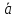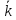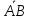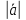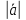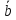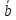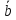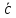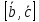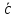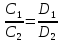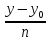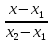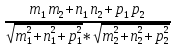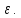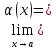1.
Матрица
Это
прямоугольная таблица, состоящая из
m×n
элементов и содержащая m
строк и n
столбцов.
Числовая
матрица
– все элементы матрицы числа.
Квадратная
матрица
– m=n.
Операции
над матрицами
Сложение
– складываются все элементы, стоящие
на одинаковых местах (только у
равноразмерных).
Произведение
– каждый элемент матрицы умножается
на число (с).
2
Транспонирование
Транспонированная
матрица – это матрица, полученная из
матрицы А заменой строк столбцами.
Умножение
матриц
Вводится
только для согласованных матриц (число
столбцов м-цы А должно совпадать со
строками м-цы В).
При
умножении матриц появляется новая
матрица, элементы которой вычисляются
по формуле: c11=a11b11+a12b21+…(1
элемент 1 строки умножаем на 1 э-т 1
столбца + 2 э-т 1 с-ки на 2 э-т 2 с-ца, и т.д.)
3.
Определители
2 и 3 порядков
Определители
вводятся только для квадратных матриц.
Определителем (Δ) или детерминалом
матрицы А называется число det
A.
Для
2-го порядка Δ вычисляется по формуле:
a11a22-a12a21
(крест накрест).
Для
3-го порядка по правилу треугольников.
Свойства:
1)
Δ
единичной матрицы =1. 2) Δ треугольной
матрицы = произведению элементов,
стоящих на главной диагонали. 3)
det(A*B)=detA*detB.
4) если строка или столбец = 0, то Δ=0.
4.Определитель
n-го порядка
Определитель
n-го
порядка находится либо разложением по
элементам строки (столбца), либо
приведением определителя к треугольному
виду.
Миноры
и алгебраические дополнения
Минор
матрицы А соответствующей элементу
Aij
– это Δ
(n-1)
порядка, получаемый путём вычёркивания
i-ой
строки или j-го
столбца. Aij=(-1)i+jMij
называется алгебраическим дополнением
к элементу aij.
Разложение
определителя
Δ
раскладывается по элементам i-ой
строки или j-го
столбца по формуле:
Δ = ai1Ai1+
ai2Ai2+…+
ainAin
5.
Обратная
матрица. Теорема о существовании
обратной матрицы
Обратная
матрица существует только для квадратных
матриц.
Если
обратная матрица существует, то она
единственна.
Матрица
А-1
обратная
А,
если выполняется условие: А-1А=А
А-1=Е
(единичная матрица).
Для
того чтобы матрица А была обратной,
необходимо чтобы она была невырожденной
(Δ не должен =0).
Матрица,
состоящая из алгебр. дополнений,
полученная путём транспонирования
называется союзной
(Ас).
Вычисление
обратной матрицы: 1) Находим Δ
2) Вычислем алгебр. доп., 3) Строим Ас
и
вычисляем:
А-1=
Ас
, 4) Делаем проверку А-1А=Е
6.
Ранг
матрицы
Ранг
матрицы
– это максимальный порядок минора,
отличный от нуля. Способы вычисления:
1)Если существует минор Mk
(k
— какой-то порядок минора) и все Mk+1=0,
то ранг М=k.
2) Метод элементарных преобразований
(матрицу приводят к треугольной и
трапециевидной форме).
Элементарные
преобразования
1)
сложение 2-х любых строк матрицы. 2)
Умножение элементов строки на число.
Теорема
о базисном миноре
Базисный
минор – это минор, не равный 0, порядок
которого равен рангу матрицы.
7.
СЛАУ
(система линейных алгебраических
уравнений)
Если
эта система имеет хотя бы одно решение,
то она называется совместной, в противном
случае несовместной. (b1,
b2,
b3)
– столбец свободных членов. (x1,
x2,
x3)
– решение системы, если при подстановке
их в систему получаются верные равенства.
Решение
систем по формулам Крамера
Сначала
находим Δ
и убеждаемся, что он не равен 0. Затем
по формулам Крамера находим определители
уже как бы новых матриц с заменой
определённого столбца на столбец
свободных членов. Находим переменные
(x,
y,
z)
по формулам Δx
Δ
и
т.д. Делаем проверку.
8.
СЛАУ
(система линейных алгебраических
уравнений)
Если
эта система имеет хотя бы одно решение,
то она называется совместной, в противном
случае несовместной. (b1,
b2,
b3)
– столбец свободных членов. (x1,
x2,
x3)
– решение системы, если при подстановке
их в систему получаются верные равенства.
Матричный
метод
Сначала
находим Δ
и убеждаемся, что он не равен 0. Находим
союзную матрицу, а затем обратную по
формуле А-1=
Ас.
Затем находим переменные (x,
y,
z)
и делаем проверку.
9.
Решение
произвольных СЛАУ
Берём
обычную систему уравнений, где А –
матрица системы, а добавление к матрице
А столбец свободных членов даёт нам
расширенную матрицу

Теорема
Кренекера-Капелли
Для
того, чтобы система уравнений была
совместна, необходимо чтобы ранг А =
рангу

Если:
1) rA=
то система имеет единственное решение.
n
– последний член элемента (a1n)
2)
rA=
то система имеет бесконечное кол-во
решений.
10.
Векторы
в пространстве
Вектор
– это направленный отрезок.
– свободный;
– имеющий точку приложения. Длина
вектора – модуль.
Линейные
операции над векторами
1)
сложение (по правилу треугольника и
параллелограмма). Суммой 2 векторов
и
явл.
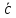
начало которого совпадает с началом 1
вектора (
а конец — с концом 2 вектора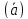
2)
вычитание (
Разностью
и
явл.

конец которого совпадает с концом

а начало — с концом
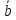
3)
умножение на число (Условия: 1) существует

2)
и
направлены одинаково если с
11.
Координаты
вектора в пространстве.
3
вектора (
образую
базис в пространстве если они взаимно
⊥
и имеют единичную длину.


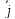
=
(x2—x1,
y2—y1,
z2—z1).

– длина
вектора
Направляющие
косинусы вектора
ax
= ПрOx
=

= ПрOy
=
cosβ;
az
= ПрOz
=
cosγ;
cosα=
Проекции
вектора на ось
образованный
с помощью осей Ox,
Oy,
Oz,
образует углы
α,
β, γ.
12.
Скалярное
произведение 2 векторов
Это
число, равное произведению длин этих
векторов на cos
угла между ними.
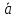
=
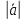

Свойство:
1)

=

2)
(
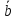
=



3)
Скалярное произведение на число =
произведение числа на один из векторов
и * на 2 вектор.
4)

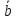
если
вектора
и
явл. Ортогональными (
⊥

13.
Векторное
произведение 2 векторов

произведением 2 векторов
и
явл.
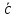
который удовлетворяет условиям: 1)
⊥


2)


– правая тройка векторов. 3)
=


(модуль произв. 2 векторов – площадь
параллелограмма)
Свойство:
1)

—

2)
=

3)

0 если
//
14.
Смешанное
произведение 3 векторов
Это
число = скалярному произведению 3-го
вектора на векторное произведение 2-х
первых векторов.
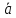

= (
—
объём параллелепипеда.
Свойство:
1)
От перемены мест множителей произведение
не меняется.
=
=
2)
Если умножить на число, то оно умножается
с одним из членов произведения.
3)
(α-
β)(
= α(
β (
15.
Базис
в пространстве
Компланарные
векторы лежат в одной плоскости.
3
любых некомпланарных вектора образуют
базис в пространстве.
Разложение
вектора по базису
Любой
вектор можно разложить по базису таким
способом: допустим B
(

– базис, а (α,
β, γ)
координаты определённого вектора,
например

Тогда разложение
по базису имеет вид:
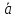
α
β
γ
16.
Прямая
на плоскости
Вектором
нормали
называется вектор перпендикулярный
плоскости. Пусть вектор
= (𝐴,
𝐵)
является вектором нормали к прямой 𝑙.
Произвольная точка плоскости 𝑀(𝑥,
𝑦)
принадлежит прямой 𝑙
тогда и только тогда, когда
⊥
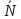
т.е. скалярное произведение этих векторов


0
Её
уравнения
1)
Уравнение прямой, проходящей через
заданную точку и имеющей заданный
вектор нормали 𝐴(𝑥–𝑥0)+𝐵(𝑦−𝑦0)=0
2)
Общее уравнение прямой: 𝐴𝑥
+ 𝐵𝑦
+ 𝐶
= 0
17.
Различные
уравнения плоскости
а)
Общее уравнение плоскости: Ax
+ By + Cz + D = 0
б)
Уравнение проходящее через точку
M0(x0,y0,z0)
и ⊥
вектору нормали

A(x—x0)
+ B(y—y0)
+C(z—z0)=0
в)
Уравнение плоскости, проходящей через
3 заданные точки.
г)
Уравнение плоскости в отрезках:
18.
Угол
между плоскостями
Допустим,
мы имеем 2 уравнения плоскости (α: A1x
+ B1y
+ C1z
+ D1
= 0
и β: A2x
+ B2y
+ C2z
+ D2
= 0)
и нам нужно вычислить угол между 2
плоскостями – двугранный
угол.
Он вычисляется по формуле: cos
(отношение произведения


к произведению модулей векторов
нормали).
Взаимное
расположение плоскостей
Две
плоскости в пространстве либо
параллельны, либо пересекаются.
α1//α2
– коллинеарные ⇒


– условие
параллельности.
α1⊥α2
⇒

⇒

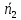

– условие
⊥.
19.
Прямая
в пространстве.
Различные
уравнения прямой в пространстве
1)
Параметрическое уравнение: x=x0+mt,
y=y0+nt,
z=z0+pt
(m,n,p)
– направляющий вектор прямой (l),
который параллелен этой прямой. M0(x0,
y0,
z0)
∈l.
2)
Каноническое уравнение:
=
=
3)
Уравнение прямой проходящей через 2
точки:
=
=
4)
Общее уравнение прямой в пространстве:
20.
Угол
между прямыми и их взаимное расположение
Допустим,
мы имеем 2 (канонических) уравнения
прямых, а также их направляющие векторы

и

Тогда угол между 2 прямыми
можно найти по формуле: cos
Условие
//-ти:

//
⇒


Условие
⊥—ти:
Расстояние
от точки до прямой в пространстве
У
нас есть уравнение прямой
=
=

её направляющий вектор
(m,n,p)
и точка не принадлежащая этой прямой
M(x1,y1,z1).
Расстояние от точки до прямой определяется
по формуле:
21.
Угол
между прямой и плоскостью.
Допустим,
у нас есть каноническое уравнение
прямой
=
=
и уравнение плоскости Ax
+ By
+ Cz
+ D
= 0.
Тогда угол между прямой и плоскостью
можно найти по формуле: Sin
=
22.
Взаимное
расположение прямой и плоскости
Условие
//-ти:
Am+Bn+Cp
= 0
Условие
⊥—ти:
Плоскости
могут совпадать, быть параллельными
или пересекаться по прямой.
23.
Эллипс
Эллипс
– это геометрическое место точек
плоскости, расстоянием от которых до
2 заданных точек называется фокусами
есть величина постоянная.
Вывод
канонического уравнения

= 1
Геометрические
свойства
1)
Эллипс является кривой 2-го порядка.
2)
Является ограниченной фигурой.
3)
Является симметричной фигурой, оси
симметрии Ox,
Oy.
4)
a – большая ось; b
– малая ось; Вершины: А1(а,0);
А2(-а,0);
В1(0,
b);
В2(0,
—b);
5)
=
– эксцентриситет эллипса; 0
1.
6)
Прямые
x
=
– директриса эллипса. При
=1 ⇒
а=с; а=b
– уравнение окружности.


24.
Гипербола
Гипербола
– геометрическое место точек на
плоскости, модуль разности расстояний
для 2 заданных точек называется фокусами
есть величина постоянная.
Вывод
канонического уравнения
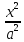
= 1
Геометрические
свойства
1)
Является кривой 2-го порядка.
2)
Является неограниченной кривой.
3)
Является симметричной фигурой.
4)
Пересекает Ox
в 2 точках, не пересекает ось Oy.
a – действительная полуось; b
– мнимая полуось;
5)
=
– эксцентриситет эллипса;

6)
x
=
– директриса.
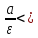
7)
y
=

– асимптоты
25.
Парабола
Парабола
– геометрическое место точек плоскости,
расстояние каждой из которых до заданной
точки называется фокусом и до определённой
прямой L,
называемой директрисой. (F∉L)
Вывод
канонического уравнения
p-
(параметр) расстояние от F
до L.
F(
– фокус параболы. x=
Уравнение: y2=2px
Геометрические
свойства
1)
Является кривой 2-го порядка.
2)
Симметричная фигура, ось симметрии –
Ox.
3)
Неограниченная фигура
4)
= 1
– эксцентриситет
26.
Числовая
последовательность
Если
каждому натуральному числу из множества
N
поставлено в соответствие некоторое
число или величина, то множество
последних образует последовательность.
xn
– числовая последовательность.
Предел
Число
a
называется пределом числовой
последовательности, если для любого
положительного числа существует
N-число,
такое, что для всех номеров N
последующий больше, чем это число по
модулю.
Теорема
о сходимости
Если
xn
имеет
предел, то он единственный. xn
наз.
ограниченной, если существует n
и все члены удовлетворяют

n
27.
Предел
функции
Если
к каждому числу из множества x
поставлено в соответствие одно число
и множество y,
то на множестве x
задана функция y=f(x)
Число
b
называется пределом функции f(x)
при x→a,
если для любого положительного
существует положительная дельта,
зависящая от
Теорема
о существовании предела функции
Для
того, чтобы f(x)
имела предел в точке a,
необходимо чтобы левый и правый пределы
были равны.
28.
Односторонние
пределы функции
Левый
и правый пределы называют односторонними
пределами.
1)
Число b
называется правым пределом функции
при x→a
справа если для всех

существует дельта от
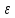
такой что 0
модуль f(x)-b

следовательно x
2)
Число b
называется левым пределом функции при
x→a
слева если для всех

существует дельта от

такой что —b
следовательно модуль f(x)-b
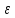
следовательно x
Теорема
о существовании предела функции
Для
того, чтобы f(x)
имела предел в точке a,
необходимо чтобы левый и правый пределы
были равны.
29.
Бесконечно-малые
и их свойства.
Бесконечно
малая функция
– это функция, предел которой в
данной точке равен нулю. Функция
α(x)
– бесконечно-малая при x→a,
если lim
α(x)
= 0.
При
x→a
lim
=
предел не существует.
Основные
свойства
1°
Сумма конечного числа б.м функций
является функцией б.м.
3°
Произведение двух б.м функций есть
функция б.м.
4°
Произведение б.м функции на константу
является б.м функцией.
5°
Частное от деления б.м функции на
функцию, предел которой
не равен нулю, есть функция б.м.
6°
Функция 
обратная
к б.м функции α(x)
0,
есть функция бесконечно большая. Верно
и обратное.
30.
Бесконечно-большие
функции.
Бесконечно
большая функция
– это функция, предел которой
стремится к
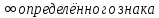
Теорема
о связи бесконечно-большой и
бесконечно-малой функции
Теорема.
Функция обратная бесконечно малой,
является бесконечно большой и наоборот.
Доказательство: Пусть предел функции
равен 0, а сама функция не = 0, при x→a,
т.е. задаём бесконечно-малую функцию

Тогда для любого числа 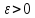
такое число дельта

что для всех x,
удовлетворяющих неравенству

выполняется неравенство 
т.е.

А из этого следует, что функция 
бесконечно большая.

Математический анализ. Шпаргалка для студента №11
Автор:
Михаль Ю.О.
Размер:
1,58 мб
Формат:
djvu
16964

Формулы по интегралам, производным и тригонометрическим функциям
Размер:
8 кб
Формат:
doc
9811

Шпаргалки по высшей математике
Размер:
178 кб
Формат:
doc
20413

Шпаргалка по высшей математике за 2 курс 3 семестр
Размер:
111 кб
Формат:
doc
21342

Шпаргалка по дискретной математике и булевой алгебре. Множества, логика, комбинаторика.
Размер:
196 кб
Формат:
doc
10235

Таблица интегралов шпаргалка
Размер:
42 кб
Формат:
rtf
21356

Шпаргалки по линейной и векторной алгебре
Автор:
Орлов Н.Г.
Размер:
104 кб
Формат:
doc
12477
Здесь представлены шпаргалки по математике, которые можно скачать бесплатно.
Шпаргалка по высшей математике для студентов технических вузов, Учебное пособие, Попов М.Л., 2007.
Пособие содержит справочные материалы по всему курсу высшей математики для физико- математических и технических специальностей, в полном соответствии с Государственным образовательным стандартом. Материал пособия охватывает следующие разделы программы: элементы линейной алгебры и аналитической геометрии; введение в математический анализ; дифференциальное исчисление функции одной и нескольких переменных; интегральное исчисление функции одной переменной; числовые и функциональные ряды; гармонический анализ; дифференциальные уравнения и элементы качественной теории диф. уравнений; кратные, криволинейные и поверхностные интегралы; теория поля; теория функций комплексной переменной; операционное исчисление; уравнения математической физики; теория вероятностей; математическая статистика; основы дискретной математики; методы оптимизации; численные методы. В каждом разделе приведены основные определения, теоремы с доказательствами, формулы с полным выводом, графики, рисунки. Пособие будет полезно студентам физико-математических и технических специальностей вузов и других образовательных заведений для успешной сдачи экзаменов по высшей математике.
Шпаргалка.
Для простого и эффективного использования «Шпаргалки» разрежьте каждую страницу на четыре части по пунктирной линии. Сложите полученные листы по порядку> номеров — верхний левый, верхний правый, нижний левый, нижний правый. Для удобства использования можно скрепить получившуюся стопку степлером или скрепкой в верхнем левом углу.
Содержание.
Линейная алгебра и аналитическая геометрия.
Введение в математический анализ.
Дифференциальное исчисление функций одной переменной.
Дифференциальное исчисление функций нескольких переменных.
Интегральное исчисление функций одной переменной.
Числовые и функциональные ряды.
Гармонический анализ.
Обыкновенные дифференциальные уравнения.
Операционное исчисление.
Элементы качественной теории дифференциальных уравнений.
Кратные, криволинейные и поверхностные интегралы.
Теория функций комплексной переменной.
Теория поля.
Теория вероятностей.
Уравнения математической физики.
Математическая статистика.
Методы оптимизации.
Бесплатно скачать электронную книгу в удобном формате, смотреть и читать:
Скачать книгу Шпаргалка по высшей математике для студентов технических вузов, Учебное пособие, Попов М.Л., 2007 — fileskachat.com, быстрое и бесплатное скачивание.
Скачать pdf
Ниже можно купить эту книгу по лучшей цене со скидкой с доставкой по всей России.Купить эту книгу
Скачать
— pdf — Яндекс.Диск.
Дата публикации: 07.08.2019 13:32 UTC
Теги:
шпаргалка по математике :: математика :: высшая математика :: шпаргалка :: Попов
Следующие учебники и книги:
- Сборник математических задач, Основы финансовой грамотности, 10-11 классы, Том 3, Моторо Н.П., Новожилова Н.В., Шалашова М.М., 2019
- Методические рекомендации к сборнику математических задач, Основы финансовой грамотности, 10-11 классы, Методические рекомендации, Том 3, Моторо Н.П., Новожилова Н.В., Шалашова М.М., 2019
- Методические рекомендации к сборнику математических задач, Основы финансовой грамотности, 5-9 классы, Том 2, Моторо Н.П., Новожилова Н.В., Шалашова М.М., 2019
- Сборник конкурсных задач по математике с решениями, Кущенко В.С., 1969
Предыдущие статьи:
- Математика, Решение упражнений к учебнику математики Моро М.И. и др.
- Дидактические карточки-задания по математике, 2 класс, Истомина Н.Б., Шмырева Г.Г., 2002
- Математика, Сборник упражнений, 4 класс, Шклярова Т.В., 2006
- Математика, Сборник упражнений, 3 класс, Шклярова Т.В.
1.
Матрица
Это
прямоугольная таблица, состоящая из
m×n
элементов и содержащая m
строк и n
столбцов.
Числовая
матрица
– все элементы матрицы числа.
Квадратная
матрица
– m=n.
Операции
над матрицами
Сложение
– складываются все элементы, стоящие
на одинаковых местах (только у
равноразмерных).
Произведение
– каждый элемент матрицы умножается
на число (с).
2
Транспонирование
Транспонированная
матрица – это матрица, полученная из
матрицы А заменой строк столбцами.
Умножение
матриц
Вводится
только для согласованных матриц (число
столбцов м-цы А должно совпадать со
строками м-цы В).
При
умножении матриц появляется новая
матрица, элементы которой вычисляются
по формуле: c11=a11b11+a12b21+…(1
элемент 1 строки умножаем на 1 э-т 1
столбца + 2 э-т 1 с-ки на 2 э-т 2 с-ца, и т.д.)
3.
Определители
2 и 3 порядков
Определители
вводятся только для квадратных матриц.
Определителем (Δ) или детерминалом
матрицы А называется число det
A.
Для
2-го порядка Δ вычисляется по формуле:
a11a22—a12a21
(крест накрест).
Для
3-го порядка по правилу треугольников.
Свойства:
1)
Δ
единичной матрицы =1. 2) Δ треугольной
матрицы = произведению элементов,
стоящих на главной диагонали. 3)
det(A*B)=detA*detB.
4) если строка или столбец = 0, то Δ=0.
4.Определитель
n-го порядка
Определитель
n-го
порядка находится либо разложением по
элементам строки (столбца), либо
приведением определителя к треугольному
виду.
Миноры
и алгебраические дополнения
Минор
матрицы А соответствующей элементу
Aij
– это Δ
(n-1)
порядка, получаемый путём вычёркивания
i-ой
строки или j-го
столбца. Aij=(-1)i+jMij
называется алгебраическим дополнением
к элементу aij.
Разложение
определителя
Δ
раскладывается по элементам i-ой
строки или j-го
столбца по формуле:
Δ = ai1Ai1+
ai2Ai2+…+
ainAin
5.
Обратная
матрица. Теорема о существовании
обратной матрицы
Обратная
матрица существует только для квадратных
матриц.
Если
обратная матрица существует, то она
единственна.
Матрица
А-1
обратная
А,
если выполняется условие: А-1А=А
А-1=Е
(единичная матрица).
Для
того чтобы матрица А была обратной,
необходимо чтобы она была невырожденной
(Δ не должен =0).
Матрица,
состоящая из алгебр. дополнений,
полученная путём транспонирования
называется союзной
(Ас).
Вычисление
обратной матрицы: 1) Находим Δ0,
2) Вычислем алгебр. доп., 3) Строим Ас
и
вычисляем:
А-1=*
Ас
, 4) Делаем проверку А-1А=Е
6.
Ранг
матрицы
Ранг
матрицы
– это максимальный порядок минора,
отличный от нуля. Способы вычисления:
1)Если существует минор Mk0
(k
— какой-то порядок минора) и все Mk+1=0,
то ранг М=k.
2) Метод элементарных преобразований
(матрицу приводят к треугольной и
трапециевидной форме).
Элементарные
преобразования
1)
сложение 2-х любых строк матрицы. 2)
Умножение элементов строки на число.
Теорема
о базисном миноре
Базисный
минор – это минор, не равный 0, порядок
которого равен рангу матрицы.
7.
СЛАУ
(система линейных алгебраических
уравнений)
Если
эта система имеет хотя бы одно решение,
то она называется совместной, в противном
случае несовместной. (b1,
b2,
b3)
– столбец свободных членов. (x1,
x2,
x3)
– решение системы, если при подстановке
их в систему получаются верные равенства.
Решение
систем по формулам Крамера
Сначала
находим Δ
и убеждаемся, что он не равен 0. Затем
по формулам Крамера находим определители
уже как бы новых матриц с заменой
определённого столбца на столбец
свободных членов. Находим переменные
(x,
y,
z)
по формулам Δx
Δ
и
т.д. Делаем проверку.
8.
СЛАУ
(система линейных алгебраических
уравнений)
Если
эта система имеет хотя бы одно решение,
то она называется совместной, в противном
случае несовместной. (b1,
b2,
b3)
– столбец свободных членов. (x1,
x2,
x3)
– решение системы, если при подстановке
их в систему получаются верные равенства.
Матричный
метод
Сначала
находим Δ
и убеждаемся, что он не равен 0. Находим
союзную матрицу, а затем обратную по
формуле А-1=*
Ас.
Затем находим переменные (x,
y,
z)
и делаем проверку.
9.
Решение
произвольных СЛАУ
Берём
обычную систему уравнений, где А –
матрица системы, а добавление к матрице
А столбец свободных членов даёт нам
расширенную матрицу
.
Теорема
Кренекера-Капелли
Для
того, чтобы система уравнений была
совместна, необходимо чтобы ранг А =
рангу
.
Если:
1) rA==n,
то система имеет единственное решение.
n
– последний член элемента (a1n)
2)
rA=,
то система имеет бесконечное кол-во
решений.
10.
Векторы
в пространстве
Вектор
– это направленный отрезок.
– свободный;
– имеющий точку приложения. Длина
вектора – модуль.
Линейные
операции над векторами
1)
сложение (по правилу треугольника и
параллелограмма). Суммой 2 векторов
и
явл.
,
начало которого совпадает с началом 1
вектора (),
а конец — с концом 2 вектора.
2)
вычитание (.
Разностью
и
явл.
,
конец которого совпадает с концом
,
а начало — с концом
.
3)
умножение на число (Условия: 1) существует
;
2)
и
направлены одинаково если с0.
11.
Координаты
вектора в пространстве.
3
вектора ()
образую
базис в пространстве если они взаимно
⊥
и имеют единичную длину.
=ax
+ay
+az
=
(x2—x1,
y2—y1,
z2—z1).
=
– длина
вектора
Направляющие
косинусы вектора
ax
= ПрOx
=
*cosα; ay
= ПрOy
=
cosβ;
az
= ПрOz
=
cosγ;
cosα=
Проекции
вектора на ось
образованный
с помощью осей Ox,
Oy,
Oz,
образует углы
α,
β, γ.
12.
Скалярное
произведение 2 векторов
Это
число, равное произведению длин этих
векторов на cos
угла между ними.
*
=
*
cosφ
Свойство:
1)
*
=
*
2)
(*
)
=
*
*
)
3)
Скалярное произведение на число =
произведение числа на один из векторов
и * на 2 вектор.
4)
*
=0,
если
вектора
и
явл. Ортогональными (
⊥
).
13.
Векторное
произведение 2 векторов
Векторным
произведением 2 векторов
и
явл.
,
который удовлетворяет условиям: 1)
⊥
,
;
2)
,
,
– правая тройка векторов. 3)
=
*
sinφ
(модуль произв. 2 векторов – площадь
параллелограмма)
Свойство:
1)
=
—
2)
=
+
3)
=
0 если
//
14.
Смешанное
произведение 3 векторов
Это
число = скалярному произведению 3-го
вектора на векторное произведение 2-х
первых векторов.
*
*
= ()
—
объём параллелепипеда.
Свойство:
1)
От перемены мест множителей произведение
не меняется.
=
=
2)
Если умножить на число, то оно умножается
с одним из членов произведения.
3)
(α-
β)(
= α(+
β (
15.
Базис
в пространстве
Компланарные
векторы лежат в одной плоскости.
3
любых некомпланарных вектора образуют
базис в пространстве.
Разложение
вектора по базису
Любой
вектор можно разложить по базису таким
способом: допустим B
(,
)
– базис, а (α,
β, γ)
координаты определённого вектора,
например
.
Тогда разложение
по базису имеет вид:
=
α+
β+
γ
16.
Прямая
на плоскости
Вектором
нормали
называется вектор перпендикулярный
плоскости. Пусть вектор
= (????,
????)
является вектором нормали к прямой ????.
Произвольная точка плоскости ????(????,
????)
принадлежит прямой ????
тогда и только тогда, когда
⊥
,
т.е. скалярное произведение этих векторов
*
=
0
Её
уравнения
1)
Уравнение прямой, проходящей через
заданную точку и имеющей заданный
вектор нормали ????(????–????0)+????(????−????0)=0
2)
Общее уравнение прямой: ????????
+ ????????
+ ????
= 0
17.
Различные
уравнения плоскости
а)
Общее уравнение плоскости: Ax
+ By + Cz + D = 0
б)
Уравнение проходящее через точку
M0(x0,y0,z0)
и ⊥
вектору нормали
(A,B,C):
A(x—x0)
+ B(y—y0)
+C(z—z0)=0
в)
Уравнение плоскости, проходящей через
3 заданные точки.
г)
Уравнение плоскости в отрезках:
18.
Угол
между плоскостями
Допустим,
мы имеем 2 уравнения плоскости (α: A1x
+ B1y
+ C1z
+ D1
= 0
и β: A2x
+ B2y
+ C2z
+ D2
= 0)
и нам нужно вычислить угол между 2
плоскостями – двугранный
угол.
Он вычисляется по формуле: cos=
(отношение произведения
1*
2
к произведению модулей векторов
нормали).
Взаимное
расположение плоскостей
Две
плоскости в пространстве либо
параллельны, либо пересекаются.
α1//α2
– коллинеарные ⇒
=
=
– условие
параллельности.
α1⊥α2
⇒
⊥
⇒
*
=0.
=0
– условие
⊥.
19.
Прямая
в пространстве.
Различные
уравнения прямой в пространстве
1)
Параметрическое уравнение: x=x0+mt,
y=y0+nt,
z=z0+pt
(m,n,p)
– направляющий вектор прямой (l),
который параллелен этой прямой. M0(x0,
y0,
z0)
∈l.
2)
Каноническое уравнение:
=
=
3)
Уравнение прямой проходящей через 2
точки:
=
=
4)
Общее уравнение прямой в пространстве:
20.
Угол
между прямыми и их взаимное расположение
Допустим,
мы имеем 2 (канонических) уравнения
прямых, а также их направляющие векторы
1
и
2.
Тогда угол между 2 прямыми
можно найти по формуле: cos=
Условие
//-ти:
1
//2
⇒
=
=
Условие
⊥—ти:
Расстояние
от точки до прямой в пространстве
У
нас есть уравнение прямой
=
=
,
её направляющий вектор
(m,n,p)
и точка не принадлежащая этой прямой
M(x1,y1,z1).
Расстояние от точки до прямой определяется
по формуле:
21.
Угол
между прямой и плоскостью.
Допустим,
у нас есть каноническое уравнение
прямой
=
=
и уравнение плоскости Ax
+ By
+ Cz
+ D
= 0.
Тогда угол между прямой и плоскостью
можно найти по формуле: Sin
=
22.
Взаимное
расположение прямой и плоскости
Условие
//-ти:
Am+Bn+Cp
= 0
Условие
⊥—ти:
Плоскости
могут совпадать, быть параллельными
или пересекаться по прямой.
23.
Эллипс
Эллипс
– это геометрическое место точек
плоскости, расстоянием от которых до
2 заданных точек называется фокусами
есть величина постоянная.
Вывод
канонического уравнения
+
= 1
Геометрические
свойства
1)
Эллипс является кривой 2-го порядка.
2)
Является ограниченной фигурой.
3)
Является симметричной фигурой, оси
симметрии Ox,
Oy.
4)
a – большая ось; b
– малая ось; Вершины: А1(а,0);
А2(-а,0);
В1(0,
b);
В2(0,
—b);
5)
=
– эксцентриситет эллипса; 0
1.
6)
Прямые
x
=
– директриса эллипса. При
=1 ⇒
а=с; а=b
– уравнение окружности.
+
=
24.
Гипербола
Гипербола
– геометрическое место точек на
плоскости, модуль разности расстояний
для 2 заданных точек называется фокусами
есть величина постоянная.
Вывод
канонического уравнения
—
= 1
Геометрические
свойства
1)
Является кривой 2-го порядка.
2)
Является неограниченной кривой.
3)
Является симметричной фигурой.
4)
Пересекает Ox
в 2 точках, не пересекает ось Oy.
a – действительная полуось; b
– мнимая полуось;
5)
=
– эксцентриситет эллипса;
1.
6)
x
=
– директриса.
1
7)
y
=
x
– асимптоты
25.
Парабола
Парабола
– геометрическое место точек плоскости,
расстояние каждой из которых до заданной
точки называется фокусом и до определённой
прямой L,
называемой директрисой. (F∉L)
Вывод
канонического уравнения
p—
(параметр) расстояние от F
до L.
F(;0)
– фокус параболы. x=.
Уравнение: y2=2px
Геометрические
свойства
1)
Является кривой 2-го порядка.
2)
Симметричная фигура, ось симметрии –
Ox.
3)
Неограниченная фигура
4)
= 1
– эксцентриситет
26.
Числовая
последовательность
Если
каждому натуральному числу из множества
N
поставлено в соответствие некоторое
число или величина, то множество
последних образует последовательность.
xn
– числовая последовательность.
Предел
Число
a
называется пределом числовой
последовательности, если для любого
положительного числа существует
N-число,
такое, что для всех номеров N
последующий больше, чем это число по
модулю.
Теорема
о сходимости
Если
xn
имеет
предел, то он единственный. xn
наз.
ограниченной, если существует n
и все члены удовлетворяют
M,
nN
27.
Предел
функции
Если
к каждому числу из множества x
поставлено в соответствие одно число
и множество y,
то на множестве x
задана функция y=f(x)
Число
b
называется пределом функции f(x)
при x→a,
если для любого положительного
существует положительная дельта,
зависящая от
Теорема
о существовании предела функции
Для
того, чтобы f(x)
имела предел в точке a,
необходимо чтобы левый и правый пределы
были равны.
28.
Односторонние
пределы функции
Левый
и правый пределы называют односторонними
пределами.
1)
Число b
называется правым пределом функции
при x→a
справа если для всех
0
существует дельта от
,
такой что 0следовательно
модуль f(x)-b
,
следовательно x
2)
Число b
называется левым пределом функции при
x→a
слева если для всех
0
существует дельта от
,
такой что —b
следовательно модуль f(x)-b
,
следовательно x
Теорема
о существовании предела функции
Для
того, чтобы f(x)
имела предел в точке a,
необходимо чтобы левый и правый пределы
были равны.
29.
Бесконечно-малые
и их свойства.
Бесконечно
малая функция
– это функция, предел которой в
данной точке равен нулю. Функция
α(x)
– бесконечно-малая при x→a,
если lim
α(x)
= 0.
При
x→a
lim
=
предел не существует.
Основные
свойства
1°
Сумма конечного числа б.м функций
является функцией б.м.
3°
Произведение двух б.м функций есть
функция б.м.
4°
Произведение б.м функции на константу
является б.м функцией.
5°
Частное от деления б.м функции на
функцию, предел которой
не равен нулю, есть функция б.м.
6°
Функция ,
обратная
к б.м функции α(x)
0,
есть функция бесконечно большая. Верно
и обратное.
30.
Бесконечно-большие
функции.
Бесконечно
большая функция
– это функция, предел которой
стремится к
.
Теорема
о связи бесконечно-большой и
бесконечно-малой функции
Теорема.
Функция обратная бесконечно малой,
является бесконечно большой и наоборот.
Доказательство: Пусть предел функции
равен 0, а сама функция не = 0, при x→a,
т.е. задаём бесконечно-малую функцию
.
Тогда для любого числа существует
такое число дельта
,
что для всех x,
удовлетворяющих неравенству
,
выполняется неравенство ,
т.е.
.
А из этого следует, что функция —
бесконечно большая.
31.
Бесконечно-малые
функции.
Бесконечно
малая функция
– это функция, предел которой в
данной точке равен нулю.
Функция
α(x)
– бесконечно-малая при x→a,
если lim
α(x)
= 0.
Терема
об отношении 2 бесконечно-малых функций
Предел
отношения 2 бесконечно-малых функций
= пределу отношения 2 других бесконечно-малых
функций, соотв. им пропорционально.
α1(x)
α2(x)
и β
1(x)
β
2(x)
=
32.
Замечательные
пределы.
1)
=1
2)
Раскрытие
неопределённостей
,
можно раскрыть используя правило
Лапиталя; разделяя каждый элемент на
x
в большей степени.
)
можно раскрыть используя 2 замечательный
предел.
(
сначала при помощи различных преобразований
приводим к
,
,
и раскрываем.
33.
Непрерывность
функции в точке
Функция называется
непрерывной
в точке, если: функция определена
в точке и ее окрестности; существует
конечный предел функции в точке;
этот предел равен значению функции
в точке.
Свойства
непрерывных функций
Точка,
в которой функция не является непрерывной,
называется точкой разрыва.
Если функция непрерывна
и справа и слева, то она непрерывна в
этой точке.
Если
функция y=f(x)
находится на отрезке
непрерывна в точке a
справа.
Если
функция y=f(x)
находится на отрезке
непрерывна в точке a
слева.
34.
Непрерывность фун. на интервале
Функция называется
непрерывной в интервале, если она
непрерывна в каждой точке этого интервала.
Основные
теоремы непрерывных функций
1)
Пусть заданы две функции f(x) и g(x) ,
непрерывные на некотором множестве X.
Сумма, произведение и частное (при
условии, что g(x) )
является также непрерывной функцией
на рассматриваемом множестве.
2)
Каждая элементарная функция, заданная
в окрестности некоторой точки, непрерывна
в этой точке.
3)
Пусть функция z=(x)
непрерывна
в точке x0,
а функция y=f(x)
непрерывна в точке z0,
где z0=(x0),
тогда сложная функция y=f((x))
является непрерывной в точке x0.
35.
Производная
функции
Это
предел отношения приращения функции
к приращению аргумента, когда приращение
аргумента стремится к нулю. Если функция
имеет производную в точке x0,
то в этой точке она непрерывна. Производная
в точке 0 не существует.
Геометрический
и механический смысл производной
1)
Геометрический смысл: производная
представляет собой угловой коэффициент
касательной к графику функции y=f(x) в
точке x0.
2)
Механический смысл: скорость – это
производная координаты по времени:
36.
Основные
правила дифференцирования
1)
Пусть u(x)
и v(x)
– дифференциальные функции в точке x,
тогда их произведение и частное также
дифференцируемы в точке x.
2)
Пусть сложная функция y=f(z),
где z=(x)
дифф-мы в точке z,
тогда y=f((x))
дифф-ма в точке x.
3)
Постоянный
множитель c можно выносить за знак
производной.
4)
Производная от суммы (разности) функции
= сумме (разности) производных.
37.
Производная
сложной и обратной функции
1)
Пусть сложная функция y=f(z),
где z=(x)
дифф-мы в точке z,
тогда y=f((x))
дифф-ма в точке x.
Производную сложной функции можно
найти по формуле: y‘=y‘z*z‘x.
2)
Если функции y=f(x)
и x=g(y)
— пара взаимно обратных функций, и
функция y=f(x) имеет производную f'(x),
то производная обратной функции
находится по формуле: g'(x)=1/f
‘(x).
38.
Дифференцирование
неявных функций и функций, заданных
параметрически
1)
Чтобы найти производную функции,
заданной неявно (когда слева и справа
есть переменная y)
каким-либо уравнением необходимо взять
производную из обоих частей уравнения,
затем переносим все y‘
влево и подставляем вместо y
исходное выражение.
2)
Пусть y=y(x)
задана параметрически:
,
тогда чтобы продифференцировать эту
функцию необходимо воспользоваться
формулой:
y‘x=
39.
Дифференциал
функции и её геометрический смысл
1)
Пусть функция y=f(x) дифференцируема в
точке x0,
тогда превращение можно представить
в виде
y=f
‘(x0)*x+0(
x)
y
f
‘(x0)*x
при
x→0
f
‘(x0)*x
в разложении
y
называется главной линейной относительно
х
частью превращения функции.
Главная
линейная относительно
х
функция наз. дифф-ой функцией и
обозначается dy.
dy=y‘*dx. y‘=
2)
Дифференциал функции y=f(x) в
точке x
равен приращению ординаты касательной
к графику функции в этой точке, когда x
получит приращение
х.
40.
Производные
высших порядков
Производная
от производной 1-го порядка называется
производной 2-го порядка. y‘=f
‘(x);
y»=(y’)’; yn=(yn-1)’
Дифференцируемость
функции
Пусть
функция y=f(x) дифф-ма в точке x0,
тогда превращение можно представить
в виде
y=f
‘(x0)*x+0(
x)
y
f
‘(x0)*x
при
x→0
f
‘(x0)*x
в разложении
y
называется главной линейной относительно
х
частью превращения функции.
Главная
линейная относительно
х
функция наз. дифф-ой функцией и
обозначается dy.
1
порядка)
dy=y‘*dx. y‘=
высших
порядков) d2y=y»dx2;
d3y=y»’dx3
41.
Теорема
Ролля и Лагранжа
1)
Пусть f(x)
удовлетворяет условиям: определена и
непрерывна на отрезке [a,b];
дифф-ма на (a,b,);
Значения функции на концах отрезков
совпадают f(a)=f(b).
Тогда существует точка c=(a,b)
такая что f‘(x)=0
2)
Пусть f(x)
удовлетворяет условиям: определена и
непрерывна на отрезке [a,b];
дифф-ма на (a,b,).
Тогда существует точка c
такая, что
=f
‘(c)
Правило
Лопиталя
Правило
Лопиталя используется при вычислении
предела функции и относится только для
раскрытия неопределённостей:
,
Такие пределы вычисляются по формуле:
=
42.
Условие
монотонности функции.
Пусть
f(x)
определена и непрерывна на отрезке
[a,b],
тогда если: 1) f(x)0,
для всех x
принадлежащих (a,b),
то f(x)
– не убывает; 2) f(x)0,
для всех x
принадлежащих (a,b),
то f(x)
– не возрастает;
Следовательно:
если f(x)0,
для всех x
принадлежащих (a,b),
то f(x)
– возрастает; а f(x)0
—
убывает
Необходимое
условие экстремума
Пусть
x0
– точка локального экстремума функции
f(x),
тогда f
‘(x)
обращается в 0 или не существует.
Критические
точки
— те, которые не входят в обл. определения
(чаще всего это точки разрыва).
Стационарные-точки
в которых значение производной равно
нулю (точки экстремума)
43.
Экстремум
фун. одной переменной
Пусть
у нас есть функция y=f(x)
и точка x0
– точка локального max
(min)
если существует x
принадлежащий дельта-окрестности x0,
то f(x0)f(x)
max;
f(x0)f(x)
min
Локальные
max
и min
– локальные экстремумы. x0
– точка локального максимума если
f(x0)=
максимальному
значению f(x).
Достаточные
условия экстремума
1) Пусть
функция f(x)
непрерывна в точке x0 и
имеет конечную производную f‘(x).
Если же при переходе через точку x0
производная не меняет знак, то в
точке x0 нет
экстремума.
2) Пусть
функция f(x)
дважды дифференцируема в точке x0,
причем
df(x0)
= 0, а d2f(x0)
> 0
(d2f(x0)
< 0 ).
Тогда
точка x0 есть
точка локального минимума (локального
максимума) функции f(x).
3)
Пусть
функция f(x)
имеет в точке х0 производные
f
‘(x0)
и f»(x0),
причем f‘(x0)
= 0, а f»(x0)
> 0
(f»(x0)
< 0 ).
Тогда
точка x0 есть
точка локального минимума (локального
максимума) функции f(x).
44.
Выпуклость
и вогнутость графика функции. Точки
перегиба
График
функции y=f(x)
называется вогнутым
на (a,b)
если он расположен ниже касательной,
проведённой к графику функции.
График
функции y=f(x)
называется выпуклым
на (a,b)
если он расположен выше касательной,
проведённой к графику функции.
Точка
перегиба функции
– это точка, в которой функция непрерывна
и её график имеет касательную (которая
может быть параллельна оси) и при
переходе через (x)
функция меняет направление выпуклости.
45.
Асимптоты
графика функции.
Асимптота
– значение, к которому стремится
функция. Различают вертикальные,
горизонтальные и наклонные асимптоты.
Прямая
называется вертикальной
асимптотой, если 1 из односторонних
пределов в этой точке =
.
Прямая
называется горизонтальной
асимптотой функции, если предел этой
функции при x→
= числу.
Прямая
y=kx+b
называется наклонной
асимптотой, если существуют конечные
пределы.
Схема
исследования функции
1)
Находим область определения функции.
2)
Определяем чётностьнечётность функции
и её периодичность.
3)
Находим точки пересечения с осями Ox
и Oy
(приравниваем x=0
и y=0)
4)
Исследуем функцию на наличие асимптот
5)
Определяем y‘
и её критические точки (y‘=0)
6)
Находим y»
и её критические точки.
7)
Результаты заносим в таблицу.

С помощью таблицы строим график функции.
Шпаргалки по высшей математике
Шпаргалки по математике

Скачать
1. Понятие числа (от натурального до комплексного).
2. Сложение, вычитание, умножение, делениекомплексных чисел.
3. Комплексное число в тригонометрической форме.
4. Комплексное число в степени.
5. Корень из комплексного числа.
6. Предел последовательности.
7. Свойство сходящихся последовательностей (докозательство).
8. Бесконечно малая величина и ограниченная последовательность. Свойства БМВ.
9. Сходимость знакоположительного ряда на примере.
10. Признак сравнения двух знакоположительных рядов на примере.
11. Признаки Коши и Даламбера.
12. Пример признака Лейбница. Знакопеременный ряд.
13. Примеры прямой и обратной функции.
14. Предел функции в точке.
15. Непрерывность функции в точке. Свойства непрерывных функций.
16. Степенная и линейная функции и их непрерывность.
17. Непрерывность функций В? и LOGaX.
18. Тригонометрические функции и их непрерывность.
19. Первый замечательный предел.
20. Применение второго замечательного предела для начисления непрерывных процентов.
21. Понятие производной от функции. Механический и геометрический смыслы призводной.
22. Понятие производной. Производная от сложения, вычитания, умножения двух функций.
23. Понятие производной. Производная от деления двух функций.
24. Понятие производной. Производная от Х?.
25. Понятие производной. Производная от обратных функций (LNx, e?).
26. Производная от тригонометрической функции.
27. Пример производной от сложной функции.
28. Дифференциал функции. Его геометрический смысл.
29. Исследование функций с помощью производной и пределов.
30. Нахождение и понятие асимптот.
31. Область сходимости степенного ряда.
32. Разложение функций в степенные ряды.
33. Таблица интегралов. Неопределенный интеграл.
34. Пример метода интегрирования с заменой переменных.
35. Интегрирование по частям.
36. Интегрирование с помощью разложения на элементарные дроби.
37. Свойства определенного интеграла. Формула Ньютона-Лейбница.
38. Определенные интегралы и их применение.
39. Вычисление определенных интегралов приближенным методом.
40. Интегралы несобственные.
41. Понятие частных, производных и дифференциала. Функции нескольких переменных.
42. Экстремум функций нескольких переменных.
43. Метод наименьших квадратов. Эмпирические формулы их понятие.
44. Понятие дифференциальных уравнений и методы его решения.
Также Формулы
1. Основы дифференциального исчисления . Понятие производной.
2. Правила дифференцирования
3. Таблица производных
4. Производная высших порядков.
5. Основные теоремы матим. анализа.
6. Правила Лопиталя. Раскрытие неопределенности.
7. Аналитические признаки поведения функции.
8. Поиск наибольшего и наименьшего значения непрерывных функций на замкнутом промежутке.
9. Теорема: Достаточный признак выпуклости графика функции вниз.
10. Теорема: Необходимый признак существования наклонной
11. Правила дифференцирования.
§1. Множество действительных чисел и его свойства.

§2. Модуль действ. числа и его свойства.

§3. Функция (отображение). Действительные функции.
Действительные переменные и их простейшие свойства.

§4. Числовые последовательности. Предел числовой
числовой последовательности. Число е.

§5. Предел функции в точке. Свойства функций,
имеющих предел в точке. Предел на бесконечности.
Бесконечные пределы.

§6. Бесконечно малые в точке функции и их свойства.
Необходимые и достаточные условия существования

§7. Арифметические операции над пределами.

§8. Предельный переход в неравенствах.

§9. Односторонние пределы. Необходимое и достаточное
условия существования предела в точке.

§10. Первый замечательный предел.


§11. Второй замечательный предел и связанные с ним
пределы.

§12. Непрерывность функции в точке. Свойства функций,
непрерывных в точке.

§13 Классификация точек разрыва функции одной
переменной.

§14. Свойства функций, непрерывных на отрезке.

§15. Обратная функция и ее непрерывность.

§1. Определение производной. Геометрический и
механический смысл производной.


§2.Два определения дифференцируемой в точке
функции и их эквивалентность. Дифференциал
1-го порядка и его геометрический смысл.



§3. Производные основных
элементарных функций.

§4. Правила дифференцирования.

§5. Дифференцирование обратной и сложной функции.

§6. Метод логарифмического дифференцирования.
§7. Производные высших порядков. Бином Ньютона.

§8. Дифференцирование функций,
заданных параметрически.

§9. Основные теоремы дифференциального
исчисления.


§10. Условия постоянства и монотонности функций
на интервале.

§11. Экстремум функции. Необходимые и достаточные
условия экстремума.

§12. Наибольшее и наименьшее значения функции
на отрезке.

§13. Выпуклость и вогнутость графика функции.
Точка перегиба.


§14. Асимптоты графика функции. Полное
исследование функции и построение ее графика.

§15. Раскрытие неопределенностей.
Правила Лопиталя.

§1. Первообразная и неопределенный интеграл.
Свойства неопределенного интеграла.



§2. Таблица основных интегралов.

§3. Интегрирование по частям в неопределенном
интеграле.

§4. Замена переменной в неопределенном интеграле.

§5 Интегрирование рациональных функций.


§6 Вычисление интегралов вида:

§ 7. Интегрирование выражений вида
. Подстановка Эйлера.

§8 Вычисление интегралов вида

§9 Интегрирование тригонометрических функций.

§10. Определение интеграла по Риману. Ограниченность
интегрируемой функции.

§11. Верхняя и нижняя интегральные суммы и их свойства.
Необходимые и достаточные условия интегрируемости
функции по Риману.

§12. Свойства неопределенного интеграла.

§13. Интеграл с переменным верхним пределом и его
свойства. Основная формула интегрального исчисления.

§14. Интегрирование по частям в определенном
интеграле.
§15. Замена переменной в определенном
интеграле.
§16. Вычисление площадей в прямоугольной
декартовой системе координат.

§17. Вычисление площадей в полярной системе
координат.

§18. Объем тела вращения.

§19. Спрямляемая кривая и ее длина. Вычисление
длины кривой.

§20. Площадь поверхности вращения.

§21. Применение определенных интегралов к решению
физических задач.

§22. Несобственные интегралы 1-го и 2-го рода.

Шпаргалка по высшей математике
1. Определители. Основные определения. Вычисление определителей
третьего порядка. Определитель- число, характеризующее матрицу.
Определителем матрицы 1-го порядка А=(а11) является единственный
элемент этой матрицы. Определителем 2-го порядка называется число,
характеризующее матрицу 2-го порядка, которое находится по
следующему правилу: из произведений элементов главной диагонали
вычитается произведение элементов второй диагонали матрицы А.
Определителем матрицы 3-го порядка называется число, вычисляемое по
правилу Сарруса. Правило Сарруса: определитель 3-го порядка ((3)
равен алгебраической сумме 6-ти тройных произведений элементов,
стоящих в разных строках и разных столбцах; со знаком «+» берутся
произведения, сомножители которых находятся на главной диагонали и
в вершинах треугольников, чьи основания параллельны главной
диагонали, остальные слагаемые берутся со знаком «-».
2. Свойства определителей.
1) Если к.-л. строка или столбец в матрице состоит из одних нолей,
то ( этой матрицы равен 0. 2)При транспонировании матрицы её
определитель не изменяется: (А (=( А’( . 3) Если все элементы к.-л.
строки или столбца матрицы умножить на одно и то же число, то и (
этой матрицы умножится на это же число. 4) При перестановке местами
2-х строк или столбцов матрицы её определитель меняет свой знак на
противоположный. 5) Если квадратная матрица содержит 2 одинаковых
строки или столбца, то её определитель равен 0. 6)Если 2 строки или
2 столбца матрицы пропорциональны, то её ( равен 0. 7) Сумма
произведений элементов к.-л. строки или столбца матрицы и другой
строки или столбца равна 0. 
если к элементам одной строки или столбца прибавить элементы другой
строки или столбца, умноженный на одно и то же число. 9)Если к.-л.
столбец или строка матрицы представляет собой сумму 2-х элементов,
то ( этой матрицы может быть представлен в виде суммы 2-х
определителей.
3. Минор.
Минором Мij квадратной матрицы n-го порядка для элемента аij
называется определитель (n-1)-ого порядка, полученный с данного
вычёркиванием i-ой строки и j-ого столбца.
4. Алгебраическое дополнение.
Алгебраическим дополнением Аij для элемента квадратной матрицы аij
называется минор этого элемента, взятый со знаком (-1)i+j .
5. Вычисление определителей любого порядка. Понятие определителя
n-ого порядка.
Определителем квадратной матрицы n-ого порядка называется число,
равное алгебраической сумме n членов, каждый из которых является
произведением n- элементов матрицы, взятых по одному из каждой
строки или столбца (причём знак каждого члена определяется как
(-1)r(j), где r(j)-число инверсий). Теорема Лапласа: определитель
квадратной матрицы равен сумме произведений элементов к.-л. строки
или столбца на их алгебраические дополнения.
6. Матрицы. Основные определения.
Матрицей размера mxn называется прямоугольная таблица чисел,
содержащая m строк и n столбцов. Вектор-строкой называют матрицу,
состоящую из одной строки. Вектор-столбцом — из одного столбца.
Матрица, у которой количество столбцов равно количеству строк,
называется квадратной матрицей n-ого порядка. Элементы матрицы, у
которых номер строки и номер столбца совпадает, называются
диагональными и образуют главную диагональ матрицы. Если все
недиагональные элементы матрицы равны нулю, то матрицу называют
диагональной. Если у диагональной матрицы n-ого порядка на главной
диагонали все элементы равны 1, то матрица называется единичной и
обозначается Е. Матрица любого размера, все элементы которой равны
0, называется нуль-матрицей.
7. Операции над матрицами.
1)Умножение матрицы на число: условий нет, умножить на число можно
любую матрицу. Произведением матрицы А на число ( называется
матрица В, равная (А, каждый элемент которой находится по формуле:
bij =( x aij. Для того, чтобы умножить матрицу на число необходимо
умножить на это число каждый элемент матрицы. 2)Сложение 2-х
матриц: условие — складывать можно только матрицы одинакового
размера. Суммой 2-х матриц А и В называется матрица С=А+В, каждый
элемент которой находится по формуле Сij=aij+bij. Для того, чтобы
сложить 2 матрицы, необходимо складывать между собой элементы,
стоящие на одинаковых местах. 3)Вычитание 2-х матриц: операция
аналогична сложению. 4)Умножение 2-х матриц: умножение А на В
возможно тогда и только тогда, когда число столбцов А равно числу
строк В; произведением матрицы А размера mxk на матрицу В размера
kxn называется матрица С размера mxn, каждый элемент которой равен
сумме произведений элементов i-ой строки матрицы А на
соответствующие элементы j-ого столбца матрицы В. 5)Возведение в
степень: возводить в степень можно только квадратные матрицы; целой
положительной степенью квадратной матрицы Аm называется
произведение m-матриц, равных А. 6)Транспонирование: условий нет;
транспонирование-операция, в результате которой строчки и столбцы
матрицы меняются местами с сохранением порядка элемента, при этом
элементы главной диагонали остаются на своих местах.
8. Понятие обратной матрицы и алгоритм её вычисления.
Матрица А-1 называется обратной по отношению к квадратной матрице
А, если при умножении её на заданную как справа так и слева
получатся единичная матрица. Теорема (необходимое и
достаточн.условие сущ-я обратн.матрицы): обратная матрица А-1 сущ-т
и единственна тогда и только тогда, когда заданная матрица не
вырожденная. Матрица называется вырожденной, если её определитель
равен 0, в противном случае она – не вырожденная. Алгоритм:
1)Определитель заданной матрицы. 2)Транспонирование.
3)Алгебраические дополнения всех элементов транспонированной
матрицы. 4) Присоед.матрица А( (на месте каждого эл-та Ат его
алгебраич.доп-я). 5) А-1= 1/(А (((. 6) Проверка((А-1 (А=Е.
9. Ранг матрицы. Элементарные преобразования.
Рангом матрицы А называется наивысший порядок отличных от 0 миноров
этой матрицы (rang A=r(A)(. Ранг матрицы не изменяется при
проведении элементарных преобразований. Преобразования:
1)отбрасывание строки или столбца, состоящих из одних нулей;
2)умножение всех эл-ов к.-л. строки или столбца матрицы на одно и
то же число, отличное от 0; 3)изменение порядка строк или столбцов
матрицы; 4)прибавление к каждому эл-ту к.-л. строки или столбца
эл-ов др. строки или столбца, умноженных на одно и то же число, не
равное 0; 5) транспонирование матрицы.
10. Системы линейных алгебраических уравнений. Основные
определения. Матричная форма записи.
Линейным ур-ем относительно неизвестных x1,x2,…,xn называется
выражение вида a1x1+a2x2+…+anxn=b, где a1,a2,…,an и b- простые
числа, причём a1,a1,…,an называются коэффициентами при неизвестных,
а b- свободным коэффициентом. Последовательность чисел k1,k2,…,kn
называется решением ур- я, если при подстановке этих чисел в ур-е
оно обращается в верное равенство. Два линейных ур-я называются
равносильными, если их решения совпадают. Чтобы получить
равносильное ур-е из заданного, необходимо осуществить следующие
преобразования: 1) перенос слагаемых из одной части ур-я в другую;
2) поэлементное умножение всего ур-я на одно и то же число,
отличное от ноля. Решить линейное ур-е –это значит найти все его
решения или установить, что их нет. Система уравнений называется
совместной, если она имеет хотя бы одно решение. Система ур-ий
называется определённой, если она имеет одно единственное решение,
и неопределённой, если решений множество. Неизвестное x1 называется
разрешённым, если к.-н. ур-е системы содержит неизвестное x1 с
коэффициентом, равным 1, а во все др. ур-я системы неизвестное x1
не входит. Если каждое ур-е системы содержит разрешённое
неизвестное, то такую систему называют разрешённой. Неизвестные
СЛУ, которые не входят в разрешённый набор, называются свободными.
Разрешённая СЛУ всегда совместна, она будет определённой, если
число ур-ий равно числу неизвестных; и неопределённой, если число
неизвестных больше, чем ур-ий. Для того, чтобы определить совместна
система или нет, не решая её, можно воспользоваться теоремой
Кронекера-Капелли. Матрица, эл-тами которой являются коэффициенты
при неизвестных системы, называется матрицей системы. Матрица
системы, дополненная столбцом свободных коэффициентов, называется
расширенной матрицей.
11. Правило Крамера.
Правило Крамера: пусть (А-определитель матрицы системы, а
(j-определитель матрицы, полученной из матрицы системы заменой
j-ого столбца на столбец свободных коэффициентов; тогда, если (А(0,
то система имеет единственное решение, определяемое по формуле (
Xj= (j/ (A.
12. Теорема Кронекера-Капелли.
Теорема Кронекера-Капелли: СЛУ совместна тогда и только тогда,
когда ранг матрицы системы равен рангу расширенной матрицы этой
системы. Система ур-ий называется совместной, если она имеет хотя
бы одно решение.
13. Решение систем линейных алгебраических ур-ий методом
Гаусса.
Метод Гаусса: каждую СЛУ при помощи конечного числа преобразований
можно превратить в разрешённую системы ур-ий или в систему,
содержащую противоречивое ур-е. Противоречивым называется ур-е вида
OX1+OX2+…+OXn=b. Если каждое ур-е системы содержит разрешённое
неизвестное, то такую систему называют разрешённой. Неизвестное x1
называют разрешённым, если к.-н. ур-е системы содержит неизвестное
x1 с коэффициентом, равным 1, а во все другие ур-я системы
неизвестное x1 не входит.
14. Матричный метод решения системы линейных алгебраических
уравнений.
Этим способом можно решить лишь те системы, в которых число
неизвестных равно числу уравнений. Алгоритм: 1)Записать матрицу
системы (А); 2) Найти обратную матрицу для матрицы системы (А-1);
3) Умножить А-1 на матрицу свободных коэффициентов (В) (
X=A-1(B.
15. Однородная система линейных алгебраических уравнений.
Система m линейных ур-ий с n переменными называется системой
линейных однородных уравнений, если все свободные члены равны 0.
Система линейных однородных ур-ий всегда совместна, т.к. она всегда
имеет, по крайней мере, нулевое решение. Система линейных
однородных ур-ий имеет ненулевое решение тогда и только тогда,
когда ранг её матрицы коэффициентов при переменных меньше числа
переменных, т.е. при rang A ( n. Всякая лин. комбинация решений
системы лин. однородн. ур-ий также является решением этой системы.
Система лин.независимых решений е1, е2,…,еk называется
фундаментальной, если каждое решение системы является линейной
комбинацией решений. Теорема: если ранг r матрицы коэффициентов при
переменных системы линейных однородных уравнений меньше числа
переменных n, то всякая фундаментальная система решений системы
состоит из n-r решений. Поэтому общее решение системы лин. однордн.
ур-ий имеет вид: с1е1+с2е2+…+сkеk, где е1, е2,…, еk – любая
фундаментальная система решений, с1, с2,…,сk – произвольные числа и
k=n-r. Общее решение системы m линейных ур-ий с n переменными равно
сумме общего решения соответствующей ей системы однородн. линейных
ур-ий и произвольного частного решения этой системы.
1 (16). Скалярные и векторные величины. Основные определения.
В математике используется 2 вида величин: а) скалярные – величины,
которые полностью определяются заданием их числовых значений
(длина, площадь, объём, масса и т.д.); б) векторные – величины, для
полного определения которых помимо численного значения требуются
ещё и направления в пространстве (изображаются при помощи
векторов). Вектор – направленный отрезок на плоскости или в
пространстве, имеющий определённую длину, у которого одна из точек
принята за начало, а другая за конец. Координатами вектора (а
являются координаты его конечной точки. Длиной вектора (нормой) или
модулем называется число, равное длине отрезка, изображающего
вектор ((a(((x2+y2(+z2)(. Если начало и конец вектора совпадают, то
такой вектор называется нулевым и обозначается (0. ( направление (0
произвольно, не определено). Для каждого (а, отличного от 0,
существует противоположный -(а, который имеет модуль, равный (а(,
коллиниарен с ним, но направлен в другую сторону. Два вектора (а
и(в называются коллинеарными, если они расположены на одной прямой
или на параллельных прямых. Два вектора называются равными, если
они: 1)имеют равные модули; 2)коллиниарны; 3)направлены в одну
сторону.
2 (17). Линейные операции над векторами. Свойства линейных
операций.
1)Сложение 2-х векторов: (правило треугольников) суммой 2-х
векторов (а и(в называют вектор (с =(а +(в, начало которого
совпадает с началом (а, а конец- с концом (в при условии, что
начало (в совпадает с концом(а. 2) Сложение нескольких векторов:
(правило многоугольника) сумма 4-х векторов (а,(в,(с,(d есть
вектор(е =(а +(в +(с +(d, начало которого совпадает с началом (а, а
конец- с концом(d. (правило параллелепипеда) сумма 3-х векторов
(а,(в,(с определяется как (d =(а +(в +(с. 3)Вычитание 2-х векторов:
разностью 2-х векторов (а и (в называется сумма (а и -(в
(противоположного). 4) Суммой 2-х векторов одинаковой размерности n
называется вектор, каждая компонента которого равна сумме
соответствующих компонент слагаемых вектора: (( = (x +(y, (i=xi +
yi (i.
5) Произведением (x на действительное число а называется (в = а(x,
каждая компонента которого равна а((xi. Cвойства лин. операций над
векторами: 1)коммутативное св-во суммы (переместительное);
2)ассоциативное св-во суммы (сочетательное); 3)ассоциативное
относительно числового множителя: ((( (((( ( ((((((;
4)дистрибьютивное (распределительное; 5)существование нулевого
вектора, такого, что ((((((( ((( ; 6)для любого (( существует такой
противоположный -(( , что (((((((((((((; 7)для любого ((
справедливо: (((((((.
3 (18). Векторное пространство, его размерность. Понятие
Базиса.
N-мерным вектором называется упорядоченная совокупность
n-действительных чисел, записанных в виде (x=(x1,x2,xi,xn), где
Xi-компонента (X. Два N- мерных вектора равны тогда и только тогда,
когда равны их соответствующие компоненты: (x =(y, если xi=yi (i.
Множество векторов с действительными компонентами, в котором
определены операции сложения векторов и умножения вектора на число,
удовлетворяющее всем сво-вам суммы( коммутативное, ассоциативные),
называется векторным пространством. Размерность векторного
пространства равна количеству векторов в базисе этого пространства.
Совокупность n-мерных векторов, рассматриваемая с определёнными в
ней операциями сложения векторов и умножения вектора на число,
называется n- мерным координатным пространством. Система n—мерных
лин. независимых векторов называется базисом Rn
(R2-плоскость,R3-пространство), если каждый вектор этого
пространства R разлагается по векторам этой системы. Базисом
называется совокупность всех лин. независимых векторов системы
пространства. Теорема: для того, чтобы — 1)2 вектора на плоскости
(2)3-в пространстве) были линейно не зависимы необходимо и
достаточно, чтобы они были не 1) коллиниарны (2) компланарны).
Векторы называются компланарными, если они лежат в одной плоскости
или параллельны одной плоскости. Два вектора (а и(в называются
коллинеарными, если они расположены на одной прямой или на
параллельных прямых. Теорема: если диагональная система является
частью n-мерных векторов, то она же является базисом этой системы.
Теорема: любой вектор системы векторов единственным образов
разлагается по векторам её базиса.
4 (19). Базис на плоскости. Разложение вектора по базису R.
Система n—мерных лин. независимых векторов называется базисом Rn
(R2- плоскость,R3-пространство), если каждый вектор этого
пространства R разлагается по векторам этой системы. Базисом
называется совокупность всех лин. независимых векторов системы
пространства.
5 (20). Базис в пространстве. Разложение вектора по базису R.
Система n—мерных лин. независимых векторов называется базисом Rn
(R2- плоскость,R3-пространство), если каждый вектор этого
пространства R разлагается по векторам этой системы. Базисом
называется совокупность всех лин. независимых векторов системы
пространства.
6 (21). Линейные операции над векторами, заданные координатами.
7 (22). Проекция вектора а на вектор b. Направляющие косинусы
вектора.
8 (23). Скалярное произведение векторов. Свойства скалярного
произведения.
Скалярным произведением 2-х векторов (а и(в называется число,
равное произведению модулей, перемноженных на cos угла между ними:
а ((в(((а ((((в ((Cos(, где (-угол(а между(в. Скалярное
произведение может быть найдено также по формуле: (а ((в =((а ((
пр.а (в =((в(( пр.в (а( скалярное произведение 2-х векторов равно
произведению модуля одного из них на проекцию на него другого
вектора. Свойства скалярного произведения: 1)Переместительное
((а((в=(в ((а); 2)Сочетательное относительно числового множителя
((((а ((в)=((а (((в); 3)Распорядительное ( ((а +(в )((с=(а ((с
((в((с); 4)Если скалярное пр-е равно 0, то либо равен 0 один из
перемножаемых векторов, любо Cos угла между ними, т.е. векторы
перпендикулярны. Скалярное произведение само на себя равно квадрату
его модуля.
9 (24). Скалярное произведение ортов.
Скалярное произведение
векторов, заданных координатами.
10 (25). Определение угла между двумя векторами.
11 (26). Условия параллельности и перпендикулярности двух
векторов.
12 (27). Векторное произведение.
Векторным произведением вектора (а на вектор (в называется вектор
(с, который определяется следующим образом: 1) модуль (с численно
равен площади параллелограмма, построенного на перемножаемых
векторах как на сторонах (с(=(а(((в( (Sin(. 2) вектор с
перпендикулярен обоим перемножаемым векторам; 3) направление
вектора с таково, что если смотреть из его конца вдоль вектора а к
вектору в, осуществляется против часовой стрелки. Геометрич. смысл
векторного произведения –модуль векторн.пр-я равен площади
параллелограмма, построенного на перемножаемых векторах. Если
векторы заданы в координатной форме, то их векторн. Произведение
находится по формуле: (а ((в =( i j k(
(ax ay az(
(bx by bz(.
13 (28). Свойства векторного произведения.
1. При перестановке сомножителей векторное произведение меняет свой
знак на противоположный, сохраняя при этом свой модуль: (а ((в
=((в) ((а. 2)Векторн.пр-е обладает сочетательным св-вом
относительно числового (скалярного) множителя:
((((а((в(((((а(((в((а(((((в(. 3)Векторн.пр-е обладает
распределительным св-ом. 4) Если векторн.пр-е 2-х векторов равно 0-
вектору, то либо равен 0 один из перемножаемых векторов, любо синус
угла между ними, т.е. векторы коллиниарны (параллельны). (Для того,
чтобы 2 ненулевых вектора были коллиниарны необходимо и достаточно,
чтобы их векторное пр-е было равно нуль-вектору.
14 (29). Векторное произведение ортов.
15 (30). Векторное произведение векторов, заданных проекциями.
16 (31). Смешанное произведение векторов. Свойства смешанного
произведения. Геометрический смысл смешанного произведения.
Рассмотрим произведение векторов а, в и с, составленное следующим
образом: ((а ((в) – векторно, а затем полученной произведение
умножают на (с скалярно. ((а ((в) ((с. Такое произведение
называется векторно-скалярным или смешанным. Оно представляет собой
некоторое число. Скалярным произведением двух векторов называется
произведение длин двух векторов на косинус угла между ними.
Смешанное произведение равно определителю 3-го порядка, в строках
которого стоят соответствующие проекции перемножаемых векторов.
Свойства: 1)если внутри смешанного произведения в векторном
произведении поменять множители местами, то смешанное пр-е поменяет
свой знак на противоположный, т.е. ((а ((в) ((с = — ((в ((а) ((с;
((а ((в) ((с = (с ( ((а ((в). 2)Для того, чтобы 3 вектора а, в и с
были компланарны, необходимо и достаточно, чтобы их смешанное
произведение равнялось 0: ((а ((в) ((с=0. Векторы, параллельные
одной плоскости или лежащие в одной плоскости, называются
компланарными. Геометрич. смысл смешанного произведения: состоит в
том, что смешанное пр-е с точностью до знака равно объёму
параллелепипеда, построенного на этих векторах как на рёбрах.
1 (32). Координаты на прямой. Деление отрезка в данном
отношении.
Положение каждой точки на оси определяется числом, равным отношению
длины отрезка прямой от точки 0 до заданной точки к выбранной
единице длины. Положение каждой точки на вертикальной оси
определяется координатой, которая называется ордината. Координата
на горизонтальной оси называется абсцисса. Метод координат на
плоскости ставит в соответствие каждой точки плоскости
упорядоченную пару действительных чисел – координаты этой точки.
Расстояние между 2-мя точками возможно найти 2-мя путями: 1)если
обе точки лежат на одной оси, то расстояние между ними по оси
ординат (или абсцисс) равно 0, а по оси абсцисс (ординат)
абсолютной величине разности между абсциссами конца и начала
отрезка +рис.; 2) если 2 точки лежат в одной плоскости, длина
отрезка равна квадратному корню из суммы квадратов разностей
соответствующих координат концов отрезков.
Деление отрезков в данном отношении: даны 2 точки М1(((((( и
М2((((((. Требуется найти внутри отрезка точку М с координатами
((;((, такую, что отрезок М1М2 поделится точкой М в соотношении
М1М/М2М=(. Найти координаты М, удовлетворяющие данному равенству.
Решение: М1М/М2М=АА1/АА2. АА1=X-X1, AA2=X2-X. M1M/M2M=(X-X1)/(X2-X)
=(. X-X1=((X2-X), X-X1=(X2-(X. X+(X=X1+(X2(X (1+() =X1+(X2,
X=X1+(X2/1+(.
2 (33). Общее уравнение прямой и его исследование.
Рассмотрим ур-е первой степени с двумя переменными в общем виде:
Ax+By+C=0, в котором коэффициенты А и В не равны одновременно нулю,
т.е.А2+В2 (0. 1)Пусть В(0. Тогда ур-е Аx+By+C=0 можно записать в
виде y= -Ax/B – C/B. Обозначим k= -А/В, b= -C/B. Если А(0, С(0, то
получим y=kx+b (ур-е прямой, проходящей ч/з начало координат); если
А=0, С(0, то y=b (ур-е прямой, параллельной оси Оy); если А=0, С=0,
то y=0 (ур-е оси Оx). 2)Пусть В=0, А(0. Тогда ур-е Аx+By+C=0 примет
вид x= — C/A. Если С(0, то получим x=a (ур- е прямой, параллельной
оси Оy); если С=0, то x=0 (ур-е оси Оy). Таким образом, при любых
значениях коэффициентов А, В (не равных одновременно нулю) и С ур-е
Ax+By+C=0 есть ур-е некоторой прямой линии на плоскости Оxy. Это
ур-е называется общим ур-ем прямой. Ур-е прямой, заданное в общем
виде, не даёт представления о расположении прямой на плоскости, но
из него легко находятся все основные хар-ки прямой: 1)k= -A/B;
2)начальная ордината b= — C/B; 3) отрезки, отсекаемые прямой на
осях ординат: Ax+By+C=0 /((- C)
-Ax/C-By/C=1
a= — C/A; b= — C/B.
3 (34). Уравнение прямой, проходящей через точку М (x, y)
перпендикулярно нормальному вектору n (A, B).
4 (35). Уравнение прямой, проходящей через точку М (x, y)
параллельно направляющему вектору q (l, m).
5 (36). Уравнение прямой, проходящей через две точки М 1(x1, y1) М2
(x2, y2).
Это ур-е является частным случаем ур-я пучка прямых. Прямая задана
2-мя лежащими на ней точками М1 (x1;y1) и M2(x2;y2), x1(x2,
y1(y2(при равенстве — применение ур-япрямой, проход.ч.з 2 точки,
невозможно). Для составления ур-я прямой М1М2 необходимо ур-е пучка
прямых, проходящих ч/з точку М1: y- y1=k(x-x1). Т.к. точка
M2(x2;y2) лежит на данной прямой, то чтобы выделить её из пучка,
подставим в ур-е пучка прямых координаты М2 и найдём угловой
коэффициент: k=y2-y1/x2-x1.
Теперь ур-е прямой, проходящеё через 2 заданные точки, примет вид:
y-y1=(x- x1) ( y2-y1/x2-x1( y-y1/y2-y1=x-x1/x2-x1.
(др. способ: после ур-я углового коэф-та вывожу: tg (=M2(N/M1(N,
M2N=y2-y1; M1N=x2-x1( tg (=K=y2-y1/x2-x1. Подставим это ур-е в ур-е
пучка прямых: y- y1=(x-x1)(y2-y1/
/x2-x1 ((( y2-y1)( y-y1/y2-y1=x-x1/x2-x1. )
6 (37). Уравнение прямой в отрезках.
Прямая задана отрезками, которые она отсекает на осях координат.
Найду ур-е прямой по заданным отрезкам а(0 и b(0, отсекаемым на
осях координат. Используя ур-е прямой, проходящей через точки
А(а;0) и В(0;b) — y-y1/y2- y1=x-x1/x2-x1—ур-е прямой в отрезках
примет вид: y-0/b-0= x-a/0-a или: -ay= b(x-a), -ay-bx+ab=0 ((ab;
-y/b-x/a+1=0 (((-1);
x/a+y/b=1. А-отрезок, отсекаемый на оси Оx; В-отрезок на оси Оy.
Тогда прямую можно определить как прямую, заданную двумя
точками(A(a;b) на осиOx и B(0:b) на оси Oy. Подставив координаты
этих точек в ур-е прямой, проходящей через две заданные точки,
получим ур-е прямой в отрезках.
7 (38). Уравнение прямой с угловым коэффициентом.
Угловой коэффициент прямой- одна из характеристик расположения
прямой на плоскости; её наклон относительно оси Оx (за угол наклона
принимается ((, отсчитываемый от оси Оx против движения часовой
стрелки до этой прямой); tg угла наклона этой прямой к оси Оx. Если
k((, то ( -острый; если (=0, то k=0, прямая параллельна оси Оx;
если (=90(, то прямая параллельна оси Оy, k- не существует. Пусть
положение прямой в прямоугольной системе координат задано величиной
отрезка, отсекаемого этой прямой на оси Оy и k этой прямой. Возьмём
произвольную точку М ((;(). Тогда tg угла ( наклона прямой найдём
из прямоугольного треугольника МВN: tg ( = MN/NB= y-b/x. Введём
угловой коэффициент прямой k=tg (; получим k=y-b/x. y=kx+b — ур-е
прямой с угловым коэффициентом. В зависимости от величин k и b
возможны следующие варианты расположения прямой: 1) при в(0, прямая
пересекает ось Оx выше начала координат; при в(0, прямая ( Оx ниже
начала координат. 2)при k(0, прямая образует острый угол с Оx; при
k(0,-тупой угол; при k=0-параллельна оси Оx; при
k=(-перпендикулярна Оx.
8 (39). Уравнение прямой, проходящей через данную точку М (x, y) с
данным угловым коэффициентом k.
9 (40). Нормальное уравнение плоскости.
Нормальное ур-е плоскости: x(Cos () +y(Cos ()+z(Cos ()+(=0, где Cos
(, Cos (, Cos (-направляющие Cos –сы нормального вектора;
(-расстояние от начала координат до плоскости. Общее ур-е
приводится к нормальному виду путём умножения на нормирующий
множитель.
10 (41). Условие параллельности и перпендикулярности прямых.
1)Если прямые параллельны, то они образуют с осью OX одинаковые
углы. Поэтому угловые коэф-ты k1 и k2 этих прямых равны. Обратно,
если k1= k2, то углы наклона прямых к оси OX одинаковы, откуда
следует, что данные прямые параллельны. Условием параллельности 2-х
прямых яв-ся равенство их угловых коэффициентов. 2)Формула
tg(=k2-k1/1+k1k2 определяет угол ( между пересекающимися прямыми
через tg(. Если (=90, то эта формула оказывается неприменимой, т.к.
tg=90 не существует. Если прямые взаимно перпендикулярны, то
(2=(1+90, откуда tg(2= tg ((1+90)= -Сtg(1. tg(2= — 1/ tg(1. Заменяя
tg(1 и Сtg(2 через k1 и k2, находим: k2= 1/ k1 или 1+ k1k2=0.
Обратно, пусть k2= 1/ k1, это значит, что tg(2= -1/tg(1 откуда
получаем (2=(1+90. Следовательно, угол между двумя данными прямыми
равен 90, т.е. прямые взаимно перпендикулярны. Условие
перпендикулярности 2-х прямых состоит в том, что угловые коэф-ты
этих прямых обратны по абсолютной величине и противоположны по
знаку: k2= -1/ k1.
11 (42). Угол между прямыми.
Угол ( между 2-мя параллельными прямыми равен 0, тогда tg(=0; с
другой стороны, из условия параллельности, т.е. из равенства k1=
k2, следует, что k1- k2=0 и по формуле tg(=k2-k1/1+k1k2-угол между
2-мя пересекающимися прямыми-получаем: k1-k2/1+k1k2=0.
12 (43). Плоскость в пространстве. Виды уравнений плоскости.
Существуют следующие виды ур-ий плоскости: 1) Общее ур-е плоскости:
Ax+By+Cz+D=0, где (n=(A,B,C)- нормальный вектор плоскости. 2) ур-е
плоскости, проходящей через точку М1(x1;y1;z1) перпендикулярно
вектору (n=(A,B,C): A(x-x1)+B(y-y1)+C(z-z1)=0. 3)Ур-е плоскости в
отрезках: x/a+y/b+z/c=1, где a,b,c-величины отрезков, отсекаемых
плоскостью на осях координат. 4)Нормальное ур-е плоскости: x(Cos ()
+y(Cos ()+z(Cos ()+(=0, где Cos (, Cos (, Cos (-направляющие Cos
–сы нормального вектора; (- расстояние от начала координат до
плоскости. Общее ур-е приводится к нормальному виду путём умножения
на нормирующий множитель. 5)Ур-е плоскости, проходящей через три
заданные точки: М1(x1;y1;z1), М2(x2;y2;z2), М3(x3;y3;z3).
(x-x1 y-y1 z-z1(
(x2-x1 y2-y1 z2-z1( =0.
(x3-x1 y3-y1 z3-z1(
13 (44). Условие параллельности и перпендикулярности
плоскостей.
14 (45). Прямая в пространстве. Виды уравнений прямой в
пространстве.
Взаимное ур-е 2-х прямых в пространстве: а) пусть прямые заданы
своими канонич.ур-ями: x-x1/L1=y-y1/m1=z-z1/n1,
x-x2/L2=y-y2/m2=z-z2/n2; где (q 1(L1;m1;n1), (q2 (L2;m2;n2)-
направляющие векторы. Тогда прямые параллельны, если параллельны их
направляющие векторы:(q1 (((q2 ( L1/L2=m1/m2=n1/n2. б) пусть прямые
заданы аналогично случаю а). Две прямые ( тогда и только тогда,
когда их направляющие векторы перпендикулярны ((q1((q2).
L1L2+m1m2+n1n2=0. Существуют следующие виды ур-ий прямой в
пространстве: 1)Общее ур-е прямой: прямая задаётся как линия
пересечения 2-х плоскостей.
(A1x+B1y+C1z+D1=0
(A2x+B2y+C2z+D2=0, где А1, В1,С1-непропорциональные коэффициентам
А2, В2, С2.
2)Ур-е прямой, проходящей через две точки (выводится аналогично
ур-ю прямой на плоскости):
x-x2/x2-x1=y-y2/y2-y1=z-z2/z2-z1.
3)Каноническое уравнение прямой в пространстве (ур-е прямой,
проходящей ч/з заданную точку М0 (x0;y0;z0), параллельно
направляющему вектору (q (l;m;n)):
x-x0/l=y-y0/m=z-z0/n.
4)Параметрическое ур-е прямой: прямая задаётся при помощи точки,
лежащей на прямой, и направляющего вектора. М0(x0;y0;z0), (q
(l;m;n). (x=x0+lt
(y=y0+mt
( z=z0+nt, t- параметр.
5)Угол между 2-мя прямыми в пространстве – это, практически, угол
между их направляющими векторами:
Cos(=L1L2+m1m2+n1n2/( L12 +m12+n12 (( L22+m22+n22 .
15 (46). Взаимное расположение прямой и плоскости.
1)Угол между прямой и плоскостью вычисляется по формуле:
Cos(=(Al+Bm+Cn(((A2+B2+C2 ((l2+m2+n2. Где l, m, n- координаты
направляющего вектора прямой; A, B, C- координаты (n. В этом случае
прямая может быть задана каноническим или параметрическим ур-ем
прямой, а плоскость – общим. 2)Прямая и плоскость в пространстве
параллельны: тогда и только тогда, когда скалярное произведение
направляющего вектора прямой и нормального вектора плоскости равно
0. (n(A,B,C)(q (l;m;n)( Ax+By+Cz+D=0 (общее ур-е плоскости);
x-x0/l=y-y0/m=z-z0/n. Т.к. (n ((q=0 (Al+Bm+Cn=0. 3)прямая и
плоскость в пространстве перпендикулярны: тогда и только тогда,
когда направляющий вектор прямой и нормальный вектор плоскости
коллинеарные (параллельны). Два вектора коллинеарны тогда и только
тогда, когда их векторное произведение равно 0 или координаты
пропорциональны. Т.к. (n ((q=0, А/l=B/m=C/n. 4)условия, при которых
прямая принадлежит плоскости: а)скалярное произведение(n ((q=0,
т.е. Al+Bm+Cn=0; б) при подстановке координат точки, лежащей на
прямой, в общее ур-е плоскости получается верное равенство(
Ax0+By0+Cz0+D=0
(x=x0+lt,
(y=y0+mt,
(z=z0+nt (параметрич. ур-е прямой).
5)точка пересечения прямой и плоскости: для того, чтобы найти
координаты точки пересечения прямой и плоскости в пространстве,
необходимо совместно решить систему, составленную из ур-ий:
x-x0/l=y-y0/m=z-z0/n (канонич. ур-е прямой), Ax+By+Cz+D=0 (общее
ур-е плоскости). Для того,чтобы решить такую систему необходимо
перейти от канонич. ур-я к параметрическому:
(x=x0+lt,
(y=y0+mt,
(z=z0+nt (параметрич. ур-е прямой)
( Ax+By+Cz+D=0.
16 (47). Кривые второго порядка. Окружность.
Кривой 2-го порядка называется линия, определяемая уравнением 2-ой
степени относительно текущих декартовых координат. В общем виде
ур-е принимает вид: Ax2+2Bxy+Cy2+2Dx+2Ey+F=0, где A, 2B, C, 2D, 2E,
F- действительные числа. Кроме того, по крайней мере, одно из этих
чисел (0. Окружность-множество точек, равно удалённых от данной
точки (центра). Если обозначить через R радиус окр., а через
С(x0,y0) –центр окружности, то исходя из этого определения :
Возьмём на окр. произвольную точку М (x,y). По определению,
расстояние СМ= R. Выражу СМ ч/з координаты заданных точек: СМ =(
(x-x0)2+(y-y0)2 = R (R2=(x-x0)2+(y-y0)2 -ур-е окр. С центром в
точке С(x0,y0). Это ур-е называется нормальным ур-ем окружности.
Ax2+2Bxy+Cy2+2Dx+2Ey+F=0-ур-е второй степени с 2-мя переменными в
общем виде. Ax2++Cy2 =(-кривая второго порядка, где А,В,С не равны
0 одновременно, т.е. А2+В2+С2(0. x2+y2-2x0x- 2y0y+x02+y02-R2=0;
B=0, A/1=C/1(A=C(0 (т.к. A2+B2+C2(0, B=0). Получаем ур- е:
Ax2+Ay2+Dx+Ey+F=0- общее ур-е оркужности. Поделим обе части этого
ур-я на А(0 и, дополнив члены, содержащие x,y, до полного квадрата,
получаем: (x+(D/2A))2+(y+(E/2A))2=(D2+E2-4AF)/4A2. Cравнивая это
ур-е с нормальным ур- ем окр., можно сделать вывод, что ур-е:
Ax2+Bxy+Cy2+Dx+Ey+F=0-ур-е действительной окружности, если:1)А=С;
2)В=0; 3) D2+E2-4AF(0. При выполнении этих условий центр окр.
расположен в точке О(-D/2A;-E/2A), а её радиус R=(D2+E2-4AF/2A.
17 (48). Кривые второго порядка. Эллипс.
Кривой 2-го порядка называется линия, определяемая уравнением 2-ой
степени относительно текущих декартовых координат. В общем виде
ур-е принимает вид: Ax2+2Bxy+Cy2+2Dx+2Ey+F=0, где A, 2B, C, 2D, 2E,
F- действительные числа. Кроме того, по крайней мере одно из этих
чисел (0. Эллипс (кривая эллиптического типа) — кривая 2-го
порядка, где коэффициенты А и С имеют одинаковые знаки.
18 (49). Кривые второго порядка. Гипербола.
Кривой 2-го порядка называется линия, определяемая уравнением 2-ой
степени относительно текущих декартовых координат. В общем виде
ур-е принимает вид: Ax2+2Bxy+Cy2+2Dx+2Ey+F=0, где A, 2B, C, 2D, 2E,
F- действительные числа. Кроме того, по крайней мере одно из этих
чисел (0. Кривая 2-го порядка называется гиперболой (или кривой
гиперболического типа), если коэффициенты А и С имеют
противоположные знаки, т.е. АС(0. Кривые 2го порядка описываются с
помощью общего ур-я:
Ax2+2Bxy+Cy2+2Dx+2Ey+F=0, где
[pic]
а) Каноническое ур-е параболы: y2=2px или y=ax2
19 (50). Кривые второго порядка. Парабола.
Кривой 2-го порядка называется линия, определяемая уравнением 2-ой
степени относительно текущих декартовых координат. В общем виде
ур-е принимает вид: Ax2+2Bxy+Cy2+2Dx+2Ey+F=0, где A, 2B, C, 2D, 2E,
F- действительные числа. Кроме того, по крайней мере одно из этих
чисел (0.
———————— 2)
Понравилась работу? Лайкни ее и оставь свой комментарий!
Для автора это очень важно, это стимулирует его на новое творчество!