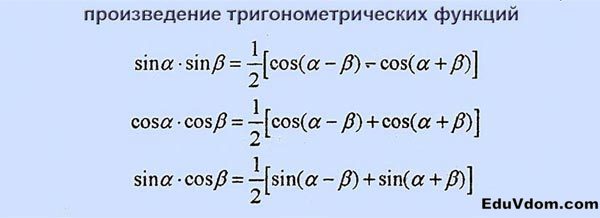- ЕГЭ по математике профиль
Для профильной математики на ЕГЭ в компактном виде для распечатки на принтере.
→ скачать docx
→ скачать pdf
Включены основные формулы:
— по алгебре (Формулы сокращенного умножения, Арифметическая прогрессия, Делимость натуральных чисел, Правила вычисления первообразной функции и т.д.)
— основные тригонометрические формулы (Формулы суммы функций, Формулы суммы аргументов, Формулы произведения функций, Формулы половинного аргумента и т.д.)
— по геометрии (Теорема косинусов, синусов; Конус; Длина окружности, площадь; Основные соотношения в треугольнике и т.д.)
Связанные страницы:
10 июля 2022
В закладки
Обсудить
Жалоба
Шпаргалка по задачам профильного ЕГЭ по математике
Сжатая информация по всем задачам профильного ЕГЭ по математике.
Часть 1
Все ответы к заданиям 1-11 по условиям экзамена даются в виде целого числа или десятичной дроби.
sh-m1.pdf
Часть 2
Для успешного решения заданий второй части нужно знать весь материал, относящийся к первой части плюс факты, перечисленные ниже.
Желательно уметь всё это доказывать!
sh-m2.pdf
Автор: Андрей Павликов.
Источник: vk.com/lomonosov_math
От Мои ответы и задания 18 июня, 2020 Сборники ЕГЭ и ОГЭ
Полезная шпаргалка для 11 класса по математике профильный уровень ЕГЭ. Справочные материалы и все формулы для решения заданий. Можно взять на ЕГЭ, чтобы было легче решать задания на экзамене.
Ссылка для скачивания шпаргалки ЕГЭ: скачать в формате PDF
Шпаргалка ЕГЭ по математике профильный уровень онлайн:
Смотрите также на нашем сайте полезные материалы:
МА1900201-МА1900212 статград математика 10 класс ответы и задания 6 февраля 2020
29 января 2020 ответы и задания по математике 11 класс статград МА1910301-МА1910312
Метки: ЕГЭматематика 11 классшпаргалка
Лучшие шпаргалки по математике. Качественно. Ничего лишнего.
Просто кликните по картинке. Подробно — в разделе «Решение задач ЕГЭ по математике».
Самое популярное. Тригонометрия и площади фигур
Тригонометрический круг
Синус, косинус, тангенс…
Формулы тригонометрии
Геометрия. Площади фигур
Геометрия на ЕГЭ по математике. Треугольники, четырехугольники, окружности.
Высоты, медианы, биссектрисы
Параллелограмм, ромб, квадрат и их свойства
Касательная к окружности
Центральные и вписанные углы
Стереометрия: формулы объема и площади поверхности.
Вписанные и описанные треугольники
Вписанные и описанные четырехугольники
Стереометрия: Формулы объема и площади поверхности.
Чертежи в задачах по стереометрии
Классическая стереометрия и метод координат
Основы стереометрии. Часть 1.
Основы стереометрии. Часть 2.
Стереометрия: Векторы и координаты.
Как расположить прямоугольную систему координат
Алгебра
Таблица производных.
Преобразования графиков функций. Задача С5.
Если вам нравятся наши материалы — записывайтесь на курсы подготовки к ЕГЭ по математике онлайн
Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Лучшие шпаргалки по математике. Качественно. Ничего лишнего.» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена:
09.03.2023
- 09.09.2012
Подборка шпаргалок по МАТЕМАТИКЕ.
Дата обновления: 01.11.2022
Полный набор теоретического материала для подготовки к ЕГЭ по математике — профильной и базовой. Таблицы, схемы, формулы, вся теория по заданимя. Всё, что необходимо для самостоятельной работы по математике.
- Тренировочные варианты ЕГЭ по профильной математике
- Тренировочные варианты по базовой математике
Что содержите в себе сборник шпаргалок по математике
- Числа, степени, модуль
- Уравнения, углы, прямые
- Справочные материалы по тригонометрии
- Решение текстовых задач
- Производная и первообразная
- Шпаргалка для экономических задач
- Шпоры по тригонометрии
- Шпаргалки по математике в картинках
Для чтения шпаргалок необходимы бесплатные программы: WinDJView и Adobe Reader
СКАЧАТЬ
https://down.ctege.info/ege/obshee/shpory/matem-ege-shpora.zip
Основные формулы и свойства на одном листе
Вернуться назад на сайт »
Формулы для профильного ЕГЭ-2022 по математике
Формулы сокращённого умножения
Арифметическая и геометрическая прогрессии
Вероятность
Свойства степеней
Свойства логарифмов
Тригонометрия
Производные
Первообразные
Геометрия
Формулы сокращённого умножения
| `(a + b)^2=a^2 + 2ab + b^2` | |
| `(a − b)^2=a^2 − 2ab + b^2` | |
| `a^2 − b^2=(a + b)(a − b)` | |
| `a^3 + b^3=(a + b)(a^2 − ab + b^2)` | |
| `a^3 − b^3=(a − b)(a^2 + ab + b^2)` | |
| `(a + b)^3=a^3 + 3a^2b + 3ab^2 + b^3` | |
| `(a − b)^3=a^3 − 3a^2b + 3ab^2 − b^3` |
Прогрессии
Арифметическая прогрессия:
| `a_n=a_(n-1)+d` |
| `a_n=a_1+(n-1)*d` |
| `S_n=((a_1+a_n)*n)/2` |
Геометрическая прогрессия:
| `b_n=b_(n-1)*q` |
| `b_n=b_1*q^(n-1)` |
| `S_n=((q^n-1)*b_1)/(q-1)` |
| Бесконечно убывающая: `S=b_1/(1-q)` |
Вероятность
| Вероятность события A: | `P(A)=m/n` | |
| События происходят A и B происходят одновременно | `A*B` | |
| Независимые события: | `P(A*B)=P(A)*P(B)` | |
| Зависимые события: | `P(A*B)=P(A)*P(B|A)` | |
| Происходит или событие A, или B | `A+B` | |
| Несовместные события: | `P(A+B)=P(A)+P(B)` | |
| Совместные события: | `P(A+B)=P(A)+P(B)-P(A*B)` |
Свойства степеней
| `a^0=1` | `a^1=a` |
| `a^(-1)=1/a` | `a^(-n)=1/a^n` |
| `a^(1/2)=sqrt(a)` | `a^(1/n)=root(n)(a)` |
| `a^m*a^n=a^(m+n)` | `a^m/a^n=a^(m-n)` |
| `(a*b)^n=a^n*b^n` | `(a/b)^n=a^n/b^n` |
| `(a^m)^n=a^(m*n)` | `a^(m/n)=root(n)(a^m)` |
Свойства логарифмов
| `log_ab=c``a^c=b` | |
| `log_a1=0` | |
| `log_aa=1` | |
| `log_a(b*c)=log_ab+log_ac` | |
| `log_a(b/c)=log_ab-log_ac` | |
| `log_ab^n=n*log_ab` | |
| `log_(a^m)b=1/m*log_ab` | |
| `log_ab=1/(log_ba)` | |
| `log_ab=(log_cb)/(log_ca)` | |
| `a^(log_cb)=b^(log_ca)` | |
| `a^(log_ab)=b` |
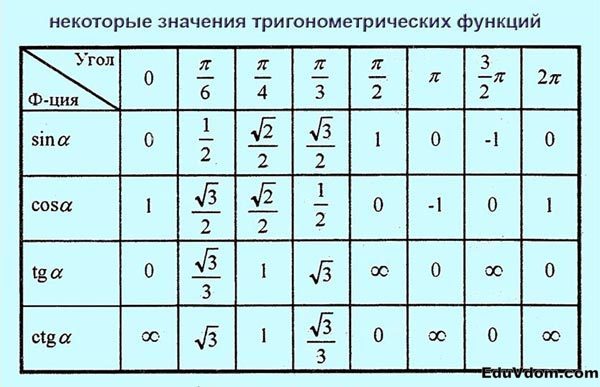
Тригонометрия
| `alpha` | `0` | `pi/6` | `pi/4` | `pi/3` | `pi/2` | `pi` | `(3pi)/2` | `2pi` |
|---|---|---|---|---|---|---|---|---|
| `0^circ` | `30^circ` | `45^circ` | `60^circ` | `90^circ` | `180^circ` | `270^circ` | `360^circ` | |
| `sinalpha` | `0` | `1/2` | `sqrt(2)/2` | `sqrt(3)/2` | `1` | `0` | `-1` | `0` |
| `cosalpha` | `1` | `sqrt(3)/2` | `sqrt(2)/2` | `1/2` | `0` | `-1` | `0` | `1` |
| `text(tg)alpha` | `0` | `sqrt(3)/3` | `1` | `sqrt(3)` | `infty` | `0` | `infty` | `0` |
| `text(ctg)alpha` | `infty` | `sqrt(3)` | `1` | `sqrt(3)/3` | `0` | `infty` | `0` | `infty` |
Основные соотношения
| `sin^2alpha+cos^2alpha=1` | |
| `text(tg)alpha=sinalpha/cosalpha=1/(text(ctg)alpha)` |
Формулы двойного угла
| `cos2alpha={(cos^2alpha-sin^2alpha),(1-2sin^2alpha),(2cos^2alpha-1):}` | |
| `sin2alpha=2sinalphacosalpha` | |
| `text(tg)2alpha=(2text(tg)alpha)/(1-text(tg)^2alpha)` |
Формулы суммы и разности аргументов
| `sin(alpha+-beta)=sinalphacosbeta+-cosalphasinbeta` |
| `cos(alpha+-beta)=cosalphacosbeta∓sinalphasinbeta` |
| `text(tg)(alpha+-beta)=(text(tg)alpha+-text(tg)beta)/(1∓text(tg)alpha*text(tg)beta)` |
Преобразование суммы и разности в произведение
| `sinalpha+-sinbeta=2sin((alpha+-beta)/2)cos((alpha∓beta)/2)` |
| `cosalpha+cosbeta=2cos((alpha+beta)/2)cos((alpha-beta)/2)` |
| `cosalpha-cosbeta=-2sin((alpha+beta)/2)sin((alpha-beta)/2)` |
Формулы половинного аргумента
| `sin(alpha/2)=+-sqrt((1-cosalpha)/2)` | |
| `cos(alpha/2)=+-sqrt((1+cosalpha)/2)` | |
| `text(tg)(alpha/2)=+-sqrt((1-cosalpha)/(1+cosalpha))=(1-cosalpha)/sinalpha=sinalpha/(1+cosalpha)` |
Обратные тригонометрические функции
| `sinx=A` | `x=(-1)^k*arcsinA + pik` или `{(x=arcsinA + 2pik),(x=pi-arcsinA+2pik):}` |
`kinZZ` |
| `cosx=A` | `x=±arccosA + 2pik` | `kinZZ` |
| `tg x=A` | `x=text(arctg) A + pik` | `kinZZ` |
| `ctg x=A` | `x=text(arcctg) A + pik` | `kinZZ` |
Также некоторые тригонометрические соотношения смотрите в разделе Геометрия.
Производные
Основные правила дифференцирования
| `(u+-v)’=u’+-v’` | |
| `(u*v)’=u’*v+u*v’` | |
| `(u/v)^’=(u’*v-u*v’)/v^2` | |
| `[f(g(x))]’=f'(g(x))*g'(x)` |
Уравнение касательной
| `y=f(x_0)+f'(x_0)*(x-x_0)` |
Производные элементарных функций
| `C’=0` | `(C*x)’=C` | |
| `(x^m)’=mx^(m-1)` | `(sqrtx)’=1/(2sqrtx)` | |
| `(1/x)^’=-1/x^2` | ||
| `(e^x)’=e^x` | `(lnx)’=1/x` | |
| `(a^x)’=a^x*lna` | `(log_ax)’=1/(xlna)` | |
| `(sinx)’=cosx` | `(cosx)’=-sinx` | |
| `(text(tg)x)’=1/cos^2x` | `(text(ctg)x)’=-1/sin^2x` | |
| `(arcsinx)’=1/sqrt(1-x^2)` | `(arccosx)’=-1/sqrt(1-x^2)` | |
| `(text(arctg))=1/(1+x^2)’` | `(text(arcctg))’=-1/(1+x^2)` |
Также некоторые сведения про производные смотрите в описании задач
№14 (база), №7 (профиль), №12 (профиль).
Первообразные
| Первообразная: | `F'(x)=f(x)` | |||
| Неопределённый интеграл: | `intf(x)dx=F(x)+C` | |||
| Определённый интеграл (формула Ньютона-Лейбница): | `int_a^bf(x)dx=F(b)-F(a)` |
Таблица первообразных
| `f(x)` | `F(x)` | `f(x)` | `F(x)` | |
|---|---|---|---|---|
| `a` | `ax` | |||
| `x^n` | `x^(n+1)/(n+1)` | `1/x` | `lnx` | |
| `e^x` | `e^x` | `a^x` | `a^x/lna` | |
| `sinx` | `-cosx` | `cosx` | `sinx` | |
| `1/cos^2x` | `text(tg)x` | `1/sin^2x` | `-text(ctg)x` | |
| `1/(x^2+a^2)` | `1/atext(arctg)x/a` | `1/(x^2-a^2)` | `1/(2a)ln|(x-a)/(x+a)|` | |
| `1/sqrt(a^2-x^2)` | `text(arcsin)x/a` | `1/sqrt(x^2+a)` | `ln|x+sqrt(x^2+a)|` |
Геометрия
Планиметрия (2D)
Площади фигур:
| Окружность: | `S=pir^2` | |
| Треугольник: | `S=1/2ah` | |
| Параллелограмм: | `S=ah` | |
| Четырёхугольник: | `S=1/2d_1d_2sinvarphi` | |
| Трапеция: | `S=(a+b)/2*h` |
Стереометрия (3D)
| Призма: | `V=S_(осн)h` | |
| Пирамида: | `V=1/3S_(осн)h` | |
| Конус: | `V=1/3S_(осн)h` | |
| `S_(бок)=pirl` | ||
| Цилиндр: | `V=pir^2h` | |
| `S_(бок)=2pirh` | ||
| Шар: | `V=4/3pir^3` | |
| `S=4pir^2` |
Полный сборник красиво оформленных школьных формул по алгебре и геометрии.
В пособии содержатся все разделы школьной математики, все формулы и даны подробные описания к каждому из них.
Смотреть в PDF: Скачайте pdf файл.
Можете записаться на занятия к репетитору математики, если что-то не понятно.
По разделам:
Степени и корни:
Сокращенное умножение
:
Квадратный трехчлен: квадратное уравнение, формулы Виета, разложение на множители:
Логарифмы:
Формулы тригонометрии, тождества:
Тригонометрические уравнения:
Значения тригонометрических функций:
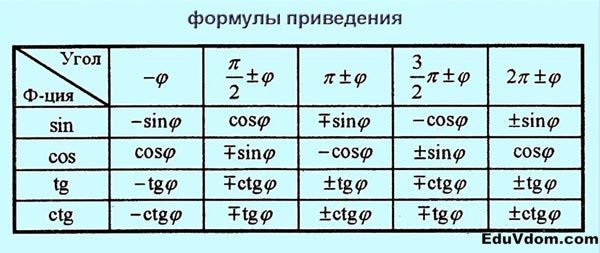
Формулы приведения:
Сумма и разность углов:
Формулы двойного и тройного аргумента:
Формулы половинного аргумента:
Сумма и разность тригонометрических функций:
Произведение тригонометрических функций:
Производная: признаки возрастания, убывания, минимума функции:
Дифференциальное исчисление:
Геометрия: формулы площадей. Прямоугольники, окружности, трапеции:
Стереометрия: объёмы, площади поверхностей:
Обратиться к репетитору по математике.
DOC-шпаргалка — подборка всех основных формул по разделам, которые нужны при решении заданий ЕГЭ по математике базового или профильного уровня…
Скачать шпаргалку
Скриншот:
Рейтинг: 3.6 из 5.0
Проголосовало: 17
Комментарии
Всего комментариев: 0
Этапы закрепощения крестьян в России
Крепостное право на Руси появилось позже, чем во многих средневековых европейских королевствах. Это было связано с объективными причинами – низкая плотность населения, зависимость от ордынского ига.
Задания 12-18 досрочного ЕГЭ по математике
3 примера по каждому заданию. Досрочный ЕГЭ по математике прошёл 28 марта.
ОГЭ по математике. Тренировочный вариант СтатГрад
Видеоуроки ОГЭ | Вчера, 21:46
Решение тестовой части (№1-19) тренировочной работы по математике от 18 апреля 2022 года.
Удержать в голове абсолютно все изученные в курсе алгебры и геометрии формулы к моменту сдачи ЕГЭ по математике практически невозможно. Поэтому, чтобы подойти к экзамену во всеоружии, стоит «вычислить» и запомнить те из них, которые могут понадобиться для решения типовых заданий КИМов.
Формулы по базовой математике для ЕГЭ
Разработчики КИМ считают, что для решения задач математики ЕГЭ базового уровня достаточно знания формул, представленных в справочных материалах – они выдаются на экзамене в индивидуальном комплекте вместе с КИМ. В «официальную шпаргалку», которой можно пользоваться во время проведения ЕГЭ, входят:
- таблица квадратных чисел от 0 до 99;
- свойства арифметического квадратного корня;
- формулы сокращенного умножения;
- корни квадратного уравнения;
- свойства степени и логарифма;
- теорема Пифагора;
- формула расчета длины окружности и площади круга;
- расчет средней линии треугольника и трапеции;
- радиус вписанной и описанной окружности правильного треугольника;
- формулы расчета площади планиметрических фигур;
- вычисление поверхностей и объемов тел;
- основные тригонометрические функции и тождества;
- график линейной функции;
- геометрический смысл производной.
Понять, нужны ли еще какие-то формулы для ЕГЭ по математике, поможет решение тренировочных тестов, например, содержащихся в открытом банке заданий на сайте ФИПИ. Для подстраховки можно изучить КЭС (кодификатор элементов содержания), актуальный в текущем учебном году. В нем перечислены все темы, которые выносятся на экзамен.
Основные формулы для профильного ЕГЭ
Выпускники, планирующие сдавать профиль, ставятся в более жесткие условия, чем те, кто выбрал базовый уровень. Учитывая то, что они видят перспективу своего дальнейшего обучения по направлениям, тесно или напрямую связанным с математикой, к их знаниям предъявляются повышенные требования. В частности, на официальные справочные материалы особенно рассчитывать не приходится. Все, что в них есть, это 5 тригонометрических тождеств.
Естественно, чтобы сдать профильную математику, для ЕГЭ потребуется запомнить намного больше формул. Выяснить, на какие темы нужно обратить внимание, можно по тому же алгоритму, что и для базы (из КЭС или, решая тренировочные задания).
Основываясь на данных, опубликованных на сайте ФИПИ, с большой долей вероятности потребуется знание следующих формул для сдачи ЕГЭ по профильной математике:
- правила сокращенного умножения;
- арифметическая и геометрическая прогрессии;
- основы вероятностной теории;
- свойства степеней и логарифмов;
- азы тригонометрии (формулы двойного угла, суммы и разности аргументов; алгоритм преобразования разности и суммы в произведение; обратные функции);
- производная (правила дифференцирования, элементарнее функции и уравнение касательной);
- первообразная;
- двухмерная планиметрия;
- правила нахождения площадей геометрических фигур;
- трехмерная стереометрия.
Опытные учителя и репетиторы собрали все формулы по математике, которые приходилось использовать на ЕГЭ в последние три года:
- ЕГЭ по математике – формулы для алгебры и начал анализа
- Формулы ЕГЭ – математика, раздел геометрия
Материалы для скачивания – в формате pdf.
Выученные назубок формулы к ЕГЭ по математике – это только часть пути к успешной сдаче, надо еще научиться правильно применять их. Хорошую практику даст решение сложных задач.
Математика
+27
баллов
к ЕГЭ
Курсы подготовки к ЕГЭ по математике
Русский язык
+30
баллов
к ЕГЭ
Курсы подготовки к ЕГЭ по русскому языку
Обществознание
+25
баллов
к ЕГЭ
Курсы подготовки к ЕГЭ по обществознанию
Физика
+31
балл
к ЕГЭ
Курсы подготовки к ЕГЭ по физике
Английский язык
+24
балла
к ЕГЭ
Курсы подготовки к ЕГЭ по английскому языку
Биология
+29
баллов
к ЕГЭ
Курсы подготовки к ЕГЭ по биологии