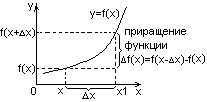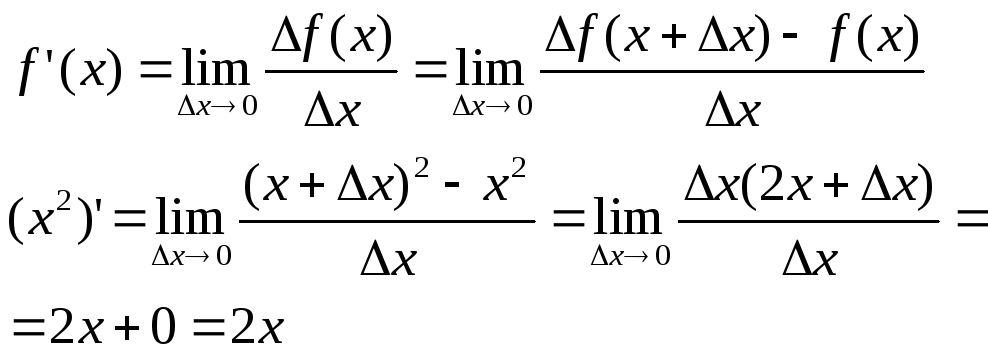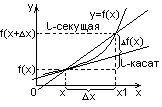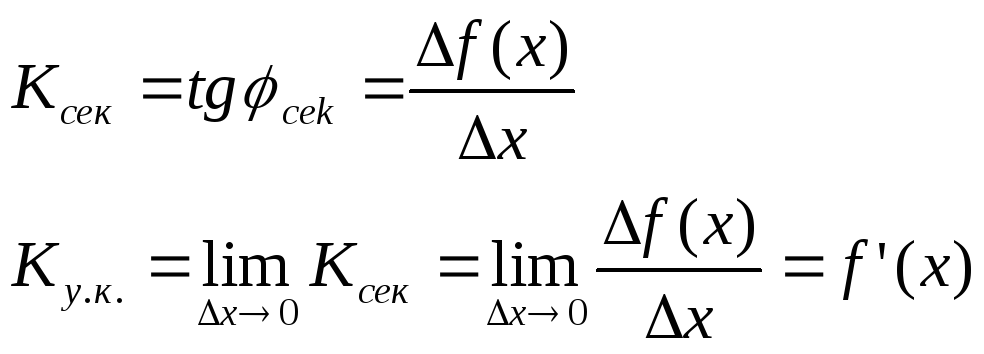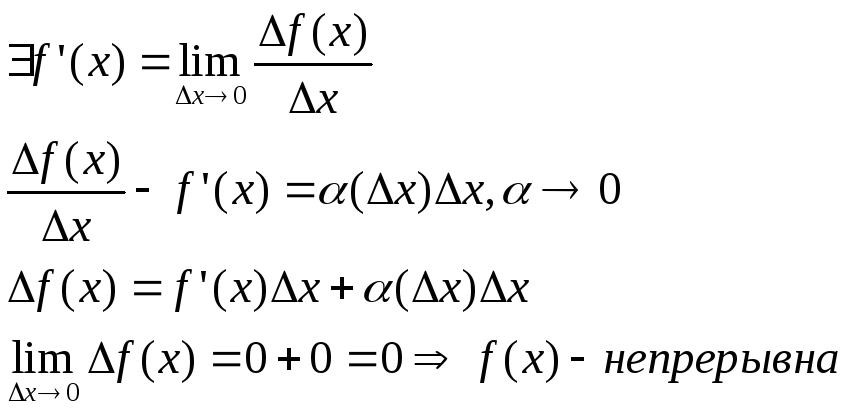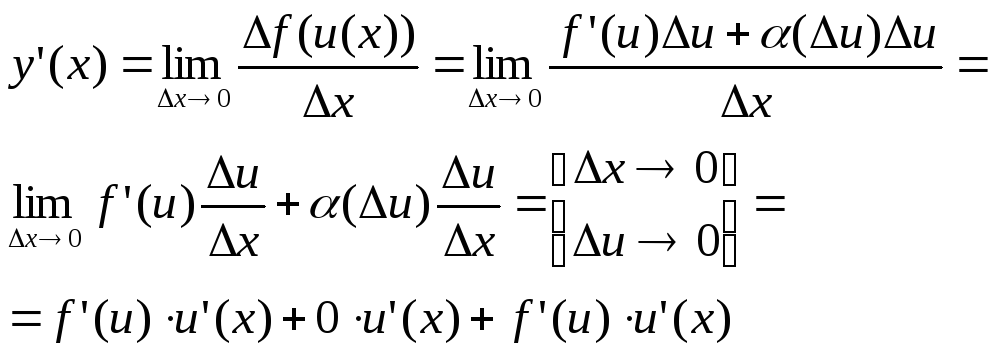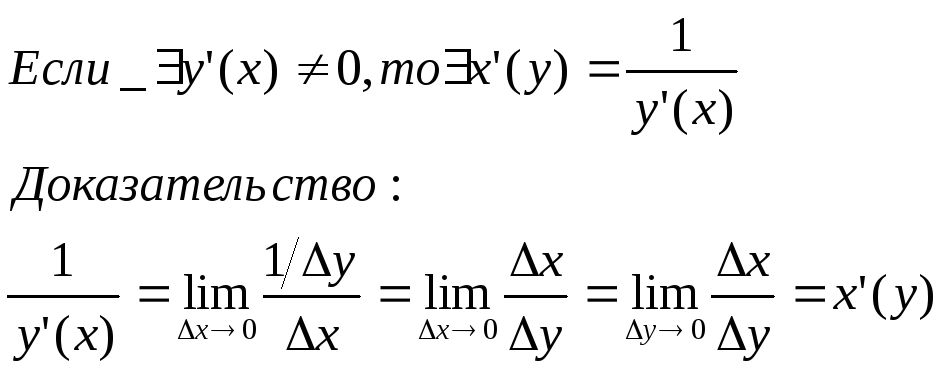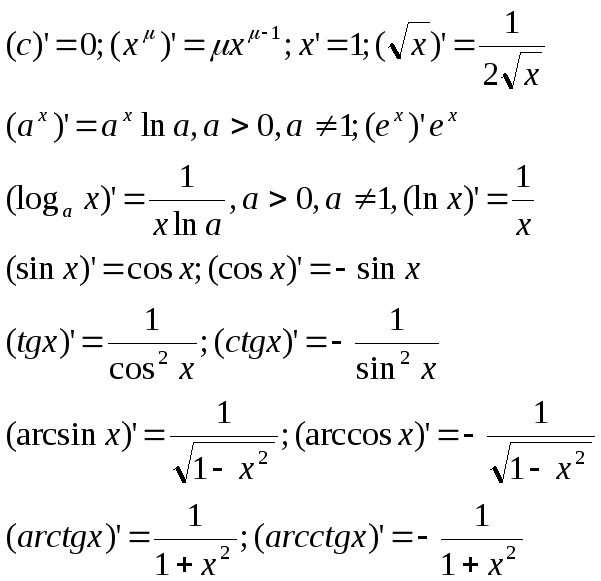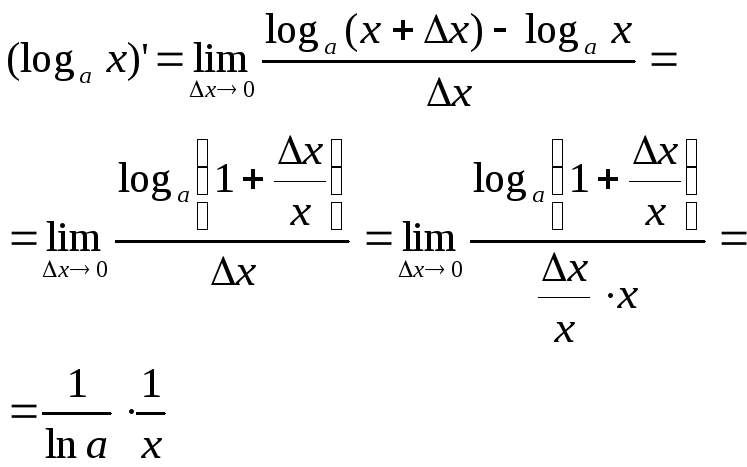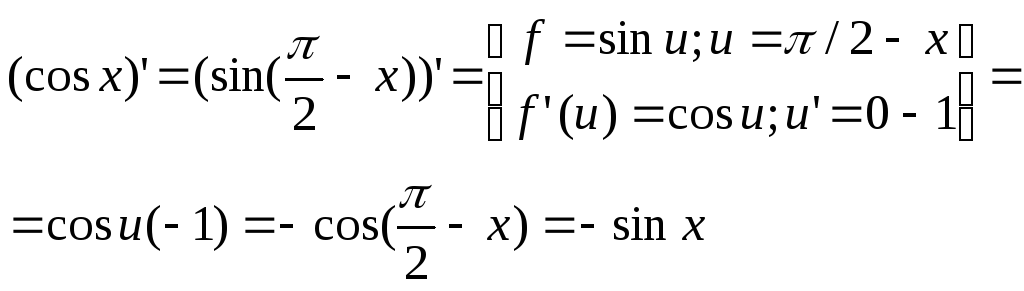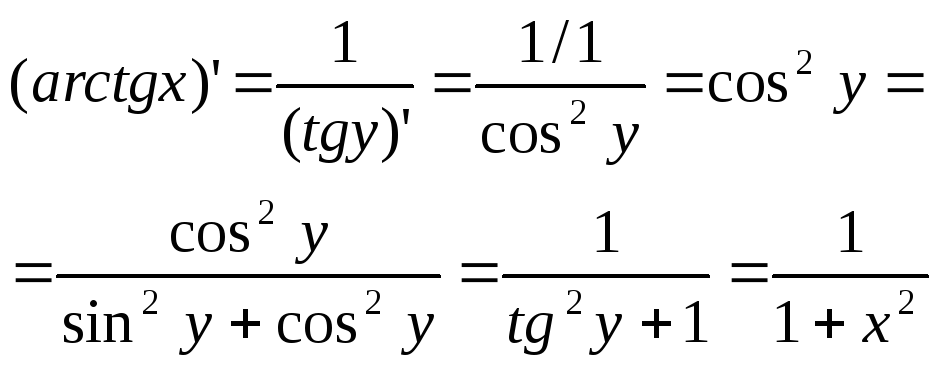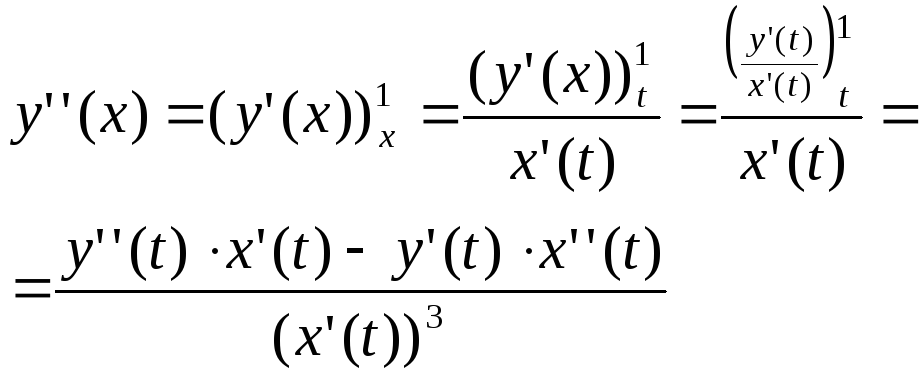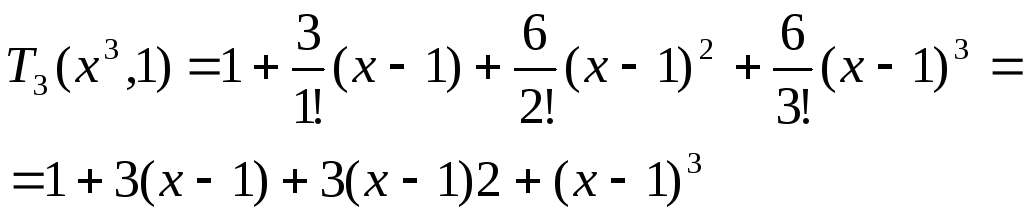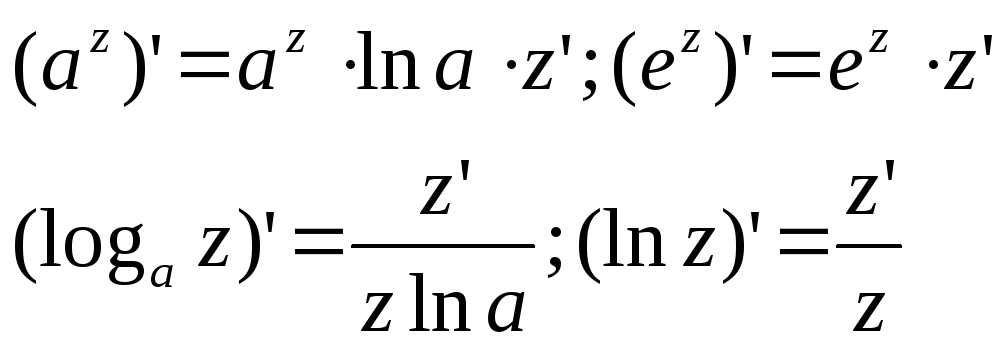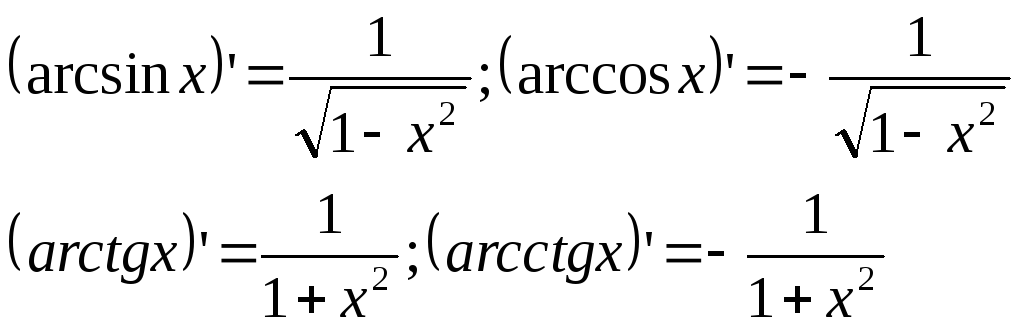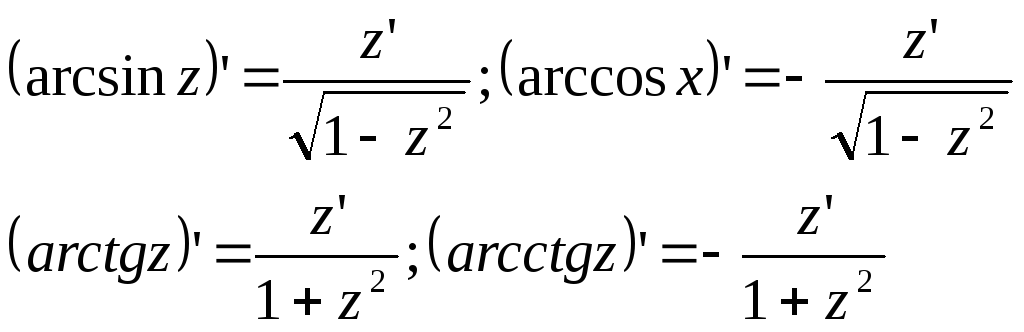Консультация и поддержка студентов в учёбе
Главная » Бесплатные рефераты » Бесплатные рефераты по математическому анализу »
Бесплатные Шпаргалки по предмету Математический анализ
Бесплатные Шпаргалки по предмету Математический анализ для студентов на разные темы можно скачать бесплатно.
Контрольные работы
Рефераты
Задачи
КОПРы
Шпаргалки
Добавить работу
Шпаргалки по темам
Найдено работ: 3
Страницы:
1
Страницы:
1
Консультация и поддержка студентов в учёбе
Ставлю 10/10
Все нравится, очень удобный сайт, помогает в учебе. Кроме этого, можно заработать самому, выставляя готовые учебные материалы на продажу здесь. Рейтинги и отзывы на преподавателей очень помогают сориентироваться в начале нового семестра. Спасибо за такую функцию. Ставлю максимальную оценку.
Отлично
Лучшая платформа для успешной сдачи сессии
Познакомился со СтудИзбой благодаря своему другу, очень нравится интерфейс, количество доступных файлов, цена, в общем, все прекрасно. Даже сам продаю какие-то свои работы.
Отлично
Студизба ван лав ❤
Очень офигенный сайт для студентов. Много полезных учебных материалов. Пользуюсь студизбой с октября 2021 года. Серьёзных нареканий нет. Хотелось бы, что бы ввели подписочную модель и сделали материалы дешевле 300 рублей в рамках подписки бесплатными.
Отлично
Отличный сайт
Лично меня всё устраивает — и покупка, и продажа; и цены, и возможность предпросмотра куска файла, и обилие бесплатных файлов (в подборках по авторам, читай, ВУЗам и факультетам). Есть определённые баги, но всё решаемо, да и администраторы реагируют в течение суток.
Отлично
Маленький отзыв о большом помощнике!
Студизба спасает в те моменты, когда сроки горят, а работ накопилось достаточно. Довольно удобный сайт с простой навигацией и огромным количеством материалов.
Хорошо
Студ. Изба как крупнейший сборник работ для студентов
Тут дофига бывает всего полезного. Печально, что бывают предметы по которым даже одного бесплатного решения нет, но это скорее вопрос к студентам. В остальном всё здорово.
Отлично
Спасательный островок
Если уже не успеваешь разобраться или застрял на каком-то задание поможет тебе быстро и недорого решить твою проблему.
Отлично
Всё и так отлично
Всё очень удобно. Особенно круто, что есть система бонусов и можно выводить остатки денег. Очень много качественных бесплатных файлов.
Отлично
Отзыв о системе «Студизба»
Отличная платформа для распространения работ, востребованных студентами. Хорошо налаженная и качественная работа сайта, огромная база заданий и аудитория.
Хорошо
Отличный помощник
Отличный сайт с кучей полезных файлов, позволяющий найти много методичек / учебников / отзывов о вузах и преподователях.
Отлично
Отлично помогает студентам в любой момент для решения трудных и незамедлительных задач
Хотелось бы больше конкретной информации о преподавателях. А так в принципе хороший сайт, всегда им пользуюсь и ни разу не было желания прекратить. Хороший сайт для помощи студентам, удобный и приятный интерфейс. Из недостатков можно выделить только отсутствия небольшого количества файлов.
Отлично
Спасибо за шикарный сайт
Великолепный сайт на котором студент за не большие деньги может найти помощь с дз, проектами курсовыми, лабораторными, а также узнать отзывы на преподавателей и бесплатно скачать пособия.
Отлично
1
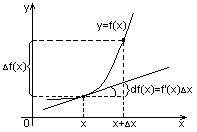
Основы дифференциального исчисления . Понятие производной.
X=X1-X
– приращение аргумента.
f(X)=f(X+X)-f(X)
– приращение функции.
Пример:
Определение:
Произв. функ. f(x)
в точке Х наз. предел отношения приращения
функ. к приращению аргум., когда последнее
стремится к 0.
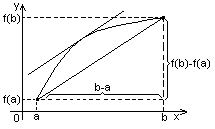
Геометрический
смысл производной.
Ку.к. – угловой
коэф. касательной.
Ксек – угловой
коэф. секущей.
Таким образом
угловой коэффициент касательной
совпадает со значение производной в
данной точке.
Уравнение касательной
к графику функции y=f(x)
в точке М0 (x0,y0)
имеет вид:
Физический смысл
производной.
S(t)
– путь за данное время.
S(t)
– приращение пути.
S(t)/
t
–средняя скорость на участке.
мгновен. скорость
на участке:
произв. пути от
скорости: S'(t)=U(t)
Теорема:
Связь между непрерывной и дифференцируемой
функцией.
Функция наз.
диферинцируемой если она имеет
производную.
Если функция диффер.
в точке х, то она и непрерывна в этой
точке.
Доказательство:
2
Правила дифференцирования
Теорема: Если f(x)
и g(x)
дифферен. в точке х, то:
Доказательство 2-го правила. Теорема о произв. Сложной функции.
Если y(x)=f(u(x))
и существует f’(u)
и u’(x),
то существует y’(x)=f(u(x))u’(x).
Доказательство:
Рассмотрим f(x)
в задан. промеж.: [a,b].
g(y):
[f(a),f(b)]
– наз. обратной к f(x),
если g(f(x))=x,
для любого
X
[a,b]
f(g(y))=y,
для любого у [f(a),f(b)]
y=sin x
[-/2,
/2],
тогда
x
y, y[1,1]
sin
arcsin y = y;
a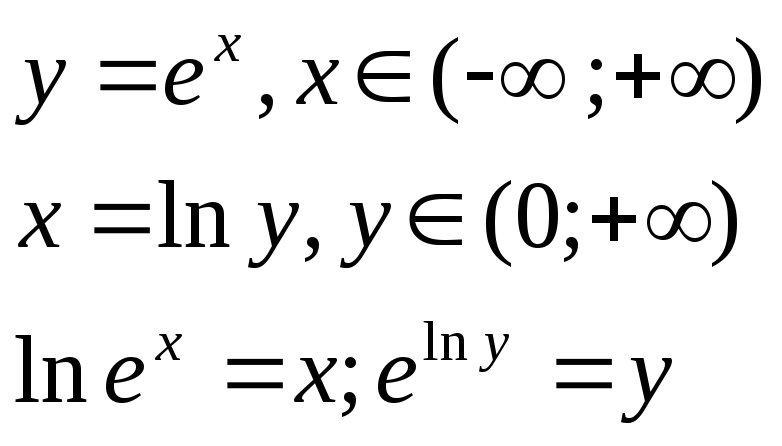
* sin x=x
Теорема о произв.
обратной функции.
Таблица производных:
3
Таблица производных:
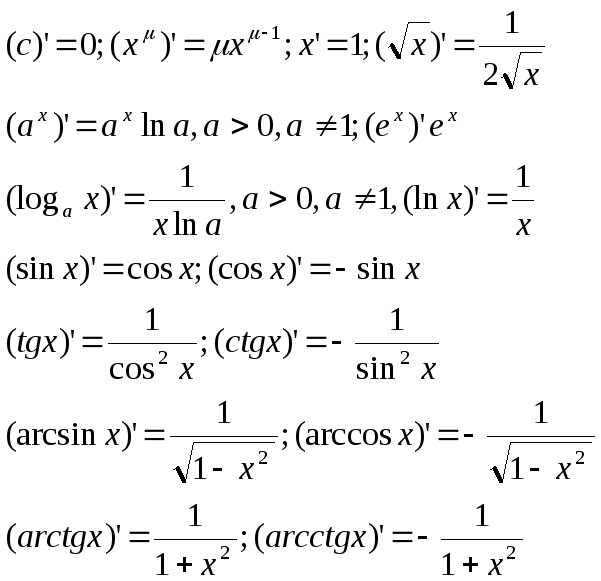
Дифференциал
функции.
Определение:
Если Х независимая переменная, то
дифференциал функции f(x)
наз. f’(x)x=u
обозначают df(x).
Теорема об
инвариантной форме первого дифференциала.
df(x)=f’(x)dx
Доказательство:
1).
2).
4
Производная
высших порядков.
Определение:
Производная второго порядка называется
производная производной данной функции:
Определение:
Производная
n-го
порядка называется производной
производной n-1-го
порядка.
Пример:
Используя метод
математической индукции несложно
показать, что:
1). n-ая
производная обладает свойством
линейности, т.е.:
2).
3).
4).
5).
6).
Дифференцирование
функций заданных параметрически.
Пример 1:
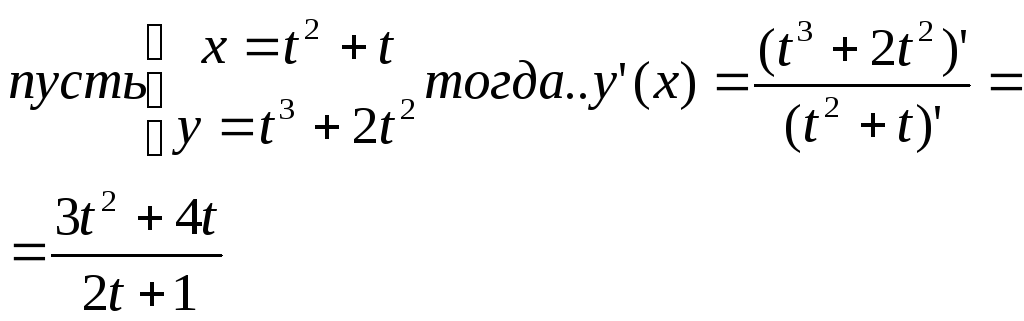
t=1,
тогда x=2,
y=3;
y’(2)=7/3
Пример
2:
5
Основные теоремы
матим. анализа.
1. Теорема Ферма.
Если f(x)
дифф. в точке x0
и принимает в хтой точке наибольш. или
наименьш. значение для некоторой
окресности точки x0,
то f’(x)=0.
Доказательство:
пусть f(x0)
– наибольшая.
2.Теорема Ролля.
Если функция f(x)
непрерывна на заданном промеж/ [a,b]
деффер. на интервале (a,b)
f(a)=f(b)
то существует т. с
из интерв. (a,b),
такая, что f’(c)=0.
3. Теорема Коши.
Если f(x),
g(x)
удовл. трем условиям:
1). f(x),
g(x)
непрерыв. на промеж [a,b]
2). f(x),
g(x)
деффер. на интервале (a,b)
3). g’(x)0
на интер. (a,b),
то сущ. т. с
g(b)g(a)
(неравны по теореме Ролля).

F(x)
– непрерывна на [a,b]
2). F(x)
– дефференцированна на (a,b)
3).
F(a)=0 ; F(b)=0
по теореме Ролля
сущ. с(a,b);
F’(с)=0
4.Теорема Лагранжа.
Если функция f(x)
непрерывна на [a,b]
и дефференцирована на (a,b),
то сущест.
т.
с(a,b),
такая,
что:
f(b)-f(a)=f’(c)(b-a).
Доказательство:
применим
т.Коши, взяв только g(x)=x,
тогда g’(x)=10.
6
Правила Лопиталя.
Раскрытие
неопределенности.
Теорема: Если
функция f(x),
g(x)
дефференцирована в окресности т. а,
причем f(a)=g(a)=0
и существует предел
Доказательство:
Формула Тейлора.
Определение:
многочлен Тейлора n-го
порядка функции f(x)
в точке x0
назыв.
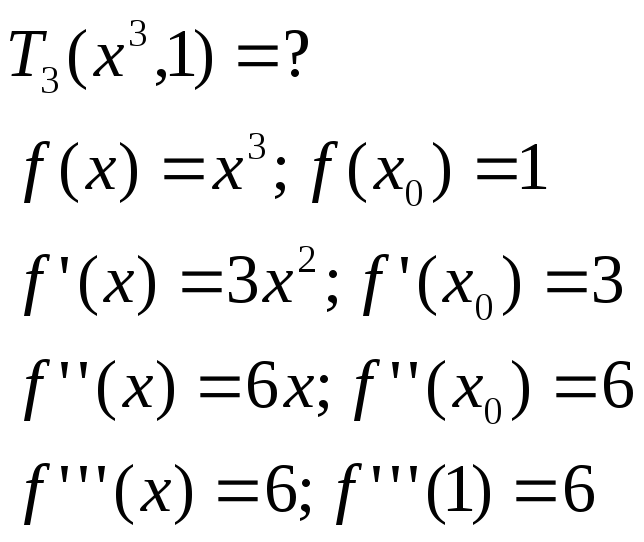
Определение:
остаточным членам формулю Тейлора n-го
порядка наз.:
Теорема:
Если функция F(x)
(n+1)
– дефферен. в окресности точки x0,
то для любого x
из этой окресн. сущ. т. с(x0,
x)
0
Правила
дифференцирования.
Производные
степенных и тригонометрических функций.
Основные формулы:
Производная
сложной функции.
Производные
показательных и логарифмических функций.
Основные формулы:
Если z=z(x)
– дифференцируемая функция от x, то
формулы имеют вид:
Производные
обратных тригонометрических функций.
Основные формулы:
Для сложных функций:
7
Соседние файлы в папке Шпаргалки
- #
- #

Математический анализ. Шпаргалка для студента №11
Автор:
Михаль Ю.О.
Размер:
1,58 мб
Формат:
djvu
16964

Формулы по интегралам, производным и тригонометрическим функциям
Размер:
8 кб
Формат:
doc
9811

Шпаргалки по высшей математике
Размер:
178 кб
Формат:
doc
20413

Шпаргалка по высшей математике за 2 курс 3 семестр
Размер:
111 кб
Формат:
doc
21342

Шпаргалка по дискретной математике и булевой алгебре. Множества, логика, комбинаторика.
Размер:
196 кб
Формат:
doc
10235

Таблица интегралов шпаргалка
Размер:
42 кб
Формат:
rtf
21356

Шпаргалки по линейной и векторной алгебре
Автор:
Орлов Н.Г.
Размер:
104 кб
Формат:
doc
12478
Здесь представлены шпаргалки по математике, которые можно скачать бесплатно.