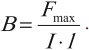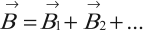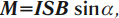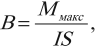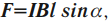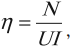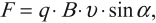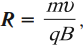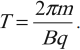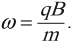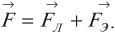Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Прямолинейный проводник длиной L с током I помещен в однородное магнитное поле так, что направление вектора магнитной индукции B перпендикулярно проводнику. Если силу тока уменьшить в 2 раза, а индукцию магнитного поля увеличить в 4 раза, то действующая на проводник сила Ампера
1) увеличится в 2 раза
2) уменьшится в 4 раза
3) не изменится
4) уменьшится в 2 раза
2
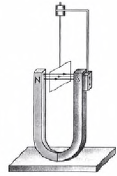
Протон p, влетевший в зазор между полюсами электромагнита, имеет скорость
перпендикулярно вектору индукции B магнитного поля, направленному вертикально. Куда направлена действующая на протон сила Лоренца F?
1) от наблюдателя
2) к наблюдателю
3) горизонтально вправо
4) вертикально вниз
3
Прямолинейный проводник длиной L с током I помещен в однородное магнитное поле перпендикулярно линиям индукции B. Как изменится сила Ампера, действующая на проводник, если его длину увеличить в 2 раза, а силу тока в проводнике уменьшить в 4 раза?
1) не изменится
2) уменьшится в 4 раза
3) увеличится в 2 раза
4) уменьшится в 2 раза
4
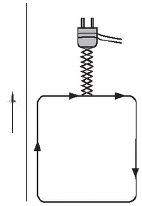
Электрическая цепь, состоящая из четырех прямолинейных горизонтальных проводников (1−2, 2−3, 3−4, 4−1) и источника постоянного тока, находится в однородном магнитном поле. Вектор магнитной индукции В направлен горизонтально вправо (см. рис., вид сверху). Куда направлена вызванная этим полем сила Ампера, действующая на проводник 1−2?
1) горизонтально влево
2) горизонтально вправо
3) перпендикулярно плоскости рисунка вниз
4) перпендикулярно плоскости рисунка вверх
5
Протон p влетает по горизонтали со скоростью υ в вертикальное магнитное поле индукцией B между полюсами электромагнита (см. рис.). Куда направлена действующая на протон сила Лоренца F?
1) вертикально вниз
2) вертикально вверх
3) горизонтально к нам
4) горизонтально от нас
Пройти тестирование по этим заданиям
Магнитное поле. Силы
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: сила Ампера, сила Лоренца.
В отличие от электрического поля, которое действует на любой заряд, магнитное поле действует только на движущиеся заряженные частицы. При этом оказывается, что сила зависит не только от величины, но и от направления скорости заряда.
Сила Лоренца
Сила, с которой магнитное поле действует на заряженную частицу, называется силой Лоренца. Опыт показывает, что вектор силы Лоренца находится следующим образом.
1. Абсолютная величина силы Лоренца равна:
(1)
Здесь — абсолютная величина заряда,
— скорость заряда,
— индукция магнитного поля,
— угол между векторами
и
.
2. Сила Лоренца перпендикулярна обоим векторам и
. Иными словами, вектор
перпендикулярен плоскости, в которой лежат векторы скорости заряда и индукции магнитного поля.
Остаётся выяснить, в какое полупространство относительно данной плоскости направлена сила Лоренца.
3. Взаимное расположение векторов ,
и
для положительного заряда
показано на рис. 1.
Рис. 1. Сила Лоренца
Направление силы Лоренца определяется в данном случае по одному из двух альтернативных правил.
Правило часовой стрелки. Сила Лоренца направлена туда, глядя откуда кратчайший поворот вектора скорости частицы v к вектору магнитной индукции B виден против часовой стрелки.
Правило левой руки . Располагаем левую руку так, чтобы четыре пальца указывали направление скорости частицы, а линии поля входили в ладонь. Тогда оттопыренный большой палец укажет направление силы Лоренца.
Для отрицательного заряда направление силы Лоренца меняется на противоположное.
Всё вышеперечисленное является обобщением опытных фактов. Формула (1) позволяет связать размерность индукции магнитного поля с размерностями других физических величин:
Сила Ампера
Если металлический проводник с током поместить в магнитное поле, то на этот проводник со стороны магнитного поля будет действовать сила, которая называется силой Ампера.
Происхождение силы Ампера легко понять. Ведь ток в металле является направленным движением электронов, а на каждый электрон действует сила Лоренца. Все эти силы Лоренца, действующие на свободные электроны, имеют одинаковое направление и одинаковую величину; они складываются друг с другом и дают результирующую силу Ампера.
Направление силы Ампера определяется по тем же двум правилам, сформулированным выше.
Правило часовой стрелки . Сила Ампера направлена туда, глядя откуда кратчайший поворот тока к полю виден против часовой стрелки .
Правило левой руки . Располагаем левую руку так, чтобы четыре пальца указывали направление тока, а линии поля входили в ладонь. Тогда оттопыренный большой палец укажет направление силы Ампера .
Взаимное расположение тока, поля и силы Ампера указано на рис. 2.
Рис. 2. Сила Ампера
На этом рисунке проводник имеет длину , а угол между направлениями тока и поля равен
. Мы сейчас выведем выражение для абсолютной величины силы Ампера.
На каждый свободный электрон действует сила Лоренца:
где — скорость направленного движения свободных электронов в проводнике.
Пусть — число свободных электронов в данном проводнике,
— их концентрация (число в единице объёма). Тогда:
где — объём проводника,
— площадь его поперечного сечения. Получаем:
Мы не случайно выделили скобками четыре сомножителя. Ведь это есть не что иное, как сила тока: (вспомните выражение силы тока через скорость направленного движения свободных зарядов!). В результате приходим к окончательной формуле для силы Ампера:
(2)
Хорошую возможность поупражняться в нахождении направлений магнитного поля и силы Ампера даёт взаимодействие параллельных токов. Оказывается, два параллельных провода отталкиваются, если направления токов в них противоположны, и притягиваются, если направления токов совпадают (рис. 3).
Рис. 3. Взаимодействие параллельных токов
Обязательно убедитесь в этом самостоятельно! Делаем так. Сначала берём произвольную точку на первом проводе и определяем направление магнитного поля, создаваемого в этой точке вторым проводом (правило вам известно — см. предыдущий листок>). Ну а затем находим направление силы Ампера, действующей на первый провод со стороны магнитного поля второго провода.
Рамка с током в магнитном поле
В листках по термодинамике мы говорили о важности циклически работающих машин: они снабжают нас энергией. Понимание законов термодинамики позволило сконструировать тепловые двигатели, которые исправно служат нам и по сей день.
Понимание же законов электромагнетизма дало возможность создать циклическую машину другого типа — электродвигатель.
Мы рассмотрим один из элементов электродвигателя — рамку с током в магнитном поле. Разобравшись в её поведении, мы сможем уловить основную идею функционирования электродвигателя.
Пусть прямоугольная рамка может вращаться вокруг горизонтальной оси (рис. 4, слева). Рамка находится в вертикальном однородном магнитном поле
. Ток течёт по рамке в направлении
; это направление показано соответствующими стрелками.
Рис. 4. Рамка с током в магнитном поле
Вектор называется вектором нормали; он перпендикулярен плоскости рамки и направлен туда, глядя откуда ток кажется циркулирующим против часовой стрелки. (Иными словами, вектор
сонаправлен с вектором индукции магнитного поля, которое создаётся током в рамке.) Поворот рамки измеряется углом
между векторами
и
.
Теперь определим направления сил Ампера, которые действуют на рамку со стороны магнитного поля. Эти силы расставлены на рисунке; вот вам ещё одно упражнение на правило часовой стрелки (левой руки) — обязательно проверьте правильность указанных направлений!
Силы и
, приложенные к сторонам
и
, действуют вдоль оси вращения. Они лишь растягивают рамку и не вызывают её вращение.
Куда более интересны силы и
, приложеные соответственно к сторонам
и
. Они лежат в горизонтальной плоскости и перпендикулярны оси вращения. Эти силы вращают рамку в направлении по часовой стрелке, если смотреть справа (рис. 4, правая часть). Вычислим момент этой пары сил относительно оси
вращения рамки.
Пусть длина стороны равна
. Тогда
Пусть длина стороны равна
. Плечо
силы
, как видно из рис. 4 (справа) равно:
Таким же будет плечо силы . Отсюда получаем момент сил, вращающий рамку:
Теперь заметим, что — площадь рамки. Окончательно имеем:
(3)
В этой формуле площадь служит единственной геометрической характеристикой рамки.Это наводит на мысль, что только площадь рамки и существенна в выражении для вращающего момента. И действительно, можно доказать (разбивая рамку на бесконечно узкие полоски, неотличимые от прямоугольников), что формула (3) справедлива для рамки любой формы с площадью .
Как видно из формулы (3), максимальный вращающий момент равен:
Эта максимальная величина момента достигается при , то есть когда плоскость рамки параллельна магнитному полю.
Вращающий момент становится равным нулю при и
. Оба этих положения по-своему интересны.
При плоскость рамки перпендикулярна полю, а векторы
и
направлены в разные стороны. Данное положение является положением неустойчивого равновенсия: стоит хоть немного шевельнуть рамку, как силы Ампера начнут её вращать в том же направлении, поворачивая вектор
к вектору
(убедитесь!).
При плоскость рамки также перпендикулярна полю, а векторы
и
сонаправлены. Это — положение устойчивого равновенсия: при отклонении рамки возникает вращающий момент, стремящийся вернуть рамку назад (убедитесь!). Начнутся колебания рамки, постепенно затухающие из-за трения. В конце концов рамка остановится в положении
; в этом положении вектор индукции магнитного поля рамки сонаправлен с вектором
индукции внешнего магнитного поля (вот почему при намагничивании вещества элементарные токи ориентируются так, что их поля направлены в сторону внешнего магнитного поля). Полезное сопоставление: рамка занимает такое положение, что её положительная нормаль ориентируется в том же направлении, что и северный конец стрелки компаса, помещённой в это магнитное поле.
Таким образом, поведение рамки в магнитном поле становится ясным: если отклонить рамку от положения устойчивого равновесия и отпустить, то рамка будет совершать колебания. С точки зрения совершения механической работы это не очень хорошо: если намотать нить на ось вращения и подвесить к нити груз, то груз будет то подниматься, то опускаться.
Но вот если исхитриться и заставить ток менять направление в нужные моменты, то вместо колебаний рамки начнётся её непрерывное вращение и, соответственно, непрерывный подъём подвешенного груза. Тогда-то и получится полноценный электродвигатель; идея с переменой направления тока реализуется с помощью коллектора и щёток.
Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Магнитное поле. Силы» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена:
08.03.2023
Тема 13.
Магнитное поле. Электромагнитная индукция
13
.
01
Сила Ампера. Сила Лоренца
Вспоминай формулы по каждой теме
Решай новые задачи каждый день
Вдумчиво разбирай решения
ШКОЛКОВО.
Готовиться с нами — ЛЕГКО!
Подтемы раздела
магнитное поле. электромагнитная индукция
13.01Сила Ампера. Сила Лоренца
13.02Поток вектора магнитной индукции
13.03Электромагнитная индукция
13.04Явление самоиндукции. Катушка индуктивности
Решаем задачи
Показать ответ и решение
Две частицы с Сила Лоренца:
где – модуль вектора магнитной индукции,
– скорость заряда,
– заряд,
– угол между вектором магнитного поля и
скоростью движения частицы.
Тогда
Показать ответ и решение
Заряды, движущиеся перпендикулярно силовым линиям магнитного поля, движутся равномерно по окружности
Сила Лоренца:
где – модуль вектора магнитной индукции,
– скорость заряда,
– заряд,
– угол между вектором магнитного поля и
скоростью движения частицы. Второй закон Ньютона:
Распишем центростремительное ускорение, как
Выразим радиус вращения
Заменим на импульс:
Показать ответ и решение
Заряды, движущиеся перпендикулярно силовым линиям магнитного поля, движутся равномерно по окружности
Сила Лоренца:
где – модуль вектора магнитной индукции,
– скорость заряда,
– заряд,
– угол между вектором магнитного поля и
скоростью движения частицы. Второй закон Ньютона:
Распишем центростремительное ускорение, как
Выразим радиус вращения
Найдите ускорение (в ) протона, который движется со скоростью 2 м/с в магнитном поле с индукцией 3 мТл
перпендикулярно линиям поля. Отношение заряда протона к его массе Кл/кг.
Показать ответ и решение
Заряды, движущиеся перпендикулярно силовым линиям магнитного поля, движутся равномерно по окружности
Сила Лоренца:
где – модуль вектора магнитной индукции,
– скорость заряда,
– заряд,
– угол между вектором магнитного поля и
скоростью движения частицы. Второй закон Ньютона:
В однородное магнитное поле перпендикулярно линиям индукции влетают протон и альфа-частица. Во
сколько раз скорость альфа-частицы больше скорости протона, если сила, действующая
со стороны магнитного поля на альфа-частицу, в 8 раз больше, чем сила, действующая на
протон?
Показать ответ и решение
Альфа-частица – это ядро гелия, оно состоит из 2 протонов и 2 нейтронов, поэтому заряд альфа-частицы в 2 раза больше заряда
протона.
Сила Лоренца:
где – модуль вектора магнитной индукции,
– скорость заряда,
– заряд,
– угол между вектором магнитного поля и
скоростью движения частицы. Из формулы силы Лоренца можно сделать вывод, что скорость альфа-частицы в 4 раза больше
скорости протона.
Во сколько раз электрическая сила, действующая на электрон, больше магнитной силы,
если напряженность электрического поля 1,5 кВ/м, а индукция магнитного поля 0,1 Тл?
Скорость электрона равна 200 м/с и направлена перпендикулярно линиям индукции магнитного
поля.
Показать ответ и решение
Электрическая сила:
где – заряд,
– напряженность
Сила Лоренца:
где – модуль вектора магнитной индукции,
– скорость заряда,
– заряд,
– угол между вектором
магнитного поля и скоростью движения частицы, следовательно, отношение электрической силы к силе Лоренца
равно
С какой силой взаимодействуют два параллельных провода с токами силой 300 А, если длина проводов
50 м и каждый из них создает в месте расположения другого провода магнитное поле с индукцией 1,2
мТл?
Показать ответ и решение
Сила Ампера:
где – модуль вектора магнитной индукции,
– сила тока,
– длина проводника,
– угол между вектором магнитного
поля и направлением тока в проводнике.
Прямой проводник с током помещен в однородное магнитное поле перпендикулярно линиям индукции.
Во сколько раз уменьшится сила, действующая на проводник со стороны магнитного поля, если его
повернуть так, чтобы направление тока в проводнике составляло угол с вектором индукции
поля?
Показать ответ и решение
Сила Ампера:
где – модуль вектора магнитной индукции,
– сила тока,
– длина проводника,
– угол между вектором магнитного
поля и направлением тока в проводнике.
В первом случае , во втором
, а значит отношение сил для первого и второго случаев
На проводник длиной 0,5 м с током силой 20 А в однородном магнитном поле с индукцией 0,1 Тл
действует сила 0,5 Н. Какой угол (в градусах) составляет направление тока в проводнике с вектором
магнитной индукции?
Показать ответ и решение
Сила Ампера:
где – модуль вектора магнитной индукции,
– сила тока,
– длина проводника,
– угол между вектором магнитного
поля и направлением тока в проводнике. Отсюда синус угла
а значит угол
Заряженная частица движется по окружности в однородном магнитном поле. Во сколько увеличится
частота обращения частицы, если уменьшить ее кинетическую энергию в 2 раза?
Показать ответ и решение
Для частицы в магнитном поле справедливо следующее:
где – сила Лоренца ,
– масса частицы,
– центростремительное ускорение. Подставим вместо силы Лоренца
, а
вместо центростремительного ускорения
Формула для нахождения периода:
Получаем, что период вращения не зависит от скорости частицы, а значит, не зависит от кинетической энергии
частицы. Так как период и частота вращения обратно пропорциональные величины, значит, частота вращения не
изменится.
Электрон влетает в однородное магнитное поле с индукцией 5 Тл со скоростью 1 км/с, направленной под некоторым углом к
силовым линиям магнитного поля. Найдите максимально возможное значение модуля силы Лоренца, действующей на электрон.
Ответ дайте в Н, умножив на
Показать ответ и решение
Сила Лоренца:
где – модуль вектора магнитной индукции,
– скорость заряда,
– заряд,
– угол между вектором магнитного поля и
скоростью движения частицы. Максимальное силы Лоренца значение при угле .
Прямолинейный проводник длиной 0,5 м, по которому течет ток 6 А, находится в однородном магнитном поле. Модуль вектора
магнитной индукции 0,2 Тл, проводник расположен под углом к вектору В. Какова сила, действующая на проводник со
стороны магнитного поля? (Ответ дать в ньютонах.)
Показать ответ и решение
Сила Ампера:
где – модуль вектора магнитной индукции,
– сила тока,
– длина проводника,
– угол между вектором магнитного
поля и направлением тока в проводнике.
Показать ответ и решение
Сила Ампера:
где – модуль вектора магнитной индукции,
– сила тока,
– длина проводника,
– угол между вектором магнитного
поля и направлением тока в проводнике. Увеличивая длину проводника в 2 раза и уменьшая силу тока в 4 раза, сила Ампера
уменьшится в 2 раза.
15. Магнитное поле. Оптика
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Сила Ампера и сила Лоренца
Прямолинейный проводник длиной (L) с током (I) помещен в однородное магнитное поле перпендикулярно линиям индукции (B). Во сколько раз уменьшится сила Ампера, действующая на проводник, если его длину увеличить в 2 раза, а силу тока в проводнике уменьшить в 4 раза?
Сила Ампера: [F_a=BIlsinalpha,] где (B) – модуль вектора магнитной индукции, (I) – сила тока, (l) – длина проводника, (alpha) – угол между вектором магнитного поля и направлением тока в проводнике. Увеличивая длину проводника в 2 раза и уменьшая силу тока в 4 раза, сила Ампера уменьшится в 2 раза.
Ответ: 2
Прямолинейный проводник длиной 0,5 м, по которому течет ток 6 А, находится в однородном магнитном поле. Модуль вектора магнитной индукции 0,2 Тл, проводник расположен под углом (30^{circ}) к вектору В. Какова сила, действующая на проводник со стороны магнитного поля? (Ответ дать в ньютонах.)
Сила Ампера: [F_a=BILsinalpha,] где (B) – модуль вектора магнитной индукции, (I) – сила тока, (l) – длина проводника, (alpha) – угол между вектором магнитного поля и направлением тока в проводнике. [F_a=0,2text{ Тл}cdot0,5text{ м}cdot6text{ А}cdotfrac{1}{2}=0,3text{ Н}]
Ответ: 0,3
Электрон влетает в однородное магнитное поле с индукцией 5 Тл, направленной под некоторым углом к силовым линиям магнитного поля, со скоростью 1 км/с. Найдите максимально возможное значение модуля силы Лоренца, действующей на электрон. Ответ дайте в Н, умноженных на (10^{16})
Сила Лоренца: [F_l=Bvqsinalpha,] где (B) – модуль вектора магнитной индукции, (v) – скорость заряда, (q) – заряд, (alpha) – угол между вектором магнитного поля и скоростью движения частицы. Максимальное силы Лоренца значение при угле (alpha=dfrac{pi}{2}). [F_{lmin}=Bvqsinalpha=0] [F_{lmax}=Bvqsinalpha=5text{ Тл}cdot10^3text{ м/с}cdot1,6cdot10^{-19}text{ Кл}=8cdot10^{-16} text{ Н}]
Ответ: 8
Заряженная частица движется по окружности в однородном магнитном поле. Во сколько увеличится частота обращения частицы, если уменьшить ее кинетическую энергию в 2 раза?
Для частицы в магнитном поле справедливо следующее: [F_l=ma_{text{ цс}},] где (F_l) – сила Лоренца , (m) – масса частицы, (a_{text{ цс}}) – центростремительное ускорение. Подставим вместо силы Лоренца (Bvq), а вместо центростремительного ускорения (dfrac{v^2}{R}) [Bvq=frac{mv^2}{R}] [Bq=frac{mv}{R}] Формула для нахождения периода: [T=frac{2pi R}{v}] [frac{v}{R}=frac{2pi}{T}] [Bq=frac{2pi m}{T}] [T=frac{2pi m}{Bq}] Получаем, что период вращения не зависит от скорости частицы, а значит, не зависит от кинетической энергии частицы. Так как период и частота вращения обратно пропорциональные величины, значит, частота вращения не изменится.
Ответ: 1
На проводник длиной 0,5 м с током силой 20 А в однородном магнитном поле с индукцией 0,1 Тл действует сила 0,5 Н. Какой угол (в градусах) составляет направление тока в проводнике с вектором магнитной индукции?
Сила Ампера: [F_A=BIlsinalpha,] где (B) – модуль вектора магнитной индукции, (I) – сила тока, (l) – длина проводника, (alpha) – угол между вектором магнитного поля и направлением тока в проводнике. Отсюда синус угла (alpha) [sinalpha=frac{F_a}{BIl}=frac{0,5text{ м}}{0,1text{ Тл}cdot20text{ А}cdot0,5text{ Н}}=frac{1}{2},] а значит угол (alpha) [alpha=30^{circ}]
Ответ: 30
Прямой проводник с током помещен в однородное магнитное поле перпендикулярно линиям индукции. Во сколько раз уменьшится сила, действующая на проводник со стороны магнитного поля, если его повернуть так, чтобы направление тока в проводнике составляло угол (30^{circ}) с вектором индукции поля?
Сила Ампера: [F_A=BIlsinalpha,] где (B) – модуль вектора магнитной индукции, (I) – сила тока, (l) – длина проводника, (alpha) – угол между вектором магнитного поля и направлением тока в проводнике.
В первом случае (alpha_1=90^{circ}), во втором (alpha_2=30^{circ}), а значит отношение сил для первого и второго случаев [frac{F_{a1}}{F_{a2}}=frac{BILsinalpha_1}{BILsinalpha_2}=frac{sinalpha_1}{sinalpha_2}=frac{1}{0,5}=2]
Ответ: 2
С какой силой взаимодействуют два параллельных провода с токами силой 300 А, если длина проводов 50 м и каждый из них создает в месте расположения другого провода магнитное поле с индукцией 1,2 мТл?
Сила Ампера: [F_A=BIlsinalpha,] где (B) – модуль вектора магнитной индукции, (I) – сила тока, (l) – длина проводника, (alpha) – угол между вектором магнитного поля и направлением тока в проводнике. [F_A=1,2cdot10^{-3}text{ Тл}cdot300text{ А}cdot50text{ м}=18 text{ Н}]
Ответ: 18

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Магнитное поле. Взаимодействие магнитов
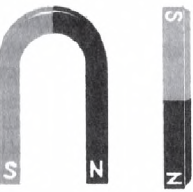
Явление взаимодействия постоянных магнитов (установление магнитной стрелки вдоль магнитного меридиана Земли, притяжение разноименных полюсов, отталкивание одноименных) известно с древних времен и систематически исследовано У. Гильбертом (результаты опубликованы в 1600 г. в его трактате «О магните, магнитных телах и о большом магните — Земле»).
Природные (естественные) магниты
Магнитные свойства некоторых природных минералов были известны уже в древности. Так, имеются письменные свидетельства более чем 2000-летней давности об использовании в Китае естественных постоянных магнитов в качестве компасов. О притяжении и отталкивании магнитов и намагничивании ими железных опилок упоминается в трудах древнегреческих и римских ученых (например, в поэме «О природе вещей» Лукреция Кара).
Природные магниты представляют собой куски магнитного железняка (магнетита), состоящего из $FeO$ (31 %) и $Fe_2O$ (69 %). Если такой кусок минерала поднести к мелким железным предметам — гвоздям, опилкам, тонкому лезвию и т. д., они к нему притянутся.
Искусственные постоянные магниты
Постоянный магнит — это изделие из материала, являющегося автономным (самостоятельным, изолированным) источником постоянного магнитного поля.
Искусственные постоянные магниты изготавливают из специальных сплавов, в которые входят железо, никель, кобальт и др. Эти металлы приобретают магнитные свойства (намагничиваются), если их поднести к постоянным магнитам. Поэтому, чтобы изготовить из них постоянные магниты, их специально держат в сильных магнитных полях, после чего они сами становятся источниками постоянного магнитного поля и способны длительное время сохранять магнитные свойства.
На рисунке изображены дугообразный и полосовой магниты.
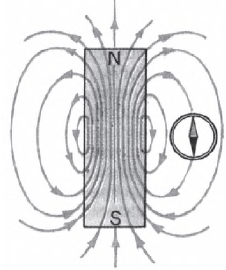
На рис. даны картины магнитных полей этих магнитов, полученных методом, который впервые применил в своих исследованиях М. Фарадей: с помощью железных опилок, рассыпанных на листе бумаги, на котором лежит магнит. У каждого магнита есть два полюса — это места наибольшего сгущения магнитных силовых линий (их называют также линиями магнитного поля, или линиями магнитной индукции поля). Это места, к которым сильнее всего притягиваются железные опилки. Один из полюсов принято называть северным (($N$), другой — южным ($S$). Если поднести два магнита друг к другу одноименными полюсами, можно увидеть, что они отталкиваются, а если разноименными — притягиваются.
На рис. наглядно видно, что магнитные линии магнита — замкнутые линии. Показаны силовые линии магнитного поля двух магнитов, обращенных друг к другу одноименными и разноименными полюсами. Центральная часть этих картин напоминает картины электрических полей двух зарядов (разноименных и одноименных). Однако существенным различием электрического и магнитного полей является то, что линии электрического поля начинаются на зарядах и заканчиваются на них. Магнитных же зарядов в природе не существует. Линии магнитного поля выходят из северного полюса магнита и входят в южный, они продолжаются и в теле магнита, т. е., как было сказано выше, являются замкнутыми линиями. Поля, силовые линии которых замкнуты, называются вихревыми. Магнитное поле — это вихревое поле (в этом его отличие от электрического).
Применение магнитов
Самым древним магнитным прибором является всем хорошо известный компас. В современной технике магниты используются очень широко: в электродвигателях, в радиотехнике, в электроизмерительной аппаратуре и т. д.
Магнитное поле Земли
Земной шар является магнитом. Как у всякого магнита, у него есть свое магнитное поле и свои магнитные полюсы. Именно поэтому стрелка компаса ориентируется в определенном направлении. Понятно, куда именно должен указывать северный полюс магнитной стрелки, ведь притягиваются разноименные полюсы. Поэтому северный полюс магнитной стрелки указывает на южный магнитный полюс Земли. Этот полюс находится на севере земного шара, несколько в стороне от северного географического полюса (на острове Принца Уэльского — около $75°$ северной широты и $99°$ западной долготы, на расстоянии примерно $2100$ км от северного географического полюса).
При приближении к северному географическому полюсу силовые линии магнитного поля Земли все под большим углом наклоняются к горизонту, и в области южного магнитного полюса становятся вертикальными.
Северный магнитный полюс Земли находится вблизи южного географического полюса, а именно на $66.5°$ южной широты и $140°$ восточной долготы. Здесь силовые линии магнитного поля выходят из Земли.
Другими словами, магнитные полюсы Земли не совпадают с ее географическими полюсами. Поэтому направление магнитной стрелки не совпадает с направлением географического меридиана, и магнитная стрелка компаса лишь приблизительно показывает направление на север.
На стрелку компаса могут влиять также некоторые природные явления, например, магнитные бури, которые являются временными изменениями магнитного поля Земли, связанными с солнечной активностью. Солнечная активность сопровождается выбросом с поверхности Солнца потоков заряженных частиц, в частности, электронов и протонов. Эти потоки, движущиеся с большой скоростью, создают свое магнитное поле, взаимодействующее с магнитным полем Земли.
На земном шаре (кроме кратковременных изменений магнитного поля) встречаются области, в которых наблюдается постоянное отклонение направления магнитной стрелки от направления магнитной линии Земли. Это области магнитной аномалии (от греч. anomalia — отклонение, ненормальность). Одной из самых больших таких областей является Курская магнитная аномалия. Причиной аномалий являются огромные залежи железной руды на сравнительно небольшой глубине.
Земное магнитное поле надежно защищает поверхность Земли от космического излучения, действие которого на живые организмы разрушительно.
Полеты межпланетных космических станций и кораблей позволили установить, что у Луны и планеты Венера отсутствует магнитное поле, а у планеты Марс оно очень слабое.
Опыты Эрстедаи Ампера. Индукция магнитного поля
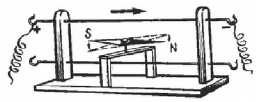
В 1820 г. датский ученый Г. X. Эрстед обнаружил, что магнитная стрелка, помещенная вблизи проводника, по которому течет ток, поворачивается, стремясь расположиться перпендикулярно к проводнику.
Схема опыта Г. X. Эрстеда изображена на рисунке. Проводник, включенный в цепь источника тока, расположен над магнитной стрелкой параллельно ее оси. При замыкании цепи магнитная стрелка отклоняется от своего первоначального положения. При размыкании цепи магнитная стрелка возвращается в свое первоначальное положение. Отсюда следует, что проводник с током и магнитная стрелка взаимодействуют друг с другом. На основании этого опыта можно сделать вывод о существовании магнитного поля, связанного с протеканием тока в проводнике и о вихревом характере этого поля. Описанный опыт и его результаты явились важнейшей научной заслугой Эрстеда.
В том же году французский физик Ампер, которого заинтересовали опыты Эрстеда, обнаружил взаимодействие двух прямолинейных проводников с током. Оказалось, что если токи в проводниках текут в одну сторону, т. е. параллельны, то проводники притягиваются, если в противоположные стороны (т. е. антипараллельны), то отталкиваются.
Взаимодействия между проводниками с током, т. е. взаимодействия между движущимися электрическими зарядами, называют магнитными, а силы, с которыми проводники с током действуют друг на друга, — магнитными силами.
Согласно теории близкодействия, которой придерживался М. Фарадей, ток в одном из проводников не может непосредственно влиять на ток в другом проводнике. Аналогично случаю с неподвижными электрическими зарядами, вокруг которых существует электрическое поле, был сделан вывод, что в пространстве, окружающем токи, существует магнитное поле, которое действует с некоторой силой на другой проводник с током, помещенный в это поле, либо на постоянный магнит. В свою очередь, магнитное поле, создаваемое вторым проводником с током, действует на ток в первом проводнике.
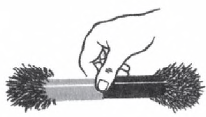
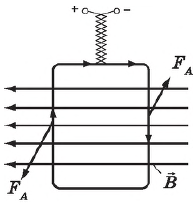
Подобно тому как электрическое поле обнаруживается по его воздействию на пробный заряд, внесенный в это поле, магнитное поле можно обнаружить по ориентирующему действию магнитного поля на рамку с током малых (по сравнению с расстояниями, на которых магнитное поле заметно меняется) размеров.
Провода, подводящие ток к рамке, следует сплести (или расположить близко друг к другу), тогда результирующая сила, действующая со стороны магнитного поля на эти провода, будет равна нулю. Силы же, действующие на такую рамку с током, будут ее поворачивать, так что ее плоскость установится перпендикулярно линиям индукции магнитного поля. В примере, рамка повернется так, чтобы проводник с током оказался в плоскости рамки. При изменении направления тока в проводнике рамка повернется на $180°$. В поле между полюсами постоянного магнита рамка повернется плоскостью перпендикулярно магнитным силовым линиям магнита.
Магнитная индукция
Магнитная индукция ($В↖{→}$) — это векторная физическая величина, характеризующая магнитное поле.
За направление вектора магнитной индукции $В↖{→}$ принимается:
1) направление от южного полюса $S$ к северному полюсу $N$ магнитной стрелки, свободно устанавливающейся в магнитном поле, или
2) направление положительной нормали к замкнутому контуру с током на гибком подвесе, свободно устанавливающемся в магнитном поле. Положительной считается нормаль, направленная в сторону перемещения острия буравчика (с правой нарезкой), рукоятку которого вращают по направлению тока в рамке.
Ясно, что направления 1) и 2) совпадают, что было установлено еще опытами Ампера.
Что касается величины магнитной индукции (т. е. ее модуля) $В$, которая могла бы характеризовать силу действия поля, то экспериментами было установлено, что максимальная сила $F$, с которой поле действует на проводник с током (помещенный перпендикулярно линиям индукции магнитного поля), зависит от силы тока $I$ в проводнике и от его длины $∆l$ (пропорциональна им). Однако сила, действующая на элемент тока (единичной длины и силы тока), зависит только от самого поля, т. е. отношение ${F}/{I∆l}$ для данного поля является величиной постоянной (аналогично отношению силы к заряду для электрического поля). Эту величину и определяют как магнитную индукцию.
$B={F}/{I∆l}$
Индукция магнитного поля в данной точке равна отношению максимальной силы, действующей на проводник с током, к длине проводника и силе тока в проводнике, помещенном в эту точку.
Чем больше магнитная индукция в данной точке поля, тем с большей силой будет действовать поле в этой точке на магнитную стрелку или движущийся электрический заряд.
Единицей магнитной индукции в СИ является тесла (Тл), названная в честь сербского электротехника Николы Теслы. Как видно из формулы, $1$ Тл $=l{H}/{A·м}$
Если имеется несколько различных источников магнитного поля, векторы индукции которых в данной точке пространства равны ${В_1}↖{→}, {В_2}↖{→}, {В_3}↖{→},…$, то, согласно принципу суперпозиции полей, индукция магнитного поля в этой точке равна сумме векторов индукции магнитных полей, создаваемых каждым источником.
$В↖{→}={В_1}↖{→}+{В_2}↖{→}+{В_3}↖{→}+…$
Линии магнитной индукции
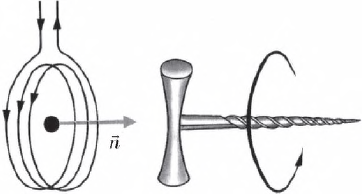
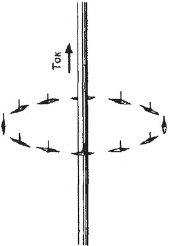
Для наглядного представления магнитного поля М. Фарадей ввел понятие магнитных силовых линий, которые он неоднократно демонстрировал в своих опытах. Картина силовых линий легко может быть получена с помощью железных стружек, насыпанных на картон. На рисунке представлены: линии магнитной индукции прямого тока, соленоида, кругового тока, прямого магнита.
Линиями магнитной индукции, или магнитными силовыми линиями, или просто магнитными линиями называют линии, касательные к которым в любой точке совпадают с направлением вектора магнитной индукции $В↖{→}$ в этой точке поля.
Если вместо железных опилок вокруг длинного прямолинейного проводника с током поместить маленькие магнитные стрелки, то можно увидеть не только конфигурацию силовых линий (концентрические окружности), но и направление силовых линий (северный полюс магнитной стрелки указывает направление вектора индукции в данной точке).
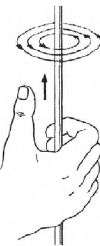
Направление магнитного поля прямого тока можно определить по правилу правого буравчика.
Если вращать рукоятку буравчика так, чтобы поступательное движение острия буравчика указывало направление тока, то направление вращения рукоятки буравчика укажет направление силовых линий магнитного поля тока.
Направление магнитного поля прямого тока можно определять также и с помощью первого правила правой руки.
Если охватить проводник правой рукой, направив отогнутый большой палец по направлению тока, то кончики остальных пальцев в каждой точке покажут направление вектора индукции в этой точке.
Вихревое поле
Линии магнитной индукции являются замкнутыми, это свидетельствует о том, что в природе нет магнитных зарядов. Поля, силовые линии которых замкнуты, называют вихревыми полями. То есть магнитное поле — это вихревое поле. Этим оно отличается от электрического поля, создаваемого зарядами.
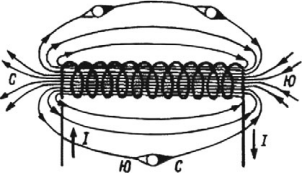
Соленоид
Соленоид — это проволочная спираль с током.
Соленоид характеризуется числом витков на единицу длины $n$, длиной $l$ и диаметром $d$. Толщина провода в соленоиде и шаг спирали (винтовой линии) малы по сравнению с его диаметром $d$ и длиной $l$. Термин «соленоид» применяют и в более широком значении — так называют катушки с произвольным сечением (квадратный соленоид, прямоугольный соленоид), и не обязательно цилиндрической формы (тороидальный соленоид). Различают длинный соленоид ($l>>d$) и короткий ($l << d$). В тех случаях, когда соотношение между $d$ и $l$ специально не оговаривается, подразумевается длинный соленоид.
Соленоид был изобретен в 1820 г. А. Ампером для усиления открытого X. Эрстедом магнитного действия тока и применен Д. Араго в опытах по намагничиванию стальных стержней. Магнитные свойства соленоида были экспериментально изучены Ампером в 1822 г. (тогда же им был введен термин «соленоид»). Была установлена эквивалентность соленоида постоянным природным магнитам, что явилось подтверждением электродинамической теории Ампера, которая объясняла магнетизм взаимодействием скрытых в телах кольцевых молекулярных токов.
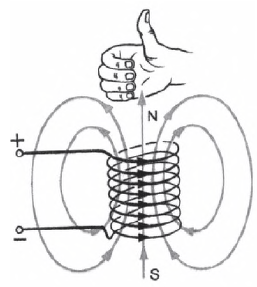
Силовые линии магнитного поля соленоида изображены на риcунке. Направление этих линий определяют с помощью второго правила правой руки.
Если обхватить соленоид ладонью правой руки, направив четыре пальца по току в витках, то отставленный большой палец укажет направление магнитных линий внутри соленоида.
Сравнив магнитное поле соленоида с полем постоянного магнита, можно заметить, что они очень похожи. Как и у магнита, у соленоида есть два полюса — северный ($N$) и южный ($S$). Северным полюсом называют тот, из которого магнитные линии выходят; южным полюсом — тот, в который они входят. Северный полюс у соленоида всегда располагается с той стороны, на которую указывает большой палец ладони при ее расположении в соответствии со вторым правилом правой руки.
Соленоид в виде катушки с большим числом витков используют в качестве магнита.
Исследования магнитного поля соленоида показывают, что магнитное действие соленоида увеличивается с увеличением силы тока и числа витков в соленоиде. Кроме того, магнитное действие соленоида или катушки с током усиливается при введении в него железного стержня, который называют сердечником.
Электромагниты
Соленоид с железным сердечником внутри называется электромагнитом.
Электромагниты могут содержать не одну, а несколько катушек (обмоток) и иметь при этом разные по форме сердечники.
Подобный электромагнит впервые был сконструирован английским изобретателем У. Стердженом в 1825 г. При массе $0.2$ кг электромагнит У. Стерджена удерживал груз весом $36$ Н. В том же году Дж. Джоуль увеличил подъемную силу электромагнита до $200$ Н, а через шесть лет американский ученый Дж. Генри построил электромагнит массой $300$ кг, способный удерживать груз массой $1$ т!
Современные электромагниты могут поднимать грузы массой несколько десятков тонн. Они используются на заводах при перемещении тяжелых изделий из чугуна и стали. Электромагниты используются также в сельском хозяйстве для очистки зерен ряда растений от сорняков и в других отраслях промышленности.
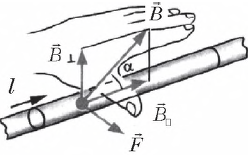
Сила Ампера
На прямолинейный участок проводника $∆l$, по которому течет ток $I$, в магнитном поле с индукцией $В$ действует сила $F$.
Для вычисления этой силы используют выражение:
$F=B|I|∆lsinα$
где $α$ — угол между вектором $B↖{→}$ и направлением отрезка проводника с током (элементом тока); за направление элемента тока принимают направление, в котором по проводнику течет ток. Сила $F$ называется силой Ампера в честь французского физика А. М. Ампера, который первым обнаружил действие магнитного поля на проводник с током. (На самом деле Ампер установил закон для силы взаимодействия между двумя элементами проводников с током. Он был сторонником теории дальнодействия и не пользовался понятием поля.
Однако по традиции и в память о заслугах ученого выражение для силы, действующей на проводник с током со стороны магнитного поля, также называют законом Ампера.)
Направление силы Ампера определяется с помощью правила левой руки.
Если расположить ладонь левой руки так, чтобы силовые линии магнитного поля входили в нее перпендикулярно, а четыре вытянутых пальца указывали направление тока в проводнике, то отставленный большой палец укажет направление силы, действующей на проводник с током. Таким образом, сила Ампера всегда перпендикулярна как вектору индукции магнитного поля, так и направлению тока в проводнике, т. е. перпендикулярна плоскости, в которой лежат эти два вектора.
Следствием действия силы Ампера является вращение рамки с током в постоянном магнитном поле. Это находит практическое применение во многих устройствах, например, в электроизмерительных приборах — гальванометрах, амперметрах, где подвижная рамка с током вращается в поле постоянного магнита и по углу отклонения стрелки, неподвижно связанной с рамкой, можно судить о величине тока, протекающего в цепи.
Благодаря вращающему действию магнитного поля на рамку с током возможным стало также создание и использование электродвигателей — машин, в которых электрическая энергия превращается в механическую.
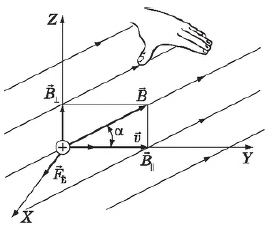
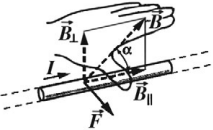
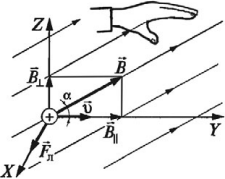
Сила Лоренца
Сила Лоренца — это сила, действующая на движущийся точечный электрический заряд во внешнем магнитном поле.
Нидерландский физик X. А. Лоренц в конце XIX в. установил, что сила, действующая со стороны магнитного поля на движущуюся заряженную частицу, всегда перпендикулярна направлению движения частицы и силовым линиям магнитного поля, в котором эта частица движется.
Направление силы Лоренца можно определить с помощью правила левой руки.
Если расположить ладонь левой руки так, чтобы четыре вытянутых пальца указывали направление движения заряда, а вектор магнитной индукции поля входил в ладонь, то отставленный большой палец укажет направление силы Лоренца, действующей на положительный заряд.
Если заряд частицы отрицательный, то сила Лоренца будет направлена в противоположную сторону.
Модуль силы Лоренца легко определяется из закона Ампера и составляет:
$F=|q|υBsinα$
где $q$ — заряд частицы, $υ$ — скорость ее движения, $α$ — угол между векторами скорости и индукции магнитного поля.
Если кроме магнитного поля есть еще и электрическое поле, которое действует на заряд с силой ${F_{эл}}↖{→}=qE↖{→}$, то полная сила, действующая на заряд, равна:
$F↖{→}={F_{эл}}↖{→}+{F_л}↖{→}$
Часто именно эту полную силу называют силой Лоренца, а силу, выраженную формулой $F=|q|υBsinα$, называют магнитной частью силы Лоренца.
Поскольку сила Лоренца перпендикулярна направлению движения частицы, она не может изменить ее скорость (она не совершает работы), а может изменить лишь направление ее движения, т. е. искривить траекторию.
Такое искривление траектории электронов в кинескопе телевизора легко наблюдать, если поднести к его экрану постоянный магнит: изображение исказится.
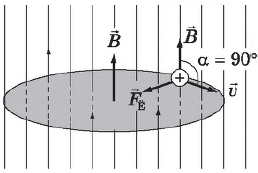
Движение заряженной частицы в однородном магнитном поле. Пусть заряженная частица влетает со скоростью $υ$ в однородное магнитное поле перпендикулярно линиям напряженности. Сила, действующая со стороны магнитного поля на частицу, заставит ее равномерно вращаться по окружности радиусом г, который легко найти, воспользовавшись вторым законом Ньютона, выражением для центростремительного ускорения и формулой $F=|q|υBsinα$:
${mυ^2}/{r}=|q|υB$
Отсюда получим
$r={mυ}/{|q|B}$
где $m$ — масса частицы.
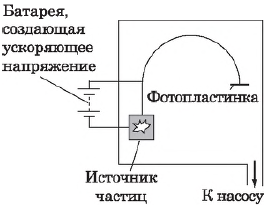
Применение силы Лоренца. Действие магнитного поля на движущиеся заряды применяется, например, в масс-спектрографах, позволяющих разделять заряженные частицы по их удельным зарядам, т. е. по отношению заряда частицы к ее массе, и по полученным результатам точно определять массы частиц.
Вакуумная камера прибора помещена в поле (вектор индукции $B↖{→}$ перпендикулярен рисунку). Ускоренные электрическим полем заряженные частицы (электроны или ионы), описав дугу, попадают на фотопластину, где оставляют след, позволяющий с большой точностью измерить радиус траектории $r$. По этому радиусу определяется удельный заряд иона. Зная заряд иона, легко вычислить его массу.
Магнитные свойства веществ
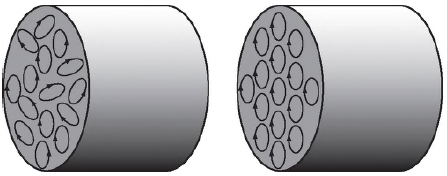
Для того, чтобы объяснить существование магнитного поля постоянных магнитов, Ампер предположил, что в веществе, обладающем магнитными свойствами, существуют микроскопические круговые токи (они были названы молекулярными). Идея эта впоследствии, после открытия электрона и строения атома, блестяще подтвердилась: эти токи создаются движением электронов вокруг ядра и, будучи ориентированы одинаково, в сумме создают поле вокруг и внутри магнита.
На рис. плоскости, в которых расположены элементарные электрические токи, ориентированы беспорядочно вследствие хаотического теплового движения атомов, и вещество не проявляет магнитных свойств. В намагниченном состоянии (под действием, например, внешнего магнитного поля) эти плоскости ориентированы одинаково, и их действия складываются.
Магнитная проницаемость. Реакция среды на воздействие внешнего магнитного поля с индукцией $В_0$ (поле в вакууме) определяется магнитной восприимчивостью $μ$:
$μ={B}/{B_0}$
где $В$ — индукция магнитного поля в веществе. Магнитная проницаемость аналогична диэлектрической проницаемости $ε$.
По своим магнитным свойствам вещества делятся на диамагнетики, парамагнетики и ферромагнетики. У диамагнетиков коэффициент $μ$, характеризующий магнитные свойства среды, меньше $1$ (например, у висмута $μ = 0.999824$); у парамагнетиков $μ > 1$ (у платины $μ = 1.00036$); у ферромагнетиков $μ >> 1$ (железо, никель, кобальт).
Диамагнетики отталкиваются от магнита, парамагнетики — притягиваются. По этим признакам их можно отличить друг от друга. У большинства веществ магнитная проницаемость практически не отличается от единицы, только у ферромагнетиков намного превосходит ее, достигая нескольких десятков тысяч единиц.
Ферромагнетики. Наиболее сильные магнитные свойства проявляют ферромагнетики. Магнитные поля, создаваемые ферромагнетиками, намного сильнее внешнего намагничивающего поля. Правда, магнитные поля ферромагнетиков создаются не вследствие обращения электронов вокруг ядер — орбитального магнитного момента, а вследствие собственного вращения электрона — собственного магнитного момента, называемого спином.
Температура Кюри ($Т_с$) — это температура, выше которой ферромагнитные материалы теряют свои магнитные свойства. Для каждого ферромагнетика она своя. Например, для железа $Т_с = 753°$С, для никеля $Т_с = 365°$С, для кобальта $Т_с = 1000°$ С. Существуют ферромагнитные сплавы, у которых $Т_с < 100°$ С.
Первые детальные исследования магнитных свойств ферромагнетиков были выполнены выдающимся русским физиком А. Г. Столетовым (1839-1896).
Применяются ферромагнетики очень широко: в качестве постоянных магнитов (в электроизмерительных приборах, громкоговорителях, телефонах и т. д.), стальных сердечников в трансформаторах, генераторах, электродвигателях (для усиления магнитного поля и экономии электроэнергии). На магнитных лентах, изготовленных из ферромагнетиков, осуществляется запись звука и изображения для магнитофонов и видеомагнитофонов. На тонкие магнитные пленки производится запись информации для запоминающих устройств в электронно-вычислительных машинах.
Сила Ампера, сила
Лоренца
1.

проводник длиной 0,2 м находится в однородном магнитном поле с
индукцией 4 Тл и расположен под углом к
вектору индукции. Чему равен модуль силы, действующей на проводник со
стороны магнитного поля при силе тока в нем 2 А?
1) 0,2 Н
2) 0,8 Н
3) 3,2 Н
4) 20 Н
2.
Прямолинейный
проводник длиной L с током I помещен в
однородное магнитное поле так, что направление вектора магнитной индукции B перпендикулярно
проводнику. Если силу тока уменьшить в 2 раза, а индукцию магнитного
поля увеличить в 4 раза, то действующая на проводник сила Ампера
1) увеличится в 2 раза
2) уменьшится в 4 раза
3) не изменится
4) уменьшится в 2 раза
3.

влетевший в зазор между полюсами электромагнита, имеет скорость , перпендикулярно
вектору индукции B магнитного поля, направленному
вертикально.Куда направлена действующая на протон сила Лоренца F?
1) от наблюдателя
2) к наблюдателю
3) горизонтально вправо
4) вертикально вниз
4.
Прямолинейный
проводник длиной L с током I помещен в
однородное магнитное поле перпендикулярно линиям индукции B.
Как изменится сила Ампера, действующая на проводник, если его длину
увеличить в 2 раза, а силу тока в проводнике уменьшить в 4 раза?
1)
не изменится
2)
уменьшится в 4 раза
3)
увеличится в 2 раза
4)
уменьшится в 2 раз
5.
. 
цепь, состоящая из четырех прямолинейных горизонтальных проводников
(1—2, 2—3, 3—4, 4—1) и источника постоянного тока, находится в однородном
магнитном поле. Вектор магнитной индукции В направлен горизонтально
вправо (см. рисунок, вид сверху). Куда направлена вызванная этим полем
сила Ампера, действующая на проводник 1—2?
1) горизонтально влево
2) горизонтально вправо
3) перпендикулярно плоскости рисунка вниз
4) перпендикулярно плоскости рисунка вверх
6.
Протон р влетает по
горизонтали со скоростью у в вертикальное магнитное поле индукцией В между
полюсами электромагнита (см. рисунок). Куда направлена действующая
на протон сила Лоренца Р.
1) вертикально вниз
2) вертикально вверх
3) горизонтально к нам
4) горизонтально от нас
7.
Прямолинейный
проводник длиной 0,5 м, по которому течет ток 6 А, находится
в однородном магнитном поле. Модуль вектора магнитной индукции
0,2 Тл, проводник расположен под углом к
вектору В. Сила, действующая на проводник со стороны магнитного
поля, равна
1) 0,075 Н
2) 0,3 Н
3) 0,6 Н
4) 120 Н
8.
Какое
явление наблюдалось в опыте Эрстеда?
1) взаимодействие двух параллельных проводников с током
2) взаимодействие двух магнитных стрелок
3) поворот магнитной стрелки вблизи проводника при пропускании
через него тока
4) возникновение электрического тока в катушке при вдвигании
в нее магнита
9. На участок
прямого проводника длиной 50 см в однородном магнитном поле с
индукцией 2 Тл при силе тока в проводнике 20 А и направлении
вектора индукции магнитного поля под углом к
проводнику ,
действует
сила Ампера, приблизительно равная
1) 12 Н
2) 16 Н
3) 1 200 Н
4) 1 600 Н
10.
Как направлена сила
Ампера, действующая на проводник № 1 (см. рисунок), если все три
проводника тонкие, лежат в одной плоскости, параллельны друг другу и
расстояния между соседними проводниками одинаково? (I —
сила тока.)
1) к нам
2) от нас
3) вверх
4) вниз
11.

в однородном магнитном поле в плоскости линий магнитной индукции
(см. рисунок). Направление тока в рамке показано стрелками. Как направлена
сила, действующая на сторону bc рамки со стороны внешнего
магнитного поля ?
1) перпендикулярно плоскости чертежа, от нас
2) вдоль направления линий магнитной индукции
3) сила равна нулю
4) перпендикулярно плоскости чертежа, к нам
12.

времени скорость электрона
, движущегося
в магнитном поле, направлена вдоль оси х (см. рисунок).
Как направлен вектор магнитной индукции ,
если в этот момент сила Лоренца, действующая на электрон, направлена
вдоль оси у?
1) из плоскости чертежа от нас
2) в отрицательном направлении оси х
3) в положительном направлении оси х
4) из плоскости чертежа к нам
13.

направления движения трех электронов в однородном магнитном поле.
На какой из электронов не действует сила со стороны магнитного поля?
14.
Заряженная
частица движется по окружности в однородном магнитном поле. Как изменится
частота обращения частицы, если уменьшить ее кинетическую энергию
в 2 раза?
1) уменьшится в 2 раза
2) уменьшится в раз
3) не изменится
4) увеличится в раз
15.
. 
магнитное поле со скоростью . Укажите
правильную траекторию альфа-частицы в магнитном поле. Силой тяжести
пренебречь.
16.

магнитное поле со скоростью . Укажите
правильную траекторию нейтрона в магнитном поле. Силой тяжести пренебречь.
17.
Проводник
с током длиной
2 м находится в однородном магнитном поле с индукцией . Причем
направление магнитного поля составляет с
направлением тока. Чему равна сила со стороны магнитного поля, действующая
на проводник?
1) 7 Н
2) 5 Н
3) 8,66 Н
4) 2 Н
18.
В
каком направлении нужно двигать в однородном магнитном поле точечный
заряд , для
того, чтобы действующая на него сила Лоренца при одинаковой по модулю
скорости этого движения была максимальной?
19.
Электрон
влетает в однородное магнитное поле с индукцией 5 Тл со скоростью 1
км/с, направленной под некоторым углом к силовым линиям магнитного
поля. Найдите все возможные значения модуля силы Лоренца, действующей
на электрон.
Справочные
данные: элементарный электрический заряд
1)
2) от 0 до
3) от 0 до
4) Модуль силы может принимать любое значение
20.

частица движется в однородном магнитном поле со скоростью , направленной
перпендикулярно вектору магнитной индукции (см.
рисунок). Как направлена сила Лоренца, действующая на частицу?
1) к нам
2) от нас
3) вдоль вектора
4) вдоль вектора
Магнитное поле
Магнитное поле – особая форма материи, существующая вокруг движущихся электрических зарядов – токов.
Источниками магнитного поля являются постоянные магниты, проводники с током. Обнаружить магнитное поле можно по действию на магнитную стрелку, проводник с током и движущиеся заряженные частицы.
Для исследования магнитного поля используют замкнутый плоский контур с током (рамку с током).
Впервые поворот магнитной стрелки около проводника, по которому протекает ток, обнаружил в 1820 году Эрстед. Ампер наблюдал взаимодействие проводников, по которым протекал ток: если токи в проводниках текут в одном направлении, то проводники притягиваются, если токи в проводниках текут в противоположных направлениях, то они отталкиваются.
Свойства магнитного поля:
- магнитное поле материально;
- источник и индикатор поля – электрический ток;
- магнитное поле является вихревым – его силовые линии (линии магнитной индукции) замкнутые;
- величина поля убывает с расстоянием от источника поля.
Важно!
Магнитное поле не является потенциальным. Его работа на замкнутой траектории может быть не равна нулю.
Магнитным взаимодействием называют притяжение или отталкивание электрически нейтральных проводников при пропускании через них электрического тока.
Магнитное взаимодействие движущихся электрических зарядов объясняется так: всякий движущийся электрический заряд создает в пространстве магнитное поле, которое действует на движущиеся заряженные частицы.
Силовая характеристика магнитного поля – вектор магнитной индукции ( vec{B} ). Модуль вектора магнитной индукции равен отношению максимального значения силы, действующей со стороны магнитного поля на проводник с током, к силе тока в проводнике ( I ) и его длине ( l ):
Обозначение – ( vec{B} ), единица измерения в СИ – тесла (Тл).
1 Тл – это индукция такого магнитного поля, в котором на каждый метр длины проводника при силе тока 1 А действует максимальная сила 1 Н.
Направление вектора магнитной индукции совпадает с направлением от южного полюса к северному полюсу магнитной стрелки (направление, которое указывает северный полюс магнитной стрелки), свободно установившейся в магнитном поле.
Направление вектора магнитной индукции можно определить по правилу буравчика:
если направление поступательного движения буравчика совпадает с направлением тока в проводнике, то направление вращения ручки буравчика совпадает с направлением вектора магнитной индукции.
Для определения магнитной индукции нескольких полей используется принцип суперпозиции:
магнитная индукция результирующего поля, созданного несколькими источниками, равна векторной сумме магнитных индукций полей, создаваемых каждым источником в отдельности:
Поле, в каждой точке которого вектор магнитной индукции одинаков по величине и направлению, называется однородным.
Наглядно магнитное поле изображают в виде магнитных линий или линий магнитной индукции. Линия магнитной индукции – это воображаемая линия, в любой точке которой вектор магнитной индукции направлен по касательной к ней.
Свойства магнитных линий:
- магнитные линии непрерывны;
- магнитные линии замкнуты (т.е. в природе не существует магнитных зарядов, аналогичных электрическим зарядам);
- магнитные линии имеют направление, связанное с направлением тока.
Густота расположения позволяет судить о величине поля: чем гуще расположены линии, тем сильнее поле.
На плоский замкнутый контур с током, помещенный в однородное магнитное поле, действует момент сил ( M ):
где ( I ) – сила тока в проводнике, ( S ) – площадь поверхности, охватываемая контуром, ( B ) – модуль вектора магнитной индукции, ( alpha ) – угол между перпендикуляром к плоскости контура и вектором магнитной индукции.
Тогда для модуля вектора магнитной индукции можно записать формулу:
где максимальный момент сил соответствует углу ( alpha ) = 90°.
В этом случае линии магнитной индукции лежат в плоскости рамки, и ее положение равновесия является неустойчивым. Устойчивым будет положение рамки с током в случае, когда плоскость рамки перпендикулярна линиям магнитной индукции.
Содержание
- Взаимодействие магнитов
- Магнитное поле проводника с током
- Сила Ампера
- Сила Лоренца
- Основные формулы раздела «Магнитное поле»
Взаимодействие магнитов
Постоянные магниты – это тела, длительное время сохраняющие намагниченность, то есть создающие магнитное поле.
Основное свойство магнитов: притягивать тела из железа или его сплавов (например стали). Магниты бывают естественные (из магнитного железняка) и искусственные, представляющие собой намагниченные железные полосы. Области магнита, где его магнитные свойства выражены наиболее сильно, называют полюсами. У магнита два полюса: северный ( N ) и южный ( S ).
Важно!
Вне магнита магнитные линии выходят из северного полюса и входят в южный полюс.
Разделить полюса магнита нельзя.
Объяснил существование магнитного поля у постоянных магнитов Ампер. Согласно его гипотезе внутри молекул, из которых состоит магнит, циркулируют элементарные электрические токи. Если эти токи ориентированы определенным образом, то их действия складываются и тело проявляет магнитные свойства. Если эти токи расположены беспорядочно, то их действие взаимно компенсируется и тело не проявляет магнитных свойств.
Магниты взаимодействуют: одноименные магнитные полюса отталкиваются, разноименные – притягиваются.
Магнитное поле проводника с током
Электрический ток, протекающий по проводнику с током, создает в окружающем его пространстве магнитное поле. Чем больше ток, проходящий по проводнику, тем сильнее возникающее вокруг него магнитное поле.
Магнитные силовые линии этого поля располагаются по концентрическим окружностям, в центре которых находится проводник с током.
Направление линий магнитного поля вокруг проводника с током всегда находится в строгом соответствии с направлением тока, проходящего по проводнику.
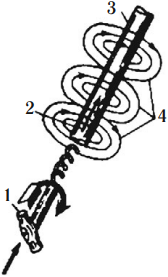
Направление магнитных силовых линий можно определить по правилу буравчика: если поступательное движение буравчика (1) совпадает с направлением тока (2) в проводнике, то вращение его рукоятки укажет направление силовых линий (4) магнитного поля вокруг проводника.
При изменении направления тока линии магнитного поля также изменяют свое направление.
По мере удаления от проводника магнитные силовые линии располагаются реже. Следовательно, индукция магнитного поля уменьшается.
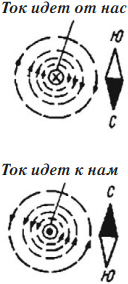
Направление тока в проводнике принято изображать точкой, если ток идет к нам, и крестиком, если ток направлен от нас.
Для получения сильных магнитных полей при небольших токах обычно увеличивают число проводников с током и выполняют их в виде ряда витков; такое устройство называют катушкой.
В проводнике, согнутом в виде витка, магнитные поля, образованные всеми участками этого проводника, будут внутри витка иметь одинаковое направление. Поэтому интенсивность магнитного поля внутри витка будет больше, чем вокруг прямолинейного проводника. При объединении витков в катушку магнитные поля, созданные отдельными витками, складываются. При этом концентрация силовых линий внутри катушки возрастает, т. е. магнитное поле внутри нее усиливается.
Чем больше ток, проходящий через катушку, и чем больше в ней витков, тем сильнее создаваемое катушкой магнитное поле. Магнитное поле снаружи катушки также складывается из магнитных полей отдельных витков, однако магнитные силовые линии располагаются не так густо, вследствие чего интенсивность магнитного поля там не столь велика, как внутри катушки.
Магнитное поле катушки с током имеет такую же форму, как и поле прямолинейного постоянного магнита: силовые магнитные линии выходят из одного конца катушки и входят в другой ее конец. Поэтому катушка с током представляет собой искусственный электрический магнит. Обычно для усиления магнитного поля внутрь катушки вставляют стальной сердечник; такую катушку называют электромагнитом.
Направление линий магнитной индукции катушки с током находят по правилу правой руки:
если мысленно обхватить катушку с током ладонью правой руки так, чтобы четыре пальца указывали направление тока в ее витках, тогда большой палец укажет направление вектора магнитной индукции.
Для определения направления линий магнитного поля, создаваемого витком или катушкой, можно использовать также правило буравчика:
если вращать ручку буравчика по направлению тока в витке или катушке, то поступательное движение буравчика укажет направление вектора магнитной индукции.
Электромагниты нашли чрезвычайно широкое применение в технике. Полярность электромагнита (направление магнитного поля) можно определить и с помощью правила правой руки.
Сила Ампера
Сила Ампера – сила, которая действует на проводник с током, находящийся в магнитном поле.
Закон Ампера: на проводник c током силой ( I ) длиной ( l ), помещенный в магнитное поле с индукцией ( vec{B} ), действует сила, модуль которой равен:
где ( alpha ) – угол между проводником с током и вектором магнитной индукции ( vec{B} ).
Направление силы Ампера определяют по правилу левой руки: если ладонь левой руки расположить так, чтобы перпендикулярная к проводнику составляющая вектора магнитной индукции ( B_perp ) входила в ладонь, а четыре вытянутых пальца указывали направление тока в проводнике, то отогнутый на 90° большой палец покажет направление силы Ампера.
Сила Ампера не является центральной. Она направлена перпендикулярно линиям магнитной индукции.
Сила Ампера широко используется. В технических устройствах создают магнитное поле с помощью проводников, по которым течет электрический ток. Электромагниты используют в электромеханическом реле для дистанционного выключения электрических цепей, магнитном подъемном кране, жестком диске компьютера, записывающей головке видеомагнитофона, в кинескопе телевизора, мониторе компьютера. В быту, на транспорте и в промышленности широко применяют электрические двигатели. Взаимодействие электромагнита с полем постоянного магнита позволило создать электроизмерительные приборы (амперметр, вольтметр).
Простейшей моделью электродвигателя служит рамка с током, помещенная в магнитное поле постоянного магнита. В реальных электродвигателях вместо постоянных магнитов используют электромагниты, вместо рамки – обмотки с большим числом витков провода.
Коэффициент полезного действия электродвигателя:
где ( N ) – механическая мощность, развиваемая двигателем.
Коэффициент полезного действия электродвигателя очень высок.
Алгоритм решения задач о действии магнитного поля на проводники с током:
- сделать схематический чертеж, на котором указать проводник или контур с током и направление силовых линий поля;
- отметить углы между направлением поля и отдельными элементами контура;
- используя правило левой руки, определить направление силы Ампера, действующей на проводник с током или на каждый элемент контура, и показать эти силы на чертеже;
- указать все остальные силы, действующие на проводник или контур;
- записать формулы для остальных сил, упоминаемых в задаче. Выразить силы через величины, от которых они зависят. Если проводник находится в равновесии, то необходимо записать условие его равновесия (равенство нулю суммы сил и моментов сил);
- записать второй закон Ньютона в векторном виде и в проекциях;
- решить полученную систему уравнений относительно неизвестной величины;
- решение проверить.
Сила Лоренца
Сила Лоренца – сила, действующая на движущуюся заряженную частицу со стороны магнитного поля.
Формула для нахождения силы Лоренца:
где ( q ) – заряд частицы, ( v ) – скорость частицы, ( B ) – модуль вектора магнитной индукции, ( alpha ) – угол между вектором скорости частицы и вектором магнитной индукции.
Направление силы Лоренца определяют по правилу левой руки: если ладонь левой руки расположить так, чтобы перпендикулярная к проводнику составляющая вектора магнитной индукции ( B_perp ) входила в ладонь, а четыре вытянутых пальца указывали направление скорости положительно заряженной частицы, то отогнутый на 90° большой палец покажет направление силы Лоренца.
Если заряд частицы отрицательный, то направление силы изменяется на противоположное.
Важно!
Если вектор скорости сонаправлен с вектором магнитной индукции, то частица движется равномерно и прямолинейно.
В однородном магнитном поле сила Лоренца искривляет траекторию движения частицы.
Если вектор скорости перпендикулярен вектору магнитной индукции, то частица движется по окружности, радиус которой равен:
где ( m ) – масса частицы, ( v ) – скорость частицы, ( B ) – модуль вектора магнитной индукции, ( q ) – заряд частицы.
В этом случае сила Лоренца играет роль центростремительной и ее работа равна нулю. Период (частота) обращения частицы не зависит от радиуса окружности и скорости частицы. Формула для вычисления периода обращения частицы:
Угловая скорость движения заряженной частицы:
Важно!
Сила Лоренца не меняет кинетическую энергию частицы и модуль ее скорости. Под действием силы Лоренца изменяется направление скорости частицы.
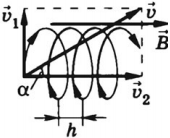
Если вектор скорости направлен под углом ( alpha ) (0° < ( alpha ) < 90°) к вектору магнитной индукции, то частица движется по винтовой линии.
В этом случае вектор скорости частицы можно представить как сумму двух векторов скорости, один из которых, ( vec{v}_2 ), параллелен вектору ( vec{B} ), а другой, ( vec{v}_1 ), – перпендикулярен ему. Вектор ( vec{v}_1 ) не меняется ни по модулю, ни по направлению. Вектор ( vec{v}_2 ) меняется по направлению. Сила Лоренца будет сообщать движущейся частице ускорение, перпендикулярное вектору скорости ( vec{v}_1 ). Частица будет двигаться по окружности. Период обращения частицы по окружности – ( T ).
Таким образом, на равномерное движение вдоль линии индукции будет накладываться движение по окружности в плоскости, перпендикулярной вектору ( vec{B} ). Частица движется по винтовой линии с шагом ( h=v_2T ).
Важно!
Если частица движется в электрическом и магнитном полях, то полная сила Лоренца равна:
Особенности движения заряженной частицы в магнитном поле используются в масс-спектрометрах – устройствах для измерения масс заряженных частиц; ускорителях частиц; для термоизоляции плазмы в установках «Токамак».
Алгоритм решения задач о действии магнитного (и электрического) поля на заряженные частицы:
- сделать чертеж, указать на нем силовые линии магнитного (и электрического) поля, нарисовать вектор начальной скорости частицы и отметить знак ее заряда;
- изобразить силы, действующие на заряженную частицу;
- определить вид траектории частицы;
- разложить силы, действующие на заряженную частицу, вдоль направления магнитного поля и по направлению, ему перпендикулярному;
- составить основное уравнение динамики материальной точки по каждому из направлений разложения сил;
- выразить силы через величины, от которых они зависят;
- решить полученную систему уравнений относительно неизвестной величины;
- решение проверить.
Основные формулы раздела «Магнитное поле»
Магнитное поле
3.2 (64%) 120 votes