Объем погруженной части тела равен объему вытесненной жидкости.
Сила Архимеда: FA = ρgV, где
ρ — плотность жидкости/газа, [кг/м3];
g — ускорение свободного падения, [м/с2];
V — объем погруженной части тела, [м3].
Условия плавания тел:
Если тело плавает в равновесии (полностью или частично погружено в воду), то сила Архимеда уравновешивает силу тяжести.
FA=mg.
Объем погруженной части тела:
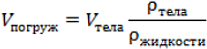
где V погруж — объем погруженной части тела, [м3];
V тела — объем тела, [м3];
ρ жидкости — плотность жидкости, [кг/м3];
ρ тела — плотность тела, [кг/м3]
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
2
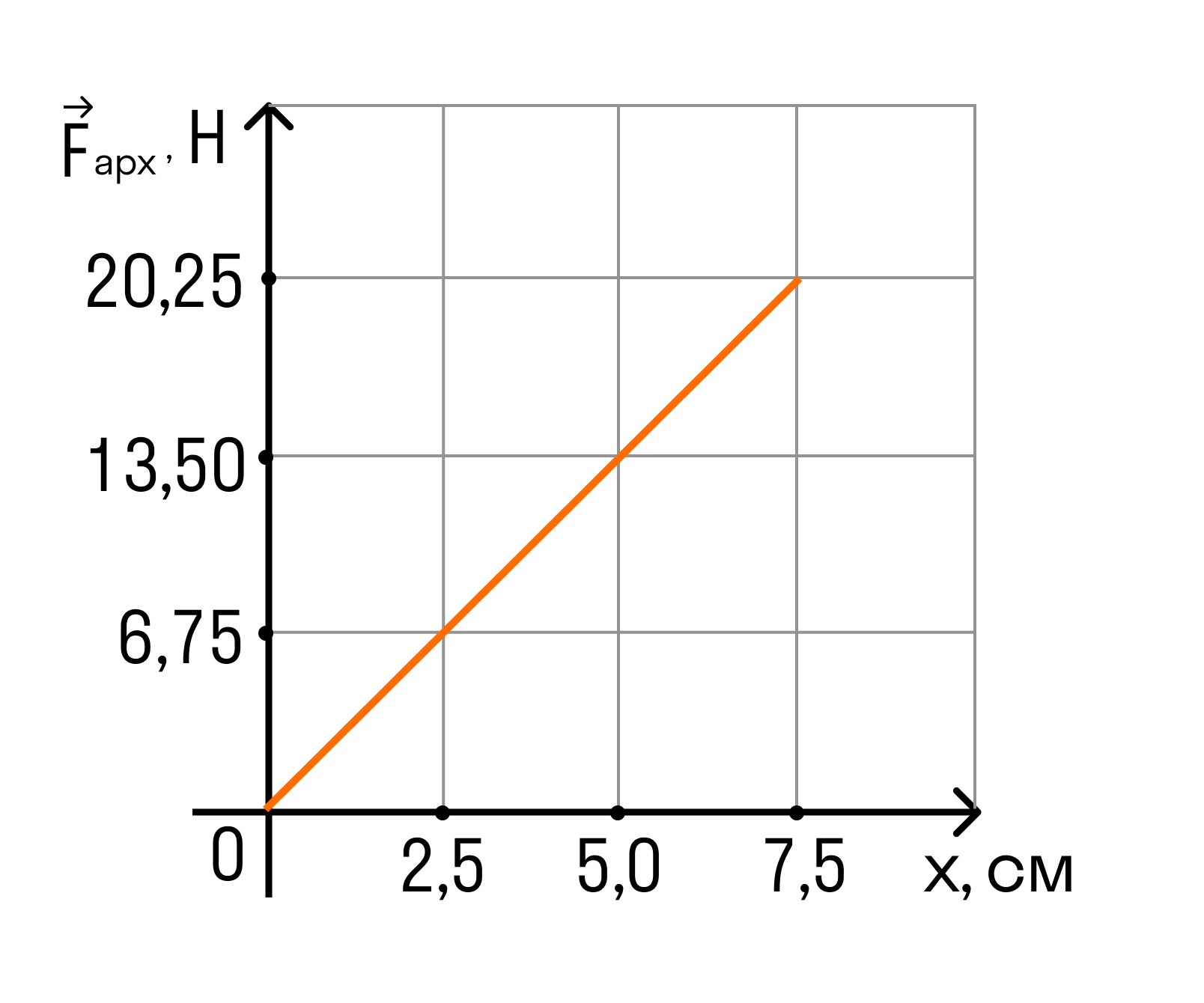
На графике показана зависимость модуля силы Архимеда FАрх, действующей на медленно погружаемый в жидкость кубик, от глубины погружения x. Длина ребра кубика равна 10 см, его нижнее основание всё время параллельно поверхности жидкости. Определите плотность жидкости. Ответ приведите в килограммах на кубический метр. Ускорение свободного падения принять равным 10 м/с2.
3
В четыре сосуда, вертикальные сечения которых показаны на рисунке, налита вода. Одна клеточка на рисунке соответствует 10 см.
В одном из этих сосудов гидростатическое давление на дно максимально. Чему оно равно? (Ответ дайте в паскалях.) Ускорение свободного падения принять равным 10 м/с2.
4
Кубик из пробки с ребром 10 см опускают в воду. Каково отношение объёма кубика, находящегося над водой, к объёму кубика, находящегося под водой? Плотность пробки 0,25 г/см3.
5
Пустой цилиндрический стеклянный стакан плавает в воде, погрузившись на половину своей высоты. Дно стакана при плавании горизонтально, плотность стекла 2500 кг/м3. Чему равно отношение внутреннего объёма стакана к его наружному объёму? Ответ представьте в виде десятичной дроби, округлив до десятых долей.
Пройти тестирование по этим заданиям
4. Статика и механические колебания
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Гидростатика. Сила Архимеда
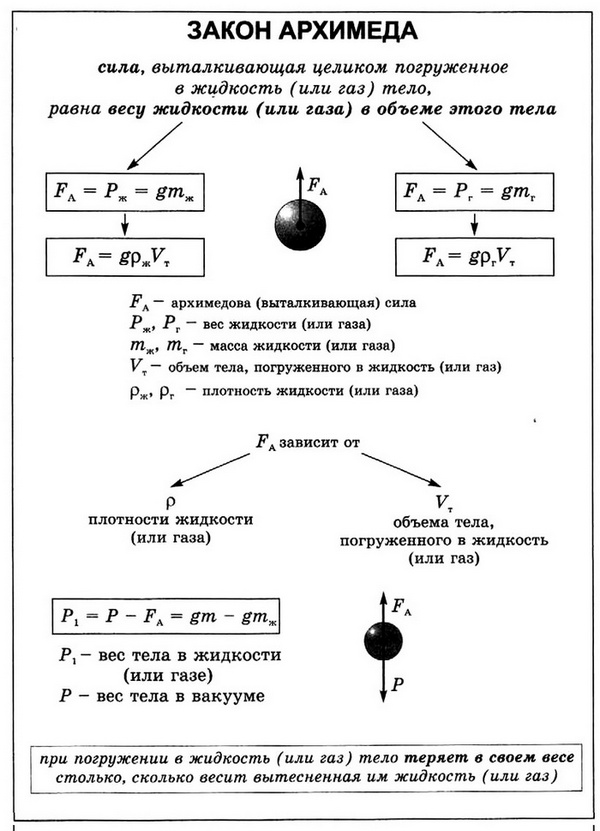
Закон Архимеда
На погружённое в жидкость или газ тело действует выталкивающая сила, и равная весу среды, объём которой равен объёму тела.
Выталкивающая сила (сила Архимеда) равна
[F_A=rho_text{ж} g V_text{пчт}] где (displaystyle V_text{пчт}) — объём погружённой части тела, (displaystyle rho_text{ж}) — плотность жидкости.
Плавание тел
Рассмотрим тело плотности (rho) и жидкость плотности (rho_0). Допустим, тело полностью погрузили в жидкость и отпустили. Сразу после отпускания на тело действуют лишь сила тяжести (mg) и архимедова сила (F_A). Если объём тела равен V, то
[mg=rho g V,] [F_A=rho_0 g V]
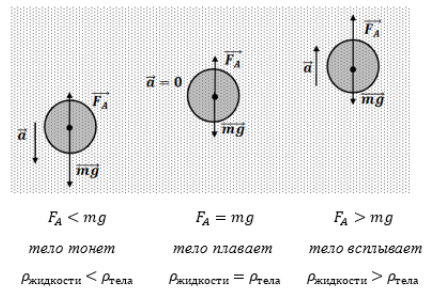
Имеются три возможности дальнейшего движения тела.
Сила тяжести больше архимедовой силы: (displaystyle mg > F_A), или (displaystyle rho>rho_0). В этом случае тело тонет.
Сила тяжести равна архимедовой силе: (displaystyle mg = F_A), или (displaystyle rho=rho_0). В этом случае тело остаётся неподвижным в состоянии безразличного равновесия.
Сила тяжести меньше архимедовой силы: (displaystyle mg < F_A), или (displaystyle rho<rho_0). В этом случае тело всплывает, достигая поверхности жидкости.
Таким образом, условие плавания тела можно записать в виде неравенства (displaystyle rholeq rho_0).
Два жестко связанные друг с другом одинаковых бруска, имеющие толщину (h=5) см, плавают в воде так, что уровень воды приходится на границу между ними (см. рисунок). Насколько изменится глубина погружения, если на два бруска положить ещё пять таких же? (Ответ дайте в сантиметрах.)
Два одинаковых связанных бруска погрузились наполовину в воду (из условия). Пусть
(displaystylerho_1) – плотность материала, из которого изготовлены бруски, а (displaystyle V) – объем двух брусков. Тогда масса этих брусков будет равна [displaystyle m=rho_1V] Сила, с которой льдинки действуют на воду, равна силе тяжести [displaystyle F=mg=rho_1Vg] Сила, с которой бруски выталкиваются из воды, равна силе Архимеда [F_text{Арх}=rho gfrac{V}2,] где (displaystyle rho) – плотность воды, (displaystyle frac{V}2) – объем погруженного в воду тела (бруски погружены только
наполовину). Так как они плавают на поверхности воды, то эти силы уравновешивают друг друга, значит, имеем: [rho_1Vg=rho gfrac{V}2,] откуда (displaystyle rho_1=dfrac{rho}2,) то есть плотность материала, из которого сделаны бруски в 2 раза меньше плотности воды. Это говорит о том, что если взять семь брусков, то они также будут погружены наполовину, то есть на величину [frac72h=3,5cdot5text{ см}=17,5 text{ см}.] Глубина увеличится на (displaystyle 17,5 -5=12,5) см.
Ответ: 12,5
Подвешенный на нити алюминиевый кубик целиком погружен в воду и не касается дна сосуда. Плотность алюминия равна (displaystyle rho_text{ ал}=2700 text{ кг}/text{м}^3. ) Какова длина ребра куба, если выталкивающая сила равна (displaystyle F_text{Арх}=33,75text{ Н}?) (Ответ дайте в сантиметрах.)
Выталкивающая сила равна по определению [F_text{Арх}=rho_text{в} gV,] где (displaystyle rho_text{в}) – плотность жидкости, в которую погружен кубик, (displaystyle V) – объем погруженной части тела. Так как куб погружен целиком, то (displaystyle V=a^3), получим: [F_text{Арх}=rho_text{в} ga^3] Выразив из этой формулы сторону (displaystyle a), получаем [a=sqrt[3]{frac{F_text{Арх}}{rho_text{в}g }}] Подставив значения в формулу, получим: [a=sqrt[3]{frac{33,75text{ Н}}{10text{ м}/{c^2}cdot1000text{ кг}/text{м}^3}}=0,15text{ м}=15text{ cм }]
Ответ: 15
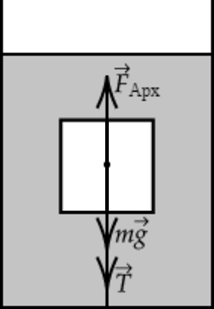
Однородный цилиндр, изготовленный из материала плотностью (displaystyle rho=600) кг/м(^3), с радиусом основания (displaystyle R=25) см и высотой (displaystyle H=20) см привязан нитью ко дну сосуда, наполненного водой. Найдите силу натяжения нити. (Ответ дайте в ньютонах.)
Сделаем рисунок с указанием сил, действующих в системе. Можем записать II закон Ньютона в векторной форме: [vec T+vec F_text{Арх}+mvec g=mvec a,] так как цилиндр покоится, то ускорение равно нулю, в проекции на ось, направленную вертикально вниз, 2 закон Ньютона можно записать следующим образом: [T- F_text{Арх}+mg=0, quad(1)] массу цилиндра можно рассчитать, исходя из формулы (displaystyle rho=frac {m}{V} Rightarrow m=rho V,) где V – объем цилиндра, который можно вычислить по формуле [V=pi R^2 H] Из формулы (1) выразим силу натяжения нити T:[T=F_text{Арх}-mg=rho_text{в}gV-rho gV=Vg(rho_text{в}-rho)=pi R^2 Hg(rho_text{в}-rho),] где (displaystyle rho_text{в}) – плотность воды, подставим в получившееся выражение численные значения:[T=3,14cdot0,25^2text{ м}cdot0,2text{ м}cdot 10text{ м}/text{с}^2 cdot (1000text{ кг}/text{м}^3-600text{ кг}/text{м}^3)=157text{ Н }]
Ответ: 157
Однородный кубический предмет с ребром (displaystyle a=18) см опускают в эфир. На сколько сантиметров длина части стороны, находящейся под жидкостью отличается от длины части над эфиром? Плотность вещества, из которого изготовлен куб равна (displaystyle rho_text{др}=340) кг/м(^3), плотность эфира (displaystyle rho_text{э}=720) кг/м(^3). (Ответ дайте в сантиметрах.)
Запишем условие равновесия кубика на поверхности эфира: [F_text{ Арх}=mg, quad(1)] где (F_text{ Арх}) – выталкивающая сила, действующая на брусок, (displaystyle m) – масса кубика, которую можно рассчитать, исходя из формулы (displaystyle rho_text{др}=frac {m}{V} Rightarrow m=rho_text{др} V,) где V – объем кубика, который можно вычислить по формуле [V=a^3.] Выталкивающая сила равна: [F_text{ Арх}=rho_text{э}gV_text{пчт},] где (displaystyle V_text{пчт}) – объем погруженной части кубика,[V_text{пчт}=xa^2,] где (displaystyle x) – длина части стороны, находящейся под эфиром, значит, выражение (1) можно записать в следующем виде: [rho_text{э}gxa^2=rho_text{др}a^3] [rho_text{э}x=rho_text{др}a, text{ выразим } x=frac{rho_text{др}a}{rho_text{э}}.] Пусть (displaystyle y) – длина части стороны, находящейся над эфиром, можем записать: [y=a-x,] искомая разница длин (displaystyle delta=y-x=a-2x=a-2cdot dfrac{rho_text{др}a}{rho_text{э}}=a(1-2cdot dfrac{rho_text{др}}{rho_text{э}})) подставим в получившееся выражение численные значения: [displaystyle delta=0,18text{ м}(1-2cdot dfrac{340text{ кг}/text{м}^3}{720text{ кг}/text{м}^3})=0,01text{ м}=1text{ см}]
Ответ: 1
В некий резервуар было налито 1000 литров жидкости плотностью (displaystyle rho_1=1500) кг/м(^3). В этой жидкости в равновесии плавает кубик, погруженный в воду на (displaystyle x=130) см. Длина стороны кубика равна (displaystyle a=200) см. В сосуд доливают ещё 1000 литров жидкости плотностью (displaystyle rho_2=1100) кг/м(^3) и перемешивают. Чему после этого будет равна длина погруженной части кубика при плавании в равновесии? Обе жидкости хорошо смешиваются, и при смешивании суммарный объём сохраняется. (Ответ дайте в метрах.)
В условии сказано, что жидкости хорошо перемешиваются. Из этого следует, что при смешивании получается новая жидкость, плотность которой является средним арифметическим изначальных, так как взятые объемы одинаковы. [rho_text{нов}=dfrac{rho_1+rho_2}{2}] Так как кубик плавает на поверхности, то можно записать: [mg=F_text{Арх},] сила тяжести, действующая на тело не изменяется, значит, выталкивающая сила тоже остается постоянной. Сначала сила Архимеда равна:[F_text{Арх1}=rho_1 g V_text{пчт1},] где (displaystyle V_text{пчт1}=a^2x) – объем погруженной части куба до смешивания. После смешения жидкостей в сосуде: [F_text{Арх2}=rho_text{нов} g V_text{пчт2}=dfrac{rho_1+rho_2}{2}g V_text{пчт2},]где (displaystyle V_text{пчт2}=a^2y) – объем погруженной части куба до смешивания, (displaystyle y) – длина погруженной части стороны куба после смешивания жидкостей. Можем приравнять получившиеся выражения, получим [rho_1 g a^2x=dfrac{rho_1+rho_2}{2} g a^2y] [rho_1x=dfrac{rho_1+rho_2}{2}y,] выразим отсюда y: [y=frac{2rho_1 x}{rho_1+rho_2},] подставим в получившееся выражение численные значения: [y=frac{2cdot1500text{ кг}/text{м}^3 cdot1,3text{ м}}{1500text{ кг}/text{м}^3+1100text{ кг}/text{м}^3}=1,5text{ м}]
Ответ: 1,5
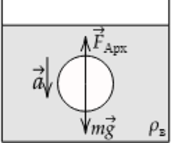
Стеклянный шарик опускается в воде с ускорением (displaystyle a=6) м/с(^2). Найти плотность стекла. Плотность воды (displaystyle rho_text{в}=1000) кг/м(^3). Силами вязкого трения пренебречь. (Ответ дайте в кг/м(^3).)
При движении шарика в воде на него действует сила тяжести (displaystyle mvec g) и сила Архимеда (displaystyle F_text{Арх}). Сделаем рисунок с указанием сил, действующих в системе. Можем записать 2 закон Ньютона в векторной форме: [vec F_text{Арх}+mvec g=mvec a,] в проекции на ось, направленную вертикально вниз, 2 закон Ньютона можно записать следующим образом: [mg- F_text{Арх}=ma,] Отсюда с учетом выражения для силы Архимеда (displaystyle F_text{Арх}=rho_text{в} g V), где V – объем шарика, а
(displaystyle rho_text{в}) – плотность воды, получим: [mg- rho_text{в} g V=ma,] Выразим массу шарика:[m=frac{rho_text{в} g V}{g-a}.] Исходя из формулы, плотность стекла равна [displaystyle rho_text{ст}=frac {m}{V}=frac{rho_text{в} g V}{(g-a)V}=frac{rho_text{в} g }{g-a},] подставим в получившееся выражение численные значения: [rho_text{ст}=frac{1000 text{ кг}/text{м}^3cdot 10text{ м}/text{с}^2 }{10text{ м}/text{с}^2-6text{ м}/text{с}^2}=2500text{ кг}/text{м}^3]
Ответ: 2500
Однородный шарик, изготовленный из материала плотностью (displaystyle rho=2000) кг/м(^3) погружен в воду. Чему равен радиус шара, если выталкивающая сила равна
(displaystyle F_text{Арх}=100) Н? (Ответ дайте в сантиметрах и округлите до целых.)
Выталкивающая сила равна по определению [F_text{Арх}=rho_text{в} gV_text{пчт},] где (displaystyle rho_text{в}) – плотность воды, (displaystyle V_text{пчт}) – объем погруженной части тела. Так как шар полностью опущен в воду, то [V_text{пчт}=frac43pi R^3,] где (displaystyle R) – радиус шара, получим: [F_text{Арх}=rho_text{в} gfrac43pi R^3, (1)] выразим из формулы R: [R=sqrt[3]{frac{3F_text{Арх}}{4rho_text{в}gpi}}] Подставив значения в формулу, получим: [R=sqrt[3]{frac{3 cdot100text{ Н}} {4 cdot1000 text{ кг}/text{м}^3cdot10text{ м}/{c^2}cdot3,14}} approx0,13text{ м}=13text{ см }]
Ответ: 13

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Закон Архимеда. Плавание тел
Сумму сил гидростатического давления, действующих на тело, покоящееся внутри жидкости, называют силой Архимеда.
Закон Архимеда. На погружённое в жидкость (или газ) тело действует выталкивающая и направленная вертикально вверх сила, равная по модулю весу вытесненной этим телом жидкости (или газа).
FА = pж • g • Vж = mж • g = Pж
где: FА — Архимедова сила, pж — плотность жидкости, g — ускорение свободного падения, Vж — объем жидкости, mж — масса жидкости, Pж — вес жидкости.
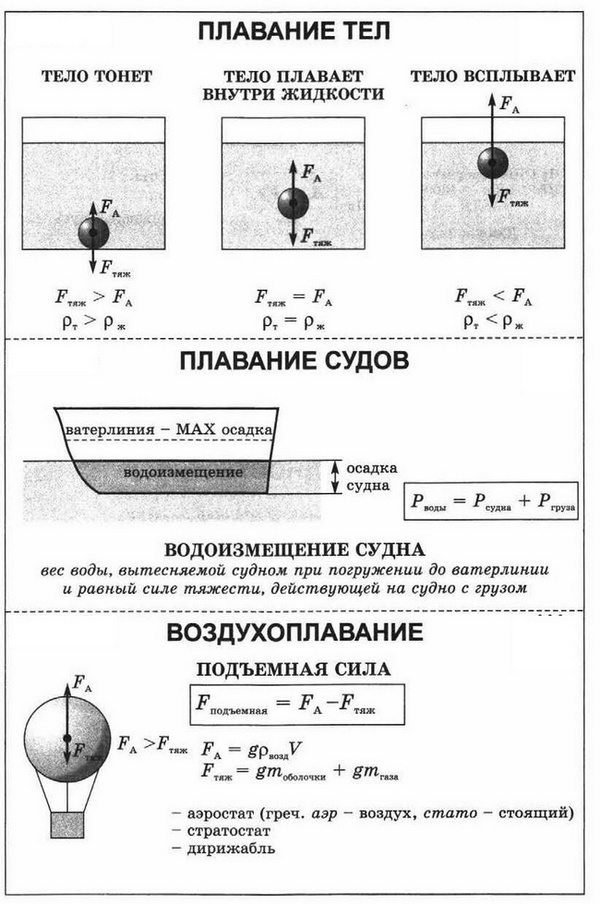
Плавание — это способность тела удерживаться на поверхности жидкости или на определённом уровне внутри жидкости. На любое тело, находящееся в жидкости, действуют две силы, направленные в противоположные стороны: сила тяжести и архимедова сила. Сила тяжести равна весу тела и направлена вниз, архимедова же сила зависит от плотности жидкости и направлена вверх.
Тело тонет, если рт > рж ; тело всплывает, если рт < рж .
Условие плавания тела на поверхности жидкости: для плавания тела на поверхности жидкости необходимо, чтобы сила тяжести уравновешивалась выталкивающей силой: Fв = М • g
Условие плавания тела на поверхности жидкости можно представить в виде рт • Vт = рж • Vж .
Конспект урока «Архимедова сила».
Следующая тема: «Сообщающиеся сосуды. Шлюзы».
Сила: что это за величина
Прежде чем говорить о силе Архимеда, нужно понять, что это вообще такое — сила.
В повседневной жизни мы часто видим, как физические тела деформируются (меняют форму или размер), ускоряются и тормозят, падают. В общем, чего только с ними не происходит! Причина любых действий или взаимодействий тел — ее величество сила.
Сила — это физическая векторная величина, которая воздействует на данное тело со стороны других тел. Сила измеряется в ньютонах — единице измерения, которую назвали в честь Исаака Ньютона.
Поскольку сила — величина векторная, у нее, помимо модуля, есть направление. От того, куда направлена сила, зависит результат.
Вот стоите вы на лонгборде: можете оттолкнуться вправо, а можете влево — в зависимости от того, в какую сторону оттолкнетесь, результат будет разный. В этом случае результат выражается в направлении движения.
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
Практикующий детский психолог Екатерина Мурашова
Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков
Открытие закона Архимеда
Так вышло, что закон Архимеда известен не столько своей формулировкой, сколько историей возникновения.
Легенда гласит, что царь Герон II попросил Архимеда определить, из чистого ли золота сделана его корона, при этом не причиняя вреда самой короне. То есть расплавить корону или растворить — нельзя.
Взвесить корону Архимеду труда не составило, но этого было мало — нужно ведь определить объем короны, чтобы рассчитать плотность металла, из которого она отлита.
Рассчитать плотность металла, чтобы установить, золотая ли корона, можно по формуле плотности.
Формула плотности тела
ρ = m/V
ρ — плотность тела [кг/м3]
m — масса тела [кг]
V — объем тела [м3]
Дальше, согласно легенде, Архимед, озабоченный мыслями о том, как определить объем короны, погрузился в ванну — и вдруг заметил, что уровень воды в ванне поднялся. Тут ученый осознал, что объем его тела вытеснил равный ему объем воды, следовательно, и корона, если ее опустить в заполненный до краев таз, вытеснит из него объем воды, равный ее объему.
Решение задачи было найдено и, согласно самой расхожей версии легенды, ученый закричал «Эврика!» и побежал докладывать о своей победе в царский дворец (и так торопился, что даже не оделся). 🤦🏻♂️
Попробуйте онлайн-курс подготовки к ЕГЭ по физике с опытным преподавателем в Skysmart!
Формула и определение силы Архимеда для жидкости
На поверхность твердого тела, погруженного в жидкость, действуют силы давления. Эти силы увеличиваются с глубиной погружения, и на нижнюю часть тела будет действовать со стороны жидкости большая сила, чем на верхнюю.
Равнодействующая всех сил давления, действующих на поверхность тела со стороны жидкости, называется выталкивающей силой или силой Архимеда. Истинная причина появления выталкивающей силы — наличие различного гидростатического давления в разных точках жидкости.
Определение архимедовой силы для жидкостей звучит так:
Выталкивающая сила, действующая на тело, погруженное в жидкость, равна по модулю весу вытесненной жидкости и противоположно ему направлена.
Формула архимедовой силы для жидкости
FАрх = ρжgVпогр
ρж — плотность жидкости[кг/м3]
Vпогр — объем погруженной части тела [м3]
g — ускорение свободного падения [м/с2]
На планете Земля g = 9,8 м/с 2.
А теперь давайте порешаем задачки, чтобы закрепить, как вычислить архимедову силу.
Задача 1
В сосуд погружены три железных шарика равных объемов. Одинаковы ли силы, выталкивающие шарики? Плотность жидкости вследствие ничтожно малой сжимаемости на любой глубине считать примерно одинаковой.
Решение
Да, так как объемы одинаковы, а архимедова сила зависит от объема погруженной части тела, а не от глубины.
Задача 2
На графике показана зависимость модуля силы Архимеда FАрх, действующей на медленно погружаемый в жидкость кубик, от глубины погружения x. Длина ребра кубика равна 10 см, его нижнее основание все время параллельно поверхности жидкости. Определите плотность жидкости. Ускорение свободного падения принять равным 10 м/с2.
Решение
Сила Архимеда, действующая на кубик, равна FАрх = ρжgVпогр.
Vпогр. — объем погруженной части кубика,
ρж — плотность жидкости.
Учитывая, что нижнее основание кубика все время параллельно поверхности жидкости, можем записать:
FАрх = ρжgV погр = ρжga 2x
где а — длина стороны кубика.
Выразим плотность:
ρ = FАрх / ga2x
Рассматривая любую точку данного графика, получим:
ρ = FАрхga2x = 20,25 / 10 × 7,5 × 10-2 = 2700 кг/м3
Ответ: плотность жидкости равна 2700 кг/м 3.
Условия плавания тел
Из закона Архимеда вытекают следствия об условиях плавания тел.
Почему корабли не тонут?
Корабль сделан из металла, плотность которого больше плотности воды. И, по идее, он должен тонуть. Но дело в том, что корпус корабля заполнен воздухом, поэтому общая плотность судна оказывается меньше плотности воды, и сила Архимеда выталкивает его на поверхность. Если корабль получит пробоину, то пространство внутри заполнится водой — следовательно, общая плотность корабля увеличится. Судно утонет.
В подводных лодках есть специальные резервуары, которые заполняют водой или сжатым воздухом. Если нужно уйти на глубину — водой, если подняться — сжатым воздухом. Рыбы используют такой же принцип в плавательном пузыре — наполняют его воздухом, чтобы подняться наверх.
Человеку, чтобы не утонуть, тоже достаточно набрать в легкие воздух и не двигаться — вода будет выталкивать тело на поверхность. Именно поэтому важно не тратить силы и кислород в легких на панику и борьбу, а расслабиться и позволить физическим законам сделать все за нас.
Формула и определение силы Архимеда для газов
На самом деле тут все очень похоже на жидкости. Начнем с формулировки закона Архимеда:
Выталкивающая сила, действующая на тело, погруженное в газ, равна по модулю весу вытесненного газа и противоположно ему направлена.
Формула архимедовой силы для газов
FАрх = ρгgVпогр
ρг — плотность газа [кг/м3]
Vпогр — объем погруженной части тела [м3]
g — ускорение свободного падения [м/с2]
На планете Земля g = 9,8 м/с 2.
Сила Архимеда для газов действует аналогично архимедовой силе для жидкостей. Давайте убедимся в этом, решив задачку.
Задача
Груз какой максимальной массы может удерживать воздушный шар с гелием объема 0,3 м3, находясь в атмосфере Земли? Плотность воздуха равна 1,3 кг/м 3. Гелий считать невесомым.
Решение
Подставляем значения и получаем:
FАрх = ρгgVпогр = 1,3 × 10 × 0,3 = 0,39 Н
По второму закону Ньютона для инерциальных систем отсчета:
FАрх = mg
Выражаем массу груза и подставляем значения:
m = FАрх / g = 0,39 / 10 = 0, 039 кг = 39 кг
Ответ: груз максимальной массы 39 г может удержать данный шарик с гелием.
Когда сила Архимеда не работает
Архимедова сила не работает лишь в трех случаях:
-
Невесомость. Главное условие возникновения Архимедовой силы — это наличие веса у среды. Если мы находимся в невесомости, холодный воздух не опускается, а горячий, наоборот, не поднимается.
-
Тело плотно прилегает к поверхности. Отсутствие газа или жидкости между поверхностью и телом свидетельствует об отсутствии выталкивающей силы — телу просто неоткуда выталкиваться.
-
Растворы и смеси. Если взять спирт, плотность которого меньше плотности воды, и смешать его с водой, получится раствор. На него не будет действовать сила Архимеда, несмотря на то, что плотность спирта меньше плотности воды — он просто растворится.
Давление. Атмосферное давление. Закон Паскаля. Закон Архимеда
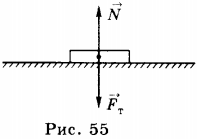
1. Твёрдые тела оказывают давление на опору. На тело, стоящее на опоре, действуют сила тяжести ( vec{F}_т=mvec{g} ) и сила реакции опоры ( vec{N} ) (рис. 55).
Если опора неподвижна, то это тело действует на неё с силой ( vec{F} ), называемой силой давления и равной в этом случае по модулю силе тяжести: ( F=mg ).
Физическая величина, равная отношению силы давления ( F ) к площади поверхности ( S ) называется давлением и обозначается буквой ( p ):
[ p=F/S ]
Единицей давления является 1 паскаль (1 Па):
[ [,p,]=1Н/1м^2=1,Н/м^2=1,Па ]
Более крупная единица давления — килопаскаль.
[ 1, кПа = 1000, Па ]
Как видно из формулы, давление на поверхность зависит от площади поверхности. Так, человек проваливается в снег при ходьбе по нему и спокойно перемещается на лыжах. В том случае, когда нужно увеличить давление на твёрдое тело, используют заострённые предметы, например, булавки, гвозди, ножи и т.п.
2. Жидкости и газы тоже оказывают давление на сосуд, в котором они находятся. Так, молекулы газа, находящегося в воздушном шаре, непрерывно движутся и при этом соударяются со стенками шара. Эти удары и вызывают давление газа на стенки шара и любого другого сосуда, в котором газ находится. Удар одной молекулы слаб, но внутри шара находится огромное число молекул, поэтому
их суммарное давление на стенки шара ощутимо.
Чем выше температура газа, чем с большей скоростью движутся молекулы и чем чаще и сильнее ударяются они о стенки сосуда, тем, следовательно, давление газа на стенки сосуда больше.
Если уменьшить объём газа в сосуде, не меняя его массу, то число молекул в единице объёма увеличится, увеличится и плотность газа. Число ударов молекул о стенки сосуда при этом возрастёт, следовательно, увеличится давление газа. При увеличении объёма газа при той же массе уменьшится его плотность и число ударов молекул о стенки сосуда. Давление уменьшится.
Таким образом, давление газа тем больше, чем выше его температура и меньше объём при неизменной массе. При повышении температуры и уменьшении объёма молекулы с большей силой и чаще ударяются о стенки сосуда.
3. Опыт показывает, что давление, производимое на жидкость или газ, передаётся по всем направлениям. Если шар с отверстиями, соединённый с трубкой, внутри которой находится поршень, наполнить водой, а затем нажать на поршень, то можно заметить, что вода брызнет из всех отверстий. При этом струйки вытекающей воды будут примерно одинаковыми. Это говорит о том, что давление, которое мы создаём, действуя на воду, передаётся водой по всем направлениям одинаково. Тот же эффект можно наблюдать, если шар заполнить дымом. Дым тоже будет передавать производимое на него давление по всем направлениям одинаково.
То, что газы и жидкости передают давление по всем направлениям, объясняется подвижностью их молекул. Она проявляется в том, что слои и частицы жидкостей и газов могут свободно перемещаться друг относительно друга но разным направлениям. Благодаря подвижности молекул давление, которое оказывает поршень на ближайший к нему слой, передаётся последующим слоям. Молекулы газа и жидкости движутся хаотически, поэтому и их действие распределяется равномерно по всему объёму шара. Таким образом, давление, производимое на жидкость или газ, передаётся по всем направлениям без изменения в каждую точку жидкости или газа. Это утверждение называется законом Паскаля.
4. Закон Паскаля находит применение в гидравлических машинах.
Основной частью любой гидравлической машины являются два соединенных между собой цилиндра разного диаметра. Цилиндры заполнены жидкостью, чаще всего маслом, и в них помещены поршни.
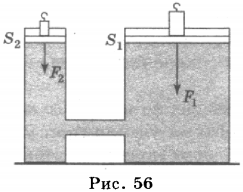
Пусть на большой поршень площадью ( S_1 ) действует сила ( F_1 ) (рис. 56). Эта сила будет оказывать на поршень давление ( p_1 ): ( p_1=F_1/S_1 ).
Это давление ( p_1 ) будет передаваться жидкости, находящейся под большим поршнем. Согласно закону Паскаля, давление, производимое на жидкость или газ, передаётся по всем направлениям без изменения. Следовательно, давление будет передаваться жидкости, находящейся под меньшим поршнем, и на меньший поршень со стороны жидкости будет действовать давление ( p_2=p_1 ). Соответственно, на меньший поршень со стороны жидкости будет действовать сила ( F_2=p_2S_2 ), направленная вверх. Откуда ( p_2=F_2/S_2 ).
Чтобы жидкость и поршни находились в равновесии, на меньший поршень следует подействовать силой, равной по модулю силе ( F_2 ), направленной вертикально вниз. Для этого можно, например, положить на поршень груз.
Так как ( p_1=p_2 ), то ( F_1/S_1=F_2/S_2 ) или ( F_1/F_2=S_1/S_2 ).
Таким образом, гидравлическая машина даёт выигрыш в силе во столько раз, во сколько раз площадь большего поршня больше площади меньшего поршня.
Это означает, что с помощью некоторой силы, приложенной к малому поршню гидравлической машины, можно уравновесить существенно большую силу, приложенную к большему поршню.
Гидравлическая машина, так же как и любой простой механизм, даёт выигрыш в силе, но не даёт выигрыша в работе.
5. Твёрдые тела производят давление на опору вследствие действия на них силы тяжести. Поскольку на жидкости тоже действует сила тяжести, то и жидкости оказывают давление на дно сосуда. Это можно доказать экспериментально.
Если в трубку, дно которой затянуто плёнкой, налить воду, то плёнка заметно прогнётся. Это происходит потому, что на воду действует сила тяжести, и каждый слой воды давит на слои воды, лежащие ниже, и соответственно на дно сосуда.
Давление производится жидкостью не только на дно сосуда, оно существует внутри жидкости на любой её глубине. При этом производимое давление передаётся по закону Паскаля по всем направлениям одинаково.
Если в трубку с дном, затянутым плёнкой, добавить воды, то плёнка прогнётся сильнее. Это происходит потому, что увеличивается вес воды и соответственно давление воды на дно трубки. Таким образом, давление жидкости на дно сосуда тем больше, чем больше высота столба жидкости.
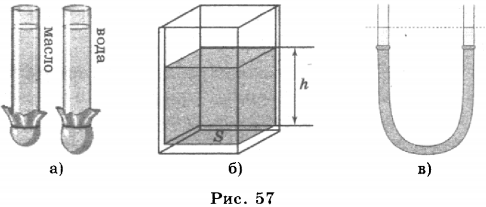
Если теперь в трубку до той же высоты налить масло, плотность которого меньше плотности воды, то плёнка прогнётся меньше, чем в том случае, когда в ней была вода (рис. 57 а). Это означает, что давление на дно сосуда тем больше, чем больше плотность жидкости.
Сила ( F ), с которой жидкость давит на дно, равна её весу ( P ). Вес жидкости ( P ) равен произведению её массы ( m ) и ускорения свободного падения ( g ): ( F=P=mg ).
Масса жидкости ( m ) равна произведению её плотности ( rho ) и объёма ( V ): ( m=rho V ), где ( V=Sh ) (рис. 57 б). Тогда ( F=mg=rho V!g=rho Shg ).
Разделив вес жидкости (силу, с которой она давит на дно сосуда) на площадь дна, получим давление жидкости ( p ): ( p=F/S ) или ( p=rho gSh/S ), т.е. ( p=rho gh )
Давление жидкости на дно и стенки сосуда равно произведению плотности жидкости, ускорения свободного падения и высоты столба жидкости.
6. Два или более сосудов, соединённых между собой у дна, называются сообщающимися сосудами. Примерами сообщающихся сосудов могут служить гидравлические машины и жидкостный манометр. Самым простым сообщающимся сосудом, которым вы пользуетесь каждый день, является чайник.
Если две стеклянные трубки соединить резиновой трубкой (рис. 57 в), то получатся сообщающиеся сосуды. Наливая в одну трубку воду, можно заметить, что она будет перетекать и в другую трубку. При этом уровни воды в трубках будут все время одинаковы.
Можно поднять одну из трубок или наклонить ее, в любом случае друг относительно друга уровни воды или любой другой жидкости останутся одинаковыми, т.е. будут лежать в одной и той же горизонтальной плоскости.
Можно сделать вывод: в сообщающихся сосудах поверхности однородной жидкости всегда устанавливаются на одном уровне.
Это верно при условии, что давление на поверхность жидкости одинаково. При использовании сообщающихся сосудов в качестве жидкостного манометра именно по разности уровней жидкости в трубках можно судить о значении давления.
Объяснить то, что в сообщающихся сосудах однородная жидкость устанавливается на одном уровне, можно следующим образом. Жидкость в сосудах не перемещается, следовательно, её давления в сосудах на одном уровне, в том числе и на дно, одинаковы. Она имеет одинаковую плотность, т.к. она однородная. Следовательно, в соответствии с формулой ( p=rho gh ) высоты жидкости тоже одинаковы.
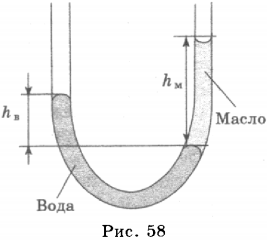
Если в одну трубку налить воду, а в другую масло, плотность которого меньше плотности воды, то уровень воды будет ниже, чем уровень масла в другой трубке (рис. 58).
Это объясняется тем, что давление жидкости на дно сосуда зависит от высоты столба жидкости и от её плотности. При одинаковом давлении, чем больше плотность жидкости, тем меньше высота её столба. Поскольку плотность масла меньше плотности воды, то столб масла выше столба воды. Жидкости, имеющие разную плотность, устанавливаются в сообщающихся сосудах на разных уровнях; во сколько раз плотность одной жидкости больше плотности другой, во столько раз меньше высота её столба.
7. Земля окружена воздушной оболочкой — атмосферой. Воздух, как и газы, входящие в состав атмосферы, имеет массу. Соответственно, на него действует сила тяжести, и он оказывает давление на поверхность Земли.
Давление воздушной оболочки на поверхность Земли и находящиеся на ней тела называется атмосферным давлением.
В существовании атмосферного давления легко убедиться на опытах. Если опустить в воду трубку с плотно прилегающим к её стенкам поршнем и поднимать поршень вверх, то вода будет подниматься по трубке вслед за поршнем.
Это происходит потому, что при подъёме поршня между ним и поверхностью воды образуется разреженное пространство. На поверхность воды в сосуде действует атмосферное давление, которое в соответствии с законом Паскаля передаётся по всем направлениям, в том числе и в направлении трубки. Оно и заставляет воду подниматься за поршнем.
Для расчёта атмосферного давления нельзя использовать формулу, по которой рассчитывается давление столба жидкости, так как для этого нужно знать высоту атмосферы и плотность воздуха. Но атмосфера не имеет определённой границы, а плотность воздуха изменяется с высотой. Однако атмосферное давление можно измерить.
Опыт по измерению атмосферного давления был предложен итальянским ученым Торричелли в XVII в. Стеклянную трубку длиной 1 м, запаянную с одного конца, заполнили ртутью. Закрыв другой конец трубки, её перевернули и опустили в сосуд с ртутью. Затем этот конец трубки открыли, и часть ртути вылилась из неё в сосуд, а часть осталась в трубке. Высота столба ртути, оставшейся в трубке, оказалась равной примерно 760 мм.
Объясняется это следующим образом: атмосферное давление действует на ртуть в сосуде, это давление передаётся по всем направлениям и действует на ртуть в основании трубки снизу вверх. Это давление уравновешивает давление столба ртути в трубке. Таким образом, атмосферное давление равно давлению, которое оказывает у основании трубки столб ртути высотой 760 мм. Это давление называют нормальным атмосферным давлением.
Если атмосферное давление выше нормального, то высота столба ртути больше, если — меньше нормального, то столб ртути опустится ниже.
Нормальное атмосферное давление равно 101 300 Па.
Атмосферное давление чаще выражают не в паскалях, а в миллиметрах ртутного столба (мм рт.ст.). 1 мм рт.ст. = 133,3 Па.
Если к трубке в опыте Торричелли прикрепить шкалу и проградуировать её в миллиметрах, то получим прибор — ртутный барометр, с помощью которого можно измерять атмосферное давление.
В быту и технике для измерения атмосферного давления применяют более удобный в обращении металлический барометр, называемый анероидом.
Атмосферное давление зависит от высоты. Это объясняется тем, что воздух хорошо сжимаем, так же как и все газы. Верхние слои воздуха давят на лежащие ниже и сжимают их, соответственно плотность слоёв воздуха, а следовательно и давление, у поверхности Земли больше, чем на некоторой высоте от неё.
Так, в местности, лежащей на уровне моря, давление равно примерно 760 мм рт. ст., т.е. нормальному атмосферному. В горах оно выше. Измерения показывают, что на каждые 12 м подъёма атмосферное давление уменьшается примерно на 1 мм рт.ст.
8. Если подвешенный к пружине динамометра шарик опустить в сосуд с водой, то можно заметить, что показание динамометра уменьшится.
Точно так же можно изменить показания динамометра, если подействовать на шарик рукой снизу вверх. Следовательно, когда шарик опустили в воду, на него, помимо силы тяжести и силы упругости пружины динамометра, стала действовать сила, направленная вверх. Эту силу называют выталкивающей или архимедовой силой.
Выталкивающая сила возникает за счёт разности давления воды на нижнюю поверхность шарика и давления на его верхнюю поверхность, поскольку давление жидкости зависит от высоты её столба.
Сила давления ( F_1 ), действующая на верхнюю поверхность шарика, направлена вниз, сила давления ( F_2 ), действующая на нижнюю поверхность шарика, направлена вверх. Так как ( F_2 ) больше ( F_1 ), то результирующая этих двух сил, являющаяся выталкивающей силой, будет направлена вверх.
Выталкивающая сила тем больше, чем больше плотность жидкости, в которую погружено тело, и чем больше объём тела, погружённого в жидкость.
Опыт показывает, что выталкивающая сила ( F ) может быть вычислена по формуле: ( F=rho gV ), где ( rho ) — плотность жидкости, в которую погружено тело, ( V ) — объём погружённой части тела.
Выталкивающая сила равна произведению плотности жидкости, ускорения свободного падения и объёма погружённой части тела.
Этот закон называют законом Архимеда.
В воздухе, так же как и в любом другом газе, на тело действует выталкивающая сила. Она имеет ту же природу, что и выталкивающая сила, действующая на тело в жидкости. Её происхождение обусловлено разностью давлений на нижнюю и верхнюю грани тела. Однако, поскольку плотность газа намного меньше плотности жидкости, выталкивающая сила, действующая на тело, в газе меньше, чем в жидкости. Часто при решении задач пренебрегают выталкивающей силой, действующей на тело в воздухе, и считают, что вес покоящегося тела в воздухе равен по модулю действующей на него силе тяжести.
Содержание
- ПРИМЕРЫ ЗАДАНИЙ
- Часть 1
- Часть 2
- Ответы
ПРИМЕРЫ ЗАДАНИЙ
Часть 1
1. Ребёнка везут на санках по свежевыпавшему снегу. Какие санки — с широкими или узкими полозьями — следует выбрать, чтобы не проваливаться в снег?
1) с широкими
2) с узкими
3) безразлично
4) ответ зависит от веса санок
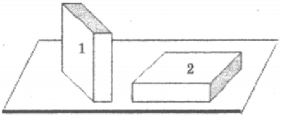
2. Брусок в форме прямоугольного параллелепипеда положили на стол сначала узкой гранью (1), а затем — широкой (2). Сравните силы давления (( F_1 ) и ( F_2 )) и давления (( p_1 ) и ( p_2 )), производимые бруском на стол в этих случаях.
1) ( F_1=F_2; p_1>p_2 )
2) ( F_1=F_2; p_1<p_2 )
3) ( F_1<F_2; p_1<p_2 )
4) ( F_1=F_2; p_1=p_2 )
3. Сила ( F_1 ), действующая со стороны жидкости на один поршень гидравлической машины, в 16 раз меньше силы ( F_2 ), действующей на другой поршень. Как соотносятся модули работы ( (A_1) ) и ( (A_2) ) этих сил, совершаемой при перемещении поршней? Трением пренебречь.
1) ( A_1=A_2 )
2) ( A_1=16A_2 )
3) ( A_2=16A_1 )
4) ( A_1=4A_2 )
4. В сосуды различной формы налита одна и та же жидкость. Высота уровня жидкости во всех сосудах одинакова. В каком из сосудов давление на дно наименьшее?
1) в сосуде А
2) в сосуде Б
3) в сосуде В
4) во всех сосудах одинаковое
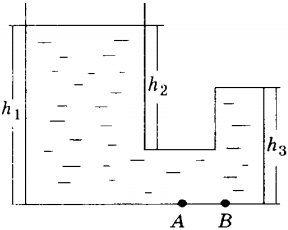
5. Стеклянный сосуд, правое колено которого запаяно, заполнен жидкостью плотностью с (см. рисунок). Давление, оказываемое жидкостью на дно сосуда в точке Б, равно
1) ( rho gh_3 )
2) ( rho gh_1 )
3) ( rho g(h_1-h_2) )
4) ( rho gh_2 )
6. Атмосферное давление на вершине горы Казбек
1) меньше, чем у её подножия
2) больше, чем у её подножия
3) равно давлению у её подножия
4) может быть больше или меньше, чем у её подножия, в зависимости от погоды
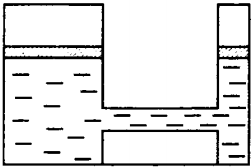
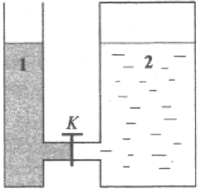
7. В открытых сосудах 1 и 2 находятся соответственно ртуть и вода. Если открыть кран К, то
1) ни вода, ни ртуть перетекать не будут
2) вода начнёт перетекать из сосуда 2 в сосуд 1
3) перемещение жидкостей будет зависеть от атмосферного давления
4) ртуть начнёт перетекать из сосуда 1 в сосуд 2
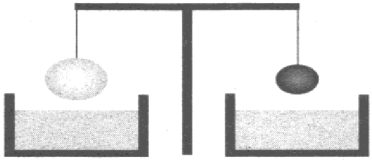
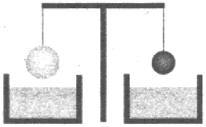
8. Два однородных шара, один из которых изготовлен из стали, а другой — из олова, уравновешены на рычажных весах (см. рисунок). Нарушится ли равновесие весов,
если шары опустить в воду?
1) Равновесие весов не нарушится, так как шары одинаковой массы.
2) Равновесие весов нарушится — перевесит шар из стали.
3) Равновесие весов нарушится — перевесит шар из олова.
4) Равновесие весов не нарушится, так как шары опускают в одну и ту же жидкость.
9. Алюминиевый шар, подвешенный на нити, опущен в крепкий раствор поваренной соли. Затем шар перенесли из раствора поваренной соли в дистиллированную воду. При этом сила натяжения нити
1) может остаться неизменной или измениться в зависимости от объёма шара
2) не изменится
3) увеличится
4) уменьшится
10. Теплоход переходит из устья реки в солёное море. При этом архимедова сила, действующая на теплоход,
1) увеличится
2) уменьшится или увеличится в зависимости от размера теплохода
3) не изменится
4) уменьшится
11. Шарик, опущенный в жидкость, начинает опускаться на дно. Как по мере движения шарика в жидкости изменяются выталкивающая сила, действующая на него, вес шарика, давление жидкости? Установите соответствие между физическими величинами и характером их изменения. Запишите в таблицу выбранные цифры под соответствующими буквами.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ
A) выталкивающая сила
Б) вес
B) давление жидкости
ХАРАКТЕР ИЗМЕНЕНИЯ ВЕЛИЧИН
1) увеличивается
2) уменьшается
3) не изменяется
12. Из перечня приведённых ниже высказываний выберите два правильных и запишите их номера в таблицу.
1) атмосферное давление можно рассчитать так же, как давление жидкости на дно сосуда.
2) в опыте Торричелли можно ртуть заменить водой при той же длине трубки.
3) для того, чтобы столб воды производил на дно сосуда такое же давление, что и столб керосина, его высота должна составлять 0,8 от высоты столба керосина.
4) на вершине горы атмосферное давление меньше, чем у её подножия.
5) закон Паскаля справедлив для газов, жидкостей и твёрдых тел.
Часть 2
13. Камень весит в воздухе 6 Н, а в воде 4 Н. Чему равен объём этого камня?
Ответы
Давление. Атмосферное давление. Закон Паскаля. Закон Архимеда
2.9 (58.53%) 68 votes