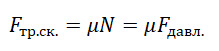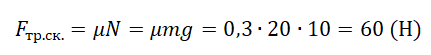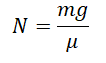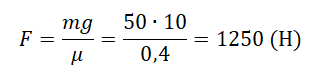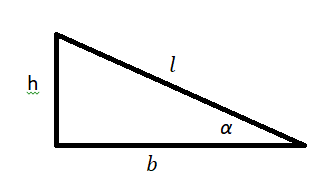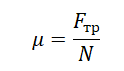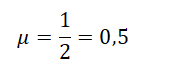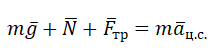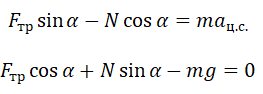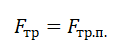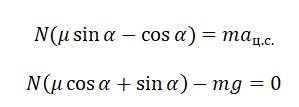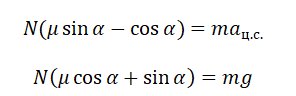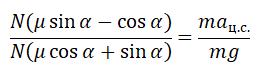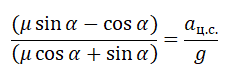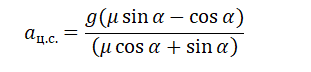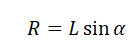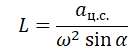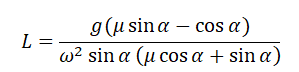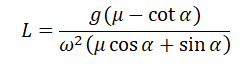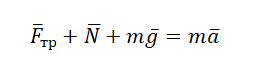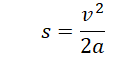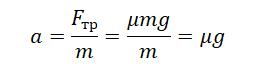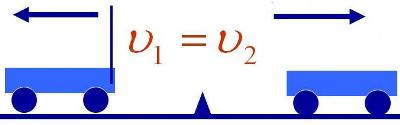в условии
в решении
в тексте к заданию
в атрибутах
Категория:
Атрибут:
Всего: 523 1–20 | 21–40 | 41–60 | 61–80 …
Добавить в вариант
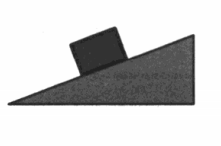
На шероховатой наклонной плоскости покоится однородный тяжёлый брусок. Угол α наклона плоскости увеличивают так, что брусок не скользит. Как в результате этого изменятся модуль действующей на брусок силы трения и момент действующей на брусок силы тяжести относительно точки O?
Для каждой величины определите соответствующий характер изменения:
1) увеличивается
2) уменьшается
3) не изменяется
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Модуль действующей
на брусок силы трения |
Момент действующей на брусок
силы тяжести относительно точки O |
На наклонной плоскости находится брусок массой 1,5 кг, для которого составлена таблица зависимости модуля силы трения Fтр от угла наклона плоскости к горизонту с погрешностью, не превышающей 0,01 Н. На основании данных, приведённых в таблице, используя закон сухого трения, выберите все верные утверждения.
| 0 | 0,05 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 | |
| Fтр, Н | 0 | 1,0 | 2,0 | 3,86 | 3,76 | 3,63 | 3,46 | 3,25 | 3,01 | 2,75 | 2,45 | 2,13 |
1) Сила трения покоя не зависит от угла
2) При уменьшении угла наклонной плоскости к горизонту модуль силы трения скольжения увеличивается.
3) С ростом угла наклона модуль силы трения покоя увеличивается.
4) Коэффициент трения скольжения больше 0,3.
5) Когда угол наклона больше 0,6 рад, брусок скользит по наклонной плоскости.
На брусок массой 5 кг, движущийся по горизонтальной поверхности, действует сила трения скольжения 20 Н. Чему будет равна сила трения скольжения после уменьшения массы тела в 2 раза, если коэффициент трения не изменится? (Ответ дайте в ньютонах.)
На брусок массой 5 кг, движущийся по горизонтальной поверхности, действует сила трения скольжения 20 Н. Чему будет равна сила трения скольжения, если коэффициент трения уменьшится в 2 раза при неизменной массе? (Ответ дайте в ньютонах.)
На брусок массой 5 кг, движущийся по горизонтальной поверхности, действует сила трения скольжения 20 Н. Чему будет равна сила трения скольжения, если коэффициент трения уменьшится в 4 раза при неизменной массе? (Ответ дайте в ньютонах.)
На брусок массой 5 кг, движущийся по горизонтальной поверхности, действует сила трения скольжения 20 Н. Чему будет равна сила трения скольжения, если, не изменяя коэффициент трения, уменьшить в 4 раза массу бруска? (Ответ дайте в ньютонах.)
На брусок массой 5 кг, движущийся по горизонтальной поверхности, действует сила трения скольжения 10 Н. Чему будет равна сила трения скольжения после уменьшения массы тела в 2 раза, если коэффициент трения не изменится? (Ответ дайте в ньютонах.)
При движении по горизонтальной поверхности на тело массой 40 кг действует сила трения скольжения 10 Н. Какой станет сила трения скольжения после уменьшения массы тела в 5 раз, если коэффициент трения не изменится? (Ответ дайте в ньютонах.)
На брусок массой 5 кг, движущийся по горизонтальной поверхности, действует сила трения скольжения 10 Н. Чему будет равна сила трения скольжения после увеличения коэффициента трения в 4 раза при неизменной массе? (Ответ дайте в ньютонах.)
На брусок массой 5 кг, движущийся по горизонтальной поверхности, действует сила трения скольжения 10 Н. Чему будет равна сила трения скольжения, если массу бруска увеличить в 2 раза, не изменяя коэффициента трения? (Ответ дайте в ньютонах.)
На брусок массой 5 кг, движущийся по горизонтальной поверхности, действует сила трения скольжения 10 Н. Если, не изменяя коэффициента трения, увеличить в 4 раза массу бруска, чему будет равна сила трения скольжения? (Ответ дайте в ньютонах.)
К неподвижному телу начинают прикладывать силу F, вызывающую ускорение В таблице приведена взаимосвязь между этими величинами. Действует ли на тело сила трения? Если да, то чему равно ее максимальное значение? (Ответ дать в ньютонах.)
| F, H | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| a, м/с2 | 0 | 0 | 0 | 1 | 2 | 3 | 4 | 5 |
Школьник скатывается на санках со склона широкого оврага и затем с разгона сразу же начинает заезжать на санках вверх, на противоположный склон оврага. Коэффициент трения полозьев санок о снег всюду одинаков, углы наклона склонов оврага к горизонту всюду одинаковы. Как в результате переезда с одного склона на другой изменяются следующие физические величины: модуль действующей на санки силы трения, модуль ускорения санок, модуль работы силы тяжести при перемещении санок вдоль склона на 1 метр?
Для каждой величины определите соответствующий характер изменения:
1) увеличивается;
2) уменьшается;
3) не изменяется.
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ
A) Модуль действующей на санки силы трения
Б) Модуль ускорения санок
B) Модуль работы силы тяжести при перемещении вдоль склона на 1 метр
ИХ ИЗМЕНЕНИЕ
1) Увеличивается
2) Уменьшается
3) Не изменяется
На покоящееся тело, находящееся на шероховатой горизонтальной плоскости, начинает действовать горизонтально направленная сила. Зависимость модуля этой силы F от времени t показана на рисунке 1. На рисунке 2 показана соответствующая зависимость модуля ускорения a этого тела от t.
Выберите все верные утверждения на основании анализа представленных графиков.
1) В момент времени t = 5 с модуль силы трения меньше модуля силы F
2) В момент времени t = 2 с сила трения равна 4 Н.
3) В интервале времени (0 с) ≤ t < (4 с) тело двигалось с отличной от нуля постоянной скоростью.
4) В интервале времени (0 с) ≤ t < (4 с) внешняя сила F не совершает работу.
5) В интервале времени (0 с) ≤ t < (4 с) сила трения совершает отрицательную работу.
В первой серии опытов брусок с грузом перемещали при помощи нити равномерно и прямолинейно вверх по наклонной плоскости. Во второй серии опытов точно так же перемещали этот брусок, но сняв с него груз. Как изменились при переходе от первой серии опытов ко второй модуль работы силы трения при перемещении бруска на одинаковые расстояния и коэффициент трения между бруском и плоскостью?
Для каждой величины определите соответствующий характер изменения:
1) увеличилась
2) уменьшилась
3) не изменилась
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Модуль работы силы
трения |
Коэффициент трения |
Источник: ЕГЭ по физике 2020. Досрочная волна. Вариант 2
Гонщик на мощном «болиде» стартует по горизонтальному прямому треку, вдавив педаль газа «в пол». Вначале ведущие колеса пробуксовывают, резина «горит», болид ускоряется, и пробуксовка в некоторый момент заканчивается. Далее мощность двигателя уже расходуется, кроме ускорения, на преодоление потерь на трение о дорогу и о воздух. Проанализируйте физические процессы, происходящие при ускорении этого автомобиля из состояния покоя до максимально возможной скорости при существующих условиях, оцените эту максимальную скорость и постройте примерный график зависимости скорости автомобиля от времени. Считайте, что максимальная мощность двигателя P = 1000 л. с. (1 лошадиная сила = 736 Вт), доля «мощности, подводимой к колёсам» (КПД трансмиссии) — а сила трения о воздух определяется «скоростным напором»
где плотность воздуха
эффективная площадь поперечного сечения «болида»
На брусок массой 5 кг, движущийся по горизонтальной поверхности, действует сила трения скольжения 20 Н.
Если, не изменяя коэффициента трения, уменьшить в 4 раза силу давления бруска на поверхность, чему будет равна сила трения скольжения? (Ответ дайте в ньютонах.)
На брусок массой 5 кг, движущийся по горизонтальной поверхности, действует сила трения скольжения 10 Н.
Если, не изменяя коэффициента трения, увеличить в 2 раза силу давления бруска на плоскость, чему будет равна сила трения скольжения? (Ответ дайте в ньютонах.)
Всего: 523 1–20 | 21–40 | 41–60 | 61–80 …
Инерциальные системы отсчета. Первый закон Ньютона. Принцип относительности Галилея
Инерциальная система отсчета — это система отсчета, в которой справедлив закон инерции: материальная точка, когда на нее не действуют никакие силы (или действуют силы, взаимно уравновешенные), находится в состоянии покоя или равномерного прямолинейного движения.
Закон этот был открыт Галилеем в 1632 г. и сформулирован Ньютоном в 1687 г. как первый закон механики.
Любая система отсчета, движущаяся по отношению к инерциальной системе отсчета поступательно, равномерно и прямолинейно, также является инерциальной системой отсчета, т. е. в ней выполняется первый закон Ньютона. Следовательно, инерциальных систем отсчета может быть сколь угодно много. Система отсчета, движущаяся с ускорением по отношению к инерциальной системе отсчета, неинерциальна и закон инерции в ней не выполняется.
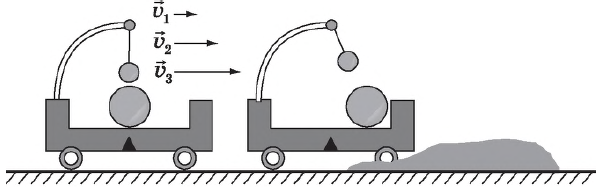
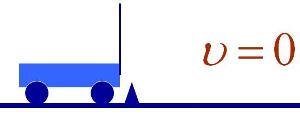
Сказанное подтверждается опытом, изображенным на рисунке. Сначала тележка движется прямолинейно и равномерно относительно земли. На ней находятся два шарика, один из которых лежит на горизонтальной поверхности, а другой подвешен на нити. Силы, действующие на каждый шарик по вертикали, уравновешены, по горизонтали никакие силы на шарики не действуют (силой сопротивления воздуха в данном случае можно пренебречь).
Шарики будут находиться в покое относительно тележки при любой скорости ее движения ($υ_1, υ_2, υ_3$ и т. д.) относительно Земли — главное, чтобы эта скорость была постоянна.
Но когда тележка попадает на песчаную насыпь, ее скорость быстро уменьшается, в результате чего тележка останавливается. Во время торможения тележки оба шарика приходят в движение, т. е. изменяют свою скорость относительно тележки, хотя нет никаких сил, которые толкали бы их.
Здесь первой (условно неподвижной) системой отсчета является Земля. Второй системой отсчета, движущейся относительно первой, является тележка. Пока тележка двигалась прямолинейно и равномерно, шарики находились в состоянии покоя относительно тележки, т. е. закон инерции выполнялся. Как только тележка начала тормозить, т. е. начала двигаться с ускорением относительно первой инерциальной системы отсчета (Земли), закон инерции перестал выполняться.
Если относительно какой-нибудь системы отсчета тело движется с ускорением, не вызванным действием на него других тел, то такую систему называют неинерциальной.
В неинерциальных системах отсчета основное положение механики о том, что ускорение тела вызывается воздействием на него других тел, не выполняется.
Следует отметить, что невозможно найти строго инерциальную систему отсчета. Реальная система отсчета всегда связывается с каким-нибудь конкретным телом (Землей, корпусом корабля или самолета и т. и.), по отношению к которому и изучается движение различных объектов. Поскольку все реальные тела движутся с тем или иным ускорением, любая реальная система отсчета может рассматриваться как инерциальная лишь приближенно.
С очень высокой степенью точности инерциальной можно считать гелиоцентрическую систему, связанную с центром Солнца и с координатными осями, направленными на три далекие звезды. Эта система используется в задачах небесной механики и космонавтики. Для решения большинства технических задач инерциальной системой отсчета можно считать любую систему, жестко связанную с Землей (или с любым телом, которое покоится или движется равномерно и прямолинейно относительно поверхности Земли).
Первый закон Ньютона
Любое тело продолжает удерживаться в своем состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменить это состояние.
Так был сформулирован Ньютоном в 1687 г. первый закон механики, или закон инерции.
Суть закона инерции впервые была изложена в одной из книг итальянского ученого Галилео Галилея, опубликованной в начале XVII в.
Ньютон обобщил выводы Галилея, сформулировав закон инерции, и включил его в качестве первого из трех законов в основу механики. Поэтому данный закон называют первым законом Ньютона.
Однако со временем выяснилось, что первый закон Ньютона выполняется не во всех системах отсчета, а только в инерциальных. Поэтому с точки зрения современных представлений первый закон Ньютона формулируется так:
Существуют системы отсчета, называемые инерциальными, относительно которых свободные тела движутся прямолинейно и равномерно.
Под свободным телом здесь понимают тело, на которое не оказывают воздействие другие тела.
Следует помнить, что в первом законе Ньютона речь идет о телах, которые могут рассматриваться как материальные точки.
Принцип относительности Галилея
Принцип относительности Галилея гласит:
Во всех инерциальных системах отсчета законы механики имеют одинаковый вид.
Это означает, что уравнения, выражающие законы механики, не меняются (инвариантны) при преобразованиях Галилея.
Преобразования Галилея заключаются в преобразовании координат $r↖{→} (х, у, z)$ и времени $t$ движущейся материальной точки при переходе от одной инерциальной системы отсчета (ИСО) к другой:
$r↖{→}={r’}↖{→}+υ↖{→}t, t=t’$ (1.47)
Для координаты $х$, например, это означает:
$x=x’+υt, t=t’,$
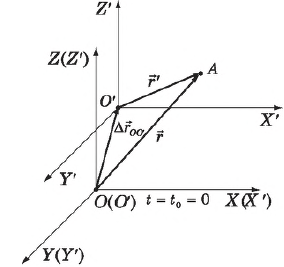
где $υ$ — относительная скорость (постоянная) движения двух ИСО, $r↖{→}$ и ${r’}↖{→}$ — радиус-векторы, а х и х1 — координаты точки в этих двух ИСО. Согласно преобразованию Галилея (1.47), время не изменяется при переходе из одной ИСО в другую: принцип относительности Галилея основан на представлениях об абсолютном времени и абсолютном пространстве, что означает одинаковость (одновременность) протекания событий во всех ИСО. Преобразования координат легко понять, если в некоторый момент времени $t_0$, принятый за начальный $t_0=0$, одну из систем координат $К(ХYZ)$ — неподвижную — совместить с другой — $К'(Х’Y’Z’)$ — подвижной и зафиксировать систему $К$.
Тогда в любой последующий момент времени положение некоторой точки $А$, движущейся относительно обеих систем координат, определяется в системе $К$ радиус-вектором $r↖{→}$, а в системе $К’$ — радиус-вектором ${r’}↖{→}$. Вектор, соединяющий начала координат $О$ неподвижной и $О’$ — подвижной систем координат, равен вектору перемещения системы $К’$ относительно $К:{OO’}↖{-}=∆r↖{→}{OO}$. Согласно правилу сложения векторов
$r↖{→}={r’}↖{→}+∆r↖{→}{OO}$
Однако вектор перемещения можно выразить через скорость движение системы $К’$ относительно $К: ∆r↖{→}{OO}=υ↖{→}t$. Поэтому
$r↖{→}={r’}↖{→}+υ↖{→}t$
что совпадает с (1.47).
Из уравнения (1.47) вытекает закон сложения скоростей:
$u↖{→}={u’}↖{→}+υ↖{→},$
где $u$ и $u’$ — скорости точки относительно систем $К$ и $К’$ соответственно.
Принцип относительности Галилея означает, что никакими механическими опытами нельзя обнаружить движение одной инерциальной системы координат относительно другой. Именно поэтому, находясь в салоне сверхзвукового самолета, пассажиры могут спокойно передвигаться, не чувствуя его скорости.
Не нужно, однако, думать, что выполнение принципа относительности означает полную тождественность движения одного и того же тела относительно разных инерциальных систем координат. Тождественны лишь законы движения. Характер же движения определяется начальными условиями (начальными скоростями и координатами тела), которые различны в разных системах отсчета.
Так, камень, выпущенный из рук в движущемся вагоне поезда, будет падать вертикально лишь относительно стен вагона, а для наблюдателя, находящегося на платформе, он будет двигаться по параболе. Объясняется это тем, что начальные скорости разные: относительно стен вагона начальная скорость равна нулю, а относительно Земли она равна скорости движения вагона.
Взаимодействие. Сила. Принцип суперпозиции сил
Взаимодействие в физике — это воздействие тел или частиц друг на друга, приводящее к изменению их движения.
Близкодействие и дальнодействие (или действие на расстоянии). О том, как осуществляется взаимодействие тел, в физике издавна существовали две точки зрения. Первая из них предполагала наличие некоторого агента (например, эфира), через который одно тело передает свое влияние на другое, причем с конечной скоростью. Это теория близкодействия. Вторая предполагала, что взаимодействие между телами осуществляется через пустое пространство, не принимающее никакого участия в передаче взаимодействия, причем передача происходит мгновенно. Это теория дальнодействия. Она, казалось бы, окончательно победила после открытия Ньютоном закона всемирного тяготения. Так, например, считалось, что перемещение Земли должно сразу же приводить к изменению силы тяготения, действующей на Луну. Кроме самого Ньютона, позднее концепции дальнодействия придерживались Кулон и Ампер.
После открытия и исследования электромагнитного поля теория дальнодействия была отвергнута, так как было доказано, что взаимодействие электрически заряженных тел осуществляется не мгновенно, а с конечной скоростью (равной скорости света: $c=3·10^8$ м/с) и перемещение одного из зарядов приводит к изменению сил, действующих на другие заряды, не мгновенно, а спустя некоторое время. Возникла новая теория близкодействия, которая была затем распространена и на все другие виды взаимодействий. Согласно теории близкодействия взаимодействие осуществляется посредством соответствующих полей, окружающих тела и непрерывно распределенных в пространстве (т. е. поле является тем посредником, который передает действие одного тела на другое). Взаимодействие электрических зарядов — посредством электромагнитного поля, всемирное тяготение — посредством гравитационного поля.
На сегодняшний день физике известны четыре типа фундаментальных взаимодействий, существующих в природе (в порядке возрастания интенсивности): гравитационное, слабое, электромагнитное и сильное взаимодействия.
Фундаментальными называются взаимодействия, которые нельзя свести к другим типам взаимодействий.
Фундаментальные взаимодействия отличаются интенсивностью ж радиусом действия. Под радиусом действия понимают максимальное расстояние между частицами, за пределами которого их взаимодействием можно пренебречь.
По радиусу действия фундаментальные взаимодействия делятся на дальнодействующие (гравитационное и электромагнитное) и короткодействующие (слабое и сильное).
Гравитационное взаимодействие универсально: в нем участвуют все тела в природе — от звезд, планет и галактик до микрочастиц: атомов, электронов, ядер. Его радиус действия равен бесконечности. Однако как для элементарных частиц микромира, так и для окружающих нас предметов макромира силы гравитационного взаимодействия настолько малы, что ими можно пренебречь. Оно становится заметным с увеличением массы взаимодействующих тел и потому определяющим в поведении небесных тел и образовании и эволюции звезд.
Основные характеристики фундаментальных взаимодействий
| Взаимодействие | Взаимодействующие частицы | Радиус действия, $м$ | Относительная интенсивность |
| Гравитационное | Все | $∞$ | 1 |
| Слабое | Все, кроме фотона | $10^{-17}$ | $10^{32}$ |
| Электромагнитное | Заряженные частицы | $∞$ | $10^{36}$ |
| Сильное | Адроны | $10^{-15}$ | $10^{38}$ |
Слабое взаимодействие присуще всем элементарным частицам, кроме фотона. Оно отвечает за большинство ядерных реакций распада и многие превращения элементарных частиц.
Электромагнитное взаимодействие определяет структуру вещества, связывая электроны и ядра в атомах и молекулах, объединяя атомы и молекулы в различные вещества. Оно определяет химические и биологические процессы. Электромагнитное взаимодействие является причиной таких явлений, как упругость, трение, вязкость, магнетизм и составляет природу соответствующих сил. На движение макроскопических электронейтральных тел оно существенного влияния не оказывает.
Сильное взаимодействие осуществляется между адронами, именно оно удерживает нуклоны в ядре.
В 1967 г. Шелдон Глэшоу, Абдус Салам и Стивен Вайнберг создали теорию, объединяющую электромагнитное и слабое взаимодействия в единое электрослабое взаимодействие с радиусом действия $10^{-17} м$, в пределах которого исчезает различие между слабым и электромагнитным взаимодействиями.
В настоящее время выдвинута теория великого объединения, согласно которой существуют лишь два типа взаимодействий: объединенное, куда входят сильное, слабое и электромагнитное взаимодействия, и гравитационное взаимодействие.
Есть также предположение, что все четыре взаимодействия являются частными случаями проявления единого взаимодействия.
В механике взаимное действие тел друг на друга характеризуется силой. Более общей характеристикой взаимодействия является потенциальная энергия.
Силы в механике делятся на гравитационные, упругости и трения. Как уже упоминалось выше, природа механических сил обусловлена гравитационным и электромагнитным взаимодействиями. Только эти взаимодействия можно рассматривать как силы в смысле механики Ньютона. Сильные (ядерные) и слабые взаимодействия проявляются на таких малых расстояниях, при которых законы механики Ньютона, а вместе с ними и понятие механической силы теряют смысл. Поэтому термин «сила» в этих случаях следует воспринимать как «взаимодействие».
Сила
Сила в механике — это величина, являющаяся мерой взаимодействия тел.
При механическом движении проявляются следующие виды сил: силы упругости, силы трения и гравитационные силы (всемирного тяготения).
Действие одного тела на другое приводит как к изменению скорости всего тела как целого, так и к изменению скорости отдельных его частей.
Мерой этого действия является сила. Часто не указывают, какое тело и как действовало на данное тело. Просто говорят, что на тело действует сила, или к нему приложена сила.
Действие одного тела на другое может производиться как при непосредственном контакте (давление, трение), так и посредством создаваемых телами полей (электромагнитное поле, гравитационное поле).
Проявлением действия силы является изменение ускорения тела.
Сила, как и скорость, — векторная величина, т. е. имеет не только численное значение, но и направление. Сила обычно обозначается буквой $F↖{→}$, модуль силы — буквой $F$ (без стрелки). Прямая, вдоль которой направлена сила, называется линией действия силы. Когда говорят о силе, важно указать, к какой точке тела приложена действующая на него сила. Если речь идет об абсолютно твердом (недеформируемом) теле, то можно считать, что сила приложена к любой точке на линии ее действия.
Итак, результат действия силы на тело зависит от ее модуля, направления и точки приложения.
Иначе говоря, сила — векторная величина, характеризующаяся численным значением, направлением в пространстве и точкой приложения.
Единицей силы в СИ является ньютон (H). Один ньютон (1 H) — это сила, которая за $1$с изменяет скорость тела массой $1$ кг на $1$ м/с. Эта единица названа в честь великого английского ученого Исаака Ньютона (1642-1727). На практике применяются также килоньютоны и миллиньютоны:
$1кH|=1000H, 1мH=0.001H.$
Принцип суперпозиции сил
Обычно на любое движущееся тело действует не одна, а сразу несколько сил. Так, например, на парашютиста, спускающегося на землю, действуют сила тяжести и сила сопротивления воздуха. На тело, висящее на пружине, действуют две силы: сила тяжести и сила упругости пружины.
В каждом подобном случае несколько сил, приложенных к телу, можно заменить одной суммарной силой $F↖{→}$, равноценной по своему действию этим силам. Сила, производящая на тело такое же действие, как несколько одновременно действующих сил, называется равнодействующей этих сил:
$F↖{→}=∑↙{i=1}↖{n}{F_i}↖{→}={F_1}↖{→}+{F_2}↖{→}+…+{F_n}↖{→}$
В этом состоит принцип суперпозиции (наложения) сил.
Равнодействующая сила, действующая на частицу со стороны других тел, равна векторной сумме сил, с которыми каждое из этих тел действует на частицу.
Для нахождения равнодействующей силы пользуются правилами сложения векторов (поскольку сила — векторная величина), в частности, сложение двух сил производится по правилу параллелограмма.
О двух силах, равных по величине и направленных вдоль одной прямой в противоположные стороны, говорят, что они уравновешивают, или компенсируют друг друга. Равнодействующая $F$ таких сил всегда равна нулю и потому изменить скорость тела не может.
Для изменения скорости тела относительно Земли необходимо, чтобы равнодействующая всех приложенных к телу сил была отлична от нуля. В том случае, когда тело движется в направлении равнодействующей силы, его скорость возрастает; при движении в противоположном направлении скорость тела убывает. Таким образом, направление скорости не всегда совпадает с направлением действующей силы $F$, а вот изменение направления скорости (а следовательно, и направление ускорения) всегда совпадает с направлением действующей силы.
Второй закон Ньютона
Второй закон Ньютона формулируется так:
Ускорение тела прямо пропорционально равнодействующей всех сил, приложенных к телу, и обратно пропорционально его массе. Направление ускорения совпадает с направлением равнодействующей всех сил.
Следует помнить, что во втором законе Ньютона, так же, как и в первом, под телом подразумевается материальная точка, движение которой рассматривается в инерциальной системе отсчета.
Математически второй закон Ньютона выражается формулой:
$a↖{→}={F↖{→}}/{m}$
В скалярном виде второй закон можно записать:
${a_x}↖{→}={{F_x}↖{→}}/{m}$
$a={F}/{m}$
Отсюда можно вывести два следствия:
- Чем больше сила, приложенная к телу, тем больше его ускорение, и следовательно, тем быстрее изменяется скорость движения этого тела.
- Чем больше масса тела, тем меньшее ускорение оно получает в результате действия данной силы и потому тем медленнее изменяет свою скорость.
Из формулы $a↖{→}={F↖{→}}/{m}$ следует:
$F↖{→}=a↖{→}m$
Формулировка второго закона механики, данная самим Ньютоном, такова:
Изменение количества движения пропорционально приложенной движущей силе и происходит по направлению той прямой, по которой эта сила действует.
В современном виде закон этот записывается следующим образом:
${d(mυ↖{→})}/{dt}=F↖{→}$
где $mυ↖{→}$ — количество движения тела. Количество движения называют также импульсом тела $p↖{→}$:
$p↖{→}=mυ↖{→}$
Когда равнодействующая сил, приложенных к телу, постоянна ($F↖{→}=const$), дифференцирование в ${d(mυ↖{→})}/{dt}=F↖{→}$ можно заменить разностью $∆$, поскольку изменение скорости (ускорение) постоянно:
$∆p↖{→}=F↖{→}∆t$
Второй закон Ньютона иногда называют основным законом динамики. После его открытия стало возможным решать такие задачи о движении тел, которые до Ньютона казались неразрешимыми. Многие казавшиеся ранее непонятными явления теперь были объяснены на основе открытых законов физики.
На основании второго закона Ньютона вводится единица силы в СИ — ньютон (Н). Один ньютон ($1Н$) — это сила, с которой нужно действовать на тело массой в $1$ кг, чтобы сообщить ему ускорение в $1$ м/$с^2$.
Подставив в формулу значения ускорения и массы с их размерностями из приведенного определения, выразим размерность силы в $1Н$ через основные единицы СИ:
$1H=1кг·1$м/$с^2=1кг·$м/$с^2$
Третий закон Ньютона
Третий закон Ньютона гласит:
Действию всегда есть равное и противоположное противодействие, иначе — взаимодействия двух тел друг на друга между собой равны и направлены в противоположные стороны.
В своем первом законе Ньютон описал движение тела, не подверженного действию других тел. В этом случае тело либо сохраняет свое состояние покоя, либо движется равномерно и прямолинейно (относительно инерциальной системы отсчета).
Во втором законе Ньютона речь идет о прямо противоположной ситуации. Теперь на данное тело действуют внешние тела, причем их количество может быть произвольным. Под действием окружающих тел рассматриваемое тело начинает двигаться с ускорением, причем произведение массы данного тела на его ускорение оказывается равным действующей силе.
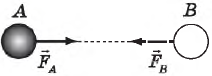
Сформулировав эти два закона, Ньютон обратился к анализу ситуации, когда во взаимодействии участвуют только два тела. Допустим, имеются два тела $А$ и $В$, которые притягивают друг друга с силами $F$ и $F’$, Может ли одна из этих сил быть больше другой? Размышление над этой проблемой привело Ньютона к выводу, что такого быть не может: силы взаимодействия двух тел всегда равны друг другу. Каким образом Ньютон пришел к такому заключению? Вот как он рассуждал: «Относительно притяжения дело может быть изложено вкратце следующим образом: между двумя взаимно притягивающимися телами надо вообразить какое-либо препятствие, мешающее их сближению. Если бы одно из тел $А$ притягивалось телом $В$ сильнее, нежели тело $В$ притягивается телом $А$, то препятствие испытывало бы со стороны тела $А$ большее давление, нежели со стороны тела $В$, и, следовательно, не осталось бы равновесия. Преобладающее давление вызвало бы движение системы, состоящей из этих двух тел и препятствия, в сторону тела $В$, ив свободном пространстве эта система, двигаясь ускоренно, ушла бы в бесконечность. Такое заключение нелепо и противоречит первому закону. Отсюда следует, что оба тела давят на препятствие с равными силами, а значит, и притягиваются взаимно с таковыми же».
Следует помнить, что силы, о которых говорится в законе Ньютона, никогда не уравновешивают друг друга, поскольку они приложены к разным телам. Две равные по модулю и противоположно направленные силы уравновешивают друг друга в том случае, если они приложены к одному телу. Тогда их равнодействующая равна нулю, и тело при этом находится в равновесии, т. е. либо покоится, либо движется равномерно и прямолинейно.
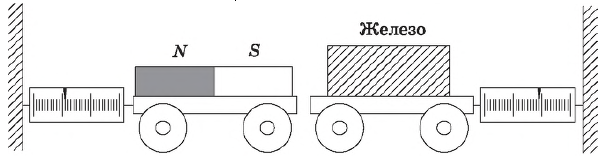
Опыты подтверждают вывод Ньютона. Если, например, взять две тележки и на одной из них закрепить магнит, а на другой кусок железа, а затем соединить их с динамометрами, то мы увидим, что показания этих приборов совпадут. Это означает, что сила, с которой магнит притягивает к себе железо, равна по величине силе, с которой железо притягивает к себе магнит. Эти силы равны по абсолютной величине и противоположны по направлению: сила притяжения к магниту направлена влево, а сила притяжения к железу вправо.
Итак, третий закон Ньютона на более привычном для нас языке может быть сформулирован так:
Силы, с которыми взаимодействуют любые два тела, всегда равны по величине и противоположны по направлению.
Математически он записывается в следующем виде:
${F_1}↖{→}=-{F_2}↖{→}$
Знак «минус» показывает, что векторы сил направлены в противоположные стороны. Используя второй закон Ньютона, можно записать:
$m_1{a_1}↖{→}=-m_2{a_2}↖{→}$
Отсюда следует, что
${a_1}/{a_2}={m_2}/{m_1}$
Таким образом, отношение модулей ускорений двух взаимодействующих тел определяется исключительно их массами (чем меньше масса тела, тем большее ускорение оно приобретает) и не зависит от природы сил взаимодействия.
Третий закон Ньютона обосновывает введение самого термина «взаимодействие»: если одно тело действует на другое, то второе также действует на первое. Другими словами, не может быть такого, чтобы одно тело на другое действовало, а второе на первое — нет. Как писал сам Ньютон, «если кто нажимает пальцем на камень, то и палец его также нажимается камнем. Если лошадь тащит камень, привязанный к канату, то и обратно (если можно так выразиться) она с равным усилием оттягивается к камню».
Трение — вариант взаимодействия двух тел. Оно возникает при движении одного тела по поверхности другого. При этом тела действуют друг на друга с силой, которая называется силой трения. Сила трения имеет электромагнитную природу.
Сила трения — сила, возникающая между телами при их движении или при попытке их сдвинуть. Обозначается как Fтр. Единица измерения — Н (Ньютон).
Трение бывает сухим и жидким. В школьном курсе физике изучается сухое трение.
Виды сухого трения:
- трение скольжения;
- трение качения;
- трение покоя.
Трение скольжения
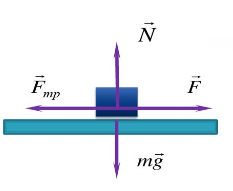
Трение скольжения — трение, возникающее при скольжении одного тела по поверхности другого. Сила трения скольжения направлена противоположно направлению движения тела: Fтр↑↓v.
Сила трения скольжения определяется формулой:
μ — коэффициент трения, N — сила реакции опоры, Fдавл. — сила нормального давления
Сила реакции опоры и сила нормального давления — равные по модулю, но противоположные по направлению силы. Если тело не перемещается с ускорением относительно оси ОУ, модули силы реакции опоры и силы нормального давления равны модулю силы тяжести, действующей на это тело.
Силу трения скольжения зависит от степени неровности (шероховатости) поверхности. Поэтому ее можно легко менять.
Чтобы увеличить силу трения скольжения, нужно сделать поверхность тела более шероховатой. Так, чтобы зимой автомобили не скользили по голому льду, автомобилисты используют зимние шины. От летних они отличаются глубоким протектором и наличием шипов, создающих дополнительную неровность.
Чтобы уменьшить силу трения скольжения, нужно сделать поверхность более ровной. Ее можно отшлифовать или смазать. Так, чтобы лыжи скользили по снегу лучше, их смазывают специальными мазями или парафинами.
Полезные факты
- Если тело движется по гладкой поверхности, сила трения между ними отсутствует.
- Сила трения скольжения не зависит от площади соприкосновения тел.
- Сила трения качения обычно в несколько раз меньше силы трения скольжения. Поэтому тяжелые грузы перемещают не волоком, а с помощью тележек на колесах.
Пример №1. Конькобежец массой 70 кг скользит по льду. Какова сила трения, действующая на конькобежца, если коэффициент трения скольжения коньков по льду равен 0,002?
Сила реакции опоры по модулю равна силе тяжести, действующей на конькобежца. Отсюда:
Трение покоя
Трение покоя возникает при попытке сдвинуть предмет с места. Трение покоя противоположно направлено приложенной к телу силе (в сторону возможного движения).
Сила трения покоя всегда больше нуля, но всегда меньше силы трения скольжения:
0 < Fтр.пок. < Fтр. ск.
Способы определения вида силы трения, возникающей между телами, и ее модуля:
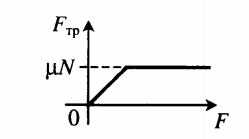
- Когда к телу прикладывается сила F , модуль которой меньше силы трения скольжения, возникает сила трения покоя. Тело продолжает покоиться. При этом модуль силы трения покоя равен модулю прикладываемой к телу силы. Если F < Fтр. ск., Fтр.пок. = F.
- Когда к телу прикладывается сила, модуль которой равен силе трения скольжения или превышает ее, возникает сила трения скольжения. Тело при этом начинает двигаться. Сила трения определяется формулой силы трения скольжения. Если F ≥ Fтр. ск., Fтр. = Fтр.ск.
Графически это можно изобразить так:
Пример №2. На горизонтальном полу стоит ящик массой 20 кг. Коэффициент трения между полом и ящиком равен 0,3. К ящику в горизонтальном направлении прикладывают силу 36 Н. Какова сила трения между ящиком и полом?
Чтобы определить вид трения, возникающего между ящиком и полом, нужно найти силу трения скольжения и сравнить с ней приложенную к ящику силу.
Сила, приложенная к ящику, меньше силы трения скольжения. Значит, между ящиком и полом возникает сила трения покоя. Модуль силы трения покоя равен модулю приложенной силы:
Fтр.пок. = F = 36 (Н).
Описание движения тел с учетом сил трения
Тело может двигаться по горизонтальной, наклонной или вертикальной плоскости. Оно может покоиться, двигаться равномерно или с ускорением, а сила тяги, под действием которой движется тело, может быть направлена, как в сторону движения тела, так и под углом к плоскости. Поэтому применение законов Ньютона к каждому из случаев имеет свои особенности.
Движение тела по горизонтальной плоскости
Равноускоренное движение по горизонтали, сила тяги параллельная плоскости |
|
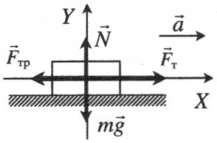 |
Второй закон Ньютона в векторной форме:
mg + N + Fт + Fтр = ma Проекция на ось ОХ: Fт – Fтр = ma Проекция на ось ОУ: N – mg = 0 |
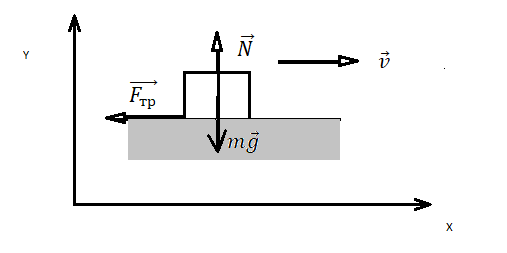
Равнозамедленное движение по горизонтали, сила тяги параллельная плоскости |
|
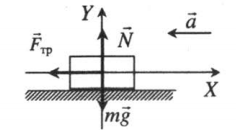 |
Второй закон Ньютона в векторной форме:
mg + N + Fт + Fтр = ma Проекция на ось ОХ: – Fтр = –ma Проекция на ось ОУ: N – mg = 0 |
Ускоренное движение по горизонтали, сила тяги направлена под углом к горизонту (вверх) |
|
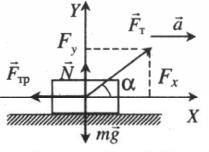 |
Второй закон Ньютона в векторной форме:
mg + N + Fт + Fтр = ma Проекция на ось ОХ: Fтcosα – Fтр = ma Проекция на ось ОУ: Fтsinα + N – mg = 0 |
Ускоренное движение по горизонтали, сила тяги направлена под углом к горизонту (вниз) |
|
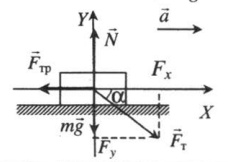 |
Второй закон Ньютона в векторной форме:
mg + N + Fт + Fтр = ma Проекция на ось ОХ: Fтcosα – Fтр = ma Проекция на ось ОУ: N – Fтsinα – mg = 0 |
Внимание! В случаях, когда сила тяги Fт направлена под углом к плоскости движения, сила реакции опоры не равна силе тяжести: N ≠ mg.
Пример №3. Брусок массой 1 кг движется равноускоренно по горизонтальной поверхности под действием силы 10 Н, как показано на рисунке. Коэффициент трения скольжения равен 0,4, а угол наклона α — 30 градусов. Чему равен модуль силы трения?
Сила трения равна произведению коэффициента трения скольжения на силу реакции опоры:
Fтр = μN
Проекция сил на ось ОУ выглядит так:
N – Fтsinα – mg = 0
Отсюда силы реакции опоры равна:
N = Fтsinα + mg
Подставим ее в формулу для вычисления силы трения и получим:
Fтр = μN = μ (Fтsinα + mg) = 0,4(10∙0,5 + 1∙10) = 6 (Н)
Движение тела по вертикальной плоскости
Тело прижали к вертикальной плоскости и удерживают |
|
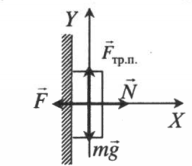 |
Второй закон Ньютона в векторной форме:
mg + N + Fт + Fтр = ma Проекция на ось ОХ: N – F = 0 Проекция на ось ОУ: Fт.п. – mg = 0 |
Тело поднимается под действием силы тяги, направленной под углом к вертикали |
|
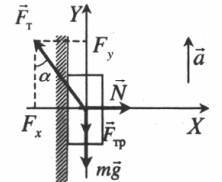 |
Второй закон Ньютона в векторной форме:
mg + N + Fт + Fтр = ma Проекция на ось ОХ: N – Fтsinα = 0 Проекция на ось ОУ: Fтcosα – Fтр – mg = 0 |
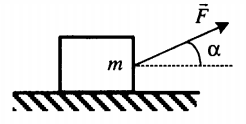
Пример №4. Груз массой 50 кг удерживают на вертикальной плоскости, коэффициент трения которой равен 0,4. Определить, какую силу нужно приложить, чтобы груз оставался в состоянии покоя.
Проекция на ось ОХ:
N – F = 0
Отсюда следует, что сила должна быть равна силе реакции опоры.
Проекция на ось ОУ:
Fт.п. – mg = 0
Перепишем, выразив силу трения через силу реакции опоры:
μN – mg = 0
Отсюда выразим силу реакции опоры:
Следовательно:
Движение тела по наклонной плоскости
Движение вниз без трения |
|
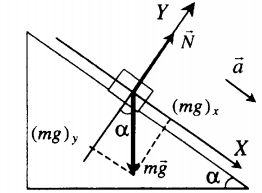 |
Второй закон Ньютона в векторной форме: |
|
mg + N = ma |
|
| Проекция на ось ОХ: | |
|
mg sinα = ma |
|
| Проекция на ось ОУ: | |
|
N – mg cosα = 0 |
|
Тело покоится на наклонной плоскости |
|
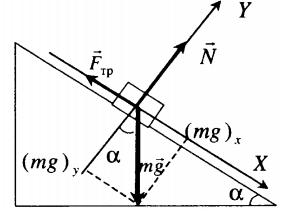 |
Второй закон Ньютона в векторной форме: |
|
mg + N + Fтр = ma |
|
| Проекция на ось ОХ: | |
|
mg sinα – Fтр.п. = 0 |
|
| Проекция на ось ОУ: | |
|
N – mg cosα = 0 |
|
Тело удерживают на наклонной плоскости |
|
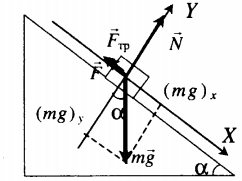 |
Второй закон Ньютона в векторной форме: |
|
mg + N + F + Fтр = ma |
|
| Проекция на ось ОХ: | |
|
F + Fтр. – mg sinα = ma |
|
| Проекция на ось ОУ: | |
|
N – mg cosα = 0 |
|
Равноускоренное движение вверх с учетом силы трения |
|
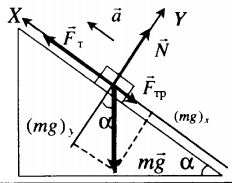 |
Второй закон Ньютона в векторной форме: |
|
mg + N + Fт + Fтр = ma |
|
| Проекция на ось ОХ: | |
|
Fт – mg sinα – Fтр. = ma |
|
| Проекция на ось ОУ: | |
|
N – mg cosα = 0 |
|
Равномерное движение вверх с учетом силы трения |
|
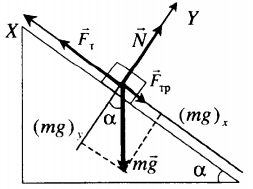 |
Второй закон Ньютона в векторной форме: |
|
mg + N + F + Fтр = ma |
|
| Проекция на ось ОХ: | |
|
Fт – mg sinα – Fтр. = 0 |
|
| Проекция на ось ОУ: | |
|
N – mg cosα = 0 |
Пример №5. Брусок массой 200 г покоится на наклонной плоскости. Коэффициент трения между поверхностью бруска и плоскостью равен 0,6. Определите величину силы трения, если угол наклона плоскости к горизонту равен 30 градусам.
Переведем массу в килограммы: 200 г = 0,2 кг.
Проекция сил, действующих на тело, на ось ОХ:
mg sinα – Fтр.п. = 0
Отсюда сила трения равна:
Fтр.п. = mg sin α
Подставляем известные данные и вычисляем:
Fтр.п. = 0,2∙10∙sin30o = 2∙0,5 = 1 (Н)
Полезная информация
Задание EF18204
При исследовании зависимости силы трения скольжения Fтр от силы нормального давления Fд были получены следующие данные:
|
Fтр, Н |
1,0 |
2,0 |
3,0 |
4,0 |
|
Fд, Н |
2,0 |
4,0 |
6,0 |
8,0 |
Из результатов исследования можно сделать вывод, что коэффициент трения скольжения равен:
а) 0,2
б) 2
в) 0,5
г) 5
Алгоритм решения
1.Записать формулу, связывающую силу трения с силой нормального давления.
2.Выразить из нее коэффициент трения.
3.Взять значения силы трения и силы нормального давления из любого опыта (из любого столбца таблицы).
4.Вычислить коэффициент трения на основании табличных данных.
Решение
Силу трения и силу нормального давления связывает формула:
Fтр = μN
Отсюда коэффициент трения равен:
Сделаем расчет коэффициента трения на основании данных первого опыта (1 столбца):
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF17513
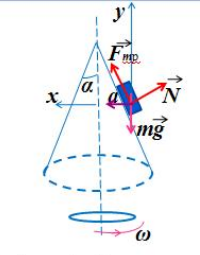
Полый конус с углом при вершине 2α вращается с угловой скоростью ω вокруг вертикальной оси, совпадающей с его осью симметрии. Вершина конуса обращена вверх. На внешней поверхности конуса находится небольшая шайба, коэффициент трения которой о поверхность конуса равен μ. При каком максимальном расстоянии L от вершины шайба будет неподвижна относительно конуса? Сделайте схематический рисунок с указанием сил, действующих на шайбу.
Алгоритм решения
1.Построить чертеж. Указать все силы, действующие на шайбу. Выбрать систему координат.
2.Записать второй закон Ньютона для описания движения шайбы в векторном виде.
3.Записать второй закон Ньютона в виде проекций на оси.
4.Через систему уравнений вывести искомую величину.
Решение
Так как шайба вращается, покоясь на поверхности конуса, на нее действуют четыре силы: сила трения, сила тяжести, сила реакции опоры и центростремительная сила. Изобразим их на чертеже. Выберем систему координат, параллельную оси вращения.
Второй закон Ньютона в векторном виде выглядит следующим образом:
Теперь запишем этот закон в проекциях на оси ОХ и ОУ соответственно:
Так как шайба покоится относительно поверхности конуса, сила трения равна силе трения покоя:
Максимальное значение силы трения равно:
Принимая в учет силу трения покоя, проекции на оси ОХ и ОУ примут следующий вид:
Запишем систему уравнение в следующем виде:
Поделим первое уравнение на второе и получим:
Сделаем сокращения и получим:
Отсюда центростремительное ускорение равно:
Но также известно, что центростремительное ускорение равно произведению квадрата угловой скорости на радиус окружности:
Радиус окружности, по которой вращается шайба вместе с конусом, можно вычислить по формуле:
Отсюда центростремительное ускорение равно:
Выразим искомую величину L:
Подставим в это выражение выведенную для центростремительного ускорения формулу и получим:
Поделим числитель на синус угла α, чтобы упростить выражение, и получим:
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF18051
Грузовик массой m, движущийся по прямолинейному горизонтальному участку дороги со скоростью υ, совершает торможение до полной остановки. При торможении колёса грузовика не вращаются. Коэффициент трения между колёсами и дорогой равен μ. Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать.
К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.
Алгоритм решения
1.Записать исходные данные.
2.Сделать чертеж. Указать все силы, действующие на грузовик во время торможения. Выбрать систему координат.
3.Записать второй закон Ньютона в векторной форме.
4.Записать второй закон Ньютона в виде проекций на оси ОХ и ОУ.
5.Записать формулу для нахождения силы трения скольжения.
6.Записать формулу для расчета перемещения при движении с постоянным ускорением.
7.Использовать второй закон Ньютона для определения тормозного пути.
Решение
Из условий задачи нам известны следующие величины:
• Начальная скорость грузовика (до начала торможения) v0 = v.
• Коэффициент трения между колесами и дорогой μ.
Выполним чертеж. Выберем такую систему координат, в которой направление движения грузовика во время торможения совпадает с направлением оси ОХ:
Запишем второй закон Ньютона в векторной форме:
Запишем второй закон Ньютона в проекциях на оси:
Fтр = ma
N – mg = 0
Известно, что сила трения скольжения определяется формулой:
Fтр = μN = μmg
Значит, в первую ячейку таблицы мы должны поставить «1».
Перемещение при равнозамедленном движении определяется формулой (учтем, что конечная скорость равна 0, так как грузовик остановился):
Выразим ускорение через проекцию сил на ось ОХ:
Подставим найденное ускорение в формулу тормозного пути и получим:
Следовательно, во вторую ячейку таблицы мы должны поставить «4».
Полный ответ: «14».
Ответ: 14
pазбирался: Алиса Никитина | обсудить разбор | оценить
Алиса Никитина | Просмотров: 13.1k
Взаимодействие тел. Понятие силы. Принцип суперпозиции. Сила упругости, силы трения.
Краткий ответ
Жизненный опыт показывает, что скорость тела меняется только в результате действия на него другого тела.
Действие тел друг на друга называют взаимодействием.
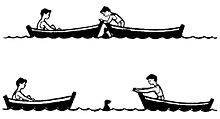
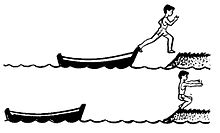
Если человек, сидящий в лодке, отталкивает от себя другую лодку, то происходит взаимодействие. Обе лодки приходят в движение.
В повседневной жизни мы постоянно встречаемся с различными видами воздействий одних тел на другие. Чтобы открыть дверь, нужно «подействовать» на нее рукой, от воздействия ноги мяч летит в ворота, даже присаживаясь на стул, вы действуете на него. В то же время, открывая дверь, мы ощущаем ее воздействие на нашу руку, действие мяча на ногу особенно ощутимо, если вы играете в футбол босиком, а действие стула не позволяет нам упасть на пол. То есть действие всегда является взаимодействием: если одно тело действует на другое, то и другое тело действует на первое. Эти примеры подтверждают вывод ученых о том, что в природе мы всегда имеем дело с взаимодействием, а не с односторонним действием.
Величину, характеризующую взаимодействие тел, называют сила.
Сила — физическая величина, которая определяет меру воздействия одного тела на другое.
F — обозначение силы
Сила – векторная величина; она характеризуется:
- модулем (абсолютной величиной);
- направлением;
- точкой приложения.
Измеряется сила при помощи прибора «динамометр».
Единица измерения силы в Международной системе единиц (СИ) — Ньютон, обозначение [Н].
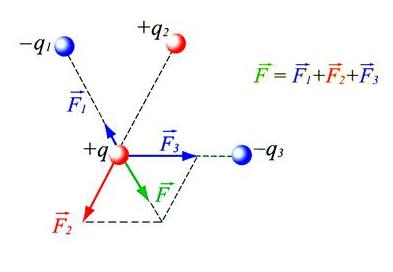
Если на тело одновременно действуют несколько сил (например,F1,F2 и F3) то под силой, действующей на тело, нужно понимать равнодействующую всех сил: F=F1+F2+F3
Принцип суперпозиции сил: если тело взаимодействует одновременно с несколькими телами, то результирующая сила, действующая на данное тело, равна векторной сумме сил, действующих на это тело со стороны всех других тел.
Для заряженных тел:
Основные виды сил: сила тяжести, сила трения, сила упругости.
При соприкосновении двух движущихся тел возникает сила, направленная против движения и препятствующая движению — сила трения.
Сила трения — это сила, возникающая при движении одного тела по поверхности другого, приложенная к движущемуся телу и направлена против движения.
Сила трения — это сила электромагнитной природы.
Возникновение силы трения объясняется двумя причинами:
1) Шероховатостью поверхностей
2) Проявлением сил молекулярного взаимодействия.
Силы трения всегда направлены по касательной к соприкасающимся поверхностям и подразделяются на силы трения покоя, силы трения скольжения, силы трения качения.
Fтр = м*N, где м – коэффициент трения , N – сила реакции опоры.
Сила упругости – сила, которая возникает при любом виде деформации тел и стремится вернуть тело в первоначальное состояние.
Fупрx = — k*x, где k – жесткость тела [Н/м], х — абсолютное удлинение тела.
Сила упругости перпендикулярна поверхности взаимодействующих тел и направлена всегда против деформации.
Развернутый ответ
Изменение скорости тела происходит под действием другого тела. Покажем это.
Опыт с тележками. К тележке прикрепим упругую пластинку. Затем изогнем ее и свяжем нитью. Тележка относительно стола находится в покое.
Станет ли двигаться тележка, если упругая пластинка выпрямится? Для этого перережем нить. Пластинка выпрямится. Тележка же останется на прежнем месте.
Затем вплотную к согнутой пластинке поставим еще одну такую же тележку.
Вновь пережжем нить. После этого обе тележки приходят в движение относительно стола. Они разъезжаются в разные стороны.
Чтобы изменить скорость тележки, понадобилось второе тело. Опыт показал, что скорость тела меняется только в результате действия на него другого тела (второй тележки). В нашем опыте мы наблюдали, что в движение пришла и вторая тележка. Обе стали двигаться относительно стола.
Тележки действуют друг на друга , т.е они взаимодействуют. Значит, действие одного тела на другое не может быть односторонним, оба тела действуют друг на друга, т. е. взаимодействуют.
Действие тел друг на друга называют взаимодействием.
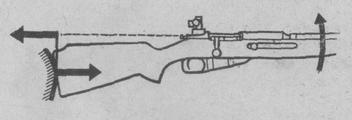
Пуля также находится в покое относительно ружья перед выстрелом. При взаимодействии (во время выстрела) пуля и ружье движутся в разные стороны. Получается явление — отдачи.
Если человек, сидящий в лодке, отталкивает от себя другую лодку, то происходит взаимодействие. Обе лодки приходят в движение.
Если человек прыгает с лодки на берег, то лодка отходит в сторону, противоположную прыжку. Человек подействовал на лодку. В свою очередь, и лодка действует на человека. Он приобретает скорость, которая направлена к берегу.
Итак, в результате взаимодействия оба тела могут изменить свою скорость.
Рассмотрим более подробно некоторые виды взаимодействий.
Типы фундаментальных взаимодействий.
Попытки классификации взаимодействий привели к идее выделения минимального набора фундаментальных взаимодействий, при помощи которых можно объяснить все наблюдаемые явления. По мере развития естествознания этот набор менялся. В настоящее время принят набор из четырех типов фундаментальных взаимодействий: гравитационные, электромагнитные, сильное и слабые ядерные. Все остальные, известные на сегодняшний день, могут быть сведены к суперпозиции перечисленных.
Гравитационные взаимодействия обусловлены наличием у тел массы и являются самыми слабыми из фундаментального набора. Они доминируют на расстояниях космических масштабов (в мега-мире).
Электромагнитные взаимодействия обусловлены специфическим свойством ряда элементарных частиц, называемым электрическим зарядом. Играют доминирующую роль в макро мире и микромире вплоть на расстояниях, превосходящих характерные размеры атомных ядер.
Ядерные взаимодействия играют доминирующую роль в ядерных процессах и проявляются лишь на расстояниях, сравнимых с размером ядра, где классическое описание заведомо неприменимо.
В повседневной жизни мы постоянно встречаемся с различными видами воздействий одних тел на другие. Чтобы открыть дверь, нужно «подействовать» на нее рукой, от воздействия ноги мяч летит в ворота, даже присаживаясь на стул, вы действуете на него. В то же время, открывая дверь, мы ощущаем ее воздействие на нашу руку, действие мяча на ногу особенно ощутимо, если вы играете в футбол босиком, а действие стула не позволяет нам упасть на пол. То есть действие всегда является взаимодействием: если одно тело действует на другое, то и другое тело действует на первое.
Эти примеры подтверждают вывод ученых о том, что в природе мы всегда имеем дело с взаимодействием, а не с односторонним действием.
Величину, характеризующую взаимодействие тел, называют сила.
Сила — физическая величина, которая определяет меру воздействия одного тела на другое.
— обозначение силы
Сила – векторная величина; она характеризуется:
- модулем (абсолютной величиной);
- направлением;
- точкой приложения.
Измеряется при помощи прибора «динамометр».
Единица измерения силы в Международной системе единиц (СИ) — Ньютон, обозначение [Н].
Если на тело одновременно действуют несколько сил (например,F1,F2 и F3) то под силой, действующей на тело, нужно понимать равнодействующую всех сил: F=F1+F2+F3
В этом выражается принцип суперпозиции сил: если тело взаимодействует одновременно с несколькими телами, то результирующая сила, действующая на данное тело, равна векторной сумме сил, действующих на это тело со стороны всех других тел.
Для заряженных тел:
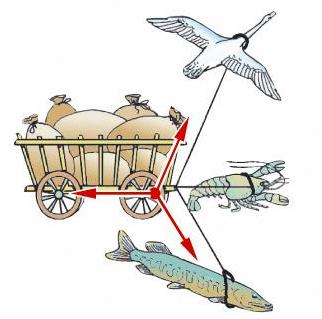
В басне Крылова «Лебедь, рак и щука» они не могли сдвинуть телегу, т.к. равнодействующая сил, приложенных к телеге была равна нулю.
В природе существуют различные силы.
Гравитационные силы действуют между всеми телами – все тела притягиваются друг к другу. Но это притяжение существенно лишь тогда, когда хотя бы одно из взаимодействующих сил так же велико, как Земля или луна.
Электромагнитные силы действуют между заряженными частицами. В атомах, молекулах, живых организмах именно они являются главными.
Область ядерных сил очень ограничена. Они заметны только внутри атомных ядер (т.е. на расстоянии 10-12 см.)
Слабые взаимодействия проявляются на ещё меньших расстояниях. Они вызывают превращение элементарных частиц друг в друга.
Основные виды сил: сила тяжести, сила трения, сила упругости.
При соприкосновении двух движущихся тел возникает сила, направленная против движения и препятствующая движению — сила трения.
Сила трения — это сила, возникающая при движении одного тела по поверхности другого, приложенная к движущемуся телу и направлена против движения.
Сила трения — это сила электромагнитной природы.
Возникновение силы трения объясняется двумя причинами:
1) Шероховатостью поверхностей
2) Проявлением сил молекулярного взаимодействия.
Силы трения всегда направлены по касательной к соприкасающимся поверхностям и подразделяются на силы трения покоя, силы трения скольжения, силы трения качения.
Fтр = м*N, где м – коэффициент трения , N – сила реакции опоры.
Сила упругости – сила, которая возникает при любом виде деформации тел и стремится вернуть тело в первоначальное состояние.
Fупрx = — k*x, где k – жесткость тела [Н/м], х — абсолютное удлинение тела.
Сила упругости перпендикулярна поверхности взаимодействующих тел и направлена всегда против деформации.