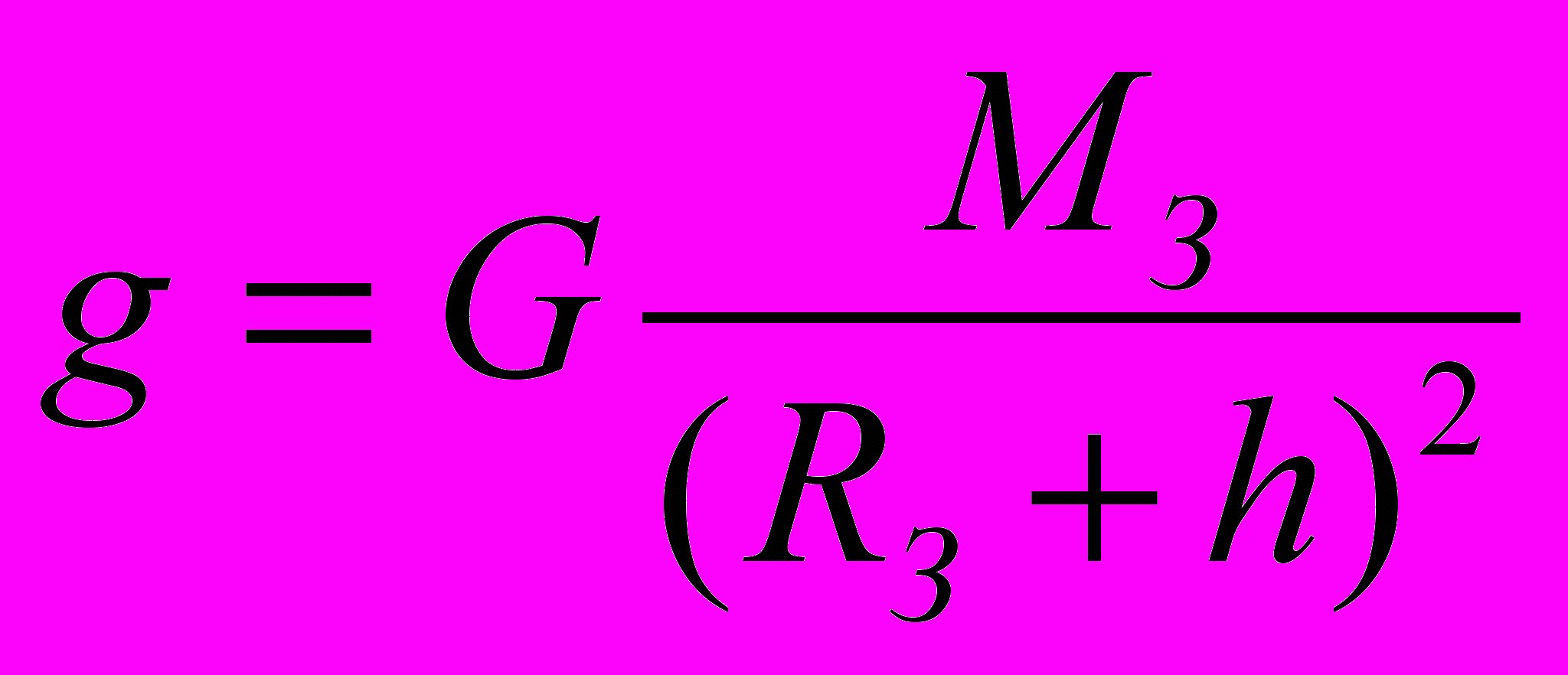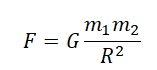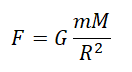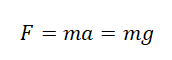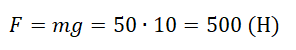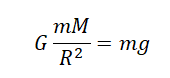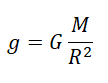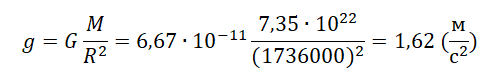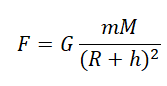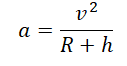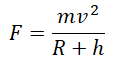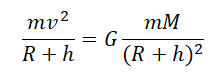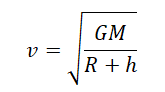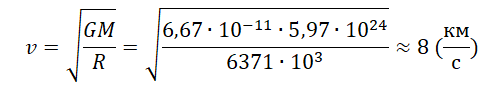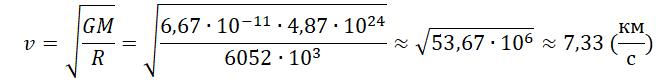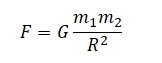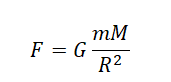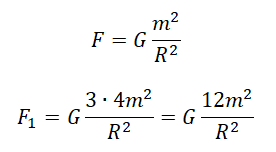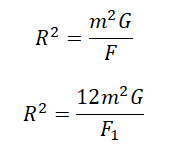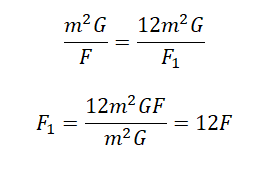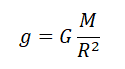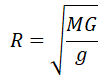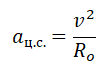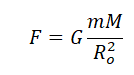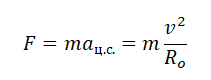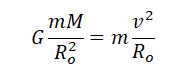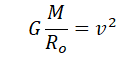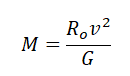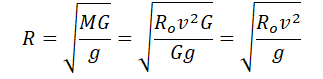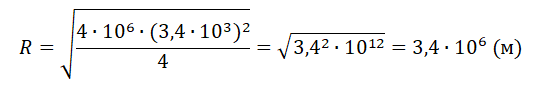Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Земля притягивает к себе подброшенный мяч с силой 5 Н. С какой силой этот мяч притягивает к себе Землю? (Ответ дайте в ньютонах.)
2
Две планеты с одинаковыми массами обращаются по круговым орбитам вокруг звезды. У первой из них радиус орбиты вдвое больше, чем у второй. Каково отношение сил притяжения первой и второй планет к звезде ?
3
Две планеты с одинаковыми массами обращаются по круговым орбитам вокруг звезды. Для первой из них сила притяжения к звезде в 4 раза больше, чем для второй. Каково отношение радиусов орбит первой и второй планет?
4
Две планеты с одинаковыми массами обращаются по круговым орбитам вокруг звезды. Для первой из них сила притяжения к звезде в 4 раза меньше, чем для второй. Каково отношение радиусов орбит первой и второй планет?
5
У поверхности Земли на космонавта действует сила тяготения 720 Н. Какая сила тяготения действует со стороны Земли на того же космонавта в космическом корабле, движущемся по круговой орбите вокруг Земли на расстоянии трёх земных радиусов от её центра? (Ответ дайте в ньютонах.)
Пройти тестирование по этим заданиям
Закон всемирного тяготения
Закон всемирного тяготения (закон тяготения Ньютона) был открыт великим английским ученым Исааком Ньютоном в конце 60-х годов XVII века и опубликован в 1687 г. Он гласит:
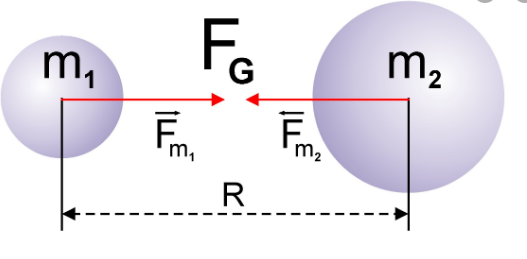
Сила гравитационного притяжения двух тел с массами $m_1$ и $m_2$ прямо пропорциональна массе каждого из тел и обратно пропорциональна квадрату расстояния $r^2$ между ними:
$F=G{m_1m_2}/{r^2},$
где $G$ — гравитационная постоянная. Значение гравитационной постоянной было определено экспериментально в 1798 г. английским физиком Г. Кавендишем и составляет $6.67·10^{-11}H·м^2$/$кг^2$. Гравитацией (от лат. gravitas — тяжесть) называется притяжение всех тел во Вселенной друг к другу.
Закон всемирного тяготения имеет всеобъемлющий характер. Притяжение существует не только между Землей и телами, находящимися на ней. Все тела притягиваются друг к другу. Притягиваются между собой Земля и Луна. Притяжение Земли к Луне вызывает приливы и отливы воды. Огромные массы воды поднимаются в океанах и морях дважды в сутки на много метров. Земля и другие планеты движутся вокруг Солнца, притягиваясь друг к другу.
Необходимо помнить, что закон тяготения как всеобщий закон справедлив для материальных точек, и силы гравитационного взаимодействия направлены вдоль линии, соединяющей эти точки. Такие силы называются центральными.
При расчетах силы тяготения между двумя телами под расстоянием $г$ между ними имеется в виду расстояние между центрами тяжести этих тел. Это особенно важно в том случае, когда размеры тел сопоставимы с расстоянием между ними (тогда форма тела имеет значение). Как показывают расчеты, точные значения силы тяжести можно определить в следующих случаях:
- размеры тел пренебрежимо малы по сравнению с расстоянием между ними;
- имеются два однородных шара (произвольного размера);
- форма одного из тел — шар, а размеры и масса его тела намного больше, чем у второго тела (произвольной формы), которое находится вблизи поверхности первого.
Благодаря последнему случаю можно рассчитать силу притяжения к Земле любого предмета, находящегося на ней.
Сила тяжести
Сила, с которой Земля притягивает к себе тело, находящееся вблизи ее поверхности, называется силой тяжести.
То, что Земля притягивает к себе все тела, находящиеся на ее поверхности и вблизи нее (деревья, воду, дома, Луну и т. д.), или явление тяготения, следует из простых наблюдений за окружающим миром. Так, мяч, брошенный в горизонтальном направлении, через некоторое время оказывается на земле; камень, выпущенный из рук, падает вниз; прыгнувший вверх человек вскоре снова оказывается внизу. Благодаря явлению тяготения искусственный спутник, запущенный с Земли, летит не по прямой, а движется вокруг Земли.
Сила тяжести всегда направлена вертикально вниз, к центру Земли. Обозначается она обычно латинской буквой $F$ со значком «т» (тяжесть) внизу — $F_т$. Сила тяжести приложена к центру тяжести тела.
Центр тяжести тела произвольной формы находят так: подвешивают тело на нити за разные его точки. Точка пересечения всех направлений, отмеченных нитью, и будет центром тяжести тела. Для тел правильной формы центр тяжести находится в центре симметрии тела, и точка эта не обязательно принадлежит телу (например, центр симметрии кольца).
Сила тяжести для тела, находящегося вблизи поверхности Земли, равна:
$F_3=G{M_3m}/{R_3^2},$
где $M_3$ — масса Земли, $m$ — масса тела, $R_3$ — радиус Земли.
Согласно второму закону Ньютона, сила тяжести может быть определена как произведение массы тела на ускорение, которое в данном случае называется ускорением свободного падения $g$:
$F_т=mg$
Сопоставляя две последние формулы, получим выражение для ускорения свободного падения:
$g={GM_3}/{R_3^2}$
Таким образом, ускорение, с которым тело падает на Землю, — ускорение свободного падения — не зависит от массы тела, а также от других его характеристик (объема, плотности и т. д.)
Вблизи поверхности Земли оно составляет $9.8$ м/$с^2$.
Земной шар немного сплюснут у полюсов, поэтому тела, находящиеся около полюсов, расположены немного ближе к центру Земли. В связи с этим сила тяжести на полюсе немного больше, чем на экваторе и других широтах (на экваторе $g = 9.78$ м/$с^2$, на Северном полюсе $g = 9.832$ м/$с^2$).
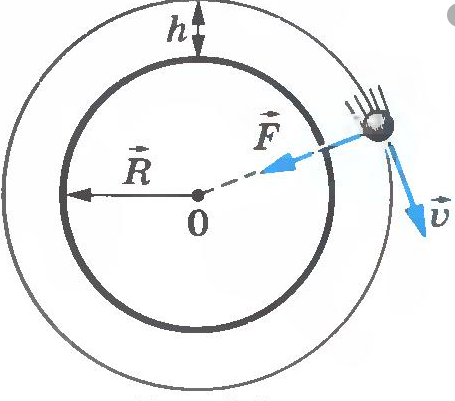
Сила тяжести, а значит, и ускорение свободного падения уменьшается при удалении от поверхности Земли. Для тела, находящегося на высоте $h$ над поверхностью Земли выражение для силы тяжести следует писать в виде:
$F_3=G{M_3m}/{(R_3+h)^2}$
Соответственно, для ускорения свободного падения:
$g=G{M_3}/{(R_3+h)^2}$
Из приведенной формулы следует, что лишь при подъеме на высоту $300$ км ускорение свободного падения уменьшается на $1$ м/$с^2$, т. е. всего на $10%$, а на высотах не только в несколько десятков или сотен метров, но и многих километров сила тяжести может считаться постоянной, не зависящей от положения тела. Именно благодаря этому свободное падение вблизи Земли можно считать равноускоренным движением.
Вес тела, невесомость, перегрузка
Вес — это сила, с которой любое тело вследствие притяжения Земли действует на опору или подвес.
Вес тела — векторная физическая величина, его обозначают буквой $Р$. Вес покоящегося, а также равномерно и прямолинейно движущегося (относительно Земли) тела по своему численному значению равен действующей на него силе тяжести:
$P=F_т=mg$
где $m$ — масса, $g$ — ускорение свободного падения.
Вес и сила тяжести приложены к разным телам, а именно: вес приложен к опоре или подвесу, а сила тяжести — к телу.
Вес и сила тяжести имеют разную физическую природу. Сила тяжести возникает вследствие взаимодействия тела и Земли. Вес тела возникает в результате взаимодействия тела и опоры (подвеса). Опора (подвес) и тело при этом деформируются, что приводит к появлению силы упругости. Из третьего закона Ньютона следует, что вес тела, т. е. сила, с которой тело давит на опору (или растягивает подвес), совпадает по величине с силой, действующей со стороны опоры на данное тело. Сила, с которой опора давит на находящееся на ней тело, называется силой реакции опоры. Обозначив силу реакции опоры через $N$, мы можем записать:
$P=N$
Полученная формула является более общей, чем $P=mg$, так как она остается справедливой и в том случае, когда тело вместе с опорой совершает ускоренное движение.
Вес тела не следует путать с его массой. Масса тела является скалярной величиной и измеряется в килограммах, а вес тела (как и любая другая сила) — векторная величина и измеряется в ньютонах.
Поскольку вес тела пропорционален ускорению свободного падения, которое различно на различных широтах, то вес тела зависит от географической широты и высоты местности (на полюсах вес несколько больше, чем на экваторе).
Вес можно измерять с помощью пружинных весов (динамометра).
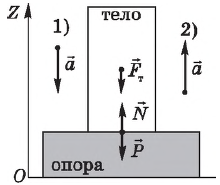
Состояние невесомости — это состояние, в котором находится материальное тело, свободно движущееся в поле тяготения Земли (или другого небесного тела) под действием только сил тяготения. Отличительной особенностью такого состояния является отсутствие давления как на все тело в целом, так и на отдельные его части.
Рассмотрим условие достижения невесомости.
Если опора движется вместе с телом с ускорением а, направление которого совпадает с направлением ускорения свободного падения, то вес тела (определяемый из векторного уравнения $N↖{→}+{F_т}↖{→}=m{a}↖{→}$) в проекции на вертикальную ось $OZ$, направленную вверх, равен:
$P=N=m(g-a)$
Когда $g=a$, $P=0$, наступает невесомость.
При движении тела и опоры в направлении, противоположном направлению свободного падения, получим:
$P=N=m(g+a)$
В этом случае наступает перегрузка — вес тела увеличивается.
Движение небесных тел
Вокруг Солнца движутся девять больших планет. Все они удерживаются около Солнца силами тяготения. Эти силы очень велики. Например, между Солнцем и Землей действует сила тяготения, равная примерно $3⋅10^{22}Н$. Большое числовое значение этой силы объясняется тем, что массы Солнца и Земли очень велики.
Среди больших планет Солнечной системы наименьшую массу имеет Меркурий — его масса почти в $19$ раз меньше массы Земли. Вокруг многих планет движутся их спутники, которые также удерживаются вблизи планет силами тяготения. Спутник нашей Земли — Луна — самое близкое к нам небесное тело. Расстояние между Землей и Луной равно в среднем $380000$ км. Масса Луны в $81$ раз меньше массы Земли.
Чем меньше масса планеты, тем с меньшей силой она притягивает к себе тела. Сила тяжести на поверхности любой планеты рассчитывается по формуле:
$F_т=mg=GMm$/$R^2$
где $m$ — масса тела, $g$ — ускорение свободного падения на данной планете, $М$ — масса планеты, $R$ — радиус планеты, $G$ — гравитационная постоянная.
Космические скорости
Первая космическая скорость — это скорость, которую необходимо сообщить телу, чтобы оно стало искусственным спутником Земли, т. е. двигалось вокруг нее с постоянной скоростью по круговой орбите под действием силы тяжести.
Скорость эта определяется с учетом скорости равномерного движения по окружности и закона всемирного тяготения.
Центростремительное ускорение $а$ тела, равномерно движущегося по окружности, определяется выражением $a_n={υ^2}/{R}$. Поскольку в данном случае $а$ равно $g$ — ускорению свободного падения (т. к. тело движется в поле тяжести Земли), то, подставляя в $a_n={υ^2}/{R}$ вместо $а$ выражение для $g$ из $g=G{M_3}/{(R_3+h)^2}$, получим:
$υ=√{G{M_3}/{R_3+h}}$
Здесь $G$ — гравитационная постоянная, $М_3$ — масса Земли, $R_3$ — радиус Земли, $h$ — высота тела над поверхностью Земли. Это и есть формула круговой скорости спутника Земли. С такой скоростью движется спутник Земли по круговой орбите на высоте $h$ от поверхности Земли.
Пренебрегая $h$ по сравнению с $R$, получим:
$υ_1=√{G{M_3}/{R_3}}$
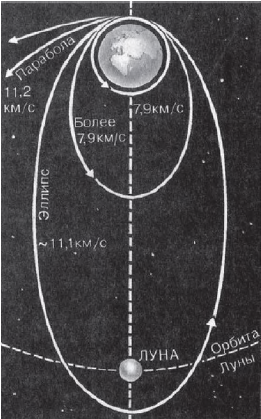
Это формула для расчета первой космической скорости при запуске спутника, т. е. той горизонтальной скорости, которую необходимо сообщить телу вблизи поверхности Земли, чтобы оно стало ее спутником. Запуск искусственного спутника осуществляется с помощью ракеты-носителя, которая поднимает тело спутника на высоту порядка $300$ км (это та высота, на которой уже почти не сказывается сопротивление атмосферы) и придает ему горизонтальную скорость $υ_1$. Спутник отделяется от ракеты-носителя и продолжает свое движение в гравитационном поле Земли. Численное значение первой космической скорости составляет $7.9$ км/с. Если придать телу большую скорость, оно будет двигаться по эллиптической орбите. По мере увеличения начальной скорости, придаваемой телу при запуске, орбита его будет вытягиваться, пока наконец не превратится в незамкнутую кривую — параболу.
Вторая космическая (параболическая) скорость — это скорость, которую надо придать телу у поверхности Земли, чтобы оно ее покинуло, двигаясь по параболической траектории. Эта скорость в $√2$ раза больше первой космической: $υ_{II}=√2·υ_{I}=11.2$ км/с. При второй космической скорости тело покидает Землю, но остается в пределах Солнечной системы. Оно становится спутником Солнца.
Третья космическая скорость — это та наименьшая скорость, при которой тело, начиная движение вблизи поверхности Земли, покидает сначала Землю, а затем преодолевает притяжение Солнца, покидая Солнечную систему. Она равна $υ_{III}=16.7$ км/с.
Видеоурок: Закон всемирного тяготения
Лекция: Закон всемирного тяготения. Сила тяжести. Зависимость силы тяжести от высоты над поверхностью планеты

До некоторого времени Ньютон не задумывался о том, что его предположения справедливы для всех тех, находящихся во Вселенной. Спустя некоторое время им были изучены законы Кеплера, а также законы, которых придерживаются тела, что свободно падают на поверхность Земли. Данные мысли не были зафиксированы на бумаге, а только остались заметки про яблоко, упавшее на Землю, а также о Луне, которая вращается вокруг планеты. Он считал, что
-
все тела рано или поздно упадут на Землю;
-
они падают с одинаковым ускорением;
-
Луна двигается по окружности с постоянным периодом;
-
размеры Луны практически в 60 раз меньше, чем у Земли.
В результате всего это был сделан вывод, что все тела притягиваются друг к другу. При этом, чем больше масса тела, тем с большей силой оно притягивает к себе окружающие объекты.
В результате этого был открыт закон всемирного притяжения:
Любые материальные точки притягиваются друг к другу с силой, увеличивающейся в зависимости от роста их масс, но при этом уменьшается в квадратной пропорциональности в зависимости от расстояния между этими телами.
F – сила гравитационного притяжения
m1, m2 – массы взаимодействующих тел, кг
r – расстояние между телами (центрами масс тел), м
G – коэффициент (гравитационная постоянная) ≈ 6,67*10-11 Нм2/кг2

Коэффициент пропорциональности из закона всемирного тяготения был определен экспериментальным путем ученым Г.Кавендишем. Гравитационная постоянная равна силе, с которой притягиваются килограммовые тела на расстоянии одного метра:
G = 6,67*10-11 Нм2/кг2
Взаимное притяжение тел объясняется гравитационным полем, подобным электрическому, которое находится вокруг всех тел.

Вокруг Земли также существует такое поле, его еще называют полем земного притяжения. Все тела, что находятся в местах его действия, притягиваются к Земле.
Сила тяжести — это равнодействующая гравитационной силы, а также центростремительной силы, направленной по оси вращения.

Характеристика силы тяжести:
1. Точка приложения: центр масс тела.
2. Направление: к центру Земли.
3. Модуль силы определяется по формуле:
Fтяж = gm
g = 9,8 м/с2 — ускорение свободного падения
m — масса тела
Так как сила тяжести — это частный случай закона гравитационного взаимодействия, то ускорение свободного падения определяется по формуле:
g — ускорение свободного падения, м/с2
G — гравитационная постоянная, Нм2/кг2
M3 — масса Земли, кг
R3 — радиус Земли
Из этого можно сделать
вывод:
-
чем больше масса космического объекта, тем больше ускорение свободного падения;
-
чем больше расстояние до космического объекта, тем меньше ускорение свободного падения.
Более того, на данную величину влияет и период вращения планеты вокруг оси.
Если тело находится на некотором расстоянии от поверхности Земли, то определить ускорение можно по следующей формуле:
Если же с увеличением высоты уменьшается ускорение, то можно сделать вывод, что сила тяжести так же уменьшается.
Сила тяготения. Задачи второго уровня.
Всем доброго времени суток! Сегодня на повестке дня задачи на отыскание силы тяготения, скоростей, ускорений и весов тел на различных высотах и на разных планетах: словом, все, что связано с законом всемирного тяготения!
Поскольку задач много, а времени – мало (как обычно), то хочется разобрать не самые простые задачи. Надеюсь, данная подборка задач будет вам интересна, потому что решений этих задач я не нашла в Интернете – и по этой же причине не хочу рассматривать совсем простые задачи, решения которых в сети легко отыскать.
Начнем, пожалуй.
Задача 1. Два одинаковых однородных шара, соприкасаясь, притягивают друг друга с силой . Как изменится сила, если увеличить массу каждого шара в
раз? Плотность шаров не изменяется.
Два шара
Сила тяготения равна — поэтому неплохо бы узнать радиус шариков. Вспомним формулу объема шара:
, откуда
, то есть
Масса и объем связаны плотностью вещества:
Тогда
То есть сила тяготения равна
Если масса шаров изменится в раз при той же плотности, то это означает, что изменятся их радиусы, так как зависимость объема от радиуса шара – прямая:
Сила тоже изменится:
Найдем теперь отношение сил:
Ответ:
Задача 2. Две точечные массы и
расположены на расстоянии
друг от друга. Где следует расположить точечную массу
, чтобы сила гравитационного воздействия на нее со стороны масс
и
равнялась
?
Так как силы в данном случае направлены от первого тела к телу
(вправо) и от второго тела
к телу
(влево), то есть такое положение массы
, что эти силы станут равны и друг друга скомпенсируют. Тогда можем записать:
Расположение масс
Так как , то
Раскрыв скобки, можем записать ,
Или
Ответ:
Задача 3. Два шарика массами , соединенные стержнем пренебрежимо малой массы, образуют гантель. Расстояние между центрами шариков
. Найти силу, действующую на гантель в поле тяжести точечной массы
, находящейся на расстоянии
от середины гантели.
. Исследовать полученные выражения для силы при
,
, при каком
она максимальна и чему будет равна.
Легкая штанга
Запишем расстояние от каждого из шариков до точечной массы :
Тогда силы взаимного притяжения каждого из шариков и массы М такие:
Эти силы можно разложить каждую на два составляющих вектора – на вектора, направленные от одного шарика к другому, вдоль гантели (вследствие равенства по длине и противоположного направления они компенсируют друг друга), и перпендикулярные к гантели. Эти две составляющие сонаправлены, поэтому именно их сумма определяет силу взаимодействия.
Определим эти составляющие сил:
Так как эти силы равны, и направлены в одну сторону, сложим их:
При условии пренебрежем величиной
в знаменателе, тогда
При условии пренебрежем величиной
в знаменателе, тогда
Ответ: ,
,
Задача 4. Три материальные точки массами кг,
кг,
кг находятся в точках с радиус-векторами
,
,
. Найти гравитационную силу, действующую на частицу, имеющую массу
, со стороны частиц с массами
и
.
Рассмотрим рисунок. Из него видно, что сила, которую мы ищем – это равнодействующая сил и
(изображена красным вектором). Найти ее можно как векторную сумму сил
и
.
Взаимное влияние точек
Для определения сил тяготения между массами нам понадобится знать расстояния между ними. Определим их, зная радиус-векторы точечных масс, так же, как определяют длину отрезка по координатам его концов. Тогда
Модуль силы равен:
Модуль силы равен:
Равнодействующая:
Сила направлена вдоль оси
— так как тела
и
лежат на одной вертикали:
Силу возможно разложить на две составляющие, направленные по осям. Разложим силу
:
Равнодействующая тогда будет равна:
Определим и
: так как
, следовательно,
, а
.
Тогда:
Подставляем числа:
Ответ:
Задача 5. С какой силой притягивается к центру земли тело массой , находящееся в глубокой шахте, если расстояние от него до центра земли равно
? Плотность земли считать постоянной и равной
.
Здесь надо понимать, что тело будет притягиваться только той частью массы планеты, которая находится «под» ним. Силы, с которыми тело будет притягивать та часть планеты, что «выше» тела, будут компенсированы силами, с которыми тело будет притягивать та часть планеты, которая «выше» тела, но в противоположном полушарии (на рисунке зеленым и красным цветами показаны силы, которые компенсируют друг друга).
Глубокая шахта
Здесь — «внутренняя часть» планеты, та, что «под» телом.
Ответ:
Задача 6. Определить максимальную скорость камня, брошенного без начальной скорости в прямой тоннель, прорытый через центр Земли с одной стороны на другую. Вращение Земли не учитывать.
Камень будет лететь равноускоренно, по крайней мере, до центра. Но, так как полет будет все время сокращать расстояние между камнем и центром планеты, то ускорение свободного падения будет все время уменьшаться, пока не станет равным нулю в середине тоннеля. Поэтому для расчета возьмем среднее ускорение: .
Тогда расстояние, которое камень пролетит до центра, равно радиусу Земли – 6400 км.
Отсюда :
Скорость при равноускоренном движении без начальной скорости:
Таким образом, скорость, которую приобретет камень, будет равна первой космической скорости, или 8000 м/c.
Задача 7. Две звезды вращаются вокруг общего центра масс с периодом и постоянными по модулю скоростями
и
. Найти массы звезд и расстояние между ними.
Две звезды
Так как звезды вращаются вокруг одного центра, не обгоняя друг друга, следовательно, у них одна и та же угловая скорость вращения: , и, очевидно, один и тот же период обращения:
. Период – время прохождения одного круга. Первая звезда проходит круг длиной
, а вторая —
, то есть скорость первой —
, скорость второй —
. Ну а расстояния звезд от центра вращения —
,
. Сумма расстояний – это как раз расстояние между звездами:
Чтобы найти массы звезд, используем силу тяготения между ними. Раз система в равновесии, значит, сила тяготения равна центробежной силе. Сила тяготения между звездами:
Центростремительное ускорение для первой звезды:
Центробежная сила:
Приравниваем силу тяготения и центробежную:
Сокращаем и «вытаскиваем» массу
:
Вместо подставим
, вместо
.
Тогда:
Аналогично, приравнивая центробежную силу для звезды массой и силу тяготения, получим:
Сокращаем и «вытаскиваем» массу
:
Вместо подставим
, вместо
.
Тогда:
Ответ: ,
,
.
Задача 8. Определить силу натяжения троса, связывающего два спутника массой каждый, которые обращаются вокруг Земли на расстояниях
и
так, что трос всегда направлен радиально. Масса Земли
.
К задаче 8
Силой тяготения между спутниками пренебрежем. Следовательно, на каждый из них действует сила тяготения земли, сила натяжения троса и центробежная сила. Так как канат всегда направлен радиально (по радиусу), то у спутников одна и та же угловая скорость: .
Центростремительное ускорение первого спутника: , второго спутника
.
Центробежная сила, действующая на первый спутник: , на второй спутник:
.
Уравнение по второму закону Ньютона для первого спутника:
Уравнение по второму закону Ньютона для второго спутника:
Здесь и
— силы тяготения между спутниками и Землей:
Сложим уравнения, составленные по второму закону Ньютона. Получим:
Или:
Так как угловая скорость спутников одна и та же , то можно записать, что
, а
Подставим:
«Вытащим» :
Определим теперь силу натяжения каната:
Подставляем в это выражение квадрат скорости, полученный выше:
Или, наконец,
Ответ:
Данная тема посвящена решению задач
на закон всемирного тяготения и силу тяжести.
Задача 1. Масса Юпитера равна 1,9 ∙ 1027 кг, а
его средний радиус — 70000 км. Определите ускорение свободного падения вблизи
поверхности планеты. Какую минимальную скорость нужно сообщить телу на Юпитере,
чтобы оно стало искусственным спутником?
Задача 2. Спутник движется вокруг Земли на высоте 1700 км над
ее поверхностью. Считая орбиту спутника круговой, определите модуль его
линейной скорости и период обращения спутника по орбите, если средний радиус
Земли составляет 6400 км. (g = 10 м/с2.)
Задача 3. На некоторой планете тела на экваторе невесомы.
Определите среднюю плотность вещества планеты, если период ее обращения вокруг
своей оси составляет 50000 с.
«Если запастись
терпением и проявить старание,
то посеянные семена
знания непременно
дадут добрые всходы.
Ученья корень горек,
да плод сладок»
Леонардо да Винчи
Целью данной статьи является подготовка к ЕГЭ по физике, мы займёмся изучением вышеперечисленных тем раздела динамики.
Сила тяжести. Зависимость силы тяжести от высоты h над поверхностью планеты радиусом R0
Силой тяжести является сила притяжения тел к нашей планете.
Рассмотрим характеристики силы тяжести:
– Точкой приложения является центр массы тела;
– Сила тяжести направлена к центру Земли;
– Модуль силы тяжести определяют в соответствии с формулой: F тяж = gm, при этом, g = 9,8 м / с^2 – ускорение свободного падения, m – масса тела.
Сила тяжести является случаем из закона гравитационного взаимодействия, исходя из этого, ускорение свободного падения вычисляют по следующей формуле:
g = G * M3 / R3^2 = 9,8 м / с^2, здесь: g – является ускорением свободного падения, измеряется в м / с^2, G – гравитационной постоянной, обозначается в Нм^2 / кг^2, M3 – массой земли, в килограммах, R3 – радиусом Земли.
Рассмотрим примеры решения задач.
- Масса тела равна четырём килограммам. Нужно найти его силу тяжести (F).
Решение:
m = 4 кг, g = 9,8 Н / кг. Применяем следующую формулу: F тяж = gm. Подставляем в формулу значение массы: F тяж = 9,8 Н / кг * 4 кг = 40 Н.
Ответ: сила тяжести предмета равна 40 Н.
- Объём воды равен 3 дм^3.
Найти: её вес (Р).
Решение: V = 3 дм^3 = 0,003 м^3, g = 9,8 Н / кг.
Для нахождения веса воды, применяем формулу: Р = mg. Массу воды мы сможем определить при известной плотности воды.
M = p * М.
Найдём массу воды: m = 1000 кг / м^3 * 0,003 м^3 = 3 кг.
Далее находим вес воды: Р = 3 кг * 9,8 Н / кг = 29,4 Н.
Ответ: вес воды равен 29,4 Н
Сделаем выводы по данной теме:
– Ускорение свободного падения зависит от массы космического объекта;
– Ускорение свободного падения будет меньше, если расстояние до объекта будет большим.
Переходим к рассмотрению второй темы. Тема, касающаяся движения небесных тел, а также космической скорости обычно встречается в задании № 24 ЕГЭ по физике, сначала рассмотрим определения темы, далее – перейдём к решению задач.
Движение небесных тел и их искусственных спутников. Первая космическая скорость. Вторая космическая скорость.
Искусственным спутником Земли является космический аппарат, который вращается вокруг нашей планеты по орбите, называемой гелиоцентрической.
Для того, чтобы осуществлять движение по орбите вокруг планеты, у спутника должна быть определённая скорость, которая равна либо больше первой космической скорости. Спутник летает на большом расстоянии, обычно оно составляет сотни тысяч километров. Период вращения спутника по орбите составляет от нескольких часов до нескольких лет. Особое внимание уделяют спутникам, находящимся на геостационарной орбите. Это обусловлено тем, что они вращаются на протяжении одних суток.
Первой космической скорость (её также называют круговой с) является скорость, необходимую для объекта, не имеющего двигатель. Такой вид скорости является минимальным, при ней движущееся в горизонтальном направлении тело, не будет падать, оно будет продолжать движение по орбите.
Формула для определения этой скорости: U1 = √G * (M / R).
Второй космической скоростью (её также называют параболической либо скоростью убегания) является минимальная скорость, необходимая для объекта. Считают, что после того, как тело приобретёт эту скорость, оно перестаёт получать негравитационное ускорение.
Формула для нахождения данной скорости = √2G * (M / R).
Решим задачи по этой теме.
- Масса Солнца равна 2 * 1030 кг, его диаметр= 1,4 * 109 м.
Найти: первую космическую скорость Солнца.
Решение: известно, что спутник движется в соответствии с силой тяготения. Применяем второй закон Ньютона, получается: mv1^2 / Rc = G mM / Rc^2.
Далее: u1 = √ GM / Rc = 437 км / с.
Ответ: первая космическая скорость Солнца приблизительно равна 437 км /с.
- Период обращения Сатурна вокруг Солнца составляет 29,5 лет. Масса Солнца составляет 2 * 1030 кг.
Найти: расстояние от Сатурна до Солнца (расстояние должно быть средним).
Решение: известно, что рассматриваемая планета движется по орбите Солнца. Используем второй закон Ньютона: mv^2 / r = G mMc / r^2, здесь: m – является массой Сатурна, r – расстоянием от планеты Сатурн к Солнцу, Мс – масса Солнца.
Период обращения Сатурна вычислим по формуле: Т = 2пr / u, получается: u = 2 пr / T.
Подставляем выражение в уравнение, получается: (2пr / T)^2 = G Mc / r.
Находим расстояние от Сатурна до Солнца: r = 3 √ GM cT^2 / 4п^2 = 1,42 * 10^12 м.
Ответ: 1,42 * 10^12 м.
В ходе подготовке к экзамену рекомендуем просмотреть демонстрационные варианты ЕГЭ по физике, так вы сможете понять примерную формулировку и тему заданий.
Сила трения. Сухое трение. Сила трения покоя. Коэффициент трения.
Переходим к рассмотрению следующей темы – сила трения, сухое трение.
Трение определяют как один из видов взаимодействия среди тел.
Внешним является трение, в ходе которого тела взаимодействуют с помощью своих поверхностей.
Внутренним трением называют движущиеся жидкости и газы.
У силы трения существуют определённые характеристики:
– Направление силы трения – противоположная сторона равнодействующей силы;
– Точкой приложения силы трения располагается на плоскости поверхностей, которые соприкасаются;
– Существует определённая формула, по которой находят модуль силы трения: F mp = μN, здесь: F mp – является силой трения скольжения, μ – коэффициентом трения, N – силой реакции опоры.
N – рассматривают, как силу, реагирующую с опорой на вес тела, а также одну из видов сил. Коэффициент трения находят в соответствующих таблицах.
Сила трения скольжения.
Сухим трением является взаимодействие, которое возникает при касании тел, при этом, между данными телами не должно быть газов и жидкостей.
Существуют несколько видов сухого трения:
– Скольжение;
– Покоя;
– Качения.
Силой трения покоя называют силу, препятствующую движению тел. Эту силу принять считать наибольшей.
Сила трения скольжения появляется в момент преодоления силы покоя. При этом коэффициенты силы трения должны уменьшаться. Для беспрепятственного скольжения следует полировать поверхность. Следует иметь в виду, что при полном устранении неровностей поверхности, коэффициент трения будет возрастать (это происходит по причине сближения молекул тела).
Сила трения качения является наиболее малой по сравнению с другими видами сил. Примером является тумба на колёсах, её горазда легче передвинуть, чем тумбу на опоре.
Существует определённый коэффициент трения. Им является характеристика трения в качестве давления.
Коэффициент трения находят по формуле: F tr = μN.
Коэффициент не имеет зависимости от площадей поверхностей, которые соприкасаются.
В некоторых случаях коэффициент трения заменяют углом трения.
Рассмотрим задачу по данной теме.
Бревно, у которого масса составляет пять килограммов, скользит по поверхности, являющейся горизонтальной. Известно, что сила трения скольжения = 20Н.
Найти: силу трения, при условии, что масса бревна будет меньше в два раза.
Решение: F mp = μN. N = mg. N1 = mg / 2 = N / 2, далее: F mp1 = F mp / 2 = 20 Н / 2 = 10 Н.
Ответ: сила трения равна 10 Н.
Рассмотрим ещё одну небольшую тему, встречающую в разделе динамики ЕГЭ по физике, это тема давления.
Давление
Давлением называют силу, которая приходится на определённую площадь поверхности.
Давление измеряется в Паскалях. Давление принято измерять в миллиметрах ртутного столба, а большое давление – в атмосферах или барах. Относительным атмосферным давлением считают 10^5 Па, или 760 миллиметров ртутного столба.
Таким образом, мы завершили рассмотрение тем из раздела динамики, встречающиеся в КИМах ЕГЭ по физике, изучили основные определения, характеристики, а также решили задачи.
Все тела взаимодействуют друг с другом. Так, две материальные точки, обладающие массой, притягиваются друг к другу с некоторой силой, которую называют гравитационной, или силой всемирного тяготения.
Сила всемирного тяготения — сила, с которой все тела притягиваются друг к другу.
Закон всемирного тяготения
Сила взаимного притяжения двух тел прямо пропорциональна произведению масс этих тел и обратно пропорциональна квадрату расстояния между ними.
F — сила всемирного тяготения, m1 и m2 — массы двух притягивающихся друг к другу тел, R — расстояние между этими телами, G — гравитационная постоянная (G = 6,67∙10–11 Н ∙ м2/кг2).
Сила всемирного тяготения направлена по линии, соединяющей центры двух тел.
Гравитационная постоянная численно равна силе притяжения между двумя точечными телами массой 1 кг каждое, если расстояние между ними равно 1 м. Если R = 1 м, m1 = 1 кг и m2 = 1 кг, то F = G.
G = 6,67∙10–11 Н ∙ м2/кг2.
Сила тяжести
Согласно закону всемирного тяготения, все тела притягиваются между собой. Так, Земля притягивает к себе падающий на нее мяч, а мяч притягивает к себе Землю.
Сила тяжести — сила, с которой Земля притягивает к себе тела.
Сила тяжести действует на все тела, находящиеся в поле притяжения Земли. Она всегда направлена к центру нашей планеты.
Расчет силы тяжести на Земле
Силу тяжести можно рассчитать с помощью закона всемирного тяготения. Тогда одна из масс будет равна массе земли. Обозначим ее большой буквой M. Вторая масса будет принадлежать телу, притягивающемуся к Земли. Обозначим его m. В качестве R будет служить радиус Земли. В таком случае сила тяжести будет определяться формулой:
Вывод формулы ускорения свободного падения
Согласно второму закону Ньютона, сила, которая действует на тело, сообщает ему ускорение. Поэтому силу тяжести также можно выразить через это ускорение. Обозначим его g — ускорение свободного падения.
Пример №1. Мальчик массой 50 кг прыгнул под углом 45 градусов к горизонту. Найти силу тяжести, действующую на него во время прыжка.
Сила тяжести зависит только от массы тела и ускорения свободного падения. Направлена она всегда к центру Земли, и от характера движения тела не зависит. Поэтому:
Мы получили две формулы для вычисления силы тяжести: одну — исходя из закона всемирного тяготения, вторую — исходя из второго закона Ньютона. Приравняем правые части формул и получим:
Отсюда:
Формула расчета ускорения свободного падения
Вместо массы и радиуса Земли можно взять массы и радиусы любых планет. Так можно рассчитать ускорение свободного падения для любого космического тела.
Пример №2. Рассчитать ускорение свободного падения на Луне. Считать, что радиус Луны равен 1736 км, а ее масса — 7,35∙1022 кг.
Переведем километры в метры: 1736 км = 1736000 м.
Первая космическая скорость
Исаак Ньютон смог доказать, что причиной падения тел на Землю, движения Луны вокруг Земли и движения Земли вокруг Солнца является сила тяготения. Если камень бросить в горизонтальном направлении, его траектория будет отклонена от прямой линии под действием земной силы тяжести. Если же придать этому камню большую скорость, камень приземлится на большем расстоянии. Значит, существует такая скорость, при которой камень не приземлится, а начнет бесконечно вращаться вокруг Земли.
ОпределениеПервая космическая скорость — минимальная (для заданной высоты над поверхностью планеты) горизонтальная скорость, которую необходимо придать объекту, чтобы он совершал движение по круговой орбите вокруг планеты.
Вывод формулы первой космической скорости
Когда тело массой m вращается на некоторой высоте h, расстояние между ним и центром Земли равно сумме этой высоты и радиуса Земли. Поэтому сила тяготения между этим телом и Землей будет равна:
Движение тела вокруг планеты — частный случай движения тела по окружности с постоянной по модулю скоростью. Мы уже знаем, что такое тело движется с центростремительным ускорением, направленным к центру окружности. В данном случае центростремительное ускорение будет направлено к центру Земли. Это ускорение сообщает телу сила тяготения.
Так как тело движется на некоторой высоте h от поверхности Земли, центростремительное ускорение будет определяться формулой:
Подставив это ускорение в формулу второго закона Ньютона, получим силу, с которой Земля притягивает к себе тело массой m:
Приравняем правые части формул, следующих из закона всемирного тяготения и второго закона Ньютона, и получим:
Отсюда скорость, с которой должно тело массой m бесконечно вращаться вокруг Земли на высоте h, равна:
Скорость бесконечно вращающегося вокруг Земли тела не зависит от его массы. Она зависит только от высоты, на которой оно находится. Чем выше высота, тем меньше скорость его вращения.
Тело, вращающееся вокруг планеты, называется ее спутником. Чтобы любое тело стало спутником Земли, нужно сообщить ему некоторую скорость на поверхности планеты в горизонтальном направлении. Высота h в этом случае равна 0. Тогда эта скорость будет равна:
8 км/с — первая космическая скорость Земли.
Пример №3. Рассчитать первую космическую скорость для Венеры. Считать, что масса Венеры равна 4,87∙1024 кг, а ее радиус равен 6052 км.
Задание EF18521
Сила гравитационного притяжения между двумя шарами, находящимися на расстоянии 2 м друг от друга, равна 9 нН. Какова будет сила притяжения между ними, если расстояние увеличить до 6 м? Ответ выразите в наноньютонах (нН).
Алгоритм решения
- Записать исходные данные.
- Записать закон всемирного тяготения.
- Установить зависимость между силой гравитационного притяжения и расстоянием между телами.
- На основании вывода о зависимости двух величин вычислить гравитационное притяжение между двумя шарами при изменении расстояния между ними.
Решение
Запишем исходные данные:
- Расстояние между двумя шарами в первом случае: R1 = 2 м.
- Расстояние между двумя шарами во втором случае: R2 = 6 м.
- Сила гравитационного притяжения между двумя шарами в первом случае: F1 = 9 нН.
Запишем закон всемирного тяготения:
Из формулы видно, что сила гравитационного притяжения обратно пропорционально квадрату расстояния между телами массами m1 и m2.
R2 больше R1 втрое (6 больше 2 в 3 раза). Следовательно, расстояние между шарами тоже увеличилось втрое. В таком случае сила гравитационного притяжения между ними уменьшится в 32 раз, или в 9 раз. Так как в первом случае эта сила была равна 1 нН, то во втором она составит в 9 раз меньше, или 1 нН.
Ответ: 1
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF17569
Две звезды одинаковой массы m притягиваются друг к другу с силами, равными по модулю F. Чему равен модуль сил притяжения между другими двумя звёздами, если расстояние между их центрами такое же, как и в первом случае, а массы звёзд равны 3m и 4m?
а) 7F
б) 9F
в) 12F
г) 16F
Алгоритм решения
1.Записать закон всемирного тяготения.
2.Применить закон всемирного тяготения для первой и второй пары звезд.
3.Из каждого выражения выразить расстояние между звездами.
4.Приравнять правые части уравнений и вычислить силу притяжения между второй парой звезд.
Решение
Закон всемирного тяготения выглядит так:
Примерим этот закон для первой и второй пары звезд:
Выразим квадраты радиусов, так как они в обоих случаях одинаковые:
Приравняем правые части выражений и выразим силу притяжения во втором случае:
Ответ: в
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF18678
Высота полёта искусственного спутника над Землёй увеличилась с 400 до 500 км. Как изменились в результате этого скорость спутника и его потенциальная энергия?
Для каждой величины определите соответствующий характер изменения:
| 1) | увеличилась |
| 2) | уменьшилась |
| 3) | не изменилась |
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Скорость
спутника |
Потенциальная энергия спутника |
Алгоритм решения
1.Записать закон всемирного тяготения и формулу центростремительного ускорения для движения тела по окружности с постоянной по модулю скоростью.
2.Установить зависимость скорости от высоты спутника над поверхностью Земли.
3.Записать формулу потенциальной энергии и установить, как она зависит от высоты.
Решение
На спутник действует сила притяжения Земли, которая сообщает ему центростремительное ускорение:
F=maц=GmM(R+h)2
Отсюда центростремительное ускорение равно:
aц=GM(R+h)2
Но центростремительное ускорение также равно:
aц=v2(R+h)
Приравняем правые части выражений и получим:
GM(R+h)2=v2(R+h)
v2=MG(R+h)(R+h)2=MG(R+h)
Квадрат скорости спутника обратно пропорционален радиусу вращения. Следовательно, при увеличении высоты увеличивается радиус вращения, а скорость уменьшается.
Потенциальная энергия спутника определяется формулой:
Ep = mgh
Видно, что потенциальная энергия зависит от высоты прямо пропорционально. Следовательно, при увеличении высоты потенциальная энергия спутника тоже увеличивается.
Верная последовательность цифр в ответе: 21.
Ответ: 21
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF17578
Искусственный спутник обращается вокруг планеты по круговой орбите радиусом 4000 км со скоростью 3,4 км/с. Ускорение свободного падения на поверхности планеты равно 4 м/с2. Чему равен радиус планеты? Ответ запишите в километрах.
Алгоритм решения
1.Записать исходные данные. Перевести единицы измерения в СИ.
2.Записать формулу ускорения свободного падения и выразить через нее радиус планеты.
3.Записать формулу, раскрывающая взаимосвязь между линейной скоростью и радиусом окружности, по которой движется тело.
4.Записать закон всемирного тяготения применительно к спутнику.
5.Вывести формулу для расчета радиуса планеты.
6.Подставить известные данные и произвести вычисление.
Решение
Запишем исходные данные:
• Линейная скорость спутника: v = 3,4 км/с, или 3,4∙103 м/с.
• Радиус орбиты спутника: Rо = 4000 км, или 4∙106 м.
• Ускорение свободного падения у поверхности планеты: g = 4 м/с2.
Ускорение свободного падения определяется формулой:
Отсюда радиус равен:
Линейная скорость и радиус орбиты связываются формулой:
Используя закон всемирного тяготения, запишем силы, с которой притягивается спутник к планете:
Согласно второму закону Ньютона, сила — это произведение массы на ускорение тела. Следовательно:
Отсюда:
Поделим обе части выражения на массу спутника и радиус его орбиты. Получим:
Из этой формулы выразим массу планеты:
Подставим массу планеты в формулу для нахождения ее радиуса:
Подставляем известные данные и вычисляем:
Этот радиус соответствует 3400 км.
Ответ: 3400
pазбирался: Алиса Никитина | обсудить разбор | оценить
Алиса Никитина | Просмотров: 17.1k