Сила упругости егэ физика - Помощь в подготовке к экзаменам и поступлению

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

На сколько сантиметров растянется пружина, жёсткость которой под действием силы 100 H? Пружину считайте идеальной.

На рисунке изображен лабораторный динамометр.

Шкала проградуирована в ньютонах. Каким будет растяжение пружины динамометра, если к ней подвесить груз массой 200 г? (Ответ дайте в сантиметрах.) Ускорение свободного падения считать равным 10 м/с².

Под действием силы 4,5 Н пружина удлинилась на 6 см. Чему равен модуль силы, под действием которой удлинение этой пружины составит 4 см? (Ответ дайте в ньютонах.)

На сколько растянется пружина жесткостью под действием силы 1000 Н? (Ответ дайте в сантиметрах.)

Пройти тестирование по этим заданиям

Источник

Упругость — свойство тел изменять форму и размеры (деформироваться) под действием нагрузок и самопроизвольно восстанавливать первоначальные форму и размеры при прекращении внешних воздействий.

Деформацией (от лат. deformatio — искажение) называют любое изменение размеров и формы тела.

Деформации бывают разных видов: растяжения, сжатия, сдвига, изгиба, кручения. Все перечисленные виды деформации возможны в твердых телах. В жидкостях и газах возможны только деформации объемного сжатия и растяжения, т. к. эти среды не обладают упругостью формы, а только объема (как известно, жидкость принимает форму сосуда, в котором находится, а газ занимает весь предоставленный ему объем).

Деформация называется упругой, если она возникает и исчезает одновременно с внешним воздействием.

Деформация, которая не исчезает после прекращения внешнего воздействия, называется пластической.

Если, например, пружину несколько растянуть, а затем отпустить, то она снова примет свою первоначальную форму. Но ту же пружину можно растянуть настолько, что после того, как ее отпустят, она так и останется растянутой.

При деформации тел возникают силы упругости, которые используются, например, в динамометрах. Пластические деформации применяют при лепке из пластилина и глины, при обработке металлов — ковке, штамповке.

Сила, возникающая в теле в результате его деформации и стремящаяся вернуть тело в исходное положение, называется силой упругости.

Сила упругости возникает и при растяжении (например, если подвесить гирю на нить), и при изгибе, и при других видах деформации.

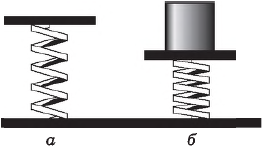
Возникновение силы упругости можно понять из следующего опыта. На рисунке, изображена ненагруженная пружина. Если на нее сверху поместить гирю, то под действием силы тяжести гиря начнет двигаться вниз, сжимая пружину, т. е. деформируя ее, но через некоторое время остановится. Так как тело (гиря) неподвижно, значит, силы, действующие на него, уравновешены, т. е. сила тяжести уравновешена силой, действующей на гирю со стороны сжатой пружины. Это и есть сила упругости.

Если на опору поместить достаточно легкий предмет, то ее деформация может оказаться столь незначительной, что изменение формы опоры будет незаметным. Но деформация все равно будет иметь место, а вместе с ней будет действовать и сила упругости, препятствующая падению тел, находящихся на данной опоре. В случае, когда деформация тела незаметна и изменением размеров опоры можно пренебречь, силу упругости называют силой реакции опоры.

Силы упругости возникают всегда при попытке изменить форму или объем твердого тела, при изменении объема жидкости или газа.

В отличие от сил тяготения, которые действуют между телами всегда, силы упругости возникают в теле лишь при определенном условии: тело должно быть деформировано.

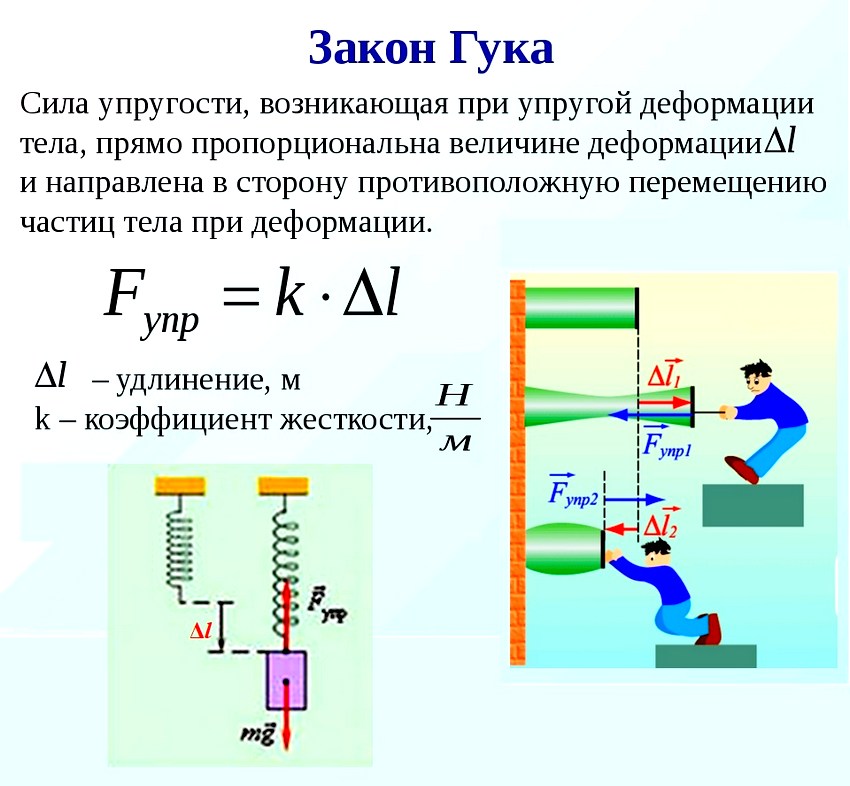
Закон Гука

Закон Гука — основной закон теории упругости. Он был открыт английским ученым Робертом Гуком в 1660 г., когда ему было 25 лет. Закон Гука гласит:

Сила упругости, возникающая при упругой деформации растяжения или сжатия тела, пропорциональна абсолютному значению изменения длины тела.

Если удлинение тела обозначить через $х$, а силу упругости через $F{упр}$, то закон Гука можно записать в виде следующей математической формулы:

$F_{упр}=-kx$

где $k$ — коэффициент пропорциональности, называемый жесткостью тела. Знак минус перед правой частью уравнения указывает на противоположные направления силы упругости и удлинения $х$. Единицей жесткости в СИ является ньютон на метр ($1$ Н/м).

У каждого тела своя жесткость. Чем больше жесткость тела (пружины, проволоки, стержня и т. д.), тем меньше оно изменяет свою длину под действием данной силы.

Следует помнить, что закон Гука справедлив только для упругой деформации. Закон Гука хорошо выполняется только при малых деформациях. При больших деформациях изменение длины перестает быть прямо пропорциональным приложенной силе, а при очень больших деформациях тело разрушается.

Источник

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

Сила упругости

Сила упругости — это сила, возникающая при упругой деформации тела и направленная в сторону, противоположную смещению частиц тела в процессе деформации. Силы, возникающие при пластических деформациях, не относятся к силам упругости.

Понятие о деформациях

Деформация — это изменение формы и размеров тела.

К деформациям относятся: растяжение, сжатие, кручение, сдвиг, изгиб.

Деформации бывают упругими и пластическими.

Закон Гука

Абсолютная величина силы упругости прямо пропорциональна величине деформации. В частности, для пружины, сжатой или растянутой на величину (displaystyle x) (разница между крайними положениями), сила упругости задается формулой [F=kx] где (displaystyle k) — коэффициент жесткости пружины.

Единицы измерения коэффициента жесткости: (k=)[Н/м].

Закон Гука о линейной зависимости силы упругости от величины деформации справедлив лишь при малых деформациях тела.

На штативе закреплён школьный динамометр. К нему подвесили груз массой 0,1 кг. Пружина динамометра при этом удлинилась на 2,5 см. Чему будет равно удлинение пружины, если масса груза увеличится втрое? (Ответ дайте в сантиметрах)

Согласно закону Гука [F=kDelta x] где k – жесткость пружины, ( Delta x) – удлинение пружины.
Найдем жесткость пружины, зная, что ( Delta x) = 2,5 см = 0,025 м при приложении силы, равно ( F=m_1g=0,1cdot 10=1text{ H} ): [k=dfrac{F}{Delta x}=dfrac{1}{0,025}=40text{ H/кг}] Если массу груза увеличить в 3 раза, то есть, (m_2=0,3) кг, то удлинение пружины будет равно: [Delta x=dfrac{F}{k}=dfrac{m_2g}{k}=dfrac{3cdot0,1cdot10text{ H}}{40text{ H/кг}}=0,075text{ м}=7,5text{ см}]

Ответ: 7,5

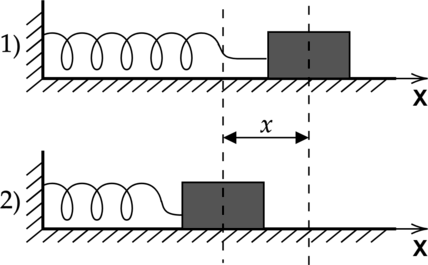
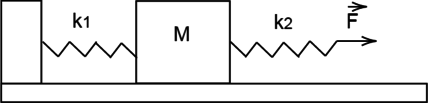
К системе из кубика массой M = 3 кг и двух пружин приложена постоянная горизонтальная сила F величиной 20 Н (см. рисунок). Между кубиком и опорой трения нет. Система покоится. Жёсткость первой пружины (k_1 = 400 text{ Н/м}). Жёсткость второй пружины (k_2 = 800 text{ Н/м}). Каково удлинение первой пружины? (Ответ дайте в сантиметрах)

Согласно закону Гука удлинение (Delta x) пружины связано с ее жесткостью k и приложенной к ней силе F выражением (F=kDelta x). На первую пружину действует такая же сила F, что и на вторую, так как трения между кубиком и опорой нет. То, что первая пружина соединена со второй через кубик, здесь не имеет никакого значения, соответственно удлинение первой пружины – это величина, равная: [Delta x=dfrac{F}{k_1}=dfrac{20text{ H}}{400text{ H/м}}=0,05 text{ м}=5 text{ см}]

Ответ: 5

Определите силу, под действием которой пружина жёсткостью 200 Н/см удлинится на 5 мм.

Согласно закону Гука ( F=kDelta x ), где k – жесткость пружины, ( Delta x) – удлинение пружины, получаем: [F=kDelta x=(dfrac{200}{0,01})text{H/м}cdot(5cdot10^{-3})text{м}=100text{ H}]

Ответ: 100

Пружина одним концом прикреплена к неподвижной опоре, к другому концу приложили силу равную 1500 Н, при этом пружина растянулась на 0,2 м. Определите жесткость данной пружины. Ответ дать в Н/м.

После растяжения, пружина покоится и на неё действуют 2 силы направленные в противоположные направления: (F_{text{упр}}) – сила упругости и F – приложенная сила.
Тогда по первому закону Ньютона: [F_{text{упр}}=F] По закону Гука: [F_{text{упр}}=kx] Приравниваем эти формулы: [F=kx] Тогда [k=frac{F}{x}=frac{1500}{0,2}=7500 text{ Н/м}]

Ответ: 7500

К потолку прикреплены одним концом две пружины с одинаковой жесткостью. За другой конец первую пружину растягивают с силой (F_{text{1}}), которая в 2,5 раза больше силы (F_{text{2}}), растягивающей вторую пружину. При этом вторая пружина растянулась на 0,4 м. Насколько растянулась первая пружина? Ответ дать в метрах.

После растяжения обе пружины находятся в покое и на них, кроме данных сил действует сила упругости. Тогда по первому закону Ньютона: [F_{text{упр1}}=F_{text{1}}] [F_{text{упр2}}=F_{text{2}}] где (F_{text{упр1}}) – сила упругости, действующая на первую пружина, (F_{text{упр2}}) – на вторую.
По закону Гука: [F_{text{упр}}=kx] Воспользуемся этим законом в вышенаписанных формулах: [kx_{1}=F_{1}quad(1)] [kx_{2}=F_{text{2}}quad(2)] где (x_{1}) – удлинение первой пружины, (x_{2}) – второй. Разделим (1) на (2), получится: [frac{x_{1}}{x_{2}}=frac{F_{text{1}}}{F_{text{2}}}Rightarrow x_{1}=dfrac{F_{text{1}}x_{2}}{F_{text{2}}}=2,5cdot0,4=1text{ м}]

Ответ: 1

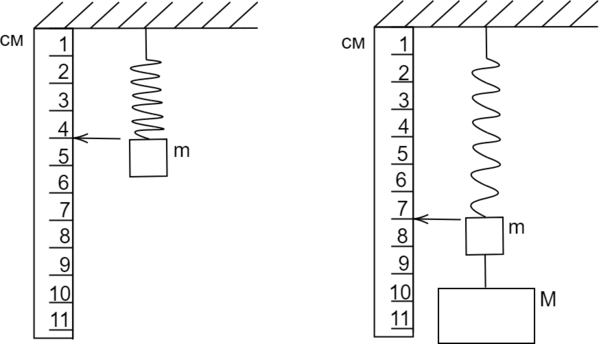
К грузу массой (m) аккуратно подвесили другой груз массой (M), при этом пружина с жесткостью 1200 Н/м удлинилась так, как показано на рисунке. Найдите массу (M). Ускорение свободного падения считать равным 10 м/(c^{2}). Ответ дать в кг.

Рассмотрим ситуацию до подвешивания груза: система тел “груз и пружина” покоится, на неё действуют 2 силы, направленные в противоположные стороны: сила тяжести и сила упругости.
Тогда по первому закону Ньютона: [mg=F_{text{упр}1}] Рассмотрим ситуацию после подвешивания груза: систама тел “2 груза и пружина” покоится, на неё действуют 2 силы, направленные в противоположные стороны: сила тяжести и сила упругости.
Тогда по первому закону Ньютона: [mg+Mg=F_{text{упр2}}] По закону Гука: [F_{text{упр}}=kx] Воспользуемся этим законом в вышенаписанных формулах: [mg=kx_{1}quad(1)] [mg+Mg=kx_{2}quad(2)] Вычтем (1) из (2), получится: [Mg=k(x_{2}-x_{1})Rightarrow M=dfrac{k(x_{2}-x_{1})}{g}=frac{1200cdot0,03}{10}=3,6text{ кг}]

Ответ: 3,6

Кубик массой (M = 2) кг, сжатый с боков пружинами, покоится на гладком горизонтальном столе. Первая пружина сжата на 2 см, а вторая сжата на 6 см. Жёсткость первой пружины (k_1 = 1200) Н/м. Чему равна жёсткость второй пружины (k_2)? Ответ выразите в Н/м.

По второму закону Ньютона силы упругости пружин будут уравновешивать друг друга, следовательно: [k_1Delta x_1=k_2Delta x_2] где (Delta x_1) и (Delta x_2) – сжатие первой и второй пружины соответственно.
Откуда жесткость второй пружины [k_2=dfrac{k_1 Delta x_1}{Delta x_2}= dfrac{1200text{ Н/м}cdot 2text{ см}}{6text{ см}}=400text{ Н/м}]

Ответ: 400

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ

Источник

Сила упругости. Закон Гука

Закон Гука: Ut tensio sic vis — каково растяжение, такова и сила. Закон выражает зависимость между размерами малых деформаций тел и силами или силой, вызывающей данные деформации. Его можно записать так: . Здесь — сила, воздействующая на тело, она может как сжимать тело, так и растягивать его, — жесткость материала — коэффициент, разный для разных материалов. Чем он больше, тем жестче материал и его труднее сжать или растянуть. — это удлинение. Вообще в формуле присутствует знак «минус»: F=-k*x . Он свидетельствует о том, что сила упругости всегда направлена в сторону, противоположную деформации.

Также закон Гука можно записать и в другой форме: . В этой форме закона Гука — нормальное напряжение в поперечном сечении (нормальное — значит, перпендикулярное срезу) — это, по сути, плотность силы: (S — площадь среза, или поперечного сечения). Е — коэффициент, называемый Модулем Юнга — его можно определить по справочнику для разных материалов, — относительное удлинение, .

Задачи.

1. На сколько удлинится рыболовная леска жесткостью 0,3 кН/м при поднятии вверх рыбы весом 300 г?

Сначала определим силу, которая возникает, когда мы что-то поднимаем. Это, конечно, сила тяжести. Если принять ускорение свободного падения равным 10 м/с*с, то модуль силы тяжести равен (не забываем массу представить в единицах СИ — килограммах): Н. Тогда по закону Гука определим модуль удлинения лески:

Выражаем модуль удлинения:

Подставим числа, жесткость лески при этом выражаем в Ньютонах: $delim{|}{x}{|}=3/{0,3*10^3}=10^{-2}=0,01$ м, или 1 см.

Ответ: 1 см.

2. На рисунке представлены графики зависимости удлинения от модуля приложенной силы для стальной 1 и медной 2 проволок равной длины и диаметра. Сравнить жесткости проволок.

Задача 2

На рисунке видно, что при воздействии одной и той же силы F удлинение стальной проволоки вдвое меньше, чем медной. Значит, стальную растянуть вдвое труднее — или ее жесткость вдвое больше.

3. Найти удлинение буксирного троса жесткостью 100 кН/м при буксировке автомобиля массой 2 тонны с ускорением 0,5 м/с*с. Трением пренебречь.

В этой задаче также сначала определим силу. Силу, которая действует на конец троса со стороны буксируемого автомобиля, можно определить по второму закону Ньютона: ведь ускорение, с которым двигается тело, прямо пропорционально силе и обратно пропорционально массе тела, в данном случае выражение записано для модуля силы: F=ma . Выразив массу машины в килограммах, определим этот модуль силы: Н. Тогда модуль удлинения троса , вычисляем:

$delim{|}{x}{|}=10^3/{100*10^3}=1/100$ м, или 1 см.

Ответ: 1 см.

4. Подвешенное к тросу тело массой 10 кг поднимается вертикально. С каким ускорением движется тело, если трос жесткостью 59 кН/м удлинился на 2 мм?

Это обратная двум предыдущим задача. Здесь сначала мы определим модуль силы упругости:

, при подстановке важно не забывать применять в расчетах величины, представленные в единицах СИ: $F=59*10^3*2*10^{-3}=118$ .

Зная силу, можно определить и ускорение (модуль ускорения): для этого воспользуемся вторым законом Ньютона: F-mg=ma ,откуда

Таким образом, получили ответ: 2 м/c*c

5. С каким максимальным ускорением можно поднимать с помощью веревки тело массой 200 кг, если веревка выдерживает неподвижный груз массой 240 кг?

Веревка выдерживает висящее тело массой 240 кг — а на висящее тело действует сила тяжести, равная Н (если принять равным 10 ускорение свободного падения). Тогда по второму закону Ньютона F-mg=ma такая сила может заставить тело массой 200 кг двигаться с ускорением:.

Ответ: 2 м/c*c

6. Жесткость одной пружины равна k_1 , а другой — k_2 . Какова жесткость пружины, составленной из этих двух пружин, соединенных последовательно?

Запишем для каждой из пружин закон Гука. Для первой: $F=k_1*delim{|}{x_1}{|}$ .

Для второй: $F=k_2*delim{|}{x_2}{|}$ — иными словами, пружины с разной жесткостью можно растянуть по-разному при воздействии одной и той же силы. Первую можно удлинить так: $delim{|}{x_1}{|}=F/{k_1}$ , вторую же можно удлинить так: $delim{|}{x_2}{|}=F/{k_2}$ Наконец, соединим их и снова будем растягивать с той же силой: . Удлинение такой составной пружины сложится из удлинений первой и второй: $delim{|}{x_1}{|}+delim{|}{x_2}{|}=F/{k_1}+F/{k_2}=delim{|}{x}{|}$ .

Вынесем за скобку силу: $delim{|}{x}{|}=F(1/{k_1}+1/{k_2})$ и приведем к общему знаменателю сумму в скобках:

$delim{|}{x}{|}=F({k_1}+{k_2})/{k_1*k_2}$

Отсюда $F=delim{|}{x}{|}*{{k_1}*{k_2}}/{k_1+k_2}$ , а жесткость составной пружины $k={{k_1}*{k_2}}/{k_1+k_2}$

7. Жесткость данного куска проволоки равна k. Чему равна жесткость половины этого куска проволоки?

Эту задачу можно решить, воспользовавшись второй формой закона Гука. Тогда для целой проволоки имеем: ${sigma_1}=E{varepsilon_1}$ , а для половины ${sigma_2}=E{varepsilon_2}$ .

Так как это одна и та же проволока, то модуль Юнга у обоих кусков одинаков. Также одинаково у обоих кусков и нормальное напряжение: ведь на оба куска воздействуют с одной и той же силой, и сечение также одинаково. Поэтому из закона Гука заключаем, что относительное удлинение также одинаково: ${varepsilon_1}={varepsilon_2}$ . Для целого куска относительное удлинение равно: ${varepsilon_1}={Delta{x_1}}/x$ , а для второго куска ${varepsilon}={Delta{x_2}}/{{1/2}x}$ . Приравняем оба выражения, тогда:

${Delta{x_1}}/x={Delta{x_2}}/{{1/2}x}$ , или ${Delta{x_1}}=2{Delta{x_2}}$ .

Теперь вспомним первую форму закона: $F=k_1*delim{|}{x_1}{|}=k_2*delim{|}{x_2}{|}$ .
Подставив соотношение относительных удлинений, полученное выше, имеем: $k_1*2*delim{|}{x_2}{|}=k_2*delim{|}{x_2}{|}$ , или , то есть жесткость половинки вдвое больше, чем целой проволоки — действительно, чем короче кусок, тем труднее его растянуть.

8. Жесткость пружины равна 50 Н/м. Если с помощью этой пружины равномерно тянуть по полу коробку массой 2 кг, то длина пружины увеличивается с 10 до 15 см. Какова сила упругости в этом случае? Чему равна сила трения коробки о пол?

Удлинение пружины здесь равно 15-10=5 см. Выразим в метрах: 0,05 м. Тогда по закону Гука: $F=k*delim{|}{x_1}{|}=50*0,05=2,5$ Н — силу упругости нашли. Теперь определим силу трения о пол. Какие силы действуют на коробку? 1. Сила тяжести. 2. Сила реакции опоры. 3. Сила, с которой коробку тянут. 4. Сила трения. Так как сила тяжести уравновешена силой реакции опоры, то остались две силы, очевидно, что между ними также равновесие, тогда сила трения равна силе упругости, и равна 2,5Н.

Ответ: 2,5 Н.

Источник

Задачи на силу упругости с решениями

Формулы, используемые на уроке «ЗАДАЧИ на силу упругости с решениями»

Название величины	Обозначение	Единицы измерения	Формула

Сила упругости	F_упр	H	F_упр = –kx F_упр = k•Δl
Коэффициент упругости (жесткость)	k	H/м, кг/с²	k = ES/L
Модуль Юнга (модуль упругости)	E	Н/м²	E = σ/ε

Тренировочные задания для подготовки к контрольным, самостоятельным, проверочным и диагностическим работам.

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Задача № 1.
Под действием груза в 200 Н пружина динамометра удлинилась на 0,5 см. Каково удлинение пружины под действием груза в 700 Н?

ОТВЕТ: 1,75 см.

Задача № 2.
Под действием силы давления вагона 50 кН буферные пружины между вагонами сжимаются на 1 см. С какой силой давит вагон, если пружины сжались на 4 см?

ОТВЕТ: 200 кН.

Задача № 3.
Резиновая лента удлинилась на 10 см под действием силы 10 Н. Какова ее жесткость?

ОТВЕТ: 100 Н/м.

Задача № 4.
Пружина без нагрузки длиной 20 см имеет коэффициент жесткости 20 Н/м. Какой станет длина пружины под действием силы 2 Н?

ОТВЕТ: на 0,1 м.

Задача № 5.
На сколько удлинится пружина под нагрузкой 12,5 Н, если под нагрузкой в 10 Н пружина удлинилась на 4 см?

ОТВЕТ: на 5 см.

Задачи на силу упругости

Задача № 6.
Какой груз нужно подвесить к пружине, жесткость которой 1000 Н/м, чтобы растянуть ее на 10 см?

ОТВЕТ: m ≈ 10 кг.

Нажмите на спойлер, чтобы увидеть РЕШЕНИЕ

Задача № 7.
Грузовик взял на буксир легковой автомобиль «Волга» массой m = 2 т и, двигаясь равноускоренно, за 50 с проехал путь 400 м. На сколько удлинился при этом трос, соединяющий автомобили, если его жесткость 2 • 10⁶ Н/м? Трением пренебречь.

ОТВЕТ: на 0,32 мм.

Нажмите на спойлер, чтобы увидеть РЕШЕНИЕ

Задача № 8.
На рисунке приведен график зависимости удлинения резинового жгута от модуля приложенной к нему силы. Найти жесткость жгута.

ОТВЕТ: 10 Н/м.

Нажмите на спойлер, чтобы увидеть РЕШЕНИЕ

Задача № 9.
Две пружины равной длины, скрепленные одними концами, растягивают за свободные концы руками. Пружина жесткостью 200 Н/м удлинилась на 4 см. Какова жесткость второй пружины, если ее удлинение равно 2 мм?

ОТВЕТ: 4000 Н/м.

Нажмите на спойлер, чтобы увидеть РЕШЕНИЕ

Краткая теория к теме
«Задачи на силу упругости»

В физике упругость — это свойство твёрдых материалов возвращаться в свою первоначальную форму и размер после устранения сил, которые применялись при деформации. Виды упругих деформаций: растяжение, сжатие, кручение, изгиб, сдвиг, срез.

Силы упругости — силы, возникающие при деформации тела и направленные в сторону, противоположную деформации. При небольших деформациях растяжения или сжатия силу упругости можно определить по закону Гука: F_упр = –kx, где x — удлинение/сжатие тела (всегда положительное значение), k — коэффициент пропорциональности (коэффициент упругости), названный жесткостью тела Знак «минус» в законе означает, что сила упругости всегда направлена в сторону, противоположную деформации. Единицы измерения жесткости тела в СИ: 1 Н/м.

В некоторых учебниках и задачниках закон Гука выражают формулой F_упр = k • Δl. В этом случае: Δl — удлинение/сжатие тела (всегда отрицательное значение), k — коэффициент упругости (жесткость) тела.

Иногда, силу упругости, возникающую при деформации опоры, называют силой реакции опоры и обозначают буквой N. Силу упругости, возникающую при деформации нити или каната, называют силой натяжения нити (каната) и обозначают буквой Т.

Модуль Юнга (модуль упругости) — это физическая величина, которая характеризует свойства какого-либо материала сгибаться или растягиваться под воздействием силы; по сути именно от этого зависит жёсткость тела. Низкое значение модуля Юнга означает, что изучаемое твёрдое тело является эластичным. Высокое значение модуля Юнга означает, что изучаемое твёрдое тело является неэластичным или жёстким.

Конспект урока по физике «ЗАДАЧИ на силу упругости». Тренировочные задания для подготовки к контрольным, самостоятельным, проверочным и диагностическим работам. Выберите дальнейшее действие:

Вернуться к Списку конспектов по физике для 7-11 классов
Найти конспект через Кодификатор ОГЭ по физике
Найти конспект через Кодификатор ЕГЭ по физике

Источник

Видеоурок 1: Закон Гука — Физика в опытах и экспериментах

Видеоурок 2: Сила упругости. Закон Гука

Лекция: Сила упругости. Закон Гука

Деформации

В результате того, что тела взаимодействуют, они не только изменяют друг другу характеристики движения, но и причиняют внешние изменения.

Деформации — это процесс изменения расположения любых точек в теле, который произошел в результате применения силы.

Деформации могут быть упругими и неупругими. Если на объект прекратить действовать силой и он возвращается в исходное положение, то такие деформации — упругие.

Любое твердое тело подвержено следующим видам деформации: сжатия, растяжения, сгибания, скручивания и сдвигу.

Иногда внешне не всегда можно увидеть изменения тела, однако расположение структурных единиц и расстояния между ними меняются. Во время прикладывания некоторой силы к телу, его структурные частицы приобретают ускорение, поэтому все изменения, происходящие в теле в результате деформации, называются электромагнитными.

Сила упругости

Силы, возникающие в теле во время деформаций, называются силами упругости.

Все тела, деформация над которыми упругая, называются упругими.

Для таких тел справедлив закон Гука:

Сила упругости напрямую зависит от удлинения тела и имеет направление, противоположное активной силы, приводящей к деформации.

k — коэффициент упругости — табличное значение для различных материалов.

Жесткость — это свойство любого тела противостоять деформации.

Для неупругих деформаций свойственны процессы, показанные на графике:

ОА — место, где справедлив закон Гука.

АВ — участок, где тело еще может вернуться в исходное положение без видимых изменений.

ВС — место, где материал начинает течь.

СД — материал становится пластичным.

Точка Е — предел прочности, если приложить граничную силу, тело разрушается.

После точки Е напряжение в теле снижается из-за происшедшего разрыва.

Источник

Закон Гука

Сила упругости

Сила упругости. Закон Гука

Задачи на силу упругости с решениями

Название величины

Обозначение

Единицы измерения

Формула

Сила упругости

Fупр

H

Fупр = –kx Fупр = k•Δl

Коэффициент упругости (жесткость)

k

H/м,

кг/с2

k = ES/L

Модуль Юнга (модуль упругости)

E

Н/м2

E = σ/ε

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Краткая теория к теме «Задачи на силу упругости»

F_упр

F_упр = –kx
F_упр = k•Δl

кг/с²

Н/м²

Краткая теория к теме
«Задачи на силу упругости»