а) Решите уравнение sin2x+sqrt(3)sinx=0.
б) Найдите все корни этого уравнения, принадлежащие отрезку [5π/2 ; 7π/2].
математика 10-11 класс
56141
По формуле синуса двойного угла
sin2x=2*sinx*cosx
2*sinx*cosx+sqrt(3)sinx=0
sinx*(2cosx+sqrt(3))=0
sinx=0 или 2cosx+sqrt(3)=0
x=πk, k∈Z или сosx=-sqrt(3)/2
x=± arccos(-sqrt(3)/2)+2πn, n∈Z
x=± (π- arccos sqrt(3)/2)+2πn, n∈Z
x=± (π- (π/6))+2πn, n∈Z
x=± (5π/6))+2πn, n∈Z
О т в е т. а)πk; ± (5π/6))+2πn, k, n∈Z
б) Найдем корни, принадлежащие отрезку [5π/2 ; 7π/2].
Для этого составим неравенство
5π/2 < πk < 7π/2, k∈Z
или
5/2 < k < 7/2, k∈Z — неравенство верно при k=3
Значит х=π*3=3π — корень из первой серии ответов, принадлежащий указанному промежутку.
Составим второе неравенство
5π/2 < (5π/6))+2πn < 7π/2, n∈Z
или
5/2 < (5/6)+2n < 7/2, n∈Z
Умножим на 6
15 < 5 +12n < 21, n∈Z
или
10 < 12n < 16 — неравенство верно при n=1
Значит х=(5π/6)+2π= 17π/6 — корень из второй серии ответов, принадлежащий указанному промежутку.
Составим третье неравенство
5π/2 < (-5π/6))+2πn < 7π/2, n∈Z
или
5/2 < (-5/6)+2n < 7/2, n∈Z
Умножим на 6
15 < -5 +12n < 21, n∈Z
или
20 < 12n < 26 — неравенство верно при n=2
Значит х=(-5π/6)+2π*2= 19π/6 — корень из второй серии ответов, принадлежащий указанному промежутку.
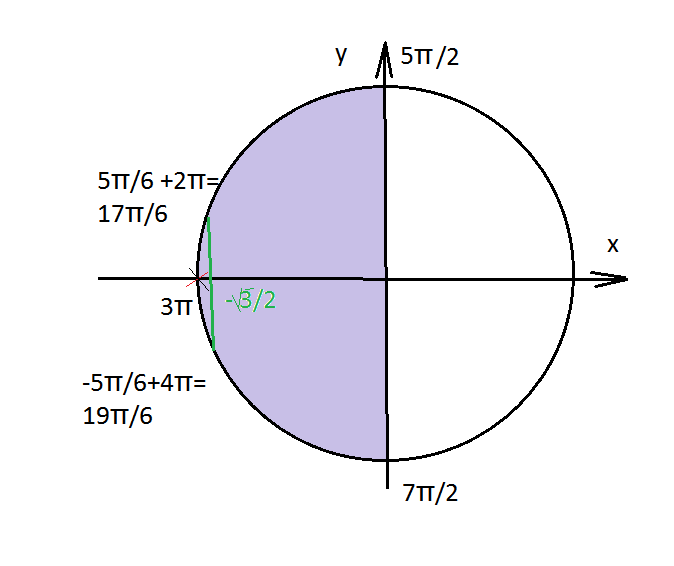
Можно рассмотреть эти корни на единичной окружности.
О т в е т. б) 17π/6; 3π; 19π/6.
Алёна Демидова 22.04.2013 19:02
По формуле для нахождения корней у косинуса, периодичность равна а в вашей формуле не та периодичность, и, следовательно, один лишний корень в выборе корней на промежутке.
Константин Лавров
Странно, что вы обращаете внимание на «лишний» корень уже только при выборе корней, а не с самого начала. Но у нас все верно, периодичность косинуса тут не причем, просто решены сразу оба уравнения.
Надежда Калинкина 21.05.2013 10:55
Если в ответе пункта А) напишу засчитают?
Виктория Григорьева 01.06.2013 07:28
Я заменила на
Из уравнения с синусом ответ получился
б)корни
Это правильное решение?
Евгений Ощепков 04.03.2014 21:35
периодичность у арккосинуса ведь 2П, а если через синус решать то там так выходит. Я прав?
Константин Лавров
впрочем, как и
не являются периодическими функциями.
Борис Синицын 11.07.2016 12:43
Вы потеряли два корня 5п/6 + 2пk и -5п/6 +2пk
Борис Синицын
Указанные Вами корни не потеряны.
входит в серию
,
входит в серию
, где
Борис Синицын 11.07.2016 12:44
возможен ответ?
а) п±п/6+2пk, ±п/6+2пk, k∈Z.
Лидия Огнева 10.02.2017 09:56
1-2sin^2x-(sin pi/2*cosx-cos pi/2*sinx)^2=1-2sin^2x-cos^2x=-2sin^2x+sin^2x=-sin^2x=-0,25 => sin^2x=0,25 => 1) sinx = 0,5 или 2) sinx = -0,5
=> x=+-pi/6+2pi*n или x=+-5pi/6+2pi*n
Объясните, пожалуйста, где моя ошибка. Почему у меня получается +-5pi/6+2pi*n?
Александр Иванов
У Вас верно.
Посмотрите комментарии к вопросам выше
39 месяцев назад
Ответы1
- В задании дано тригонометрическое уравнение sin(2 * x) + √(3) * sinx = 0. Однако, сопровождающее требование к нему отсутствует. По всей видимости, составители задания хотели решить данное уравнение. Для выполнения требования задания, воспользуемся свойствами тригонометрических функций.
- Используя формулу sin(2 * α) = 2 * sinα * cosα (синус двойного угла), преобразуем данное уравнение следующим образом: 2 * sinх * cosх + √(3) * sinx = 0. Выводим за скобки общий для обоих слагаемых множитель sinx. Тогда, имеем: sinх * (2 * cosх + √(3)) = 0.
- Произведение двух сомножителей равно нулю тогда и только тогда, когда хотя бы один из них равен нулю. Используя этот факт, вместо последнего уравнения рассмотрим по отдельности следующие два уравнения: sinх = 0 и 2 * cosх + √(3) = 0.
- Первое уравнение sinх = 0 является простейшим тригонометрическим уравнением. Выпишем его решение: х = π * m, где m – целое число.
- Второе уравнение перепишем в виде 2 * cosх = -√(3). Поделим обе части последнего уравнения на 2. Тогда, получим уравнение cosх = -√(3) / 2, которое также является простейшим тригонометрическим уравнением. Выпишем его решение: х = ±5 * π/6 + 2 * π * n, где n – целое число.
Ответ: х = π * m и х = ±5 * π/6 + 2 * π * n, где m и n – целые числа.
Опубликовано 03.01.2018 по предмету
Алгебра
от Гость
А) Решите уравнение sin2x+√3sinx=0. б) Найдите все корни этого уравнения, принадлежащие отрезку [5П/2;7П/2].
Ответ оставил Гость
2sinxcosx+√3sinx=0
sinx(2cosx+√3)=0
sinx=0⇒x=πn x=3π∈[5π/2;7π/2]
cosx=-√3/2⇒x1=5π/6+2πn
x=17π/6∈[5π/2;7π/2] U x2=-5π/6+2πn x=19π/6∈[5π/2;7π/2]
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
Не нашел нужный ответ?
Если ответ по предмету Алгебра отсутствует или он оказался неправильным, то попробуй воспользоваться поиском других ответов во всей базе сайта.
Найти другие ответы

