Системы логических уравнений егэ информатика

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Пройти тестирование по этим заданиям

Автор материалов — Лада Борисовна Есакова.

Решение систем логических уравнений методом замены переменных

Метод замены переменных применяется, если некоторые переменные входят в состав уравнений только в виде конкретного выражения, и никак иначе. Тогда это выражение можно обозначить новой переменной.

Пример 1.

Сколь­ко су­ще­ству­ет раз­лич­ных на­бо­ров зна­че­ний ло­ги­че­ских пе­ре­мен­ных x1, х2, х3, х4, х5, х6, х7, х8, ко­то­рые удо­вле­тво­ря­ют всем пе­ре­чис­лен­ным ниже усло­ви­ям?

(x1 → х2) → (х3→ х4) = 1

(х3 → х4) → (х5 → х6) = 1

(х5 → х6) → (х7 → х8) = 1

В от­ве­те не нужно пе­ре­чис­лять все раз­лич­ные на­бо­ры зна­че­ний пе­ре­мен­ных x1, х2, х3, х4, х5, х6, х7, х8, при ко­то­рых вы­пол­не­на дан­ная си­сте­ма ра­венств. В ка­че­стве от­ве­та Вам нужно ука­зать ко­ли­че­ство таких на­бо­ров.

Решение:

Сде­ла­ем за­ме­ну пе­ре­мен­ных:

(x1 → х2) = y1; (х3 → х4) = y2; (х5 → х6) = y3; (х7 → х8) = y4.

Тогда можно за­пи­сать си­сте­му в виде од­но­го урав­не­ния:

(y1 → y2) ∧ (y2 → y3) ∧ (y3 → y4) = 1. Конъюнкция равна 1 (истинна), когда каждый операнд принимает значение 1. Т.е. каждая из импликаций должна быть истинна, а это выполняется при всех значениях, кроме (1  → 0). Т.е. в таблице значений переменных y1, y2, y3, y4 единица не должна стоять левее нуля:

y1	y2	y3	y4
0	0	0	0
0	0	0	1
0	0	1	1
0	1	1	1
1	1	1	1

Т.е. условия выполняются для 5 наборов y1-y4.

Т.к. y1 = x1 → x2, то значение y1 = 0  достигается на единственном наборе x1, x2: (1, 0), а значение y1 = 1 – на трех наборах x1, x2: (0,0) , (0,1), (1,1). Аналогично для y2, y3, y4.

Поскольку каждый набор (x1,x2) для переменной y1 сочетается с каждым набором (x3,x4) для переменной y2 и т.д., то количества наборов переменных x перемножаются:

y1	y2	y3	y4	Кол-во наборов на x1…x8
0	0	0	0	1*1*1*1 = 1
0	0	0	1	1*1*1*3 = 3
0	0	1	1	1*1*3*3 = 9
0	1	1	1	1*3*3*3 = 27
1	1	1	1	3*3*3*3 = 81

Сло­жим ко­ли­че­ство наборов: 1 + 3 + 9 + 27 + 81 = 121.

Ответ: 121

Пример 2.

Сколько существует различных наборов значений логических переменных x1, x2, … x9, y1, y2, … y9, которые удовлетворяют всем перечисленным ниже условиям?

(¬ (x1 ≡ y1)) ≡ (x2 ≡ y2)

(¬ (x2 ≡ y2)) ≡ (x3 ≡ y3)

…

(¬ (x8 ≡ y8)) ≡ (x9 ≡ y9)

В ответе не нужно перечислять все различные наборы значений переменных x1, x2, … x9, y1, y2, … y9, при которых выполнена данная система равенств. В качестве ответа Вам нужно указать количество таких наборов.

Решение:

Сде­ла­ем за­ме­ну пе­ре­мен­ных:

(x1 ≡ y1) = z1, (x2 ≡ y2) = z2,…. ,(x9 ≡ y9) = z9

Систему можно записать в виде одного уравнения:

(¬ z1 ≡ z2) ∧ (¬ z2 ≡ z3) ∧ …..∧ (¬ z8 ≡ z9)

Эквивалентность истинна, только если оба операнда равны. Решениями этого уравнения будут два набора:

z1	z2	z3	z4	z5	z6	z7	z8	z9
0	1	0	1	0	1	0	1	0
1	0	1	0	1	0	1	0	1

Т.к. zi = (xi ≡ yi), то значению zi = 0 соответствуют два набора (xi,yi): (0,1) и (1,0), а значению zi = 1 — два набора (xi,yi): (0,0) и (1,1).

Тогда первому набору z1, z2,…, z9 соответствует 2⁹ наборов (x1,y1), (x2,y2),…, (x9,y9).

Столько же соответствует второму набору z1, z2,…, z9. Тогда всего 2⁹ +2⁹ = 1024 наборов.

Ответ:1024

Решение систем логических уравнений методом визуального определения рекурсии.

Этот метод применяется, если система уравнений достаточно проста и порядок увеличения количества наборов при добавлении переменных очевиден.

Пример 3.

Сколь­ко раз­лич­ных ре­ше­ний имеет си­сте­ма урав­не­ний

¬x1 ∨ x2 = 1

¬x2 ∨ x3 = 1

…

¬x9 ∨ x10 = 1,

где x1, x2, … x10 — ло­ги­че­ские пе­ре­мен­ные?

В от­ве­те не нужно пе­ре­чис­лять все раз­лич­ные на­бо­ры зна­че­ний x1, x2, … x10, при ко­то­рых вы­пол­не­на дан­ная си­сте­ма ра­венств. В ка­че­стве от­ве­та Вам нужно ука­зать ко­ли­че­ство таких на­бо­ров.

Решение:

Решим первое уравнение. Дизъюнкция равна 1, если хотя бы один из ее операндов равен 1. Т.е. решениями являются наборы:

 

Для x1=0 существуют два значения x2 ( 0 и 1), а для x1=1 только одно значение x2 (1), такие, что набор (x1,x2) является решением уравнения. Всего 3 набора.

Добавим переменную x3 и рассмотрим второе уравнение. Оно аналогично первому, значит для x2=0 существуют два значения x3 ( 0 и 1), а для x2=1 только одно значение x3 (1), такие, что набор (x2,x3) является решением уравнения. Всего 4 набора.

 

Несложно заметить, что при добавлении очередной переменной добавляется один набор. Т.е. рекурсивная формула количества наборов на (i+1) переменных:

N_i+1 = N_i + 1. Тогда для десяти переменных получим 11 наборов.

Ответ: 11

Решение систем логических уравнений различного типа

Пример 4.

Сколь­ко су­ще­ству­ет раз­лич­ных на­бо­ров зна­че­ний ло­ги­че­ских пе­ре­мен­ных x₁, …, x₄, y₁,…, y₄, z₁,…, z₄, ко­то­рые удо­вле­тво­ря­ют всем пе­ре­чис­лен­ным ниже усло­ви­ям?

(x₁ → x₂) ∧ (x₂ → x₃) ∧ (x₃ → x₄) = 1

(y₁ → y₂) ∧ (y₂ → y₃) ∧ (y₃ → y₄) = 1

(z₁ → z₂) ∧ (z₂→ z₃) ∧ (z₃ → z₄) = 1

x₄ ∧ y₄ ∧ z₄ = 0

В от­ве­те не нужно пе­ре­чис­лять все раз­лич­ные на­бо­ры зна­че­ний пе­ре­мен­ных x₁, …, x₄, y₁, …, y₄, z₁, …, z₄, при ко­то­рых вы­пол­не­на дан­ная си­сте­ма ра­венств.

В ка­че­стве от­ве­та Вам нужно ука­зать ко­ли­че­ство таких на­бо­ров.

Решение:

Заметим, что три уравнения системы одинаковы на различных независимых наборах переменных.

Рассмотрим первое уравнение. Конъюнкция истинна (равна 1) только тогда, когда все ее операнды истинны (равны 1). Импликация равна 1 на всех наборах, кроме (1,0). Значит, решением первого уравнения будут такие наборы x1, x2, x3, x4, в которых 1 не стоит левее 0 (5 наборов):

x1	x2	x3	x4
0	0	0	0
0	0	0	1
0	0	1	1
0	1	1	1
1	1	1	1

Аналогично, решениями второго и третьего уравнений будут абсолютно такие же наборы y1,…,y4 и z1,…, z4.

Теперь проанализируем четвертое уравнение системы: x₄ ∧ y₄ ∧ z₄ = 0. Решением будут все наборы x4, y4, z4, в которых хотя бы одна из переменных равна 0.

Т.е. для x4 = 0 подойдут все возможные наборы (y4, z4), а для x4 = 1 подойдут наборы (y4, z4), в которых присутствует хотя бы один ноль : (0, 0), (0,1) , (1,0).

x1	x2	x3	x4	Кол-во наборов  (y4, z4)
0	0	0	0	5*5 = 25
0	0	0	1	1 + 4 + 4 = 9
0	0	1	1	1 + 4 + 4 = 9
0	1	1	1	1 + 4 + 4 = 9
1	1	1	1	1        + 4 + 4 = 9

Общее количество наборов 25 + 4*9 = 25 + 36 = 61.

Ответ: 61

Решение систем логических уравнений методом построения рекуррентных формул

Метод построения рекуррентных формул применяется при решении сложных систем, в которых порядок увеличения количества наборов неочевиден, а построение дерева невозможно из-за объемов.

Пример 5.

Сколь­ко су­ще­ству­ет раз­лич­ных на­бо­ров зна­че­ний ло­ги­че­ских пе­ре­мен­ных x1, x2, … x7, y1, y2, … y7, ко­то­рые удо­вле­тво­ря­ют всем пе­ре­чис­лен­ным ниже усло­ви­ям?

(x1 ∨ y1) ∧ ((x2 ∧ y2) → (x1 ∧ y1)) = 1

(x2 ∨ y2) ∧ ((x3 ∧ y3) → (x2 ∧ y2)) = 1

…

(x6 ∨ y6) ∧ ((x7 ∧ y7) → (x6 ∧ y6)) = 1

(x7 ∨ y7) = 1

В от­ве­те не нужно пе­ре­чис­лять все раз­лич­ные на­бо­ры зна­че­ний пе­ре­мен­ных x1, x2, …, x7, y1, y2, …, y7, при ко­то­рых вы­пол­не­на дан­ная си­сте­ма ра­венств. В ка­че­стве от­ве­та Вам нужно ука­зать ко­ли­че­ство таких на­бо­ров.

Решение:

Заметим, что первые шесть уравнений системы одинаковы и отличаются только набором переменных. Рассмотрим первое уравнение. Его решением будут следующие наборы переменных:

 

Обозначим:

число наборов (0,0) на переменных (x1,y1) через A₁,

число наборов (0,1) на переменных (x1,y1) через B₁,

число наборов (1,0) на переменных (x1,y1) через C₁,

число наборов (1,1) на переменных (x1,y1) через D₁.

число наборов (0,0) на переменных (x2,y2) через A₂,

число наборов (0,1) на переменных (x2,y2) через B₂,

число наборов (1,0) на переменных (x2,y2) через C₂,

число наборов (1,1) на переменных (x2,y2) через D₂.

Из дерева решений видим, что

A₁=0, B₁=1, C₁=1, D₁=1.

Заметим, что набор (0,0) на переменных (x2,y2) получается из наборов (0,1), (1,0) и (1,1) на переменных (x1,y1). Т.е. A₂=B₁+C₁+D₁.

Набор (0,1) на переменных (x2,y2) получается из наборов (0,1), (1,0) и (1,1) на переменных (x1,y1). Т.е. B₂=B₁+C₁+D₁.

Аналогично рассуждая, заметим, что С₂=B₁+C₁+D₁. D₂= D₁.

Таким образом, получаем рекуррентные формулы:

A_i+1 = B_i + C_i + D_i

B_i+1 = B_i + C_i + D_i

C_i+1 = B_i + C_i + D_i

D_i+1 = A_i +B_i + C_i + D_i

Составим таблицу

Наборы	Обозн.	Формула	Количество наборов
i=1	i=2	i=3	i=4	i=5	i=6	i=7
(0,0)	Ai	Ai+1=Bi+Ci+Di	0	3	7	15	31	63	127
(0,1)	Bi	Bi+1=Bi+Ci+Di	1	3	7	15	31	63	127
(1,0)	Ci	Ci+1=Bi+Ci+Di	1	3	7	15	31	63	127
(1,1)	Di	Di+1=Di	1	1	1	1	1	1	1

Последнему уравнению (x7 ∨ y7) = 1 удовлетворяют все наборы, кроме тех, в которых x7=0 и y7=0. В нашей таблице число таких наборов A₇.

Тогда общее количество наборов равно B₇ + C₇ + D₇ = 127+127+1 = 255

Ответ: 255

Методика решения задач ЕГЭ

по теме

«Системы логических

уравнений»

Учитель информатики

Шахова Е.А.

ГБОУ «Гимназия №1

им. А.С. Пушкина»

Севастополь, 2017

Формулировка задания

Сколько существует различных наборов значений логических переменных х1, х2,… (y1, y2, …), которые удовлетворяют всем перечисленным ниже условиям:

… (система логических уравнений)

В ответе не нужно перечислять все различные наборы х1, х2, … (y1, y2, …), при которых выполняется данная система равенств. В качестве ответа необходимо указать количество таких наборов

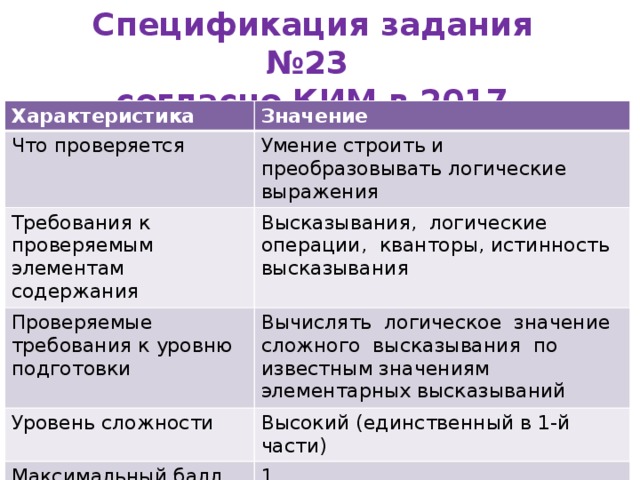
Спецификация задания №23

согласно КИМ в 2017 ( «ФИПИ»)

Характеристика

Значение

Что проверяется

Умение строить и преобразовывать логические выражения

Требования к проверяемым элементам содержания

Высказывания, логические операции, кванторы, истинность высказывания

Проверяемые требования к уровню подготовки

Вычислять логическое значение сложного высказывания по известным значениям элементарных высказываний

Уровень сложности

Высокий (единственный в 1-й части)

Максимальный балл

1

Примерное время выполнения

10 мин

Особенности решения

• Задание сложное, его невозможно формализовать;
• Большое количество приемов и методов решения;
• Большая сложность при маленьком количестве баллов (лучше решить №24, чем №23);
• Требует базовых знаний по комбинаторике.

Необходимые знания и умения

• Базовые и дополнительные логические операции;
• Законы алгебры логики;
• Структуры данных – деревья;
• Метод замены переменных;
• Метод отображения (динамическое программирование);
• Основы комбинаторики;
• Навыки преобразования и анализа логических выражений.

Условные обозначения (в порядке приоритета операций)

• отрицание (НЕ) :  A , , not A
• конъюнкция (И) : A ˄ B , A  B, AB, А&B, A and B
• дизъюнкция (ИЛИ) : A ˅ B , A+ B, A | B, А or B
• импликация (следствие) : А  B
• эквивалентность (равенство): A  В, A  B, A  B
• исключающее «или» (сложение по модулю 2) : A  B , A xor B

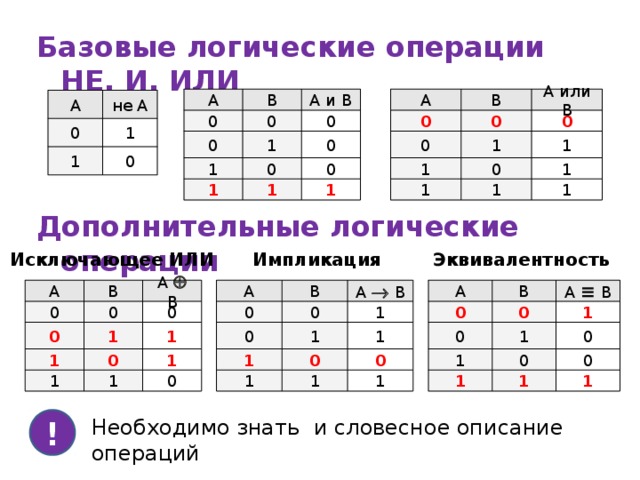
Базовые логические операции НЕ, И, ИЛИ

А или B

B

A

A

B

А и B

не А

А

0

0

0

0

0

0

1

0

0

1

1

1

0

0

0

1

0

1

0

0

1

1

1

1

1

1

1

1

Дополнительные логические операции

Импликация

Эквивалентность

Исключающее ИЛИ

A

A

B

А  B

A

B

А ≡ B

А  B

B

0

1

0

0

0

1

0

0

0

0

1

0

1

1

0

1

1

0

0

1

0

0

1

0

0

1

1

1

1

1

0

1

1

1

1

1

Необходимо знать и словесное описание операций

!

Основные законы логики

Свойства логических операций

И

ИЛИ

НЕ

Название

Переместительный

Закон в логике

Аналог в алгебре

А ˅ B = B ˅ A

А + B=B + A

Сочетательный

А ˄ B = B ˄ A

А * B=B * A

(А ˅ B) ˅ C =А ˅( B˅ C)

Распределительный

(А + B) + C =А +( B+ C)

(А ˄ B) ˄ C =А ˄ ( B˄ C)

(А*B) * C =А *( B* C)

(А ˅ B) ˄ C = (А ˄ C) ˅ (B ˄ C)

(А +B) *C = (А*C) +(B*C)

(А ˄ B) ˅ C = (А ˅ C ) ˄(B˅ C)

Аналога нет

Основные законы логики

Законы де Моргана:

Формулы склеивания:

Формулы поглощения:

Преобразование операций

Метод замены переменных

Применяется, если можно выделить одинаковые выражения в уравнениях, между которыми нет общих переменных .

ПРИМЕР:

((x1 ≡ x2) / (x3 ≡ x4)) / (¬(x1 ≡ x2) / ¬(x3 ≡ x4)) =1

((x3 ≡ x4) / (x5 ≡ x6)) / (¬(x3 ≡ x4) / ¬(x5 ≡ x6)) =1

((x5 ≡ x6) / (x7 ≡ x8)) / (¬(x5 ≡ x7) / ¬(x7 ≡ x8)) =1

((x7 ≡ x8) / (x9 ≡ x10)) / (¬(x7 ≡ x8) / ¬(x9 ≡ x10)) =1

ЗАМЕНА:

t1 = (x1  x2)

t2 = (x3  x4)

t3 = (x5  x6)

t4 = (x7  x8)

t5 = (x9  x10)

= Решение в новых переменных (2 набора) t1 0 t2 1 1 t3 0 t4 0 t5 1 1 0 0 1 » width=»640″

Метод замены переменных

Получаем после преобразования

=

=

Решение в новых переменных (2 набора)

t1

0

t2

1

1

t3

0

t4

0

t5

1

1

0

0

1

Метод замены переменных

Для каждой комбинации из 5-ти значений t 1 … t 5 существует по 2 решения:

если t 1 = 0 , то x 1 =1, x 2 =0

или x 1 =0, x 2 =1

если t 1 = 1 , то x 1 =1, x 2 =1

или x 1 =0, x 2 =0

t 1 = ( x 1 ≡ x 2 )

t 2 = ( x 3 ≡ x 4 )

t 3 = ( x 5 ≡ x 6 )

t 4 = ( x 7 ≡ x 8 )

t 5 = ( x 9 ≡ x 10 )

То есть 2 варианта по 5 переменным дают 2 5 =32 решения, 32+32=64

Метод замены переменных

Для закрепления

Информатика и ИКТ. Подготовка к ЕГЭ-2016. 20 тренировочных вариантов по демоверсии на 2016 год: учебно-методическое пособие / Под ред. Л. Н. Евич, С.Ю. Кулабухова. – Ростов-на-Дону: Легион, 2015.

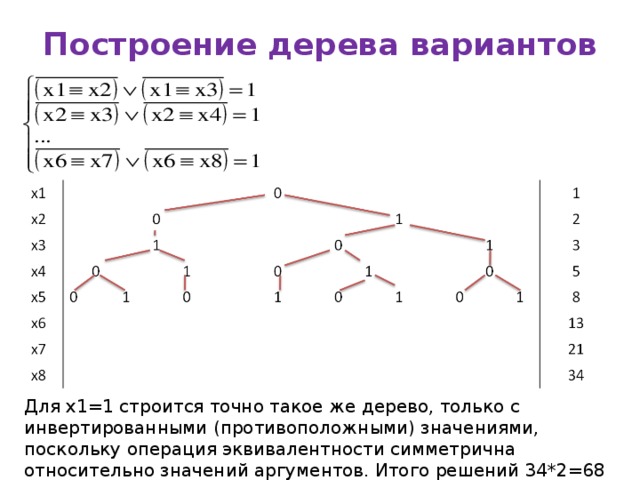
Построение дерева вариантов

Сколько существует различных наборов значений логических переменных х1, х2,…х8, которые удовлетворяют всем перечисленным ниже условиям:

Информатика и ИКТ. Подготовка к ЕГЭ-2016. 20 тренировочных вариантов по демоверсии на 2016 год: учебно-методическое пособие / Под ред. Л. Н. Евич, С.Ю. Кулабухова. – Ростов-на-Дону: Легион, 2015.

Построение дерева вариантов

ИЛИ

Построение дерева вариантов

Для x1=1 строится точно такое же дерево, только с инвертированными (противоположными) значениями, поскольку операция эквивалентности симметрична относительно значений аргументов. Итого решений 34*2=68

Построение дерева вариантов

Плюсы:

• Универсальность (можно использовать всегда);
• Наглядность.

Минусы:

— Громоздкость решения в некоторых случаях;

— Сложность выявить закономерность при больших размерностях.

Вывод : максимально упрощать выражения, при возможности использовать частные методы решения и логику.

!

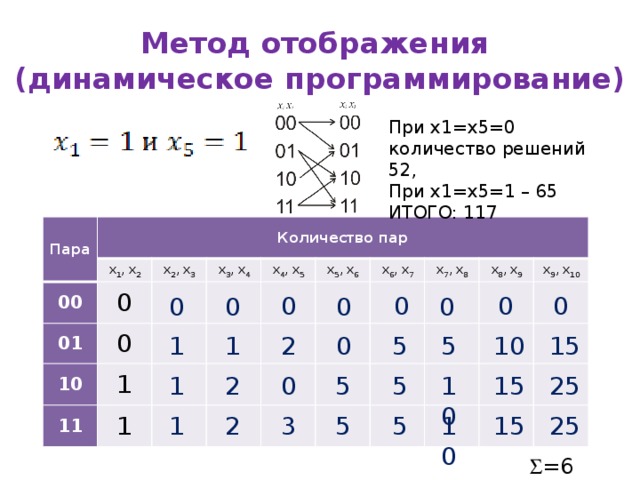
Метод отображения (динамическое программирование)

Используется, когда система состоит из уравнений, отличающихся только индексами.

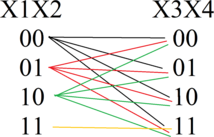
Метод отображения (динамическое программирование)

Значения пары (x1,x2) определяют возможные значения переменной x3. Т.к. другие уравнения аналогичны ,то пары (x2,x3) влияют на x4 и т.д. Выявим закономерности получения пар значений

x1

x2

0

0

X3

1

1

0

1

0

1

0

1

1

0

(x1,x2)

00

(x2,x3)

01

00

01

10

11

10

11

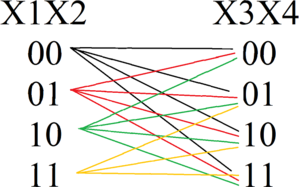
Метод отображения (динамическое программирование)

(x1,x2)

(x2,x3)

00

00

01

01

10

10

11

11

00

(x1,x2)

(x2,x3)

01

1

(x3,x4)

10

1

(x4,x5)

11

1

(x5,x6)

1

(x6,x7)

(x7,x8)

5

8

13

8

8

13

8

5

13

21

21

13

2

3

1

5

3

2

2

5

3

1

2

3

 =68

Метод отображения (динамическое программирование)

Сложность использования: наличие ограничений.

x1

x2

0

x3

0

0

1

1

0

1

1

0

1

1

0

1

Проблема : Как исключить из таблицы варианты, которые не удовлетворяют последнему уравнению.

?

Метод отображения (динамическое программирование)

Решение: рассмотрим все пары, удовлетворяющие последнему уравнению, построим отдельные таблицы.

1)

Пара

Количество пар

00

x 1 , x 2

1

01

x 2 , x 3

x 3 , x 4

10

1

x 4 , x 5

11

0

x 5 , x 6

0

x 6 , x 7

x 7 , x 8

x 8 , x 9

x 9 , x 10

1

1

1

1

1

1

1

1

13

7

0

6

1

2

5

1

19

12

4

0

1

2

5

6

19

12

0

2

6

0

1

5

 =52

Метод отображения (динамическое программирование)

При x1=x5=0 количество решений 52,

При x1=x5=1 – 65

ИТОГО: 117

Пара

Количество пар

00

x 1 , x 2

x 2 , x 3

01

0

x 3 , x 4

10

0

11

x 4 , x 5

1

1

x 5 , x 6

x 6 , x 7

x 7 , x 8

x 8 , x 9

x 9 , x 10

0

0

0

0

0

0

0

0

2

15

5

10

5

1

0

1

25

15

0

5

10

2

5

1

15

5

25

3

10

2

1

5

 =65

Задачи

Ответ: 149

1)

2)

Ответ: 73

1) в-4 2) в-9 3) в-12

3)

Ответ: 5

24

Задачи

4)

Ответ: 165

5)

Ответ: 73

4) в-13 5) в-16

24

Список использованных источников

• Информатика и ИКТ. Подготовка к ЕГЭ-2016. 20 тренировочных вариантов по демоверсии на 2016 год: учебно-методическое пособие / Под ред. Л. Н. Евич, С.Ю. Кулабухова. – Ростов-на-Дону: Легион, 2015.
• Презентация Лимаренко Андрея Ивановича, учителя информатики гимназии 446 на тему «Мастер класс: Логические задачи. Подготовка к ЕГЭ, В15»
• Презентация Мирончик Ел. А., Мирончик Ек. А. на тему «Системы логических уравнений. Метод отображения.» г. Новокузнецк, 2012.
• Презентация Вишневской М.П., МАОУ «Гимназия №3» на тему «Решение задания В15 (системы логических уравнений)» 2013 г., г. Саратов .

Егэ системы логических уравнений по информатике

Сколько существует различных наборов значений логических переменных x1, x2, x3, x4, x5, y1, y2, y3, y4, y5, которые удовлетворяют всем перечисленным ниже условиям?

(x1 → x2) ∧ (x2 → x3) ∧ (x3 → x4) ∧ (x4 → x5 ) = 1

(y1 → y2) ∧ (y2 → y3) ∧ (y3 → y4) ∧ (y4 → y5 ) = 1

В ответе не нужно перечислять все различные наборы значений переменных x1, x2, x3, x4, x5, y1, y2, y3, y4, y5, при которых выполнена данная система равенств. В качестве ответа Вам нужно указать количество таких наборов.

1) Из последнего уравнения следует, что глобально мы имеем три варианта — x1=1, y1=1; x1=0, y1=1; x1=1, y1=0.

2) Логическое И истинно, только тогда, когда истины все утверждения, а импликация ложна только в случае, если из истинного следует ложное.

3) Уравнение (1) описывает ряд переменных . Так как из переменной с более низким номером всегда следует переменная с более высоким, если любую переменную из этого ряда приравнять 1, то все следующие должны также быть равны 1. Для уравнения (2) существует то же самое правило. Иначе говоря, если записать переменные x (или y) в порядке возрастания их номеров, слева будут нули, а справа — единицы.

4) Рассмотрим вариант x1=1, y1=1. Так как первые числа каждого ряда равны 1, то все следующие тоже равны 1. Существует только одна комбинация для этого варианта.

5) Рассмотрим вариант x1=0, y1=1. Для y-ряда все переменные равны 1, для x же существует 5 комбинаций, так как в ряде x может быть от 1 до 5 нолей включительно.

6) Последний вариант рассмотрим аналогично предыдущему. Там существует всего 5 комбинаций.

Правильный ответ: 5+5+1=11 комбинаций.

Сколько существует различных наборов значений логических переменных x1, x2, x3, x4, y1, y2 y3, y4, которые удовлетворяют всем перечисленным ниже условиям?

(x1 → x2) ∧ (x2 → x3) ∧ (x3 → x4) = 1

(¬y1 ∨ y2) ∧ (¬y2 ∨ y3) ∧ (¬y3 ∨ y4) = 1

(y1 → x1) ∧ (y2 → x2) ∧ (y3 → x3) ∧ (y4 → x4) = 1

В ответе не нужно перечислять все различные наборы значений переменных x1, x2, x3, x4, y1, y2 y3, y4, при которых выполнена данная система равенств. В качестве ответа Вам нужно указать количество таких наборов.

Конъюнкция истина тогда и только тогда, когда каждое высказывание истинно.

Для первого выражения это означает, что, если х1 равен 1, то х2, х3 и х4 также равны 1, т. е. для х1. х4 решения существуют только в виде «1111», «0111», «0011», «0001» и «0000».

Применив преобразование импликации ко второму выражению, увидим, что оно аналогично первому.

В третьем выражении из «y» следует соответствующее ему «x», это означает, что если y = 1, то и x = 1.

Следовательно, первому набору для x «1111» соответствует 5 наборов y. Второму — 4, третьему — 3, и. т. д.

Следовательно, ответ: 5 + 4 + 3 + 2 + 1 = 15.

Сколько существует различных наборов значений логических переменных x₁, x₂, x₃, x₄, y₁, y₂, y₃, y₄, z₁, z₂, z₃, z₄, которые удовлетворяют всем перечисленным ниже условиям?

(x1→x2) ∧ (x2→x3) ∧ (x3→x4) = 1

(¬x1 ∧ y1 ∧ z1) ∨ (x1 ∧ ¬y1 ∧ z1) ∨ (x1 ∧ y1 ∧ ¬z1) = 1

(¬x2 ∧ y2 ∧ z2) ∨ (x2 ∧ ¬y2 ∧ z2) ∨ (x2 ∧ y2 ∧ ¬z2) = 1

(¬x3 ∧ y3 ∧ z3) ∨ (x3 ∧ ¬y3 ∧ z3) ∨ (x3 ∧ y3 ∧ ¬z3) = 1

(¬x4 ∧ y4 ∧ z4) ∨ (x4 ∧ ¬y4 ∧ z4) ∨ (x4 ∧ y4 ∧ ¬z4) = 1

В ответе не нужно перечислять все различные наборы значений переменных

x₁, x₂, x₃, x₄, y₁, y₂, y₃, y₄, z₁, z₂, z₃, z₄, при которых выполнена данная система равенств. В качестве ответа Вам нужно указать количество таких наборов.

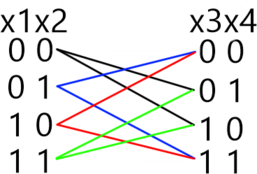
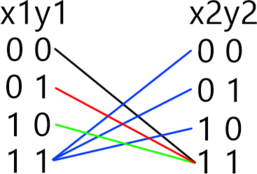
Рассмотрим первое уравнение. Ему удовлетворяют следующие наборы переменных x₁, x₂, x₃, x₄: 1111, 0111, 0011, 0001, 0000.

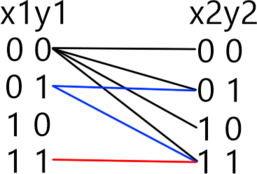
Рассмотрим оставшиеся уравнения для первого набора x₁, x₂, x₃, x₄: 1111. Во втором уравнении первая скобка будет равна 0. Из второй и третьей скобок ясно, что переменные y₁ и z₁ могут принимать значения 01 или 10. Имеем два набора решений второго уравнения. Аналогично для третьего, четвёртого и пятого уравнений. Таким образом, для набора x₁, x₂, x₃, x₄: 1111, получаем 16 наборов переменных y₁, y₂, y₃, y₄, z₁, z₂, z₃, z₄ (см. рис).

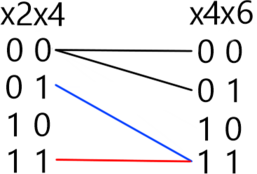
Рассмотрим второй набор переменных x₁, x₂, x₃, x₄: 0111. В этом случае из второго уравнения ясно, что переменные y₁ и z₁ могут принимать значения 11. Для оставшихся уравнений ситуация аналогична первому набору. Таким образом, для набора x₁, x₂, x₃, x₄: 0111, получаем 8 наборов переменных y₁, y₂, y₃, y₄, z₁, z₂, z₃, z₄ (см. рис).

Проведя аналогичные рассуждения для наборов 0011, 0001 и 0000, получаем, соответственно 4, 2 и 1 набор переменных y₁, y₂, y₃, y₄, z₁, z₂, z₃, z₄ соответственно.

Задача №23. Решение систем логических уравнений.

Решение систем логических уравнений методом замены переменных

Метод замены переменных применяется, если некоторые переменные входят в состав уравнений только в виде конкретного выражения, и никак иначе. Тогда это выражение можно обозначить новой переменной.

Сколь­ко су­ще­ству­ет раз­лич­ных на­бо­ров зна­че­ний ло­ги­че­ских пе­ре­мен­ных x1, х2, х3, х4, х5, х6, х7, х8, ко­то­рые удо­вле­тво­ря­ют всем пе­ре­чис­лен­ным ниже усло­ви­ям?

(x1 → х2) → (х3→ х4) = 1

(х3 → х4) → (х5 → х6) = 1

(х5 → х6) → (х7 → х8) = 1

В от­ве­те не нужно пе­ре­чис­лять все раз­лич­ные на­бо­ры зна­че­ний пе­ре­мен­ных x1, х2, х3, х4, х5, х6, х7, х8, при ко­то­рых вы­пол­не­на дан­ная си­сте­ма ра­венств. В ка­че­стве от­ве­та Вам нужно ука­зать ко­ли­че­ство таких на­бо­ров.

Сде­ла­ем за­ме­ну пе­ре­мен­ных:

(x1 → х2) = y1; (х3 → х4) = y2; (х5 → х6) = y3; (х7 → х8) = y4.

Тогда можно за­пи­сать си­сте­му в виде од­но­го урав­не­ния:

(y1 → y2) ∧ (y2 → y3) ∧ (y3 → y4) = 1. Конъюнкция равна 1 (истинна), когда каждый операнд принимает значение 1. Т.е. каждая из импликаций должна быть истинна, а это выполняется при всех значениях, кроме (1 → 0). Т.е. в таблице значений переменных y1, y2, y3, y4 единица не должна стоять левее нуля:

Т.е. условия выполняются для 5 наборов y1-y4.

Т.к. y1 = x1 → x2, то значение y1 = 0 достигается на единственном наборе x1, x2: (1, 0), а значение y1 = 1 – на трех наборах x1, x2: (0,0) , (0,1), (1,1). Аналогично для y2, y3, y4.

Поскольку каждый набор (x1,x2) для переменной y1 сочетается с каждым набором (x3,x4) для переменной y2 и т.д., то количества наборов переменных x перемножаются:

Кол-во наборов на x1…x8

Сло­жим ко­ли­че­ство наборов: 1 + 3 + 9 + 27 + 81 = 121.

Сколько существует различных наборов значений логических переменных x1, x2, . x9, y1, y2, . y9, которые удовлетворяют всем перечисленным ниже условиям?

В ответе не нужно перечислять все различные наборы значений переменных x1, x2, . x9, y1, y2, . y9, при которых выполнена данная система равенств. В качестве ответа Вам нужно указать количество таких наборов.

Сде­ла­ем за­ме­ну пе­ре­мен­ных:

(x1 ≡ y1) = z1, (x2 ≡ y2) = z2,…. ,(x9 ≡ y9) = z9

Систему можно записать в виде одного уравнения:

(¬ z1 ≡ z2) ∧ (¬ z2 ≡ z3) ∧ …..∧ (¬ z8 ≡ z9)

Эквивалентность истинна, только если оба операнда равны. Решениями этого уравнения будут два набора:

z1	z2	z3	z4	z5	z6	z7	z8	z9
0	1	0	1	0	1	0	1	0
1	0	1	0	1	0	1	0	1

Т.к. zi = (xi ≡ yi), то значению zi = 0 соответствуют два набора (xi,yi): (0,1) и (1,0), а значению zi = 1 — два набора (xi,yi): (0,0) и (1,1).

Тогда первому набору z1, z2,…, z9 соответствует 2 9 наборов (x1,y1), (x2,y2),…, (x9,y9).

Столько же соответствует второму набору z1, z2,…, z9. Тогда всего 2 9 +2 9 = 1024 наборов.

Решение систем логических уравнений методом визуального определения рекурсии.

Этот метод применяется, если система уравнений достаточно проста и порядок увеличения количества наборов при добавлении переменных очевиден.

Сколь­ко раз­лич­ных ре­ше­ний имеет си­сте­ма урав­не­ний

где x1, x2, … x10 — ло­ги­че­ские пе­ре­мен­ные?

В от­ве­те не нужно пе­ре­чис­лять все раз­лич­ные на­бо­ры зна­че­ний x1, x2, … x10, при ко­то­рых вы­пол­не­на дан­ная си­сте­ма ра­венств. В ка­че­стве от­ве­та Вам нужно ука­зать ко­ли­че­ство таких на­бо­ров.

Решим первое уравнение. Дизъюнкция равна 1, если хотя бы один из ее операндов равен 1. Т.е. решениями являются наборы:

Для x1=0 существуют два значения x2 ( 0 и 1), а для x1=1 только одно значение x2 (1), такие, что набор (x1,x2) является решением уравнения. Всего 3 набора.

Добавим переменную x3 и рассмотрим второе уравнение. Оно аналогично первому, значит для x2=0 существуют два значения x3 ( 0 и 1), а для x2=1 только одно значение x3 (1), такие, что набор (x2,x3) является решением уравнения. Всего 4 набора.

Несложно заметить, что при добавлении очередной переменной добавляется один набор. Т.е. рекурсивная формула количества наборов на (i+1) переменных:

N_i+1 = N_i + 1. Тогда для десяти переменных получим 11 наборов.

Решение систем логических уравнений различного типа

Сколь­ко су­ще­ству­ет раз­лич­ных на­бо­ров зна­че­ний ло­ги­че­ских пе­ре­мен­ных x₁, . x₄, y₁. y₄, z₁. z₄, ко­то­рые удо­вле­тво­ря­ют всем пе­ре­чис­лен­ным ниже усло­ви­ям?

В от­ве­те не нужно пе­ре­чис­лять все раз­лич­ные на­бо­ры зна­че­ний пе­ре­мен­ных x₁, . x₄, y₁, . y₄, z₁, . z₄, при ко­то­рых вы­пол­не­на дан­ная си­сте­ма ра­венств.

В ка­че­стве от­ве­та Вам нужно ука­зать ко­ли­че­ство таких на­бо­ров.

Заметим, что три уравнения системы одинаковы на различных независимых наборах переменных.

Рассмотрим первое уравнение. Конъюнкция истинна (равна 1) только тогда, когда все ее операнды истинны (равны 1). Импликация равна 1 на всех наборах, кроме (1,0). Значит, решением первого уравнения будут такие наборы x1, x2, x3, x4, в которых 1 не стоит левее 0 (5 наборов):

Задание 23. Алгебра логики. Системы логических уравнений. ЕГЭ 2022 по информатике

Задачи для практики

Задача 1

У исполнителя Увеличитель две команды, которым присвоены номера:

2. Увеличь цифру в старшем разряде числа на 1.

Первая из них увеличивает данное число на 2, вторая — увеличивает цифру в старшем разряде числа на 1, например, число 34 с помощью этой команды превратится в число 44. Программа для исполнителя Увеличитель — это последовательность команд.

Определите количество программ, которые число 20 преобразуют в число 44.

Решение

Будем решать поставленную задачу последовательно для чисел 20, 21, 22, . . . , 44 (то есть для каждого из чисел определим, сколько программ исполнителя существует для его получения). Количество программ, которые преобразуют число 20 в число n, будем обозначать через R(n). Будем считать, что R(20) = 1. Заметим, что команда 2 для чисел, меньших 90, соответствует условию «прибавь 10». С помощью каждой из команд 1 и 2, применяя их последовательно к числам, получаемым из числа 29, можно получить только чётные числа. Числа 20, 22, . . . , 28 можно получить из предыдущего числа только с помощью команды 1. Значит, количество искомых программ для каждого из таких чисел равно количеству программ для предыдущего числа: R(i) = R(i − 2), i—чётное, 22 ≤ i ≤ 28.

Получаем R(20) = R(22) = · · · = R(28) = 1. Для чисел, больших 28 и не превосходящих 44, вариантов последней команды два: прибавь 2 и прибавь 10, то есть R(i) = R(i − 2) + R(i − 10), i — чётное, 30 ≤ i ≤ 44. Заполним соответствующую таблицу по приведённым формулам слева направо:

20	22	24	26	28	30	32	34	36	38	40	42	44
1	1	1	1	1	2	3	4	5	6	8	11	15

Задача 2

У исполнителя Удвоитель две команды, которым присвоены номера:

Первая из них увеличивает данное число на 2, вторая — увеличивает его в 5 раз. Программа для исполнителя Удвоитель — это последовательность команд.

Определите количество программ, которые число 1 преобразуют в число 37.

Решение

Заметим, что все числа, получаемые с помощью заданных команд из числа 1, — нечётные. Будем решать поставленную задачу последовательно для чисел 1, 3, 5, . . . , 37 (то есть для каждого нечётного числа определим, сколько программ исполнителя существует для его получения). Количество программ, которые преобразуют число 1 в число n, будем обозначать через R(n). Будем считать, что R(1) = 1. Для каждого следующего числа рассмотрим, из какого числа оно может быть получено за одну команду исполнителя. Если число не делится на 5, то оно может быть получено только из предыдущего с помощью команды прибавь 2. Значит, количество искомых программ для такого числа равно количеству программ для предыдущего числа: R(i) = R(i − 2), i — нечётное. Если число на 5 делится, то вариантов последней команды два: прибавь 2 и умножь на 5, тогда R(i) = R(i−2)+R(i/5), i — нечётное. Заполним соответствующую таблицу по приведенным формулам слева направо:

1	3	5	7	9	11	13	15	17	19	21	23	25	27
1	1	2	2	2	2	2	3	3	3	3	3	5	5
29	31	33	35	37
5	5	5	7	7

Задача 3

У исполнителя X157 три команды, которым присвоены номера:

Первая из них увеличивает число на экране на 1, вторая — на 5, а третья — в 7 раз. Программа для исполнителя X157 — это последовательность команд.

Сколько есть программ, которые число 1 преобразуют в число 20?

Скачать материал

Скачать материал

Описание презентации по отдельным слайдам:

• 

  1 слайд

  Метод подстановки
  ЕГЭ 23_7-15

• 

  2 слайд

  Содержание ЕГЭ23
  Вариант 2_2019
  Вариант 11_2019
  Вариант 12_2019
  Вариант 13_2019
  Вариант 14_2019
  Вариант 15_2019
  Вариант 16_2019
  Вариант 17_2019
  Вариант 18_2019
  Вариант 20_2019

• 

  3 слайд

  Вариант 2_2019
  Сколько существует различных наборов значений логических переменных x1, x2, … x12, которые удовлетворяют всем перечисленным ниже условиям?

  ¬(x1 ≡ x2) → (x3 ∧  x4) = 0
  ¬(x3 ≡ x4) → (x5 ∧  x6) = 0
  ¬(x5 ≡ x6) → (x7 ∧  x8) = 0
  ¬(x7 ≡ x8) → (x9 ∧  x10) = 0
  ¬(x9 ≡ x10) → (x11 ∧  x12) = 0
  (x1 ≡ x4) ∨ (x5 ≡ x8) ∨ (x2 ≡ x12) = 1

  В качестве ответа Вам нужно указать количество таких наборов.
  Ответ: 84

• 

  4 слайд

  Решение
  В первых пяти выражениях имеем импликацию, которая ложна. Импликация ложна в единственном случае 1 → 0 = 0. То есть в этих выражениях левая часть (посылка) должна быть везде = 1, а правая часть 0.
  Первые пять условий можно решить методом отображений. Для этого построим схему отображений: ¬(x1 ≡ x2) → (x3 ∧  x4) = 0

  F(00)
  F(01) = F(01)+F(10)
  F(10)

• 

  5 слайд

  Решение
  В первых пяти выражениях имеем импликацию, которая ложна. Импликация ложна в единственном случае 1 → 0 = 0. То есть в этих выражениях левая часть (посылка) должна быть везде = 1, а правая часть 0.
  Первые пять условий можно решить методом отображений. Для этого построим схему отображений: ¬(x1 ≡ x2) → (x3 ∧  x4) = 0

  F(00)
  F(01) = F(01)+F(10)
  F(10)

• 

  6 слайд

  построим таблицу отображений:
  F(00)
  F(01) = F(01)+F(10)
  F(10)

• 

  7 слайд

  В последнем уравнении
  ((x1 ≡ x4) (x5 ≡ x8) ∨ (x2 ≡ x12) = 1) имеем дизъюнкцию, которая равна 1.
  Для дизъюнкции всегда проще найти ложный случай (когда она = 0), так как это единственный вариант в таблице истинности дизъюнкции (0 ∨ 0 = 0). Найдем количество таких решений, т.е. найдем решения уравнения: (x1 ≡ x4) ∨ (x5 ≡ x8) ∨ (x2 ≡ x12) = 0
  Построим побитовую маску для данного уравнения:

• 

  8 слайд

  (x1 ≡ x4) ∨ (x5 ≡ x8) ∨ (x2 ≡ x12) = 0
  Построим побитовую маску для данного уравнения:

• 

  9 слайд

  Так как в схеме отображений значения для пары x1 и x2 равные 00 и 11 не используются, не будем использовать в последующих вычислениях. Выпишем оставшиеся варианты и обозначим строки цифрами :

• 

  10 слайд

  Построим таблицу отображений отдельно для каждой получившейся строки
  Строка (1)
  F(00)
  F(01) = F(01)+F(10)
  F(10)

• 

  11 слайд

  Построим таблицу отображений отдельно для каждой получившейся строки
  Строка (2)
  F(00)
  F(01) = F(01)+F(10)
  F(10)

• 

  12 слайд

  Построим таблицу отображений отдельно для каждой получившейся строки
  Строка (3)
  F(00)
  F(01) = F(01)+F(10)
  F(10)

• 

  13 слайд

  Построим таблицу отображений отдельно для каждой получившейся строки
  Строка (4)
  F(00)
  F(01) = F(01)+F(10)
  F(10)

• 

  14 слайд

  Число решений для всех полученных строк: 4 + 4 + 2 + 2 = 12
  Эти решения необходимо исключить, т.к. мы рассмотрели ложный случай уравнения 6:
  96 — 12 = 84

  Итого решений 84

• 

  15 слайд

  Вариант 11_2019
  Сколько существует различных наборов значений логических переменных x1, x2, … x8, y1, y2, … y8, которые удовлетворяют всем перечисленным ниже условиям?

  ¬(((x1 ∧   y1) ≡ (x3 ∧   y3)) → (x2 ∧   y2))
  ¬(((x2 ∧   y2) ≡ (x4 ∧   y4)) → ¬(x3 ∧   y3))
  ¬(((x3 ∧   y3) ≡ (x5 ∧   y5)) → (x4 ∧   y4))
  ¬(((x4 ∧   y4) ≡ (x6 ∧   y6)) → ¬(x5 ∧   y5))
  ¬(((x5 ∧   y5) ≡ (x7 ∧   y7)) → (x6 ∧   y6))
  ¬(((x6 ∧   y6) ≡ (x8 ∧   y8)) → ¬(x7 ∧   y7))

  В качестве ответа Вам нужно указать количество таких наборов.

• 

  16 слайд

  ЕГЭ 23_11
  ¬(((x1 ∧   y1) ≡ (x3 ∧   y3)) → (x2 ∧   y2))
  ¬(((x2 ∧   y2) ≡ (x4 ∧   y4)) → ¬(x3 ∧   y3))

  Введем обозначения a1= x1 ∧  y1; a2= x2 ∧  y2; …; a8= x8 ∧  y8;
  Освободимся от отрицания
  (a1 ≡ a3) → (a2)=0
  Правая часть выражения в импликации должна быть равна 0.
  Из первого уравнения
  a1= a3;
  Из последнего уравнения
  a8= a6;
  1
  0

• 

  17 слайд

  ЕГЭ 23_11
  К содержанию
  (a1 ≡ a3) → (a2)=0

  a1= x1 ∧  y1; a2= x2 ∧  y2; …; a8= x8 ∧  y8;
  1 может получиться только в одном случае, когда ху=(11)
  0 в трёх случаях, когда ху=(00, 01, 10)

  Итого решений 34*14=81

• 

  18 слайд

  ЕГЭ 23_вариант 12_2019
  Сколько существует различных наборов значений логических переменных x1, x2, … x9, y1, y2, … y9, которые удовлетворяют всем перечисленным ниже условиям?

  ¬(((x1 ∨   y1) ≡ (x3 ∨   y3)) → (x2 ∨   y2))
  ¬(((x2 ∨   y2) ≡ (x4 ∨   y4)) → ¬(x3 ∨   y3))
  …
  ¬(((x6 ∨   y6) ≡ (x8 ∨   y8)) → ¬(x7 ∨   y7))
  ¬(((x7 ∨   y7) ≡ (x9 ∨   y9)) → (x8 ∨   y8))

  В качестве ответа Вам нужно указать количество таких наборов.

• 

  19 слайд

  ЕГЭ 23_12
  ¬(((x1 ∨   y1) ≡ (x3 ∨   y3)) → (x2 ∨   y2))
  ¬(((x2 ∨   y2) ≡ (x4 ∨   y4)) → ¬(x3 ∨   y3))

  Введем обозначения a1= x1 ∨  y1; a2= x2 ∨ y2; …; a9= x9 ∨ y9;
  Освободимся от отрицания
  (a1 ≡ a3) → (a2)=0
  Правая часть выражения в импликации должна быть равна 0.
  Из первого уравнения
  a1= a3;
  Из последнего уравнения
  a9= a7;
  1
  1

• 

  20 слайд

  ЕГЭ 23_12
  К содержанию
  (a1 ≡ a3) → (a2)=0

  a1= x1 ∨   y1; a2= x2 ∨ y2; …; a8= x8 ∨ y8;
  0 может получиться только в одном случае, когда ху=(00)
  1 в трёх случаях, когда ху=(01, 10, 11)

  Итого решений 35*14=243

• 

  21 слайд

  ЕГЭ 23_13
  Сколько существует различных наборов значений логических переменных x1, x2, … x7, y1, y2, … y7, которые удовлетворяют всем перечисленным ниже условиям?

  ¬(((x1 ∧   y1) ≡ (x3 ∧   y3)) → (x2 ∧   y2))
  ¬(((x2 ∧   y2) ≡ (x4 ∧   y4)) → (x3 ∧   y3))
  ¬(((x3 ∧   y3) ≡ (x5 ∧   y5)) → (x4 ∧   y4))
  ¬(((x4 ∧   y4) ≡ (x6 ∧   y6)) → (x5 ∧   y5))
  ¬(((x5 ∧   y5) ≡ (x7 ∧   y7)) → (x6 ∧   y6))

  В качестве ответа Вам нужно указать количество таких наборов.

• 

  22 слайд

  ЕГЭ 23_13
  ¬(((x1 ∧   y1) ≡ (x3 ∧   y3)) → (x2 ∧   y2))
  ¬(((x2 ∧   y2) ≡ (x4 ∧   y4)) → (x3 ∧   y3))

  Введем обозначения a1= x1 ∧  y1; a2= x2 ∧  y2; …; a7= x7 ∧  y7;
  Освободимся от отрицания
  (a1 ≡ a3) → (a2)=0
  Правая часть выражения в импликации должна быть равна 0.
  Из первого уравнения
  a1= a3;
  Из последнего уравнения
  a7= a5;
  0
  0

• 

  23 слайд

  ЕГЭ 23_13
  К содержанию
  (a1 ≡ a3) → (a2)=0

  a1= x1 ∧  y1; a2= x2 ∧  y2; …;
  0 в трёх случаях, когда ху=(00, 01, 10)

  Итого решений 37=2187

• 

  24 слайд

  ЕГЭ 23_14
  Сколько существует различных наборов значений логических переменных x1, x2, … x9, y1, y2, … y9, которые удовлетворяют всем перечисленным ниже условиям?

  ¬(((x1 ≡   y1) ≡ (x3 ≡   y3)) → (x2 ≡   y2))
  ¬(((x2 ≡   y2) ≡ (x4 ≡   y4)) → (x3 ≡   y3))
  …
  ¬(((x6 ≡   y6) ≡ (x8 ≡   y8)) → (x7 ≡   y7))
  ¬(((x7 ≡   y7) ≡ (x9 ≡   y9)) → (x8 ≡   y8))

  В качестве ответа Вам нужно указать количество таких наборов.

• 

  25 слайд

  ЕГЭ 23_14
  ¬(((x1 ∨   y1) ≡ (x3 ∨   y3)) → (x2 ∨   y2))
  ¬(((x2 ∨   y2) ≡ (x4 ∨   y4)) → ¬(x3 ∨   y3))

  Введем обозначения a1= x1 ∨  y1; a2= x2 ∨ y2; …; a9= x9 ∨ y9;
  Освободимся от отрицания
  (a1 ≡ a3) → (a2)=0
  Правая часть выражения в импликации должна быть равна 0.
  Из первого уравнения
  a1= a3;
  Из последнего уравнения
  a9= a7;
  0
  0

• 

  26 слайд

  ЕГЭ 23_14
  К содержанию
  (a1 ≡ a3) → (a2)=0

  a1= (x1 ≡   y1); a2= (x2 ≡ y2); …; a9= (x9 ≡ y9);
  0 может получиться только в двух случаях, когда ху=(01, 10)

  Итого решений 29=512

• 

  27 слайд

  ЕГЭ 23_15
  Сколько существует различных наборов значений логических переменных x1, x2, … x9, y1, y2, … y9, которые удовлетворяют всем перечисленным ниже условиям?

  ¬(((x1 ∨   y1) ≡ (x2 ∨   y2)) → (x3 ∨   y3))
  ¬(((x2 ∨   y2) ∨ ¬(x3 ∨   y3)) → (x4 ∨   y4))
  …
  ¬(((x6 ∨   y6) ∨ ¬(x7 ∨   y7)) → (x8 ∨   y8))
  ¬(((x7 ∨   y7) ≡ (x8 ∨   y8)) → (x9 ∨   y9))

  В качестве ответа Вам нужно указать количество таких наборов.

• 

  28 слайд

  ЕГЭ 23_15
  ¬(((x1 ∨   y1) ≡ (x2 ∨   y2)) → (x3 ∨   y3))
  ¬(((x2 ∨   y2) ∨ ¬(x3 ∨   y3)) → (x4 ∨   y4))

  Введем обозначения a1= x1 ∨  y1; a2= x2 ∨ y2; …; a9= x9 ∨ y9;
  Освободимся от отрицания
  (a1 ≡ a2) → (a3)=0
  Правая часть выражения в импликации должна быть равна 0.
  Из второго уравнения
  a2= (0,1) , т.к. ¬a3=1;
  Из первого уравнения
  a1= a2;
  0/1
  0/1

• 

  29 слайд

  ЕГЭ 23_15
  К содержанию
  Итого решений 10
  F00=F00
  F01=F01+F10+F11
  F10=F01+F10+F11
  F11=F01+F10+F11

• 

  30 слайд

  ЕГЭ 23_16
  Сколько существует различных наборов значений логических переменных x1, x2, … x6, y1, y2, … y6, которые удовлетворяют всем перечисленным ниже условиям?

  ¬(((x1 ∧   y1) ≡ (x2 ∧   y2)) → (x3 ∧   y3))
  ¬(((x2 ∧   y2) ∨ ¬(x3 ∧   y3)) → (x4 ∧   y4))
  ¬(((x3 ∧   y3) ∨ ¬(x4 ∧   y4)) → (x5 ∧   y5))
  ¬(((x4 ∧   y4) ≡ (x5 ∧   y5)) → (x6 ∧   y6))

  В качестве ответа Вам нужно указать количество таких наборов.

• 

  31 слайд

  ЕГЭ 23_16
  ¬(((x1 ∧   y1) ≡ (x2 ∧   y2)) → (x3 ∧   y3))
  ¬(((x2 ∧   y2) ∨ ¬(x3 ∧   y3)) → (x4 ∧   y4))

  Введем обозначения a1= x1 ∨  y1; a2= x2 ∨ y2; …; a6= x6 ∨ y6;
  Освободимся от отрицания
  (a1 ∧ a2) → (a3)=0
  Правая часть выражения в импликации должна быть равна 0.
  Из второго уравнения
  a2= (0,1) , т.к. ¬a3=1;
  Из первого уравнения
  a1= a2;
  0/1
  0/1

• 

  32 слайд

  ЕГЭ 23_16
  К содержанию
  Итого решений 10*34=810
  F00=F00
  F01=F01+F10+F11
  F10=F01+F10+F11
  F11=F01+F10+F11

• 

  33 слайд

  ЕГЭ 23_17
  Сколько существует различных наборов значений логических переменных x1, x2, … x6, y1, y2, … y6, которые удовлетворяют всем перечисленным ниже условиям?

  (x1 ∨   y1)  (x2 ∧ y2) = 0
  (x2 ∨   y2)  (x3 ∧   y3) = 0
  …
  (x5 ∨   y5)  (x6 ∧   y6) = 0

  В качестве ответа Вам нужно указать количество таких наборов.

• 

  34 слайд

  ЕГЭ 23_17
  (x1 ∨   y1) =1 (x2 ∧  y2)=0

  F01=F01+F10+F11
  F10=F01+F10+F11
  F00=F01+F10+F11

• 

  35 слайд

  ЕГЭ 23_17
  К содержанию
  Итого решений 144
  F01=F01+F10+F11
  F10=F01+F10+F11
  F00=F01+F10+F11

• 

  36 слайд

  ЕГЭ 23_18
  Сколько существует различных наборов значений логических переменных x1, x2, … x10, которые удовлетворяют всем перечисленным ниже условиям?
  ((x1 ≡   х3) ∨ (x2 ≡  х4)) ∧ (¬(x1 ≡   х3) ∨ ¬(x2 ≡  х4))
  ((x2 ≡  х4) ∨ (x5 ≡  х7)) ∧ (¬(x2 ≡  х4) ∨ ¬(x5 ≡  х7))
  ((x5 ≡   х7) ∨ (x6 ≡  х8)) ∧ (¬(x5 ≡   х7) ∨ ¬(x6 ≡  х8))
  ((x6 ≡  х8) ∨ (x9 ≡  х10)) ∧ (¬(x6 ≡  х8) ∨ ¬(x9 ≡  х10))
  В качестве ответа Вам нужно указать количество таких наборов.

• 

  37 слайд

  ЕГЭ 23_18
  ((x1 ≡   х3) ∨ (x2 ≡  х4)) ∧ (¬(x1 ≡   х3) ∨ ¬(x2 ≡  х4))

  Введем обозначения a1= (x1 ≡   х3); a2= (x2 ≡   х4); a3= (x5 ≡   х7); a4= (x6 ≡   х8); a5= (x9 ≡  х10);
  После упрощения
  (a1 ≠ a2) =1

  Из первого уравнения
  a1 ≠ a2;
  Из второго уравнения
  a2 ≠ a3;
  a1 a2 =(01, 10)
  0
  К содержанию
  Итого решений 2*25=64

• 

  38 слайд

  ЕГЭ 23_18
  .

  F01=F00+F11
  F10=F00+F11
  F00=F01+F10
  F11= F01+F10
  a1 a2 =(01, 10)
  a1= (x1 ≡   х3); a2= (x2 ≡   х4)

• 

  39 слайд

  ЕГЭ 23_20
  Сколько существует различных наборов значений логических переменных x1, x2, … x10, которые удовлетворяют всем перечисленным ниже условиям?
  ((x1 ≡   х3) ∨ (x2 ≡  х4)) ∧ (¬((x1 ≡   х3) ∧ (x2 ≡  х4))) = 0
  ((x2 ≡  х4) ∨ (x5 ≡  х7)) ∧ (¬((x2 ≡  х4) ∧ (x5 ≡  х7)))= 0
  ((x5 ≡   х7) ∨ (x6 ≡  х8)) ∧ (¬((x5 ≡   х7) ∧ (x6 ≡  х8))) = 0
  ((x6 ≡  х8) ∨ (x9 ≡  х10)) ∧ (¬((x6 ≡  х8) ∧ (x9 ≡  х10))) = 0
  ((x1 ≡   х3)  (x2 ≡  х4))  ((x6 ≡   х8) ∨ (x9 ≡  х10))=1
  В качестве ответа Вам нужно указать количество таких наборов.

• 

  40 слайд

  ЕГЭ 23_20
  ((x1 ≡   х3) ∨ (x2 ≡  х4)) ∧ (¬(x1 ≡   х3) ∧ (x2 ≡  х4)) = 0
  Введем обозначения a1= (x1 ≡   х3); a2= (x2 ≡   х4); a3= (x5 ≡   х7); a4= (x6 ≡   х8); a5= (x9 ≡  х10);
  После упрощения
  (a1 ≠ a2) =0; (a1 = a2) =1

  Из первого уравнения
  a1 = a2;
  Из второго уравнения
  a2 = a3;
  a1 a2 =(00, 11)
  К содержанию

• 

  41 слайд

  ЕГЭ 23_20
  ((x1 ≡   х3) ∨ (x2 ≡  х4)) ∧ (¬(x1 ≡   х3) ∧ (x2 ≡  х4)) = 0
  Введем обозначения a1= (x1 ≡   х3); a2= (x2 ≡   х4); a3= (x5 ≡   х7); a4= (x6 ≡   х8); a5= (x9 ≡  х10);

  Подключаем последнее уравнение
  (a1  a2)  (a4 ∨ a5)=1

  Т.к. (a1  a2)=1, то и
  (a4 ∨ a5) = 1
  Первая строка не подходит

  0
  К содержанию
  Итого решений 25=32

• 

  42 слайд

  ЕГЭ 23_20
  .

  F00=F00+F11
  F11=F00+F11
  F01=F01+F10
  F10= F01+F10
  a1 a2 =(00, 11)
  a1= (x1 ≡   х3); a2= (x2 ≡   х4)

Краткое описание документа:

Это пособие по решению заданий 23 ЕГЭ «Системы логических уравнений» высокого уровня сложности. В работе дан разбор заданий 23 из сборника Крылова С.С., Чуркиной Т.Е. «Типовые экзаменационные варианты» ФИПИ 2019 и 2020 год. Рассмотрены наиболее сложные задания. Данная презентация будет полезна учащимся 10-11 классов при подготовке к ЕГЭ по информатике, а также учителям информатики.

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

6 155 190 материалов в базе

• Выберите категорию:

• Выберите учебник и тему

• Выберите класс:

• Тип материала:

  • Все материалы

  • Статьи

  • Научные работы

  • Видеоуроки

  • Презентации

  • Конспекты

  • Тесты

  • Рабочие программы

  • Другие методич. материалы

Найти материалы

Вам будут интересны эти курсы:

• Курс повышения квалификации «Информационные технологии в деятельности учителя физики»

• Курс повышения квалификации «Развитие информационно-коммуникационных компетенций учителя в процессе внедрения ФГОС: работа в Московской электронной школе»

• Курс повышения квалификации «Использование компьютерных технологий в процессе обучения в условиях реализации ФГОС»

• Курс повышения квалификации «Введение в программирование на языке С (СИ)»

• Курс профессиональной переподготовки «Теория и методика обучения информатике в начальной школе»

• Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»

• Курс повышения квалификации «Современные языки программирования интегрированной оболочки Microsoft Visual Studio C# NET., C++. NET, VB.NET. с использованием структурного и объектно-ориентированного методов разработки корпоративных систем»

• Курс повышения квалификации «Применение интерактивных образовательных платформ на примере платформы Moodle»

Логические уравнения

Системы ло­ги­че­ских уравнений, со­дер­жа­щие
однотипные уравнения

За­да­ние 1 Сколь­ко су­ще­ству­ет раз­лич­ных
на­бо­ров зна­че­ний ло­ги­че­ских пе­ре­мен­ных x1, х2, хЗ, х4, х5, хб, х7,
х8, ко­то­рые удо­вле­тво­ря­ют всем пе­ре­чис­лен­ным ниже усло­ви­ям?

(x1 —> х2) —> (хЗ—> х4) = 1

(хЗ —> х4) —> (х5 —> хб) = 1

(х5 —> хб) —> (х7 —> х8) = 1

В от­ве­те не нужно пе­ре­чис­лять все раз­лич­ные на­бо­ры
зна­че­ний пе­ре­мен­ных x1, х2, хЗ, х4, х5, хб, х7, х8, при ко­то­рых вы­пол­не­на
дан­ная си­сте­ма ра­венств. В ка­че­стве от­ве­та Вам нужно ука­зать ко­ли­че­ство
таких на­бо­ров.

По­яс­не­ние.

Сде­ла­ем за­ме­ну пе­ре­мен­ных:

(x1 —> х2) = y1; (хЗ—> х4) = y2; (х5 —> хб) =
y3; (х7 —> х8) = y4.

Тогда можно за­пи­сать си­сте­му в виде од­но­го урав­не­ния:

(y1 —> y2) ∧ (y2 —>
y3) ∧
(y3 —>
y4) = 1.

Для того, чтобы это ра­вен­ство было вы­пол­не­но, ни
одна из им­пли­ка­ций не долж­на быть лож­ной

Вот все воз­мож­ные ва­ри­ан­ты зна­че­ний
«y» (клю­че­вым яв­ля­ет­ся тот факт, что пе­ре­мен­ные y не­за­ви­си­мы):

Им­пли­ка­ция x1 —> х2 дает «0» при одном
на­бо­ре пе­ре­мен­ных и «1» при трех на­бо­рах пе­ре­мен­ных.

По­сколь­ку каж­дая из пе­ре­мен­ных «y» не­за­ви­си­ма
от дру­гой, для каж­дой стро­ки по­лу­чен­ной таб­ли­цы пе­ре­мно­жа­ем ко­ли­че­ство
ва­ри­ан­тов ком­би­на­ций ис­ход­ных пе­ре­мен­ных:

Сло­жим ко­ли­че­ство ва­ри­ан­тов: 1 + 3 + 9 + 27 +
81 = 121.

За­да­ние
2. Сколь­ко су­ще­ству­ет раз­лич­ных
на­бо­ров зна­че­ний ло­ги­че­ских пе­ре­мен­ных x1, х2, хЗ, х4, х5, хб, х7,
х8, ко­то­рые удо­вле­тво­ря­ют всем пе­ре­чис­лен­ным ниже усло­ви­ям?

(x1 —> х2) —> (хЗ—> х4) = 1

(хЗ —> х4) —> (х5 —> хб) = 1

(х5 —> хб) —> (х7 —> х8) = 1

(х7 —> х8) —> (х9 —> х10) = 1

В от­ве­те не нужно пе­ре­чис­лять все раз­лич­ные на­бо­ры
зна­че­ний пе­ре­мен­ных x1, х2, хЗ, х4, х5, хб, х7, х8, при ко­то­рых вы­пол­не­на
дан­ная си­сте­ма ра­венств. В ка­че­стве от­ве­та Вам нужно ука­зать ко­ли­че­ство
таких на­бо­ров.

По­яс­не­ние.

Сде­ла­ем за­ме­ну пе­ре­мен­ных:

(x1 —> х2) = y1; (хЗ—> х4) = y2; (х5 —> хб) =
y3; (х7 —> х8) = y4; (х9 —> х10) = y5.

Тогда можно за­пи­сать си­сте­му в виде од­но­го урав­не­ния.

(y1 —> y2) ∧ (y2 —>
y3) ∧
(y3 —>
y4) ∧
(y4 —>
y5) = 1.

Для того, чтобы это ра­вен­ство было вы­пол­не­но, ни
одна из им­пли­ка­ций не долж­на быть лож­ной

Вот все воз­мож­ные ва­ри­ан­ты зна­че­ний
«y»(клю­че­вым яв­ля­ет­ся тот факт, что пе­ре­мен­ные y не­за­ви­си­мы):

Им­пли­ка­ция x1 —> х2 дает «0» при одном
на­бо­ре пе­ре­мен­ных и «1» при трех на­бо­рах пе­ре­мен­ных.

По­сколь­ку каж­дая из пе­ре­мен­ных «y» не­за­ви­си­ма
от дру­гой, для каж­дой стро­ки по­лу­чен­ной таб­ли­цы пе­ре­мно­жа­ем ко­ли­че­ство
ва­ри­ан­тов ком­би­на­ций ис­ход­ных пе­ре­мен­ных:

Сло­жим ко­ли­че­ство ва­ри­ан­тов: 1 + 3 + 9 + 27 +
81 + 243 = 364.

За­да­ние 3. Сколь­ко су­ще­ству­ет раз­лич­ных на­бо­ров зна­че­ний
ло­ги­че­ских пе­ре­мен­ных x1, x2, x3, x4, x5, x6, x7, x8 ко­то­рые удо­вле­тво­ря­ют
всем пе­ре­чис­лен­ным ниже усло­ви­ям?

(x1≡x2)—>(x2≡x3) = 1

(x2≡x3)—>(x3≡x4) = 1

…

(x6≡x7)—>(x7≡x8) = 1

В от­ве­те не нужно пе­ре­чис­лять
все раз­лич­ные на­бо­ры зна­че­ний пе­ре­мен­ных x1, x2, x3, x4, x5, x6, x7,
x8 при ко­то­рых вы­пол­не­на дан­ная си­сте­ма ра­венств. В ка­че­стве от­ве­та
Вам нужно ука­зать ко­ли­че­ство таких на­бо­ров.

По­яс­не­ние.

За­пи­шем пе­ре­мен­ные в строч­ку: x₁x₂x₃x₄x₅x₆x₇x₈.
Им­пли­ка­ция ложна толь­ко в том слу­чае, когда из ис­ти­ны сле­ду­ет ложь.
Усло­вие не вы­пол­ня­ет­ся, если в ряде после оди­на­ко­вых цифр при­сут­ству­ет
дру­гая цифра. На­при­мер, «11101…» что озна­ча­ет не­вы­пол­не­ние
вто­ро­го усло­вия.

Рас­смот­рим ком­би­на­ции пе­ре­мен­ных, удо­вле­тво­ря­ю­щие
всем усло­ви­ям. Вы­пи­шем ва­ри­ан­ты, при ко­то­рых все цифры че­ре­ду­ют­ся,
таких два: 10101010 и 01010101. Те­перь для пер­во­го ва­ри­ан­та, на­чи­ная с
конца, будем уве­ли­чи­вать ко­ли­че­ство по­вто­ря­ю­щих­ся под­ряд цифр (на­столь­ко,
на­сколь­ко это воз­мож­но). Вы­пи­шем по­лу­чен­ные ком­би­на­ции:
«10101011; 10101111…» таких ком­би­на­ций во­семь. Ана­ло­гич­но
для вто­ро­го ва­ри­ан­та: «01010101; 01010100…». Таким об­ра­зом,
по­лу­ча­ем 8 + 8 = 16 ре­ше­ний.

За­да­ние
4. Сколь­ко су­ще­ству­ет раз­лич­ных
на­бо­ров зна­че­ний ло­ги­че­ских пе­ре­мен­ных x1, x2, x3, x4, x5, x6, x7, ко­то­рые
удо­вле­тво­ря­ют всем пе­ре­чис­лен­ным ниже усло­ви­ям?

(x1≡x2)—>(x2≡x3) = 1

(x2≡x3)—>(x3≡x4) = 1

…

(x5≡x6)—>(x6≡x7) = 1

В от­ве­те не нужно пе­ре­чис­лять все раз­лич­ные на­бо­ры
зна­че­ний пе­ре­мен­ных x1, x2, x3, x4, x5, x6, x7, при ко­то­рых вы­пол­не­на
дан­ная си­сте­ма ра­венств. В ка­че­стве от­ве­та Вам нужно ука­зать ко­ли­че­ство
таких на­бо­ров.

По­яс­не­ние.

За­пи­шем пе­ре­мен­ные в строч­ку: x₁x₂x₃x₄x₅x₆x₇.
Им­пли­ка­ция ложна толь­ко в том слу­чае, когда из ис­ти­ны сле­ду­ет ложь.
Усло­вие не вы­пол­ня­ет­ся, если в ряду после оди­на­ко­вых цифр при­сут­ству­ет
дру­гая цифра. На­при­мер, «11101…» что озна­ча­ет не­вы­пол­не­ние
вто­ро­го усло­вия.

Рас­смот­рим ком­би­на­ции пе­ре­мен­ных, удо­вле­тво­ря­ю­щие
всем усло­ви­ям. Вы­пи­шем ва­ри­ан­ты, при ко­то­рых все цифры че­ре­ду­ют­ся,
таких два: 1010101 и 0101010. Те­перь для пер­во­го ва­ри­ан­та, на­чи­ная с
конца, будем уве­ли­чи­вать ко­ли­че­ство по­вто­ря­ю­щих­ся под­ряд цифр(на­столь­ко,
на­сколь­ко это воз­мож­но). Вы­пи­шем по­лу­чен­ные ком­би­на­ции:
«1010111; 1011111…» таких ком­би­на­ций во­семь. Ана­ло­гич­но для
вто­ро­го ва­ри­ан­та: «0101011; 0101111…». Учтём, что при подсчёте
ком­би­на­ция для вто­ро­го ва­ри­ан­та ком­би­на­ции 0000000 и 1111111 были
учте­ны два­жды. Таким об­ра­зом, по­лу­ча­ем 8 + 8 − 2 = 14 ре­ше­ний.

Ответ: 14.

За­да­ние
5. Сколь­ко су­ще­ству­ет раз­лич­ных
на­бо­ров зна­че­ний ло­ги­че­ских пе­ре­мен­ных x₁, x₂,
… x₈, ко­то­рые удо­вле­тво­ря­ют всем пе­ре­чис­лен­ным ниже усло­ви­ям?

((x₁ ≡ x₂) ∨ (x₃ ≡ x₄)) ∧ (¬(x₁ ≡ x₂) ∨ ¬(x₃ ≡ x₄)) = 1

((x₃ ≡ x₄) ∨ (x₅ ≡ x₆)) ∧ (¬(x₃ ≡ x₄) ∨ ¬(x₅ ≡ x₆)) = 1

((x₅ ≡ x₆) ∨ (x₇ ≡ x₈)) ∧ (¬(x₅ ≡ x₆) ∨ ¬(x₇ ≡ x₈)) = 1

В от­ве­те не нужно пе­ре­чис­лять
все раз­лич­ные на­бо­ры зна­че­ний пе­ре­мен­ных x₁, x₂,
… x₈ при ко­то­рых вы­пол­не­на дан­ная си­сте­ма ра­венств. В
ка­че­стве от­ве­та Вам нужно ука­зать ко­ли­че­ство таких на­бо­ров.

По­яс­не­ние.

По­стро­им древо ре­ше­ний пер­во­го урав­не­ния:

За­ме­тим, что вы­ра­же­ние (x₃ ≡ x₄)
в двух слу­ча­ях равно 1 и в двух слу­ча­ях равно 0. Таким об­ра­зом, одно урав­не­ние
имеет во­семь ре­ше­ний.

Вто­рое урав­не­ние свя­за­но с пер­вым толь­ко через
вы­ра­же­ние (x₃ ≡ x₄). По­стро­им древо ре­ше­ний
вто­ро­го урав­не­ния:

 

Для каж­до­го из зна­че­ний 0 и 1 вы­ра­же­ния (x₃ ≡
x₄) су­ще­ству­ет че­ты­ре на­бо­ра пе­ре­мен­ных x₁, x₂,…,x₄,
удо­вле­тво­ря­ю­щих пер­во­му урав­не­нию (см. пер­вый ри­су­нок). Таким
об­ра­зом, си­сте­ма из двух урав­не­ний имеет 4 · 4 = 16
ре­ше­ний.

Тре­тье урав­не­ние свя­за­но со вто­рым толь­ко через
вы­ра­же­ние (x₅ ≡ x₆). По­стро­им древо ре­ше­ний
тре­тье­го урав­не­ния:

 

Для каж­до­го из зна­че­ний 0 и 1 вы­ра­же­ния (x₅ ≡
x₆) су­ще­ству­ет 2 · 4 = 8 на­бо­ров пе­ре­мен­ных
x₁, x₂,…,x₆, удо­вле­тво­ря­ю­щих пер­во­му
урав­не­нию (см. пер­вый и вто­рой ри­су­нок). Таким об­ра­зом, си­сте­ма
из трёх урав­не­ний имеет 8 · 4 = 32 ре­ше­ния.

Ответ: 32.

За­да­ние
6. Сколь­ко су­ще­ству­ет раз­лич­ных
на­бо­ров зна­че­ний ло­ги­че­ских пе­ре­мен­ных x₁, x₂,
… x₁₀, ко­то­рые удо­вле­тво­ря­ют всем пе­ре­чис­лен­ным ниже
усло­ви­ям?

((x₁ ≡ x₂) ∨ (x₃ ≡ x₄)) ∧ (¬(x₁ ≡ x₂) ∨ ¬(x₃ ≡ x₄)) = 1

((x₃ ≡ x₄) ∨ (x₅ ≡ x₆)) ∧ (¬(x₃ ≡ x₄) ∨ ¬(x₅ ≡ x₆)) = 1

…

((x₇ ≡ x₈) ∨ (x₉ ≡ x₁₀)) ∧ (¬(x₇ ≡ x₈) ∨ ¬(x₉ ≡ x₁₀)) = 1

В от­ве­те не нужно пе­ре­чис­лять
все раз­лич­ные на­бо­ры зна­че­ний пе­ре­мен­ных x₁, x₂,
… x₁₀ при ко­то­рых вы­пол­не­на дан­ная си­сте­ма ра­венств. В
ка­че­стве от­ве­та Вам нужно ука­зать ко­ли­че­ство таких на­бо­ров.

По­яс­не­ние.

По­стро­им древо ре­ше­ний пер­во­го урав­не­ния:

 

За­ме­тим, что вы­ра­же­ние (x₃ ≡ x₄)
в двух слу­ча­ях равно 1 и в двух слу­ча­ях равно 0. Таким об­ра­зом, одно урав­не­ние
имеет во­семь ре­ше­ний.

Вто­рое урав­не­ние свя­за­но с пер­вым толь­ко через
вы­ра­же­ние (x₃ ≡ x₄). По­стро­им древо ре­ше­ний
вто­ро­го урав­не­ния:

 

Для каж­до­го из зна­че­ний 0 и 1 вы­ра­же­ния (x₃ ≡
x₄) су­ще­ству­ет че­ты­ре на­бо­ра пе­ре­мен­ных x₁, x₂,…,x₄,
удо­вле­тво­ря­ю­щих пер­во­му урав­не­нию (см. пер­вый ри­су­нок). Таким
об­ра­зом, си­сте­ма из двух урав­не­ний имеет 4 · 4 = 16
ре­ше­ний.

Тре­тье урав­не­ние свя­за­но со вто­рым толь­ко через
вы­ра­же­ние (x₅ ≡ x₆). По­стро­им древо ре­ше­ний
тре­тье­го урав­не­ния:

 

Для каж­до­го из зна­че­ний 0 и 1 вы­ра­же­ния (x₅ ≡
x₆) су­ще­ству­ет 2 · 4 = 8 на­бо­ров пе­ре­мен­ных
x₁, x₂,…,x₆, удо­вле­тво­ря­ю­щих пер­во­му
урав­не­нию (см. пер­вый и вто­рой ри­су­нок). Таким об­ра­зом, си­сте­ма
из трёх урав­не­ний имеет 8 · 4 = 32 ре­ше­ния, си­сте­ма
из четырёх — 64.

Ответ: 64.

За­да­ние 7. Сколь­ко су­ще­ству­ет раз­лич­ных на­бо­ров зна­че­ний
ло­ги­че­ских пе­ре­мен­ных x₁, x₂, … x₁₀,
ко­то­рые удо­вле­тво­ря­ют всем пе­ре­чис­лен­ным ниже усло­ви­ям?

((x₁ ≡ x₂) ∧ (x₃ ≡ x₄)) ∨ (¬(x₁ ≡ x₂) ∧ ¬(x₃ ≡ x₄)) = 0

((x₃ ≡ x₄) ∧ (x₅ ≡ x₆)) ∨ (¬(x₃ ≡ x₄) ∧ ¬(x₅ ≡ x₆)) = 0

((x₅ ≡ x₆) ∧ (x₇ ≡ x₈)) ∨ (¬(x₅ ≡ x₆) ∧ ¬(x₇ ≡ x₈)) = 0

((x₇ ≡ x₈) ∧ (x₉ ≡ x₁₀)) ∨ (¬(x₇ ≡ x₈) ∧ ¬(x₉ ≡ x₁₀)) = 0

В от­ве­те не нужно пе­ре­чис­лять
все раз­лич­ные на­бо­ры зна­че­ний пе­ре­мен­ных x₁, x₂,
… x₁₀ при ко­то­рых вы­пол­не­на дан­ная си­сте­ма ра­венств. В
ка­че­стве от­ве­та Вам нужно ука­зать ко­ли­че­ство таких на­бо­ров.

По­яс­не­ние.

По­стро­им древо ре­ше­ний пер­во­го урав­не­ния:

 

За­ме­тим, что вы­ра­же­ние (x₃ ≡ x₄)
в двух слу­ча­ях равно 1 и в двух слу­ча­ях равно 0. Таким об­ра­зом, одно урав­не­ние
имеет во­семь ре­ше­ний.

Вто­рое урав­не­ние свя­за­но с пер­вым толь­ко через
вы­ра­же­ние (x₃ ≡ x₄). По­стро­им древо ре­ше­ний
вто­ро­го урав­не­ния:

 

Для каж­до­го из зна­че­ний 0 и 1 вы­ра­же­ния (x₃ ≡
x₄) су­ще­ству­ет че­ты­ре на­бо­ра пе­ре­мен­ных x₁, x₂,…,x₄,
удо­вле­тво­ря­ю­щих пер­во­му урав­не­нию (см. пер­вый ри­су­нок). Таким
об­ра­зом, си­сте­ма из двух урав­не­ний имеет 4 · 4 = 16
ре­ше­ний.

Тре­тье урав­не­ние свя­за­но со вто­рым толь­ко через
вы­ра­же­ние (x₅ ≡ x₆). По­стро­им древо ре­ше­ний
тре­тье­го урав­не­ния:

Для каж­до­го из зна­че­ний 0 и 1 вы­ра­же­ния (x₅ ≡
x₆) су­ще­ству­ет 2 · 4 = 8 на­бо­ров пе­ре­мен­ных
x₁, x₂,…,x₆, удо­вле­тво­ря­ю­щих пер­во­му
урав­не­нию (см. пер­вый и вто­рой ри­су­нок). Таким об­ра­зом, си­сте­ма
из трёх урав­не­ний имеет 8 · 4 = 32 ре­ше­ния.

Ана­ло­гич­но си­сте­ма из четырёх урав­не­ний будет
иметь 64 ре­ше­ния.

Ответ: 64.

За­да­ние 8. Сколь­ко су­ще­ству­ет раз­лич­ных на­бо­ров зна­че­ний
ло­ги­че­ских пе­ре­мен­ных x₁, x₂, … x₈, ко­то­рые
удо­вле­тво­ря­ют всем пе­ре­чис­лен­ным ниже усло­ви­ям?

¬(x₁ ≡
x₂) ∧ (
(x₁ ∧ ¬x₃) ∨ (¬x₁ ∧ x₃) ) = 0

¬(x₂ ≡
x₃) ∧ (
(x₂ ∧ ¬x₄) ∨ (¬x₂ ∧ x₄) ) = 0

…

¬(x₆ ≡
x₇) ∧ ¬( (x₆ ∧ ¬x₈) ∨ (¬x₆ ∧ x₈) ) = 0

В от­ве­те не нужно пе­ре­чис­лять
все раз­лич­ные на­бо­ры зна­че­ний пе­ре­мен­ных x₁, x₂,
… x₈ при ко­то­рых вы­пол­не­на дан­ная си­сте­ма ра­венств. В
ка­че­стве от­ве­та Вам нужно ука­зать ко­ли­че­ство таких на­бо­ров.

По­яс­не­ние.

Рас­смот­рим пер­вое урав­не­ние.

При x₁ = 1 воз­мож­ны два слу­чая:
x₂ = 0 и x₂ = 1. В пер­вом слу­чае x₃ =
1. Во вто­ром — x₃ либо 0, либо 1. При x₁ = 0
также воз­мож­ны два слу­чая: x₂ = 0 и x₂ = 1.
В пер­вом слу­чае x₃   либо 0, либо 1. Во вто­ром — x₃ =
0. Таким об­ра­зом, урав­не­ние имеет 6 ре­ше­ний (см. ри­су­нок).

 

Рас­смот­рим си­сте­му из двух урав­не­ний.

Пусть x₁ = 1. При x₂ = 0
воз­мо­жен лишь один слу­чай: x₃ = 1, пе­ре­мен­ная x₄ =
0. При x₂ = 1 воз­мож­но два слу­чая: x₃ = 0
и x₃ = 1. В пер­вом слу­чае x₄ = 1, во вто­ром — x₄ либо
0, либо 1. Всего имеем 4 ва­ри­ан­та.

Пусть x₁ = 0. При x₂ = 1
воз­мо­жен лишь один слу­чай: x₃ = 0, пе­ре­мен­ная x₄ =
1. При x₂ = 0 воз­мож­но два слу­чая: x₃ = 0
и x₃ = 1. В пер­вом слу­чае x₄ либо 1,
либо 0, во вто­ром — x₄ = 0. Всего имеем 4 ва­ри­ан­та.

Таким об­ра­зом, си­сте­ма из двух урав­не­ний имеет 4
+ 4 = 8 ва­ри­ан­тов (см. ри­су­нок).

 

Си­сте­ма из трёх урав­не­ний будет иметь 10 ре­ше­ний,
из четырёх — 12. От­ри­ца­ние в по­след­нем урав­не­нии дей­ству­ет
толь­ко на ком­би­на­цию пе­ре­мен­ных, не свя­зан­ных с с преды­ду­щи­ми урав­не­ни­я­ми.
По­это­му, ко­ли­че­ство ре­ше­ний дан­ной в усло­вии си­сте­мы сов­па­да­ет с
ко­ли­че­ством ре­ше­ний си­сте­мы из шести од­но­тип­ных урав­не­ний (си­сте­мы,
в ко­то­рой в по­след­нем урав­не­нии нет знака от­ри­ца­ния после конъ­юнк­ции),
и равно 16.

Ответ: 16.

За­да­ние
9. Сколь­ко су­ще­ству­ет раз­лич­ных
на­бо­ров зна­че­ний ло­ги­че­ских пе­ре­мен­ных x₁, x₂,
… x₈, ко­то­рые удо­вле­тво­ря­ют всем пе­ре­чис­лен­ным ниже усло­ви­ям?

((x₁ ≡ x₂) ∧ (x₃ ≡ x₄)) ∨ (¬(x₁ ≡ x₂) ∧ ¬(x₃ ≡ x₄)) = 0

((x₃ ≡ x₄) ∧ (x₅ ≡ x₆)) ∨ (¬(x₃ ≡ x₄) ∧ ¬(x₅ ≡ x₆)) = 0

((x₅ ≡ x₆) ∧ (x₇ ≡ x₈)) ∨ (¬(x₅ ≡ x₆) ∧ ¬(x₇ ≡ x₈)) = 0

В от­ве­те не нужно пе­ре­чис­лять
все раз­лич­ные на­бо­ры зна­че­ний пе­ре­мен­ных x₁, x₂,
… x₈ при ко­то­рых вы­пол­не­на дан­ная си­сте­ма ра­венств. В
ка­че­стве от­ве­та Вам нужно ука­зать ко­ли­че­ство таких на­бо­ров.

По­яс­не­ние.

По­стро­им древо ре­ше­ний пер­во­го урав­не­ния:

 

За­ме­тим, что вы­ра­же­ние (x₃ ≡ x₄)
в двух слу­ча­ях равно 1 и в двух слу­ча­ях равно 0. Таким об­ра­зом, одно урав­не­ние
имеет во­семь ре­ше­ний.

Вто­рое урав­не­ние свя­за­но с пер­вым толь­ко через
вы­ра­же­ние (x₃ ≡ x₄). По­стро­им древо ре­ше­ний
вто­ро­го урав­не­ния:

 

Для каж­до­го из зна­че­ний 0 и 1 вы­ра­же­ния (x₃ ≡
x₄) су­ще­ству­ет че­ты­ре на­бо­ра пе­ре­мен­ных x₁, x₂,…,x₄,
удо­вле­тво­ря­ю­щих пер­во­му урав­не­нию (см. пер­вый ри­су­нок). Таким
об­ра­зом, си­сте­ма из двух урав­не­ний имеет 4 · 4 = 16
ре­ше­ний.

Тре­тье урав­не­ние свя­за­но со вто­рым толь­ко через
вы­ра­же­ние (x₅ ≡ x₆). По­стро­им древо ре­ше­ний
тре­тье­го урав­не­ния:

 

Для каж­до­го из зна­че­ний 0 и 1 вы­ра­же­ния (x₅ ≡
x₆) су­ще­ству­ет 2 · 4 = 8 на­бо­ров пе­ре­мен­ных
x₁, x₂,…,x₆, удо­вле­тво­ря­ю­щих пер­во­му
урав­не­нию (см. пер­вый и вто­рой ри­су­нок). Таким об­ра­зом, си­сте­ма
из трёх урав­не­ний имеет 8 · 4 = 32 ре­ше­ния.

Ответ: 32.

За­да­ние
10. Сколь­ко су­ще­ству­ет раз­лич­ных
на­бо­ров зна­че­ний ло­ги­че­ских пе­ре­мен­ных x₁, x₂,
… x₁₂, ко­то­рые удо­вле­тво­ря­ют всем пе­ре­чис­лен­ным ниже
усло­ви­ям?

((x₁ ≡ x₂) ∧ (x₃ ≡ x₄)) ∨ (¬(x₁ ≡ x₂) ∧ ¬(x₃ ≡ x₄)) = 0

((x₃ ≡ x₄) ∧ (x₅ ≡ x₆)) ∨ (¬(x₃ ≡ x₄) ∧ ¬(x₅ ≡ x₆)) = 0

…

((x₉ ≡ x₁₀) ∧ (x₁₁ ≡ x₁₂)) ∨ (¬(x₉ ≡ x₁₀) ∧ ¬(x₁₁ ≡ x₁₂)) = 0

В от­ве­те не нужно пе­ре­чис­лять
все раз­лич­ные на­бо­ры зна­че­ний пе­ре­мен­ных x₁, x₂,
… x₁₂ при ко­то­рых вы­пол­не­на дан­ная си­сте­ма ра­венств. В
ка­че­стве от­ве­та Вам нужно ука­зать ко­ли­че­ство таких на­бо­ров.

По­яс­не­ние.

По­стро­им древо ре­ше­ний пер­во­го урав­не­ния:

За­ме­тим, что вы­ра­же­ние (x₃ ≡ x₄)
в двух слу­ча­ях равно 1 и в двух слу­ча­ях равно 0. Таким об­ра­зом, одно урав­не­ние
имеет во­семь ре­ше­ний.

Вто­рое урав­не­ние свя­за­но с пер­вым толь­ко через
вы­ра­же­ние (x₃ ≡ x₄). По­стро­им древо ре­ше­ний
вто­ро­го урав­не­ния:

 

Для каж­до­го из зна­че­ний 0 и 1 вы­ра­же­ния (x₃ ≡
x₄) су­ще­ству­ет че­ты­ре на­бо­ра пе­ре­мен­ных x₁, x₂,…,x₄,
удо­вле­тво­ря­ю­щих пер­во­му урав­не­нию (см. пер­вый ри­су­нок). Таким
об­ра­зом, си­сте­ма из двух урав­не­ний имеет 4 · 4 = 16
ре­ше­ний.

Тре­тье урав­не­ние свя­за­но со вто­рым толь­ко через
вы­ра­же­ние (x₅ ≡ x₆). По­стро­им древо ре­ше­ний
тре­тье­го урав­не­ния:

 

Для каж­до­го из зна­че­ний 0 и 1 вы­ра­же­ния (x₅ ≡
x₆) су­ще­ству­ет 2 · 4 = 8 на­бо­ров пе­ре­мен­ных
x₁, x₂,…,x₆, удо­вле­тво­ря­ю­щих пер­во­му
урав­не­нию (см. пер­вый и вто­рой ри­су­нок). Таким об­ра­зом, си­сте­ма
из трёх урав­не­ний имеет 8 · 4 = 32 ре­ше­ния.

Ана­ло­гич­но си­сте­ма из четырёх урав­не­ний будет
иметь 64 ре­ше­ния, си­сте­ма из пяти урав­не­ний — 128.

Ответ: 128.

Логические уравнения

За­да­ние
1. Сколь­ко раз­лич­ных ре­ше­ний имеет
урав­не­ние J ∧ ¬K ∧ L ∧ ¬M ∧ (N ∨ ¬N)
= 0, где J,
K, L, M, N — ло­ги­че­ские пе­ре­мен­ные?

В от­ве­те не нужно пе­ре­чис­лять все раз­лич­ные на­бо­ры
зна­че­ний J, K, L, M и N, при ко­то­рых вы­пол­не­но дан­ное ра­вен­ство. В ка­че­стве
от­ве­та нужно ука­зать ко­ли­че­ство таких на­бо­ров.

По­яс­не­ние.

Вы­ра­же­ние (N ∨ ¬N) ис­тин­но при любом N, по­это­му

J ∧ ¬K ∧ L ∧ ¬M =
0.

При­ме­ним от­ри­ца­ние к обеим ча­стям ло­ги­че­ско­го
урав­не­ния и ис­поль­зу­ем закон де Мор­га­на ¬ (А ∧ В) = ¬ А ∨ ¬ В . По­лу­чим

¬J ∨ K ∨ ¬L ∨ M = 1.

Ло­ги­че­ская сумма равна 1, если хотя бы одно из со­став­ля­ю­щих
ее вы­ска­зы­ва­ний равно 1. По­это­му по­лу­чен­но­му урав­не­нию удо­вле­тво­ря­ют
любые ком­би­на­ции ло­ги­че­ских пе­ре­мен­ных кроме слу­чая, когда все вхо­дя­щие
в урав­не­ние ве­ли­чи­ны равны 0. Каж­дая из 4 пе­ре­мен­ных может быть равна
либо 1, либо 0, по­это­му все­воз­мож­ных ком­би­на­ций 2·2·2·2 = 16.
Сле­до­ва­тель­но, урав­не­ние имеет 16 −1 = 15 ре­ше­ний.

Оста­лось за­ме­тить, что най­ден­ные 15 ре­ше­ний со­от­вет­ству­ют
лю­бо­му из двух воз­мож­ных зна­че­ний зна­че­ний ло­ги­че­ской пе­ре­мен­ной
N, по­это­му ис­ход­ное урав­не­ние имеет 30 ре­ше­ний.

За­да­ние
2. Сколь­ко раз­лич­ных ре­ше­ний имеет
урав­не­ние

((J → K) → (M
∧ N ∧ L)) ∧ ((J ∧ ¬K) → ¬ (M
∧ N ∧ L)) ∧ (M → J) = 1

где
J, K, L, M, N – ло­ги­че­ские пе­ре­мен­ные?

В от­ве­те не нужно пе­ре­чис­лять все раз­лич­ные на­бо­ры
зна­че­ний J, K, L, M и N, при ко­то­рых вы­пол­не­но дан­ное ра­вен­ство. В ка­че­стве
от­ве­та нужно ука­зать ко­ли­че­ство таких на­бо­ров.

По­яс­не­ние.

Ис­поль­зу­ем фор­му­лы A → B = ¬A ∨ B и ¬(А ∨ В) =
¬А ∧ ¬В

Рас­смот­рим первую под­фор­му­лу:

(J → K) → (M
∧ N ∧ L) = ¬(¬J ∨ K) ∨ (M ∧ N ∧ L) = (J ∧ ¬K) ∨ (M ∧ N ∧ L)

Рас­смот­рим вто­рую под­фор­му­лу

(J ∧ ¬K) → ¬(M ∧ N ∧ L) = ¬(J ∧ ¬K) ∨ ¬(M ∧ N ∧ L) = (¬J ∨ K) ∨ ¬M ∨ ¬N ∨ ¬L

Рас­смот­рим тре­тью под­фор­му­лу

1) M → J = 1 сле­до­ва­тель­но,

а)
M = 1 J = 1

(J ∧ ¬K) ∨ (M ∧ N ∧ L) = (1 ∧ ¬K) ∨ (1 ∧ N ∧ L) = ¬K ∨ N ∧ L;

(0 ∨ K) ∨ 0 ∨ ¬N ∨ ¬L = K ∨ ¬N ∨ ¬L;

Объ­еди­ним:

¬K ∨ N ∧ L ∧ K ∨ ¬N ∨ ¬L = 0 ∨ L ∨ 0 ∨ ¬L =
L ∨ ¬L = 1 сле­до­ва­тель­но, 4
ре­ше­ния.

б)
M = 0 J = 1

(J ∧ ¬K) ∨ (M ∧ N ∧ L) = (1 ∧ ¬K) ∨ (0 ∧ N ∧ L) = ¬K;

(¬J ∨ K) ∨ ¬M ∨ ¬N ∨ ¬L =
(0 ∨ K)
∨ 1 ∨ ¬N ∨ ¬L =
K ∨ 1 ∨ ¬N ∨ ¬L

Объ­еди­ним:

K ∨ 1 ∨ ¬N ∨ ¬L ∧ ¬K =
1 ∨ ¬N ∨ ¬L сле­до­ва­тель­но, 4 ре­ше­ния.

в) M = 0 J = 0.

(J ∧ ¬K) ∨ (M ∧ N ∧ L) = (0 ∧ ¬K) ∨ (0 ∧ N ∧ L) = 0.

(¬J ∨ K) ∨ ¬M ∨ ¬N ∨ ¬L =
(1 ∨ K)
∨ 1 ∨ ¬N ∨ ¬L.

Ответ: 4 + 4 = 8.

За­да­ние
3. Сколь­ко раз­лич­ных ре­ше­ний имеет
урав­не­ние: 

¬((J
→ K) → (L
∧ M ∧ N)) ∨ ¬((L
∧ M ∧ N) → (¬J ∨ K)) ∨ (M ∧ J) = 0

По­яс­не­ние.

Ис­поль­зу­ем фор­му­лу A → B = ¬A ∨ B

Рас­смот­рим первую под­фор­му­лу:

¬((¬J
∨ K)
→ (M ∧ N ∧ L)) = ¬(¬(¬J ∨ K) ∨ (M ∧ N ∧ L)) = ¬((J
∧ ¬K) ∨ (M ∧ N ∧ L)) =

Учи­ты­вая, что ¬(А ∨ В) =
¬А ∧ ¬В,

=
(¬J ∨ K)
∧ (¬M ∨ ¬N ∨ ¬L)

Рас­смот­рим вто­рую под­фор­му­лу

¬((L
∧ M ∧ N) → (¬J ∨ K)) = ¬(¬(L ∧ M ∧ N) ∨ (¬J ∨ K)) = L ∧ M ∧ N ∧ J ∧ ¬K

При­ме­ним от­ри­ца­ние к левой и пра­вой части урав­не­ния,
по­лу­чит­ся

[(J
∧ ¬K) ∨ (M ∧ N ∧ L)] ∧ [¬L ∨ ¬M ∨ ¬N ∨ ¬J ∨ K] ∧ [¬M ∨ ¬J] = 1

1) (¬M ∨ ¬J)
= 1, сле­до­ва­тель­но,

а)
M = 0 J = 0

0 ∧ ¬K ∧ ¬L ∨ ¬N ∨ K, сле­до­ва­тель­но, 0
ре­ше­ний.

б)
M = 1 J = 0

[(0
∧ ¬K) ∨ (1 ∧ N ∧ L)] ∧ [¬L ∨ 0 ∨ ¬N ∨ 1 ∨ K] ∧ [¬M ∨ 1] = N ∧ L ∧ ¬L ∨ ¬N ∨ 1 ∨ K = 1 => L=N=1, сле­до­ва­тель­но, 2 ре­ше­ния.

в)
M = 0 J = 1

[(1
∧ ¬K) ∨ (0 ∧ N ∧ L)] ∧ [¬L ∨ ¬0 ∨ ¬N ∨ ¬1∨ K]
∧ [¬0 ∨ ¬1]
= 1, сле­до­ва­тель­но, 4 ре­ше­ния.

Ответ: 2 + 4 = 6.

За­да­ние
4. Сколь­ко раз­лич­ных ре­ше­ний имеет
урав­не­ние

((K ∨ L) → (L ∧ M ∧ N)) = 0

где
K, L, M, N – ло­ги­че­ские пе­ре­мен­ные? В От­ве­те не нужно пе­ре­чис­лять
все раз­лич­ные на­бо­ры зна­че­ний K, L, M и N, при ко­то­рых вы­пол­не­но дан­ное
ра­вен­ство. В ка­че­стве От­ве­та Вам нужно ука­зать ко­ли­че­ство таких на­бо­ров.

По­яс­не­ние.

пе­ре­пи­шем
урав­не­ние, ис­поль­зуя более про­стые обо­зна­че­ния опе­ра­ций:

((K + L) → (L
· M · N)) = 0

1) из таб­ли­цы ис­тин­но­сти опе­ра­ции «им­пли­ка­ция»
(см. первую за­да­чу) сле­ду­ет, что это ра­вен­ство верно тогда и толь­ко
тогда, когда од­но­вре­мен­но

K + L = 1 и L · M · N = 0

2) из пер­во­го урав­не­ния сле­ду­ет, что хотя бы
одна из пе­ре­мен­ных, K или L, равна 1 (или обе вме­сте); по­это­му рас­смот­рим
три слу­чая

3) если K = 1 и L = 0, то вто­рое ра­вен­ство вы­пол­ня­ет­ся
при любых М и N; по­сколь­ку су­ще­ству­ет 4 ком­би­на­ции двух ло­ги­че­ских
пе­ре­мен­ных (00, 01, 10 и 11), имеем 4 раз­ных ре­ше­ния

4) если K = 1 и L = 1, то вто­рое ра­вен­ство вы­пол­ня­ет­ся
при М · N = 0; су­ще­ству­ет 3 таких ком­би­на­ции (00, 01 и 10), имеем еще 3
ре­ше­ния

5) если K = 0, то обя­за­тель­но L = 1 (из пер­во­го
урав­не­ния); при этом вто­рое ра­вен­ство вы­пол­ня­ет­ся при М · N = 0; су­ще­ству­ет
3 таких ком­би­на­ции (00, 01 и 10), имеем еще 3 ре­ше­ния

6) всего по­лу­ча­ем 4 + 3 + 3 = 10 ре­ше­ний.

Ответ: 10

За­да­ние
5. Сколь­ко раз­лич­ных ре­ше­ний имеет
урав­не­ние

(K ∧ L) ∨ (M ∧ N) = 1

где
K, L, M, N – ло­ги­че­ские пе­ре­мен­ные? В от­ве­те не нужно пе­ре­чис­лять
все раз­лич­ные на­бо­ры зна­че­ний K, L, M и N, при ко­то­рых вы­пол­не­но дан­ное
ра­вен­ство. В ка­че­стве от­ве­та вам нужно ука­зать толь­ко ко­ли­че­ство
таких на­бо­ров.

По­яс­не­ние.

Вы­ра­же­ние ис­тин­но в трех слу­ча­ях, когда (K ∧ L) и (M ∧ N) равны со­от­вет­ствен­но 01, 11, 10.

1) «01» K ∧ L = 0; M ∧ N = 1, => M, N равны 1, а K и L любые, кроме как од­но­вре­мен­но 1. Сле­до­ва­тель­но 3 ре­ше­ния.

2) «11» K ∧ L = 1; M ∧ N = 1. => 1 ре­ше­ние.

3) «10» K ∧ L = 1; M ∧ N = 0. => 3 ре­ше­ния.

За­да­ние
6. Сколь­ко раз­лич­ных ре­ше­ний имеет
урав­не­ние

(X ∧ Y ∨ Z) → (Z ∨ P) = 0

где
X, Y, Z, P – ло­ги­че­ские пе­ре­мен­ные? В от­ве­те не нужно пе­ре­чис­лять
все раз­лич­ные на­бо­ры зна­че­ний, при ко­то­рых вы­пол­не­но дан­ное ра­вен­ство.
В ка­че­стве от­ве­та вам нужно ука­зать толь­ко ко­ли­че­ство таких на­бо­ров.

По­яс­не­ние.

При­ме­ним пре­об­ра­зо­ва­ние им­пли­ка­ции:

(X ∧ Y ∨ Z) → (Z ∨ P) = 0 =>

¬(X
∧ Y ∨ Z) ∨ (Z ∨ P) = 0;

(¬X
∨ ¬Y ∧ ¬Z) ∨ (Z ∨ P) = 0;

Ло­ги­че­ское ИЛИ ложно толь­ко в одном слу­чае: когда
оба вы­ра­же­ния ложны.

Сле­до­ва­тель­но,

(Z ∨ P) = 0 => Z = 0, P = 0.

¬X ∨ ¬Y ∧ ¬Z =
0 => ¬X ∨ ¬Y ∧ 1 = 0 =>

¬X ∨ ¬Y = 0 => X = 1; Y = 1.

Сле­до­ва­тель­но, су­ще­ству­ет толь­ко одно ре­ше­ние
урав­не­ния.

За­да­ние
7. Сколь­ко раз­лич­ных ре­ше­ний имеет
урав­не­ние

(X ∨ Y ∨ Z) → (X ∧ P) = 1

где
X, Y, Z, P – ло­ги­че­ские пе­ре­мен­ные? В от­ве­те не нужно пе­ре­чис­лять
все раз­лич­ные на­бо­ры зна­че­ний, при ко­то­рых вы­пол­не­но дан­ное ра­вен­ство.
В ка­че­стве от­ве­та вам нужно ука­зать толь­ко ко­ли­че­ство таких на­бо­ров.

По­яс­не­ние.

При­ме­ним пре­об­ра­зо­ва­ние им­пли­ка­ции:

(X ∨ Y ∨ Z) → (X ∧ P) = 1;

¬(X
∨ Y ∨ Z) ∨ (X ∧ P) = 1;

(¬X ∧ ¬Y ∧ ¬Z) ∨ (X ∧ P) = 1; (1)

Ло­ги­че­ское «ИЛИ» ложно , когда ложны оба
утвер­жде­ния.

Ло­ги­че­ское «И» ис­тин­но толь­ко тогда,
когда ис­тин­ны оба утвер­жде­ния.

Ва­ри­ант 1.

(¬X ∧ ¬Y ∧ ¬Z) = 1 тогда X = 0, Y = 0, Z = 0.

Тогда из (1) сле­ду­ет, что P может быть как 1, так и
0, то есть 2 на­бо­ра ре­ше­ний.

Ва­ри­ант 2.

(¬X ∧ ¬Y ∧ ¬Z) = 0, (X ∧ P) = 1.

Тогда P = 1, X = 1.

(0 ∧ ¬Y ∧ ¬Z) = 0 => есть 4 ре­ше­ния.

В итоге 6 ре­ше­ний.

За­да­ние
8. Сколь­ко раз­лич­ных ре­ше­ний имеет
урав­не­ние

(K ∨ L) ∧ (M ∨ N) = 1

где
K, L, M, N – ло­ги­че­ские пе­ре­мен­ные? В от­ве­те не нужно пе­ре­чис­лять
все раз­лич­ные на­бо­ры зна­че­ний K, L, M и N, при ко­то­рых вы­пол­не­но дан­ное
ра­вен­ство. В ка­че­стве от­ве­та вам нужно ука­зать толь­ко ко­ли­че­ство
таких на­бо­ров.

По­яс­не­ние.

Ло­ги­че­ское И ис­тин­но толь­ко в одном слу­чае:
когда все вы­ра­же­ния ис­тин­ны.

K ∨ L = 1, M ∨ N = 1.

Каж­дое из урав­не­ний дает по 3 ре­ше­ния.

Рас­смот­рим урав­не­ние А ∧ В = 1 если и А и В при­ни­ма­ют ис­тин­ные зна­че­ния в трех слу­ча­ях каж­дое, то в целом урав­не­ние
имеет 9 ре­ше­ний.

Сле­до­ва­тель­но ответ 9.

За­да­ние
9. Сколь­ко раз­лич­ных ре­ше­ний имеет
урав­не­ние

((A → B)∧ C) ∨ (D ∧ ¬D)=
1,

где
A, B, C, D – ло­ги­че­ские пе­ре­мен­ные?

В от­ве­те не нужно пе­ре­чис­лять все раз­лич­ные на­бо­ры
зна­че­ний A, B, C, D, при ко­то­рых вы­пол­не­но дан­ное ра­вен­ство. В ка­че­стве
от­ве­та вам нужно ука­зать ко­ли­че­ство таких на­бо­ров.

По­яс­не­ние.

Ло­ги­че­ское «ИЛИ» ис­тин­но , когда ис­тин­но
хотя бы одно из утвер­жде­ний.

(D ∧ ¬D)= 0 при любых D.

Сле­до­ва­тель­но,

(A → B)∧ C) = 1 => C = 1; A → B
= 1 => ¬ A ∨ B = 1, что дает нам 3 ва­ри­ан­та ре­ше­ний при каж­дом D.

(D ∧ ¬
D)= 0 при любых D, что дает нам два ва­ри­ан­та ре­ше­ний
(при D = 1, D = 0).

Сле­до­ва­тель­но: всего ре­ше­ний 2*3 = 6.

Итого 6 ре­ше­ний.

За­да­ние
10. Сколь­ко раз­лич­ных ре­ше­ний имеет
урав­не­ние

(¬K ∨ ¬L ∨ ¬M) ∧ (L ∨ ¬M ∨ ¬N) = 0

где
K, L, M, N – ло­ги­че­ские пе­ре­мен­ные? В от­ве­те не нужно пе­ре­чис­лять
все раз­лич­ные на­бо­ры зна­че­ний K, L, M и N, при ко­то­рых вы­пол­не­но дан­ное
ра­вен­ство. В ка­че­стве от­ве­та вам нужно ука­зать толь­ко ко­ли­че­ство таких
на­бо­ров.

По­яс­не­ние.

При­ме­ним от­ри­ца­ние к обеим ча­стям урав­не­ния:

(K ∧ L ∧ M) ∨ (¬L ∧ M ∧ N) = 1

Ло­ги­че­ское ИЛИ ис­тин­но в трех слу­ча­ях.

Ва­ри­ант 1.

K ∧ L ∧ M = 1, тогда K, L, M = 1, а ¬L ∧ M ∧ N = 0. N любое, то есть 2 ре­ше­ния.

Ва­ри­ант 2.

¬L ∧ M ∧ N = 1, тогда N, M = 1; L = 0, K любое, то есть 2 ре­ше­ния.

Сле­до­ва­тель­но, ответ 4.

Системы логических уравнений, содержащие не однотипные
уравнения

За­да­ние
1. Сколь­ко су­ще­ству­ет раз­лич­ных
на­бо­ров зна­че­ний ло­ги­че­ских пе­ре­мен­ных x1, x2, x3, x4, x5, y1, y2,
y3, y4, y5, ко­то­рые удо­вле­тво­ря­ют всем пе­ре­чис­лен­ным ниже усло­ви­ям?

(x1 → x2) ∧ (x2 → x3) ∧ (x3 → x4) ∧ (x4 → x5 ) = 1

(y1 → y2) ∧ (y2 → y3) ∧ (y3 → y4) ∧ (y4 → y5 ) = 1

x1 ∨ y1 = 1

В от­ве­те не нужно пе­ре­чис­лять все раз­лич­ные на­бо­ры
зна­че­ний пе­ре­мен­ных x1, x2, x3, x4, x5, y1, y2, y3, y4, y5, при ко­то­рых
вы­пол­не­на дан­ная си­сте­ма ра­венств. В ка­че­стве от­ве­та Вам нужно ука­зать
ко­ли­че­ство таких на­бо­ров.

По­яс­не­ние.

1) Из по­след­не­го урав­не­ния сле­ду­ет, что гло­баль­но
мы имеем три ва­ри­ан­та — x1=1, y1=1; x1=0, y1=1; x1=1, y1=0.

2) Ло­ги­че­ское И ис­тин­но, толь­ко тогда, когда ис­ти­ны
все утвер­жде­ния, а им­пли­ка­ция ложна толь­ко в слу­чае, если из ис­тин­но­го
сле­ду­ет лож­ное.

3) Урав­не­ние (1) опи­сы­ва­ет ряд пе­ре­мен­ных {x1,
x2, x3, x4, x5}. Так как из пе­ре­мен­ной с более низ­ким но­ме­ром все­гда сле­ду­ет
пе­ре­мен­ная с более вы­со­ким, если любую пе­ре­мен­ную из этого ряда при­рав­нять
1, то все сле­ду­ю­щие долж­ны также быть равны 1. Для урав­не­ния (2) су­ще­ству­ет
то же самое пра­ви­ло. Иначе го­во­ря, если за­пи­сать пе­ре­мен­ные x (или y)
в по­ряд­ке воз­рас­та­ния их но­ме­ров, слева будут нули, а спра­ва — еди­ни­цы.

4) Рас­смот­рим ва­ри­ант x1=1, y1=1. Так как пер­вые
числа каж­до­го ряда равны 1, то все сле­ду­ю­щие тоже равны 1. Су­ще­ству­ет
толь­ко одна ком­би­на­ция для этого ва­ри­ан­та.

5) Рас­смот­рим ва­ри­ант x1=0, y1=1. Для y-ряда все
пе­ре­мен­ные равны 1, для x же су­ще­ству­ет 5 ком­би­на­ций, так как в ряде x
может быть от 1 до 5 нолей вклю­чи­тель­но.

6) По­след­ний ва­ри­ант рас­смот­рим ана­ло­гич­но
преды­ду­ще­му. Там су­ще­ству­ет всего 5 ком­би­на­ций.

Пра­виль­ный ответ: 5+5+1=11 ком­би­на­ций.

За­да­ние
2. Сколь­ко су­ще­ству­ет раз­лич­ных
на­бо­ров зна­че­ний ло­ги­че­ских пе­ре­мен­ных x1, x2, x3, x4, x5, y1, y2,
y3, y4, y5, ко­то­рые удо­вле­тво­ря­ют всем пе­ре­чис­лен­ным ниже усло­ви­ям?

(x1 → x2) ∧ (x2 → x3) ∧ (x3 → x4) ∧ (x4 → x5 ) = 1

(y5 → y4) ∧ (y4 → y3) ∧ (y3 → y2) ∧ (y2 → y1 ) = 1

x3 ∧ y3 = 1

В от­ве­те не нужно пе­ре­чис­лять
все раз­лич­ные на­бо­ры зна­че­ний пе­ре­мен­ных x1, x2, x3, x4, x5, y1, y2,
y3, y4, y5, при ко­то­рых вы­пол­не­на дан­ная си­сте­ма ра­венств. В ка­че­стве
от­ве­та Вам нужно ука­зать ко­ли­че­ство таких на­бо­ров.

По­яс­не­ние.

1) Из по­след­не­го урав­не­ния сле­ду­ет, что гло­баль­но
мы имеем x3=1, y3=1.

2) Ло­ги­че­ское И ис­тин­но, толь­ко тогда, когда ис­ти­ны
все утвер­жде­ния, а им­пли­ка­ция ложна толь­ко в слу­чае, если из ис­тин­но­го
сле­ду­ет лож­ное.

3) Урав­не­ние (1) опи­сы­ва­ет ряд пе­ре­мен­ных {x1,
x2, x3, x4, x5}. Так как из пе­ре­мен­ной с более низ­ким но­ме­ром все­гда сле­ду­ет
пе­ре­мен­ная с более вы­со­ким, если любую пе­ре­мен­ную из этого ряда при­рав­нять
1, то все сле­ду­ю­щие долж­ны также быть равны 1. Для урав­не­ния (2) су­ще­ству­ет
то же самое пра­ви­ло, толь­ко на­о­бо­рот: из пе­ре­мен­ной с более вы­со­ким
но­ме­ром все­гда сле­ду­ет пе­ре­мен­ная с более низ­ким. Иначе го­во­ря, если
за­пи­сать пе­ре­мен­ные x в по­ряд­ке воз­рас­та­ния их но­ме­ров, спра­ва
будут еди­ни­цы, а слева — нули, в y — на­про­тив, слева еди­ни­цы, спра­ва —
нули.

4) Рас­смот­рим ва­ри­ант x3=1, y3=1. Тогда все сле­ду­ю­щие:
x4, x5, y2, y1 тоже равны 1. Оста­ют­ся пе­ре­мен­ные x1, x2, y4, y5. Так как
x2 сле­ду­ет из x1, для них мы имеем 3 ва­ри­ан­та, ана­ло­гич­но для y4 и y5.
33=9.

Ответ — 9.

За­да­ние
3. Сколь­ко су­ще­ству­ет раз­лич­ных
на­бо­ров зна­че­ний ло­ги­че­ских пе­ре­мен­ных x1, x2, x3, x4, y1, y2 y3, y4,
ко­то­рые удо­вле­тво­ря­ют всем пе­ре­чис­лен­ным ниже усло­ви­ям?

(x1 → x2) ∧ (x2 → x3) ∧ (x3 → x4) = 1

(¬y1 ∨ y2) ∧ (¬y2 ∨ y3) ∧ (¬y3 ∨ y4) = 1

(y1 → x1) ∧ (y2 → x2) ∧ (y3 → x3) ∧ (y4 → x4) = 1

В от­ве­те не нужно пе­ре­чис­лять все раз­лич­ные на­бо­ры
зна­че­ний пе­ре­мен­ных x1, x2, x3, x4, y1, y2 y3, y4, при ко­то­рых вы­пол­не­на
дан­ная си­сте­ма ра­венств. В ка­че­стве от­ве­та Вам нужно ука­зать ко­ли­че­ство
таких на­бо­ров.

По­яс­не­ние.

Конъ­юнк­ция ис­ти­на тогда и толь­ко тогда, когда каж­дое
вы­ска­зы­ва­ние ис­тин­но.

Для пер­во­го вы­ра­же­ния это озна­ча­ет, что, если
х1 равен 1, то х2, х3 и х4 также равны 1, т. е. для х1…х4 ре­ше­ния су­ще­ству­ют
толь­ко в виде «1111», «0111», «0011»,
«0001» и «0000».

При­ме­нив пре­об­ра­зо­ва­ние им­пли­ка­ции ко вто­ро­му
вы­ра­же­нию, уви­дим, что оно ана­ло­гич­но пер­во­му.

В тре­тьем вы­ра­же­нии из «y» сле­ду­ет со­от­вет­ству­ю­щее
ему «x», это озна­ча­ет, что если y = 1, то и x = 1.

Сле­до­ва­тель­но, пер­во­му на­бо­ру для x
«1111» со­от­вет­ству­ет 5 на­бо­ров y. Вто­ро­му — 4, тре­тье­му —
3, и. т. д.

Сле­до­ва­тель­но, ответ: 5 + 4 + 3 + 2 + 1 = 15.

За­да­ние
4. Сколь­ко су­ще­ству­ет раз­лич­ных
на­бо­ров зна­че­ний ло­ги­че­ских пе­ре­мен­ных x1, x2, x3, x4, x5, y1, y2,
y3, y4, y5, ко­то­рые удо­вле­тво­ря­ют всем пе­ре­чис­лен­ным ниже усло­ви­ям?

(x1
→ x2) ∧ (x2 → x3) ∧ (x3 → x4) ∧ (x4 → x5 ) = 1

(y1
→ y2) ∧ (y2 → y3) ∧ (y3 → y4) ∧ (y4 → y5 ) = 1

x1 → y1 = 1

В
от­ве­те не нужно пе­ре­чис­лять все раз­лич­ные на­бо­ры зна­че­ний пе­ре­мен­ных
x1, x2, x3, x4, x5, y1, y2, y3, y4, y5, при ко­то­рых вы­пол­не­на дан­ная си­сте­ма
ра­венств. В ка­че­стве от­ве­та Вам нужно ука­зать ко­ли­че­ство таких на­бо­ров.

По­яс­не­ние.

1) Из по­след­не­го урав­не­ния сле­ду­ет, что гло­баль­но
мы имеем три ва­ри­ан­та — x1=1, y1=1; x1=0, y1=1; x1=0, y1=0.

2) Ло­ги­че­ское И ис­тин­но, толь­ко тогда, когда ис­ти­ны
все утвер­жде­ния, а им­пли­ка­ция ложна толь­ко в слу­чае, если из ис­тин­но­го
сле­ду­ет лож­ное.

3) Урав­не­ние (1) опи­сы­ва­ет ряд пе­ре­мен­ных {x1,
x2, x3, x4, x5}. Так как из пе­ре­мен­ной с более низ­ким но­ме­ром все­гда сле­ду­ет
пе­ре­мен­ная с более вы­со­ким, если любую пе­ре­мен­ную из этого ряда при­рав­нять
1, то все сле­ду­ю­щие долж­ны также быть равны 1. Для урав­не­ния (2) су­ще­ству­ет
то же самое пра­ви­ло. Иначе го­во­ря, если за­пи­сать пе­ре­мен­ные x (или y)
в по­ряд­ке воз­рас­та­ния их но­ме­ров, спра­ва будут еди­ни­цы, а слева —
нули.

4) Рас­смот­рим ва­ри­ант x1=1, y1=1. Так как пер­вые
числа каж­до­го ряда равны 1, то все сле­ду­ю­щие тоже равны 1. Су­ще­ству­ет
толь­ко одна ком­би­на­ция для этого ва­ри­ан­та.

5) Рас­смот­рим ва­ри­ант x1=0, y1=1. Для y-ряда все
пе­ре­мен­ные равны 1, для x же су­ще­ству­ет 5 ком­би­на­ций, так как в ряде x
может быть от 1 до 5 нолей вклю­чи­тель­но.

6) По­след­ний ва­ри­ант рас­смот­рим ана­ло­гич­но
преды­ду­ще­му. Там су­ще­ству­ет всего 25 ком­би­на­ций.

Пра­виль­ный ответ: 25+5+1=31 ком­би­на­ция.

За­да­ние
5. Сколь­ко су­ще­ству­ет раз­лич­ных
на­бо­ров зна­че­ний ло­ги­че­ских пе­ре­мен­ных x1, х2, хЗ, х4, х5, хб, y1,
у2, уЗ, у4, у5, у6 ко­то­рые удо­вле­тво­ря­ют всем пе­ре­чис­лен­ным ниже усло­ви­ям?

(x1 → х2) ∧ (х2 → хЗ) ∧ (хЗ → х4) ∧ (х4 → х5) ∧ (х5 → х6) = 1

(y1 → y2) ∧ (у2 → уЗ) ∧ (уЗ → у4) ∧ (у4 → у5) ∧ (у5 → у6) = 1

x1 ∨ y1 = 1

В от­ве­те не нужно пе­ре­чис­лять
все раз­лич­ные на­бо­ры зна­че­ний пе­ре­мен­ных x1, х2, хЗ, х4, х5, y1, у2,
уЗ, у4, у5, при ко­то­рых вы­пол­не­на дан­ная си­сте­ма ра­венств. В ка­че­стве
от­ве­та Вам нужно ука­зать ко­ли­че­ство таких на­бо­ров.

По­яс­не­ние.

1) Из по­след­не­го урав­не­ния сле­ду­ет, что гло­баль­но
мы имеем три ва­ри­ан­та — x1=1, y1=1; x1=0, y1=1; x1=1, y1=0.

2) Ло­ги­че­ское И ис­тин­но, толь­ко тогда, когда ис­ти­ны
все утвер­жде­ния, а им­пли­ка­ция ложна толь­ко в слу­чае, если из ис­тин­но­го
сле­ду­ет лож­ное.

3) Урав­не­ние (1) опи­сы­ва­ет ряд пе­ре­мен­ных {x1,
x2, x3, x4, x5, x6}. Так как из пе­ре­мен­ной с более низ­ким но­ме­ром все­гда
сле­ду­ет пе­ре­мен­ная с более вы­со­ким, если любую пе­ре­мен­ную из этого
ряда при­рав­нять 1, то все сле­ду­ю­щие долж­ны также быть равны 1. Для урав­не­ния
(2) су­ще­ству­ет то же самое пра­ви­ло. Иначе го­во­ря, если за­пи­сать пе­ре­мен­ные
x (или y) в по­ряд­ке воз­рас­та­ния их но­ме­ров, спра­ва будут нули, а слева
— еди­ни­цы.

4) Рас­смот­рим ва­ри­ант x1=1, y1=1. Так как пер­вые
числа каж­до­го ряда равны 1, то все сле­ду­ю­щие тоже равны 1. Су­ще­ству­ет
толь­ко одна ком­би­на­ция для этого ва­ри­ан­та.

5) Рас­смот­рим ва­ри­ант x1=0, y1=1. Для y-ряда все
пе­ре­мен­ные равны 1, для x же су­ще­ству­ет 6 ком­би­на­ций, так как в ряде x
может быть от 1 до 6 нолей вклю­чи­тель­но.

6) По­след­ний ва­ри­ант рас­смот­рим ана­ло­гич­но
преды­ду­ще­му. Там су­ще­ству­ет всего 6 ком­би­на­ций.

Пра­виль­ный ответ: 6+6+1=13 ком­би­на­ций.

За­да­ние
6. Сколь­ко су­ще­ству­ет раз­лич­ных
на­бо­ров зна­че­ний ло­ги­че­ских пе­ре­мен­ных x1, х2, хЗ, х4, х5, y1, у2,
уЗ, у4, у5, ко­то­рые удо­вле­тво­ря­ют всем пе­ре­чис­лен­ным ниже усло­ви­ям?

(x1 → х2) ∧ (х2 → хЗ) ∧ (хЗ → х4) ∧ (х4 → х5 )
= 1

(y1 → y2) ∧ (у2 → уЗ) ∧ (уЗ → у4) ∧ (у4 → у5 )
= 1

x1 ∨ y1 = 1

В от­ве­те не нужно пе­ре­чис­лять все раз­лич­ные на­бо­ры
зна­че­ний пе­ре­мен­ных x1, х2, хЗ, х4, х5, y1, у2, уЗ, у4, у5, при ко­то­рых
вы­пол­не­на дан­ная си­сте­ма ра­венств. В ка­че­стве от­ве­та Вам нужно ука­зать
ко­ли­че­ство таких на­бо­ров.

По­яс­не­ние.

1) Из по­след­не­го урав­не­ния сле­ду­ет, что гло­баль­но
мы имеем три ва­ри­ан­та — x1=1, y1=1; x1=0, y1=1; x1=1, y1=0.

2) Ло­ги­че­ское И ис­тин­но, толь­ко тогда, когда ис­ти­ны
все утвер­жде­ния, а им­пли­ка­ция ложна толь­ко в слу­чае, если из ис­тин­но­го
сле­ду­ет лож­ное.

3) Урав­не­ние (1) опи­сы­ва­ет ряд пе­ре­мен­ных {x1,
x2, x3, x4, x5}. Так как из пе­ре­мен­ной с более низ­ким но­ме­ром все­гда сле­ду­ет
пе­ре­мен­ная с более вы­со­ким, если любую пе­ре­мен­ную из этого ряда при­рав­нять
1, то все сле­ду­ю­щие долж­ны также быть равны 1. Для урав­не­ния (2) су­ще­ству­ет
то же самое пра­ви­ло. Иначе го­во­ря, если за­пи­сать пе­ре­мен­ные x (или y)
в по­ряд­ке воз­рас­та­ния их но­ме­ров, спра­ва будут нули, а слева — еди­ни­цы.

4) Рас­смот­рим ва­ри­ант x1=1, y1=1. Так как пер­вые
числа каж­до­го ряда равны 1, то все сле­ду­ю­щие тоже равны 1. Су­ще­ству­ет
толь­ко одна ком­би­на­ция для этого ва­ри­ан­та.

5) Рас­смот­рим ва­ри­ант x1=0, y1=1. Для y-ряда все
пе­ре­мен­ные равны 1, для x же су­ще­ству­ет 5 ком­би­на­ций, так как в ряде x
может быть от 1 до 5 нолей вклю­чи­тель­но.

6) По­след­ний ва­ри­ант рас­смот­рим ана­ло­гич­но
преды­ду­ще­му. Там су­ще­ству­ет всего 5 ком­би­на­ций.

Пра­виль­ный ответ: 5+5+1=11 ком­би­на­ций.

За­да­ние
7. Сколь­ко су­ще­ству­ет раз­лич­ных
на­бо­ров зна­че­ний ло­ги­че­ских пе­ре­мен­ных x1, x2, x3, x4, x5, y1, y2,
y3, y4, y5, ко­то­рые удо­вле­тво­ря­ют всем пе­ре­чис­лен­ным ниже усло­ви­ям?

(x1 → x2) ∧ (x2 → x3) ∧ (x3 → x4) ∧ (x4 → x5 ) = 1

(y1 → y2) ∧ (y2 → y3) ∧ (y3 → y4) ∧ (y4 → y5 ) = 1

y5 → x5 = 1

В от­ве­те не нужно пе­ре­чис­лять все раз­лич­ные на­бо­ры
зна­че­ний пе­ре­мен­ных x1, x2, x3, x4, x5, y1, y2, y3, y4, y5, при ко­то­рых
вы­пол­не­на дан­ная си­сте­ма ра­венств. В ка­че­стве от­ве­та Вам нужно ука­зать
ко­ли­че­ство таких на­бо­ров.

По­яс­не­ние.

1) Из по­след­не­го урав­не­ния сле­ду­ет, что гло­баль­но
мы имеем три ва­ри­ан­та: x5=1, y5=1; x5=0, y5=0; x5=0, y5=1.

2) Ло­ги­че­ское И ис­тин­но, толь­ко тогда, когда ис­ти­ны
все утвер­жде­ния, а им­пли­ка­ция ложна толь­ко в слу­чае, если из ис­тин­но­го
сле­ду­ет лож­ное.

3) Урав­не­ние (1) опи­сы­ва­ет ряд пе­ре­мен­ных {x1,
x2, x3, x4, x5}. Так как из пе­ре­мен­ной с более низ­ким но­ме­ром все­гда сле­ду­ет
пе­ре­мен­ная с более вы­со­ким, если любую пе­ре­мен­ную из этого ряда при­рав­нять
1, то все сле­ду­ю­щие долж­ны также быть равны 1. Для урав­не­ния (2) су­ще­ству­ет
то же самое пра­ви­ло. Иначе го­во­ря, если за­пи­сать пе­ре­мен­ные x в по­ряд­ке
воз­рас­та­ния их но­ме­ров, спра­ва будут нули, а слева — еди­ни­цы, в y — так
же.

4) Рас­смот­рим ва­ри­ант x5=1, y5=1. Тогда осталь­ные
пе­ре­мен­ные могут при­ни­мать любые зна­че­ния: всего таких ком­би­на­ций 25.

5) Рас­смот­рим ва­ри­ант х5=0, у5=0. Тогда все пе­ре­мен­ные
равны 0, сле­до­ва­тель­но, 1 ком­би­на­ция.

6) Рас­смот­рим ва­ри­ант х5=0, у5=1. Тогда все пе­ре­мен­ные
х равны 0, а пе­ре­мен­ные у могут при­ни­мать любые зна­че­ния. Всего таких
ком­би­на­ций 5.

Ответ: 31.

За­да­ние
8. Сколь­ко су­ще­ству­ет раз­лич­ных
на­бо­ров зна­че­ний ло­ги­че­ских пе­ре­мен­ных x1, х2, хЗ, х4, х5, у1, у2,
уЗ, у4, у5, ко­то­рые удо­вле­тво­ря­ют всем пе­ре­чис­лен­ным ниже усло­ви­ям?

В от­ве­те не нужно пе­ре­чис­лять
все раз­лич­ные на­бо­ры зна­че­ний пе­ре­мен­ных x1, х2, хЗ, х4, х5, у1, у2,
уЗ, у4, у5, при ко­то­рых вы­пол­не­на дан­ная си­сте­ма ра­венств. В ка­че­стве
от­ве­та Вам нужно ука­зать ко­ли­че­ство таких на­бо­ров.

По­яс­не­ние.

За­ме­тим, что пер­вые два урав­не­ния свя­за­ны друг
с дру­гом толь­ко через тре­тье.

Най­дем ко­ли­че­ство ре­ше­ний пер­во­го урав­не­ния.
Каж­дая из пе­ре­мен­ных x1, … , x5 может при­ни­мать толь­ко два зна­че­ния.
Им­пли­ка­ция ложна толь­ко тогда, когда из ис­ти­ны сле­ду­ет ложь. Если за­пи­сать
зна­че­ния пе­ре­мен­ных под­ряд, то можно уви­деть, что для того, чтобы ра­вен­ство
вы­пол­ня­лось, не­об­хо­ди­мо, чтобы после «1» ни­ко­гда не стоял
«0». Сле­до­ва­тель­но, по­лу­ча­ем такие ре­ше­ния: (x1,x2,x3,x4,x5)
= 00000, 00001, 00011, 00111, 01111, 11111.

Во вто­ром урав­не­нии не­об­хо­ди­мо, чтобы после
«0» ни­ко­гда не сто­я­ла «1». Сле­до­ва­тель­но, по­лу­ча­ем
такие ре­ше­ния: (y1,y2,y3,y4,y5) = 00000, 10000, 11000, 11100, 11110, 11111.
Таким об­ра­зом, си­сте­ма из двух урав­не­ний имеет 6·6 = 36 ре­ше­ний:
для каж­до­го на­бо­ра пе­ре­мен­ных y су­ще­ству­ет 6 на­бо­ров пе­ре­мен­ных
x.

Тре­тье урав­не­ние ложно, когда (x1,y1) = 00. Вы­черк­нем
из нашей таб­ли­цы те ре­ше­ния, для ко­то­рых (x1,y1) = 00.

Таким об­ра­зом, име­ет­ся 31 набор пе­ре­мен­ных, удо­вле­тво­ря­ю­щих
си­сте­ме.

За­да­ние 9. Сколь­ко су­ще­ству­ет раз­лич­ных на­бо­ров зна­че­ний
ло­ги­че­ских пе­ре­мен­ных x1, х2, хЗ, х4, х5, х6, у1, у2, уЗ, у4, у5, у6, ко­то­рые
удо­вле­тво­ря­ют всем пе­ре­чис­лен­ным ниже усло­ви­ям?

В от­ве­те не нужно пе­ре­чис­лять
все раз­лич­ные на­бо­ры зна­че­ний пе­ре­мен­ных x1, х2, хЗ, х4, х5, х6, у1,
у2, уЗ, у4, у5, у6, при ко­то­рых вы­пол­не­на дан­ная си­сте­ма ра­венств. В
ка­че­стве от­ве­та Вам нужно ука­зать ко­ли­че­ство таких на­бо­ров.

По­яс­не­ние.

За­ме­тим, что пер­вые два урав­не­ния свя­за­ны друг
с дру­гом толь­ко через тре­тье.

Най­дем ко­ли­че­ство ре­ше­ний пер­во­го урав­не­ния.
Каж­дая из пе­ре­мен­ных x1, … , x6 может при­ни­мать толь­ко два зна­че­ния.
Им­пли­ка­ция ложна толь­ко тогда, когда из ис­ти­ны сле­ду­ет ложь. Если за­пи­сать
зна­че­ния пе­ре­мен­ных под­ряд, то можно уви­деть, что для того, чтобы ра­вен­ство
вы­пол­ня­лось, не­об­хо­ди­мо, чтобы после «1» ни­ко­гда не стоял
«0». Сле­до­ва­тель­но, по­лу­ча­ем такие ре­ше­ния: (x1,x2,x3,x4,x5,
x6) = 000000, 000001, 000011, 000111, 001111, 011111, 111111.

Во вто­ром урав­не­нии не­об­хо­ди­мо, чтобы после
«0» ни­ко­гда не сто­я­ла «1». Сле­до­ва­тель­но, по­лу­ча­ем
такие ре­ше­ния: (y1,y2,y3,y4,y5, y6) = 000000, 100000, 110000, 11100, 111100,
111110, 111111. Таким об­ра­зом, си­сте­ма из двух урав­не­ний имеет
7·7 = 49 ре­ше­ний: для каж­до­го на­бо­ра пе­ре­мен­ных y су­ще­ству­ет
7 на­бо­ров пе­ре­мен­ных x.

Тре­тье урав­не­ние ложно, когда (x1,y1) = 00. Вы­черк­нем
из нашей таб­ли­цы те ре­ше­ния, для ко­то­рых (x1,y1) = 00.

Таким об­ра­зом, име­ет­ся 43 на­бо­ров пе­ре­мен­ных,
удо­вле­тво­ря­ю­щих си­сте­ме.

За­да­ние
10. Сколь­ко су­ще­ству­ет раз­лич­ных
на­бо­ров зна­че­ний ло­ги­че­ских пе­ре­мен­ных x₁, x₂,
… x₁₂, ко­то­рые удо­вле­тво­ря­ют всем пе­ре­чис­лен­ным ниже
усло­ви­ям?

((x₁ ≡ x₂) ∨ (x₃ ≡ x₄)) ∧ (¬(x₁ ≡ x₂) ∨ ¬(x₃ ≡ x₄)) = 1

((x₃ ≡ x₄) ∨ (x₅ ≡ x₆)) ∧ (¬(x₃ ≡ x₄) ∨ ¬(x₅ ≡ x₆)) = 1

…

((x₉ ≡ x₁₀) ∨ (x₁₁ ≡ x₁₂)) ∧ (¬(x₉ ≡ x₁₀) ∨ ¬(x₁₁ ≡ x₁₂)) = 1

В от­ве­те не нужно пе­ре­чис­лять
все раз­лич­ные на­бо­ры зна­че­ний пе­ре­мен­ных x₁, x₂,
… x₁₂ при ко­то­рых вы­пол­не­на дан­ная си­сте­ма ра­венств. В
ка­че­стве от­ве­та Вам нужно ука­зать ко­ли­че­ство таких на­бо­ров.

По­яс­не­ние.

По­стро­им древо ре­ше­ний пер­во­го урав­не­ния:

 

За­ме­тим, что вы­ра­же­ние (x₃ ≡ x₄)
в двух слу­ча­ях равно 1 и в двух слу­ча­ях равно 0. Таким об­ра­зом, одно урав­не­ние
имеет во­семь ре­ше­ний.

Вто­рое урав­не­ние свя­за­но с пер­вым толь­ко через
вы­ра­же­ние (x₃ ≡ x₄). По­стро­им древо ре­ше­ний
вто­ро­го урав­не­ния:

Для каж­до­го из зна­че­ний 0 и 1 вы­ра­же­ния (x₃ ≡
x₄) су­ще­ству­ет че­ты­ре на­бо­ра пе­ре­мен­ных x₁, x₂,…,x₄,
удо­вле­тво­ря­ю­щих пер­во­му урав­не­нию (см. пер­вый ри­су­нок). Таким
об­ра­зом, си­сте­ма из двух урав­не­ний имеет 4 · 4 = 16
ре­ше­ний.

Тре­тье урав­не­ние свя­за­но со вто­рым толь­ко через
вы­ра­же­ние (x₅ ≡ x₆). По­стро­им древо ре­ше­ний
тре­тье­го урав­не­ния:

 

Для каж­до­го из зна­че­ний 0 и 1 вы­ра­же­ния (x₅ ≡
x₆) су­ще­ству­ет 2 · 4 = 8 на­бо­ров пе­ре­мен­ных
x₁, x₂,…,x₆, удо­вле­тво­ря­ю­щих пер­во­му
урав­не­нию (см. пер­вый и вто­рой ри­су­нок). Таким об­ра­зом, си­сте­ма
из трёх урав­не­ний имеет 8 · 4 = 32 ре­ше­ния. Си­сте­ма
из четырёх — 128.

Ответ: 128.