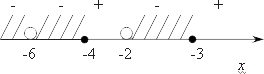Системы неравенств егэ фипи

в условии
в решении
в тексте к заданию
в атрибутах

Категория:

Атрибут:

Всего: 191    1–20 | 21–40 | 41–60 | 61–80 …

Добавить в вариант

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

Всего: 191    1–20 | 21–40 | 41–60 | 61–80 …

24 марта 2020

В закладки

Обсудить

Жалоба

Система неравенств из открытого банка ФИПИ

Раздел: Уравнения и неравенства.

Решите систему неравенств:

Решение задачи

В данном уроке рассматривается метод решения системы неравенств с одним неизвестным. Решить систему неравенств — это значит найти все значения неизвестного, которые удовлетворяют каждому неравенству системы. Таким образом, сначала решается каждое неравенство системы по отдельности. Так, первое неравенство представляется в виде произведения линейных двучленов, а дальнейшее решение проводится методом интервалов. Второе неравенство, содержащее модуль, решается методом возведения в квадрат неравенства. Затем полученный числитель раскладывается на множители по формуле разности квадратов, и далее — на произведение линейных двучленов. Полученное неравенство решается методом интервалов, при этом следует учесть область определения неравенства и исключить значения, обращающие знаменатель в нуль. Далее решения двух неравенств совмещаются на одной числовой оси. Общий для обоих неравенств отрезок числовой прямой и является решением системы неравенств.

Решением данной задача целесообразно будет воспользоваться при подготовке к ЕГЭ в качестве примера решения задач С3.

6 мая 2014

В этом видеоуроке я подробно разобрал довольно серьезную задачу 15 из ЕГЭ по математике, которая содержит и логарифмическое, и дробно-рациональное неравенство. Особое внимание уделено теореме Безу (для поиска корней многочлена), а также методике деления многочленов уголком (для разложения на множители).

В этом уроке мы разберем систему из двух неравенств из ЕГЭ по математике:

⎧⎩⎨⎪⎪log7−2x(x+6)≤0x−x−3x+6−x2+27x+90x2+8x+12≤−1left{ begin{align}& {{log }_{7-2x}}left( x+6 right)le 0 \& x-frac{x-3}{x+6}-frac{{{x}^{2}}+27x+90}{{{x}^{2}}+8x+12}le -1 \end{align} right.

Решение системы неравенств

Как видите, система состоит из логарифмического неравенства, а также классического дробно-рационального неравенства, однако в процессе решения мы обнаружим, что данное неравенство не так уж и просто, как может показаться на первый взгляд. Начнем с логарифмического. Для этого выпишем его отдельно:

log7−2x(x+6)≤ 0

{{log }_{7-2x}}left( x+6 right)le text{ }0

Как и любое логарифмическое неравенство, данная конструкция приводится к каноническому виду, т. е. слева мы оставляем все без изменения, а вот справа запишем следующим образом:

log7−2x(x+6)≤log7−2x1

{{log }_{7-2x}}left( x+6 right)le {{log }_{7-2x}}1

Как использовать метод рационализации

Теперь воспользуемся методом рационализации. Напомню, что если у нас есть неравенство вида

logk(x)f(x)⋃logk(x)g(x),

{{log }_{kleft( x right)}}fleft( x right)bigcup {{log }_{kleft( x right)}}gleft( x right),

то мы можем перейти вот к такой конструкции:

(f(x)−g(x))(k(x)−1)⋃0

left( fleft( x right)-gleft( x right) right)left( kleft( x right)-1 right)bigcup 0

Разумеется, в этом неравенстве не учтена область определения логарифма:

f(x)>0

fleft( x right)>0

g(x)>0

gleft( x right)>0

1≠k(x)>0

1ne kleft( x right)>0

Данные неравенства мы должны просчитать отдельно, а затем пересечь со вторым решением. Но, как правило, учет ОДЗ в решении логарифмических неравенств не представляет, поэтому давайте вернемся к решению элемента нашей системы.

Итак, в роли f(x)fleft( x right) выступает линейная функция x+6x+6, а в роли g(x)gleft( x right) выступает просто 1. Поэтому переписываем наше логарифмическое неравенство системы следующим образом:

(x+6−1)(7−2x−1)

left( x+6-1 right)left( 7-2x-1 right)

Последняя 1 — это та самая x−1x-1, которая стоит во второй скобке. Все это меньше или равно 0. Знак неравенства при выполнении данного преобразования сохраняется. Приведем подобные в каждой скобке:

(x+5)(6−2x)≤0

left( x+5 right)left( 6-2x right)le 0

Применение метода интервалов

Очевидно, перед нами простейшее неравенство, которое легко решается методом интервалов. Приравняем каждую скобку к 0:

(+5)=0→=−5

left( +5 right)=0to =-5

6−2=0→2=6

6-2=0to 2=6

x=3

x=3

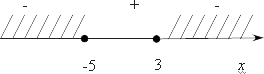
Отметим все эти точки (таких точек получилось две) на координатной прямой. При этом заметим, что они являются закрашенными: 

Отметим знаки. Для этого возьмем любое число, больше 3. Первым будет стоять «минус». Затем знаки везде чередуются, потому что корней четной кратности нет. Нас интересует знак меньше или равно, т. е. знак «минус». Закрашиваем нужные области. Напомню, что при решении неравенств методом интервалов мы подставляем 1 млрд. в последнее выражение, которое получили перед переходом к уравнениям.

Итак, мы нашли множества. Но, как понимаете, это еще не решение неравенства. Теперь от нас требуется найти область определения логарифма. Для этого выпишем следующие функции:

Erroneous nesting of equation structures

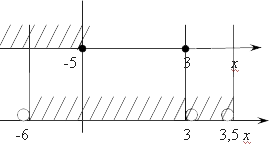
left[ begin{align}& x+6>0 \& 7-2x>0 \& 7-2xne 1 \end{align} right.=>left[ begin{align}& x>-6 \& 7>2x \& 6ne 2x \end{align} right.=>left[ begin{align}& \& x<text{ }3,5 \& xne text{ }3 \end{align} right.

Итак, мы получили три одновременных требования, т. е. все эти неравенства должны выполняться одновременно. Давайте начертим прямую, параллельную нашему кандидату на ответ:

Мы получили итоговый ответ для первого элемента системы:

(−6;−5]⋃(3;3,5)

left( -6;-5 right]bigcup left( 3;3,5 right). На этом моменте у многих учеников возникает вопрос. Взгляните, 3 — с одной стороны она выколота, но с другой стороны, эта же точка закрашена. Так как же отметить ее в результате? Для того, чтобы корректно и раз и навсегда разобраться с этим вопросом, запомните одно простое правило.

Что значит пересечение множеств? Это такое множество, которое одновременно входит и в первое множество и во второе. Другими словами, заполняя картинку, нарисованную ниже, мы ищем такие точки, которые одновременно принадлежат и первой, и второй прямой. Следовательно, если какая-либо точка не принадлежит хотя бы одной из этих прямых, то независимо от того, как она выглядит на второй прямой, она нас не устраивает. И, в частности, с 3, происходит именно такая история: с одной стороны в кандидатах на ответ точка 3 нас устраивает, потому что она закрашена, но с другой стороны 3 выколота в силу области определения логарифма, а, значит, и в итоговом множестве эта точка должна быть выколота. Все, ответ на первое логарифмическое неравенство системы полностью обоснован. Для надежности я еще раз продублирую его:

(−6;−5]⋃(3;3,5)

left( -6;-5 right]bigcup left( 3;3,5 right)

Решение дробно-рационального неравенства

Идем далее и решаем дробно-рациональное неравенство из нашей системы. Очевидно, что его мы тоже будем решать методом интервалов. Выпишем его:

x−x−3x+6−x2+27x+90x2+8x+12≤−1x-frac{x-3}{x+6}-frac{{{x}^{2}}+27x+90}{{{x}^{2}}+8x+12}le -1

Теперь перенесем -1 влево:

x+1−x−3x+6−x2+27x+90(x+6)(x+2)≤0x+1-frac{x-3}{x+6}-frac{{{x}^{2}}+27x+90}{left( x+6 right)left( x+2 right)}le 0

x+11−x−3x+6−x2+27x+90(x+6)(x+2)≤0frac{x+1}{1}-frac{x-3}{x+6}-frac{{{x}^{2}}+27x+90}{left( x+6 right)left( x+2 right)}le 0

Приводим всю конструкцию к общему знаменателю:

(x+1)(x+6)(x+2)−(x−3)(x+2)−(x2+27x+90)(x+6)(x+2)≤0frac{left( x+1 right)left( x+6 right)left( x+2 right)-left( x-3 right)left( x+2 right)-left( {{x}^{2}}+27x+90 right)}{left( x+6 right)left( x+2 right)}le 0

Раскроем скобки:

(x+2)((x+1)(x+6)−(x−3))−x2−27x−90(x+6)(x+2)≤0frac{left( x+2 right)left( left( x+1 right)left( x+6 right)-left( x-3 right) right)-{{x}^{2}}-27x-90}{left( x+6 right)left( x+2 right)}le 0

x3+6x2+9x+2x2+12x+18−x2−27x−90(x+6)(x+2)≤0frac{{{x}^{3}}+6{{x}^{2}}+9x+2{{x}^{2}}+12x+18-{{x}^{2}}-27x-90}{left( x+6 right)left( x+2 right)}le 0

x3+7x2−6x−72(x+6)(x+2)≤0frac{{{x}^{3}}+7{{x}^{2}}-6x-72}{left( x+6 right)left( x+2 right)}le 0

Что можно сказать про полученное неравенство? Во-первых, оно дробно-рациональное, при этом знаменатель уже разложен на множители. Следовательно, наиболее оптимальным вариантом будет решать это неравенство методом интервалов. Однако для того, чтобы решать его методом интервалов, необходимо и числитель разложить на множители. В этом и состоит основная сложность, потому что числитель представляет собой многочлен третьей степени. Кто помнит формулу корней третьей степени? Лично я не помню. Но это нам не потребуется.

Все, что нам потребуется, это теорема Безу, точнее, не сама теорема, а одно из важнейших ее следствии, которое гласит следующее: если многочлен с целыми коэффициентами имеет корень x1{{x}_{1}}, причем он является целым числом, то свободный коэффициент (в нашем случае 72) обязательно будет делиться на x1{{x}_{1}}. Другими словами, если мы хотим найти корни этого кубического уравнения, то все, что нужно, это просто «покопаться» в множителях, на которые раскладывается число 72.

Давайте разложим число 72 на простые множители:

72=8⋅9=2⋅2⋅2⋅3⋅3

72=8cdot 9=2cdot 2cdot 2cdot 3cdot 3

Итак, нам нужно перебрать все комбинации двоек т троек, чтобы получить хотя бы один корень нашего кубического выражения. На первый взгляд может показаться, что это комбинаторная задача, однако на самом деле все не так страшно. Давайте начнем с минимального числа:

x=2

x=2

Проверим, является ли 2 ответом. Для этого вспомним, что такое корень. Это такое число, которое будучи подставленным в многочлен, обращает его в 0. Давайте подставим:

(2)=8+28−12−72<0

left( 2 right)=8+28-12-72<0

Получаем, что x−2x-2 не подходит. Идем дальше. Давайте возьмем 4:

=4

=4

(4)=64+112−24−72>0

left( 4 right)=64+112-24-72>0

x=4x=4 также не является корнем нашей конструкции.

Идем дальше. Какой следующий xx мы будем разбирать? Для ответа на этот вопрос давайте заметим интересный факт: при x−2x-2 наш многочлен был отрицательным, а при x=4x=4 он оказался уже положительным. Это значит, что где-то между точками 2 и 4 наш многочлен пересекает ось xx. Другими словами, где-то на этом отрезке наш он обращается в 0. Это значит, что данная точка будет искомым числом. Давайте подумаем, какое целое число лежит между 4 и 2. Очевидно, что только 3, и 3 присутствует в разложении, следовательно, она действительно может являться корнем нашего выражения. Рассмотрим этот вариант:

x=3

x=3

(3)=27+63−18−72=90−90=0

left( 3 right)=27+63-18-72=90-90=0

Прекрасно, наша гипотеза подтвердилась. Действительно, x=3x=3 является корнем нашей конструкции. Но как это поможет нам разложить данный многочлен на множители? Очень просто. Все из той же самой теоремы Безу следует, что если x1{{x}_{1}} является корнем многочлена p(x)pleft( x right), то значит, что мы можем записать следующее:

x1:p(x)=Q(x)(x−x1)

{{x}_{1}}:pleft( x right)=Qleft( x right)left( x-{{x}_{1}} right)

Другими словами, зная x1{{x}_{1}} мы можем утверждать, что в разложении нашего выражения на множители обязательно будет присутствовать множитель x1{{x}_{1}}. В нашем случае мы можем записать, что наш многочлен обязательно имеет в своем разложении множитель (x−3)left( x-3 right), потому что 3 является его корнем.

Идем дальше. Мы нашли один из корней данного многочлена, но как найти остальные? И здесь нам приходит на помощь деление уголком. Давайте запишем наш исходный многочлен и разделим его:

x3+7x2−6x−72x−3=x2+10x+24frac{{{x}^{3}}+7{{x}^{2}}-6x-72}{x-3}={{x}^{2}}+10x+24

Другими словами, наше неравенство из системы мы можем переписать следующим образом:

(x+3)(x2+10x+24)(x+6)(x+2)≤0frac{left( x+3 right)left( {{x}^{2}}+10x+24 right)}{left( x+6 right)left( x+2 right)}le 0

Заметим, что во второй скобке числителя стоит квадратный трехчлен, который тоже очень просто раскладывается на множители, получим:

(x+3)(x+6)(x+4)(x+6)(x+2)≤0frac{left( x+3 right)left( x+6 right)left( x+4 right)}{left( x+6 right)left( x+2 right)}le 0

Вот и все, осталось просто выписать корни:

x=3

x=3

≠−6(2k)

ne -6left( 2k right)

=−4

=-4

≠−2

ne -2

Давайте отметим все эти точки, которые могут быть решением системы, на координатной прямой xx: 

Для того, чтобы определить знаки, берем любое число, больше 3, подставляем в каждую из этих скобок и получаем пять положительных чисел, т. е. справа от 3 стоит знак «плюс». Затем везде знаки меняются, а вот в -6 ничего не меняется, потому что -6 — корень второй кратности. Нас интересуют те области, где знак функции отрицательный, поэтому заштриховываем «минусы».

Итого, мы можем записать решение нашего исходного неравенства — оно будет следующим:

(−∞;−6)⋃(−6;−4]⋃(−2;3]

left( -infty ;-6 right)bigcup left( -6;-4 right]bigcup left( -2;3 right]

Заключительные шаги

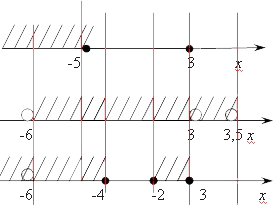
Мы решили второе неравенство нашей системы, а теперь осталось решить, собственно, систему, т. е. пересечь полученные нами множества. Для этого я предлагаю построить еще одну прямую, параллельную двум нашим старым прямым, отвечающим за логарифмическое неравенство из системы: 

Мы можем записать итоговый ответ второго элемента системы неравенств: (−6;−5]left( -6;-5 right]. Теперь можно вернуться к нашей системе и записать итоговое множество:

x∈(−6; −5]

xin left( -6;text{ }-5 right]

Ключевые моменты

Ключевых моментов в данной задаче сразу несколько:

1. Нужно уметь решать логарифмические неравенства с помощью перехода к канонической форме.
2. Нужно уметь работать с дробно-рациональными неравенствами. Это вообще материал 8-9 класса, поэтому если вы работаете с логарифмами, то уж с дробно-рациональными неравенствами разберетесь.
3. Теорема Безу. Важнейшим следствием из этой теоремы является тот факт, что корни многочлена с целыми коэффициентами являются делителями его свободного члена.

В остальном это несложная, хотя довольно объемная задача на решение системы уравнений. Определенные трудности при решении системы могут возникнуть также в пересечении всех множеств, особенно связанных с точкой 3. Тут все очень просто: достаточно запомнить, что пересечение означает требование одновременного выполнения всех неравенств, т. е. искомая точка должна быть закрашена на всех трех осях. Если хотя бы на одной оси она не закрашена или выколота, то такая точка не может быть частью ответа. 

Смотрите также:

1. Сравнение корней и учёт области определения в логарифмических неравенства из ЕГЭ.
2. Что делать, если в показателе стоит логарифм
3. Тест к уроку «Что такое логарифм» (средний)
4. Комбинированные задачи B12
5. Изюм и виноград (смеси и сплавы)
6. Задача B4: транзит нефти