Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Два мотоциклиста стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой трассы, длина которой равна 14 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного из них на 21 км/ч больше скорости другого?
2
Из одной точки круговой трассы, длина которой равна 14 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 80 км/ч, и через 40 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.
3
Из пункта A круговой трассы выехал велосипедист. Через 30 минут он еще не вернулся в пункт А и из пункта А следом за ним отправился мотоциклист. Через 10 минут после отправления он догнал велосипедиста в первый раз, а еще через 30 минут после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна 30 км. Ответ дайте в км/ч.
4
Часы со стрелками показывают 8 часов ровно. Через сколько минут минутная стрелка в четвертый раз поравняется с часовой?
5
Два гонщика участвуют в гонках. Им предстоит проехать 60 кругов по кольцевой трассе протяжённостью 3 км. Оба гонщика стартовали одновременно, а на финиш первый пришёл раньше второго на 10 минут. Чему равнялась средняя скорость второго гонщика, если известно, что первый гонщик в первый раз обогнал второго на круг через 15 минут? Ответ дайте в км/ч.
Пройти тестирование по этим заданиям
11. Сюжетные текстовые задачи
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Задачи на круговое движение
Верны те же формулы: [{large{S=vcdot t quad quad quad v=dfrac
St quad quad quad
t=dfrac Sv}}]
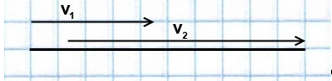
(blacktriangleright) Пусть два тела начали движение из одной точки в одном направлении со скоростями (v_1>v_2).
Тогда если (l) — длина круга, (t_1) — время, через которое они окажутся в одной точке в первый раз, то:
То есть за (t_1) первое тело пройдет расстояние на (l) большее, чем второе тело.
Если (t_n) — время, через которое они в (n)–ый раз окажутся в одной точке, то справедлива формула: [{large{t_n=ncdot t_1}}]
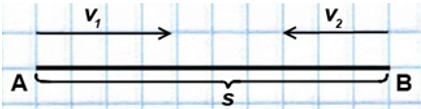
(blacktriangleright) Пусть два тела начали движение из разных точек в одном направлении со скоростями (v_1>v_2).
Тогда задача легко сводится к предыдущему случаю: нужно найти сначала время (t_1), через которое они окажутся в одной точке в первый раз.
Если на момент начала движения расстояние между ними (buildrelsmileover{A_1A_2}=s), то:
Задание
1
#2677
Уровень задания: Легче ЕГЭ
Два спортсмена стартуют в одном направлении из диаметрально противоположных точек круговой дорожки. Они бегут с разными непостоянными скоростями. Известно, что в тот момент, когда спортсмены впервые поравнялись, они прекратили тренировку. На сколько кругов больше пробежал спортсмен с большей средней скоростью, чем другой спортсмен?
Назовём спортсмена с большей средней скоростью первым. Сначала первому спортсмену нужно было пробежать полкруга, чтобы достичь места старта второго спортсмена. После этого ему предстояло пробежать столько же, сколько пробежал второй спортсмен (грубо говоря, после того, как первый спортсмен пробежал полкруга, ему до встречи надо было пробежать каждый метр дорожки, который пробежал второй спортсмен, причём столько же раз, сколько этот метр пробежал второй).
Таким образом, первый спортсмен пробежал на (0,5) круга больше.
Ответ: 0,5
Задание
2
#2115
Уровень задания: Легче ЕГЭ
Кот Мурзик бегает от пса Шарика по кругу. Скорости Мурзика и Шарика постоянны. Известно, что Мурзик бежит в (1,5) раза быстрее Шарика и за (10) минут они в сумме пробегают два круга. За сколько минут Шарик пробежит один круг?
Так как Мурзик бежит в (1,5) раза быстрее Шарика, то за (10) минут Мурзик и Шарик в сумме пробегают такое же расстояние, которое пробежал бы Шарик за (10cdot (1 + 1,5) = 25) минут. Следовательно, Шарик пробегает два круга за (25) минут, тогда один круг Шарик пробегает за (12,5) минут
Ответ: 12,5
Задание
3
#823
Уровень задания: Равен ЕГЭ
Из точки A круговой орбиты далёкой планеты одновременно в одном направлении вылетели два метеорита. Скорость первого метеорита на 10000 км/ч больше, чем скорость второго. Известно, что впервые после вылета они встретились через 8 часов. Найдите длину орбиты в километрах.
В тот момент, когда они впервые встретились, разница расстояний, которые они пролетели, равна длине орбиты.
За 8 часов разница стала (8 cdot 10000 = 80000) км.
Ответ: 80000
Задание
4
#821
Уровень задания: Равен ЕГЭ
Вор, укравший сумочку, убегает от хозяйки сумочки по круговой дороге. Скорость вора на 0,5 км/ч больше, чем скорость хозяйки сумочки, которая бегает за ним. Через сколько часов вор догонит хозяйку сумочки во второй раз, если длина дороги, по которой они бегают, равна 300 метрам (считайте, что в первый раз он её догнал уже после кражи сумочки)?
Первый способ:
Вор догонит хозяйку сумочки во второй раз в тот момент, когда расстояние, которое он пробежит, станет на 600 метров больше, чем расстояние, которое пробежит хозяйка сумочки (с момента кражи).
Так как его скорость на (0,5) км/ч больше, то за час он пробегает на 500 метров больше, тогда за (1 : 5 = 0,2) часа он пробегает на (500 : 5 = 100) метров больше. На 600 метров больше он пробежит за (1 + 0,2 = 1,2) часа.
Второй способ:
Пусть (v) км/ч – скорость хозяйки сумочки, тогда
(v + 0,5) км/ч – скорость вора.
Пусть (t) ч – время, через которое вор догонит хозяйку сумочки во второй раз, тогда
(vcdot t) – расстояние, которое пробежит хозяйка сумочки за (t) ч,
((v + 0,5)cdot t) – расстояние, которое пробежит вор за (t) ч.
Вор догонит хозяйку сумочки во второй раз в тот момент, когда пробежит ровно на 2 круга больше неё (то есть на (600) м = (0,6) км), тогда [(v + 0,5)cdot t — vcdot t = 0,6qquadLeftrightarrowqquad 0,5cdot t = 0,6,] откуда (t = 1,2) ч.
Ответ: 1,2
Задание
5
#822
Уровень задания: Равен ЕГЭ
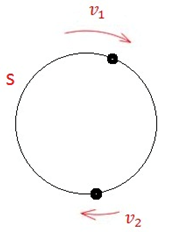
Два мотоциклиста стартуют одновременно из одной точки круговой трассы в разных направлениях. Скорость первого мотоциклиста в два раза больше, чем скорость второго. Через час после старта они встретились в третий раз (считайте, что в первый раз они встретились уже после старта). Найдите скорость первого мотоциклиста, если длина трассы 40 км. Ответ дайте в км/ч.
В тот момент, когда мотоциклисты встретились в третий раз, суммарное расстояние, которое они проехали, было (3 cdot 40 = 120) км.
Так как скорость первого в 2 раза больше, чем скорость второго, то он проехал из 120 км часть в 2 раза большую, чем второй, то есть 80 км.
Так как встретились в третий раз они через час, то 80 км первый проехал за час. Его скорость 80 км/ч.
Ответ: 80
Задание
6
#824
Уровень задания: Равен ЕГЭ
Два бегуна стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой дорожки, длина которой 400 метров. Через сколько минут бегуны поравняются в первый раз, если первый бегун за час пробегает на 1 километр больше, чем второй?
За час первый бегун пробегает на 1000 метров больше, чем второй, значит на 100 метров больше он пробежит за (60 : 10 = 6) минут.
Изначальное расстояние между бегунами равно 200 метров. Они поравняются, когда первый бегун пробежит на 200 метров больше, чем второй.
Это произойдёт через (2 cdot 6 = 12) минут.
Ответ: 12
Задание
7
#825
Уровень задания: Равен ЕГЭ
Из города M по круговой дороге длиной 220 километров вышел турист, а через 55 минут следом за ним из города M отправился автомобилист. Через 5 минут после отправления он догнал туриста в первый раз, а еще через 4 часа после этого догнал его во второй раз. Найдите скорость туриста. Ответ дайте в км/ч.
Первый способ:
После первой встречи автомобилист догнал туриста (во второй раз) через 4 часа. К моменту второй встречи автомобилист проехал на круг больше, чем прошёл турист (то есть на (220) км).
Так как за эти 4 часа автомобилист обогнал туриста на (220) км, то скорость автомобилиста на (220 : 4 = 55) км/ч больше, чем скорость туриста.
Пусть теперь скорость туриста (v) км/ч, тогда до первой встречи он успел пройти [v cdot left(dfrac{55}{60} + dfrac{5}{60}right) = v text{км},] автомобилист успел проехать [(v + 55)dfrac{5}{60} = dfrac{v + 55}{12} text{км}.] Тогда [dfrac{v + 55}{12} = v,] откуда находим (v = 5) км/ч.
Второй способ:
Пусть (v) км/ч – скорость туриста.
Пусть (w) км/ч – скорость автомобилиста. Так как (55) минут (+ 5) минут (= 1) час, то
(vcdot 1) км – расстояние, которое прошёл турист до первой встречи. Так как (5) минут (= dfrac{1}{12}) часа, то
(wcdot dfrac{1}{12}) км – расстояние, которое проехал автомобилист до первой встречи. Расстояния, которые они проехали до первой встречи, равны: [wcdot dfrac{1}{12} = vcdot 1.] За следующие 4 часа автомобилист проехал больше, чем прошёл турист на круг (на (220) км), тогда (wcdot 4 = vcdot 4 + 220), итого: [v = dfrac{1}{12}w,] что равносильно (w = 12cdot v)
(4w = 4v + 220), откуда с учётом предыдущего уравнения [48v = 4v + 220.] Решая эту систему на (v) и (w), находим (v = 5) км/ч, (w = 60) км/ч.
Ответ: 5
Как научиться быстро и правильно решать задачи на круговое движение в ЕГЭ по математике? Этот вопрос в преддверии аттестационного испытания возникает у школьников все чаще. О том, как максимально эффективно подготовиться к экзамену, расскажет образовательный портал «Школково».
Основные моменты
В задачах ЕГЭ на круговое движение перемещение могут осуществлять 2 объекта. В этом случае следует учитывать их скорость сближения или удаления.
[T=dfrac S {V_1-V_2}]
[T=dfrac S {V_1+V_2}]
При использовании в упражнении величин, которые связаны с расстоянием (скорость, длина круга), решить их можно путем сведения к перемещению по прямой.
[S=Vcdot t]
Наибольшую сложность у школьников Москвы и других городов, как показывает практика, вызывают задачи на круговое движение в ЕГЭ, поиск ответа в которых связан с применением угла. Для решения упражнения длину окружности можно задать как часть круга.
Повторить эти и другие алгебраические формулы вы можете в разделе «Теоретическая справка». Для того чтобы научиться применять их на практике, прорешайте упражнения по данной теме в «Каталоге».

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Текстовые задачи на движение – легко! Алгоритм решения и успех на ЕГЭ
Смотри видео «Текстовые задачи на ЕГЭ по математике».
Почему текстовые задачи относятся к простым?
Во-первых, все такие задачи решаются по единому алгоритму, о котором мы вам расскажем. Во-вторых, многие из них однотипны — это задачи на движение или на работу. Главное — знать к ним подход.
Внимание! Чтобы научиться решать текстовые задачи, вам понадобится всего три-четыре часа самостоятельной работы, то есть два-три занятия. Всё, что нужно, — это здравый смысл плюс умение решать квадратное уравнение. И даже формулу для дискриминанта мы вам напомним, если вдруг забыли.
Прежде чем перейти к самим задачам — проверьте себя.
Запишите в виде математического выражения:
на
больше
;
в пять раз больше
;
на
меньше, чем
;
меньше
в
раза;
на
меньше, чем
;
- частное от деления
на
в полтора раза больше
;
- квадрат суммы
и
равен
;
составляет
процентов от
;
больше
на
процентов.
Пока не напишете — в ответы не подглядывайте! 
Казалось бы, на первые три вопроса ответит и второклассник. Но почему-то у половины выпускников они вызывают затруднения, не говоря уже о вопросах и
. Из года в год мы, репетиторы, наблюдаем парадоксальную картину: ученики одиннадцатого класса долго думают, как записать, что «
на
больше
». А в школе в этот момент они «проходят» первообразные и интегралы

Итак, правильные ответы:
больше, чем
. Разница между ними равна пяти. Значит, чтобы получить большую величину, надо к меньшей прибавить разницу.
больше, чем
, в пять раз. Значит, если
умножить на
, получим
.
меньше, чем
. Разница между ними равна
. Чтобы получить меньшую величину, надо из большей вычесть разницу.
меньше, чем
. Значит, если из большей величины вычтем разницу, получим меньшую.
На всякий случай повторим терминологию:
Сумма — результат сложения двух или нескольких слагаемых.
Разность — результат вычитания.
Произведение — результат умножения двух или нескольких множителей.
Частное — результат деления чисел.
Мы помним, что.
Еслипринять за
, то
на
процентов больше, то есть
.
Начнем мы с задач на движение. Они часто встречаются в вариантах ЕГЭ. Здесь всего два правила:
- Все эти задачи решаются по одной-единственной формуле:
, то есть расстояние
скорость
время. Из этой формулы можно выразить скорость
или время
.
- В качестве переменной
удобнее всего выбирать скорость. Тогда задача точно решится!
Для начала очень внимательно читаем условие. В нем все уже есть. Помним, что текстовые задачи на самом деле очень просты.
. Из пункта
в пункт
, расстояние между которыми
км, одновременно выехали автомобилист и велосипедист. Известно, что в час автомобилист проезжает на
км больше, чем велосипедист. Определите скорость велосипедиста, если известно, что он прибыл в пункт
на
часа позже автомобилиста. Ответ дайте в км/ч.
Что здесь лучше всего обозначить за ? Скорость велосипедиста. Тем более, что ее и надо найти в этой задаче. Автомобилист проезжает на
километров больше, значит, его скорость равна
.
Нарисуем таблицу. В нее сразу можно внести расстояние — и велосипедист, и автомобилист проехали по км. Можно внести скорость — она равна
и
для велосипедиста и автомобилиста соответственно. Осталось заполнить графу «время».
Его мы найдем по формуле: . Для велосипедиста получим
, для автомобилиста
.
Эти данные тоже запишем в таблицу.
Вот что получится:
| велосипедист | |||
| автомобилист |
Остается записать, что велосипедист прибыл в конечный пункт на часа позже автомобилиста. Позже — значит, времени он затратил больше. Это значит, что
на четыре больше, чем
, то есть
Решаем уравнение.
Приведем дроби в левой части к одному знаменателю.
Первую дробь домножим на , вторую — на
.
Если вы не знаете, как приводить дроби к общему знаменателю (или — как раскрывать скобки, как решать уравнение…), подойдите с этим конкретным вопросом к вашему учителю математики и попросите объяснить. Бесполезно говорить учительнице: «Я не понимаю математику» — это слишком абстрактно и не располагает к ответу. Учительница может ответить, например, что она вам сочувствует. Или, наоборот, даст какую-либо характеристику вашей личности. И то и другое неконструктивно.
А вот если вы зададите конкретный вопрос: «Как приводить дроби к одному знаменателю?» или «Как раскрывать скобки?» — вы получите нужный вам конкретный ответ. Вам ведь необходимо в этом разобраться! Если педагог занят, договоритесь о времени, когда вы можете с ним (или с ней) встретиться, чтобы получить консультацию. Используйте ресурсы, которые у вас под рукой!
Получим:
Разделим обе части нашего уравнения на . В результате уравнение станет проще. Но почему-то многие учащиеся забывают это делать, и в результате получают сложные уравнения и шестизначные числа в качестве дискриминанта.
Умножим обе части уравнения на . Получим:
Раскроем скобки и перенесем всё в левую часть уравнения:
Мы получили квадратное уравнение. Напомним, что квадратным называется уравнение вида . Решается оно стандартно — сначала находим дискриминант по формуле
, затем корни по формуле
В нашем уравнении ,
,
.
Найдем дискриминант и корни:
,
.
Ясно, что не подходит по смыслу задачи — скорость велосипедиста не должна быть отрицательной.
Ответ: .
Следующая задача — тоже про велосипедиста.
2. Велосипедист выехал с постоянной скоростью из города в город
, расстояние между которыми равно
км. На следующий день он отправился обратно со скоростью на
км/ч больше прежней. По дороге он сделал остановку на
часа. В результате он затратил на обратный путь столько же времени, сколько на путь из
в
. Найдите скорость велосипедиста на пути из
в
. Ответ дайте в км/ч.
Пусть скорость велосипедиста на пути из в
равна
. Тогда его скорость на обратном пути равна
. Расстояние в обеих строчках таблицы пишем одинаковое —
километров. Осталось записать время. Поскольку
, на путь из
в
велосипедист затратит время
, а на обратный путь время
.
| туда | |||
| обратно |
На обратном пути велосипедист сделал остановку на часа и в результате затратил столько же времени, сколько на пути из
в
. Это значит, что на обратном пути он крутил педали на
часа меньше.
Значит, на три меньше, чем
. Получается уравнение:
Как и в предыдущей задаче, сгруппируем слагаемые:
Точно так же приводим дроби к одному знаменателю:
Разделим обе части уравнения на
Напомним — если вам непонятны какие-либо действия при решении уравнений, обращайтесь к учительнице! Показывайте конкретную строчку в решении задачи и говорите: «Пожалуйста, объясните, как это делать». Для нее такое объяснение — дело пятнадцати минут, а вы наконец научитесь решать уравнения, что очень важно для сдачи ЕГЭ по математике.
Умножим обе части уравнения на , раскроем скобки и соберем все в левой части.
Находим дискриминант. Он равен .
Найдем корни уравнения:
. Это вполне правдоподобная скорость велосипедиста. А ответ
не подходит, так как скорость велосипедиста должна быть положительна.
Ответ: .
Следующий тип задач — когда что-нибудь плавает по речке, в которой есть течение. Например, теплоход, катер или моторная лодка. Обычно в условии говорится о собственной скорости плавучей посудины и скорости течения. Собственной скоростью называется скорость в неподвижной воде.
При движении по течению эти скорости складываются. Течение помогает, по течению плыть — быстрее.
Скорость при движении по течению равна сумме собственной скорости судна и скорости течения.
А если двигаться против течения? Течение будет мешать, относить назад. Теперь скорость течения будет вычитаться из собственной скорости судна.
3. Моторная лодка прошла против течения реки км и вернулась в пункт отправления, затратив на обратный путь на
часа меньше. Найдите скорость лодки в неподвижной воде, если скорость течения равна
км/ч. Ответ дайте в км/ч.
Пусть скорость лодки в неподвижной воде равна .
Тогда скорость движения моторки по течению равна , а скорость, с которой она движется против течения
.
Расстояние и в ту, и в другую сторону одинаково и равно км.
Занесем скорость и расстояние в таблицу.
Заполняем графу «время». Мы уже знаем, как это делать. При движении по течению , при движении против течения
, причем
на два часа больше, чем
.
| по течению | |||
| против течения |
Условие « на два часа больше, чем «
» можно записать в виде:
Составляем уравнение:
и решаем его:
Приводим дроби в левой части к одному знаменателю:
Раскрываем скобки:
Делим обе части на , чтобы упростить уравнение:
Умножаем обе части уравнения на
Вообще-то это уравнение имеет два корня: и
(оба этих числа при возведении в квадрат дают
). Но конечно же, отрицательный ответ не подходит — скорость лодки должна быть положительной.
Ответ: .
4. Теплоход проходит по течению реки до пункта назначения км и после стоянки возвращается в пункт отправления. Найдите скорость течения, если скорость теплохода в неподвижной воде равна
км/ч, стоянка длится
часов, а в пункт отправления теплоход возвращается через
часов после отплытия из него. Ответ дайте в км/ч.
Снова обозначим за скорость течения. Тогда скорость движения теплохода по течению равна
, скорость его движения против течения равна
. Расстояния — и туда, и обратно — равны
км.
Теперь графа «время».
Поскольку , время
движения теплохода по течению равно
, которое теплоход затратил на движение против течения, равно
.
| по течению | |||
| против течения |
В пункт отправления теплоход вернулся через часов после отплытия из него. Стоянка длилась
часов, следовательно,
часов теплоход плыл — сначала по течению, затем против.
Значит,
Прежде всего разделим обе части уравнения на . Оно станет проще!
Мы не будем подробно останавливаться на технике решения уравнения. Всё уже понятно — приводим дроби в левой части к одному знаменателю, умножаем обе части уравнения на , получаем квадратное уравнение
. Поскольку скорость течения положительна, получаем:
.
Ответ: .
Наверное, вы уже заметили, насколько похожи все эти задачи. Текстовые задачи хороши еще и тем, что ответ легко проверить с точки зрения здравого смысла. Ясно, что если вы получили скорость течения, равную километров в час — задача решена неверно.
5. Баржа в вышла из пункта
в пункт
, расположенный в
км от
. Пробыв в пункте
час
минут, баржа отправилась назад и вернулась в пункт
в
. Определите (в км/час) скорость течения реки, если известно, что собственная скорость баржи равна
км/ч.
Пусть скорость течения равна . Тогда по течению баржа плывет со скоростью
, а против течения со скоростью
.
Сколько времени баржа плыла? Ясно, что надо из вычесть
, а затем вычесть время стоянки. Обратите внимание, что
час
минут придется перевести в часы:
час
минут
часа. Получаем, что суммарное время движения баржи (по течению и против) равно
часа.
| по течению | |||
| против течения |
Возникает вопрос — какой из пунктов, или
, расположен выше по течению? А этого мы никогда не узнаем!

Да и какая разница — ведь в уравнение входит сумма , равная
.
Итак,
Решим это уравнение. Число в правой части представим в виде неправильной дроби:
.
Приведем дроби в левой части к общему знаменателю, раскроем скобки и упростим уравнение. Получим:
Работать с дробными коэффициентами неудобно! Если мы разделим обе части уравнения на и умножим на
, оно станет значительно проще:
Поскольку скорость течения положительна, .
Ответ: 2.
Еще один тип текстовых задач в вариантах ЕГЭ по математике — это задачи на работу.
Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Текстовые задачи на движение – легко! Алгоритм решения и успех на ЕГЭ» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена:
09.03.2023
На чтение 9 мин Просмотров 18.2к. Опубликовано 16 ноября, 2020
Задачи на движение начинают проходить в 5 классе и решают все оставшиеся учебные годы вплоть до 11 класса. В ЕГЭ по математике вы найдете задачи на движение в задании 11, в котором собраны все текстовые задачи. Рассмотрим как надо решать задачи на движение из ЕГЭ. Но сначала немного теории.
Содержание
- Как решать задачи на движение
- Примеры решения
- Виды задач на движение
- Движение навстречу друг другу, движение в противоположных направлениях
- Движение друг за другом (вдогонку)
- Задачи на движение по кругу
- Задачи на движение мимо объекта
- Задачи на движение по течению и против течения
- Задачи на движение из ЕГЭ по математике (профильный уровень)
- Задача 1.
- Задача 2.
- Задача 3
- Задача 4
- Задача 5
Как решать задачи на движение
Решение задач на движение подчиняется четкому алгоритму, который состоит из нескольких этапов:
- Анализ данных.
- Составление таблицы.
- Составление уравнения.
- Решение уравнения.
Остановимся подробно на каждом пункте:
1. Первое, с чего нужно начать — медленно и вдумчиво прочитать условие задачи, то есть проанализировать данные.
Чтобы наглядно представить задачу, необходимо сделать рисунок и отобразить на нем все известные по условию задачи величины.
2. Второй шаг — составить таблицу по условию задачи, внести в таблицу известные величины и ввести неизвестные.
Таблица состоит из трех столбцов S, v и t (путь, скорость и время) и нескольких строк. При заполнении каждой строки сначала выбираем и заполняем тот столбец, информация о котором дана в задаче. Еще один столбец записываем в роли неизвестного (чаще всего, это то, что требуется найти в задаче). В третью, оставшуюся колонку вписываем связь характеристик из двух уже заполненных столбцов по формуле:
S = v · t.
В таблице получается столько строчек, сколько каждый из объектов задачи действовал (то есть, перемещался) или мог бы действовать.
3. Следующий шаг — при помощи сделанного рисунка и заполненной таблицы составить уравнение или систему уравнений.
По окончании заполнения таблицы оказывается, что есть часть информации, которая не вошла в таблицу. Эта информация характеризует те значения величин в колонках, которые вычисляются в третью очередь, то есть по формуле. На основании этой информации и данных из третьей колонки составляем уравнение.
4. Решить полученное уравнение и прийти к ответу.
Когда уравнение составлено, последний шаг — это решить его, и, в конце концов, получить ответ.
Будьте внимательны, если за неизвестное вы приняли не то, что требуется найти в задаче. В этом случае следует выразить то, что нужно найти через полученное решение уравнения.
Если, решив уравнение, вы получили несколько ответов, то следует отобрать только имеющие смысл решения. Помните, что путь, скорость и время не могут быть отрицательными.
Примеры решения
Пример:
Два велосипедиста одновременно отправляются в 60-километровый пробег. Первый едет со скоростью на 10 км/ч большей, чем второй, и прибывает к финишу на 3 часа раньше второго. Найдите скорость велосипедиста, пришедшего к финишу вторым.
Решение:
В задаче требуется найти скорость второго, более медленного, велосипедиста. Примем его скорость за x. Заполним таблицу:
| v, км/ч | t, ч | S, км | |
| Первый велосипедист | x + 10 | 60 | |
| Второй велосипедист | x | 60 |
В условии задачи сказано, что первый велосипедист прибыл к финишу на 3 часа раньше второго. На основании этого составим уравнение:
3x2 + 90x = 600 + 60x;
x2 + 10x – 200 = 0.
Получаем два корня, x1 = 10 и x2 = –20. Второй корень не подходит, так как скорость не может быть отрицательной.
Ответ: 10 км/ч.
Виды задач на движение
Движение навстречу друг другу, движение в противоположных направлениях
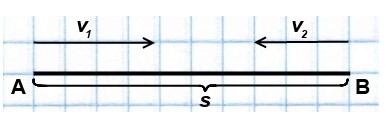
Если два объекта движутся навстречу друг другу, то они сближаются:
При движении в противоположном направлении объекты удаляются:
В обоих случаях объекты как бы «помогают» друг другу преодолеть общее для них расстояние, «действуют сообща». Поэтому чтобы найти их совместную скорость (это и будет скорость сближения или удаления), нужно складывать скорости объектов:
v = v1 + v2.
Движение друг за другом (вдогонку)
При движении в одном направлении объекты также могут как сближаться, так и удаляться. В этом случае они как бы «соревнуются» в преодолении общего расстояния, «действуют друг против друга». Поэтому их совместная скорость будет равна разности скоростей.
Если скорость идущего впереди объекта меньше скорости объекта, следующего за ним, то они сближаются. Чтобы найти скорость сближения, надо из большей скорости вычесть меньшую:
Если объект, идущий впереди, движется с большей скоростью, чем идущий следом за ним, то они удаляются. Чтобы найти скорость удаления, надо из большей скорости вычесть меньшую:
Таким образом:
При движении навстречу друг другу и движении в противоположных направлениях скорости складываем.
При движении в одном направлении скорости вычитаем.
Задачи на движение по кругу
При движении по кругу объекты могут:
При этом пройденные расстояния измеряются длиной круговой трассы, равной S.
- Если два объекта начинают движение по кругу из одной и той же точки, то в момент первой встречи более быстрый объект пройдет расстояние на один круг больше.
- Если два объекта начинают движение по кругу из разных точек, расстояние между которыми равно S0, то в момент первой встречи догоняющий объект пройдет на S0 км большее расстояние, чем догоняемый.
- Если через определенное время t первый объект опережает второй на m кругов, то разница пройденных объектами расстояний будет равна m · S: S1 – S2 = m · S.
Задачи на движение мимо объекта
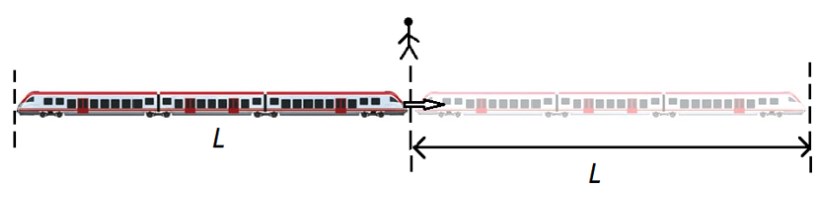
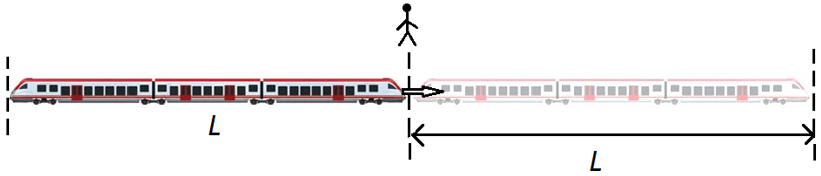
В задачах на движение мимо объекта обязательно присутствуют протяженные тела — поезда, туннели, корабли и т. п. Зачастую движущимся объектом является поезд.
Если поезд длиной L движется мимо точечного объекта (столба, светофора, человека), то он проходит расстояние, равное его длине L:
S = L = v0 · t.
При этом, если точечный объект (пешеход, велосипедист) тоже движется, то совместная скорость равна сумме скоростей, если поезд и объект двигаются в разных направлениях (как в пункте 1), и равна разности скоростей, если они двигаются в одном направлении (как в пункте 2).
Если поезд длиной L1 движется мимо протяженного объекта (туннеля, лесополосы) длиной L2, то он проходит расстояние, равное сумме длин самого поезда и протяженного объекта:
S = L1 + L2 = v0 · t.
При этом, если протяженный объект (например, другой поезд) тоже движется, то совместная скорость равна сумме скоростей, если оба объекта двигаются в разных направлениях, и равна разности скоростей (из большей вычитается меньшая), если они двигаются в одном направлении.
Задачи на движение по течению и против течения
В задачах на движение помимо собственной скорости плывущего тела нужно учитывать скорость течения.
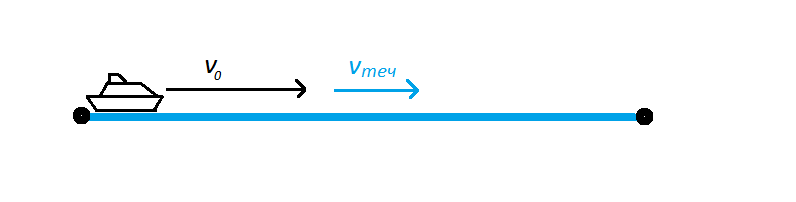
При движении по течению скорость течения прибавляется к скорости плывущего тела: v = v0 + vтеч.
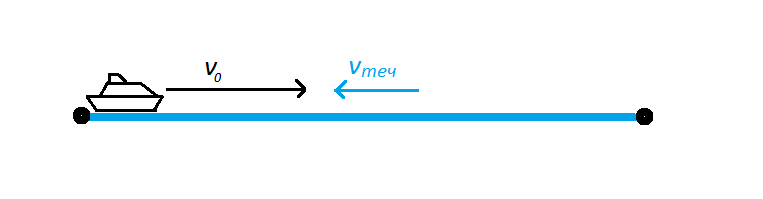
При движении против течения скорость течения отнимается от скорости плывущего тела: v = v0 – vтеч.
Задачи на движение из ЕГЭ по математике (профильный уровень)
Задача 1.
Из одной точки круговой трассы, длина которой равна 44 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 112 км/ч, и через 48 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.
Решение: Пусть скорость второго автомобиля равна v км/ч. За 4/5 часа первый автомобиль прошел на 44 км больше, чем второй, отсюда имеем:
112 ∙ = v ∙
= v ∙
+ 44 ⇔ 4 ∙ v = 112 ∙ 4 – 44 ∙ 5 ⇔ v = 57.
Следовательно, скорость второго автомобиля была равна 57 км/ч.
Ответ: 57 км/ч.
Задача 2.
Из пункта A круговой трассы выехал велосипедист, а через 10 минут следом за ним отправился мотоциклист. Через 2 минуты после отправления он догнал велосипедиста в первый раз, а еще через 3 минуты после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна 5 км. Ответ дайте в км/ч.
Решение:
До первой встречи велосипедист провел на трассе 1/5 часа, а мотоциклист 1/30 часа. Пусть скорость мотоциклиста равна v км/ч, тогда скорость велосипедиста равна
Тогда если скорость велосипедиста – это 1 единица отношения, то скорость мотоциклиста – это 6 единиц отношения.
Так как они едут в одном направлении, их общая скорость 5 единиц отношения.
∙5 ед.отн. = 5
1 ед.отн. = 20
6 ед.отн. = 120
Таким образом, скорость мотоциклиста была равна 120 км/ч.
Ответ: 120 км/ч.
Задача 3
Часы со стрелками показывают 3 часа ровно. Через сколько минут минутная стрелка в девятый раз поравняется с часовой?
Решение: Скорость движения минутной стрелки 12 делений/час (под одним делением здесь подразумевается расстояние между соседними цифрами на циферблате часов), а часовой ― 1 деление/час. До девятой встречи минутной и часовой стрелок минутная должна сначала 8 раз «обогнать» часовую, то есть пройти 8 кругов по 12 делений. Пусть после этого до четвертой встречи часовая стрелка пройдет L делений. Тогда общий путь минутной стрелки складывается из найденных 96 делений, ещё 3 изначально разделяющих их делений (поскольку часы показывают 3 часа) и последних L делений. Приравняем время движения для часовой и минутной стрелок:
, отсюда
, отсюда
и
.
Ответ: через 9 минут.
Задача 4
Из одной точки круговой трассы, длина которой равна 14 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 80 км/ч, и через 40 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.
Решение:
Данную задачу можно интерпретировать (представить её, как задачу на линейное движение): Два автомобиля одновременно начинают движение в одном направлении. Скорость первого равна 80 км/ч. Через 40 минут он опережает второго на 14 км (т. к. сказано, что на один круг). Найти скорость второго. Очень важно в заданиях на движение представить сам процесс этого движения.
Сравнение так же производим по расстоянию.
За x принимаем искомую величину ― скорость второго. Время движения 40 минут (2/3 часа) для обоих. Заполним графу «расстояние»:
| v | t | S | |
| 1 | 80 | 2/3 | |
| 2 | x | 2/3 |
Расстояние, пройденное первым, больше расстояния, который прошёл второй на 14 км.
80 ∙ больше, чем x ∙
больше, чем x ∙
на 14.
80 ∙ = x ∙
= x ∙
+ 14;
–
–
= x ∙
;
160 – 42 = х ∙ 2;
х = 59.
Скорость второго автомобиля 59 (км/ч).
Ответ: 59 км/ч.
Задача 5
Из пункта A в пункт B, расстояние между которыми 75 км, одновременно выехали автомобилист и велосипедист. Известно, что за час автомобилист проезжает на 40 км больше, чем велосипедист. Определите скорость велосипедиста, если известно, что он прибыл в пункт B на 6 часов позже автомобилиста. Ответ дайте в км/ч.
Решение:
Пусть v км/ч – скорость велосипедиста, тогда скорость автомобилиста равна v + 40 км/ч. Велосипедист был в пути на 6 часов больше, отсюда имеем:
Таким образом, скорость велосипедиста была равна 10 км/ч.
Ответ: 10 км/ч.
На чтение 10 мин. Просмотров 4.4k.
Вычислить скорость, время и расстояние часто бывает необходимо в повседневной жизни, когда мы рассчитываем время на дорогу. Все эти величины (время, расстояние и скорость) связаны между собой математической формулой и зная две из них всегда можно найти третью. Мы с вами рассмотрим, что понимается под этими величинами, как их найти, решим несколько задач.
Скорость, время и расстояние — это ключевые параметры при решении задач на движение. Эти задачи есть и в ЕГЭ и в ОГЭ по математике. Сегодня мы подробнее остановимся на этих величинах.
Расстояние
Расстояние — это физическая величина, означающая длину между двумя объектами. Расстояние обозначается буквой S и измеряется в единицах длины: метрах. Метр — это международно-принятая единица измерения длины. Однако встречаются и другие единицы длины — километр, сантиметр, миллиметр. В этом случае целесообразно перевести единицы длины в международную систему единиц (СИ).
Например: расстояние от Земли до Солнца равно 149 597 870 700 метров.
Расстояние связано со скоростью и временем:
S=v cdot t
Вот тут таблица длин и их перевода в международную систему единиц — то есть в метры.
| Единицы длины | СИ |
| 1 сантиметр | 0,01 м |
| 1 километр | 1000 м |
| 1 дециметр | 0,1 м |
| 1 миллиметр | 0,001 м |
| 1 микрометр | 1·10-6 м |
| 1 миля | 1609,34 м |
| 1 фут | 0,3048 м |
| 1 ярд | 0,9144 м |
| 1 дюйм | 0,0254 м |
| 1 морская миля | 1852 м |
Время
Время — это физическая величина, которая обозначает непрерывное и необратимое (возможно) движение от прошлого к будущему через настоящее. Это фундаментальная физическая величина, единица измерения времени — секунда. Однако, в задачах могут использоваться и другие единицы времени — часы, минуты, дни.
Время можно найти по формуле:
t=frac{S}{v}
Ученые о времени
По словам греческого философа Парменида (ок. 450 г. до н.э.), время и движение были иллюзиями. Его ученик Зенон Элейский разработал два знаменитых парадокса: «Ахиллес и черепаха» и «Парадокс летящей стрелы», чтобы доказать его утверждения. Платон, живший на пару поколений позже, считал, что время создано вместе со вселенной и существует независимо. Он рассматривал время как пустой контейнер, который можно заполнить движущимися вещами и событиями. Его ученик Аристотель считал, что время не существует независимо от событий, но время есть изменение и движение.
Аристотель пришел к выводу, что время не состоит из последовательных неделимых моментов «сейчас», как пытался сказать Зенон с помощью своего парадокса стрелы. Согласно Аристотелю, не существует серии моментов «сейчас», потому что такие моменты не могли бы исчезнуть в течение их собственной длительности или в следующий момент «сейчас». Исааку Ньютону (1642–1726) время понадобилось в качестве переменной в его уравнениях, и он начал думать о времени с научной точки зрения. Ньютон поддерживал идею Платона о независимости времени. Он разделил время на абсолютное (математическое) время и относительное (обычное) время.
Абсолютное время, или продолжительность, является реальным и математическим, и оно течет неуклонно, независимо от чего-либо внешнего. Относительное время кажущееся и является внешней мерой длительности, которая может быть обнаружена органами чувств с помощью движения, которое может быть точным или неточным.
Готфрид Лейбниц (1646–1716) был согласен с Аристотелем и думал, что без событий и перемен не было бы времени. Физик- теоретик Ли Смолин писал в 2010 году, что исследования квантовой гравитации подтверждают, что четырехмерное пространство-время имеет смысл только в том случае, если время реально, фундаментально и даже является единственным аспектом реальности, который мы непосредственно ощущаем.
Скорость
Скорость обозначается буквой — это физическая величина, которая обозначает какое расстояние проходит объект в единицу времени. Единица измерения скорости — м/с. Однако, встречаются также и км/ч и см/с (эти измерения не входят в международную систему единиц измерения). Скорость показывает как быстро изменяется расстояние во времени.
Например, выражение 9 м/с означает, что тело за 1 секунду проходит 9 метров. То есть за 1 секунду 9 метров, за 2 секунду еще 9 метров, итого за 2 секунду — 18 метров. В курсе школьной математики мы считаем, что скорость равномерная во времени. То есть тело за равные промежутки времени проходит равные расстояния. То есть 9 м/с означает 9 метров в любую из секунд движения тела. Однако, в реальности движение бывает равномерное и неравномерное. Мы не рассматриваем неравномерное движение в курсе математики (1-6 класс), однако в курсе алгебры элементы кинематики с неравномерным движением рассматриваются.
Еще примеры: скорость 100 км/ч — это прохождение расстояния в 100 километров за 1 час.
Формула скорости
Скорость можно найти через расстояние и время по формуле:
v=frac{S}{t}
Средняя скорость
Если движение тела можно разбить на несколько участков и в пределах каждого участка скорость тела не меняется, то целесообразно говорить о средней скорости.
Формула средней скорости:
v=frac{S_{весь ; путь}}{t_{всё ; время}}=frac{S_1+S_2+…+ S_n}{t_1+t_2+…+ t_n}
То есть средняя скорость это отношение всего пути, ко всему времени.
Скорости сближения и удаления
Понятие скорости ученики изучают еще в 4 классе, а далее это понятие расширяется и уточняется. Вводятся такие понятия как скорость сближения и скорость удаления. Не все педагоги используют эти понятия в своей работе, поскольку эти понятия можно использовать только при решении небольшого класса задач на движение и они ограничивают решение задач и другими условиями (например, если тела удаляются или сближаются не по одной прямой, а по перпендикулярным прямым). И все же, давайте мы уточним, о чем вообще идет речь.
Скорость удаления
Если два тела удаляются друг от друга, двигаясь по одной прямой, то в таких случаях говорят о скорости удаления. То есть скорость удаления характеризует расстояние, которое увеличивается по мере удаления двух тел в единицу времени.
Допустим есть два пешехода, которые удаляются друг от друга, первый пешеход удаляется со скоростью 3 км/ч, а второй пешеход со скоростью 4 км/ч. Тогда скорость удаления будет:
3+4=7 км/ч.
Действительно, расстояние, пройденное первым пешеходом за один час будет 3 километра, а расстояние, пройденное вторым пешеходом за то же время будет 4 километра. Тогда при удалении пешеходов друг от друга расстояние между ними увеличивается на 7 километров в каждый час или наши пешеходы удаляются со скоростью 7 км/ч. Мы должны сложить скорости объектов.
Формула скорости удаления:
v_{удаления}=v_1+v_2
где
— скорость одного тела,
— скорость другого тела.
Напомним, что это понятие можно использовать только если тела двигаются в разных направлениях, располагаемых на одной прямой.
Скорость сближения двух тел
Аналогично, рассмотрим ситуацию, если два пешехода двигаются навстречу друг к другу. Один пешеход за один час проходит расстояние 2 км, а второй пешеход за то же время проходит 5 км.
Значит, расстояние между ними будем уменьшаться со скоростью 5+2 = 7 км/ч.
Формула скорости сближения:
v_{сближения}=v_1+v_2
где
— скорость одного тела,
— скорость другого тела.
Если один пешеход догоняет другого. То скорость сближения при движении в одном направлении можно определить, если вычесть из большей скорости меньшую.
То есть, если у нас второго пешехода (=3км/ч) догоняет первый пешеход (
=5 км/ч), то скорость их сближения будет 2 км/ч:
Формула скорости сближения при движении вдогонку:
v_{сближения}=v_1-v_2
где
— скорость одного тела,
— скорость другого тела. При этом
Таблица «скорость, время, расстояние» при решении задач на движение
При решении задач на движение очень удобно пользоваться такой таблицей, в которой три столбца с данными по скорости, времени движения тел и расстоянию, которое они проходят. Эта таблица, кстати помогает легко запомнить формулы скорости, времени и расстояния, если представить что первый столбец — это первый множитель, второй столбец — второй множитель, а третий столбец — произведение.
| Скорость, v, м/с | Время, t, с | Расстояние, S, м |
Простой пример, найти скорость велосипедиста, если за 5 часов он прошел 45 километров.
Составляем таблицу и записываем в нее данные:
| Скорость, v, км/ч | Время, t, ч | Расстояние, S, км |
| ? | 5 | 45 |
Теперь видно, что неизвестна скорость в первом столбце, значит, неизвестен первый множитель. Чтобы определить неизвестный множитель надо произведение разделить на известный множитель: = 45/5 = 9 км/ч.
Важно! В задачах все единицы измерения должны быть приведены либо к международной системе единиц (метр, секунда, м/с) либо к одним единицам измерения (то есть если в задаче есть и м/с и км/ч можно привести всё либо к м/с (тогда и время в секундах и расстояние в метрах), либо к км/ч (тогда и время в часах будет и расстояние в километрах))
Рассмотрим теперь некоторые примеры решения задач
Примеры задач на движение
Задача 1
Школьник идет домой со скоростью 2 км/ч. Расстояние от школы до дома 1 км. За какое время школьник дойдет до дома?
Решение:
Найдем время по формуле: displaystyle t=frac{S}{v}=frac{1}{2}ч.
Школьник дойдет до дома за полчаса.
Ответ: 0,5 ч.
Задача 2
Автомобилист и велосипедист выехали в город из деревни одновременно. Скорость автомобилиста 50 км/ч. Расстояние до города 100 км. Какова скорость велосипедиста, если известно, что он прибыл в город на 8 часов позже автомобилиста?
Решение: Составим таблицу
| Скорость, v, км/ч | Время, t, ч | Расстояние, S, км | |
| Автомобилист | 50 | 100/50 | 100 |
| Велосипедист | x | 100/x | 100 |
Пусть скорость велосипедиста x. В таблице мы сразу смогли написать соотношения для времени движения. По условию задачи дано, что велосипедист прибыл в город на 8 часов позже автомобилиста. Запишем это:
displaystyle frac{100}{x}-frac{100}{50}=8
Мы отнимаем от времени, которое потратил велосипедист (он же потратил больше времени) время, которое потратил автомобилист и получаем 8 часов.
Решим полученное уравнение.
displaystyle frac{100}{x}-2=8
displaystyle frac{100}{x}=10
x=10
Ответ: 10 км/ч
Задача 3
Стрела пролетает 180 метров за 0,05 минуты. Найдите ее скорость.
Решение: прежде чем решать задачу, переведем все единицы в одну систему единиц. Минуты переведем в секунды.
В одной минуте 60 секунд. Значит, чтобы узнать сколько секунд в 0,05 минутах, умножим 0,05 на 60, получим:
0,05 cdot 60=3 c.
Тогда displaystyle v= frac{180}{3}=60 м/с.
Ответ: 60 м/с
Задача 4
Турист прошел лесной участок длиной 10 км со скоростью 5 км/ч, а затем шел по полю 20 км, со скоростью 4 км/ч. Какова средняя скорость туриста?
Решение:
Определим весь путь который прошел турист:
displaystyle S_{весь ; путь}=S_1+S_2=10+20=30 км.
Для прохождения лесного участка турист потратил: displaystyle t_1= frac{S_1}{v_1}=frac{10}{5}=2ч, а на второй участок времени ушло: displaystyle t_2= frac{S_2}{v_2}=frac{20}{4}=5ч
Все время: displaystyle t_{всё ; время}=t_1+t_2=2+5=7ч
Тогда найдем среднюю скорость:
displaystyle v_{ср}= frac{S_{весь ; путь}}{t_{всё ; время}}=frac{30}{7}=4 frac{2}{7} км/ч.
Ответ: displaystyle v_{ср}=4 frac{2}{7}
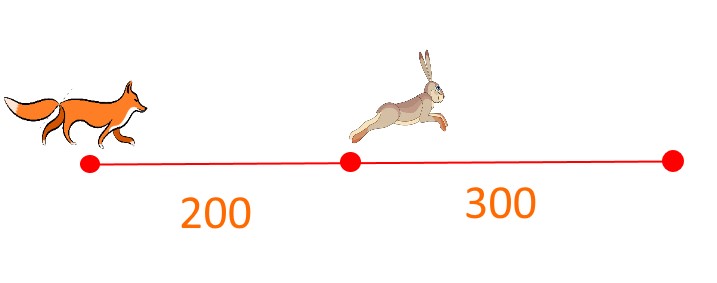
Задача 5
Лиса гонится за зайцем. Скорость лисы 20 м/с, а скорость зайца 15 м/с. Догонит ли лиса зайца, если заяц находится на расстоянии 300 метров от безопасного места, а лиса находится на расстоянии 200 метров от зайца?
Решение:
Заяц добежит до норы за displaystyle t= frac{300}{15}=20 секунд.
Лиса же за 20 секунд пробежит расстояние displaystyle S= 20 cdot 20=400 метров.
Лиса не догонит зайца.
Действительно, скорость сближения лисы и зайца:
displaystyle v=v_{лисы}-v_{зайца}=20-15=5 м/с
То есть, чтобы преодолеть расстояние 200 метров, которое изначально существует между лисой и зайцем, лисе понадобиться displaystyle t=frac{200}{5}=40 с
Заяц же уже 20 секунд будет в безопасном месте.
Ответ: лиса зайца не догонит.
Содержание материала
- Задачи на скорость сближения
- Видео
- Скорость сближения
- Задачи на течение реки
- Скорость
- Задача на движение объектов в одном направлении
- Движение в противоположных направлениях
- Относительное движение
- Примеры решения задач
Задачи на скорость сближения
Скорость сближения — это скорость, с которой объекты сближаются друг с другом.
Чтобы найти скорость сближения двух объектов, которые движутся в одном направлении, надо из большей скорости вычесть меньшую.
Задача 1. Из города выехал автомобиль со скоростью 40 км/ч. Через 4 часа вслед за ним выехал второй автомобиль со скоростью 60 км/ч. Через сколько часов второй автомобиль догонит первый?
Решение: Так как на момент выезда второго автомобиля из города первый уже был в пути 4 часа, то за это время он успел удалиться от города на:
40 · 4 = 160 (км).
Второй автомобиль движется быстрее первого, значит каждый час расстояние между автомобилями будет сокращаться на разность их скоростей:
60 — 40 = 20 (км/ч) — это скорость сближения автомобилей.
Разделив расстояние между автомобилями на скорость их сближения, можно узнать, через сколько часов они встретятся:
160 : 20 = 8 (ч).
Решение задачи по действиям можно записать так:
1) 40 · 4 = 160 (км) — расстояние между автомобилями,
2) 60 — 40 = 20 (км/ч) — скорость сближения автомобилей,
3) 160 : 20 = 8 (ч).
Ответ: Второй автомобиль догонит первый через 8 часов.
Задача 2. Из двух посёлков между которыми 5 км, одновременно в одном направлении вышли два пешехода. Скорость пешехода, идущего впереди, 4 км/ч, а скорость пешехода, идущего позади 5 км/ч. Через сколько часов после выхода второй пешеход догонит первого?
Решение: Так как второй пешеход движется быстрее первого, то каждый час расстояние между ними будет сокращаться. Значит можно определить скорость сближения пешеходов:
5 — 4 = 1 (км/ч).
Оба пешехода вышли одновременно, значит расстояние между ними равно расстоянию между посёлками (5 км). Разделив расстояние между пешеходами на скорость их сближения, узнаем через сколько второй пешеход догонит первого:
5 : 1 = 5 (ч).
Решение задачи по действиям можно записать так:
1) 5 — 4 = 1 (км/ч) — это скорость сближения пешеходов,
2) 5 : 1 = 5 (ч).
Ответ: Через 5 часов второй пешеход догонит первого.
Видео
Скорость сближения
Скорость сближения — это расстояние, пройденное двумя объектами навстречу друг другу за единицу времени.
Например, если из двух пунктов навстречу друг другу отправятся два пешехода, причем скорость первого будет 100 м/м, а второго — 105 м/м, то скорость сближения будет составлять 100 + 105, то есть 205 м/м. Это значит, что каждую минуту расстояние между пешеходами будет уменьшáться на 205 метров
Чтобы найти скорость сближения, нужно сложить скорости объектов.
Предположим, что пешеходы встретились через три минуты после начала движения. Зная, что они встретились через три минуты, мы можем узнать расстояние между двумя пунктами.
Каждую минуту пешеходы преодолевали расстояние равное двухсот пяти метрам. Через 3 минуты они встретились. Значит умножив скорость сближения на время движения, можно определить расстояние между двумя пунктами:
205 × 3 = 615 метров
Можно и по другому определить расстояние между пунктами. Для этого следует найти расстояние, которое прошел каждый пешеход до встречи.
Так, первый пешеход шел со скоростью 100 метров в минуту. Встреча состоялась через три минуты, значит за 3 минуты он прошел 100 × 3 метров
100 × 3 = 300 метров
А второй пешеход шел со скоростью 105 метров в минуту. За три минуты он прошел 105 × 3 метров
105 × 3 = 315 метров
Теперь можно сложить полученные результаты и таким образом определить расстояние между двумя пунктами:
300 м + 315 м = 615 м
Задача 1. Из двух населенных пунктов навстречу друг другу выехали одновременно два велосипедиста. Скорость первого велосипедиста 10 км/ч, а скорость второго — 12 км/ч. Через 2 часа они встретились. Определите расстояние между населенными пунктами
Решение
Найдем скорость сближения велосипедистов
10 км/ч + 12 км/ч = 22 км/ч
Определим расстояние между населенными пунктами. Для этого скорость сближения умножим на время движения
22 × 2 = 44 км
Решим эту задачу вторым способом. Для этого найдем расстояния, пройденные велосипедистами и сложим полученные результаты.
Найдем расстояние, пройденное первым велосипедистом:
10 × 2 = 20 км
Найдем расстояние, пройденное вторым велосипедистом:
12 × 2 = 24 км
Сложим полученные расстояния:
20 км + 24 км = 44 км
Ответ: расстояние между населенными пунктами составляет 44 км.
Задача 2. Из двух населенных пунктов, расстояние между которыми 60 км, навстречу друг другу выехали одновременно два велосипедиста. Скорость первого велосипедиста 14 км/ч, а скорость второго — 16 км/ч. Через сколько часов они встретились?
Решение
Найдем скорость сближения велосипедистов:
14 км/ч + 16 км/ч = 30 км/ч
За один час расстояние между велосипедистами уменьшается на 30 километров. Чтобы определить через сколько часов они встретятся, нужно расстояние между населенными пунктами разделить на скорость сближения:
60 : 30 = 2 часа
Значит велосипедисты встретились через два часа
Ответ: велосипедисты встретились через 2 часа.
Задача 3. Из двух населенных пунктов, расстояние между которыми 56 км, навстречу друг другу выехали одновременно два велосипедиста. Через два часа они встретились. Первый велосипедист ехал со скоростью 12 км/ч. Определить скорость второго велосипедиста.
Решение
Определим расстояние пройденное первым велосипедистом. Как и второй велосипедист в пути он провел 2 часа. Умножив скорость первого велосипедиста на 2 часа, мы сможем узнать сколько километров он прошел до встречи
12 × 2 = 24 км
За два часа первый велосипедист прошел 24 км. За один час он прошел 24:2, то есть 12 км. Изобразим это графически
Вычтем из общего расстояния (56 км) расстояние, пройденное первым велосипедистом (24 км). Так мы определим сколько километров прошел второй велосипедист:
56 км − 24 км = 32 км
Второй велосипедист, как и первый провел в пути 2 часа. Если мы разделим пройденное им расстояние на 2 часа, то узнаем с какой скоростью он двигался:
32 : 2 = 16 км/ч
Значит скорость второго велосипедиста составляет 16 км/ч.
Ответ: скорость второго велосипедиста составляет 16 км/ч.
Задачи на течение реки
Теперь, когда ты отлично решаешь задачи «на суше», перейдем в воду, и рассмотрим страаашные задачи, связанные с течением.
Особенность этих задач в том, что к скорости, с которой движется тело по воде добавляется (или вычитается) скорость течения реки.
Давай разберемся.
Скорость
Двигаться со скоростью черепахи — значит медленно, а со скоростью света — значит очень быстро. Сейчас узнаем, как пишется скорость в математике и как ее найти по формуле.
Скорость определяет путь, который преодолеет объект за единицу времени. Скорость обозначается латинской буквой v.
Проще говоря, скоростью называют расстояние, пройденное телом за единицу времени.
Впервые формулу скорости проходят на математике в 5 классе. Сейчас мы ее сформулируем и покажем, как ее использовать.
Формула скорости
Чтобы найти скорость, нужно разделить путь на время:
v = s : t
Показатели скорости чаще всего выражаются в м/сек или км/час.
Скорость сближения — это расстояние, на которое сблизились два объекта за единицу времени. Чтобы найти скорость сближения двух объектов, которые движутся навстречу друг другу, надо сложить скорости этих объектов.
Скорость удаления — расстояние, на которое отдалились друг от друга два объекта за единицу времени.
Чтобы найти скорость удаления объектов, которые движутся в противоположных направлениях, нужно сложить скорости этих объектов.
Чтобы найти скорость удаления при движении с отставанием или скорость сближения при движении вдогонку, нужно из большей скорости вычесть меньшую.
Онлайн-курсы по математике для детей — отличный способ разобраться в сложных темах под руководством внимательного преподавателя.
Задача на движение объектов в одном направлении
В предыдущей теме мы рассматривали задачи в которых объекты (люди, машины, лодки) двигались либо навстречу другу другу либо в противоположных направлениях. При этом мы находили различные расстояния, которые изменялись между объектами в течении определенного времени. Эти расстояния были либо скоростями сближения либо скоростями удаления.
В первом случае мы находили скорость сближения — в ситуации, когда два объекта двигались навстречу друг другу. За единицу времени расстояние между объектами уменьшалось на определенное расстояние
Движение в противоположных направлениях
Если два объекта движутся в противоположных направлениях, то они удаляются. Чтобы найти скорость удаления, надо сложить скорости этих объектов:

Скорость удаления больше скорости любого из них.
Задача 1
Из поселка вышли одновременно в противоположных направлениях два пешехода. Средняя скорость одного пешехода – 5 км/ч, другого – 4 км/ч. Через сколько часов расстояние между ними будет 27 км ?
Решение:
Чтобы найти время движения пешеходов, нужно знать расстояние и скорость пешеходов. Мы знаем, что за каждый час один пешеход удаляется от поселка на 5 км, а другой пешеход удаляется от поселка на 4 км. Можем найти их скорость удаления.
1. (км/ч)
Мы знаем скорость удаления и знаем все расстояние – 27 км. Можем найти время, через которое пешеходы удалятся друг от друга на 27 км, для этого нужно расстояние разделить на скорость.
2. (ч)
Ответ: Через три часа расстояние между переходами будет 27 км.
Задача 2
Из поселка вышли одновременно в противоположных направлениях два пешехода. Через 3 часа расстояние между ними было 27 км. Первый пешеход шел со скоростью 5 км/ч. С какой скоростью шел второй пешеход ?

Решение:
Чтобы узнать скорость второго пешехода, надо знать расстояние, которое он прошел, и его время в пути. Чтобы узнать, какое расстояние прошел второй пешеход, надо знать, какое расстояние прошел первый пешеход и общее расстояние. Общее расстояние мы знаем. Чтобы найти расстояние, которое прошел первый пешеход, надо знать его скорость и его время в пути. Средняя скорость движения первого пешехода – 5 км/ч, его время в пути – 3 часа. Если среднюю скорость умножить на время в пути, получим расстояние, которое прошел пешеход:
1. (км)
Мы знаем общее расстояние и знаем расстояние, которое прошел первый пешеход. Можем теперь узнать, какое расстояние прошел второй пешеход.
2. (км)
Теперь мы знаем расстояние, которое прошел второй пешеход, и время, проведенное им в пути. Можем найти его скорость.
3. (км/ч)
Ответ: Скорость второго пешехода – 4 км/ч.
Задача 3
Товарный и пассажирский поезда движутся в противоположных направлениях. Скорость товарного 45 км/ч, скорость пассажирского — 70 км/ч. Сейчас между ними 20 км. Какое расстояние будет между ними через 2 часа ?
Решение:
1) 70+45=115 (км/ч) скорость удаления поездов
2) 115∙2=230 (км) пройдут поезда вместе за 2 часа
3) 230+20=250 (км) такое расстояние между поездами будет через 2 часа.
Ответ: Через 2 часа расстояние между поездами составит 250 км.
Задача 4
Из одного пункта одновременно в противоположных направлениях выехали два мотоциклиста. Скорость одного из них — 60 км/ч, скорость другого — 40 км/ч. Через какое время расстояние между ними станет равным 300 км?

Решение:
1) 60+40=100 (км/ч) скорость удаления мотоциклистов
2) 300:100=3 (ч) через такое время расстояние между ними будет 300 км.
Ответ: Расстояние между мотоциклистами станет 300 км через 3 часа.
Относительное движение
Если какие-то тела движутся друг относительно друга, часто бывает полезно посчитать их относительную скорость. Она равна:
- сумме скоростей, если тела движутся навстречу друг другу;
- разности скоростей, если тела движутся в одном направлении.
Примеры решения задач
Два туриста на велосипедах отправились в одно и то же время из разных пунктов в точку назначения. Время в пути первого велосипедиста составило 2 ч. Для того чтобы прибыть в точку назначения одновременно с первым туристом, второму велосипедисту потребовалось проехать каждый последующий км пути на 1 мин быстрее по сравнению с предыдущим. Расстояние, которое преодолел второй турист на велосипеде больше на 6 км, чем путь первого туриста. Требуется определить скорости первого и второго велосипедистов.
Решение
Предположим, что первый турист на велосипеде преодолевал каждый км пути за х мин. Тогда его скорость равна 60/х км/ч. В таком случае, скорость второго велосипедиста составит 60/(х-1) км/ч. Составим уравнение:
60/(х–1)*2–(60/х)*2=6
х1=5
х2=–4
Второй корень является посторонним.
Ответ: скорость первого велосипедиста 12 км/ч, второй велосипедист двигался со скоростью 15 км/ч.
Теги
Решение текстовых задач на движение подчиняется четкому алгоритму, который состоит из нескольких этапов:
- Анализ данных.
- Составление таблицы.
- Составление уравнения.
- Решение уравнения.
Остановимся подробно на каждом пункте:
1. Первое, с чего нужно начать — медленно и вдумчиво прочитать условие задачи, то есть проанализировать данные.
Чтобы наглядно представить задачу, необходимо сделать рисунок и отобразить на нем все известные по условию задачи величины.
2. Второй шаг — составить таблицу по условию задачи, внести в таблицу известные величины и ввести неизвестные.
Таблица состоит из трех столбцов S, v и t (путь, скорость и время) и нескольких строк. При заполнении каждой строки сначала выбираем и заполняем тот столбец, информация о котором дана в задаче. Еще один столбец записываем в роли неизвестного (чаще всего, это то, что требуется найти в задаче). В третью, оставшуюся колонку вписываем связь характеристик из двух уже заполненных столбцов по формуле:
S = v · t.
В таблице получается столько строчек, сколько каждый из объектов задачи действовал (то есть, перемещался) или мог бы действовать.
3. Следующий шаг — при помощи сделанного рисунка и заполненной таблицы составить уравнение или систему уравнений.
По окончании заполнения таблицы оказывается, что есть часть информации, которая не вошла в таблицу. Эта информация характеризует те значения величин в колонках, которые вычисляются в третью очередь, то есть по формуле. На основании этой информации и данных из третьей колонки составляем уравнение.
4. Решить полученное уравнение и прийти к ответу.
Когда уравнение составлено, последний шаг — это решить его, и, в конце концов, получить ответ.
- Будьте внимательны, если за неизвестное вы приняли не то, что требуется найти в задаче. В этом случае следует выразить то, что нужно найти через полученное решение уравнения.
- Если, решив уравнение, вы получили несколько ответов, то следует отобрать только имеющие смысл решения. Помните, что путь, скорость и время не могут быть отрицательными.
Пример:
Два велосипедиста одновременно отправляются в 60-километровый пробег. Первый едет со скоростью на 10 км/ч большей, чем второй, и прибывает к финишу на 3 часа раньше второго. Найдите скорость велосипедиста, пришедшего к финишу вторым.
Решение:
В задаче требуется найти скорость второго, более медленного, велосипедиста. Примем его скорость за x. Заполним таблицу:
| v, км/ч | t, ч | S, км | |
|---|---|---|---|
|
Первый велосипедист |
x + 10 |
$ frac{60}{x+10} $ |
60 |
|
Второй велосипедист |
x |
$ frac{60}{x} $ |
60 |
В условии задачи сказано, что первый велосипедист прибыл к финишу на 3 часа раньше второго. На основании этого составим уравнение:
$ frac{60}{x+10}+3=frac{60}{x} $
$ frac{60+3x+30}{x+10}=frac{60}{x} $
3x2 + 90x = 600 + 60x;
x2 + 10x – 200 = 0.
Получаем два корня, x1 = 10 и x2 = –20. Второй корень не подходит, так как скорость не может быть отрицательной.
Ответ: 10 км/ч.
Виды задач на движение:
1. Движение навстречу друг другу, движениев противоположных направлениях:
Если два объекта движутся навстречу друг другу, то они сближаются:
При объекты удаляются:
В обоих случаях объекты как бы «помогают» друг другу преодолеть общее для них расстояние, «действуют сообща». Поэтому чтобы найти их совместную скорость (это и будет скорость сближения или удаления), нужно складывать скорости объектов:
v = v1 + v2.
2. Движение друг за другом (вдогонку):
При движении в одном направлении объекты также могут как сближаться, так и удаляться. В этом случае они как бы «соревнуются» в преодолении общего расстояния, «действуют друг против друга». Поэтому их совместная скорость будет равна разности скоростей.
Если скорость идущего впереди объекта меньше скорости объекта, следующего за ним, то они сближаются. Чтобы найти скорость сближения, надо из большей скорости вычесть меньшую:
$ {upsilon_{c}=upsilon_{1}-upsilon_{2};\ upsilon_{1}>upsilon_{2}.} $
Если объект, идущий впереди, движется с большей скоростью, чем идущий следом за ним, то они удаляются. Чтобы найти скорость удаления, надо из большей скорости вычесть меньшую:
$ {upsilon_{y}=upsilon_{2}-upsilon_{1};\ upsilon_{2}>upsilon_{1}.} $
Таким образом:
- При движении навстречу друг другу и движении в противоположных направлениях скорости складываем.
- При движении в одном направлении скорости вычитаем.
3. Движение по кругу:
При движении по кругу объекты могут:
- сближаться, если скорость догоняющего больше скорости догоняемого. Скорость сближения будет равна $ upsilon_{c}=upsilon_{1}-upsilon_{2}; $
- отдаляться, если скорость догоняющего меньше скорости догоняемого. Скорость удаления будет равна $ upsilon_{y}=upsilon_{2}-upsilon_{1}. $
При этом пройденные расстояния измеряются длиной круговой трассы, равной S.
- Если два объекта начинают движение по кругу из одной и той же точки, то в момент первой встречи более быстрый объект пройдет расстояние на один круг больше.
- Если два объекта начинают движение по кругу из разных точек, расстояние между которыми равно S0, то в момент первой встречи догоняющий объект пройдет на S0км большее расстояние, чем догоняемый.
- Если через определенное время t первый объект опережает второй на m кругов, то разница пройденных объектами расстояний будет равна m · S:
S1 – S2 = m · S.
4. Движение мимо объекта:
В задачах на движение мимо объекта обязательно присутствуют протяженные тела — поезда, туннели, корабли и т. п. Зачастую движущимся объектом является поезд.
- Если поезд длиной L движется мимо точечного объекта (столба, светофора, человека), то он проходит расстояние, равное его длине L:
S = L = v0 · t.
При этом, если точечный объект (пешеход, велосипедист) тоже движется, то совместная скорость равна сумме скоростей, если поезд и объект двигаются в разных направлениях (как в пункте 1), и равна разности скоростей, если они двигаются в одном направлении (как в пункте 2).
- Если поезд длиной L1 движется мимо протяженного объекта (туннеля, лесополосы) длиной L2, то он проходит расстояние, равное сумме длин самого поезда и протяженного объекта:
S = L1 + L2 = v0 · t.
При этом, если протяженный объект (например, другой поезд) тоже движется, то совместная скорость равна сумме скоростей, если оба объекта двигаются в разных направлениях, и равна разности скоростей (из большей вычитается меньшая), если они двигаются в одном направлении.
5. Движение по воде:
В задачах на движение помимо собственной скорости плывущего тела нужно учитывать скорость течения.
- При движении по течению скорость течения прибавляется к скорости плывущего тела: v = v0 + vтеч.
- При движении против течения скорость течения отнимается от скорости плывущего тела: v = v0 – vтеч.
- Скорость плота считается равной скорости течения.