На сегодняшний день ЕГЭ по математике является обязательным. Наверняка, не всех радует этот факт. Но есть хорошая новость: сдавать ЕГЭ по математике вы можете либо на базовом, либо на профильном уровне. Выбор за вами! И чем раньше вы определитесь, тем больше у вас будет времени и возможностей для подготовки.
Базовый и профильный уровень ЕГЭ
Базовый уровень ЕГЭ по математике
На базовом уровне вполне достаточно знаний из обычной школьной программы. В бланке пишутся только ответы в виде цифр, развернутых решений здесь не требуется. В тесте 20 заданий примерно одного уровня сложности, которые нужно решить за 3 часа. Они включают в себя:
- 10 задач по алгебре;
- 4 задачи по геометрии;
- 1 задача на функции;
- 3 задачи на уравнения и неравенства;
- 1 задача на начала математического анализа;
- 1 задача из комбинаторики и теории вероятностей.
Чтобы получить оценку “удовлетворительно”, вам необходимо правильно решить 6 задач, что соответствует 27 баллам.
Рассмотрим несколько подобных задач.
Задание (задача из категории 6 “Простейшие текстовые задачи”):
В магазине вся мебель продается в разобранном виде. Покупатель может заказать сборку мебели на дому, стоимость которой составляет 15 % от стоимости купленной мебели. Шкаф стоит 3000 рублей. Во сколько рублей обойдётся покупка этого шкафа вместе со сборкой?
Решение:
Рассчитаем стоимость сборки шкафа: 300015100=450 рублей.
Теперь прибавим к стоимость шкафа стоимость сборки: 3000+450=3450 рублей.
Записываем в бланк ответ в виде цифр: 3450.
Теперь рассмотрим задачу по геометрии.
Задание (задача из категории 13 “Стереометрия”):
Даны два дара с радиусами 5 и 1. Во сколько раз площадь поверхности первого шара больше площади поверхности второго?
Решение:
Площади поверхности первого и второго шаров можно записать в виде: S1=4R12 и S2=4R22.
Поделим площадь поверхности первого шара S1 на площадь поверхности второго шара S2:
S1S2=4R124R22=R1R22=512=25
Записываем в бланк ответов: 25.
Задание (задача из категории 10 “Начала теории вероятностей”)
В офисе работают 20 человек. С помощью жребия они выбирают 4 человек, которые должны пойти на курсы повышения квалификации. Работник Петров хотел бы повысить квалификацию, но он подчиняется жребию. Какова вероятность того, что он попадет на эти курсы?
Решение:
Всего исходов n=20, из них благоприятных исходов m=4.
По классической формуле расчета вероятности получим: P=mn=420=0,2
Записываем ответ в бланк: 0,2.
Видно, что каждая из задач решается элементарно за пару минут. Главное – будьте предельно внимательны и не допустите ошибок в арифметике.
Однако помните, что сдав ЕГЭ по математике на базовом уровне, вы получите аттестат, но возможность поступления в нужный вам ВУЗ будет под вопросом.
Профильный уровень ЕГЭ по математике
Для профильного уровня характерно то, что задания имеют разную степень сложности:
- 8 заданий базового уровня;
- 9 заданий повышенного уровня;
- 2 задания высокого уровня.
Если в первых восьми заданиях достаточно простого ответа в виде цифры, то в заданиях повышенного и высокого уровня сложности требуется подробное описание хода решения задач. Проверяются такие задачи независимыми экспертами.
На решение всего теста у вас есть 2 часа 55 минут. Для оценки “удовлетворительно” нужно набрать 27 баллов.
Тематически задания включают в себя:
- 4 задачи по алгебре;
- 5 задач по геометрии;
- 2 задачи на функции;
- 5 задач на уравнения и неравенства;
- 2 задачи на начала математического анализа;
- 1 задача из комбинаторики и теории вероятностей.
Решим для примера задачу из профильного уровня.
Задание (задача из категории 17 “Финансовая математика”):
В марте ИП Иванов планирует взять кредит в банке на сумму 9 млн. Рублей на некоторый срок (целое число лет). Условия его возврата таковы:
– каждый январь долг возрастает на 20% по сравнению с концом предыдущего года;
– с января по июнь каждого года необходимо выплатить часть долга;
– в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
Чему будет равна общая сумма выплат после полного погашения кредита, если наибольший годовой платеж составит 3,6 млн. Рублей?
Решение:
Наибольшим будет первый платеж, поскольку он соответствует максимальной сумме долга.
Примем, что кредит размером S взят на n лет. Тогда первый платеж можно записать в виде:
9n+90.2=3.6(млн. руб.)
Решая уравнение, найдем n=5.
Если принять, что кредит берется под r% годовых, то выплата составит:
S+n+1200rS=9+5+1200209=14,4 млн. рублей.
Записываем ответ в бланке: 14,4.
Чувствуете отличие от базового уровня? В таких заданиях нужно не просто пользоваться готовыми формулами и производить несложные вычисления, а еще и уметь анализировать. Это достигается долгой и упорной работой.
Мало кому под силу набрать 100 баллов. Для этого нужно иметь определенный склад ума, уметь “чувствовать” математику.
Что делать, если вы не сдали ЕГЭ по математике
Если вы не сдали ЕГЭ по математике на профильном уровне, то у вас есть возможность пересдать предмет в резервные сроки. В этом случае вы можете изменить уровень на базовый.
Как готовиться к ЕГЭ?
Как бы странно это ни звучало, правильнее всего начинать готовиться к ЕГЭ практически с 5 класса! Ведь математика не тот предмет, который можно выучить за пару месяцев. Знания наслаиваются из темы в тему. И порой один небольшой пробел влечет за собой в будущем много сложностей. Не ленитесь прорабатывать сложные моменты.
Подготовка должна быть комплексной. Это значит, что просто решать однотипные задачи из демо-версий или учебников недостаточно. Нужно и теорию повторять, и решать задачи по тематическим блокам из разных тем. Это позволит улучшить аналитическое мышление, и вы сможете решать не только задачи по шаблону.
Если знаний, полученных в школе, вам не хватает, обращайтесь к репетиторам. Если нет возможности нанять репетитора, ищите проверенные сайты, каналы на ютубе. Помните: кто ищет, тот всегда найдет!
Полезные советы перед сдачей ЕГЭ по математике:
- Не торопитесь, внимательно читайте задания. Очень обидно получить ноль за ту задачу, которую вы умеете решать, но допустили ошибку в исходных данных.
- Следите за арифметикой! Тщательно прописывайте все вычисления. Это поможет вам избежать самых распространенных ошибок или “опечаток” в виде потери знака минус, неправильного раскрытия скобок, перед которыми стоит все тот же минус, и так далее.
- Если не знаете, как решать задачу, не сидите над ней долго. За это время вы, возможно, успеете решить три другие задачи. Двигайтесь дальше, а к ней потом вернетесь.
- Расписывайте ход решения задач в их логической последовательности. Не пишите решения “абы как”. Если вдруг поймете, что где-то допущена ошибка, вам будет проще ее обнаружить.
- Не торопитесь вписать полученный ответ в бланк ответов. Вполне возможно, что у вас останется время и будет возможность проверить задачи (очень рекомендуем это сделать).
Обычно базовую математику выбирают ребята, у которых есть план: надо как можно скорее разделаться с бесполезным для поступления предметом и сосредоточиться на своем наборе вступительных. Из этой статьи вы узнаете, как сдать базовую математику максимально быстро и просто.
В этом материале мы сделаем акцент на простых номерах, которые принесут вам балл почти задаром! Они обозначены пометкой «Обязательно делать» — таких заданий 10. Как раз с запасом на ошибки, ведь минимум для сдачи базовой математики — 7 баллов.
Для тех, кто хочет получить выше тройки — это 12 баллов и выше, — мы дали рекомендации по еще 3 задачам. В сумме получается 13 номеров. Решите их все, и твердая четверка у вас в кармане.
Какие задания решать, чтобы сдать базовую математику
Задание 1: обязательно делать
Проверяется ваше умение разделить случаи, когда требуется округлить величину в большую сторону, а когда — в меньшую.
Если вы ходите в магазин с наличными, то сталкиваетесь с подобными задачами каждый день. Разделим 100 рублей на стоимость одной упаковки йогурта. Не забывайте приводить все величины к одной размерности:
100 : 14,6 = 6, 849…
Так сколько баночек йогурта вам продадут? На 7 штук денег не хватает, значит, округлить полученную величину надо до целого в меньшую сторону. Математическое правило округление в этой задаче не поможет.
Ответ: 6.
Если одна пачка рассчитана на 6 рулонов, то на 63 рулона:
63 : 6 = 10,5.
Но полпачки вам не продаст. Включаем логику: возьмем меньше — не хватит еще половины пачки на три последних рулона. Значит, округлить надо в большую сторону, взять клей с небольшим запасом. Математическое правило округления снова игнорируем.
Ответ: 11.
Задание 2: обязательно делать
Это задача на здравый смысл. Нужно соотнести величины с их возможными значениями.
Вряд ли грузовой автомобиль может весить как 3 шоколадки (300 г), а взрослый человек — 8 т.
Давайте вместе подберем значения.
- Взрослый человек обычно весит от 50 до 100 кг — что из этого подходит? Конечно, 65 кг.
- Грузовой автомобиль достаточно большой и тяжелый, скорее всего, он весит несколько тонн. Нам подходит 8 т.
- Книга обычно не такая большая и весит до 1 кг. Из оставшегося подойдет 300 г.
- А пуговка совсем маленькая. Значит, берем самый легкий вес — 5 г.
Ответ:
Главное — внимательно перенести ответы в бланк: 3142.
Задание 3: обязательно делать
Задание на работу с графиком, диаграммой или таблицей. Вооружайтесь карандашом, читайте условие с предельной внимательностью и безжалостно отмечайте нужные по условию значения на изображении в КИМ. Вы и представить не можете, сколько выпускников теряет тут баллы по невнимательности.
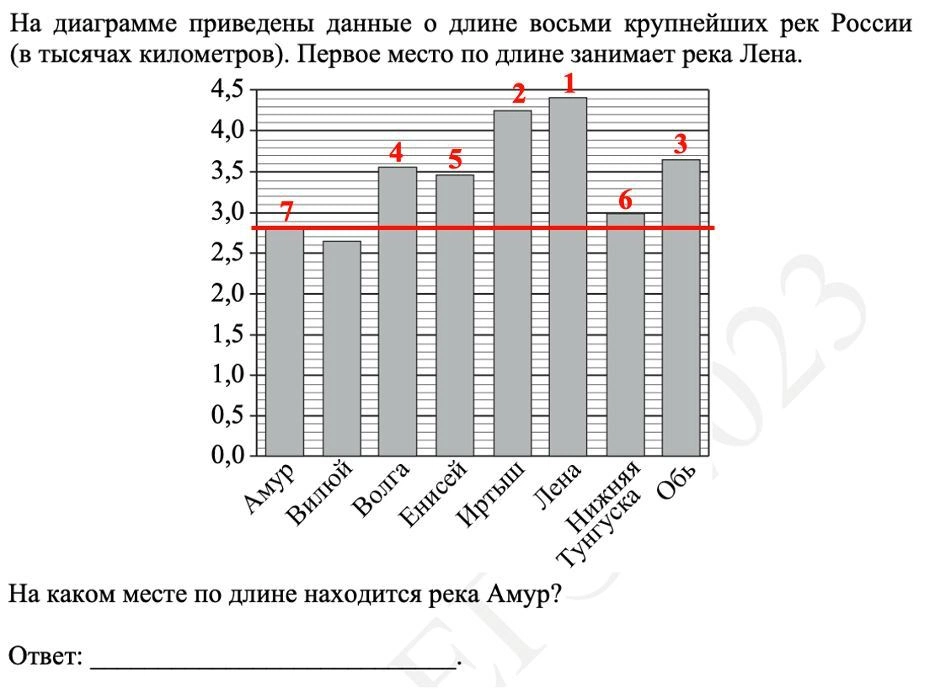
Мы ярко отметили уровень, соответствующий Амуру, в итоге посчитать все более длинные реки стало проще простого. У вас на экзамене будет так же наглядно!
Ответ: 7.
Задание 4: обязательно делать
Задание проверяет навык работы с формулами. Алгоритм решения напоминает решение задачек на уроке по физике:
- Выписываем формулу из условия.
- Определяем, что нужно найти: единственную букву, значение которой не дано.
- Выражаем искомую величину.
- Подставляем значения из условия в формулу.
- Ищем неизвестное.
Самое трудное тут — правильно выразить искомую величину. Для этого повторяем порядок выполнения арифметических операций, свойства умножения, тренируемся перекидывать через равно множители и слагаемые.
И да, в базе эта задача проста настолько, что даже перекидывать ничего не придется. Нужная величина уже будет слева от равно.
Задание 5: обязательно делать
Простая задача на определение вероятности, которая поможет вам точно сдать базовую математику.
Решаем с помощью формулы:
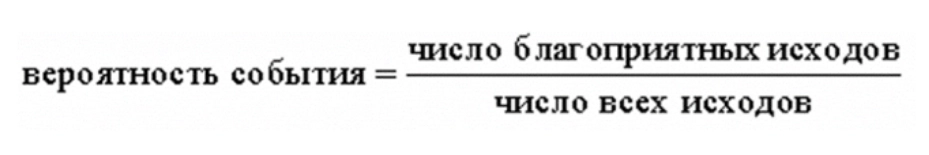
Внимательно читайте вопрос: спрашивают вероятность купить исправную лампочку. Если из ста 3 неисправны, значит, остальные в порядке и подойдет любая из оставшихся 97. Это и есть наши благоприятные исходы из формулы.
97 : 100 = 0,97.
Ответ: 0,97.
Будьте внимательны: иногда в задаче есть указание к округлению. Значит, ответ у вас выйдет некрасивый, в виде бесконечной десятичной дроби, которую вы округлите до нужного разряда.
Еще один подвох: формулировка с предлогом «на». К примеру, «На 100 лампочек 3 неисправны. Найдите вероятность купить неисправную». Подходящие исходы тут даны явно: 3 неисправные лампочки. А вот число всех исходов спрятано, и найти его будет нужно сложением исправных и неисправных лампочек: 100 + 3 = 103.
Задание 6: обязательно делать
Задание проверяет навык чтения информации из таблицы и подбора подходящего по условию варианта.
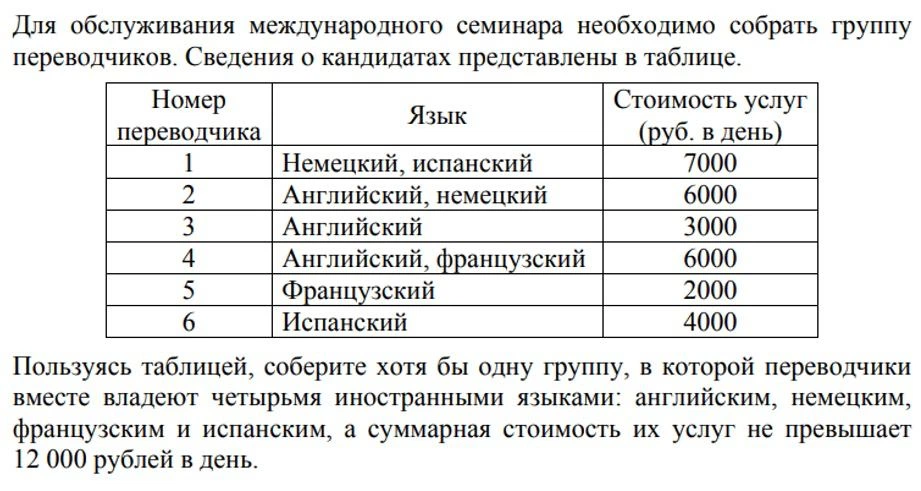
Например, вы нашли вариант позвать первого, третьего и пятого переводчиков. Получите весь набор языков как раз за 12 тысяч. Но обратите внимание, что это решение далеко не единственное.
Ответ: 135.
Задание 7
Мы не выделяем это задание в обязательные, так как для его выполнения понадобится навык анализа поведения функции по графику. Но, как его решать, сейчас коротко расскажем.
Запомним: точка максимума будет на «горке», точка минимума — в «ямке». Функция убывает, если идет вниз слева направо. Возрастает, если идет вверх слева направо.
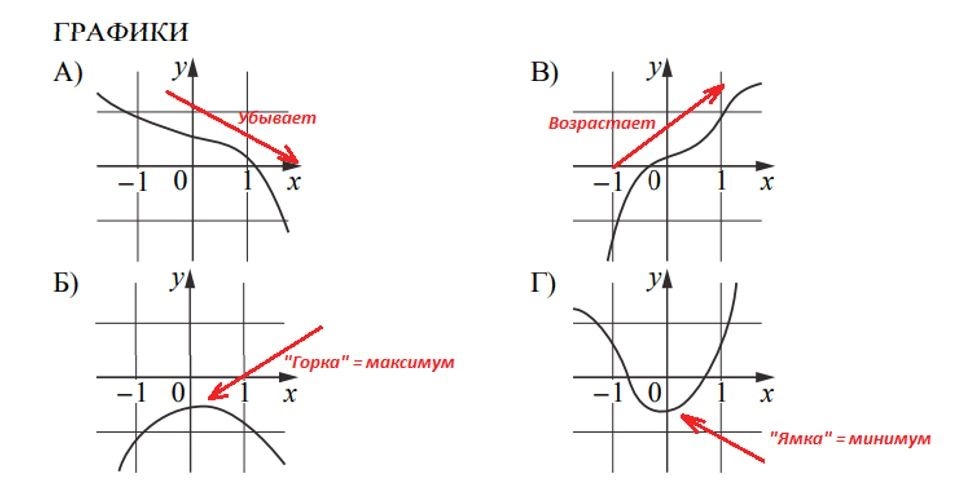
Если не повезет, то придется вспомнить азы теории по производной.
Здесь все дело в касательных. Нужно внимательно к ним присмотреться. Если касательная к графику возрастает, то значение производной будет положительное, если убывает — отрицательное. Производная будет тем больше по величине (модулю), чем быстрее возрастает или убывает касательная.
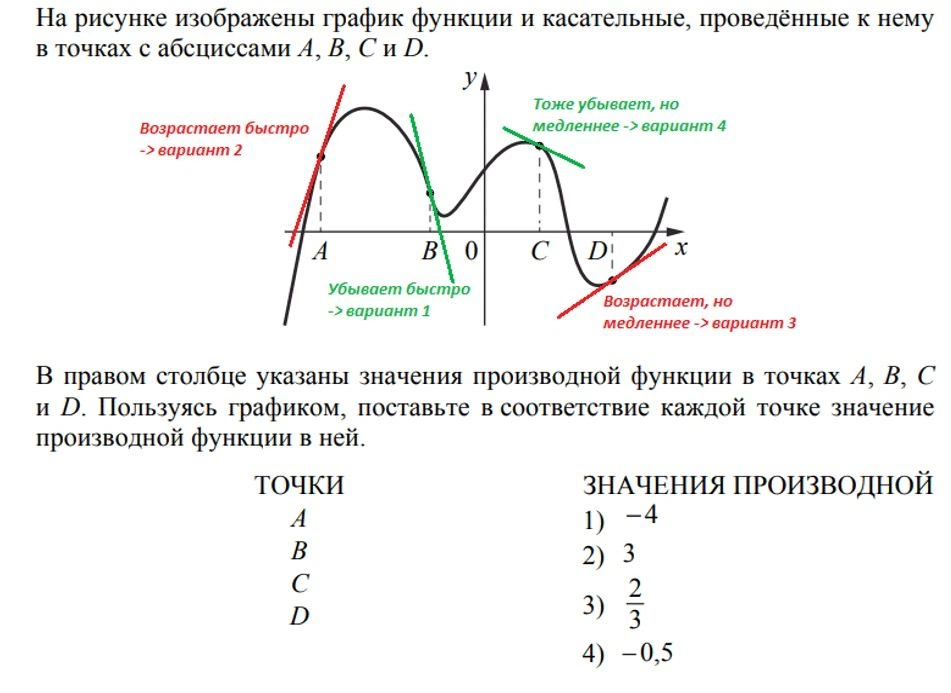
Ответ: 2143.
Задание 8: обязательно делать
Задача проверяет умение делать логичные выводы из утверждения. Иногда попадаются совсем простые задания, к таким даже дополнительно готовиться не надо.
Все, что от вас требуется, — схематично изобразить на черновике ясень, рябину и осину, указать известную разницу в высоте и внимательно сопоставить картинку с утверждениями.
Важно: не додумывайте дополнительные условия, не указанные в тексте задачи. Учитесь читать строго то, что написано.
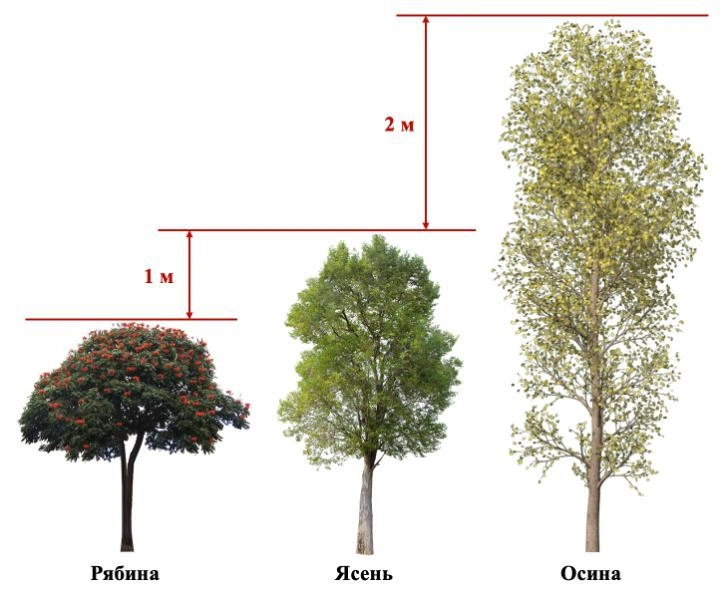
Исходя из рисунка выше получаем, что верны только утверждения 1 и 4.
Ответ: 14.
А бывают случаи, когда с визуализацией задачки придется постараться.
Тут иллюстрация не так очевидна, но нам помогут круги Эйлера. Этот инструмент позволяет наглядно изобразить множество объектов. В данном случае — школьников. Давайте прикинем, как ребята могут распределиться по кружкам.
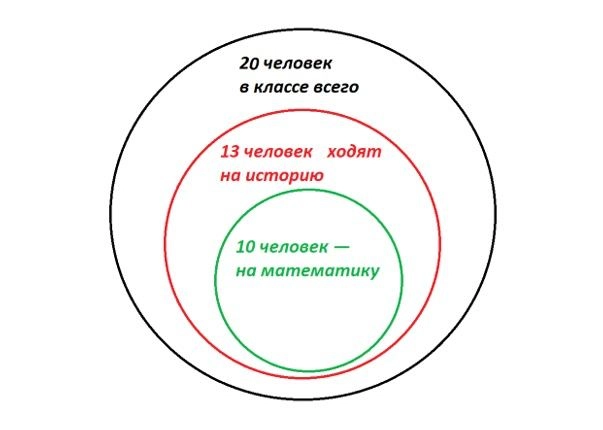
Например, так. Тут из 20 человек на кружки в итоге ходят 13. Причем 10 из них очень активны и выбрали сразу два предмета. Трое ограничились только историей.
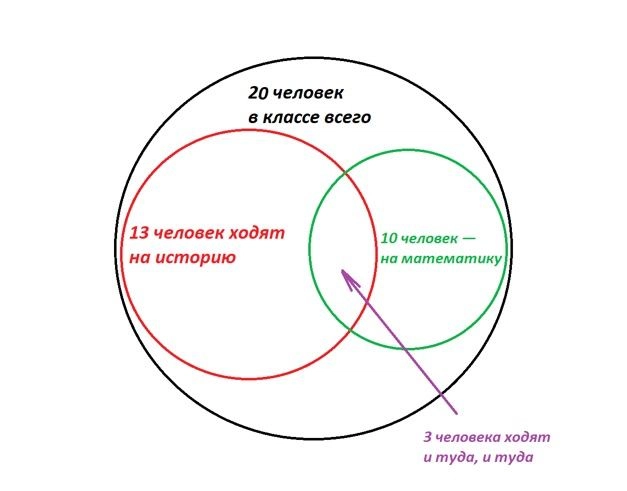
Или вот так. Если ребята задались целью по максимуму не пересекаться на дополнительных занятиях, то… У них не получится, и как минимум трое запишутся сразу на оба факультатива.
Конечно, возможны еще промежуточные варианты, но мы нарисовали два крайних. Теперь попробуем ответить на вопросы.
- Смотрим на первую картинку. Даже если все ребята будут очень стараться посетить оба кружка, они ограничены условиями задачи и максимум на оба попадут 10 человек из 20. Нет.
- Тут надо рассмотреть другую крайность, которую мы изобразили на второй картинке. Как бы ребята ни старались не встречаться на кружках, хотя бы трое попадут на оба сразу. Да.
- Уж точно неверно. На обеих наших картинках есть ребята, которые ходят на историю, но не ходят на математику. Нет.
- Смотрим на первую картинку. Оба кружка могут посещать максимум 10 человек.
Ответ: 24.
Так что для решения иногда мало логики — понадобится еще немного воображения. Потренируйтесь, и ваши шансы получить балл увеличатся.
Задание 14: обязательно делать
Задание проверяет базовые навыки счета, которым учат в 5–6-м классах. Чтобы получить балл и сдать базовую математику, надо:
- уметь выполнять арифметические действия с обыкновенными и десятичными дробями;
- правильно расставлять порядок действий;
- быть предельно внимательными.
Уделите пару вечеров отработке алгоритмов сложения, вычитания, умножения и деления обыкновенных и десятичных дробей, и это задание у вас в кармане.
Задание 15
Составители экзамена проверяют ваш навык работы с процентами и единицами отношения. Такие задачи бывают четырех типов.
Тип 1. Найти часть от числа
Часть может быть выражена в процентах или сразу в виде дроби. Например, придется искать треть от чего-то.
Рассмотрим на примере реальной задачи из экзамена:
Прочувствуйте специфику задачи: нам известно целое — вся зарплата до вычета налога. А работать мы будем с кусочком — 13 процентами. Сколько это в рублях, нам еще предстоит узнать.
Чтобы ответить на вопрос задачи, нужно сделать три шага:
1. Перевести процент в десятичную дробь.
Для этого всегда надо количество процентов поделить на 100.
13 : 100 = 0,13.
2. Найти, сколько это от зарплаты в рублях.
Запоминаем главное правило для этого типа задач: чтобы найти дробь от числа, надо число умножить на эту дробь.
12 500 ∙ 0,13 = 1 625 (руб.) — налог, который удержат с зарплаты Ивана Кузьмича.
3. Ответить на вопрос задачи.
У нас просили зарплату после вычета налога, а не сам налог.
12 500 – 1625 = 10 875 (руб.).
Ответ: 10 875.
Будьте внимательны: многие совершают ошибку именно на последнем шаге!
Тип 2. Найти число по его части
Прочувствуйте разницу с прошлой задачей: тут 124 — и есть 25%, то есть одна и та же величина выражена в процентах и в абсолютных величинах, в данном случае — в учениках. Просят узнать целое — 100%.
1. Переводим процент в десятичную дробь:
25 : 100 = 0,25.
2. Находим, сколько учеников всего.
Правило для этого типа задач: чтобы найти целое, надо часть разделить на дробь.
124 : 0,25 = 496 (уч.) — всего.
Ответ: 496.
Тип 3. Найти, сколько процентов часть составляет от целого
Особенность подобных заданий: не дано процентов, есть только абсолютные величины. В данном случае — стоимость футболки в рублях.
1. Находим, какую долю новая цена составляет от первоначальной.
Запоминаем правило: чтобы найти, какую долю часть составляет от целого, надо часть разделить на целое.
680 : 800 = 0,85.
2. Переводим долю в процент.
В прошлых задачах мы уже дважды выполнили обратное действие. В этот раз сделаем наоборот: умножим полученную дробь на 100.
0,85 ∙ 100 = 85% — столько процентов новая цена составляет от старой.
3. Отвечаем на вопрос задачи.
Нас спросили, на сколько процентов цена снизилась, что стала 85% от первоначальной. Конечно, изначально она была 100%. Итого:
100 – 85 = 15%.
Ответ: 15%.
Тип 4. Задачи на соотношение
Если перефразировать условие, то за первого кандидата проголосовали 3 части избирателей, а за второго — 2 части. Особенность этих частей в том, что они одинаковые по величине.
Если одна будет состоять из 10 человек, то за первого кандидата будет 30, а за второго — 20.
1. Считаем общее количество частей:
3 + 2 = 5.
2. Узнаем, сколько голосов составляет одна такая часть.
Тут речь о процентах проголосовавших. Сколько всего проголосовало? Конечно, 100%! Значит, каждая из пяти частей «весит»
100 : 5 = 20%.
3. Отвечаем на вопрос задачи.
За проигравшего проголосовало меньше частей избирателей. В нашем случае 2.
20 ∙ 2 = 40%.
Ответ: 40%.
Решение этих задач удобнее всего оформить табличкой:
1 часть = 100% : 5 = 20%.
Если рассчитываете решать текстовую задачу, включите здравый смысл. Ответ всегда можно проверить на адекватность благодаря обычной логике.
Задание 16: обязательно делать
Задание на решение выражения. На самом деле оно проверяет знание теории, так как в этом задании вам могут встретиться:
- выражения со степенями,
- иррациональные выражения,
- логарифмические выражения,
- тригонометрические выражения.
Ваша задача, соответственно, — знать:
- свойства степеней
- свойства корней
- свойства логарифмов
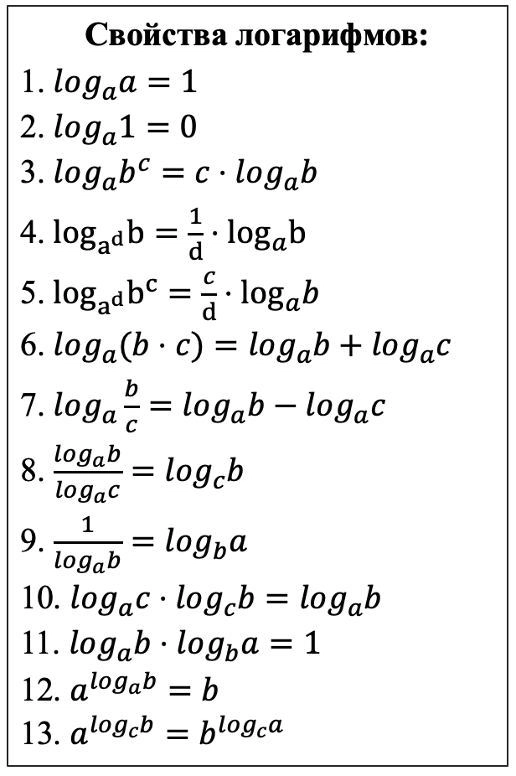
- формулы тригонометрии
Вы можете подробно ознакомиться с ними и научиться выводить в этой статье.
Обратите внимание: нужная теория будет в справочных материалах на экзамене, но это не поможет, если вы не научитесь применять ее для решения заданий. Практика обязательна!
Задание 17: обязательно делать
В номере с уравнениями вам не встретятся тригонометрические. Зато вы точно увидите там:
- линейные уравнения
Раскрываем скобки, если они есть, слагаемые с х переносим в одну сторону от равно, без х — в другую. Приводим подобные и решаем простейшее уравнение.
- квадратные уравнения
Бывают полные и неполные, всего надо повторить три алгоритма решения! А формула дискриминанта еще и в справочных материалах есть.
- иррациональные уравнения
Это те, что с корнем. Чтобы избавиться от корня, возводим обе части уравнения в квадрат и решаем получившееся уравнение. Есть нюансы с областью допустимых значений: подставьте полученные корни в исходное уравнение и проверьте, выполняется ли равенство. Если нет, то подставленное значение решением не будет.
- показательные уравнения
Ваша задача — с помощью формул свойств степеней привести уравнение к виду, когда слева и справа от равно в основании степени будет одно и то же число. После приравниваем показатели и решаем. Вот так:
Ответ: 7.
- логарифмические уравнения
С помощью формул свойств логарифмов приводим уравнение к виду, когда слева и справа от равно будет логарифм с одинаковым основанием. После приравниваем выражения под логарифмом и решаем.
Ответ: 67.
Прелесть уравнений в том, что ответ всегда можно проверить подстановкой вместо x в уравнение. Не забывайте проверять, ведь это возможность убедиться на 100%, что вы не упустите заветный балл.
Задание 19
Если хотите сдать базовую математику и решить номер 19, надо ознакомиться со свойствами целых чисел и признаками делимости. Иногда решение можно найти даже подбором! Попробуйте — времени на базовом ЕГЭ вам точно хватит.
Для начала нужно запомнить все признаки делимости.
А теперь посмотрим на типичное задание 19.
Тут помогут признаки делимости. Отдельного признака для 12 нет, потому нам надо разложить его на множители, признаки делимости для которых есть.
- На 3: сумма всех цифр делится на 3.
- На 4: число, образованное последними двумя цифрами, делится на 4.
Начнем с признака для 4. Пока что наше число заканчивается на 13 и на 4 не делится. Попробуем вычеркнуть последнюю цифру, и число будет заканчиваться на 61. Тоже не подходит. Вычеркнем еще одну: теперь на конце 76… Вот оно! От изначального числа осталось 751576, две цифры уже вычеркнули, осталось убрать одну.
Теперь проверим признак для 3: 7 + 5 + 1 + 5 + 7 + 6 = 31. Какое ближайшее число разделится на 3? Конечно, 30. Если мы вычеркнем единичку, все сойдется.
Ответ: 75576.
Другой вариант задания:
А задание такого типа можно попытаться подобрать, расположений не слишком много. Мы все же постараемся порассуждать, чтобы уменьшить количество возможных вариантов.
Чтобы число делилось на 10, оно должно заканчиваться на 0. Например, это получится, если сложить 7 + □7 + □□6. Уже немного легче. Остальное просто подберем. Под условие задачи подойдет 7 + 27 + 356 = 390.
Ответ: 390.
Какие задания мы не разобрали и почему
Теперь вы знаете, как сдать базовую математику, решив всего семь заданий. Но некоторые номера базового ЕГЭ включают слишком большое разнообразие прототипов, и методы их решения не ограничиваются парой простых алгоритмов.
Например, в эту группу относятся все задания по геометрии: с 9 по 13. Чтобы решать геометрию, мало знать основные фигуры и формулы. Необходим навык, который вырабатывается только практикой. Однако у нас есть статья про окружность — в ней вы найдете много полезной информации.
Задание 18 обычно, хотя и не всегда, содержит неравенство.
Это объемный блок теории, которую тоже необходимо подкреплять практикой. Но, может, вам повезет и попадется задачка на расположение значений на числовой прямой.
Тут достаточно примерно прикинуть значения и аккуратно внести ответы в бланк. Ясно, что 7/3 больше 2, но меньше 3. Корень из 26 равен 5 с копейками, а степень –1 из 3/5 сделает 5/3, или чуть больше 1,5. Подобные задания надо пытаться делать обязательно!
Задание 20. С этим заданием ученики знакомы еще с 9-го класса, так как оно было под номером 21 на ОГЭ. Это текстовая задача:
- на производительность,
- движение (по прямой, воде, окружности),
- сплавы и смеси,
- проценты (пиджаки, рубашки, брюки; бюджет семьи; акции, которые растут и падают),
- прогрессии.
В задании 21 на ОГЭ не было прогрессий, но они были в первой части на ОГЭ, так что ничего нового.
Задание 21. Здесь попадаются разные типы неочевидных задач на логику — чем-то они даже похожи на олимпиадные. Решение каждой нужно рассматривать отдельно и подробно. Если хотите прочитать о том, какие задачи бывают в 21-м номере, пишите в комментариях, и Maximum поделится своими методами решения!
Не знаете, какой вуз выбрать? Воспользуйтесь бесплатной консультацией в нашем центре. Что это такое? Все просто: вы расскажете о себе и о своих интересах. А специалист посоветует, на какие специальности обратить внимание, в какой вуз поступать, какие ЕГЭ сдавать. Так вы сэкономите время на подготовку и сможете выбрать образование, которое точно окажется для вас интересным и полезным!
Что нужно делать школьнику, чтобы получить 100 баллов?
Чтобы получить 100 баллов, надо любить и понимать математику (быть математиком — по сути, по настроению, по образу жизни). Если школьник рассматривает математику как второстепенный предмет, как предмет, который просто необходимо сдать, например, когда речь идет о поступлении на экономические направления, он не сможет получить 100 баллов ни при каком раскладе. Максимальный балл требует, чтобы человек всем своим «нутром и состоянием своего мозга» был ориентирован на математику. Потому что есть задачи, которые требуют четкого, хорошего логического мышления и владения абсолютно всем материалом. В нужный момент необходимо выудить необходимые знания и применить их для решения задачи. Есть такие задачи, на которые натаскать по принципу «делай вот так» просто нельзя (например, задача № 19). Даже если школьник прекрасно знает математику, 100 баллов получить очень сложно. Это единичные случаи.
По вашему опыту преподавания, какие разделы математики самые сложные и вызывают наибольшие затруднения?
Сегодня для школьника самое сложное — это геометрия. К сожалению, культура геометрии в школе просто отсутствует. И еще, конечно, задачи с параметрами. Старшеклассники их панически боятся. Но ученик, который понимает математику, и с этими задачами справляется. Для их решения требуется именно понимание, а все необходимые для этого знания изложены в курсе школьной математики.
А вообще, в любой теме есть простой материал (азы), который лежит в основе задач из первой части ЕГЭ, и сложный материал, который лежит в основе задач второй части. Думаю, что если есть желание, то каждый в состоянии освоить азы любой темы из школьной программы по математике, а вот более глубокое понимание этих тем и умение решать сложные задачи по силам не всем.
Ни о каком везении разговора быть не может, если школьник хочет получить больше 80 баллов
А какие темы можно назвать самыми простыми?
Обычно школьники легко решают линейные и квадратные уравнения, но только в том случае, если в них нет параметра. Так что по темам «Линейная функция» и «Квадратичная функция» есть простые задачи, а есть сложные. И так по любой теме. Можно сформулировать простую задачу, а можно такую, что никто не решит.
Простыми темами можно считать те, на большинство задач по которым можно школьника натаскать. Простая задача — это гарантированно правильно решенная. А про ЕГЭ (особенно про задачи первой части) так вообще нельзя говорить. Например, школьник знает, как решить задачу, но допускает арифметическую ошибку или невнимательно читает условие (ищет одну величину, а для ответа надо еще что-то с ней сделать). В итоге получается неверный ответ. И задача не решена. И не важно, простая она была или сложная.
Присутствует ли на ЕГЭ по математике фактор везения? Возможно ли получить высокий балл, если знаешь предмет на более скромный результат?
Да, это возможно, но только если речь идет о результате в районе 75 баллов или меньше. Ни о каком везении разговора быть не может, если школьник хочет получить больше 80 баллов. Там нужно решать сложные задачи из второй части, а они требуют четкого обоснования решения, что для большинства является непосильным. Здесь должна быть стабильность.
А можно завалить экзамен, если знаешь предмет очень хорошо?
Элементарно. Арифметические ошибки, невнимательное чтение условия задачи и просто паника. Все это приводит талантливых учеников к более скромным результатам.
Что же делать? Есть «формула успеха», которая поможет подготовиться к ЕГЭ по математике?
Учить математику! Не натаскиваться по вариантам ЕГЭ, а систематически учить темы, разбираться, стараться понять. Тогда до многих задач школьник дойдет сам, своим умом, а это и есть залог успешной подготовки и высоких баллов. Математика — это, в первую очередь, понимание, а потом уже формулы и схемы решения. При подготовке методом натаскивания потолок — это 75 баллов. Одна и та же задача, сформулированная просто «с другого конца», натасканного ребенка деморализует. Он не может узнать знакомую задачу, а разобраться в «новой» сам не в состоянии.
Вот, например, задача № 17. Когда она появилась в вариантах диагностических работ, детям в школе начали давать формулы для ее решения. И школьники заучивали эти формулы, сопротивляясь попыткам учителей объяснить, откуда они взялись. Многие действовали методом «я знаю формулу и по ней буду решать». А на самом экзамене в условие внесли незначительное изменение, и ни одна из выученных формул не подходила. Как получить ту, которая позволит решить задачу, дети не знали. Вроде бы решили все 120 вариантов задания № 17, а на ЕГЭ дали 121-й вариант. В итоге те, кто не разбирался, задачу не решили.
Надо выбросить калькулятор и научиться считать без него
До ЕГЭ по математике осталось 3,5 месяца. Как вы посоветуете выпускникам распределить время, чтобы подготовиться наилучшим образом?
Во-первых, выбросить калькулятор и научиться считать без него. Во-вторых, повторить теорию и выучить формулы (именно сейчас, а не перед экзаменом): то есть подготовить базу, а дальше решать задачи. Можно решать из сборников вариантов ЕГЭ, но, к сожалению, там их не очень много и они часто повторяются.
Каждый ребенок ставит для себя определенную планку в зависимости от того, куда собирается поступать и как знает предмет. Если говорить о заданиях второй части ЕГЭ, то во время подготовки необходимо прежде всего обратить внимание на задачи № 13, № 15 и № 17. Их можно научиться решать. Если решение не вызывает проблем, можно переходить к задачам № 14 и № 16.
Задачи № 18 и № 19 — это, конечно, уже очень высокий уровень, но попробовать можно. Если эти задачи идут хорошо, то я не думаю, что надо тратить оставшееся время на курсы. Лучше решить больше задач самостоятельно. Если же возникают проблемы или неуверенность, что вы все решаете верно, не откладывая обращайтесь за помощью. Эффективная стратегия на этот период — решать, решать и решать!
Как готовиться к заданиям повышенной сложности
| Задание № 10 | Задача легкая. Здесь важно внимательно читать условие. Внимание на единицы измерения! Все величины подставлять в одних единицах измерения. |
| Задание № 11 | Текстовая задача. Не считаю ее сложной. Обратите внимание на вопрос задачи, что именно спрашивают в условии и в каких единицах измерения необходимо записать ответ. Часто школьники пишут скорость не того пешехода или производительность не той трубы. |
| Задания № 13, № 15 | Задания решаемые, но должна быть база по всем темам алгебры. Особенное внимание необходимо обратить на область определения (в особенности это касается логарифма, тангенса и котангенса). Нужно уметь применять те тождественные преобразования, которые помогут решить задачу, а не заведут в тупик, и знать все формулы наизусть. |
| Задания № 14, № 16 | Задачи по геометрии. Самое сложное в них — это умение доказать. Для этого школьник должен владеть всем материалом планиметрии и стереометрии, знать все теоремы и следствия из них, уметь их доказывать. И еще важен чертеж! Он может либо стать эффективным инструментом и подсказать правильный ход решения, либо, если сделан некорректно, помешать решению задачи. |
| Задание № 17 | Несложная задача. Это задание на умение формализовать текстовую задачу, то есть записать условие задачи в виде уравнений или неравенств (этого же требует и решение задачи № 11). На ЕГЭ под этим номером пока стабильно дают задачу на проценты. Теоретически может быть и задача на поиск оптимального решения, но такие варианты пока встречались только в диагностических работах. После формализации условия получается стандартная математическая задача о нахождении экстремума функции или на нахождение наибольшего (наименьшего) значения функции на отрезке (аналогично задаче № 12). Здесь важно не пользоваться готовыми формулами, а разбираться, почему в этой задаче так, а в другой иначе. Только тогда можно научиться переводить условие текстовой задачи на язык математики. |
| Задание № 18 | Для решения этой задачи необходимо отличное владение предметом. Поможет ее решить знание свойств элементарных функций, умение исследовать функции и строить их графики. Все это есть в школьном курсе математики. |
| Задание № 19 | Это задача для тех, кому интересна математика. В ходе решения может возникнуть необходимость обратиться к любому разделу предмета из программы любого класса. Нужно найти в своей голове и грамотно применить эти знания. В одной задаче может сочетаться арифметическая прогрессия со свойствами делимости чисел и нахождением наибольшего значения. Для решения этой задачи нужно понимать, когда достаточно привести пример, а когда необходимо строгое обоснование. |
Есть два уровня ЕГЭ по математике: базовый и профильный. В середине последнего школьного учебного года надо будет определиться, какой из них предпочесть для экзамена. Выбор зависит от того, на какую специальность вы хотите поступить в вуз.
Сейчас существует множество бесплатных инструментов, которые позволяют подготовиться к ЕГЭ и увеличить балл на 40% с минимальными временными затратами.
Наиболее эффективными являются подписки на видеокурсы. Попробовать можно с
компанией Twostu
,
тем более здесь это ничего не стоит.
Содержание
- Секрет подготовки
- Самостоятельная работа
- Какова цель вашей подготовки
- Каким заданиям необходимо уделить больше времени
- Рекомендации от репетиторов
Профильный ЕГЭ придется сдавать тем, кому для успешного преодоления конкурса на выбранную специальность потребуются высокие баллы по математике. Если в списке экзаменов на ваш факультет математики нет, достаточно будет сдать ЕГЭ базового уровня.
В случае если вы завалите ЕГЭ по математике, будет возможность пересдать его в резервный день. Но повторно сдавать профильную математику в этот же год нельзя: вместо этого вам предложат базовый тест.
Секрет подготовки
Трудно ли сдавать ЕГЭ по математике? Если выбран профиль, то справиться с экзаменом, получив хорошие баллы, почти невозможно, не готовясь специально.
В отличие от ЕГЭ по русскому языку, к которому каждый может подготовиться, просто ответственно делая домашние задания и внимательно слушая учителя на уроках, математика требует дополнительной работы.
Большинство педагогов рекомендует начинать подготовку к ЕГЭ по математике как можно раньше. Обычно специализированные курсы и программы репетиторов рассчитаны на срок от 6 до 12 месяцев. Если у вас нет возможности ходить в учебный центр или нанять преподавателя, то к усиленным самостоятельным занятиям надо приступать примерно в такие же сроки. У опытного педагога есть программа, по которой он работает с абитуриентами, несколько проверенных пособий и задачников, методика подачи теоретического материала. Вам же придется своимим силами разбираться в теории, проверять решение всех задач и исправлять ошибки, самостоятельно подбирая учебники и задачники.
Самостоятельная работа
Демонстрационные варианты ЕГЭ по математике дадут примерное представление о типах заданий, но не помогут детально разобраться во всех темах. В открытой базе вопросов слишком много, чтобы зубрить способ решения или ответ на каждый из них. Намного полезнее получить системное представление о предмете, изучить перечисленные в кодификаторе темы так, чтобы быть в состоянии решить любую или почти любую задачу. Достичь такого уровня возможно, нужно только захотеть. Читайте учебники и справочники, попросите учителей посоветовать вам хорошие задачники. Не стесняйтесь просить о помощи школьных педагогов, членов семьи, одноклассников, знакомых студентов и специалистов.
Какова цель вашей подготовки
Прежде чем начать подготовку, определите свои цели. Нужно ли вам просто набрать проходной балл или жизненно необходимо сдать ЕГЭ по математике на 90 баллов? От того, в какой вуз вы хотите поступить, зависит выбор уровня – базового или профильного – и стратегия подготовки.
Если вам достаточно сдать базовый ЕГЭ по математике на 3, сначала сосредоточьтесь на подготовке по тем темам, которые даются относительно легко. Рассчитайте, сколько нужно сделать заданий, чтобы набрать нужный балл (на тройку хватит семи). Решайте уравнения и неравенства, а также задачи на проценты – часто на школьных уроках им уделяется недостаточно внимания. Обязательно попробуйте разобраться в новых для себя темах – скорее всего, у вас останется на это время. Пусть у вас будет запас верно выполненных заданий на случай, если вы не заметите на экзамене какую-нибудь ошибку и за нее снимут баллы.
Тот, кто сдает профильный ЕГЭ по математике, поставил перед собой цель, достойную уважения. Чтобы ее достичь, придется много заниматься, даже если нет проблем с математикой в школе. Но все равно опытные педагоги рекомендуют начинать подготовку с повторения и отработки базовых знаний умений.
Каким заданиям нужно уделить больше времени
ЕГЭ по математике состоит из заданий четырех типов: базовых, алгебраических, геометрических и повышенной сложности.
Постройте свою подготовку так, чтобы охватить все темы, входящие в ЕГЭ. Составьте себе программу, переходите от тех тем и заданий, которые даются проще всего, к самым сложным. Не забывайте о повторении, чередуйте его с изучением новых тем. Уделяйте внимание теории, ведь вам важно разобраться в материале, а не зазубрить.
На предпоследнем этапе подготовки уделите время заданиям повышенной сложности. Вы заметите, что они уже не кажутся невыполнимыми, потому что любое из них можно свести к нескольким простым, для решения которых хватит тех знаний, которые у вас уже есть.
Последним этапом подготовки педагоги рекомендуют сделать «контрольное» решение демонстрационных вариантов ЕГЭ, чтобы выявить «слабое звено» в системе знаний. Если все еще остаются пробелы, все внимание надо сосредоточить на их устанении.
Работа с демонстрационными тестами нужна еще для того, чтобы знать, сколько времени уходит на выполнение того или иного задания. «Предварительные замеры» помогут выработать стратегию поведения на ЕГЭ и просчитать, какие задания и в каком порядке выполнять, чтобы успеть сделать как можно больше. Не забывайте, что обязательно нужно перепроверить все ответы. Если ваша цель – набрать проходной балл, все равно для подстраховки сделайте на несколько заданий больше, чем планировали. Если поставлена задача сдать ЕГЭ по математике на 90 баллов и выше, постарайтесь ответить на все вопросы. Даже если не уверены в ответе, но у вас нет другого варианта, вносите в бланк полученный результат. Есть шанс, что он окажется верным и принесет несколько дополнительных баллов.
Рекомендации от репетиров
Не слушайте учителей, которые считают этот экзамен тяжелейшим испытанием, после которого выживают немногие. Действительно, он не из легких, но успешно сдать ЕГЭ по математике можно. Помните, что КИМ составляются так, чтобы соответствовать школьной программе и быть по силам любому старшекласснику. Чем лучше вы подготовлены, тем больше шансов решить все задания правильно, и тем увереннее вы себя чувствуете. Волнение перед экзаменом – это совершенно нормально, только не позволяйте тревоге отнимать все ваши силы и время. Планируйте занятия разумно, соотнося их со школьным расписанием, графиком посещения спортивных секций или творческих кружков — не забывайте об отдыхе, движении, общении с семьей и друзьями.
Правильный настрой поможет сдать ЕГЭ относительно легко. Ни пуха, ни пера!