Сложно ли сдать экзамен по математике

Обычно базовую математику выбирают ребята, у которых есть план: надо как можно скорее разделаться с бесполезным для поступления предметом и сосредоточиться на своем наборе вступительных. Из этой статьи вы узнаете, как сдать базовую математику максимально быстро и просто.

В этом материале мы сделаем акцент на простых номерах, которые принесут вам балл почти задаром! Они обозначены пометкой «Обязательно делать» — таких заданий 10. Как раз с запасом на ошибки, ведь минимум для сдачи базовой математики — 7 баллов.

Для тех, кто хочет получить выше тройки — это 12 баллов и выше, — мы дали рекомендации по еще 3 задачам. В сумме получается 13 номеров. Решите их все, и твердая четверка у вас в кармане.

Какие задания решать, чтобы сдать базовую математику

Задание 1: обязательно делать

Проверяется ваше умение разделить случаи, когда требуется округлить величину в большую сторону, а когда — в меньшую.

Если вы ходите в магазин с наличными, то сталкиваетесь с подобными задачами каждый день. Разделим 100 рублей на стоимость одной упаковки йогурта. Не забывайте приводить все величины к одной размерности:

100 : 14,6 = 6, 849…

Так сколько баночек йогурта вам продадут? На 7 штук денег не хватает, значит, округлить полученную величину надо до целого в меньшую сторону. Математическое правило округление в этой задаче не поможет.

Ответ: 6.

Если одна пачка рассчитана на 6 рулонов, то на 63 рулона:

63 : 6 = 10,5. 

Но полпачки вам не продаст. Включаем логику: возьмем меньше — не хватит еще половины пачки на три последних рулона. Значит, округлить надо в большую сторону, взять клей с небольшим запасом. Математическое правило округления снова игнорируем.

Ответ: 11.

Задание 2: обязательно делать

Это задача на здравый смысл. Нужно соотнести величины с их возможными значениями.

Вряд ли грузовой автомобиль может весить как 3 шоколадки (300 г), а взрослый человек — 8 т.

Давайте вместе подберем значения.

• Взрослый человек обычно весит от 50 до 100 кг — что из этого подходит? Конечно, 65 кг.
• Грузовой автомобиль достаточно большой и тяжелый, скорее всего, он весит несколько тонн. Нам подходит 8 т.
• Книга обычно не такая большая и весит до 1 кг. Из оставшегося подойдет 300 г.
• А пуговка совсем маленькая. Значит, берем самый легкий вес — 5 г.

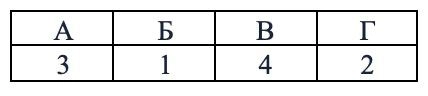
Ответ:

Главное — внимательно перенести ответы в бланк: 3142.

Задание 3: обязательно делать

Задание на работу с графиком, диаграммой или таблицей. Вооружайтесь карандашом, читайте условие с предельной внимательностью и безжалостно отмечайте нужные по условию значения на изображении в КИМ. Вы и представить не можете, сколько выпускников теряет тут баллы по невнимательности.

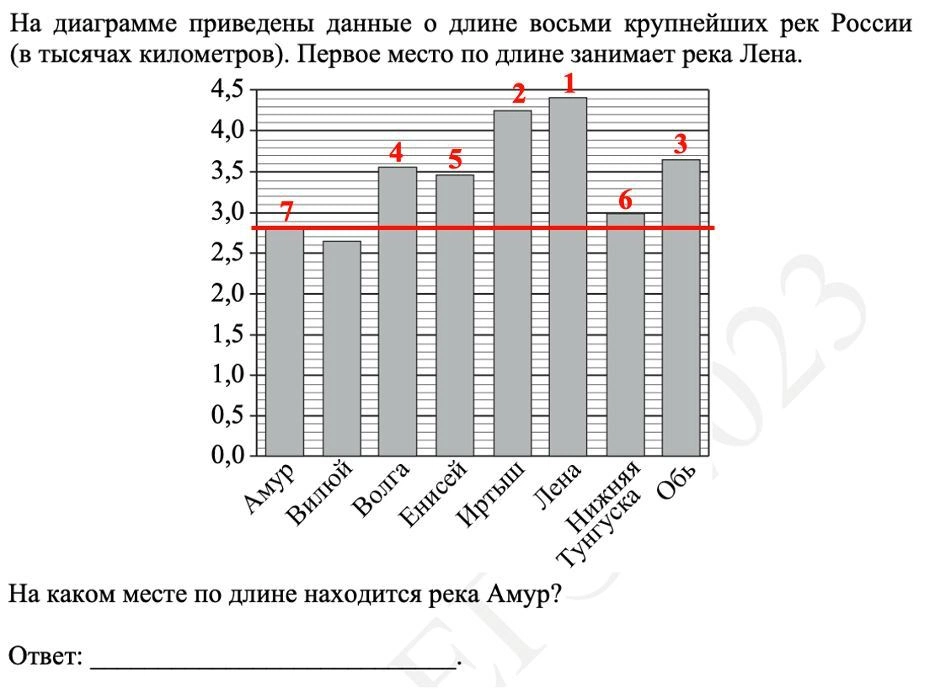
Мы ярко отметили уровень, соответствующий Амуру, в итоге посчитать все более длинные реки стало проще простого. У вас на экзамене будет так же наглядно!

Ответ: 7.

Задание 4: обязательно делать

Задание проверяет навык работы с формулами. Алгоритм решения напоминает решение задачек на уроке по физике:

• Выписываем формулу из условия.
• Определяем, что нужно найти: единственную букву, значение которой не дано.
• Выражаем искомую величину.
• Подставляем значения из условия в формулу.
• Ищем неизвестное.

Самое трудное тут — правильно выразить искомую величину. Для этого повторяем порядок выполнения арифметических операций, свойства умножения, тренируемся перекидывать через равно множители и слагаемые.

И да, в базе эта задача проста настолько, что даже перекидывать ничего не придется. Нужная величина уже будет слева от равно.

Задание 5: обязательно делать

Простая задача на определение вероятности, которая поможет вам точно сдать базовую математику.

Решаем с помощью формулы:

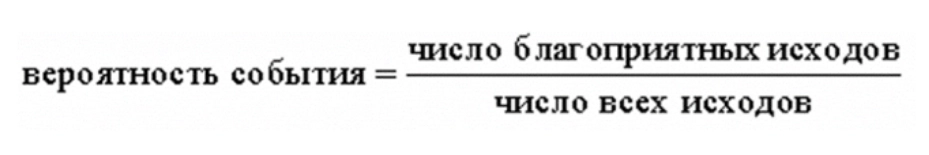
Внимательно читайте вопрос: спрашивают вероятность купить исправную лампочку. Если из ста 3 неисправны, значит, остальные в порядке и подойдет любая из оставшихся 97. Это и есть наши благоприятные исходы из формулы.

97 : 100 = 0,97.

Ответ: 0,97.

Будьте внимательны: иногда в задаче есть указание к округлению. Значит, ответ у вас выйдет некрасивый, в виде бесконечной десятичной дроби, которую вы округлите до нужного разряда.

Еще один подвох: формулировка с предлогом «на». К примеру, «На 100 лампочек 3 неисправны. Найдите вероятность купить неисправную». Подходящие исходы тут даны явно: 3 неисправные лампочки. А вот число всех исходов спрятано, и найти его будет нужно сложением исправных и неисправных лампочек: 100 + 3 = 103.

Задание 6: обязательно делать

Задание проверяет навык чтения информации из таблицы и подбора подходящего по условию варианта.

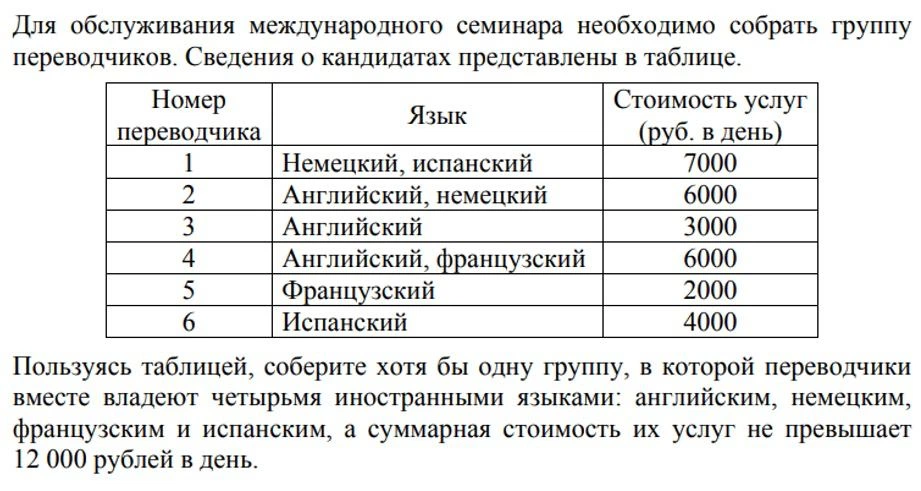
Например, вы нашли вариант позвать первого, третьего и пятого переводчиков. Получите весь набор языков как раз за 12 тысяч. Но обратите внимание, что это решение далеко не единственное.

Ответ: 135.

Задание 7

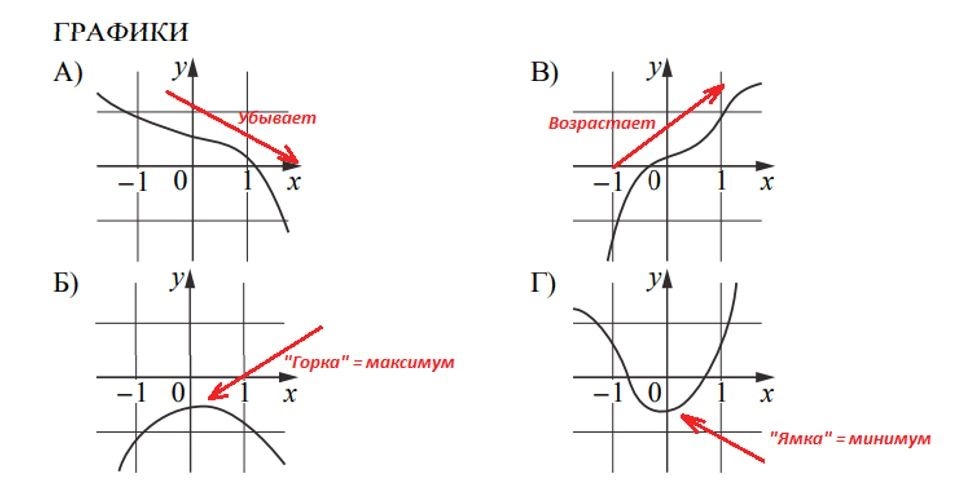
Мы не выделяем это задание в обязательные, так как для его выполнения понадобится навык анализа поведения функции по графику. Но, как его решать, сейчас коротко расскажем.

Запомним: точка максимума будет на «горке», точка минимума — в «ямке». Функция убывает, если идет вниз слева направо. Возрастает, если идет вверх слева направо.

Если не повезет, то придется вспомнить азы теории по производной.

Здесь все дело в касательных. Нужно внимательно к ним присмотреться. Если касательная к графику возрастает, то значение производной будет положительное, если убывает — отрицательное. Производная будет тем больше по величине (модулю), чем быстрее возрастает или убывает касательная.

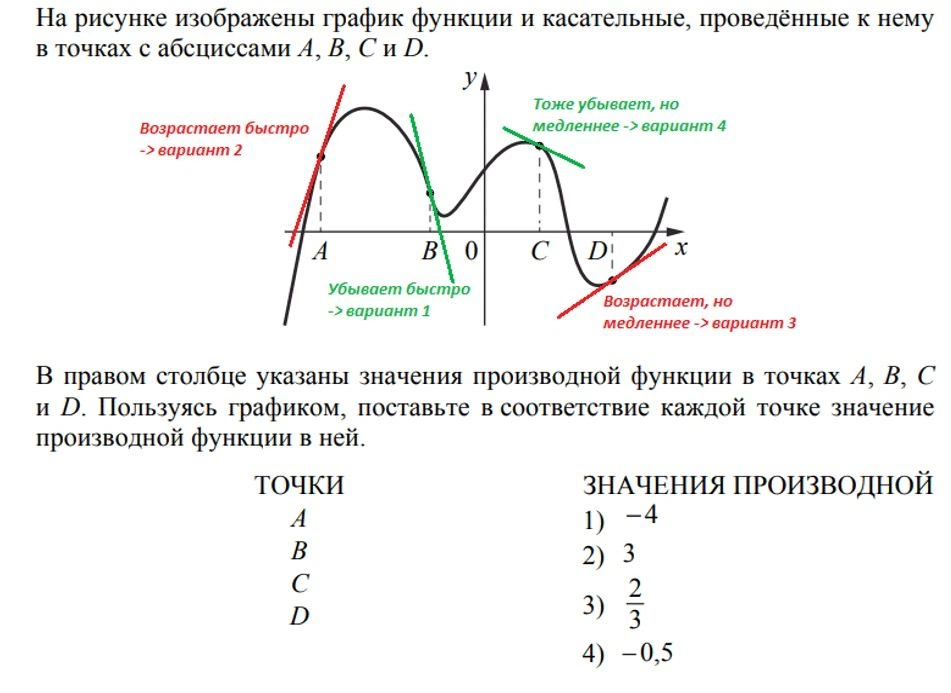
Ответ: 2143.

Задание 8: обязательно делать

Задача проверяет умение делать логичные выводы из утверждения. Иногда попадаются совсем простые задания, к таким даже дополнительно готовиться не надо.

Все, что от вас требуется, — схематично изобразить на черновике ясень, рябину и осину, указать известную разницу в высоте и внимательно сопоставить картинку с утверждениями.

Важно: не додумывайте дополнительные условия, не указанные в тексте задачи. Учитесь читать строго то, что написано.

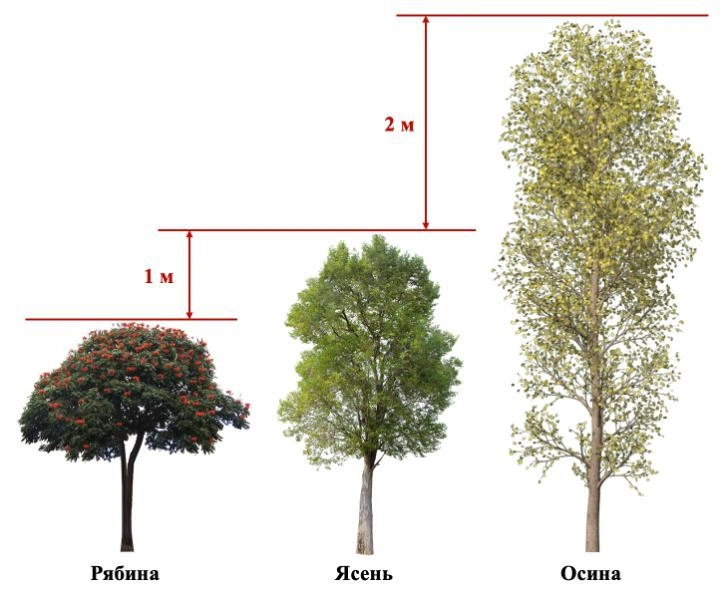
Исходя из рисунка выше получаем, что верны только утверждения 1 и 4.

Ответ: 14.

А бывают случаи, когда с визуализацией задачки придется постараться.

Тут иллюстрация не так очевидна, но нам помогут круги Эйлера. Этот инструмент позволяет наглядно изобразить множество объектов. В данном случае — школьников. Давайте прикинем, как ребята могут распределиться по кружкам.

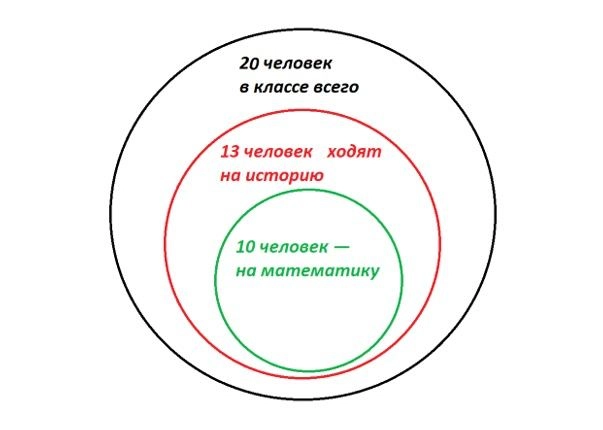
Например, так. Тут из 20 человек на кружки в итоге ходят 13. Причем 10 из них очень активны и выбрали сразу два предмета. Трое ограничились только историей.

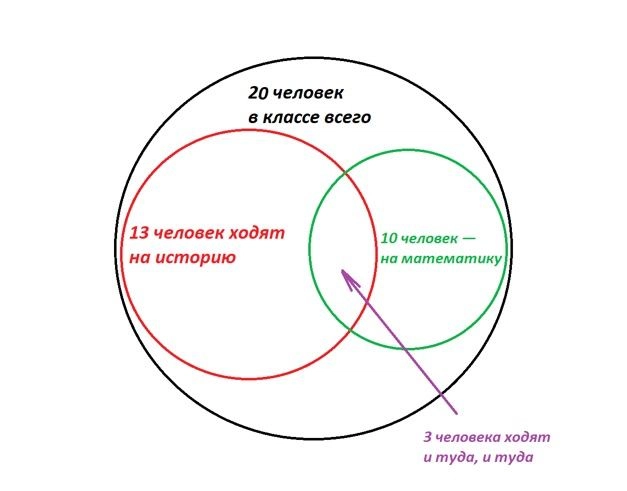
Или вот так. Если ребята задались целью по максимуму не пересекаться на дополнительных занятиях, то… У них не получится, и как минимум трое запишутся сразу на оба факультатива.

Конечно, возможны еще промежуточные варианты, но мы нарисовали два крайних. Теперь попробуем ответить на вопросы.

1. Смотрим на первую картинку. Даже если все ребята будут очень стараться посетить оба кружка, они ограничены условиями задачи и максимум на оба попадут 10 человек из 20. Нет.
2. Тут надо рассмотреть другую крайность, которую мы изобразили на второй картинке. Как бы ребята ни старались не встречаться на кружках, хотя бы трое попадут на оба сразу. Да.
3. Уж точно неверно. На обеих наших картинках есть ребята, которые ходят на историю, но не ходят на математику. Нет.
4. Смотрим на первую картинку. Оба кружка могут посещать максимум 10 человек. 

Ответ: 24.

Так что для решения иногда мало логики — понадобится еще немного воображения. Потренируйтесь, и ваши шансы получить балл увеличатся.

Задание 14: обязательно делать

Задание проверяет базовые навыки счета, которым учат в 5–6-м классах. Чтобы получить балл и сдать базовую математику, надо:

• уметь выполнять арифметические действия с обыкновенными и десятичными дробями;
• правильно расставлять порядок действий;
• быть предельно внимательными.

Уделите пару вечеров отработке алгоритмов сложения, вычитания, умножения и деления обыкновенных и десятичных дробей, и это задание у вас в кармане.

Задание 15

Составители экзамена проверяют ваш навык работы с процентами и единицами отношения. Такие задачи бывают четырех типов.

Тип 1. Найти часть от числа

Часть может быть выражена в процентах или сразу в виде дроби. Например, придется искать треть от чего-то.

Рассмотрим на примере реальной задачи из экзамена:

Прочувствуйте специфику задачи: нам известно целое — вся зарплата до вычета налога. А работать мы будем с кусочком — 13 процентами. Сколько это в рублях, нам еще предстоит узнать.

Чтобы ответить на вопрос задачи, нужно сделать три шага:

1. Перевести процент в десятичную дробь.

Для этого всегда надо количество процентов поделить на 100.

13 : 100 = 0,13.

2. Найти, сколько это от зарплаты в рублях.

Запоминаем главное правило для этого типа задач: чтобы найти дробь от числа, надо число умножить на эту дробь.

12 500 ∙ 0,13 = 1 625 (руб.) — налог, который удержат с зарплаты Ивана Кузьмича.

3. Ответить на вопрос задачи.

У нас просили зарплату после вычета налога, а не сам налог.

12 500 – 1625 = 10 875 (руб.).

Ответ: 10 875.

Будьте внимательны: многие совершают ошибку именно на последнем шаге!

Тип 2. Найти число по его части

Прочувствуйте разницу с прошлой задачей: тут 124 — и есть 25%, то есть одна и та же величина выражена в процентах и в абсолютных величинах, в данном случае — в учениках. Просят узнать целое — 100%.

1. Переводим процент в десятичную дробь:

25 : 100 = 0,25.

2. Находим, сколько учеников всего.

Правило для этого типа задач: чтобы найти целое, надо часть разделить на дробь.

124 : 0,25 = 496 (уч.) — всего.

Ответ: 496.

Тип 3. Найти, сколько процентов часть составляет от целого

Особенность подобных заданий: не дано процентов, есть только абсолютные величины. В данном случае — стоимость футболки в рублях.

1. Находим, какую долю новая цена составляет от первоначальной.

Запоминаем правило: чтобы найти, какую долю часть составляет от целого, надо часть разделить на целое.

680 : 800 = 0,85.

2. Переводим долю в процент.

В прошлых задачах мы уже дважды выполнили обратное действие. В этот раз сделаем наоборот: умножим полученную дробь на 100.

0,85 ∙ 100 = 85% — столько процентов новая цена составляет от старой.

3. Отвечаем на вопрос задачи.

Нас спросили, на сколько процентов цена снизилась, что стала 85% от первоначальной. Конечно, изначально она была 100%. Итого:

100 – 85 = 15%.

Ответ: 15%.

Тип 4. Задачи на соотношение

Если перефразировать условие, то за первого кандидата проголосовали 3 части избирателей, а за второго — 2 части. Особенность этих частей в том, что они одинаковые по величине.

Если одна будет состоять из 10 человек, то за первого кандидата будет 30, а за второго — 20.

1. Считаем общее количество частей:

3 + 2 = 5.

2. Узнаем, сколько голосов составляет одна такая часть.

Тут речь о процентах проголосовавших. Сколько всего проголосовало? Конечно, 100%! Значит, каждая из пяти частей «весит»

100 : 5 = 20%.

3. Отвечаем на вопрос задачи.

За проигравшего проголосовало меньше частей избирателей. В нашем случае 2.

20 ∙ 2 = 40%.

Ответ: 40%.

Решение этих задач удобнее всего оформить табличкой:

1 часть = 100% : 5 = 20%.

Если рассчитываете решать текстовую задачу, включите здравый смысл. Ответ всегда можно проверить на адекватность благодаря обычной логике. 

Задание 16: обязательно делать

Задание на решение выражения. На самом деле оно проверяет знание теории, так как в этом задании вам могут встретиться:

• выражения со степенями,
• иррациональные выражения,
• логарифмические выражения,
• тригонометрические выражения.

Ваша задача, соответственно, — знать:

• свойства степеней

• свойства корней

• свойства логарифмов

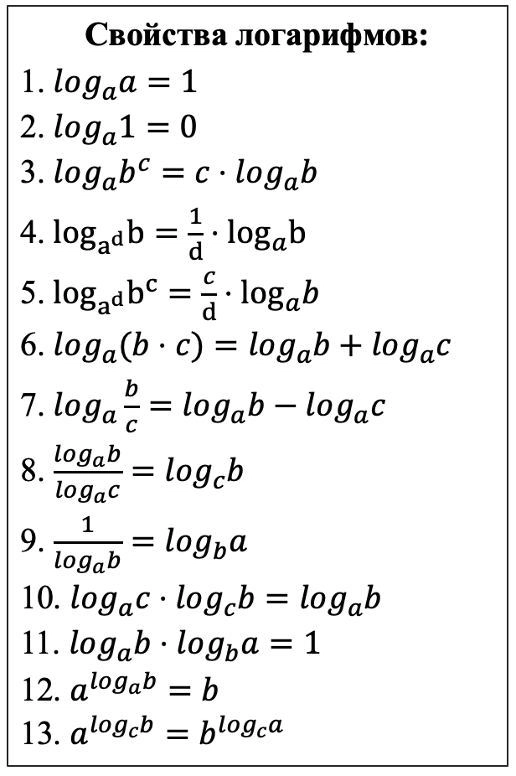
• формулы тригонометрии

Вы можете подробно ознакомиться с ними и научиться выводить в этой статье.

Обратите внимание: нужная теория будет в справочных материалах на экзамене, но это не поможет, если вы не научитесь применять ее для решения заданий. Практика обязательна!

Задание 17: обязательно делать

В номере с уравнениями вам не встретятся тригонометрические. Зато вы точно увидите там:

• линейные уравнения

Раскрываем скобки, если они есть, слагаемые с х переносим в одну сторону от равно, без х — в другую. Приводим подобные и решаем простейшее уравнение.

• квадратные уравнения

Бывают полные и неполные, всего надо повторить три алгоритма решения! А формула дискриминанта еще и в справочных материалах есть.

• иррациональные уравнения

Это те, что с корнем. Чтобы избавиться от корня, возводим обе части уравнения в квадрат и решаем получившееся уравнение. Есть нюансы с областью допустимых значений: подставьте полученные корни в исходное уравнение и проверьте, выполняется ли равенство. Если нет, то подставленное значение решением не будет.

• показательные уравнения

Ваша задача — с помощью формул свойств степеней привести уравнение к виду, когда слева и справа от равно в основании степени будет одно и то же число. После приравниваем показатели и решаем. Вот так:

Ответ: 7.

• логарифмические уравнения

С помощью формул свойств логарифмов приводим уравнение к виду, когда слева и справа от равно будет логарифм с одинаковым основанием. После приравниваем выражения под логарифмом и решаем.

Ответ: 67.

Прелесть уравнений в том, что ответ всегда можно проверить подстановкой вместо x в уравнение. Не забывайте проверять, ведь это возможность убедиться на 100%, что вы не упустите заветный балл.

Задание 19

Если хотите сдать базовую математику и решить номер 19, надо ознакомиться со свойствами целых чисел и признаками делимости. Иногда решение можно найти даже подбором! Попробуйте — времени на базовом ЕГЭ вам точно хватит.

Для начала нужно запомнить все признаки делимости.

А теперь посмотрим на типичное задание 19.

Тут помогут признаки делимости. Отдельного признака для 12 нет, потому нам надо разложить его на множители, признаки делимости для которых есть. 

• На 3: сумма всех цифр делится на 3.
• На 4: число, образованное последними двумя цифрами, делится на 4.

Начнем с признака для 4. Пока что наше число заканчивается на 13 и на 4 не делится. Попробуем вычеркнуть последнюю цифру, и число будет заканчиваться на 61. Тоже не подходит. Вычеркнем еще одну: теперь на конце 76… Вот оно! От изначального числа осталось 751576, две цифры уже вычеркнули, осталось убрать одну.

Теперь проверим признак для 3: 7 + 5 + 1 + 5 + 7 + 6 = 31. Какое ближайшее число разделится на 3? Конечно, 30. Если мы вычеркнем единичку, все сойдется.

Ответ: 75576.

Другой вариант задания:

А задание такого типа можно попытаться подобрать, расположений не слишком много. Мы все же постараемся порассуждать, чтобы уменьшить количество возможных вариантов.

Чтобы число делилось на 10, оно должно заканчиваться на 0. Например, это получится, если сложить 7 + □7 + □□6. Уже немного легче. Остальное просто подберем. Под условие задачи подойдет 7 + 27 + 356 = 390.

Ответ: 390.

Какие задания мы не разобрали и почему

Теперь вы знаете, как сдать базовую математику, решив всего семь заданий. Но некоторые номера базового ЕГЭ включают слишком большое разнообразие прототипов, и методы их решения не ограничиваются парой простых алгоритмов.

Например, в эту группу относятся все задания по геометрии: с 9 по 13. Чтобы решать геометрию, мало знать основные фигуры и формулы. Необходим навык, который вырабатывается только практикой. Однако у нас есть статья про окружность — в ней вы найдете много полезной информации.

Задание 18 обычно, хотя и не всегда, содержит неравенство.

Это объемный блок теории, которую тоже необходимо подкреплять практикой. Но, может, вам повезет и попадется задачка на расположение значений на числовой прямой.

Тут достаточно примерно прикинуть значения и аккуратно внести ответы в бланк. Ясно, что 7/3  больше 2, но меньше 3. Корень из 26 равен 5 с копейками, а степень –1 из 3/5 сделает 5/3, или чуть больше 1,5. Подобные задания надо пытаться делать обязательно!

Задание 20. С этим заданием ученики знакомы еще с 9-го класса, так как оно было под номером 21 на ОГЭ. Это текстовая задача:

• на производительность,
• движение (по прямой, воде, окружности),
• сплавы и смеси,
• проценты (пиджаки, рубашки, брюки; бюджет семьи; акции, которые растут и падают),
• прогрессии.

В задании 21 на ОГЭ не было прогрессий, но они были в первой части на ОГЭ, так что ничего нового.

Задание 21. Здесь попадаются разные типы неочевидных задач на логику — чем-то они даже похожи на олимпиадные. Решение каждой нужно рассматривать отдельно и подробно. Если хотите прочитать о том, какие задачи бывают в 21-м номере, пишите в комментариях, и Maximum поделится своими методами решения!

Не знаете, какой вуз выбрать? Воспользуйтесь бесплатной консультацией в нашем центре. Что это такое? Все просто: вы расскажете о себе и о своих интересах. А специалист посоветует, на какие специальности обратить внимание, в какой вуз поступать, какие ЕГЭ сдавать. Так вы сэкономите время на подготовку и сможете выбрать образование, которое точно окажется для вас интересным и полезным!

Колледж экономических международных связей

Для выпускников 9 и 11 классов.

Высшее образование онлайн

Федеральный проект дистанционного образования.

Я б в нефтяники пошел!

Пройди тест, узнай свою будущую профессию и как её получить.

Технологии будущего

Вдохновитесь идеей стать крутым инженером, чтобы изменить мир

Студенческие проекты

Студенты МосПолитеха рассказывают о своих изобретениях

Химия и биотехнологии в РТУ МИРЭА

120 лет опыта подготовки

Международный колледж искусств и коммуникаций

МКИК — современный колледж

Английский язык

Совместно с экспертами Wall Street English мы решили рассказать об английском языке так, чтобы его захотелось выучить.

15 правил безопасного поведения в интернете

Простые, но важные правила безопасного поведения в Сети.

Олимпиады для школьников

Перечень, календарь, уровни, льготы.

Первый экономический

Рассказываем о том, чем живёт и как устроен РЭУ имени Г.В. Плеханова.

Билет в Голландию

Участвуй в конкурсе и выиграй поездку в Голландию на обучение в одной из летних школ Университета Радбауд.

Цифровые герои

Они создают интернет-сервисы, социальные сети, игры и приложения, которыми ежедневно пользуются миллионы людей во всём мире.

Работа будущего

Как новые технологии, научные открытия и инновации изменят ландшафт на рынке труда в ближайшие 20-30 лет

Профессии мечты

Совместно с центром онлайн-обучения Фоксфорд мы решили узнать у школьников, кем они мечтают стать и куда планируют поступать.

Экономическое образование

О том, что собой представляет современная экономика, и какие карьерные перспективы открываются перед будущими экономистами.

Гуманитарная сфера

Разговариваем с экспертами о важности гуманитарного образования и областях его применения на практике.

Молодые инженеры

Инженерные специальности становятся всё более востребованными и перспективными.

Табель о рангах

Что такое гражданская служба, кто такие госслужащие и какое образование является хорошим стартом для будущих чиновников.

Карьера в нефтехимии

Нефтехимия — это инновации, реальное производство продукции, которая есть в каждом доме.

Структура экзамена

На выполнение всей экзаменационной работы дается 3 часа 55 минут. КИМ в 2022 году будет состоять из 25 заданий. Для первой части определено 19 заданий, на которые нужно дать короткие ответы:

1. Первые 5 вопросов относятся к разделу «реальная математика». Они направлены на раскрытие умения применять науку в реальной жизни.
2. Вопросы 6−15 относятся к обычной алгебре. В этом блоке представлены задания на вычисление и преобразование, уравнения, практические задачи, графики функций.
3. Вопросы 16−19 посвящены решению задач по геометрии: нахождению векторов, координат и значений разных фигур.

Вторая часть работы включает 6 достаточно сложных заданий. В этом разделе потребуется умение четко и грамотно расписывать ход решения для комплексных и планиметрических задач.

Перед вопросами в бланке находятся справочные материалы: формулы по алгебре и геометрии, таблица квадратов двузначных чисел. Они помогут облегчить решение задач и сэкономить время.

Максимально можно получить 31 балл. Итоговое количество баллов определяет отметку по пятибалльной системе оценивания:

• чтобы получить оценку «пять», ученик должен набрать от 22 баллов;
• «четверку» ставят тем, кто смог решить на 15−21 балл;
• «тройку» получают за 8−14 баллов.

Не менее 2 баллов необходимо получить за задания по геометрии.

Какие задания требуют особого внимания

Вопрос 5 из первой части зачастую вызывает трудности. Он содержит разные виды сюжета: например, план домохозяйства или квартиры, план местности, телефонный тариф. Используя условие задачи и таблицу, и сравнив два или несколько вариантов, требуется вычислить наиболее дешевый или выгодный. Верный ход решения выглядит следующим образом:

• прочитать условие и вычеркнуть в таблице ненужные данные;
• внимательно посчитать стоимость товаров или услуг для каждого варианта;
• сравнить и выбрать самый выгодный.

В задание 11 включены графики функций, где нужно установить соответствие между графиком и его функцией. Нередко школьники путают параболу с гиперболой и их формулы. Важно помнить отличия между графиками функций, положительные и отрицательные значения, направления ветвей.

Вопрос 13 содержит 4 подтемы с разными типами неравенств:

• линейные;
• квадратные;
• рациональные;
• системы неравенств.

Для начала следует решить неравенство, раскрывая скобки и меняя, при необходимости, знаки, затем полученный результат соотнести с рисунком. В этом вопросе важна внимательность: получив верный ответ, нужно указать правильный рисунок.

Для выполнения задания 14 нужно хорошо понимать геометрическую и алгебраическую прогрессии, чтобы подставить верные значения в формулу.

Задача 24 по геометрии относится к повышенному уровню сложности. Ее решение требует твердых аргументов. Рекомендуется тщательно изучить теоремы, понять их логику. Все шаги доказательства должны быть обоснованы.

Особенности подготовки

Перед началом подготовки школьнику стоит ознакомиться с официальными документами по экзамену, утвержденными ФИПИ — демоверсией и кодификатором. Их можно найти на сайте университета «Синергия» во вкладке ОГЭ. Там же находятся разборы заданий и теоретическая часть.

Рекомендуется периодически проходить тренировочные экзамены с использованием настоящих КИМов. Такие пробники помогут школьнику научиться развить скорость решения типичных задач и правильно рассчитывать время на экзамене. Обязательно должно остаться не менее 15 минут на перепроверку ответов.

Как показывает опыт прошлых лет, ученики особенно сложными находят построение графиков, уравнения с корнями, задачи на вписанную и описанную окружность. Также стоит проработать тему подобных треугольников, а именно их 3 признака.

После каждой пройденной темы рекомендуется практиковаться в решении заданий. Для разбора задач, можно использовать сборники упражнений и онлайн-ресурсы. Неясные моменты станут понятнее, если просмотреть лекции или вебинары, где подробно рассказывают ход решения.

Сдать экзамен по математике нетрудно, если тщательно изучить теорию и проработать типовые задания. В университете «Синергия» можно пройти подготовку к ОГЭ на онлайн-курсах.