Топ сложных заданий ЕГЭ по математике, в которых ошибается каждый третий
Математика — царица наук, а ты в её королевстве даже не холоп, а пятое дерево в седьмом ряду? У тебя ещё есть возможность это исправить, ведь мы собрали для тебя самые сложные задания в ЕГЭ по математике, чтобы знал, на что обратить внимание и не допускал в них ошибок.
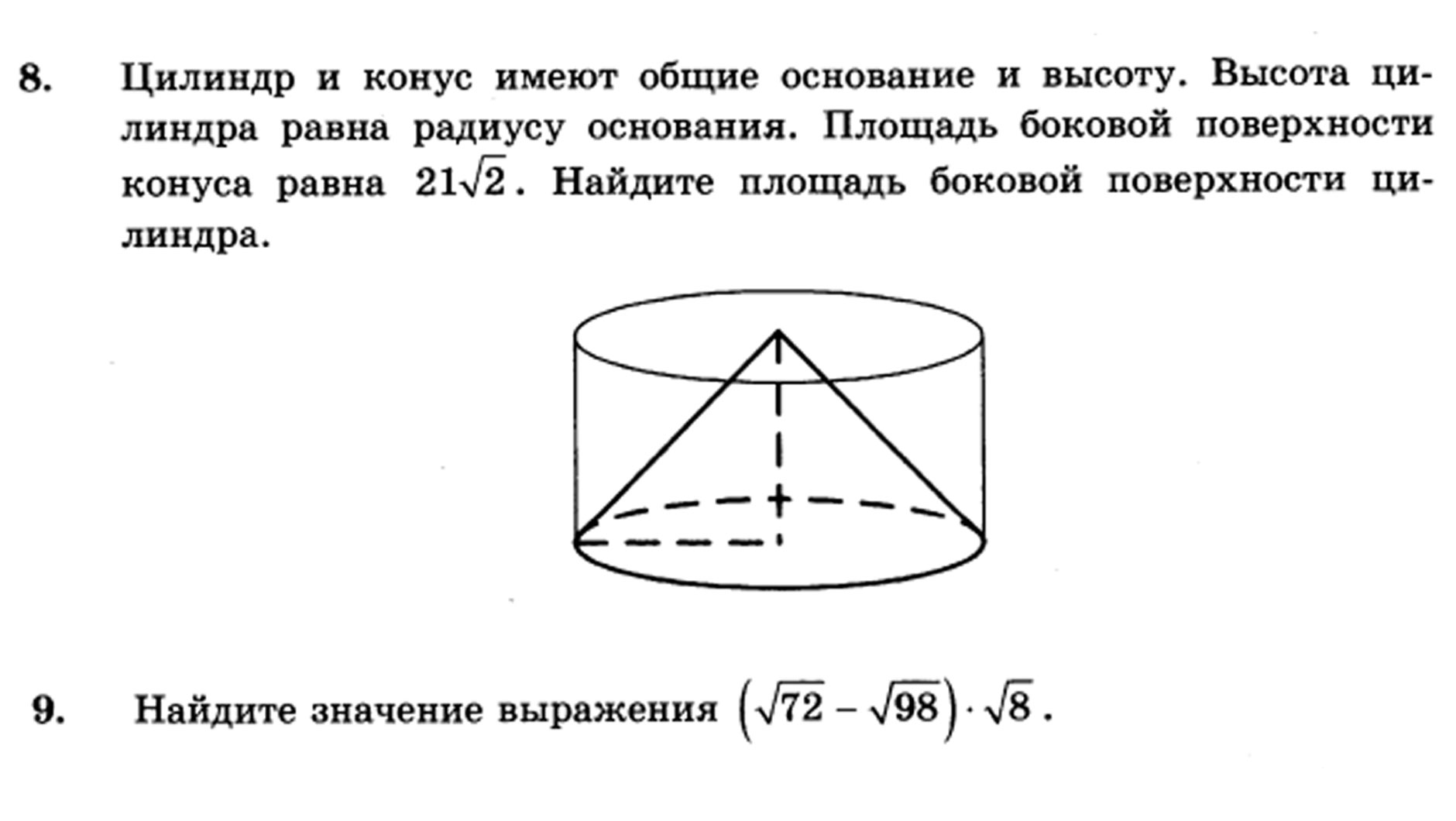
Задание 8
Для того, чтобы решить это задание, тебе нужно научиться представлять объёмную фигуру в пространстве, а также уметь соотносить размеры одной фигуры с другой. Для более чёткого понимания этой темы можешь склеить модели фигур из бумаги и использовать их при подготовке.
Задание 9
Чтобы получить максимальный балл за это задание, тебе нужно уделить особое внимание преобразованию тригонометрических выражений и их вычислению. В учебнике этому посвящён целый раздел, не поленись его изучить, если рассчитываешь на хороший результат.
Задание 14
В любой геометрической задаче важно знать свойства фигуры, которая в ней дана. Именно из-за недостаточных теоретических знаний выпускники путаются в последовательности решения, неправильно строят чертёж и пытаются самостоятельно вывести формулу вместо того, чтобы использовать уже существующую и не тратить время на долгие логические рассуждения.
Демоварианты ЕГЭ 2021: как сделать подготовку с их помощью эффективнее
Задание 16
Больше всего сложностей в этом задании возникает на этапе построения чертежа, поэтому важно быть внимательным. Неправильный рисунок разрушит твои шансы на успех ещё до того, как приступишь к расчётам. Баллы теряют также из-за неправильного построения доказательств, поэтому внимательно изучи теоремы, которые даются в учебнике, чтобы понять логику и не ошибиться.
Задание 17
Это пункт лучше всего показывает, как математика может помочь тебе в обычной жизни. Чаще всего ошибки в нём допускаются при вычислении и составлении модели задачи — выпускники не видят взаимосвязи между величинами и из-за этого путаются в них. И не забывай писать пояснения к своим действиям, так ты не запутаешься и не потеряешь драгоценные баллы.
Задание 19
Многие абитуриенты надеются на удачу и в этом задании пишут ответ да или нет наугад. Но даже в случае угадывания, этого недостаточно. Комиссии необходимо видеть аргументированное решение с пояснениями. Поэтому обрати внимание на раздел, который посвящён вероятности.
Решай как можно больше заданий из демовариантов и не забывай, что в борьбе за высокий балл на ЕГЭ у тебя всегда есть помощники. Заглядывай на наш канал, там много полезной информации для подготовки. Спасибо, что дочитал до конца. Мы рады, что были полезны. Чтобы получить больше информации, посмотри ещё:
Курсы подготовки к ЦТ 2021 в образовательном центре Адукар
Курсы подготовки к ЕГЭ 2021 в образовательном центре Адукар
Каталог учебных заведений Адукар
Не пропускай важные новости и подписывайся на наш YouTube, ВК, Instagram, Telegram, Facebook и уведомления на adukar.by.
***
Если хотите разместить этот текст на своём сайте или в социальной сети, свяжись с нами по адресу info@adukar.by. Перепечатка материалов возможна только с письменного согласия редакции.
Хочешь быть в курсе новостей ЦТ?
Подписывайся на Адукар в соцсетях!
Начни подготовку к ЦТ и ЦЭ прямо сейчас!

Адукар обещает крутых преподавателей и много полезной практики.
итоговые занятия перед ЦТ? Такие занятия мы проводим уже четвёртый год, и преподаватели нашего учебного центра
научились достаточно точно предсказывать, какие вопросы будут на ЦТ. На этом занятии мы прорешаем их вместе с тобой!
Регистрируйся,
если еще не сделал этого — и увеличь свои шансы на поступление!
Каким был ЕГЭ-2020 по математике?
Когда я увидела московский вариант ЕГЭ – он мне сразу понравился.
Вот разбор этого варианта на Ютьюбе:
Я сказала ученикам, что вариант простой. И что я решила его за максимально короткое время.
Смотрите сами. В этом варианте:
Стандартная задача № 13 (Тригонометрия).
Простые задачи № 14 (Стереометрия) и 15 (Неравенство).
Задача по планиметрии (№16) вызывает ощущение, что мы ее где-то видели. Стандартная, решается быстро.
«Экономическая» задача (№17) – обыкновенная.
Задача с параметром (№18) – новая. Уровень сложности – обычный.
И наконец, задача 19 на числа и их свойства – просто подарок. Легко, приятно, один за другим решаются все пункты – (а), (б) и (в).
Но оказалось, что я рано обрадовалась. И легким был только московский вариант.
Очень странно, что в разных городах на ЕГЭ дали разные по сложности варианты. Например, в краснодарском варианте более сложная, чем в московском, задача с параметром (№18). В варианте, который дали в Санкт-Петербурге, задача 16 более замысловатая, чем в московском. Что касается задачи 19 из питерского варианта – первые два пункта решаются легко, а пункт (в) невозможно решить обычными школьными методами. Скорее всего, составители варианта некорректно сформулировали условие.
Это не всё. Дмитрий Гущин, автор сайта РешуЕГЭ, отметил, что задание 15 (неравенство) оказалось одинаковым во всех регионах нашей большой страны. Неужели составители забыли, что в России одиннадцать часовых поясов? Когда выпускники в Магадане уже написали ЕГЭ, московские школьники еще не проснулись. А проснувшись, заглянули в соцсети и увидели, какие задачи были в других городах.
Так не должно быть. Не должно быть одинаковых заданий в разных регионах. Не должно быть вариантов, значительно отличающихся по уровню сложности. И тем не менее, они были!
Борис Трушин даже записал на эту тему видео: «ЕГЭ сломался, несите новый!» Но может быть, все-таки этот починить?
Давайте разберемся, что же там было, на ЕГЭ-2020. Какие сложные и необычные задачи достались выпускникам.
Санкт-Петербург, №14
В правильной четырёхугольной пирамиде SABCD сторона основания AB = 4, а боковое ребро SA = 7. На рёбрах AB и SB отмечены точки M и K соответственно, причём AM = SK = 1.
а) Докажите, что плоскость CKM перпендикулярна плоскости ABC.
б) Найдите объём пирамиды BCKM.
Посмотреть решение
Санкт-Петербург, №16
На сторонах AB, BC и AC треугольника ABC отмечены точки C1, A1 и B1 соответственно, причём AC1 : C1B = 8 : 3, BA1 : A1C = 1 : 2, CB1 : B1A = 3 : 1. Отрезки BB1 и CC1 пересекаются в точке D.
а) Докажите, что ADA1B1 — параллелограмм.
б) Найдите CD, если отрезки AD и BC перпендикулярны, AC = 28, BC = 18.
Посмотреть решение
Разберем несколько задач из варианта, который получили выпускники Краснодара. Задачи 16 и 17 – стандартные, задача 18 – сложная, задача 19 – обычный уровень сложности.
Краснодар, №16
Дан прямоугольный треугольник ABC. На катете AC отмечена точка M, а на продолжении катета BC за точку C — точка N так, что CM = CB и CA = CN.
а) Пусть CH и CF — высоты треугольников ABC и NMC соответственно. Докажите, что CF и CH перпендикулярны.
б) Пусть L — это точка пересечения BM и AN, BC = 2, AC = 5. Найдите ML.
Посмотреть решение
Краснодар, №17
В кредит взяли 220 тыс. рублей на 5 лет под r% годовых. По условиям кредита, на конец первых трех лет задолженность остается неизменной и равной 220 тысячам рублей, а выплаты последних двух лет равны. На конец пятого года кредит должен быть погашен. Найдите r если известно, что сумма всех выплат составит 420 тысяч рублей.
Посмотреть решение
Краснодар, №18
При каких значениях a система
имеет ровно два решения?
Посмотреть решение
Краснодар, №19
На доске написано несколько различных натуральных чисел, которые делятся на 3 и оканчиваются на 4.
а) Может ли сумма составлять 282?
б) Может ли их сумма составлять 390?
в) Какое наибольшее количество чисел могло быть на доске, если их сумма равна 2226?
Посмотреть решение
И наконец, та самая задача.
Санкт-Петербург, №19
На доске написано несколько различных натуральных чисел. Эти числа разбили на три группы, в каждой из которых оказалось хотя бы одно число. К каждому числу из первой группы приписали справа цифру 6, к каждому числу из второй группы приписали справа цифру 9, а числа третьей группы оставили без изменений.
а) Могла ли сумма всех этих чисел увеличиться в 9 раз?
б) Могла ли сумма всех этих чисел увеличиться в 19 раз?
в) В какое наибольшее число раз могла увеличиться сумма всех этих чисел?
Посмотреть решение
Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «ЕГЭ-2020 по математике. Сложные задачи, неравноценные варианты и одно неравенство для всей страны» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
09.03.2023
Выпускные экзамены по математике относятся к категории сложных. Поэтому требуют хороших знаний и предварительной подготовки, желательно с репетитором. Что нужно знать о самых сложных заданиях в математике по ЕГЭ 2023 г., есть ли изменения к КИМ, рекомендованные ФИПИ по предмету, и на какие нюансы стоит обратить детальное внимание, предлагаем узнать из нашей статьи.
Нововведения 2023 г.
ЕГЭ по математике имеет свои особенности, и будет оцениваться по пятибалльной (для базовой части) и четырехбальной (профильной) системе. Особенность сдачи предмета состоит в том, что учащийся должен заранее определиться, какой именно он будет сдавать экзамен – базовый или профильный.
Базовый после 11 класса сдается всеми выпускниками, относится к части №1 в ЕГЭ, и не подходит для поступления в ВУЗы и колледжи на такие специальности, как: инженерия, экономика, ИТ-сфера, физика, экономика, техника и т.д. Для его успешной сдачи достаточно школьной программы и основной теории.
Профильный экзамен, напротив, считается более углубленным, нужен для ВУЗа, требует основательной подготовки и хороших знаний. Важным нововведением части №1 (базовой) ЕГЭ по математике в 2023 г., для профильного экзамена, является требование к оцифровке ответов техническими средствами. Часть №2 будут проверять эксперты.
Для упрощенного базового ЕГЭ по математике в 2023 г. предложено 21 задание, каждое из них будет оцениваться по 1 ПБ (первичному баллу). Для получения положительного ответа школьнику достаточно выполнить всего 7 заданий. Наглядно оценивание выглядит таким образом:
Тематические разделы
|
Тематические разделы |
Количество заданий по ЕГЭ |
Процент общего оценивания |
|
Алгебра |
10 |
47% |
|
Геометрия |
5 |
24% |
|
Неравенства, уравнения, системы |
3 |
14% |
|
Начала математического анализа |
1 |
5% |
|
Функции |
1 |
5% |
|
Теория вероятности, статистика |
1 |
5% |
Из таблицы видно, что большинство баллов могут быть получены при решении стандартных заданий по базовой основе курса алгебры + геометрии + неравенств, уравнений и систем. Поэтому при подготовке к экзамену на них стоит обратить самое пристальное внимание.
Выставление баллов за задания по профильному экзамену осуществляется в 4 балла:
- 1 ПБ – № 1-11.
- 2 ПБ – № 12, 14, 15.
- 3 ПБ – № 13, 16.
- 4 ПБ – № 17, 18.
Полученные первичные баллы переводятся в 100-бальную систему:
Перевод баллов по ЕГЭ (математика) в 2023 г.
|
Перевод баллов по ЕГЭ (математика) в 2023 г. |
|
|
Первичный балл |
Тестовый балл |
|
1 |
5 |
|
2 |
9 |
|
3 |
14 |
|
4 |
18 |
|
5 |
23 |
|
6 |
27 |
|
7 |
33 |
|
8 |
39 |
|
9 |
45 |
|
10 |
50 |
|
11 |
56 |
|
12 |
62 |
|
13 |
68 |
|
14 |
70 |
|
15 |
72 |
|
16 |
74 |
|
17 |
76 |
|
18 |
78 |
|
19 |
80 |
|
20 |
82 |
|
21 |
84 |
|
22 |
86 |
|
23 |
88 |
|
24 |
90 |
|
25 |
92 |
|
26 |
94 |
|
27 |
96 |
|
28 |
98 |
|
29 |
99 |
|
30 |
100 |
|
31 |
100 |
В новом ЕГЭ 2023 г. все задания, кроме № 11, поменяли нумерацию. Задания с векторами и комплексными числами в экзамен включены не были.
Разбор демоверсии
По сложным заданиям, встречающимся в профильном ЕГЭ, желательно поработать заранее. Они требуют детального расписывания решения, которое должно соответствовать критериям оценивания.
Первые вопросы по математике – стандартные, по геометрии и стереометрии.
- 3, 4 – теория вероятности, в четвертом предлагается вариант с %.
- 5, 6 –уравнения и выражения, тригонометрия и степени.
- 7 – задание по графикам и производным.
- 8 – задача по формуле величин с подстановкой.
- 9 – вторая задача по теме динамики движений по прямой, окружности или молекул в составах.
- 10 – построение графика.
- 11 – вычисление графических производных, точек максимума/минимума
- 12 – требуется решение тригонометрического уравнения.
- 13 – задание по стереометрии с треугольной призмой.
- 14 – неравенства с логарифмами.
- 15 – экономическая задача про клиента банка, которому нужен расчет % и сумм выплат за взятый займ.
- 16 – задача по планиметрии про две окружности.
- 17 – требуется решение задания на параметры.
- 18 – сложная задача на целые числа.
Демоверсия доступна на официальном сайте ФИПИ. Можно посмотреть, как задания примерно будут выглядеть в бумажном файле. Если у учащегося возникают трудности с предметом, подготовиться к ЕГЭ по математике он может с репетитором.
Подводя итоги
Чтобы лучше разбираться в деталях экзамена, желательно скачать демоверсию КИМ, спецификации и кодификатор с сайта ФИПИ. При подготовке необходимо повторить функции тригонометрии, уметь решать обычные и квадратные уравнения, а также задания на поиск %.
ЕГЭ по математике 2023 г. состоит из 2-х частей:
- 1 часть – 35%, 11 ПБ по 11 заданиям с кратким ответом.
- 2 часть – 65%, 20 ПБ по 7 заданиям развернутого характера.
Для получения более 80 ТБ за профильный экзамен, необходимо решить 1 часть без ошибок, и обязательно выполнить задания № 12, 14, 15, 18 (а, б). Получить 100 ТБ помогут задачи по стереометрии и планиметрии. Длится профильный ЕГЭ по математике в 2023 г. 235 минут.
СДАМ ГИА:
РЕШУ ЕГЭ
Образовательный портал для подготовки к экзаменам
Математика профильного уровня
Математика профильного уровня
≡ Математика
Базовый уровень
Профильный уровень
Информатика
Русский язык
Английский язык
Немецкий язык
Французский язык
Испанский язык
Физика
Химия
Биология
География
Обществознание
Литература
История
Сайты, меню, вход, новости
СДАМ ГИАРЕШУ ЕГЭРЕШУ ОГЭРЕШУ ВПРРЕШУ ЦТ
Об экзамене
Каталог заданий
Варианты
Ученику
Учителю
Школа
Эксперту
Справочник
Карточки
Теория
Сказать спасибо
Вопрос — ответ
Чужой компьютер
Зарегистрироваться
Восстановить пароль
Войти через ВКонтакте
Играть в ЕГЭ-игрушку
Новости
10 марта
Как подготовиться к ЕГЭ и ОГЭ за 45 дней
6 марта
Изменения ВПР 2023
3 марта
Разместили утвержденное расписание ЕГЭ
27 января
Вариант экзамена блокадного Ленинграда
23 января
ДДОС-атака на Решу ЕГЭ. Шантаж.
6 января
Открываем новый сервис: «папки в избранном»
22 декабря
Открыли новый портал Решу Олимп. Для подготовки к перечневым олимпиадам!
4 ноября
Материалы для подготовки к итоговому сочинению 2022–2023
31 октября
Сертификаты для учителей о работе на Решу ЕГЭ, ОГЭ, ВПР
21 марта
Новый сервис: рисование
31 января
Внедрили тёмную тему!
НАШИ БОТЫ
Все новости
ЧУЖОЕ НЕ БРАТЬ!
Экзамер из Таганрога
10 апреля
Предприниматель Щеголихин скопировал сайт Решу ЕГЭ
Наша группа
Каталог заданий
Задания Д8 C1. Уравнения, системы уравнений. Сложные уравнения смешанного типа
Пройти тестирование по 10 заданиям
Пройти тестирование по всем заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Задания Д8 C1 № 505640
а) Решите уравнение
б) Найдите все корни на промежутке
Источник: А. Ларин: Тренировочный вариант № 48.
Классификатор алгебры: Показательные уравнения, Тригонометрические уравнения, Тригонометрические уравнения, решаемые разложением на множители, Уравнения смешанного типа
Методы алгебры: Формулы двойного угла
Решение
·
·
Сообщить об ошибке · Помощь
2
Задания Д8 C1 № 505646
а) Решите уравнение
б) Найдите все корни на промежутке
Аналоги к заданию № 505646: 506044 Все
Источник: А. Ларин: Тренировочный вариант № 49.
Классификатор алгебры: Показательные уравнения, Тригонометрические уравнения
Методы алгебры: Формулы двойного угла
Решение
·
·
Сообщить об ошибке · Помощь
3
Задания Д8 C1 № 505706
а) Решите уравнение
б) Найдите все корни на промежутке
Источник: А. Ларин: Тренировочный вариант № 59.
Классификатор алгебры: Логарифмические уравнения, Однородные тригонометрические уравнения, Тригонометрические уравнения, Тригонометрические уравнения, сводимые к целым на тангенс или котангенс, Уравнения смешанного типа
Решение
·
·
Сообщить об ошибке · Помощь
4
Задания Д8 C1 № 505766
а) Решите уравнение
б) Найдите все корни на промежутке
Источник: А. Ларин: Тренировочный вариант № 69.
Классификатор алгебры: Логарифмические уравнения, Тригонометрические уравнения, Тригонометрические уравнения, решаемые разложением на множители, Уравнения смешанного типа
Методы алгебры: Формулы двойного угла
Решение
·
·
Сообщить об ошибке · Помощь
5
Задания Д8 C1 № 505790
а) Решите уравнение
б) Найдите все корни на промежутке
Источник: А. Ларин: Тренировочный вариант № 73.
Классификатор алгебры: Логарифмические уравнения, Тригонометрические уравнения
Методы алгебры: Формулы двойного угла
Решение
·
·
Сообщить об ошибке · Помощь
Пройти тестирование по этим заданиям
О проекте · Редакция · Правовая информация · О рекламе
© Гущин Д. Д., 2011—2023
Задания ЕГЭ с развернутым ответом — самые сложные в экзамене по любому предмету. А о математике так вообще ходят легенды! Выпускники настолько боятся этих задач, что даже не пытаются к ним готовиться, пропускают, не читая, во время экзамена. И это стоит им стольких баллов!
Что из себя представляют задания с развернутым ответом в ЕГЭ по математике?
Вторая часть экзамена по профильной математике целиком состоит из заданий ЕГЭ с развернутым ответом — от №12 до №18. Они проверяют углубленное знание предмета, поэтому без решения хотя бы их части невозможно получить 80+ баллов.
Задание №12 — это решение сложного уравнения и определение корней в рамках обозначенного отрезка. За него можно получить максимум 2 балла.
Задание №13 — это геометрическая задача на доказательство утверждения и нахождение одного из показателей. Максимальный балл — 3.
Задание №14 — это решение сложного неравенства (например, логарифмического). Максимальный балл — 2.
Задание №15 — классическая экономическая задача. За нее можно получить до 2 баллов.
Задание №16 — сложная геометрическая задача, с которой справляются только 2.7% выпускников. Проверяется примерно то же, что в №13, и приносит также 3 балла.
Задание №17 — это решение системы уравнений. При этом, нужно будет найти все возможные переменные, соответствующие заданному условию (например, положительные, при которых система имеет только одно решение). Максимальный балл — 4.
Задание №18 — это работа с теорией чисел, в которой придется руководствоваться не только знаниями, но и старым добрым логическим подбором. Максимальный балл — 4.
В чем их основная сложность?
Задания ЕГЭ с развернутым ответом №12, 14, 15 самые легкие из второй части, поэтому их желательно научиться решать в первую очередь. Они принесут дополнительные баллы и позволят получить высокий результат на экзамене.
А вот №16–18 — номера повышенной сложности, с которыми удается справиться далеко не каждому выпускнику. Для их решения потребуется основательная подготовка.
При этом, при подготовке и решении второй части ЕГЭ по математике нужно помнить об оформлении и доказательной базе. Забытое ОДЗ при решении уравнения или неравенства или непоясненное действие при доказательстве может стоить драгоценных баллов!
Как решать задания с развернутым ответом?
Решать задания ЕГЭ с развернутым ответом нужно с самых простых задач: например, с простых алгебраических вычислений (№12, 14). После подготовки и регулярного нарешивания они не займут на самом экзамене много времени. После можно выполнить экономическую задачу и все, что получается решить. В оставшееся время нужно проверить ответы и попытаться решить оставшееся.
При подготовке можно руководствоваться правилами оформления прошлого года, но нужно помнить про изменившуюся нумерацию!
Почему стоит браться за эти задачи?
Большинство выпускников в принципе не берется за решение второй части, поэтому правильно решенная первая часть и задачи из второй — сильное конкурентное преимущество. Именно они станут залогом 90+ за математику и позволят поступить на бюджет в самые престижные вузы страны.
Что говорит статистика?
И преимущество перед другими будет действительно колоссальным, потому что по статистике правильно решают задачи второй части единицы:
- около 30% — за №12,
- около 2% — за №13,
- около 12% — за №14,
- около 15% — за №15,
- около 2,7% — за №16,
- около 1% — за №17 и №18.
Без подготовки решить вторую часть по математике практически нереально. Именно этим объясняются неутешительные проценты выполнения номеров и средние баллы по предмету. Но такая сложность — это конкурентное преимущество подготовившихся учеников, которое поможет поступить в вуз мечты!
4. Введение в теорию вероятностей
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
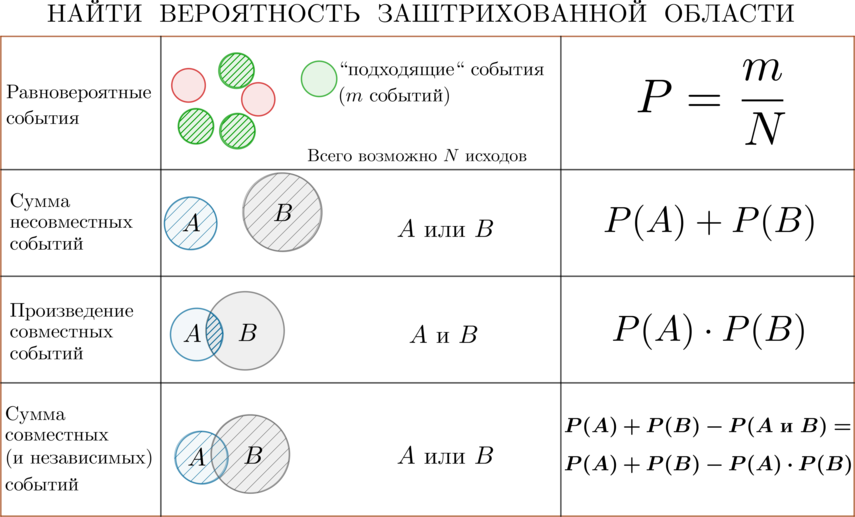
Сложные задачи по теории вероятности
Общая памятка по всем разделам теории вероятностей:
Задание
1
#3858
Уровень задания: Равен ЕГЭ
Чтобы пройти в следующий круг соревнований, футбольной команде нужно набрать хотя бы (4) очка в двух играх. Если команда выигрывает, она получает (3) очка, в случае ничьей — (1) очко, если проигрывает — (0) очков. Найдите вероятность того, что команде удастся выйти в следующий круг соревнований. Считайте, что в каждой игре вероятности выигрыша и проигрыша одинаковы и равны (0,3).
Чтобы команда в двух играх набрала не менее (4) очков, ей нужно: либо 1) выиграть обе игры, либо 2) выиграть в одной из игр и сыграть вничью в другой игре.
Так как вероятности выиграть и проиграть одинакова и равна (0,3), то вероятность сыграть вничью равна (1-0,3-0,3=0,4).
Следовательно, вероятности в этих случаях равны соответственно:
1) (0,3cdot 0,3)
2) (0,3cdot 0,4+0,4cdot 0,3) (выиграть в первой игре и сыграть вничью во второй или сыграть вничью в первой и выиграть во второй).
Следовательно, вероятность того, что команда выйдет в следующий круг соревнований, равна [0,3cdot 0,3+0,3cdot 0,4+0,4cdot 0,3=0,33]
Ответ: 0,33
Задание
2
#2739
Уровень задания: Сложнее ЕГЭ
Илья решает задачу по геометрии, в которой дан четырёхугольник (ABCD), причём (AB = 5), (BC = 6), (CD = 4), (AD = 10). В условии задачи сказано, что одна из вершин является центром некоторой окружности и Илья думает, какую вершину ему выбрать в качестве центра этой самой окружности.
Известно, что вероятность выбора каждой конкретной вершины пропорциональна сумме длин сторон четырёхугольника (ABCD), проходящих через эту вершину. Какова вероятность того, что Илья выберет вершину (B)?
Через вершину (A) проходят стороны (AB) и (AD), их сумма: (AB + AD = 15).
Через вершину (B) проходят стороны (AB) и (BC), их сумма: (AB + BC = 11).
Через вершину (C) проходят стороны (BC) и (CD), их сумма: (BC + CD = 10).
Через вершину (D) проходят стороны (CD) и (DA), их сумма: (CD + DA = 14).
Обозначим вероятность выбора вершины (A) через (P(A)) (для остальных вершин аналогично). Тогда по условию имеем: [P(A) = 15k,qquad P(B) = 11k,qquad P(C) = 10k,qquad P(D) = 14k,,] но (P(A) + P(B) + P(C) + P(D) = 1), тогда (k = 0,02), откуда находим: (P(B) = 0,22).
Ответ: 0,22
Задание
3
#191
Уровень задания: Сложнее ЕГЭ
Монетку подбросили 10 раз. Какова вероятность того, что выпало не менее 9 орлов? Ответ округлите до тысячных.
Условие того, что выпало не менее 9 орлов эквивалентно тому, что выпало не более 1 решки, то есть либо ровно 1 решка, либо 0 решек.
Количество всевозможных различных исходов в серии из 10 испытаний равно (2^{10} = 1024).
Среди них есть 11 исходов, подходящих под условие: (Орёл; Орёл; …; Орёл), (Орёл; Орёл; …; Орёл; Решка), (Орёл; Орёл; …; Решка; Орёл), …, (Решка; Орёл; …; Орёл), следовательно, искомая вероятность равна [dfrac{11}{1024}.] После округления получим (0,011).
Ответ: 0,011
Задание
4
#190
Уровень задания: Сложнее ЕГЭ
Монетку подбросили 3 раза. Какова вероятность того, что выпало не менее 3 орлов? Ответ округлите до тысячных.
Условие того, что выпало не менее 3 орлов эквивалентно тому, что выпали только орлы.
Количество всевозможных различных исходов в серии из 3 испытаний равно (2^3 = 
Ответ: 0,125
Задание
5
#189
Уровень задания: Сложнее ЕГЭ
Монетку подбросили 2 раза. Какова вероятность того, что выпало не менее 1 орла? Ответ округлите до тысячных.
Всевозможных исходов в серии из 2 подбрасываний может быть (2^2 = 4): (Орёл; Орёл), (Орёл; Решка), (Решка; Орёл), (Решка; Решка).
Среди выписанных (всевозможных) исходов под условие задачи подходят первые 3, следовательно, искомая вероятность равна [dfrac{3}{4} = 0,75.]
Ответ: 0,75
Задание
6
#2658
Уровень задания: Сложнее ЕГЭ
Игорь трижды подбрасывает правильную игральную кость. Какова вероятность того, что за эти три подбрасывания ровно один раз выпадет число, кратное трём, а сумма результатов подбрасываний не будет делиться на (3)? Ответ округлите до сотых.
Так как игральная кость правильная, то вероятность выпадения каждой грани равна (dfrac{1}{6}). Среди чисел на гранях есть два числа, дающих при делении на (3) остаток (0), два числа, дающих при делении на (3) остаток (1) и два числа, дающих при делении на (3) остаток (2).
Тогда вероятность за одно подбрасывание получить, например, число, дающее при делении на (3) остаток (1), равна (dfrac{1}{3}). С другими остатками аналогично.
Условие задачи можно переформулировать в следующем виде: какова вероятность за три подбрасывания получить результаты, остатки от деления на (3) которых будут содержать единственный (0) и два одинаковых числа?
Таким образом, нас устраивают исходы, остатки от деления на (3) которых будут иметь вид:
[begin{aligned}
&0,quad 1,quad 1\
&1,quad 0,quad 1\
&1,quad 1,quad 0\
&0,quad 2,quad 2\
&2,quad 0,quad 2\
&2,quad 2,quad 0,.
end{aligned}]
Вероятность любого из выписанных исходов равна [dfrac{1}{3}cdot dfrac{1}{3}cdot dfrac{1}{3},.] При этом различных исходов здесь шесть, следовательно, вероятность получения подходящего исхода равна [6cdot dfrac{1}{3}cdot dfrac{1}{3}cdot dfrac{1}{3} = dfrac{2}{9},.] После округления получим ответ (0,22).
Ответ: 0,22
Задание
7
#2765
Уровень задания: Сложнее ЕГЭ
Таня заметила, что в казино “Подкинем” используют неправильную игральную кость (т.е. не у всех граней вероятности выпадения одинаковы). При этом она установила, что вероятность выпадения чётного числа равна (0,6); вероятность выпадения числа, делящегося на (3), равна (0,3); вероятность того, что выпадет (1) или (5), равна (0,22). Найдите вероятность того, что на этой игральной кости выпадет число (3). Ответ округлите до сотых.
Вероятность выпадения числа (n) обозначим через (P({n})), вероятность выпадения одного из чисел (m) и (n) обозначим через (P({m; n})), а вероятность выпадения одного из чисел (m), (n) и (k) обозначим через (P({m; n; k})). Тогда [P({2; 4; 6}) = 0,6qquadLeftrightarrowqquad P({1; 3; 5}) = 1 — 0,6 = 0,4]
При этом (P({1; 5}) = 0,22), но ведь (P({1; 3; 5}) — P({1; 5}) = P({3})), следовательно, [P({3}) = 0,4 — 0,22 = 0,18,.]
Ответ: 0,18
Если выпускник готовится к сдаче ЕГЭ по математике профильного уровня, ему необходимо научиться решать задачи на применение теории вероятности повышенной сложности. Как показывает практика многих лет, такие задания являются обязательной частью программы аттестационного испытания. Поэтому если учащийся не до конца понимает принцип решения сложных задач на теорию вероятности, ему обязательно стоит вновь разобраться в данной теме.
Вместе с образовательным порталом «Школково» старшеклассники смогут качественно подготовиться к прохождению аттестационного испытания. Наш сайт позволит определить наиболее сложные темы и восполнить пробелы в знаниях. Опытные специалисты «Школково» подготовили весь необходимый материал, изложив его таким образом, чтобы школьники с любым уровнем подготовки смогли легко справиться с решением сложных задач ЕГЭ на теорию вероятности. Базовая информация по данной теме представлена в разделе «Теоретическая справка».
Чтобы попрактиковаться в выполнении сложных задач ЕГЭ по теории вероятности, школьники могут выполнить соответствующие упражнения. Простые и сложные задания, подобранные нашими специалистами, содержат подробные алгоритмы решения и правильные ответы. База заданий регулярно обновляется и дополняется.
Выполнять упражнения школьники из Москвы и других российских городов могут в онлайн-режиме. При необходимости задания по теории вероятности в ЕГЭ можно сохранить в разделе «Избранное». Благодаря этому вы сможете быстро найти интересующие примеры и обсудить алгоритмы нахождения правильного ответа с преподавателем.

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ