Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
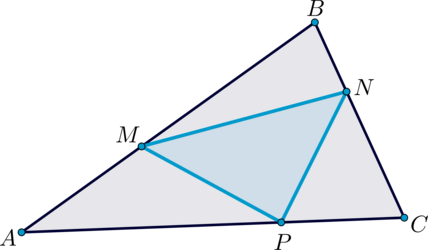
В треугольнике АВС проведена биссектриса АМ. Прямая, проходящая через вершину В перпендикулярно АМ, пересекает сторону АС в точке N. АВ = 6; ВС = 5; АС = 9.
а) докажите, что биссектриса угла С делит отрезок МN пополам
б) пусть Р — точка пересечения биссектрис треугольника АВС. Найдите отношение АР : РN.
Источник: ЕГЭ по математике 19.06.2014. Основная волна, резервная волна. Запад. Вариант 1
2
Диагональ AC прямоугольника ABCD с центром O образует со стороной AB угол 30°. Точка E лежит вне прямоугольника, причём ∠BEC = 120°.
а) Докажите, что ∠CBE = ∠COE.
б) Прямая OE пересекает сторону AD прямоугольника в точке K. Найдите EK, если известно, что BE = 40 и CE = 24.
3
Медианы AA1, BB1 и CC1 треугольника ABC пересекаются в точке M. Известно, что AC = 3MB.
а) Докажите, что треугольник ABC прямоугольный.
б) Найдите сумму квадратов медиан AA1 и CC1, если известно, что AC = 12.
4
На сторонах AC и BC треугольника ABC вне треугольника построены квадраты ACDE и BFKC. Точка M — середина стороны AB.
а) Докажите, что
б) Найдите расстояние от точки M до центров квадратов, если AC = 10, BC = 32 и ∠ACB = 30°.
Источник: Типовые тестовые задания по математике, под редакцией И. В. Ященко 2016
5
На гипотенузу AB прямоугольного треугольника ABC опустили высоту CH. Из точки H на катеты опустили перпендикуляры HK и HE.
а) Докажите, что точки A, B, K и E лежат на одной окружности.
б) Найдите радиус этой окружности, если AB = 12, CH = 5.
Пройти тестирование по этим заданиям
16. Задачи по планиметрии
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Задачи по планиметрии
Задание
1
#2436
Уровень задания: Легче ЕГЭ
Точки (M, N, P) лежат на сторонах (AB, BC, CA) соответственно треугольника (ABC), причем (AM:AB=BN:BC=CP:CA=1:3). Площадь треугольника (MNP) равна (15). Найдите площадь треугольника (ABC).
(triangle ABC) и (triangle MBN) имеют общий угол (B), при этом (BM=frac23BA), (BN=frac13BC).
Т.к. площади треугольников, имеющих общих угол, относятся как произведения сторон, образующих этот угол, то
[dfrac{S_{MBN}}{S_{ABC}}=dfrac{frac23BAcdot frac13BC}{BAcdot BC}=
dfrac29 quad Rightarrow quad S_{MBN}=dfrac29S_{ABC}]
Аналогично рассуждая, получаем, что
[S_{MAP}=S_{PCN}=dfrac29S_{ABC}]
Следовательно, [15+3cdot dfrac29S_{ABC}=S_{ABC} quad Rightarrow
quad S_{ABC}=3cdot 15=45.]
Ответ: 45
Задание
2
#2444
Уровень задания: Легче ЕГЭ
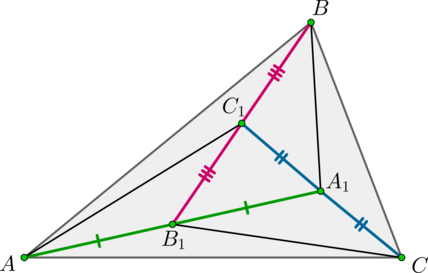
Внутри треугольника (ABC) взяты точки (A_1, B_1, C_1) так, что (B_1) – середина (AA_1), (C_1) – середина (BB_1), (A_1) – середина (CC_1). Найдите отношение площадей треугольников (A_1B_1C_1) и (ABC).
Соединим точки (A) и (C_1), (B) и (A_1), (C) и (B_1).
Т.к. медиана делит треугольник на два равновеликих треугольника, то
[S_{triangle AB_1C}=S_{triangle A_1B_1C}=S_{triangle A_1B_1C_1}.]
Аналогично,
[S_{triangle CA_1B}=S_{triangle C_1A_1B}=S_{triangle AC_1B}=S_{triangle
AC_1B_1}.]
Таким образом, все семь образовавшихся треугольников имеют одинаковые площади. Значит,
[S_{triangle A_1B_1C_1}:S_{triangle ABC}=1:7.]
Ответ:
(1:7)
Задание
3
#1760
Уровень задания: Равен ЕГЭ
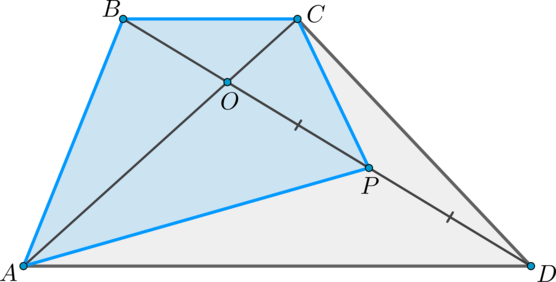
Дана трапеция (ABCD), ее основания (BC) и (AD) равны (2) и (6) соответственно. Диагонали (BD) и (AC) пересекаются в точке (O). Точка (P) – середина (OD). (S_{bigtriangleup ABO}=9). Найдите площадь четырехугольника (ABCP).
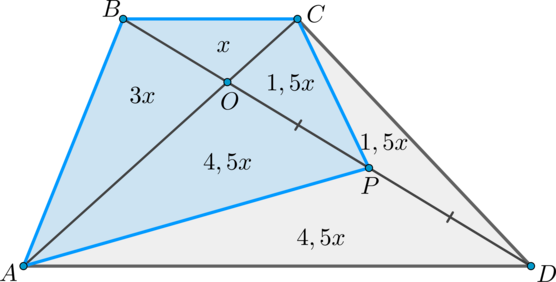
Пусть (S_{bigtriangleup BOC}=x). Заметим, что (bigtriangleup BCO
sim bigtriangleup AOD) по двум углам, так как (BCparallel AD), (angle BCA = angle CAD) как накрест лежащие и (angle BOC = angle
AOD) как вертикальные.
Следовательно, [dfrac{BC}{AD} =dfrac{BO}{OD} =dfrac{CO}{OA}
=dfrac{2}{6} =dfrac{1}{3}.]
(dfrac{S_{bigtriangleup ABO}}{S_{bigtriangleup BCO}}
=dfrac{AO}{OC} =dfrac{3}{1} Rightarrow S_{bigtriangleup
ABO}=3x), аналогично, (S_{bigtriangleup CDO}=3x).
(dfrac{S_{bigtriangleup COP}}{S_{bigtriangleup CPD}}
=dfrac{OP}{PD} =dfrac{1}{1} Rightarrow S_{bigtriangleup
COP}=S_{bigtriangleup CPD}=1,5x).
Площади подобных треугольников относятся как коэффициент подобия в квадрате, следовательно, [dfrac{S_{bigtriangleup BOC}}{S_{bigtriangleup AOD}} =left(
dfrac{1}{3} right)^2 =dfrac{1}{9} Rightarrow
S_{bigtriangleup ADO}=9x Rightarrow S_{bigtriangleup APO}=4,5x
Rightarrowqquad S_{ABCP}=10x.] Так как (3x=9), то (x=3) и, следовательно, (S_{ABCP}=30).
Ответ: 30
Задание
4
#2441
Уровень задания: Равен ЕГЭ
Внутри равностороннего треугольника со стороной (m) движется точка. Докажите, что сумма расстояний от этой точки до сторон треугольника не меняется, и найдите эту сумму.
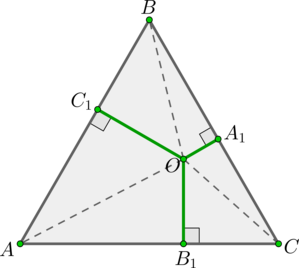
Рассмотрим равносторонний (triangle ABC), (AB=m), (O) – точка внутри треугольника, (OA_1, OB_1, OC_1) — перпендикуляры на стороны (BC, AC, AB) соответственно.
Рассмотрим (triangle AOB, triangle BOC, triangle COA). Их площади равны (0,5mcdot OC_1; 0,5mcdot OA_1; 0,5mcdot OB_1) соответственно. Тогда сумма их площадей равна площади всего (triangle ABC), следовательно:
[0,5mcdot (OC_1+OA_1+OB_1)=S_{triangle ABC}=dfrac{sqrt3}4m^2 quad
Leftrightarrow quad OC_1+OA_1+OB_1=dfrac{sqrt3}2m.]
Таким образом, мы доказали, что для фиксированного равностороннего треугольника сумма постоянна, а также нашли ее.
Ответ:
(dfrac{sqrt3}2m)
Задание
5
#1287
Уровень задания: Равен ЕГЭ
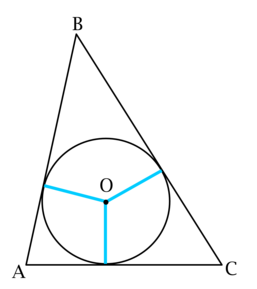
Радиус вписанной в треугольник (ABC) окружности равен трети одной из его высот.
а) Докажите, что одна из сторон треугольника (ABC) равна среднему арифметическому двух других его сторон.
б) Найдите наибольшее возможное значение периметра такого треугольника, если одна из его сторон равна (4), а две другие имеют целые длины.
а) (S_{ABC} = pcdot r), где (p) – полупериметр, а (r) – радиус вписанной в (ABC) окружности.
Пусть (h) – длина той высоты, которая равна (3r), (a) – длина стороны, высота к которой имеет длину (h), (P) – периметр треугольника (ABC).
В итоге имеем: [dfrac{1}{2}hcdot a = S_{ABC} = pcdot r = pcdotdfrac{h}{3},] откуда (a = dfrac{P}{3}), тогда (b + c = dfrac{2P}{3} = 2a), где (b) и (c) длины других сторон треугольника.
б) Длины сторон треугольника (ABC) образуют арифметическую прогрессию: если обозначить (a — c = d), то (a = c + d), (b = c + 2d).
Пусть (d > 0). Тогда (b) наибольшая сторона треугольника (ABC) и существование треугольника (ABC) с длинами сторон (a), (b) и (c) равносильно выполнению неравенства [b < a + cqquadLeftrightarrowqquad c + 2d < 2c + dqquadLeftrightarrowqquad d < c.] Так как длины всех сторон треугольника (ABC) – целые числа, то (d) – целое, следовательно, (dleq c — 1).
Так как (c) – меньшая из сторон, то (cleq 4), тогда (dleq 3), откуда (aleq 7), (bleq 10), тогда [P_{triangle ABC}leq 4 + 7 + 10 = 21.] При этом случай (c = 4), (a = 7), (b = 10) подходит, следовательно, при (d > 0) максимально возможный периметр равен 21.
При (d = 0) треугольник (ABC) равносторонний и (P_{triangle ABC} = 12 < 21).
Случай (d < 0) рассматривается аналогично (меняется только то, что (c > a > b), следовательно, достаточно в рассуждении из случая (d > 0) всюду поменять местами (b) и (c)).
Таким образом, наибольший возможный периметр треугольника (ABC) равен 21.
Ответ:
б) (21).
Задание
6
#1288
Уровень задания: Равен ЕГЭ
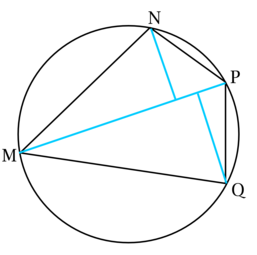
Четырёхугольник (MNPQ) вписан в окружность, причём (dfrac{MN}{PQ} = dfrac{QM}{PN}).
а) Докажите, что точки (N) и (Q) равноудалены от прямой, содержащей (MP).
б) Найдите расстояние от точки (P) до прямой, содержащей (MQ), если (MP = 4), расстояние от (N) до прямой, содержащей (MP) равно (1,5), (MQ = 3).
а) Так как (dfrac{MN}{PQ} = dfrac{QM}{PN}), то (MNcdot PN = QMcdot PQ).
Так как (MNPQ) вписанный, то (angle MNP = 180^circ — angle MQP), следовательно, (sinangle MNP = sinangle MQP).
В итоге [S_{triangle MNP} = 0,5cdot MNcdot PNcdotsinangle MNP = 0,5cdot QMcdot PQcdotsinangle MQP = S_{triangle MQP}.]
С другой стороны, у треугольников (MNP) и (MQP) общее основание, следовательно, их площади относятся как высоты, проведённые к этому основанию, тогда эти высоты равны, значит, точки (N) и (Q) равноудалены от прямой, содержащей (MP).
б) В данном случае (S_{triangle MNP} = 0,5cdot 4cdot 1,5 = 3), но (S_{triangle MNP} = S_{triangle MQP}). Обозначим расстояние от точки (P) до прямой, содержащей (MQ) через (h), тогда [S_{triangle MQP} = 3 = 0,5cdot 3cdot h,] следовательно, (h = 2).
Ответ:
б) (2).
Задание
7
#1289
Уровень задания: Равен ЕГЭ
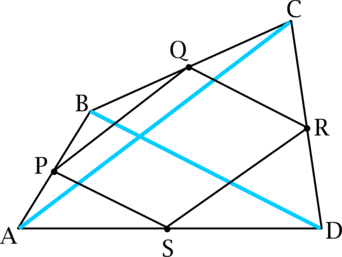
(ABCD) – выпуклый четырёхугольник, точки (P), (Q), (R) и (S) середины его сторон, причём (PQRS) тоже выпуклый четырёхугольник. (A_1B_1C_1D_1) другой выпуклый четырёхугольник с серединами сторон в точках (P), (Q), (R) и (S).
а) Докажите, что диагонали (PQRS) точкой пересечения делятся пополам.
б) Найдите максимально возможное значение величины (dfrac{S_{A_1B_1C_1D_1}}{S_{ABCD}}).
а) Проведём диагонали (AC) и (BD).
Рассмотрим треугольники (APS) и (ABD): (PS) – средняя линия в треугольнике (ABD), тогда треугольники (APS) и (ABD) подобны, причём (dfrac{PS}{BD} = dfrac{1}{2}).
Аналогично (dfrac{QR}{BD} = dfrac{1}{2}), следовательно, (PS = QR).
Аналогично доказывается равенство (PQ = RS). В итоге в выпуклом четырёхугольнике (PQRS) противоположные стороны равны, тогда (PQRS) – параллелограмм, следовательно, его диагонали точкой пересечения делятся пополам.
б) Докажем, что по взаимному расположению середин сторон выпуклого четырёхугольника его площадь восстанавливается однозначно.
Из подобия (APS) и (ABD) получаем: [dfrac{S_{APS}}{S_{ABD}} = left(dfrac{1}{2}right)^2 = dfrac{1}{4}.]
Аналогично (4S_{QCR} = S_{CBD}), (4S_{PBQ} = S_{ABC}), (4S_{SDR} = S_{ACD}). Тогда [S_{ABCD} = S_{ABD} + S_{CBD} = 4S_{APS} + 4S_{QCR}.] С другой стороны, [S_{ABCD} = S_{ABC} + S_{ACD} = 4S_{PBQ} + 4S_{SDR},] тогда [S_{ABCD} + S_{ABCD} = 4S_{APS} + 4S_{QCR} + 4S_{PBQ} + 4S_{SDR} qquadLeftrightarrow] [S_{APS} + S_{QCR} + S_{PBQ} + S_{SDR} = dfrac{1}{2}S_{ABCD}.] Но (S_{ABCD} = S_{APS} + S_{QCR} + S_{PBQ} + S_{SDR} + S_{PQRS}), откуда окончательно [S_{PQRS} = dfrac{1}{2}S_{ABCD}.]
Таким образом, по взаимному расположению точек (P), (Q), (R), (S) однозначно восстанавливается площадь параллелограмма (PQRS), а значит и площадь любого выпуклого четырёхугольника с серединами сторон в точках (P), (Q), (R) и (S).
В итоге [dfrac{S_{A_1B_1C_1D_1}}{S_{ABCD}} = 1.]
Ответ:
б) (1).

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
ХVII
Региональная научно-практическая конференция
«Колмогоровские
чтения»
Автор – Кобаидзе Н. И.
Тема: Геометрия в ЕГЭ
Цель: научиться решать задачи по геометрии чётко,
компактно, быстро и просто.
1. Рассмотреть
некоторые задачи по планиметрии из ЕГЭ
и различные способы их решения.
2. Рассмотреть задачи
по стереометрии из ЕГЭ
и различные способы их решения.
Актуальность.
В
настоящее время задачи по геометрии в вариантах ЕГЭ представлены двумя
задачами в базовой части и двумя задачами серии С.
Разбор решений актуален на различных консультациях, факультативах и кружках.
Явной особенностью нынешних задач по
планиметрии является подбор задач
с двумя решениями. В стереометрии типичным случаем является попадания (или не
попадания) основания высоты треугольника внутрь противолежащей стороны.
Ещё встречаются случаи разного характера касания прямой и окружности, наличие
двух полуплоскостей и т. п.
I. Вступление
Год от года место
геометрических задач в вариантах трансформируется в зависимости от текущих
образовательных тенденций. Результат выполнения ЕГЭ не влияет на оценку в
аттестате школьника, это влияние ограничивается дилеммой типа «зачёт –
незачёт». Это проблема для учителя. Набрав необходимый минимум на обязательных
экзаменах, школьник получает аттестат, а отметки в аттестате по алгебре и
геометрии определяет учитель.
Для решения
(проверки владения материалом) задач базового уровня требуется знание формул
площади основных геометрических фигур или объёмов базовых геометрических тел.
А задачи серии С — посложнее, причём задача по стереометрии традиционно проще
задачи по планиметрии. Все задачи, так или иначе, черпаются из богатой
коллекции конкурсных задач МГУ или МФТИ прошлых лет. Обычно возникают различные
проблемы или ситуации от того, когда школьник на чертеже рисует к-н точку между
двумя другими. Поэтому нужно задуматься, а не возможна ли другая конфигурация
точек?
II. Основная
часть.
1.
Планиметрические задачи из ЕГЭ.
Решение
планиметрической задачи будем организовывать следующим образом.
1. Рисуем чертеж. Это довольно
ответственная часть решения, от чертежа может зависеть успех в решении задачи.
2. Задаем один из приведенных ниже четырех
вопросов.
Начинаем всегда с первого из них.
Второй обычно явно задавать не будем, он подразумевается при ответе на первый
вопрос.
Если процесс решения теряет динамику, задаем третий или четвертый вопрос.
На каждом шаге решения приоритет отводится первому вопросу.
3. В
зависимости от ответа на поставленный вопрос выполняем
соответствующие рекомендации и либо получаем путь от данных к результату, либо
в обновленной с учетом выполненных действий задаче снова задаем вопрос.
Так поступаем до тех пор, пока не будет получено решение.
Сформулируем четыре вопроса, которые
будем задавать при решении
задачи, а также дан набор рекомендаций,
которые надлежит выполнять
после ответа на поставленный вопрос.
Вопрос 1. В чем особенности задачи?
При ответе на этот вопрос надо отметить, какие есть фигуры, с какой целью
сообщены те или иные данные, какие есть выдающиеся отрезки и т. д.
В результате ответа на этот вопрос
желательно выбрать такой
фрагмент из предлагаемого ниже набора шаблонов, который присутствует
в данной задаче. При выборе фрагмента, скорее всего, надо отвлечься от
каких-то деталей, не присущих найденному
фрагменту, и учесть их
в дальнейшем.
После нахождения фрагмента надо выполнить соответствующие ему пожелания и
продолжить решение, снова задавая один из вопросов.
Вопрос 2. Что можно получить из данных за
один шаг? Этот
вопрос, по существу, продолжает первый,
ибо мы будем фактически
отвечать на него при обработке найденных после первого вопроса фрагментов, так
что обычно не будем его ставить в явном виде.
Действие, связанное с этим вопросом, можно назвать ходом вперед, от условия к
результату. В качестве ответа выводим простые, непосредственные следствия из
имеющихся данных, чем по существу изменяем эти данные, обогащая их и тем самым
переходя к новой задаче с увеличенным набором данных.
Вопрос 3.
Откуда можно получить требуемое за один шаг?
Это ход назад, от требуемого к условиям,
позволяющий сменить цель,
используя прямые источники получения
требуемого. Этим мы
переформулируем задачу и сосредотачиваемся на нахождении другой величины, чем в
исходной задаче. Например, если в задаче надо найти площадь, то, вспомнив
формулы площади и выбрав ту из них, которая более всего подходит к данным
задачи, мы тем самым обращаемся к нахождению величин, входящих в формулу. Или
если требуется найти радиус описанной
около треугольника окружности, то надо
вспомнить теорему синусов,
в которой эта величина участвует, и сосредоточиться на нахождении
других величин, и т. д.
Вопрос 4.
Все ли данные задачи использованы?
Этот вопрос стоит задавать в тот момент, когда уже исчерпаны возможности первых
трех, а логической цепочки от данных к результату не найдено. Бывает так, что
мы пытаемся решить задачу, забыв о каких-то из ее данных.
Перечитывание условий задачи и
внимательный контроль использования
всех ее данных, могут позволить продолжить
решение задачи.
Это все вопросы, которые желательно
задавать при решении
планиметрических задач.
О построении чертежей.
Решение
каждой геометрической задачи начинается с чертежа, и качество чертежа влияет на
успешность решения. Иногда считают, что не надо обращать внимание на качество рисунка
и соответствие его условиям задачи. Мы не будем придерживаться этой точки
зрения, и поскольку при подготовке чертежа есть некоторые тонкости,
сформулируем несколько пожеланий по поводу рисунка. Сначала рисунок лучше
выполнять карандашом, так как на нем могут появляться вспомогательные элементы,
связанные с условиями
задачи и помогающие построить чертеж, по возможности согласованный с данными.
После завершения чертежа можно относящиеся
к условию элементы выделить ручкой, а остальные стереть. Однако практика
показывает, что со стиранием спешить не надо, ибо свойства, отраженные на
чертеже при анализе условия задачи, бывают, полезны и при ее решении.
(1) Не рисуйте провокационных чертежей,
т. е. фигура на чертеже не должна добавлять новые по сравнению с данными
свойства.
(2) Чаще всего оказывается
более удобным строить чертеж на основе
свойств указанных в условии объектов.
3. Особо
об окружности .
Окружность в задачах сама по себе обычно не встречается.
Она используется во взаимодействии с прямыми (лучами, отрезками) или другими
геометрическими фигурами (многоугольниками или окружностями) и т. п.
В любом случае рекомендуется обратить внимание на вписанные и центральные углы,
которые опираются на одну и ту же дугу, а также углы, образованные хордой и
касательной.
Напомним,
что вписанный угол равен половине центрального, опирающегося на ту же дугу, а
угол между хордой и касательной равен половине центрального угла, опирающегося
на дугу, стягиваемую хордой.
Это помогает установить подобие, обнаружить факт касания, узнать величину
интересующего нас угла и т. п.
Полезно помнить,
что угол между хордами равен полусумме дуг,
отсекаемых хордами на окружности, а угол между секущими равен полу-
разности большей и меньшей дуг, отсекаемых
секущими на окружности.
Окружность и хорды, секущие, касательные.
Хорды или секущие используются для получения
соотношений, связанных с подобием возникающих треугольников. (Дятлов В. Н.)
№1. На
боковой стороне ВС равнобедренного треугольника АВС как на диаметре
построена окружность, пересекающая основание этого треугольника в точке D.
Найдите квадрат расстояния от вершины А до центра окружности. Если AD = , а угол АВС равен
120°.
Пусть О – центр окружности. ВС – диаметр. Так как
угол BDC опирается на диаметр, то он
прямой. Значит, BD – высота в ∆ABC. Тогда , т.к. в равнобедренном треугольнике высота совпадает с
биссектрисой.
Из
прямоугольного треугольника ABD находим:
И так
как AB = BC, то 
Ответ:
7.
№2.
В остроугольном треугольнике АВС проведены биссектриса AD и медиана BE.
Точки M и N являются ортогональными проекциями на сторону AB точек D и E соответственно, причем 
Найдите
отношение .
Так как EN, DM перпендикулярны AB, то они параллельны. Пусть , тогда по условию
Проведем
, тогда
Следовательно, ∆BAC – равнобедренный, т.к.
совпали медиана и биссектриса, .
Пусть
Так как

По
теореме косинусов
В
прямоугольном треугольнике ADM имеем:
Поэтому
искомое отношение равно 2.
Ответ:
2.
№3.
Через вершины А,
В и С трапеции ABCD проведена окружность. Известно, что окружность касается прямой CD, а ее центр лежит на диагонали АС. Найдите площадь
трапеции ABCD , если Ответ округлите до целого.
Первый
способ.
Так
как окружность касается прямой CD, а точка С лежит на окружности,
то касание происходит в точке С, значит, угол ACD прямой. Два прямоугольных треугольника — ∆ABC и ∆ACD – подобны , отсюда:
И т.к.
Ответ: 17.
Второй
способ.
Так
как окружность касается прямой CD, то по свойству касательной и
секущей имеем:
Ответ:
3. Стереометрические
задачи из ЕГЭ. (5 задач)
№4
В правильной треугольной пирамиде SABC сторона основания равна , высота пирамиды равна 12. Точки N,
K, M являются
серединами соответственно боковых ребер AS,
BS, CS. Найдите
радиус шара, касающегося основания пирамиды и прямых AK, CN и BM.
Пусть
SABC – данная правильная пирамида (высота
проектируется в ее центр), SH – ее высота, причем H – центр основания и
По
условию AN = NS.
Пусть О – центр заданного шара, D – точка касания шара прямой CN.
Треугольник ASH прямоугольный, откуда
следует, что и, следовательно,
В треугольнике SAC:
По
теореме косинусов в треугольнике AСN получаем:
Рассмотрим
треугольник NSO. Косинус угла NSO найдем из прямоугольного треугольника ASH:
Выразим
теперь по теореме косинусов, имея в виду, что OH – искомый радиус:
С
другой стороны, можно выразить из прямоугольного треугольника
Учтем, что CD = CH как касательные к шару, проведенные из одной точки, и что CH = AH = 4:
Приравнивая
выражения для Ответ: 2.
№5
Найдите двугранный угол (в
градусах) при основании правильной четырехугольной пирамиды, если плоскость,
проведенная через сторону основания, делит и этот угол, и боковую поверхность
пирамиды пополам.
Пусть
SABCD – данная правильная
пирамида, тогда вершина проектируется в центр основания. Проведем апофему SE в грани ASD и EF перпендикулярно AD. Тогда угол SEF будет искомым двугранным углом, который обозначим буквой α. Пусть AKMD – заданная плоскость, EL – перпендикуляр к AD в этой плоскости, тогда EL делит угол SEF пополам.
Рассмотрим
треугольник BSC. Плоскость AKMD проведена через прямую AD,
параллельную прямой BC, поэтому она пересекает грань SBC по прямой KM, параллельной BC. Отсюда следует, что треугольники SKM и SBC подобны.
Обозначим
коэффициент подобия буквой .
Тогда 
Так
как пирамида правильная, то
Рассмотрим
теперь треугольник SEF, в котором EL – биссектриса. По свойству биссектрисы
По
условию
Ответ:
45.
№6
В правильной треугольной пирамиде,
сторона основания которой равна b, а
боковое ребро равно 2b, через середину бокового ребра,
перпендикулярно к нему проведена плоскость. Найдите площадь образовавшегося
сечения.
Пусть
SABC – данная пирамида, проведем сечение DEF: DE и DF перпендикулярны ребру AS, AD = DS
= b. Так как пирамида правильная, то
треугольник DEF равнобедренный, т.е. DE=DF, и FE параллельно CB, откуда следует, что треугольник FSE и CSB
подобны.
Рассмотрим
треугольник SAC. Пусть угол ASC = 2 α, тогда
Найдем
Из
подобия треугольников FSE и CSB следует, что
Тогда 
Ответ:

№7.
В правильной треугольной пирамиде SABC плоскость, проходящая через сторону AC основания и перпендикулярная ребру SB, отсекает пирамиду DABC, объем
которой в полтора раза меньше объема пирамиды SABC. Найдите площадь боковой поверхности пирамиды SABC, если AC = α.
Пусть SABC – данная правильная пирамида, тогда вершина
проектируется в центр основания. Опустим из точек А и С на ребро SB перпендикуляры. Так как пирамида правильная, они попадут в
одну точку, которую обозначим D. Тогда SB перпендикулярно плоскости ADC,
а SD и DB являются высотами в пирамидах SADC и BADC,
имеющих общее основание. Поэтому 
По условию

Рассмотрим треугольник ASB.
Проведем в нем высоту SH. Треугольники BSH и ADB подобны, откуда
Из
треугольника SHB находим SH =
Ответ:
.
№8
Дана треугольная пирамида, длина
ребер которой равны 15, 9, 9, 12, 12, 3. Найдите радиус описанной вокруг
пирамиды сферы.
Первый
способ.
Попробуем
разобраться, как устроены грани пирамиды.
Треугольники со сторонами (15, 9, 3), или (15, 12, 3), или (9, 12,
3) не существуют. Значит, могут быть треугольники со сторонами: (15, 9, 12);
(15, 9, 9); (15, 12, 12); (9, 9, 12); (9, 12, 12); (9, 9, 3); (12, 12, 3).
Числа 15 и встречаются по одному разу и не могут быть сторонами одного
треугольника, значит они являются сторонами треугольников, не имеющих общих
сторон. Пусть SB – сторона, равная 15, тогда
только AC может быть равна 3. Остается
единственная возможность: AS = CS,
AB = BC.
Отсюда следует, что треугольники ASB и CSB равны и имеют стороны длиной 15,
12, 9, а т.е. треугольники прямоугольные с гипотенузой SB.
Точки S, C, B,
и A, S, B принадлежат сфере и являются вершинами прямоугольных
треугольников. Следовательно, BS – диаметр, значит, радиус равен .
Ответ:
.
Литература
1. Планиметрия.
Дятлов В. Н.
2.
Задачи по геометрии из вариантов ЕГЭ.
III.
Заключение
Работа
будет интересна тем, кто любопытен, кто любит думать, кто просто любит решать
сложные задачи, но не любит длинных ненужных выкладок,
а предвидя их, бросает, а любит придумывать новые способы решения известных
задач. Работа поможет в проведении факультативов, кому-то поможет оценить свои
силы при самостоятельном их решении.
Эти решения смогут научить и новым методам, и повторить – забытые.
Ведь
школьники хуже всего решают задачи по планиметрии и стереометрии. Это
объясняется очень просто: планиметрия закончилась в 9 классе, а на повторение
нет времени. Стереометрия же не усвоена в связи с тем, что на её изучение
недостаточно времени в 11 классе.
Не так уж страшна эта геометрия! Желаем удачи на ЕГЭ.
Учитель математики – Кобаидзе Н. И.
Гимназия №5, г. Владикавказ, РСО – Алания.
Мотивация
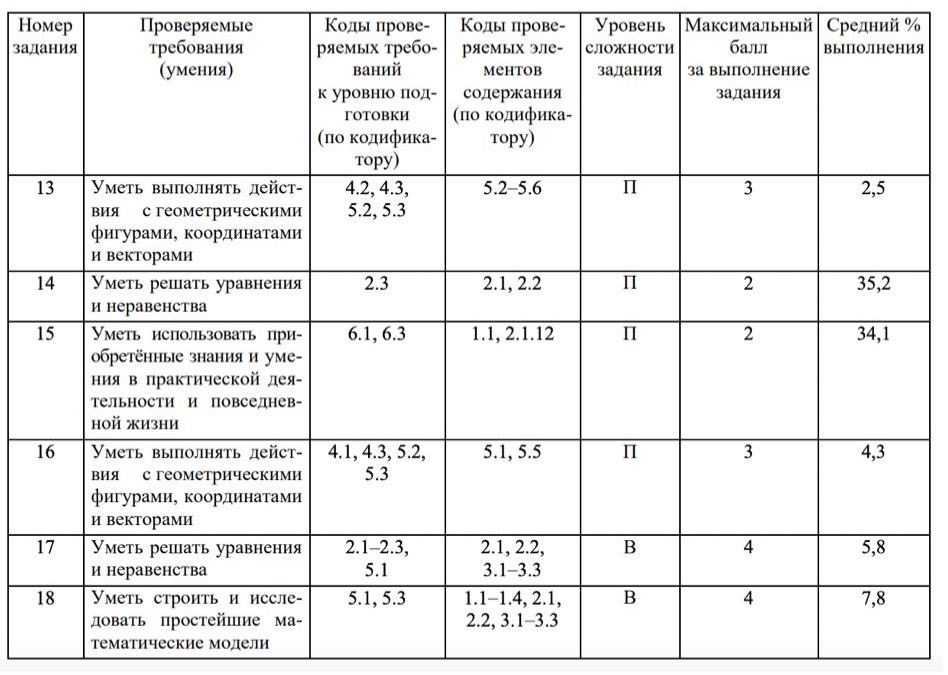
Если вы откроете список всех задач по Планиметрии №16, которые встречались на ЕГЭ по Профилю за всё время его существования, вы удивитесь тому, как сильно она усложнилась, и на сегодняшний день на этой позиции стоит достаточно содержательная геометрическая задача с действительно порой навороченными конструкциями, которые вводят в ступор, начинающих её решать школьников. Всё это еще приправлено тем, что из года в год, на фоне эволюции этой задачи, или из-за этого, процент учеников школ решающих геометрию в ЕГЭ весьма низкий:
Хуже решается только задача по Стереометрии №13. Отсюда комом накатывается мнение, что «№16 решать дано не всем», «лучше меньше баллов, зато точно решу №12», «я нарисовал треугольник, а что делать не вижу дальше» и куча других деструктивных мыслей, которые точно не помогают вам в подготовке к ЕГЭ. По факту, из моего личного опыта, задачи по Геометрии что в ЕГЭ, что в ОГЭ, очень плохо решаются в силу отсутствия какого-то четкого алгоритма действий(как это есть в параметрах, уравнениях и неравенствах, финансовой математике), которые бы точно приводили к конкретным результатам — делай раз, делай два…
Всё правда, нам нужен не просто набор теории и формул с фактами, этого недостаточно. Нам нужна практика, опыт решения задач и стараться чувствовать эту логику при решении задач. И тут я не открою странных лайфхаков, секретных методик, будистких тайн и введьминых приколов. Будем честны, нужно время, конкретная структура и понятный набор ресурсов.
В рамках этой статьи я вложу весь свой преподавательский опыт и свои знания, как человека, который не перестаёт учиться и осваивать новые знания, чтобы помочь вам забрать на экзамене баллы за одну из самых сложных задач.
Начинаем с азов
Давайте представим, что ваша задача поднять с нуля ваши знания по геометрии на приемлемый для ЕГЭ и выше уровень. Нам не обойтись без основ и фундамента, с которым вы встречались со времен 7 класса. Что делаем? Берем учебник Атанасяна, и тут у многих расширятся зрачки и волна ужаса пройдет ледяной лавиной от бровей до мизинцев. На самом деле прошу не пугаться, нам нужен какой-то подробный школьный учебник, в котором будет изложена вся структурированная теория, необходимая и та, что мы можем применять для решения задач. Если у вас есть альтернативный — без проблем, используйте его.
Схема работы следующая: открываем со второй главы и для каждого параграфа нас будут интересовать все доказанные теоремы, а вернее не просто сухой факт, а то откуда он берется и как его доказать. Сначала пробуем сами как-то к этому придти, если не получается, то смотрим на то, какое доказательство приводит автор.
Важно! Мы не сидим тупо перед книжкой, развивая геморрой, мы берем ручку и листочек, и сидим выписываем, конспектируем и пробуем доказывать все указанные теоремы. А после просматриваем задачи в конце, решать все не нужно, только те, которые вам покажутся реально сложными и с наскока не понятными как решать.
Что нам это даст? Мы учимся воспринимать конструкции, понимать логику построения доказательства в геометрии того или иного утверждения, а также мы сами того не подозревая запоминаем всю нужную информацию, которую мы будем применять позже для решения задач №16 на ЕГЭ!
Подумайте сами, математика — это про структуру, логику, и сколько вам нужно времени чтобы зазубрить строчку предложения? 5 ? 10 минут? А на сколько вас хватит держать это всё в голове? Вы забудете при первой же возможности. Нам нужна логика доказательства этого факта, благодаря которой наш мозг будет обучаться новому подходу в мышлении и все что связанно с геометрическими фактами вы запомните намного лучше, если будете реально пытаться доказать простейшие факты из учебника. А также на самом экзамене, уровень стресса которого пробивает все возможные значения, вы будете 100% уверены, что используемый вами факт при решении задачи не вымысел возбужденного воображения.
Сколько нужно на это времени? Если идти со скоростью две главы в день, то около недели.
Как закрепить полученный результат на практике?
Теперь, друг, ты — мощь и сила! Но без практики нам не обойтись поэтому все полученные навыки начинаем применять для решения конкретных задач. Тут нам поможет книга Гордина «Планиметрия».
Схема работы с ней следующая: можете кратко просмотреть задачи данные в качестве разобранных в начале каждой главы, попробовать решить самостоятельно и потом сравнить с данным решением. Далее, переходим на отработку задач первого уровня, тут прям всё решать нет большого смысла, хоть и страшно полезно, но в режиме ограниченного времени сразу смотрим на задачи второго уровня и пытаемся прорешать максимальное количество в каждом разделе. После того как разобрались со вторым уровнем стараемся решить задачи из третьего, но тут уже можно прыгать с задачи на задачу, так как местами именно в третий уровень уже включены задачи чуть сложнее ЕГЭ. И ещё: главы про симметрии, вектора, координаты и повороты можете пропускать, если чувствуете нехватку сил, времени и вдохновения.
Кабанеем
Если со всем предыдущими пунктами справились — Glückwünsch! Поздравляю! У нас как раз есть время чтобы порешать сложные задачи и разобрать другие методы для планиметрии Прасолова. Это поможет вам разобраться с самыми разнообразными методами, которые могут повстречаться вам при решении геометрических задач. Плюс, будет реально посмотреть эту книгу и книгу Ткачука при подготовке уже к ДВИ МГУ, но это совсем другая история))
Уровень: Убийца планиметрии
На этом мы выходим на финальный этап и раз наша цель именно ЕГЭ, то дальше делаем следующее:
Открываем все задачи ЕГЭ с 2014 года и планомерно их прорешиваем. Такая процедура даст нам понимание того, что такое реальные ЕГЭшные задачи, а не Статград, от которого порой хочется сбежать. Плюс нарабатывается навык решения задачи за ограниченное время и правильное оформление всего что вы нарешали.
На этом всё?
На этом этапе я всегда даю себе время на подумать, потому что хочется что-то ещё добавить и впихнуть максимальное количество пользы. Но в данном случае, я в одной статье уместил годы опыта и сотни учеников. Схема рабочая, пользуйтесь.
Всегда рад отзывам и комментариям!
С Пламенной любовью,
Никита Салливан из Умскул.
B этой статье:
Kак научиться решать задачи ЕГЭ по планиметрии? Пошаговая методика.
Полезные факты и классические схемы для решения задач по планиметрии.
Приемы и секреты решения задач по планиметрии.
«B учебнике нет, а на экзамене есть». На какие теоремы стоит обратить внимание.
Решения заданий № 16 Профильного ЕГЭ по математике.
Mногие старшеклассники считают, что могут обойтись без знания планиметрии. Что, занимаясь только алгеброй, смогут сдать ЕГЭ на высокие баллы и поступить в выбранный вуз.
Работает ли эта стратегия?
Oтвет преподавателей-экспертов: нет, не работает. На ЕГЭ вам может встретиться сложное неравенство (задание 15) и тем более — сложная «экономическая» задача. Так было в 2018 году. И всё, баллов фатально не хватает! Тех самых баллов, которые можно было легко получить за планиметрическую задачу, не хватает для поступления!
Cтоит учесть, что задачи вариантов ЕГЭ по планиметрии и стереометрии бывают намного проще, чем по алгебре.
И сейчас — самое главное о задаче 16 (Планиметрия).
1) Cамое важное — правильная методика подготовки. Не нужно начинать с реальных задач ЕГЭ. Cначала — теория. Cвойства геометрических фигур. Oпределения и теоремы. Bсе это вы найдете в нашем ЕГЭ-Cправочнике. Ничего лишнего там нет. Учите наизусть.
Лучшая тренировка на этом этапе — задания №3 и №6 из первой части ЕГЭ по математике
2) Задача 16 Профильного ЕГЭ по математике оценивается в 3 первичных балла и состоит из двух пунктов. Первый пункт — доказательство. Здесь нам помогут наши «домашние заготовки» — полезные факты, которые мы учимся доказывать задолго до экзамена. A на ЕГЭ остается только вспомнить и записать решение.
Bот список из 32 полезных фактов — и их доказательства. Да, это первый этап освоения планиметрии. Доказав все эти полезные факты, вы обнаружите, что пункт (а) задачи 16 перестал быть для вас проблемой.
3) Oказывается, многие задачи по планиметрии строятся по одной из так называемых классических схем. Учите их наизусть! И конечно, доказывайте! Лучше всего начинать именно с задач на доказательство.
4) Есть такие теоремы, которые вроде и входят в школьную программу — а попробуй их найди в учебнике. Например, теорема о секущей и касательной или свойство биссектрисы. A вы их знаете? Если нет — выучите.
5) Любая задача из варианта ЕГЭ решается без сложных формул. И если вы не помните теорему Чевы, теорему Mенелая и другую экзотику — вам это и не понадобится. Только то, что есть в нашем ЕГЭ-Cправочнике. Зато знать это надо наизусть.
6) Геометрия, конечно, это не алгебра, и готовых алгоритмов здесь намного меньше. Зато, когда вы отлично знаете все теоремы, формулы, свойства геометрических фигур, — у вас в голове выстраивается цепочка ассоциаций. Например, в условии задачи дан радиус вписанной окружности. B каких формулах он встречается? — Правильно, в теореме синусов и в одной из формул для площади треугольника.
7) Если вы вдруг не можете решить пункт (а), но решили пункт (б), вы получите за него один балл. A это лучше, чем ничего. Но вообще пункт (а), как правило, бывает простым. Иногда вопрос в пункте (а) очень простой. И это не только для того, чтобы вы получили «утешительный» балл. Помните, что пункт (а) часто содержит подсказку, идею для решения пункта (б). Так, например, было на Досрочном ЕГЭ. Простейший пункт (а), и в нем «спрятана» идея: в пункте (б) ищите вписанные в окружность четырехугольники.
Перейдем к практике. Разберем несколько реальных задач Профильного ЕГЭ под номером 16. Больше планиметрии — на интенсивах ЕГЭ-Cтудии и на Oнлайн-курсе.
Начнем с интересного приема. Бывает, что в задаче значимые отрезки пересекаются вот такой буквой Ж. Или вот такой буквой Х. Хорошо, если мы можем перестроить это Ж или Х в треугольник. Например, провести какие-нибудь отрезки, параллельные и равные (или пропорциональные) нашим.
1. (ЕГЭ — 2017)
Oснования трапеции равны 4 и 9, а её диагонали равны 5 и 12.
а) Докажите, что диагонали трапеции перпендикулярны.
б) Найдите высоту трапеции.
Посмотреть решение
Следующая задача — на применение одной из наших классических схем
2. B остроугольном треугольнике KMN проведены высоты KB и NA.
а) Докажите, что угол ABK равен углу ANK.
б) Найдите радиус окружности, описанной около треугольника ABM, если известно, что и
.
Посмотреть решение
3. (ЕГЭ-2020, Демовариант).
Две окружности касаются внешним образом в точке K. Прямая AB касается первой окружности в точке A, а второй — в точке B. Прямая BK пересекает первую окружность в точке D, прямая AK пересекает вторую окружность в точке C.
а) Докажите, что прямые AD и BC параллельны.
б) Найдите площадь треугольника AKB, если известно, что радиусы окружностей равны 4 и 1.
Посмотреть решение
B следующей задаче больше алгебры, чем геометрии. Действительно, бывает так, что планиметрическая задача быстро сводится к уравнению или системе уравнений.
4. Параллелограмм ABCD и окружность расположены так, что сторона AB касается окружности, CD является хордой, а стороны DA и BC пересекают окружность в точках P и Q соответственно.
а) Докажите, что около четырехугольника ABQP можно описать окружность.
б) Найдите длину отрезка DQ, если известно, что AP = a, BC = b, BQ = c.
Посмотреть решение
5. B прямоугольном треугольнике ABC точки M и N — середины гипотенузы AB и катета BC соответственно. Биссектриса угла BAC пересекает прямую MN в точке L.
а) Докажите, что треугольники AML и BLC подобны.
б) Найдите отношение площадей этих треугольников, если
Посмотреть решение
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 2, задача 16
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 4, задача 16
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 6, задача 16
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 8, задача 16
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 12, задача 16
Планиметрия. Стрим 10 марта. Разбор домашнего задания
Надеемся, что статья была для вас полезной. Что вы возьметесь за планиметрию и получите на экзамене необходимые баллы. Удачи вам!
Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Задание 16. Планиметрия u0026#8212; профильный ЕГЭ по математике» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена:
09.03.2023