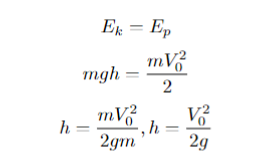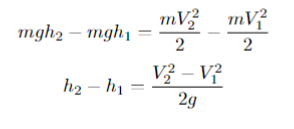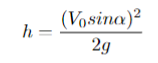Сложные задачи по механике егэ - Помощь в подготовке к экзаменам и поступлению

ЕГЭ Решение задач по физике. Глава 1. МЕХАНИКА (кинематика, динамика, статика, колебания и волны).

Задачи ЕГЭ по физике М11 — М20 с указаниями, подсказками, ответами и решениями (ГДЗ по ЕГЭ). Материал для подготовки к ЕГЭ по физике может быть использован репетиторами, учителями и самими учащимися.

Вернуться к Списку заданий тренинга по физике.

Задачи по физике.
Механика 11-20

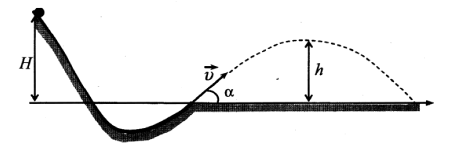
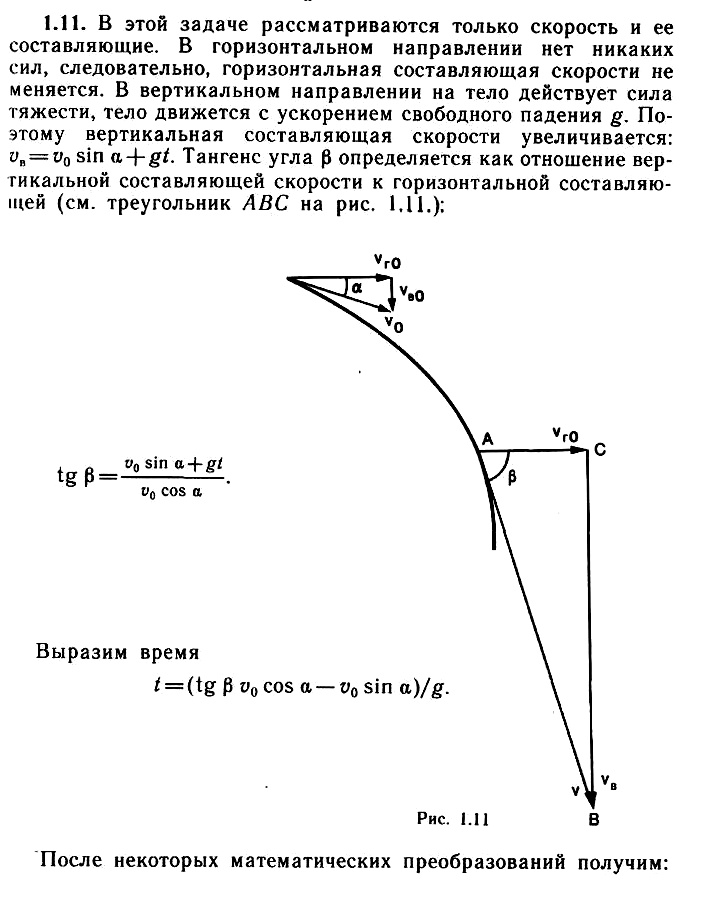
Задача 1.11. Тело массой m = 400 г брошено с некоторой высоты по направлению к земле под углом α = 30° к горизонту. Начальная скорость тела ʋ₀ = 20 м/с. Определите, через сколько времени скорость тела будет направлена под углом β = 60° к горизонту. Определите изменение потенциальной энергии тела за это время. Ускорение свободного падения g ≈ 10 м/с².

Указания (подсказка)

Покажите на рисунке направление горизонтальной, вертикальной и полной скоростей тела в начальный момент времени и в искомый момент времени. Учтите, что горизонтальная составляющая скорости не изменяется, а вертикальная увеличивается с течением времени. Вспомните определение тангенса угла и из треугольника скоростей получите уравнение для времени. Изменение потенциальной энергии определите из закона сохранения энергии или как работу силы тяжести за указанный промежуток времени.

Решение и ответ

Задача 1.12. Тело массой m = 0,5 кг брошено со скоростью ʋ₀ = 20 м/с под углом α = 30° к горизонту. Определите наибольшую высоту полета н изменение импульса за время полета. Сопротивлением воздуха можно пренебречь. Примите g ≈ 10 м/с².

Указания (подсказка)

Наибольшую высоту подъема определите или из уравнения движения, или из закона сохранения энергии (см. задачу 1.10). Изменение импульса определите как разность векторов конечного и начального импульсов. Внимание! Не забывайте о векторном характере импульса. Можно воспользоваться вторым законом Ньютона. Изменение импульса системы равно импульсу внешней силы. Этой силой является сила тяжести.

Решение и ответ

Задача 1.13. Катер пересекает реку шириной l = 360 м. Скорость течения ʋ = 2 м/с. Рулевой держит курс перпендикулярно течению. Двигатель обеспечивает постоянное ускорение а = 0,1 м/с². Начальная скорость катера равна нулю. Определите, через сколько времени катер пересечет реку. На какое расстояние он будет снесен течением?

Указания (подсказка)

Катер участвует в двух движениях: по течению реки он движется равномерно, а перпендикулярно течению относительно воды его движение равноускоренное.

Решение и ответ

Задача 1.14. Из окна вагона поезда, движущегося по горизонтальной дороге со скоростью ʋ = 54 км/ч, бросают в горизонтальном направлении предмет. Предмет падает на землю на расстоянии s = 12,1 м от места, над которым он находился в момент бросания. Определите скорость ʋ₀ предмета относительно вагона сразу после бросания, если она была направлена перпендикулярно скорости движения поезда. Высота окна над поверхностью земли H = 2,5 м. Сопротивлением воздуха можно пренебречь.

Указания (подсказка)

Необходимо воспользоваться принципом относительности движения, рассматривая движение одного тела относительно другого или относительно Земли. Вспомните правило сложения скоростей: скорость тела относительно неподвижной системы отсчета равна векторной сумме скорости тела относительно подвижной системы отсчета и скорости этой подвижной системы относительно неподвижной. Помните о векторном характере скоростей. Если вам трудно запомнить такие «сложные» закономерности, вспомните простое правило сложения скоростей для лодки, переплывающей реку: течение ее сносит вдоль берега, а рулевой стремится переправиться на противоположный берег. И тогда любая задача, связанная с относительностью движения, будет вами решена.

Решение и ответ

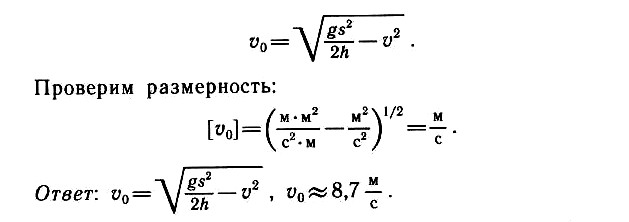
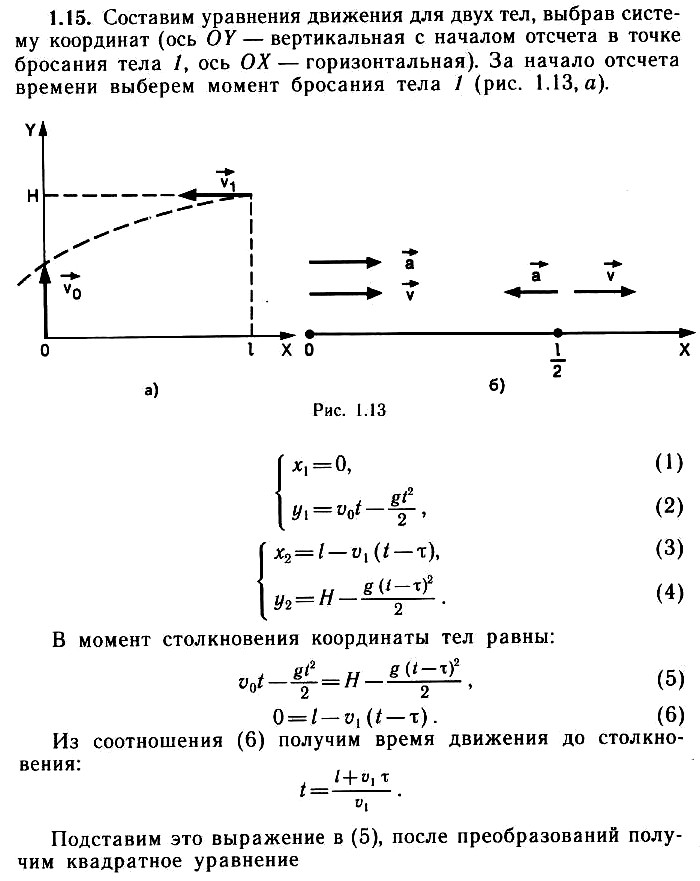
Задача 1.15. Тело 1 бросают вертикально вверх с начальной скоростью ʋ₀ = 30 м/с. Тело 2, находящееся на высоте Н = 40 м по вертикали и на расстоянии l = 20 м по горизонтали от точки бросания тела 1, бросают горизонтально со скоростью ʋ₁ =20 м/с. Определите, с каким запаздыванием или опережением т надо бросить тело 2, чтобы тела столкнулись в полете. Ускорение свободного падения g ≈ 10 м/с².

Указания (подсказка)

Решение и ответ

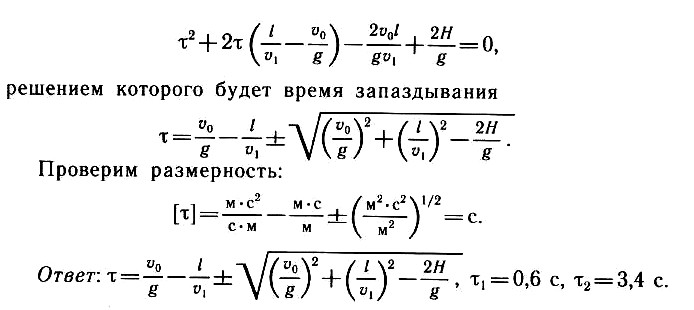
Задача 1.16. Человек начинает подниматься по движущемуся вверх эскалатору метро с ускорением а = 0,21 м/с². Добежав до середины эскалатора, он останавливается, поворачивает и начинает спускаться вниз с тем же ускорением. Определите, сколько времени человек находится на эскалаторе. Длина эскалатора l = 100 м, а скорость его движения ʋ = 2 м/с.

Указания (подсказка)

Смотрите указание к задаче 1.14

Решение и ответ

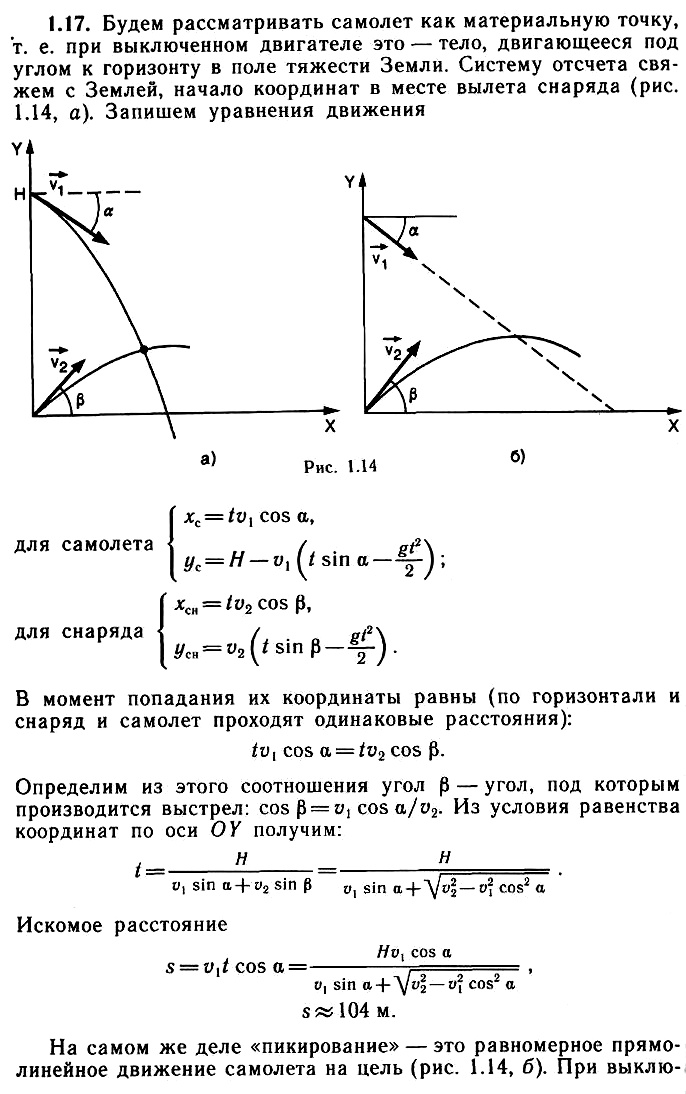
Задача 1.17. Самолет, пролетая над зенитной батареей на высоте H = 1 км, начинает пикировать с выключенным двигателем на цель со скоростью ʋ₁ = 540 км/ч, направленной под углом а = 60° к горизонту. Самолет сбивают выстрелом из орудия, произведенным в тот момент времени, когда он находился над батареей. Определите, на каком расстоянии от батареи, считая по горизонтальному направлению, снаряд попал в сaмолет. Скорость снаряда при вылете из ствола орудия ʋ₂ = 600 м/с. Сопротивлением воздуха можно пренебречь.

Указания (подсказка)

Смотрите указание к задаче 1.14. Выберите систему отсчета, связанную с Землей, и составьте уравнения движения для снаряда и самолета. Равенство соответствующих координат и означает момент столкновения.

Решение и ответ

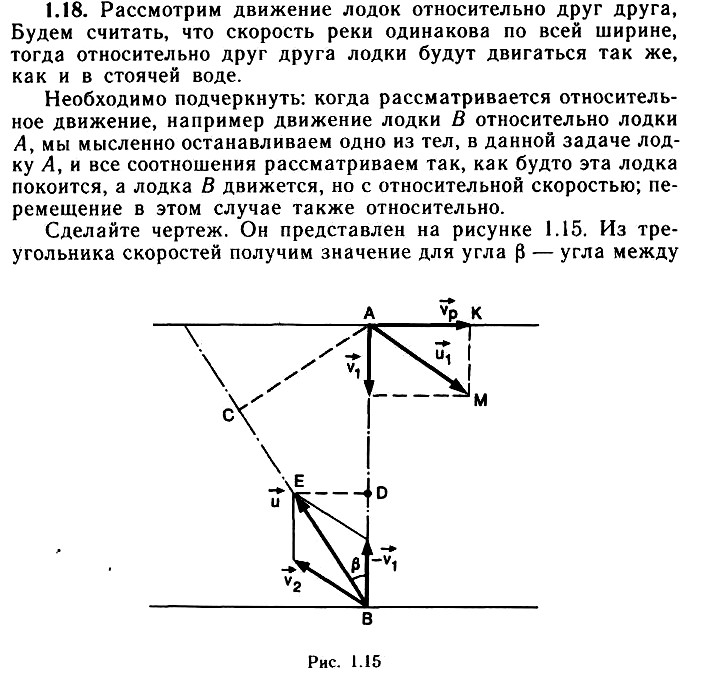
Задача 1.18. Две лодки переплывают реку, отправляясь одновременно из пунктов A и В, расположенных на противоположных берегах реки против друг друга. Скорость течения реки ʋ_p = 20 м/мин, ширина реки l = 200 м. Скорости лодок относительно воды равны ʋ₁ = 15 м/мин, ʋ₂ = 20 м/мин. Первая лодка начала движение перпендикулярно течению, а вторая держит курс под углом α = 150° к скорости течения реки. Определите, на каком расстоянии от пункта А будет находиться первая лодка, когда расстояние между лодками будет наименьшим.

Указания (подсказка)

После построения векторов скоростей учтите, что наименьшее расстояние между лодками будет определяться перпендикуляром из точки А на направление относительной скорости для лодки, выходящей из пункта В. Для того чтобы это понять, мысленно остановите лодку в пункте А, тогда вторая лодка должна двигаться в направлении относительной скорости, это ее перемещение, а наименьшее расстояние есть перпендикуляр, опущенный из точки на выбранное направление!

Решение и ответ

Задача 1.19. Лодочник отплывает из пункта А, держа курс перпендикулярно берегу. Скорость течения реки ʋ_p = 2 м/с, ее ширина h = 144 м. Лодка в течение времени t₁движется равноускоренно с ускорением а = 1 м/с², а затем в течение промежутка времени t₂ движется равномерно и, наконец, в течение промежутка времени t₃ – равнозамедленно с тем же ускорением а. Определите промежутки времени t₁ и t₂, если известно, что лодка пришла в пункт В, расположенный на противоположном берегу реки на расстоянии l = 80 м вниз по течению. Постройте траекторию движения лодки в системе координат (XOY), связанной с берегом.

Указания (подсказка)

Выберите оси координат по течению реки и в перпендикулярном направлении. Запишите уравнения движения по обеим осям. Решите полученную систему.

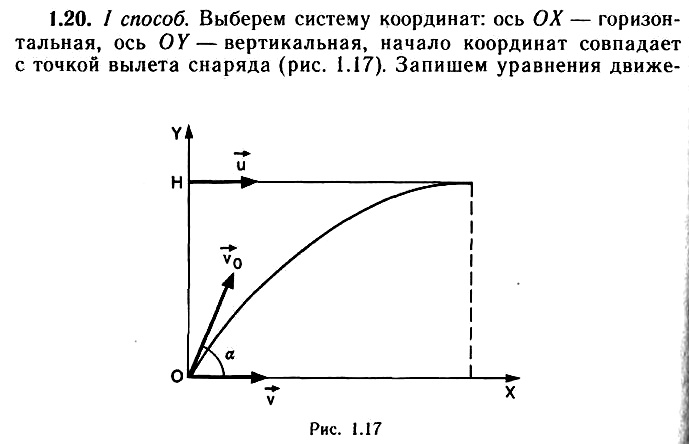
Задача 1.20. Из танка, движущегося со скоростью ʋ = 70 км/ч, стреляют по горизонтально летящему на высоте Н = 6 км самолету. Скорость самолета ʋ = 790 км/ч, а ее направление совпадает с направлением движения танка. Определите угол вылета α снаряда относительно горизонта. Известно, что в момент выстрела самолет находился над танком, а снаряд попал в самолет в высшей точке траектории.

Указания (подсказка)

Выберите систему отсчета, связанную с Землей, и составьте уравнения движения для снаряда и самолета. Равенство соответствующих координат и означает момент столкновения.

Решение и ответ

Вы смотрели «ЕГЭ Решение задач по физике. Механика 11-20». Задачи ЕГЭ по физике с указаниями, подсказками, ответами и решениями (ГДЗ по ЕГЭ). Материал для подготовки к ЕГЭ по физике.

Вернуться к Списку заданий тренинга по физике.

Источник

в условии
в решении
в тексте к заданию
в атрибутах

Категория:

Атрибут:

Всего: 36 1–20 | 21–36

Добавить в вариант

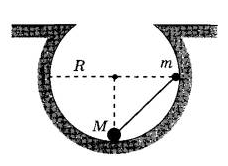
На гладком горизонтальном столе покоится брусок с прикреплённой к нему гладкой изогнутой в вертикальной плоскости тонкой жёсткой трубкой (см. рис.). Общая масса бруска с трубкой равна M = 0,8 кг. В верхний конец вертикальной части трубки, находящийся на высоте H = 70 см над бруском, опускают без начальной скорости маленький шарик массой m = 50 г. Другой конец трубки наклонён к горизонту под углом α = 30° и находится на высоте h = 20 см над бруском. Найдите модуль скорости, с которой будет двигаться брусок после того, как шарик вылетит из трубки.

Какие законы Вы используете для описания движения и взаимодействия трубки и шарика? Обоснуйте их применение к данному случаю.

Источник: Тренировочная работа по физике 28.04.2017, вариант ФИ10503

Задания Д1 B1 № 131

Лодка должна попасть на противоположный берег реки по кратчайшему пути в системе отсчета, связанной с берегом. Скорость течения реки u, а скорость лодки относительно воды v . Чему должен быть равен модуль скорости лодки относительно берега?

Автобус везёт пассажиров по прямой дороге со скоростью 10 м/с. Пассажир равномерно идёт по салону автобуса со скоростью 1 м/с относительно автобуса, двигаясь от задней двери к кабине водителя. Чему равен модуль скорости пассажира относительно дороги? (Ответ дайте в метрах в секунду.)

Задания Д29 C2 № 9072

Задания Д1 B1 № 5952

Два камня одновременно бросили из одной точки: первый  — вертикально вверх, второй  — под углом 45° к горизонту. Сопротивление воздуха пренебрежимо мало. Как движется первый камень в системе отсчёта, связанной со вторым камнем?

1)  покоится

2)  движется по параболе

3)  движется равномерно и прямолинейно

4)  движется по дуге окружности

Задания Д1 B1 № 5987

Два камня одновременно бросили из одной точки: первый  — вертикально вверх, второй  — под углом 30° к горизонту. Сопротивление воздуха пренебрежимо мало. Как движется второй камень в системе отсчёта, связанной с первым камнем?

1)  покоится

2)  движется по параболе

3)  движется равномерно и прямолинейно

4)  движется по дуге окружности

Мотоцикл едет по прямой дороге с постоянной скоростью 50 км/ч. По той же дороге навстречу ему едет автомобиль с постоянной скоростью 70 км/ч. Чему равен модуль скорости движения мотоцикла относительно автомобиля? (Ответ дайте в километрах в час.)

Мотоцикл едет по прямой дороге с постоянной скоростью 50 км/ч. По той же дороге в том же направлении едет автомобиль с постоянной скоростью 70 км/ч. Чему равен модуль скорости движения мотоцикла относительно автомобиля? (Ответ дайте в километрах в час.)

Задания Д2 B2 № 6637

Маша взяла в руку монету и, стоя в комнате своей квартиры, выпустила её из пальцев без начальной скорости. Монета полетела вдоль вертикали и упала на пол комнаты. Затем Маша вышла из дома, села в подъехавший автобус и, дождавшись, пока он начнёт двигаться равномерно и прямолинейно по горизонтальной дороге, повторила опыт с бросанием монеты. Оказалось, что монета в равномерно движущемся автобусе падает точно так же, как и в квартире. Иллюстрацией какого закона или принципа может служить этот опыт?

1)  первого закона Ньютона

2)  второго закона Ньютона

3)  третьего закона Ньютона

4)  принципа относительности Галилея

Задания Д2 B2 № 6676

Саша взял в руку монету и, стоя в равномерно движущемся вниз лифте, выпустил её из пальцев без начальной скорости. Монета полетела вдоль вертикали и упала на пол лифта. Затем Саша вышел из дома, сел в подъехавший автобус и, дождавшись, пока он начнёт двигаться равномерно и прямолинейно по горизонтальной дороге, повторил опыт с бросанием монеты. Оказалось, что монета в равномерно движущемся автобусе падает точно так же, как и в равномерно опускающемся лифте. Иллюстрацией какого закона или принципа может служить этот опыт?

1)  Первого закона Ньютона

2)  Второго закона Ньютона

3)  Третьего закона Ньютона

4)  принципа относительности Галилея

Задания Д1 B1 № 125

Вертолет поднимается вертикально вверх. Какова траектория движения точки на конце лопасти винта вертолета в системе отсчета, связанной с винтом?

1)  точка

2)  прямая

3)  окружность

4)  винтовая линия

Задания Д3 B3 № 4412

Два бруска массой m и равномерно движутся вдоль прямой OX (см. рис.). В системе отсчёта, связанной с бруском модуль импульса второго бруска равен

1)   6mV

2)   4mV

3)   3mV

4)   2mV

Задания Д3 B3 № 4447

Два бруска массой m и равномерно движутся вдоль прямой OX (см. рис.). В системе отсчёта, связанной с бруском модуль импульса первого бруска равен

1)  mV

2)   2mV

3)   3mV

4)   4mV

Из двух городов навстречу друг другу с постоянной скоростью движутся два автомобиля. На графике показано изменение расстояния между автомобилями с течением времени. Каков модуль скорости первого автомобиля в системе отсчёта, связанной со вторым автомобилем? Ответ приведите в метрах в секунду.

Источник: Демонстрационная версия ЕГЭ—2020 по физике.

Задания Д1 B1 № 3357

Вертолет равномерно поднимается вертикально вверх. Какова траектория крайней точки лопасти вертолета в системе отсчета, связанной с корпусом вертолета?

1)  прямая линия

2)  винтовая линия

3)  окружность

4)  эллипс

Пловец плывет по течению реки. Определите скорость пловца относительно берега, если скорость пловца относительно воды 0,4 м/с, а скорость течения реки 0,3 м/с. (Ответ дайте в метрах в секунду.)

Из незакреплённой пушки стреляют снарядом массой 20 кг, который вылетает из ствола в горизонтальном направлении со скоростью 102 м/с относительно пушки. Пушка при этом откатывается, приобретая относительно земли скорость 2 м/с. Чему равна масса пушки, если массой сгоревшего порохового заряда можно пренебречь? Ответ дайте в килограммах.

Из незакреплённой пушки массой 800 кг стреляют снарядом, который вылетает из ствола в горизонтальном направлении со скоростью 102 м/с относительно пушки. Пушка при этом откатывается, приобретая относительно земли скорость 2 м/с. Чему равна масса снаряда, если массой сгоревшего порохового заряда можно пренебречь? Ответ дайте в килограммах.

Пароход движется по реке против течения со скоростью 5 м/с относительно берега. Определите скорость течения реки, если скорость парохода относительно берега при движении в обратном направлении равна 8 м/с. (Ответ дайте в метрах в секунду.)

Всего: 36 1–20 | 21–36

Источник

В ЕГЭ по физике примерно 11 задач по механике, включая три сложные задачи из второй части. Так получилось потому, что этот раздел науки в школьной программе изучают дольше всего.

Хорошо разбираясь в механике, можно набрать достаточно большое количество баллов! Мы разберем один из часто встречающихся типов задач.

С чего начать

Все задачи по механике можно условно разделить на четыре раздела (плюс один дополнительный). Это задачи типа 3-8 в бланке ЕГЭ:

описание движения (кинематика),
сила и импульс (динамика),
работа и энергия (механическое действие),
условия равновесия и рычаги (статика, механизмы),
дополнительный раздел “Механические колебания” (маятники).

В сложных задачах механика может встретиться в заданиях типа 25, 26: одна из них качественного характера, другая расчётная.

Последняя задача строго механическая и считается самой сложной — за нее дают аж 4 первичных балла. Также механика часто встречается там, где комбинируют два раздела физики, например: механика и термодинамика, или механика и электричество.

Поэтому учителю при подготовке ученика к ЕГЭ стоит много времени уделить именно механике – уж очень много баллов можно собрать именно с этого раздела.

В этой статье мы обратим внимание на те задачи, которые могут попасться в типе задач 3, 5-8 в первой части и 25, 30 во второй части.

Задачи на броски

Часто встречающийся формат задач – это броски. Они делятся на два основных вида:

броски ровно вертикально,
броски под углом к горизонту.

При этом сразу отметим, что можно применять в решении два основных подхода: систему уравнений движения и закон сохранения энергии.

Задачи на броски вертикально вверх

Здесь четыре типа движения:

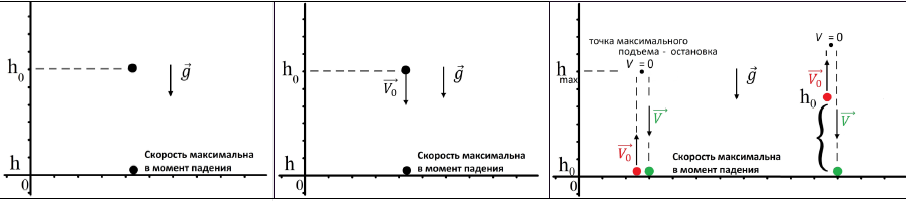
падение объекта,
бросок объекта вниз,
бросок объекта вверх,
бросок объекта с определенной высоты.

Подпись к фото: на схемах изображены все типы движения

При любом из типов вертикального движения мы можем использовать систему уравнения движения. Давайте выведем, например, для случая «бросок вверх» максимальную высоту подъема через скорость и ускорение, ведь ускорение нам известно (g примерно 10):

А теперь найдем выражение для той же самой высоты, но уже через закон сохранения энергии, зная, что вся кинетическая энергия перейдет в потенциальную:

Как мы видим, формулы идентичные. Следовательно, при решении задач можно использовать либо один подход, либо другой.

Но главное, что нужно понимать: скорость будет соответствовать высоте. Необязательно брать начальную скорость и максимальную высоту, можно взять изменение высоты и изменения скорости:

Это вывод нужно обязательно показать ученику, ведь гораздо проще понять смысл и запомнить, как решаются задачи или какие принципы используются, если есть доказательства и пояснения.

Стоит отметить, что применять уравнения движения мы можем абсолютно всегда. Но когда речь идет о законах сохранения, мы можем применять их только тогда, когда система замкнутая, то есть нет воздействия внешних сил.

Лайфхак: можно посоветовать ученику при чтении условия обратить внимание на то, что в задаче дано.

— Если в задаче не дано время, то, скорее всего, данную задачу можно решить двумя способами, и быстрее вывести уравнение через закон сохранения энергии.
— Если же есть время, то лучше воспользоваться уравнением движения, а потом проверить с помощью закона сохранения.

Задачи на броски под углом к горизонту

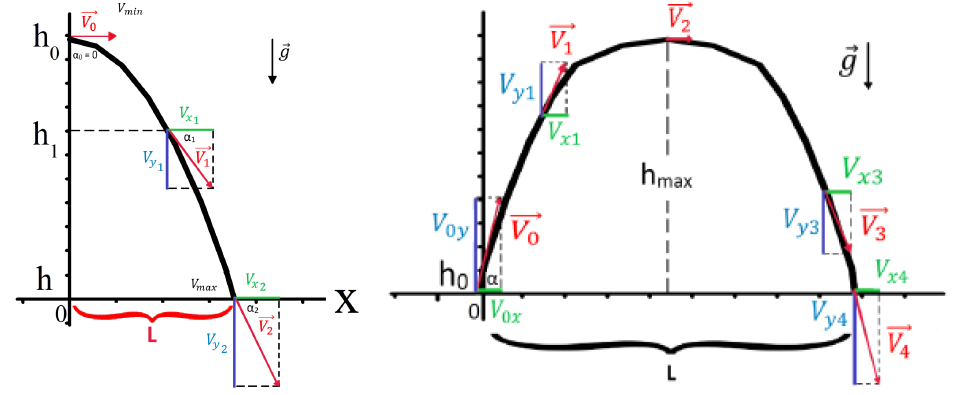
Броски к горизонту бывают всего двух типов. Либо бросают с какой-то высоты (чаще всего горизонтально), либо бросают с поверхности земли под углом (бывают еще броски из ям, но такие задачи в ЕГЭ крайне редки).

Важно пояснить ученику, что в таких типах задач ничего принципиально другого нет. Единственное — мы должны рассматривать в таких задачах два типа движения.

Стандартное равномерное движение по оси Х и с ускорением вертикальное по оси У. А также скорость, которая была в формулах ранее, изменится на две составляющие — по оси Х и по оси У:

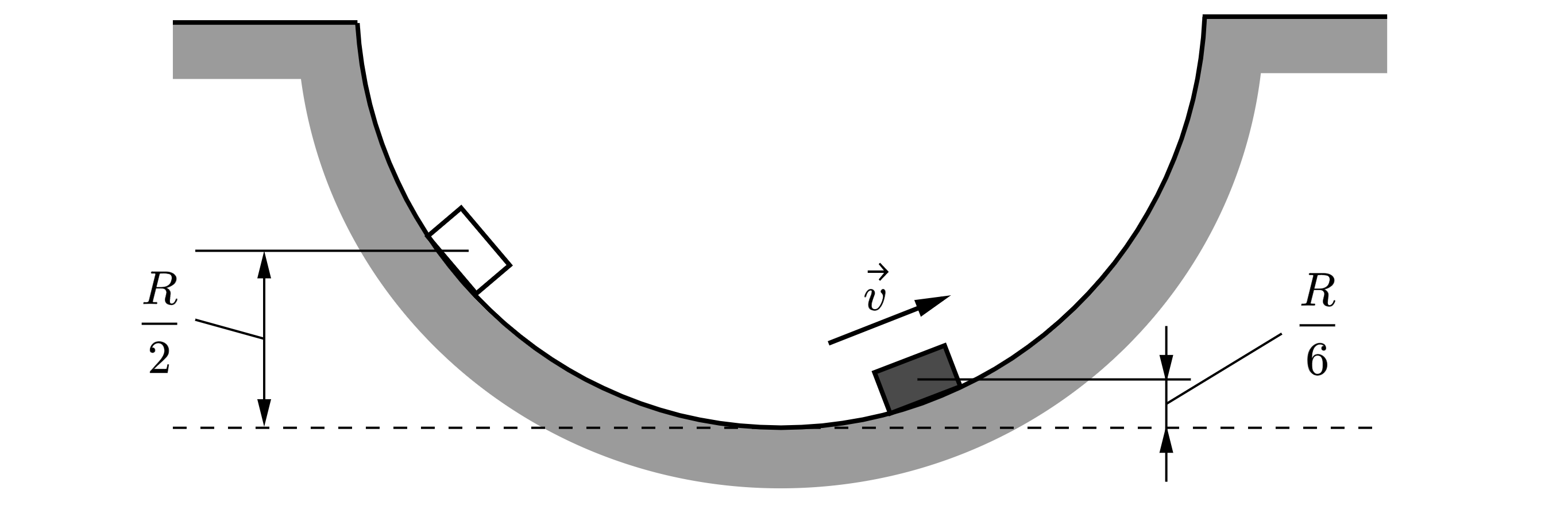
Все остальное останется таким же, и в итоге мы получаем следующую формулу для максимальной высоты:

Примеры задачи

Рассмотрим, как применить эти два метода, чтобы решить задачи из ЕГЭ.

Тело брошено вертикально вверх. Через 0,5 с после броска его скорость 20 м/с. На какой высоте окажется тело? Сопротивлением воздуха пренебречь. (Ответ дайте в метрах.)

Сначала решим методом уравнения движения:

А теперь решим с помощь закона сохранения энергии:

Единственное, что нужно учесть — при уменьшении кинетической энергии увеличивается потенциальная, поэтому в конце минус пропадает.

Таким образом, мы получили одинаковые ответы двумя способами.

Краткий вывод

Такого рода задания достаточно часто встречаются в ЕГЭ как в первой, так и во второй части, поэтому важно знать два метода решения, чтобы у ученика были запасные варианты проверки правильного ответа.

И помните: «Fortis fortuna adiuvat» — удача на стороне сильных. Старайтесь, и все будет хорошо!

Источник

Тема 24.

Качественная задача

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.

Готовиться с нами — ЛЕГКО!

Подтемы раздела

качественная задача

24.01Механика

24.02Молекулярная физика. Термодинамика

24.03Электродинамика

24.04Оптика

24.05Квантовая физика

Решаем задачи

Два деревянных кольца детских пирамидок № 1 и № 2, способных без трения скользить по оси,
соединили с основаниями двумя одинаковыми лёгкими пружинками (см. рисунок). Пирамидку № 2
поместили в прочный сосуд с водой, прикрепив основание к его дну. Обе пирамидки покоятся
относительно Земли. Как изменится по сравнению с этим случаем (увеличится, уменьшится или
останется прежней) длина пружин пирамидок 1 и № 2 во время свободного падения с балкона высокого
дома? Сопротивлением воздуха пренебречь. Ответ поясните, указав, какие физические закономерности
Вы использовали

Показать ответ и решение

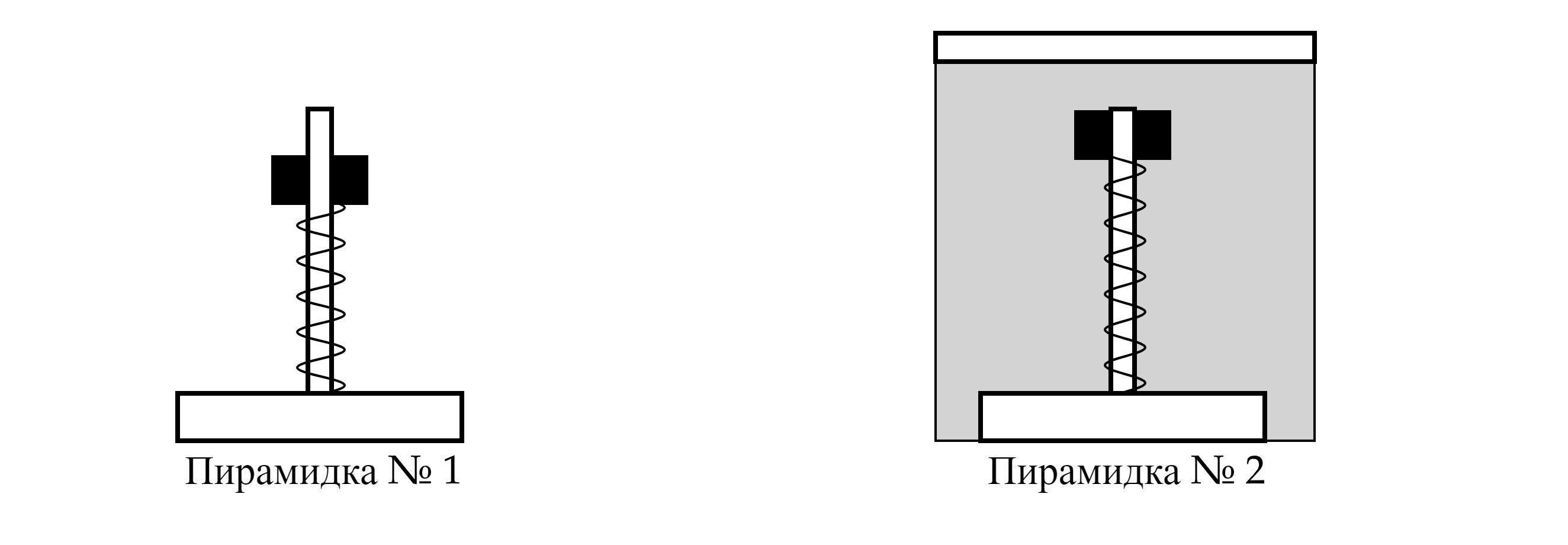
На кольцо в первом случае действует сила упругости пружины Fy1 , сила тяжести кольца . Во
втором случае на тело действует сила Архимеда Fарх , сила упругости Fy2 и сила тяжести . Пусть
плотность дерева , объём кольца , а плотность воды ρ
0 . Тогда сила тяжести равна ρgV , а сила
Архимеда ρ0gV . Так как , то сила Архимеда по модулю больше, чем сила тяжести. Сделаем
рисунок с расстановкой сил.

В первом случае пружина сжата, а во втором растянута (из-за того, что сила Архимеда больше силы
тяжести кольца). При свободном падении тело испытывает состояние невесомости: невесомы стали и
кольцо, и вода. Сила Архимеда стала равна нулю. Вес всех предметов стал равен нулю и перестал
действовать на пружины и они вернулись в недеформированное состояние: пружина 1 растянулась,
пружина 2 – сжалась

Критерии оценки

3 балла ставится за задачу если:

_________________________________________________________________________________________________________________

Приведено полное правильное решение, включающее правильный ответ (в данном случае — сказано,
как изменится длина пружин) и исчерпывающие верные рассуждения с прямым указанием
наблюдаемых явлений и законов (в данном случае — явление невесомости, закон Архимеда, формула
связи массы и плотности вещества)

2 балла ставится за задачу если:

_________________________________________________________________________________________________________________
Дан правильный ответ, и приведено объяснение, но в решении имеются один или несколько из
следующих недостатков. В объяснении не указано или не используется одно из физических явлений,
свойств, определений или один из законов (формул), необходимых для полного верного объяснения.
(Утверждение, лежащее в основе объяснения, не подкреплено соответствующим законом, свойством,
явлением, определением и т.п.)

I) Указаны все необходимые для объяснения явления и законы, закономерности, но в них содержится
один логический недочёт.

II) В решении имеются лишние записи, не входящие в решение (возможно, неверные), которые не отделены
от решения (не зачёркнуты; не заключены в скобки, рамку и т.п.).

III) В решении имеется неточность в указании на одно из физических явлений, свойств, определений,
законов (формул), необходимых для полного верного объяснения.

IV) При неверном построении или отсутствии рисунка и (или) графика за задачу ставится 2
балла.

1 балл ставится за задачу если:

_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.

Дан правильный ответ на вопрос задания, и приведено объяснение, но в нём не указаны два явления
или физических закона, необходимых для полного верного объяснения.

Указаны все необходимые для объяснения явления и законы, закономерности, но имеющиеся
рассуждения, направленные на получение ответа на вопрос задания, не доведены до конца.

Указаны все необходимые для объяснения явления и законы, закономерности, но имеющиеся рассуждения,
приводящие к ответу, содержат ошибки.

Указаны не все необходимые для объяснения явления и законы, закономерности, но имеются верные
рассуждения, направленные на решение задачи.

Во всех остальных случаях за задачу выставляется 0 баллов.

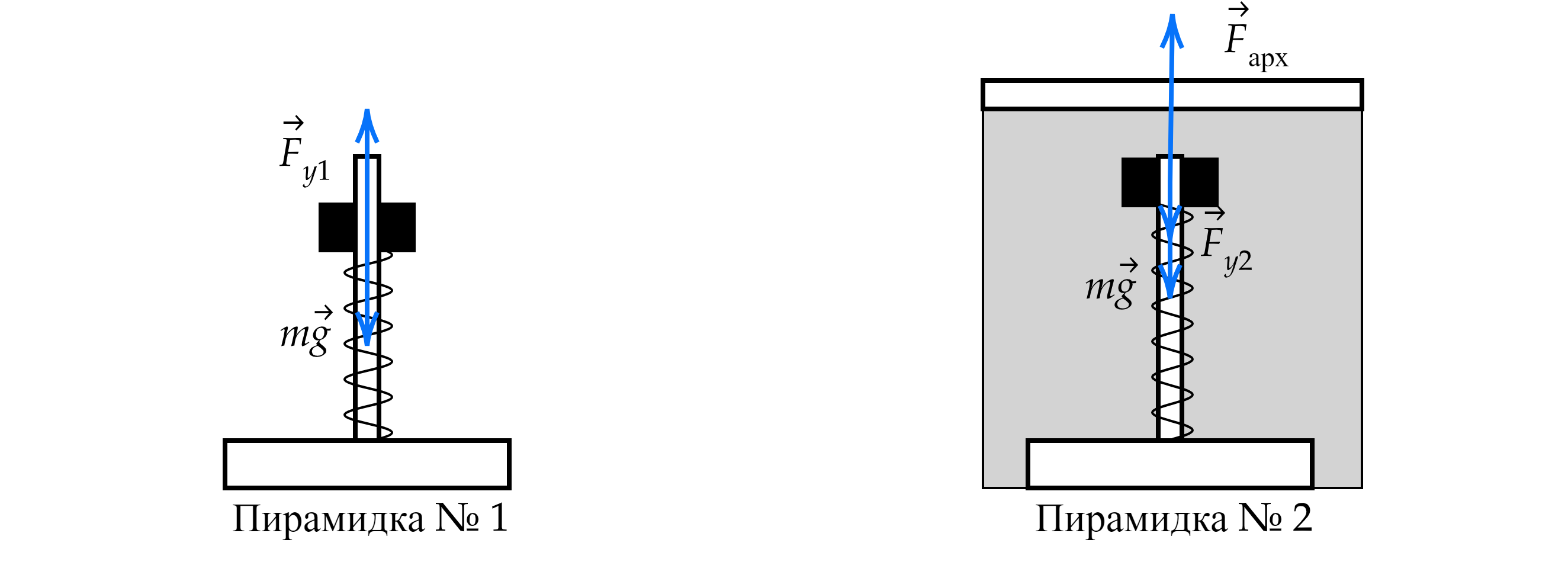
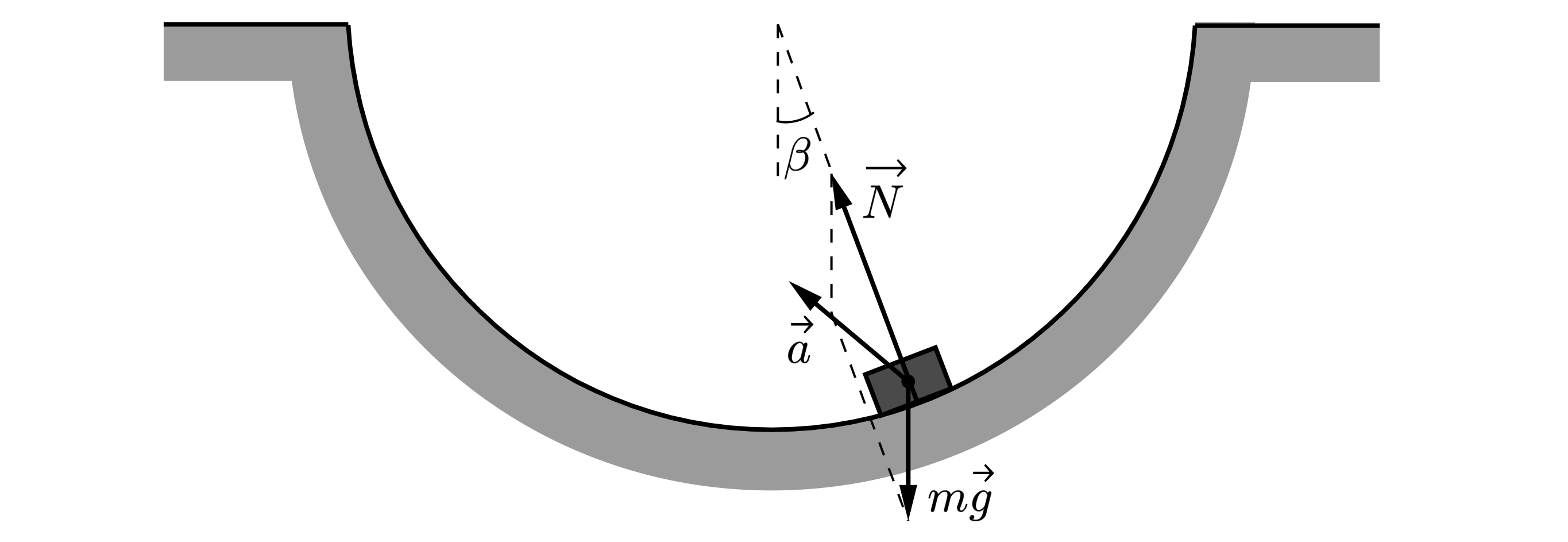
Маленькая шайба движется из состояния покоя по неподвижной гладкой сферической поверхности
радиусом . Начальное положение шайбы находится на высоте R
--
2 относительно нижней точки
поверхности. Сделайте рисунок с указанием сил, действующих на шайбу в момент, когда она движется
вправо-вверх, находясь на высоте R
--
6 над нижней точкой поверхности (см. рис). Покажите на этом
рисунке, куда направлено в этот момент ускорение шайбы (по радиусу поверхности, по касательной к
поверхности, внутрь поверхности, наружу от поверхности). обоснуйте. Сопротивление воздуха не
учитывать.
Основная волна 2014

Показать ответ и решение

К шайбе приложены сила тяжести , направленная вертикально вниз, и сила реакции поверхности
, направленная по радиусу вверх. Ускорение шайбы направлено внутрь траектории левее
направления силы (см. рисунок).

В точке R ∕6 скорость шайбы не равна 0, значит, у шайбы есть центростремительное ускорение ,
направленное в центр окружности траектории движения.
Так же у шайбы есть ускорение на касательную к траектории, которое равно gsinβ , то есть
есть тангенциальное ускорение , не равное нулю и направленное влево в нижнюю точку
сферы.
Общее ускорение будет равно

которое будет направляться внутрь поверхности

Критерии оценки

3 балла ставится за задачу если:

2 балла ставится за задачу если:

IV) При неверном построении или отсутствии рисунка и (или) графика за задачу ставится 2
балла.

1 балл ставится за задачу если:

Во всех остальных случаях за задачу выставляется 0 баллов.

Будет ли разница в действии гидравлического пресса на земле и на луне

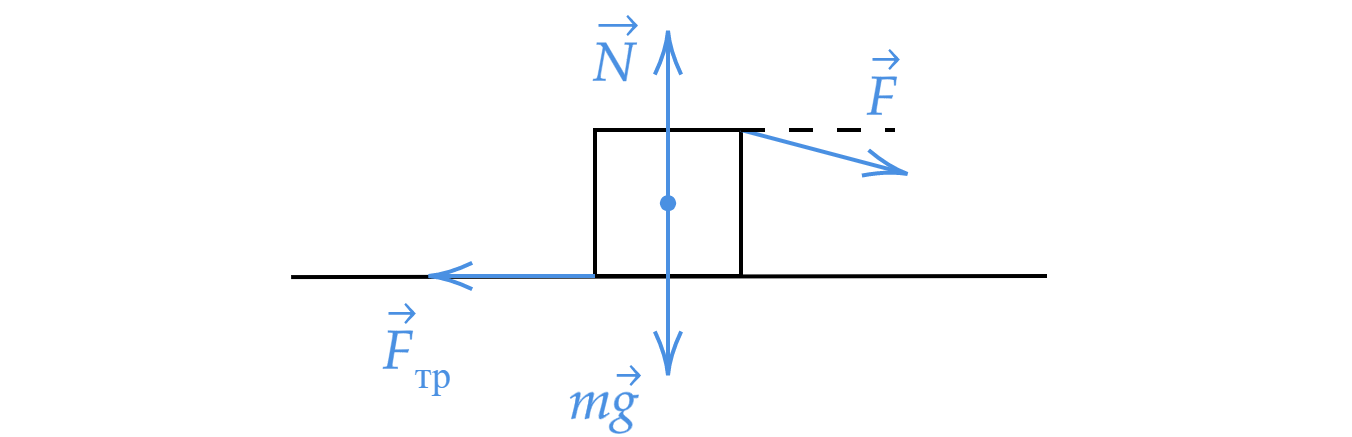
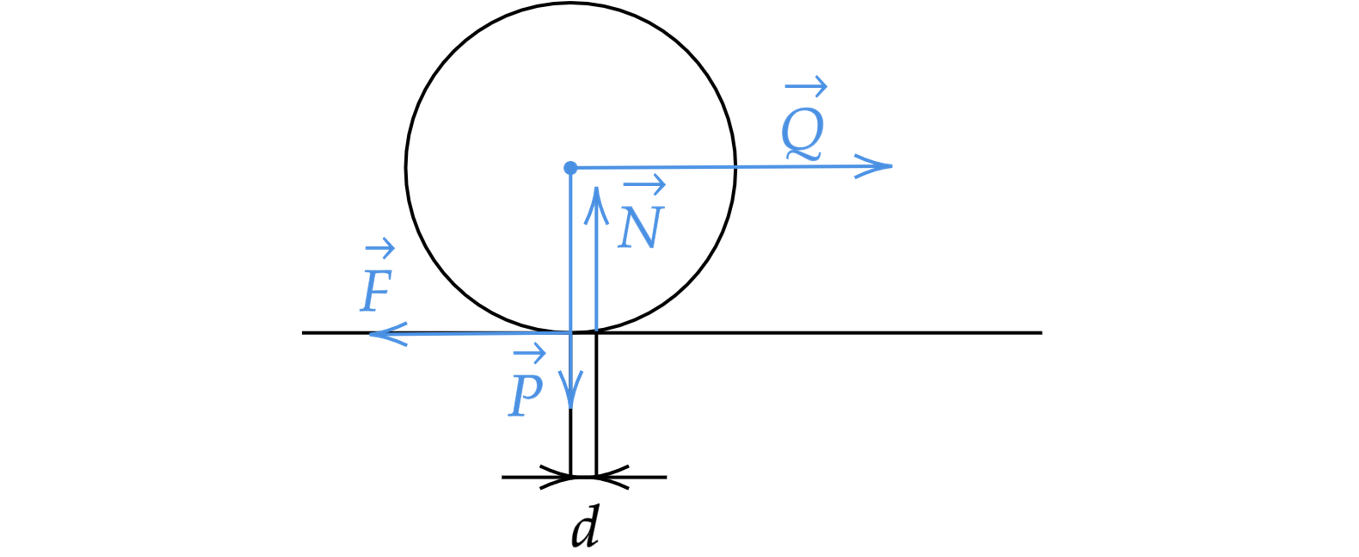
На горизонтальной поверхности стоит куб. Под каким углом и в какой точке на верхней стороне куба
нужно приложить силу, чтобы перевернуть куб без проскальзывания? Найти минимально возможную
силу, если масса куба , а коэффициента трения . Ответ дайте, основываясь на
законах физики. Сделайте схематический рисунок с указанием всех сил, действующих на
куб.

Показать ответ и решение

Введем оси и , направленные вертикально и горизонтально соответственно запишем второй
закон Ньютона относительно каждой из осей, а также правило моментов относительно точки
приложения силы

(
|
||{ Ox F cos α − F тр = 0
Oy N − F sinα − mg = 0
||
|( M A − F тр ⋅ a + mg a-= 0
2

где – угол между силой и горизонталью Из последнего уравнения выразим силу
трения

mg--
F тр = 2 (1)

Откуда сила

--mg---
F = 2 cosα

Чтобы косинус угла был максимален, угол должен быть минимален, следовательно, надо расположить
силу под углом 90 к поверхности куба.
Также проверим, подходит ли эта сила под условие коэффициента трения.
Сила трения равна

А
сила реакции опоры из второго уравнения системы

Объединяем (1) – (3) с учетом, что α = 0 и получаем

mg 1
-2--≤ μmg ⇒ μ ≥ 2-

Коэффициент трения входит в наш диапазон, следовательно, ответ верный.

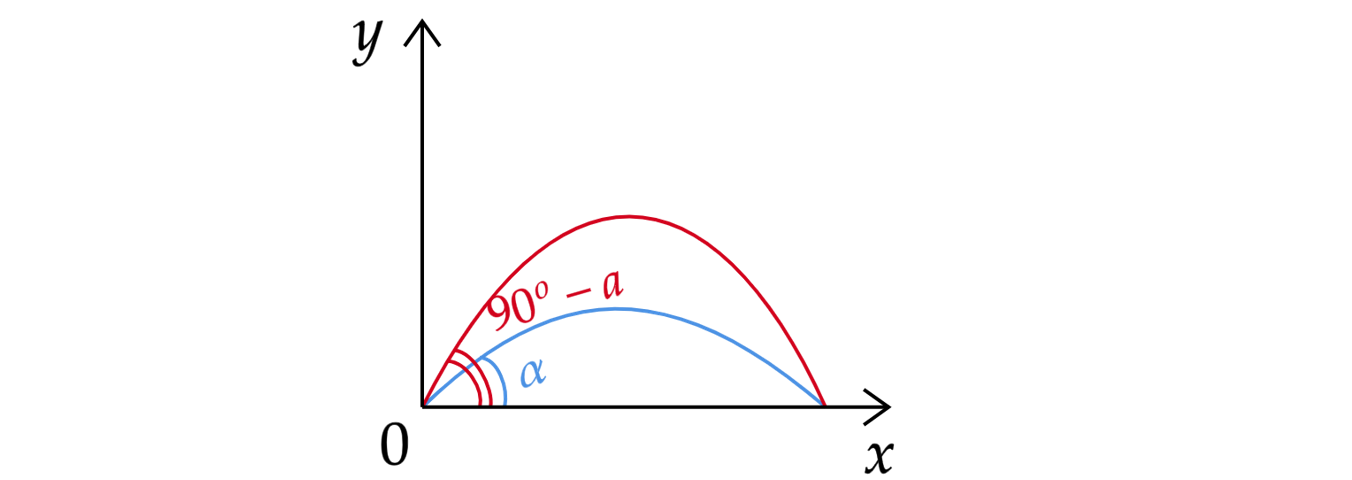
Тело бросили два раза под углами и к горизонту. Найдите отношение дальностей полета
тела в первом и во втором случае. Ответ дайте, основываясь на законах физики. Нарисуйте схематично
траекторию движения тела в обоих случаях.

Показать ответ и решение

Выведем формулу дальности полета тела.
Время подъема тела на максимальную высоту (снижение до земли с максимальной высоты)
равно

v0 sin α
0 = v0sinα − gt ⇒ t = -------
g

Откуда время всего полета тела

2v0 sin α
τ = 2t = --------- (1 )
g

Дальность полета тела выражена формулой

Объединим (1) и (2) и получим

2 2
2-⋅ v0 sinα-cos-α v-0 sin-2α
L = g = g

Подставим наши углы и

v20 sin2α-
Lα = g

v20 sin(180 − 2α) v20 sin2α
L90−α = ----------------= ---------
g g

Получились две одинаковые формулы, следовательно, дальности полетов одинаковые. Нарисуем
траектории движения

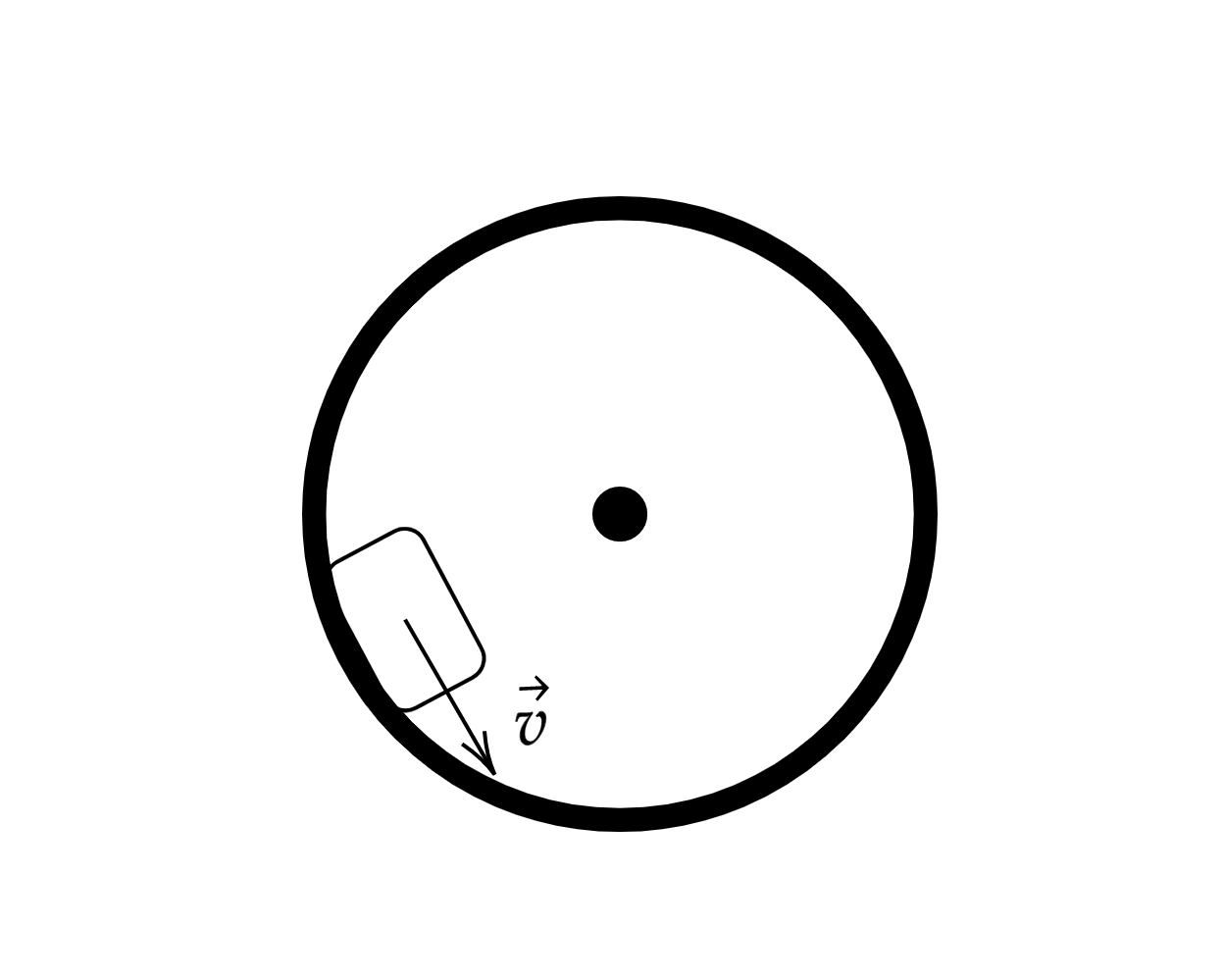
Небольшое тело вращается в вертикальной плоскости по закрепленному кольцу. Основываясь на
законах физики, объясните, в какой точке колеса давление на колесо со стороны тела будет
максимальным? Сделайте схематичный рисунок с указанием всех сил, действующих на тело. Трением
пренебречь.

Показать ответ и решение

Пусть радиус кольца, – скорость тела в верхней точке, – скорость тела в какой-то другой
точке кольца.

Сила давления тела на поверхность кольца равна силе реакции опоры со стороны кольца. Введем ось
, направленную в центр кольца, тогда сила реакции опоры в проекции на ось равна
. По второму закону Ньютона

2 2
mv--= N − mg cosα ⇒ N = mv---+ mg cos α.
R R

Из закона сохранения энергии можно найти

mv21- mv2-- mv2-- mv21-
2 + 2mgR = 2 + mgR (1 − cosα ) ⇒ R = R + 2mg (1 + cosα ),

Откуда

mv2
N = ---1-+ 2mg (1 + cosα ) + mg cosα,
R

Для того, чтобы было максимально, нужно чтобы cosα тоже был максимален, то есть α = 0 и
это соответствует нижней точке.

Сила реакции опоры равняется силе давления на колесо по третьему закон Ньютона, значит, в той
точке, где сила реакции опоры максимальна, максимальна будет и сила, с которой тело действует на
кольцо

Критерии оценки

3 балла ставится за задачу если:

_________________________________________________________________________________________________________________
Приведено полное правильное решение, включающее правильный ответ (в данном случае сделан
верный чертеж с указанием всех сил действующих на тело) и исчерпывающие верные
рассуждения с прямым указанием наблюдаемых явлений и законов (в данном случае: для
произвольного момента времени записан второй закон Ньютона в векторной форме и в проекции на
координатную ось, проходящую через центр колеса, на основе анализа записи второго закона
Ньютона в проекции на ось сделан верный вывод о положении точки на колесе, в которой
сила реакции опоры принимает наибольшее значение, с использованием третьего закона
Ньютона сделан вывод о численном равенстве силы реакции опоры и силы давления тела на
колесо)

2 балла ставится за задачу если:

IV) При неверном построении или отсутствии рисунка и (или) графика за задачу ставится 2
балла.

1 балл ставится за задачу если:

Во всех остальных случаях за задачу выставляется 0 баллов.

Известно, что слуховой аппарат человека чувствителен к изменениям атмосферного давления — если оно
быстро меняется, то уши закладывает. От этого ощущения можно избавиться, если определённым
образом глотнуть воздух. Объясните, основываясь на физических законах и закономерностях,
наблюдаемое явление и оцените, при спуске на лифте с какого этажа Главного здания (ГЗ) МГУ им.
М.В. Ломоносова это закладывание произойдёт, если в среднем уши человека чувствуют изменение
давления на 9 мм ртутного столба. Высота каждого этажа в ГЗ 5 м, а атмосферные условия близки к
нормальным. Лифт опускается на первый этаж. Считайте, что в пределах высоты ГЗ плотность
атмосферного воздуха не меняется.

Показать ответ и решение

Найдем, при какой разности давления в паскалях начинает закладывать уши

3
Δp = ρрт. ⋅ g ⋅ h = 13600 кг/ м ⋅ 10 Н/к г ⋅ 0,009 м ≈ 1224 П а

Найдем также высоту поднятия, необходимую для такой же разности давления, плотность воздуха
выразим из уравнения Клапейрона – Менделеева

-μp-
ρ = RT ,

где
– молярная масса воздуха, – нормальное атмосферное давление, – температура воздуха в
Кельвинах.

Найдем количество этажей

H--
n = 5 ≈ 10

Критерии оценки

3 балла ставится за задачу если:

_________________________________________________________________________________________________________________
Приведено полное правильное решение, включающее правильный ответ (в данном случае найдено число
этажей) и исчерпывающие верные рассуждения с прямым указанием наблюдаемых явлений и законов
(в данном случае: уравнение Менделеева-Клапейрона, формула гидростатического давления столба
жидкости))

2 балла ставится за задачу если:

IV) При неверном построении или отсутствии рисунка и (или) графика за задачу ставится 2
балла.

1 балл ставится за задачу если:

Во всех остальных случаях за задачу выставляется 0 баллов.

На каких колесах ехать легче: немного спущенных или полностью накаченных? Свой ответ объясните,
основываясь на законах физики.

Показать ответ и решение

Пусть к оси катка, имеющего вес , приложена сила , достаточно большая для того, чтобы
каток сдвинулся с места. Трение качения вызвано деформацией катящегося тела и поверхности. Сила
реакции опоры при этом смещена от вертикали, проходящей через центр колеса. Момент силы
трения качения равен

Если
колеса велосипеда немного спущены, то деформация колеса становится больше, увеличиваются
смещение силы реакции опоры и момент силы трения качения. Поэтому ехать становится
тяжелее.

Два абсолютно упругих шарика подвешены на длинных нерастяжимых нитях одинаковой длины. Один
из шариков массивный, а другой намного легче, чем первый. Они подвешены так, что центры шариков
находятся на одной высоте и шарики касаются друг друга. Вначале отклоняют в сторону в плоскости
нитей лёгкий шарик, отпускают его, и после лобового удара о тяжёлый шар лёгкий шарик
отскакивает и поднимается на некоторую высоту . Затем такой же опыт проводят, отклоняя
из начального положения на ту же высоту тяжёлый шар. Во сколько раз высота подъёма
лёгкого шарика после удара по нему тяжёлым шаром будет отличаться от той, что была в
первом случае? Потерями энергии можно пренебречь. Ответ поясните, опираясь на законы
механики.

Показать ответ и решение

1) Высота подъёма лёгкого шарика в первом случае, очевидно, будет равна той, на которую его
подняли. Это следует из законов сохранения импульса и механической энергии при абсолютно упругом
ударе о массивный шар — лёгкий шарик просто отскакивает от неподвижного тяжёлого с той же по
модулю скоростью, с какой он к нему приближался, и поднимается на исходную высоту. 2) При
отклонении тяжелого шарика его вся потенциальная энергия перейдет в кинетическую, и его скорость
перед столкновением будет равна скорости маленького шарика 3) Запишем закон сохранения импульса и
энергии

(
|{
M v1 = M V1 + mV2
| M--v21 M--V21- mV-22-
( 2 = 2 + 2

где и – массы большого и маленького шариков, – скорость большого шарика перед
столкновением, и – скорости большого и маленьких шариков после столкновения. Сгруппируем
слагаемые

(
|{ M v1 − M V1 = mV2
2 2 2
|( M--v1 − M-V-1-= mV-2-
2 2 2

Заметим разность квадратов и раскроем ее, умножив второе уравнение на 2

(
{ M v1 − M V1 = mV2

( M ((v1 − V1)(V1 + V1)) = mV 22

Поделим второе на первое

Выразим скорость большого шарика после столкновения и подставим в закон сохранения
импульса

Так
как

m ≪ M

, то
массой маленького можно пренебречь.

4)
Запишем закон сохранения энергии для маленького шарика с переходом в потенциальную
энергию

mV-22 4mv21-
2 = mgH ⇒ 2 = mgH

Значит и высота увеличиться в 4 раза.

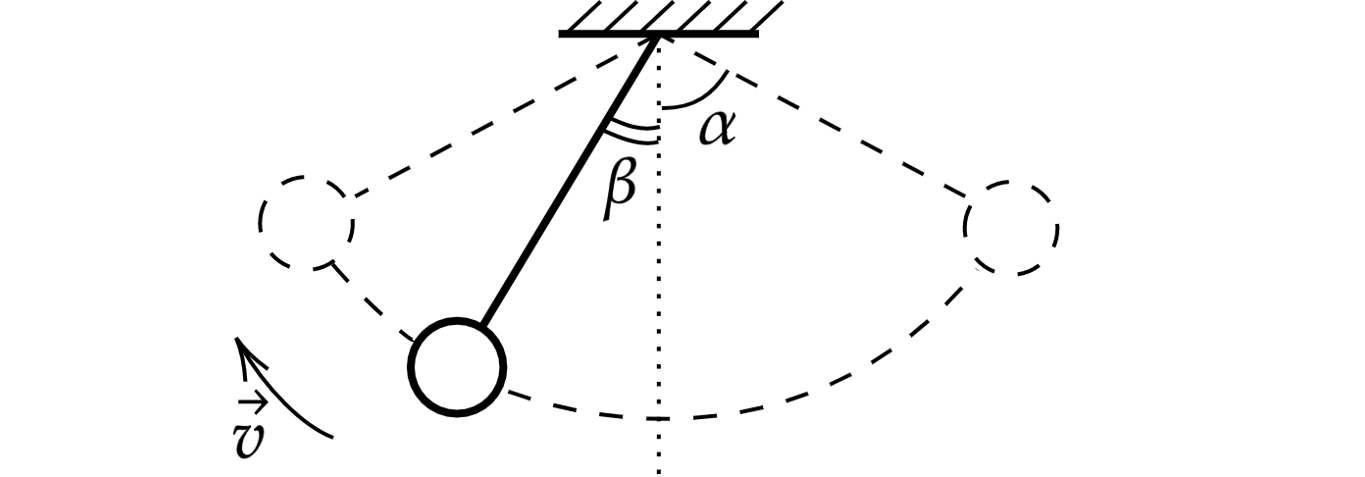
Маленький шарик, подвешенный к потолку на лёгкой нерастяжимой нити, совершает колебания в
вертикальной плоскости. Максимальное отклонение нити от вертикали составляет угол ∘
α = 60 .
Сделайте рисунок с указанием сил, приложенных к шарику в тот момент, когда шарик движется
влево-вверх, а нить образует угол с вертикалью (см. рисунок). Покажите на этом рисунке,
куда направлено в этот момент ускорение шарика (по нити, перпендикулярно нити, внутрь
траектории, наружу от траектории). Ответ обоснуйте. Сопротивление воздуха не учитывать.

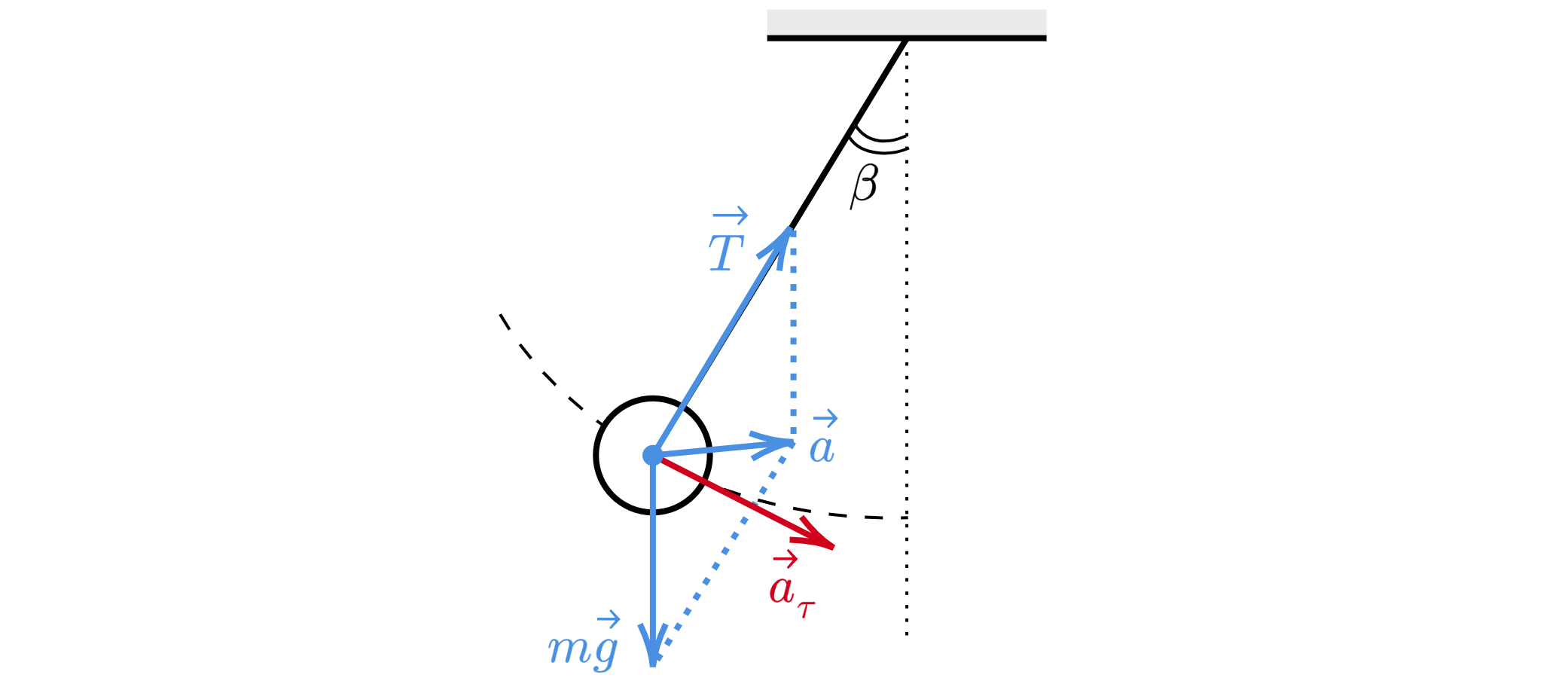
Показать ответ и решение

1) Сделаем рисунок с расставлением всех сил

2) Также у шарика при v ⁄= есть центростремительное и тангенциальное ускорение . Причем
тангенциальное ускорение направлено к положению равновесия и равно , а центростремительное
ускорение направлено в центр.
3) Ускорение тела будет равно векторному сложению тангенциального и центростремительного
ускорений

Значит ускорение направлено под некоторым углом правее внутрь траектории.

Критерии оценки

3 балла ставится за задачу если:

2 балла ставится за задачу если:

IV) При неверном построении или отсутствии рисунка и (или) графика за задачу ставится 2
балла.

1 балл ставится за задачу если:

Во всех остальных случаях за задачу выставляется 0 баллов.

Объясните, происхождение подъёмной силы гелиевых шариков и определите, насколько она изменится,
если вместо гирлянды из 27 шаров, в каждый из которых накачали по 1 молю гелия, надуть
тем же количеством гелия один большой шар? Толщина резиновой оболочки у всех шаров
одинакова, давление и температура близки к нормальным, а подъёмная сила гирлянды равна
Н. Ответ поясните, указав, какие физические закономерности вы использовали для
объяснения.

Показать ответ и решение

1) Подъемная сила возникает при условии, что сила Архимеда больше, чем сила тяжести.
2) Найдем подъемную силу 1 моль гелия, она равна

где и – молярные массы воздуха и гелия.
Для n = 27 моль гелия

Так как количество гелия и гирлянде и в одном большом шаре не изменяется, то и подъемная сила
будет оставаться той же.
3) Найдем опускающую силу (вес) гирлянды и одного большого шара.
Для гирлянды вес равен

Так как у нас шары, то их объем пропорционален кубу радиуса шара, а их площадь
пропорциональна квадрату радиуса.
Так как объем большого шара равен 27 объемам маленьких шаров, то радиус большого равен 3
радиусам маленького . Площадь оболочки будет в 3 раза меньше, чем площадь маленького. Значит, вес
большого шара равен

P = 5,-23-Н ≈ 1,74 Н
n 3

4) Найдем подъемную силу большого шара

А увеличится она по сравнению с гирляндой

Объясните, почему у басовых труб органа длины большие, а у труб с высокими тонами —
маленькие. Органная труба открыта с обоих концов и звучит при продувании через неё потока
воздуха. Ответ поясните, указав, какие физические закономерности вы использовали для
объяснения.

Показать ответ и решение

1) Громкий звук бывает, когда на конце трубы устанавливается пучность стоячей волны, так как вблизи
пучности колебания происходят с максимальной амплитудой, а чем больше амплитуда, тем громче
звук.
2) Поскольку труба открыта с обоих концов, то пучность также должна устанавливаться и на входе
трубы. Поэтому для наиболее громкого звучания минимальная длина трубы должна быть равна
половине длины волны — при этом посередине трубы находится узел стоячей волны, а на её концах — две
пучности.
3) Звуки низкой частоты (басы) соответствуют большим длинам волн, а высокой частоты —
маленьким длинам волн, поскольку длина волны v
λ = --
ν , а скорость звука не зависит от его
частоты.

Как известно, при долгом использовании автомобиля диск сцепления в нем начинает стираться, а сила
его прижатия к маховику уменьшается, и сцепление начинает пробуксовывать. На каких передачах —
«пониженных» или «повышенных» — следует двигаться в этом случае, чтобы добраться до ближайшей
станции техобслуживания?

Справка: при движении автомобиля с определённой скоростью на «пониженных» передачах (1, 2, 3
…) двигатель работает на больших оборотах, а на «повышенных» (4, 5, …) — на меньших оборотах
при той же скорости движения.

Показать ответ и решение

1) При износе диска уменьшается сила прижатия к маховику, а значит и уменьшается максимальная
сила трения и её момент, что приводит к пробуксовке сцепления на режимах движения с
использованием максимальной мощности двигателя.
2) Мощность силы равна модулю силы умножить на скорость перемещения точки приложения данной
силы. Значит, для того, чтобы сохранить, при уменьшении силы (максимальной силы трения)
необходимо увеличить частоту вращения диска, то есть увеличивать скорость вращения диска сцепления
или обороты двигателя.
3) Из пункта 2 следует, что при возникновении пробуксовки сцепления нужно переходить с повышенных
передач на пониженные, когда двигатель при той же скорости движения автомобиля работает на более
высоких оборотах.

Критерии оценки

3 балла ставится за задачу если:

2 балла ставится за задачу если:

IV) При неверном построении или отсутствии рисунка и (или) графика за задачу ставится 2
балла.

1 балл ставится за задачу если:

Во всех остальных случаях за задачу выставляется 0 баллов.

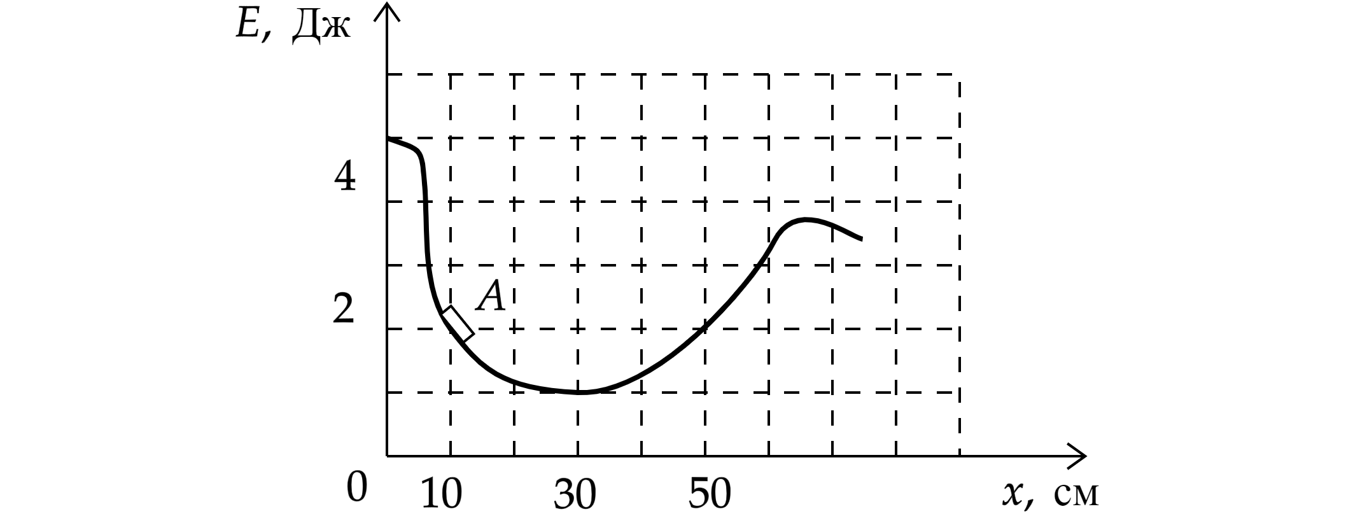
Льдинку толкнули в яму с гладкими стенами, в которой она движется без трения. На рисунке приведен
график зависимости энергии взаимодействия льдинки с Землей от её координаты в яме.

В некоторый момент времени льдинка находилась в точке и двигалась влево, имея кинетическую
энергию, равную 2 Дж. Сможет ли льдинка выскользнуть из ямы? Ответ поясните, указав, какие
физические закономерности вы использовали для объяснения.

Показать ответ и решение

1) Посмотрим по рисунку, какой энергией должна обладать льдинка, чтобы выскочить с левого или с
правого краев. Слева надо иметь запас механической энергии 5 Дж, а справа запас должен быть меньше
4 Дж.
2) В самом начале движения льдинка обладала кинетической и потенциальной энергиями, равными
2 Дж, а значит ее запас механической энергии равен сумме этих энергий и равен E = 4
Дж.
3) По пункту 1 и 2 мы можем сделать вывод, что льдинка не выскочит слева, но выскочит справа, так
как ее запас механической энергии равен 4 Дж, чтобы выскочить справа нужно иметь чуть меньше, чем
4 Дж.

Критерии оценки

3 балла ставится за задачу если:

2 балла ставится за задачу если:

IV) При неверном построении или отсутствии рисунка и (или) графика за задачу ставится 2
балла.

1 балл ставится за задачу если:

Во всех остальных случаях за задачу выставляется 0 баллов.

На поверхности Земли покоится миска с водой и деревянным бруском. Как изменится глубина
погружения бруска в воду, если миска будет стоять на полу лифта, движущегося с ускорением,
направленным вертикально вверх? Ответ поясните, используя физические закономерности.

Показать ответ и решение

1) Когда миска с водой и брусок покоятся относительно Земли сила Архимеда уравновешивает силу
тяжести бруска, поэтому масса бруска и масса вытесненной воды равны.
2) Когда миска, брусок и вода покоятся относительно друг друга, но движутся с ускорением
относительно Земли, то сила Архимеда и сила тяжести сообщают одно и то же ускорение , а
значит:

где – масса бруска, m
1 – масса вытесненной воды.
Так как m = m1 , а масса бруска постоянна, то и масса вытесненной воды не изменяется. Вода
практически несжимаема, поэтому плотность воды в обоих случаях одинакова. Значит, объем
вытесненной воды не изменяется, глубина погружения бруска в лифте остается прежней.

Критерии оценки

3 балла ставится за задачу если:

2 балла ставится за задачу если:

IV) При неверном построении или отсутствии рисунка и (или) графика за задачу ставится 2
балла.

1 балл ставится за задачу если:

Во всех остальных случаях за задачу выставляется 0 баллов.

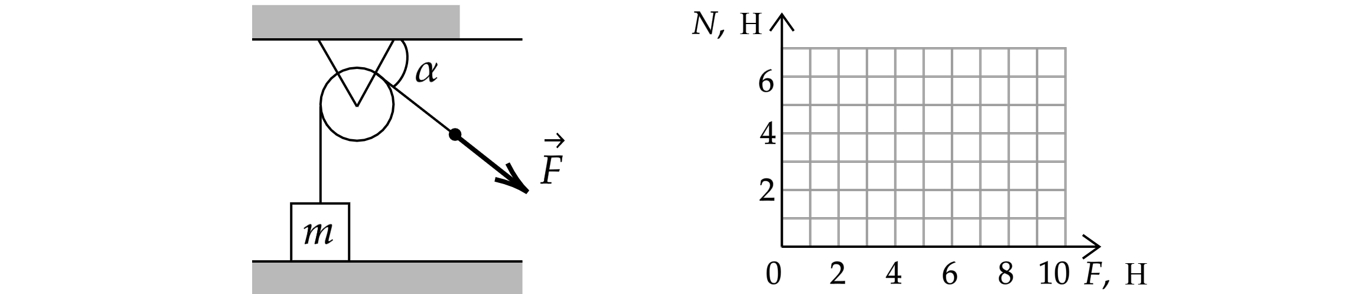
Лёгкая нить, привязанная к грузу массой m = 0,4 кг, перекинута через идеальный неподвижный блок.
К правому концу нити приложена постоянная сила . Левая часть нити вертикальна, а правая
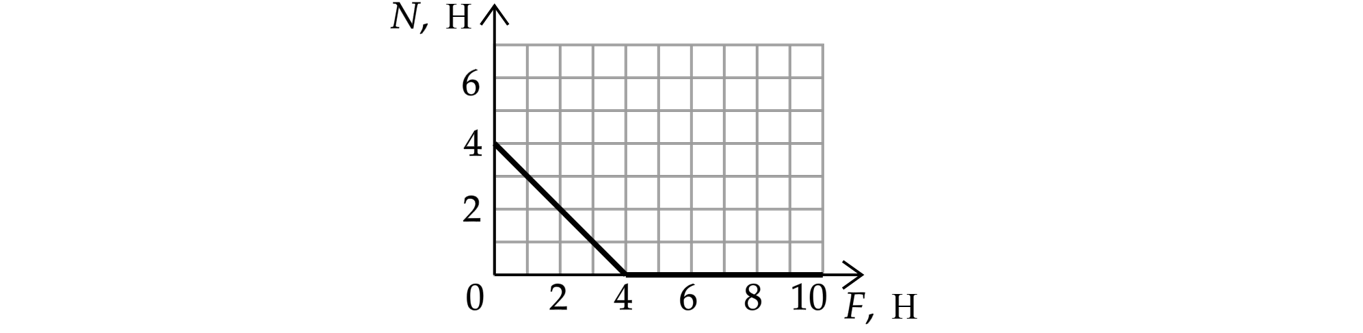
наклонена под углом к горизонту (см. рисунок). Постройте график зависимости модуля силы
реакции стола N от F на отрезке Н. Ответ поясните, указав, какие физические явления и
закономерности Вы использовали для объяснения. Сделайте рисунок с указанием сил, приложенных к
грузу.

Демоверсия 2021

Показать ответ и решение

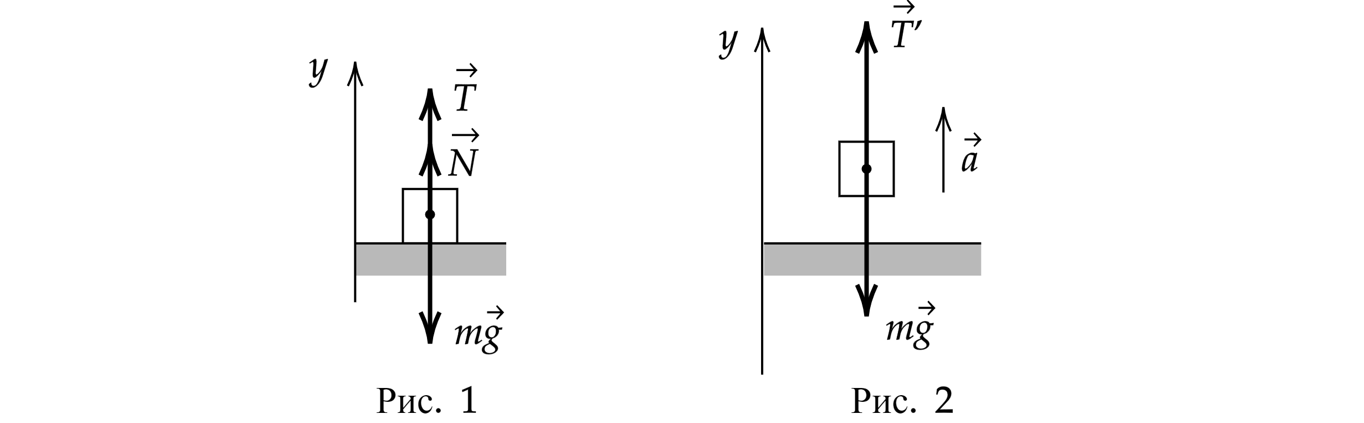
В начале сила натяжения нити, равная силе будет меньше, чем сила mg = 4 Н, поэтому по
второму закону Ньютона

пока тело покоится, ускорение равно нулю, при F = 0 , Н.
При силе от 0 до 4 Н,
При силе больше 4 Н, груз начнет отрываться от стола и двигаться с ускорением, а сила реакции опоры
станет равна 0.

Критерии оценки

3 балла ставится за задачу если:

_________________________________________________________________________________________________________________
Приведено полное правильное решение, включающее правильный ответ (в данном случае сделан верный
рисунок с указанием всех сил приложенных к грузу, построен график зависимости модуля силы
реакции поверхности стола N от F) и исчерпывающие верные рассуждения с прямым указанием
наблюдаемых явлений и законов (в данном случае: записан и назван второй закон Ньютона, записано
условие отрыва груза от поверхности стола)

2 балла ставится за задачу если:

IV) При неверном построении или отсутствии рисунка и (или) графика за задачу ставится 2
балла.

1 балл ставится за задачу если:

Во всех остальных случаях за задачу выставляется 0 баллов.

Источник

Задача 1

К одному концу лёгкой пружины жёсткостью k = 100 Н/м прикреплён массивный груз, лежащий на горизонтальной плоскости, другой конец пружины закреплён неподвижно (см. рисунок). Коэффициент трения груза по плоскости Груз смещают по горизонтали, растягивая пружину, затем отпускают с начальной скоростью, равной нулю. Груз движется в одном направлении и затем останавливается в положении, в котором пружина уже сжата. Максимальное растяжение пружины, при котором груз движется таким образом, равно d = 15 см. Найдите массу m груза.

Решение

1. Начальная энергия системы равна потенциальной энергии растянутой пружины: После того, как пружину отпустили, она остановится в положении, при котором она сжата на величину Тогда конечная энергия системы равна потенциальной энергии сжатой пружины:

Изменение полной энергии системы равно работе силы трения

где — модуль силы реакции опоры.

2. В момент, когда груз остановился, по второму закону Ньютона равнодействующая всех сил стала равна нулю. Пружина сжата, поэтому сила упругости пружины направлена вправо. Её уравновешивает сила трения покоя, которая направлена против возможного движения, причём эта сила максимальна, т. к. по условию начальное положение пружины соответствует максимальному растяжению пружины, при котором груз движется таким образом.

Запишем закон Ньютона для горизонтальной и вертикальной осей:

3. Подставим полученное выражение для в равенство из пункта 1:

После подстановки получим

Ответ:

Задача 2

Из пружинного пистолета выстрелили вертикально вниз в мишень, находящуюся на расстоянии 2 м от него. Совершив работу 0,12 Дж, пуля застряла в мишени. Какова масса пули, если пружина была сжата перед выстрелом на 2 см, а ее жесткость 100 Н/м?

Решение

Согласно закону сохранения механической энергии, имеем два равенства:

где и — скорости летящей пули соответственно на высоте и непосредственно перед мишенью. Вся энергия подлетевшей к мишени пули потрачена на механическую работу, так что

Решая полученную систему уравнений, находим массу пули:

Задача 3

Небольшая шайба после толчка приобретает скорость v = 2 м/с и скользит по внутренней поверхности гладкого закрепленного кольца радиусом R = 0,14 м. На какой высоте h шайба отрывается от кольца и начинает свободно падать?

Решение

Согласно закону сохранения энергии:

, (1)

где — скорость шайбы в момент отрыва от кольца на высоте .

В точке отрыва сила нормальной реакции опоры равна 0; . Центростремительное ускорение шайбы найдём из второго закона Ньютона (см. рис.):

. (2)

. (3)

Объединяя (1), (2) и (3), получим:

м.

Ответ: 0,18.

Задача 4

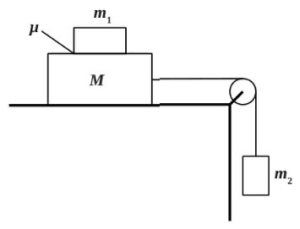
Грузы массами M = 1 кг и m связаны легкой нерастяжимой нитью, переброшенной через блок, по которому нить может скользить без трения (см. рис.). Груз массой М находится на шероховатой наклонной плоскости (угол наклона плоскости к горизонту а = 30°, коэффициент трения = 0,3). Чему равно минимальное значение массы m, при котором система грузов еще не выходит из первоначального состояния покоя?

Решение

Если масса m достаточно мала, но грузы ещё покоятся, то сила трения покоя, действующая на груз массой М, направлена вверх вдоль наклонной плоскости. Запишем второй закон Ньютона для каждого из покоящихся тел в проекциях на оси введенной системы координат. На первое тело действуют сила тяжести, сила нормальной реакции опоры, сила натяжения нити и сила трения:

(ось направлена вниз вдоль наклонной плоскости);

(ось направлена вверх перпендикулярно наклонной плоскости).

На второе тело действуют сила тяжести и сила натяжения нити:

(ось направлена вертикально вниз).

Учитывая, что (нить легкая, между блоком и нитью трения нет), то (сила трения покоя). Получим:

кг.

Ответ: 0,24.

Задача 5

Тело, брошено с поверхности земли со скоростью v под углом a к горизонту. Сопротивление воздуха пренебрежимо мало.

Установите соответствие между физическими величинами, характеризующими движение тела, и формулами, по которым их можно определить.

К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры.

Решение

Рассмотрим динамику движения тела, брошенного под углом к горизонту с начальной скоростью . В задаче нас интересует вертикальное движение тела.

Из рисунка видно, что проекция начальной скорости на ось Oy равна

Проекция ускорения равна

где м/с2 – ускорение свободного падения. Таким образом, скорость тела вдоль оси Oy будет меняться по закону

Можно заметить, что в точке максимального подъема скорость , получаем уравнение

То есть для буквы «А» соответствует формула под номером 4.

Для определения максимальной высоты , запишем формулу движения тела, подброшенного вертикально вверх:

и, учитывая, что , , а время для достижения максимальной высоты составляет , получаем выражение:

То есть для буквы «Б» соответствует формула под номером 1.

Ответ: А4, Б1.

Задача 6

Воздушный шар объемом V = 2500 м3 с массой оболочки = 400 кг имеет внизу отверстие, через которое воздух в шаре нагревается горелкой. До какой минимальной температуры t1 нужно нагреть воздух в шаре, чтобы шар взлетел вместе с грузом (корзиной и воздухоплавателем) массой = 200 кг? Температура окружающего воздуха t = 7 °С, его плотность = 1,2 кг/м3. Оболочку шара считать нерастяжимой.

Решение

Шар взлетает, когда сила тяжести, действующая на него, равна силе Архимеда

, (1)

где m — масса воздуха в шаре. Из уравнения Менделеева-Клапейрона

, , (2)

где , , — молярная масса воздуха. Объединяя (1) и (2), получим:

соответственно °С.

Ответ: 350.

Задача 7

Брусок массой m₁ = 500 г соскальзывает по наклонной плоскости с некоторой высоты h и, двигаясь по горизонтальной поверхности, сталкивается с неподвижным бруском массой m₂ = 300 г. Считая столкновение абсолютно неупругим, определите высоту h, если общая кинетическая энергия брусков после столкновения равна 2,5 Дж. Трением при движении пренебречь. Считать, что наклонная плоскость плавно переходит в горизонтальную.

Решение

Кинетическая энергия брусков после столкновения где v — скорость системы после удара, определяемая из закона сохранения импульса на горизонтальном участке: m₁v₁ = (m₁ + m₂)v.

Исключая из системы уравнений скорость v, получим:

Кинетическая энергия первого бруска перед столкновением определяется из закона сохранения механической энергии при скольжении по наклонной плоскости: что даёт выражение

Подставляя значения масс и энергии из условия, получим численное значение h = 0,8 м

Ответ: h = 0,8 м.

Задача 8

Небольшой груз, прикрепленный к нити длиной l = 15 см, вращается вокруг вертикальной оси так, что нить отклоняется от вертикали на угол a = 60°. С какой скоростью движется груз?

Решение

На груз действуют сила натяжения нити и сила тяжести , как указано на рисунке.

В инерциальной системе отсчёта, связанной с Землёй, ускорение тела определяется вторым законом Ньютона:

Здесь — центростремительное ускорение. Решая полученную систему, получим:

м/с.

Ответ: 1,5.

Задача 9

Камень массой m = 4 кг падает под углом a = 30° к вертикали со скоростью 10 м/с в тележку с песком общей массой M = 16 кг, покоящуюся на горизонтальных рельсах. Определите скорость тележки с камнем после падения в нее камня.

Решение

Общая инерция камня, падающего в тележку, равна . Величина инерции, в горизонтальном направлении от падения камня составит . Тогда из закона сохранения инерции, учитывая, что тележка вначале была неподвижной, а после падения в нее камня увеличила свою массу на массу камня, получаем

откуда

м/с

Ответ: 1.

Задача 10

Два груза одинаковой массы М, связанные нерастяжимой и невесомой нитью, движутся прямолинейно по гладкой горизонтальной поверхности под действием горизонтальной силы F, приложенной к одному из грузов (см. рис.). Минимальная сила F, при которой нить обрывается, равна 12 Н. При какой силе натяжения обрывается нить?

Решение

Сила, под действием которой движутся грузы массой M – это равнодействующая, то есть учитывающая силу трения. Следовательно, из второго закона Ньютона можно записать , где — ускорение, с которым движутся грузы. Сила натяжения нити T создается последним грузом, который перемещается с тем же ускорением , но имеет массу M, т.е. . Выражая ускорение как , получаем силу натяжения, равную Н.

Ответ: 6.

Задача 11

Груз, лежащий на столе, связан легкой нерастяжимой нитью, переброшенной через идеальный блок, с грузом массой 0,25 кг. На первый груз действует горизонтальная постоянная сила F, равная 9 Н (см. рис.). Второй груз движется с ускорением 2 м/с2, направленным вверх. Трением между грузом и поверхностью стола пренебречь. Какова масса первого груза?

Решение

На второй груз действует сила тяжести и противоположная сила тяги первого груза Н (трение здесь не учитывается). Таким образом, для системы из двух грузов массами и можем записать

где — масса первого груза. Отсюда получаем:

Подставляем числовые значения, находим

кг.

Ответ: 3.

Задача 12

Маленький шарик падает сверху на наклонную плоскость и упруго отражается от неё. Угол наклона плоскости к горизонту равен На какое расстояние по горизонтали перемещается шарик между первым и вторым ударами о плоскость? Скорость шарика непосредственно перед первым ударом направлена вертикально вниз и равна 1 м/с.

Решение

Выберем следующую систему координат: ось направим вдоль плоскости, а ось — перпендикулярно ей. Тогда кинематические уравнения движения шарика имеют вид:

В момент второго соударения шарика с плоскостью

Решая систему уравнений, получаем:

Из рисунка видно, что

Ответ:

Задача 13

На гладкой горизонтальной поверхности стола покоится горка с двумя вершинами, высоты которых h и 5/2*h (см. рисунок). На правой вершине горки находится шайба. От незначительного толчка шайба и горка приходят в движение, причём шайба движется влево, не отрываясь от гладкой поверхности горки, а поступательно движущаяся горка не отрывается от стола. Скорость шайбы на левой вершине горки оказалась равной v. Найдите отношение масс шайбы и горки.

Решение

На систему тел «шайба + горка» действуют внешние силы (тяжести и реакции стола), направленные по вертикали, поэтому проекция импульса системы на горизонтальную ось Ох системы отсчёта, связанной со столом, сохраняется.

В начальный момент , а в момент . Из закона сохранения импульса получим: , где m — масса шайбы, М — масса горки.

Работа сил тяжести определяется изменением потенциальной энергии, а суммарная работа сил реакции равна нулю, так как поверхности гладкие. Следовательно, полная механическая энергия системы тел, равная сумме кинетической и потенциальной, сохраняется. Так как потенциальная энергия горки не изменилась, получаем уравнение

Решение системы дает отношение масс

Ответ: .

Задача 14

Снаряд, движущийся со скоростью v0 разрывается на две равные части, одна из которых продолжает движение по направлению движения снаряда, а другая движется в противоположную сторону. В момент разрыва суммарная кинетическая энергия осколков увеличивается за счёт энергии взрыва на величину ∆E. Скорость осколка, движущегося вперёд по направлению движения снаряда, равна v1. Найдите массу m осколка.

Решение

Введём обозначение: v2 — модуль скорости летящего назад осколка снаряда. Система уравнений для решения задачи:

Выразим v2 из первого уравнения: — и подставим во второе уравнение. Получим: . Отсюда следует:

Ответ: .

Задача 15

Снаряд массой 2m разрывается в полёте на две равные части, одна из которых продолжает движение по направлению движения снаряда, а другая — в противоположную сторону. В момент разрыва суммарная кинетическая энергия осколков увеличивается за счёт энергии взрыва на величину ∆Е. Модуль скорости осколка, движущегося по направлению движения снаряда, равен v1, а модуль скорости второго осколка равен v2. Найдите ∆Е.

Решение

Введём обозначение: v0 — модуль скорости снаряда до разрыва. Система уравнений для решения задачи:

Выразим v0 из первого уравнения: и подставим во второе уравнение. Получим:

Отсюда следует:

Ответ: .

Задача 16

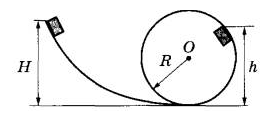
При выполнении трюка «Летающий велосипедист» гонщик движется по гладкому трамплину под действием силы тяжести, начиная движение из состояния покоя с некоторой высоты (см. рисунок). На краю трамплина скорость гонщика направлена под углом α = 60° к горизонту. Пролетев по воздуху, он приземляется на горизонтальный стол, поднявшись в полёте на высоту h над краем трамплина. С какой высоты H начинал движение гонщик?

Решение

Применим закон сохранения энергии и найдём скорость велосипедиста при отрыве от трамплина.

Рассмотрим проекции скорости на горизонтальную и вертикальную оси:

В тот момент, когда велосипедист достигнет наивысшей точки полёта вертикальная проекция его скорости станет равной нулю, при этом в горизонтальном направлении он пролетит половину пути. Найдём время, за которое велосипедист достигнет наивысшей точки.

Координата зависит от времени по закону Значит, максимальная высота полёта велоспедиста

Откуда

Ответ:

Задача 17

После толчка льдинка закатилась в яму с гладкими стенками, в которой она может двигаться практически без трения. На рисунке приведен график зависимости энергии взаимодействия льдинки с Землей от её координаты в яме.

В некоторый момент времени льдинка находилась в точке А с координатой и двигалась влево, имея кинетическую энергию, равную 2 Дж. Сможет ли льдинка выскользнуть из ямы? Ответ поясните, указав, какие физические закономерности вы использовали для объяснения.

Решение

1) Льдинка сможет выскользнуть из ямы через ее правый край.

2) Трения при движении льдинки нет, поэтому ее механическая энергия сохраняется. Запас кинетической энергии льдинки в точке A позволяет ей подняться до уровня, где ее потенциальная энергия составит 4 Дж.

3) Левый край ямы поднят до большей высоты. Следовательно, этого края льдинка не достигнет и заскользит вправо. Правый же край ямы ниже: на верху этого края потенциальная энергия льдинки меньше 4 Дж. Поэтому льдинка выскользнет из ямы через правый край.

Задача 18

Гладкий клин массой M с углом при основании стоит на горизонтальной плоскости, часть которой под ним и левее — гладкая, а часть — справа от него — шероховатая (см. рис.). На вершине клина, на высоте H над плоскостью находится маленький брусок массой m, коэффициент трения которого о шероховатую часть плоскости равен Брусок отпускают без начальной скорости, он скатывается по клину и далее скользит по шероховатой плоскости и останавливается на некотором расстоянии L по горизонтали от своего начального положения. Найдите это расстояние L, если в точке перехода с клина на плоскость есть гладкое закругление, так что скорость бруска при переходе с клина на плоскость не уменьшается.

Решение

При соскальзывании бруска с клина выполняются законы сохранения горизонтальной проекции импульса и механической энергии данной системы тел: где v и V — скорости бруска и клина, соответственно, после соскальзывания бруска с клина. Из этих уравнений следует, что скорость бруска перед его попаданием на шероховатый участок плоскости равна:

До попадания на этот участок брусок сдвинется из начального положения по горизонтали без трения на расстояние равное, очевидно, длине основания клина, а затем пройдёт по шероховатой плоскости расстояние на котором его кинетическая энергия будет израсходована на работу против силы сухого трения скольжения. По закону Амонтона — Кулона эта сила равна так как сила N давления бруска на неподвижную горизонтальную плоскость равна mg. Таким образом, и Искомое расстояние L в результате равно сумме l₁ и l₂:

Ответ:

Задача 19

В системе, изображённой на рисунке, трения нет, блоки невесомы, нить невесома и нерастяжима, m₁ = 2 кг, m₂ = 4 кг, m₃ = 1 кг. Найдите модуль и направление ускорения груза массой m₃.

Решение

1. Введём на рисунке неподвижную систему координат, у которой ось x горизонтальна и направлена вправо, а ось y направлена вертикально вниз. Обозначим также силы, определяющие ускорения тел вдоль направлений их движения: силу T натяжения нити, которая, как следует из условия задачи, постоянна по модулю вдоль всей нити, и силу тяжести

2. Записывая второй закон Ньютона в проекциях на оси x и y для трёх грузов, имеем:

3. Поскольку нить нерастяжима, из постоянства её длины получаем следующее соотношение для координат грузов:

Отсюда следует связь между ускорениями грузов:

4. Решая полученную систему уравнений, находим модуль искомого ускорения:

вектор направлен вниз.

Ответ: вектор направлен вниз.

Задача 20

К двум вертикально расположенным пружинам одинаковой длины подвесили однородный стержень длиной L = 30 см. Если к этому стержню подвесить груз массой m = 3 кг на расстоянии d = 5 см от правой пружины, то стержень будет расположен горизонтально, и растяжения обеих пружин будут одинаковы (см. рисунок). Жёсткость левой пружины в 2 раза меньше, чем правой. Чему равна масса стержня М? Сделайте рисунок с указанием используемых в решении сил.

Решение

1. Укажем на рисунке силы действующие на стержень. Приравняем моменты сил, действующих на стержень, относительно центра стержня, т.е. точки А:

Учтем, что стержень расположен горизонтально, т.е. удлинения пружин равны, а также, что жесткость правой пружины в два раза больше левой:

2. Приравняем моменты сил, действующих на стержень, относительно точки Б, которая находится в месте крепления правой пружины:

3. Найдем массу стержня:

Ответ:

Задача 21

Найдите модуль ускорения a груза массой m в системе, изображённой на рисунке. Трения нет, блоки невесомы, нити лёгкие и нерастяжимые, их участки, не лежащие на блоках, вертикальны, масса второго груза M, ускорение свободного падения равно g.

Решение

Введём координатную ось Х, направленную вниз, и отметим на ней координаты грузов М и m: x_M и x_m (см. рис.). Пронумеруем блоки цифрами 1, 2, 3 и укажем на рисунке силы натяжения нитей и силы тяжести, действующие на грузы. Согласно условию, в силу невесомости нитей и блоков, а также отсутствия сил трения, первая нить, охватывающая блоки 1 и 2, натянута с силой T, а вторая — с силой 2T, так что на груз m действует направленная вверх сила 4T. Если сместить груз М вдоль оси Х вниз на расстояние Δx_M, то в силу нерастяжимости нитей блок 2 сместится, как следует из рисунка, на −Δx_M/2, а блок 3 и груз m — на Δx_m = −Δx_M/4. Таким образом, Δx_M + 4Δx_m = 0.

Отсюда получаем уравнение кинематической связи: A + 4a = 0, где A и a — проекции ускорений грузов М и m на ось Х. Уравнения движения грузов (второй закон Ньютона) в проекциях на ось Х имеют вид: МA = Мg – T, ma = mg – 4T. Решая полученную систему из трех уравнений, находим, что модуль ускорения груза М равен:

Ответ:

Задача 22

Тонкий однородный стержень АВ шарнирно закреплён в точке А и удерживается горизонтальной нитью ВС (см. рисунок). Трение в шарнире пренебрежимо мало. Масса стержня m = 1 кг, угол его наклона к горизонту α = 45°. Найдите модуль силы действующей на стержень со стороны шарнира. Сделайте рисунок, на котором укажите все силы, действующие на стержень.

Решение

1. Изобразим на рисунке силы, действующие на стержень, и систему координат Оху.

Здесь — сила натяжения нити, — сила тяжести, и — вертикальная и горизонтальная составляющие силы, действующей на стержень со стороны шарнира.

2. В положении равновесия равны нулю сумма моментов сил, действующих на стержень, относительно оси, проходящей через точку А перпендикулярно плоскости рисунка, сумма горизонтальных и сумма вертикальных составляющих сил, действующих на стержень:

где — длина стержня; (1)

(2)

(3)

3. Модуль силы реакции шарнира

Из (1) получим Окончательно

Ответ:

Задача 23

Из двух ровных досок сделан желоб, представляющий собой двугранный угол с раствором Желоб закреплен так, что его ребро горизонтально, а доски симметричны относительно вертикали. В желобе на боковой поверхности лежит цилиндр массой Коэффициент трения между досками и цилиндром равен К торцу цилиндра приложена горизонтально направленная сила Найдите модуль ускорения цилиндра.

Решение

Изобразим вид на желоб со стороны торца цилиндра. На цилиндр в плоскости чертежа действуют направленная вниз сила тяжести и две равные по модулю силы реакции досок, направленные перпендикулярно стенкам желоба. Так как цилиндр не движется в вертикальном направлении, то, в соответствии со вторым законом Ньютона, сумма проекций этих трех сил на вертикаль равна нулю:

где

Отсюда В горизонтальном направлении (вдоль желоба) на цилиндр действуют сила а также, в противоположном направлении, две силы сухого трения Предположим, что цилиндр будет двигаться по желобу. Тогда по закону Амонтона — Кулона для силы сухого трения скольжения можно записать:

Записывая второй закон Ньютона в проекции на горизонтальную ось, направленную вдоль ребра желоба, получим:

где — модуль искомого ускорения цилиндра. Заметим, что Это означает, что приложенная к торцу цилиндра сила превышает силу трения покоя, то есть цилиндр и в самом деле будет скользить вдоль желоба.

Следовательно, Подставляя числовые данные и проверяя размерность, окончательно получим:

Ответ:

Задача 24

Равносторонний треугольник, состоящий из трёх жёстких лёгких стержней, может вращаться без трения вокруг горизонтальной оси, совпадающей с одной из его сторон. В точке пересечения двух других его сторон к треугольнику прикреплён массивный грузик (см. рисунок). Как и во сколько раз изменится период малых колебаний грузика около его положения равновесия, если ось вращения наклонить под углом к горизонту?

Решение

Обозначим расстояние от оси вращения треугольника до грузика через Тогда период колебаний при горизонтальном положении оси равен, очевидно,

После наклона оси на угол возвращающая сила при отклонении треугольника от положения равновесия уменьшится: составляющая силы тяжести вдоль оси, равная (здесь — масса грузика), будет компенсироваться силами реакции со стороны подшипников, в которых закреплена эта ось, а в направлении, перпендикулярном оси, будет действовать эффективная «сила тяжести», равна Поэтому период малых колебаний грузика при наклоненной оси будет равен

Таким образом, период колебаний увеличится в раз.

Ответ: период колебаний увеличится в раз.

Задача 25

На гладкой горизонтальной плоскости лежат два груза массами и соединённые невесомой нерастяжимой нитью, перекинутой через два неподвижных (А и В) и один подвижный (О) невесомые блоки, как показано на рисунке. Оси блоков горизонтальны, трения в осях блоков нет. К оси О подвижного блока приложена направленная вертикально вниз сила F = 4 Н. Найдите ускорение этой оси. Сделайте схематический рисунок с указанием сил, действующих на грузы и блок.

Решение

Нарисуем силы Т натяжения нити, одинаковые, в силу условия задачи, вдоль всей нити и действующие на грузы и блок О (см. рисунок). Введём систему координат XY, как показано на рисунке, и запишем уравнения движения грузов в проекции на ось X:

В силу невесомости блока О имеем или

В силу нерастяжимости нити (длиной L) и неподвижности блоков А и В (их координаты и постоянны) имеется следующая кинематическая связь между координатами и грузов и координатой блока О (здесь — радиус блоков А и В, R — радиус блока О):

или

и значит

Решаем записанную систему уравнений и получаем ответ:

Ответ:

Задача 26

Два вращающихся вала соединены замкнутым ремнём, который не проскальзывает относительно валов. Радиус первого вала равен R, радиус второго вала равен 2R. Чему равно отношение угловой скорости точки A к угловой скорости вращения первого вала

Решение

Скорость движения точек первого вала, находящихся на расстоянии от его центра, даётся формулой Угловая скорость вращения точки А равна угловой скорости вращения второго вала. Валы связаны ремнём, поэтому скорости ободов у валов одинаковы, а их угловые скорости

В итоге получаем

Ответ: 0,5.

Задача 28

Два велосипедиста совершают кольцевую гонку с одинаковой угловой скоростью. Положения и траектории движения велосипедистов показаны на рисунке. Чему равно отношение центростремительных ускорений велосипедистов ?

Решение

При движении по окружности угловая и линейная скорости тела связаны с радиусом окружности соотношением: Центростремительное ускорение равно Поскольку велосипедисты едут с одинаковым угловыми скоростями, для отношения центростремительных ускорения велосипедистов имеем:

Ответ: 2.

Задача 29

Прибор наблюдения обнаружил летящий снаряд и зафиксировал его горизонтальную координату и высоту м над Землёй (см. рисунок). Через 3 с снаряд упал на Землю и взорвался на расстоянии м от места его обнаружения. Известно, что снаряды данного типа вылетают из ствола пушки со скоростью 800 м/с. Какова была максимальная высота Н траектории снаряда, если считать, что сопротивление воздуха пренебрежимо мало? Пушка и место взрыва находятся на одной горизонтали.

Первое решение

Найдём горизонтальную скорость снаряда:

Найдём вертикальную проекцию скорости снаряда в момент обнаружения:

Определим, за какое время снаряд долетел из верхней точки траектории в точку, в которой был зафиксирован:

Таким образом, время опускания снаряда составляет

Таким образом, максимальная высота снаряда:

Второе решение

Найдём горизонтальную скорость снаряда: эта скорость остается постоянной на протяжении всего полета. Определим величину вертикальной проекции скорости в начальный момент: Используя формулу для максимальной высоты брошенного под углом к горизонту тела, получаем:

Ответ: около 16 км.

Задача 30

К концу вертикального стержня привязана лёгкая нерастяжимая нить с маленьким грузиком на конце. Грузик раскрутили на нити так, что она отклонилась от вертикали на угол α = 30º (см. рисунок). Как и во сколько раз надо изменить угловую скорость ω вращения грузика вокруг стержня для того, чтобы этот угол стал равным β = 60º?

Решение

1. Обозначим силу натяжения нити T, массу грузика m, длину нити l, радиус окружности, по которой вращается грузик, R, и изобразим систему на рисунке (см. рисунок).

2. Запишем уравнение движения грузика по окружности вокруг стержня в проекциях на вертикальную ось и на радиус окружности с учётом выражения для центростремительного ускорения грузика: , .

3. Из написанных соотношений следует, что , а .

4. Для того, чтобы угол отклонения нити стал равным β, угловая скорость вращения грузика должна увеличиться в

раза.

Ответ: 1,3 раза.

Задача 31

В аттракционе человек массой 80 кг движется на тележке по рельсам и совершает «мертвую петлю» в вертикальной плоскости. Каков радиус круговой траектории, если при скорости 10 м/с, направленной вертикально вверх, сила нормального давления человека на сидение тележки равна 1 600 Н? Ускорение свободного падения равно

Задача 32

На рисунке приведен график зависимости проекции скорости тела от времени. Чему равна проекция ускорения тела в момент времени 45 с? Ответ выразите в м/с².

Решение

Из графика видно, что скорость в интервале времени от 40 с до 50 с меняется линейно, значит, ускорение постоянно. На всём этом интервале времени ускорение такое же, как и в момент времени 45 с. Найдём это ускорение:

Ответ: 2.

Задача 32

Два небольших тела с массами 2 кг и 3 кг висят на разных концах невесомой нерастяжимой нити, перекинутой через гладкий неподвижный блок. Первое тело находится на высоте 40 см ниже второго. Тела пришли в движение без начальной скорости. Через какое время они окажутся на одной высоте? Сделайте схематический рисунок с указанием сил, действующих на тела. Обоснуйте применимость используемых законов к решению задачи.

Решение

Задача 33

Система грузов M, m₁ и m₂, показанная на рисунке, движется из состояния покоя. Поверхность стола — горизонтальная гладкая. Коэффициент трения между грузами M и m₁ равен μ = 0,3. Грузы M и m₂ связаны легкой нерастяжимой нитью, которая скользит по блоку без трения. Пусть M = 2,4 кг, m₁ = m₂ = m. При каких значениях m грузы M и m₁ движутся как одно целое? Сделайте рисунок с указанием сил, действующих на грузы.

Решение

Задача 34

Небольшие шарики, массы которых m и M, соединены лёгким стержнем и помещены в гладкую сферическую выемку радиусом R = 20 см. В начальный момент шарики удерживаются в положении, изображённом на рисунке. Когда их отпустили без толчка, шарики стали скользить по поверхности выемки. Минимальная высота, на которой оказался шарик m в процессе движения, равна 4 см от нижней точки выемки. Определите отношение масс M и m.

Решение

Задача 35

Небольшой брусок массой m начинает соскальзывать с высоты H по гладкой горке, переходящей в мёртвую петлю (см. рисунок). Определите высоту отрыва бруска, если высота горки H. Радиус окружности R. Сделайте рисунок с указанием сил, поясняющий решение.

Решение

Направим ось Ох вдоль ускорения и пусть сила тяжести образует с этой осью угол α Запишем второй закон Ньютона для бруска на высоте h:

Выразим отсюда скорость бруска, учитывая, что и по третьему закону Ньютона N=F :

На высоте h брусок обладает как кинетической, так и потенциальной энергией. Из закона сохранения энергии найдём искомую высоту H:

откуда

Задача 36

В маленький шар массой M=100г, висящий на нити длиной l=50 см, попадает и застревает в нем пулька массой m=20г, летящая под углом 30 град к горизонту (см рисунок). Какую скорость v имела пуля перед попаданием в шар, если после соударения шар с застрявшей в нем пулей отклонился по вертикали на угол 60 град? Сопротивлением воздуха пренебречь. Какие законы вы использовали для описания взаимодействия пульки с шаром и подьема тел? Обоснуйте их применимость к данному случаю.

Решение

Задача 37

При выполнение трюка летающий велосипедист гонщик движется по трамплину под действием силы тяжести, начиная движение из состояния покоя с высоты H. На краю трамплина скорость гонщика направлена под таим углом к горизонту, что дальность его полета максимальна. Пролетев по воздуху, гонщик приземляется на горизонтальный стол, находящейся на той же высоте, что и край трамплина. Какова высота полета h на этом трамплине? Сопротивлением воздуха и трением пренебречь.

Решение

Источник

: ЕГЭ по физике

Задачи по механике для подготовки к ЕГЭ по физике.

Большинство заданий с ответами.

→ скачать сборник

→ презентация: «Задачи по механике»

Пример заданий:

1. Начальная скорость снаряда, выпущенного из пушки вертикально вверх, равна v₀ = 10 м/с. В точке максимального подъема снаряд разорвался на два осколка, массы которых относятся как 2 : 1. Осколок большей массы упал на землю первым со скоростью v₁ = 2v₀. До какой максимальной высоты поднялся осколок меньшей массы?

2. Начальная скорость снаряда, выпущенного из пушки вертикально вверх, равна v₀ = 10 м/с. В точке максимального подъема снаряд разорвался на два осколка, массы которых относятся как 1 : 2. Осколок меньшей массы упал на землю со скоростью v₁ = 2v₀. Какова скорость большего осколка при падении на землю? Считать поверхность земли плоской и горизонтальной.

17. Звезда и массивная планета обращаются вокруг общего неподвижного центра масс по круговым орбитам. Найдите радиус орбиты планеты r, если известно, что масса планеты равна m, а период обращения звезды и радиус ее орбиты равны Т и R соответственно.

27. Пуля летит горизонтально со скоростью v0 = 160 м/с, пробивает стоящую на горизонтальной шероховатой поверхности коробку и продолжает движение в прежнем направлении со скоростью v0/4. Масса коробки в 12 раз больше массы пули. Коэффициент трения скольжения между коробкой и поверхностью μ = 0,3. На какое расстояние S переместится коробка к моменту, когда его скорость уменьшится на 20 % ?

Связанные страницы:

Источник

Эксперт ЕГЭ Н. Л. Точильникова
Задача 29 на ЕГЭ по физике – это расчетная задача на механику. До 2014 года включительно она фигурировала под номером «С2».

Это может быть кинематика, динамика, динамика движения по окружности, задача на законы сохранения в механике, статику или гидростатику.

Например, задача на движение тела, брошенного под углом к горизонту:

1. Маленький шарик падает сверху на наклонную плоскость и упруго отражается от нее. Угол наклона плоскости к горизонту равен $30^{circ}$ . На какое расстояние по горизонтали перемещается шарик между первым и вторым ударами о плоскость? Скорость шарика в момент первого удара направлена вертикально вниз и равна м/с.

Запишем «дано»:
V_0=1 м/с
$alpha = 30^{circ}$

Найти: .

Решение:

В задачах части «С» необходимо описывать все параметры, которых нет в дано, иначе оценку снижают на один балл.
Поэтому пишем:
– расстояние по горизонтали между первым и вторым ударами о плоскость.
Нарисуем наклонную плоскость и начальную скорость шарика $overrightarrow{mkern -5mu V_0}$ . Как известно из геометрии, углы с перпендикулярными сторонами равны. Начальная скорость шарика перпендикулярна основанию наклонной плоскости. Восстановим перпендикуляр к наклонной плоскости в точке падения на нее шарика. Тогда угол между этим перпендикуляром и вектором начальной скорости равен углу наклона плоскости к горизонту (углы с перпендикулярными сторонами, зеленые пунктирные линии на рисунке). Угол падения шарика (с перпендикуляром) равен углу отражения $alpha = 30^{circ}$ . Тогда угол между начальной скоростью отскочившего шарика и наклонной плоскостью равен $beta = 90^{circ} - alpha = 90^{circ} - 30^{circ} = 60^{circ} = 2 alpha$ . Модуль скорости не меняется, так как удар упругий.

Итак, убираем построения, которые нам больше не нужны:

Тело будет двигаться по параболе и упадет на расстоянии от точки бросания вдоль наклонной плоскости. Это не то расстояние, которое нам надо найти, мы ищем — расстояние по горизонтали. Но, если мы знаем , найти очень легко: .

Теперь нужно выбрать систему отсчета. С началом отсчета все ясно, очевидно, мы берем его в точке падения шарика. А вот с направлениями осей все не так просто.

Можно выбрать оси традиционным способом: «» горизонтально и «» вертикально:

Но при таком выборе осей трудно определить точку падения. Поэтому в подобных задачах оси обычно выбирают иначе: «» вдоль наклонной плоскости, а «» перпендикулярно наклонной плоскости:

При таком выборе осей точка падения определяется элементарно: там координата «» обращается в ноль. Зато движение становится равноускоренным по двум осям, поскольку ускорение проектируется на обе оси:

— противолежащий катет;
— прилежащий катет.

Начальная скорость $overrightarrow{mkern -3mu V_0mkern 3mu}$ также проектируется на обе оси:

$V_{0x} = V_0 cdot cos 2 alpha$ – прилежащий катет;
$V_{0y} = V_0 cdot sin 2 alpha$ – противолежащий катет

Зависимости координат от времени при равноускоренном движении выражаются формулами:

$x= x_0 + V_{0x}t + genfrac{}{}{}{0}{alpha_x t^2}{2}$

$y= y_0 + V_{0y}t + genfrac{}{}{}{0}{alpha_y t^2}{2}$

Подставляя значения проекций скорости и ускорения, получаем:

$left{begin{matrix}x=V_0 cdot cos 2 alpha cdot t +g cdot sin alpha cdot genfrac{}{}{}{0}{t^2}{2}=l\y = V_0 cdot sin 2 alpha cdot t - g cdot cos alpha cdot genfrac{}{}{}{0}{t^2}{2}=0end{matrix}right.$

Начальные координаты: ;

Конечная координата y также равна нулю, так как тело падает на наклонную плоскость.

Из второго уравнения получаем:

$tleft ( V_0 sin 2 alpha - g cos alpha genfrac{}{}{}{0}{t}{2}right ) = 0$

Это уравнение равносильно совокупности:

$left[ begin{matrix} t=0 phantom{sin 2 alpha - g cos alpha genfrac{}{}{}{0}{t}{2}}\V_0sin 2 alpha - g cos alpha genfrac{}{}{}{0}{t}{2}=0 end{matrix}right.$

Из второго уравнения находим :

$V_0 sin 2 alpha= g cos alpha genfrac{}{}{}{0}{t}{2}$

$t = genfrac{}{}{}{0}{2V_0 sin 2 alpha}{g cos alpha}$

Подставляем в уравнение для :

$l = V_0 cos 2 alphagenfrac{}{}{}{0}{2V_0 sin 2 alpha}{g cos alpha} + g sin alphagenfrac{}{}{}{0}{left (genfrac{}{}{}{0}{2V_0 sin 2 alpha}{g cos alpha} right ) ^2}{2},$

Откуда:

$l=2{V_0}^2 cos 2 alpha genfrac{}{}{}{0}{sin 2 alpha}{g cos alpha} + g sin alpha genfrac{}{}{}{0}{4{V_0}^2(sin 2 alpha)^2}{2 g^2 (cos alpha)^2},$

$l= genfrac{}{}{}{0}{2{V_0}^2 sin 2 alpha ( cos 2 alpha cos alpha+ sin alphasin 2 alpha)}{g (cos alpha)^2},$

Тогда:

$L=l cos alpha= genfrac{}{}{}{0}{2{V_0}^2 sin 2 alpha ( cos 2 alpha cos alpha+ sin alphasin 2 alpha)}{g (cos alpha)^2}cos alpha=$

$= genfrac{}{}{}{0}{2{V_0}^2 sin 2 alpha ( cos 2 alpha cos alpha+ sin alphasin 2 alpha)}{g cos alpha}$

Но $sin 2 alpha = sin 60^{circ} = cos 30^{circ} = cos alpha$ и $cos 2 alpha = cos 60^{circ} = sin 30^{circ} = sin alpha$

То есть:

$L= genfrac{}{}{}{0}{2{V_0}^2 sin alpha cos alpha }{g}= genfrac{}{}{}{0}{2{V_0}^2 sin 2 alpha}{g}$

$L =genfrac{}{}{}{0}{2{V_0}^2 sin 2 alpha}{g}$

$L = 2 cdot 1^2genfrac{}{}{}{0}{sin 60^{circ}}{10}= 2 cdot genfrac{}{}{}{0}{sqrt{3}}{2}cdot genfrac{}{}{}{0}{1}{10}=0,173$ м

Задача 30 на ЕГЭ по физике

Задача 30 на ЕГЭ по физике (раньше называлась С3) – это задача на газовые законы или термодинамику.

Например:

2. Вертикально расположенный замкнутый цилиндрический сосуд высотой см разделен подвижным поршнем весом 110 H на две части, в каждой из которых содержится одинаковое количество идеального газа при температуре 361 K . Сколько молей газа находится в каждой части цилиндра, если поршень расположен на высоте см от дна сосуда? Толщиной поршня пренебречь.

Дано:

H=50 см = 0,5 м
P=110 H
T=361 K
h=20 см = 0,2 м

Найти: (число молей в каждой части цилиндра.)

p_1 – давление в верхней части цилиндра;

p_2 – давление в нижней части цилиндра;

– площадь сечения поршня.

p_1S – сила давления на поршень газа в верхней части цилиндра;

p_2S — сила давления на поршень газа нижней части цилиндра.

Так как поршень неподвижен, сумма всех действующих на него сил равна нулю.

То есть:

Запишем уравнение Менделеева-Клапейрона для верхней и нижней частей цилиндра:

Где – объем верхней части цилиндра;

V_2=hS — объем нижней части цилиндра.

Выражаем p_1 и p_2 :

$p_1 = genfrac{}{}{}{0}{nu RT}{V_1};$

$p_2 = genfrac{}{}{}{0}{nu RT}{V_2}$

И подставляем в уравнение для сил:

$genfrac{}{}{}{0}{nu RT}{V_2}S=genfrac{}{}{}{0}{nu RT}{V_1}S+P$

Подставляем выражения для объемов:

$genfrac{}{}{}{0}{nu RT}{hS}S=genfrac{}{}{}{0}{nu RT}{(H-h)S}S+P$

Сокращаем :

$genfrac{}{}{}{0}{nu RT}{h}=genfrac{}{}{}{0}{nu RT}{H-h}+P$

$genfrac{}{}{}{0}{nu RT}{h}-genfrac{}{}{}{0}{nu RT}{H-h}=P$

$nu RT left ( genfrac{}{}{}{0}{1}{h}-genfrac{}{}{}{0}{1}{H-h} right ) =P$

$nu RT left ( genfrac{}{}{}{0}{H-h-h}{h(H-h)} right ) =P$

Откуда:

$nu = genfrac{}{}{}{0}{Ph(H-h)}{RT(H-2h)}$

$nu = genfrac{}{}{}{0}{110 cdot 0,5 cdot (0,5-0,2)}{8,31 cdot 361(0,5-2 cdot 0,2)} = 0,022$ моль

Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Задачи 29 и 30 на ЕГЭ по физике» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Публикация обновлена:
09.03.2023

Источник

Задачи по физике. Механика 11-20

С чего начать

Задачи на броски

Задачи на броски вертикально вверх

Задачи на броски под углом к горизонту

Примеры задачи

Краткий вывод

Задача 30 на ЕГЭ по физике

Задачи по физике.
Механика 11-20