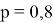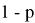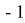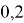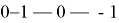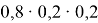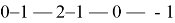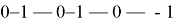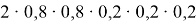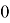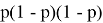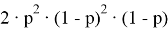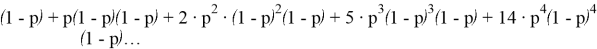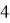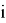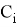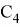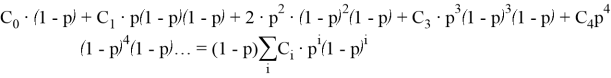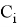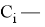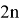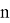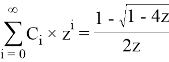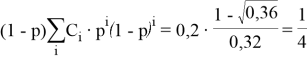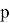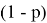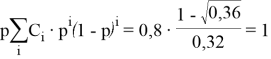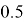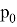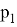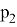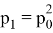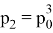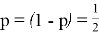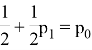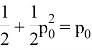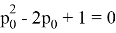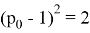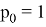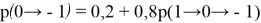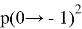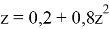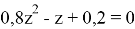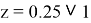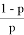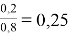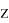Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Какова вероятность того, что случайно выбранный телефонный номер оканчивается двумя чётными цифрами?
2
Если шахматист А. играет белыми фигурами, то он выигрывает у шахматиста Б. с вероятностью 0,52. Если А. играет черными, то А. выигрывает у Б. с вероятностью 0,3. Шахматисты А. и Б. играют две партии, причём во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет оба раза.
3
На рисунке изображён лабиринт. Паук заползает в лабиринт в точке «Вход». Развернуться и ползти назад паук не может, поэтому на каждом разветвлении паук выбирает один из путей, по которому ещё не полз. Считая, что выбор дальнейшего пути чисто случайный, определите, с какой вероятностью паук придёт к выходу
4
Вероятность того, что в случайный момент времени температура тела здорового человека окажется ниже чем 36,8 °С, равна 0,81. Найдите вероятность того, что в случайный момент времени у здорового человека температура окажется 36,8 °С или выше.
5
При изготовлении подшипников диаметром 67 мм вероятность того, что диаметр будет отличаться от заданного не больше, чем на 0,01 мм, равна 0,965. Найдите вероятность того, что случайный подшипник будет иметь диаметр меньше чем 66,99 мм или больше чем 67,01 мм.
Пройти тестирование по этим заданиям
Рассмотрим решение новых задач по теории вероятностей, которые появятся в ЕГЭ по математике в 2022 году.
Вы можете попробовать решить задачи самостоятельно, а потом сверить свое решение с предложенным.
1. № 508755
Игральный кубик бросают дважды. Известно, что в сумме выпало 8 очков. Найдите вероятность того, что в первый раз выпало 6 очков.
Решение. показать
2. № 508769
Игральную кость бросили два раза. Известно, что три очка не выпали ни разу. Найдите при этом условии вероятность события «сумма выпавших очков окажется равна 8».
Решение. показать
3. № 508781
Симметричную монету бросают 11 раз. Во сколько раз вероятность события «выпадет ровно 5 орлов» больше вероятности события «выпадет ровно 4 орла»?
Решение. показать
4. № 508791
В одном ресторане в г. Тамбове администратор предлагает гостям сыграть в «Шеш-беш»: гость бросает одновременно две игральные кости. Если он выбросит комбинацию 5 и 6 очков хотя бы один раз из двух попыток, то получит комплимент от ресторана: чашку кофе или десерт бесплатно. Какова вероятность получить комплимент? Результат округлите до сотых.
Решение. показать
5. № 508793
Игральную кость бросили один или несколько раз. Оказалось, что сумма всех выпавших очков равна 4. Какова вероятность того, что потребовалось сделать три броска? Результат округлите до сотых.
Решение. показать
6. № 508798
Игральную кость бросали до тех пор, пока сумма выпавших очков не превысила число 3. Какова вероятность того, что для этого потребовалось 3 броска? Ответ округлите до сотых.
Решение. показать
7. № 508809
Телефон передает SMS-сообщение. В случае неудачи телефон делает следующую попытку. Вероятность того, что сообщение удастся передать без ошибок в каждой отдельной попытке, равна 0,2. Найдите вероятность того, что для передачи сообщения потребуется не больше двух попыток.
Решение. показать
8. № 508820
При подозрении на наличие некоторого заболевания пациента отправляют на ПЦР-тест. Если заболевание действительно есть, то тест подтверждает его в 91% случаев. Если заболевание нет, то тест выявляет отсутствие заболевания в среднем в 93% случаев. Известно, что в среднем тест оказывается положительным у 10% пациентов, направленных на тестирование. При обследовании некоторого пациента врач направил его на ПЦР-тест, который оказался положительным. Какова вероятность того, что пациент действительно имеет это заболевание? Результат округлите до сотых.
Решение. показать
9. № 508831
Стрелок в тире стреляет по мишени до тех пор, пока не поразит ее. Известно, что он попадает в цель с вероятностью 0,2 при каждом отдельном выстреле. Сколько патронов нужно дать стрелку, чтобы он поразил цель с вероятностью не менее 0,5?
Решение. показать
10. № 508843
В ящике три красных и три синих фломастера. Фломастеры вытаскивают по очереди в случайном порядке. Какова вероятность того, что в первый раз синий фломастер появится третьим по счету?
Решение. показать
11. №508851
Стрелок стреляет по пяти одинаковым мишеням. На каждую мишень дается не более двух выстрелов, и известно, что вероятность поразить мишень каждым отдельным выстрелом равна 0,6. Во сколько раз вероятность события «стрелок поразит ровно три мишени» больше вероятность события «стрелок поразит ровно две мишени».
Решение. показать
12. № 508868
В викторине участвуют 10 команд. Все команды разной силы, и в каждой встрече выигрывает та команда, которая сильнее. В первом раунде встречаются две случайно выбранные команды. Ничья невозможна. Проигравшая команда выбывает из викторины, а победившая команда играет со следующим случайно выбранным соперником. Известно, что в первых шести играх победила команда А. Какова вероятность, что эта команда выиграет седьмой раунд.
Решение. показать
13. № 508871
Турнир по настольному теннису проводится по олимпийской системе: игроки случайным образом разбиваются на пары; проигравший в каждой паре выбывает из турнира, а победитель выходит в следующий тур, где встречается со следующим противником, который определен жребием. Всего в турнире 8 игроков, все они играют одинаково хорошо, поэтому в каждой встрече вероятность выигрыша и поражения у каждого игрока равна 0,5. Среди игроков два друга — Иван и Алексей. Какова вероятность того, что этим двоим в каком-то туре придется сыграть друг с другом?
Решение. показать
14. № 508887
Первый игральный кубик обычный, а на гранях второго кубика нет четных чисел, а нечетные числа встречаются по два раза. В остальном кубики одинаковые. Один случайно выбранный кубик бросают два раза. Известно, что в каком-то порядке выпали 3 и 5 очков. Какова вероятность, что бросали второй кубик?
Решение. показать
15. № 509078
Маша коллекционирует принцесс из Киндер-сюрпризов. Всего в коллекции 10 разных принцесс, и они равномерно распределены, то есть в каждом Киндер-сюрпризе может с равными вероятностями оказаться любая из 10 принцесс. У Маши есть две разные принцессы из коллекции. Какова вероятность того, что для получения следующей принцессы Маше придется купить еще 2 или 3 шоколадных яйца?
Решение. показать
15. № 508885
Первый член последовательности целых чисел равен 0. Каждый следующий член последовательности с вероятность на единицу больше предыдущего и с вероятность
на единицу меньше предыдущего. Какова вероятность того, что какой-то член этой последовательности окажется равен -1?
Решение. показать
И.В. Фельдман, репетитор по математике
4. Введение в теорию вероятностей
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Сложные задачи по теории вероятности
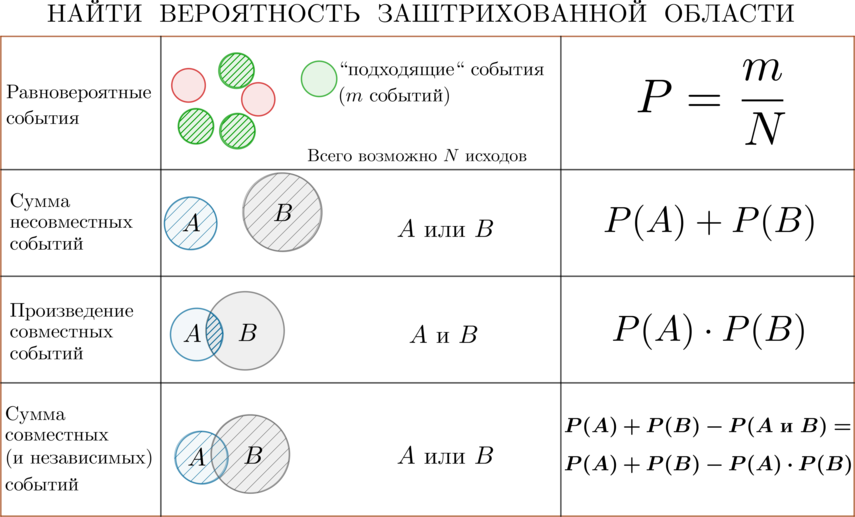
Общая памятка по всем разделам теории вероятностей:
Задание
1
#3858
Уровень задания: Равен ЕГЭ
Чтобы пройти в следующий круг соревнований, футбольной команде нужно набрать хотя бы (4) очка в двух играх. Если команда выигрывает, она получает (3) очка, в случае ничьей — (1) очко, если проигрывает — (0) очков. Найдите вероятность того, что команде удастся выйти в следующий круг соревнований. Считайте, что в каждой игре вероятности выигрыша и проигрыша одинаковы и равны (0,3).
Чтобы команда в двух играх набрала не менее (4) очков, ей нужно: либо 1) выиграть обе игры, либо 2) выиграть в одной из игр и сыграть вничью в другой игре.
Так как вероятности выиграть и проиграть одинакова и равна (0,3), то вероятность сыграть вничью равна (1-0,3-0,3=0,4).
Следовательно, вероятности в этих случаях равны соответственно:
1) (0,3cdot 0,3)
2) (0,3cdot 0,4+0,4cdot 0,3) (выиграть в первой игре и сыграть вничью во второй или сыграть вничью в первой и выиграть во второй).
Следовательно, вероятность того, что команда выйдет в следующий круг соревнований, равна [0,3cdot 0,3+0,3cdot 0,4+0,4cdot 0,3=0,33]
Ответ: 0,33
Задание
2
#2739
Уровень задания: Сложнее ЕГЭ
Илья решает задачу по геометрии, в которой дан четырёхугольник (ABCD), причём (AB = 5), (BC = 6), (CD = 4), (AD = 10). В условии задачи сказано, что одна из вершин является центром некоторой окружности и Илья думает, какую вершину ему выбрать в качестве центра этой самой окружности.
Известно, что вероятность выбора каждой конкретной вершины пропорциональна сумме длин сторон четырёхугольника (ABCD), проходящих через эту вершину. Какова вероятность того, что Илья выберет вершину (B)?
Через вершину (A) проходят стороны (AB) и (AD), их сумма: (AB + AD = 15).
Через вершину (B) проходят стороны (AB) и (BC), их сумма: (AB + BC = 11).
Через вершину (C) проходят стороны (BC) и (CD), их сумма: (BC + CD = 10).
Через вершину (D) проходят стороны (CD) и (DA), их сумма: (CD + DA = 14).
Обозначим вероятность выбора вершины (A) через (P(A)) (для остальных вершин аналогично). Тогда по условию имеем: [P(A) = 15k,qquad P(B) = 11k,qquad P(C) = 10k,qquad P(D) = 14k,,] но (P(A) + P(B) + P(C) + P(D) = 1), тогда (k = 0,02), откуда находим: (P(B) = 0,22).
Ответ: 0,22
Задание
3
#191
Уровень задания: Сложнее ЕГЭ
Монетку подбросили 10 раз. Какова вероятность того, что выпало не менее 9 орлов? Ответ округлите до тысячных.
Условие того, что выпало не менее 9 орлов эквивалентно тому, что выпало не более 1 решки, то есть либо ровно 1 решка, либо 0 решек.
Количество всевозможных различных исходов в серии из 10 испытаний равно (2^{10} = 1024).
Среди них есть 11 исходов, подходящих под условие: (Орёл; Орёл; …; Орёл), (Орёл; Орёл; …; Орёл; Решка), (Орёл; Орёл; …; Решка; Орёл), …, (Решка; Орёл; …; Орёл), следовательно, искомая вероятность равна [dfrac{11}{1024}.] После округления получим (0,011).
Ответ: 0,011
Задание
4
#190
Уровень задания: Сложнее ЕГЭ
Монетку подбросили 3 раза. Какова вероятность того, что выпало не менее 3 орлов? Ответ округлите до тысячных.
Условие того, что выпало не менее 3 орлов эквивалентно тому, что выпали только орлы.
Количество всевозможных различных исходов в серии из 3 испытаний равно (2^3 = 
Ответ: 0,125
Задание
5
#189
Уровень задания: Сложнее ЕГЭ
Монетку подбросили 2 раза. Какова вероятность того, что выпало не менее 1 орла? Ответ округлите до тысячных.
Всевозможных исходов в серии из 2 подбрасываний может быть (2^2 = 4): (Орёл; Орёл), (Орёл; Решка), (Решка; Орёл), (Решка; Решка).
Среди выписанных (всевозможных) исходов под условие задачи подходят первые 3, следовательно, искомая вероятность равна [dfrac{3}{4} = 0,75.]
Ответ: 0,75
Задание
6
#2658
Уровень задания: Сложнее ЕГЭ
Игорь трижды подбрасывает правильную игральную кость. Какова вероятность того, что за эти три подбрасывания ровно один раз выпадет число, кратное трём, а сумма результатов подбрасываний не будет делиться на (3)? Ответ округлите до сотых.
Так как игральная кость правильная, то вероятность выпадения каждой грани равна (dfrac{1}{6}). Среди чисел на гранях есть два числа, дающих при делении на (3) остаток (0), два числа, дающих при делении на (3) остаток (1) и два числа, дающих при делении на (3) остаток (2).
Тогда вероятность за одно подбрасывание получить, например, число, дающее при делении на (3) остаток (1), равна (dfrac{1}{3}). С другими остатками аналогично.
Условие задачи можно переформулировать в следующем виде: какова вероятность за три подбрасывания получить результаты, остатки от деления на (3) которых будут содержать единственный (0) и два одинаковых числа?
Таким образом, нас устраивают исходы, остатки от деления на (3) которых будут иметь вид:
[begin{aligned}
&0,quad 1,quad 1\
&1,quad 0,quad 1\
&1,quad 1,quad 0\
&0,quad 2,quad 2\
&2,quad 0,quad 2\
&2,quad 2,quad 0,.
end{aligned}]
Вероятность любого из выписанных исходов равна [dfrac{1}{3}cdot dfrac{1}{3}cdot dfrac{1}{3},.] При этом различных исходов здесь шесть, следовательно, вероятность получения подходящего исхода равна [6cdot dfrac{1}{3}cdot dfrac{1}{3}cdot dfrac{1}{3} = dfrac{2}{9},.] После округления получим ответ (0,22).
Ответ: 0,22
Задание
7
#2765
Уровень задания: Сложнее ЕГЭ
Таня заметила, что в казино “Подкинем” используют неправильную игральную кость (т.е. не у всех граней вероятности выпадения одинаковы). При этом она установила, что вероятность выпадения чётного числа равна (0,6); вероятность выпадения числа, делящегося на (3), равна (0,3); вероятность того, что выпадет (1) или (5), равна (0,22). Найдите вероятность того, что на этой игральной кости выпадет число (3). Ответ округлите до сотых.
Вероятность выпадения числа (n) обозначим через (P({n})), вероятность выпадения одного из чисел (m) и (n) обозначим через (P({m; n})), а вероятность выпадения одного из чисел (m), (n) и (k) обозначим через (P({m; n; k})). Тогда [P({2; 4; 6}) = 0,6qquadLeftrightarrowqquad P({1; 3; 5}) = 1 — 0,6 = 0,4]
При этом (P({1; 5}) = 0,22), но ведь (P({1; 3; 5}) — P({1; 5}) = P({3})), следовательно, [P({3}) = 0,4 — 0,22 = 0,18,.]
Ответ: 0,18
Если выпускник готовится к сдаче ЕГЭ по математике профильного уровня, ему необходимо научиться решать задачи на применение теории вероятности повышенной сложности. Как показывает практика многих лет, такие задания являются обязательной частью программы аттестационного испытания. Поэтому если учащийся не до конца понимает принцип решения сложных задач на теорию вероятности, ему обязательно стоит вновь разобраться в данной теме.
Вместе с образовательным порталом «Школково» старшеклассники смогут качественно подготовиться к прохождению аттестационного испытания. Наш сайт позволит определить наиболее сложные темы и восполнить пробелы в знаниях. Опытные специалисты «Школково» подготовили весь необходимый материал, изложив его таким образом, чтобы школьники с любым уровнем подготовки смогли легко справиться с решением сложных задач ЕГЭ на теорию вероятности. Базовая информация по данной теме представлена в разделе «Теоретическая справка».
Чтобы попрактиковаться в выполнении сложных задач ЕГЭ по теории вероятности, школьники могут выполнить соответствующие упражнения. Простые и сложные задания, подобранные нашими специалистами, содержат подробные алгоритмы решения и правильные ответы. База заданий регулярно обновляется и дополняется.
Выполнять упражнения школьники из Москвы и других российских городов могут в онлайн-режиме. При необходимости задания по теории вероятности в ЕГЭ можно сохранить в разделе «Избранное». Благодаря этому вы сможете быстро найти интересующие примеры и обсудить алгоритмы нахождения правильного ответа с преподавателем.

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Подборка сложных задач с ответами из открытого банка ФИПИ задание №10 теория вероятностей ЕГЭ 2022 математика 11 класс профильный уровень.
Скачать задачи из ФИПИ
Тренировочные варианты ЕГЭ 2022 с ответами
Задание 10 теория вероятностей ЕГЭ 2022 профиль ФИПИ
задание10_егэ2022_профиль_математика_фипи
Задания и ответы с ФИПИ
1)Если шахматист А. играет белыми фигурами, то он выигрывает у шахматиста Б. с вероятностью 0,6. Если А. играет чёрными, то А. выигрывает у Б. с вероятностью 0,45. Шахматисты А. и Б. играют две партии, причём во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет оба раза.
Ответ: 0,27
2)Если шахматист А. играет белыми фигурами, то он выигрывает у шахматиста Б. с вероятностью 0,5. Если А. играет чёрными, то А. выигрывает у Б. с вероятностью 0,3. Шахматисты А. и Б. играют две партии, причём во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет оба раза.
Ответ: 0,15
3)Стрелок в тире стреляет по мишени до тех пор, пока не поразит её. Известно, что он попадает в цель с вероятностью 0,5 при каждом отдельном выстреле. Какое наименьшее количество патронов нужно дать стрелку, чтобы он поразил цель с вероятностью не меньше 0,7?
Ответ: 2
4)Стрелок в тире стреляет по мишени до тех пор, пока не поразит её. Известно, что он попадает в цель с вероятностью 0,5 при каждом отдельном выстреле. Какое наименьшее количество патронов нужно дать стрелку, чтобы он поразил цель с вероятностью не меньше 0,8?
Ответ: 3
5)Стрелок стреляет по одному разу в каждую из четырёх мишеней. Вероятность попадания в мишень при каждом отдельном выстреле равна 0,9. Найдите вероятность того, что стрелок попадёт в первую мишень и не попадёт в три последние.
Ответ: 0,0009
6)Стрелок стреляет по одному разу в каждую из четырёх мишеней. Вероятность попадания в мишень при каждом отдельном выстреле равна 0,8. Найдите вероятность того, что стрелок попадёт в первую мишень и не попадёт в три последние.
Ответ: 0,0064
7)Автоматическая линия изготавливает батарейки. Вероятность того, что готовая батарейка неисправна, равна 0,01. Перед упаковкой каждая батарейка проходит систему контроля качества. Вероятность того, что система забракует неисправную батарейку, равна 0,96. Вероятность того, что система по ошибке забракует исправную батарейку, равна 0,06. Найдите вероятность того, что случайно выбранная изготовленная батарейка будет забракована системой контроля.
Ответ: 0,069
8)Автоматическая линия изготавливает батарейки. Вероятность того, что готовая батарейка
неисправна, равна 0,01. Перед упаковкой каждая батарейка проходит систему контроля качества.
Вероятность того, что система забракует неисправную батарейку, равна 0,95. Вероятность того,
что система по ошибке забракует исправную батарейку, равна 0,05. Найдите вероятность того,
что случайно выбранная изготовленная батарейка будет забракована системой контроля.
Ответ: 0,059
9)В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в первом автомате закончится кофе, равна 0,1. Вероятность того, что кофе закончится во втором автомате, такая же. Вероятность того, что кофе закончится в двух автоматах, равна 0,03. Найдите вероятность того, что к концу дня кофе останется в двух автоматах.
Ответ: 0,83
10)В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в первом автомате закончится кофе, равна 0,1. Вероятность того, что кофе закончится во втором автомате, такая же. Вероятность того, что кофе закончится в двух автоматах равна 0,05. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.
Ответ: 0,85
11)В коробке 11 синих, 6 красных и 8 зелёных фломастеров. Случайным образом выбирают два фломастера. Найдите вероятность того, что окажутся выбраны один синий и один красный фломастеры.
Ответ: 0,22
12)В коробке 12 синих, 6 красных и 7 зелёных фломастеров. Случайным образом выбирают два фломастера. Найдите вероятность того, что окажутся выбраны один синий и один красный фломастеры.
Ответ: 0,24
13)Помещение освещается тремя лампами. Вероятность перегорания каждой лампы в течение года равна 0,8. Лампы перегорают независимо друг от друга. Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит.
Ответ: 0,488
14)Помещение освещается тремя лампами. Вероятность перегорания каждой лампы в течение года равна 0,9. Лампы перегорают независимо друг от друга. Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит.
Ответ: 0,271
15)Чтобы пройти в следующий круг соревнований, футбольной команде нужно набрать хотя бы 4 очка в двух играх. Если команда выигрывает, она получает 3 очка, в случае ничьей — 1 очко, если проигрывает — 0 очков. Найдите вероятность того, что команде удастся выйти в следующий круг соревнований. Считайте, что в каждой игре вероятности выигрыша и проигрыша одинаковы и равны 0,3.
Ответ: 0,33
16)Чтобы пройти в следующий круг соревнований, футбольной команде нужно набрать хотя бы 4 очка в двух играх. Если команда выигрывает, она получает 3 очка, в случае ничьей — 1 очко, если проигрывает — 0 очков. Найдите вероятность того, что команде удастся выйти в следующий круг соревнований. Считайте, что в каждой игре вероятности выигрыша и проигрыша одинаковы и равны 0,2.
Ответ: 0,28
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
-
Густав 11 июля 2022 23:16 |
Цитировать |
Ответить
+1
Задача 3 проще значительно решается. Общее число вариантов выбора 2 фломастеров из 25 — это число сочетаний из 25 по 2 и равно 25!/23!/2!=300. Общее число вариантов выбора синего и красного 10*9 (выбрав 1 синий, мы можем 9 способами выбрать красный, для 10 синих — число способов = произведение их количеств). 90/300=0.3
-
-
October 17 2021, 20:23
- Образование
- Наука
- Cancel
Сложные задачи по теории вероятностей на ЕГЭ
Как известно, с 2022 года в профильный ЕГЭ по математике добавили сложную задачу по теории вероятностей (номер 10)
Поэтому перед учителями и репетиторами теперь стоит задача рассказать ученикам про деревья, условную вероятность, комбинаторику и тд
Иван Ростиславович Высоцкий рассказала учителям, как просто рассказать о сложном
https://events.webinar.ru/29143559/9139569/record-new/9370643
Старшеклассникам и родителям тоже можно посмотреть.
Напоминаю про два полезных сайта.
Открытый банк задач — задача 10
Решу ЕГЭ — задача 10
В статье автор разбирает решение одной из новых задач по теории вероятностей, введённой в ЕГЭ-2022. Рассматриваются как классический вариант решения, не приводящий к решению, так и альтернативные, которые оказываются наиболее оптимальными. Приводятся аргументы, критикующие повышенную сложность данной задачи относительно стандартов школьной программы.
Ключевые слова:
ЕГЭ, теория вероятностей, числа Каталана, задача о пьянице, бесконечная сумма.
В 2022 году, в первой части профильного ЕГЭ по математике будет впервые присутствовать 2 задачи на теорию вероятностей. Первая задача (номер 2) не изменится, а вторая (номер 10), по нашему мнению, будет в разы сложнее. Это задача требует более глубокого анализа, и включает несколько шагов, для получения верного ответа. Пример данных задач, был опубликован на официальном сайте «Открытый банк задач ЕГЭ по математике».
Несмотря на то, что это первая часть экзамена (размышление над задачами которой, подразумевает порядка 5 минут времени), здесь встречаются задачи, которые могут быть сложнее всей содержательной части ЕГЭ. Рассмотрим пример одной из таких задач.
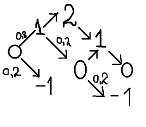
«Первый член бесконечной последовательности целых чисел равен 0. Каждый последующий член данной последовательности с вероятностью
на единицу больше предыдущего, и с вероятностью
меньше предыдущего. Найдите вероятность того, что среди членов этой последовательности можно найти число
» [1].
Есть множество вариантов попадания в
. Рассмотрим некоторые из них (рис.1):
Рис. 1. Математическая модель задачи
-
Возможно, попасть в
с первого хода. Тогда вероятность равна
-
, тогда вероятность равна:
-
или
. Здесь, вероятность равна:
.
Но что делать дальше? Ведь этим можно заниматься бесконечно! Начнём с классического способа, заключающегося в нахождении бесконечной суммы ряда (что не входит в школьную программу, за одним исключением — суммы бесконечно-убывающей геометрической прогрессии).
Итак, посчитаем сумму вероятностей попадания в
.
-
Вероятность попасть из
в
=
-
Можно из
попасть в
, а затем спуститься в
. Вероятность будет равна
-
Попасть в
можно также с вероятностью:
Так можно считать до бесконечности. Получаем следующее выражение:
Нахождение способов подняться до
, а потом спустить до
уже вызывает проблемы. В связи с этим просто посчитать сумму ряда, по крайней мере со знаниями школьной программы не видится возможным. Соответственно, классический способ решения на этом заканчивается и не даёт никакого решения.
Приходится искать альтернативные методы решения, и такие, как оказалось, есть. Первый — заключается в привлечении расширенных знаний по комбинаторике, а второй с широким кругозором знаний различных математических головоломок. Начнём с первого.
Очевидно, что нам мешает старший коэффициент, выражающий количество способов подняться до
-го числа и опуститься до
. Обозначим количество этих способов коэффициентом
.
Тогда, например, количество способов подняться до 4 и опуститься до
будет обозначено, как
.
Перепишем наше выражение, полученное суммированием:
Теперь, используем знания комбинаторики [2, 3]. Оказывается, что у наших коэффициентов
есть название — числа Каталана.
Числа Каталана
это количество правильных скобочных последовательностей длины
, то есть таких последовательностей из
левых и
правых скобок, в которых количество открывающихся скобок равно количеству закрывающихся. То есть ((())) или (())().
Теперь, для решения нашей задачи, требуется воспользоваться производящей функцией. Данное понятие выходит далеко за рамки школьной программы, а также программы некоторых высших учебных заведений. Благо в данном контексте, глубокое понимание данного термина не требуется, однако его привлечение вызывает множество вопросов.
Стоит отметить, что данную функцию можно вывести, как показано, например в [4]. Но, по нашему мнению, процесс вывода достаточно трудоемкий, и точно не имеет место быть на экзамене, когда на счету каждая минута. Итак, воспользуемся производящей функцией для чисел Каталана [4]:
Теперь, с помощью данной функции, мы можем найти сумму ряда без значительных проблем.
Ответ получен, однако сколько времени для его получения бы затратил среднестатистический школьник? Отметим, также, что данный способ решения избавляет от следующей проблемы.
Если поменять вероятности
и
местами, т. е. мы будем удаляться от
с меньшей вероятностью, то мы получим в ответе 1.
Когда мы будем рассматривать следующий способ, мы заметим, что у нас будет два ответа и выбор из них — проблема.
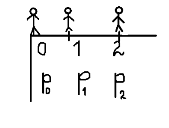
Итак, рассмотрим второй способ решения, за счёт широкого кругозора. В книге Мостеллера [5] была приведена следующая задача «На краю утеса» (рис. 2):
Есть пьяница, стоящий на обрыве. С вероятностью
он каждую секунду делает шаг вправо или влево. Какая вероятность того, что когда-нибудь он упадет?
Рис. 2. Вырезка из книги
Опустим полное решение, описанное в данной книге, и приведём её урезанный вариант.
Вероятность того, что он упадет из точки 0 —
.
Из точки 1 —
, а из точки 2 —
(рис. 3). Что же должно произойти, чтобы человек свалился?
- Гуляя, человек должен оказаться в точке 0
- А после этого, он должен упасть
Рис. 3. Иллюстрация к задаче
Какова вероятность того, что человек из единицы попадет в ноль? Заметим, что мы можем мысленно сдвинуть обрыв, получая тем сам аналогичную задачу (отметим, что это возможно благодаря тому, что ряд бесконечный, и сдвиг или удаление/добавление ограниченного количества элементов не меняет предел). Соответственно, вероятность упасть из позиции 1 есть вероятность того, что мы когда-нибудь сместимся на шаг назад, т. е.
. Это вероятность того, что человек сместится влево. Получаем, что
,
и т. д. Значит, нам осталось лишь найти
.
Находясь в точке 0, человек может сразу пойти влево, или же сделать шаг вправо, а потом когда-нибудь влево. Тогда мы получаем равенство, зная, что
.
Теперь, решим полученное равенство, пользуясь тем, что
:
Это означает, что как бы далеко от обрыва не стоял человек, рано или поздно он упадет. Заметим, что, данное рассуждение достаточно сложно провести, не зная его заранее. Также стоит отметить, что в данной задаче вероятности
и
были равны. Посмотрим, что будет в нашем случае.
Вернемся к исходной задаче (рис. 1). Какова вероятность попасть в
? Можно сразу из точки
попасть в
, а можно сначала попасть в
, потом в
, а потом в
:
Вероятность попасть из единицы в минус единицу, по аналогии с данной задачей, будет равна
Выполнив замену, получаем равенство:
Итак, мы получаем два ответа, причём правильным из них оказывается 0,25. Но почему?
Насколько нам известно, ответ будет зависеть от следующего частного
. В случае, если его значение больше 1, в ответе всегда получится 1 (что автоматически решает задачу, еще на стадии её задания, и моментально выписывается ответ, целесообразность чего мы не понимаем), если же значение меньше 1, как в нашем случае (
), то мы получаем ответ.
Отметим, что данный вывод достаточно очевиден, если понимать основы случайных процессов (также не изучающщихся в школьной программе). В случае если частное больше 1, подразумевается, что вероятность спуститься ниже выше, а следовательно, в среднем, на каждый шаг вверх, приходится
шагов вниз. В таком случае, очевидно, что мы всегда достигнем значения
, сколь долго мы бы не удалялись от него.
В обратном случае ситуация противоположная, и шанс опуститься до
снижается в зависимости от уменьшения значения
.
На фоне этого, возникает максимально оптимальный вариант решения данной задачи — алгоритмический. Алгоритм, следующий:
Рассмотрим частное
, ответом
будет следующее значение:
Отметим, что данный способ полностью обесценивает какие-либо рассуждения данной задачи, и позволяет, даже не читать задачу, а просто записать ответ, что очевидно, не соответствует уровню итогового экзамена, проверяющего знания.
Также, в заключении отметим, что большинство элементов, рассмотренных в данной статье отсутствуют в подавляющем числе школьных учебников, что напрямую увеличивает нагрузку как на педагогов, за счёт поиска и подготовки данного материала, а также сложность грамотной передачи знаний в головы учащихся, а также увеличивает нагрузку на учащихся в плане восприятия новой для них информации, и форсированного расширения кругозора знаний.
Использование же, последнего приведённого способа помимо обесценивания задачи, приводит также к банальной зубрежке формулы, что для изучения математики грозит резким снижением качества образования.
Литература:
- Открытый банк математических задач ЕГЭ. Профильный уровень. https://prof.mathege.ru/
- Спивак А. Числа Каталана. // Квант. 2004. — № 3. — с. 2–10.
- Гарднер М. Числа Каталана. // Квант. 1978. — № 7. — с. 20–26.
- Числа Каталана. https://internat.msu.ru/media/uploads/2015/12/CHisla-Katalana_jk.pdf
- Мостеллер, Ф. Пятьдесят занимательных вероятностных задач с решениями / Ф. Мостеллер. — М.: Наука, 1971. — 103 с.