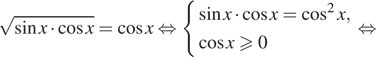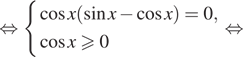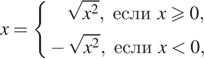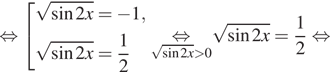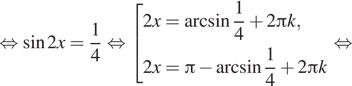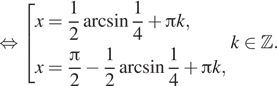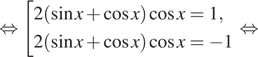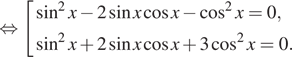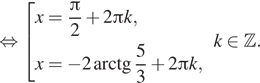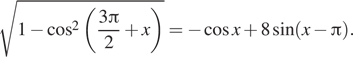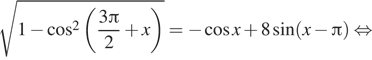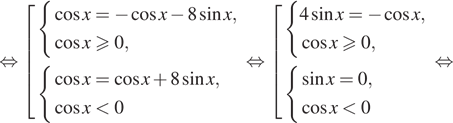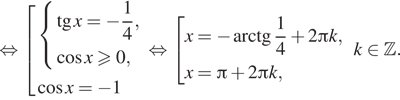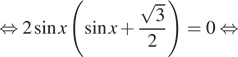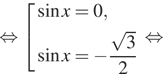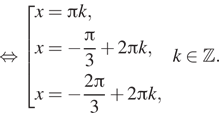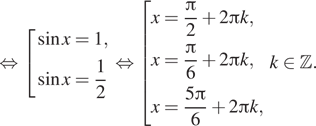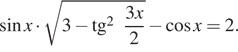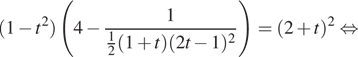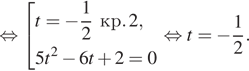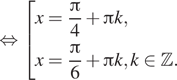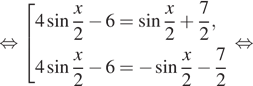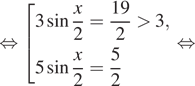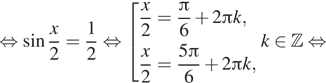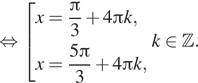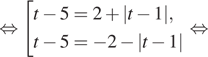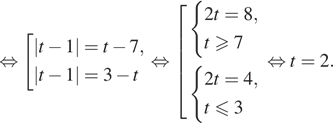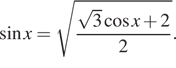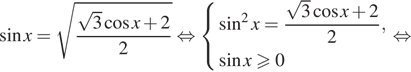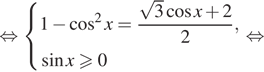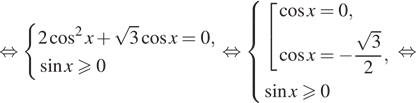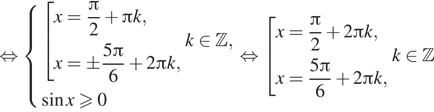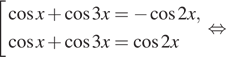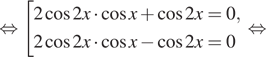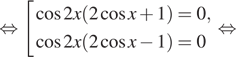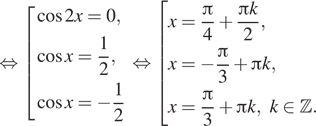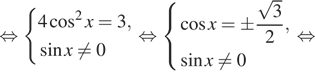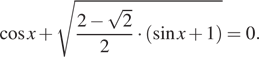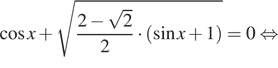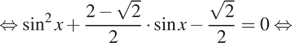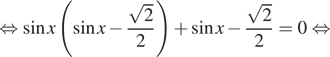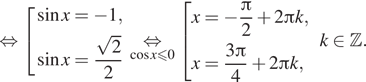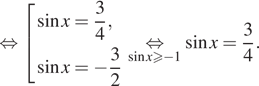Смешанные тригонометрические уравнения егэ


Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

1

а)  Решите уравнение левая круглая скобка 2 синус x плюс корень из 3 правая круглая скобка умножить на корень из косинус x=0.

б)  Найдите все корни этого уравнения, принадлежащие отрезку левая квадратная скобка дробь: числитель: 3 Пи , знаменатель: 2 конец дроби ; дробь: числитель: 7 Пи , знаменатель: 2 конец дроби правая квадратная скобка .

2

а)  Решите уравнение 15 в степени левая круглая скобка косинус x правая круглая скобка = 3 в степени левая круглая скобка косинус x правая круглая скобка умножить на 5 в степени левая круглая скобка синус x правая круглая скобка .

б)  Найдите все корни этого уравнения, принадлежащие отрезку левая квадратная скобка 5 Пи , дробь: числитель: 13 Пи , знаменатель: 2 конец дроби правая квадратная скобка .

Источник: ЕГЭ по математике 03.06.2013. Основная волна. Центр. Вариант 1.

3

а)  Решите уравнение дробь: числитель: 3 в степени левая круглая скобка косинус x правая круглая скобка , знаменатель: 9 в степени левая круглая скобка косинус в квадрате x правая круглая скобка конец дроби =4 в степени левая круглая скобка 2 косинус в квадрате x минус косинус x правая круглая скобка .

б)  Укажите корни этого уравнения, принадлежащие отрезку левая квадратная скобка минус дробь: числитель: 3 Пи , знаменатель: 2 конец дроби ; дробь: числитель: Пи , знаменатель: 6 конец дроби правая квадратная скобка .

Источник: РЕШУ ЕГЭ — Предэкзаменационная работа 2014 по математике.

4

а)  Решите уравнение левая круглая скобка 27 в степени левая круглая скобка косинус x правая круглая скобка правая круглая скобка в степени левая круглая скобка синус x правая круглая скобка = 3 в степени левая круглая скобка tfrac3 косинус x правая круглая скобка 2.

б)  Найдите все корни этого уравнения, принадлежащие отрезку левая квадратная скобка минус Пи , дробь: числитель: Пи , знаменатель: 2 конец дроби правая квадратная скобка .

Источник: ЕГЭ по математике 03.06.2013. Основная волна. Урал. Вариант 203., Задания 13 (С1) ЕГЭ 2013

5

а)  Решите уравнение 9 в степени левая круглая скобка синус x правая круглая скобка плюс 9 в степени левая круглая скобка минус синус x правая круглая скобка = дробь: числитель: 10, знаменатель: 3 конец дроби .

б)  Укажите корни этого уравнения, принадлежащие отрезку совокупность выражений минус дробь: числитель: 7 Пи , знаменатель: 2 конец дроби , минус 2 Пи конец совокупности правая квадратная скобка .

Источник: Задания 13 (С1) ЕГЭ 2017, ЕГЭ 28.04.2014 по математике. Досрочная волна. Вариант 1., Задания 13 (С1) ЕГЭ 2014

Пройти тестирование по этим заданиям

Источник
Skip to content

ЕГЭ Профиль №13. Уравнения смешанного типа, содержащие тригонометрические функции

ЕГЭ Профиль №13. Уравнения смешанного типа, содержащие тригонометрические функцииadmin2021-05-06T21:27:04+03:00

Источник


1. Вспоминай формулы по каждой теме


2. Решай новые задачи каждый день


3. Вдумчиво разбирай решения

Показательные, логарифмические, тригонометрические уравнения

(blacktriangleright) На ОДЗ верны следующие формулы:

[large{begin{array}{|ll|}
hline a^0=1 &a^1=a\
a^{nm}=(a^n)^m &a^ncdot a^m=a^{n+m}\
dfrac{a^n}{a^m}=a^{n-m}&a^{-n}=dfrac{1}{a^n}\
a^ncdot b^n=(acdot b)^n &\
a^{frac{k}{r}}=sqrt[r]{a^k} qquad qquad qquad qquad&
dfrac{a^n}{b^n}=left(dfrac{a}{b}right)^n\&\
a,b>0, a,bne 1, kin mathbb{Z},& rinmathbb{N}, m,ninmathbb{R}\
hline
end{array}}]

[large{begin{array}{|lcl|}
hline log_a1=0& qquad & log_aa=1\
&&\
log_{a^n}{b^m}=frac mnlog_{|a|}{|b|}&& a^{log_bc}=c^{log_ba}\
&&\
log_a{bc}=log_a{|b|}+log_a{|c|}&& log_a{dfrac bc}=log_a{|b|}-log_a{|c|}\
&&\
log_abcdot log_bc=log_ac & Longleftrightarrow & log_bc=dfrac{log_ac}{log_ab}\
&&\
log_abcdot log_ba=1 & Longleftrightarrow & log_ab=dfrac1{log_ba}\
&&\
hline
end{array}}]


Задание
1

#3823

Уровень задания: Равен ЕГЭ

а) Решите уравнение [(2cos^2x+11cos x+5)cdot log_{18}(sin
x)=0]

б) Найдите все корни этого уравнения, принадлежащие промежутку ([0;pi].)

а) Произведение равно нулю тогда и только тогда, когда один из множителей равен нулю, а другие при этом не теряют смысла: [left[begin{gathered}begin{aligned}
&2cos^2x+11cos x+5=0\[1ex]
&log_{18}(sin
x)=0end{aligned}end{gathered}right.quadLeftrightarrowquad
begin{cases}
left[begin{gathered}begin{aligned}
&2cos^2x+11cos x+5=0\[1ex]
&sin x=18^0end{aligned}end{gathered}right.\
sin x>0end{cases}] Назовем (sin x>0) ОДЗ.

1) Рассмотрим первое уравнение. Заменой (cos x=t), (-1leqslant
tleqslant 1), данное уравнение сводится к квадратному: (2t^2+11t+5=0). Корнями будут (t_1=-frac12) и (t_2=-5). Видим, что корень (t_2) не подходит. Таким образом: [cos x=-dfrac12quadLeftrightarrowquad x=pm dfrac{2pi}3+2pi n,
ninmathbb{Z}] Заметим, что углы (x=dfrac{2pi}3+2pi n) находятся во второй четверти, где (sin x>0), следовательно, подходят по ОДЗ. Углы (x=-dfrac{2pi}3+2pi n) находятся в третьей четверти, где (sin x
<0), следовательно, не подходят по ОДЗ. Итог: [x=dfrac{2pi}3+2pi n,
ninmathbb{Z}]

2) Рассмотрим второе уравнение: (sin x=1) (подходит под ОДЗ). Решением будут [x=dfrac{pi}2+2pi k, kinmathbb{Z}]

б) Отберем корни.
 
1) (0leqslant dfrac{2pi}3+2pi nleqslant pi
quadRightarrowquad n=0 quadRightarrowquad
x=dfrac{2pi}3)
 
2) (0leqslant dfrac{pi}2+2pi kleqslant pi
quadRightarrowquad k=0quadRightarrowquad x=dfrac{pi}2)

Ответ:

а) (dfrac{2pi}3+2pi n, dfrac{pi}2+2pi k; k, ninmathbb{Z})

б) (dfrac{pi}2; dfrac{2pi}3)


Задание
2

#3821

Уровень задания: Равен ЕГЭ

а) Решите уравнение [{large{dfrac{4^{sin 2x}-2^{2sqrt3sin
x}}{sqrt{7sin x}}=0}}]

б) Найдите все корни этого уравнения, принадлежащие промежутку (left[-dfrac{13pi}2; -5pi right].)

а) Дробь равна нулю тогда и только тогда, когда числитель равен нулю, а знаменатель при этом не равен нулю: [begin{cases}
4^{sin 2x}-2^{2sqrt3sin x}=0\[1ex]
sqrt{7sin x}ne 0end{cases}] Так как ОДЗ выражения (sqrt{7sin
x}) — это (sin xgeqslant 0), но (sqrt{7sin x}ne 0), то есть (sin xne 0), то данная система равносильна: [begin{cases}
4^{sin 2x}-2^{2sqrt3sin x}=0\[1ex]
sin x>0end{cases}] Назовем неравенство ОДЗ.
Рассмотрим уравнение системы: [2^{2sin 2x}=2^{2sqrt3sin x}quadLeftrightarrowquad
2cdot 2sin xcos x=2sqrt3sin xquadLeftrightarrowquad sin
x(2cos x-sqrt3)=0] Следовательно:

1) (sin x=0). Данное уравнение не удовлетворяет ОДЗ (sin x>0).

или

2) (cos x=dfrac{sqrt3}2), что равносильно (x=dfrac{pi}6+2pi n) или (x=-dfrac{pi}6+2pi m), (n,minmathbb{Z}).
Так как по ОДЗ (sin x>0), то серия корней (x=-dfrac{pi}6+2pi m) нам не подходит, так как эти углы находятся в четвертой четверти, где (sin x<0).

Следовательно, ответом будут: (x=dfrac{pi}6+2pi n), (ninmathbb{Z}).

б) Отберем корни.

(-dfrac{13pi}2leqslant dfrac{pi}6+2pi nleqslant
-5piquadLeftrightarrowquad -dfrac{10}3leqslant nleqslant
-dfrac{31}{12}quadRightarrowquad n=-3quadRightarrowquad
x=-dfrac{35pi}6)

Ответ:

а) (dfrac{pi}6+2pi n), (ninmathbb{Z})

б) (-dfrac{35pi}6)


Задание
3

#3822

Уровень задания: Равен ЕГЭ

а) Решите уравнение [{large{dfrac{log^2_2(sin x)+log_2(sin
x)}{2cos x-sqrt3}=0}}]

б) Найдите все корни этого уравнения, принадлежащие промежутку (left[dfrac{pi}2; 2piright].)

а) Дробь равна нулю тогда и только тогда, когда числитель равен нулю, а знаменатель при этом не равен нулю: [begin{cases}
log^2_2(sin x)+log_2(sin
x)=0\[1ex]
2cos x-sqrt3ne 0end{cases}] Неравенство (cos xne
dfrac{sqrt3}2) назовем ОДЗ.
Рассмотрим уравнение системы: (log^2_2(sin x)+log_2(sin x)=0).
Сделаем замену (log_2(sin x)=t). Тогда уравнение примет вид [t^2+t=0quadLeftrightarrowquad t(t+1)=0quadLeftrightarrowquad
left[begin{gathered}begin{aligned} &t=0\
&t=-1end{aligned}end{gathered}right.] Следовательно, [left[begin{gathered}begin{aligned}
&log_2(sin x)=0\
&log_2(sin x)=-1
end{aligned}end{gathered}right.quadLeftrightarrowquad
left[begin{gathered}begin{aligned}
&sin x=2^0=1\[1ex]
&sin x=2^{-1}=dfrac12
end{aligned}end{gathered}right.quadLeftrightarrowquad
left[begin{gathered}begin{aligned}
&x_1=dfrac{pi}2+2pi n\[2ex]
&x_2=dfrac{pi}6+2pi m\[2ex]
&x_3=dfrac{5pi}6+2pi k
end{aligned}end{gathered}right.] (n,m,kinmathbb{Z}).
Вернемся к ОДЗ. По ОДЗ (xne dfrac{pi}6+2pi l) и (xne
-dfrac{pi}6+2pi p), (l,pinmathbb{Z}).
Таким образом мы видим, что серия корней (x_2) не подходит под ОДЗ, значит, не будет входить в ответ.
Ответом будут являться серии (x_1) и (x_3).

б) Отберем корни.
 
1) (dfrac{pi}2leqslant dfrac{pi}2+2pi nleqslant 2pi
quadLeftrightarrowquad 0leqslant nleqslant
dfrac34quadRightarrowquad n=0quadRightarrowquad
x=dfrac{pi}2)
 
2) (dfrac{pi}2leqslant dfrac{5pi}6+2pi kleqslant 2pi
quadLeftrightarrowquad -dfrac16leqslant kleqslant
dfrac7{12}quadRightarrowquad k=0quadRightarrowquad
x=dfrac{5pi}6)

Ответ:

а) (dfrac{pi}2+2pi n, dfrac{5pi}6+2pi k), (n,kinmathbb{Z})

б) (dfrac{pi}2; dfrac{5pi}6)


Задание
4

#3971

Уровень задания: Равен ЕГЭ

а) Решите уравнение [(10cos^2x-7cos x-6)cdot log_{8}(-sin
x)=0]

б) Найдите все корни этого уравнения, принадлежащие отрезку (left[2pi;dfrac{7pi}2right]).

а) Произведение равно нулю тогда и только тогда, когда один из множителей равен нулю, а другие при этом не теряют смысла: [begin{cases}
left[begin{gathered}begin{aligned}
&10cos^2x-7cos x-6=0\
&log_{8}(-sin x)=0
end{aligned}end{gathered}right. \
-sin x>0end{cases} quadLeftrightarrowquad
begin{cases}
left[begin{gathered}begin{aligned}
&10cos^2x-7cos x-6=0\
&sin x=-1
end{aligned}end{gathered}right. \
sin x<0end{cases}] Назовем (sin x<0) – ОДЗ.

1) Рассмотрим первое уравнение. Заменой (cos x=t), (-1leqslant
tleqslant 1), данное уравнение сводится к квадратному (10t^2-7t-6=0). Корнями будут (t=-frac12) и (t=frac65). Видим, что второй корень не подходит. Таким образом: [cos x=-dfrac12quadLeftrightarrowquad
x=pm dfrac{2pi}3+2pi n, ninmathbb{Z}] Заметим, что углы (x=dfrac{2pi}3+2pi n), (ninmathbb{Z}) находятся во второй четверти, где (sin x>0), следовательно, не подходят по ОДЗ. Углы (x=-dfrac{2pi}3+2pi n), (ninmathbb{Z}) находятся в третьей четверти, где (sin x<0), следовательно, подходят по ОДЗ. Итог: [x=-dfrac{2pi}3+2pi n, ninmathbb{Z}]

2) Рассмотрим второе уравнение: (sin x=-1) (подходит по ОДЗ). Решением будут [x=-dfrac{pi}2+2pi k, kinmathbb{Z}]

б) Отберем корни.
 
(2pileqslant -dfrac{2pi}3+2pi nleqslant
dfrac{7pi}2quadLeftrightarrowquad dfrac43leqslant nleqslant
dfrac{25}{12}quadRightarrowquad
n=2quadRightarrowquad x=dfrac{10pi}3)
 
(2pi leqslant -dfrac{pi}2+2pi kleqslant
dfrac{7pi}2quadLeftrightarrowquad dfrac54leqslant kleqslant
2quadRightarrowquad k=2quadRightarrowquad x=dfrac{7pi}2)

Ответ:

а) (-dfrac{2pi}3+2pi n, -dfrac{pi}2+2pi k, n,kinmathbb{Z})

б) (dfrac{10pi}3; dfrac{7pi}2)


Задание
5

#3972

Уровень задания: Равен ЕГЭ

а) Решите уравнение [dfrac{log^2_2(sin x)+log_2(sin x)}{2cos
x+sqrt3}=0]

б) Найдите все корни этого уравнения, принадлежащие отрезку (left[0;dfrac{3pi}2right]).

а) ОДЗ уравнения: (sin x>0) и (cos xne -frac{sqrt3}2).
Решим уравнение на ОДЗ: [dfrac{log_2(sin x)cdot left(log_2(sin x)+1right)}{2cos x+sqrt3}=0
quadRightarrowquad left[begin{gathered}begin{aligned}
&log_2(sin x)=0\ &log_2(sin x)=-1
end{aligned}end{gathered}right.
quadRightarrowquad left[begin{gathered}begin{aligned} &sin
x=1\[2ex]
&sin x=dfrac12
end{aligned}end{gathered}right.] Видим, что оба уравнения подходят под условие (sin x>0) из ОДЗ.
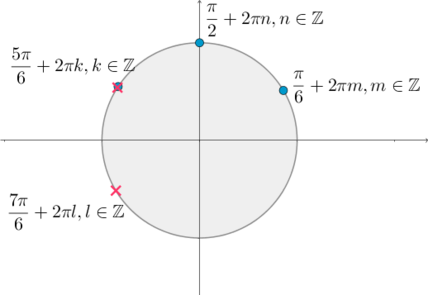
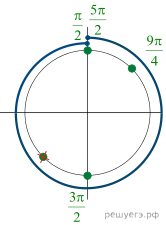
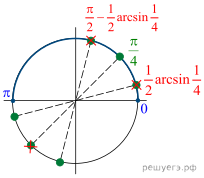
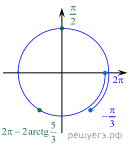
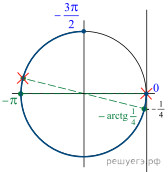
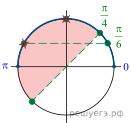
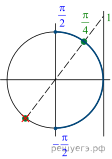
Таким образом, нам нужно отобрать корни, которые подходят под условие (cos xne -dfrac{sqrt3}2). Сделаем это по окружности:


Таким образом, видим, что отбрасывается только одна серия корней: (dfrac{5pi}6+2pi k). Итоговый ответ: [x= dfrac{pi}2+2pi n; dfrac{pi}6+2pi m; n,minmathbb{Z}]

б) Отберем корни.
 
(0leqslant dfrac{pi}2+2pi nleqslant
dfrac{3pi}2quadLeftrightarrowquad -dfrac14leqslant nleqslant
dfrac12quadRightarrowquad n=0quadRightarrowquad
x=dfrac{pi}2)
 
(0leqslant dfrac{pi}6+2pi mleqslant
dfrac{3pi}2quadLeftrightarrowquad -dfrac1{12}leqslant
mleqslant dfrac23quadRightarrowquad m=0quadRightarrowquad
x=dfrac{pi}6)

Ответ:

а) (dfrac{pi}2+2pi n, dfrac{pi}6+2pi m, n,minmathbb{Z})

б) (dfrac{pi}6; dfrac{pi}2)

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ

Источник

Уравнения
из материалов ЕГЭ профильного уровня смешанного тип

         Иррациональные и тригонометрические уравнения.

1. а)  Решите
уравнение левая круглая скобка 2 синус x плюс корень из 3 правая круглая скобка умножить на корень из косинус x=0.

б)  Найдите все корни этого уравнения, принадлежащие
отрезку левая квадратная скобка дробь: числитель: 3 Пи , знаменатель: 2 конец дроби ; дробь: числитель: 7 Пи , знаменатель: 2 конец дроби правая квадратная скобка .

Решение. а)  Решим
уравнение

левая круглая скобка 2 синус x плюс корень из 3 правая круглая скобка умножить на корень из косинус x=0 равносильно
равносильно система выражений совокупность выражений косинус x=0, синус x= минус дробь: числитель: корень из 3 , знаменатель: 2 конец дроби конец системы . , косинус xgeqslant0 конец совокупности . равносильно совокупность выражений x= дробь: числитель: Пи , знаменатель: 2 конец дроби плюс Пи k,x= минус дробь: числитель: Пи , знаменатель: 3 конец дроби плюс 2 Пи k, конец совокупности . k принадлежит Z .

https://math-ege.sdamgia.ru/get_file?id=50342&png=1

б)  С помощью числовой окружности отберём корни,
принадлежащие отрезку левая квадратная скобка дробь: числитель: 3 Пи , знаменатель: 2 конец дроби ; дробь: числитель: 7 Пи , знаменатель: 2 конец дроби правая квадратная скобка . Получим
числа: дробь: числитель: 3 Пи , знаменатель: 2 конец дроби ; дробь: числитель: 5 Пи , знаменатель: 3 конец дроби ; дробь: числитель: 5 Пи , знаменатель: 2 конец дроби ; дробь: числитель: 7 Пи , знаменатель: 2 конец дроби .

Ответ: а) левая фигурная скобка дробь: числитель: Пи , знаменатель: 2 конец дроби плюс Пи k, минус дробь: числитель: Пи , знаменатель: 3 конец дроби плюс 2 Пи k: k принадлежит Z правая фигурная скобка ; б)
дробь: числитель: 3 Пи , знаменатель: 2 конец дроби ; дробь: числитель: 5 Пи , знаменатель: 3 конец дроби ; дробь: числитель: 5 Пи , знаменатель: 2 конец дроби ; дробь: числитель: 7 Пи , знаменатель: 2 конец дроби .

2. а)  Решите
уравнение корень из синус x умножить на косинус x= косинус x.

б)  Укажите корни этого уравнения, принадлежащие
отрезку левая квадратная скобка дробь: числитель: Пи , знаменатель: 2 конец дроби ; дробь: числитель: 5 Пи , знаменатель: 2 конец дроби правая квадратная скобка .

Решение. а)  Воспользуемся
тем, что

корень из f = g равносильно система выражений g больше или равно 0,f=g в квадрате , конец системы .

https://math-ege.sdamgia.ru/get_file?id=103707&png=1

и произведем эквивалентые преобразования уравнения:

корень из синус x умножить на косинус x= косинус x равносильно система выражений синус x умножить на косинус x= косинус в квадрате x, косинус x больше или равно 0 конец системы . равносильно
равносильно система выражений косинус x левая круглая скобка синус x минус косинус x правая круглая скобка =0, косинус x больше или равно 0 конец системы . равносильно

равносильно система выражений совокупность выражений косинус x=0, синус x = косинус x, конец системы .} косинус x больше или равно 0 конец совокупности . равносильно совокупность выражений x= дробь: числитель: Пи , знаменатель: 2 конец дроби плюс Пи k, x= дробь: числитель: Пи , знаменатель: 4 конец дроби плюс 2 Пи k, конец совокупности .k принадлежит Z .

б)  Отберем корни при помощи единичной окружности.
Подходят дробь: числитель: Пи , знаменатель: 2 конец дроби , дробь: числитель: 3 Пи , знаменатель: 2 конец дроби , дробь: числитель: 9 Пи , знаменатель: 4 конец дроби , дробь: числитель: 5 Пи , знаменатель: 2 конец дроби .

Ответ: а) левая фигурная скобка дробь: числитель: Пи , знаменатель: 2 конец дроби плюс Пи k, дробь: числитель: Пи , знаменатель: 4 конец дроби плюс 2 Пи k : k принадлежит Z правая фигурная скобка ; б)
дробь: числитель: Пи , знаменатель: 2 конец дроби , дробь: числитель: 3 Пи , знаменатель: 2 конец дроби , дробь: числитель: 9 Пи , знаменатель: 4 конец дроби , дробь: числитель: 5 Пи , знаменатель: 2 конец дроби .

3. а)  Решите
уравнение 2 синус 2x минус синус x умножить на корень из 2ctg x=1.

б)  Укажите корни этого уравнения, принадлежащие
отрезку левая квадратная скобка 0; Пи правая квадратная скобка .

Решение. а)  Заметим,
что

x= система выражений корень из x в квадрате ,если xgeqslant0, минус корень из x в квадрате ,если x меньше 0, конец системы .

поэтому, внося синус xпод знак корня, необходимо
рассмотреть два случая:

синус x корень из 2 умножить на дробь: числитель: косинус x, знаменатель: синус x конец дроби = система выражений корень из 2 синус x косинус x, синус x больше 0, минус корень из 2 синус x косинус x, синус x меньше 0 конец системы . =
= система выражений корень из синус 2x, синус x больше 0, минус корень из синус 2x, синус x меньше 0. конец системы .

https://math-ege.sdamgia.ru/get_file?id=46175&png=1

В случае синус x больше 0имеем:

2 синус 2x минус корень из синус 2x минус 1=0 равносильно равносильно
равносильно совокупность выражений корень из синус 2x=1, корень из синус 2x= минус дробь: числитель: 1, знаменатель: 2 конец дроби конец совокупности . underset корень из синус 2x больше 0mathop равносильно корень из синус 2x=1 равносильно

равносильно синус 2x=1 равносильно 2x= дробь: числитель: Пи , знаменатель: 2 конец дроби плюс 2 Пи k равносильно x= дробь: числитель: Пи , знаменатель: 4 конец дроби плюс Пи k,k принадлежит Z .

Условию синус x больше 0удовлетворяет
серия x= дробь: числитель: Пи , знаменатель: 4 конец дроби плюс 2 Пи k,k принадлежит Z .

В случае синус x меньше 0имеем:

2 синус 2x плюс корень из синус 2x минус 1=0 равносильно
равносильно совокупность выражений корень из синус 2x= минус 1, корень из синус 2x= дробь: числитель: 1, знаменатель: 2 конец дроби конец совокупности . underset корень из синус 2x больше 0mathop равносильно корень из синус 2x= дробь: числитель: 1, знаменатель: 2 конец дроби равносильно

равносильно синус 2x= дробь: числитель: 1, знаменатель: 4 конец дроби равносильно совокупность выражений 2x= арксинус дробь: числитель: 1, знаменатель: 4 конец дроби плюс 2 Пи k,2x= Пи минус арксинус дробь: числитель: 1, знаменатель: 4 конец дроби плюс 2 Пи k конец совокупности . равносильно
равносильно совокупность выражений x= дробь: числитель: 1, знаменатель: 2 конец дроби арксинус дробь: числитель: 1, знаменатель: 4 конец дроби плюс Пи k,x= дробь: числитель: Пи , знаменатель: 2 конец дроби минус дробь: числитель: 1, знаменатель: 2 конец дроби арксинус дробь: числитель: 1, знаменатель: 4 конец дроби плюс Пи k, конец совокупности . k принадлежит Z .

Условию синус x меньше 0удовлетворяют
серии x= Пи плюс дробь: числитель: 1, знаменатель: 2 конец дроби арксинус дробь: числитель: 1, знаменатель: 4 конец дроби плюс 2 Пи kи
x= дробь: числитель: 3 Пи , знаменатель: 2 конец дроби минус дробь: числитель: 1, знаменатель: 2 конец дроби арксинус дробь: числитель: 1, знаменатель: 4 конец дроби плюс 2 Пи k, k принадлежит Z .

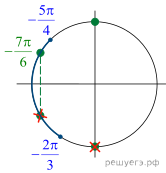
б)  Отберём корни, принадлежащие отрезку левая квадратная скобка 0; Пи правая квадратная скобка ,при помощи
тригонометрической окружности (см. рис.). Получим дробь: числитель: Пи , знаменатель: 4 конец дроби .

Ответ: а) левая фигурная скобка дробь: числитель: Пи , знаменатель: 4 конец дроби плюс 2 Пи k; Пи плюс дробь: числитель: 1, знаменатель: 2 конец дроби арксинус дробь: числитель: 1, знаменатель: 4 конец дроби плюс 2 Пи k; дробь: числитель: 3 Пи , знаменатель: 2 конец дроби минус дробь: числитель: 1, знаменатель: 2 конец дроби арксинус дробь: числитель: 1, знаменатель: 4 конец дроби плюс 2 Пи k : k принадлежит Z правая фигурная скобка ; б)
дробь: числитель: Пи , знаменатель: 4 конец дроби .

4. а)  Решите
уравнение корень из синус левая круглая скобка дробь: числитель: Пи , знаменатель: 4 конец дроби плюс x правая круглая скобка косинус левая круглая скобка дробь: числитель: Пи , знаменатель: 4 конец дроби минус x правая круглая скобка умножить на косинус x= дробь: числитель: 1, знаменатель: 2 корень из 2 конец дроби .

б)  Укажите корни этого уравнения, принадлежащие
отрезку левая квадратная скобка минус дробь: числитель: Пи , знаменатель: 4 конец дроби ; Пи правая квадратная скобка .

Решение. Уравнение имеет корни,
только если косинус x больше 0.При этом
условии обе части уравнения неотрицательны и можно возвести их в квадрат.
Выполним преобразования:

корень из синус левая круглая скобка дробь: числитель: Пи , знаменатель: 4 конец дроби плюс x правая круглая скобка косинус левая круглая скобка дробь: числитель: Пи , знаменатель: 4 конец дроби минус x правая круглая скобка умножить на косинус x= дробь: числитель: 1, знаменатель: 2 корень из 2 конец дроби равносильно
равносильно синус левая круглая скобка дробь: числитель: Пи , знаменатель: 4 конец дроби плюс x правая круглая скобка косинус левая круглая скобка дробь: числитель: Пи , знаменатель: 4 конец дроби минус x правая круглая скобка умножить на косинус в квадрате x= дробь: числитель: 1, знаменатель: 8 конец дроби равносильно

равносильно 4 левая круглая скобка 1 плюс синус 2x правая круглая скобка косинус в квадрате x=1 равносильно
равносильно 4 левая круглая скобка синус в квадрате x плюс 2 синус x косинус x плюс косинус в квадрате x правая круглая скобка косинус в квадрате x = 1 равносильно

равносильно 4 левая круглая скобка синус x плюс косинус x правая круглая скобка в квадрате косинус в квадрате x = 1 равносильно
равносильно левая круглая скобка 2 левая круглая скобка синус x плюс косинус x правая круглая скобка косинус x правая круглая скобка в квадрате = 1 равносильно

равносильно совокупность выражений 2 левая круглая скобка синус x плюс косинус x правая круглая скобка косинус x=1,2 левая круглая скобка синус x плюс косинус x правая круглая скобка косинус x = минус 1 конец совокупности . равносильно
равносильно совокупность выражений синус в квадрате x минус 2 синус x косинус x минус косинус в квадрате x =0, синус в квадрате x плюс 2 синус x косинус x плюс 3 косинус в квадрате x =0. конец совокупности .

https://math-ege.sdamgia.ru/get_file?id=46848&png=1Разделим второе
уравнение совокупности на косинус в квадрате x,получим тангенс в квадрате x плюс 2 тангенс x плюс 3 =0,это уравнение не имеет
решений. Умножим обе части первого уравнения на −1 и воспользуемся
формулами двойного угла. Получим:

синус 2x = минус косинус 2x равносильно тангенс 2x = минус 1 равносильно
равносильно 2x = минус дробь: числитель: Пи , знаменатель: 4 конец дроби плюс Пи k равносильно x = минус дробь: числитель: Пи , знаменатель: 8 конец дроби плюс дробь: числитель: Пи k, знаменатель: 2 конец дроби , k принадлежит Z .

Из найденных серий условию косинус x больше 0удовлетворяют
только x = минус дробь: числитель: Пи , знаменатель: 8 конец дроби плюс 2 Пи k.и
x = дробь: числитель: 3 Пи , знаменатель: 8 конец дроби плюс 2 Пи k, k принадлежит Z .

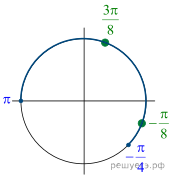
Отберем корни при помощи тригонометрической окружности
(см. рис.), получим числа минус дробь: числитель: Пи , знаменатель: 8 конец дроби и дробь: числитель: 3 Пи , знаменатель: 8 конец дроби .

Ответ: а) левая фигурная скобка минус дробь: числитель: Пи , знаменатель: 8 конец дроби плюс 2 Пи k, дробь: числитель: 3 Пи , знаменатель: 8 конец дроби плюс 2 Пи k : k принадлежит Z правая фигурная скобка ;б)
минус дробь: числитель: Пи , знаменатель: 8 конец дроби и дробь: числитель: 3 Пи , знаменатель: 8 конец дроби .

5. а)  Решите
уравнение корень из 2 синус в квадрате дробь: числитель: x, знаменатель: 2 конец дроби левая круглая скобка 1 минус косинус x правая круглая скобка = минус синус левая круглая скобка минус x правая круглая скобка минус 5 косинус x.

б)  Укажите корни этого уравнения принадлежащие
отрезку совокупность выражений минус дробь: числитель: Пи , знаменатель: 3 конец дроби ;2 Пи конец совокупности правая квадратная скобка .

Решение. а)  Заметим,
что 1 минус косинус x = 2 синус в квадрате дробь: числитель: x, знаменатель: 2 конец дроби ,получим
в левой части

корень из 2 синус в квадрате дробь: числитель: x, знаменатель: 2 конец дроби левая круглая скобка 1 минус косинус x правая круглая скобка = корень из 4 синус в степени 4 дробь: числитель: x, знаменатель: 2 конец дроби =2 синус в квадрате дробь: числитель: x, знаменатель: 2 конец дроби .

Далее, используя формулы минус синус левая круглая скобка минус x правая круглая скобка = синус x, синус x = 2 синус дробь: числитель: x, знаменатель: 2 конец дроби косинус дробь: числитель: x, знаменатель: 2 конец дроби , косинус x = косинус в квадрате { дробь: числитель: x, знаменатель: 2 конец дроби минус синус в квадрате { дробь: числитель: x, знаменатель: 2 конец дроби , перейдем
к половинному аргументу в правой части и сведем уравнение к однородному
тригонометрическому второй степени:

https://math-ege.sdamgia.ru/get_file?id=47473&png=1

2 синус в квадрате дробь: числитель: x, знаменатель: 2 конец дроби = синус x минус 5 косинус x равносильно
равносильно 2 синус в квадрате дробь: числитель: x, знаменатель: 2 конец дроби =2 синус дробь: числитель: x, знаменатель: 2 конец дроби косинус дробь: числитель: x, знаменатель: 2 конец дроби минус 5 левая круглая скобка косинус в квадрате { дробь: числитель: x, знаменатель: 2 конец дроби минус синус в квадрате { дробь: числитель: x, знаменатель: 2 конец дроби правая круглая скобка равносильно

равносильно 3 синус в квадрате дробь: числитель: x, знаменатель: 2 конец дроби плюс 2 синус дробь: числитель: x, знаменатель: 2 конец дроби косинус дробь: числитель: x, знаменатель: 2 конец дроби минус 5 косинус в квадрате дробь: числитель: x, знаменатель: 2 конец дроби =0 равносильно
равносильно 3 тангенс в квадрате дробь: числитель: x, знаменатель: 2 конец дроби плюс 2 тангенс дробь: числитель: x, знаменатель: 2 конец дроби минус 5=0 равносильно

равносильно совокупность выражений тангенс дробь: числитель: x, знаменатель: 2 конец дроби =1, тангенс дробь: числитель: x, знаменатель: 2 конец дроби = минус дробь: числитель: 5, знаменатель: 3 конец дроби конец совокупности . равносильно совокупность выражений дробь: числитель: x, знаменатель: 2 конец дроби = дробь: числитель: Пи , знаменатель: 4 конец дроби плюс Пи k, дробь: числитель: x, знаменатель: 2 конец дроби = минус арктангенс дробь: числитель: 5, знаменатель: 3 конец дроби плюс Пи k конец совокупности . равносильно
равносильно совокупность выражений x= дробь: числитель: Пи , знаменатель: 2 конец дроби плюс 2 Пи k, x= минус 2 арктангенс дробь: числитель: 5, знаменатель: 3 конец дроби плюс 2 Пи k, конец совокупности . k принадлежит Z .

б)  Отберем корни при помощи единичной окружности,
подходят дробь: числитель: Пи , знаменатель: 2 конец дроби и 2 Пи минус 2 арктангенс дробь: числитель: 5, знаменатель: 3 конец дроби .

Ответ: а) левая фигурная скобка дробь: числитель: Пи , знаменатель: 2 конец дроби плюс 2 Пи k, минус 2 арктангенс дробь: числитель: 5, знаменатель: 3 конец дроби плюс 2 Пи k: k принадлежит Z правая фигурная скобка ; б)
дробь: числитель: Пи , знаменатель: 2 конец дроби , 2 Пи минус 2 арктангенс дробь: числитель: 5, знаменатель: 3 конец дроби .

6. а)  Решите
уравнение корень из 1 минус косинус в квадрате левая круглая скобка дробь: числитель: 3 Пи , знаменатель: 2 конец дроби плюс x правая круглая скобка = минус косинус x плюс 8 синус левая круглая скобка x минус Пи правая круглая скобка .

б)  Укажите корни этого уравнения, принадлежащие
отрезку левая квадратная скобка минус дробь: числитель: 3 Пи , знаменатель: 2 конец дроби ; 0 правая квадратная скобка .

Решение. а)  Преобразуем
уравнение с помощью формул приведения и основного тригонометрического
тождества:

корень из 1 минус косинус в квадрате левая круглая скобка дробь: числитель: 3 Пи , знаменатель: 2 конец дроби плюс x правая круглая скобка = минус косинус x плюс 8 синус левая круглая скобка x минус Пи правая круглая скобка равносильно
равносильно корень из 1 минус синус в квадрате x= минус косинус x минус 8 синус x равносильно

равносильно корень из косинус в квадрате x= минус косинус x минус 8 синус x равносильно | косинус x|= минус косинус x минус 8 синус x равносильно

https://math-ege.sdamgia.ru/get_file?id=48246&png=1

равносильно совокупность выражений новая строка система выражений новая строка косинус x= минус косинус x минус 8 синус x, новая строка косинус xgeqslant0, конец системы . новая строка система выражений новая строка косинус x= косинус x плюс 8 синус x, новая строка косинус x меньше 0 конец системы . конец совокупности . равносильно совокупность выражений новая строка система выражений новая строка 4 синус x= минус косинус x, новая строка косинус xgeqslant0, конец системы . новая строка система выражений новая строка синус x=0, новая строка косинус x меньше 0 конец системы . конец совокупности . равносильно

равносильно совокупность выражений новая строка система выражений новая строка тангенс x= минус дробь: числитель: 1, знаменатель: 4 конец дроби , новая строка косинус xgeqslant0, конец системы . новая строка косинус x= минус 1 конец совокупности . равносильно совокупность выражений новая строка x= минус арктангенс дробь: числитель: 1, знаменатель: 4 конец дроби плюс 2 Пи k, новая строка x= Пи плюс 2 Пи k, конец совокупности .k принадлежит Z .

б)  Отберём корни. принадлежащие отрезку. Для первой
серии получаем:

минус дробь: числитель: 3 Пи , знаменатель: 2 конец дроби меньше или равно минус арктангенс дробь: числитель: 1, знаменатель: 4 конец дроби плюс 2 Пи kleqslant0 равносильно
равносильно минус дробь: числитель: 3 Пи , знаменатель: 2 конец дроби плюс арктангенс дробь: числитель: 1, знаменатель: 4 конец дроби leqslant2 Пи k меньше или равно арктангенс дробь: числитель: 1, знаменатель: 4 конец дроби равносильно k = 0,

откуда корень минус арктангенс дробь: числитель: 1, знаменатель: 4 конец дроби .Для
второй серии имеем:

минус дробь: числитель: 3 Пи , знаменатель: 2 конец дроби меньше или равно Пи плюс 2 Пи k leqslant0 равносильно минус дробь: числитель: 5 Пи , знаменатель: 2 конец дроби leqslant2 Пи kleqslant минус Пи равносильно k = минус 1,

откуда корень минус Пи .

Ответ: а) левая фигурная скобка минус арктангенс дробь: числитель: 1, знаменатель: 4 конец дроби плюс 2 Пи k, Пи плюс 2 Пи k : k принадлежит Z правая фигурная скобка ;б)
минус арктангенс дробь: числитель: 1, знаменатель: 4 конец дроби , минус Пи .

7. а)  Решите
уравнение корень из синус в квадрате x плюс корень из 3 синус x плюс 1= косинус x.

б)  Укажите корни этого уравнения, принадлежащие
отрезку левая квадратная скобка минус дробь: числитель: 3 Пи , знаменатель: 2 конец дроби ; Пи правая квадратная скобка .

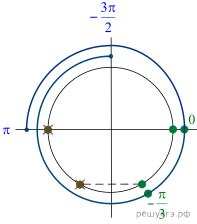
Решение. https://math-ege.sdamgia.ru/get_file?id=60645&png=1а)  При
условии косинус x geqslant0исходное
уравнение равносильно следующим:

синус в квадрате x плюс корень из 3 синус x плюс 1= косинус в квадрате x равносильно
равносильно синус в квадрате x плюс корень из 3 синус x плюс 1=1 минус синус в квадрате x равносильно

равносильно 2 синус в квадрате x плюс корень из 3 синус x=0, равносильно
равносильно 2 синус x левая круглая скобка синус x плюс дробь: числитель: корень из 3, знаменатель: 2 конец дроби правая круглая скобка =0 равносильно

равносильно совокупность выражений новая строка синус x=0, новая строка синус x= минус дробь: числитель: корень из 3, знаменатель: 2 конец дроби конец совокупности . равносильно
равносильно совокупность выражений новая строка x= Пи k, новая строка x= минус дробь: числитель: Пи , знаменатель: 3 конец дроби плюс 2 Пи k, новая строка x= минус дробь: числитель: 2 Пи , знаменатель: 3 конец дроби плюс 2 Пи k, конец совокупности . k принадлежит Z .

Условию косинус xgeqslant0удовлетворяет
только x=2 Пи k,x= минус дробь: числитель: Пи , знаменатель: 3 конец дроби плюс 2 Пи k, k принадлежит Z .

б)  Отберем корни при помощи единичной окружности,
подходят минус дробь: числитель: Пи , знаменатель: 3 конец дроби и 0.

Ответ: а) левая фигурная скобка минус дробь: числитель: Пи , знаменатель: 3 конец дроби плюс 2 Пи k; 2 Пи k : k принадлежит Z правая фигурная скобка ; б)
минус дробь: числитель: Пи , знаменатель: 3 конец дроби ; 0.

8. а)  Решите
уравнение левая круглая скобка косинус 2x плюс 3 синус x минус 2 правая круглая скобка умножить на корень из косинус x минус синус x = 0.

б)  Укажите корни этого уравнения, принадлежащие
отрезку левая квадратная скобка 0; Пи правая квадратная скобка .

Решение. а)  Левая
часть уравнения обращается в нуль в двух случаях. Если второй множитель равен
нулю:

косинус x минус синус x = 0 равносильно тангенс x= 1 равносильно x = дробь: числитель: Пи , знаменатель: 4 конец дроби плюс Пи k, k принадлежит Z .

Или если первый множитель равен нулю, а второй при этом определён.

Решим уравнение:

косинус 2x плюс 3 синус x минус 2 = 0 равносильно левая круглая скобка 1 минус 2 синус в квадрате x правая круглая скобка плюс 3 синус x минус 2 = 0 равносильно

равносильно 2 синус в квадрате x минус 3 синус x плюс 1 = 0 равносильно
равносильно совокупность выражений синус x = 1, синус x = дробь: числитель: 1, знаменатель: 2 конец дроби конец совокупности . равносильно совокупность выражений x = дробь: числитель: Пи , знаменатель: 2 конец дроби плюс 2 Пи k , x = дробь: числитель: Пи , знаменатель: 6 конец дроби плюс 2 Пи k, x = дробь: числитель: 5 Пи , знаменатель: 6 конец дроби плюс 2 Пи k, . конец совокупности k принадлежит Z .

https://math-ege.sdamgia.ru/get_file?id=94514&png=1

Решим неравенство:

косинус x минус синус x больше или равно 0 равносильно минус дробь: числитель: 3 Пи , знаменатель: 4 конец дроби плюс 2 Пи n меньше или равно x меньше или равно дробь: числитель: Пи , знаменатель: 4 конец дроби плюс 2 Пи n, n принадлежит Z .

Неравенству удовлетворяют только корни серии дробь: числитель: Пи , знаменатель: 6 конец дроби плюс 2 Пи k.

Объединяя два рассмотренных случая, заключаем, что решениями
уравнения являются x = дробь: числитель: Пи , знаменатель: 6 конец дроби плюс 2 Пи k и x = дробь: числитель: Пи , знаменатель: 4 конец дроби плюс Пи k, k принадлежит Z .

б)  Для отбора корней воспользуемся тригонометрической
окружностью (см. рис.). На отрезке левая квадратная скобка 0; Пи правая квадратная скобка лежат корни дробь: числитель: Пи , знаменатель: 4 конец дроби и дробь: числитель: Пи , знаменатель: 6 конец дроби

Ответ: а) левая фигурная скобка дробь: числитель: Пи , знаменатель: 6 конец дроби плюс 2 Пи k; дробь: числитель: Пи , знаменатель: 4 конец дроби плюс Пи k : k принадлежит Z правая фигурная скобка ; б)
дробь: числитель: Пи , знаменатель: 4 конец дроби , дробь: числитель: Пи , знаменатель: 6 конец дроби .

9. а)  Решите
уравнение синус x умножить на корень из 3 минус тангенс в квадрате дробь: числитель: 3x, знаменатель: 2 конец дроби минус косинус x=2.

б)  Укажите корни этого уравнения, принадлежащие
отрезку левая квадратная скобка минус 17; 2 правая квадратная скобка .

Решение. а)  Перенесем
косинус xв правую часть, заметим, что сумма 2 плюс косинус xне
принимает отрицательных значений. Следовательно, при условии синус x больше или равно 0возведение обеих частей уравнения в квадрат
является равносильным преобразованием. Имеем:

синус в квадрате x умножить на левая круглая скобка 3 минус тангенс в квадрате дробь: числитель: 3x, знаменатель: 2 конец дроби правая круглая скобка = левая круглая скобка 2 плюс косинус x правая круглая скобка в квадрате

Выразим множители, стоящие в левой части уравнения, через косинус x.В силу основного тригонометрического тождества синус в квадрате x = 1 минус косинус в квадрате x.Чтобы преобразовать
первый множитель, воспользуемся формулой тангенс в квадрате альфа = дробь: числитель: 1, знаменатель: конец дроби косинус в квадрате альфа минус 1,откуда
получим: 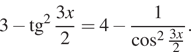3 минус тангенс в квадрате дробь: числитель: 3x, знаменатель: 2 конец дроби = 4 минус дробь: числитель: 1, знаменатель: конец дроби косинус в квадрате дробь: числитель: 3x, знаменатель: 2 конец дроби . Далее
применим формулы косинуса тройного угла косинус 3 альфа = 4 косинус в кубе альфа } минус 3 косинус альфа }и
косинуса половинного угла косинус в квадрате дробь: числитель: x, знаменатель: 2 конец дроби = дробь: числитель: 1, знаменатель: 2 конец дроби левая круглая скобка 1 плюс косинус x правая круглая скобка :

косинус в квадрате дробь: числитель: 3x, знаменатель: 2 конец дроби = левая круглая скобка 4 косинус в кубе дробь: числитель: x, знаменатель: 2 конец дроби минус 3 косинус дробь: числитель: x, знаменатель: 2 конец дроби правая круглая скобка в квадрате =
= косинус в квадрате дробь: числитель: x, знаменатель: 2 конец дроби левая круглая скобка 4 косинус в квадрате дробь: числитель: x, знаменатель: 2 конец дроби минус 3 правая круглая скобка в квадрате = дробь: числитель: 1, знаменатель: 2 конец дроби левая круглая скобка 1 плюс косинус x правая круглая скобка умножить на левая круглая скобка 2 левая круглая скобка 1 плюс косинус x правая круглая скобка минус 3 правая круглая скобка в квадрате .

Пусть t = косинус x,тогда имеем:

левая круглая скобка 1 минус t в квадрате правая круглая скобка левая круглая скобка 4 минус дробь: числитель: 1, знаменатель: конец дроби дробь: числитель: 1, знаменатель: 2 конец дроби левая круглая скобка 1 плюс t правая круглая скобка левая круглая скобка 2t минус 1 правая круглая скобка в квадрате правая круглая скобка = левая круглая скобка 2 плюс t правая круглая скобка в квадрате равносильно
равносильно 4 левая круглая скобка 1 минус t в квадрате правая круглая скобка минус дробь: числитель: 2 левая круглая скобка 1 минус t в квадрате правая круглая скобка , знаменатель: левая круглая скобка 1 плюс t правая круглая скобка умножить на левая круглая скобка 2t минус 1 правая круглая скобка в квадрате конец дроби = t в квадрате плюс 4t плюс 4 равносильно

равносильно дробь: числитель: 2 левая круглая скобка t минус 1 правая круглая скобка , знаменатель: левая круглая скобка 2t минус 1 правая круглая скобка в квадрате конец дроби = 5 t в квадрате плюс 4t, t не равно минус 1 равносильно
равносильно 2t минус 2 = левая круглая скобка 5t в квадрате плюс 4t правая круглая скобка левая круглая скобка 2t минус 1 правая круглая скобка в квадрате , t не равно минус 1, t не равно дробь: числитель: 1, знаменатель: 2 конец дроби равносильно

равносильно 2t минус 2 = левая круглая скобка 5t в квадрате плюс 4t правая круглая скобка левая круглая скобка 4t в квадрате минус 4t плюс 1 правая круглая скобка равносильно
равносильно 20t в степени 4 минус 4t в кубе минус 11t в квадрате плюс 2t плюс 2 = 0 равносильно
равносильно совокупность выражений t = минус дробь: числитель: 1, знаменатель: 2 конец дроби кр. 2,5t в квадрате минус 6t плюс 2 =0 конец совокупности . равносильно t = минус дробь: числитель: 1, знаменатель: 2 конец дроби .

Вернемся к исходной переменной, получим уравнение косинус x = минус дробь: числитель: 1, знаменатель: 2 конец дроби , откуда
x = pm дробь: числитель: 2 Пи , знаменатель: 3 конец дроби плюс 2 Пи k, k принадлежит Z . Учитывая
условие синус x больше или равно 0,окончательно
получаем: x = дробь: числитель: 2 Пи , знаменатель: 3 конец дроби плюс 2 Пи k, k принадлежит Z .

б)  Чтобы найти корни на заданном отрезке, решим двойное
неравенство:

минус 17 меньше или равно дробь: числитель: 2 Пи , знаменатель: 3 конец дроби плюс 2 Пи k меньше или равно 2 равносильно минус дробь: числитель: 17, знаменатель: Пи конец дроби меньше или равно дробь: числитель: 2, знаменатель: 3 конец дроби плюс 2k меньше или равно дробь: числитель: 2, знаменатель: Пи конец дроби равносильно
равносильно минус дробь: числитель: 17, знаменатель: 2 Пи конец дроби минус дробь: числитель: 1, знаменатель: 3 конец дроби меньше или равно k меньше или равно дробь: числитель: 1, знаменатель: Пи конец дроби минус дробь: числитель: 1, знаменатель: 3 конец дроби .

Так как 3 меньше Пи меньше 4,правая часть
полученного двойного неравенства лежит в интервале (−1; 0). Значения k
целые, поэтому наибольшее значение k = −1. Оценим
левую часть:

минус дробь: числитель: 17}6 меньше минус дробь: числитель: 17, знаменатель: 2 Пи конец дроби меньше минус дробь: числитель: 17, знаменатель: 8 конец дроби равносильно минус дробь: числитель: 19}6 меньше минус дробь: числитель: 17, знаменатель: 2 Пи конец дроби минус дробь: числитель: {, знаменатель: 1 конец дроби , знаменатель: 3 конец дроби меньше минус дробь: числитель: {, знаменатель: 5 конец дроби 9, знаменатель: 24 конец дроби .

Поскольку минус дробь: числитель: 59, знаменатель: 24 конец дроби меньше минус 2, подходит
также значение k = −2. Поскольку минус дробь: числитель: 19, знаменатель: 6 конец дроби больше минус 4, осталось
проверить значение k = −3. Покажем, что минус дробь: числитель: 17, знаменатель: 2 Пи конец дроби минус дробь: числитель: 1, знаменатель: 3 конец дроби меньше минус 3:

минус дробь: числитель: 17, знаменатель: 2 Пи конец дроби минус дробь: числитель: 1, знаменатель: 3 конец дроби меньше минус 3 равносильно дробь: числитель: 8, знаменатель: 3 конец дроби меньше дробь: числитель: 17, знаменатель: 2 Пи конец дроби равносильно Пи меньше дробь: числитель: 51, знаменатель: 16 конец дроби равносильно Пи меньше 3,1875.

Итак k = −3, k = −2
или k = −1. Найденным значениям k соответствуют
корни минус дробь: числитель: 16 Пи , знаменатель: 3 конец дроби , минус дробь: числитель: 10 Пи , знаменатель: 3 конец дроби , и минус дробь: числитель: 4 Пи , знаменатель: 3 конец дроби .

Ответ: а) левая фигурная скобка дробь: числитель: 2 Пи , знаменатель: 3 конец дроби плюс 2 Пи k : k принадлежит Z правая фигурная скобка ; б)
минус дробь: числитель: 16 Пи , знаменатель: 3 конец дроби , минус дробь: числитель: 10 Пи , знаменатель: 3 конец дроби , минус дробь: числитель: 4 Пи , знаменатель: 3 конец дроби .

10. а)  Решите
уравнение корень из синус x минус косинус x левая круглая скобка ctg x минус корень из 3 правая круглая скобка =0.

б)  Укажите корни этого уравнения, принадлежащие
отрезку левая квадратная скобка дробь: числитель: 3 Пи , знаменатель: 2 конец дроби ; 3 Пи правая квадратная скобка .

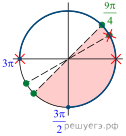
Решение. https://math-ege.sdamgia.ru/get_file?id=65002&png=1а)   При
условии синус x минус косинус x geqslant0и
синус x не равно 0исходное уравнение эквивалентно совокупности

совокупность выражений синус x минус косинус x=0,ctg x минус корень из 3=0 конец совокупности . равносильно совокупность выражений тангенс x =1,ctg x= корень из 3 конец совокупности . равносильно
равносильно совокупность выражений x= дробь: числитель: Пи , знаменатель: 4 конец дроби плюс Пи k,x= дробь: числитель: Пи , знаменатель: 6 конец дроби плюс Пи k, k принадлежит Z . конец совокупности .

Условию удовлетворяют серии корней x= дробь: числитель: Пи , знаменатель: 4 конец дроби плюс Пи k и x= дробь: числитель: 7 Пи , знаменатель: 6 конец дроби плюс 2 Пи k, k принадлежит Z .

б)  Отберём корни при помощи единичной
тригонометрической окружности. На заданном отрезке лежит только один
корень  — число дробь: числитель: 9 Пи , знаменатель: 4 конец дроби .

Ответ: а) левая фигурная скобка дробь: числитель: Пи , знаменатель: 4 конец дроби плюс Пи k; дробь: числитель: 7 Пи , знаменатель: 6 конец дроби плюс 2 Пи k : k принадлежит Z правая фигурная скобка ; б)
дробь: числитель: 9 Пи , знаменатель: 4 конец дроби .

11. а)  Решите
уравнение корень из косинус 2x минус синус в кубе x плюс 3 = синус x.

б)  Укажите корни этого уравнения, принадлежащие
промежутку левая круглая скобка дробь: числитель: 73 Пи , знаменатель: 2 конец дроби ; 41 Пи правая квадратная скобка .

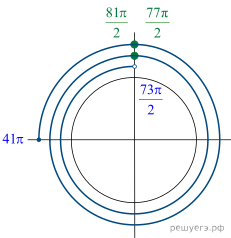
Решение. https://math-ege.sdamgia.ru/get_file?id=68780&png=1a)  Уравнение
корень из x = yравносильно уравнению x = y в квадрате при
условии y больше или равно 0.Возведем обе
части исходного уравнения в квадрат при условии синус x больше или равно 0,получим:

косинус 2x минус синус в кубе x плюс 3= синус в квадрате x равносильно
равносильно 1 минус 2 синус в квадрате x минус синус в кубе x плюс 3= синус в квадрате x равносильно

равносильно синус в кубе x плюс 3 синус в квадрате x минус 4=0 равносильно
равносильно синус в кубе x минус 1 плюс 3 синус в квадрате x минус 3=0 равносильно

равносильно левая круглая скобка синус x минус 1 правая круглая скобка левая круглая скобка синус в квадрате x плюс синус x плюс 1 правая круглая скобка плюс 3 левая круглая скобка синус x минус 1 правая круглая скобка левая круглая скобка синус x плюс 1 правая круглая скобка =0 равносильно

равносильно левая круглая скобка синус x минус 1 правая круглая скобка левая круглая скобка синус в квадрате x плюс 4 синус x плюс 4 правая круглая скобка =0 равносильно
равносильно левая круглая скобка синус x минус 1 правая круглая скобка левая круглая скобка синус x плюс 2 правая круглая скобка в квадрате =0 равносильно

равносильно синус x=1 равносильно x= дробь: числитель: знаменатель: p конец дроби i 2 плюс 2 Пи k, k принадлежит Z .

Полученный корень удовлетворяет исходному ограничению.

б)  Отберем корни при помощи единичной окружности
(см. рис.), подходят числа дробь: числитель: 77 Пи , знаменатель: 2 конец дроби и  дробь: числитель: 81 Пи , знаменатель: 2 конец дроби .

Ответ: а) левая фигурная скобка дробь: числитель: знаменатель: p конец дроби i 2 плюс 2 Пи k : k принадлежит Z правая фигурная скобка ;б)
дробь: числитель: 77 Пи , знаменатель: 2 конец дроби , дробь: числитель: 81 Пи , знаменатель: 2 конец дроби .

12. а)  Решите
уравнение корень из синус в квадрате 0,5x плюс 2 синус 0,5x плюс 1 минус корень из левая круглая скобка 4 синус 0,5x минус 6 правая круглая скобка в квадрате = минус 2,5.

б)  Укажите корни этого уравнения, принадлежащие
отрезку левая квадратная скобка минус Пи ; дробь: числитель: 3 Пи , знаменатель: 2 конец дроби правая квадратная скобка .

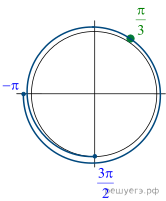
Решение. https://math-ege.sdamgia.ru/get_file?id=80832&png=1а)  Под
знаками обоих радикалов находятся полные квадраты:

корень из синус в квадрате 0,5x плюс 2 синус 0,5x плюс 1 минус корень из левая круглая скобка 4 синус 0,5x минус 6 правая круглая скобка в квадрате = минус 2,5 равносильно

равносильно left| синус дробь: числитель: x, знаменатель: 2 конец дроби плюс 1 | минус left|4 синус дробь: числитель: x, знаменатель: 2 конец дроби минус 6|= минус дробь: числитель: 5, знаменатель: 2 конец дроби underset синус альфа плюс 1 больше или равно 0 mathop равносильно
underset синус альфа плюс 1 больше или равно 0 mathop равносильно left|4 синус дробь: числитель: x, знаменатель: 2 конец дроби минус 6|= синус дробь: числитель: x, знаменатель: 2 конец дроби плюс дробь: числитель: 7, знаменатель: 2 конец дроби равносильно

равносильно совокупность выражений 4 синус дробь: числитель: x, знаменатель: 2 конец дроби минус 6= синус дробь: числитель: x, знаменатель: 2 конец дроби плюс дробь: числитель: 7, знаменатель: 2 конец дроби ,4 синус дробь: числитель: x, знаменатель: 2 конец дроби минус 6= минус синус дробь: числитель: x, знаменатель: 2 конец дроби минус дробь: числитель: 7, знаменатель: 2 конец дроби конец совокупности . равносильно
равносильно совокупность выражений 3 синус дробь: числитель: x, знаменатель: 2 конец дроби = дробь: числитель: 19, знаменатель: 2 конец дроби больше 3,5 синус дробь: числитель: x, знаменатель: 2 конец дроби = дробь: числитель: 5, знаменатель: 2 конец дроби конец совокупности . равносильно

равносильно синус дробь: числитель: x, знаменатель: 2 конец дроби = дробь: числитель: 1, знаменатель: 2 конец дроби равносильно совокупность выражений дробь: числитель: x, знаменатель: 2 конец дроби = дробь: числитель: Пи , знаменатель: 6 конец дроби плюс 2 Пи k, дробь: числитель: x, знаменатель: 2 конец дроби = дробь: числитель: 5 Пи , знаменатель: 6 конец дроби плюс 2 Пи k, конец совокупности . k принадлежит Z равносильно
равносильно совокупность выражений x= дробь: числитель: Пи , знаменатель: 3 конец дроби плюс 4 Пи k,x= дробь: числитель: 5 Пи , знаменатель: 3 конец дроби плюс 4 Пи k, конец совокупности . k принадлежит Z .

б)  Отберём корни при помощи единичной окружности.
Подходит дробь: числитель: Пи , знаменатель: 3 конец дроби .

Ответ: а) левая фигурная скобка дробь: числитель: Пи , знаменатель: 3 конец дроби плюс 4 Пи k; дробь: числитель: 5 Пи , знаменатель: 3 конец дроби плюс 4 Пи k:k принадлежит Z правая фигурная скобка ; б)
дробь: числитель: Пи , знаменатель: 3 конец дроби .

13. а)  Решите
уравнение left| 2 тангенс x минус 5 | минус left| 2 тангенс x минус 1 |=2.

б)  Укажите корни этого уравнения, принадлежащие
отрезку левая квадратная скобка минус дробь: числитель: Пи , знаменатель: 2 конец дроби ; дробь: числитель: Пи , знаменатель: 2 конец дроби правая квадратная скобка .

Решение. а)  Сделаем
замену переменной t = 2 тангенс x,тогда:

https://math-ege.sdamgia.ru/get_file?id=60588&png=1

|t минус 5| минус |t минус 1| = 2 равносильно |t минус 5|=2 плюс |t минус 1| равносильно
равносильно совокупность выражений t минус 5=2 плюс |t минус 1|,t минус 5= минус 2 минус |t минус 1| конец совокупности . равносильно

равносильно совокупность выражений |t минус 1| = t минус 7,|t минус 1| = 3 минус t конец совокупности . равносильно совокупность выражений система выражений 2t=8,t geqslant7 конец системы . система выражений 2t =4, t leqslant3 конец системы . конец совокупности . равносильно t=2.

Таким образом, 2 тангенс x =2,откуда x = дробь: числитель: Пи , знаменатель: 4 конец дроби плюс Пи k, k принадлежит Z .

б)  Отберем корни при помощи единичной окружности.
Точка дробь: числитель: Пи , знаменатель: 4 конец дроби удовлетворяет
заданному интервалу.

Ответ: а) левая фигурная скобка дробь: числитель: Пи , знаменатель: 4 конец дроби плюс Пи k : k принадлежит Z rigth правая фигурная скобка ; б)
дробь: числитель: Пи , знаменатель: 4 конец дроби .

Примечание.

Уравнение |t минус 5| минус |t минус 1| = 2удобно
решить, используя геометрический смысл модуля. Действительно, с геометрической
точки зрения левая часть уравнения представляет собой разность расстояний от
точки с координатой t до точек с координатами 5 и 1 на числовой
оси. Эта разность равна в точке t = 2;для точек, лежащих на
числовой оси правее числа 2, эта разность расстояний будет меньше двух, а для
точек, лежащих левее  — больше двух.

14. а)  Решите
уравнение корень из синус в квадрате 0,5x плюс 2 синус 0,5x плюс 1 минус корень из левая круглая скобка 4 синус 0,5x минус 6 правая круглая скобка в квадрате = минус 2,5.

б)  Укажите корни этого уравнения, принадлежащие
отрезку левая квадратная скобка минус Пи ; дробь: числитель: 3 Пи , знаменатель: 2 конец дроби правая квадратная скобка .

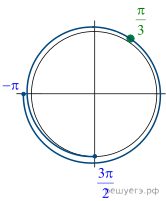
Решение. https://math-ege.sdamgia.ru/get_file?id=80832&png=1а)  Под
знаками обоих радикалов находятся полные квадраты:

корень из синус в квадрате 0,5x плюс 2 синус 0,5x плюс 1 минус корень из левая круглая скобка 4 синус 0,5x минус 6 правая круглая скобка в квадрате = минус 2,5 равносильно

равносильно left| синус дробь: числитель: x, знаменатель: 2 конец дроби плюс 1 | минус left|4 синус дробь: числитель: x, знаменатель: 2 конец дроби минус 6|= минус дробь: числитель: 5, знаменатель: 2 конец дроби underset синус альфа плюс 1 больше или равно 0 mathop равносильно
underset синус альфа плюс 1 больше или равно 0 mathop равносильно left|4 синус дробь: числитель: x, знаменатель: 2 конец дроби минус 6|= синус дробь: числитель: x, знаменатель: 2 конец дроби плюс дробь: числитель: 7, знаменатель: 2 конец дроби равносильно

равносильно совокупность выражений 4 синус дробь: числитель: x, знаменатель: 2 конец дроби минус 6= синус дробь: числитель: x, знаменатель: 2 конец дроби плюс дробь: числитель: 7, знаменатель: 2 конец дроби ,4 синус дробь: числитель: x, знаменатель: 2 конец дроби минус 6= минус синус дробь: числитель: x, знаменатель: 2 конец дроби минус дробь: числитель: 7, знаменатель: 2 конец дроби конец совокупности . равносильно
равносильно совокупность выражений 3 синус дробь: числитель: x, знаменатель: 2 конец дроби = дробь: числитель: 19, знаменатель: 2 конец дроби больше 3,5 синус дробь: числитель: x, знаменатель: 2 конец дроби = дробь: числитель: 5, знаменатель: 2 конец дроби конец совокупности . равносильно

равносильно синус дробь: числитель: x, знаменатель: 2 конец дроби = дробь: числитель: 1, знаменатель: 2 конец дроби равносильно совокупность выражений дробь: числитель: x, знаменатель: 2 конец дроби = дробь: числитель: Пи , знаменатель: 6 конец дроби плюс 2 Пи k, дробь: числитель: x, знаменатель: 2 конец дроби = дробь: числитель: 5 Пи , знаменатель: 6 конец дроби плюс 2 Пи k, конец совокупности . k принадлежит Z равносильно
равносильно совокупность выражений x= дробь: числитель: Пи , знаменатель: 3 конец дроби плюс 4 Пи k,x= дробь: числитель: 5 Пи , знаменатель: 3 конец дроби плюс 4 Пи k, конец совокупности . k принадлежит Z .

б)  Отберём корни при помощи единичной окружности.
Подходит дробь: числитель: Пи , знаменатель: 3 конец дроби .

Ответ: а) левая фигурная скобка дробь: числитель: Пи , знаменатель: 3 конец дроби плюс 4 Пи k; дробь: числитель: 5 Пи , знаменатель: 3 конец дроби плюс 4 Пи k:k принадлежит Z правая фигурная скобка ; б)
дробь: числитель: Пи , знаменатель: 3 конец дроби .

15. а)  Решите
уравнение синус x= корень из дробь: числитель: корень из 3 косинус x плюс 2, знаменатель: 2 конец дроби .

б)  Укажите корни этого уравнения, принадлежащие
отрезку левая квадратная скобка минус дробь: числитель: 5 Пи , знаменатель: 4 конец дроби ; минус дробь: числитель: 2 Пи , знаменатель: 3 конец дроби правая квадратная скобка .

Решение. а)  Преобразуем
уравнение:

синус x= корень из дробь: числитель: корень из 3 косинус x плюс 2, знаменатель: 2 конец дроби равносильно система выражений синус в квадрате x= дробь: числитель: корень из 3 косинус x плюс 2, знаменатель: 2 конец дроби , синус xgeqslant0 конец системы . равносильно
равносильно система выражений 1 минус косинус в квадрате x= дробь: числитель: корень из 3 косинус x плюс 2, знаменатель: 2 конец дроби , синус xgeqslant0 конец системы . равносильно

равносильно система выражений 2 косинус в квадрате x плюс корень из 3 косинус x=0, синус xgeqslant0 конец системы . равносильно система выражений совокупность выражений косинус x=0, косинус x= минус дробь: числитель: корень из 3 , знаменатель: 2 конец дроби , конец системы . синус xgeqslant0 конец совокупности . равносильно
равносильно система выражений совокупность выражений x= дробь: числитель: Пи , знаменатель: 2 конец дроби плюс Пи k,x=pm дробь: числитель: 5 Пи , знаменатель: 6 конец дроби плюс 2 Пи k, конец системы .k принадлежит Z , синус xgeqslant0 конец совокупности . равносильно совокупность выражений x= дробь: числитель: Пи , знаменатель: 2 конец дроби плюс 2 Пи k,x= дробь: числитель: 5 Пи , знаменатель: 6 конец дроби плюс 2 Пи k, конец совокупности .k принадлежит Z

https://math-ege.sdamgia.ru/get_file?id=85607&png=1

б)  Отберём корни при помощи единичной окружности.
Подходит минус дробь: числитель: 7 Пи , знаменатель: 6 конец дроби .

Ответ: а) левая фигурная скобка дробь: числитель: Пи , знаменатель: 2 конец дроби плюс 2 Пи k; дробь: числитель: 5 Пи , знаменатель: 6 конец дроби плюс 2 Пи k:k принадлежит Z правая фигурная скобка ; б)
минус дробь: числитель: 7 Пи , знаменатель: 6 конец дроби .

16. а)  Решите
уравнение | косинус x плюс косинус 3x|= минус косинус 2x.

б)  Укажите корни этого уравнения, принадлежащие
отрезку левая квадратная скобка минус Пи ; дробь: числитель: Пи , знаменатель: 2 конец дроби правая квадратная скобка .

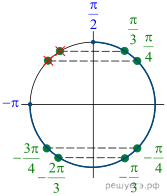
Решение. https://math-ege.sdamgia.ru/get_file?id=64292&png=1а)  Исходное
уравнение имеет смысл только при косинус 2x меньше или равно 0,тогда
это эквивалентно совокупности:

совокупность выражений косинус x плюс косинус 3x = минус косинус 2x, косинус x плюс косинус 3x = косинус 2x конец совокупности . равносильно
равносильно совокупность выражений 2 косинус 2x умножить на косинус x плюс косинус 2x=0,2 косинус 2x умножить на косинус x минус косинус 2x = 0 конец совокупности . равносильно

равносильно совокупность выражений косинус 2x левая круглая скобка 2 косинус x плюс 1 правая круглая скобка =0, косинус 2x левая круглая скобка 2 косинус x минус 1 правая круглая скобка =0 конец совокупности . равносильно
равносильно совокупность выражений косинус 2x=0, косинус x = дробь: числитель: 1, знаменатель: 2 конец дроби , косинус x = минус дробь: числитель: 1, знаменатель: 2 конец дроби конец совокупности . равносильно совокупность выражений x= дробь: числитель: Пи , знаменатель: 4 конец дроби плюс дробь: числитель: Пи k, знаменатель: 2 конец дроби ,x= минус дробь: числитель: Пи , знаменатель: 3 конец дроби плюс Пи k, x= дробь: числитель: Пи , знаменатель: 3 конец дроби плюс Пи k, k принадлежит Z . конец совокупности .

Все найденные серии корней удовлетворяют условию косинус 2x меньше или равно 0.

б)  Отберем корни при помощи единичной окружности
(см. рис.), получим: минус дробь: числитель: 3 Пи , знаменатель: 4 конец дроби , минус дробь: числитель: 2 Пи , знаменатель: 3 конец дроби , минус дробь: числитель: Пи , знаменатель: 3 конец дроби , минус дробь: числитель: Пи , знаменатель: 4 конец дроби , дробь: числитель: Пи , знаменатель: 4 конец дроби и дробь: числитель: Пи , знаменатель: 3 конец дроби .

Ответ: а) левая фигурная скобка дробь: числитель: Пи , знаменатель: 4 конец дроби плюс дробь: числитель: Пи k, знаменатель: 2 конец дроби , минус дробь: числитель: Пи , знаменатель: 3 конец дроби плюс Пи k, дробь: числитель: Пи , знаменатель: 3 конец дроби плюс Пи k: k принадлежит Z правая фигурная скобка ; б)
минус дробь: числитель: 3 Пи , знаменатель: 4 конец дроби , минус дробь: числитель: 2 Пи , знаменатель: 3 конец дроби , минус дробь: числитель: Пи , знаменатель: 3 конец дроби , минус дробь: числитель: Пи , знаменатель: 4 конец дроби , дробь: числитель: Пи , знаменатель: 4 конец дроби и дробь: числитель: Пи , знаменатель: 3 конец дроби .

17. а)  Решите
уравнение корень из 2 тангенс левая круглая скобка дробь: числитель: 3 Пи , знаменатель: 2 конец дроби минус x правая круглая скобка синус левая круглая скобка 3 Пи минус 2x правая круглая скобка = минус тангенс дробь: числитель: 2 Пи , знаменатель: 3 конец дроби .

б)  Укажите корни этого уравнения, принадлежащие
отрезку левая квадратная скобка минус Пи ; минус дробь: числитель: Пи , знаменатель: 3 конец дроби правая квадратная скобка .

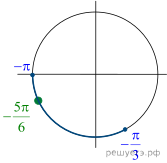
Решение. https://math-ege.sdamgia.ru/get_file?id=86862&png=1а)  Преобразуем
уравнение:

корень из 2 тангенс левая круглая скобка дробь: числитель: 3 Пи , знаменатель: 2 конец дроби минус x правая круглая скобка синус левая круглая скобка 3 Пи минус 2x правая круглая скобка = минус тангенс дробь: числитель: 2 Пи , знаменатель: 3 конец дроби равносильно
равносильно 2ctg x синус 2x=3 равносильно

равносильно система выражений 4 косинус в квадрате x=3, синус x не равно 0 конец системы . равносильно система выражений косинус x=pm дробь: числитель: корень из 3, знаменатель: 2 конец дроби , синус x не равно 0 конец системы . равносильно
равносильно x=pm дробь: числитель: Пи , знаменатель: 6 конец дроби плюс Пи k,k принадлежит Z .

б)  Отберём корни при помощи единичной окружности.
Получим минус дробь: числитель: 5 Пи , знаменатель: 6 конец дроби .

Ответ: а) левая фигурная скобка pm дробь: числитель: Пи , знаменатель: 6 конец дроби плюс Пи k:k принадлежит Z правая фигурная скобка ; б)
минус дробь: числитель: 5 Пи , знаменатель: 6 конец дроби .

18. а)  Решите
уравнение корень из косинус 2x минус синус 5x= минус 2 косинус x.

б)  Укажите корни этого уравнения, принадлежащие
отрезку левая квадратная скобка 2 Пи ; 4 Пи правая квадратная скобка .

Решение. а)  При
условии косинус x меньше или равно 0,исходное
уравнение эквивалентно следующим:

косинус 2x минус синус 5x=4 косинус в квадрате x равносильно косинус 2x минус синус 5x=2 косинус 2x плюс 2 равносильно
равносильно синус 5x плюс косинус 2x= минус 2. qquad левая круглая скобка * правая круглая скобка

Каждое из слагаемых в левой части не меньше −1, поэтому их
сумма равна −2 тогда и только тогда, когда каждое слагаемое равно
−1. Решим уравнение косинус 2x = минус 1,получим 2x = Пи плюс 2 Пи k,то есть x = дробь: числитель: Пи , знаменатель: 2 конец дроби плюс Пи k, k принадлежит Z . Проверим
для найденных решений выполнение условия синус 5x = минус 1.Используем
периодичность синуса, применим формулу приведения, получаем:

синус левая круглая скобка дробь: числитель: 5 Пи , знаменатель: 2 конец дроби плюс 5 Пи k правая круглая скобка = синус левая круглая скобка 2 Пи плюс дробь: числитель: Пи , знаменатель: 2 конец дроби плюс 4 Пи k плюс Пи k правая круглая скобка =
= синус левая круглая скобка дробь: числитель: Пи , знаменатель: 2 конец дроби плюс Пи k правая круглая скобка = косинус Пи k.

Выражение косинус Пи kравно −1 для
всех нечетных k и только для них. Следовательно, решениями уравнения
(⁎) являются числа дробь: числитель: Пи , знаменатель: 2 конец дроби плюс Пи k,где k  —
любое нечетное число. Эти числа удовлетворяют условию косинус x меньше или равно 0,поскольку обращают косинус в нуль. Тем
самым все они являются корнями исходного уравнения.

б)  Решим двойное неравенство:

2 Пи меньше или равно дробь: числитель: Пи , знаменатель: 2 конец дроби плюс Пи k меньше или равно 4 Пи равносильно 2 меньше или равно дробь: числитель: 1, знаменатель: 2 конец дроби плюс k меньше или равно 4 равносильно
равносильно целая часть: 1, дробная часть: числитель: 1, знаменатель: 2 меньше или равно k меньше или равно целая часть: 3, дробная часть: числитель: 1, знаменатель: 2 underset k принадлежит Z mathop равносильно совокупность выражений k=2,k=3. конец совокупности .

Следовательно, k = 3 и подходит корень дробь: числитель: 7 Пи , знаменатель: 2 конец дроби

 Ответ: а) левая фигурная скобка дробь: числитель: Пи , знаменатель: 2 конец дроби плюс Пи k : k минус нечётное число правая фигурная скобка ; б)
дробь: числитель: 7 Пи , знаменатель: 2 конец дроби .

 Примечание.Ответ к пункту а) можно записать в виде левая фигурная скобка дробь: числитель: Пи , знаменатель: 2 конец дроби плюс Пи левая круглая скобка 2n плюс 1 правая круглая скобка : n принадлежит Z правая фигурная скобка .

19. а)  Решите
уравнение косинус x плюс корень из дробь: числитель: 2 минус корень из 2, знаменатель: 2 конец дроби умножить на левая круглая скобка синус x плюс 1 правая круглая скобка =0.

б)  Найдите все корни уравнения, принадлежащие отрезку
левая квадратная скобка минус дробь: числитель: 11 Пи , знаменатель: 2 конец дроби ; минус 4 Пи правая квадратная скобка .

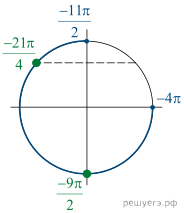
Решение. https://math-ege.sdamgia.ru/get_file?id=117181&png=1а) Заметим, что
уравнение может иметь решения только при косинус x меньше или равно 0.Преобразуем его при этом условии:

косинус x плюс корень из дробь: числитель: 2 минус корень из 2, знаменатель: 2 конец дроби умножить на левая круглая скобка синус x плюс 1 правая круглая скобка =0 равносильно
равносильно корень из дробь: числитель: 2 минус корень из 2, знаменатель: 2 конец дроби умножить на левая круглая скобка синус x плюс 1 правая круглая скобка = минус косинус x undersetmathclap косинус x меньше или равно 0 равносильно дробь: числитель: 2 минус корень из 2, знаменатель: 2 конец дроби умножить на левая круглая скобка синус x плюс 1 правая круглая скобка = косинус в квадрате x равносильно равносильно синус в квадрате x плюс дробь: числитель: 2 минус корень из 2, знаменатель: 2 конец дроби умножить на синус x минус дробь: числитель: корень из 2, знаменатель: 2 конец дроби =0 равносильно
равносильно синус x левая круглая скобка синус x минус дробь: числитель: корень из 2, знаменатель: 2 конец дроби правая круглая скобка плюс синус x минус дробь: числитель: корень из 2, знаменатель: 2 конец дроби =0 равносильно равносильно левая круглая скобка синус x минус дробь: числитель: корень из 2, знаменатель: 2 конец дроби правая круглая скобка левая круглая скобка синус x плюс 1 правая круглая скобка =0 равносильно
равносильно совокупность выражений синус x= минус 1, синус x= дробь: числитель: корень из 2}2 конец совокупности . undersetmathclap{ косинус x меньше или равно 0, знаменатель: равносильно конец дроби совокупность выражений x= минус дробь: числитель: Пи , знаменатель: 2 конец дроби плюс 2 Пи k,x= дробь: числитель: 3 Пи , знаменатель: 4 конец дроби плюс 2 Пи k , конец совокупности . k принадлежит Z .

б)  Отберём корни, принадлежащие отрезку левая квадратная скобка минус дробь: числитель: 11 Пи , знаменатель: 2 конец дроби ; минус 4 Пи правая квадратная скобка , при
помощи тригонометрической окружности. Подходят минус дробь: числитель: 21 Пи , знаменатель: 4 конец дроби , минус дробь: числитель: 9 Пи , знаменатель: 2 конец дроби .

Ответ: а) левая фигурная скобка минус дробь: числитель: Пи , знаменатель: 2 конец дроби плюс 2 Пи k, дробь: числитель: 3 Пи , знаменатель: 4 конец дроби плюс 2 Пи k : k принадлежит Z правая фигурная скобка ; б)
минус дробь: числитель: 21 Пи , знаменатель: 4 конец дроби , минус дробь: числитель: 9 Пи , знаменатель: 2 конец дроби .

20. а)  Решите
уравнение дробь: числитель: 6 синус x минус 2 косинус 2 x минус 4 косинус в квадрате x минус 3, знаменатель: корень из 7 синус x минус 3 косинус x конец дроби =0.

б)  Найдите все корни уравнения, принадлежащие отрезку
левая квадратная скобка минус 4 Пи ; минус 3 Пи правая квадратная скобка .

Решение. а)  Знаменатель
дроби должен быть отличен от нуля, то есть

корень из 7 синус x минус 3 косинус xnot=0 равносильно тангенс x not= дробь: числитель: 3, знаменатель: корень из 7 конец дроби .

При этом условии числитель дроби должен быть равен нулю. Применим
формулы косинус в квадрате x = 1 минус синус в квадрате x и косинус 2x = 1 минус 2 синус в квадрате x,получим:

6 синус x минус 2 косинус 2 x минус 4 косинус в квадрате x минус 3=0 равносильно
равносильно 6 синус x минус 2 левая круглая скобка 1 минус 2 синус в квадрате x правая круглая скобка минус 4 левая круглая скобка 1 минус синус в квадрате x правая круглая скобка минус 3 = 0 равносильно
равносильно 8 синус в квадрате x плюс 6 синус x минус 9=0 равносильно
равносильно совокупность выражений синус x= дробь: числитель: 3, знаменатель: 4 конец дроби , синус x= минус дробь: числитель: 3, знаменатель: 2 конец дроби конец совокупности . underset синус x больше или равно минус 1 mathop равносильно синус x= дробь: числитель: 3, знаменатель: 4 конец дроби .

Если синус x= дробь: числитель: 3, знаменатель: 4 конец дроби и угол х
лежит в первой четверти, то 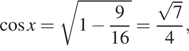косинус x = корень из 1 минус дробь: числитель: 9, знаменатель: 16 конец дроби = дробь: числитель: корень из 7 , знаменатель: 4 конец дроби , а
тогда тангенс x = дробь: числитель: 3, знаменатель: корень из 7 конец дроби , что
обращает знаменатель в нуль. Если же синус x= дробь: числитель: 3, знаменатель: 4 конец дроби и угол х
лежит во второй четверти, то 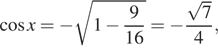косинус x = минус корень из 1 минус дробь: числитель: 9, знаменатель: 16 конец дроби = минус дробь: числитель: корень из 7 , знаменатель: 4 конец дроби , а
тогда тангенс x = минус дробь: числитель: 3, знаменатель: корень из 7 конец дроби , что
допустимо. Следовательно, решением уравнения является серия x= Пи минус арксинус дробь: числитель: 3, знаменатель: 4 конец дроби плюс 2 Пи k,k принадлежит Z .

б)  Отберем корни, решая двойное неравенство:

минус 4 Пи меньше Пи минус арксинус дробь: числитель: 3, знаменатель: 4 конец дроби плюс 2 Пи k меньше минус 3 Пи равносильно
равносильно минус 5 Пи плюс арксинус дробь: числитель: 3, знаменатель: 4 конец дроби меньше 2 Пи k меньше минус 4 Пи плюс арксинус дробь: числитель: 3, знаменатель: 4 конец дроби .

Акрсинус положительного числа лежит в интервале левая круглая скобка 0; дробь: числитель: знаменатель: p конец дроби i2 правая круглая скобка ,поэтому
левая часть двойного неравенства больше  –5π, а
правая  — меньше –4,5π. Следовательно, число 2πk
лежит в интервале (–5π; –4,5π), а значит, k= минус 2.Найденному значению параметра соответствует корень минус 3 Пи минус арксинус дробь: числитель: 3, знаменатель: 4 конец дроби .

Ответ: а) левая фигурная скобка Пи минус арксинус дробь: числитель: 3, знаменатель: 4 конец дроби плюс 2 Пи k : k принадлежит Z правая фигурная скобка ; б)
минус 3 Пи минус арксинус дробь: числитель: 3, знаменатель: 4 конец дроби .

                                    
Решить
самостоятельно.

1. а)  Решите уравнение левая круглая скобка 2x в квадрате минус 5x минус 12 правая круглая скобка левая круглая скобка 2 косинус x плюс 1 правая круглая скобка =0.

б)  Найдите все корни этого уравнения, принадлежащие
промежутку левая квадратная скобка минус дробь: числитель: Пи , знаменатель: 2 конец дроби ; Пи правая квадратная скобка .

2. а)  Решите уравнение корень из синус в квадрате x плюс 3 синус x минус дробь: числитель: 17, знаменатель: 9 конец дроби = минус косинус x.

б)  Укажите корни этого уравнения, принадлежащие
отрезку левая квадратная скобка минус дробь: числитель: 3 Пи , знаменатель: 2 конец дроби ; Пи правая квадратная скобка .

3. а)  Решите уравнение 2 синус 2x минус синус x умножить на корень из 2ctg x=1.

б)  Укажите корни этого уравнения, принадлежащие
отрезку левая квадратная скобка 0; Пи правая квадратная скобка .

4. а)  Решите уравнение корень из ctg x левая круглая скобка синус в квадрате x минус дробь: числитель: 1, знаменатель: 4 конец дроби правая круглая скобка =0.

б)  Укажите корни этого уравнения, принадлежащие
отрезку левая квадратная скобка минус дробь: числитель: 3 Пи , знаменатель: 2 конец дроби ; 0 правая квадратная скобка .

5. а)  Решите уравнение левая круглая скобка 2 минус 3x минус 2x в квадрате правая круглая скобка левая круглая скобка 2 синус x минус корень из 3 правая круглая скобка =0.

б)  Найдите все корни этого уравнения, принадлежащие
промежутку левая квадратная скобка минус Пи ; дробь: числитель: Пи , знаменатель: 2 конец дроби правая квадратная скобка .

6. а)  Решите уравнение левая круглая скобка тангенс в квадрате x минус 3 правая круглая скобка корень из 18 косинус x=0.

б)  Найдите все корни этого уравнения, принадлежащие
отрезку левая квадратная скобка 4 Пи ; дробь: числитель: 11 Пи , знаменатель: 2 конец дроби правая квадратная скобка .

7. а)  Решите уравнение корень из синус x минус косинус x умножить на левая круглая скобка косинус x плюс косинус 2x правая круглая скобка =0.

б)  Укажите корни этого уравнения, принадлежащие
отрезку левая квадратная скобка минус дробь: числитель: Пи , знаменатель: 2 конец дроби ; дробь: числитель: Пи , знаменатель: 2 конец дроби правая квадратная скобка .

8. а)  Решите уравнение корень из 4 косинус 2x минус 2 синус 2x=2 косинус x.

б)  Укажите корни этого уравнения, принадлежащие
отрезку левая квадратная скобка минус дробь: числитель: 5 Пи , знаменатель: 2 конец дроби ; 0 правая квадратная скобка .

                                              
Ответы.

1. а) левая фигурная скобка 4; минус дробь: числитель: 3, знаменатель: 2 конец дроби ; дробь: числитель: 2 Пи , знаменатель: 3 конец дроби плюс 2 Пи k; минус дробь: числитель: 2 Пи , знаменатель: 3 конец дроби плюс 2 Пи k: k принадлежит Z правая фигурная скобка ; б)
минус дробь: числитель: 3, знаменатель: 2 конец дроби , дробь: числитель: 2 Пи , знаменатель: 3 конец дроби .     (№17)

2. : а) левая фигурная скобка Пи минус арксинус дробь: числитель: 2, знаменатель: 3 конец дроби плюс 2 Пи k : k принадлежит Z правая фигурная скобка ; б)
минус Пи минус арксинус дробь: числитель: 2, знаменатель: 3 конец дроби , Пи минус арксинус дробь: числитель: 2, знаменатель: 3 конец дроби .     (№40)

3. : а) левая фигурная скобка дробь: числитель: Пи , знаменатель: 4 конец дроби плюс 2 Пи k; Пи плюс дробь: числитель: 1, знаменатель: 2 конец дроби арксинус дробь: числитель: 1, знаменатель: 4 конец дроби плюс 2 Пи k; дробь: числитель: 3 Пи , знаменатель: 2 конец дроби минус дробь: числитель: 1, знаменатель: 2 конец дроби арксинус дробь: числитель: 1, знаменатель: 4 конец дроби плюс 2 Пи k : k принадлежит Z правая фигурная скобка ; б)
дробь: числитель: Пи , знаменатель: 4 конец дроби .   (№31)

4. : а) левая фигурная скобка дробь: числитель: Пи , знаменатель: 2 конец дроби плюс Пи k; дробь: числитель: Пи , знаменатель: 6 конец дроби плюс Пи k: k принадлежит Z правая фигурная скобка ; б)
минус дробь: числитель: 3 Пи , знаменатель: 2 конец дроби , минус дробь: числитель: 5 Пи , знаменатель: 6 конец дроби , минус дробь: числитель: Пи , знаменатель: 2 конец дроби .    (№47)

5. : а) левая фигурная скобка минус 2; дробь: числитель: 1, знаменатель: 2 конец дроби ; дробь: числитель: Пи , знаменатель: 3 конец дроби плюс 2 Пи n; дробь: числитель: 2 Пи , знаменатель: 3 конец дроби плюс 2 Пи n :n принадлежит Z правая фигурная скобка ; б)
минус 2 , дробь: числитель: 1, знаменатель: 2 конец дроби , дробь: числитель: Пи , знаменатель: 3 конец дроби .   (№55)

6. а) левая фигурная скобка дробь: числитель: Пи , знаменатель: 3 конец дроби плюс 2 Пи k; минус дробь: числитель: Пи , знаменатель: 3 конец дроби плюс 2 Пи k:k принадлежит Z правая фигурная скобка ; б)
дробь: числитель: 13 Пи , знаменатель: 3 конец дроби .    (№67)

7. а) левая фигурная скобка дробь: числитель: Пи , знаменатель: 4 конец дроби плюс Пи k; дробь: числитель: Пи , знаменатель: 3 конец дроби плюс 2 Пи k; Пи плюс 2 Пи k:k принадлежит Z правая фигурная скобка ; б)
дробь: числитель: Пи , знаменатель: 4 конец дроби , дробь: числитель: Пи , знаменатель: 3 конец дроби .    (№68)

8. : а) левая фигурная скобка 2 Пи k; минус дробь: числитель: Пи , знаменатель: 4 конец дроби плюс 2 Пи k:k принадлежит Z правая фигурная скобка ; б)
минус дробь: числитель: 9 Пи , знаменатель: 4 конец дроби , минус 2 Пи , минус дробь: числитель: Пи , знаменатель: 4 конец дроби , 0.    (№71)

Уравнения из материалов ЕГЭ профильного уровня смешанного тип

Уравнения из материалов ЕГЭ профильного уровня смешанного тип

Отберем корни при помощи единичной окружности

Отберем корни при помощи единичной окружности

В случае имеем: Условию удовлетворяет серия

В случае имеем: Условию удовлетворяет серия

Укажите корни этого уравнения, принадлежащие отрезку

Укажите корни этого уравнения, принадлежащие отрезку

Укажите корни этого уравнения принадлежащие отрезку

Укажите корни этого уравнения принадлежащие отрезку

Отберём корни. принадлежащие отрезку

Отберём корни. принадлежащие отрезку

Решение. а) При условии исходное уравнение равносильно следующим:

Решение. а) При условии исходное уравнение равносильно следующим:

Решим неравенство: Неравенству удовлетворяют только корни серии

Решим неравенство: Неравенству удовлетворяют только корни серии

Пусть тогда имеем:

Пусть тогда имеем:

Ответ: а) б) 10. а)

Ответ: а) б) 10. а)

Полученный корень удовлетворяет исходному ограничению

Полученный корень удовлетворяет исходному ограничению

Отберём корни при помощи единичной окружности

Отберём корни при помощи единичной окружности

Решите уравнение б) Укажите корни этого уравнения, принадлежащие отрезку

Решите уравнение б) Укажите корни этого уравнения, принадлежащие отрезку

Решите уравнение б) Укажите корни этого уравнения, принадлежащие отрезку

Решите уравнение б) Укажите корни этого уравнения, принадлежащие отрезку

Решение. а) Исходное уравнение имеет смысл только при тогда это эквивалентно совокупности:

Решение. а) Исходное уравнение имеет смысл только при тогда это эквивалентно совокупности:

Отберём корни при помощи единичной окружности

Отберём корни при помощи единичной окружности

Решите уравнение б) Найдите все корни уравнения, принадлежащие отрезку

Решите уравнение б) Найдите все корни уравнения, принадлежащие отрезку

При этом условии числитель дроби должен быть равен нулю

При этом условии числитель дроби должен быть равен нулю

Решить самостоятельно. 1. а)

Решить самостоятельно. 1. а)

Ответы. 1. а) б) (№17) 2

Ответы. 1. а) б) (№17) 2

Источник

Задание 907

Дано уравнение $$sqrt{1-sin ^{2}x}=sin x$$.

a) Решите уравнение.

б) Найдите корни этого уравнения, принадлежащие отрезку $$left [frac{5pi}{2};4pi right ]$$

Ответ: А) $$frac{pi}{4}+2pi n;frac{3pi}{4}+2pi m,n,min Z$$ Б) $$frac{11pi}{4}$$

Скрыть

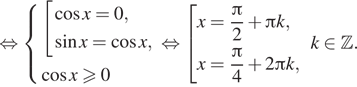
$$ sqrt{1-sin ^{2}x}=sin x Leftrightarrow left{begin{matrix}sqrt{1-sin ^{2}x}geq 0\ sin xgeq 0\ 1-sin ^{2}x=sin ^{2} xend{matrix}right.$$ $$Leftrightarrow left{begin{matrix} 1-sin ^{2}xgeq 0\ sin xgeq 0\ 1-sin ^{2}x=sin ^{2} xend{matrix}right.$$ $$Leftrightarrow left{begin{matrix}sin ^2 xleq 1\ sin xgeq 0\ 1=2sin ^{2} xend{matrix}right.$$ $$Leftrightarrow left{begin{matrix}sin ^{2}xleq 1\ sin xgeq 0\ sin x = pm frac{sqrt{2}}{2}end{matrix}right.$$ $$Leftrightarrow sin x = frac{sqrt{2}}{2}$$ $$Leftrightarrow left{begin{matrix} x=frac{pi}{4}+2pi n , nin Z\ x=frac{3pi}{4}+2pi n nin Zend{matrix}right.$$

Задание 3248

Дано уравнение $$log_{2}sin xcdotlog_{sin x}cos^{2}x=-1$$ .
А) Решите уравнение.
Б) Укажите корни этого уравнения, принадлежащие отрезку

Ответ: а) $$frac{pi}{4}+2pi n$$; $$frac{3pi}{4}+2pi n$$; б) $$frac{17pi}{4}$$; $$frac{19pi}{4}$$

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Скрыть

$$log_{2}sin xcdotlog_{sin x}cos^{2}x=-1$$ $$left{begin{matrix}sin x>0\cos^{2}x>0\sin xneq1end{matrix}right.$$ $$left{begin{matrix}xin(2pi n;pi+2pi n)\xneqfrac{pi}{2}+pi nend{matrix}right.$$ $$frac{1}{log_{sin x}2}cdotlog_{sin x}cos^{2}x=-1$$ $$frac{log_{sin x}cos^{2}x}{log_{sin x}2}=-1$$ $$log_{2}cos^{2}x=-1$$ $$cos^{2}x=frac{1}{2}$$ $$left{begin{matrix}cos x=frac{sqrt{2}}{2}\cos x=-frac{sqrt{2}}{2}end{matrix}right.$$ $$left{begin{matrix}x=pmfrac{pi}{4}+2pi n\x=pmfrac{3pi}{4}+2pi nend{matrix}right.$$ $$nin Z$$ С учетом ОДЗ: $$x_{1}=frac{pi}{4}+2pi n$$ $$x_{2}=frac{3pi}{4}+2pi n$$ б) $$4pi+frac{pi}{4}=frac{17pi}{4}$$ $$5pi-frac{pi}{4}=frac{19pi}{4}$$

Задание 4068

а)Решите уравнение $$5^{2sin 2x}=(frac{1}{25})^{cos (frac{3pi}{2}+x)}$$
б)Найдите все корни этого уравнения, принадлежащие отрезку $$[frac{3pi}{2};3pi]$$

Ответ:

Задание 4082

Решите систему уравнений
$$left{begin{matrix} 16^{cos x}-10*4^{cos x}+16=0\ sqrt{y}+2cos x=0 end{matrix}right.$$

Ответ:

Задание 4083

Решите систему уравнений
$$left{begin{matrix} y^{2}=x\ sin y^{2}=cos x end{matrix}right.$$

Ответ:

Задание 4084

Решите систему уравнений
$$left{begin{matrix} 2cos 2x +3sin x = 1\ y^{2}cos x + ycos x + frac{sqrt{15}}{2}=0 end{matrix}right.$$

Ответ:

Задание 4085

Решите уравнение $$(sin x — frac{sqrt{3}}{2})sqrt{3x^{2}-7x+4}=0$$

Ответ:

Задание 4086

а) Решите уравнение $$ (frac{4}{9})^{cos x}+2*(frac{2}{3})^{cos x}-3=0$$
б) Найдите все корни этого уравнения, принадлежащие отрезку $$[frac{5pi}{2};4pi]$$

Ответ:

Задание 4087

а) Решите уравнение $$12^{sin x}=4^{sin x}*3^{-sqrt{3}cos x}$$
б) Найдите все корни этого уравнения, принадлежащие отрезку $$[frac{5pi}{2};4pi]$$

Ответ:

Задание 4088

а) Решите уравнение $$(25^{cos x})^{sin x}=5^{cos x}$$
б) Найдите все корни этого уравнения, принадлежащие отрезку $$[-frac{5pi}{2};-pi]$$

Ответ:

Задание 4089

а) Решите уравнение $$4^{sin x} + 4^{-sin x}=frac{5}{2}$$
б) Укажите корни этого уравнения, принадлежащие отрезку $$[frac{5pi}{2};4pi]$$

Ответ:

Задание 4090

а) Решите уравнение $$(frac{2}{5})^{cos x} + (frac{5}{2})^{cos x}=2$$
б) Укажите корни этого уравнения, принадлежащие отрезку $$[2pi;frac{7pi}{2}]$$

Ответ:

Задание 4091

а) Решите уравнение $$5^{2sin 2x}=(frac{1}{25})^{cos (frac{3pi}{2}+x)}$$
б) Найдите все корни этого уравнения, принадлежащие отрезку $$[frac{3pi}{2};3pi]$$

Ответ:

Задание 4116

а) Решите уравнение $$log_2 (cos x + sin 2x +8) =3$$
б) Найдите все корни этого уравнения, принадлежащие отрезку $$[frac{3pi}{2};3pi]$$

Ответ:

Задание 4117

а) Решите уравнение $$2log_{2} ^{2} (2cos x) — 9log_{2} (2cos x) +4 =0$$
б) Найдите корни этого уравнения, принадлежащие отрезку $$[-2pi;-frac{pi}{2}]$$

Ответ:

Источник

Уравнения смешанного типа

Смешанные уравнения – это уравнения, в которых переменная находится в функциях разных типов.

Решение смешанного уравнения

Каждое такое уравнение решается очень индивидуально. Общего метода решения – нет. В некоторых уравнениях нужно умело использовать формулы. В других помогут графики функций.

Пример. Решить уравнение (log_2⁡x=-x+1).
Решение: Здесь никакие преобразования не помогут найти корень . Это отличительный признак уравнений, решающихся графически.
Представим левую и правую части уравнения как функции: (f(x)=log_2⁡x) и (g(x)=-x+1). Уравнения требует, чтоб они были равны – значит, графики этих функций должны пересекаться, а точка пересечения и будет корнем уравнения.
Построим графики функций и найдем точки пересечений.

Единственная точка пересечения — ((1;0)). Значит, корнем уравнения будет значение (x=1). Проверим это подстановкой:

Конечно, некоторые из вас сразу нашли этот корень простым подбором, но это не будет полноценным решением. Почему? Потому что вы не можете быть уверены, что других корней нет, а график функций снимает этот вопрос — он четко показывает: корень здесь только один.

Это показательно — тригонометрическое уравнение.
Обратим внимание, что (15) можно представить как (3cdot 5). Вряд ли это простое совпадение. Используя свойства степеней разложим (15) на множители.

Перенесем выражение из правой части в левую.

В какую степень надо возвести тройку, чтоб она стала нулем? Ни в какую, положительное число в любой степени останется положительным числом. Поэтому у первого уравнения нет решения.
Во втором уравнении перенесем (5^<sin⁡x>) вправо.

Имеем показательное уравнение . Решаем его как обычно — «убираем» основания степеней.

Делим уравнение на (sin⁡x). Это можно сделать т.к. (sin⁡x=0) не будет решением уравнения. Значит синус икс – не ноль, и поэтому на него можно делить.

Конспект по математике 11 класс «Смешанные тригонометрические уравнения»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику


Тип урока: Урок обобщения и систематизации.

-исследовательский – решение познавательных обобщающих задач;

Цель урока: Обобщить и систематизировать знания по теме «Тригонометрические уравнения», решение смешанных тригонометрических уравнений, продолжить работу по подготовке к ЕГЭ.

● Устная работа (разминка)

● Самостоятельная работа (повторение)

● Проверка вариантов ЕГЭ (домашняя работа)

● Демонстрация решённых самостоятельно смешанных тригонометрических уравнений

● Самостоятельное решение смешанных уравнений.

● Индивидуально — консультационная работа.

Крылатые выражения (девиз урока)

Сегодня на уроке мы продолжим работу над обобщением и систематизацией полученные знания по теме «Тригонометрические уравнения». На этом занятии мы будем решать смешанные тригонометрические уравнения, и тем самым – продолжаем подготовку к ЕГЭ. Работаем по следующему плану:

Устная работа. Диктант «Верно — неверно»

● Самостоятельная работа (повторение)

Для каждого варианта — задания на слайде, продолжите каждую запись. Время выполнения 3 минуты.

Критерий оценки: «5» — все 9 «+», «4» — 8 «+», «3» — 6-7 «+»

● Проверка вариантов ЕГЭ (домашняя работа).

● Демонстрация решённых самостоятельно смешанных тригонометрических уравнений. Отсканированные работы на слайдах. Ход решения кратко рассказывают ученики.

№ 511105. а) Решите уравнение

б) Найдите все корни этого уравнения, принадлежащие отрезку

а) Преобразуем уравнение:

б) С помощью единичной окружности отберём корни на отрезке

Получаем:

Ответ: а) б)

№ 501689. а) Решите уравнение

б) Найдите все корни этого уравнения, принадлежащие отрезку

а) Преобразуем исходное уравнение:

б) С помощью числовой окружности отберем корни, принадлежащие отрезку Получим числа:

Ответ : а) б)

№ 502313. а) Решите уравнение

б) Найдите все корни этого уравнения, принадлежащие отрезку

а) Запишем исходное уравнение в виде:

Значит, либо откуда либо откуда или

б) С помощью числовой окружности отберём корни, принадлежащие отрезку Получим числа:

Ответ : а) б)

№ 505565. а) Решите уравнение

б) Укажите корни этого уравнения, принадлежащие отрезку

Заметим, что: Далее имеем:

Заданному промежутку принадлежат числа

Ответ: а) б)

а) Решите уравнение

б) Найдите все корни этого уравнения, принадлежащие отрезку

а) Последовательно получаем:

б) Условию удовлетворяет только числа

Ответ: а) ; б)

● Самостоятельное решение смешанных уравнений.

log 5 ( cos x − sin 2 x + 25) = 2

Перепишем Все уравнение с учетом этого факта:

Перед нами каноническое логарифмическое уравнение . В нем мы можем смело убрать знаки логарифма (т.е. просто приравнять аргументы логарифмов). Получим:

cos x − sin 2 x + 25 = 25

Перед нами тригонометрическое уравнение. Переносим 25 влево и получаем:

cos x − sin 2 x = 0

Формула синуса двойного угла

В данном случае все очень легко. Вспоминаем формулу синуса двойного угла:

sin 2 x = 2sin x · cos x

Подставляем это выражение в наше уравнение:

cos x − 2sin x · cos x = 0

Мы видим, что и в первом, и во втором слагаемом есть cos x . Выносим его за скобку:

cos x (1- 2sin x ) = 0

Произведение равно нулю, когда хотя бы один из множителей равен нулю:

либо cos x = 0, либо 1 − 2sin x = 0

Перед нами совокупность из двух простейших тригонометрических уравнений:

cos x = 0; 1 — 2sin x = 0.

Вспоминаем, что cos x = 0 — это частный случай, поэтому x = π/2 + π n , n ∈ Z .

2). ( 2sinx — )∙ log 3 (tgx) = 0.

Решение: ( 2sinx — )∙ log 3 (tgx) = 0, ОДЗ: tgx > 0

2sinx — = 0 или log 3 (tgx) = 0

sinx = tgx = 1

х =

Заметим, что x= не удовлетворяет ОДЗ

Ответ: ; .

● Индивидуально — консультационная работа. Ученики могут начинать решение с любого уравнения при необходимости за советом или помощью обращаются к одноклассникам или ко мне.

№ 484551. Решите уравнение

Уравнение равносильно системе

Из неравенства получаем, что . В уравнении сделаем замену и решим уравнение или Равенствам и на тригонометрической окружности соответствует четыре точки. Две из них, находящиеся в верхней полуплоскости, не удовлетворяют условию

Получаем решения:

Ответ:

№ 484552. Решите уравнение

Уравнение равносильно системе

Тогда или . Последнее уравнение не имеет решений, а из первого, учитывая, что , получаем: .

Ответ: .

№ 507620. Решите уравнение:

Уравнение равносильно системе:

Уравнение решений не имеет. Учитывая, что получаем:

Ответ:

№ 507633. Решите уравнение

Левая часть уравнения имеет смысл при Приравняем числитель к нулю:

Учитывая условие получаем, что числа не являются решениями данного уравнения. Учитывая условие получаем, что числа не являются решениями данного уравнения.

Ответ:

№ 507656. Решите уравнение

Перейдём к системе:

Решим первое уравнение:

Учитывая, что получаем:

Ответ:

№ 507659. Решите уравнение

Найдем нули числителя:

Учитывая, что получаем:

Ответ:

Тригонометрические уравнения смешанного типа определение

Методы решения тригонометрических уравнений.

1. Алгебраический метод.

( метод замены переменной и подстановки ).

2. Разложение на множители.

П р и м е р 1. Решить уравнение: sin x + cos x = 1 .

Р е ш е н и е . Перенесём все члены уравнения влево:

sin x + cos x – 1 = 0 ,

преобразуем и разложим на множители выражение в

левой части уравнения:

П р и м е р 2. Решить уравнение: cos 2 x + sin x · cos x = 1.

Р е ш е н и е . cos 2 x + sin x · cos x – sin 2 x – cos 2 x = 0 ,

sin x · cos x – sin 2 x = 0 ,

sin x · ( cos x – sin x ) = 0 ,

П р и м е р 3. Решить уравнение: cos 2 x – cos 8 x + cos 6 x = 1.

Р е ш е н и е . cos 2 x + cos 6 x = 1 + cos 8 x ,

2 cos 4x cos 2x = 2 cos ² 4x ,

cos 4x · ( cos 2x – cos 4x ) = 0 ,

cos 4x · 2 sin 3x · sin x = 0 ,

1). cos 4x = 0 , 2). sin 3x = 0 , 3). sin x = 0 ,

3. Приведение к однородному уравнению.

а) перенести все его члены в левую часть;

б) вынести все общие множители за скобки;

в) приравнять все множители и скобки нулю;

г ) скобки, приравненные нулю, дают однородное уравнение меньшей степени, которое следует разделить на

cos ( или sin ) в старшей степени;

д) решить полученное алгебраическое уравнение относительно tan .

П р и м е р . Решить уравнение: 3 sin 2 x + 4 sin x · cos x + 5 cos 2 x = 2.

Р е ш е н и е . 3sin 2 x + 4 sin x · cos x + 5 cos 2 x = 2sin 2 x + 2cos 2 x ,

sin 2 x + 4 sin x · cos x + 3 cos 2 x = 0 ,

tan 2 x + 4 tan x + 3 = 0 , отсюда y 2 + 4y +3 = 0 ,

корни этого уравнения: y 1 = — 1, y 2 = — 3, отсюда

1) tan x = –1, 2) tan x = –3,

4. Переход к половинному углу.

П р и м е р . Решить уравнение: 3 sin x – 5 cos x = 7.

Р е ш е н и е . 6 sin ( x / 2 ) · cos ( x / 2 ) – 5 cos ² ( x / 2 ) + 5 sin ² ( x / 2 ) =

= 7 sin ² ( x / 2 ) + 7 cos ² ( x / 2 ) ,

2 sin ² ( x / 2 ) – 6 sin ( x / 2 ) · cos ( x / 2 ) + 12 cos ² ( x / 2 ) = 0 ,

tan ² ( x / 2 ) – 3 tan ( x / 2 ) + 6 = 0 ,

5. Введение вспомогательного угла.

где a , b , c – коэффициенты; x – неизвестное.

Теперь коэффициенты уравнения обладают свойствами синуса и косинуса , а именно : модуль ( абсолютное значение ) каждого из них не больше 1, а сумма их квадратов равна 1 . Тогда можно обозначить их соответственно как cos и sin ( здесь — так называемый вспомогательный угол ), и наше уравнение прини мает вид:

6. Преобразование произведения в сумму.

П р и м е р . Решить уравнение: 2 sin x · sin 3 x = cos 4 x .

Р е ш е н и е . Преобразуем левую часть в сумму:

источники:

http://infourok.ru/konspekt-po-matematike-klass-smeshannie-trigonometricheskie-uravneniya-1448867.html

http://www.sites.google.com/site/trigonometriavneskoly/metody-resenia-trigonometriceskih-uravnenij

Источник

Понравилась статья? Поделить с друзьями:
  • Смешанные неравенства егэ профиль
  • Смешанные неравенства 15 задание егэ
  • Смешанная экономика это егэ
  • Смешанная форма республики егэ
  • Смешанная рыночная экономика егэ