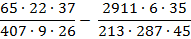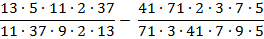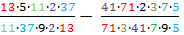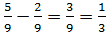Дроби появились в глубокой древности, когда древний человек решил разделить добычу с себе подобным. При разделе добычи, при измерениях величин, да и в других похожих случаях люди столкнулись с необходимостью делить что-то на равные части, т. е. наряду с необходимостью считать предметы у людей с древних времён появилась потребность измерять длину, площадь, объём, время и другие величины. Результат измерений не всегда удавалось выразить натуральным числом, приходилось учитывать и части употребляемой меры. Так возникли дроби. Так русское слово дробь, как и его аналоги в других языках, происходят от латинского слова fractura, которое, в свою очередь, является переводом арабского с тем же значением: ломать, раздроблять. Первой дробью, с которой познакомились люди, была половина. Следующей дробью была треть. В древности у разных народов использовались разные дроби и разные записи дробей.
Оцени ответ
ДРОБИ В НАШЕЙ ЖИЗНИ
- Авторы
- Руководители
- Файлы работы
- Наградные документы
Гугунава Г.Г. 1
1Гимназия»Жуковка»
Дунаева С.С. 1
1Гимназия»Жуковка»
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
Введение
В свободное от учебы время я занимаюсь музыкой. Играю на трубе. При изучении нотной грамоты я столкнулся с понятиями доли и дроби. 6/8 – это три четверти и что в одной половине 8/16. Разучивая новую пьесу, я вслух отсчитываю каждую ноту в такте «раз, и два, и…». Я даже и не подозревал раньше, что считал обыкновенные дроби.
Мы часто отвечаем на вопрос «который час?» дробями. «Без четверти десять» без пятнадцати минут десять; «Сейчас три часа без четверти» -2 час 45 минут; «Четверть второго» -1 час 15 минут.
Меня заинтересовало, а где еще в нашей повседневной жизни мы еще сталкиваемся с понятием дроби.
Тема моей проектно-исследовательской работы «Дроби в нашей жизни»
Объектом исследования являются дроби. Предмет исследования – использование дробей в нашей повседневной жизни.
Цель: выяснить историю происхождения дробей, их применение в различных областях жизни и деятельности человека. Найти и решить интересные старинные задачи на дроби
Задачи исследования:
Изучить литературу, связанную с историей возникновения дробей
Исследовать, где в нашей жизни встречаются дроби;
Провести опрос, определяющий степень значимости дробей в нашей повседневной жизни;
Собрать и решить интересные задачи по теме дроби.
Для решения поставленных задач использовались следующие методы исследования:
теоретические (анализ литературы по данной теме);
общенаучные (личные наблюдения, опросы);
статистические (обработка результатов опроса).
Гипотеза: дроби проникли во все сферы нашей повседневной жизни
Глава 1. История возникновения дробей.
Наряду с необходимостью считать предметы у людей с древних времён появилась потребность измерять длину, площадь, объём, время и другие величины. Результат измерений не всегда удавался выразить натуральным числом, приходилось учитывать и части употребляемой меры. Потребность в более точных измерениях привела к тому, что начальные единицы меры начали дробить на 2, 3 и более частей. Более мелкой единице меры, которую получали как следствие раздробления, давали индивидуальное название, и величины измеряли уже этой более мелкой единицей.
В связи с этой необходимой работой люди стали употреблять выражения: половина, треть, два с половиной шага. Откуда можно было сделать вывод, что дробные числа возникли как результат измерения величин. Народы прошли через многие варианты записи дробей, пока не пришли к современной записи.
Дроби в Древнем Египте
В Древнем Египте архитектура достигла высокого развития. Для того, чтобы строить грандиозные пирамиды и храмы, чтобы вычислять длины, площади и объемы фигур, необходимо было знать арифметику.
Из расшифрованных сведений на папирусах ученые узнали, что египтяне 4 000 лет назад имели десятичную (но не позиционную) систему счисления, умели решать многие задачи, связанные с потребностями строительства, торговли и военного дела.
В Древнем Египте некоторые дроби имели свои особые названия – а именно, часто возникающие на практике 1/2, 1/3, 2/3, 1/4, 3/4, 1/6 и 1/8. Кроме того, египтяне умели оперировать с так называемыми аликвотными дробями (от лат. aliquot – несколько) типа 1/n – их поэтому иногда также называют «египетскими»; эти дроби имели свое написание: вытянутый горизонтальный овальчик и под ним обозначение знаменателя. Что касается остальных дробей, то их следовало раскладывать в сумму египетских. Древние египтяне уже знали, как поделить 2 предмета на троих, для этого числа — 2/3 — у них был специальный значок. Это была единственная дробь в обиходе египетских писцов, у которой в числителе не стояла единица — все остальные дроби непременно имели в числителе единицу (так называемые основные дроби). Если египтянину нужно было использовать другие дроби, он представлял их в виде суммы основных дробей. Например, вместо 8/15 писали 1/3+1/5. Иногда это бывало удобно.Умели египтяне также умножать и делить дроби. Но для умножения приходилось умножать доли на доли, а потом, быть может, снова использовать таблицу. Ещё сложнее обстояло с делением. Важную работу по исследованию египетских дробей провёл математик XIII века Фибоначчи.
В Древнем Египте пользовались только простейшими дробями, у которых числитель равен единице (те, которые мы называем «долями»). Математики называют такие дроби аликвотными (от лат. aliquot – несколько). Эти дроби обозначались так:
Кроме того, египтяне использовали формы записи, основанные на иероглифе Глаз Гора (Уаджет). Для древних людей характерно переплетение образа Солнца и глаза. В египетской мифологии часто упоминается бог Гор, олицетворяющий крылатое Солнце и являющийся одним из самых распространенных сакральных символов. В битве с врагами Солнца, воплощенными в образе Сета, Гор сначала терпит поражение. Сет вырывает у него Глаз — чудесное око — и разрывает его в клочья. Тот — бог учения, разума и правосудия — снова сложил части глаза в одно целое, создав «здоровый глаз Гора». Изображения частей разрубленного Ока использовались при письме в Древнем Египте для обозначения дробей от
Таблица обозначений иероглифов дробей
|
Иероглиф |
Значение |
Примерная величина |
|
большая часть глаза |
1/2 (или 32/64) |
|
|
зрачок |
1/4 (или 16/64) |
|
|
бровь |
1/8 (или 8/64) |
|
|
меньшая часть глаза |
1/16 (или 4/64) |
|
|
капля слезы |
1/32 (или ²/64) |
|
|
знак сокола |
1/64 |
|
|
Уаджет |
63/64 |
Египтяне писали на папирусах, т.е на свитках, изготовленных из стебля крупных тропических растений, носивших то же название. Важнейшим по содержанию является папирус Ахмеса, названный так по имени одного из древнеегипетских писцов. Рукою которого он был написан. Его длина 544см, а ширина 33 см.
Дроби в Древней Греции
Египетские дроби продолжались использоваться в древней Греции и впоследствии математиками всего мира до средних веков, несмотря на имеющиеся к ним замечания древних математиков (к примеру, Клавдий Птолемей говорил о неудобстве использования египетских дробей по сравнению с Вавилонской системой). Максим Плануд греческий монах, ученый, математик в 13 веке ввел название числителя и знаменателя
В Греции употреблялись наряду с единичными, «египетскими» дробями и общие обыкновенные дроби. Среди разных записей употреблялась и такая: сверху знаменатель, под ним – числитель дроби. Например, означало три пятых. Еще за 2-3 столетия до Евклида и Архимеда греки свободно владели арифметическими действиями с дробями. Учение об отношениях, о дробях и связывалось у греков с музыкой. Кроме арифметики и геометрии, в греческую математику входила музыка. Музыкой греки называли ту часть арифметики, в которой говорится об отношениях и пропорциях. Греки создали и научную теорию музыки. Они знали: чем длиннее натянутая струна, тем «ниже» получается звук, который она издает; что короткая струна издает высокий звук. Однако у музыкального инструмента не одна, а несколько струн, и для того, чтобы все струны при игре звучали «согласно», приятно для уха, длина звучащих частей их должна быть в определенном отношении. Например, чтобы высоты звуков, издаваемых двумя струнами, различались на октаву, нужно, чтобы их длины относились как 1:2. Подобным же образом квинте соответствует отношение 2:3, кварте – отношение 3:4 и т.д.
Дроби в Индии.
Современную систему записи дробей создали в Индии. Только там писали знаменатель сверху, а числитель снизу, и не писали дробной черты. Зато вся дробь помещалась в прямоугольную рамку. Иногда использовалось и «трехэтажное» выражение с тремя числами в одной рамке; в зависимости от контекста это могло обозначать неправильную дробь (a + b/c) или деление целого числа a на дробь b/c. Правила действий над дробями почти не отличались от современных.
Дроби у арабов.
Записывать дроби как сейчас стали арабы. Средневековые арабы пользовались тремя системами записи дробей. Во-первых, на индийский манер записывая знаменатель под числителем; дробная черта появилась в конце XII – начале XIII в. Во-вторых, чиновники, землемеры, торговцы пользовались исчислением аликвотных дробей, похожим на египетское, при этом применялись дроби со знаменателями, не превышающими 10 (только для таких дробей арабский язык имеет специальные термины); часто использовались приближенные значения; арабские ученые работали над усовершенствованием этого исчисления. В-третьих, арабские ученые унаследовали вавилонско-греческую шестидесятеричную систему, в которой, как и греки, применяли алфавитную запись, распространив ее и на целые части.
Дроби в Вавилоне
Вавилоняне пользовались всего двумя цифрами. Вертикальная черточка обозначала одну единицу, а угол из двух лежащих черточек – десять. Эти черточки у них получались в виде клиньев, потому что вавилоняне писали острой палочкой на сырых глиняных дощечках, которые потом сушили и обжигали.
В древнем Вавилоне предпочитали постоянный знаменатель, равный 60-ти. Исследователи по-разному объясняют появление у вавилонян шестидесятеричной системы счисления. Скорее всего здесь учитывалось основание 60, которое кратно 2, 3, 4, 5, 6, 10, 12, 15, 20, 30 и 60, что значительно облегчает всякие расчеты.
Но было неудобно работать над натуральными числами, записанными по десятичной системе, и дробями, записанными по шестидесятеричной. А работать с обыкновенными дробями было уже совсем трудно. Поэтому голландский математик Симон Стевин предложил перейти к десятичным дробям.
Дроби в Древнем Китае
В Древнем Китае уже пользовались десятичной системой мер, обозначали дробь словами, используя меры длины чи: цуни, доли, порядковые, шерстинки, тончайшие, паутинки. Дробь вида 2,135436 выглядела так: 2 чи, 1 цунь, 3 доли, 5 порядковых, 4 шерстинки, 3 тончайших, 6 паутинок. Так записывались дроби на протяжении двух веков, а в V веке китайский ученый Цзу-Чун-Чжи принял за единицу не чи, а чжан = 10 чи, тогда эта дробь выглядела так: 2 чжана, 1 чи, 3 цуня, 5 долей, 4 порядковых, 3 шерстинки, 6 тончайших, 0 паутинок.
Дроби в Древнем Риме
Интересная система дробей была в Древнем Риме. Она основывалась на делении на 12 долей единицы веса, которая называлась асс. Двенадцатую долю асса называли унцией. А путь, время и другие величины сравнивали с наглядной вещью — весом. Например, римлянин мог сказать, что он прошел семь унций пути или прочел пять унций книги. При этом, конечно, речь шла не о взвешивании пути или книги. Имелось в виду, что пройдено 7/12 пути или прочтено 5/12 книги. А для дробей, получающихся сокращением дробей со знаменателем 12 или раздроблением двенадцатых долей на более мелкие, были особые названия.
Даже сейчас иногда говорят: «Он скрупулёзно изучил этот вопрос.» Это значит, что вопрос изучен до конца, что не одной самой малой неясности не осталось. А происходит странное слово «скрупулёзно» от римского названия 1/288 асса — «скрупулус». В ходу были и такие названия: «семис»- половина асса, «секстанс»- шестая его доля, «семиунция»- половина унции, т.е. 1/24 асса и т.д. Всего применялось 18 различных названий дробей. Чтобы работать с дробями, надо было помнить для этих дробей таблицу сложения и таблицу умножения. Поэтому римские купцы твёрдо знали, что при сложении триенса (1/3 асса) и секстанса получается семис, а при умножении беса (2/3 асса) на сескунцию (2/3 унции, т.е.1/8 асса) получается унция. Для облегчения работы составлялись специальные таблицы, некоторые из которых дошли до нас.
Дроби на Руси
В русском языке слово «дробь» появилось лишь в VIII веке. Происходит слово «дробь» от слова «дробить, разбивать, ломать на части». У других народов название дроби также связано с глаголами «ломать», «разбивать», «раздроблять». В первых учебниках дроби назывались «ломанные числа». В старых руководствах находили следующие названия дробей на Руси:
– половина, полтина, – треть,
– четь, – полтреть,
– полчеть, – полполтреть,
– полполчеть, – полполполтреть (малая треть),
– полполполчеть (малая четь), – пятина,
– седьмина, – десятина.
Глава 2 Значение дробей в жизни современного общества
а) Дроби и музыка.Ноты отличаются по длительности их звучания. Знаком обозначают целую ноту, ноту вдвое короче – половинную — , четвертную — ,восьмую — , шестнадцатую — .б) Дроби в медицине
Врачи в рецептах указывают больному в каких частях принимать лекарство
Провизоры используют дроби при приготовлении лекарств. В состав одной таблетки цитрамона входит: кислоты ацетилсалициловой – 0,24 г, парацетамола – 0,18 г, кофеина – 0, 03г.
В медицине, например, известно, что «великан» среди микробов имеет размер 0,1 мм, а наибольший мелкий вирус имеет размер 16 миллимикрон, т. е. (0,1: 1000 : 1000) х 16=0,0000016 (мм). Сравнивая размеры, медики определяют, чем вызвано заболевание (микробом или вирусом?), и узнают, какая болезньв) Дроби в кулинарии.В кулинарии (как и во всем поварском деле) все основывается на долях, на соотношениях. В различных рецептах приготовления блюд требуется взять 0,5 стакана сахара, 0,7 кг муки, 0,5 чайных ложки соды и т.д.
г) Дроби в космосе.В геодезии существует метод съемки земли, называемый космическое зондирование. Этот очень сложный метод можно упростить, используя дроби при расчетах формул. Благодаря им, геодезисты могут получить наиболее качественное изображение поверхности Земли.
д) Дроби в танцах.В русском танце имеется весьма распространенный вид движений выполняемых сильными, четкими, короткими, частыми ударами ног об пол. такие движения русской пляски называются “ дроби”. Дроби весьма разнообразны по ритму и технике исполнения.е) Дроби в строительстве.Без знаний дробей невозможно построить здания, возвести мосты, проложить асфальт и т. д. Чтобы сделать строительный раствор необходимо знать дроби.
В строительстве прорабы используют дроби при составлении сметы на строительство чего-либо.ж) Дроби в рисовании.Для построения изображения головы человека высоту головы делим на 7 частей. Расстояние между глазами равно длине глаз. Ширина головы = 34 высоты головыз) Дроби в нумерации домов.Дроби в нумерации домов Номер через дробь ставят у домов, пронумерованным по двум пересекающимся улицам.и ) Дроби в стихах.Древний выдумал мыслитель Знаменатель и числитель, Чем и вызвал интерес К своей особе. Чтобы выглядеть отменно, Чтобы мыслить современно, Изучайте непременно Чудо — дроби. к) Дроби в фигурном катании.В фигурном катании десятичные дроби применяются при подсчете баллов для выявления победителей среди сильнейших фигуристов.
л))Дроби вгеографии Участки земной поверхности изображаются на карте в уменьшенном виде, для этого используется понятие масштаба: отношение длины отрезка на карте к длине соответствующего отрезка на местности.Например: масштаб карты означает, что 1см на карте соответствует 10000см на местности.
м) Дроби в парикмахерской.
Парикмахер использует дроби для приготовления раствора для окрашивания волос.
Наша повседневная жизнь состоит из постоянных мелких подсчётов: скидки в магазине, расчёт сдачи и времени до посадки на самолёт.
Наша гипотеза: «дроби проникли во все сферы нашей повседневной жизни» полностью подтвердилась.
Глава 3 Социологический опрос
Среди сотрудников гимназии «Жуковка» и родителей, учащихся был проведен социологический опрос. Целью опроса было определить степень значимости дробей в нашей повседневной жизни.
В опросе приняло участие 44 респондента различной возрастной категории (от 21 года до 67 лет).
В результате обработки полученных данных выяснилось:
84% опрошенных считают ,что дроби очень значимы в нашей повседневной жизни и без них нельзя обойтись ни в одной сфере деятельности;
9% опрошенных считают, что с дробями они сталкиваются только в быту; 7% опрошенных не помнят и не умеют работать с дробями.
Как показал опрос большинство респондентов уверены в том, что без дробей нельзя обойтись ни в одной сфере деятельности в нашей повседневной жизни.( Приложение 1. )
Глава 4. Старинные задачи на дроби и их решение.
Из различных источников я нашёл интересные задачи, которые были использованы в различные исторические периоды.
Задача Герона Александрийского (I в. н. э. ), древнегреческий инженер, физик, механик, математик, изобретатель
Бассейн вместимостью 12 куб. ед. наполняется через две трубы, из которых через одну поступает в каждый час 1 куб. ед. воды, а через другую — 4 куб. ед. За какое время наполнится бассейн при совместном действии обеих труб?
1)4+1=5(куб. ед. ) наполняют обе трубы за 1 час совместной работы.
2)12:5=(часа) наполнят трубы бассейн.
Ответ: за 2 часа 24 минуты наполнится весь бассейн.
Задача из «Арифметики» Леонтия Филипповича Магницкого. Учебник арифметики, по которому учился Михаил Васильевич Ломоносов. Эта задача трехвековой давности.
Один человек выпьет бочонок за 14 дней, а с женой выпьет тот же бочонок за 10 дней. За сколько дней жена его отдельно выпьет этот бочонок?
Решение 1 способом. Весь бочонок принят за — 1.
1)1:14=бочонка пьёт один человек в день.
1:10=бочонка пьёт муж и жена в день.
2) пьёт жена в день.
3)1:дней понадобится жене чтобы выпить бочонок.
Ответ:35 дней понадобится жене чтобы выпить бочонок.
Анания Ширакаци (615 г. ) — армянский философ, математик и географ середины 7 века.
Задача В городе Афины был водоем, в который проведены три трубы. Одна из труб может наполнить водоем за 1 ч, другая, более тонкая, — за 2 ч, третья, еще более тонкая, — за 3 ч. За какую часть часа все три трубы вместе наполнят водоем?
Решение. Весь водоём принят за — 1.
1)1:1==1 (водоёма) наполняет первая труба за 1 ч.
2)1:2= (водоёма) наполняет вторая труба за 1 ч.
3)1:3= (водоёма) наполняет третья труба за 1 ч.
4) 1+ (часа) понадобится всем трубам чтобы наполнить водоём.
Ответ: 2 ч понадобится трубам чтобы наполнить водоём.
Задача С. Сатина из журнала «Крокодил» (1990. № 34):
За десять дней пират Ерема
Способен выпить бочку рома.
А у пирата у Емели
Ушло б на это две недели.
За сколько дней прикончат ром
Пираты, действуя вдвоем?
Решение. вся бочка принята за — 1.
1)1:10=бочки рома выпивает пират Ерёма в день.
1:14=бочки рома выпивает пират Емеля в день.
2) бочки рома выпивают оба пирата в день.
3)1: дней выпьют бочку рома оба пирата.
Ответ: за 5 дней выпьют бочку рома оба пирата совместно.
Задача Четыре плотника хотят построить дом. Первый плотник может построить дом за год, второй — за 2 года, третий — за 3 года, четвертый — за 4 года. За сколько лет они построят дом при совместной работе?
Решение. Способ 1. Вся работа принята за – 1.
1) 1:1=1за 1 год 1-ый плотник сделает всю работу.
1:2=(работы) делает 2-ой плотник за 1 год.
1:3=(работы) делает 3-ий плотник за 1 год.
1:4=(работы) делает 4-ый плотник за 1 год.
2)1+(домов) сделают плотники за 1 год, работая совместно.
3)1:(года) понадобится плотникам, чтобы сделать 1 дом.
Ответ: за года или 175 дней часа сделают плотники 1 дом работая совместно.
Решение. Способ 2. Пусть все мастера работали 12 лет.
1)12:1=12(домов) построит 1-ый плотник за 12 лет.
12:2=6(домов) построит 2-ой плотник за 12 лет.
12:3=4(дома) построит 3-ий плотник за 12 лет.
12:4=3(дома) построит 4-ый плотник за 12 лет.
2)12+6+4+3=25(домов) построят плотники за 12 лет.
3)12:25=(года) построят плотники 1 дом совместно.
Ответ: за 175 дней часа построят плотники 1 дом, работая совместно.
Задача . Для переписки сочинения наняты 4 писца; первый мог бы один переписать сочинение за 24 дня, второй — за 36, третий — за 20 и четвертый — 18 дней. Какую часть сочинения напишут они за один день, если будут работать вместе?
Решение. Всё сочинение принято за — 1.
1)1:24=сочинения пишет первый писец за 1 день.
1:36= сочинения пишет второй писец за 1 день.
1:20= сочинения пишет третий писец за 1 день.
1:18= сочинения пишет четвёртый писец за 1 день.
2) сочинения пишет первый и второй писец за 1 день.
3) сочинения пишет первый, второй и третий писец за 1 день.
4) сочинения пишут все писцы за 1 день.
5)1: дня напишут сочинение писцы работая вместе.
Ответ: за 5 дня напишут писцы сочинение, работая вместе.
Задача Старинная задача (Китай, II в. ).
Дикая утка от южного моря до северного моря летит 7 дней. Дикий гусь от северного моря до южного моря летит 9 дней. Теперь дикая утка и дикий гусь вылетают одновременно. Через сколько дней они встретятся?
Решение. Весь путь принят за — 1.
1)1:7=(пути) пролетает дикая утка в день.
1:9=(пути) пролетает дикий гусь в день.
2) (пути) пролетают дикий гусь и дикая утка в день.
3)1:(дней) встретятся дикая утка и дикий гусь.
Ответ: за 3 дней встретятся дикая утка и дикий гусь.
8. Старинная Задача
Лошадь съедает воз сена за месяц, коза – за 2 месяца, овца – за 3 месяца. За какое время лошадь, коза и овца съедят вместе такой же воз сена?
Решение. Всё сено принято за — 1.
1)1:1=(сена) съедает лошадь за 1 месяц
1:2=(сена) съедает коза за 1 месяц
1:3=(сена) съедает осёл за 1 месяц
2)1+=2(месяца) хватит на всех (лошадь, коза, овца) сена.
Ответ: на 2 месяца хватит сена для животных.
1 )Задача Эйлера.
Леонард Эйлер (4 апреля 1707г.- 18 сентября 1783г.) — является основателем русской научной математической школы. Полное собрание его сочинений насчитывает более 70 томов, а списки его трудов – более 850 названий.
Решив все свои сбережения поделить поровну между всеми сыновьями, некто составил завещание. «Старший из моих сыновей должен получить 1000 рублей и восьмую часть остатка; следующий – 2000 рублей и восьмую часть нового остатка; третий сын – 3000 рублей и восьмую часть следующего остатка и т. д.». Определите число сыновей и размер завещанного сбережения.
Решение: так как все сыновья получили поровну, то восьмая часть каждого нового остатка была на 1000 рублей меньше восьмой части предыдущего остатка, а, значит, весь новый остаток был на 8000 рублей меньше предыдущего. Так как по условию все деньги были поделены полностью, то, когда младший сын получил по завещанию, кроме нескольких тысяч рублей, ещё восьмую часть остатка, этого остатка не оказалось. Но тогда предыдущий остаток 8000 рублей. Из него предпоследний сын получил восьмую часть, равную 1000 рублей, а остальные 7000 рублей получил младший сын, который, таким образом, был седьмым сыном: сыновей было семь, а завещанная сумма 49000 рублей..
2) Известный физик А. В. Цингер в своих воспоминаниях о Л. Н. Толстом рассказывает о следующей задаче, которая очень нравилась известному писателю:
«Артели косцов надо было скосить два луга, один вдвое больше другого. Половину дня артель косила большой луг. После этого артель разделилась пополам: первая половина осталась на большом лугу и докосила его к вечеру до конца; вторая же половина косила малый луг, на котором к вечеру ещё остался участок, скошенный на другой день косцом за один день работы. Сколько косцов было в артели?»Решение: если большой луг полдня косила вся артель и полдня пол — артели, то ясно, что за полдня пол-артели скашивает луга. Следовательно, на малом лугу остался нескошенным участок в . Если один косец скашивает в день луга, а скошено было , то косцов было восемь.
В начале XVIII века в России было немного образованных людей. Одним из авторитетных учёных был Леонтий Филиппович Магницкий (), который в 1703 году издал первый печатный учебник по математике «Арифметика». По этому учебнику обучались многие поколения русских людей. В книге Магницкого много задач с разным содержанием, включая и дроби.
3) «Един человек выпьет кадь пития в 14 дней, а со женою выпьет тое же кадь в 10 дней. И ведательно есть, в колико дней жена его выпьет тое же кадь»
Решение: муж за день будет выпивать часть кади, а вместе с женой — часть, значит, жена за один день выпьет часть кади, а всё содержимое выпьет за 35 дней.
4) «Воз сена».
Лошадь съедает воз сена за месяц, коза — за два месяца, овца – за три месяца. За какое время лошадь, коза и овца вместе съедят такой же воз сена?
Решение: Поскольку лошадь съедает воз сена за месяц, то за год (12 месяцев) она съест 12 возов сена. Так как коза съедает воз сена за 2 месяца, то за год она съест 6 возов. Овца съедает воз сена за три месяца, значит, за год она съест 4 воза. Вместе за год они съедят 12+6+4=22 воза сена. Тогда один воз сена они вместе съедят за 12:22= месяца.
5) «Далеко ли до деревни?
Прохожий, догнавший другого, спросил: «Как далеко до деревни, которая у нас впереди?». Ответил другой прохожий: «Расстояние от той деревни, от которой ты идёшь, равно третьей части всего расстояния между деревнями, а если ещё пройдёшь три версты, тогда будешь ровно посередине между деревнями». Сколько вёрст осталось ещё идти первому прохожему?
Решение:До середины расстояния между деревнями первому прохожему нужно идти 2 версты, и это составляет — = часть всего расстояния между деревнями. Поэтому расстояние между деревнями равно 12 верстам, к моменту встречи первый прохожий прошёл *12 = 4 версты и осталось ему ещё идти 8 вёрст.
6) «С чем иностранка к россам привезена?»
Нововыезжей в Россию иностранной мадаме
Вздумалось оценить своё богатство в чемодане:
Новой выдумки нарядное фуро
И праздничный чепец а ля фигаро.
Оценщик был русак,
Сказал мадаме так:
«Богатства твоего первая вещь фуро
Вполчетверта дороже чепца фигаро;
Вообще же стоят не с половиною четыре алтына,
Но настоящая им цена только сего половина».
Спрашивается каждой вещи цена,
С чем иностранка к россам привезена.
(Вполчетверта – в 3 раза)
Задача ИЗ АКМИМСКОГО ПАПИРУСА
Некто взял из сокровищницы 1/13. Из того, что осталось, другой взял 1/17. Оставил же в сокровищнице 192. Мы хотим узнать, сколько было в сокровищнице первоначально?
Решение: 1)1-1/13=12/13(ч) сокровищ осталось 2)12/13-1/17=191/221(ч) сокровищ осталось 191/221 составляет 191 3)191:191*221=221
Ответ: 221 было первоначально.
Задача Магавиры
Найти число павлинов в стае, 1/16 которой, умноженная на себя, сидит на манговом дереве, а квадрат 1/9
остатка вместе с 14 другими павлинами – на дереве тамала.
Из четырех жертвователей второй дал вдвое больше
первого, третий – втрое больше второго, четвертый –
вчетверо больше третьего, а вместе дали 132. Сколько
дал первый?
Некто сказал своему другу: ≪ Дай мне 100 рупий, и я
буду вдвое богаче тебя≫, на что последний ответил: ≪
Если ты мне дашь только 10 рупий, я стану вшестеро
богаче тебя≫. Спрашивается, сколько было у каждого?
ЗАДАЧИ ИНДИИ
Наиболее известными индийскими математиками
являются Ариабхата (конец Iв.), Брамагупта (VII) и
Бхаскара (ХII). Индийские математики далекого
прошлого любили состязаться на публичных народных
собраниях. Поэтому поводу один индийский автор VII
века, заканчивая свою книгу, писал: «Подобно тому, как
солнце затмевает своим блеском звезды, так мудрец
затмевает славу других людей, предлагая и особенно
решая на народных собраниях математические
задачи.
1. Старинная задача (Индия, XI в.)
Есть кадамба цветок,
На один лепесток
Пчелок пятая часть опустилась.
Рядом тут же росла
Вся в цвету сименгда
И на ней третья часть
поместилась.
Разность их ты найди,
Ее трижды сложи
И тех пчел на Кутай посади.
Лишь одна не нашла
Себе места нигде
Все летала то взад, то вперед и везде
Ароматом цветов наслаждалась.
Назови теперь мне,
Подсчитавши в уме,
Сколько пчелок всего здесь собралось.
И вы подсчитайте в уме, как говорит автор, сколько пчелок
собралось на цветке.
Решение
+ =(часть пчёл сидит на цветах)
— =(разность)
+= ; +=; 1=
(ответ: 15 пчёлок всего)
Задача Брахмагупты
Найти высоту свечи, зная длины теней, отбрасываемых
вертикальным шестом в двух различных положениях,
и расстояние между ними .
Задача Брахмагупты (около 600 г.)
Слон, слониха и слонёнок пришли напиться к озеру,
чтобы напиться воды. Слон может выпить озеро за 3ч,
слониха — за 5ч, а слонёнок — за 6ч. За сколько времени
они все вместе выпьют озеро?
(за 1 час вместе)
Ответ: за 1
Дикая утка от южного моря до северного моря летит 7 дней. Дикий гусь от северного моря до южного моря летит 9 дней. Теперь дикая утка и гусь вылетают одновременно. Через сколько дней они встречаются?
Решение:
Ответ: за 3
(Древняя Греция ,1 в. До н. э.)
Бассейн может заполнять через четыре фонтана. Если открыт только первый фонтан, бассейн наполнится за день, только второй за два дня. Только третий за три дня, только четвёртый за 4 дня. За какое время наполнится бассейн, если открыты все четыре крана?
Решение: Посмотрим, сколько бассейнов могут заполнить фонтаны за12 дней.
Первые 12 бассейнов
Второй 6 бассейнов.
Третий четыре бассейна
Четвёртый 3 бассейн. Значит, всего они могут заполнить бассейнов за 12 дней 12+6+4+3=25. Поэтому один бассейн вместе они заполнят за 12:25=Ответ:
Путник, догнав другого, спросил его: «далеко ли до деревни, которая впереди?». Другой путник ответил: «Расстояние от деревни, из которой ты идёшь, равно трети всего пути всего расстояния между деревнями. А если пройдёшь ещё 2 версты, будет ровно посередине между деревнями». Сколько вёрст осталось идти путнику?
Решение: Две версты, которые нужно пройти первому путнику до середины между деревнями, составляют пути-1/3=1/6 часть всерасстояния между деревнями. Значит расстояние между деревнями в 6 раз больше и равно 2* 6=12верс. Так как к моменту встречи путник прошёл треть пути, т.е. 12*1/3=4 версты, ему осталось пройти 12-4=8 вёрст.
Ответ:8 вёрст
Китай, II век н.э. Дикая утка от южного моря до северного моря летит 7 дней. Дикий гусь от северного моя до южного моря летит 9 дней. Теперь утка и гусь вылетают одновременно. Через сколько дней они встретятся? Решение: утка 7 дн. 9раз 63 дня гусь 9 дн. 7раз 63 дня 1)7+9=16 раз 2) 63:16= 3 15/16 ( дней) 1) 1:7=1/7пути утка 1 д. 2) 1:9=1/9пути гусь 1 д. 3) 1/7+1/9=16/63 вместе 4) 1:16/63=3 15/16 дней Ответ: через 3 15/16 дней.
В знаменитой книге «1001 ночь» мудрец задаёт юной деве следующую задачу: Одна женщина отправилась в сад собирать яблоки. Чтобы выйти из сада, ей нужно было пройти через четыре двери, у каждой из которых стоял стражник. Стражнику у первых дверей женщина отдала половину сорванных ею яблок. Дойдя до второго стражника, женщина отдала ему половину оставшихся. Так же она поступила и с третьим стражником, а когда она поделилась яблоками с четвёртым стражником, у неё осталось 10 яблок. Сколько яблок она собрала в саду? Решение: I способ: 1) 1-1/2=1/2(ч) осталась 2) 1/2-1/4=1/4(ч) осталась 3) 1/4-1/8=1/8(ч) осталась 4) 1/8-1/16=1/16(ч) осталась 1/16 составляет 10 яблок 5) 10*16=160(яблок) IIспособ: 1)2*2*2*2=16(раз) 2)10*16=160(яблок) III способ: 1) 10*2=20(яблок) 2) 20*2=40(яблок) 3) 40*2=80(яблок) 4) 80*2=160(яблок) Ответ: 160 яблок.
Заключение
В результате проведенной исследовательской работы мной изучены
теоретические основы понятия дроби, история развития дробей. Исследовано где в нашей повседневной жизни мы встречаемся с дробями. Среди сотрудников гимназии и родителей проведен социологический опрос, в котором приняли участие 44 респондента разной возрастной категории.
После обработки полученных данных выяснилось, 84% опрошенных считают ,что дроби очень значимы в нашей повседневной жизни и без них нельзя обойтись ни в одной сфере деятельности;
9% опрошенных считают, что с дробями они сталкиваются только в быту; 7% опрошенных не помнят и не умеют работать с дробями.
Как показал опрос большинство респондентов уверены в том, что без дробей нельзя обойтись ни в одной сфере деятельности в нашей повседневной жизни. Мною найдены и решены интересные старинные задачи.
Подводя итоги проектно-исследовательской работы можно сказать, что все поставленные задачи выполнены, цель достигнута. Гипотеза подтвердилась.
Математика всегда была неотъемлемой и существеннейшей составной частью человеческой культуры, она является ключом к познанию окружающего мира. Сегодня можно с уверенностью сказать, что дроби – неотъемлемая часть нашей жизни. С их помощью строят дома, лечат людей, измеряют время, пишут музыку, шьют одежду, пишут картины … Значение дробей трудно переоценить.
Материалы проектно-исследовательской работы можно использовать не только на уроках математики , но и на занятиях математического кружка и при проведении внеклассных мероприятий по математике.
В перспективе планирую продолжить сбор старинных задач на дроби, а также создать мини-брошюру со старинными задачами на дроби, а также задачами на применение дробей в различных профессиях и в жизненных ситуациях.
Список использованных источников и литературы
1. Виленкин Н.Я. Жохов В.И. Чесноков А.С.Шварцбурд С.И. «Математика, 5кл.» — М.: Мнемозина, 2015.
2.Глейзер Г.И. «История математики в школе». – М.: Просвещение, 1981.
3.Дорофеев Г.В. ,Шарыгин И.Ф. «Математика, 5 кл.»/М.: Просвещение,1998.
4.Нагибин Ф. Канин Е. «Математическая шкатулка» — М.: Просвещение, 1984.
5. «Энциклопедия для детей», т.11: Математика /Глав.ред. М.Д.Аксёнова. – М.:Аванта +, 2000.
Интернет-ресурсы:
6. Д Буравлева. Дроби:история дробей .История возникновения дробей. http://schools.keldysh.ru/sch1905/drobi/history.htm
Историческая справка
http://www.webmath.ru/poleznoe/formules_12_0.php
8.Когда появились дроби? http://allforchildren.ru/why/when9.php
9. https://ru.wikipedia.org/wiki/%D0%94%D1%80%D0%BE%D0%B1%D1%8C
10. https://7lafa.com/pageanswer.php?id=25527
Приложение 1.
Дроби проникли даже в детскую художественную литературу! Н.Н.Носов. «Витя Малеев в школе и дома». Автор на 2,5 страницах подробно описывает, как главный герой решал задачу на части.
С.Я.Маршак. «Про одного ученика и шесть единиц». И здесь одну из единиц ученик получил за неумение решать задачи на дроби.
Л.Гераскина. «В стране невыученных уроков», где несчастный Витя Перестукин встретил ответ своей задачи -1,5 землекопа.
Просмотров работы: 23970
Руководитель:
Яруллина Гульсиня Ситдиковна
Учреждение:
Школа МБОУ «Гимназия №1» г. Абдулино
В данном исследовательском проекте по математике на тему «Обыкновенные дроби в жизни людей» автор изучает историю возникновения дробей, даёт определение «обыкновенная дробь», а также наглядно показывает обыкновенные дроби.
Подробнее о проекте:
В авторском исследовательском проекте по математике «Обыкновенные дроби в жизни людей» ученик 5 класса стремится показать, что дроби нужны не только в математике, но и в повседневной жизни. Учащийся дает развернутое определение понятия «дроби в математике», а также приводит подробную характеристику обыкновенных дробей.
Автор творческого проекта по математике на тему «Обыкновенные дроби в жизни людей» изучил использование обыкновенных дробей в профессиональной деятельности человека, а также порассуждал и аргументированно доказал важность знания и применения дробей для профессии «Разметчик». Также в работе можно найти определение других математических дробей.
Оглавление
Введение
1. Теоретическая часть.
1.1 Понятие дроби.
1.2 История возникновения дробей.
1.3 Использование обыкновенных дробей в профессиональной деятельности человек.
1.3.1 Дроби для профессии «Разметчик».
2. Практическая часть.
2.1. Мои наблюдения.
Заключение
Список использованной литературы
Введение
Уважаемые друзья! Ответственно вам сообщаю, есть люди, которые считают, будто дробям нет места в нашей жизни. За примерами далеко ходить не надо. Когда я учился в начальных классах, думал: «Зачем математики придумали дроби?» Наверное, только для того, чтобы портить жизнь школьникам. Другого объяснения не знал, пока не начали изучать в 5 классе тему «Дроби»
С первого знакомства с дробями было понятно, что они очень необычные числа, начиная с их непривычной записи и заканчивая сложными правилами действий с ними.
В обычной жизни, и взрослым, и детям каждый день приходится сталкиваться с проблемой деления целого на части, и даже в определенный момент кажется, что нас больше окружают не целые, а дробные числа, что является актуальностью данной темы.
Мне стало интересно узнать: как и когда появились дроби? В какой сфере жизни больше всего практически их применяют? Хотелось в ходе исследования этого вопроса убедиться и убедить других в необходимости дробей в повседневной жизни.
Объект исследования: обыкновенные дроби
Предмет исследования: использование дробей в нашей повседневной жизни.
Цель: показать, что дроби нужны не только в математике, но и в повседневной жизни.
Задачи:
- Узнать, что такое дробь, какие виды дроби существуют
- Изучить историю возникновения дробей.
- Рассмотреть применение дробей в повседневной жизни.
- Оценить достижения науки в данной области.
Понятие дроби
Дробь в математике — число, состоящее из одной или нескольких частей (долей) единицы. Дробь выражается отношением двух целых чисел m/n, где n — показывает на сколько долей разделена единица, а m – показывает сколько таких долей содержится в дроби.
В математике применяются следующие виды дробей:
- обыкновенная дробь;
- правильная дробь;
- неправильная дробь;
- смешанная дробь;
- десятичная дробь.
Дроби разные нужны, дроби всякие важны
Обыкновенная дробь имеет вид n/m или m/n где m и n — натуральные числа. Делимое (m) — называют числителем дроби, делитель (n) — называют знаменателем данной дроби. Горизонтальная или косая линия в дроби обозначает деление. Черта наклонная называется — «солидус», а горизонтальная – «винкулум».
Если числитель дроби меньше знаменателя, то дробь называется правильной (например 3/7), если больше или равен — неправильной (например 7/3).
Числа, в состав которых входит целое число и правильная дробь, называются смешанными. Целое число называют целой частью смешанного числа, а правильная дробь называется дробной частью смешанного числа. Например, для смешанной дроби число 3 — целая часть, 2/5 — дробная.
Десятичная дробь, это дробь, которая записывается без знаменателя.
Выглядят они так: 5,6; 3,17; 0,17 и т.д. На самом деле это особая запись обыкновенных дробей, у которых знаменатель равен 10, 100, 1000 и т. д.
История возникновения дробей
Память человечества не сохранила для нас имя изобретателя колеса. Также невозможно назвать точно даже тот отрезок времени, когда появились дроби.
Можно предположить, что потребность делить целое на части возникала ещё в первобытном обществе. Могло быть и так…
Были у древнего человека жена и двое детей. Вот пошла однажды древняя женщина собирать плоды и нашла всего лишь 1 яблоко. Детей у неё двое, а яблоко одно. Наверное, она догадалась: взяла каменный нож да и разделила это яблоко на 2 половины.
А в это время самый — самый древний человек пошёл на охоту и убил самого — самого древнего кабана. Пришёл домой и разделил свою добычу на четыре равные части: себе, жене, сыну и дочке. Конечно, эти древние люди и не догадывались, что, разделив целое число на части, они занимались таким трудным разделом математики, который впоследствии назовут «дроби». Итак, дроби появились в тот период времени, когда в трудовой деятельности людей появилась потребность более точно измерять какие-то величины, хотя делением на части люди пользовались, наверное, с древнейших времён.
Дроби в Древнем Египте
На протяжении многих веков египтяне именовали дроби «ломаным числом», а первая дробь, с которой они познакомились, была 1/2 . За ней последовали 1/4, 1/8 , 1/16, … затем 1/3, 1/6, … т.е. самые простые дроби, называемые единичными или основными дробями.
У них числитель всегда единица. Лишь значительно позже у греков, затем у индийцев и других народов стали входить в употребление и дроби общего вида, называемые обыкновенными, у которых числитель и знаменатель могут быть любыми натуральными числами. В Древнем Египте архитектура достигла высокого развития. Чтобы строить грандиозные пирамиды и храмы, чтобы вычислять длины, площади и объемы фигур, необходимо было знать арифметику.
Из расшифрованных сведений на папирусах ученые узнали, что египтяне 4000 лет назад имели десятичную систему счисления, умели решать многие задачи, связанные с потребностями строительства, торговли и военного дела.
Одним из первых известных упоминаний о дробях является математический папирус Ринда. Три более древних текста, в которых упоминаются дроби — это Египетский математический кожаный свиток, Московский математический папирус и Деревянная табличка Ахмима. Папирус Ринда включает таблицу египетских дробей для рациональных чисел вида 1/n, а также 84 математических задачи, их решения и ответы, записанные в виде египетских дробей.
Египтяне ставили иероглиф (ер, «один из» или ре, рот) над числом для обозначения единичной дроби в обычной записи, а в священных текстах использовали линию. У них также были специальные символы для дробей 1/2, 2/3 и 3/4, которыми можно было записывать также другие дроби.
Остальные дроби они записывали в виде суммы долей. Дробь 7/8 они записывали в виде ½ ¼ 1/8, но знак «+» не указывали. А сумму 4+1/3 записывали в виде 41/3. Такая запись смешанных чисел (без знака «+») сохранилась до сих пор.
Вавилонские дроби
Жители древнего Вавилона примерно за 3000 лет до нашей эры создали систему мер аналогичную нашей метрической, только в основе её лежало не число 10, а число 60, в которой меньшая единица измерения составляла 1/60 часть высшей единицы. Полностью эта система выдерживалась у вавилонян для измерения времени и углов, и мы унаследовали от них деление часа и градуса на 60 минут, а минуты на 60 секунд.
Исследователи по-разному объясняют появление у вавилонян шестидесятеричной системы. Число 60 прекрасно делится на 2, 3, 4, 5, 6, 10, 12, 15, 20, 30 и 60, что значительно облегчает всякие расчеты. Шестидесятые доли были привычны в жизни вавилонян.
Вот почему они пользовались шестидесятеричными дробями, имеющими знаменателем всегда число 60 или его степени: 602, 603 и т.д. В этом отношении шестидесятеричные дроби можно сравнить с нашими десятичными дробями.
Вавилонская математика оказала влияние на греческую математику. Следы вавилонской шестидесятеричной системы счисления удержались в современной науке при измерении времени и углов. До наших дней сохранилось деление часа на 60 мин., минуты на 60 с, окружности на 360˚, градуса на 60 мин., минуты на 60с.
Вавилоняне внесли ценный вклад в развитие астрономии. Шестидесятеричными дробями пользовались в астрономии ученые всех народов до XVII века, называя их астрономическимидробями. В отличие от них, дроби общего вида, которыми пользуемся мы, были названы обыкновенными.
Дроби в Древней Греции
Греки работали с обыкновенными дробями не часто, поэтому использовали различные обозначения. Герон и Диофант, самые известные арифметики среди древнегреческих математиков, записывали дроби в алфавитной форме, причем числитель располагали под знаменателем. Но в принципе предпочтение отдавалось либо дробям с единичным числителем, либо шестидесятеричным дробям.
Недостатки греческой системы счисления относят к их любви к строгости, которое заметно увеличило трудности, связанные с анализом отношения несоизмеримых величин. Слово «число» греки понимали, как набор единиц, поэтому то, что мы теперь рассматриваем как единое число – дробь, – греки понимали, как отношение двух целых чисел. Именно этим объясняется, почему обыкновенные дроби редко встречались в греческой арифметике.
Дроби в Древнем Китае
В Древнем Китае уже пользовались десятичной системой мер, обозначали дробь словами, используя меры длины чи: цуни, доли, порядковые, шерстинки, тончайшие, паутинки. Дробь вида 2,135436 выглядела так: 2 чи, 1 цунь, 3 доли, 5 порядковых, 4 шерстинки, 3 тончайших, 6 паутинок. Так записывались дроби на протяжении двух веков, а в V веке китайский ученый Цзу-Чун-Чжи принял за единицу не чи, а чжан = 10 чи, тогда эта дробь выглядела так: 2 чжана, 1 чи, 3 цуня, 5 долей, 4 порядковых, 3 шерстинки, 6 тончайших, 0 паутинок.
Дроби на Руси
В русском языке слово «дробь» появилось лишь в VIII веке. Происходит оно от слова «дробить, разбивать, ломать на части». В русских рукописных арифметиках XVII в. дроби называли долями, позднее «ломаными числами». В старых руководствах существуют следующие названия дробей на Руси:
| 1/2 — половина, полтина | 1/3 – треть |
| 1/4 – четь | 1/6 – полтреть |
| 1/8 — полчеть | 1/12 –полполтреть |
| 1/16 — полполчеть | 1/24 – полполполтреть (малая треть) |
| 1/32 – полполполчеть (малая четь) | 1/5 – пятина |
| 1/7 — седьмина | 1/10 — десятина |
Славянская нумерация употреблялась в России до XVI века, затем в страну начала постепенно проникать десятичная система счисления. Она окончательно вытеснила славянскую нумерацию при Петре I.
Дроби в других государствах древности
В китайской «Математике в девяти разделах» уже имеют место сокращения дробей и все действия с дробями. У индийского математика Брахмагупты найдена достаточно развитую систему дробей. У него встречаются разные дроби: и основные, и производные с любым числителем. Числитель и знаменатель записываются так же, как и у нас сейчас, но без горизонтальной черты, а просто размещаются один над другим.
Арабы первыми начали отделять чертой числитель от знаменателя.
Леонардо Пизанский уже записывает дроби, помещая в случае смешанного числа, целое число справа, но читает так, как принято у нас. В XV – XVI столетиях учение о дробях приобретает уже знакомый нам теперь вид и оформляется приблизительно в те самые разделы, которые встречаются в наших учебниках.
Следует отметить, что раздел арифметики о дробях долгое время был одним из наиболее трудных. Недаром у немцев сохранилась поговорка: «Попасть в дроби», что означало – зайти в безвыходное положение. Считалось, что тот, кто не знает дробей, не знает и арифметики.
Использование обыкновенных дробей в профессиональной деятельности человека
Живя в окружении дробей, мы не всегда их явно замечаем. И все же, мы сталкиваемся с ним очень часто: дома, на улице, в магазине, на работе и так далее. Покажу лишь малую часть того, где мы можно увидеть присутствие дробей.
В медицине. Чтобы приготовить необходимое лекарство нужно знать его состав, записанный с помощью дробей, или, когда врач назначает больному ½ таблетки.
Дроби в кулинарии. Поварам нужны дроби для соблюдения пропорции при приготовлении блюда. В рецептах очень часто используются такие фразы, например, как одна вторая стакана, четверть столовой ложки.
Дроби в музыке. Учащиеся музыкальной школы знакомятся с дробями раньше, чем в общеобразовательной школе. С первых дней занятий дети знакомятся с такими понятиями как размер и длительности нот. Древнегреческий философ Пифагор (570 г. до н. э.), один из самых первых установил связь музыки и математики. Он создал учение о звуке. Пифагор связал длительность звучания нот с дробями.
Счёт длительностей в музыке ведётся от целой ноты, которая считается до четырёх. В целой ноте 2 половинные, 4 четверти, 8 восьмых, 16 шестнадцатых. Так музыка живёт в согласии с математикой.
Дроби в географии: Материк Евразия занимает 1/3 часть суши;
Масштаб карты равен 1/50000
Участки земной поверхности изображаются на карте в уменьшенном виде, для этого используется понятие масштаба: отношение длины отрезка на карте к длине соответствующего отрезка на местности.
Например, масштаб карты 1/10000 означает, что 1см на карте соответствует 10000 см на местности.
Дроби в спорте. Когда смотрим ½ финала матча по футболу.
Дроби в пропорции человека тоже связаны с дробями. Голова маленького ребенка составляет 1/5 часть роста человека. Голова подростка – 1/6. А голова взрослого человека – 1/8 часть роста. Основываясь на этих данных, была создана кукла «Барби».
Дроби в юридической деятельности. Взрослые в жизни встречаются с такими ситуациями: в наследство каждый по завещанию получили, например А- 1/8 имущества наследодателя; Б. – 6/17; В. — завещано всё остальное . Какие доли достались каждому из наследников?
Дроби для портных. Портной при раскрое одежды использует дроби. (рукав длины три четверти — ¾ или брюки длины 7/8)
В настоящее время невозможно представить ни одну отрасль промышленности или сельского хозяйства, или строительства, где бы в расчётах не встречалось дробных чисел.
Дроби для профессии «Разметчик»
На машиностроительных заводах есть очень увлекательная профессия, называется она — разметчик. Разметчик намечает на заготовке линии, по которым эту заготовку следует обрабатывать, чтобы придать ей необходимую форму.
Разметчику приходится решать интересные и подчас нелегкие геометрические задачи, производить арифметические расчеты и т. д.
«Понадобилось как-то распределить 7 одинаковых прямоугольных пластинок равными долями между 12 деталями. Принесли эти 7 пластинок разметчику и попросили его, если можно, разметить пластинки так, чтобы не пришлось дробить ни одной из них на очень мелкие части. Значит, простейшее решение — резать каждую пластинку на 12 равных частей — не годилось, так как при этом получалось много мелких долей. Как же быть?
Возможно ли деление данных пластинок на более крупные доли? Разметчик подумал, произвел какие-то арифметические расчеты с дробями и нашел все-таки самый экономный способ деления данных пластинок.
Впоследствии он легко дробил 5 пластинок для распределения их равными долями между шестью деталями, 13 пластинок для 12 деталей, 13 пластинок для 36 деталей, 26 для 21 и т.п.
Оказывается, разметчик представил дробь 712 в виде суммы единичных дробей 13 + 14. Значит, если из 7 данных пластинок 4 разрезать на три равные части каждую, то получим 12 третей, то есть по одной трети для каждой детали. Остальные 3 пластинки разрежем 4 равные части каждую, получим 12 четвертей, то есть по одной четверти для каждой детали. Аналогично, используя представления дробей в виде суммы единичных дробей 56 = 12+13; 1312 =13+34; 1336 =14+19.
Практическая часть. Мои наблюдения
Дроби в часах. «Встреча». Видеоролик. (Приложение 1)
Мы часто отвечаем на вопрос «который час?» дробями. «Без четверти пять» без пятнадцати минут пять; «Сейчас три часа без четверти» -2 час 45 минут; «Половина второго» -1 час 30 минут.
Ситуация 1. В парке стоит молодой человек с букетом цветов:
- Извините. Не подскажете который час? — спрашивает у прохожего.
- «Без четверти пять», — отвечает прохожий.
- Что опаздывает?
- Да, на целых ¾ часа.
- Сочувствую.
- Спасибо.
Дроби в кулинарии. «Пряники». Видеоролик. (Приложение 2)
Поварам нужны дроби для соблюдения пропорции при приготовлении блюда. В рецептах очень часто используются такие фразы, например, как одна вторая стакана, четверть столовой ложки.
Ситуация 2. Ученик в одежде повара. Готовит тесто для пряников.
— Для пряников понадобится 1 яйцо, один с четвертью стакана муки, две с половиною столовой ложки меда, треть чайной ложки соли, половина чайной ложки имбиря. Всё тщательно перемешиваем и печем пряники.
Дроби в кулинарии. «Пирожное». Видеоролик (Приложение 3)
Приготовленные блюда нужно умело делить на порции.
Ситуация 3. На столе стоит тарелка. В ней 5 пирожное.
— На день рождения пришли 6 друзей. Передо мной встал вопрос: «Как поровну разделить 5 пирожное между 6 человек»?
Решение было такое: нужно 5 пирожное разделить пополам каждый. Затем ещё 2 пирожное разделить на 3 части. Получается 6 абсолютно равных частей.
Дроби в математике.
Учитель математики после изучения сокращения дробей задал домашнее задание. Найти значение выражения рациональным способом.
65 : (407 : 9) 22 (37 : 26) — (2911 : 213) 6 (35: 287) : 45
На первый взгляд, обыкновенные натуральные числа. Сначала надо решить действия в скобках, потом делить и умножать. Но, здесь должна быть какая-то хитрость?! Надо найти рациональный способ. Я решил данное выражение так:
1) Записал выражение в виде дроби.
2) Преобразовал каждое натуральное число в виде произведения двух множителей.
3) В полученных дробях получились числа, которых можно сократить.
4) Получил ответ
Заключение
При выполнении своего проекта, я узнал много нового и интересного о дробях. Думаю, что эти знания пригодятся в учебе. Прочитал много книг и разделов из энциклопедий. Познакомился с первыми дробями, которыми оперировали люди, узнал новые для меня имена ученых, внесших свой вклад в развитие учения о дробях. А особенно то, что дроби используются почти во всех сферах деятельности человека, а это значит, что людям всех профессий нужно обязательно изучать дроби! Уметь решать задачи на дроби, знать правила сложения и вычитания, умножения и деления дробей.
Без знания математики, особенно знания дробей вся современная жизнь была бы невозможна. Например, у нас не было бы хороших домов, потому что строители должны уметь измерять, считать, сооружать. Наша одежда была бы очень грубой, так как ее нужно хорошо скроить, то есть точно все измерить, Не было бы ни какой большой промышленности, ни какой коммерции.
И конечно, не было бы радио, телевидения, кино, телефона и тысяч других вещей, составляющих часть нашей цивилизации. Использование дробей, измерения «на сколько?», «как долго?» являются жизненно необходимой частью мира, в котором мы живем.
В заключении можно сказать, что дроби бывают разные, дроби бывают важные. Знание понятия математическая дробь очень важно!
Считаю, что материалы моей работы будут интересными для других учащихся. Они могут быть использованы как на уроке, так и для проведения учителями внеклассных мероприятий по математике.
Список использованной литературы
- Анищенко Е. А. Число как основное понятие математики. Мариуполь, 2002.
- Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика. 5 класс: учеб.для общеобразовательных учреждений/- 26-е изд., стер. – М.: Мнемозина, 2009. — 280 с.
- Гейзер Г.И. История математики в школе. Пособие для учителей. – М.: Просвещение, 1981. – 239 с.
- Математика. 5 класс: учеб.для общеобразоват. учреждений. [СМ. Никольский, М.К.Потапов, Н.Н.Решетников, А.В. Шевкин]. — 11-е изд, дораб. — М.: Просвещение, 2016. — 272 с. — (МГУ — школе).
- Математический энциклопедический словарь. – М., 1988.
Если страница Вам понравилась, поделитесь в социальных сетях:
| Меню сайта |
 |
| Новости образовани |
 |
| Поиск |
 |
| Статистика |
|
Онлайн всего: 1 Гостей: 1 Пользователей: 0 |
 |
 |
 |
|||||||||
Главная » 2011 » Март » 19 » Сочинения 5 класса на тему,, дроби,,
Добавлять комментарии могут только зарегистрированные пользователи. [ Регистрация | Вход ] |
||||||||||
 |
 |