Методика подготовки к ЕГЭ по математике. Автор: Анна Георгиевна Малкова.
-
Основные принципы методики Анны Малковой:
-
Программа Полного курса подготовки к ЕГЭ по математике для учащихся групп «М-100».
-
Сентябрь.
-
Текстовые задачи на ЕГЭ по математике.
-
Октябрь.
-
Геометрия и стереометрия на ЕГЭ по математике, часть 1.
-
Октябрь — ноябрь.
-
Алгебра на ЕГЭ по математике, часть 1.
-
Тригонометрия на ЕГЭ по математике.
-
Декабрь.
-
Производная функции. Геометрический смысл производной.
-
Стереометрия на ЕГЭ по математике.
-
Январь.
-
Неравенства на ЕГЭ по математике.
-
Февраль.
-
Геометрия на ЕГЭ по математике. Задача С4.
-
Задачи с экономическим содержанием на ЕГЭ по математике.
-
Март.
-
Задачи с параметрами на ЕГЭ по математике.
-
Апрель.
-
Нестандартные задачи на ЕГЭ по математике (С6).
-
Май.
-
Повторение всех тем и решение вариантов ЕГЭ.
-
Рекомендуемый хронометраж для учащихся, претендующих на 90-100 баллов ЕГЭ:
-
Дополнения к Авторской методике Анны Малковой:
-
Приложение к методике: Обучающие комплекты видеокурсов Анны Малковой «Получи пятерку» и «Премиум».
-
Авторское право.
Внимание! Методика подготовки к ЕГЭ Анны Георгиевны Малковой защищена законом об авторских правах. Все материалы, находящиеся в данном файле, не подлежат воспроизведению в какой-либо форме или каким-либо образом без предварительного письменного разрешения ООО «ЕГЭ-Студия» и Анны Георгиевны Малковой. © 2017.
Методика подготовки к профильному ЕГЭ по математике Анны Малковой является результатом многолетнего опыта репетиторской и преподавательской работы. Анна Малкова преподает математику более 25 лет и за это время разработала целостную систему, включающую эффективные приемы объяснения той или иной темы школьной программы, пошаговое повышение мотивации учащихся и контроль достигнутых ими успехов.
Методика Анны Малковой рассчитана на обычного среднестатистического школьника и позволяет ему получить результат 90-100 баллов на ЕГЭ по математике профильного уровня за один учебный год подготовки.
Методика Анны Малковой предназначена для учителей, выпускающих 11 класс, преподавателей курсов подготовки к ЕГЭ и репетиторов, готовящих к ЕГЭ по математике.
Рассмотрим основные цели и задачи, стоящие перед репетитором-математиком (учителем, преподавателем), который готовит ученика к ЕГЭ или дополнительным вступительным экзаменам в вузы.
— Глобальная цель: пройти с учеником весь курс математики 10-11 класса. При необходимости – повторить отдельные темы или весь курс математики 5-9 класса.
Часто говорят, что репетитор «натаскивает» перед экзаменом, то есть сообщает, в каких задачах какие именно механические действия надо сделать, чтобы магическим образом получить ответ. Этот миф о репетиторах не имеет с реальностью ничего общего, и таким способом подготовить к экзамену невозможно.
Задача репетитора – не «натаскать перед экзаменом», а передать ученику полное и целостное понимание всего курса школьной математики. Не показать разрозненные приемы решения отдельных задач, а научить решать творчески и при этом математически грамотно любую экзаменационную задачу.
— При работе с учеником репетитору необходимо выявить пробелы, возникшие при изучении тех или иных тем в школе, и проработать эти темы наиболее тщательно.
К сожалению, старшеклассник, обучающийся в среднестатистической школе, практически всегда имеет такие пробелы и не скрывает, что некоторых тем в математике не понимает совсем.
Это связано с тем, что в разных школах преподавание математики ведется по различным программам, часто не состыкованным друг с другом. Смена учителя и тем более смена школы ведет к еще большей несогласованности пройденных тем.
— Одна из задач репетитора — дать навыки решения простых задач ЕГЭ быстро и без калькулятора.
Как показывает статистика, большая часть ошибок на ЕГЭ связана с арифметическими вычислениями. Именно из-за ошибок в вычислениях выпускник часто теряет драгоценные баллы и получает результат ниже, чем рассчитывал. Связано это с тем, что на уроках в школе и тем более при выполнении домашних заданий школьник привыкает пользоваться калькулятором, при этом часто забывая, как «в столбик» поделить одно число на другое.
— Следующая задача репетитора (преподавателя) — научить выпускника рассчитывать время на экзамене.
Профильный ЕГЭ по математике – фактически два экзамена в одном. Это и относительно простые 12 (в 2015 году — 14) задач части 1, или части В, которые можно считать выпускным экзаменом за курс средней школы, и 7 задач части 2 (которую еще недавно называли «Часть С»), которые по уровню сложности и требованиям к оформлению близки к традиционным задачам вступительных экзаменов в вузы. На все эти задачи дается 3 часа 55 минут. Это значит, что у ученика нет времени «изобретать» решение задачи на экзамене. Ему необходимо заранее знать все алгоритмы и нюансы решения каждой задачи, уметь доводить решение до результата, не бросая на полпути, уметь адекватно оценивать и проверять результат, а также следить за временем, зная, сколько минут можно потратить на решение тех или иных задач.
— Одна из важнейших задач репетитора (учителя, преподавателя курсов подготовки к ЕГЭ) — дать абитуриенту базу для дальнейшего освоения высшей математики и других связанных с математикой дисциплин при учебе в вузе.
Как правило, с поступлением абитуриента в вуз работа репетитора (учителя, преподавателя курсов подготовки к ЕГЭ) счастливо завершается, но на этом не заканчивается знакомство его ученика с математикой. Чем более качественной была подготовка к ЕГЭ, тем проще учащемуся, теперь уже студенту, будут даваться математический анализ, аналитическая геометрия, дифференциальные уравнения, математическая статистика и другие изучаемые в вузе науки.
Методика Анны Малковой отвечает всем этим требованиям.
к оглавлению ▴
Основные принципы методики Анны Малковой:
— Любую тему школьной математики можно объяснить просто и понятно, сохраняя при этом необходимую математическую строгость изложения. Это особенно важно при изучении таких традиционно трудных для школьников понятий, как понятия алгебраических преобразований, арифметического квадратного корня, модуля числа, степени с действительным показателем, обратной функции и многих других.
— Изучение каждой темы начинается с основных понятий, определений, связи этих понятий с уже пройденными темами, иными словами – с нуля. Любой новый термин, который вводится в курсе, объясняется через уже известные ученику.
— Курс математики изучается как целостная система. При этом репетитор (преподаватель) знает, какое место займет данная тема в общей математической картине учащегося, когда она понадобится в будущем и как связана с темами, которые еще предстоит пройти.
— Каждая тема в авторском курсе Анны Малковой занимает свое определенное место, в соответствии с Авторской программой подготовки к ЕГЭ Анны Малковой. Перестановка тем, пропуск тем или разделов или добавление других тем являются отступлением от методики. Такой порядок тем обусловлен необходимостью построить систему знаний, прежде всего понятную для ученика, где каждый новый «уровень» логически опирается на предыдущие.
— Основа мотивации учащихся – небольшие ежедневные успехи в освоении математики и отсутствие «провалов», то есть непонятных или неподъемных тем. Программа Анны Малковой построена так, чтобы ученик, независимо от предыдущего уровня подготовки, видел результаты занятий с первых же пройденных тем. Тогда его мотивация становится выше, самооценка растет, и за счет этого недавний троечник, занимающийся по методике Анны Малковой, выходит на уровень 80-90 баллов ЕГЭ.
— Один из основных принципов методики Анны Малковой – понимание вместо зубрежки. Большинство математических понятий, которые в школе бессмысленно заучиваются, вводятся на понятном уровне, причем не изолированно, а как элементы системы, связанные и с пройденным ранее материалом, и с тем, который будет в дальнейшем.
— Освоение каждой темы предполагает решение 50-100 практических задач по данной теме. Часть из этих задач разбирается на занятиях, часть задается на дом или изучается самостоятельно по видеоматериалам и Годовому онлайн-курсу Анны Малковой.
— Методика подготовки к ЕГЭ Анны Малковой основана на традициях советской математической школы и прежде всего на системе обучения, принятой в МФТИ, и полностью адаптирована к задаче подготовки к ЕГЭ.
— Методика Анны Малковой рассчитана на учащихся общеобразовательной школы и отличается от обычной школьной программы прежде всего системностью и практичностью, при этом без ущерба для математической культуры и грамотности.
— Для качественного освоения методики Анны Малковой каждая тема сопровождается авторскими методическими материалами:
1) Книга «ЕГЭ по математике. Полный курс подготовки».
2) Полный онлайн-курс подготовки к ЕГЭ по математике (включает 9 мастер-классов по 8 часов + домашние задания).
3) Полный видеокурс для подготовки к ЕГЭ по математике (12 дисков на физических или электронных носителях).
к оглавлению ▴
Программа Полного курса подготовки к ЕГЭ по математике для учащихся групп «М-100».
Программа рассчитана на учащихся 11 класса, которые готовятся к ЕГЭ 1 год, с сентября по май, 4 часа в неделю на занятиях + самостоятельная подготовка. Начальный уровень – около 50-60 баллов. Начальный уровень определяется на входном тестировании. Результат по окончании курса: 80-100 баллов. Программа расписана по занятиям, из расчета: 2 занятия в неделю. Праздничные дни при этом являются учебными, каникулы с 30 декабря по 5 января.
к оглавлению ▴
Сентябрь.
Текстовые задачи на ЕГЭ по математике.
1. Задачи на проценты на ЕГЭ по математике.
2. Текстовые задачи на движение и работу.
3. Задачи на сплавы, смеси, растворы.
4. Задачи на движение протяженных тел, на среднюю скорость и движение по окружности.
5. Алгебраические задачи с физическим содержанием.
6. Теория вероятностей на ЕГЭ по математике.
7. Задачи с экономическим содержанием (подготовительные занятия).
8. Знакомство с нестандартными задачами на ЕГЭ по математике (С6).
Дополнительно: приемы быстрого счета без калькулятора. Приемы решения алгебраических уравнений и систем уравнений. Алгебраические преобразования.
Первый блок Полного курса подготовки к ЕГЭ традиционно посвящен алгебре. Курс начинается с тем «Задачи на проценты» и «Текстовые задачи». Это материал 5-8 класса, который чаще всего к 11 классу оказывается благополучно забытым.
Почему именно эти темы рекомендованы для старта в методике Анны Малковой?
Цели такой компоновки следующие:
— Повторить и улучшить основные математические навыки учащихся.
— Вспомнить (или заново освоить) навыки составления и решение уравнений. Построение математических моделей.
— Освоить навыки быстрого счета и проверки ответа. На ЕГЭ пользоваться калькулятором не разрешается, поэтому выпускнику надо уметь считать быстро без калькулятора.
— Повторить основные темы алгебры: арифметические действия, порядок действий, десятичные и обыкновенные дроби и действия с ними, решение квадратных и дробно-рациональных уравнений.
Темы «Текстовые задачи» и «Задачи на проценты» являются выгодными для репетитора и преподавателя. Их освоение сразу дает быстрые результаты. Здесь не требуется сложного математического аппарата. Достаточно нескольких простых правил, которые школьнику легко запомнить. Таким образом, уже с первых уроков работы по данным темам ученик получает заметный, измеримый результат. Даже если у него «никогда и ничего не получалось» или «ненавидел математику» — первый результат помогает учащемуся поверить в себя и повысить самооценку. При этом также растет авторитет преподавателя – поскольку объяснил то, что раньше было недоступным.
Задачи на сплавы, смеси, растворы – также выигрышная тема для преподавателя или репетитора. Из курса химии у старшеклассника эта тема чаще всего остается непонятной. Несколько простых приемов помогают освоить эту тему.
Задачи на движение протяженных тел, на среднюю скорость и движение по окружности – приятный бонус: решаются за счет знания нескольких «репетиторских секретов», которые трудно найти в учебниках. Такие «секреты» особенно любят и ценят школьники.
Теория вероятностей – тема, отсутствующая в большинстве школьных учебников и совсем недавно появившаяся в программе ЕГЭ по математике. Авторский курс Анны Малковой по теории вероятностей, свободно доступный в Интернете, на сегодняшний день наиболее популярный среди школьников и учителей по данной теме.
Задачи с физическим содержанием – тема, которую учащиеся 11 класса признают страшной. За исключением учащихся физмат школ, старшеклассники боятся «физики», часто не знают основных физических законов и от любых физических формул приходят в ужас. Конечно, включение задач с физическим содержанием в курс математики не может восполнить пробел в знаниях по физике, зато на примере этой темы можно отлично проиллюстрировать понятие функции как зависимости одной физической величины от другой по определенному закону. Часто такие задачи решаются с помощью графиков функций.
И наконец, на первом этапе репетитор (преподаватель) знакомит учащегося с отдельными и специально подобранными сложными задачами из части 2. Это задачи с экономическим содержанием, недавно появившиеся в ЕГЭ по математике, и нестандартные задачи (С6). Следует помнить, что это только первое знакомство, подготовительные занятия, которые тем не менее повышают самооценку ученика и помогают ему получить баллы за эти задачи на первом сентябрьском пробном ЕГЭ по математике.
к оглавлению ▴
Октябрь.
Геометрия и стереометрия на ЕГЭ по математике, часть 1.
1. Планиметрия, основные формулы. Вычисление площадей фигур на клетчатой бумаге. Вывод формулы площади прямоугольника, параллелограмма, треугольника, трапеции.
2. Тригонометрия на ЕГЭ по математике. Определения синуса, косинуса, тангенса угла в прямоугольном треугольнике.
3. Внешний угол треугольника – как найти его синус, косинус и тангенс. Понятие смежных углов. Высота в прямоугольном треугольнике.
4. Определения медианы, биссектрисы, высоты. Простые геометрические построения. Сумма углов треугольника.
5. Краткий курс геометрии. Программа здесь.
6. Векторы на плоскости.
7. Стереометрия. Формулы объема и площади поверхности многогранников и тел вращения.
8. Все задачи по стереометрии из Первой части ЕГЭ по математике.
Планиметрия и тем более стереометрия – темы, по которым даже школьные хорошисты в начале курса подготовки к ЕГЭ показывают практически нулевые знания.
Геометрии и стереометрии в школьной программе по математике уделяется значительно меньше внимания, чем алгебре. Уроки геометрии и стереометрии учителя часто заменяют алгеброй, поскольку отдельного обязательного экзамена по геометрии в школе теперь нет.
Особенно катастрофически сказалось на изучении геометрии и стереометрии в школе то, что из школьной программы исчез такой предмет, как черчение, и только в первом-втором классе сохранилось рисование. При этом школьная программа по геометрии и стереометрии никак не скорректирована и не адаптирована к этим изменениям.
Изучение планиметрии в школьной математике в 7 классе начинается с аксиом и доказательства очевидных для ученика утверждений. Как правило, ученик уже на этом этапе перестает что-либо понимать. В 10 классе, опять с непонятных аксиом, начинается стереометрия.
Школьные учебники по геометрии и стереометрии авторов Погорелова и Атанасяна в целом лучше, чем учебники по алгебре. Однако они не рассчитаны на то мизерное количество часов, которое в школе отводится на изучение этих дисциплин. В них не всегда можно выделить главные, ключевые моменты, и сделать это может только высококвалифицированный учитель.
В авторском курсе Анны Малковой изучение геометрии начинается с темы «площади фигур». Формулы для площадей прямоугольника, параллелограмма, треугольника, трапеции иллюстрируются простыми и наглядными примерами.
К сожалению, большая часть наших старшеклассников не понимает, что такое «длина отрезка» и как посчитать площадь квадрата. Методика Анны Малковой учитывает этот нулевой уровень владения навыками и помогает освоить геометрию начиная с самых основ.
Обязательным для изучения и запоминания является авторский комплект «шпаргалок», своего рода краткий конспект с рисунками, содержащий определения, формулы, основные свойства геометрических фигур.
Весь этот теоретический материал сразу же применяется на практике, при решении задач части 1 ЕГЭ.
На этом этапе вводятся также понятия синуса, косинуса, тангенса и котангенса острого угла в прямоугольном треугольнике, основные формулы тригонометрии в прямоугольном треугольнике, формулы для тригонометрических функций смежных углов.
Подбор задач осуществлен строго по уровню сложности, для того чтобы результатом каждого занятия становился рост понимания и уверенности учащегося.
В этом же блоке, после изучения тригонометрии в прямоугольном треугольнике и основ геометрии, дается тема «Векторы на плоскости», традиционно сложная для школьников.
Аналогичным образом в методике Анны Малковой происходит изучение стереометрии.
Изучение стереометрии начинается со знакомства с основными типами многогранников и тел вращения, понятия объема и площади поверхности, формулы для вычисления объемов и площадей поверхности.
На этом этапе используются для наглядности объемные модели многогранников и тел вращения. То, что можно подержать в руках, повернуть и рассмотреть с разных сторон, оказывается для начинающего более понятным и применимым, чем оперирующие отвлеченными понятиями аксиомы.
В блоках «Геометрия, часть 2, задача С4» и «Стереометрия, часть 2, задача С2» эта тема получит дальнейшее развитие. Основное внимание в решении задач по геометрии и стереометрии части 2.
ЕГЭ по математике в методике Анны Малковой уделяется строгим математическим доказательствам и корректному решению и оформлению задач.
к оглавлению ▴
Октябрь — ноябрь.
Алгебра на ЕГЭ по математике, часть 1.
9. Корни и степени.
10. Понятие функции. Исследование графика функции. Понятия возрастания и убывания функции, нулей функции, промежутков знакопостоянства, точек максимума и минимума функции, четности и нечетности функции.
11. Квадратичная функция и квадратичные неравенства.
12. Дробно-рациональная функция и метод интервалов. Решение дробно-рациональных неравенств.
13. Модуль числа. Уравнения и неравенства с модулем.
14. Показательная функция. Показательные уравнения (часть 1 + задачи из классических сборников).
15. Логарифмы. Преобразования логарифмических выражений. Логарифмические уравнения (часть 1 + задачи из классических сборников).
16. Логарифмическая функция. Понятие обратной функции.
17. Задачи с физическим содержанием по пройденным темам.
Этот блок методики Анны Малковой посвящен понятию функции в математике – ключевому в курсе алгебры 10-11 класса.
В школьной программе тема «Функции» дана фрагментарно, начиная с линейной и квадратичной функций в 7 классе, причем семиклассники чаще всего воспринимают эту тему поверхностно, не понимая, зачем она нужна. Далее, при изучении других типов функций, в школе самому определению функции уже не уделяется достаточного внимания, поскольку формально его «прошли» в 7 классе. В итоге абитуриент, закончив общеобразовательную школу и став студентом, обычно не готов к изучению математического анализа и тоже заучивает его формально, чтобы только сдать сессию.
В методике Анны Малковой определение функции считается одним из важнейших во всей школьной программе. Оно дается несколькими способами, раскрывающими различные грани этого понятия. Показано практическое применение того или иного определения, а также их взаимосвязь.
После изучения показательных и логарифмических функций учащийся получает представление о 5 типах элементарных функций, с каждым из которых связаны определенные способы решения уравнений, о сложной и обратной функции, а также о построении (пока без производной) и преобразованиях графиков функций.
Темы этого блока методики Анны Малковой содержат максимальное, по сравнению с другими, количество строгих определений и математических формулировок, без знания которых ученик не может понять последующий материал. Это, например, определения модуля, арифметического квадратного корня, логарифма, точек максимума и минимума функции. К сожалению, большинство учителей и репетиторов либо пропускает эти определения, считая, что школьник «и так их знает», либо дает их в неточной формулировке.
Очевидно, что учитель (преподаватель, репетитор) обязан дать все эти формулировки, не пропуская и не модифицируя их, так же, как учитель русского языка должен передать ученику правила русского языка без собственных добавок и видоизменения.
Это определяет высокие требования к уровню математической культуры учителей и преподавателей, работающих по данной методике.
И закреплением темы являются задачи с физическим содержанием, теперь уже включающие в себя показательные, логарифмические и степенные зависимости одной величины от другой.
к оглавлению ▴
Тригонометрия на ЕГЭ по математике.
18. Определения синуса, косинуса, тангенса для произвольного угла.
19. Тригонометрический круг. Тригонометрические функции.
20. Формулы тригонометрии.
21. Тригонометрические преобразования. Простейшие тригонометрические уравнения.
22. Обратные тригонометрические функции и их графики.
23. Тригонометрические уравнения (часть 2).
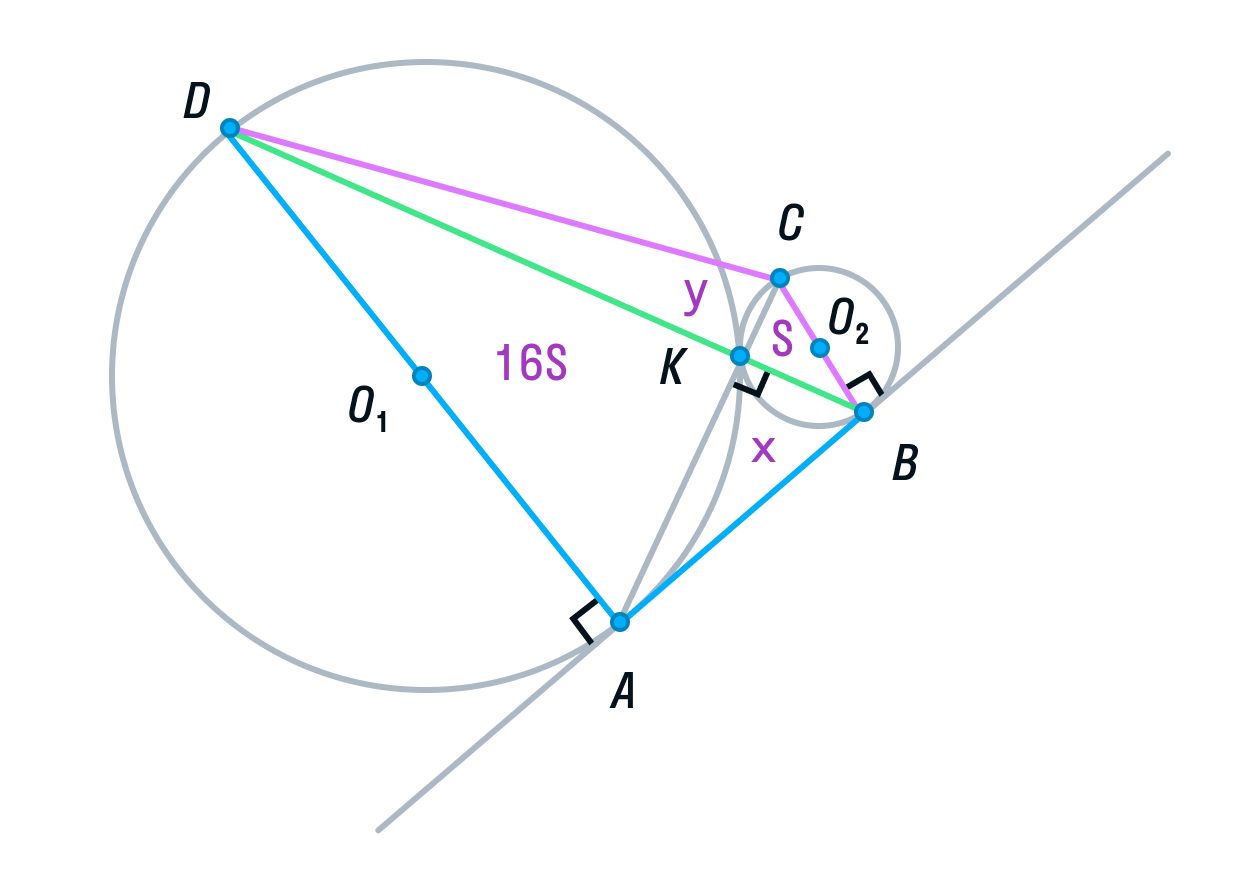
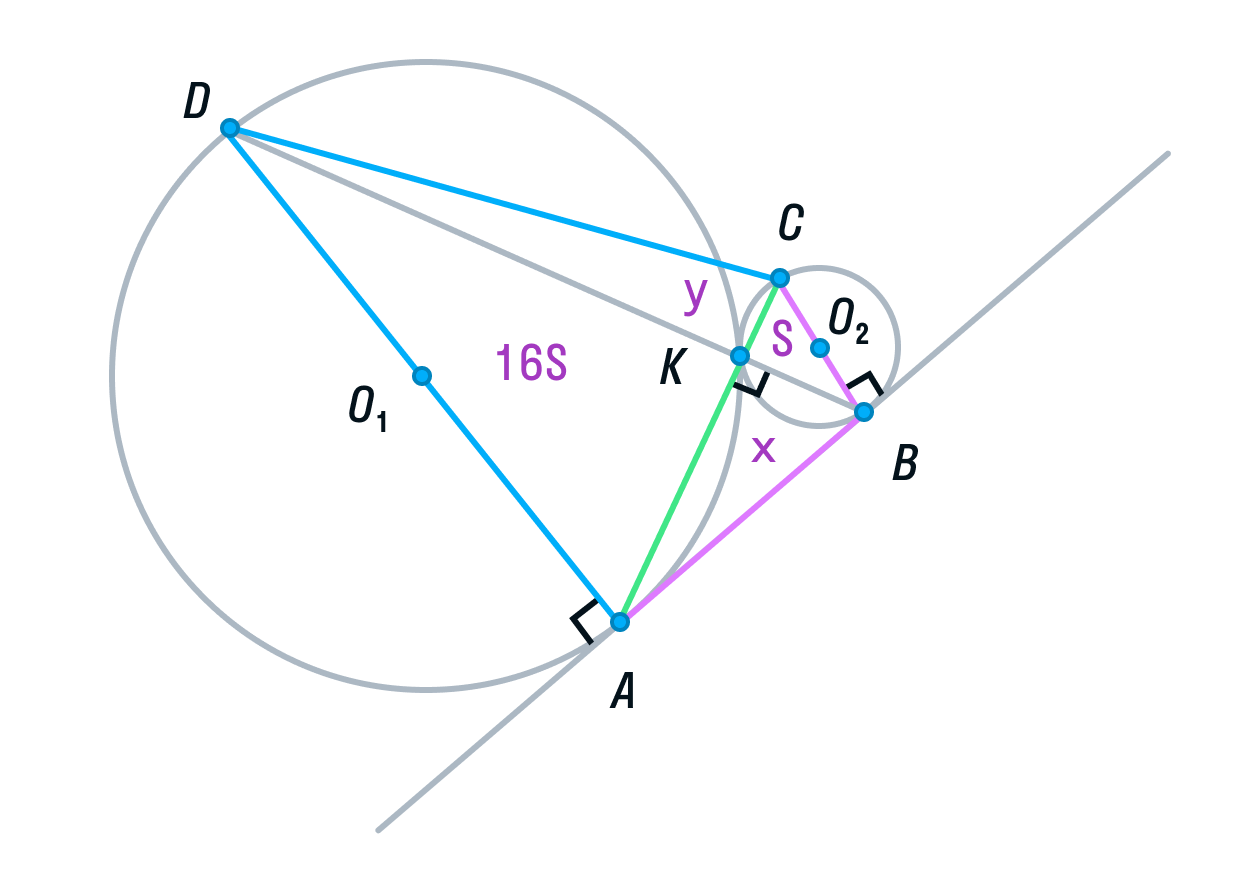
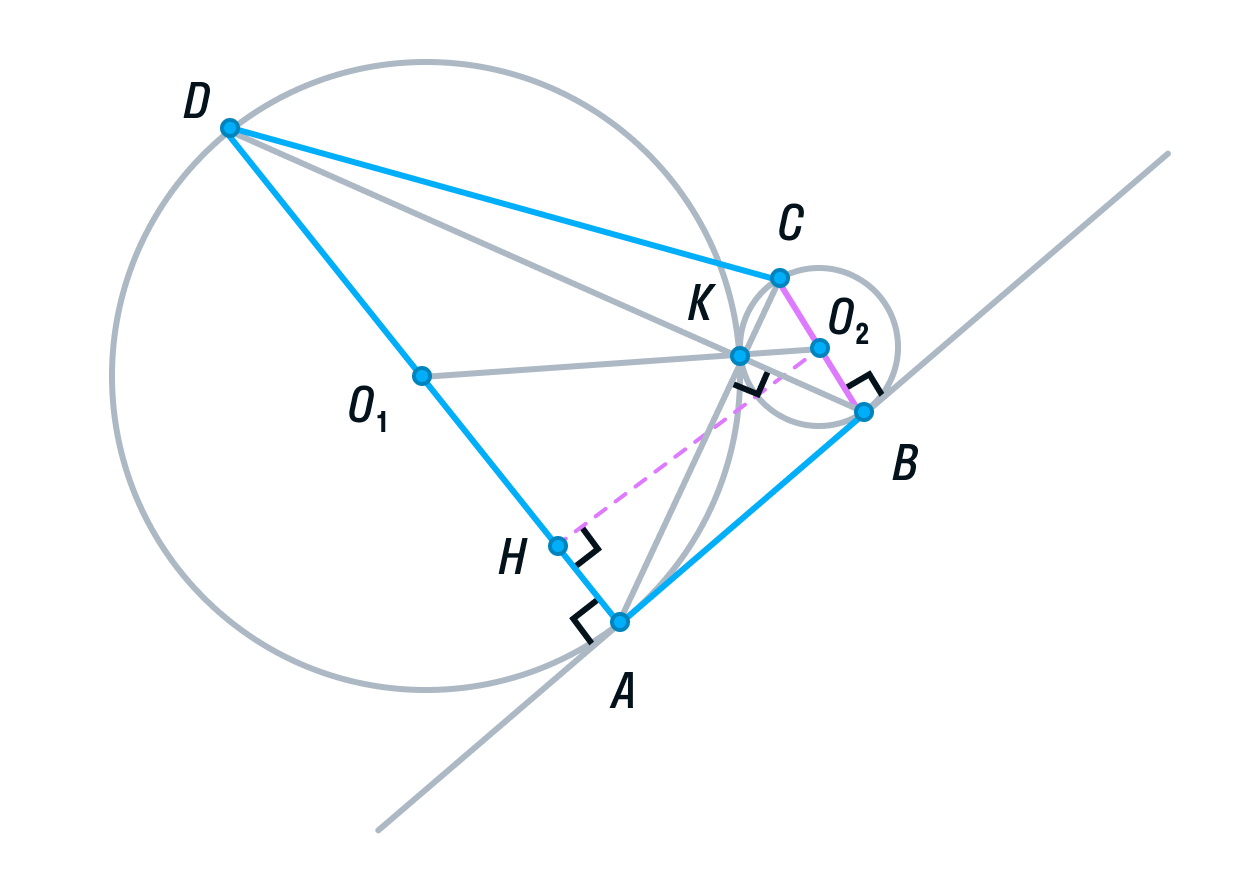
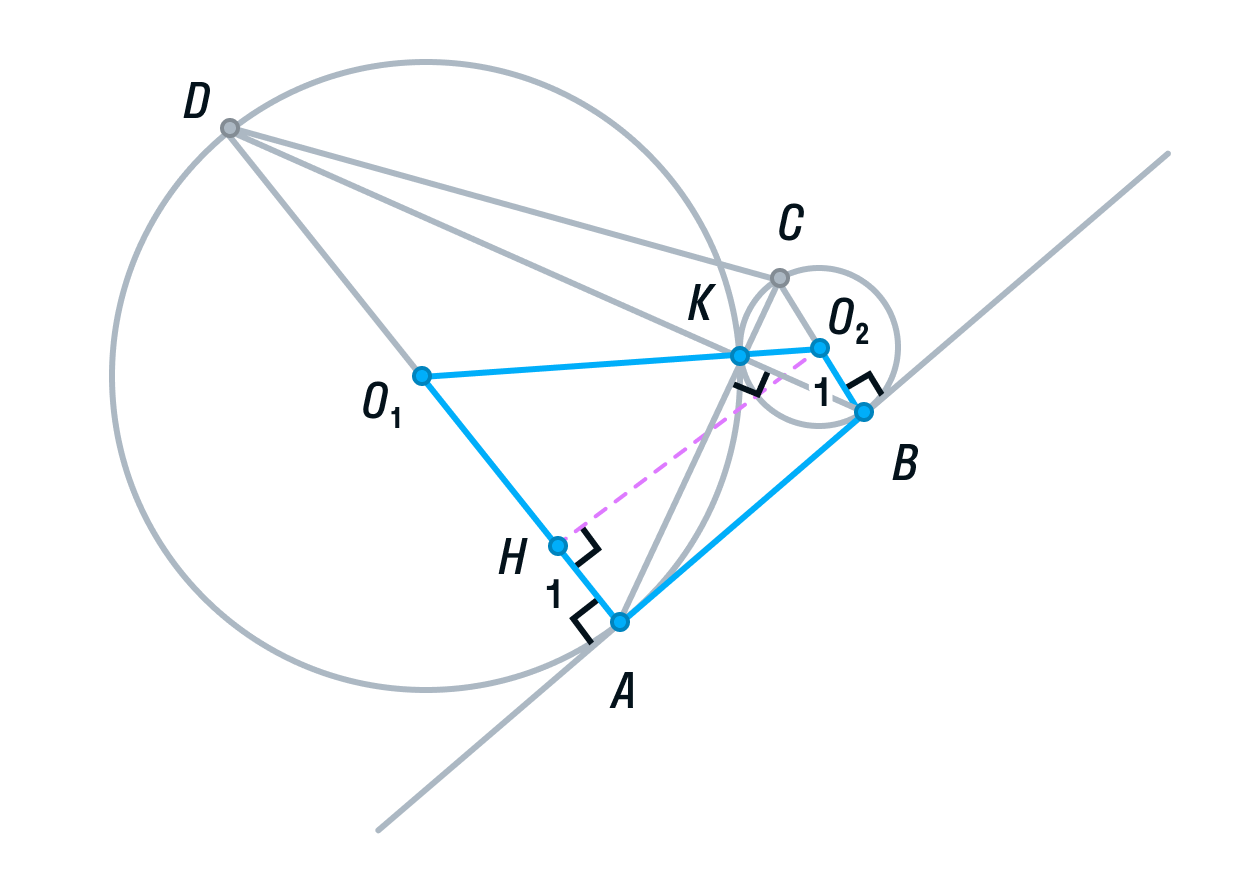
Тема «Тригонометрия» базируется на знаниях, полученных в теме «Геометрия и стереометрия на ЕГЭ по математике. Часть 1» и начинается с повторения понятий тригонометрических функций острого угла в прямоугольном треугольнике. Для введения определений тригонометрических функций произвольного угла используется Тригонометрический круг – авторская разработка Анны Малковой. Конечно, тригонометрический круг не изобретен Анной Малковой, он существовал и раньше. Авторскими являются сам рисунок тригонометрического круга, порядок объяснения, иллюстрация с помощью тригонометрического круга основных закономерностей тригонометрии.
Особое внимание уделяется тому, что тригонометрический круг изображен в привычной школьнику декартовой системе координат, а также пониманию того, что уже известные тригонометрические функции острого угла в прямоугольном треугольнике являются частным случаем тригонометрии для произвольного угла. С помощью тригонометрического круга объясняются понятия и правила, которые в школьной программе ученику часто приходится бессмысленно зубрить (или писать по ним шпаргалки). Эта удобная иллюстрация заменяет десяток таблиц.
Один из основных принципов методики Анны Малковой – минимум зубрежки, максимум понимания. В методике Анны Малковой такие понятия, как четность и нечетность тригонометрических функций, их периодичность, знаки тригонометрических функций в координатных четвертях не заучиваются бессмысленно, а объясняются с помощью тригонометрического круга.
По сравнению с другими методиками и особенно по сравнению с распространенными в интернете шпаргалками, в методике Анны Малковой дается минимальное количество (порядка 25 штук) формул тригонометрии, причем формулы разделены по смысловым блокам. Для тренировки в применении этих формул, кроме типичных заданий ЕГЭ на вычисление или преобразование тригонометрических выражений, даются также задачи из классических сборников – Сканави и других.
Особая тема – решение простейших тригонометрических уравнений и обратные тригонометрические функции. Здесь также применяется принцип методики Анны Малковой — минимум зубрежки, максимум понимания. В частности, формулы для решения простейших тригонометрических уравнений не заучиваются, как заклинания, а выводятся из простых соображений и определений. Тема «Обратные тригонометрические функции» является логическим продолжением темы «Обратная функция», пройденной в блоке 3 (Алгебра).
Завершение темы – решение тригонометрических уравнений. Здесь рекомендуется не ограничиваться только задачами ЕГЭ по тригонометрии и использовать также классические сборники для поступающих в вузы. Количество способов решения тригонометрических уравнений здесь больше, чем в программе общеобразовательной школы: кроме способов замены переменной, разложения на множители, сведения к квадратному уравнению и частных случаев введения дополнительного угла, дается также метод решения однородных уравнений, метод введения дополнительного угла в общем виде, метод оценки, универсальная тригонометрическая замена и другие методы. Все эти методы пригодятся учащемуся позже, при решении задач с параметрами (С5).
В последние годы в сборниках вариантов ЕГЭ по математике появились комбинированные задачи по тригонометрии, включающие в себя и показательные, и логарифмические, и тригонометрические компоненты. Это дает возможность повторить пройденные ранее темы «Показательные и логарифмические уравнения».
к оглавлению ▴
Декабрь.
Производная функции. Геометрический смысл производной.
24. Производная функции. Исследование функции с помощью производной.
25. Первообразная функции.
Тема «Производная функции» закономерно изучается после того, как учащемуся уже знакомы тригонометрические функции. Точнее, к этому моменту учащийся уже знаком со всеми пятью типами элементарных функций: степенными, показательными, логарифмическими, тригонометрическими и обратными тригонометрическими, знает особенности их графиков, а также знаком с основными характеристиками поведения функции, такими, как возрастание и убывание функции, точка минимума и точка максимума, наибольшее и наименьшее значение функции на отрезке. Также к этому моменту ученик владеет методом интервалов и знает, как находить промежутки закон постоянства дробно-рациональной функции.
В общеобразовательной школе понятие производной обычно вводится как «предел отношения приращения функции к приращению аргумента при приращении аргумента, стремящемся к нулю». Естественно, обычный старшеклассник (а иногда и учитель) всего этого заклинания запомнить не может, смутно представляет себе, что такое приращение, вообще не понимает, что такое предел, а в итоге как-то укладывает в свою голову, что «производная – это штрих» и худо-бедно зазубривает таблицу производных.
В методике Анны Малковой понятие производной функции дается на основе геометрического смысла производной – как скорость изменения функции и как тангенс угла наклона, или угловой коэффициент касательной. Здесь также действует принцип «Понимание вместо зубрежки». Понятие предела функции при этом не вводится, поскольку эта непростая тема требует более высокого, чем у среднего старшеклассника, уровня математической подготовки.
Особое внимание уделяется связи поведения функции с поведением производной. Часто ученик не понимает, что это два разных объекта, и на этом построено множество задач-ловушек в вариантах ЕГЭ. Исследование поведения функции на отрезке, нахождение наибольших и наименьших значений функции – здесь везде есть свои нюансы, которые преподавателю, работающему по методике Анны Малковой, необходимо соблюдать в точности.
к оглавлению ▴
Стереометрия на ЕГЭ по математике.
26. Программа по стереометрии.
27. Классический метод решения задач по стереометрии.
28. Векторы в пространстве. Векторно-координатный метод.
Задача С2 (стереометрия) традиционно считается одной из самых сложных для учащихся 11 класса, и многие школьники за нее даже не берутся.
В методике Анны Малковой тема «Стереометрия, часть 2» начинается с подготовительной работы – изучения авторского краткого курса стереометрии, то есть основных определений, аксиом, теорем. Все разделы этого курса сопровождаются авторскими иллюстрациями, которые выдаются учащимся также в виде таблиц. Для наглядности дополнительно используются объемные модели многогранников и тел вращения.
Следующая подготовительная тема – методы построения сечений объемных тел и развитие пространственного мышления учащихся. При этом важно не просто нарисовать сечение, а описать его построение и положение вершин сечения относительно исходного объемного тела.
Для решения задач С2 в методике Анны Малковой даются два способа – классический и векторно-координатный.
В классическом способе особое внимание уделяется грамотному и математически корректному оформлению решения, строгому доказательству каждого утверждения, построению дополнительных чертежей и пошаговому сведению объемной, стереометрической задачи – к планиметрической.
Векторно-координатный способ дается в объеме школьной программы, без использования вузовских приемов аналитической геометрии, причем особое значение также имеет грамотное и математически корректное оформлению решения.
Учащиеся получают рекомендации по применению каждого из методов в тех или иных задачах.
к оглавлению ▴
Январь.
Неравенства на ЕГЭ по математике.
29. Неравенства на ЕГЭ по математике.
30. Показательные и логарифмические неравенства. (часть 2 ЕГЭ по математике).
31. Метод рационализации (замены множителя). Метод оценки.
Тема «Неравенства» (задача С3 на ЕГЭ по математике) отличается обманчивой легкостью и рекордным количеством ошибок среди абитуриентов, причем они даже не подозревают, где именно их делают. Именно здесь возникает больше всего ситуаций типа «Я все сделал правильно и получил 0 баллов».
Именно здесь проходит граница между «неплохо сдал ЕГЭ» и «поступил в престижный вуз». Задача С3 многим открывает дорогу в вузы с профильной математикой и может считаться критерием профессионализма репетитора или учителя.
Без С3 становится недоступной и более сложная С5 (задача с параметрами).
В методике Анны Малковой даются приемы решения неравенств различных типов: иррациональных неравенств, неравенств с модулем, логарифмических и показательных неравенств. Показывается правильное оформление решений, что особенно важно для тех, кто сдает ЕГЭ и ДВИ на высокие баллы.
Особое внимание уделяется разбору типичных ошибок и отработке навыков правильного решения и оформления.
к оглавлению ▴
Февраль.
Геометрия на ЕГЭ по математике. Задача С4.
32. Что такое математическое доказательство. Задачи на доказательство.
33. Задачи части 2 ЕГЭ, Геометрия.
К решению задачи С4 (Геометрия, часть 2) учащиеся, занимающиеся по методике Анны Малковой, уже подготовлены. Ведь уже пройдены темы «Геометрия на ЕГЭ по математике, часть 1» и «Стереометрия на ЕГЭ по математике».
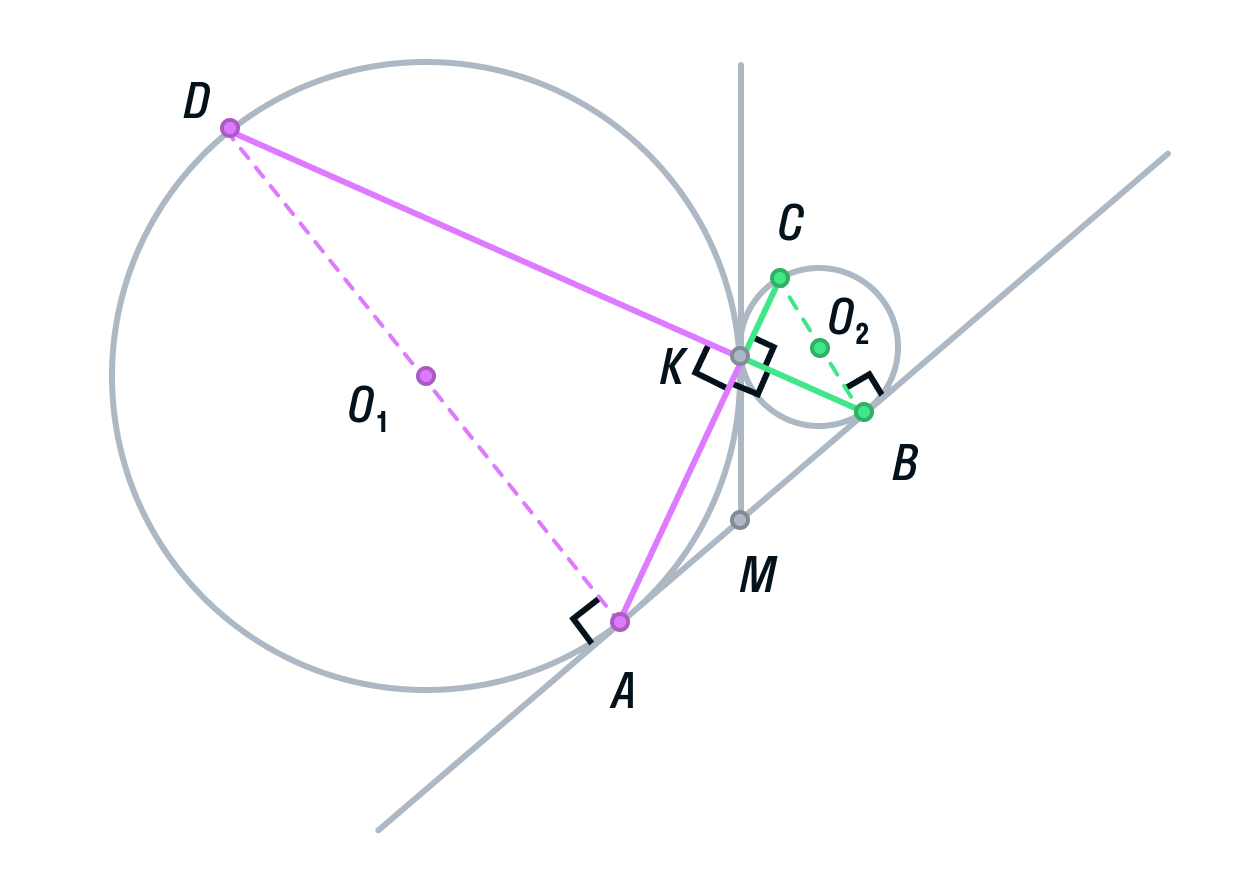
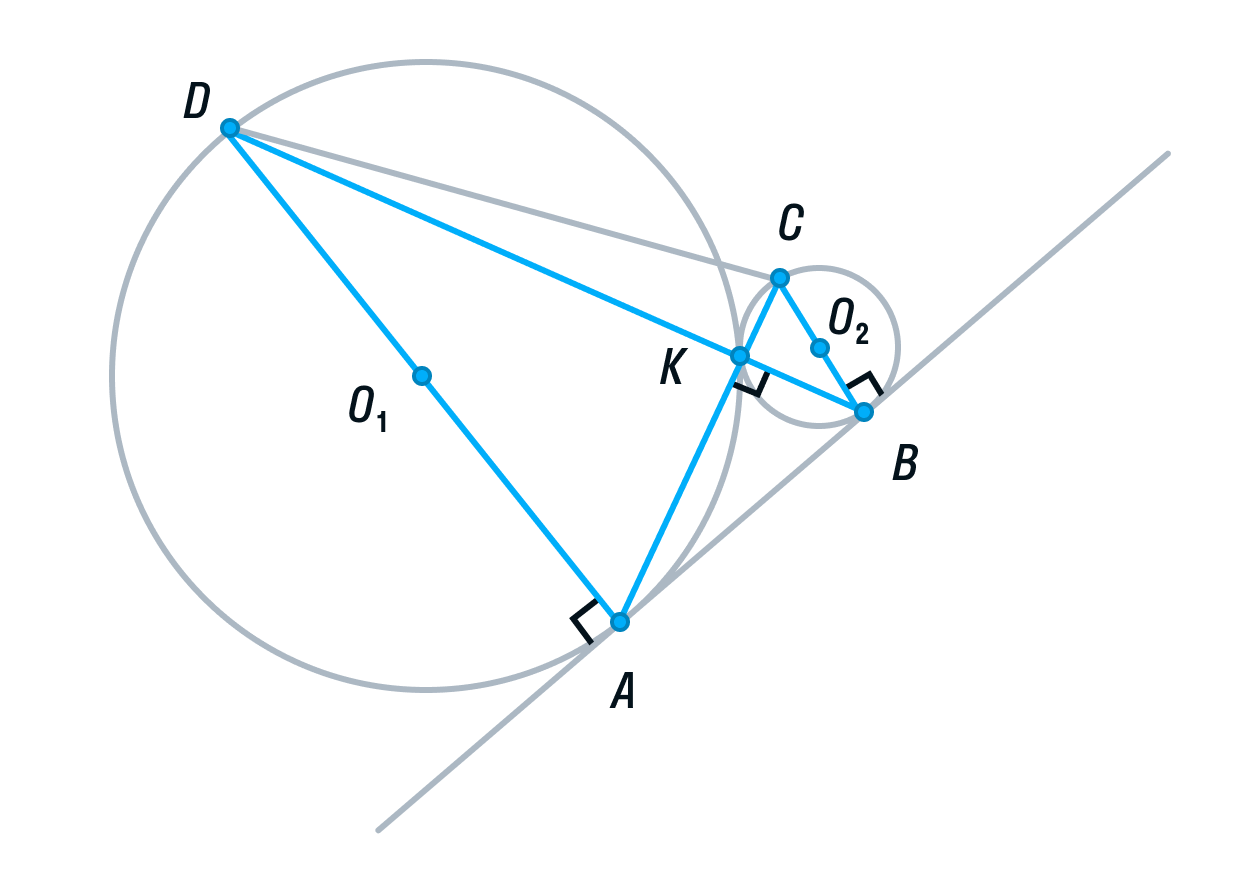
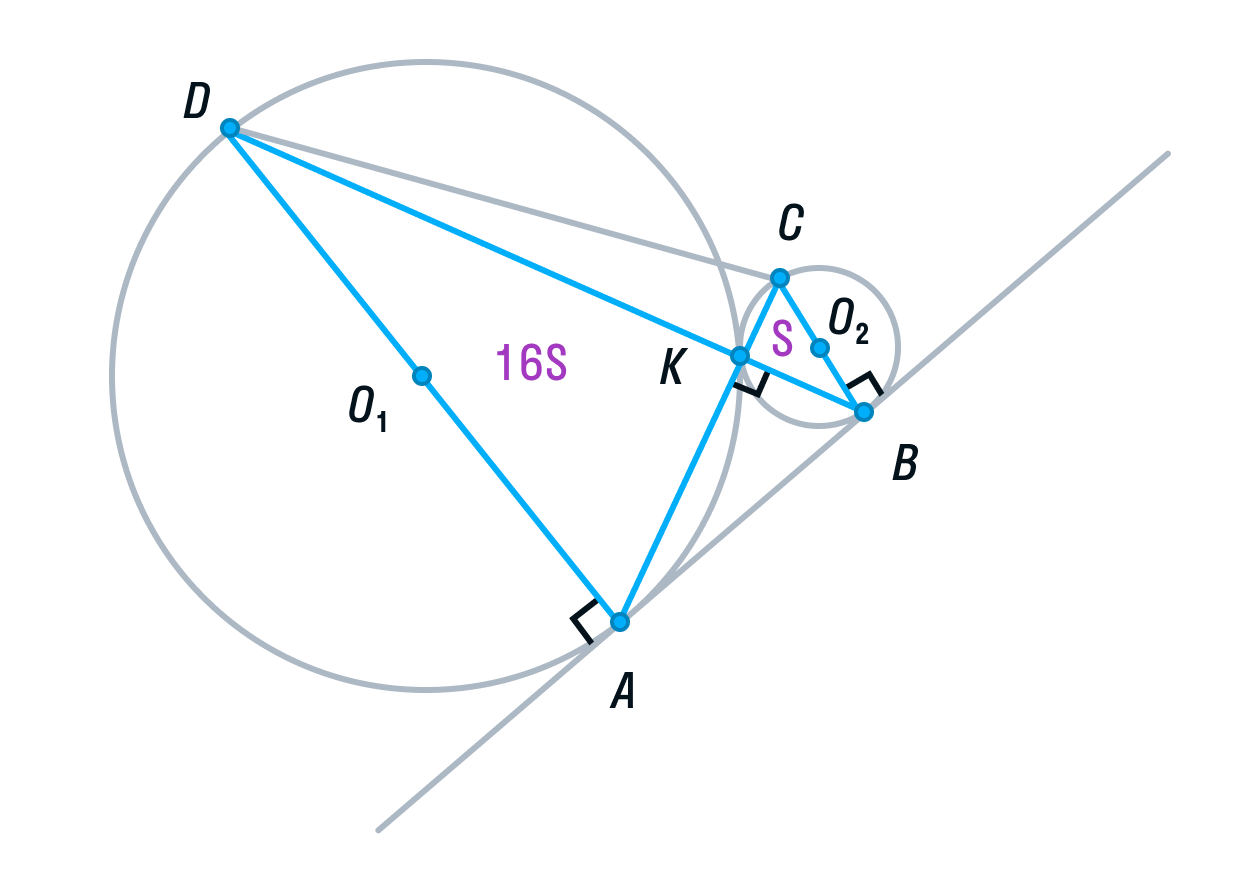
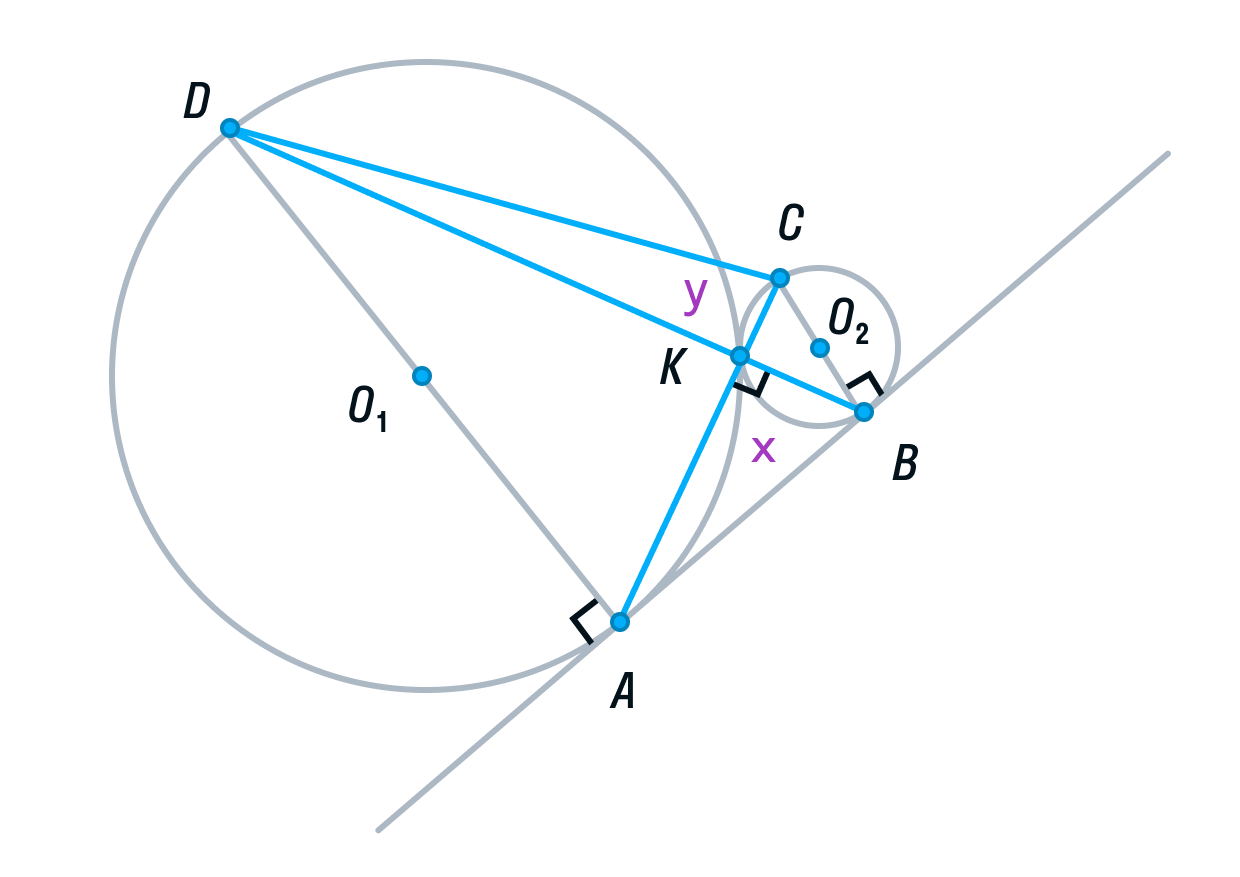
Перед тем, как перейти непосредственно к экзаменационным задачам, необходим подготовительный период – решение задач на доказательство. Для этого разработан специальный материал «Доказательство полезных фактов», где задачи на доказательство расположены по возрастанию сложности. Каждая из таких задач является схемой для решения реальных экзаменационных. Особое внимание уделяется методам доказательства и решения, таким, как удвоение медианы, перестроение чертежа, задаче о трех точках, лежащих на одной прямой, применению равенства и подобия треугольниках в задачах.
Геометрия многим учащимся представляется сложнее алгебры, потому что здесь нет готовых алгоритмов решения (как в теме 1 – текстовых задачах). Зато намного большее значение имеет система ассоциаций и умение комбинировать различные приемы решения.
к оглавлению ▴
Задачи с экономическим содержанием на ЕГЭ по математике.
34. Задачи с экономическим содержанием на ЕГЭ по математике.
35. Арифметическая и геометрическая прогрессии.
36. Формулы для решения задач с экономическим содержанием.
Задачи с экономическим содержанием появились в ЕГЭ по математике совсем недавно, и даже многие учителя не знают, как к ним подойти.
Однако задачи такого типа считаются традиционными на олимпиадах по экономике, а также на 1 курсе экономического факультета МГУ и других вузов. Методика Анны Малковой дает способы решения таких задач, а также готовые формулы и приемы. Методические материалы по этой теме, как и по другим, постоянно дорабатываются, чтобы находиться в соответствии с последними тенденциями ЕГЭ по математике.
к оглавлению ▴
Март.
Задачи с параметрами на ЕГЭ по математике.
37. Элементарные функции и их графики.
38. Преобразования графиков функций.
39. Множества точек на плоскости. «Базовые» схемы решения. Окружность, круг, полуокружность, ромбик, сумма модулей, полуплоскость, полоса, отрезок.
40. Тренировочные задачи с параметрами.
41. Квадратичные уравнения и неравенства с параметрами.
42. Графический метод решения задач с параметрами.
43. Метод симметрии, параметр как переменная и другие методы.
Методика Анны Малковой позволяет за короткие сроки научить абитуриентов решать такую традиционно сложную задачу, как С5 (задача с параметрами). Эта задача – из тех, о которых не пишут в школьных учебниках.
Необходимая подготовительная работа в изучении данной темы – это типы элементарных функций и их графики (5 типов), преобразования графиков функций (сдвиги, растяжения-сжатия, инверсии по горизонтали и вертикали), построение графиков сложных функций. Весь этот материал в программе средней школы дается фрагментарно и факультативно, или же не дается совсем.
От привычных функций одной переменной и их графиков происходит плавный переход к неявным функциям, задающих множества точек на плоскости. Учащийся знакомится с такими базовыми схемами решения задач с параметрами, как окружность, круг, полуокружность, ромбик, сумма модулей, полуплоскость, полоса, отрезок, и с уравнениями, задающими эти объекты на плоскости.
Методика Анны Малковой включает около 15 различных методов решения задач с параметрами, и все они изучаются в течение курса. Это и метод оценки, и критерии единственности решения квадратного уравнения, и метод симметрии, и многие другие.
к оглавлению ▴
Апрель.
Нестандартные задачи на ЕГЭ по математике (С6).
44. Делимость. Признаки делимости. Деление с остатком.
45. Метод «Оценка плюс пример».
46. Реальные нестандартные задачи на ЕГЭ по математике.
Задача С6, последняя в вариантах ЕГЭ по математике, считается самой необычной. В учебниках для 10-11 класса нет даже намеков на существование таких задач.
Долгое время и школьники, и учителя просто боялись таких задач и не приступали к ним. О методах их решения не говорилось ничего, кроме «как-нибудь попробуйте догадаться сами». При этом методы решения задачи С6 существуют и успешно могут быть освоены, о чем свидетельствуют высокие результаты учеников Анны Малковой и других преподавателей, занимающихся этими задачами. Теоретической основной решения задачи С6 являются признаки делимости, приемы записи для деления с остатком, знание об арифметической и геометрической прогрессиях, в том числе целочисленных, основная теорема алгебры (о каноническом разложении натурального числа на множители).
Среди методов одним из основных является «Оценка плюс пример». Сложность С6 еще и в том, что эта задача подразумевает умение выражать свои мысли точным математическим языком, требует определенной математической культуры. Методика Анны Малковой дает ученику возможность решить С6 и понять, что это не задача для избранных, а реальный источник баллов на ЕГЭ.
к оглавлению ▴
Май.
Повторение всех тем и решение вариантов ЕГЭ.
Методика Анны Малковой отличается от многих других еще и тем, что решение вариантов ЕГЭ происходит на заключительном этапе, как итоговая тренировка. На первых этапах подготовки, пока большая часть тем еще не освоена, решение вариантов ЕГЭ может привести лишь к разочарованию учащихся в своих способностях. Это часто и бывает, когда ученик начинает занятия самостоятельно «по интернету» или занимается с неопытным репетитором.
Пробные ЕГЭ для учащихся, занимающихся по методике Анны Малковой, проводятся 1 раз в месяц, причем задачи, не пройденные к данному моменту, не обязательны для решения. На заключительном этапе подготовки обязательны все задачи.
Заключительная часть подготовки к ЕГЭ по методике Анны Малковой нацелена на тренировку решения варианта ЕГЭ без ошибок и в точно отведенное время. Не следует приступать к решению нескольких задач одновременно, так как результат при этом чаще всего нулевой.
к оглавлению ▴
Рекомендуемый хронометраж для учащихся, претендующих на 90-100 баллов ЕГЭ:
1. 20-25 минут – решение, проверка и запись ответов задач части 1 (1-12).
2. 50-60 минут – решение и оформление на чистовике задач 13-15 (С1, С2 и С3).
3. Теперь, когда обязательная программа выполнена, рекомендуется из задач №16-19 выбрать наиболее простую и знакомую, решить ее, проверить и полностью оформить. После этого переходить к решению следующей из оставшихся по тому же принципу.
к оглавлению ▴
Дополнения к Авторской методике Анны Малковой:
1. Программа синхронизирована с Годовым курсом подготовки к ЕГЭ по математике.
2. Каждая тема завершается контрольной работой или зачетом.
3. Материалы и ресурсы для подготовки:
1) Мастер-классы Анны Малковой;
2) Видеокурсы Анны Малковой;
3) Материалы для подготовки бесплатно;
5) Полезные сайты:
www.ege-study.ru — сайт Образовательной компании «ЕГЭ-Студия». В разделе «Материалы ЕГЭ» — полный курс математики. Просто, понятно, без «воды». Вся теория и разбором задач ЕГЭ по математике.
www.reshuege.ru — дистанционная обучающая система для подготовки к ЕГЭ по математике «РЕШУ ЕГЭ». Автор — Дмитрий Гущин. Тысячи заданий ЕГЭ с решениями и ответами.
www.alexlarin.net — сайт Александра Ларина, на котором постоянно публикуются варианты пробных и реальных ЕГЭ. Тренировочные варианты ЕГЭ с разбором на форуме.
к оглавлению ▴
Приложение к методике: Обучающие комплекты видеокурсов Анны Малковой «Получи пятерку» и «Премиум».
Видеокурсы «Получи пятерку» и «Премиум» являются авторскими методическими разработками Анны Малковой. Задача автора видеокурсов — объяснить каждую тему так, чтобы ученик понял, запомнил и смог применять на практике полученные знания.
1. Ученик, который смотрит видеокурс, не может задать автору вопрос, как на уроке. Это означает, что видеокурс должен быть для него максимально понятным. Для этого применены следующие принципы:
1) Чтобы максимально приблизиться к атмосфере урока (или занятия с репетитором), Анна Малкова пользуется обычной белой маркерной доской. Принцип «Учитель в кадре» считается предпочтительным.
2) При этом условия задач, как правило, выводятся на экран на специальных текстовых «плашках».
3) Монтаж видео позволяет оставить «за кадром» моменты написания на доске объемных математических преобразований или наоборот, стирания решенной задачи с доски. Это придает видеокурсу необходимую динамичность.
4) В видеокурсах Анны Малковой используются также средства компьютерной графики и анимации. Например, в ряде видеокурсов появляются забавные мультипликационные персонажи.
2. Есть также ряд чисто методических принципов, по которым построены видеокурсы. Вот некоторые из них:
1) Каждая задача в видеокурсе подобрана так, чтобы лучше всего проиллюстрировать определенную тему, или теорему, или математический прием.
2) Принцип «Одна сложность – в одну единицу времени». Например, при объяснении новой и сложной темы дается задача с максимально простыми вычислениями, чтобы внимание ученика было сконцентрировано именно на новой теме.
3) Еще один принцип. Вводя новое понятие или новый термин, обязательно объясняется, что он значит. Иначе непонятное слово оказывается барьером в восприятии.
4) Для того чтобы усвоить новую тему, необходимо повторение, причем не однократно, а несколько раз.
5) Комплект видеокурсов Анны Малковой построен по определенному принципу – каждая тема является фундаментом для следующей. При этом постоянно отмечаются взаимосвязи между различными разделами математики.
6) Особое внимание уделяется вычислительным приемам. Поскольку на ЕГЭ недопустимо пользоваться калькулятором, в первом же видеокурсе дается ряд приемов быстрого счета без калькулятора. Этими приемами Анна Малкова пользуется в каждом видеокурсе, специально акцентируя на них внимание.
7) Одной из основных проблем старшеклассников является неумение оформить решение задачи части С (части 2) так, как это необходимо для получения высокого балла на ЕГЭ по математике. В видеокурсах даются не только методы решения задач, но и полное, как на экзамене, математически грамотное оформление решения.
Для подготовки видеокурсов использованы как задачи ЕГЭ прошлых лет, так и множеством «классических» задач из сборников для поступающих в вузы. Результатом является полный спектр приемов и «инструментов» для успешного решения любой задачи ЕГЭ по математике.
Внимание! Методика подготовки к ЕГЭ Анны Георгиевны Малковой защищена законом об авторских правах. Все материалы, находящиеся в данном файле, не подлежат воспроизведению в какой-либо форме или каким-либо образом без предварительного письменного разрешения ООО «ЕГЭ-Студия» и Анны Георгиевны Малковой. © 2017.
к оглавлению ▴
Авторское право.
Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Методика подготовки к ЕГЭ по математике. Автор: Анна Георгиевна Малкова.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена:
08.03.2023
Скачать материал

Скачать материал


- Сейчас обучается 234 человека из 62 регионов


- Сейчас обучается 140 человек из 49 регионов


- Сейчас обучается 98 человек из 32 регионов


Описание презентации по отдельным слайдам:
-
1 слайд
МБОУ СОШ № 39
Учитель математики: Кашка Светлана Васильевна
Эффективные методы
подготовки к ЕГЭ по математике -
2 слайд
«Недостаточно лишь понять задачу, необходимо желание решить ее. Без сильного желания решить трудную задачу невозможно, но при наличии такового возможно. Где есть желание, найдется путь!»
Пойа Д.1
-
3 слайд
Сегодня я хочу вам представить свой опыт работы по теме: «Эффективные методы подготовки к ЕГЭ по математике». Основная задача, которая стоит перед каждым учителем, это как можно лучше подготовить учащихся к сдаче ЕГЭ. Потому что результаты, полученные выпускниками на ЕГЭ, это и оценка работы учителя. И учащиеся, и их учителя все больше заинтересованы в получении как можно лучших результатов. Поэтому каждый педагог ищет и применяет в своей работе наиболее эффективные методы, формы и технологии обучения.
Ведущая идея моего опыта — повышение качества математической подготовки школьников на основе использования различных форм и технологий. Работа над этой проблемой у меня началась несколько лет назад. Первоначально это было знакомство с нормативно-правовыми документами, изучение КИМ разных лет, опыта работы других учителей по этой проблеме. Затем начался поиск и отбор форм и методов обучения, которые мне казались эффективными. И только в 2007 году я начала реализовывать свои идеи в работе. Я остановлюсь на тех формах работы и технологиях, которые оказались, на мой взгляд, самыми эффективными.
Жизнь украшается двумя вещами: занятием математикой и её преподаванием!
С.Пуассон
2 -
4 слайд
Основным направлением работы учителя является методическая подготовка к ЕГЭ, которую я провожу в двух направлениях: тематической и по содержательным линиям курса математики. Выстроить подготовку можно следующим образом: разбить материал на несколько крупных тематических блоков, выстроив повторение по содержательным линиям:
1. Числа и вычисления.
Проценты. Пропорции. Решение текстовых задач.
2. Выражения и преобразования.
Корень степени n. Степень с рациональным показателем. Логарифм. Синус, косинус, тангенс, котангенс.
3. Уравнения и неравенства.
Уравнения с одной переменной. Равносильность уравнений: распознавать равносильные уравнения. Общие приемы решения уравнений. Решение простейших уравнений. Системы уравнений с двумя переменными. Неравенства с одной переменной. Системы неравенств. Совокупность неравенств.
4. Функции.
Числовые функции и их свойства. Производная функции. Исследование функции с помощью производной.
5. Геометрические фигуры и их свойства. Измерение геометрических величин.
Признаки равенства и подобия треугольников. Решение треугольников (сумма углов треугольника. Неравенство треугольника. Теорема Пифагора. Теорема синусов и теорема косинусов). Площадь треугольника. Многоугольники. Окружность. Равные векторы. Координаты вектора. Сложение векторов. Умножение вектора на число. Угол между векторами. Скалярное произведение векторов. Многогранники. Тела вращения. Объем тел. Комбинации тел.
Такой подход будет способствовать формированию более прочных знаний и, как следствие, более уверенному поведению выпускника на экзамене вне зависимости от того, в какой форме экзамен будет проводиться.
3 -
5 слайд
Тематическую подготовку начинаю в 10 классе. Начать подготовку к экзамену можно с проведения уже в начале учебного года диагностической работы, которая, с одной стороны поможет выявить пробелы в подготовке учащихся, а с другой стороны, ознакомит учащихся с экзаменационной работой, ее структурой и основными особенностями.
Анализируя работы учащихся, выявляются следующие проблемы:
— неумение выполнять операции с отрицательными числами;
— низкий процент верно решивших геометрические задачи, а большинство вообще не приступали к решению этих задач;
— в заданиях ЕГЭ содержится много нехарактерных вопросов для разных типов учебных задач (например, нужно не просто решить уравнение, а указать наибольший, наибольший целый корень, сумму корней и т.д.);
— проблемы оформления решений в заданиях с развернутым ответом: многословность пояснения очевидных фактов, небрежность работы с модулем, ошибки при внесении переменной под знак корня, небрежность в обосновании решения иррационального уравнения.
4 -
6 слайд
Итоговое повторение в 11-м классе целесообразно организовать «по содержательным блокам».
Тема предваряется необходимой справочной информацией, представленной в максимально сжатой форме.
Затем подробно разбирается большое количество примеров (практически на каждый прием, когда-либо встречавшийся в заданиях ЕГЭ). В этой части присутствуют пример, к которому приведено решение, или несколько аналогичных примеров с небольшими нюансами в решениях.
Затем идут тренировочные упражнения, которые даются в традиционной форме.
Повторение темы должно заканчиваться выполнением тематического теста.
Предлагаю вашему вниманию фрагменты некоторых из них.
5 -
7 слайд
Задание В 1
Тип задания: Задание на вычислениеХарактеристика задания: Задание, моделирующее реальную или близкую к реальной ситуацию. Для решения задачи достаточно уметь выполнять арифметические действия, делать прикидку и оценку, знать, что процент – одна сотая часть числа
Комментарий: Для успешного решения задачи достаточно умения выполнять арифметические действия с целыми и дробными числами, вычислять проценты, читать и понимать условие задачи
6 -
8 слайд
1. Один килограмм огурцов стоит 15 рублей. Мама купила 2 кг 400 г огурцов. Сколько сдачи она должна получить со 100 рублей?
Ответ: 64
2. Андрей Петрович купил автомобиль, на спидометре которого скорость измеряется в милях в час. Миля равна 1609 м. Какова скорость автомобиля в километрах в час, если спидометр показывает 42 мили в час? Ответ округлить до целых
Ответ: 68
3. 1 киловатт-час электроэнергии стоит 1 рубль 60 копеек. Счетчик электроэнергии 1 ноября показывал 32544 киловатт-часа, а 1 декабря 32726 киловатт-часов. Сколько нужно заплатить за электроэнергию за ноябрь? Ответ дать в рублях Ответ: 291,2
4. Пакет сока стоит 32 рубля. Какое наибольшее количество пакетов сока можно купить на 200 рублей? Ответ: 6
5. В пачке бумаги 500 листов. За неделю в офисе расходуется 1200 листов. Какое наименьшее количество пачек бумаги нужно купить в офис на 8 недель? Ответ: 20
6. В магазине проходит рекламная акция: заплатив за 2 шоколадки, покупатель покупает третью в подарок. Шоколадка стоит 35 рублей. Какое наибольшее число шоколадок можно получить на 200 рублей? Ответ: 7
7. Рубашка стоит 450 рублей. Во время распродажи скидка на все товары составляет 20%. Сколько рублей стоит рубашка во время распродажи? Ответ: 360
8. В сентябре 1 кг слив стоил 60 рублей. В октябре сливы подорожали на 25%. Сколько рублей стоил 1 кг слив после подорожания в октябре? Ответ: 75
9. Магазин делает пенсионерам скидку на определенное количество процентов от цены покупки. Пакет кефира стоит в магазине 40 рублей. Пакет заплатил за пакет кефира 38 рублей. Сколько процентов составляет скидка для пенсионеров? Ответ: 5
10. В июне 1 кг огурцов стоил 50 рублей. В июле огурцы подешевели еще на 20%, а в августе – еще на 50%. Сколько рублей стоил 1 кг огурцов после снижения цены в августе? Ответ: 20
11. В городе живет 300000 жителей. Среди них 20% детей и подростков. Среди взрослых 35% не работает (пенсионеры, студенты, домохозяйки и т.п.). Сколько жителей города работает? Ответ: 156000
12. Клиент взял в банке кредит на сумму 30000 рублей с годовой процентной ставкой 14%. Он должен погашать кредит, внося в банк ежемесячно одинаковую сумму денег, чтобы через год выплатить всю сумму, взятую в кредит, вместе с процентами. Сколько рублей он должен вносить в банк ежемесячно? Ответ: 28507
-
9 слайд
Тип задания: Задание на чтение графика функции
Характеристика задания: Задание, моделирующее реальную или близкую к реальной ситуацию. График характеризует изменение в зависимости от времени некоторой величины (температуры, стоимости акций и т.д.). Как правило, в задании требуется найти наибольшее (наименьшее) значение этой величины, разность между наибольшим и наименьшим значением (возможно за определенный период времени), время, когда величина достигает данного значения
Комментарий: Простейшее задание на считывание информации, представленной в виде графика
Задание В 2
8 -
10 слайд
На рисунке показано изменение температуры воздуха в Москве с 14 по 21 января 2006 года. По горизонтали указываются числа января, по вертикали – температура в градусах Цельсия.
а)Определить наименьшую температуру 14 январяб) Определить наибольшую температуру 21 января Ответ: — 22
в) Определить какого числа произошло резкое похолодание (более чем на 15 градусов) Ответ: 16
г) Найти разность между наибольшей и наименьшей температурой за те сутки, когда произошло резкое похолодание Ответ: 19Ответ: — 2
9
-
11 слайд
2. На рисунке жирными точками показана среднемесячная цена нефти во все месяцы 1998 и 1999 годов. По горизонтали указываются месяцы, по вертикали – цена барреля нефти (в долларах)
Определить среднемесячную цену нефти в мае 1998 Ответ: 14
Определить сколько раз за указанный период среднемесячная цена нефти была ровно 14 долларов Ответ: 3
Определить во сколько раз среднемесячная цена нефти в августе 1999 года превосходила среднемесячную цену нефти в декабре 1998Ответ: 2
Определить сколько раз среднемесячная цена нефти принимала наименьшее значение Ответ: 2
Определить разность между наибольшей и наименьшей среднемесячной ценой нефти в указанный период Ответ: 16
10
-
12 слайд
Задание В 3
Тип задания: Уравнение
Характеристика задания: Несложное показательное, логарифмическое или иррациональное уравнение
Комментарий: Уравнение сводится в одно действие к линейному или квадратному (в последнем случае в зависимости от условия в ответе нужно указать только один из корней – меньший или больший). Неправильные ответы связаны в основном с арифметическими ошибками или неуверенным владением понятия степени (особенно с отрицательным показателем)
11
-
13 слайд
Найдите корень уравнения.
12 -
14 слайд
Найдите корень уравнения.
13 -
-
16 слайд
Найдите корень уравнения. Если уравнение имеет более одного корня, то укажите наименьший (наибольший).
15 -
17 слайд
5-x=3
x=5-3
x=2
Найдите корень уравнения
16 -
18 слайд
Задание В10
Тип задания: Задание на анализ практической ситуации, сводящееся к решению уравнения или неравенства
Характеристика задания: Текстовое задание, моделирующее реальную или близкую к реальной ситуацию (например, экономические, физические, химические и др. процессы)
Комментарий: По условию задачи требуется составить уравнение или неравенство, сводимое к линейному или квадратному, решив которое, записать в ответ искомую величину -
19 слайд
1. КПД теплового двигателя вычисляется по формуле .
При каком наименьшем значении температуры нагревателя Т1 КПД двигателя будет не менее 75%, если температура холодильника Т2 = 350 К. Ответ: 1400
2. Зависимость объема спроса на продукцию некоторой фирмы от цены продукции задается формулой q(p) = 280 – 10p, где p – цена (тыс.руб); q – спрос (единиц в месяц). Определить максимальный уровень цены (в тыс.руб), при котором значение выручки предприятия за месяц r = q·p составит не менее 960 тыс.рубОтвет: 24
3. Операционная прибыль предприятия в краткосрочном периоде вычисляются по формуле h(q) = q(p – v) – f. Компания продает свою продукцию по цене p = 400 руб. за штуку, затраты на производство одной единицы продукции составляют v = 300 руб. за штуку, постоянные расходы предприятия f = 800000 руб. в месяц. Определить наименьший месячный объём производства q (шт.), при котором прибыль предприятия будет не меньше 700000 руб. в месяц.Ответ: 15000
4. Высота столба жидкости в баке с открытым краном меняется по закону H(t) = 1,28 – 0,8t + 0,125 t2, где t – время в минутах, H – высота в метрах. Через несколько минут после открытия крана вода полностью вытечет из бака? Ответ: 3,2
5. Зависимость температуры нагревательного элемента прибора от времени имеет вид T(t) = Т0 + at + bt2 , где Т0 = 100К, a = 37,5 К/мин, b = — 0,25 К/ мин2 . Прибор может испортится при температуре свыше 1000К. Определить момент времени (в минутах), когда прибор необходимо выключить чтобы он не вышел из строя. Ответ: 30
6. В розетку электросети подключены приборы, общее сопротивление которых составляет 70 Ом. Параллельно с ними в розетку предполагается подключить электрообогреватель. Чему равно наименьшее возможное сопротивление (в Омах) этого обогревателя, если известно, что при параллельном соединении двух проводников с сопротивлениями R1 и R2 их общее сопротивление определяется формулой, а для нормального функционирования электросети общее сопротивление в ней должно быть не меньше 21 Ом? Ответ: 3017
-
20 слайд
7. Для определения эффективной температуры звезд используют закон Стефона-Больцмана, согласно которому мощность излучения нагретого тела прямопропорциональна площади поверхности и четвертой степени температуры: P = σST4 , где σ = 5,7·10-8 — числовой коэффициент, площадь измеряется в квадратных метрах, температура – в Кельвинах, а мощность – в ваттах. Известно, что некоторая звезда имеет площадь S = 1/7·1016 м2 , а излучаемая ею мощность P = 19,551·1022 Вт. Определить температуру этой звезды. Ответ: 7000
8. Изменение высоты полета брошенного вертикально вверх мяча описывается формулой h(t) = — 5t2 + 30t (h – высота в метрах, t – время в секундах. Сколько секунд мяч находился на высоте не менее 25 м? Ответ: 49. При температуре 00 С рельс имеет длину l0 = 20 м. При прокладке путей между рельсами оставили зазор в 6 мм. При возрастании температуры будет происходить тепловое расширение рельса и его длина будет меняться по закону l(t0 ) = l0 (1 + αt0 ), где α = 1,2·10-5 0С-1 — коэффициент теплового расширения, t0 — температура (в градусах Цельсия). При какой минимальной температуре между рельсами исчезнет зазор? (ответ выразить в градусах Цельсия)Ответ: 20
10. Парашютисты-экстремалы определяют высоту сооружений для будущих прыжков, засекая время падения небольших камней с вершин сооружений до поверхности приземления. Приближенная зависимость от времени свободного падения имеет вид h = 4,9t2 . Здесь y – высота в метрах, t – время в секундах. С вершины первого сооружения камень падал 4,5 с. На сколько метров второе сооружение выше первого, если с вершины второго сооружения камень падал на 1 с дольше? Ответ: 49
11. При вращении ведерка с водой на веревке в вертикальной плоскости сила давления на дно воды не остается постоянной: она максимальна в нижней точке и минимальна в верхней. Вода не будет выливаться, если сила ее давления на дно будет положительна во всех точках траектории. В верхней точке сила давления равна P = m(V2 /L – g), где m – масса воды, V – скорость движения ведерка, L – длина веревки, g – ускорение свободного падения. С какой минимальной скоростью (в м/с) надо вращать ведерко, чтобы вода не выливалась из него, если длина веревки 10 см? (g считать равным 10 м/с2 )Ответ: 3.
18
-
21 слайд
Задание В11
Тип задания: Задание на исследование функции с помощью производной
Характеристика задания: Задание на вычисление с помощью производной экстремума данной функции или наибольшего (наименьшего) значения данной функции на заданном отрезке
Комментарий: Решение задачи связано с нахождением при помощи производной точек максимума (минимума) заданной функции или ее наибольшего (наименьшего) значения на отрезке. Если функция задана формулой, то при нахождении наибольшего (наименьшего) значения функции на отрезке можно использовать стандартный алгоритм19
-
22 слайд
Таблица производных
20 -
23 слайд
Правила вычисления производных
(f(x)+g(x))´=f´(x)+g´(x)
(f(x)-g(x))´=f´(x)-g´(x)
(f(x)·g(x))´=f´(x)·g(x)+f(x)·g´(x)
(f(x)/g(x))´=(f´(x)·g(x)-f(x)·g´(x))/g2(x)
(f(g(x))´=f´(g(x))·g´(x)Алгоритм отыскания наибольшего (наименьшего) значения функции
на заданном отрезке
1. Найти производную функции
2. Найти значения х, при которых производная равна нулю
3. Выбрать из значений х, найденных в п.2 те, которые принадлежат заданному отрезку
4. Вычислить значения функции на концах заданного отрезка и в точках, определенных в п.3
5. Выбрать наибольшее (наименьшее) значение функции21
-
24 слайд
Ответ: 0
РешениеНайти наименьшее значение функции
на отрезке [-9; -7]
22 -
25 слайд
2. Найти наименьшее значение функции
на отрезке [0; π/2]
Ответ: -15
Решение
23 -
26 слайд
3. Найти наибольшее значение функции
на отрезке [0; π/2]
Ответ: 3
Решение
24 -
27 слайд
4. Найти наибольшее значение функции
на отрезке [-4; -1]
Ответ: -6
Решение
25 -
28 слайд
5. Найти точку минимума функции у = х – 5lnх
Ответ: 5
РешениеВ точке х = 5 производная меняет знак с + на -. Значит х = 5 – единственная точка минимума
26 -
29 слайд
6. Найти наибольшее значение функции у = 5 – 7х + 7ln(х + 3) на отрезке [-2,5; 0]
Ответ: 19
Решение
27 -
30 слайд
Перед началом изучения каждой темы, я обязательно просматриваю задания, которые предлагают авторы учебника и литературу по подготовке к ЕГЭ, с той целью, чтобы дополнить набор упражнений учебника, заданиями, которые могут встретиться учащимся на экзамене по изучаемой теме. Тематическую подготовку выстраиваю «по правилу спирали»,- от простых к заданиям со звездочкой в учебнике, от комплексных типовых заданий части 1 до заданий раздела части С. В конце изучения параграфа провожу уроки решения задач ЕГЭ. Это и обычные по форме уроки, и уроки организации работы в группах, когда каждый учит каждого, т.е. уроки, на которых применяется технология сотрудничества. Наблюдая за работой на уроке, заметила, что вместе учиться не только легче и интереснее, но и значительно эффективнее. При разборе задач у учащихся часто возникают различные вопросы, и оказать каждому помощь на уроке не возможно, но если ученики работают в группах, они быстрее находят пути решения и могут оказать друг другу консультативную помощь. Эта форма эффективна и при работе с тестами, т.е. тест, дается не индивидуально каждому, а паре учащихся. Причем при такой организации труда можно осуществлять и дифференцированный подход.
28 -
31 слайд
Класс условно делится на три группы. Для себя я эти группы называю
А, В, С.
Группа С — ученики, которые интересуются предметом, решают задачи
продвинутого уровня.
Группа В – самостоятельно могут решать задачи среднего уровня.
Группа А – ученики, решающие стандартные задачи, используя
образцы и алгоритмы решения. Задания для каждой группы различны.
При организации тематической подготовки к экзамену я использую такую
форму как долгосрочное домашнее задание. Учащимся предлагается
набор заданий, которые они должны выполнить в промежуток изучения
конкретной темы. Два года назад, начиная использовать эту форму работы, я не дифференцировала задание. И в результате оказывалось, что часть учеников не справлялась с большей частью заданий, а некоторые уже через несколько дней сдавали тетради на проверку, так как предложенные упражнения оказывались для них очень простыми и не развивали учеников, то есть такая организация работы не давала положительных результатов. У каждого ученика имеется тематический сборник по подготовке к ЕГЭ. Задания в нем даны по уровням. Набор заданий формирую для каждой группы отдельный: группа С — минимальное количество заданий базового уровня, задачи повышенного и высокого уровня сложности, для учеников группы В предлагаю задания базового и повышенного уровней, а для учащихся группы А основную часть составляют задачи базового уровня. Долгосрочные домашние задания выполняются в специальных тетрадях, которые затем сдают на проверку. После проверки, рекомендую выполнить работу над ошибками. Тех учеников, которые выполнили правильно менее половины задач, приглашаю во внеурочное время на дополнительное занятие, после которого они работают над ошибками. Считаю, что эту форму работы необходимо использовать, так как для успешной сдачи ЕГЭ недостаточно хорошо работать на уроках и регулярно выполнять домашние задания, необходимо ещё дополнительная подготовка. Долгосрочными домашними работами, я некоторым образом обязываю учеников заниматься дополнительно.
29 -
32 слайд
Ещё мне хочется остановиться на системе устных упражнений. Развитие скорости устных вычислений и преобразований, а также развитие навыков решения простейших задач «в уме» является важным моментом подготовки ученика к ЕГЭ. Для организации устной работы на уроке мне помогают информационные технологии, которые способствуют активизации учебного процесса, развивают познавательный интерес. Презентации незаменимы в тех случаях, когда задания содержат рисунки и графики, то есть то, что практически невозможно подготовить перед уроком на доске, а использование интерактивной доски позволяет на слайде делать необходимые пометки, в случае, если возникают какие-то вопросы. При этом следует обратить внимание и на упражнения сопутствующего повторения. Почти все уроки я начинаю с небольшой устной работы, на которой предлагаю задания по изучаемой теме и задачи на повторение. Конечно же, сопутствующее повторение это не только устные упражнения, это решение задач, требующих оформления решения. Важно, чтобы это повторение было не разовым мероприятием, а постоянным и обязательно отслеживались темы. Я поступаю следующим образом. В кодификаторе есть таблица, в которой перечислены все темы, выходящие на итоговую аттестацию. Дополняю эту таблицу столбцами справа, вверху записываю дату урока и отмечаю в таблице темы, задания по которым выполнялись на уроке. Таким образом, чтобы подготовить к уроку упражнения, мне не нужно просматривать поурочные планы, а достаточно взять таблицу и за секунды я уже могу определиться с набором заданий на планируемый урок. Организация выполнения устных упражнений на уроках дали определенный результат. Отслеживая результаты пробных ЕГЭ в прошлом году, я убедилась, что количество заданий 1 части, выполняемых учениками, увеличивалось, а время выполнения этих задач уменьшалось. К концу года большинство учеников класса выполняли 1 часть теста ЕГЭ за время, рекомендованное в спецификации.
30 -
33 слайд
В1. Тетрадь стоит 20 рублей. Какое наибольшее число таких тетрадей можно купить на 550 рублей после понижения цены на 25%?
В2. На рисунке жирными точками показана цена золота на момент закрытия биржевых торгов во все рабочие дни с 6 по 19 ноября 2008 года. По горизонтали указываются числа месяца , по вертикали – цена унции золота в долларах США. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, какого числа цена золота на момент закрытия торгов была наибольшей.В3. Найдите корень уравнения
В4. В треугольнике ABC угол C равен 900, AB=30, AC=24.
Найдите sinAВ6. Найдите площадь треугольника, изображенного на клетчатой бумаге
с размером клетки 1 см×1 см (см. рисунок).
Ответ дайте в квадратныхсантиметрах.
В7. Найдите значение выраженияВ8. На рисунке изображены график функции y=f(x) и касательная к этому графику, проведенная в точке с абсциссой х0. Найдите значение производной функции f(x) в точке х0
31 -
34 слайд
Компьютерные технологии при подготовке к ЕГЭ можно использовать и при организации других форм работы: тестирование, решение заданий ЕГЭ в режиме онлайн. Такую работу можно организовать в кабинетах информатики. Учащимся такая форма решения тестов ЕГЭ очень нравится, поэтому они продолжают эту работу дома, так как практически у всех есть компьютер и интернет.
Ежедневно в начале урока я провожу небольшие самостоятельные разноуровневые работы на время, содержащие задания из банка ЕГЭ. Эту работу можно начинать уже в 10 классе, тогда к 11 классу основная масса задач будет отработана и у учащихся будет время для выполнения более сложных задач.
У нас в школе имеется методическая копилка тренировочных тестов, это и тематические и тесты, выстроенные по содержательным линиям курса, и презентации, и просто КИМ разных лет. Конечно помогают и интернет ресурсы, и материал предлагаемый учителями МО района, ККИДППО. Эта копилка постоянно обновляется и пополняется.
Ежемесячные диагностические контрольные работы в 10 и 11 классах так же имеют положительный эффект. В диагностическую работу включаются задания различных типов и разного уровня сложности для дифференциации учащихся по уровням подготовки. Тесты выстраиваются по содержательным линиям курса математики, изученных в определенный период. После проверки учащимся рекомендуется выполнить работу над ошибками. С учащимися, не справившимися с заданиями теста, организую дополнительные консультации, после которых они выполняют подобный тест. На основе диагностических контрольных работ формирую и пополняю базу данных ЕГЭ. Распределение заданий по темам позволяет учащимся дифференцированно отрабатывать задачи по той или иной группе.
32 -
35 слайд
Особое внимание в процессе деятельности по подготовке учащихся к ЕГЭ занимает мониторинг качества обученности, который должен быть системным и комплексным. В связи с этим на каждого учащегося заводится диагностическая карта, куда в течение двух лет вносятся результаты диагностических, самостоятельных, контрольных работ, причем по каждое теме. Это позволяет проследить степень подготовки учащегося по той или иной теме и контролировать отработку навыков, готовить индивидуальные задания, дифференцированно подходить к планированию урока. Все тренировочные тесты, выполненные на листочках или на бланках ЕГЭ, учащиеся собирают в папки, которые хранятся в кабинете. Собирая тренировочные тесты, я могу отслеживать динамику роста у отдельных учеников, контролировать выполнение работы над ошибками, выявлять темы, которые на данном этапе обучения плохо усвоены, для корректировки процесса обучения через повторение, использовать для организации индивидуальной работы. Кроме того, мне нужно это для работы с родителями.
33 -
36 слайд
Диагностическая карта подготовки к ЕГЭ по математике
ученика 11 «Б» класса МОУ СОШ № 39
_______________________________________________________
(Ф.И.О.) 2010/11 учебный год
Учитель математики Кашка Светлана Васильевна
34 -
37 слайд
Важен так же и психологический настрой учащихся, так как некоторым трудно преодолеть психологическое напряжение и включиться в работу и тогда я цитирую своим ученикам совет Дейла Карнеги из его книги «Как выступать публично»:
«Смотри на присутствующих, как на людей, которые должны тебе по 100 долларов и вот уже год не отдают долг!»
И знаете — помогает, многие ребята с улыбкой делятся, что на ДКР страх уходит! И юмор никогда не повредит! А если серьезно: на стенде по подготовке к ЕГЭ в кабинете вывешиваю
ОБЩИЕ РЕКОМЕНДАЦИИ, АДРЕСОВАННЫЕ ВСЕМ УЧАЩИМСЯ35
-
38 слайд
ОБЩИЕ РЕКОМЕНДАЦИИ, АДРЕСОВАННЫЕ ВСЕМ УЧАЩИМСЯ:
1. В задачах части 1 полученный ответ часто можно проверить, поставив его исходную задач–сделайте это. Такая возможность есть.
2. Решать задачи лучше по порядку. Если задача для вас трудна, то пропустите ее и переходите к решению следующей. НЕ вписывайте придуманные ответы, лучше оставьте пустые места.
3. После того как были просмотрены и частично решены все задания части 1, вернитесь и поработайте с задачами, которые не получились с первой попытки.
4. Если после второго прохода все же останутся «белые пятна», то не следует заполнять их наугад. Постарайтесь вернуться к ним в конце всей работы.
5. На экзамене отсутствует справочный материал, поэтому постарайтесь вспомнить (вывести) необходимые формулы и т.д.
6. После выполнения заданий части 1 сделайте небольшой перерыв в 3-5 минут, постарайтесь от состояния «гонки» настроиться на спокойную и вдумчивую работу.
7. Приготовьтесь к тому, что задачи этой части имеют «подводные камни».
8. Не забывайте о краткости записи при «полном» обосновании.
9. Если задача сложная и сразу не видно способов решения, а время экзамена подходит к концу, не стремитесь начинать решение новой задачи – лучше еще раз проверьте решения заданий частей 1 и 2.
10. Для решения заданий экзамена калькулятор не предусматривается (запрещен), поэтому особое внимание уделите проверке выполнения арифметических действий.
36 -
39 слайд
В 2011 году 19 моих учеников сдавали экзамен по математике в форме ЕГЭ.
Все выпускники успешно сдали ЕГЭ.
Средний балл составил 53 балла что на 6,7 балла выше краевого показателя.
Я считаю, что кропотливая совместная работа учителя и учеников способна повысить математическую грамотность школьников и дать возможность успешно сдать ЕГЭ.
37
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 156 467 материалов в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Другие материалы
- 29.09.2015
- 1236
- 0
- 29.09.2015
- 999
- 0
Рейтинг:
5 из 5
- 29.09.2015
- 3586
- 30
- 29.09.2015
- 3250
- 12
- 29.09.2015
- 1644
- 0
- 29.09.2015
- 1475
- 0
Вам будут интересны эти курсы:
-
Курс повышения квалификации «Внедрение системы компьютерной математики в процесс обучения математике в старших классах в рамках реализации ФГОС»
-
Курс повышения квалификации «Педагогическое проектирование как средство оптимизации труда учителя математики в условиях ФГОС второго поколения»
-
Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»
-
Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Специфика преподавания основ финансовой грамотности в общеобразовательной школе»
-
Курс повышения квалификации «Специфика преподавания информатики в начальных классах с учетом ФГОС НОО»
-
Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»
-
Курс профессиональной переподготовки «Теория и методика обучения информатике в начальной школе»
-
Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
-
Курс профессиональной переподготовки «Инженерная графика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Методика преподавания курса «Шахматы» в общеобразовательных организациях в рамках ФГОС НОО»
-
Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»
-
Курс профессиональной переподготовки «Черчение: теория и методика преподавания в образовательной организации»
ДОКЛАД
Эффективные приемы и методы подготовки учащихся к успешной сдаче ЕГЭ по математики.
В основу построения рекомендаций положены принципы развития математического образования, определение приоритетных и перспективных направлений, а также анализ наиболее типичных ошибок, допущенных в решении заданий базового и профильного экзамена.
Возрастание роли математики в современной жизни привело к тому, что для адаптации в современном обществе и активному участию в нем необходимо быть математически грамотным человеком. В связи со стратегическими направлениями социально — экономического развития России до 2020 года: «Приоритетной государственной задачей является обеспечение качественного базового уровня математических и естественнонаучных знаний у всех выпускниковшколы, не только будущих ученых, но и будущих квалифицированных рабочих…» Каждый школьник в процессе обучения должен иметь возможность получить полноценную подготовку к выпускным экзаменам. Формула успеха хорошо сдать экзамен ЕГЭ и ОГЭ по математике: Высокая степень восприимчивости + мотивация + компетентный педагог.
Практика показывает, что прорешивание открытых вариантов ЕГЭ прошлых лет не даёт ожидаемого эффекта. Разобрав вариант в классе, учитель даёт аналогичный вариант для домашнего разбора. После удачного разбора в классе домашний вариант не представляет большого труда, и у обучающегося и учителя складывается ложное впечатление, что подготовка идет эффективно и цель достигнута. Многократное повторение этих манипуляций не улучшает ситуацию. Когда участник на ЕГЭ получает свой вариант, он обнаруживает, что этот вариант он с учителем не решал. Привычка повторять разобранные ранее варианты часто идет во вред обучению.
Правильным подходом является систематическое изучение материала, решение большого числа задач по каждой теме – от простых к сложным, изучение отдельных методов решения задач. Разумеется, варианты подготовительных сборников, открытые варианты можно и нужно использовать в качестве источника заданий, но их решение не должно становиться главной целью; они должны давать возможность иллюстрировать и отрабатывать те или иные методы. В любом случае, при проведении диагностических работ следует подбирать задачи, прямые аналоги которых в классе не разбирались. Только так учитель может составить верное представление об уровне знаний и умений своих учеников.
Компенсирующее обучение в старших классах.
Часто мы сталкиваемся с ситуацией, когда главенствующим методическим принципом оказывается принцип «прохождения программы», – то есть программа должна быть пройдена во что бы то ни стало, невзирая на то, что содержание этой программы может не отвечать реальным возможностям и подготовке обучающихся.
С введением нового ФГОС, реализацией Концепции развития математического образования, принятием федеральных примерных образовательных программ по математике принцип прохождения программы приобретает новый смысл – обучающийся должен участвовать в посильной интеллектуальной математической деятельности, дающей осязаемые плоды обучения.
Компенсирующая программа как вариант базовой программы для старших классов даёт возможность учителю сделать уроки математики для наименее подготовленных обучающихся осмысленными. При этом появляется реальная возможность эффективно подготовить обучающихся к решению 8 – 10 заданий профильного ЕГЭ.
Практико-ориентированная математика.
Важной частью ЕГЭ по математике и современных программ являются задачи на применение математических знаний в быту, в реальных жизненных ситуациях. Это задачи на проценты, оптимальный выбор из предложенных вариантов, чтение данных, представленных в виде диаграмм, графиков или таблиц, вычисление площадей или других геометрических величин по рисунку, задачи на вычисление по формулам и т.п.
Круг практико-ориентированных задач в ЕГЭ постоянно расширяется; дополнительно к ним следует отнести задачи вероятностно-статистического блока.
Сложилась практика, когда к практическим задачам учитель приступает только в последний год перед сдачей ЕГЭ. К этому времени обучающиеся успели прочно забыть, как вычислять проценты, как находить площади фигур с помощью палетки или на клетчатой бумаге – все эти задачи для них оказываются новыми.
На протяжении всего периода обучения математике не следует отрываться от простых практических задач; их следует включать в блоки повторения в начале и конце учебного года, в текущий, внутришкольный контроль. Задачи на вычисление сумм налогов, процентов по банковскому вкладу или кредиту, другие задачи финансового характера должны стать постоянным инструментом на уроках математики, поскольку эти задачи связывают наш предмет с окружающим миром и повседневной жизнью.
Практико-ориентированные задачи по финансовой грамотности, геометрического плана, чтение таблиц и графиков нужно включать в изучение математики в средней и старшей школе. При этом характер и трудность задач могут меняться со временем, более того, это необходимо для органического вплетения практических тем в изучение теоретических вопросов. Например, задачи на вклады и кредиты органично возникают при изучении прогрессий, показательной функции и производных. Вычисление площадей по клеточкам очень часто помогает при изучении совершенно абстрактной, казалось бы, темы «первообразная и интеграл». Чтение простых графиков помогает понять и грамотно на качественном уровне применять производную.
Отдельную важную роль в сближении школьной математики с задачами окружающего мира играют вопросы вероятностей и статистики.
Теория вероятности и статистика.
В Концепции развития математического образования ТВ и статистика названы в числе перспективных и важных направлений развития школьной математики. С 2012 года задачи по ТВ формально включаются в КИМ ОГЭ и ЕГЭ. При этом учителя понимают, что те задачи, которые сейчас есть в открытом банке заданий и те, что включены в экзамен, в большинстве случаев сводятся к перечислению равновозможных исходов.
Ясно, что роль ТВ и статистики в школьной математике будет расти. Одновременно будет расширяться круг тем, подлежащих контролю.
При обучении математике следует больше внимания уделять темам вероятности и статистики, постепенно нарабатывая опыт преподавания этих разделов, которые оказываются наиболее практически направленными. Изучение вероятности и статистики требуется вести в тесной привязке к темам алгебры и геометрии, поскольку систематический подход к вопросам ТВ требует от обучающихся знаний о свойствах геометрической прогрессии преобразованиях многочленов, корнях и степенях, площадях фигур.
Таким образом, правильно выстроенное преподавание вероятности не отнимает время, а, напротив, поддерживает изучение традиционных разделов школьной математики. В 2012 – 2014 году задачи по ТВ, появившись в экзамене, вызывали большие трудности, и выполнение этих заданий редко поднималось выше 50%. В настоящее время ситуация изменилась. На данный момент медиана выполнения задания 4 – около 90%.
Некоторые эффективные приёмы обучения математике.
Остановимся подробнее на некоторых приёмах обучения математике, доказавших свою эффективность.
1) При решении задач одним из эффективных приёмов является использование примеров и образцов. Скажем, ученик получает задачу и готовое решение, которое он должен разобрать самостоятельно. Решение может быть дополнено советами, комментариями трудных или «опасных» моментов, другими способами решения и т.п. Когнитивная нагрузка в данном случае получает управляющий импульс и осуществляется в заданном направлении. Важным условием является выход на стратегию, которую можно будет применить в дальнейшем при решении широкого круга задач. Следующим этапом может стать работа не с готовым решением, а с заданным алгоритмом решения, который ученик должен самостоятельно применить к данной ему задаче. После этого можно провести решение полностью самостоятельно. Покажем это (без потери общности) на простой задаче.
Условие. Каждый из двух друзей одновременно показывает на руке случайное количество пальцев от 1 до 5. С какой вероятностью в сумме получится число 8?
Решение. Общее число исходов равно: 25. Благоприятными событию «получится в сумме число 8» будут исходы: 3 + 5, 5 + 3, 4 + 4. Вероятность события равна: 3/25 = 0,12. Ответ: 0,12.
Комментарий. Следует различать две комбинации, когда один из друзей показывает 3 пальца, а другой – 5 пальцев. Ответ можно записать как обыкновенной дробью, так и десятичной.
Задание для самостоятельного решения. Каждый из двух друзей показывает на руке случайное количество пальцев от 1 до 5. С какой вероятностью в сумме получится число 7?
Описанный приём может использоваться применительно к отдельному заданию, однако из таких заданий – с решениями и комментариями – можно составить тематическую проверочную работу, которую можно использовать и в рамках подготовки к экзамену. Решения могут быть написаны учителем самостоятельно, могут быть взяты из публикуемых сборников для подготовки к ЕГЭ, а также из материалов журнала «Математика» или других источников.
2) Весьма эффективно использование при решении задач подсказок, то есть некоторой дополнительной информации, которая дается ученику после (что важно!) того, как он начал работать над задачей. Чем определеннее подсказка, тем больше из нее можно извлечь. Фразы: «Хорошо подумай», «Внимательно прочти условие задачи», «Подумай о других способах решения» подсказками не являются, поскольку они никак не направляют ход мысли и не помогают найти решение.
Пример. Решите уравнение.
Подсказка. Можно применить формулу синуса суммы двух углов. Подсказкой может быть похожая задача, которая решалась недавно, указание на конкретный метод. Всегда полезно использовать результаты, методы уже решённых задач, а также опыт, приобретенный при решении. Это широко используется в школьном курсе геометрии, где многие важные геометрические факты, которыми целесообразно пользоваться при решении других задач, даны не в виде утверждений (теорем), а в виде задач. Кроме того, это возможность использования еще одного метода – аналогии.
При решении тригонометрических уравнений подсказкой может быть определённая формула, а при решении логарифмического уравнения – свойство логарифма. Полезно учить пользоваться подсказками, искать их самостоятельно, а также учить давать подсказки.
3) При обучении решению сложных или трудоёмких в плане вычислений и преобразований задач полезно использовать групповые формы работы, а в качестве приёма – мозговой штурм. Основные принципы мозгового штурма: на первом этапе – предложение как можно большего количества решений, без оценки их применимости, рациональности и проч., на втором – анализ и вывод о целесообразности предложенного, выбор наиболее удачных идей и предложений. Ценность приема – в стимулировании поисковой активности на первом этапе и критичности мышления на втором. Хорошо применим данный прием при поиске различных способов решения геометрических задач и тригонометрических уравнений.
4) При решении текстовых задач важным приёмом, необходимым для усвоения, является переформулирование условия, отношений, связывающих входящие в задачу величины. Ниже приводится пример такой задачи из варианта профильного экзамена.
«Задание 11. Заказ на изготовление 323 деталей первый рабочий выполняет на 2 ч быстрее, чем второй. Сколько деталей изготавливает первый рабочий, если известно, что он изготавливает на 2 детали больше второго?»
Данную задачу экзаменуемые решили существенно хуже, чем аналогичную задачу с более привычной и хорошо отработанной фабулой, связанной с движением двух велосипедистов.
Умение переформулировать условие важно и при решении нестандартных задач, то есть таких, метод решения которых ученику не известен, не изучался и не отрабатывался на уроках.
Ещё более актуально это умение при решении практико- ориентированных задач, представляющих собой некоторую ситуацию из реальной жизни, которую необходимо преобразовать и описать на языке математики (то есть самостоятельно сформулировать задачу). В самом простом случае основа задачи будет следующая: за лестницей, которую прислонили к стене дома, надо распознать прямоугольный треугольник, гипотенузой которого и будет данная лестница.
5).В связи с введением обязательного ЕГЭ и ОГЭ по математике возникает необходимость научить учащихся решать быстро и качественно задачи базового уровня. При этом необыкновенно возрастает роль устных
вычислений, так как на экзамене не разрешается использовать калькулятор и таблицы. Можно научить учащихся выполнять простейшие (и не очень) преобразования устно. Конечно, для этого потребуется организовать отработку такого навыка до автоматизма,
на каждом уроке необходимо отводить 5 — 7 минут для проведения упражнений устных вычислений, предусмотренных программой каждого
класса. Устные упражнения активизируют мыслительную деятельность учащихся, требуют осознанного усвоения учебного материала; при их выполнении
развивается память, речь, внимание, быстрота реакции.
Если в 5 — 6 классах устный счет – это выполнение действий с числами:
натуральные числа, обыкновенные дроби, десятичные дроби, то в старших
классах – это могут быть:
7 класс: Формулы сокращенного умножения. Решение простейших ЛУР. Действия со степенью. График линейной
функции.
8 класс: Линейные неравенства и числовые промежутки.
Решение простейших линейных неравенств. Решение КВУР с помощью
теоремы Виета и частных случаев. Решение КВУР рациональными способами. Арифметический квадратный корень и его свойства. 9 класс: Решение неравенств 2 степени. Преобразование графиков функций. Формулы приведения. Значения тригонометрических функций.
10 — 11 классах: Вычисление производных. Простейшие тригонометрические неравенства. Тригонометрические формулы. Простейшие тригонометрические уравнения. Функции, обратные тригонометрическим. Преобразование графиков функций. Вычисление первообразных. Свойства логарифмов. Простейшие показательные уравнения
и неравенства. Простейшие логарифмические уравнения и неравенства. Практика показала, что систематическая работа с устным счетом способствует значительному повышению продуктивности вычислений и преобразований. Сокращается время на выполнение таких операций, что переводит их из разряда самостоятельной задачи в разряд вспомогательной и становится инструментом (“таблицей
умножения”) для решения более сложных задач. Учитель по математике, знающий, с чем придется столкнуться школьнику на экзамене, кроме фундамента уделяет большую часть времени на занятии отработке вопросов специфики ЕГЭ и ОГЭ. Правильность оформления заданий, тактика и стратегия решения в условиях дефицита выделенного времени на экзамене, а также банальная невнимательность. Эти и масса других особенностей составляют
суть специфики. Для эффективной подготовки к ЕГЭ и ОГЭ нужна тренировка, тренировка и еще раз тренировка. Довести решение задач до автоматизма.
Развитие геометрических представлений
Процент выполнения экзаменующимися геометрических заданий традиционно ниже, чем процент выполнения заданий алгебраических. Одна из основных причин – недостатки в формировании пространственного мышления учащихся. Массово эта проблема проявилась с уходом из общего образования такого учебного предмета, как черчение, и вряд ли стоит ожидать его возвращения – профессия конструктора перестала быть столь массово востребованной с приходом компьютерных технологий.
Эта проблема легла на плечи учителей математики, однако решение её известно: непрерывное развитие геометрических представлений и геометрического воображения обучающихся с 1 по 11 класс; наглядная геометрия в 1–6 классах; больше внимания геометрическому моделированию и конструированию (из плоских и пространственных фигур), геометрическим чертежам, построениям, изображениям от руки и с помощью различных чертёжных инструментов, на нелинованной и клетчатой бумаге.
Это отнюдь не означает, что всю геометрию надо свести к наглядности и к работе руками. Определения и доказательства, логика и аксиоматика важны для современного человека и для изучения геометрии не менее, но надо понимать, что в развитии человека всему отводится свое время, а несформированное наглядно-образное мышление, которое должно быть основой и этапом на пути формирования логического мышления, просто мешает его формированию.
Если вернуться к этапу обучения в старшей школе, то целесообразно использовать любые приёмы и средства, которые способствовали бы визуализации предлагаемых обучающимся задач. Это не только построение чертежей по условию задачи (что непросто сделать при проблемах с пространственным воображением), это прежде всего различные предметные модели (полезно для каждой решаемой задачи иметь соответствующую ей модель-подсказку, чтобы использовать её для визуализации условия, поиска и проверки решения), компьютерные программы, позволяющие выполнять стереометрические чертежи.
Полезно выделить эту работу в отдельный тематический практикум, на котором обучающиеся тренировались бы в изображении и моделировании пространственных тел, построении чертежей по условию задачи (в различных ракурсах, выбирая наиболее удобный для поиска решения), можно также организовать данную работу в рамках проекта.
Mногие старшеклассники считают, что могут обойтись без знания планиметрии. Что, занимаясь только алгеброй, смогут сдать ЕГЭ на высокие баллы и поступить в выбранный вуз.
Работает ли эта стратегия?
Oтвет преподавателей-экспертов: нет, не работает. На ЕГЭ вам может встретиться сложное неравенство (задание 15) и тем более — сложная «экономическая» задача. Так было в 2018 году. И всё, баллов фатально не хватает! Тех самых баллов, которые можно было легко получить за планиметрическую задачу, не хватает для поступления!
Cтоит учесть, что задачи вариантов ЕГЭ по планиметрии и стереометрии бывают намного проще, чем по алгебре.
1) Cамое важное — правильная методика подготовки. Не нужно начинать с реальных задач ЕГЭ. Cначала — теория. Cвойства геометрических фигур. Oпределения и теоремы. Учить наизусть.
Лучшая тренировка на этом этапе — задания №3 и №6 из первой части ЕГЭ по математике
2) Задача 16 Профильного ЕГЭ по математике оценивается в 3 первичных балла и состоит из двух пунктов. Первый пункт — доказательство. Здесь нам помогут наши «домашние заготовки» — полезные факты, которые мы учимся доказывать задолго до экзамена. A на ЕГЭ остается только вспомнить и записать решение.
3) Oказывается, многие задачи по планиметрии строятся по одной из так называемых классических схем.
4) Есть такие теоремы, которые вроде и входят в школьную программу — а попробуй их найди в учебнике. Например, теорема о секущей и касательной или свойство биссектрисы.
5.) Любая задача из варианта ЕГЭ решается без сложных формул. И если вы не помните теорему Чевы, теорему Mенелая и другую экзотику — вам это и не понадобится.
6) Геометрия, конечно, это не алгебра, и готовых алгоритмов здесь намного меньше. Зато, когда вы отлично знаете все теоремы, формулы, свойства геометрических фигур — у вас в голове выстраивается цепочка ассоциаций. Например, в условии задачи дан радиус вписанной окружности. B каких формулах он встречается? — Правильно, в теореме синусов и в одной из формул для площади треугольника.
7) Если вы вдруг не можете решить пункт (а), но решили пункт (б), вы получите за него один балл. A это лучше, чем ничего. Но вообще пункт (а), как правило, бывает простым. Иногда вопрос в пункте (а) очень простой. И это не только для того, чтобы вы получили «утешительный» балл. Помните, что пункт (а) часто содержит подсказку, идею для решения пункта (б).
Саморегуляция и обратная связь «ученик-учитель».
Известно, что эффективность обучения возрастает в случае самооценивания, поскольку ученик самостоятельно получает информацию о своих результатах, сам её анализирует, делает выводы о своем прогрессе, корректирует цели в случае необходимости. Но для этого необходимы критерии оценивания работы, которые должны быть у ученика не просто до начала выполнения конкретной работы, но желательно и в самом начале изучения темы. К сожалению, на практике более распространена ситуация, когда работа выдаётся ученику без критериев ее выполнения.
К саморегуляции относятся также вопросы, связанные с осознанностью знания и незнания. Объяснение учителя сродни лекционной форме предъявления новых знаний. В связи с этим подчеркнём важность обратной связи. Учитель должен получать сигналы от обучающихся: «Я понимаю, могу объяснить», «Я не уверен, правильно ли я понимаю», «Я не понимаю». Учитель может прервать своё объяснение вопросом к тем, кто ещё не понял, предложением высказать свои сомнения тем, кто не уверен в понимании, предоставлением слова тем, кто всё понял.
Доказано, что обратная связь эффективна, если ученик получает сообщение о верно выполненных заданиях, а не только об ошибках, если он получает не просто маркеры, свидетельствующие о положительном результате, не просто похвалу за решённую задачу, а и некоторый содержательный комментарий. Этот комментарий может включать в себя такую оценку, как «рациональное решение», «интересная идея», «грамотная запись». Может быть отмечена актуальность проверки результата, удачное прохождение «ловушек» и «опасных» мест и т.п.
Обратная связь эффективна в случае, если она конкретна, то есть связана с известными ученику результатами и действиями, подлежащими усвоению. Важное значение имеет информированность ученика относительно того, чему он должен научиться, какие задания должен научиться решать, а какие может научиться решать для того, чтобы получить желаемое количество баллов на экзамене. Если ученик фиксирует и отслеживает сам, умеет ли он выполнять требуемое задание или нет, то минимизируется время на выполнение заданий, при этом работа становится более эффективной и рациональной. Отсюда необходимость в открытости предъявляемых требований к результатам обучения, а на этапе подготовки к экзамену – в ориентации на конечный запланированный результат.
И еще об одном факторе следует упомянуть – это повторяющееся тестирование. Уже имеющийся опыт российской школы и более продолжительный зарубежный опыт не позволяют говорить о нём, как об эффективном факторе. Положительные эффекты возникают только в тех случаях, когда учитель учитывает результаты тестирования для корректировки процесса обучения и приспосабливает методы обучения к возможностям конкретного ученика, учитывая его сильные и слабые стороны, или при условии содержательной обратной связи, с которой ученик может работать самостоятельно, то есть имеет возможность учиться на тестах.
Завершающие рекомендации.
Необходимо отметить, что создание ЕГЭ по математике базового уровня и появление акцента на использование математических знаний в реальных ситуациях были неверно истолкованы некоторыми учителями в качестве генеральной идеи обучения, что привело к поверхностному освоению обучающимися программы старшей школы. В частности, это зафиксировано и результатами экзамена: результаты выполнения заданий по темам курса старшей школы ниже результатов выполнения заданий из «реальной математики».
Для того чтобы успешно сдать ЕГЭ по математике, важно пройти всю программу целиком, а не только «то, что пригодится на экзамене», повысить свою культуру вычислений, то есть минимизировать использование калькуляторов, развивать умение читать графики, правильно использовать терминологию и учить формулы.
Для учащихся, которые могут успешно освоить курс математики средней (полной) школы на базовом уровне, образовательный акцент должен быть сделан на полное изучение традиционных курсов алгебры и начал анализа и геометрии на базовом уровне. Помимо заданий базового уровня в образовательном процессе должны использоваться задания повышенного уровня. Количество часов математики должно быть не менее 5 часов в неделю.
Для учащихся, которые могут успешно освоить курс математики полной (средней) школы на профильном (повышенном) уровне, образовательный акцент должен быть сделан на полное изучение традиционных курсов алгебры и начал анализа и геометрии на профильном уровне. Количество часов математики должно быть не менее 6–7 часов в неделю.
В первую очередь нужно выработать у обучающихся быстрое и правильное выполнение заданий части 1, используя, в том числе и банк заданий экзамена базового уровня. Умения, необходимые для выполнения заданий базового уровня, должны быть под постоянным контролем.
Задания с кратким ответом (повышенного уровня) части 2 должны находить отражение в содержании математического образования, и аналогичные задания должны включаться в систему текущего и рубежного контроля.
В записи решений к заданиям с развернутым ответом нужно особое внимание обращать на построение чертежей и рисунков, лаконичность пояснений, доказательность рассуждений.
И в завершение необходимо отметить, что еще одним важным фактором является психологический климат в учебном коллективе: дружеские отношения среди одноклассников, спокойная рабочая атмосфера на уроке, методичная, прозрачная и последовательная подготовка к экзамену, доверительные отношения учителя с учениками, вера в достижение более высоких результатов и эмоциональная поддержка.
На занятиях стараюсь создать атмосферу комфортности,
взаимопонимания. На своих уроках я делаю установку на то, чтобы любой ребенок должен быть понят и услышан учителем и соучеником: учение должно проходить в «атмосфере непринужденности, чтобы дети и учитель свободно дышали на уроках». От учителя требуется и мастерство, и большое терпение, и любовь к учащимся. Доброжелательное отношение к ученикам снимает у них страх перед трудностями обучения: ребенок не должен бояться
ошибиться, спросить учителя, если он что то прослушал или не понял. Психологическая подготовка учащихся, может заключается в следующем:
отработка поведения в период подготовки к экзамену; обучение навыкам
саморегуляции, самоконтроля, повышение уверенности в себе, в своих силах. Методы проведения занятий по психологической подготовке учащихся разнообразны: групповая дискуссия, игровые методы, медитативные техники, Содержание занятий должно ориентироваться на следующие вопросы: как подготовиться к экзаменам, поведение на экзамене, способы снятия нервнопсихического напряжения, как противостоять стрессу.
Литература:
Методические рекомендации для учителей, подготовленные на основе анализа типичных ошибок участников ЕГЭ 2019 года по математике, подготовленные ФГБНУ «ФИПИ».
Методические рекомендации для учителей, подготовленные на основе анализа типичных ошибок участников ЕГЭ 2020 года по математике, подготовленные ФГБНУ «ФИПИ».
Бабанский Ю.К. Активность и самостоятельность учащихся в обучении / М.Ю. Бабанский М., Педагогика, 1989.
Беспалько В.П. Слагаемые педагогической технологии / Беспалько В.П. – М., 1989.
Красновский Э.А. Активизация учебного познания / Красновский Э.А. // Советская педагогика. – 1989. №5.
Эльконин Д. Б. Избранные педагогические труды. / Под ред. В.В. Давыдова, В.П. Зинченко.М., 1989.
Щукина Г.И. Активизация познавательной деятельности в учебном процессе/ Щукина Г.И. М., 1979.
Муниципальное бюджетное общеобразовательное учреждение
«Кардымовская средняя школа
имени Героя Советского Союза С.Н. Решетова»
Кардымовского района Смоленской области
Заседание МО
учителей математики,
физики и информатики
Эффективные формы и методы
подготовки к ЕГЭ по математике
(из опыта работы)
Сообщение подготовила:
Е. П. Серкова
п. Кардымово
Февраль 2017
Происходящие в последние годы значительные изменения в российской системе образования, связаны не только с демократизацией общества и переходом страны к рыночным отношениям, но и созданием условий для развития разнообразных типов и видов образовательных учреждений, внедрением в практику вариативных образовательных программ, учебников, методик и технологий обучения.
Единый государственный экзамен по математике – серьёзное испытание в жизни каждого выпускника школы. Вот уже несколько лет он является обязательным для всех учащихся 11 классов и основная его цель – независимая экспертиза качества знаний и совмещение выпускного и вступительного экзаменов.
Проблемами современного этапа математической подготовки учащихся к выпускным и вступительным экзаменам в форме ЕГЭ являются и сложность самой математики как науки, и психофизиологические основы формирования готовности старшеклассников к выпускным экзаменам по предмету.
Организация промежуточных тестирований, использование информационных технологий, проведение выпускных экзаменов за курс основной школы в режиме ЕГЭ позволяет, на мой взгляд, формировать систему общеучебных умений и навыков, прежде всего, умений и навыков самоконтроля, самоанализа и рефлексии, самообразования, выработки знаний о самом себе, об особенностях познавательного процесса при усвоении знаний.
В современных условиях совершенствование учебного процесса должно затрагивать не только выпускные классы, но и всю среднюю школу, все методические службы, системы повышения квалификации учителей математики, авторские коллективы по написанию учебников, пособий и рекомендаций для учащихся. В связи с государственным статусом ЕГЭ по математике меняются и критерии оценок работы учителей выпускных классов. Аттестационные комиссии, подвергая анализу, результаты ЕГЭ по математике, рассматривают их как показатель квалификации учителя, его профессионализма. Основная задача, которая стоит перед каждым учителем, это как можно лучше подготовить учащихся к сдаче ЕГЭ. Потому что результаты, полученные выпускниками на ЕГЭ, это и оценка работы учителя. Важным аспектом работы по подготовке к ЕГЭ является формирование позитивного отношения к тестовому итоговому контролю, как к одной из форм оценки результатов обучения. Оценка эта дается не только ученику, но и учителю, школе, региону. И учащиеся, и их учителя все больше заинтересованы в получении как можно лучших результатов. Поэтому каждый педагог ищет и применяет в своей работе наиболее эффективные методы, формы и технологии обучения. Огромная ответственность за результат легла на учителя ещё и потому, что ЕГЭ был призван заменить собой два экзамена – выпускной за среднюю школу и вступительный в высшие и средние учебные заведения.
Основная моя цель — повышение качества математической подготовки школьников на основе использования различных форм и технологий. Работа над этой проблемой у меня началась несколько лет назад. Первоначально это было знакомство с нормативно-правовыми документами, изучение КИМ разных лет, опыта работы других учителей по этой проблеме. Затем начался поиск и отбор форм и методов обучения, которые мне казались эффективными.
Главное то, что на курсах школьному учителю общеобразовательной школы была дана установка на подготовку детей к ЕГЭ. Для отработки навыков решения сложных задач необходима систематическая углублённая индивидуальная работа. Учитывая всё это, я поставила для себя конкретные задачи по подготовке школьников к ЕГЭ и с 2008 года успешно реализую их.
Задачи по подготовке детей к ЕГЭ:
1. В выпускных классах начинать консультации по подготовке к ГИА и ЕГЭ с сентября месяца.
2. Использовать готовые печатные и электронные пособия, сайты по подготовке к ГИА и ЕГЭ.
3. Учить школьников «технике сдачи теста»;
4. Психологическая подготовка к ГИА и ЕГЭ;
5. Через систему дополнительных занятий (элективных курсов, индивидуальных консультаций) повышать интерес к предмету и личную ответственность школьника за результаты обучения.
Во-первых, я никогда не пугаю школьников предстоящим ГИА и ЕГЭ. Наоборот, с первых же дней учёбы убеждаю их в том, что если очень постараться, то можно получить вполне приличный балл. Главное не упустить время.
Во-вторых, в течение всего года знакомлю детей с материалами ГИА и ЕГЭ, с новыми пособиями, с интернет сайтами.
В-третьих, знакомлю учащихся с особенностями новой формы итоговой аттестации: со структурой теста, временными рамками, нормами оценивания экзаменационной работы, условиями проведения экзамена. Начинаю обучать «технике сдачи теста»:
— обучаю строгому самоконтролю времени;
— учу определять трудность заданий;
— учу правильно заполнять бланки ответов.
Приучаю ребят к методу «пристального взгляда» — внимательно посмотри: «Нет ли короткого пути решения? Так как ты ограничен во времени». Учу определять трудность заданий? Сначала прошу учеников просмотреть тест от начала до конца и отметить карандашом те задания, которые кажутся им простыми и лёгкими и выполнить их в «режиме скорости». Затем, отметить 2-3 задания, которые им понятны по формулировке, но требуют большего времени и выполнить их; и только после этого, если останется время, можно поразмышлять над остальными.
Обязательно напоминаю о том, что полученный результат можно проверить подстановкой, т. е. «прикинуть» имеет ли он смысл. Двигаясь по тесту, дети знают, что сложность заданий нарастает, поэтому всегда советую настойчиво и добросовестно отрабатывать первую часть, только затем можно приступать ко второй части – это и есть принцип «спирального движения» по тесту. По результатам достижений сама определяю двух, трёх учеников, которых можно подготовить к выполнению более сложных заданий и работаю с ними строго индивидуально. Индивидуально работаю и со слабыми.
Чтобы работу по подготовке к экзамену проводить в течение всего учебного года в кабинете необходимо иметь огромное количество тестового материала. У меня в кабинете имеется методическая копилка тренировочных тестов, это и тематические тесты, выстроенные по содержательным линиям курса, и просто КИМ разных лет. Приобрела для кабинета большое количество методической и математической литературы по ключевым вопросам ЕГЭ. Эта копилка постоянно обновляется и пополняется.
В течение учебного года в 10-11 классе, помимо репетиционных ЕГЭ проводятся диагностические тестовые работы. В начале года входные, в конце итоговые, входящие в компетенцию администрации. В диагностическую работу включаются задания различных типов и разного уровня сложности для дифференциации учащихся по уровням подготовки. Тесты выстраиваются по содержательным линиям курса математики, изученных в определенный период. Провожу консультации со всем классом и плюс к этому индивидуальные консультации. Для хорошей подготовки к экзамену необходимо целенаправленное повторение. Организую на уроках повторение через систему упражнений, составленных на основе материалов ЕГЭ. Учебники часто не готовят детей к ЕГЭ, в них по-прежнему традиционные формулировки заданий. После объяснения нового материала и его первичного закрепления показываю, как эта тема вышла на ЕГЭ. Стараюсь при этом продемонстрировать всё разнообразие заданий из первой и второй части, используя сборники с материалами ЕГЭ разных лет. Четвёртую четверть в 9, 11 классах посвящаю переходу к комплексным тестам, учу ребят оценивать итоги работы над тестом в целом.
Все тренировочные тесты, выполненные на листочках или на бланках ЕГЭ, учащихся собираю в папки, которые хранятся в кабинете. Собирая тренировочные тесты, я могу отслеживать динамику роста у отдельных учеников, контролировать выполнение работы над ошибками, выявлять темы, которые на данном этапе обучения плохо усвоены, для корректировки процесса обучения через повторение, использовать для организации индивидуальной работы. Кроме того, мне нужно это для работы с родителями. И я считаю, что кропотливая совместная работа учителя и учеников способна повысить математическую грамотность школьников и дать возможность успешно сдать ЕГЭ.
В заключении хочу сказать, что такая система подготовки детей к итоговой аттестации помогала мне получать неплохие результаты .
Обычно базовую математику выбирают ребята, у которых есть план: надо как можно скорее разделаться с бесполезным для поступления предметом и сосредоточиться на своем наборе вступительных. Из этой статьи вы узнаете, как сдать базовую математику максимально быстро и просто.
В этом материале мы сделаем акцент на простых номерах, которые принесут вам балл почти задаром! Они обозначены пометкой «Обязательно делать» — таких заданий 10. Как раз с запасом на ошибки, ведь минимум для сдачи базовой математики — 7 баллов.
Для тех, кто хочет получить выше тройки — это 12 баллов и выше, — мы дали рекомендации по еще 3 задачам. В сумме получается 13 номеров. Решите их все, и твердая четверка у вас в кармане.
Какие задания решать, чтобы сдать базовую математику
Задание 1: обязательно делать
Проверяется ваше умение разделить случаи, когда требуется округлить величину в большую сторону, а когда — в меньшую.

Если вы ходите в магазин с наличными, то сталкиваетесь с подобными задачами каждый день. Разделим 100 рублей на стоимость одной упаковки йогурта. Не забывайте приводить все величины к одной размерности:
100 : 14,6 = 6, 849…
Так сколько баночек йогурта вам продадут? На 7 штук денег не хватает, значит, округлить полученную величину надо до целого в меньшую сторону. Математическое правило округление в этой задаче не поможет.
Ответ: 6.

Если одна пачка рассчитана на 6 рулонов, то на 63 рулона:
63 : 6 = 10,5.
Но полпачки вам не продаст. Включаем логику: возьмем меньше — не хватит еще половины пачки на три последних рулона. Значит, округлить надо в большую сторону, взять клей с небольшим запасом. Математическое правило округления снова игнорируем.
Ответ: 11.
Задание 2: обязательно делать
Это задача на здравый смысл. Нужно соотнести величины с их возможными значениями.

Вряд ли грузовой автомобиль может весить как 3 шоколадки (300 г), а взрослый человек — 8 т.
Давайте вместе подберем значения.
- Взрослый человек обычно весит от 50 до 100 кг — что из этого подходит? Конечно, 65 кг.
- Грузовой автомобиль достаточно большой и тяжелый, скорее всего, он весит несколько тонн. Нам подходит 8 т.
- Книга обычно не такая большая и весит до 1 кг. Из оставшегося подойдет 300 г.
- А пуговка совсем маленькая. Значит, берем самый легкий вес — 5 г.
Ответ:
Главное — внимательно перенести ответы в бланк: 3142.
Задание 3: обязательно делать
Задание на работу с графиком, диаграммой или таблицей. Вооружайтесь карандашом, читайте условие с предельной внимательностью и безжалостно отмечайте нужные по условию значения на изображении в КИМ. Вы и представить не можете, сколько выпускников теряет тут баллы по невнимательности.
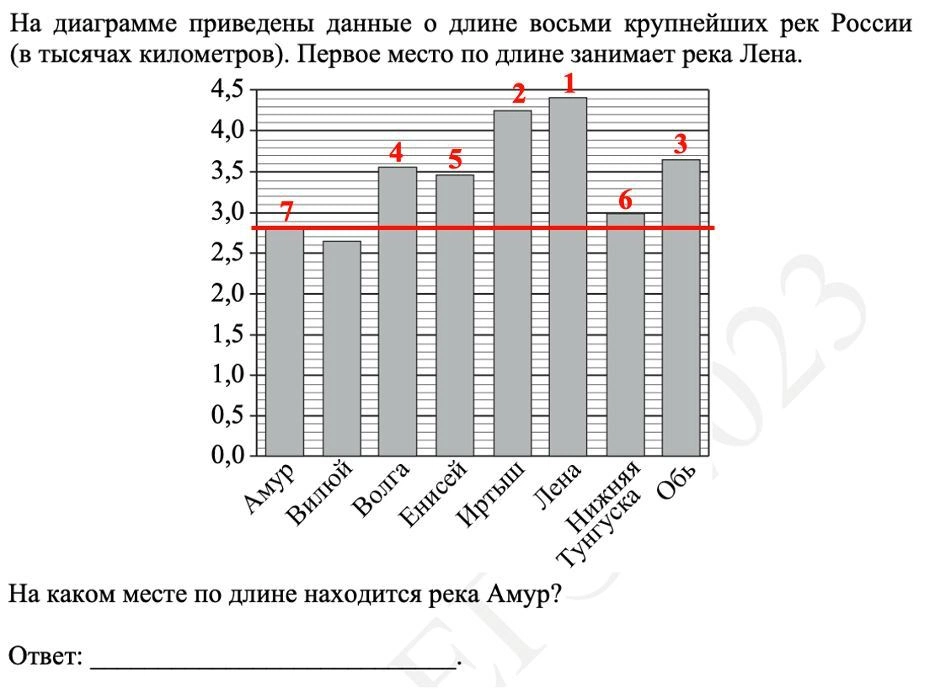
Мы ярко отметили уровень, соответствующий Амуру, в итоге посчитать все более длинные реки стало проще простого. У вас на экзамене будет так же наглядно!
Ответ: 7.
Задание 4: обязательно делать
Задание проверяет навык работы с формулами. Алгоритм решения напоминает решение задачек на уроке по физике:
- Выписываем формулу из условия.
- Определяем, что нужно найти: единственную букву, значение которой не дано.
- Выражаем искомую величину.
- Подставляем значения из условия в формулу.
- Ищем неизвестное.
Самое трудное тут — правильно выразить искомую величину. Для этого повторяем порядок выполнения арифметических операций, свойства умножения, тренируемся перекидывать через равно множители и слагаемые.
И да, в базе эта задача проста настолько, что даже перекидывать ничего не придется. Нужная величина уже будет слева от равно.
Задание 5: обязательно делать
Простая задача на определение вероятности, которая поможет вам точно сдать базовую математику.
Решаем с помощью формулы:
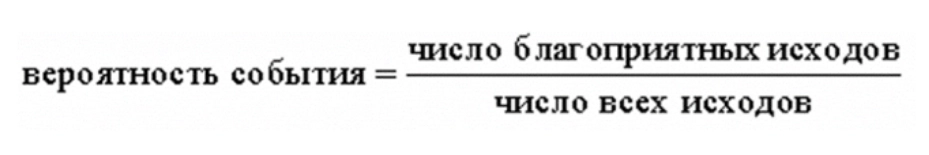

Внимательно читайте вопрос: спрашивают вероятность купить исправную лампочку. Если из ста 3 неисправны, значит, остальные в порядке и подойдет любая из оставшихся 97. Это и есть наши благоприятные исходы из формулы.
97 : 100 = 0,97.
Ответ: 0,97.
Будьте внимательны: иногда в задаче есть указание к округлению. Значит, ответ у вас выйдет некрасивый, в виде бесконечной десятичной дроби, которую вы округлите до нужного разряда.
Еще один подвох: формулировка с предлогом «на». К примеру, «На 100 лампочек 3 неисправны. Найдите вероятность купить неисправную». Подходящие исходы тут даны явно: 3 неисправные лампочки. А вот число всех исходов спрятано, и найти его будет нужно сложением исправных и неисправных лампочек: 100 + 3 = 103.
Задание 6: обязательно делать
Задание проверяет навык чтения информации из таблицы и подбора подходящего по условию варианта.
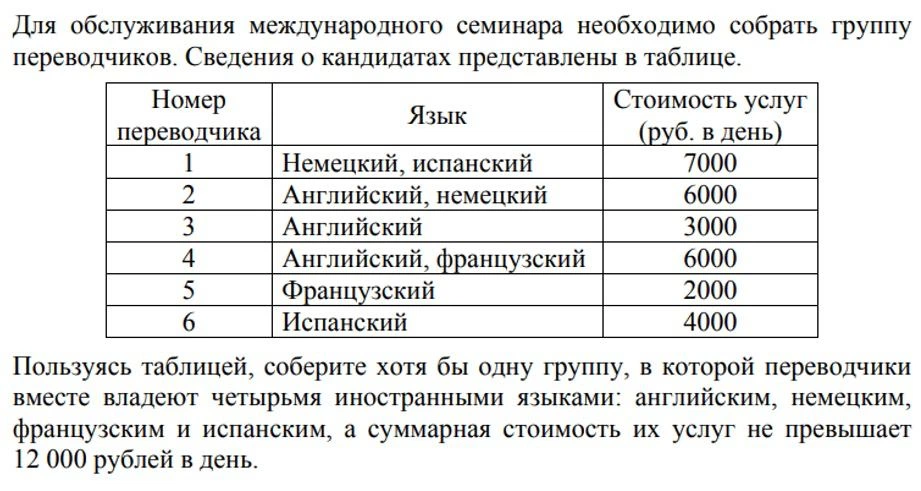
Например, вы нашли вариант позвать первого, третьего и пятого переводчиков. Получите весь набор языков как раз за 12 тысяч. Но обратите внимание, что это решение далеко не единственное.
Ответ: 135.
Задание 7
Мы не выделяем это задание в обязательные, так как для его выполнения понадобится навык анализа поведения функции по графику. Но, как его решать, сейчас коротко расскажем.
Запомним: точка максимума будет на «горке», точка минимума — в «ямке». Функция убывает, если идет вниз слева направо. Возрастает, если идет вверх слева направо.
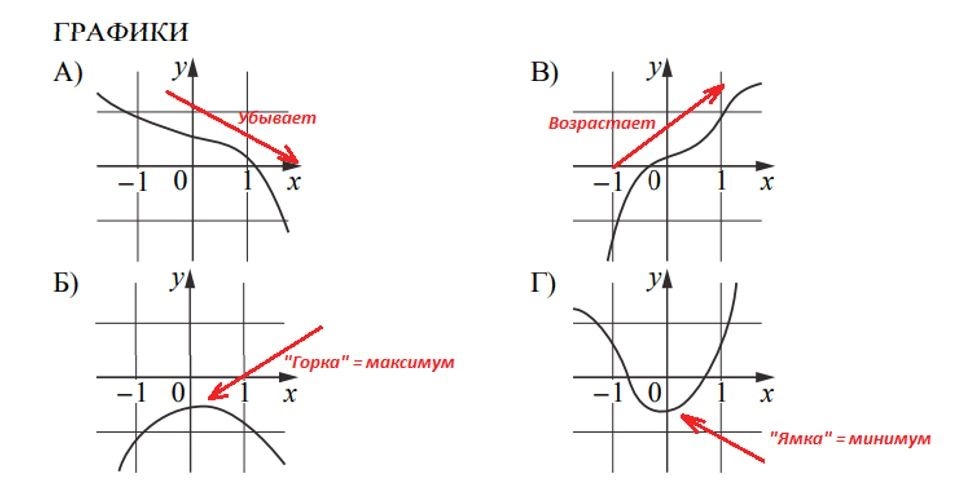
Если не повезет, то придется вспомнить азы теории по производной.
Здесь все дело в касательных. Нужно внимательно к ним присмотреться. Если касательная к графику возрастает, то значение производной будет положительное, если убывает — отрицательное. Производная будет тем больше по величине (модулю), чем быстрее возрастает или убывает касательная.
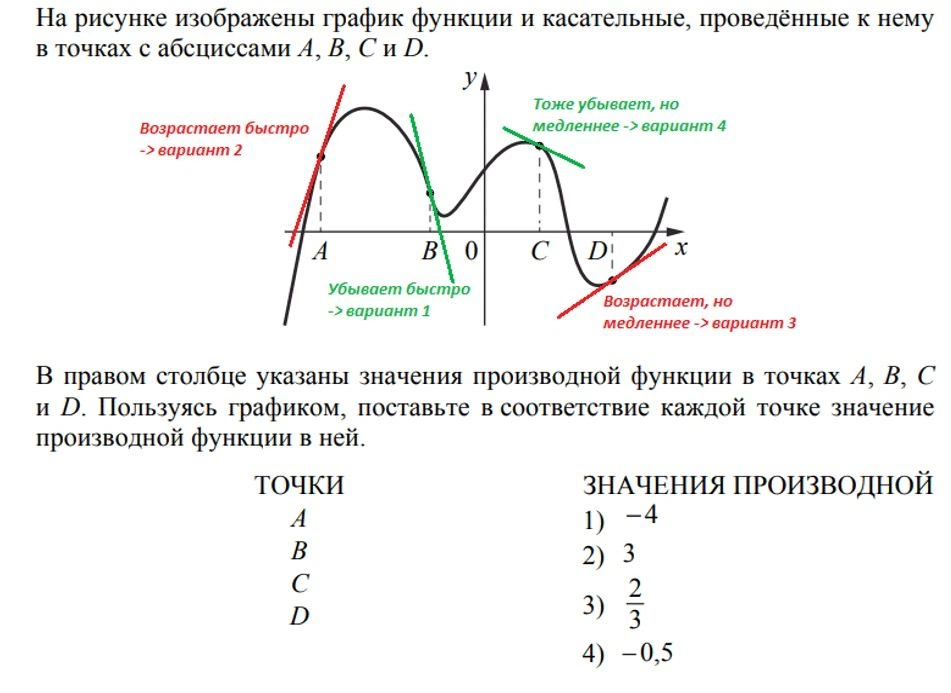
Ответ: 2143.
Задание 8: обязательно делать
Задача проверяет умение делать логичные выводы из утверждения. Иногда попадаются совсем простые задания, к таким даже дополнительно готовиться не надо.

Все, что от вас требуется, — схематично изобразить на черновике ясень, рябину и осину, указать известную разницу в высоте и внимательно сопоставить картинку с утверждениями.
Важно: не додумывайте дополнительные условия, не указанные в тексте задачи. Учитесь читать строго то, что написано.
Исходя из рисунка выше получаем, что верны только утверждения 1 и 4.
Ответ: 14.
А бывают случаи, когда с визуализацией задачки придется постараться.

Тут иллюстрация не так очевидна, но нам помогут круги Эйлера. Этот инструмент позволяет наглядно изобразить множество объектов. В данном случае — школьников. Давайте прикинем, как ребята могут распределиться по кружкам.
Например, так. Тут из 20 человек на кружки в итоге ходят 13. Причем 10 из них очень активны и выбрали сразу два предмета. Трое ограничились только историей.
Или вот так. Если ребята задались целью по максимуму не пересекаться на дополнительных занятиях, то… У них не получится, и как минимум трое запишутся сразу на оба факультатива.
Конечно, возможны еще промежуточные варианты, но мы нарисовали два крайних. Теперь попробуем ответить на вопросы.
- Смотрим на первую картинку. Даже если все ребята будут очень стараться посетить оба кружка, они ограничены условиями задачи и максимум на оба попадут 10 человек из 20. Нет.
- Тут надо рассмотреть другую крайность, которую мы изобразили на второй картинке. Как бы ребята ни старались не встречаться на кружках, хотя бы трое попадут на оба сразу. Да.
- Уж точно неверно. На обеих наших картинках есть ребята, которые ходят на историю, но не ходят на математику. Нет.
- Смотрим на первую картинку. Оба кружка могут посещать максимум 10 человек.
Ответ: 24.
Так что для решения иногда мало логики — понадобится еще немного воображения. Потренируйтесь, и ваши шансы получить балл увеличатся.
Задание 14: обязательно делать
Задание проверяет базовые навыки счета, которым учат в 5–6-м классах. Чтобы получить балл и сдать базовую математику, надо:
- уметь выполнять арифметические действия с обыкновенными и десятичными дробями;
- правильно расставлять порядок действий;
- быть предельно внимательными.
Уделите пару вечеров отработке алгоритмов сложения, вычитания, умножения и деления обыкновенных и десятичных дробей, и это задание у вас в кармане.
Задание 15
Составители экзамена проверяют ваш навык работы с процентами и единицами отношения. Такие задачи бывают четырех типов.
Тип 1. Найти часть от числа
Часть может быть выражена в процентах или сразу в виде дроби. Например, придется искать треть от чего-то.
Рассмотрим на примере реальной задачи из экзамена:

Прочувствуйте специфику задачи: нам известно целое — вся зарплата до вычета налога. А работать мы будем с кусочком — 13 процентами. Сколько это в рублях, нам еще предстоит узнать.
Чтобы ответить на вопрос задачи, нужно сделать три шага:
1. Перевести процент в десятичную дробь.
Для этого всегда надо количество процентов поделить на 100.
13 : 100 = 0,13.
2. Найти, сколько это от зарплаты в рублях.
Запоминаем главное правило для этого типа задач: чтобы найти дробь от числа, надо число умножить на эту дробь.
12 500 ∙ 0,13 = 1 625 (руб.) — налог, который удержат с зарплаты Ивана Кузьмича.
3. Ответить на вопрос задачи.
У нас просили зарплату после вычета налога, а не сам налог.
12 500 – 1625 = 10 875 (руб.).
Ответ: 10 875.
Будьте внимательны: многие совершают ошибку именно на последнем шаге!
Тип 2. Найти число по его части

Прочувствуйте разницу с прошлой задачей: тут 124 — и есть 25%, то есть одна и та же величина выражена в процентах и в абсолютных величинах, в данном случае — в учениках. Просят узнать целое — 100%.
1. Переводим процент в десятичную дробь:
25 : 100 = 0,25.
2. Находим, сколько учеников всего.
Правило для этого типа задач: чтобы найти целое, надо часть разделить на дробь.
124 : 0,25 = 496 (уч.) — всего.
Ответ: 496.
Тип 3. Найти, сколько процентов часть составляет от целого

Особенность подобных заданий: не дано процентов, есть только абсолютные величины. В данном случае — стоимость футболки в рублях.
1. Находим, какую долю новая цена составляет от первоначальной.
Запоминаем правило: чтобы найти, какую долю часть составляет от целого, надо часть разделить на целое.
680 : 800 = 0,85.
2. Переводим долю в процент.
В прошлых задачах мы уже дважды выполнили обратное действие. В этот раз сделаем наоборот: умножим полученную дробь на 100.
0,85 ∙ 100 = 85% — столько процентов новая цена составляет от старой.
3. Отвечаем на вопрос задачи.
Нас спросили, на сколько процентов цена снизилась, что стала 85% от первоначальной. Конечно, изначально она была 100%. Итого:
100 – 85 = 15%.
Ответ: 15%.
Тип 4. Задачи на соотношение

Если перефразировать условие, то за первого кандидата проголосовали 3 части избирателей, а за второго — 2 части. Особенность этих частей в том, что они одинаковые по величине.
Если одна будет состоять из 10 человек, то за первого кандидата будет 30, а за второго — 20.
1. Считаем общее количество частей:
3 + 2 = 5.
2. Узнаем, сколько голосов составляет одна такая часть.
Тут речь о процентах проголосовавших. Сколько всего проголосовало? Конечно, 100%! Значит, каждая из пяти частей «весит»
100 : 5 = 20%.
3. Отвечаем на вопрос задачи.
За проигравшего проголосовало меньше частей избирателей. В нашем случае 2.
20 ∙ 2 = 40%.
Ответ: 40%.
Решение этих задач удобнее всего оформить табличкой:

1 часть = 100% : 5 = 20%.
Если рассчитываете решать текстовую задачу, включите здравый смысл. Ответ всегда можно проверить на адекватность благодаря обычной логике.
Задание 16: обязательно делать
Задание на решение выражения. На самом деле оно проверяет знание теории, так как в этом задании вам могут встретиться:
- выражения со степенями,
- иррациональные выражения,
- логарифмические выражения,
- тригонометрические выражения.
Ваша задача, соответственно, — знать:
- свойства степеней

- свойства корней

- свойства логарифмов
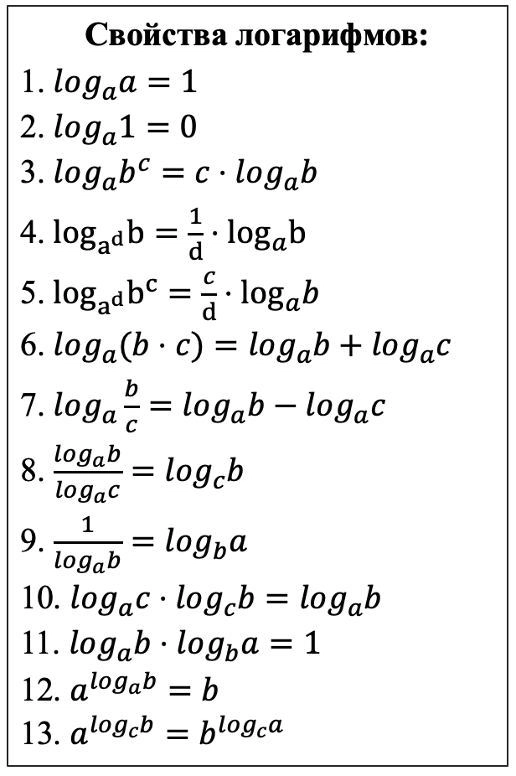
- формулы тригонометрии
Вы можете подробно ознакомиться с ними и научиться выводить в этой статье.
Обратите внимание: нужная теория будет в справочных материалах на экзамене, но это не поможет, если вы не научитесь применять ее для решения заданий. Практика обязательна!
Задание 17: обязательно делать
В номере с уравнениями вам не встретятся тригонометрические. Зато вы точно увидите там:
- линейные уравнения
Раскрываем скобки, если они есть, слагаемые с х переносим в одну сторону от равно, без х — в другую. Приводим подобные и решаем простейшее уравнение.
- квадратные уравнения
Бывают полные и неполные, всего надо повторить три алгоритма решения! А формула дискриминанта еще и в справочных материалах есть.
- иррациональные уравнения
Это те, что с корнем. Чтобы избавиться от корня, возводим обе части уравнения в квадрат и решаем получившееся уравнение. Есть нюансы с областью допустимых значений: подставьте полученные корни в исходное уравнение и проверьте, выполняется ли равенство. Если нет, то подставленное значение решением не будет.
- показательные уравнения
Ваша задача — с помощью формул свойств степеней привести уравнение к виду, когда слева и справа от равно в основании степени будет одно и то же число. После приравниваем показатели и решаем. Вот так:

Ответ: 7.
- логарифмические уравнения
С помощью формул свойств логарифмов приводим уравнение к виду, когда слева и справа от равно будет логарифм с одинаковым основанием. После приравниваем выражения под логарифмом и решаем.

Ответ: 67.
Прелесть уравнений в том, что ответ всегда можно проверить подстановкой вместо x в уравнение. Не забывайте проверять, ведь это возможность убедиться на 100%, что вы не упустите заветный балл.
Задание 19
Если хотите сдать базовую математику и решить номер 19, надо ознакомиться со свойствами целых чисел и признаками делимости. Иногда решение можно найти даже подбором! Попробуйте — времени на базовом ЕГЭ вам точно хватит.
Для начала нужно запомнить все признаки делимости.

А теперь посмотрим на типичное задание 19.

Тут помогут признаки делимости. Отдельного признака для 12 нет, потому нам надо разложить его на множители, признаки делимости для которых есть.
- На 3: сумма всех цифр делится на 3.
- На 4: число, образованное последними двумя цифрами, делится на 4.
Начнем с признака для 4. Пока что наше число заканчивается на 13 и на 4 не делится. Попробуем вычеркнуть последнюю цифру, и число будет заканчиваться на 61. Тоже не подходит. Вычеркнем еще одну: теперь на конце 76… Вот оно! От изначального числа осталось 751576, две цифры уже вычеркнули, осталось убрать одну.
Теперь проверим признак для 3: 7 + 5 + 1 + 5 + 7 + 6 = 31. Какое ближайшее число разделится на 3? Конечно, 30. Если мы вычеркнем единичку, все сойдется.
Ответ: 75576.
Другой вариант задания:

А задание такого типа можно попытаться подобрать, расположений не слишком много. Мы все же постараемся порассуждать, чтобы уменьшить количество возможных вариантов.
Чтобы число делилось на 10, оно должно заканчиваться на 0. Например, это получится, если сложить 7 + □7 + □□6. Уже немного легче. Остальное просто подберем. Под условие задачи подойдет 7 + 27 + 356 = 390.
Ответ: 390.
Какие задания мы не разобрали и почему
Теперь вы знаете, как сдать базовую математику, решив всего семь заданий. Но некоторые номера базового ЕГЭ включают слишком большое разнообразие прототипов, и методы их решения не ограничиваются парой простых алгоритмов.
Например, в эту группу относятся все задания по геометрии: с 9 по 13. Чтобы решать геометрию, мало знать основные фигуры и формулы. Необходим навык, который вырабатывается только практикой. Однако у нас есть статья про окружность — в ней вы найдете много полезной информации.
Задание 18 обычно, хотя и не всегда, содержит неравенство.

Это объемный блок теории, которую тоже необходимо подкреплять практикой. Но, может, вам повезет и попадется задачка на расположение значений на числовой прямой.

Тут достаточно примерно прикинуть значения и аккуратно внести ответы в бланк. Ясно, что 7/3 больше 2, но меньше 3. Корень из 26 равен 5 с копейками, а степень –1 из 3/5 сделает 5/3, или чуть больше 1,5. Подобные задания надо пытаться делать обязательно!
Задание 20. С этим заданием ученики знакомы еще с 9-го класса, так как оно было под номером 21 на ОГЭ. Это текстовая задача:
- на производительность,
- движение (по прямой, воде, окружности),
- сплавы и смеси,
- проценты (пиджаки, рубашки, брюки; бюджет семьи; акции, которые растут и падают),
- прогрессии.
В задании 21 на ОГЭ не было прогрессий, но они были в первой части на ОГЭ, так что ничего нового.
Задание 21. Здесь попадаются разные типы неочевидных задач на логику — чем-то они даже похожи на олимпиадные. Решение каждой нужно рассматривать отдельно и подробно. Если хотите прочитать о том, какие задачи бывают в 21-м номере, пишите в комментариях, и Maximum поделится своими методами решения!
Не знаете, какой вуз выбрать? Воспользуйтесь бесплатной консультацией в нашем центре. Что это такое? Все просто: вы расскажете о себе и о своих интересах. А специалист посоветует, на какие специальности обратить внимание, в какой вуз поступать, какие ЕГЭ сдавать. Так вы сэкономите время на подготовку и сможете выбрать образование, которое точно окажется для вас интересным и полезным!
Подготовка к ЕГЭ по математике
Из каких частей состоит ЕГЭ по математике в 2023 году
Математика — один из двух обязательных предметов на ЕГЭ. Но, в отличие от русского языка, эта дисциплина предлагает 2 уровня сложности: профильный и базовый. Какий именно вариант выбрать, зависит от вашей цели. Если вуз, в который вы хотите поступить, требует профильного уровня, нужно сдавать его. Обычно это касается технических специальностей.
Для получения аттестата выпускникам школ хватит и базового. Но финальное решение за вами. Если вы хотите сдать профильный вариант, просто чтобы проверить свои знания и уровень подготовки, — дерзайте!
Структура базового уровня ЕГЭ по математике
Базовый уровень проверяет основные знания школьника по математике. Такой экзамен не делится на части: в него входит только 21 задание с кратким ответом. Ответом может быть целое число, десятичная дробь или ряд цифр. По уровням сложности задания экзамена тоже не делятся — все задачи в нем базового уровня. Чтобы выполнить такую работу, ученику дают 180 минут.
Структура профильного уровня ЕГЭ по математике
Варианты профильного уровня проверяют основные и углубленные знания школьника. В 2023 году ЕГЭ состоит из 2 частей:
-
1-я часть: 11 задач с кратким ответом;
-
2-я часть: 7 задач с развернутым ответом.
В первой части ответом может быть целое число, десятичная дробь или ряд цифр. Во второй части — полное обоснованное решение и ответ. Чтобы выполнить задания экзамена, школьнику дают 235 минут.
Задачи ЕГЭ по математике профильного варианта делятся на категории по уровням сложности. В таблице ниже можно увидеть, как именно.
| Базовый | 6 |
| Повышенный | 10 |
| Высокий | 2 |
| Всего | 18 |
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
Реши домашку по математике на 5.
Подробные решения помогут разобраться в самой сложной теме.
Как сдать ЕГЭ по математике: разбор сложных задач
Экзамен по математике не зря считают одним из самых трудных. Даже в заданиях базового варианта можно легко ошибиться по невнимательности. Что уж говорить о действительно сложных задачах с полным решением, где много «подводных камней»? Чтобы вы знали, как подготовиться к ЕГЭ по профильной математике, мы разобрали несколько из них.
Задание 16
Две окружности касаются внешним образом в точке K. Прямая AB касается первой окружности в точке A, а второй — в точке B. Прямая BK пересекает первую окружность в точке D, прямая AK пересекает вторую окружность в точке C.
а) Докажите, что прямые AD и BC параллельны.
б) Найдите площадь треугольника AKB, если известно, что радиусы окружностей равны 4 и 1.
Совет
Для этого задания советуем повторить темы:
-
Касательные к окружности и их свойства.
-
Свойства вписанных углов.
-
Взаимное расположение окружностей.
-
Свойства прямоугольного треугольника.
-
Признаки и свойства параллельных прямых.
-
Подобные треугольники, площади подобных фигур.
-
Свойство площадей (в частности: отношение площадей треугольников с одинаковой стороной).
-
Трапеция, её свойства. Площадь трапеции.
-
Теорема Пифагора.
Проследите, чтобы они были в вашем плане подготовки к профилю ЕГЭ по математике.
Решение
а) Выполним построение.
-
Окружности с центрами О1 и О2 соответственно касаются друг друга в одной точке К.
-
Прямая АВ касается обеих окружностей в точках А и В соответственно.
-
Прямые АК и ВК пересекают окружности в точках С и D соответственно
-
Пусть общая касательная окружностей в точке К, пересекает прямую АВ в точке М.
Тогда по свойству касательных, проведенных из одной точки, AM = KM и KM = BM.
-
Рассмотрим треугольник АВК. Его медиана АМ равна половине стороны, которую она разбивает. Следовательно, делаем вывод, что треугольник АВК прямоугольный, а угол К = 90°.
-
Вписанный угол AKD является смежным углом АКВ, а значит, он тоже 90° как прямой. Следовательно, угол AKD опирается на диаметр AD. Значит, AD ⊥ AB, так как радиус, а в данном случае диаметр, перпендикулярен касательной в точке касания.
-
Аналогично рассмотрев угол ВКС, получим, что BC⊥ AB.
-
Прямые AD и ВС перпендикулярны третьей прямой АВ, следовательно, прямые AD и BC параллельны. Ч. т. д.
б) Пусть радиус первой окружности равен 4, а радиус второй окружности равен 1. Тогда АD = 8, ВС = 2.
-
Рассмотрим треугольники ADK и СВК. Они подобны, т. к. имеют два равных угла (К – вертикальный, С и А — накрест лежащие). Из подобия треугольников следует, что их площади относятся как коэффициент подобия в квадрате:
-
Обозначим площадь треугольника СВК за S, тогда площадь треугольника ADK будет равна 16S.
-
Пусть площади треугольников АВК и CDK будут равны х и у соответственно.
-
Вспомним свойство, связывающее высоты треугольников с общим основанием и получим следующие равенства: DB — общая сторона треугольников ADB и СDB, следовательно:
(равно 4 из подобия треугольников ADK и СВК, см. выше),
-
Аналогично, AC — общая сторона треугольников ADС и ABC, следовательно,
(равно 4 из подобия треугольников ADK и СВК, см. выше),
-
Решим полученную систему уравнений:
-
Из первого уравнения
подставим во второе и найдем y.
следовательно,
подставим во второе и найдем y.
-
Площадь ABCD равна 16S + 4S + 4S + S = 25S.
-
Заметим, что ABCD — прямоугольная трапеция (AD||BC, AB — перпендикулярна основаниям). Для вычисления ее площади нужно полусумму оснований умножить на высоту.
-
Для того, чтобы найти высоту, рассмотрим меньшую трапецию AO1O2B.
Ее основания равны 1 и 4, так как О2В и О1А — радиусы. O1O2 = 5, так как О2К и О1К — радиусы. О2H — высота трапеции AO1O2B.
-
По теореме Пифагора найдём О2H:
-
Вычислим площадь трапеции ABCD:
-
С другой стороны мы нашли
Отсюда S = 0,8.
-
Площадь треугольника АКВ = 4S, следовательно,
Ответ: 3,2.
Задание 18
В школах № 1 и № 2 учащиеся писали тест. В каждой школе тест писали по крайней мере 2 учащихся, а суммарно тест писали 9 учащихся. Каждый учащийся, писавший тест, набрал натуральное количество баллов. Оказалось, что в каждой школе средний балл за тест был целым числом. После этого один из учащихся, писавших тест, перешел из школы № 1 в школу № 2, а средние баллы за тест были пересчитаны в обеих школах.
а) Мог ли средний балл в школе № 1 уменьшиться в 10 раз?
б) Средний балл в школе № 1 уменьшился на 10%, средний балл в школе № 2 также уменьшился на 10%. Мог ли первоначальный средний балл в школе № 2 равняться 7?
в) Средний балл в школе № 1 уменьшился на 10%, средний балл в школе № 2 также уменьшился на 10%. Найдите наименьшее значение первоначального среднего балла в школе № 2.
Совет
Чтобы справиться с этой задачей, нужно повторить темы:
-
Понятие натурального и целого числа.
-
Среднее арифметическое.
-
Делимость чисел.
-
Процент. Нахождение процента от числа, уменьшение числа на заданный процент.
-
Составление и решение линейных уравнений.
Добавьте их в ваш план подготовки к ЕГЭ по математике, если собираетесь сдавать профиль.
Решение:
а)
-
Допустим, что в школе № 1 писали тест 2 учащихся, один из них набрал 1 балл, а второй набрал Х баллов и перешёл в другую школу. Тогда средний балл в школе был равен (1 + Х) : 2 = 10, а стал равен 1, т. е. уменьшился в 10 раз.
-
Решим уравнение и получим Х = 19 — натуральное число. Следовательно, наше предположение верно.
-
Или мы можем предположить другой вариант: что один учащийся набрал 2 балла. Тогда средний балл изначально равняется 20, а после ухода второго станет 2, т. е. изменится в 10 раз.
-
Решим уравнение (2 + Х) : 2 = 20, отсюда Х = 38 — натуральное число, что тоже удовлетворяет условию задачи.
Ответ: средний балл в школе № 1 мог уменьшиться в 10 раз.
б)
-
Пусть в школе № 2 писали тест m учащихся, n — сумма баллов m учащихся, средний балл равнялся B, а перешедший в неё учащийся набрал u баллов.
-
Умножим обе части полученного уравнения на 10, получим:
-
По условию B = 7, тогда получим, что 10u кратно 10, а
не делится на 10, так как ни один из множителей не делится на 10. Это противоречие.
Ответ: Первоначальный средний балл в школе № 2 не мог равняться 7.
в)
-
Пусть в школе № 1 средний балл равнялся A, общее количество баллов — p, количество писавших работу — (9 – m).
(из пункта б).
Следовательно,
-
Попробуем найти средний балл в школе № 2 методом подбора. Пусть:
В = 1, тогда:
кратно 10, а
не делится на 10.
В = 2, тогда:
пусть u = 1, тогда m = 4:
— не является целым числом.
u = 2 не может быть, т. к. m ≥ 1
В = 3, тогда:
кратно 10, а
не делится на 10.
В = 4, тогда:
Чтобы m было натуральным числом u должно быть четным, u = 2, тогда m = 4, что невозможно (доказали при В = 2).
u = 4, тогда m меньше 0, что невозможно т. к. m ≥ 1.
В = 5, тогда:
пусть u = 1, тогда m = 7, что невозможно (доказали в пункте б);
пусть u = 2, тогда m = 5:
— не является целым числом;
пусть u = 3, тогда m = 3:
-
Этот случай реализуется, например, в школе № 2 при m = 3, B = 5. Предположим, что каждый ученик набрал по 5 баллов. Тогда в школе № 1 писали 9 – m = 9 – 3 = 6 учащихся, 3 из них набрали по 1 баллу, а 3 – по 3 балла, тогда средний балл:
-
Переход из школы № 1 в школу № 2 совершил ученик с 3 баллами, тогда
средний балл в школе № 1 стал равен:что на 10% меньше от первоначального значения.
-
Тогда средний балл в школе № 2 стал равен:
что на 10% меньше от первоначального значения.
Ответ: наименьшее значение первоначального среднего балла в школе № 2 равно 5.
Ответ: а) да; б) нет; в) 5.
Как выставляют баллы за ЕГЭ по математике
С базовым уровнем сложности все просто: за каждый правильный ответ вашего варианта вы получаете по 1 первичному баллу. То же самое касается и первой части профиля: задания 1–11 тоже оценивают в 1 балл.
Как вы помните, во 2-й части профильного варианта нужны и решение, и ответ. Здесь задания оценивают по нескольким критериям. Они сложнее, но и баллов за них можно получить больше. Давайте же разберемся, как выставляют баллы во второй части профиля. Это поможет вам подготовиться к заданиям ЕГЭ по математике как самостоятельно, так и с учителем.
| Задание № 12 | Баллы |
|---|---|
| В обоих пунктах есть обоснованные ответы | 2 |
| Есть обоснованный ответ только в пункте а или есть неверный ответ из-за ошибки в вычислениях, но шаги в решениях обоих пунктов верные |
1 |
| Все остальные случаи | 0 |
| Максимальный балл | 2 |
| Задание № 13 | Баллы |
|---|---|
| Верно доказан пункт а, в пункте б есть обоснованный ответ | 3 |
| Есть только обоснованный ответ в пункте б или верно доказан пункт а, в пункте б шаги решения верные, но из-за ошибки в вычислении получен неверный ответ |
2 |
| Есть только верное доказательство пункта а, или в пункте б шаги решения верные, но из-за ошибки в вычислении получен неверный ответ, или есть обоснованный ответ в пункте в, который получен с помощью пункта а, но сам пункт а не выполнен |
1 |
| Все остальные случаи. | 0 |
| Максимальный балл | 3 |
| Задание № 14 | Баллы |
|---|---|
| Есть обоснованный ответ | 2 |
| Ответ обоснован, но он отличается от верного исключением точек –12 и/или 0 или шаги решения верные, но из-за ошибки в вычислениях получен неверный ответ |
1 |
| Все остальные случаи | 0 |
| Максимальный балл | 2 |
| Задание № 15 | Баллы |
|---|---|
| Есть обоснованный ответ | 2 |
| Ученик верно построил математическую модель | 1 |
| Все остальные случаи | 0 |
| Максимальный балл | 2 |
| Задание № 16 | Баллы |
|---|---|
| Верно доказан пункт а, в пункте б есть обоснованный ответ | 3 |
| Есть только обоснованный ответ в пункте б иЛИ Верно доказан пункт а, в пункте б шаги решения верные, но из-за ошибки в вычислении получен неверный ответ |
2 |
| Есть только верное доказательство пункта а, или в пункте б шаги решения верные, но из-за ошибки в вычислении получен неверный ответ, или есть обоснованный ответ в пункте в, который получен с помощью пункта а, но сам пункт а не выполнен |
1 |
| Все остальные случаи | 0 |
| Максимальный балл | 3 |
| Задание № 17 | Баллы |
|---|---|
| Есть обоснованный ответ | 4 |
| Рассуждения и значения параметра верные, но в ответе есть 1–2 неверных значения или решение недостаточно обосновано | 3 |
| Есть верное рассуждение и хотя бы одно правильное значение | 2 |
| Задача сведена к исследованию взаимного расположения 3 окружностей или двух квадратных уравнений с параметром | 1 |
| Все остальные случаи | 0 |
| Максимальный балл | 4 |
| Задание № 18 | Баллы |
|---|---|
| Есть обоснованный ответ в пунктах а, б, в | 4 |
| Есть обоснованный ответ в пункте в и есть обоснованный ответ в пунктах а или б | 3 |
| Есть обоснованный ответ в пунктах а и б или есть обоснованный ответ в пункте в. |
2 |
| Есть обоснованный ответ в пунктах а или б | 1 |
| Все остальные случаи | 0 |
| Максимальный балл | 4 |
Узнать больше о структуре экзамена, вариантах и критериях, по которым оценивают работы, можно на официальном сайте ФИПИ, в разделе «Демоверсии, спецификации, кодификаторы». Там же вы найдете методические указания для подготовки.
Сколько баллов нужно набрать, чтобы получить 3, 4 и 5
Теперь, когда мы разобрали критерии, можно посчитать, сколько баллов нужно набрать на конкретную оценку. В этом нам помогут таблицы ниже. Заодно разберемся, как первичные баллы переводятся в тестовые — финальные.
| Шкала перевода баллов в базовой математике | |
|---|---|
| Первичные баллы | Оценка |
| <7 | 2 |
| 7–11 | 3 |
| 12–16 | 4 |
| 17–21 | 5 |
| Максимальный балл | 4 |
Обратите внимание: с 2008 года официально баллы ЕГЭ не переводят в привычные нам оценки по пятибальной системе. Но если вам хочется это сделать, можно примерно оценить работу по таблице ниже.
| Шкала перевода баллов в профильной математике (неофициальная) | ||
|---|---|---|
| Первичные баллы | Тестовые баллы | Оценка |
| <5 | <27 | 2 |
| 5–8 | 27–49 | 3 |
| 8–20 | 50–67 | 4 |
| 21–31 | 68–100 | 5 |
6 советов от эксперта, как готовиться к ЕГЭ по математике
Мы занимаемся подготовкой учеников к экзамену каждый год и понимаем, насколько это важно и волнительно. Вам предстоит ответственная работа, от которой многое зависит. Чтобы облегчить ее, мы собрали несколько советов, которые помогут вам как можно лучше подготовиться к ЕГЭ по математике:
-
Осознанно выберите уровень сложности и поставьте цель в баллах.
-
Составьте план подготовки к ЕГЭ по математике: больше времени уделяйте темам, которые у вас «западают». Чтобы выявить их, ученики Skysmart проходят тест на бесплатном уроке.
-
Узнайте все о ЕГЭ: сколько времени длится экзамен, из каких частей состоит, по каким темам будут задания, сколько вариантов, какие дадут справочные материалы и т. д.
-
Составьте сбалансированное расписание для подготовки и следите, чтобы в нем было достаточно времени для отдыха.
-
Много практикуйтесь: решайте варианты из Открытого банка заданий ЕГЭ и сдавайте тестовые экзамены.
-
Систематически консультируйтесь и занимайтесь с наставником, который часто имеет дело с подготовкой к ЕГЭ — преподавателем в школе или репетитором.
Все пункты в этом списке важны для тех, кто хочет набрать 80–100 баллов, но последний — особенно. Преподаватель расскажет о том, что представляет из себя ЕГЭ, и тогда на реальном экзамене не будет неприятных сюрпризов.
На курсах подготовки к ЕГЭ по математике в Skysmart учителя помогают школьникам разобраться в КИМах и прорешать каждый тип задач. Ученики заранее знакомятся с частыми ошибками, что помогает избегать их в работе и сохранять баллы. А еще мы учим готовиться морально, чтобы не допустить ошибок из-за паники и невнимательности. Начните подготовку к ЕГЭ по математике с нуля вместе со Skysmart: первый урок — бесплатно!




























![4. Найти наибольшее значение функции
на отрезке [-4; -1]Ответ: -6Решение25 4. Найти наибольшее значение функции
на отрезке [-4; -1]Ответ: -6Решение25](https://documents.infourok.ru/f2565eb3-7000-44e5-9e2c-b981eb8d018c/0/slide_27.jpg)