Способы решения неравенств егэ - Помощь в подготовке к экзаменам и поступлению

Если в выражении с переменными вы увидели знак = , то это уравнение.

Если знак < или ˃ или ≤ или ≥ — то это, конечно, неравенство.

Как правило, неравенства решаются сложнее, чем аналогичные им уравнения. И знать надо больше – чтобы не наделать ошибок

В этом разделе – все основные способы и приемы решения неравенств на ЕГЭ по математике. Повторите их. Даже такие неравенства, как квадратичные или дробно-рациональные, содержат немало ловушек для неопытного школьника. И тем более — показательные и логарифмические. А иррациональные неравенства и неравенства с модулями вообще считаются одними из самых сложных тем школьного курса алгебры.

Здесь рассказано также о методе замены множителя (еще он называется методом рационализации неравенства). В учебнике вы его не найдете. И еще – об основных ошибках и полезных лайфхаках для решения неравенств.

^New

Решаем задачи из сборника И. В. Ященко, 2021

Квадратичные неравенства

Метод интервалов

Иррациональные неравенства

Задача 15 Репетиционного ЕГЭ онлайн, май 2020, Анна Малкова

Неравенства с модулем

Показательные неравенства

Логарифмические неравенства

Метод замены множителя (рационализации)

Решение неравенств: основные ошибки и полезные лайфхаки

Решаем задачи из сборника И. В. Ященко, 2020. Вариант 8, задача 15

Решаем задачи из сборника И. В. Ященко, 2020. Вариант 32, задача 15

Решаем задачи из сборника И. В. Ященко, 2020. Вариант 36, задача 15

Логарифмические неравенства повышенной сложности

Еще раз повторим основные правила:

— Равносильными называются неравенства, множества решений которых совпадают.

— Если обе части неравенства умножить на отрицательное число, знак неравенства поменяется на противоположный. А если на положительное число – знак неравенства останется тем же.

— Возводить обе части неравенства в квадрат можно только если они неотрицательны.

— Извлекать корень из неравенства нельзя. Нет такого действия!

— Если в неравенстве можно сделать замену переменной – сделайте замену переменной. А потом аккуратно вернитесь к той переменной, которая была вначале.

— Если вы решаете простейшее показательное или логарифмическое неравенство – не забудьте сравнить основание степени (или логарифма) с единицей.

— Если в неравенстве есть дроби, корни четной степени или логарифмы – там обязательно будет область допустимых значений.

— Решение неравенства лучше всего записывать в виде цепочки равносильных переходов.

— Если вы воспользовались методом рационализации (замены множителя) – соответствующие формулы лучше доказать.

Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Решение неравенств» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.

Публикация обновлена:
08.03.2023

Источник

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

Решение неравенств

Задание
1

#2500

Уровень задания: Легче ЕГЭ

Решите неравенство [x+10<3x^2]

Перенесем слагаемые в левую часть: [-3x^2+x+10<0] Разложим на множители выражение (-3x^2+x+10): [-3x^2+x+10=0 quad Rightarrow quad x_1=2quadtext{и}quad x_2=-dfrac53] Следовательно, (-3x^2+x+10=-3(x-2)left(x-frac53right)=-(x-2)(3x+5)).
Тогда неравенство примет вид [-(x-2)(3x+5)< 0quad Rightarrow
quad (x-2)(3x+5)>0] Решим его методом интервалов:

Таким образом, подходят (xin
left(-infty;-frac53right)cup(2;+infty)).

Ответ:

(left(-infty;-frac53right)cup(2;+infty))

Задание
2

#2501

Уровень задания: Легче ЕГЭ

Решите неравенство [x^2+34x+289>0]

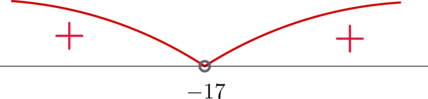
Заметим, что по формуле квадрата суммы (x^2+34x+289=(x+17)^2), следовательно, неравенство принимает вид: [(x+17)^2>0] Решим его методом интервалов:

Таким образом, нам подходят (xin(-infty;-17)cup(-17;+infty)).

Ответ:

((-infty;-17)cup(-17;+infty))

Задание
3

#2502

Уровень задания: Легче ЕГЭ

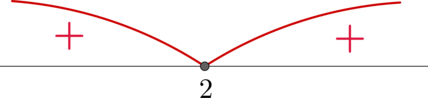
Решите неравенство [x^2-4x+4leqslant 0]

Заметим, что по формуле квадрата разности (x^2-4x+4=(x-2)^2), следовательно, неравенство принимает вид: [(x-2)^2leqslant 0] Решим его методом интервалов:

Таким образом, нам подходят (xin{2}).

Ответ:

({2})

Задание
4

#2503

Уровень задания: Легче ЕГЭ

Решите неравенство [x^2+3x+3geqslant 0]

Разложим на множители выражение (x^2+3x+3), для этого решим уравнение (x^2+3x+3=0). Оно имеет отрицательный дискриминант, следовательно, не разлагается на множители и принимает значения одного знака: либо положительно, либо отрицательно при всех (x). Проверить его знак можно, подставив вместо (x) любое число, например, (x=0): получим (3), следовательно, выражение всегда (>0).

Таким образом, нам подходят (xin mathbb{R}).

Ответ:

(mathbb{R})

Задание
5

#2412

Уровень задания: Легче ЕГЭ

Решите неравенство

[begin{aligned}
dfrac{(x — 1)(x + 2)}{(x — 3)(x + 4)}leqslant 0
end{aligned}]

ОДЗ:

[begin{aligned}
(x — 3)(x + 4)neq 0
end{aligned}]

Решим исходное неравенство методом интервалов. Для этого найдём нули числителя и знаменателя.

1) Нули числителя находятся из уравнения [(x — 1)(x + 2) = 0] Произведение выражений равно нулю в том и только том случае, когда хотя бы одно из них равно нулю и все они не теряют смысл, тогда нули числителя: [x = 1,qquadqquad x = -2]

2) Найдём нули знаменателя: [(x — 3)(x + 4) = 0qquadLeftrightarrowqquad
left[
begin{gathered}
x = 3\
x = -4
end{gathered}
right.]

По методу интервалов:

откуда [xin(-4; -2]cup[1; 3),.] В этом ответе ОДЗ уже учтено (мы учли его, когда выкололи на числовой прямой нули знаменателя).

Ответ:

((-4; -2]cup[1; 3))

Задание
6

#3762

Уровень задания: Легче ЕГЭ

Решить неравенство [dfrac 6{xsqrt3-3}+dfrac{xsqrt3-6}{xsqrt3-9}geqslant 2]

(Задача от подписчиков)

Пусть (xsqrt3-3=t). Тогда [dfrac 6t+dfrac{t-3}{t-6}geqslant 2quadLeftrightarrowquad
dfrac{t^2-15t+36}{t(t-6)}leqslant 0quadLeftrightarrowquad
dfrac{(t-3)(t-12)}{t(t-6)}leqslant 0] Решая данное неравенство методом интервалов, получим (0<tleqslant 3) или (6<tleqslant 12). Следовательно, [left[begin{gathered}begin{aligned}
&0<xsqrt3-3leqslant 3\
&6<xsqrt3-3leqslant
12end{aligned}end{gathered}right.quadLeftrightarrowquad
left[begin{gathered}begin{aligned}
&sqrt3<xleqslant 2sqrt3\
&3sqrt3<xleqslant 5sqrt3
end{aligned}end{gathered}right.]

Ответ:

((sqrt3;2sqrt3]cup(3sqrt3;5sqrt3])

Задание
7

#2413

Уровень задания: Легче ЕГЭ

Решите неравенство

[begin{aligned}
dfrac{(x + 1)(x — 2)}{(x + 3)(x^2 + 4)}leqslant 0
end{aligned}]

ОДЗ:

[begin{aligned}
(x — 3)(x^2 + 4)neq 0
end{aligned}]

Решим исходное неравенство методом интервалов. Для этого найдём нули числителя и знаменателя.

1) Нули числителя находятся из уравнения [(x + 1)(x — 2) = 0] Произведение выражений равно нулю в том и только том случае, когда хотя бы одно из них равно нулю и все они не теряют смысл, тогда нули числителя: [x = -1,qquadqquad x = 2]

2) Найдём нули знаменателя: [(x + 3)(x^2 + 4) = 0] так как (x^2geqslant 0), то (x^2 + 4geqslant 4), следовательно, нули знаменателя: [x = -3]

По методу интервалов:

откуда [xin(-infty; -3)cup[-1; 2],.] В этом ответе ОДЗ уже учтено (мы учли его, когда выкололи на числовой прямой нули знаменателя).

Ответ:

((-infty; -3)cup[-1; 2])

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ

Источник

При решении неравенств вы должны свободно владеть понятием числового неравенства, знать, что такое решение неравенства, что значит решить неравенство, помнить свойства неравенств. То же относится и к системам числовых неравенств. Все эти сведения вы можете найти в любом пособии для поступающих в вузы.
 Напомним свойства числовых неравенств.
 1. Если а > b , то b < а; наоборот, если а < b, то b > а.
 2. Если а > b и b > c, то а > c. Точно так же, если а b, то а + c > b+ c (и а – c > b – c). Если же а < b, то а + c < b+ c (и а – c b и c > d, то а + c > b + d; точно так же, если а < b и c < d, то а + c < b + d, т. е. два неравенства одинакового смысла можно почленно складывать.

Замечание.

Два неравенства одинакового смысла нельзя почленно вычитать друг из друга, так как результат может быть верным, но может быть и неверным. Например, если из неравенства 11 > 9 почленно вычесть неравенство 3 > 2, то получим верное неравенство 8 > 7. Если из неравенства 11 > 9 почленно вычесть неравенство 7 > 2, то полученное неравенство будет неверным.
 5. Если а > b и c < d, то а – c > b – d; если а d, то а – c b и m – положительное число, то m а > m b и , т.е. обе части неравенства можно умножить или разделить на одно и то же положительное число ( знак неравенства остаётся тем же ).
 Если же а > b и n – отрицательное число, то n а < n b и , т.е. обе части неравенства можно умножить или разделить на одно и то же отрицательное число, но при этом знак неравенства нужно переменить на противоположный.
 7. Если а > b и c > d , где а, b, c, d > 0, то а c > b d и если а 0, то аc < bd, т.е. неравенства одного смысла на множестве положительных чисел можно почленно перемножать.
Следствие. Если а > b, где а, b > 0, то а² > b², и если а < b, то а² < b², т.е. на множестве положительных чисел обе части неравенства можно возводить в квадрат.

8. Если а > b, где а, b > 0, то и если а < b , то .

Виды неравенств и способы их решения

1. Линейные неравенства и системы неравенств

Пример 1. Решить неравенство .
 Решение:
 .
 Ответ: х < – 2.

Пример 2. Решить систему неравенств
    Решение:
         .
    Ответ: (– 2; 0].

Пример 3. Найти наименьшее целое решение системы неравенств

    Решение:

    Ответ:

2. Квадратные неравенства

Пример 4. Решить неравенство х² > 4.
    Решение:
        х² > 4   (х – 2)∙(х + 2) > 0.
        Решаем методом интервалов.

Ответ:

3. Неравенства высших степеней

Пример 5. Решить неравенство (х + 3)∙(х² – 2х + 1) > 0.
    Решение:

    Ответ: .

Пример 6. Найти середину отрезка, который является решением неравенства 4х² – 24х + 24 < 4у², где .
 Решение:
 Область определения неравенства: .
 С учётом области определения 4х² – 24х + 24 < 4у² будет равносильно неравенству

Решаем методом интервалов.

        Решение неравенства: .
        Середина отрезка: .
    Ответ: .

4. Рациональные неравенства

Пример 7. Найти все целые решения, удовлетворяющие неравенству .
    Решение:

Методом интервалов:

        Решение неравенства: .
        Целые числа, принадлежащие полученным полуинтервалам: – 6; – 5; – 4; 1.
    Ответ: – 6; – 5; – 4; 1.

5. Иррациональные неравенства

Помните! Начинать решение иррациональных неравенств нужно с нахождения области определения.

Пример 8. Решить неравенство .
    Решение:
        Область определения: .
        Так как арифметический корень не может быть отрицательным числом, то .
    Ответ: .

Пример 9. Найти все целые решения неравенства .

Решение:

Область определения .

– быть отрицательным не может, следовательно, чтобы произведение было неотрицательным достаточно потребовать выполнения неравенства , при этом учитывая область определения. Т.е. исходное неравенство равносильно системе .

Целыми числами из этого отрезка будут 2; 3; 4.

Ответ: 2; 3; 4.

Пример 10. Решить неравенство .

Решение:

Область определения:

Преобразуем неравенство: . С учётом области определения видим, что обе части неравенства — положительные числа. Возведём обе части в квадрат и получим неравенство, равносильное исходному.

т.е. , и этот числовой отрезок включён в область определения.

Ответ: .

Пример 11. Решить неравенство .

Решение:

Раскрываем знак модуля.

Объединим решения систем 1) и 2): .

Ответ: .

6. Показательные, логарифмические неравенства и системы неравенств

Пример 12. Решите неравенство .

Решение:

Ответ: .

Пример 13. Решите неравенство .

Решение:

Ответ: .

Пример 14. Решите неравенство .

Решение:

Ответ: .

Пример 15. Решите неравенство .

Решение:

Ответ: .

Задания для самостоятельного решения

Базовый уровень

Целые неравенства и системы неравенств

1) Решите неравенство 2х – 5 ≤ 3 + х.

2) Решите неравенство – 5х > 0,25.

3) Решите неравенство .

4) Решите неравенство 2 – 5х ≥ – 3х.

5) Решите неравенство х + 2 < 5x – 2(x – 3).

6) Решите неравенство
.

7) Решите неравенство (х – 3) (х + 2) > 0.

Решить систему неравенств

9) Найдите целочисленные решения системы неравенств .

10) Решить систему неравенств .

11) Решить систему неравенств

12) Найти наименьшее целое решение неравенства

13) Решите неравенство .

14) Решите неравенство .

15) Решите неравенство .

16) Решите неравенство .

17) Найдите решение неравенства , принадлежащие промежутку .

18) Решить систему неравенств

19) Найти все целые решения системы

Рациональные неравенства и системы неравенств

20) Решите неравенство .

21) Решите неравенство .

22) Определите число целых решений неравенства .

23) Определите число целых решений неравенства .

24) Решите неравенство .

25) Решите неравенство 2^x<16 .

26) Решите неравенство .

27) Решите неравенство .

28) Решите неравенство .

29) Найдите сумму целых решений неравенства на отрезке [– 7, 7].

30) Решите неравенство .

31) Решите неравенство .

Иррациональные неравенства

32) Решите неравенство .

33) Решите неравенство

34) Решите неравенство .

Показательные, логарифмические неравенства и системы неравенств

35) Решите неравенство .

36) Решите неравенство .

37) Решите неравенство .

38) Решите неравенство .

39) Решите неравенство .

40) Решите неравенство 49∙7^х < 7^{3х + 3}.

41) Найдите все целые решения неравенства .

42) Решите неравенство .

43) Решите неравенство .

44) Решите неравенство 7^x+1-7^x<42 .

45) Решите неравенство log₃(2x²+x-1)>log₃2 .

46) Решите неравенство log_0,5(2x+3)>0 .

47) Решите неравенство .

48) Решите неравенство .

49) Решите неравенство .

50) Решите неравенство log_x+112>log_x+12 .

51) Решите неравенство log_x9<2.

52) Решите неравенство .

Повышенный уровень

53) Решите неравенство |x-3|>2x.

54) Решите неравенство 2│х + 1| > х + 4.

55) Найдите наибольшее целое решение неравенства .

56) Решить систему неравенств

57) Решить систему неравенств .

58) Решите неравенство .

59) Решите неравенство 25•2^x-10^x+5^x>25 .

60) Решите неравенство .

Ответы

1) х ≤ 8; 2) х < – 0,05; 3) х ≥ 5; 4) х ≤ 1; 5) х > –2; 6) х < 11; 7) ; (-2;0]; 9) – 1; 10) х ≥ 7,5; 11); 12) 1; 13); 14) х ≤ – 0,9; 15) х < – 1; 16) х < 24; 17); 18) ; 19) 3, 4, 5;

20) (0; 2); 21) (0; 1,5); 22) 3; 23) 6; 24) (–1; 1,5); 25) х < 4; 26); 27) (– 3; 17); 28)

; 29) – 10; 30) (0; + ∞); 31); 32) [1;17); 33) x > 17; 34) х ≥ 2; 35); 36) х < 2; 37) х > 0; 38) х ≤ 3; 39) х > – 3,5; 40) х > – 0,5; 41) 0, 1, 2, 3, 4, 5; 42) х < 3; 43) ; 44) х < 1; 45) ; 46) (– 1,5; – 1); 47) х < 0; 48); 49) ; 50) х > 0; 51) ; 52) ; 53) х < 1; 54); 55) – 1; 56) ; 57) [3,5; 10]; 58) (0, 1); 59) (0; 2); 60)

Источник

Слайд 1

Решение неравенств Разработала Желтова А.В., учитель математики (подготовка к ЕГЭ) Муниципальное бюджетное общеобразовательное учреждение школа №8 г.Кулебаки , 2021

Слайд 2

Виды неравенств — Линейные + + _ — Квадратные

Слайд 3

Виды неравенств — Рациональные + + _ _

Слайд 4

Виды неравенств — Содержащие чётную степень — Содержащие нечётную степень

Слайд 5

Виды неравенств — Иррациональные (корень чётной степени) — Иррациональные (корень нечётной степени)

Слайд 6

Виды неравенств — Показательные

Слайд 7

Виды неравенств — Логарифмические — Тригонометрические Решаем неравенства, используя тригонометрическую окружность, либо с помощью графика соответствующей функции

Слайд 8

Равносильность неравенств Перенос члена неравенства (с противоположным знаком) из одной части неравенства в другую; 2. Умножение (деление) обеих частей неравенства на положительное число; 3. Применение правил умножения многочленов и формул сокращённого умножения; 4. Приведение подобных членов многочлена; 5. Возведение неравенства в нечётную степень; 6. Логарифмирование неравенства т.е замена этого неравенства неравенством

Слайд 9

Равносильность неравенств на некотором множестве чисел Возведение неравенства в чётную степень; Потенцирование неравенства; 3. Умножение обеих частей неравенства на функцию; 4. Применение некоторых формул (логарифмических, тригонометрических и др.)

Слайд 10

Равносильны ли неравенства?

Слайд 11

Методы решения неравенств функциональный графический алгебраический геометрический

Слайд 12

Алгебраические методы решения неравенств Сведение неравенства к равносильной системе или совокупности систем Метод замены Разбиение области определения неравенства на подмножества

Слайд 13

Сведение неравенства к равносильной совокупности систем неравенств

Слайд 14

Решите неравенство Решение

Слайд 16

Если Квант № 10 1990 г . “Некоторые полезные логарифмические соотношения” Аналогично можно доказать , что если

Слайд 17

Ответ

Слайд 18

Заменяемое выражение Используемое выражение Решите неравенство Метод «рационализации»

Слайд 19

Решение. Решите неравенство

Слайд 21

Домашнее задание — обязательное задание — по желанию 2. Повторите способы решения тригонометрических неравенств 1. Решите неравенство: Решите неравенство:

Слайд 22

Литература Затакавай В. Некоторые полезные показательные и логарифмические соотношения. Журнал Квант, 1990 №10 Математика : ЕГЭ: Учебно-справочные материалы. Ю.М. Нейман, Т.М. Королёва, Е.Г. Маркарян .- М.: СПб.: Просвещение. 2011 Шестаков С. А . ЕГЭ 2018. Математика. Неравенства и системы неравенств. Задача 15 (профильный уровень).—М.: МЦНМО, 2018.—352 с. Ященко И.В., Шестаков С.А. Подготовка к ЕГЭ по математике в 2019 году. Профильный уровень. Методические указания . _ М.: МЦНМО , 2019

Источник