460 ₽552 ₽
ЕГЭ История. Картографический практикум. Тетрадь-тренажер | Ушаков Петр Афанасьевич, Пазин Роман Викторович
370 ₽
с Ozon Картой
377 ₽509 ₽
Подготовка к ЕГЭ-2023 Русский язык. 25 тренировочных вариантов по демоверсии 2023 г. | Глянцева Татьяна Николаевна, Гармаш Светлана Васильевна
329 ₽
с Ozon Картой
336 ₽453 ₽
ЕГЭ 2023 Математика. Базовый уровень. 40 тренировочных вариантов | Лысенко Федор Федорович, Коннова Елена Генриевна
326 ₽
с Ozon Картой
333 ₽483 ₽
Подготовка к ЕГЭ-2023 Математика. Профильный уровень. 40 тренировочных вариантов | Иванов Сергей Олегович, Кулабухов Сергей Юрьевич
373 ₽
с Ozon Картой
381 ₽549 ₽
Подготовка к ЕГЭ-2023 Химия. 30 тренировочных вариантов по демоверсии 2023 г. | Доронькин Владимир Николаевич, Февралева Валентина Александровна
313 ₽
с Ozon Картой
320 ₽468 ₽
ЕГЭ-2022. История. 30 тренировочных вариантов по демоверсии 2022 года | Ткачук Ирина Ивановна, Крамаров Николай Иванович
Справочник
«ОСНОВНЫЕ ТЕОРЕМЫ
ГЕОМЕТРИИ»
Содержание:
1.
Теоремы базового уровня……………………………………….3 – 11 стр.
1.1.
Теорема Фалеса Милетского……………………………..……3 стр. 1.2. Теорема
Пифагора………………………………………………3 стр. 1.3.
Теорема синусов………………………………………………..4 стр. 1.4. Теорема косинусов……………………………………………..4 стр.
1.5.
Теорема биссектрис…………………………………………….5 стр.
1.6.
Теорема о пересечении медиан треугольника……………..…5 стр. 1.7. Теорема о высотах
треугольника………………………………5 стр. 1.8.
Площади треугольников……………………………….………6 стр.
1.9.
Вписанный и центральный углы……………………………….7 стр.
1.10.
Вписанная окружность треугольника………………………..8 стр.
1.11.
Описанная окружность треугольника……………………..…8 стр.
1.12.
Вневписанная окружность треугольника……………………..8 стр. 1.13. Площади
четырехугольников……….……………………..….9 стр.
1.14.
Вписанный четырехугольник………………..………………10 стр.
1.15.
Описанный четырехугольник…………..……………………10 стр.
1.16.
Теорема о двух секущих……..………………………………11 стр. 1.17. Теорема о касательной и
секущей……………………………11 стр.
1.18. Теорема
о двух хордах………………………………………..11 стр.
2.
Теоремы профильного уровня…………………………………12 – 13 стр.
2.1.
Теорема Менелая………………………………………………12 стр. 2.2. Теорема
Чевы…………………………………………………..12 стр.
2.3.
Теорема Ван – Обеля………………………………………….12 стр.
2.4.
Теорема Стюарта………………………………………………13 стр.
2.5.
Теорема Птолемея…………………………………………….13 стр.
2.6.
Теорема Аполлония……………………………………………13 стр.
Теорема Фалеса
Милетского «Несколько параллельных прямых a║b║c║d и т.д., отсекающие на
одной из сторон угла равные отрезки, и на другой стороне угла также отсекающие
на одной из сторон угла равные отрезки, и на другой стороне угла также отсекают
равные отрезки»

Теорема Пифагора
1. Квадрат
гипотенузы прямоугольного треугольника равен сумме квадратов катетов.
2. Если
квадрат стороны треугольника равен сумме квадратов двух других его сторон, то
треугольник – прямоугольный.

Теорема синусов
Пусть a, b, c – стороны треугольника; α, β, γ –
противолежащие им углы; R – радиус описанной окружности. Тогда:
Теорема косинусов
Пусть a, b, c – стороны треугольника; α – угол,
противолежащий стороне a. Тогда:
α
Теорема биссектрис
Биссектриса треугольника делит противоположную сторону на два
отрезка, длины которых относятся так же, как длины соответствующих сторон.
Теорема о пересечении медиан треугольника
В треугольнике три медианы пересекаются в одной точке. Точка
пересечения делит каждую медиану в отношении 2:1, если считать от вершины, из
которой проведена медиана.

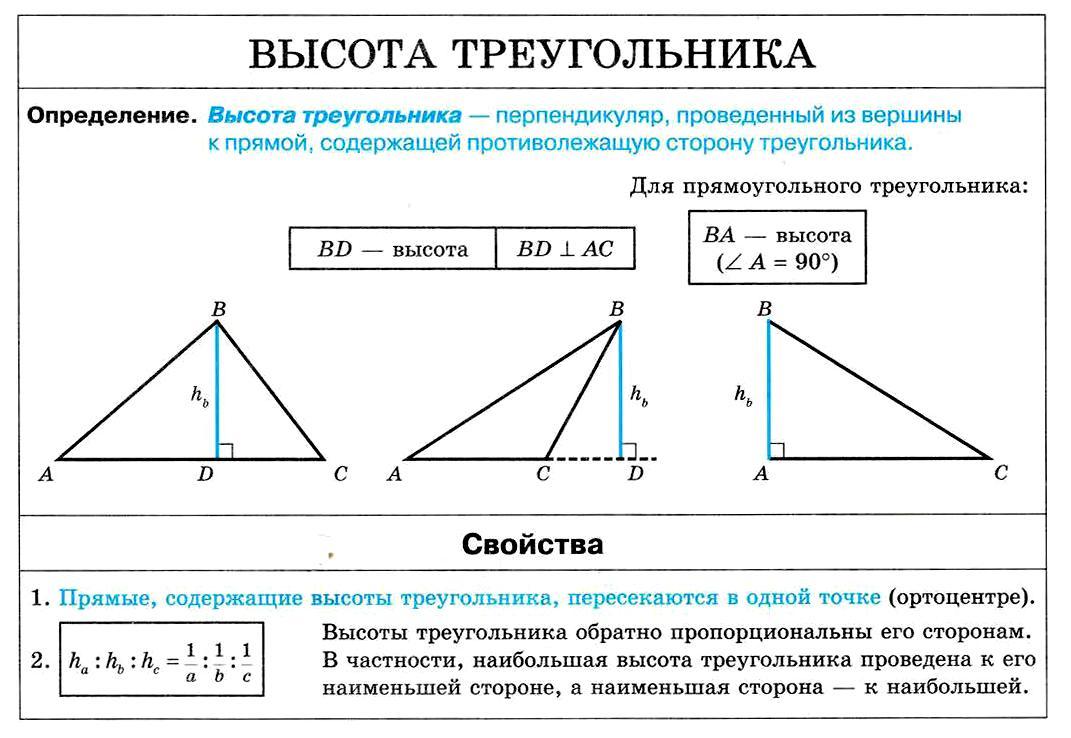
Теорема о высотах треугольника
В треугольнике высоты пересекаются в одной точке.
Площади треугольников
;
;
;
(формула
Герона)
где:
•
a,b,c – стороны треугольника
•
ha – высота треугольника
•
p – полупериметр треугольника
•
r – радиус вписанной окружности
•
R – радиус описанной окружности
•
β – угол между сторонами
Вписанный и центральный углы
Угол называется вписанным в окружность, если его вершина
лежит на окружности, а стороны пересекают эту окружность.
На рисунке вписанным углом является ABC.
Центральным называется угол вершиной в центре окружности. На
рисунке центральным углом является угол AOC.
Вписанная окружность треугольника

вписать единственную окружность. Центр окружности, вписанной в треугольник, совпадает
с точной пересечения его биссектрис.
Описанная окружность треугольника
Около любого треугольника можно описать
единственную окружность. Центр окружности, описанной около треугольника,
совпадает с точкой пресечения серединных перпендикуляров к его сторонам

Вневписанная окружность треугольника
В любом треугольнике биссектрисы двух
внешних углов и биссектриса внутреннего угла, не смежного с ними, пересекаются
в одной точке.
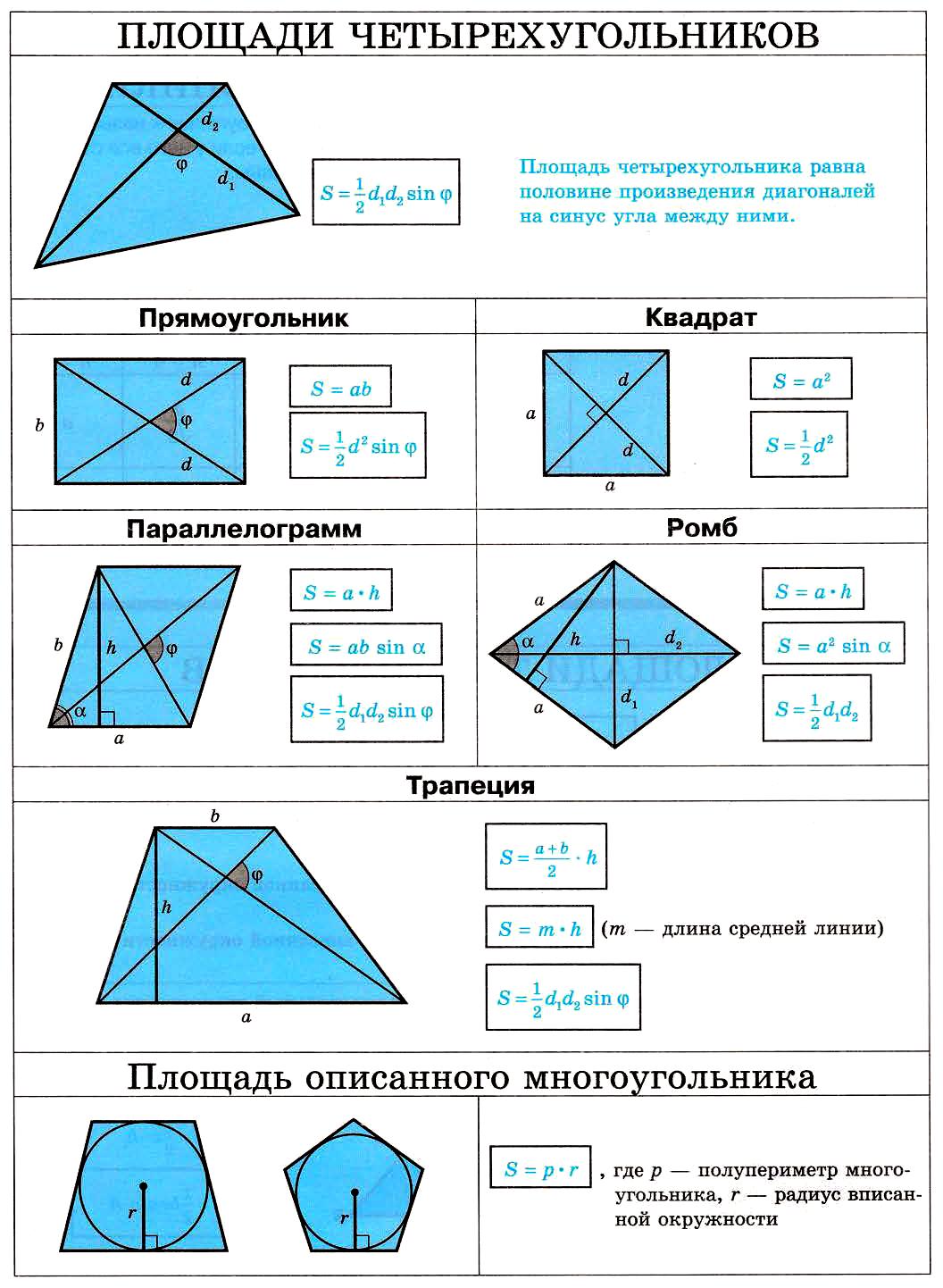
Площади четырехуголников
— площадь любого четырехугольника, где
•
d1 – первая диагональ
•
d2 – вторая диагональ
•
α – угол между диагоналями
— площадь четырехугольника,
вписанного в окружность (формула Герона), где
•
p – полупериметр четырехугольника
•
a, b, c и d – стороны четырехугольника
S = aha – площадь паралелограмма, где
•
a – основание паралелограмма
•
ha – высота, проведенная к основанию
S = ab sinβ – площадь параллелограмма, где
•
a и b – стороны паралелограмма
•
β – угол между смежными сторонами
S = ab – площадь прямоугольника, где
a и b – стороны квадрата
S = – площадь квадрата, где
a – сторона квадрата
S = aha – площадь ромба, где
•
a – сторона ромба
•
ha – высота, проведенная к стороне
S = – площадь ромба, где
•
a – сторона ромба
•
β – угол между сторонами ромба
Вписанный четырехугольник
Четырехугольник можно вписать в окружность тогда и только
тогда, когда суммы его противоположных углов равны 180.

Описанный четырехугольник
Четырехугольник можно описать вокруг окружности тогда и
только тогда, когда суммы длин его противоположных сторон равны.

DC
+ AB = DA + BC
Теорема о двух секущих
Если из точки, лежащей вне окружности, проведены две секущие,
то произведение одной секущей на ее внешнюю часть равно произведению другой
секущей на ее внешнюю часть:

MAMB = MC
MD
Теорема о касательной и секущей
Если из точки, лежащей вне окружности
проведены касательная и секущая, то квадрат длины касательной равен
произведению секущей на ее внешнюю часть

= MA MB
M
B
Теорема о двух
хордах Если две хорды окружности AB и CD пересекаются в точке S, то
произведение отрезков одной хорды равно произведению отрезков другой хорды. AS SD = CS
SB
D

SD = CS
SB
A
Теорема Менелая

Теорема Чевы
Отрезок, соединяющий вершину треугольника с точкой на
противоположной стороне или ее продолжении, называется чевианой.

Теорема Ван-Обеля

Теорема Стюарта

py
a
Теорема
Птолемея
Если
четырехугольник вписан в окружность, то
 AB
AB + AD
+ AD = AC
= AC
Теорема Аполлония
A
Если AD – медиана треугольника ABC, то
Желаем вам успехов!
31 октября 2013
В закладки
Обсудить
Жалоба
Cправочник по геометрии
Справочник был создан для учеников 7-9 классов по учебнику Л.С. Атанасяна. В нём собраны самые важные и нужные правила, свойства, которые могут пригодиться при решении различных заданий.
Пригодится как для подготовки к ГИА, так и к ЕГЭ.
Скачать справочник: spravochnik-geometriya.rar
Авторы: учителя математики Есикова Л.И. и Ушакова М.Б., МБОУ СОШ № 11 п. РАЯКОСКИ
Напомним, что в ГИА 2013 изменилась структура экзаменационной работы, в неё был включен модуль «Геометрия».
Теоремы и определения по Планиметрии
Теоремы и определения по Планиметрии. Справочник по геометрии для 7-11 классов, для подготовки к ОГЭ и ЕГЭ. Часть 1 «Планиметрия». Автор: Нелин Е.П. Использованы цитаты из пособия «Геометрия. 7-11 классы. Определения, свойства, методы решения задач в таблицах / М.: Илекса, 2018» из серии «Комплексная подготовка к ЕГЭ и ГИА (ОГЭ). Цитаты использованы в учебных целях.
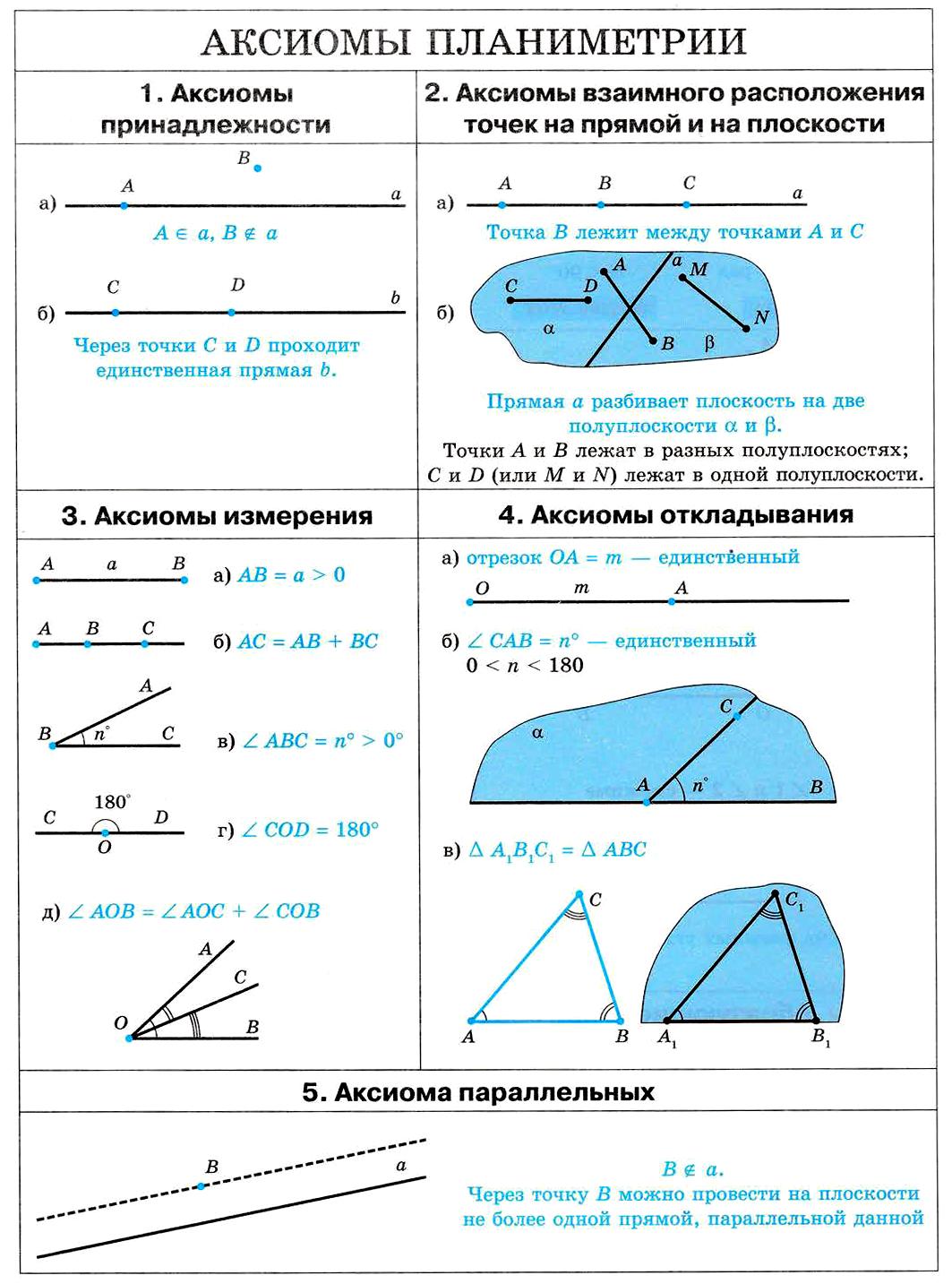
01. Аксиомы планиметрии.
Аксиомы принадлежности. Аксиомы взаимного расположения точек на прямой и плоскости. Аксиомы измерения. Аксиомы откладывания. Аксиома параллельных
02. Углы
Смежные углы. Вертикальные углы. Углы при пересечении
03. Параллельные прямые. Перпендикулярные прямые. Перпендикуляр к прямой
03. Параллельные прямые. Перпендикулярные прямые. Перпендикуляр к прямой
04. Свойства сторон и углов треугольника
Свойства сторон и углов треугольника. Внешний угол. Свойства. Неравенство треугольника. Равнобедренный треугольник
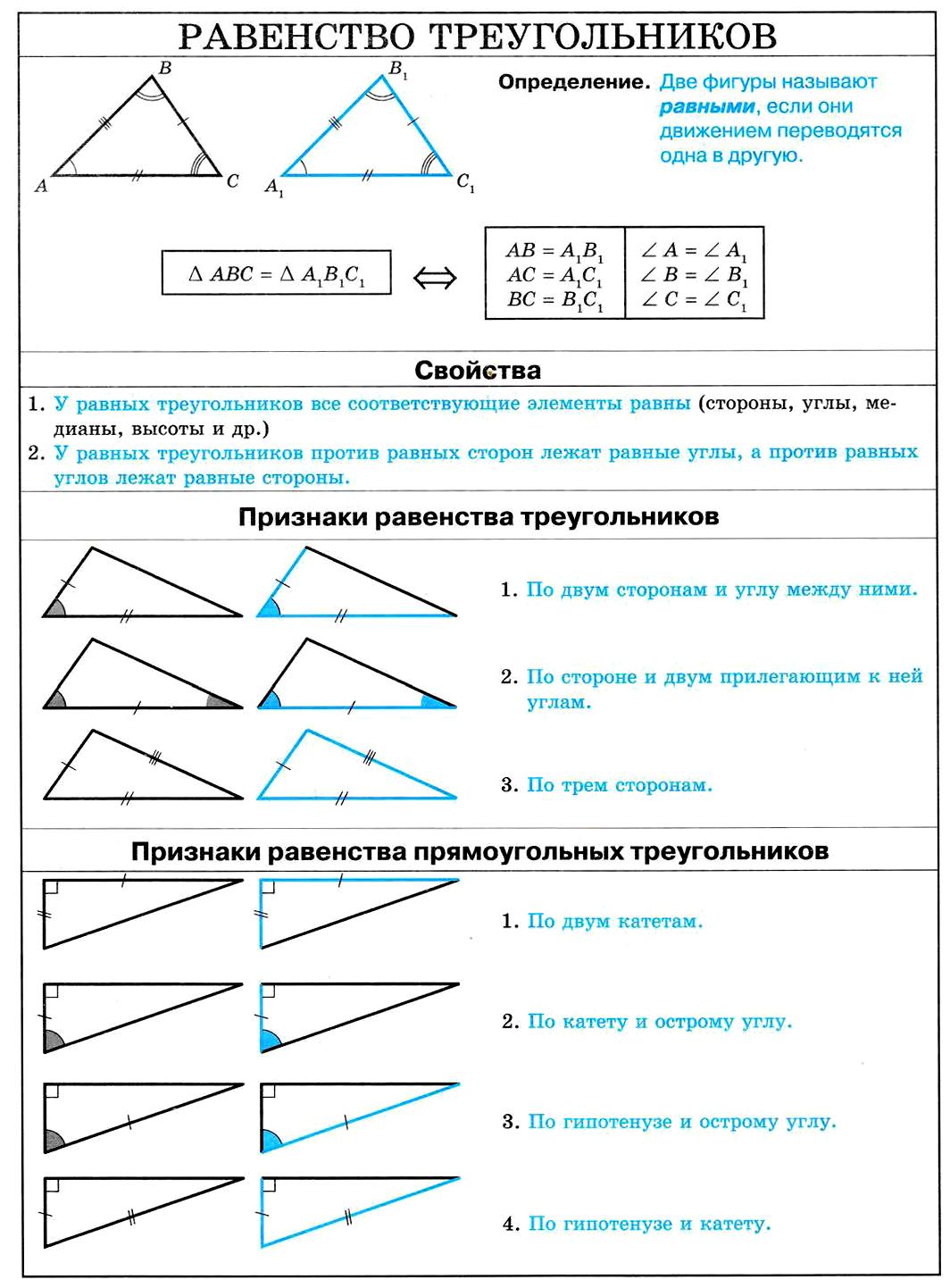
05. Равенство треугольников.
Равенство треугольников. Свойства. Признаки равенства треугольников. Признаки равенства прямоугольных треугольников
06. Медиана треугольника.
Медиана треугольника. Свойства.
07. Биссектриса треугольника.
Биссектриса треугольника. Свойства
08. Высота треугольника
Высота треугольника. Свойства
09. Средняя линия треугольника
Средняя линия треугольника. Свойства
10. Соотношение между элементами прямоугольного треугольника
Соотношение между элементами прямоугольного треугольника
11. Соотношение между сторонами и углами в произвольном треугольнике
Соотношение между сторонами и углами в произвольном треугольнике
12. Преобразование фигур. Движение
Преобразование фигур. Движение. Симметрия относительно точки. Поворот. Симметрия относительно прямой. Параллельный перенос
13. Преобразование подобия
Преобразование подобия. Свойства. Гомотетия.
14. Подобие треугольников.
Подобие треугольников. Свойства. Признаки подобия треугольников
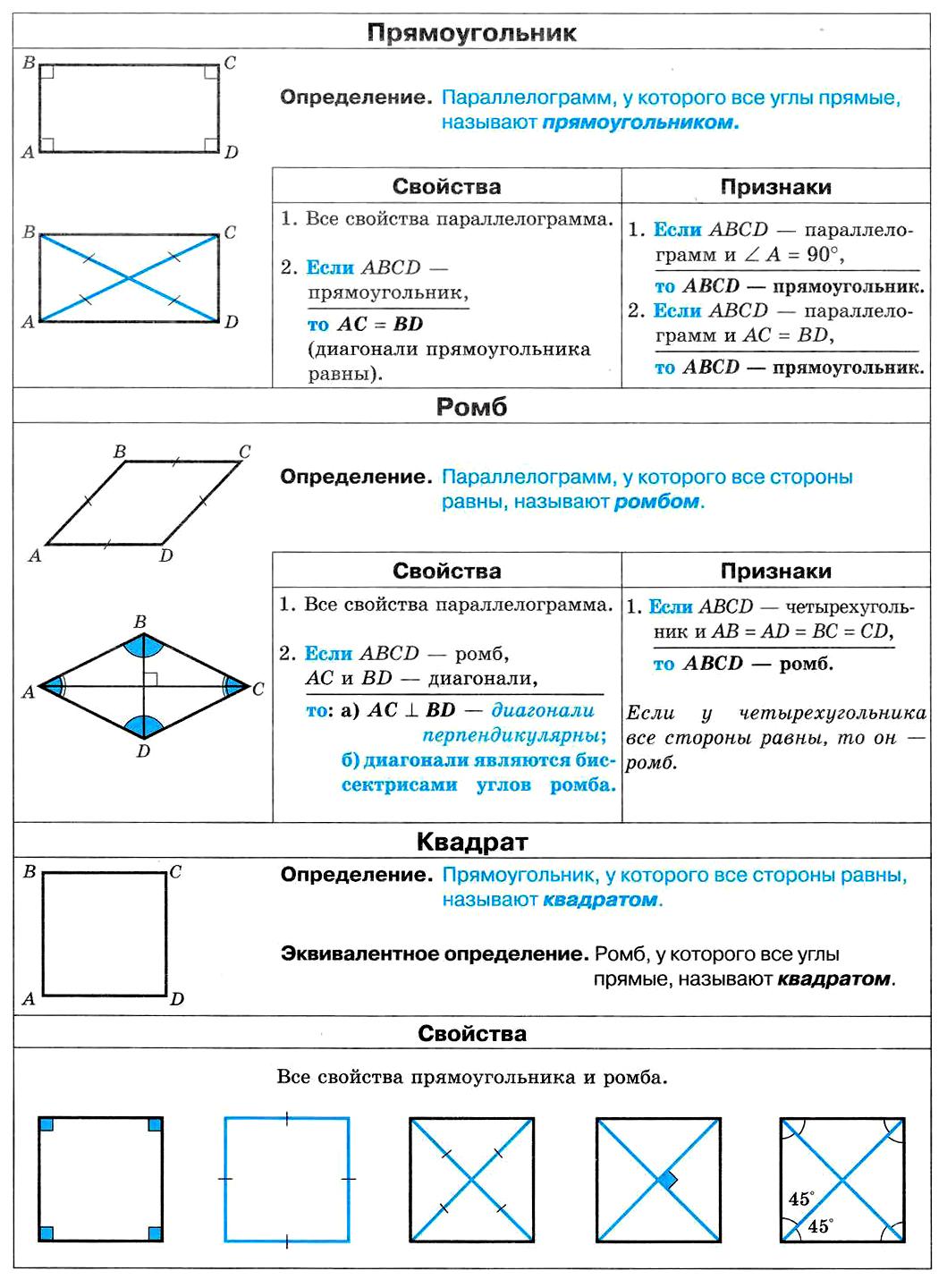
15. Параллелограмм и его виды.
Параллелограмм и его виды. Свойства. Признаки
Прямоугольник. Ромб. Квадрат.
16. Трапеция
Трапеция. Частные случаи трапеции. Средняя линия трапеции. Дополнительные построения для трапеции
17. Окружность, хорды и дуги
Окружность, хорды и дуги. Свойства
18. Окружность. Касательные и секущие.
Окружность. Касательные и секущие.
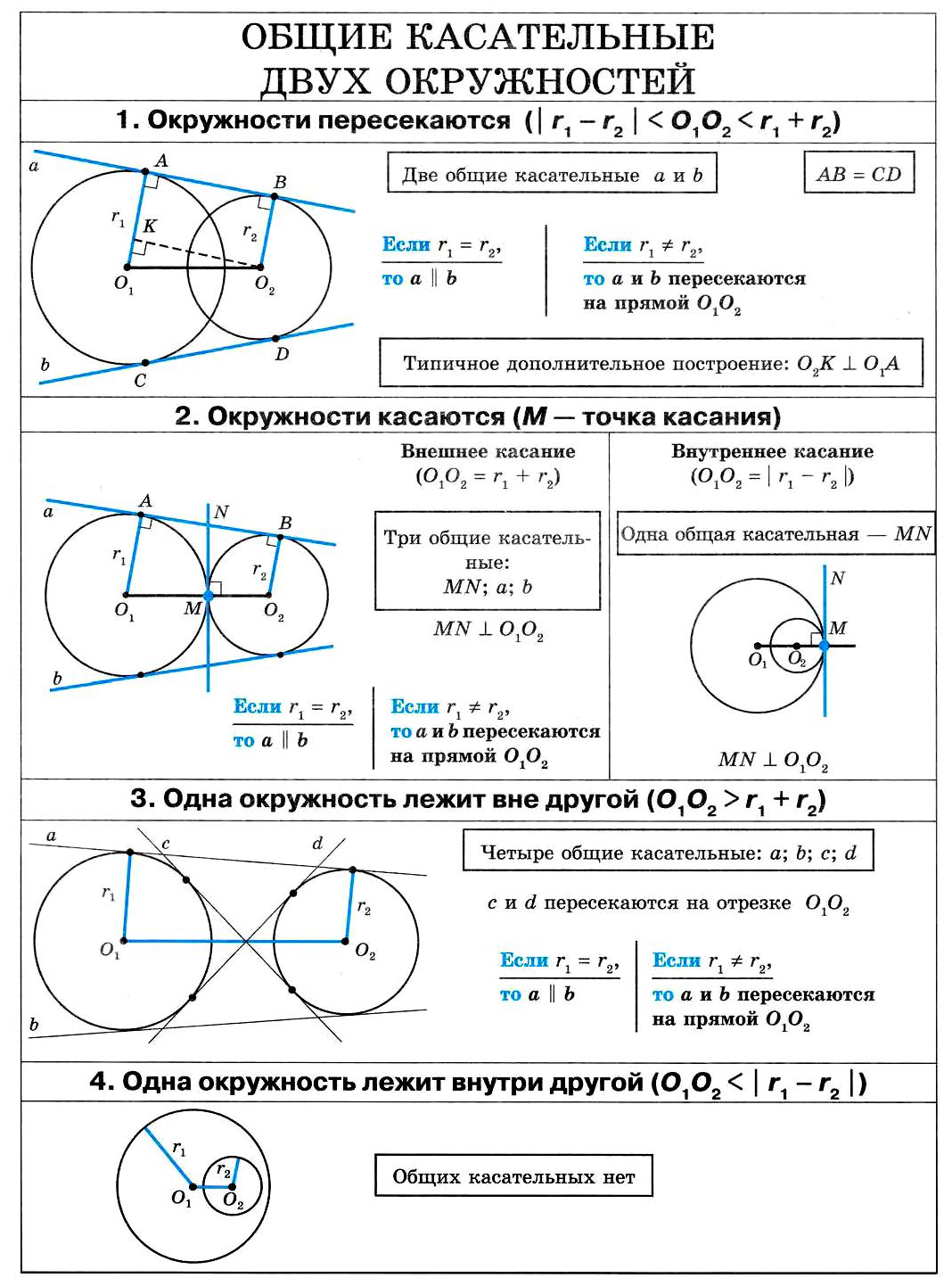
19. Взаимное расположение прямой и окружности. Взаимное расположение двух окружностей.
Взаимное расположение прямой и окружности. Взаимное расположение двух окружностей.
20. Общие касательные двух окружностей.
Общие касательные двух окружностей.
21. Углы в окружности.
Углы в окружности.
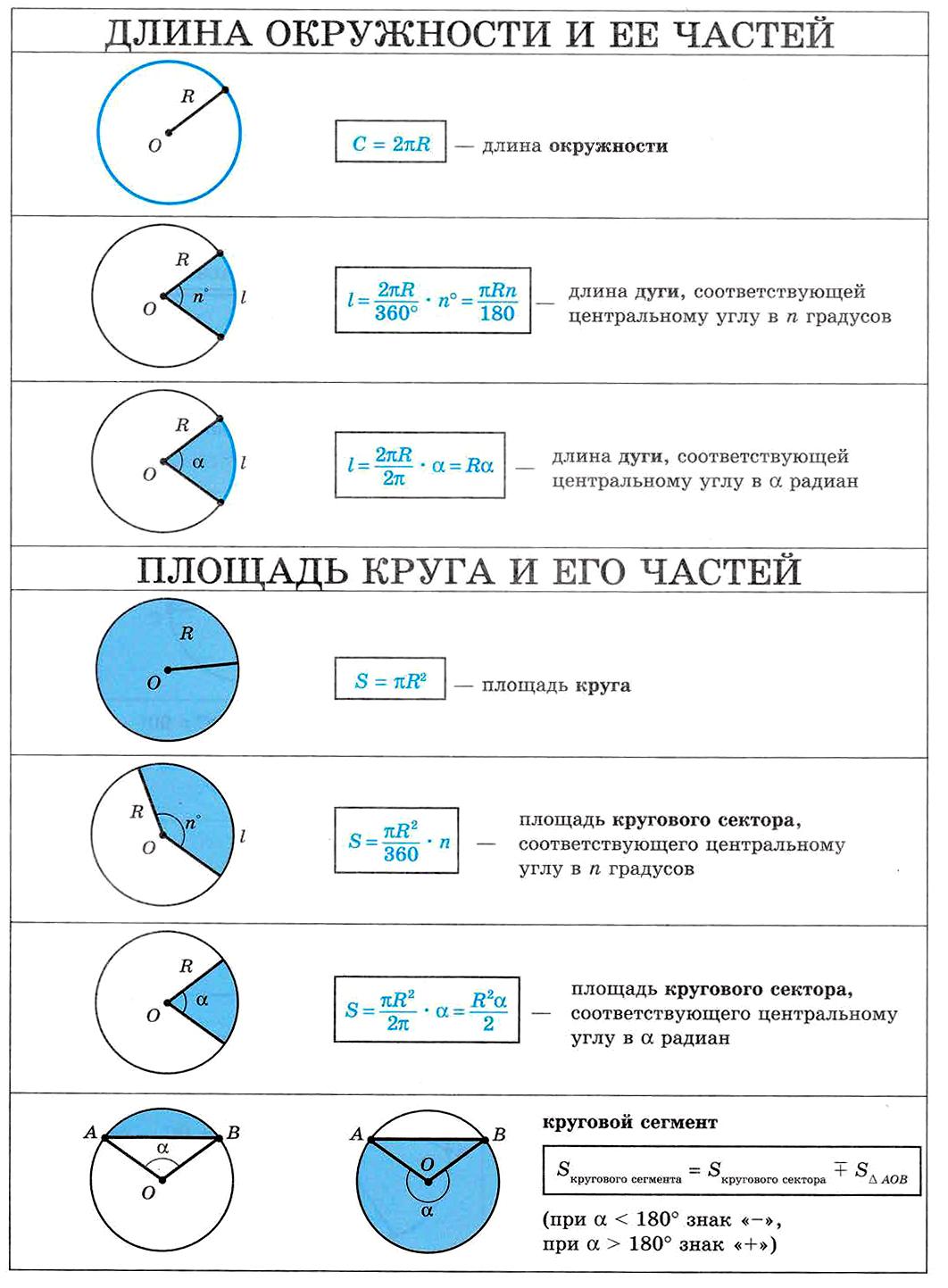
22. Длина окружности и её частей. Площадь круга и его частей
Длина окружности и её частей. Площадь круга и его частей
23. Вписанный и описанный многоугольники. Вписанный и описанный четырехугольники. Прямоугольник. Трапеция и ромб. Квадрат.
Вписанный и описанный многоугольники. Вписанный и описанный четырехугольники. Прямоугольник. Трапеция и ромб. Квадрат.
24. Окружность, описанная около треугольника, и окружность, вписанная в треугольник.
25. Окружности, описанные и вписанные в правильные многоугольники
Окружности, описанные и вписанные в правильные многоугольники
26. Площади треугольников.
Площади треугольников.
27. Площади четырехугольников.
Площади четырехугольников. Площадь описанного многоугольника
Вы смотрели справочник по геометрии для 7-11 классов «Теоремы и определения по Планиметрии».