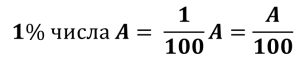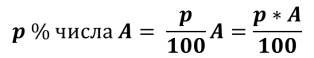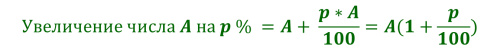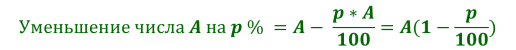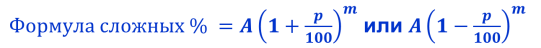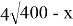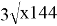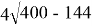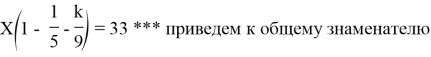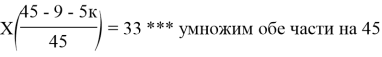Статистика решения экономических задач егэ

Чтобы сумма на банковском счёте была наибольшей необходимо, чтобы процент (r) от стоимости ценной бумаги в n-ом году был больше, чем 2000 рублей r(7000+(n-1)2000)2000

0,1(7000+2000n-2000)2000

500+200n2000

200n

n

n=8

Ответ: 8года.

3.3 Задачи на оптимизацию.

Задача №1.

У фермера есть два поля, каждое площадью 100 гектаров. На каждом поле можно выращивать картофель и свёклу, поля можно делить между этими культурами в любой пропорции. Урожайность картофеля на первом поле составляет 400 ц/га, а на втором — 300 ц/га. Урожайность свёклы на первом поле составляет 300 ц/га, а на втором — 400 ц/га.Фермер может продавать картофель по цене 10 000 руб. за центнер, а свёклу — по цене 11 000 руб. за центнер. Какой наибольший доход может получить фермер?

Решение:

Вся площадь: 100 га

Составим функцию полного дохода:

∑(x,k) = 4000000x+3300000kx→наиб

Заметим, что x+kx=100, т.е. x=где k

∑(k) = +→наиб

∑(k) = →наиб

Возьмём производную этой функции

= =

Значит функция убывает во всей области определения, т.е. принимает своё наибольшее значение при k=0. Это означает, что всё первое поле нужно засадить картофелем, при этом доход будет 4000000рублей

Из второй таблицы видно, что свекла имеет, как большую урожайность, так и большую цену за центнер, следовательно, второе поле нужно засадить свеклой.При этом доход будет 40011000рублей

Полный доход составляет 400 млн + 440 млн = 840 млн рублей.

Ответ: 840 млн рублей.

Задача №2.

У фермера есть два поля, каждое площадью 10 гектаров. На каждом поле можно выращивать картофель и свёклу, поля можно делить между этими культурами в любой пропорции. Урожайность картофеля на первом поле составляет 500 ц/га, а на втором — 300 ц/га. Урожайность свёклы на первом поле составляет 300 ц/га, а на втором – 500 ц/га. Фермер может продать картофель по цене 5000 руб. за центнер, а свёклу — по цене 8000 руб. за центнер. Какой наибольший доход может получить фермер?

Вся площадь: 10 га

Составим функцию полного дохода:

∑(x,k) = 2500000x+2400000kx→наиб

Заметим, что x+kx=10, т.е. x=где k

∑(k) = +→наиб

∑(k) = →наиб

Возьмём производную этой функции

= =

Значит функция убывает во всей области определения, т.е. принимает своё наибольшее значение при k=0. Это означает, что всё первое поле нужно засадить картофелем, при этом доход будет 2500000рублей

Из второй таблицы видно, что свекла имеет, как большую урожайность, так и большую цену за центнер, следовательно, второе поле нужно засадить свеклой. При этом доход будет 5008000рублей

Полный доход составляет 25 млн + 40 млн = 65 млн рублей.

Ответ: 65млн рублей.

Задача №3.

Предприниматель купил здание и собирается открыть в нём отель. В отеле могут быть стандартные номера площадью 27 квадратных метров и номера «люкс» площадью 45 квадратных метров. Общая площадь, которую можно отвести под номера, составляет 981 квадратный метр. Предприниматель может поделить эту площадь между номерами различных типов, как хочет. Обычный номер будет приносить отелю 2000 рублей в сутки, а номер «люкс» — 4000 рублей в сутки. Какую наибольшую сумму денег сможет заработать в сутки на своём отеле предприниматель?

Решение:

Общая площадь: 981

Составим функцию полного дохода:

∑(x,y) = 2000x+4000y→наиб

Заметим, что 27x+45y981, т.е. x где y , т.е.y

∑(y) = +4000y→наиб

∑(y) = →наиб

Возьмём производную этой функции

=

Значит функция возрастает во всей области определения, т.е. принимает своё наибольшее значение при y=21. Это означает, что номеров люкс будет 21. Проверим общую площадь: 45ер. При этом полный доход будет рублей.

Ответ: 86000 рублей.

Задача №4.

Предприниматель купил здание и собирается открыть в нем отель. В отеле могут быть стандартные номера площадью 30 квадратных метров и номера «люкс» площадью 40 квадратных метров. Общая площадь, которую можно отвести под номера, составляет 940 квадратных метров. Предприниматель может определить эту площадь между номерами различных типов, как хочет. Обычный номер будет приносить отелю 4000 рублей в стуки, а номер «люкс» — 5000 рублей в сутки. Какую наибольшую сумму денег сможет заработать в сутки на своем отеле предприниматель?

Решение:Общая площадь : 940

Составим функцию полного дохода:

∑(x,y) = 4000x+5000y→наиб

Заметим, что 30x+40y940, т.е. x где y , т.е.y

∑(y) = +5000y→наиб

∑(y) = →наиб

Возьмём производную этой функции

=

Значит функция убывает во всей области определения, т.е. принимает своё наибольшее значение при y=0. Это означает, что стандартных номеров будет 940. Проверим общую площадь: 30ер на номер люкс. При этом полный доход будет рублей.

Ответ: 125000 рублей.

Задача №5.

Антон является владельцем двух заводов в разных городах. На заводах производится абсолютно одинаковые товары при использовании одинаковых технологий. Если рабочие на одном из заводов трудятся суммарно t² часов в неделю, то за эту неделю они производят t единиц товара. За каждый час работы на заводе, расположенном в первом городе,Антон платит рабочему 250 рублей, а на заводе, расположенном во втором городе, — 200 рублей. Антон готов выделять 900 000 рублей в неделю на оплату труда рабочих. Какое наибольшее количество единиц товара можно произвести за неделю на этих двух заводах?

Решение: Оплата труда в неделю : 900000рублей

Составим функцию количества единиц товара:

∑(x,y) = x+y→наиб

Заметим, что 250+200900000, т.е. x где y

∑(y) = +y→наиб

Возьмём производную этой функции

= +1 =

Найдём нули производной: =0

=0

0,64=(3600-)

1,44=3600

y=50

Функция принимает своё наибольшее значение при y=50 (точка максимума).

x==40

Найдём количество единиц товара :+50 = 90

Ответ: 90 единиц товара.

Задача №6.

Григорий является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары, но на заводе, расположенном во втором городе, используется более совершенное оборудование. В результате, если рабочие на заводе, расположенном в первом городе, трудятся суммарно t² часов в неделю, то за эту неделю они производят 3t единиц товара; если рабочие на заводе, расположенном во втором городе, трудятся суммарно t² часов в неделю, то за эту неделю они производят 4t единиц товара. За каждый час работы (на каждом из заводов) Григорий платит рабочему 500 рублей. Готов выделять 5 000 000 рублей в неделю на оплату труда рабочих. Какое наибольшее количество единиц товара можно произвести за неделю на этих двух заводах?

Решение:Оплата труда в неделю: 5000000рублей

Составим функцию количества единиц товара:

∑(x,y) = 3x+4y→наиб

Заметим, что 500+5005000000, т.е. x где y

∑(y) =3 +4y→наиб

Возьмём производную этой функции

= 3+4 =

Найдём нули производной: =0

=0

9=16(10000-)

25=1600000

y=80

Функция принимает своё наибольшее значение при y=80 (точка максимума).

x==60

Найдём количество единиц товара: 3+480 = 180+320 = 500

Ответ: 500 единиц товара.

Задача №7.

Борис является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары при использовании одинаковых технологий. Если рабочие на одном из заводов трудятся суммарно t ² часов в неделю, то за эту неделю они производят t единиц товара.За каждый час работы на заводе, расположенном в первом городе, Борис платит рабочему 500 рублей, а на заводе, расположенном во втором городе, — 200 рублей.Борису нужно каждую неделю производить 70 единиц товара. Какую наименьшую сумму придётся тратить еженедельно на оплату труда рабочих?

Решение: 70 единиц товара

Составим функцию еженедельной оплаты труда:

∑(x,y) = 500→наим

Заметим, что x+y70, т.е. x где y

∑(y) =500→наим

∑(y) =500 =700-70000y+2450000

Возьмём производную этой функции

= 1400y-70000

Найдём нули производной: 1400y-70000=0

y=50

Функция принимает своё наименьшее значение при y=50 (точка минимума).

x

Найдёмеженедельную оплату труда:+200 = 500+200500000=700000

Ответ: 700тысяч рублей.

Задача №8.

Фёдор является владельцем двух заводов в разных городах.Назаводахпроизводятсяабсолютноодинаковыеприборы,ноназаводе,расположенном в первом городе, используется более совершенное оборудование. В результате, если рабочие на заводе, расположенном в первом городе, трудятсясуммарно 3t²часоввнеделю,тозаэтунеделюонипроизводят t приборов;если рабочие на заводе,расположенномво втором городе, трудятся суммарно 4t² часов внеделю,онипроизводят tприборов.За каждый час работы (на каждом из заводов) Фёдор платит рабочему 1тысячуруб.Необходимо,чтобызанеделюсуммарнопроизводилось30приборов.Какуюнаименьшуюсуммупридетсятратитьвладельцузаводов еженедельно на оплату трударабочих? 

Решение: 30 единиц товара

4y²

y

1000

4000

Составим функцию еженедельной оплаты труда:

∑(x,y) = 3000→наим

Заметим, что x+y30, т.е. x где y

∑(y) =3000→наим

∑(y) =3000 =7000-180000y+2700000

Возьмём производную этой функции

= 14000y-180000

Найдём нули производной: 14000y-180000=0

y==12

Функция принимает своё наименьшее значение при y=12 (точка минимума).

Пусть y=12, тогда x=18

Найдёмеженедельную оплату труда:+400 = 3000+4000000=1548000

Пусть y=13, тогда x=17

Найдёмеженедельную оплату труда:+400 = 30004000000=1543000

Ответ: 1543000 рублей.

Задача №9.

В двух областях есть по 160 рабочих, каждый из которых готов трудиться по 5 часов в сутки на добыче алюминия или никеля. В первой области один рабочий за час добывает 0,1 кг алюминия или 0,1 кг никеля. Во второй области для добычи x кг алюминия в день требуется x² человеко-часов труда, а для добычи у кг никеля в день требуется у² человеко-часов труда.

Для нужд промышленности можно использовать или алюминий, или никель, причём 1 кг алюминия можно заменить 1 кг никеля. Какую наибольшую массу металлов можно за сутки суммарно добыть в двух областях?

Решение:

Из таблицы видно, что в первой области совершенно одинаковые условия добывания алюминия и никеля. Это означает, что в первой области алюминия и никеля будут добывать поровну по = 40 кг. Всего 80 кг.

Во второй области: x² +y²=160

x² +y²=800

x=20, y=20. Всего 40 кг.

Ответ: 120кг.

Задача №10.

В двух шахтах добывают алюминий и никель. В первой шахте имеется 60 рабочих, каждый из которых готов трудиться 5 часов в день. При этом один рабочий за час добывает 2 кг алюминия или 3 кг никеля. Во второй шахте имеется 260 рабочих, каждый из которых готов трудиться 5 часов в день. При этом один рабочий за час добывает 3 кг алюминия или 2 кг никеля.

Обе шахты поставляют добытый металл на завод, где для нужд промышленности производится сплав алюминия и никеля, в котором на 2 кг алюминия приходится 1 кг никеля. При этом шахты договариваются между собой вести добычу металлов так, чтобы завод мог произвести наибольшее количество сплава. Сколько килограммов сплава при таких условиях ежедневно сможет произвести завод?

Решение: 60 человек по 5 часов в день

260 человек по 5 часов в день Получаем, что всего алюминия производят 10x+15y

никеля:15(60-x)+ 10(260-y)=3500-15x-10y

Так как для сплаванеобходимо , чтобы на2 кг алюминия приходился 1 кг никеля, то: 10x+15y=2(3500-15x-10y)

10x+15y=7000-30x-20y

40x=7000-35y

x = =

Составим функцию массы сплава:

∑(x,y) = 10x+15y+3500-15x-10y→наиб

∑(x,y) = 3500-5x+5y →наиб

∑(y) = 3500-5 +5y →наиб

∑(y) = 3500-5 +5y →наиб

∑(y) = →наиб

Возьмём производную этой функции

=

Значит функция возрастает во всей области определения, т.е. принимает своё наибольшее значение при наибольшем значенииy.

Так как x = то 1400-7y0 , y.

Проверим значение у=200, тогда x=0.

Масса сплава: 3500-5+5=4500

Ответ: 4500 кг.

Задача №11.

Фабрика, производящая пищевые полуфабрикаты, выпускает блинчики со следующими видами начинки: ягодная и творожная. В данной ниже таблице приведены себестоимость и отпускная цена, а также производственные возможности фабрики по каждому виду продукта при полной загрузке всех мощностей только данным видом продукта.

Для выполнения условий ассортиментности, которые предъявляются торговыми сетями, продукции каждого вида должно быть выпущено не менее 15 тонн. Предполагая, что вся продукция фабрики находит спрос (реализуется без остатка), найдите максимально возможную прибыль, которую может получить фабрика от производства блинчиков за 1 месяц

Решение

Пусть xтонн выпускает фабрика блинчиков с ягодами, а y тонн – с творогом. Тогда по условию имеем :x

Составим функцию прибыли:

∑(x,y) = 30x+35y→наиб

Пусть производственная возможность равна 1, тогда + = 1

75x + 90y = 6750

x = 90 – 1,2y

∑(y) = 30(90 – 1,2y)+35y→наиб

∑(y) = 2700 — y→наиб

Возьмём производную этой функции

=

Значит функция убывает во всей области определения, т.е. принимает своё наибольшее значение при y=15. Тогда x = 90-1,2

При этом максимальная прибыль будет рублей.

Ответ: 2685000 рублей.

Задача №12.

Консервный завод выпускает фруктовые компоты в двух видах тары — стеклянной и жестяной. Производственные мощности завода позволяют выпускать в день 90 центнеров компотов в стеклянной таре или 80 центнеров в жестяной таре. Для выполнения условий ассортиментности, которые предъявляются торговыми сетями, продукции в каждом из видов тары должно быть выпущено не менее 20 центнеров. В таблице приведены себестоимость и отпускная цена завода за 1 центнер продукции для обоих видов тары.

Предполагая, что вся продукция завода находит спрос (реализуется без остатка), найдите максимально возможную прибыль завода за один день (прибылью называется разница между отпускной стоимостью всей продукциии её себестоимостью).

Решение

Пусть xцентнеров выпускает фабрика в стеклянной таре, а y центнеров – в жестяной. Тогда по условию имеем :x

Составим функцию прибыли:

∑(x,y) = 600x+650y→наиб

Пусть производственная возможность равна 1, тогда + = 1

80x + 90y = 7200

x = 90 – 1,125y

∑(y) = 600(90 – 1,125y)+650y→наиб

∑(y) = 54000 — 25y→наиб

Возьмём производную этой функции

=

Значит функция убывает во всей области определения, т.е. принимает своё наибольшее значение при y=20. Тогда x = 90-1,12

При этом максимальная прибыль будет рублей.

Ответ: 53500 рублей.

3.4 Нестандартные задачи

Задача №1.

Два велосипедиста равномерно движутся по взаимно перпендикулярным дорогам по направлению к перекрестку этих дорог. Один из них движется со скоростью 40 км/ч и находится на расстоянии 5 км от перекрестка, второй движется со скоростью 30 км/ч и находится на расстоянии 3 км от перекрестка. Через сколько минут расстояние между велосипедистами станет наименьшим? Каково будет это наименьшее расстояние?

Решение:

Составим функцию квадрата расстояния между велосипедистами:

∑(t) = →наим, где t

∑(t) = 25-400t+1600→наим

∑(t) = 2500→наим

Возьмём производную этой функции

= 5000t-580

Найдём нули производной: 5000t-580=0

t===

Функция принимает своё наименьшее значение при t=ч = 60(точка минимума).

Найдём расстояние между велосипедистами: = = ===0,6

Ответ: 0,6км, 6,96 минут.

Задача №2.

Бриллиант массой 20 карат был разбит на две части после чего его стоимость уменьшилась на 25,5%.а) Найдите массы частей на которые был разбит бриллиант если известно, что цена бриллианта пропорциональнаквадрату его массы.б) На какое максимальное число процентов может уменьшиться цена бриллианта разбитого на две части.

Решение:

M=20 карат, S— стоимость бриллианта

S=km,S₁=km₁,S₂=km₂

Пустьm=x,тогдаm=20-x

1. S1+S2=0,745S

kx²+k(20-x)²=0,745k20²

x²+(20-x)²=298

x²+400-40x+102=0

x²-20x+51=0

x₁=17, x₂=3

Ответ: массы частей 17 и 3 карат.

1. Цена бриллианта максимально снизится, если обе части будут по 10 карат

S₁+S₂=aS

k10²+k10²=a20²k

100+100=a400

a=200/400=0,5

Ответ: на 50%

Задача №3

В одной стране в обращении находились 1000000 долларов, 20% из которых были фальшивыми. Некая нехорошая структура стала ввозить в страну по 100000 долларов в месяц, 10% из которых были фальшивыми. В это время другая структура стала вывозить из страны 50000 долларов ежемесячно, из которых 30% оказались фальшивыми. Через сколько месяцев содержания фальшивых долларов в стране составит 5%?

Решение:

n-количество месяцев

200000-5000n =0,05(1000000+50000n )

200000-5000n =50000+2500n

-7500n = -150000

n=20

Ответ: 20 месяцев

Задача №4

Два брокера купили акции одного достоинства на сумму 3640 рублей.Когда цена на эти акции возросла, они продали часть акций на сумму 3927 рублей. Первый брокер продал 75% своих акций, а второй – 80%. При этом сумма от продажи акций, полученная вторым брокером, на 140% больше суммы первого. На сколько процентов возросла цена одной акции?

Решение:

k— первоначальная цена 1 акции

x – штук купил первый брокер

y – штук купил второй

z – конечная цена 1 акции

Составим систему уравнений:

3)

y = = 2,25x

1. k(x+y)=3640

k(x+2.25x)=3640

k = = =

1. z(0,75x+0,8y)=3927

z(0,75х+1,8x)=3927

z2,55x=3927

z= = =

4)Найдём, на сколько процентов возросла цена одной акции

k= — 100%

z = — a%

a= 137,5%

Ответ: на 37,5%

Задача №5.

Строительство нового завода стоит 115млн рублей. Затраты на производство x тыс. единиц продукции на таком заводе равны0,5 x²+x+9млн рублей в год. Если продукцию завода продать по цене p тыс. рублей за единицу, то прибыль фирмы (в млн рублей) за один год составит

px-(0,5 x²+x+9). Когда завод будет построен, фирма будет выпускать продукцию в таком количестве, чтобы прибыль была наибольшей. При каком наименьшем значении pстроительство завода окупится не более чем за 5 лет?

Решение

Составим функцию прибыли:

∑(x,p) =px-(0,5 x²+x+9)→наиб

∑(x,p) =px-0,5 x²—x-9

Возьмём производную этой функции

= p—x-1

Найдём нули производной: p—x-1=0

x = p-1

Функция принимает своё наибольшее значение приx = p-1(точка минимума).

Найдём прибыль:

∑(p) =p(p-1)-0,5 (p-1)²-(p-1)-9 = 0,5p²—p-8,5

По условию строительство завода должно окупиться не более, чем за 5 лет. То есть за 5 лет прибыль должна быть не меньше 115млн рублей.

5(0,5p²—p-8,5115

0,5p²—p-8,5-23=0

p²-2p-63=0

p₁=9, p₂=-7

Ответ: 9 тысяч рублей.

4.Заключение

В данной работе рассмотрены основные методы решения задач на кредит, вклады и оптимизацию. Тема работы очень актуальна, так как все рассматриваемые задачи взяты из материалов по подготовке к ЕГЭ по математике «Профиль». Надеюсь, что данная работа будет полезна учащимся 10-11 класса, а также преподавателям математики.

5.Список использованной литературы:

1. ЕГЭ 2018под редакцией А. Л. Семенова, И.В. Ященко

2. Открытый банк заданий ЕГЭfipi.ru

3. Сайт «Решу ЕГЭ»

4. Сайт «Алекс Ларин»

Научно-образовательный форум школьников Республики Мордовия

Лицей федерального государственного бюджетного образовательного учреждения высшего образования «Национальный исследовательский Мордовский государственный университет им. Н.П. Огарёва»

ИССЛЕДОВАТЕЛЬСКАЯ РАБОТА

ГОТОВИМСЯ К ЕГЭ. ЭКОНОМИЧЕСКИЕ ЗАДАЧИ В ПРОФИЛЬНОЙ МАТЕМАТИКЕ

Секция: Математический калейдоскоп

Автор работы:	Душутина К. A.
	10 класс Лицей МГУ им. Н. П. Огарева
Руководитель работы:	Кубанцева А. В.
	учитель математики Лицей МГУ им Н. П. Огарева

Саранск

2021

СОДЕРЖАНИЕ

ВВЕДЕНИЕ        3

1 ТЕОРЕТИЧЕСКАЯ ЧАСТЬ        5

1.1        Содержательный смысл определения экономической науки        5

1.2        Взаимосвязь двух наук: экономики и математики        5

1.3        Основные определения и понятия        6

1.3.1        Понятие процента и процентной ставки        7

1.3.2        Понятие арифметической и геометрической прогрессий        8

1.3.3        Понятия фиксированных, аннуитетных и дифференцируемых платежей        10

2        ПРАКТИЧЕСКАЯ ЧАСТЬ        12

2.1        Типы экономических задач и способы их решения        12

2.1.1        Кредиты        12

2.1.2        Вклады        21

2.1.3        Задачи на оптимальный выбор        23

2.1.4        Нестандартные задачи        24

ЗАКЛЮЧЕНИЕ        26

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ        27

ВВЕДЕНИЕ

Современная экономическая обстановка актуализирует проблему экономического воспитания подрастающего поколения. Экономические знания современной молодежи носят сугубо теоретический характер, оторванный от реальной действительности. Причем все больше осознается необходимость в формировании экономической грамотности у старшеклассников, тех, кто стоит на пороге самостоятельной жизни и которым в ближайшем будущем предстоит занять активную позицию в обществе. От экономической грамотности выпускников школы во многом будет зависеть их успешная адаптация к социально – экономическим условиям общества. Проблема обучения старшеклассников решению задач с экономическим содержанием складывается из нескольких составляющих: наличие в таких задачах большого количества терминов, неизвестных учащимся; старшеклассники плохо ориентируются в материале, изученном в 5-9 классах и необходимом для решения задач с экономическим содержанием: темы процентов, арифметической, геометрической прогрессий вызывают затруднения.

Задачи о вкладах и кредитовании, а также задачи оптимизации производства товаров и услуг сравнительно недавно включены во вторую часть ЕГЭ по математике профильного уровня и вызывают значительные затруднения у большинства выпускников.

Актуальность данной темы обусловлена тем, что в курсе математики, изучаемой в школе, решению задач с экономическим содержанием не уделено достаточно времени. Жизнь настоятельно требует, чтобы выпускник имел развитое экономическое мышление и был готов к жизни в условиях рыночных отношений. Однако основные практические навыки и умения у большинства учеников сформированы на уровне, не удовлетворяющем требованиям подготовки к ЕГЭ и повседневной жизни.

Гипотеза исследования – в современном мире необходимы знания об экономике и в этом может помочь математика.

Объект исследования – процесс подготовки к единому государственному экзамену по математике профильного уровня.

Предмет исследования – экономические задачи №17, встречающиеся в ЕГЭ по математике профильного уровня.

Цель исследования – исследование методов решения задач с экономическим содержанием.

Для достижения поставленной цели необходимо решить следующие задачи:

1. Изучить теоретико-методологические основы экономики.

2. Провести классификацию и систематизацию типов экономических задач, включенных во вторую часть ЕГЭ по математике профильного уровня, и методов их решений.

Методы исследования – теоретический анализ и синтез научной и учебной литературы по теме исследования, сравнение, систематизация информации, обобщение, вывод, подбор и решение задач.

Научная новизна работы заключается в обобщении, систематизация, анализе экономических задач, входящих в ЕГЭ по математике профильного уровня.

Практическое значимость – возможность использования обобщенных данных при подготовке выпускников к сдаче единого государственного экзамена по математике профильного уровня, отработке решения задач экономического содержания.

1 ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

1. Содержательный смысл определения экономической науки

У всякой науки свой предмет, т.е. своя главная тема исследований. В центре внимания экономической теории – хозяйственная деятельность людей, которая осуществляется при определенных условиях, в определенной обстановке, экономической среде. [2]. В зависимости от условий, обстановки и экономической среды, термин «экономика» имеет различные определения. Приведем одно из определений экономики (экономической теории) как науки:

Экономика – это наука, изучающая типичные мотивы и модели поведения людей в процессах производства, обмена и потребления жизненных благ. [6].

Другими словами, экономика – наука об оптимальном, т.е. наилучшем в конкретных условиях, использовании ограниченных ресурсов [8].

1. Взаимосвязь двух наук: экономики и математики

Математика настолько практична, что немногое из окружающего мира может без нее функционировать. От банков и магазинов, бирж и страховых компаний до штрихкодов, прослушивания дисков и разговоров по мобильному телефону – все это и многое другое работает благодаря процессорам и математическим моделям, задача которых – постоянное выполнение математических операций.

Особенности математики, как отличительной области знаний, которые делают ее неповторимой, заключаются в следующем:

• недопустимость расхождения в определении правил и создании математических формул;
• математические формулы составляются из ряда аксиом, на основе строгих условий;  
• возможность владеть теми или иными понятиями, не раскрывая их смысла.

Именно благодаря всем вышеперечисленным особенностям математический аппарат является многофункциональным аналитическим инструментом для всех отраслей знаний. [4].

Экономика представляет собой науку, которая изучает объективные причины и условия ведения в обществе хозяйственной деятельности. В этой связи экономике изначально были присущи различные количественные характеристики, исследование и описание которых потребовало использование большого числа математических методов. Экономические объекты, процессы и явления изучаются математически формализованным образом. Роль математики в экономике заключается в том, что ее язык позволяет сформулировать содержательные и проверяемые гипотезы о многих сложных экономических явлениях. Причем большая часть этих явлений вообще не может быть изучена без привлечения математического аппарата. В частности, его использование привело к созданию математических моделей, в которых нашли отражение некоторые теоретические экономические взаимосвязи.

На сегодняшний день обширное использование математического аппарата в своих исследованиях способствует достижению наибольших успехов в разных областях. Поэтому применение математики на практике позволяет достичь более значительных результатов в изучении явлений природы и общества.

1. Основные определения и понятия

Решение финансовых задач основывается на использовании различных математических моделей: уравнений, неравенств, их систем с привлечением процентов, арифметической и геометрической прогрессий, производной. Прежде чем рассмотреть способы решения экономических задач, целесообразно привести основные определения, понятия, таблицы и формулы.

1. Понятие процента и процентной ставки

Процентом называют одну сотую часть числа. С точки зрения экономики, процент – это абсолютная часть дохода, получаемая в результате финансовой операции за определенный период времени при наращении.

При решении экономических задач часто используется определение процентной ставки за определенный период времени – величины, характеризующей относительное изменение денежной суммы F за этот период:

где – абсолютная величина изменения суммы F.

Определенная таким образом процентная ставка измеряется в процентах (%). Если относительное изменение денежной суммы не умножать на 100, то ставка будет измеряться в долях единицы (дробях).

Отрезок времени, к которому приурочена процентная ставка, называют периодом начисления. В качестве такого периода принимают год, полугодие, квартал, месяц или даже день. Чаще всего на практике имеют дело с годовыми ставками.

В зависимости от того, какая из сумм дана и какую нужно найти, выделяют два направления финансовых расчетов: наращение и дисконтирование.

Наращение – определение величины итоговой стоимости по заданной текущей стоимости. Дисконтирование – определение текущей стоимости по ожидаемой итоговой сумме в будущем. [3].

Различают простые и сложные процентные ставки, или проценты.

Для начисления простых процентов применяют постоянную базу начисления. В этом случае начисленные за весь срок проценты I составят:

 где P – первоначальная денежная сумма, n – период начисления процентов, i – ставка наращения процентов в виде десятичной дроби.

Наращенная сумма представляет собой сумму первоначальной денежной суммы и наращенных процентов:

Когда за базу принимается сумма, полученная на предыдущем этапе наращения (дисконтирования), используют сложные процентные ставки. В этом случае база начисления последовательно изменяется, то есть проценты начисляются на проценты.

В конце первого года проценты будут равны величине I = Р * i, а наращенная сумма составит S = Р + Р * i = Р * (1 + i). К концу второго года она достигнет величины Р * (1 + i) + Р * (1 + i) * i = Р * (1 + i)2 и т.д. В конце n-го года наращенная сумма будет равна:

где P – первоначальная денежная сумма, n – период начисления процентов, i – ставка наращения процентов в виде десятичной дроби.

Проценты за этот срок составят:

.

1. Понятие арифметической и геометрической прогрессий

Арифметическая прогрессия – это числовая последовательность, в которой каждый член равен предыдущему, сложенному с одним и тем же числом. Это число называется разностью арифметической прогрессии и обозначается d. [7].

 

Очевидно, что арифметическая прогрессия представляется возрастающей последовательностью, если d > 0, и убывающей, если d < 0.

Формула n-ого члена арифметической прогрессии:

Формула суммы первых n членов арифметической прогрессии:

Каждый член арифметической прогрессии, кроме первого (и последнего – в случае конечной прогрессии), равен среднему арифметическому предыдущего и последующего членов. Верно и обратное: если последовательность (an) такова, что для любого n > 1 выполняется равенство:

 

то (аn) – арифметическая прогрессия. [5].

Числовую последовательность, все члены которой отличны от нуля и каждый член которой, начиная со второго, получается из предыдущего члена умножением его на одно и то же число q, называют геометрической прогрессией. При этом число q называют знаменателем прогрессии. [1].

Формула n-ого члена геометрической прогрессии:

Формула суммы первых n членов арифметической прогрессии:

Квадрат каждого члена геометрической прогрессии, первого (и последнего – в случае конечной последовательности), равен произведению предшествующего и последующего членов. Верно и обратное: если последовательность (bn) такова, что для любого n > 1 выполняется равенство:

 то (bn) – геометрическая прогрессия. [1].

1. Понятия фиксированных, аннуитетных и дифференцируемых платежей

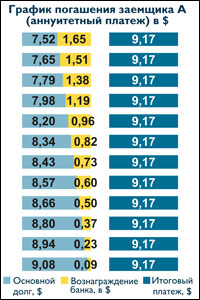
Фиксированные платежи – платежи, которые четко оговариваются в условии задачи. Аннуитетный платеж – это платеж, который устанавливается в равной сумме через равные промежутки времени. Месячный аннуитетный платеж находится по формуле:

где X – месячный платеж, S – сумма кредита, P – 1/12 процентной ставки, N – количество месяцев.

Дифференцируемый платеж – это платеж, который представляет собой неравные ежемесячные транши, пропорционально уменьшающиеся в течение срока кредитования. Если при аннуитетной схеме неизменным является сам аннуитетный платеж, то при дифференцируемой – не меняется именно взнос, идущий на погашение тела кредита. Рассчитывается он по формуле:

где St – сумма, которая идет на погашение тела кредита, S – сумма кредита, N – количество месяцев. Для расчёта доли процентов в дифференцированных платежах пользуются следующей формулой:

где In – сумма, которая идёт на погашение процентов по кредиту в данный расчётный период, Sn — остаток задолженности по кредиту, P – годовая процентная ставка. Зная долю тела кредита и долю процентов, мы можем рассчитать дифференцированный платёж, используя формулу:

где X — размер дифференцированного платежа по кредиту, St – сумма, которая идёт на погашение тела кредита, In – сумма уплачиваемых процентов. [3].

1. ПРАКТИЧЕСКАЯ ЧАСТЬ

Экономические задачи были введены в задания ЕГЭ по математике профильного уровня (№17) в 2015 году. По своей сложности задачи с экономическим содержанием находятся на одном уровне с заданиями, содержащие параметры и теорию чисел.

Низкий процент успешной сдачи решения задания №17 (за 2015 – 2020 годы – 2, 5) объясняется как трудностью самих задач, так и их отсутствием в школьном курсе математики.

Основными ошибками, которыми допускали учащиеся при решении задач финансовой математики, являются:

• неверное составление модели;
• вычислительными, или арифметические;
• прекращение решения на промежуточном шаге, то есть без доведения ответа до числового значения;
• решение методом перебора без обоснования единственности;
• решение без вывода формул. В ряде случаев трактуется как неумение строить математическую модель.

С целью подготовки учащихся к успешной ЕГЭ имеет смысл подробно рассмотреть типы экономических задач и методы их решения.

1. Типы экономических задач и способы их решения

Условно выделяют несколько типов задач экономического содержания.

Далее приведем подробные разборы примеров задания №17 каждого типа.

1. Кредиты

ПРИМЕР №1 (Подтип 1: Нахождение количества лет (месяцев) выплаты кредита). 1 января 2015 года Павел Витальевич взял в банке 1 млн рублей в кредит. Схема выплаты кредита следующая: 1 числа каждого следующего месяца банк начисляет 1 процент на оставшуюся сумму долга (то есть увеличивает долг на 1%), затем Павел Витальевич переводит в банк платёж. На какое минимальное количество месяцев Павел Витальевич может взять кредит, чтобы ежемесячные выплаты были не более 125 тыс. рублей? [10].

РЕШЕНИЕ:

СПОСОБ №1. Сначала найдем минимальное количество месяцев, за которое Павел Витальевич сможет погасить основную сумму долга, если его ежемесячный платеж будет составлять 125 тыс. рублей: 1 000 000 : 125 000 = 8 (месяцев).

Но банк ежемесячно начисляет 1% на оставшуюся сумму долга. Тем самым получаем, что общая сумма долга будет превышать 1 млн рублей.

Составим таблицу, наглядно показывающую схему кредита, и найдем № месяца, когда задолженность будет меньше, чем ежемесячная выплата:

Месяц, №	Задолженность в начале месяца, руб.	Задолженность после погашения, руб.
1	1 000 000 + 1% = 1 010 000	1 010  000 – 125 000 = 885 000
2	885 000 + 1% =893 850	893 850 – 125 000 = 768 850
3	768 850 + 1% = 776 538, 5	776 538, 5 – 125 000 = 651 538,5
4	651 538,5 + 1% = 658 054	658 054 – 125 000 = 533 054
5	533 054 + 1% = 538 385	538 385 – 125 000 = 413 385
6	413 385 + 1% = 417 519	417 519 – 125 000 = 292 519
7	292 519 + 1% = 295 445	295 445 – 125 000 = 170 445
8	170 445 + 1% = 172 150	172 150 – 125 000 = 47 150
9	47 150 + 1% = 47 622	0

СПОСОБ №2. За 8 месяцев Павел Витальевич сможет оплатить за кредит не более, чем 125 000 * 8 = 1 000 000 рублей, но с учетом начисляемых процентов общая сумма долга будет превышать 1 млн рублей.

За 9 месяцев банк начислит не более, чем 9 сумм процентов за первый месяц (максимально начисленные проценты будут составлять 10 000 рублей), то есть 10 000 * 9 = 90 000, что составляет меньше, чем ежемесячный платеж. Таким образом, Павел Витальевич полностью погасит кредит за 9 месяцев.

ОТВЕТ: на 9 месяцев.

ПРИМЕР №2 (Подтип 1: Нахождение количества лет (месяцев) выплаты кредита). В июле планируется взять кредит в банке на сумму 5 млн рублей на некоторый срок. Условия его возврата таковы:

• каждый январь долг возрастает на 15% по сравнению с концом предыдущего года;
• с февраля по июнь каждого года необходимо выплатить часть долга;
• в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года.

На какой минимальный срок следует брать кредит, чтобы наибольший годовой платёж по кредиту не превысил 1, 4 млн руб.? [11].

РЕШЕНИЕ: Чтобы найти минимальное количество лет, надо обозначить размер максимального первого платежа – 1,4 млн рублей.

Дата	Долг до выплаты, млн руб.	Выплата, млн руб.	Долг после выплаты, млн руб.
Июль 0-ого года	5
Январь 1-ого года	5 + 15% = 5,75
Февраль 1-ого года		1,4	5,75 — 1,4 = 4,35
Июль 1-ого года	4,35 (разница 0,65)
Июль 2-ого года	4,35 – 0,65 = 3,7
Июль 3-его года	3, 7 – 0,65 = 3,05
Июль 4-ого года	3,05 – 0,65 = 2,4
Июль 5-ого года	2,4 – 0,65 = 1,75
Июль 6-ого года	1,75 – 0,65 = 1,1
Июль 7-ого года	1,1 – 0,65 = 0,45
Июль 8-ого года	0

Мы можем найти оставшуюся сумму долга на июль данного года, найдя фиксированную разницу между 1-ым и 2-ым годами выплаты кредита. Как только, оставшаяся сумма долга будет меньше, чем разница, кредит будет считаться полностью оплаченным в этот год.

ОТВЕТ: 8 лет.

ПРИМЕР №3 (Подтип 2: Вычисление процентной ставки по кредиту). В июле 2019 планируется взять кредит в банке на сумму 100 000 рублей. Условия его возврата таковы:

• каждый январь долг возрастает на r% по сравнению с концом предыдущего года;
• с февраля по июнь каждого года необходимо выплатить часть долга.

Найдите число r, если известно, что кредит был полностью погашен за два года, причём в первый год было переведено 52 500 рублей, а во второй год – 67 500 рублей? [11].

РЕШЕНИЕ: Пусть банк начисляет r процентов, умножая сумму долгу на x = (1 + ). Составим схему погашения кредита:

Дата	Долг до выплаты, тыс. руб.	Выплата, тыс. руб.	Долг после выплаты, тыс. руб.
1.7.2019	100
1.1.2020	100x
1.2.2020		52,5
1.7.2020			100x – 52,5
1.1.2021	(100x – 52,5) * x = 100x2 – 52,5x
1.2.2021		67,5
1.7.2021			100x2 – 52, 5x – 67,5 = 0

Решив квадратное уравнение: 100x2 – 52, 5x – 67,5 = 0, получаем, что x1= = — 0,6 (не подходит, т. к. процентная ставка не может быть отрицательным числом) и x2 = 1, 125. Отсюда получаем: x = 1 +  = 1, 125; r = 12, 5.

ОТВЕТ: 12,5

ПРИМЕР №4 (Подтип 3: Нахождение суммы кредита). Планируется выдать льготный кредит на целое число миллионов рублей на пять лет. В середине каждого года действия кредита долг заёмщика возрастает на 20 % по сравнению с началом года. В конце 1-го, 2-го и 3-го годов заёмщик выплачивает только проценты по кредиту, оставляя долг неизменно равным первоначальному. В конце 4-го и 5-го годов заёмщик выплачивает одинаковые суммы, погашая весь долг полностью. Найдите наименьший размер кредита, при котором общая сумма выплат заёмщика превысит 10 млн. [10].

РЕШЕНИЕ:

СПОСОБ №1. Обозначим за S полную сумму кредита. Составим схему погашения кредита:

Дата	Долг до выплаты, млн руб.	Выплата, млн руб.	Долг после выплаты, млн руб.
Начало 1/2/3-ого годов	S
Середина 1/2/3-ого годов	S + 20%=1,2S
Конец 1/2/3-ого годов		0,2S	S
Начало 4-ого года	S
Середина 4-ого года	S + 20%=1,2S
Конец 4-ого года		X	1,2S — X
Начало 5-ого года	1,2S — X
Середина 5-ого года	(1,2S– X)+20% =1,44S-1,2X
Конец 5-ого года		X	1,44S — 1,2X – X = 0

Решаем уравнение 1,44S — 1,2X – X = 0. Получаем, что X = .

Общая сумма выплат составляет 0,6S + 2X = 0,6S + S = S. По условию: S > 10 млн. Получаем, что S > 5, 24 (Минимальное целочисленное решение неравенства – S = 6).

СПОСОБ №2. Обозначим за S полную сумму кредита. Каждый год заёмщик выплачивает по 0,2S млн. Всего 0,6S за три года.

Рассмотрим погашение кредита за следующие два года. В середине 4-го года долг возрастёт до 1,2S млн. Обозначим через X размер выплаты в конце 4-го и 5-го годов. После выплаты в конце 4-го года долг равен (1,2S — X), а в середине 5-го года он равен 1,2(1,2S — X). В конце 5-го года весь долг должен быть погашен. Отсюда следует, что последняя выплата равна 1,2(1,2S- X), а по условию равна X. Получаем, что X = S.

Общая сумма выплат составляет 0,6S + 2X = 0,6S + S = S. По условию, S > 10 млн. Получаем: S > 5, 24 (Минимальное целочисленное решение неравенства – S = 6).

ОТВЕТ: 6 млн рублей.

ПРИМЕР №5 (Подтип 4: Нахождение ежегодного (ежемесячного) транша). 31 декабря 2014 года Дмитрий взял в банке 4 290 000 рублей в кредит под 14,5% годовых. Схема выплаты кредита следующая – 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 14,5%), затем Дмитрий переводит в банк X рублей. Какой должна быть сумма X, чтобы Дмитрий выплатил долг двумя равными платежами (то есть за два года)? [10].

РЕШЕНИЕ: Составим схему погашения кредита:

Дата	Долг до выплаты, руб.	Выплата, руб.	Долг после выплаты, руб.
31.12.2014	4 290 000
31.12. 2015	4 290 000 + 14,5% = 4 912 050	X	4 912 050 — X
31.12. 2016	(4 912 050 – X) + 14,5% =     5 624 298 – 1,145X	X	5 624 298 – 2,145X = 0

Решаем уравнение 5 624 298 – 2,145X = 0. Получаем, что X = 2 622 050.

ОТВЕТ: 2 622 050 рублей.

ПРИМЕР №6 (Подтип 4: Нахождение ежегодного (ежемесячного) транша). Клиент взял в банке кредит 18000 рублей на год под 18 %. Он должен погашать кредит, внося в банк ежемесячно одинаковую сумму денег, с тем чтобы через год выплатить всю сумму, взятую в кредит, вместе с процентами. Сколько рублей он должен вносить в банк ежемесячно? [10].

РЕШЕНИЕ: Через год банк начисляет 18% годовых, то есть долг увеличивается в 1,18 раз. Получится, что клиент должен банку 18 000 * 1,18 = 21 240 рублей. Соответственно ежемесячная выплата составит:

 21 240 / 12 = 1 770 рублей.

ОТВЕТ: 1 770 рублей.

ПРИМЕР №7 (Подтип 5: Нахождение разницы). 31 декабря 2014 года Тимофей взял в банке 7 007 000 рублей в кредит под 20% годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 20%), затем Тимофей переводит в банк платёж. Весь долг Тимофей выплатил за 3 равных платежа. На сколько рублей меньше он бы отдал банку, если бы смог выплатить долг за 2 равных платежа? [10].

РЕШЕНИЕ: Построим схему выплаты кредита:

Дата	Долг до выплаты, руб.	Выплата, руб.	Долг после выплаты, руб.
31.12.2014	7 007 000
31.12.2015	7 007 000 + 20% = 8 408 400	X	8 408 400 – X
31.12.2016	(8 408 400 – X) + 20% = 10 090 080 – 1,2X	X	10 090 080 – 2,2X
31.12.2017	(10 090 080 – 2,2X) + 20% = 12 108 096 – 2,64X	X	12 108 096 – 3,64X

Схема №1 (3 равных платежа). Последним платежом Тимофей полностью погасит кредит. Решим уравнение 12 108 096 – 3,64X1 = 0. Получаем, что X1 = 3 326 400.

Схема №2 (2 равных платежа). Решим уравнение 10 090 080 – 2,2X2 = 0. Получаем, что X2 = 4 586 400.

Находим разницу: 3X1 – 2X2 = 9 979 200 – 9 172 800 = 806 400 рублей.

ОТВЕТ: на 806 400 рублей.

ПРИМЕР №8 (Подтип 6: Задачи, связанные с известным остатком). В январе 2020 года планируется взять кредит в банке на три года в размере 800 тыс. рублей. Условия его возврата таковы:

• каждый ноябрь долг увеличивается на 20% по сравнению с концом предыдущего года;
• в декабре каждого года необходимо выплатить одним платежом часть долга;
• в январе каждого года долг (в тыс. рублей) должен соответствовать следующей таблице:

Месяц и год	Январь 2020	Январь 2021	Январь 2022	Январь 2023
Долг, тыс. руб.	800	600	300	0

Сколько тыс. рублей нужно заплатить по кредиту в декабре 2021 года? [11].

РЕШЕНИЕ:

СПОСОБ №1. Составим схему погашения кредита:

Дата	Долг до выплаты, тыс. руб.	Выплата, тыс. руб.	Долг после выплаты, тыс. руб.
Январь 2020	800
Ноябрь 2020	800 + 20% = 960
Декабря 2020		X1 = 960 – 600 = 360
Январь 2021			960 – X1 = 600
Ноябрь 2021	600 + 20% = 720
Декабрь 2021		X2 =720 – 300 = 420
Январь 2022			720 – X2 = 300
Ноябрь 2022	300 + 20% = 360
Декабрь 2022		X3 = 360
Январь 2023			360 – X3 = 0

По таблице видим, что в декабре 2021 года клиент должен будет заплатить банку 420 тыс. рублей.

СПОСОБ №2. В ноябре 2021 года долг в размере 600 тыс. руб., который остался в 2021 году, увеличится на 20% и будет составлять 600 *1,2 = 720 тыс. руб. В январе 2022 года долг должен стать равным 300 тысячам рублей, так что в декабре 2021 года должно быть выплачено 720 – 300 = 420 тыс. руб.

ОТВЕТ: 420 руб. тыс.

ПРИМЕР №9 (Подтип 7: Задачи, связанные с дифференцированными платежами). 15 января планируется взять кредит в банке на 9 месяцев. Условия его возврата таковы:

— 1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца;

— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

— 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца.

Известно, что на пятый месяц кредитования нужно выплатить 57,5 тыс. рублей. Какую сумму нужно вернуть банку в течение всего срока кредитования? [11].

РЕШЕНИЕ: Обозначим за S размер кредита, взятого в банке 15 января. 1-го февраля он уже вырастет на 3% и будет составлять 1,03S. После этого происходит выплата так, чтобы долг менялся каждый месяц на одну и ту же величину, то есть выплата в первый месяц составит: . Составим схему выплаты кредита:

Дата	Долг до выплаты, тыс. руб.	Выплата, тыс. руб.	Долг после выплаты, тыс. руб.
15.01	S
01.02	1,03S
14.02
15.02
1.03
14.03
15.03
15.04
15.05
15.06		=57,5

Решим уравнение: . Получаем, что S = 450 тыс. руб.

Рассчитаем всю сумму, выплаченную банку за 9 месяцев:

. Подставим S = 450. Получаем:

ОТВЕТ: 517,5 тыс. руб.

ПРИМЕР №10 (Подтип 7: Задачи, связанные с дифференцированными платежами). Алексей взял кредит в банке на срок 12 месяцев. По договору Алексей должен вернуть кредит ежемесячными платежами. В конце каждого месяца к оставшейся сумме долга добавляется r % этой суммы и своим ежемесячным платежом Алексей погашает эти добавленные проценты и уменьшает сумму долга. Ежемесячные платежи подбираются так, чтобы долг уменьшался на одну и ту же величину каждый месяц (на практике такая схема называется «схемой с дифференцированными платежами»). Известно, что общая сумма, выплаченная Алексеем банку за весь срок кредитования, оказалась на 13 % больше, чем сумма, взятая им в кредит. Найдите r. [9]

РЕШЕНИЕ: Обозначим за S полную сумму кредита. По условию долг должен уменьшатся до нуля равномерно. Составим геометрическую прогрессию: S; ; …; ; ; 0.

К концу каждого месяца долг увеличивается на r%, то есть умножается на коэффициент k, равный : S; ; …; ; ; 0.

Отсюда следует, что ежемесячные выплаты должны быть представлены в следующем виде:  ; ; …; ; ; 0.

Всего следует заплатить: .

Общая сумма выплат оказалась на 13% больше суммы, взятой в кредит. Получаем: ; k =  = 1,02; r = 2%.

ОТВЕТ: 2%.

1. Вклады

ПРИМЕР №11. В банк был положен вклад под 10% годовых. Через год, после начисления процентов, вкладчик снял со счета 2000 рублей, а еще через год (опять после начисления процентов) снова внес 2000 рублей. Вследствие этих действий через три года со времени открытия вклада вкладчик получил сумму меньше запланированной (если бы не было промежуточных операций со вкладом). На сколько рублей меньше запланированной суммы он получил? [10].

РЕШЕНИЕ: Обозначим за S общую сумму вклада. Составим схему начисления процентов по вкладу:

Год, №	Реальная сумма, руб.	Запланированная сумма, руб.
0	S	S
1	1,1S	1,1S
2	1,1(1,1S – 2000)	1,1 * 1,1S
3	1,1(1,1(1,1S – 2000) + 2000) = 1,1 * (1,21S – 200) = 1, 331S -220	1,1 * 1,1 * 1,1S = 1, 331S

Найдем разницу:

 1,1(1,1(1,1S – 2000) + 2000) — 1,1 * 1,1 * 1,1S = 1, 331S – 220 – 1,331S = — 220. Таким образом, вкладчик получил на 220 рублей меньше запланированной суммы.

ОТВЕТ: на 220 рублей.

ПРИМЕР №12. По бизнес-плану предполагается изначально вложить в четырёхлетний проект 10 млн рублей. По итогам каждого года планируется прирост вложенных средств на 15% по сравнению с началом года. Начисленные проценты остаются вложенными в проект. Кроме этого, сразу после начислений процентов нужны дополнительные вложения: по целому числу n млн рублей в первый и второй годы, а также по целому числу m млн рублей в третий и четвёртый годы.

Найдите наименьшие значения n и m, при которых первоначальные вложения за два года как минимум удвоятся, а за четыре года как минимум утроятся. [11].

РЕШЕНИЕ: Составим схему увеличения вклада:

Год	Сумма вклада	Год	Сумма вклада
0	10	3	((1,15 * 10 + 4) * 1,15 +4) *1,15 + m = 21,825 * 1, 15 + m = 25,099 + m
1	1,15 * 10 + n	4	(25,099 + m) * 1, 15 + m
2	(1,15 * 10 + n) * 1,15 + n

В условии задачи сказано, что за два года первоначальные вложения как минимум удвоятся, значит, можно составить неравенство:

(1,15 * 10 + n) * 1,15 + n ≥ 20. Получаем, что n ≥ 3,5. (Минимальное целочисленное решение n = 4).

За четыре года первоначальные вложения утроятся. Составим неравенство: (25,099 + m) * 1, 15 + m ≥ 30. Получаем, что m ≥ 0,528. (Минимальное целочисленное решение m = 1).

ОТВЕТ: 4 и 1 млн рублей.

1. Задачи на оптимальный выбор

ПРИМЕР №13. В январе 2000 года ставка по депозитам в банке «Возрождение» составляла х% годовых, тогда как в январе 2001 года она составила у% годовых, причем известно, что x + y = 30. В январе 2000 года вкладчик открыл счет в банке «Возрождение», положив на него некоторую сумму. В январе 2001 года, по прошествии года с того момента, вкладчик снял со счета пятую часть этой суммы. Укажите значение х при котором сумма на счету вкладчика в январе 2002 года станет максимально возможной. [10].

РЕШЕНИЕ: Обозначим за S сумму вклада, которую положили в банк в январе 2000 года. В январе 2001 года вклад будет уже составлять S(1+0,01x), но вкладчик снял 0,2S. Поэтому на январь 2021 на вклад приходится: S(1+0,01x) – 0,2S = 0,8S +0,01Sx. В январе 2002 года вклад увеличится на y%, то есть умножится на (1 + 0,01y) = (1 + 0,01(30 – x), и будет составлять (0,8S +0,01Sx) * (1 + 0,01(30 — x)) = — 0,0001Sx2 + 0,005Sx + 1, 04S.

Функция f(x) = — 0,0001Sx2 + 0,005Sx + 1, 04S является убывающей. Найдем ее максимальное значение x0 =   = 25.

ОТВЕТ: 25.

1. Нестандартные задачи

ПРИМЕР №14. В одной стране в обращении находилось 1 000 000 долларов, 20% из которых были фальшивыми. Некая криминальная структура стала ввозить в страну по 100 000 долларов в месяц, 10% из которых были фальшивыми. В это же время другая структура стала вывозить из страны 50 000 долларов ежемесячно, из которых 30% оказались фальшивыми. Через сколько месяцев содержание фальшивых долларов в стране составит 5% от общего количества долларов? [10].

РЕШЕНИЕ: Найдем ежемесячное увеличение валютной массы, находящейся в обращении: 100 – 50 = 50 тыс. долларов. Через n месяцев в стране будет – (1 000 + 50n) тыс. долларов.

Ежемесячно количество фальшивых купюр уменьшается на 50 * 0,3 – 100 * 0, 1 = 5 тыс. долларов. Изначально их было 1 000 000 * 0, 2 = 200 000. Тогда, через n месяцев их будет – (200 – 5n) тыс. долларов, что составляет 5% от общего количества долларов. Получаем: (1 000 + 50n) * 0, 05 = 200 – 5n.

n = 20.

ОТВЕТ: через 20 месяцев.

ПРИМЕР №15. При рытье колодца глубиной свыше 10 м за первый метр заплатили 1000 руб., а за каждый следующий на 500 руб. больше, чем за предыдущий. Сверх того, за весь колодец дополнительно было уплачено 10 000 руб. Средняя стоимость 1 м оказалась равной 6250 руб. Определите глубину колодца. [10].

РЕШЕНИЕ: Обозначим за Х м глубину колодца. Тогда, часть выплат, зависящая от глубины колодца, представляет собой арифметическую прогрессию, где a1 = 1000, а d = 500. Последний член прогрессии имеет вид: 1000 + 500(X –1).

Найдем сумму всех выплат по формуле суммы n – членов арифметической прогрессии: .

Поскольку сверх этого было выплачено еще 10 000 руб., а средняя стоимость 1 м при этом составила 6250 руб., то имеет место уравнение вида: 250X2 + 750X + 10 000 = 6250X. Решим, получаем: Х1 = 2 (не подходит, т. к. Х> 10 м) и Х2 = 20.

ОТВЕТ: 20 м.

ЗАКЛЮЧЕНИЕ

В результате проведенной работы по классификации и систематизации типов задач финансовой математики, включенных во вторую часть ЕГЭ по математике профильного уровня, и методов их решений были получены следующие выводы и результаты:

1. Было дано определение экономики как науки, изучающей типичные мотивы и модели поведения людей в процессах производства, обмена и потребления жизненных благ, а также установлена ее связь с математикой, заключающаяся в построении теоретических моделей математическим методом при анализе экономических явлений и процессов.

2. Были выделены четыре типа, один из которых содержит в себе семь подтипов, экономических задач ЕГЭ по математике профильного уровня и приведены различные способы их решений.

В ходе исследования было замечено, что наиболее наглядным и понятным методом решения задач с экономических содержанием оказался табличный метод. Именно этот способ решения рекомендуется использовать учащимся для построения точной теоретической модели экономической задачи.

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

1. Алимов, Ш. А. Алгебра: учебник для учащихся 9 кл. средней школы / Ш.А. Алимов. – М.: Просвещение, 2012. – 287 с.
2. Ермаков, С. Л. Экономика: учебное пособие (Бакалавриат) / С.Л. Ермаков, С.В. Устинов, Ю.Н. Юденков. – Москва: КНОРУС, 2020. – 270 с.
3. Копнова, Е. Д. Финансовая математика: учебник и практикум для бакалавриата и магистратуры / Е. Д. Копнова. — М.: Издательство Юрайт, 2016. — 413 с.
4. Лагошина Ю.С. Взаимосвязь математики с экономическими отраслями / Ю.С. Лагошина // Международный студенческий научный вестник. – 2017. – № 4 – С. 4.
5. Мордкович, А.Г. Алгебра: Учебник. 9 класс / А.Г. Мордкович, П.В. Семенов. – М.: Мнемозина, 2010. – 224 с.
6. Носова, С.С. Основы экономики: учебник (Среднее профессиональное образование) /С. С. Носова. – Москва: КНОРУС, 2020. – 312 с.
7. Пичурин Л.Ф. За страницами учебника алгебры: Кн. Для учащихся 7-9 кл. средн. Шк. / Л.Ф. Пичурин. – М.: Просвещение, 1990. – 224 с.
8. Шимко, П. Д. Основы экономики: учебник (Среднее профессиональное образование) / П.Д. Шимко. – Москва: КНОРУС, 2021. – 292 с.
9.  fipi.ru: сайт. – 2009. – URL: https://fipi.ru/
10.  ege.sdamgia.ru: образовательный портал: сайт. – 2011. —  URL: https://ege.sdamgia.ru/ 
11.  yandex.ru/tutor: образовательный портал: сайт. – 2018. – URL: https://yandex.ru/tutor/

Муниципальное автономное общеобразовательное учреждение «Лицей №14 имени Заслуженного учителя Российской Федерации А.М. Кузьмина»

ИНДИВИДУАЛЬНЫЙ ПРОЕКТ

по теме:

«Экономические задачи ЕГЭ и способы их решения»

Выполнил:

Учащийся 11 класса «А»

Задонский Ярослав Владимирович

Подпись

Научный руководитель:

Сухненко Ирина Александровна

учитель математики

Тамбов, 2018

Содержание:

Введение…………………………………………………………………. С. 3

РАЗДЕЛ ПЕРВЫЙ. Теоретический аспект изучения экономических задач ЕГЭ ………………………………………………………………………. С. 5

Раздел второй. Типы экономических задач на аннуитетный и дифференцированный платежи ………………………………………..

Раздел третий. Особые экономические задачи

Заключение ……………………………………………………………….

Список литературы ………………………………………………………

Введение

В настоящее время общее образование находится на этапе модернизации и обновления системы и содержания в условиях введения новых федеральных государственных стандартов. Приоритетом общества и системы образования является способность вступающих в жизнь людей самостоятельно решать встающие перед ними новые, еще неизвестные задачи. На первый план наряду с общей грамотностью выступает умение выпускников, например, разрабатывать и проверять гипотезы, умение работать в проектном режиме, проявлять инициативу в принятии решений. Это и становится одним из значимых ожидаемых результатов образования и предметом стандартизации.

Русский математик и механик, основоположник Петербургской математической школы, академик Петербургской академии наук П.Л. Чебышев говорил, что «особенную важность имеют те методы науки, которые позволяют решать задачу, общую для всей практической деятельности человека: как располагать своими средствами для достижения наибольшей выгоды». С такими задачами в наше время приходится иметь дело представителям самых разных специальностей. Технологи – стараются так организовать производство, чтобы выпускалось как можно больше продукции. Конструкторы пытаются разработать прибор для космического корабля так, чтобы масса прибора была наименьшей. Экономисты стараются спланировать связи завода с источниками сырья так, чтобы транспортные расходы оказались минимальными, и т.д.

Актуальность данной темы исследования определяется тем, что начиная с 2015 года, в заданиях ЕГЭ по математике профильного уровня появилась новая практико-ориентированная задача №17, так называемая «банковская» задача. Важным видом учебной деятельности, в процессе которой усваиваются математические знания, умения и навыки, является решение задач и одними из наиболее востребованных типов задач в рамках государственного экзамена являются задачи на проценты, в частности экономические задачи. 

Объектом данного исследования являются экономические задача единого государственного экзамена.

Предметом исследования выступают способы решения экономических задач единого государственного экзамена.

Гипотеза исследования — общего способа решения экономических задач быть не может, не существует единого алгоритма, позволяющего за конечное число шагов решать эти задачи.

Продукт проекта — методические рекомендации по решению банковских задач

В связи с объектом и предметом, цель проекта заключается в нахождении решения экономических задач.

Достижение поставленной цели осуществлялось через постановку и решение следующих исследовательских задач:

— проанализировать учебную и научную литературу по теме исследования, с целью определения базовых понятий и степени изученности проблемы;

— рассмотреть теоретические аспекты изучения экономических задач;

— выделить типы экономических задач;

— рассмотреть особые способы решения экономических задач на аннуитетный и дифференцированный платежи

Все вышесказанное, подчеркивает востребованность и необходимость рассмотрения экономических задач в едином государственном экзамене.

РАЗДЕЛ ПЕРВЫЙ. Теоретический аспект изучения экономических задач

При чтении условий любой задачи можно встретить такие величины как вклады, проценты и кредиты. Потому что именно задачи с процентами с недавних пор добавлены во вторую часть единого государственного экзамена по математике. За решение этой задачи согласно спецификациям ЕГЭ предлагается сразу три первичных балла, т. е. экзаменаторы считают эту задачу одной из самых сложных.

Вместе с тем, для решения любой из указанных задач из ЕГЭ по математике необходимо знать всего лишь две формулы, каждая из которых вполне доступна любому школьному выпускнику.

Вкладываем деньги в банк

Прежде всего, хотелось бы сделать небольшое лирическое отступление, связанное с финансами, банками, кредитами и вкладами, на основании которых мы и получим те формулы, которые будем использовать для решения данной задачи. Итак, давайте немного отвлечемся от экзаменов, от предстоящих школьных проблем, и посмотрим в будущее.

Допустим, вы выросли и собираетесь покупать квартиру. Допустим, вы собираетесь покупать не какую-то плохую квартиру на окраине, а хорошую качественную квартиру за 20 миллионов рублей. При этом также предположим, что вы устроились на более-менее нормальную работу и зарабатываете по 300 тысяч рублей в месяц. В этом случае за год вы сможете отложить примерно три миллиона рублей. Разумеется, зарабатывая по 300 тысяч рублей в месяц, за год у вас получится чуть большая сумма — 3600000 — но эти 600000 пусть будут потрачены на еду, на одежду и на прочие ежедневные бытовые радости. Итого вводные данные таковы: необходимо заработать двадцать миллионов рублей, у нас же в распоряжении имеется лишь три миллиона рублей в год. Возникает естественный вопрос: сколько лет нам необходимо откладывать по три миллиона, чтобы получить эти самые двадцать миллионов. Считается это так:

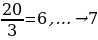
Однако как мы уже отмечали, вы зарабатываете 300 тысяч рублей в месяц, это значит, что вы умные люди и не будете откладывать деньги «под подушку», а отнесете их в банк. И, следовательно, ежегодно на те вклады, которые вы принесете в банк, будут начисляться проценты. Допустим, вы выберете надежный, но при этом более-менее прибыльный банк, и поэтому ваши вклады ежегодно будут расти на 15% годовых. Другими словами можно сказать, что сумма на ваших счетах ежегодно будет увеличиваться в 1,15 раза. Формула:

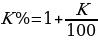
Посчитаем, сколько денег будет на ваших счетах после каждого года:

В первый год, когда вы только начнете откладывать деньги, никакие проценты не накопятся, т. е. в конце года вы отложите три миллиона рублей:

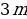
В конце второго года на те три миллиона рублей, которые остались с первого года, уже будут начислены проценты, т.е. нам нужно умножить на 1,15. Однако в течение второго года вы также доложили еще три миллиона рублей. Разумеется, на эти три миллиона еще не были начислены проценты, потому что к концу второго года эти три миллиона только появились на счету:

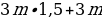
Итак, третий год. В конце третьего года на эту сумму будут начислены проценты, т. е. необходимо всю эту сумму умножить на 1,15. И опять же, в течение всего года вы усердно работали и еще отложили три миллиона рублей:

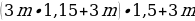
Рассчитаем еще четвертый год. Опять же, вся сумма, которая оказалась у нас к концу третьего года, умножается на 1,15, т.е. на всю сумму будут начислены проценты. В том числе, будут начислены проценты на проценты. И к этой сумме добавляется еще три миллиона, потому что в течение четвертого года вы также работали и также откладывали деньги:

⋅1,15+3m)1,15+3m

А теперь раскроем скобки и посмотрим, какая у нас будет сумма к концу четвертого года откладывания денег:

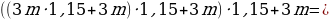
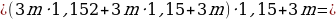
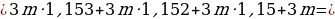
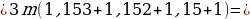
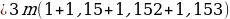
Как видим, в скобках у нас стоят элементы геометрической прогрессии, т. е. у нас стоит сумма элементов геометрической прогрессии.

Если геометрическая прогрессия задана элементом b1, а также знаменателем q, то сумма элементов будет считаться по следующей формуле:

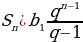
Эту формулу обязательно нужно знать и четко применять.

Обратим внимание: формула n-го элемента звучит следующим образом:

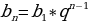
Из-за этой степени многие ученики путаются. В сумме у нас стоит просто n для суммы n-элементов, а сам n-й элемент имеет степень n−1. Другими словами, если мы сейчас попытаемся посчитать сумму геометрической прогрессии, то нужно учитывать следующее:

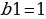
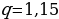
Теперь мы можем посчитать сумму:

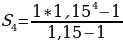
Посчитаем числитель отдельно:

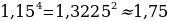
Итого, возвращаясь к сумме геометрической прогрессии, мы получим:

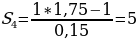
В итоге мы получаем, что за четыре года накоплений наша исходная сумма увеличится не в четыре раза, как если бы мы не клали деньги в банк, а в пять раз, т. е. пятнадцать миллионов. Давайте запишем это отдельно:

4 года → 5 раз

Забегая вперед, отмечу, что если бы мы копили не четыре года, а пять лет, то в итоге наша сумма накоплений увеличилась бы в 6,7 раза:

5 лет → 6,7 раз

Другими словами, к концу пятого года мы бы получили на счету следующую сумму:

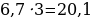
Т. е. к концу пятого года накоплений с учетом процентов по вкладу мы бы уже получили свыше двадцати миллионов рублей. Таким образом, общий счет накоплений за счет банковских процентов снизился бы с почти семи лет до пяти лет, т. е. почти на два года.

Таким образом, даже, несмотря на то, что банк начисляет достаточно низкий процент на наши вклады (15%), уже через пять лет эти самые 15% дают прибавку, существенно превышающую наш ежегодный заработок. При этом основной мультипликационный эффект приходится на последние годы и даже, скорее, на последний год накоплений.

Если мы действительно хотим приумножить свои сбережения, то вкладывать их нужно не в банк, а в реально действующий бизнес, где эти самые проценты, т. е. рентабельность в условиях российской экономики редко опускается ниже 30%, т. е. вдвое больше банковских вкладов.

А вот что действительно полезно во всех этих рассуждениях, так это формула, которая позволяет нам найти итоговую сумму вклада через размер ежегодных платежей, а также через проценты, которые начисляет банк. Так и запишем:

Сам по себе % считается по следующей формуле:

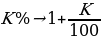
Эту формулу также необходимо знать, как и основную формулу суммы вклада. А, в свою очередь, основная формула способна значительно сократить вычисления в тех задачах с процентами, где требуется посчитать именно вклад.

Почему стоит пользоваться формулами, а не таблицами?

У многих наверняка возникнет вопрос, а к чему вообще все эти сложности, нельзя ли просто расписать каждый год в табличке, как это делают во многих учебниках, посчитать отдельно каждый год, а затем посчитать общую сумму вклада? Конечно, можно вообще забыть про сумму геометрической прогрессии и все считать с помощью классических табличек — так сделано в большинстве сборников для подготовки к ЕГЭ. Однако, во-первых, резко увеличивается объем вычислений, а во-вторых, как следствие, увеличивается вероятность допустить ошибку.

Да и вообще, использовать таблицы вместо этой замечательной формулы — это то же самое, что на стройке копать траншеи руками вместо того, чтобы использовать стоящий рядом и полностью работающий экскаватор.

Ну, или то же самое, что умножить пятерку на десятку не с помощью таблицы умножения, а складывать пятерку с самой собой десять раз подряд. Впрочем, это я уже отвлекся, поэтому еще раз повторю самую главную мысль: если есть какой-то способ упростить и сократить вычисления, то именно этим способом и надо воспользоваться.

Проценты по кредитам

Далее рассмотрим следующий вопрос, а именно — к процентам по кредитам.

Итак, пока вы копите деньги, скрупулезно планируете свой бюджет, думаете о своей будущей квартире, ваш одноклассник, а нынче простой безработный, решил жить сегодняшним днем и просто взял кредит. При этом он еще будет подкалывать и смеяться над вами, мол, у него кредитный телефон и подержанный автомобиль, взятый в кредит, а вы до сих пор ездите на метро и пользуетесь старым кнопочным телефоном. Разумеется, за все эти дешевые вещи вашему бывшему однокласснику придется дорого расплатится. Насколько дорого — вот это именно сейчас мы и посчитаем.

Для начала краткая вводная информация. Допустим, ваш бывший одноклассник взял два миллиона рублей в кредит. При этом согласно договору он должен платить x рублей в месяц. Допустим, что кредит он взял по ставке 20% годовых, что в нынешних условиях выглядит вполне прилично. Кроме того, предположим, что срок кредита составляет всего три месяца. Давайте попробуем связать все эти величины в одну формулу.

Итак, в самом начале, как только ваш бывший одноклассник вышел из банка у него в кармане два миллиона, и это и есть его долг. При этом не год прошел, и не месяц, а это только самое начало:

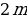
Затем спустя один месяц на сумму задолженности будут начислены проценты. Как мы уже знаем для вычисления процентов достаточно умножить исходную задолженность на коэффициент, который считается по следующей формуле:

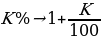
В нашем случае речь идет о ставке 20% годовых, т. е. мы можем записать:

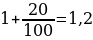
Это коэффициент суммы, которая будет начисляться в год. Однако наш одноклассник не очень умный и он не читал договор, и на деле кредит ему выдали не под 20% в год, а под 20% в месяц. И уже к концу первого месяца на эту сумму будут начислены проценты, и она увеличится в 1,2 раза. Сразу после этого человеку будет необходимо оплатить оговоренную сумму, т. е. x рублей в месяц:

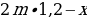
Далее к концу второго месяца уже на эту сумму будут вновь начислены проценты:

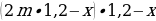
И вновь наш паренек вносит платеж в размере x рублей.

Затем к концу третьего месяца сумма его задолженности еще раз увеличивается на 20%:

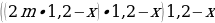
И по условию за три месяца он должен полностью расплатиться, т. е. после внесения последнего третьего платежа его объем задолженности должен быть равен нулю. Мы можем записать такое уравнение:

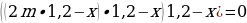
Давайте решать:

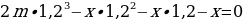
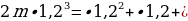
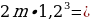
Перед нами вновь геометрическая прогрессия, а точнее, сумма трех элементов геометрической прогрессии. Давайте перепишем ее в порядке возрастания элементов:

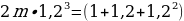
Теперь нам нужно найти сумму трех элементов геометрической прогрессии. Давайте запишем:

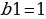
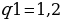
Теперь найдем сумму геометрической прогрессии:

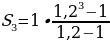
Следует напомнить, что сумма геометрической прогрессии с такими параметрами(b1;q) считается по формуле:

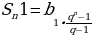
Вот этой формулой мы только что и воспользовались. Подставляем эту формулу в наше выражение:

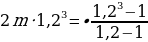
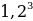
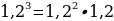
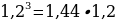
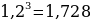
Для дальнейших вычислений нам следует узнать, чему равна  . К сожалению, в этом случае мы уже не можем расписать как в прошлый раз в виде двойного квадрата, но зато можем посчитать так:

Переписываем наше выражение:

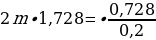
Это классическое линейное выражение. Давайте вернемся к следующей формуле:

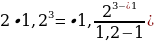
По сути, если обобщить ее, то мы получим формулу, связывающую проценты, кредиты, платежи и сроки. Формула звучит следующим образом:

}

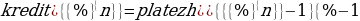
Вот она, самая главная формула, с помощью которой считается не менее 80% всех экономических задач из ЕГЭ по математике во второй части. Знать эту формулу, связывающую кредиты платежи и проценты, также необходимо как и сумму геометрической прогрессии. Именно с помощью этих формул решаются реальные экономические задачи из ЕГЭ по математике

Кредитные инструменты очень полезны и крайне необходимы нашей экономике, но только при условии, что кредит берется на развитие бизнеса. В крайнем случае, можно взять кредит на покупку жилья, т. е. ипотеку либо на неотложное медицинское лечение — все, других причин взять кредит просто не существует.

Помимо ставки вознаграждения по кредиту (проценты по кредиту), клиенту необходимо обратить внимание на такой важный показатель, как метод погашения кредита — аннуитетный и дифференцированный, или еще его называют «равными долями».

Отметим, что в то время как в России существовал только один вид платежа – дифференцированный, на западе практиковался другой – аннуитетный. Оба вида выполняют одну и ту же функцию, помогая гражданам соблюдать свои обязательства по кредиту, говоря простыми словами – выплачивать долги.    

Дифференцированный платеж

При дифференцированных платежах вся сумма кредита (основного долга) делится на равные части с учетом срока и периодичности погашения платежа по кредиту (ежемесячно, ежедневно, ежеквартально).

В даты платежа по графику клиент выплачивает часть суммы кредита (основного долга) плюс начисленные проценты.
Проценты начисляются на остаток основного долга, соответственно, сумма начисленного вознаграждения по мере погашения кредита уменьшается.

Наиболее распространенной периодичностью погашения является ежемесячный график.

Например, сумма кредита — 100 000 тенге, срок кредита — 1 год, периодичность погашения – ежемесячно (100 000:12 месяцев = 8 333,33 тенге), дополнительно к полученной сумме прибавляется сумма начисленного вознаграждения, которая производится в первый месяц от 100 000 тенге, во второй месяц — от 91 666,66 тенге (100 000 – 8 333,33 = 91 666,66) и т.д.

Недостатком дифференцированного платежа является то, что клиенту необходимо или помнить, или постоянно уточнять, сколько денег ему нужно платить в очередной раз.

При дифференцированном графике в первую половину срока кредита заемщик направляет на погашение кредита гораздо большую сумму из своего дохода, чем во второй ее половине. При таком методе слова «деньги сейчас дороже, чем потом» не работают на клиента, т.к. на деньги, которые заемщик направляет на погашение в первой половине, можно купить гораздо больше, чем через 5, 10 или 20 лет, ведь инфляция велика, и объективных признаков ее снижения в обозримом будущем нет.

Данный вид платежа приемлем для клиентов, у которых нефиксированный доход, который ежемесячно варьируется (больше или меньше). Во-вторых, по кредиту с дифференцированным платежом требования к платежеспособности выше, ведь банк оценивает максимальную сумму кредита, исходя из способности клиента «потянуть» первые платежи по кредиту. Однако учитывая возможность изменения и улучшения условий в будущем (возможное уменьшение % по кредиту, инфляцию, повышение доходов), в последующем выплаты по кредиту становятся все менее обременительными, и к концу срока фактически снижаются.

Плюсы и минусы дифференцированного платежа

Особенности дифференцированного платежа таят в себе как плюсы, так и минусы. Основным плюсом является факт более выгодного способа оплачивать кредит, поскольку данный вид платежа существенно снижает переплаты по кредиту.

Минусом являются большие размеры первоначальных платежей, поэтому дифференцированный платеж называют платежом для обеспеченных людей. Еще одним минусом является отсутствие популярности платежа у банков – большинство банков используют аннуитетную платежную систему, как более выгодную. Несмотря на то, что в России имеется порядка 6-9 банков, где предусмотрена подобная система платежа, среди населения не наблюдается особого ажиотажа – сказывается необходимость выплачивать большие суммы на первоначальном этапе.

Если кредит, к примеру, ипотечный и берется на долгие годы, то имеет смысл перераспределить «тяжесть» платежей таким образом, чтобы основная кредитная нагрузка пришлась на молодые годы, когда человек еще не обременен множеством обязательств, а поиск работы не сопряжен с возрастными ограничениями.

Аннуитетный платеж

Аннуитетный платеж остается неизменным в течение всего срока действия кредитного договора.

Это значит, что каждый месяц клиент платит за кредит одинаковую сумму, которая состоит из начисленных процентов за кредит и части суммы, списывающейся в счет основного долга.

Преимущество аннуитетных платежей заключается в их неизменности. Клиенту известна сумма, которую он должен платить каждый месяц в установленный срок. Больше никаких цифр держать в своей голове ему не надо. Это очень удобно для клиентов, имеющих фиксированный доход.

Таким образом, при выборе графика погашения необходимо выбирать наиболее подходящий для себя метод платежа с учетом текущих ежемесячных расходов, особенно это важно при оформлении кредита на длинные сроки.

К примеру, при оформлении ипотеки на 15-20 лет клиентам, имеющим доход в виде ежемесячной заработной платы, наиболее удобным при планировании семейного бюджета будет аннуитетный вид платежа.

В случае, если вы решите выбрать кредит с дифференцированными платежами, необходимо также учитывать, что максимально возможная сумма кредита может оказаться меньше в отличие от варианта с аннуитетным платежом, так как банк при расчете вашей платежеспособности будет учитывать максимально возможную сумму кредита с учетом первого платежа, который в сравнении с аннуитетом будет больше. 
Исходить нужно исключительно из своих возможностей и не забывать, что независимо от вида выбранного платежа, у вас всегда есть право досрочного погашения кредита.

Пример:

• Клиент А получил кредит 100 долларов сроком на 12 месяцев по ставке 10% (ГЭСВ 10,62 %). Выбрал аннуитетный график платежа по кредиту. 
  Отличительной особенностью данного вида платежа является фиксированный размер платежа на всем сроке кредита, что позволяет клиенту ежемесячно выделять из бюджета равную сумму денежных средств для погашения кредита.

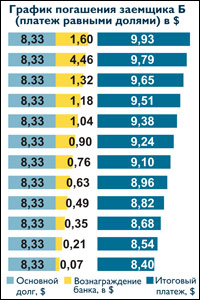
• Клиент Б получил кредит на аналогичных условиях, но выбрал график с дифференцированными платежами (погашение основного долга равными долями). 

Отличительной особенностью данного графика является то, что в течение всего срока кредита размер платежа изменяется от наибольшего к наименьшему.

 Подводя итог, отметим, что выбирая кредитную программу, потенциальные заемщики ориентируются на процентную ставку по кредиту. Но не только ставка влияет на сумму выплачиваемых процентов, а также способ их начисления и метод погашения кредита. Таких методов существует два: аннуитетные платежи и дифференцированные платежи.

На наш взгляд, наиболее выгодная схема погашения ипотечного кредита — дифференцированные платежи. Так, общая сумма выплаченных банку денег, взятых под 12 % годовых и погашенных дифференцированными платежами — намного меньше, чем взятых под 12 % годовых, но погашенных аннуитетными платежами.

Дифференцированные платежи характерны тем, что задолженность по кредиту погашается равномерно начиная с самых первых выплат, а проценты начисляются по фактическому остатку. Таким образом, каждый последующий платеж меньше предыдущего. Досрочное погашение не ограничено ни по времени, ни по сумме и позволяет существенно сэкономить на выплачиваемых процентах.

Аннуитет — начисление равных платежей на весь срок погашения кредита. При этом в первой половине срока погашения задолженность по кредиту практически не гасится — выплачиваются в большей части проценты. Эта особенность делает платежи относительно небольшими, но значительно увеличивает общую сумму начисляемых процентов.

Раздел второй. Типы экономических задач на аннуитетный и дифференцированный платежи

Приведем примеры решения задач формата ЕГЭ на аннуитетный платеж

№ 1. 31 декабря 2013 года Сергей взял в банке 9 930 000 рублей в кредит под 10% годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 10%), затем Сергей переводит в банк определённую сумму ежегодного платежа. Какой должна быть сумма ежегодного платежа, чтобы Сергей выплатил долг тремя равными ежегодными платежами?

Решение. Пусть сумма кредита равна a, ежегодный платеж равен x рублей, а годовые составляют k %. Тогда 31 декабря каждого года оставшаяся сумма долга умножается на коэффициент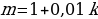 

После первой выплаты сумма долга составит:  . После второй выплаты сумма долга составит: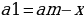

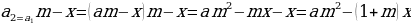
После третьей выплаты сумма оставшегося долга:

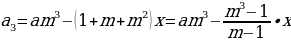
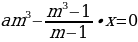
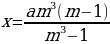
По условию тремя выплатами Сергей должен погасить кредит полностью, поэтому  откуда при  , откуда ,при a = 9 930 000 и k = 10, получаем: m = 1,1

Ответ: 3 993 000 рублей. 

№ 2. В июле планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы:

— каждый январь долг возрастает на 31% по сравнению с концом предыдущего года;

— с февраля по июнь каждого года необходимо выплатить часть долга, равную 69690821 рубль.

Сколько рублей было взято в банке, если известно, что он был полностью погашен тремя равными платежами ( то есть за три года)?

Решение.

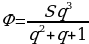
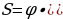
Если искомая сумма составляет S рублей, то при коэффициенте ежегодной процентной ставки q, равной 1,31, фиксированная сумма Ф, которую клиент ежегодно должен возвращать в банк в течение 3 лет, составляет , откуда .

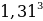
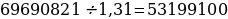
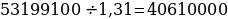
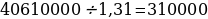
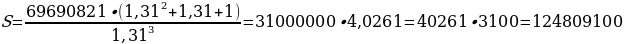
Заметим, что 69690821 кратно . Действительно, ;

 

Ответ: 124 809 100 рублей.

№ 3. 31 декабря 2014 года Алексей взял в банке 6 902 000 рублей в кредит под 12,5% годовых. Схема выплат кредита следующая — 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 12,5%), затем Алексей переводит в банк x рублей. Какой должна быть сумма x, чтобы Алексей выплатил долг четырьмя равными платежами (то есть за четыре года)?

Решение.

Пусть сумма кредита равна S, а годовые составляют a%. Тогда 31 декабря каждого года оставшаяся сумма долга умножается на коэффициент b = 1 + 0,01a. После первой выплаты сумма долга составит S₁ = Sb − x. После второй выплаты сумма долга составит:

.

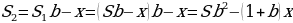
После третьей выплаты сумма оставшегося долга равна:

.

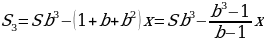
После четвёртой выплаты сумма оставшегося долга равна

.

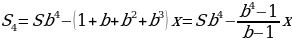
По условию четырьмя выплатами Алексей должен погасить кредит полностью, поэтому

; откуда

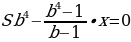
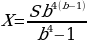
При S = 6 902 000 и a = 12,5, получаем: b = 1,125 и

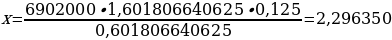
 рублей

Ответ: 2 296 350.

№ 4. 31 декабря 2014 года Тимофей взял в банке 7 007 000 рублей в кредит под 20% годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 20%), затем Тимофей переводит в банк платёж. Весь долг Тимофей выплатил за 3 равных платежа. На сколько рублей меньше он бы отдал банку, если бы смог выплатить долг за 2 равных платежа?

Решение.

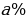
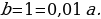
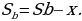
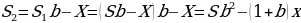
Пусть сумма кредита равна S, а годовые составляют .Тогда 31 декабря каждого года оставшаяся сумма долга умножается на коэффициент После первой выплаты сумма долга составит После второй выплаты сумма долга составит

После третей выплаты сумма оставшегося долга равна

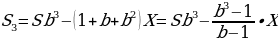
По условию тремя выплатами Тимофей погасил кредит полностью, поэтому

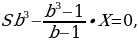
откуда .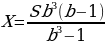

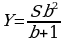
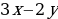
Рассуждая аналогично, находим, что если бы Тимофей гасил долг двумя равными выплатами, то каждый год он должен был бы выплачивать .рублей. Значит, он отдал банку на больше.

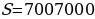
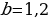
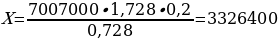
При и a=20, получаем : и (рублей).

(рублей).

Значит,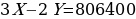

 Ответ: 806400.

№ 5. 31 декабря 2014 года Дмитрий взял в банке 4 290 000 рублей в кредит под 14,5% годовых. Схема выплаты кредита следующая — 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 14,5%), затем Дмитрий переводит в банк X рублей. Какой должна быть сумма X, чтобы Дмитрий выплатил долг двумя равными платежами (то есть за два года)?

 Решение.

Пусть сумма кредита равна S, а годовые составляют а%. Тогда 31 декабря каждого года оставшаяся сумма долга умножается на коэффициент b = 1 + 0,01а. После первой выплаты сумма долга составит S₁ = Sb − X. После второй выплаты сумма долга составит 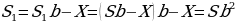–(1+b)X

По условию двумя выплатами Дмитрий должен погасить кредит полностью, поэтому  откуда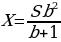 

При S = 4 290 000 и а = 14,5, получаем: b = 1,145 и 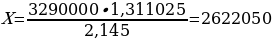 (рублей).

 Ответ: 2 622 050.

Приведем примеры решения задач формата ЕГЭ на дифференцированный платеж

№ 1. Антон взял кредит в банке на срок 6 месяцев. В конце каждого месяца общая сумма оставшегося долга увеличивается на одно и то же число процентов (месячную процентную ставку), а затем уменьшается на сумму, уплаченную Антоном. Суммы, выплачиваемые в конце каждого месяца, подбираются так, чтобы в результате сумма долга каждый месяц уменьшалась равномерно, то есть на одну и ту же величину. Общая сумма выплат превысила сумму кредита на 63%. Найдите месячную процентную ставку.

Решение.

Пусть сумма кредита S у.е., процентная ставка банка x %.

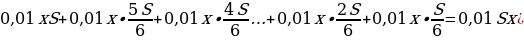
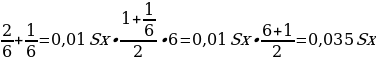
Предложение «Суммы, выплачиваемые в конце каждого месяца, подбираются так, чтобы в результате сумма долга каждый месяц уменьшалась равномерно, то есть на одну и ту же величину» означает: Антон взятую сумму возвращал в банк равными долями. Сумма, образованная применением процентной ставки, составляет: +  (у.е.)

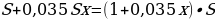
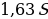
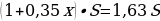
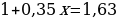
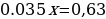
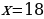
Общая сумма, выплаченная Антоном за 6 месяцев:   (у.е.). А эта сумма по условию задачи равна   у.е. Решим уравнение:

 Ответ: 18.

№2. Жанна взяла в банке в кредит 1,2 млн рублей на срок 24 месяца. По договору Жанна должна возвращать банку часть денег в конце каждого месяца. Каждый месяц общая сумма долга возрастает на 2 %, а затем уменьшается на сумму, уплаченную Жанной банку в конце месяца. Суммы, выплачиваемые Жанной, подбираются так, чтобы сумма долга уменьшалась равномерно, то есть на одну и ту же величину каждый месяц. Какую сумму Жанна вернёт банку в течение первого года кредитования?

Решение.

Пусть B_i — размер долга Жанны на конец месяца i, X_i — платеж Жанны в конце месяца i. Мы знаем, что имеет место соотношение B_i = 1,02B_{i − 1} − X_i. Кроме того, мы знаем, что последовательность (B_i) является арифметической прогрессией. При этом B₀ = 1200 тыс. руб., а B₂₄ = 0, так как в конце срока кредитования долг Жанны должен быть равен нулю. 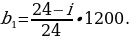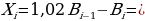Этих двух точек достаточно, чтобы узнать всю последовательность B_i:   Значит,

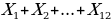
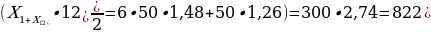
Поскольку X_i линейно зависит от i, последовательность X_i также является арифметической прогрессией. Значит, =  тыс. рублей.

 Ответ: 822 тыс. рублей.

№3 Сергей взял кредит в банке на срок 9 месяцев. В конце каждого месяца общая сумма оставшегося долга увеличивается на 12%, а затем уменьшается на сумму, уплаченную Сергеем. Суммы, выплачиваемые в конце каждого месяца, подбираются так, чтобы в результате сумма долга каждый месяц уменьшалась равномерно, то есть на одну и ту же величину.

Сколько процентов от суммы кредита составила общая сумма, уплаченная Сергеем банку (сверх кредита)?

Решение.

Предложение «Суммы, выплачиваемые в конце каждого месяца, подбираются так, чтобы в результате сумма долга каждый месяц уменьшалась равномерно, то есть на одну и ту же величину» означает: Сергей взятую сумму, без учета процентов, возвращал равными долями.

Общая сумма, уплаченная Сергеем банку сверх кредита, обусловлена только применением процентной ставки.

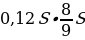
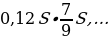
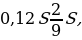
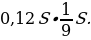
В первом месяце эта часть заплаченной суммы составляла 0,12S, во втором —  , в третьем —   в восьмом —   наконец, в последнем — 

Всего за 9 месяцев:

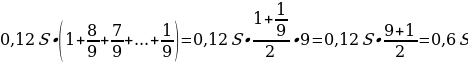
 Искомое процентное отношение есть 60 

 Ответ: 60.

№4. Алексей взял кредит в банке на срок 12 месяцев. По договору Алексей должен вернуть кредит ежемесячными платежами. В конце каждого месяца к оставшейся сумме долга добавляется r % этой суммы и своим ежемесячным платежом Алексей погашает эти добавленные проценты и уменьшает сумму долга. Ежемесячные платежи подбираются так, чтобы долг уменьшался на одну и ту же величину каждый месяц (на практике такая схема называется «схемой с дифференцированными платежами»). Известно, что общая сумма, выплаченная Алексеем банку за весь срок кредитования, оказалась на 13 % больше, чем сумма, взятая им в кредит. Найдите r.

Решение.

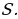
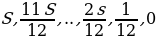
Пусть сумма кредита равна   По условию долг Алексея должен уменьшаться до нуля равномерно:

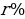
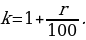
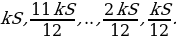
К концу каждого месяца к сумме долга добавляется  . Пусть   Тогда последовательность сумм долга вместе с процентами такова:

Следовательно, выплаты должны быть следующими:

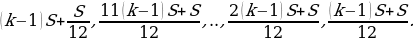
Всего следует выплатить:

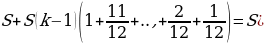
Общая сумма выплат оказалась на 13% больше суммы, взятой в кредит, поэтому:

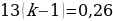
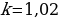
Откуда получаем, что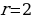 

 Ответ: 2.

№ 5.15-го января планируется взять кредит в банке на девять месяцев. Условия его возврата таковы:

— 1-го числа каждого месяца долг возрастает на r% по сравнению с концом предыдущего месяца;

— со 2-го по 14-е число месяца необходимо выплатить часть долга;

— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.

Известно, что общая сумма выплат после полного погашения кредита на 25% больше суммы, взятой в кредит. Найдите r.

Решение.

По формуле для переплаты П при выплате суммы кредита S дифференцированными платежами имеем: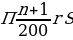

где n = 9 — число месяцев, а r — искомая величина платежной ставки в процентах. По условию, переплата П равна 0,25S, тогда: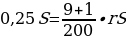

откуда r = 5.

 Приведем другое решение.

Долг уменьшается на 15-е число равномерно: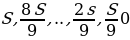 

Первого числа долг возрастает на r%, значит, долг на первое число:

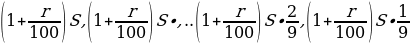
Выплаты:

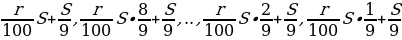
Тогда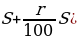

 

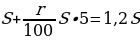
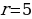
Ответ: 5.

Раздел третий. Особые экономические задачи

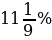
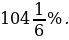
№ 1. За время хранения вклада в банке проценты по нему начислялись ежемесячно сначала в размере 5%, затем 12%, потом   и, наконец, 12,5% в месяц. Известно, что под действием каждой новой процентной ставки вклад находился целое число месяцев, а по истечении срока хранения первоначальная сумма увеличилась на   Определите срок хранения вклада.

Решение.

Известно:

1. Проценты на вклад начислялись ежемесячно.

2. Каждая последующая процентная надбавка по истечении календарного месяца начислялась с учетом вновь образованной суммы вклада и с учетом предыдущих надбавок.

Если первоначальная сумма вклада при ежемесячной 5%-ной ставке начисления процентов продержалась k месяцев, то вклад ежемесячно увеличивался в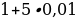   раз, и этот коэффициент будет сохранен до тех пор, пока ставка не изменится.

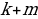
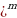
При изменении процентной надбавки с 5% на 12% (ставка 12% продержалась m месяцев) первоначальная сумма вклада за   месяцев увеличится в    раз.

Предположим, что процентная ставка 11 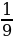  продержалась n месяцев, а процентная ставка 12,5 продержалась t месяцев. Тогда соответствующие коэффициенты повышения составят:

 и  .

Таким образом, коэффициент повышения суммы вклада в целом за весь период хранения вклада в банке составит:

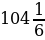
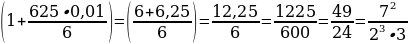
Это — с одной стороны. Но с другой стороны, согласно условию задачи первоначальная сумма вклада за это же время увеличилась на   то есть в  ( раз).

Значит,

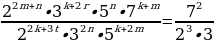
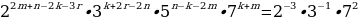
Согласно основной теореме арифметики каждое натуральное число, большее 1, можно представить в виде произведения простых множителей, и это представление единственное с точностью до порядка их следования. В таком случае:

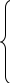
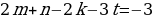
k+2t-2n=-1

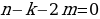
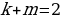
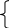
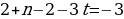
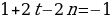
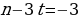
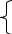
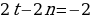
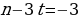
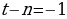
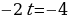
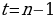
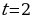
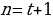
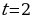
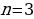
Решим эту систему относительно натуральных k,m,n и t. И з последнего уравнения системы имеем: k=m=1. При этих значениях k и m система примет вид:

 

Итак, 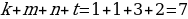  вклад в банке на хранении был 7 месяцев. При найденных значениях k,m,n и t n-k-2m действительно равно нулю.

 Ответ: 7.

№ 2. В июле 2016 года планируется взять кредит в банке на три года в размере S млн рублей, где S — целое число. Условия его возврата таковы:

− каждый январь долг увеличивается на 25% по сравнению с концом предыдущего года;

− с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;

− в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей

Месяц и год	Июль 2016	Июль 2017	Июль 2018	Июль 2019
Долг (в млн рублей)	S	0,7S	0,4S	0

 Найдите наименьшее значение S, при котором каждая из выплат будет больше 5 млн рублей.

Решение.

Долг перед банком (в млн рублей) на июль каждого года должен уменьшаться до нуля следующим образом:

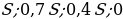
По условию, в январе каждого года долг увеличивается на 25%, значит, долг в январе каждого года равен:

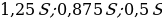
Следовательно, выплаты с февраля по июнь каждого года составляют:

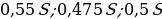
По условию, каждая из выплат должна быть больше 5 млн рублей. Это будет верно, если минимальная из выплат больше 5 млн рублей то есть если0,475S 5 Тогда:

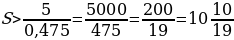
Наименьшее целое решение этого неравенства — число 11. Значит, искомый размер кредита — 11 млн рублей.

 Ответ: 11.

№ 3. В июле 2016 года планируется взять кредит в банке на четыре года в размере S млн рублей, где S — целое число. Условия его возврата таковы:

— каждый январь долг увеличивается на 15% по сравнению с концом предыдущего года;

— с февраля по июнь каждого года необходимо выплатить часть долга;

— в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей.

Месяц и год	Июль 2016	Июль 2017	Июль 2018	Июль 2019	Июль 2020
Долг (в млн рублей)	S	0,8S	0,5S	0,1S	0

Найдите наибольшее значение S, при котором общая сумма выплат будет меньше 50 млн рублей.

Решение.

Долг перед банком (в млн рублей) на июль каждого года должен уменьшаться до нуля следующим образом:

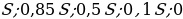
По условию, в январе каждого года долг увеличивается на 15%, значит, долг в январе каждого года равен:

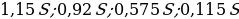
Следовательно, выплаты с февраля по июнь каждого года составляют:

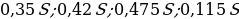
По условию, сумма выплат должна быть меньше 50 млн рублей.

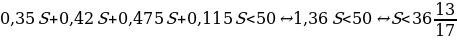
Наибольшее целое решение этого неравенства — число 36. Значит, искомый размер кредита — 36 млн рублей.

 Ответ: 36.

 №4. Вклад в размере 10 млн рублей планируется открыть на четыре года. В конце каждого года банк увеличивает вклад на 10% по сравнению с его размером в начале года. Кроме того, в начале третьего и четвёртого годов вкладчик пополняет вклад на х млн рублей, где х — целое число. Найдите наименьшее значение х, при котором банк за четыре года начислит на вклад больше 6 млн рублей.

Решение.

Составим неравенство согласно условию задачи:

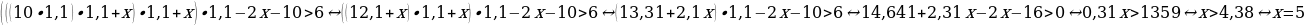
Ответ: 5.

Подводя итог, отметим, что необходимо знать для решения задания №17 на ЕГЭ

1. 1% — это сотая часть чего-либо

2. За 100% принимает ту величину, с которой сравниваем

3. Основные формулы для подсчета процентов

Если величину S увеличить на а%, то получим S(1+0,1а)

Если величину S уменьшить на а%, то получим S(1-0,1а)

Если величину S дважды увеличить на а%, то получим S(1+0,1а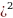

Если величину S уменьшить на а%, то получим S(1-0,01а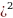

Заключение

В связи с преобразованием России из системы централизованного планирования в экономику рыночной ориентации экономические знания стали необходимыми как в профессиональной сфере, так и в повседневной жизни. Экономические знания позволяют понимать роль и права человека в обществе, готовят учеников к адекватному восприятию общества и производства, помогают им определить для себя сферу деятельности, профессию в будущем.

Эффективному постижению азов экономики поможет решение задач, в содержании которых идет речь о процентах. Понятие «проценты» буквально вошло в нашу жизнь, оно атакует нас в пору утверждения рыночных отношений в экономике, в пору банкротств, инфляций, финансовых кризисов. Сами проценты не дают экономического развития, но их знание помогает в развитии практических способностей, а также умение решать экономические задачи. Обдуманное изучение процентов может способствовать развитию таких навыков как экономичность, расчетливость.

Задачи с экономическим содержанием являются практическими задачами. А их решение, бесспорно, способствует более качественному усвоению содержания курса математики средней школы, позволяет осуществлять перенос полученных знаний и умений в экономику, что в свою очередь, активизирует интерес к задачам прикладного характера и изучению математики в целом. Такие задачи позволяют наиболее полно реализовывать прикладную направленность в обучении и способствуют более качественному усвоению самого учебного материала и формированию умения решать задачи данного типа.

На основе проанализированных задач, мы считаем, что введение такого рода заданий важно в современное время. Данные виды заданий чрезвычайно полезны так как, работая над моделями, сформулированными в условиях, они заставляют задумываться о реальной жизни. О том, что кредиты, отношения с банками, игра на бирже, колебания курсов ценных бумаг, начисление процентов дело сложное и требует больших знаний. К этому нельзя относиться легкомысленно. С чего начинать решать экономические задачи – очень внимательно читать условия задачи и по шагам распределить действия, затем постараться математически выразить их и постараться прийти к ответу.

ЛИТЕРАТУРА

1. Акимов Д.В. Решение задач по экономике: от простых до олимпиадных.М.,2016

2.Бондаренко М. Краткий курс лекций и рекомендаций по решению экономических задач. Чебоксары, 2016.

3. Гришаева Л.С. Основы экономики: задачи с решениями. М., 2016

4.Демонстрационный вариант контрольно-измерительных материалов единого государственного экзамена 2015 года по математике. Профильный уровень. Сайт http://www.ege.edu.ru/Ященко И. В. и др.

5. Колесникова С.И. Экономические задачи ЕГЭ. М., 2016

6. Малыхин В. Финансовая математика. СПб., 2014

7.Подготовка к ЕГЭ по математике в 2016 году. Базовый и профильный уровни. Методические указания / И. В. Ященко, С. А. Шестаков, А. С. Трепалин. – М.: МЦНМО, 2015.

8.Пучков Н.П. Математика в экономике. М., 2015

9.Спецификация контрольно-измерительных материалов для проведения в 2015 году единого государственного экзамена по математике. Профильный уровень. Сайт http://www.ege.edu.ru/

10. Хачатрян С. Методы и модели решения экономических задач. М., 2015

Автор: Фролов Глеб Романович

Место работы/учебы (аффилиация): ГБОУ «Брянский городской лицей №1 имени А.С.Пушкина», 10 класс

Актуальность исследовательской работы определяется  необходимостью уметь решать экономические задачи при сдаче ЕГЭ. Решение  экономических задач очень полезно, так как жизнь  современного человека тесно связана с финансовыми операциями.

Проблема заключается в отсутствии навыков применения математических и экономических знаний на практике в расчетах платежей банковских кредитов и прочих операций, а также неумение и боязнь решать экономические задачи на ЕГЭ.

Предмет исследования: различные подходы к решению  задач о кредитах, в зависимости от условия задачи.

Гипотеза: в современном мире необходимы знания об экономике и в этом может помочь математика.

Цель исследования – исследование методов решения задач с экономическим содержанием.

Задачи  исследования:

• изучить теоретический материал по выбранной теме;
• научиться решать задачи с процентами разных видов сложности;
• разобрать основные типы задач с примерами решений;
• создать таблицы для различных видов платежей;
• показать на примерах поиск решения реальной практической задачи (кредит с разными видами платежей – аннуитетные, фиксированные и дифференцированные);
• провести анкетирование среди обучающихся 11-х профильных классов с целью выяснения трудностей, которые возникают у них при решении экономической задачи №17.

Практическое решение экономических задач

• Авторы
• Руководители
• Файлы работы
• Презентация
• Наградные документы

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF

I.Введение

Экономическую задачу ввели в экзамен ЕГЭ «Профиль по математике» только с 2015 года. Она стала называться заданием № 17 и по своей сложности находится на одном уровне с заданиями на параметры и теорию чисел. Для меня эта тема особенно важна, так как я учусь в 10 социально-экономическом классе и собираюсь свою профессию связать с экономикой. Приведу примеры статистики сдачи ЕГЭ по математике (профильный уровень) с 2018 по 2020 по Брянской области, взятые на сайте Брянского центра оценки и качества образования и сайте 4ЕГЭ.[8], [7]

Год	Средний балл по Брянской области	Средний балл по России	Решили задачу №17 по Брянской области	Не решили задачу №17 по Брянской области	Количество 100-бальников по Брянской области
2018	49,1	49,8	1,5%	98,5%	2
2019	57,8	56,5	18%	82%	2
2020	55,9	53,9	10%	90%	6

Такая статистика решения экономической задачи объясняется и сложностью задания и просто тем, что такой темы просто нет в наших учебниках по алгебре. Поэтому и возникла идея написать исследовательскую работу «Практическое решение экономических задач».

Актуальность темы моей работы определяется необходимостью уметь решать экономические задачи при сдаче ЕГЭ. Решение экономических задач очень полезно, так как жизнь современного человека тесно связана с финансовыми операциями.

Проблема заключается в отсутствии навыков применения математических и экономических знаний на практике в расчетах платежей банковских кредитов и прочих операций, а также неумение и боязнь решать экономические задачи на ЕГЭ.

Объект исследования: задачи с экономическим содержанием.

Предмет исследования: различные подходы к решению задач о кредитах, в зависимости от условия задачи.

Гипотеза: в современном мире необходимы знания об экономике и в этом может помочь математика.

Цель исследования – исследование методов решения задач с экономическим содержанием.

Задачи исследования:

изучить теоретический материал по выбранной теме;

научиться решать задачи с процентами разных видов сложности;

разобрать основные типы задач с примерами решений;

создать таблицы для различных видов платежей;

показать на примерах поиск решения реальной практической задачи (кредит с разными видами платежей – аннуитетные, фиксированные и дифференцированные);

провести анкетирование среди обучающихся 11-х профильных классов с целью выяснения трудностей, которые возникают у них при решении экономической задачи №17.

Конечно, на различных сайтах и в математической литературе можно найти решения таких задач, но зачастую либо они содержат много лишней информации, либо они решены непонятным для меня способом. Я же использовал табличный метод, так как считаю его самым наглядным и простым.

II.Основная часть

2.1. Основные теоретические сведения.

2.1.1. Необходимые знания при решении экономических задач.

Решение финансовых задач основывается на использовании различных математических моделей: уравнений, неравенств, их систем с привлечением процентов, арифметической и геометрической прогрессий и производной. Я не беру производную, так как в в10 классе по учебнику Ю.М.Колягина эта тема не изучается. Приведу основные определения, понятия, таблицы и формулы.

Из необходимых знаний и умений мне понадобились:

Определение понятия «Процент»

Определение понятий «Фиксированные платежи», «Аннуитетные платежи» и «Дифференцируемые платежи».

Виды мною созданных таблиц

Определение, формулы n-ого члена и суммы n первых членов арифметической и геометрической прогрессий.

2.1.2.Проценты.

Определение: один процент – это одна сотая доля. Чтобы найти данное число процентов от числа, нужно проценты записать десятичной дробью, а затем число умножить на эту десятичную дробь.

Пример: 5% от 80 это будет 0,05

r % от 14 это будет 0,01r

При решении задач необходимо понимать механизм начисления процентов по вкладам или кредитам. Например, если банк выдаёт кредит (S) клиенту, то через год клиент должен банку не только сумму кредита, но и некий процент (r). Возникает необходимость введения нового коэффициента b, b=1+0,01r. С учётом этого, долг клиента банку через год можно записать следующим образом: S + r% от S = S + 0,01r = S (1 + 0,01r) = b·S

2.1.3.Платежи.

В задачах по теме «Кредит» используют о три основных вида платежа:

Фиксированные платежи (платежи, которые чётко оговариваются в условии задачи)

2.Аннуитетные платежи (постоянные ежемесячные или ежегодные платежи, которые не меняются на протяжении всего периода кредитования)

3.Дифференцируемые платежи— ежемесячные или ежегодные платежи, уменьшающиеся к концу срока кредитования и обеспечивающие уменьшение суммы долга на одну и ту же величину. [1]

2.1.4.Таблицы.

При решении задач, связанных с аннуитетными платежами мне было очень удобно заполнять следующую таблицу:

S – сумма кредита

r% — годовые (ежемесячные) проценты

b=1+0,01r – коэффициент

х – ежегодная (ежемесячная) выплата

Год	Долг с %	Выплата	Долг после выплаты
0			S
1 год	Sb	x	Sb-x
2 год	(Sb-x)b=Sb2-xb	x	Sb2-xb-x
3 год	(Sb2-xb-x)b=Sb3-x b2-xb	x	Sb3-x b2-xb-x
4 год	(Sb3—x b2—xb—x)b= Sb4—xb3—xb2—xb	x	Sb4—xb3—xb2—xb-x
5 год	(Sb4—xb3—xb2—xb—x)b= Sb5—xb4-xb3—xb2—xb	x	Sb5-xb4-xb3-xb2-xb-x
6 год	(Sb5—xb4-xb3—xb2—xb—x)b= Sb6—xb5—xb4-xb—3xb2—xb	x	Sb6-xb5-xb4-xb-3xb2-xb-x
n год	Sbn—xbn-1—xbn-2-…-xb2—xb	x	Полная выплата, долг равен 0

При решении задач, связанных с дифференцированными платежами я использовал следующую таблицу:

Месяц	Долг с %	Выплата	Долг после выплаты
0			S
1	Sb	Sb
2
n-1
n			0

При решении задач по теме «Вклады»

Год	Вклад с %
0
1	Sb
2	Sb2
n	Sbn

При решении задач, в которых осуществлялись какие-либо действия (пополнение или снятие денег с вклада):

х – действие

Год	Вклад с %	Действие	Вклад после действия.
0			S
1 год	Sb	+х	Sb+x
2 год	b(Sb+x)= Sb2+xb	+х	Sb2+xb+x
3 год	b(Sb2+xb+x)=Sb3_+хb2+xb	Снял вклад

2.1.5. Арифметическая и геометрическая прогрессии.[2]

Арифметическая прогрессия.

Определение. Последовательность чисел, в которой каждое следующее отличается от предыдущего ровно на одну и ту же величину, называется арифметической прогрессией. Любой член арифметической прогрессии вычисляется по формуле: = + (n-1)·d

Формула суммы n-первых членов арифметической прогрессии

S_n=

С учётом этой формулы: (n-1) + (n-2) +…+3+2+1 = =

= =

= =

Геометрическая прогрессия

Определение. Геометрической прогрессией называется последовательность отличных от нуля чисел, каждый член которой, начиная со второго, равен предыдущему члену, умноженному на одно и то же число.

Любой член геометрической прогрессии вычисляется по формуле:

b_n =b₁· q^n-1

Формула суммы n-первых членов геометрической прогрессии

S_n=

Из этой формулы следует: b^n-1+b^n-2 +…+b²+b+1=

2.2. Практическое решение экономических задач.

2.2.1. 1 тип: нахождение количества лет (месяцев) выплаты кредита.

n-? (Аннуитетные платежи)

Задача №1

Максим хочет взять кредит 1,5 млн рублей. Погашение кредита происходит раз в год равными суммами (кроме, может быть, последней) после начисления процентов. Ставка процента 10% годовых. На какое минимальное количество лет может Максим взять кредит, чтобы ежегодные выплаты были не более 350 тысяч рублей?[3]

Решение: кредит (S) 1500000 руб.

Ставка (r) 10% годовых. Введём коэффициент b=1+0,01r

Ежегодная выплата (х) ≤350000 руб.

Сколько лет (n)-?

Год	Долг с %	Платёж	Долг после выплаты
0			1500000
1 год	1500000•1,1=1650000	350000	1300000
2 год	1300000•1,1=1430000	350000	1080000
3 год	1080000•1,1=1188000	350000	838000
4 год	838000•1,1=921800	350000	571800
5 год	571800•1,1=628980	350000	278980
6 год	278980•1,1=306878	306878	0

Ответ: 6 лет.

2.2.2. 2 тип: вычисление процентной ставки по кредиту.

r-? (Фиксированные платежи)

Задача №2

31 декабря 2014 года Борис взял в банке 1 млн. рублей в кредит. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга ( то есть увеличивает долг на определенное количество процентов), затем Борис переводит очередной транш. Борис выплатил кредит за два транша, переводя в первый раз 560 тыс. рублей, во второй – 644,1 тыс. рублей. Под какой процент банк выдал кредит Борису? [3]

Решение Кредит (S) 1000000 руб.

Введём коэффициент b=1+0,01r

1 год выплата – x₁=560000руб.

2 год выплата – x₂₌644100 руб.

r-?

Год	Долг с %	Платёж	Долг после выплаты
0			S
1 год	Sb	x1	Sb-x1
2 год	b(Sb-x1) =Sb2-bx1	x2	—

Sb²-x₁b=x₂

1000000b²-560000b-644100=0

10000b²-5600b-6441=0

D=5600²+4•10000•6441=31360000+257640000=289000000

b₁= = 1,13

b₂= = — 0,57 не подходит по условию задачи. b=1+0,01r, r=13 Ответ: 13%

2.2.3. 3 тип: нахождение суммы кредита.

S-? (Аннуитетные платежи)

Задача №3.

31 декабря 2014 года Сергей взял в банке некоторую сумму в кредит под 12% годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 12%), затем Сергей переводит в банк 3512320 рублей. Какую сумму взял Сергей в банке, если он выплатил долг тремя равными платежами (то есть за три года)? [4]

Решение: ставка (r) — 12% , b=1,12

Ежегодная выплата (х) — 3512320 рублей

Количество лет (n) 3 года

Сумма кредита (S) -?

Год	Долг с %	Платёж	Долг после выплаты
0			S
1 год	Sb	х	Sb-x
2 год	b(Sb-x)= Sb2-xb	х	Sb2-xb-x
3 год	b(Sb2—xb—x )=Sb3_ хb2—xb	х	—

Sb^3_хb²-xb =x , Sb³-(1+b+b²)x=0

S=Ответ: 8436000рублей.

2.2.4. 4 тип: нахождение ежегодного (ежемесячного) транша.

х-? (Аннуитетные платежи)

Задача №4.

31 декабря 2014 года Алексей взял в банке 9282000рублей в кредит по 10% годовых. Схема выплат кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 10%), затем Алексей переводит в банк Х рублей. Какой должна быть сумма Х, чтобы Алексей выплатил долг четырьмя равными платежами ( то есть за четыре года)?[4]

Решение:

Сумма кредита (S)- 9282000рубля

Ставка (а)=10%, b=1,1

Количество лет (n) 4 года

Ежегодная выплата ( транш): х -?

Год	Долг с %	Выплата	Долг после выплаты
0			S
1 год	Sb	x	Sb-x
2 год	(Sb-x)b=Sb2-xb	x	Sb2-xb-x
3 год	(Sb2-xb-x)b=Sb3-x b2-xb	x	Sb3-x b2-xb-x
4 год	(Sb3—x b2—xb—x)b= Sb4—xb3—xb2—xb	x	Полная выплата — остаток 0

Sb⁴—xb³—xb²—xb =x

Sb⁴-(b+b²+b³)x=x

Sb⁴-(1+b+b²+b³)x=0, X=

X= .

Ответ: 2928200 рублей.

2.2.5. 5 тип: нахождение разницы (аннуитетные платежи).

Задача №5.

31 декабря 2014 года Федор взял в банке 6951000рублей в кредит под 10% годовых. Схема выплат кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 10%), затем Федор переводит в банк платеж. Весь долг Федор выплатил за 3 равных платежа. На сколько рублей меньше он бы отдал банку, если бы смог выплатить долг за 2 равных платежа?[5]

Решение: Сумма кредита (S) – 6951000 рублей

Ставка (r) -10%, b=1,1

3 равных платежа:

Год	Долг с %	Платёж	Долг после выплаты
0			S
1 год	Sb	х	Sb-x
2 год	b(Sb-x)= Sb2-xb	х	Sb2-xb-x
3 год	b(Sb2—xb—x )=Sb3_ хb2—xb	х	—

Sb³— хb²-xb=x

Sb³-(b²+b+1)x=0

X=

2 равных платежа:

Год	Долг с %	Платёж	Долг после выплаты
0			S
1 год	Sb	х	Sb-x
2 год	b(Sb-x)= Sb2-xb	х	—

Sb²-xb=x

Sb²-(1+b)x=0

X=

За три года: 2795100_·3=8385300

За два года:4005100_·2=8010200

Разница: 8385300-8010200=375100

Ответ: на 375100 рублей.

2.2.6. 6 тип: задачи, связанные с известным остатком (фиксированные платежи).

Задача №6.

15-го января был выдан полугодовой кредит на развитие бизнеса. В таблице представлен график его погашения.

Дата	15.01	15.02	15.03	15.04	15.05	15.06	15.07
Долг (в процентах от кредита)	100%	90%	80%	70%	60%	50%	0%

В конце каждого месяца, начиная с января, текущий долг увеличивался на 5%, а выплаты по погашению кредита происходили в первой половине каждого месяца, начиная с февраля. На сколько процентов общая сумма выплат при таких условиях больше суммы самого кредита?[6]

Решение: S – сумма кредита

r% — годовые (ежемесячные) проценты (5%)

b=1+0,01r – коэффициент (1,05)

Месяц	Долг с %	Выплата	Долг после выплаты
15.01			S
15.02	Sb	Sb-0,9S	0,9S
15.03	0,9Sb	0,9Sb -0,8S	0,8S
15.04	0,8Sb	0,8Sb -0,7S	0,7S
15.05	0,7Sb	0,7Sb -0,6S	0,6S
15.06	0,6Sb	0,6Sb -0,5S	0,5S
15.07	0,5Sb	0,5Sb	Полная выплата — остаток 0

Общая сумма выплат:

(Sb+0,9Sb+0,8Sb+0,7Sb+0,6Sb+0,5Sb)-(0,9S+0,8S+0,7S+0,6S+0,5S)=

4,5Sb-3,5S=S(4,5b-3,5)=S(4,5·1,05-3,5)=1,225S

Ответ: 22,5 процента.

2.2.7. 7 тип: задачи, связанные с дифференцированными платежами.

Задача №7.

Алексей взял кредит в банке на срок 12 месяцев. По договору Алексей должен вернуть кредит ежемесячными платежами. В конце каждого месяца к оставшейся сумме долга добавляется r % этой суммы и своим ежемесячным платежом Алексей погашает эти добавленные проценты и уменьшает сумму долга. Ежемесячные платежи подбираются так, чтобы долг уменьшался на одну и ту же величину каждый месяц (на практике такая схема называется «схемой с дифференцированными платежами»). Известно, что общая сумма, выплаченная Алексеем банку за весь срок кредитования, оказалась на 13 % больше, чем сумма, взятая им в кредит. Найдите r. [6]

Решение: Сумма кредита (S), ставка (r) -? %, b=1+0,01r

Месяц	Долг с %	Выплата	Долг после выплаты
0			S
1	Sb	Sb
2
3
4
5
6
7
8
9
10
11
12			0

Sb(1+ )-S )=1,13S

— =1,13S /S

— =1,13

78b=1,13·12+66 , b=1,02, r=2% Ответ: 2%.

2.2.8. Вклады. Задача №8

Владимир поместил в банк 3600 тысяч рублей под 10% годовых. В конце каждого из первых двух лет хранения после начисления процентов он дополнительно вносил на счет одну и ту же фиксированную сумму. К концу третьего года после начисления процентов оказалось, что размер вклада увеличился по сравнению с первоначальным на 48,5%. Какую сумму Владимир ежегодно добавлял к вкладу?[3]

Решение:

S=3600 тысяч – сумма вклада

r% — годовые (ежемесячные) проценты, r=10%

b=1+0,01r – коэффициент, b=1,1

n=3 года, х =? – действие

Год	Вклад с %	Действие	Вклад после действия.
0			S
1 год	Sb	+х	Sb+x
2 год	b(Sb+x)= Sb2+xb	+х	Sb2+xb+x
3 год	b(Sb2+xb+x)=Sb3_+хb2+xb	Снял вклад

Sb³+хb²+xb = 1,485S

х(b²+b) = 1,485S — Sb³

х(1,21+1,1) = 1,485S – 1,331S

2,31х = 0,154·3600

2,31х = 554,4

х = 240

Ответ: 240000.

2.3. Результаты анкетирования

В анкетировании приняли участие: 11 физико-математический, 11 инженерный, 11 социально-экономический, 11академический. Всего 74 человека. Это классы, в которых почти все обучающиеся сдают профильную математику. Мне было интересно, как будущие выпускники этого учебного года ответят на предложенные им вопросы.

Вопросы для анкетирования:

1.Какую задачу из второй части ЕГЭ вы считаете самой трудной:

№13, №14, №15, №16, №17, №18, №19?

2.У вас всегда, получается, правильно решить задачу №17?

А) Да; Б) Нет; В) Другой ответ.

3.Вы решаете задачу №17 с помощью таблицы?

А) Да; Б) Нет; В) Другой ответ.

4.Сколько в среднем я решил(а) самостоятельно задач под номером 17 в этом учебном году?

5. Хотели бы вы научиться хорошо решать задачи №17?

А) Да; Б) Нет; В) Другой ответ.

На первый вопрос ответы были следующими: самой трудной задачей выпускники считают задачу №18(28%), потом задачу №19(25%), затем №16(19%), №14(17%) и №17(11%). Экономическую задачу большинство респондентов не считают трудной, но почему тогда низкий процент её выполнения. Может ответ кроется в допущении вычислительных ошибок? Там нужно производить достаточно сложные расчеты без калькулятора. На второй вопрос, 42% респондентов решают экономическую задачу №17, 48% нет и 10% когда как, иногда получается, а иногда нет. Большинство выпускников при решении задания №17 используют таблицы(64%), остальные 36% нет. Конечно, 11-е классы готовятся к экзаменам и решают экономические задачи, но нашлись такие, которые пока не решили самостоятельно ни одной такой задачи (7%), может до №17 пока не дошла очередь. Ипри ответе на пятый вопрос 86%респондентов хотят хорошо научиться решать задачи, 6%-нет, и 8% уже хорошо научились решать экономические задачи.

Вывод: потребность в исследовании, конечно, есть. Даже 36% выпускников не пользуются таблицами, а мы ещё в 10 классе, нам многому надо учиться. Также много желающих хотят потренироватьсяв решении таких задач(86%). Более подробно ознакомиться с результатами анкетирования можно в приложении.

III. Заключение

Таким образом, понимание процентов и умение производить процентные расчеты, в настоящее время необходимы каждому человеку. Их знание помогает в развитии практических способностей, а также умение решать экономические задачи. Изучение банковских процентов может способствовать развитию таких навыков как экономичность, расчетливость.

В целом работа по данной теме для меня оказалась полезной, а также она принесла мне необходимые знания финансовой математики в сфере банковских процентов. Я считаю, цели, поставленные в работе, были достигнуты. Тема работы очень актуальна, так как все рассматриваемые задачи взяты из материалов по подготовке к ЕГЭ по математике «Профиль». Я расширил свои математические навыки и получил дополнительные теоретические знания по теме «Проценты», научился самостоятельно решать экономические задачи из кимов ЕГЭ. Ведь решение экономических задач нужно не только для сдачи экзамена, а также для повышения финансовой грамотности молодёжи.

IV. Список источников информации

1. Прокофьев А.А., Корянов А.Г. Социально – экономические задачи. «Легион». Ростов на Дону,2016.

2. Википедия – свободная энциклопедия.

3. ЕГЭ 2018 под редакцией А. Л. Семенова, И.В. Ященко.

4. Открытый банк заданий ЕГЭ fipi.ru

5. Сайт «Решу ЕГЭ».

6. Сайт «Алекс Ларин».

7. Сайт 4ЕГЭ.

8. ege32.ru ГАУ «Брянский региональный центр обработки информации».

V. Приложения

Результаты анкетирования.

Просмотров работы: 581

3 октября 2020

В закладки

Обсудить

Жалоба

Средний процент выполнения заданий профильного ЕГЭ по математике

Основные характеристики экзаменационной работы ЕГЭ 2020 г. по математике.

№	Проверяемые требования	Уровень сложности задания	Максимальный балл	Средний процент выполнения
1	Уметь использовать приобретенные знания и умения в практической деятельности и повсе­дневной жизни	Б	1	88,9
2	Уметь использовать приобретенные знания и умения в практической деятельности и повсе­дневной жизни	Б	1	98,4
3	Уметь выполнять действия с геометрическими фигурами, координатами и векторами	Б	1	89,8
4	Уметь строить и исследовать простейшие математические модели	Б	1	89,9
5	Уметь решать уравнения и неравенства	Б	1	96,1
6	Уметь выполнять действия с геометрическими фигурами, координатами и векторами	Б	1	76,8
7	Уметь выполнять действия с функциями	Б	1	63,0
8	Уметь выполнять действия с геометрическими фигурами, координатами и векторами	Б	1	63,8
9	Уметь выполнять вычисления и преобразования	П	1	65,2
10	Уметь использовать приобретенные знания и умения в практической деятельности и повсе­дневной жизни	П	1	75,7
11	Уметь строить и исследовать простейшие математические модели	П	1	57,0
12	Уметь выполнять действия с функциями	П	1	47,9
13	Уметь решать уравнения и неравенства	П	2	34,9
14	Уметь выполнять действия с геометрическими фигурами, координатами и векторами	П	2	2,5
15	Уметь решать уравнения и неравенства	П	2	14,8
16	Уметь выполнять действия с геометрическими фигурами, координатами и векторами	П	3	3,8
17	Уметь использовать приобретенные знания и умения в практической деятельности и повсе­дневной жизни	П	3	22,0
18	Уметь решать уравнения и неравенства	В	4	2,4
19	Уметь строить и исследовать простейшие мате­матические модели	В	4	10,3

Изменений в структуре КИМ ЕГЭ-2021 нет.



В статье анализируются основные вопросы, связанные с формированием основ экономической и финансовой грамотности российского общества в целом, а также формированием экономических практико-ориентированных компетенций у обучающихся российских школ в частности на примере решения задач с экономическим содержанием. Рассматриваются сущность, типы и основные особенности экономических задач в структуре единого государственного экзамена по математике (профильный уровень), а также предлагаются варианты решения данных задач и методическая база.

Ключевые слова:



единый государственный экзамен, экономическая задача, экономическая грамотность, финансовая грамотность.

The article analyzes the main issues related to the formation of the foundations of economic and financial knowledge of Russian society as a whole, as well as the formation of economic practice-oriented competencies of Russian schools` students, in particular, using the example of solving math tasks with economic content. The essence, types and main features of economic tasks in the structure of the unified state examination in mathematics (advanced level) are considered, as well as options for solving these tasks and a methodological base are proposed.

Keywords:



unified state examination, economic task, economic knowledge, financial knowledge.

Реалии современной экономической ситуации в России, обусловленные рядом политических, социальных, технологических, правовых и международных факторов, актуализируют важность и необходимость обеспечения высокого уровня экономической и финансовой грамотности российского населения. Современной России нужны люди, способные находиться в постоянном поиске путей решения экономических проблем и эффективно осуществлять экономическую деятельность. Важное значение в системе подготовки экономически грамотного населения отводится школе, так как современная социальная среда не в состоянии обеспечить детям и подросткам практико-ориентированную подготовку к решению экономических задач их повседневной жизни.

В последнее десятилетие проблеме формирования экономического практико-ориентированного мышления подрастающего поколения уделяется в системе образования значительно больше внимания, чем в предыдущие годы: организуются и проводятся курсы по формированию финансовой грамотности населения как для педагогов, так и для детей и взрослых, издается и переиздается большое количество теоретической и практической экономической литературы, разрабатываются и реализуются образовательные проекты по развитию финансовой и экономической грамотности, предпринимательству на всех уровнях системы образования. В качестве частного случая решения выше указанных задач можно выделить включение в структуру единого государственного экзамена по математике (профильный уровень) практико-ориентированной задачи с экономическим содержанием. Данная задача в структуре контрольно-измерительных материалов экзамена (КИМ ЕГЭ) предлагается участникам экзамена во второй части (задания с развернутым ответом), имеет порядковый номер задания 15 и обладает повышенным уровнем сложности, предполагаемое время решения указанной задачи участниками экзамена составляет 25–30 минут. В спецификации КИМ ЕГЭ 2022г. и кодификаторе элементов содержания КИМ по математике можно увидеть, что задача направлена на проверку умения использовать приобретенные математические знания в практической деятельности и повседневной жизни [1,2]. У обучающихся при этом проверяется умение выполнять действия с целыми и рациональными числами, с дробями, со степенями с натуральным показателем, знаний и умений обращаться с процентами, в том числе и сложными «банковскими» процентами [3].

Однако, как показывает практика проведения единого государственного профильного экзамена по математике, у выпускников школ отмечаются существенные сложности в решении задач данного типа. Сложности в решении задачи № 15 выпускниками напрямую связаны с подготовкой к экзамену в школе. В контексте проблем в подготовке к успешному решению конкретной задачи можно выделить следующие: наличие в таких задачах большого количества терминов, неизвестных учащимся; старшеклассники плохо ориентируются в материале, изученном в 5–9 классах и необходимом для решения подобных задач (темы процентов, арифметической, геометрической прогрессий вызывают затруднения); предлагаемые для решения задачи являются сразу сложными.

Таким образом, задача методической подготовки к решению задач с экономическим содержанием, в первую очередь, педагогов подтверждает свою значимость и актуальность.

Авторами настоящей статьи рекомендовано, в первую очередь, разобраться и различать несколько типов указанной задачи, а затем, для каждого типа задачи разработать и предложить обучающимся единый алгоритм решения.

Существует 5 типов задачи № 15 с экономическим содержанием:

— Задача на кредиты;

— Задача на вклады;

— Задача на нахождение экстремумов;

— Производственно-бытовая задача;

— Задача на проценты, доли и соотношения.

Базовые формулы для решения указанных типов задач следующие:

(1)

(2)

(3)

(4)

(5)

Решение задачи с экономическим содержанием, как и любой текстовой задачи происходит по следующей схеме:

1. Условие задачи необходимо «перевести» на математический язык (составление математической модели).
2. Найти решение задачи, используя знание математических формул (работа с составленной моделью).
3. Объяснить полученный для математической модели результат в терминах первоначальной задачи.

1 тип: задача на кредиты

Пример

:

31 декабря 2017 года Виталий взял в Банке 4 550 000 рублей в кредит под 20 % годовых. Схема выплаты следующая: 31 числа каждого следующего месяца Банк начисляет процент (%) на оставшуюся сумму долга (т. е. повышает долг на 20 %), затем Виталий переводит в Банк определенную сумму ежегодного платежа. Какова должна быть сумма ежегодного платежа (в рублях), если Виталий выплатит долг тремя равными ежегодными платежами.

Решение задачи

:

Обозначим сумму ежегодного платежа за Х, тогда

1 год: 4 550 000 * 1,2 — сумма к возврату после 1 года (с начисленными %)

После выплаты ежегодного платежа: 4 550 000 * 1,2 — Х

2 год: (4 550 000 * 1,2 — Х) * 1,2 — Х

3 год: ((4 550 000 * 1,2 — Х) * 1,2 — Х)* 1,2 — Х

Так как по условию задачи Виталий к концу 3 года выплатит все полностью, по состоянию на конец 3го года долг Виталия перед банком будет равен 0 рублей.

Составим уравнение (математическая модель):

((4 550 000 * 1,2 — Х) * 1,2 — Х)* 1,2 — Х = 0

Далее — математическое решение уравнения с одним неизвестным элементом.

Ответ: 2 160 000 рублей.

2 тип: задачи на вклады

Пример

:

Вкладчик внес в Банк 2 500 000 рублей в год под 10 % годовых. В конце каждого из трех лет вкладчик дополнительно вносил одну и ту же сумму денег. К концу 4-го года его вклад стал равен 4 024 350 рублей. Какую сумму вносил вкладчик в течение 1–3 лет?

Данный тип задач похож на 1 тип, только сумма на счету не уменьшается, а увеличивается.

Решение

:

Обозначим сумму ежегодного платежа, которую вносил на свой счет вкладчик, за Х, тогда

1 год: 2 500 000 * 1,1 — сумма к концу 1 года (с начисленными % по вкладу)

После внесения суммы на счет вкладчиком: 2 500 000 * 1,1 + Х

2 год: (2 500 000 * 1,1 + Х) * 1,1 + Х

3 год: ((2 500 000 * 1,1 + Х) * 1,1 + Х)* 1,1 + Х

4 год: (((2 500 000 * 1,1 + Х) * 1,1 + Х)* 1,1 + Х) * 1,1

В конце 4-го года начислены только %, так как вкладчик сумму добавлял только 1–3 года.

Составим уравнение (математическая модель):

(((2 500 000 * 1,1 + Х) * 1,1 + Х)* 1,1 + Х) * 1,1 = 4 024 350

Далее — математическое решение задачи

Ответ: 100 000 рублей

3 тип: задачи на исследование функции и


нахождение экстремумов

Пример

:

Первичная информация некоторой фирмы распределяется по Серверам 1 и 2. С Сервера 1 при объеме W2 Гбайт входящей информации выходит 3W Гбайт, а с Сервера 2 при объеме W2 Гбайт выходит 4W Гбайт. Определите наибольший общий объем Выходящей информации, если общий объем входящей информации 400 Гбайт. В ответе укажите число Гбайт.

Когда речь в Задаче идет о предельных величинах (максимальных или минимальных значениях), — значит, эта задача связана с нахождением производной функции.

Решение

:

Пусть на Сервер 1 входит Х входящей информации, а на Сервер 2 — У входящей информации, тогда

На оба Сервера будет входить Х+У = 400 Гбайт

Сервер 1: входит Х информации, выходит

Сервер 2: входит У информации, выходит

или

, таким образом, общий объём выходящей информации будет равен:

+

= F(X)

Необходимо найти точку экстремума функции

Далее — математическое решение задачи.

Х = 144 — т. е. в этом значении функции достигает максимального значения.

Найдём значение функции в указанной точке:

F (144) =

+

F (144) = 3*12+4*16 = 36+64=100

Ответ: 100 Гбайт.

4 тип: производственно-бытовые задачи

Пример

:

Общая численность персонала завода составляет более 200 человек. Пятая часть сотрудников работает в заводоуправлении, 33 сотрудника работают в сборочном цехе, а остальные — в нескольких цехах, численность в каждом из которых составляет 1/9 от всего персонала завода. Чему равна общая численность персонала завода?

В задачах такого типа важно проявить предположение, подбор чисел, элементы эрудиции, — здесь важно предположить, каким может быть ответ, ограничить область принадлежности чисел потенциального ответа и методом подбора вариантов найти верное решение. Подбор решений основывается на знаниях кратности чисел и логике.

Решение

:

Пусть общая численность персонала равна Х, тогда

X= 1/5 Х + 33+ 1/9 Х * К (К –количество цехов)

X= 1/5 Х + 33+ Х/9 * К

Х-1/5 Х — КХ/9 = 33

X (36–5K) = 33*45 *** теперь делаем предположение, каким может быть К

С одной стороны: 36–5К> 0, следовательно K≤7

С другой стороны: 33*45 = 1485 — нечетное, значит К — нечетное,

Таким образом возможные варианты К = 1,3,5,7

Проверяем все варианты:

К=7 — единственное решение задачи, в таком случае Х = 1485 человек

Ответ: 1485 человек.

5 тип: задачи на проценты, доли и


соотношения

Пример

:

Меховая шуба стоит дороже кожаной куртки на 45 %. На сколько % дешевле стоит кожаная куртка, чем меховая шуба?

В задачах такого типа важно правильно определить, что именно брать за основу, т. е. за элемент относительного сравнения (за 100 %).

Решение

:

Пусть кожаная куртка стоит Х, тогда, по условию задачи меховая шуба стоит 1,45 Х

Теперь, за основу, за базу, за 100 % возьмем меховую шубу, тогда

1,45 Х — 100 %

Х — р %

Р % = 100Х / 1,45 Х = 10 000 / 145 = 68,9 % = 69 %

Кожаная куртка составляет по стоимости в НОВОМ сравнении 69 % от меховой шубы, т. е. дешевле нее на 100 % — 69 % = 31 %

Ответ: 31 %

Вышеприведенные примеры типов задач являются авторской классификацией и могут не ограничиваться только указанными примерами. КИМ ЕГЭ пересматриваются ежегодно, дополняются и совершенствуются. Указанные типы задач предложены авторами статьи в качестве методического ориентира, базовых характеристик возможных типов содержания задачи № 15 и вариантов решения. Важно дополнительно отметить, что несмотря на свою значимость, задачи, имеющие экономическое содержание, вызывают значительные трудности у обучающихся, обусловленные отсутствием достаточного внимания к решению подобных задач в школьном курсе математики, слишком большим объёмом информации, из которой трудно выделить необходимую при самостоятельной подготовке к экзамену, отсутствием общей математической культуры и экономической грамотности.

Кроме краткосрочной цели успешного прохождения экзаменационных испытаний по окончанию школы, обучение школьников решению задач с экономическим содержанием на уроках математики важно для всех категорий обучающихся благодаря из практико-ориентированному содержанию. Использование прикладных задач с экономическим содержанием позволит сформировать у выпускников школы некоторые представления об экономике страны и её месте в мировой экономике, даст возможность изучить экономические термины, встречаемые в задачах и в жизни, лучше их понять. В настоящее время, когда возрастают требования государства и общества к воспитанию конкурентоспособной личности, умеющей адаптироваться к меняющимся условиям жизнедеятельности, социально активной и компетентной в трудовой сфере, а слова «кредит», «кредитная карта», «ипотека», «вклад», «банковские проценты» не понаслышке знакомы большинству российских семей, использование задач с экономическим содержанием на уроках математики позволит продемонстрировать учащимся практическую значимость математики и одновременно подготовить их к финансовым задачам, диктуемым жизнью, т. е. быть финансово грамотным.

В Концепции программы повышения уровня финансовой грамотности населения РФ это понятие трактуют как способность граждан [4]:

— эффективно управлять личными финансами;

— осуществлять учет расходов и доходов домохозяйства и осуществлять краткосрочное и долгосрочное финансовое планирование;

— оптимизировать соотношение между сбережениями и потреблением;

— разбираться в особенностях различных финансовых продуктов и услуг (в том числе инструментов рынка ценных бумаг и коллективных инвестиций), иметь актуальную информацию о ситуации на финансовых рынках;

— принимать обоснованные решения в отношении финансовых продуктов и услуг и осознано нести ответственность за такие решения;

— компетентно планировать и осуществлять пенсионные накопления.

Изложенные обстоятельства определяют актуальность вопросов, связанных с повышением экономической грамотности школьников, и делают проблему усиления прикладной направленности математики одним из важнейших направлений развития школьного математического образования. Задачей современной школы является подготовка учащихся к успешной социальной и профессиональной адаптации в условиях рыночной экономики, и экономическая грамотность становится одним из основных критериев развития конкурентоспособной личности, приспособленной к самостоятельной жизни [5].

Литература:

1. Спецификация контрольно-измерительных материалов единого государственного экзамена 2022 г. по математике [Электронный ресурс]. — Федеральный Институт Технических Измерений (ФИПИ). — Режим доступа: http://www.fipi.ru
2. Кодификатор требований к уровню подготовки выпускников по математике для составления контрольных измерительных материалов единого государственного экзамена 2022 г. Электронный ресурс]. — Федеральный Институт Технических Измерений (ФИПИ). — Режим доступа: http://www.fipi.ru
3. Демонстрационный вариант контрольных измерительных материалов единого государственного экзамена по математике 2022 г. [Электронный ресурс]. — Федеральный Институт Технических Измерений (ФИПИ). — Режим доступа: http://www.fipi.ru
4. Стратегия повышения финансовой грамотности в Российской Федерации на 2017‒2023 гг. утверждена распоряжением Правительства Российской Федерации от 25 сентября 2017 г. № 2039-р.
5. Чумаченко В. В., Горяев А. П. Основы финансовой грамотности: учебное пособие для общеобразовательных организаций. — М.: Просвещение, 2019.