20 октября 2016
В закладки
Обсудить
Жалоба
Средний процент выполнения заданий профильного ЕГЭ по математике
Основные характеристики экзаменационной работы ЕГЭ 2016 г.
100 баллов получили 296 участников экзамена по математике профильного уровня (в 2015 году – 66 участников).
Изменений в структуре КИМа ЕГЭ-2017 нет.
| № | Проверяемые требования (умения) | Уровень сложности задания | Максимальный балл за выполнение задания | Средний процент выполнения | |
| 1 | Уметь использовать приобре-тенные знания и умения в практической деятельности и повседневной жизни | Б | 1 | 91,4 | |
| 2 | Уметь использовать приобре-тенные знания и умения в практической деятельности и повседневной жизни | Б | 1 | 94,2 | |
| 3 | Уметь выполнять действия сгеометрическими фигурами, координатами и векторами | Б | 1 | 89,6 | |
| 4 | Уметь строить и исследоватьпростейшие математические модели | Б | 1 | 75,6 макс | |
| 5 | Уметь решать уравнения инеравенства | Б | 1 | 90,7 | |
| 6 | Уметь выполнять действия сгеометрическими фигурами, координатами и векторами | Б | 1 | 78,8 | |
| 7 | Уметь выполнять действия сфункциями | Б | 1 | 50,7 | |
| 8 | Уметь выполнять действия сгеометрическими фигурами, координатами и векторами | Б | 1 | 51,5 | |
| 9 | Уметь выполнять вычисленияи преобразования | П | 1 | 59,1 | |
| 10 | Уметь использовать приобретенные знания и умения в практической деятельности и повседневной жизни | П | 1 | 38,5 | |
| 11 | Уметь строить и исследоватьпростейшие математические модели | П | 1 | 38,4 | |
| 12 | Уметь выполнять действия сфункциями | П | 1 | 44,9 | |
| 13 | Уметь решать уравнения инеравенства | П | 2 | 1 балл | 11.1 |
| 2 балла | 40.8 | ||||
| 14 | Уметь выполнять действия с геометрическими фигурами,координатами и векторами | П | 2 | 1 балл | 4.6 |
| 2 балла | 1.2 | ||||
| 15 | Уметь решать уравнения инеравенства | П | 2 | 1 балл | 4.6 |
| 2 балла | 10.5 | ||||
| 16 | Уметь выполнять действия сгеометрическими фигурами,координатами и векторами | П | 3 | 1 балл | 1.6 |
| 2 балла | 0.31 | ||||
| 3 балла | 0.85 | ||||
| 17 | Уметь использовать приоб-ретённые знания и умения в практической деятельности и повседневной жизни | П | 3 | 1 балл | 2.7 |
| 2 балла | 2.4 | ||||
| 3 балла | 7.8 | ||||
| 18 | Уметь решать уравнения инеравенства | В | 4 | 1 балл | 2.3 |
| 2 балла | 1 | ||||
| 3 балла | <1 | ||||
| 4 балла | 1 | ||||
| 19 | Уметь строить и исследовать простейшие математические модели | В | 4 | 1 балл | 23.6 |
| 2 балла | 4.8 | ||||
| 3 балла | <1 | ||||
| 4 балла | <1 |
Из методических рекомендаций для учителей.
Статистика ЕГЭ по математике за последние несколько лет
Результаты ЕГЭ 2021 по профильной математике оказались лучше, чем в 2019 и 2020 годах. Давай рассмотрим подробней, как они менялись за последние несколько лет. Эта инфа тебе пригодится, чтобы спрогнозировать ситуацию на ЕГЭ 2022.
ЕГЭ по математике в 2016 году
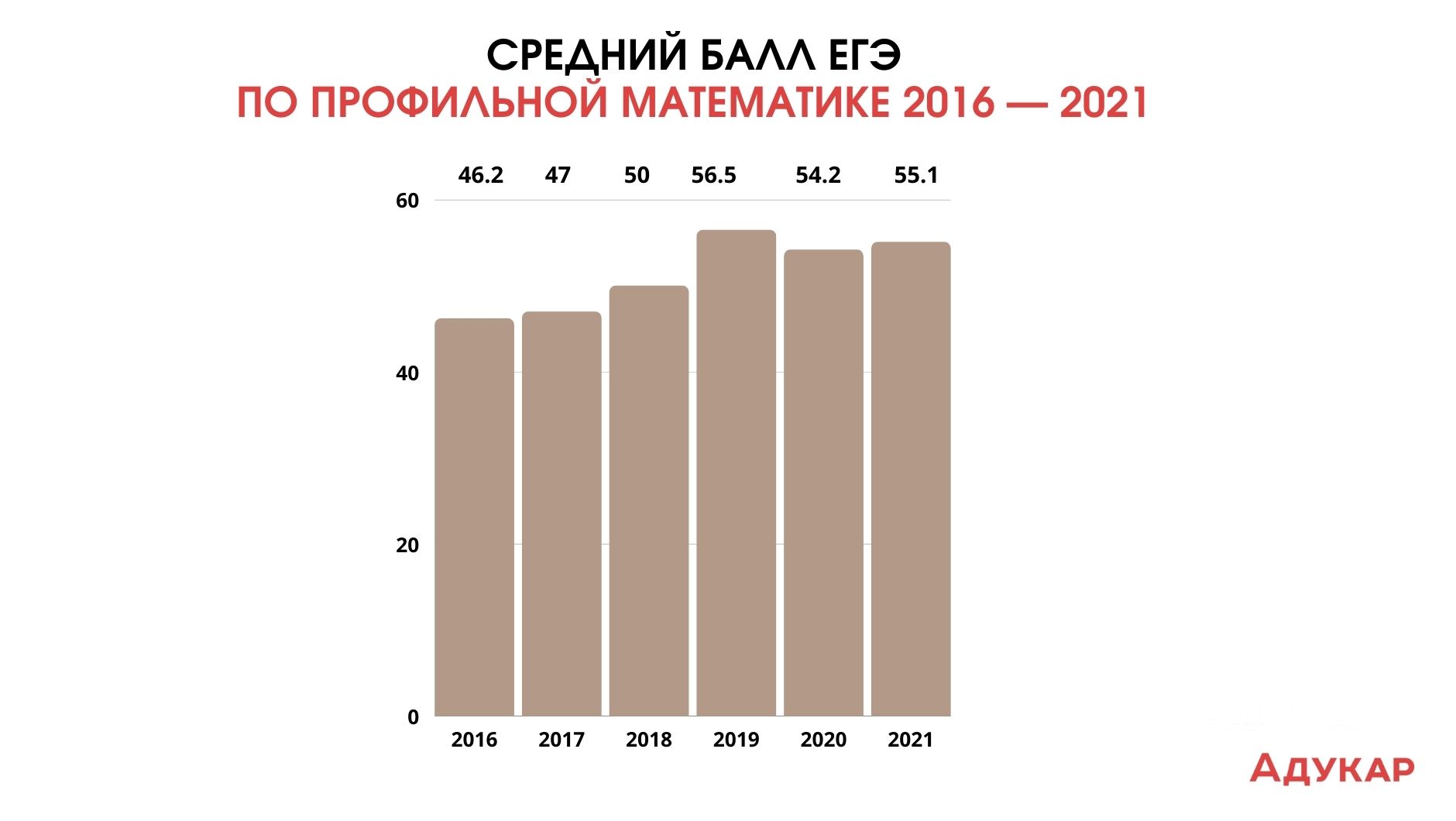
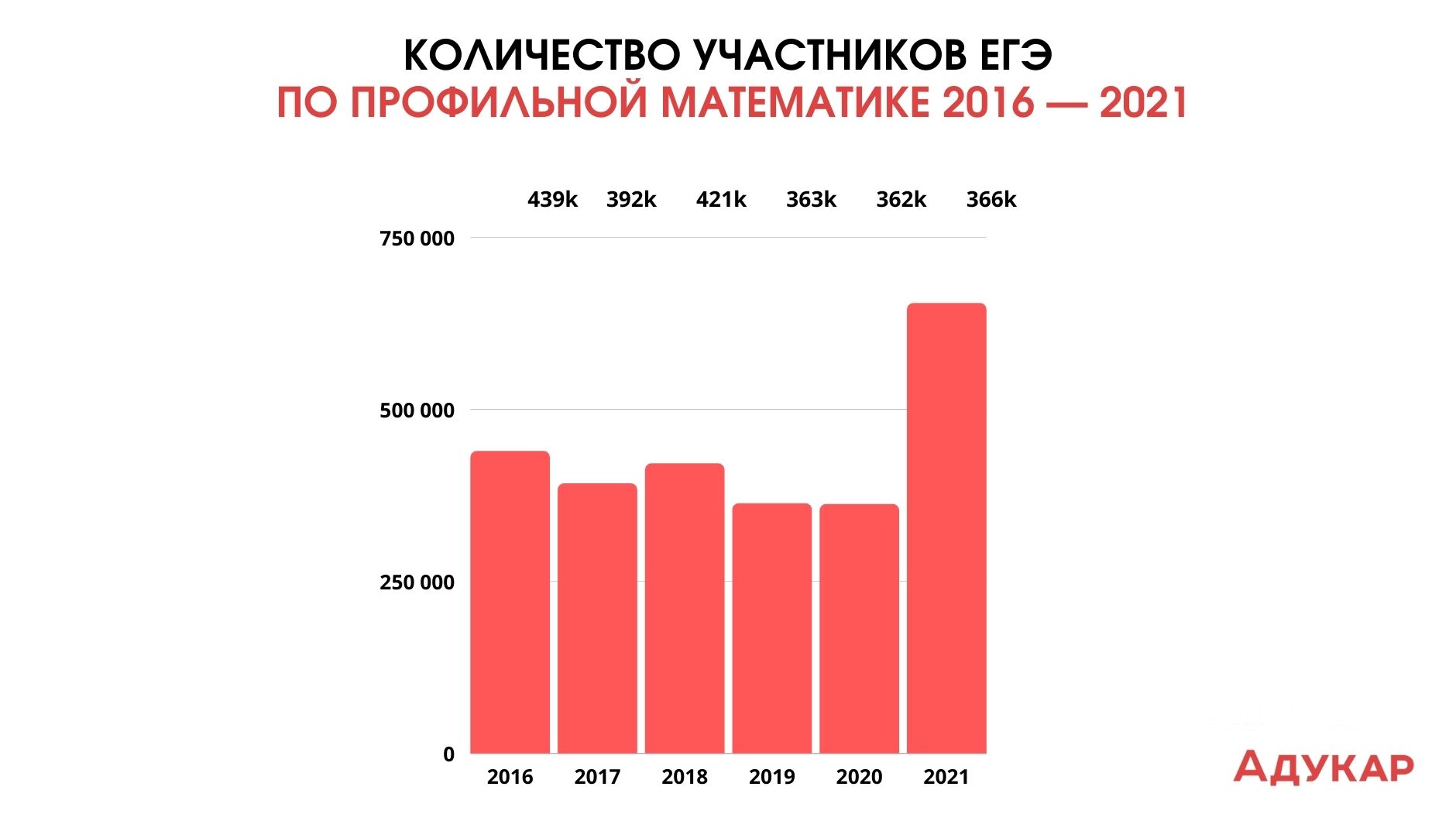
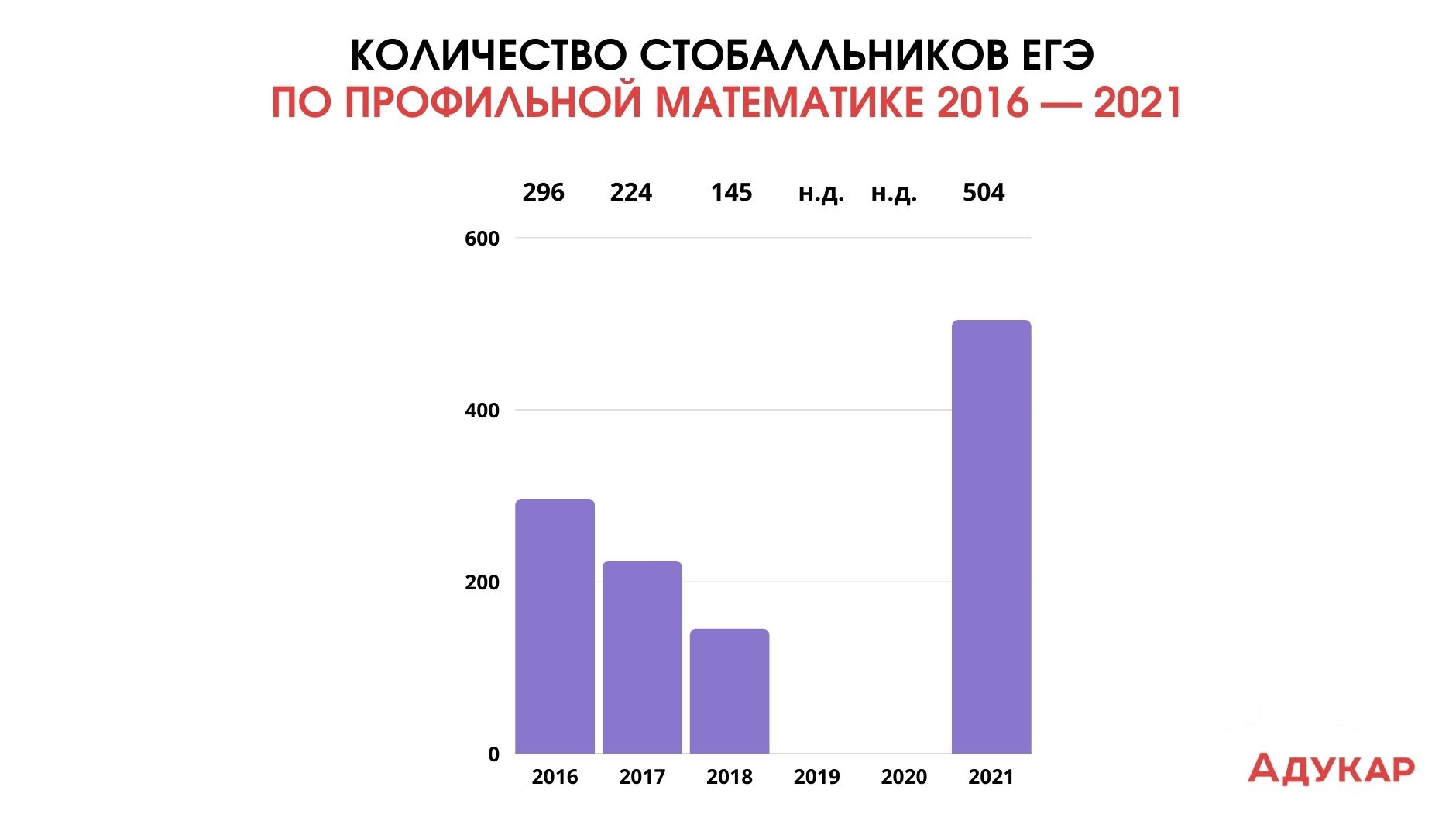
Для начала разберёмся с профильной математикой. Экзамен сдавали 439 000 учеников. В 2016 году минимальный балл для поступления в вуз был равен 27. На высокий балл в диапазоне от 81 до 100 ЕГЭ по этому предмету сдали 2,69% учеников. Всего было 296 стобалльников. Средний результат экзамена — 46,2 баллов. 15,33% абитуриентов не смогли набрать пороговый балл.
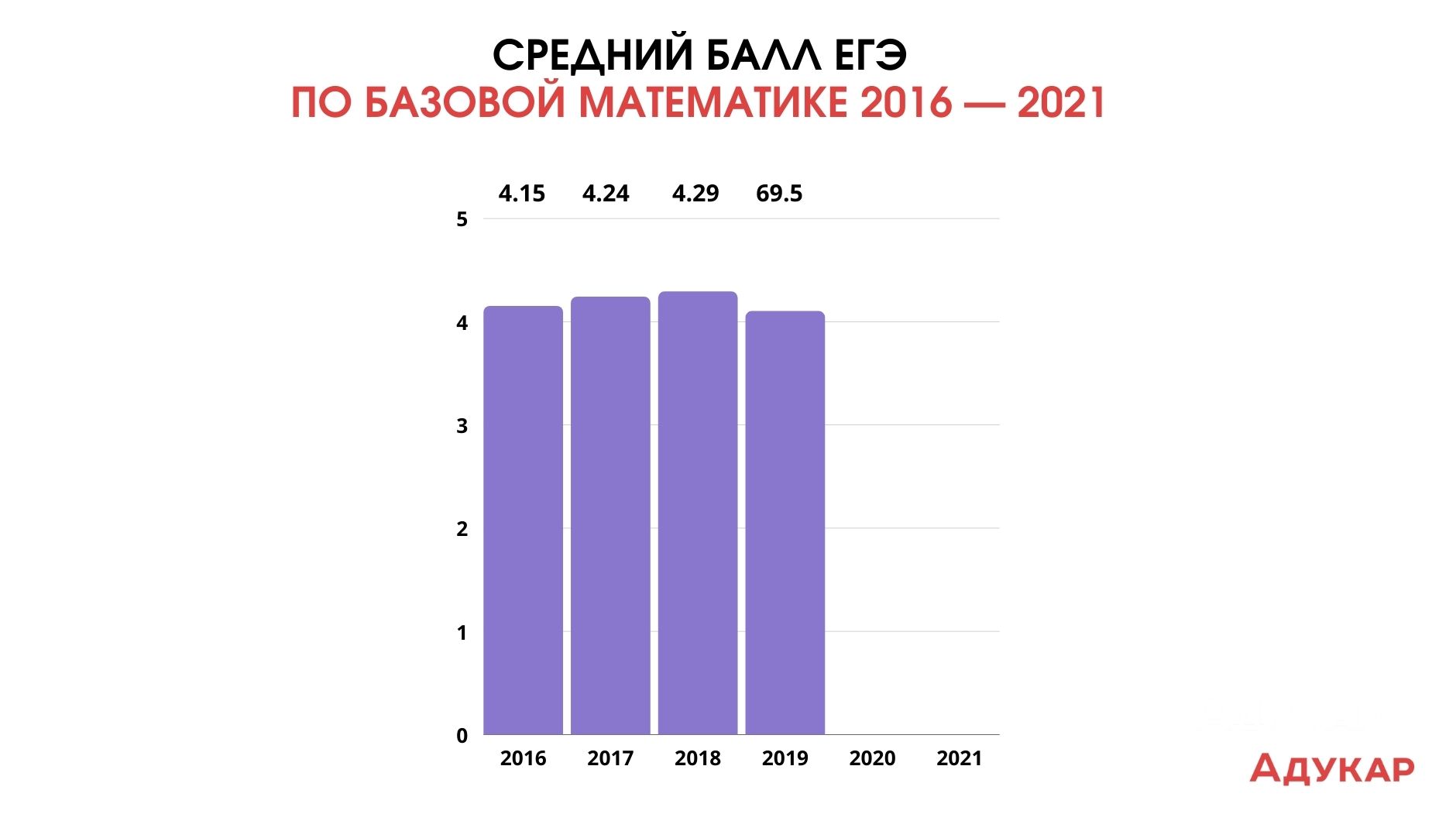
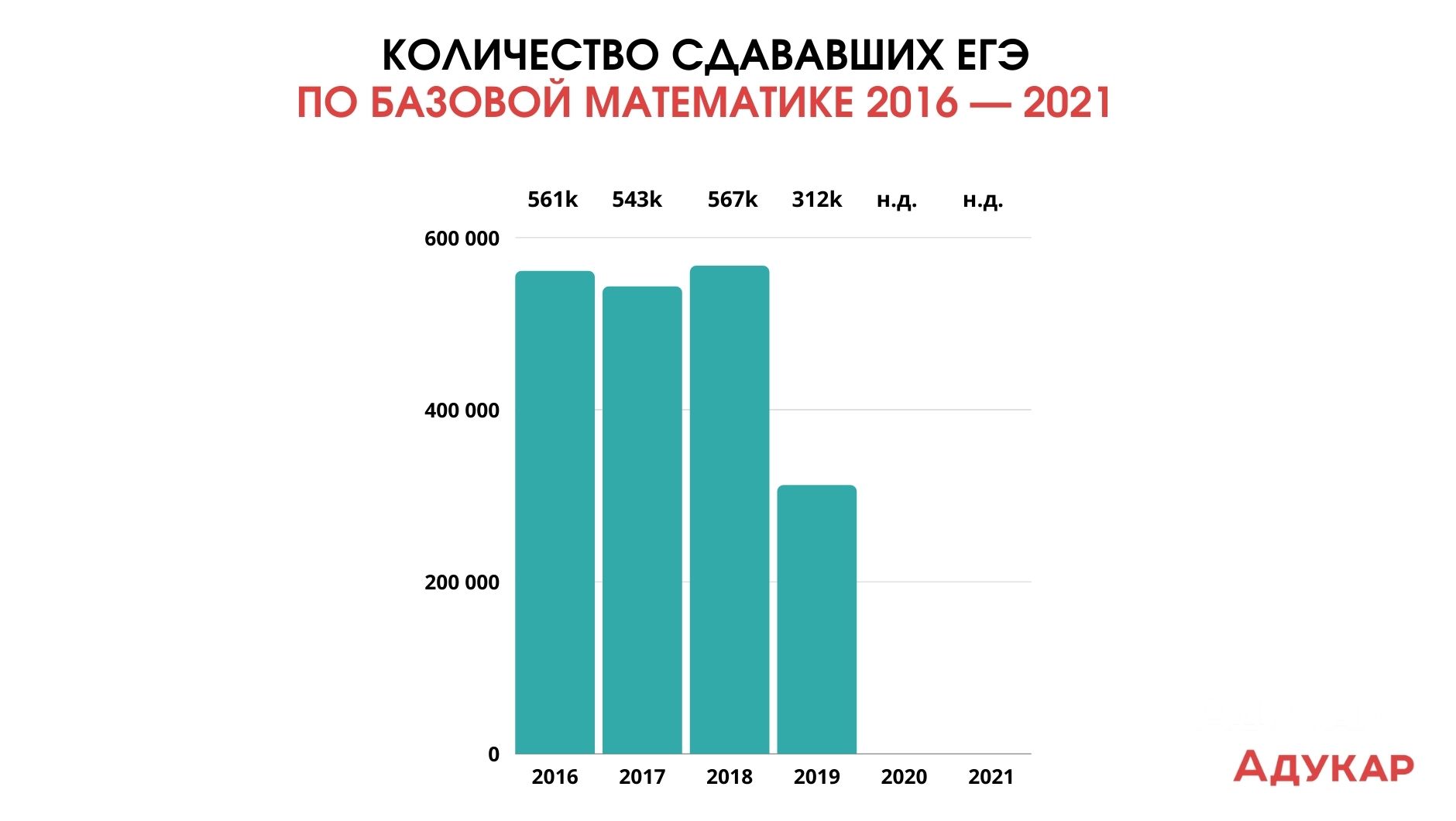
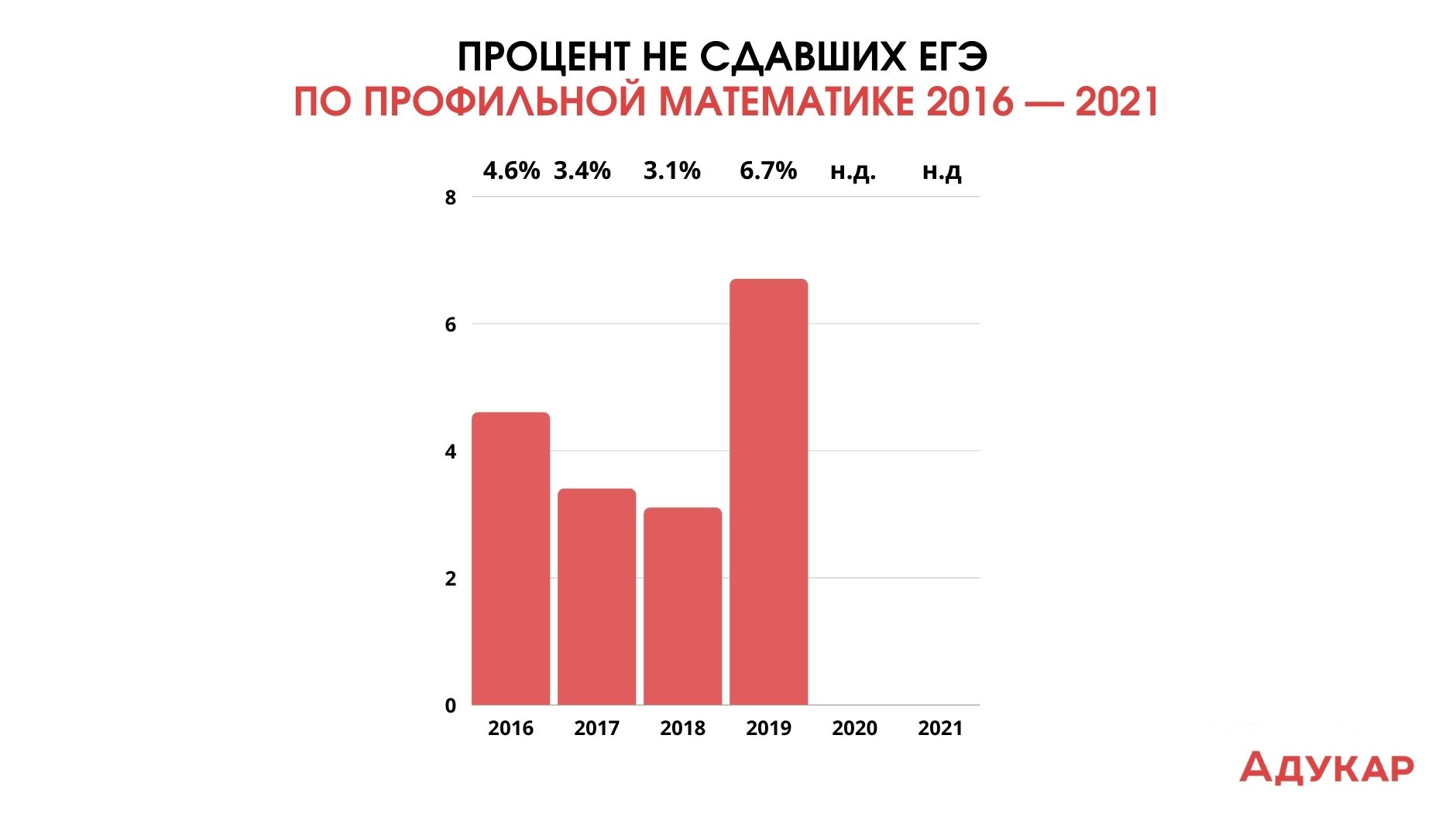
Средний результат ЕГЭ по базовой математике составил 4,15 баллов. А минимальный порог в 3 балла не преодолели 4,6% абитуриентов. Экзамен сдавали 561 000 человек. По сравнению с профилем стобалльников было больше: почти 18 000 абитуриентов.
ЕГЭ по математике в 2017 году
В 2017 году профильный ЕГЭ по математике сдавали почти 392 000 человек, а минимальный порог экзамена был 27 баллов, как и в 2016-м. Его не преодолели 14% участников экзамена. Средний результат ЕГЭ вырос до 47 баллов. Также в 2017-м по профильной математике было 4,5% высокобалльников, из них максимальных балл получили 224 человека.
Средний результат ЕГЭ по базовой математике в этом году составил 4%, при том, что экзамен сдавали 543 000 человек. Минимальный порог в 3 балла не преодолели 3,4% абитуриентов. Средний балл незначительно отличается от результата прошлого года — 4,24 (в 2016-м — 4,15).
ЕГЭ по математике в 2018 году
Спойлер: порог по профильной математике, как и ранее, остался на уровне 27 баллов. Его не преодолели 7% абитуриентов. Максимальный результат в 100 баллов получили 145 выпускников. Средний балл ЕГЭ подрос до почти до 50. При этом в экзамене участвовали 421 000 человек.
Средний балл ЕГЭ по базовой математике в 2018-м составил 4,29%, экзамен сдавали 567 000 человек (больше, чем годом ранее). Минимальный порог в 3 балла не преодолели 3,1% абитуриентов.
ЕГЭ по математике в 2019 году
В 2019-м профильную математику сдавали почти 363 000 студентов, 7% из них получили высокие баллы. Порог в 27 баллов не преодолели 6,7% учеников. В среднем ЕГЭ по математике сдали на 56,5 баллов.
Средний балл ЕГЭ по базовой математике в 2019-м составил 4,1. Сдавали его 312 000 выпускников. Порог был равен 3 баллам.
ЕГЭ по математике в 2020 году
В 2020-м году базовый экзамен по математике не проводился. Но профильный ЕГЭ был. В этом году количество выпускников, решивших сдавать математику стало меньше — 362 000. Средний балл ЕГЭ снизился до 54,2. 8,9% выпускников не смогли преодолеть минимальный порог баллов.
ЕГЭ по математике в 2021 году
В последнюю вступительную кампанию профильную математику сдавали 366 000 человек. Стобалльников было 504, высокобалльников — почти 31 000. Процент абитуриентов, которые не справились упал до 7,6%. В 2021-м средний балл по профильной математике был равен 55,1. Как и в 2020, базовая математика не проводилась.
Важные данные о ЕГЭ по математике за 2016−2021 года мы разместили в таблицах. Сохрани их, чтобы грамотно выстроить подготовку к ЕГЭ. Так ты сможешь ориентироваться по баллам, которые тебе нужны для поступления.
С каждым годом растёт минимальный порог по всем предметам. Значит надеяться на удачный случай ненадёжно. К тому же становится больше стобалльников. Конкуренция усиливается, но хорошо сдать математику реально. Если тебе хочется учить материалы и не листать скучный учебник, записывайся на бесплатное пробное занятие в Адукар.
Спасибо, что дочитал до конца. Мы рады, что были полезны. Чтобы получить больше информации, посмотри ещё:
Как успешно выбрать репетитора, чтобы сдать ЕГЭ
Как выбрать предметы ЕГЭ: 3 проверенные методики
Как написать сочинение-рассуждение на любую тему
Не пропускай важные новости и подписывайся на наш YouTube, ВК, Instagram, Telegram.
***
Если хотите разместить этот текст на своём сайте или в социальной сети, свяжись с нами по адресу info@adukar.by. Перепечатка материалов возможна только с письменного согласия редакции.
Хочешь быть в курсе новостей ЦТ?
Подписывайся на Адукар в соцсетях!
Начни подготовку к ЦТ и ЦЭ прямо сейчас!

Адукар обещает крутых преподавателей и много полезной практики.
итоговые занятия перед ЦТ? Такие занятия мы проводим уже четвёртый год, и преподаватели нашего учебного центра
научились достаточно точно предсказывать, какие вопросы будут на ЦТ. На этом занятии мы прорешаем их вместе с тобой!
Регистрируйся,
если еще не сделал этого — и увеличь свои шансы на поступление!
Автор: edu1
Методическая копилка —
Математика
АНАЛИЗ КИМ ЕГЭ
ПО МАТЕМАТИКЕ 2017
Учитель математики МБОУ СОШ № 6 г.Курчатова
Саркисова К.А.
Задание № 13 является наиболее доступным для школьников среди заданий с развёрнутым ответом. Большинство выпускников, взявшихся за решение этой задачи, проявили основные навыки решения тригонометрических уравнений. Ошибки допускались при преобразованиях тригонометрических выражений, записи решения тригонометрического уравнения простейшего вида, отборе корней, что свидетельствует о формальном, не содержательном уровне владения основными понятиями тригонометрии у многих выпускников. Следует отметить также большое количество описок и ошибок по невнимательности. Задание № 13 оказалось комбинированным уравнением, содержащим одновременно и тригонометрические, и логарифмические функции, и наряду с типичными ошибками тригонометрии нередко встречались ошибки при избавлении от логарифма.
Задание 15 проверяло умение решать неравенства. Типичные ошибки связаны с невнимательным чтением математической записи неравенства, непониманием алгоритма решения совокупностей и систем логарифмических неравенств. Очень много ошибок допущено участниками экзамена при решении дробно-рационального неравенства (забыт знаменатель). Следует отметить небрежность, которая была во многих работах, при изображении множеств на координатной прямой. При решении задания № 15 выпускники, как правило, проявляли базовые навыки преобразования сложных выражений и решения неравенств. Наиболее часто встречались ошибки при учёте ОДЗ, а также большое количество описок и ошибок в преобразовании выражений. Участники ЕГЭ зачастую упрощали дробное выражение нерациональным, громоздким способом, что приводило к увеличению количества таких ошибок.
Задание № 18 относится к задачам высокого уровня сложности. Тем не менее, значительное количество выпускников получили хотя бы один балл за эту задачу (Полные её решения были единичными). Наиболее часто встречаемые ошибки не учёт условия на правую часть после возведения уравнения в квадрат, не учёт случаев совпадения корней, описки и арифметические ошибки. Основной проблемой в решение этого задания оказалось применение графического метода решения, который, как показали работы участников экзамена, недостаточно сформирован при обучении математике – без объяснений и обоснований на координатной плоскости отмечаются какие-то графики, какие-то множества, и считывается множество значений параметра (иногда совпадающее с искомым). О недостаточной сформированности решения графическим методом свидетельствует и тот факт, что было много работ, в которых на координатной плоскости обозначено, в том числе верно, много объектов, а ответа на поставленный вопрос так и не последовало.
Достаточно успешно (по сравнению с предыдущим годом) выпускники справлялись с заданием № 17. Основные трудности вызвало построение математической модели, часто встречались также описки и арифметические ошибки.
Геометрические задания повышенного уровня. К заданиям повышенного уровня относились задания второй части 14 (стереометрия) и 16 (планиметрия) с развернутым ответом. Задания проверяли умения выполнять действия с геометрическими фигурами, координатами и векторами. Оба задания содержали два пункта. В первом пункте задание нужно доказать, а во втором пункте – вычислить.
В задаче № 14 причиной ошибкой является незнание определений стереометрических величин и способов их нахождения, незнание или неверное применение необходимых теорем стереометрии, неверное представление о стереометрической конфигурации в целом. Часто встречаются необоснованные утверждения, попытки угадать особенности стереометрической конфигурации.
Задание № 16, какпоказывает статистика проверки, – наиболее трудное, за его решение берётся небольшая часть выпускников, и лишь несколько процентов с ним справляются (хотя бы частично, причём полные, 3-балльные, решения этой задачи единичны). Это свидетельствует о том, что подавляющее большинство выпускников не обладает навыками решения сложных планиметрических задач. Проблемы вызывает как понимание и верное построение данной планиметрической конфигурации, так и незнание или неверное применение теорем. При попыткахрешения вопроса на доказательство (пункт а)) нередко встречается «логический круг» (доказываемое утверждение явно или неявно предполагается верным в начале доказательства).
Задание №19 имеет высокий уровень сложности, но процент успешных её решений (в том числе частичных) оказался достаточно большим. Тем не менее, полные или почти полные (3 и 4-балльные) решения этой задачи встречаются крайне редко. Большинство участников ЕГЭ, взявшихся за это задание, ограничиваются наиболее простой его частью – пунктом а) и/или б) и не приступают к выполнению пункта в), причём зачастую это оказывается по силам и для не очень сильного ученика. Это свидетельствует о достаточно сформированных логических навыках начального уровня, позволяющих найти решение хотя и в несложной, но нестандартной ситуации. С другой стороны, вопрос, требующий более глубокого логического анализа (пункт в)) оказывается доступен лишь немногим ученикам.Зачастую вызывало трудности понимание текстового условия задачи, и участники экзамена нередко искали ответ не на тот вопрос, который был поставлен, имея в виду неверную ситуацию. Также часто встречались описки и ошибки по невнимательности
Задание 19 проверяло умение строить и исследовать простейшие математические модели, умение осуществлять поиск решения, выбирая различные подходы из числа известных, модифицируя изученные методы решать уравнения и неравенства . Первый пункт выполнили те, кто прочитал условие, понял закономерности, попробовал исследовать несколько примеров, а потом обобщить полученный результат. Типичным заблуждением для многих оказалось, что на вопрос «Может ли?» нужно давать аргументированное решение, а не ответ «да» или «нет».
В целом результаты ЕГЭ по математике 2017 года показали положительную динамику в подготовке учеников по большинству разделов математики. Подавляющее большинство учащихся успешно справились с экзаменационными заданиями, и это свидетельствует о достаточном уровне и стабильном характере усвоения учащимися базовых знаний курса математики. В частности, можно считать достаточно сформированными у выпускников области можно считать навыки решения текстовых задач, задач по теории вероятностей, несложных задач по геометрии, несложных уравнений и неравенств. Наибольшие трудности у выпускников традиционно вызывают более сложные геометрические задачи, уравнения и неравенства, а также задачи, связанные с понятием производной. При этом навыки решения уравнений и неравенств имеют тенденцию к улучшению, но сложности с геометрией (особенно стереометрией) и применением производной сохраняются. Анализ решений этих задач выпускниками показывает, что определения и теоремы геометрии, техника преобразования выражений и решения уравнений и неравенств, понятие производной зачастую понимаются учениками формально, без знания их внутреннего смысла и границ применимости. В целом ЕГЭ по математике 2017 г. показал, что значительная часть выпускников осваивают курс математики средней (полной) школы, овладевают математическими компетенциями, необходимыми в обычной жизни и для продолжения образования по выбраннойспециальности. Выявленные проблемы преподавания математики в школе допускают возможность эффективного решения в среднесрочной перспективе.
Рекомендации для подготовки выпускников к ЕГЭ по математике на профильном уровне.
С целью существенного улучшения качества математической подготовки учащихся на профильном уровне в образовательных учреждениях области необходимо усилить системную работу.
1. Уделить особое внимание формированию у выпускников базовых математических знаний, умений и навыков. В первую очередь необходимо выработать у учащихся быстрое и правильное выполнение заданий части 1. При этом нужно использовать банк заданий экзамена базового уровня. Умения, необходимые для выполнения заданий базового уровня, должны быть под постоянным контролем.
2. Особое внимание уделять «проблемным» темам (в соответствии с итогами ЕГЭ—2017): составление математической модели, производная, стереометрия, нестандартные задачи.
3. По возможности — увеличить количество часов на изучение математики в старших классах с 5 до 8 часов.
4. Использовать дифференцированное обучение. С этой цели организовывать работу с разными категориями школьников, разработку и проведение элективных курсов по предмету, работу по индивидуальным планам обучения.
5. Выработать для каждого учащегося индивидуальную стратегию написания экзаменационной работы — от простого задания, которое выпускник способен выполнить, решить до сложного, для выполнения которого нужно больше времени. Выпускники должны знать структуру экзамена и оценивать свои возможности.
6. Необходимо детально знакомить учащихся с содержанием и структурой ЕГЭ по математике, тематикой экзаменационных задач (на примерах демонстрационного варианта и открытого банка заданий ЕГЭ). С этой целью в кабинетах математики должны быть информационные стенды с демоверсиями ЕГЭ, полезными адресами (ФИПИ, «Реши ЕГЭ», датами и сроками консультаций (индивидуальных, групповых) и др.).
7. Проводить регулярную диагностику готовности учащихся с помощью заданий, приближенных к КИМ ЕГЭ.
8. В записи решений к задачам с развернутым ответом нужно особое внимание обращать на построение чертежей и рисунков, лаконичность пояснений, доказательность рассуждений.
9. Использовать современную литературу и технические средства обучения.
10. Уделять внимание организационной и психологической подготовке учащихся к экзамену.