Задания помогут ученикам при подготовке к ЕГЭ
Скачать:
Предварительный просмотр:
Подписи к слайдам:
Слайд 2
Найдите квадрат расстояния между вершинами С и А 1 прямоугольного параллелепипеда, для которого АВ = 5 , AD = 4 , AA 1 = 3 . A A 1 B C D B 1 C 1 D 1 Ответ: 50 4 5 3 5
Слайд 3
A A 1 B C D B 1 C 1 D 1 Ответ: 5 5 4 3 4
Слайд 4
D A 1 A B C B 1 C 1 D 1 5 4 3 3 5 Ответ: 4 5
Слайд 5
1 1 1 A F E 1 1 120° 1 Ответ: 2
Слайд 6
1 1 O B E 1 1 Ответ: 2
Слайд 7
Ответ: 5
Слайд 8
1 1 2 Ответ: 2 Ответ: 60
Слайд 9
Ответ: 3 Найдите квадрат расстояния между вершинами D и C 2. Ответ: 5
Слайд 10
1 2 Ответ: 3
Слайд 11
1 1 2 Ответ: 14
Слайд 12
2 2 Ответ: 1
Слайд 13
2 Ответ: 6
Слайд 14
Ответ: 60
Слайд 15
О 3 5 Ответ: 4
Слайд 16
N 1 Ответ: 2
Слайд 17
6 4 О Ответ: 5
Слайд 18
5 30° О Ответ: 10
По теме: методические разработки, презентации и конспекты
- Мне нравится
1.
Новая Школа
Подготовка к ЕГЭ по математике 2019
2.
Стереометрия. Часть 1
Задание №8 и 14
3.
План занятия
❏
❏
❏
❏
Куб
Прямоугольный параллелепипед
Составные многогранники
Призма
4.
Куб
Куб – это прямоугольный параллелепипед, все
грани которого – равные квадраты.
5.
Куб
Если сфера вписана в куб (то есть касается всех
его граней), то ее радиус равен 0,5*a, где a –
ребро куба.
6.
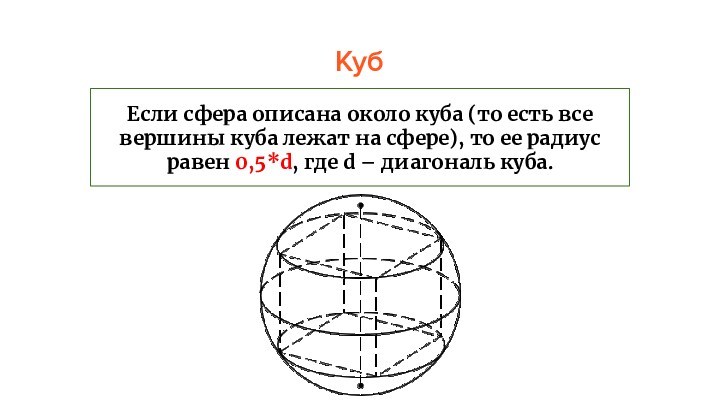
Куб
Если сфера описана около куба (то есть все
вершины куба лежат на сфере), то ее радиус
равен 0,5*d, где d – диагональ куба.
7.
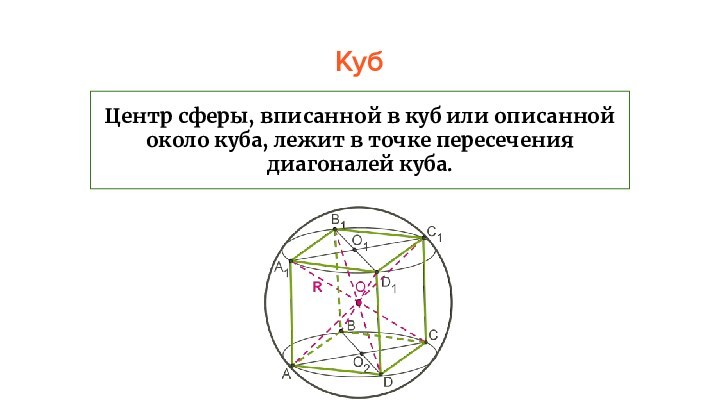
Куб
Центр сферы, вписанной в куб или описанной
около куба, лежит в точке пересечения
диагоналей куба.
8.
Задание №1
Площадь поверхности куба равна 18. Найдите его диагональ.
9.
Задание №2
Если каждое ребро куба увеличить на 1, то его площадь поверхности увеличится на 54. Найдите
ребро куба.
10.
Задание №3
11.
Задание №4
Куб описан около шара, объем которого равен 3π. Найдите объем куба.
12.
План занятия
❏
❏
❏
Куб
Прямоугольный параллелепипед
Составные многогранники
Призма
13.
Прямоугольный параллелепипед
Прямоугольный параллелепипед – это
параллелепипед, все грани которого являются
прямоугольниками.
14.
Прямоугольный параллелепипед
15.
Прямоугольный параллелепипед
16.
Задание №5
Объем прямоугольного параллелепипеда равен 24. Одно из его ребер равно 3. Найдите площадь
грани параллелепипеда, перпендикулярной этому ребру.
17.
Задание №6
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 3. Объем
параллелепипеда равен 36. Найдите его диагональ.
18.
Задание №7
19.
Задание №8
20.
Задание №9
21.
Задание №10
Объем первого прямоугольного параллелепипеда равен 105. Найдите объем второго
прямоугольного параллелепипеда, если известно, что высота первого параллелепипеда в 7 раз
больше высоты второго, ширина второго в 2 раза больше ширины первого, а длина первого в 3
раза больше длины второго.
22.
План занятия
❏
❏
Куб
Прямоугольный параллелепипед
Составные многогранники
Призма
23.
Задание №11
24.
Задание №12
25.
Задание №13
26.
Задание №14
27.
Задание №15
28.
Задание №16
29.
План занятия
❏
Куб
Прямоугольный параллелепипед
Составные многогранники
Призма
30.
Призма
В основании призмы лежат многоугольники.
Боковые грани представляют собой
параллелограммы. Высота призмы –
перпендикуляр, опущенный из вершины
одного основания к плоскости другого
основания.
31.
Призма
Площадь боковой поверхности – сумма
площадей ее боковых граней.
Площадь полной поверхности – сумма
площади боковой поверхности и площадей
оснований.
32.
Прямая призма
Призма называется прямой, если ее боковые
ребра перпендикулярны основаниям.
33.
Правильная призма
Призма называется правильной, если она
прямая и ее основания – правильные
многоугольники.
34.
Задание №17
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8,
высота призмы равна 10. Найдите площадь ее поверхности.
35.
Задание №18
Через среднюю линию основания треугольной призмы, объем которой равен 32, проведена
плоскость, параллельная боковому ребру. Найдите объем отсеченной треугольной призмы.
36.
Задание №19
37.
Задание №20
38.
Задание №21
39.
План занятия
Куб
Прямоугольный параллелепипед
Составные многогранники
Призма
40.
Спасибо за
внимание
Слайд 1Мастер-класс по теме: «Решение и оформление стереометрических задач профильного уровня при
подготовке к ГИА по математике в 11 классе»
Выполнила Позднышева С.В. ,учитель математики специализированной школы №11.
Г. Свердловск

Слайд 2При подготовке к сдаче ГИА и ЕГЭ учащиеся стараются проигнорировать задания
по геометрии, считая их сложными. Это говорит о том , что они слабо владеют изученным материалом, недостаточно развитым пространственным мышлением и способами изображения стереометрических фигур, ведь они не знакомы с таким предметом как черчение.
Все это ставит перед учителем математики сложную задачу: за короткое время постараться повторить с учащимися достаточно большой объем материала, среди которого и формулы, и теоремы для обоснования рисунка и решения задачи, научить правильно изображать геометрические фигуры , используя свойства параллельного проектирования, так чтобы рисунок был наглядным и мог бы действительно помочь в решении задачи.
Кроме этого учитель имеет как минимум три различных подхода к подготовке учащихся к экзаменам:
— Коллективное решение задачи на уроке;
— Самостоятельное решение задачи учащимися;
— Перед тем как предложить решать задачу самостоятельно, рассмотреть отдельные ее части, чтобы учащиеся, начав самостоятельные действия, не оказались в ситуации, когда они ничего не помнят и не представляют как приступить к ее решению

Слайд 3 При решении задач очень важно изобразить хороший чертеж. Для этого
используют свойства параллельного проектирования, которое сохраняет параллельность и отношение отрезков параллельных или совпадающих прямых.

Слайд 4Свойства параллельного проектирования при построении стереометрического чертежа
Внимание! При параллельном проектирование не
сохраняются ни углы, ни длины отрезков, ни отношения длин неколлинеарных отрезков (то есть отрезков, которые не лежат на параллельных прямых, или на одной прямой). Поэтому глядя на изображение проекции мы не можем определить соотношение отрезков и углов.
При изображении стандартных геометрических тел на плоскости нужно следить за тем, чтобы ребра и диагонали были все видны и не накладывались друг на друга.
В общем случае удобно строить в такой последовательности.
1. Начинаем с основания фигуры.
Если в основании треугольник, то вне зависимости от вида треугольника рисуем тупоугольный не равнобедренный треугольник,

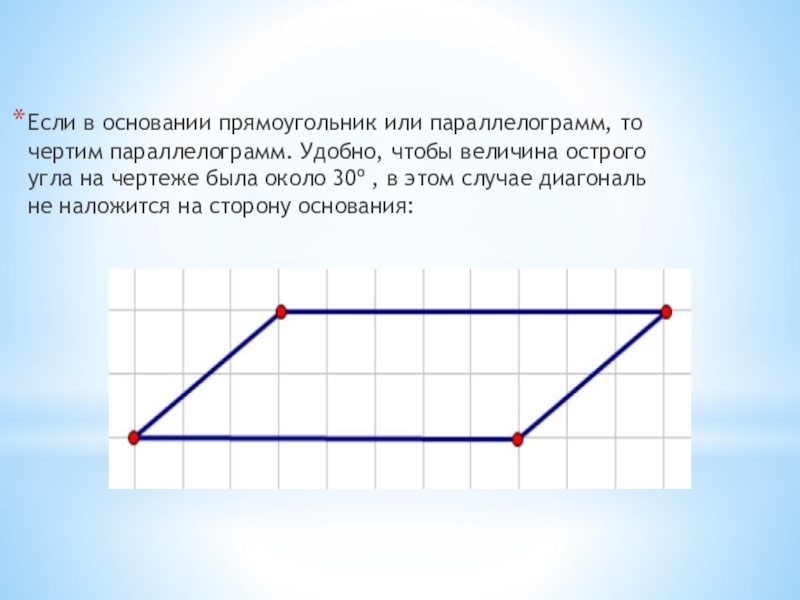
Слайд 6Если в основании прямоугольник или параллелограмм, то чертим параллелограмм. Удобно, чтобы
величина острого угла на чертеже была около 30º , в этом случае диагональ не наложится на сторону основания:
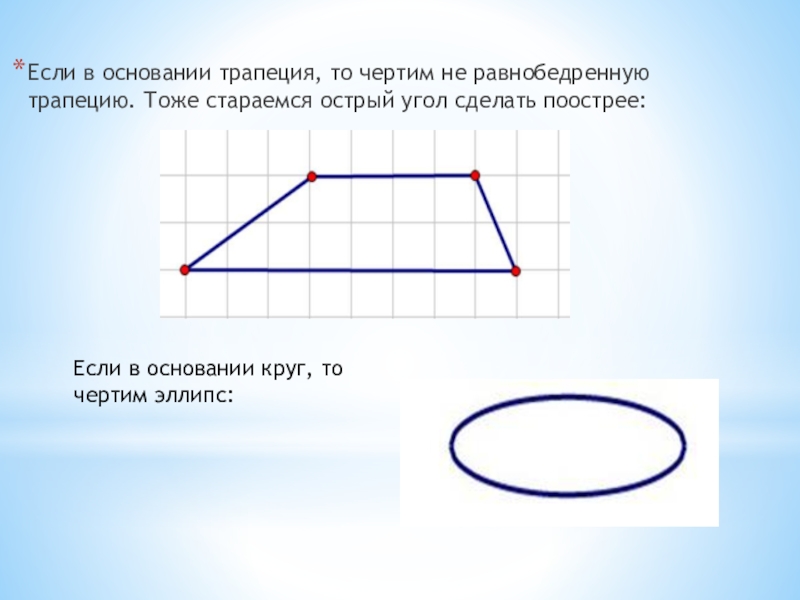
Слайд 7Если в основании трапеция, то чертим не равнобедренную трапецию. Тоже стараемся
острый угол сделать поострее:
Если в основании круг, то чертим эллипс:
Слайд 8Если в основании правильный шестиугольник, то чертим проекцию правильного шестиугольника. Следим
за тем, чтобы противоположные стороны шестиугольника были параллельны. Построение проекции правильного шестиугольника, как правило, вызывает наибольшие трудности. Поэтому если в вашем распоряжении есть листок в клеточку, то удобно строить по такому образцу:

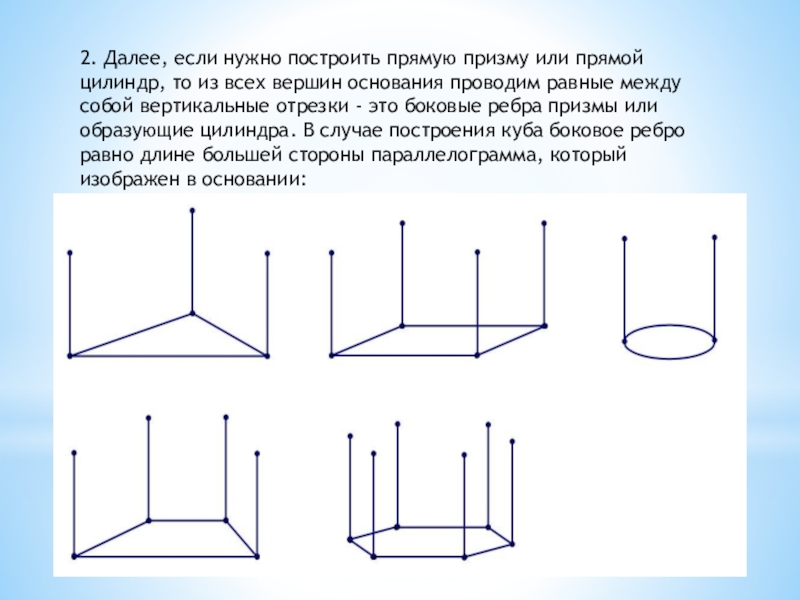
Слайд 92. Далее, если нужно построить прямую призму или прямой цилиндр, то
из всех вершин основания проводим равные между собой вертикальные отрезки — это боковые ребра призмы или образующие цилиндра. В случае построения куба боковое ребро равно длине большей стороны параллелограмма, который изображен в основании:
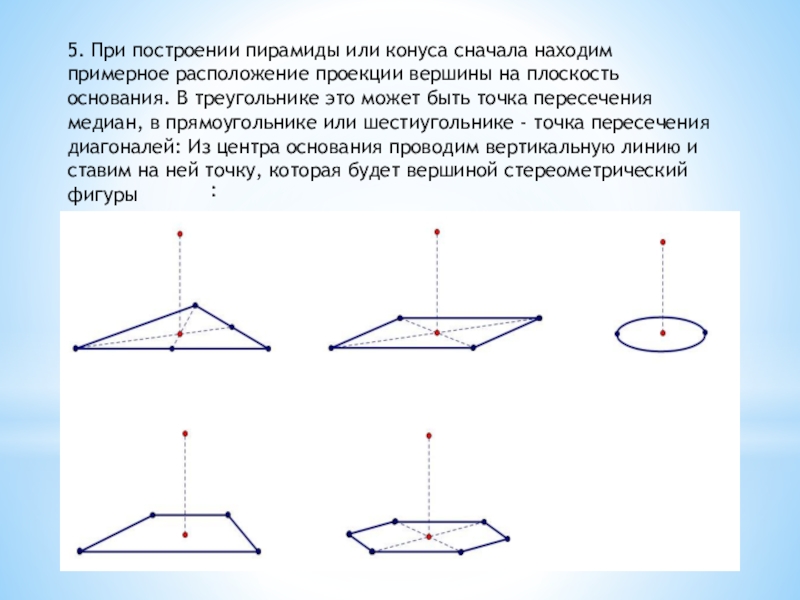
Слайд 125. При построении пирамиды или конуса сначала находим примерное расположение проекции
вершины на плоскость основания. В треугольнике это может быть точка пересечения медиан, в прямоугольнике или шестиугольнике — точка пересечения диагоналей: Из центра основания проводим вертикальную линию и ставим на ней точку, которая будет вершиной стереометрический фигуры
:
Слайд 13:
Соединяем вершину стереометрической фигуры с вершинами основания:
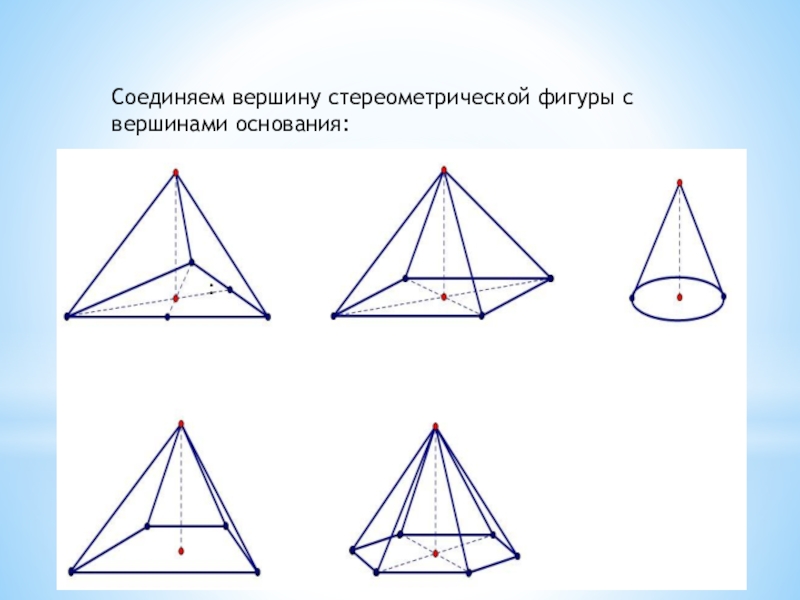
Слайд 14Приведем примеры удачных и неудачных чертежей.
Мы рисуем чертеж крупным, чтобы на нем всё было
хорошо видно. Не стоит, как «лучший в мире рисовальщик петухов» Карлсон, изображать крошечного одинокого петушка (или малюсенький кубик) в углу тетради.
Видимые линии изображаем сплошными, невидимые —пунктирными. Если вы решаете задачу векторно-координатным методом, ставьте рядом с точками их координаты. Это удобно.
Иногда одного чертежа недостаточно. Чаще всего для решения задач по стереометрии, кроме «объемного» чертежа, нужен один или несколько плоских.

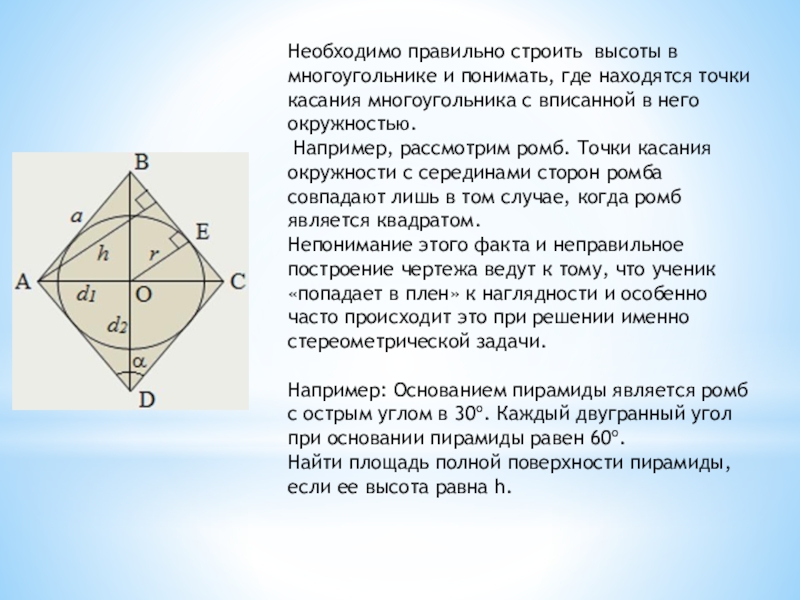
Слайд 17Необходимо правильно строить высоты в многоугольнике и понимать, где находятся точки
касания многоугольника с вписанной в него окружностью.
Например, рассмотрим ромб. Точки касания окружности с серединами сторон ромба совпадают лишь в том случае, когда ромб является квадратом.
Непонимание этого факта и неправильное построение чертежа ведут к тому, что ученик «попадает в плен» к наглядности и особенно часто происходит это при решении именно стереометрической задачи.
Например: Основанием пирамиды является ромб с острым углом в 30º. Каждый двугранный угол при основании пирамиды равен 60º.
Найти площадь полной поверхности пирамиды, если ее высота равна h.
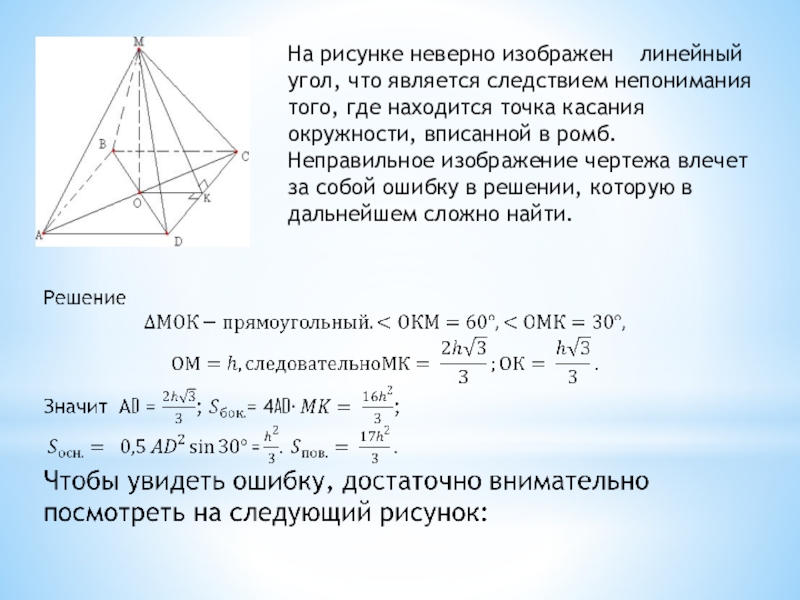
Слайд 18На рисунке неверно изображен линейный угол, что является следствием непонимания
того, где находится точка касания окружности, вписанной в ромб. Неправильное изображение чертежа влечет за собой ошибку в решении, которую в дальнейшем сложно найти.
Слайд 20Теорема о трех перпендикулярах
Имеем плоскость α . В плоскости α лежит
прямая b.
АН – перпендикуляр к плоскости α, АМ – наклонная,
МН — проекция наклонной АМ на плоскость α.
По теореме о трех перпендикулярах, наклонная перпендикулярна к прямой b тогда и только тогда, когда ее проекция перпендикулярна к прямой b.
В теореме идет речь трех перпендикулярах. Укажем их:
АH – это перпендикуляр к плоскости α, а значит, к прямой b.
HМ – проекция, перпендикуляр к прямой b.
АМ – наклонная, перпендикуляр к прямой b.

Слайд 22Чтобы легко справиться с решением задач на шар, вписанный в пирамиду,
полезно разобрать небольшой теоретический материал.
Шар вписан в пирамиду (или сфера вписана в пирамиду) — значит, шар (сфера) касаются каждой грани пирамиды. Плоскости, содержащие грани пирамиды, являются касательными плоскостями шара. Отрезки, соединяющие центр шара с точками касания, перпендикуляры к касательным плоскостям. Их длины равны радиусу шара. Центр вписанного в пирамиду шара — точка пересечения биссекторных плоскостей двугранных углов при основании (то есть плоскостей, делящих эти углы пополам).
Чаще всего в задачах речь идет о шаре, вписанном в правильную пирамиду. Шар можно вписать в любую правильную пирамиду. Центр шара в этом случае лежит на высоте пирамиды. При решении задачи удобно провести сечение пирамиды и шара плоскостью, проходящей через апофему и высоту пирамиды. Если пирамида четырехугольная или шестиугольная, сечение представляет собой равнобедренный треугольник, боковые стороны которого — апофемы, а основание — диаметр вписанной в основание окружности.

Задачи по стереометрии нужно не только уметь решать, но и грамотно оформлять. В данной работе задачи по стереометрии содержат подробные пояснения к решениям и чертежи. Решения, не являются единственно верными для конкретных задач, ведь многие типы задач по стереометрии имеют не один алгоритм решения. Этим они и интересны.
©
Бочкарева Наталья Анатольевна
Бочкарева Наталья Анатольевна
Понравилось? Сохраните и поделитесь:
Неограниченная бесплатная загрука материала «Стереометрия в задачах ЕГЭ» доступна всем пользователям. Разработка находится в разделе «Мастер-класс».
Загрузка началась…
Понравился сайт? Получайте ссылки
на лучшие материалы еженедельно!
Подарок каждому подписчику!
В презентации разбираются решения трех задач на вычисление расстояний между элементами пирамид. Работу можно использовать при подготовке к экзаменам.
Зад.ЕГЭпостереом.проф.ур.ч1.ppt
Заданий ЕГЭ по стереометрии профильного уровня (1 часть)
Заданий ЕГЭ по стереометрии профильного уровня
(1 часть)
В правильной треугольной пирамиде сторона основания равна 4, а боковое ребро равно 3
В правильной треугольной пирамиде сторона основания равна 4, а боковое ребро равно 3. Найдите расстояние от стороны основания до противоположного бокового ребра.
Задача №1
А
С
В
S
O
D
E
3
4
S В С А D 13 5 9 K В основании треугольной пирамиды
S
В
С
А
D
13
5
9
K
В основании треугольной пирамиды SABC лежит прямоугольный треугольник с прямым углом при вершине С, гипотенузой АВ = 13 и катетом ВС = 5. Найдите расстояние между ребрами AS и ВС, если длина высоты SB равна 9.
Задача №2
В основании треугольной пирамиды
В основании треугольной пирамиды SABC лежит прямоугольный треугольник с катетом ВС = 3 и гипотенузой АС = 5. Расстояние между ребрами SA и ВС равно 3. Найдите длину ребра SA, если вершина пирамиды проектируется в середину ребра АВ.
Задача №3
А
С
В
S
D
E
3
5
3
Материалы на данной страницы взяты из открытых истончиков либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.
Введите ваш emailВаш email
Единый государственный экзамен (ЕГЭ) в 11-м классе не только осуществл яю т контроль за качеством обучения школьников, полученными ими знаниями, выработанными умениями и навыками, сформированными компетенциями. Содержание и форма проведения этих экзамен ов зада ю т ориентиры всего математического образования, влияют на отбор содержания, выбор форм и методов обучения. Поэтому так важно, чтобы содержание ЕГЭ соответствовало целям и задачам математического образования школьников.
О собенности геометрических задач, отбираемых для включения в ЕГЭ по математике.
Повышение роли наглядности. К каждой задаче предполагается да вать рисунок, позволяющий лучше понять условие, представить соответствующую геометрическую ситуацию, наметить план решения, при необходимости провести дополнительные построения и вычисления.
Повышение роли конструктивных умений учащихся. Включение задач, в которых требуется не только выполнить вычисления, но и провести построения (изображения) искомых геометрических фигур.
Повышение роли геометрических задач с практической направленностью. Нахождение расстояний до недоступных объектов, величин углов, объемов и площадей поверхностей реальных предметов и др.
Традиционно геометрические задачи подразделяются на :
— задачи на вычисление (углов, длин, площадей);
— задачи на доказательство ;
— задачи на построение .
Каждый из этих типов задач выполняет важную функцию и способствует достижению результатов обучени я .
В ЕГЭ должны быть, в той или иной мере, представлены геометрические задачи всех этих типов .
Углы
Помимо планиметрических задач на нахождение углов, примеры которых рассмотрены в презентации для ГИА, в этот раздел ЕГЭ включены задачи на нахождение углов в пространстве.
1. В кубе A … D 1 найдите угол между прямыми AA 1 и BC .
Ответ. 90 о .
2. В кубе A … D 1 найдите угол между прямыми AA 1 и BC 1 .
Ответ. 45 о .
3. В кубе A … D 1 найдите угол между прямыми AB 1 и CD 1 .
Ответ. 90 о .
4. В кубе A … D 1 найдите угол между прямыми AB 1 и BC 1 .
Ответ. 60 о .
5. В правильной треугольной призме ABCA 1 B 1 C 1 , все ребра которой равны 1, найдите угол между прямыми AA 1 и BC 1 .
Ответ. 45 о .
6. В правильной треугольной призме ABCA 1 B 1 C 1 , все ребра которой равны 1, найдите угол между прямыми AB и A 1 C 1 .
Ответ. 60 о .
7. В правильной четырехугольной пирамиде SABCD , все ребра которой равны 1, найдите угол между прямыми SA и BC .
Ответ. 60 о .
8. В правильной шестиугольной призме A … F 1 , все ребра которой равны 1, найдите угол между прямыми AA 1 и BC 1 .
Ответ. 45 о .
9. В правильной шестиугольной призме A … F 1 , все ребра которой равны 1, найдите угол между прямыми AB и C 1 D 1 .
Ответ. 60 о .
10. В правильной шестиугольной призме A … F 1 , все ребра которой равны 1, найдите угол между прямыми AB и C 1 D 1 .
Ответ. 30 о .
Длины
Помимо планиметрических задач на нахождение длин, примеры которых рассмотрены в презентации для ГИА, в этот раздел ЕГЭ включены задачи на нахождение расстояний в пространстве.
1. Найдите диагональ куба, все ребра которого равны .
Ответ. 3.
2. Найдите квадрат расстояния между вершинами B и D 1 прямоугольного параллелепипеда, для которого AB = 5, AD = 4, AA 1 = 3.
Ответ. 50.
3. В правильном тетраэдре ABCD , ребра которого равны 1, найдите квадрат расстояния между серединами противоположных ребер AB и CD .
Ответ. 0,5.
4. В правильной шестиугольной призме A … F 1 , все ребра которой равны 1, найдите квадрат расстояния между точками A и С 1 .
Ответ. 4.
5. Найдите квадрат расстояния между противоположными вершинами октаэдра, ребра которого равны 1.
Ответ. 2.
6. Найдите квадрат расстояния между вершинами A и C 1 многогранника, изображенного на рисунке, все двугранные углы которого прямые.
Ответ. 19.
7. Найдите квадрат расстояния между вершинами A и C 2 многогранника, изображенного на рисунке, все двугранные углы которого прямые.
Ответ. 14.
8. Найдите квадрат расстояния между вершинами A и C 3 многогранника, изображенного на рисунке, все двугранные углы которого прямые.
Ответ. 17.
9. Найдите квадрат расстояния между вершинами A и D 3 многогранника, изображенного на рисунке, все двугранные углы которого прямые.
Ответ. 14.
10. Найдите расстояние от вершины B до прямой C 1 D 1 прямоугольного параллелепипеда, для которого AB = 5, AD = 4, AA 1 = 3.
Ответ. 5.
11. В правильной шестиугольной призме A … F 1 , все ребра которой равны 1, найдите квадрат расстояния от точки B до прямой A 1 E 1 .
Ответ. 2.
12. Найдите квадрат расстояния от вершины A до прямой CC 1 многогранника, изображенного на рисунке, все двугранные углы которого прямые.
Ответ. 18.
Площади
Помимо планиметрических задач на нахождение площадей, примеры которых рассмотрены в презентации для ГИА, в этот раздел ЕГЭ включены задачи на нахождение площадей сечений пространственных фигур.
1. Найдите площадь сечения, проходящего через вершины A , B и С 1 прямоугольного параллелепипеда ABCDA 1 B 1 C 1 D 1 , для которого AB = 5, AD = 4, AA 1 = 3.
Ответ. 25.
2. Найдите площадь сечения, проходящего через середины ребер AA 1 , BB 1 и B 1 C 1 прямоугольного параллелепипеда ABCDA 1 B 1 C 1 D 1 , для которого AB = 4, AD = 4, AA 1 = 3.
Ответ. 10.
3. Ребра правильной четырехугольной пирамиды SABCD равны 1. Найдите площадь сечения, проходящего через вершины A , C и S .
Ответ. 0,5.
4. Ребра правильной четырехугольной пирамиды SABCD равны 1. Найдите площадь сечения, проходящего через середины ребер SA , SB и SC .
Ответ. 0,25.
5. Ребра тетраэдра равны 1. Найдите площадь сечения, проходящего через середины четырех его ребер.
Ответ. 0,25.
6. Найдите площадь сечения, проходящего через середины ребер AB , BC и A 1 B 1 правильной треугольной призмы ABCA 1 B 1 C 1 , все ребра которой равны 1.
Ответ. 0,5.
7. Найдите площадь сечения, проходящего через вершины A , D и D 1 правильной шестиугольной призмы ABCDEFA 1 B 1 C 1 D 1 E 1 F 1 , все ребра которой равны 1.
Ответ. 2.
8. Найдите площадь осевого сечения конуса, радиус основания и высота которого равны 2.
Ответ. 4.
9. Найдите площадь S сечения, проходящего через вершины A , B и C 1 многогранника, изображенного на рисунке, все двугранные углы которого прямые. В ответе укажите .
Ответ. 10.
10. Найдите площадь S сечения, проходящего через середины ребер AD , BC и B 1 C 1 многогранника, изображенного на рисунке, все двугранные углы которого прямые.
Ответ. 3.
Объемы
Здесь предлагаются примеры задач на нахождение объемов и площадей поверхностей пространственных фигур.
О ни проверя ю т развитие пространственных представлений учащихся, умения проводить построения в пространстве, находить объемы и площади поверхностей многогранников, круглых тел и их комбинаций.
Для успешного решения эт их зада ч требуются знания основных формул для нахождения значений геометрических величин пространственных фигур; умения проводить дополнительные построения на изображениях пространственных фигур, работать с формулами, выполнять преобразования и производить действия с числовыми выражениями в процессе решения задачи.
1. Диагональ куба равна . Найдите его объем.
Решение. Если ребро куба равно a , то его диагональ равна . Отсюда следует, что если диагональ куба равна , то его ребро равно 2 и, значит, объем этого куба равен 8.
Ответ. 8.
2. Через среднюю линию основания треугольной призмы, объем которой равен 32, проведена плоскость, параллельная боковому ребру. Найдите объем отсеченной треугольной призмы.
Решение. Площадь основания отсеченной призмы равна четверти площади основания исходной призмы. Высота отсеченной призмы равна высоте исходной призмы. Следовательно, объем отсеченной призмы равен четверти объема исходной призмы, т.е. равен 8.
Ответ. 8.
3. Во сколько раз увеличится объем правильного тетраэдра, если все его ребра увеличить в два раза?
Решение. Воспользуемся тем, что если два тетраэдра подобны и коэффициент подобия равен k , то отношение объемов этих тетраэдров равно k 3 . Если ребра тетраэдра увеличить в два раза, то объем тетраэдра увеличится в 8 раз.
Ответ. 8.
4. Найдите площадь поверхности многогранника, изображенного на рисунке, все двугранные углы которого прямые.
Решение. Поверхность многогранника состоит из двух квадратов площад и 4, четырех прямоугольников площад и 2 и двух невыпуклых шестиугольников площад и 3. Следовательно, площадь поверхности многогранника равна 22.
Ответ. 22.
5. Найдите объем многогранника, изображенного на рисунке, все двугранные углы которого прямые.
Решение 1. М ногогранник состоит из двух прямоугольных параллелепипедов , объемы которых равн ы 2 и 4 . Следовательно, объем многогранника рав ен 6 .
Решение 2. М ногогранник получается из куба, объем которого равен 8, вырезанием прямоугольного параллелепипеда, объем которого равен 2. Следовательно, объем многогранника рав ен 6 .
Ответ. 6.
6. Найдите площадь поверхности многогранника, изображенного на рисунке, все двугранные углы которого прямые.
Решение. Поверхность многогранника состоит из двух квадратов площад и 16 , прямоугольника площади 12, трех прямоугольников площади 4 , двух прямоугольников площади 8, и двух невыпуклых восьми угольников площад и 10 . Следовательно, площадь поверхности многогранника равна 92 .
Ответ. 92.
7. Найдите объем многогранника, изображенного на рисунке, все двугранные углы которого прямые.
Решение. М ногогранник получается из прямоугольного параллелепипеда, объем которого равен 48, вырезанием прямоугольного параллелепипеда, объем которого равен 8. Следовательно, объем многогранника рав ен 40 .
Ответ. 48.
8. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Решение. Поверхность многогранника состоит из квадрат а площад и 9 , семи прямоугольников площади которых равны 3, и двух невыпуклых восьми угольников площад и которых равны 4 . Следовательно, площадь поверхности многогранника равна 38 .
Ответ. 38.
9. Найдите объем многогранника, изображенного на рисунке, все двугранные углы которого прямые.
Решение. М ногогранник составлен из двух прямоугольных параллелепипедов, объемы которых равны 9 и 1. Следовательно, объем многогранника рав ен 10 .
Ответ. 10.
10. Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите .
Ответ. 0,5.
11. Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите .
Ответ. 1,5.
12. Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите .
Ответ. 1,5.
13. Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите .
Ответ. 9.
14. Найдите объем V части конуса , изображенной на рисунке. В ответе укажите .
Ответ. 1.
15. В цилиндрический сосуд, в котором находится 6 дм 3 воды, опущена деталь. При этом уровень жидкости в сосуде поднялся в 1,5 раза. Чему равен объем детали?
Решение. Так как уровень жидкости в сосуде поднялся в 1,5 раза, то и объем увеличился в 1,5 раза, т.е. стал равен 9 дм 3 . Следовательно, объем детали равен 3 дм 3 .
Ответ. 3.
16. В цилиндрическом сосуде уровень жидкости достигает 18 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй сосуд, диаметр которого в 3 раза больше первого?
Ответ. 2 см.
17. Радиусы двух шаров равны 6 и 8. Найдите радиус шара, площадь поверхности которого равна сумме площадей их поверхностей.
Решение. Площади поверхностей данных шаров равны и . Их сумма равна . Следовательно, радиус шара, площадь поверхности которого равна этой сумме, равен 10.
Ответ. 10.
18. Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 2. Найдите объем параллелепипеда.
Решение. Ребра параллелепипеда равны 4, 4, 2 и, следовательно, его объем равен 32.
Ответ. 32.
19. В куб с ребром 6 вписан шар. Найдите объем шара, деленный на .
Решение. Радиус шара равен 3. Объем шара равен 36 , а объем, деленный на равен 36.
Ответ. 36.
Расстояния
Здесь предлагаются примеры задач повышенной трудности на нахождение расстояний в пространстве, относящихся к профильной части Единого государственного экзамена по математике.
В режиме слайдов ответ появляется после кликанья мышкой.
1. В единичном кубе A … D 1 найдите расстояние от точки A до прям ой B 1 D 1 .
В режиме слайдов ответ появляется после кликанья мышкой.
Решение: Искомое расстояние равно высоте AE равностороннего треугольника AB 1 D 1 . Имеем, AB 1 = AD 1 = B 1 D 1 = .
Следовательно, AE =
Ответ:
60
2. В единичном кубе A … D 1 найдите расстояние от точки A до прям ой BD 1 .
Решение: Искомое расстояние равно высоте AE прямоугольного треугольника ABD 1 . Имеем, AB = 1, AD 1 = , BD 1 = .
Следовательно, AE = .
В режиме слайдов ответ появляется после кликанья мышкой.
Ответ:
3. В правильной пирамиде SABCD , все ребра которой равны 1, н айдите расстояние от вершины A до прямой SC .
В режиме слайдов ответ появляется после кликанья мышкой.
Решение. Треугольник SAC прямоугольный. Искомое расстояние равно катету SA и равно 1.
Ответ: 1.
4. В правильной пирамиде SABCD , боковые ребра которой равны 2, а ребра основания – 1, н айдите расстояние от точки A до прямой SD .
В режиме слайдов ответ появляется после кликанья мышкой.
Решение. Искомое расстояние равно высоте AH равностороннего треугольника SAD. Оно равно
Ответ:
5. В правильной треугольной призме ABCA 1 B 1 C 1 , все ребра которой равны 1, найдите расстояние от точки A до прям ой B 1 C 1 .
Решение: Искомое расстояние равно высоте AD равнобедренного треугольника AB 1 C 1 . Имеем,
B 1 C 1 = 1; AB 1 = AC 1 = .
Следовательно, AD =
Ответ:
6. В правильной треугольной призме ABCA 1 B 1 C 1 , все ребра которой равны 1, найдите расстояние от точки A до прям ой BC 1 .
Решение: Искомое расстояние равно высоте AD равнобедренного треугольника ABC 1 . Имеем,
AB = 1; AC 1 = BC 1 = .
Следовательно, AD =
Ответ:
7. В правильной 6-й призме A … F 1 , ребра которой равны 1, найдите расстояние от точки A до прям ой D 1 E 1 .
Решение: Искомым расстоянием является длина отрезка AE 1 . В прямоугольном треугольнике AEE 1 имеем: EE 1 = 1, AE = . Следовательно, AE 1 = 2.
Ответ: 2.
8. В правильной 6-й призме A … F 1 , ребра которой равны 1, найдите расстояние от точки A до прям ой B 1 C 1 .
Решение: Достроим призму, присоединив к ней правильную треугольную призму ABGA 1 B 1 G 1 . Искомым расстоянием является длина отрезка AH 1 , где H 1 – середина ребра B 1 G 1 . В прямоугольном треугольнике AHH 1 имеем: HH 1 = 1, AH = Следовательно, AH 1 =
Ответ:
9. В правильной 6-й призме A … F 1 , ребра которой равны 1, найдите расстояние от точки A до прям ой BE 1 .
Решение: Искомое расстояние равно высоте AH прямоугольного треугольника ABE 1 , в котором AB = 1, AE 1 = 2, BE 1 =
Из подобия треугольников ABE 1 и BHA находим AH =
Ответ:
10. В единичном кубе A … D 1 найдите расстояние между прямыми AA 1 и BD 1 .
В режиме слайдов ответ появляется после кликанья мышкой.
Решение. Пусть P , Q – середины AA 1 , BD 1 . Искомым расстоянием является длина отрезка PQ . Она равна
Ответ:
11. В правильном тетраэдре ABCD н айдите расстояние между прямыми AD и BC .
Решение. Искомое расстояние равно длине отрезка EF , где E , F – середины ребер AD , GF . В треугольнике DAG DA = 1,
В режиме слайдов ответ появляется после кликанья мышкой.
AG = DG = Следовательно, EF =
Ответ:
12. В правильной пирамиде SABCD , все ребра которой равны 1, н айдите расстояние между прямыми SA и BD .
В режиме слайдов ответ появляется после кликанья мышкой.
Решение. Искомое расстояние равно высоте OH треугольника SAO , где O – середина BD . В прямоугольном треугольнике SAO
имеем: SA = 1, AO = SO = Следовательно, OH =
Ответ:
13. В правильной пирамиде SABCD , все ребра которой равны 1, н айдите расстояние между прямыми SA и BC .
Решение. Плоскость SAD параллельна прямой BC . Следовательно, искомое расстояние равно расстоянию между прямой BC и плоскостью SAD . Оно равно высоте EH треугольника SEF , где E , F – середины ребер BC , AD . В треугольнике SEF имеем:
EF = 1, SE = SF = Высота SO равна
Следовательно, EH =
В режиме слайдов ответ появляется после кликанья мышкой.
Ответ:
14. В правильной треугольной призме ABCA 1 B 1 C 1 , все ребра которой равны 1, найдите расстояние между прямыми: AA 1 и BC 1 .
Ответ:
15. В правильной треугольной призме ABCA 1 B 1 C 1 , все ребра которой равны 1, найдите расстояние между прямыми: AB и A 1 C .
Решение: Искомое расстояние равно расстоянию между прямой AB и плоскостью A 1 B 1 C . Обозначим D и D 1 середины ребер AB и A 1 B 1 . В прямоугольном треугольнике CDD 1 из вершины D проведем высоту DE. Она и будет искомым расстоянием.
Имеем, DD 1 = 1, CD = , CD 1 = .
Следовательно, DE =
Ответ:
16. В правильной 6-й призме A … F 1 , ребра которой равны 1, найдите расстояние между прямыми: AB и C 1 D 1 .
Ответ: 1.
17. В правильной 6-й призме A … F 1 , ребра которой равны 1, найдите расстояние между прямыми: AA 1 и C 1 D 1 .
Решение: Искомым общим перпендикуляром является отрезок A 1 C 1 . Его длина равна .
Ответ: .
18. В правильной 6-й призме A … F 1 , ребра которой равны 1, найдите расстояние между прямыми: AA 1 и B 1 C 1 .
Решение: Продолжим стороны B 1 C 1 и A 1 F 1 до пересечения в точке G . Треугольник A 1 B 1 G равносторонний. Его высота A 1 H является искомым общим перпендикуляром. Его длина равна .
Ответ: .
19. В правильной 6-й призме A … F 1 , ребра которой равны 1, найдите расстояние между прямыми: AA 1 и CE 1 .
Решение: Искомым расстоянием является расстояние между прямой AA 1 и плоскостью CEE 1 . Оно равно .
Ответ: .
20. В правильной 6-й призме A … F 1 , ребра которой равны 1, найдите расстояние между прямыми: AA 1 и CD 1 .
Решение: Искомым общим перпендикуляром является отрезок AC . Его длина равна .
Ответ: .
21. В правильной 6-й призме A … F 1 , ребра которой равны 1, найдите расстояние между прямыми: AA 1 и BC 1 .
Решение: Искомым расстоянием является расстояние между параллельными плоскостями ADD 1 и BCC 1 . Оно равно .
Ответ: .
22. В единичном кубе A … D 1 найдите расстояние от точки A до п лоскости BDA 1 .
Решение: Диагональ AC 1 куба перпендикулярна плоскости BDA 1 . Обозначим O — центр грани ABCD , E — точка пересечения AC 1 и плоскости BDA 1 . Длина отрезка AE будет искомым расстоянием. В прямоугольном треугольнике AOA 1 имеем
AA 1 = 1; AO = ; OA 1 = .
Следовательно, AE =
В режиме слайдов ответ появляется после кликанья мышкой.
Ответ:
23. В правильной треугольной призме ABCA 1 B 1 C 1 , все ребра которой равны 1, найдите расстояние от точки A до плоскости A 1 B 1 C .
Решение: Достроим данную треугольную призму до четырехугольной. Искомым расстоянием будет расстояние от точки A 1 до плоскости CDA 1 в призме A … D 1 . Это расстояние мы нашли в предыдущей задаче. Оно равно
Ответ:
24. В правильной 6-й призме A … F 1 , ребра которой равны 1, найдите расстояние от точки A до п лоскости BCC 1 .
Решение: Продолжим отрезки CB и FA до пересечения в точке G . Треугольник ABG равносторонний. Искомым расстоянием является длина высоты AH треугольника ABG. Она равна
Ответ:
25. В правильной 6-й призме A … F 1 , ребра которой равны 1, найдите расстояние от точки A до п лоскости A 1 B 1 D.
Решение: Искомым расстоянием является длина перпендикуляра AH , опущенного из точки A на прямую A 1 E . Для его нахождения рассмотрим прямоугольный треугольник AEA 1 . Имеем AA 1 = 1, AE = , A 1 E = 2. Следовательно, угол AEA 1 равен 30 о и высота AH равна .
Ответ: .
Углы
Здесь предлагаются примеры задач повышенной трудности на нахождение углов в пространстве, относящихся к профильной части Единого государственного экзамена по математике.
В режиме слайдов ответ появляется после кликанья мышкой.
1. В кубе A … D 1 найдите косинус уг ла между прямыми AA 1 и BD 1 .
В режиме слайдов ответ появляется после кликанья мышкой.
Ответ:
86
2. В правильной треугольной призме ABCA 1 B 1 C 1 , все ребра которой равны 1, найдите угол между прямыми: AB и A 1 C .
Решение: Искомый угол равен углу B 1 A 1 C . В треугольнике B 1 A 1 C проведем высоту CD 1 . В прямоугольном треугольнике A 1 CD 1 катет A 1 D 1 равен 0,5; гипотенуза A 1 C равна . Следовательно,
3. В правильной шестиугольной призме A … F 1 , все ребра которой равны 1, найдите косинус угла между прямыми AB 1 и BC 1 .
Решение 1 . Пусть O 1 – центр правильного шестиугольника A 1 … F 1 . Тогда прямая AO 1 параллельна прямой BC 1 , и искомый угол между прямыми AB 1 и BC 1 равен углу B 1 AO 1 . В равнобедренном треугольнике B 1 AO 1 имеем: O 1 B 1 = 1; AB 1 = AO 1 =
. Применяя теорему косинусов, получим .
Решение 2 . Введем систему координат, считая началом координат точку A , точка B имеет координаты (1, 0, 0), точка A 1 имеет координаты (0, 0, 1). Тогда точка С 1 имеет координаты (1,5, , 1). Вектор имеет координаты (1, 0, 1), вектор имеет координаты (0,5, , 1). Воспользуемся формулой
выражающий косинус угла между векторами через их скалярное произведение и длины. Имеем , . Следовательно, косинус уг ла между прямыми AB 1 и BС 1 равен 0,75 .
4. В правильной шестиугольной призме A … F 1 , все ребра которой равны 1, найдите косинус угла между прямыми AB 1 и BD 1 .
Решение 1 . Прямая AE 1 параллельна прямой BD 1 . Угол между прямыми AB 1 и BD 1 равен углу B 1 AE 1 . В треугольнике B 1 AE 1 имеем: AB 1 = , A E 1 = 2, B 1 E 1 = .
Применяя теорему косинусов, получим .
Решение 2 . Введем систему координат, считая началом координат точку A , точка B имеет координаты (1, 0, 0), точка A 1 имеет координаты (0, 0, 1). Тогда точка D 1 имеет координаты (1, , 1). Вектор имеет координаты (1, 0, 1), вектор имеет координаты (0, , 1). Воспользуемся формулой
выражающий косинус угла между векторами через их скалярное произведение и длины. Имеем , , . Следовательно, косинус уг ла между прямыми AB 1 и BС 1 равен .
5. В правильной шестиугольной призме A … F 1 , все ребра которой равны 1, найдите угол между прямыми AB 1 и BE 1 .
Решение 1. Докажем, что угол между прямыми AB 1 и BE 1 равен 90 о . Для этого воспользуемся теоремой о трех перпендикулярах. А именно, если ортогональная проекция наклонной на плоскость перпендикулярна прямой, лежащей в этой плоскости, то и сама наклонная перпендикулярна этой прямой. Ортогональная проекция BE 1 на плоскость ABB 1 есть прямая A 1 B , перпендикулярная AB 1 . Следовательно, прямая BE 1 также будет перпендикулярна прямой AB 1 , т.е. искомый угол равен 90 о .
Решение 2. Через точку B проведем прямую, параллельную прямой AB 1 , и обозначим G 1 ее точку пересечения с прямой A 1 B 1 . Искомый угол равен углу E 1 BG 1 . Сторона BG 1 треугольника E 1 BG 1 равна . В прямоугольном треугольнике BEE 1 катеты BE и EE 1 равны соответственно 2 и 1. Следовательно, гипотенуза BE 1 равна . В прямоугольном треугольнике G 1 A 1 E 1 катеты A 1 G 1 и A 1 E 1 равны соответственно 2 и . Следовательно, гипотенуза G 1 E 1 равна . Таким образом, в треугольнике BE 1 G 1 имеем: BG 1 = , BE 1 = , G 1 E 1 = . По теореме, обратной к теореме Пифагора, получим, что угол E 1 BG 1 равен 90 о .
Решение 3 . Введем систему координат, считая началом координат точку A , точка B имеет координаты (1, 0, 0), точка A 1 имеет координаты (0, 0, 1), точка E имеет координаты (0, , 0). Тогда точка E 1 имеет координаты (0, , 1), Вектор имеет координаты (1, 0, 1), вектор имеет координаты (-1, , 1). Воспользуемся формулой
выражающий косинус угла между векторами через их скалярное произведение и длины. Имеем и, следовательно, угол между прямыми AB 1 и BE 1 равен 90 о .
6. В кубе A … D 1 найдите уг ол между прям ой AB 1 и плоскостью ABC .
Ответ: 45 o .
7. В кубе A … D 1 найдите тангенс уг ла между прям ой AA 1 и плоскостью BC 1 D .
Ответ:
8. В кубе A … D 1 найдите уг ол между прям ой и плоскостью
AB 1 и ABC 1 .
Ответ: 30 o .
9. В кубе A … D 1 найдите уг ол между прям ой AC 1 и плоскостью BA 1 D .
Ответ: 90 o .
10. В правильной треугольной призме ABCA 1 B 1 C 1 , все ребра которой равны 1, найдите угол между прямой и плоскостью : AA 1 и AB 1 C 1 .
Ответ:
11. В кубе A … D 1 найдите тангенс уг ла между плоскостями ABC и AB 1 D 1 .
Ответ:
12. В правильной треугольной призме ABCA 1 B 1 C 1 , все ребра которой равны 1, найдите угол между плоскост ями ABC и A 1 B 1 C .
Решение: Обозначим O , O 1 — середины ребер AB и A 1 B 1 . Искомым линейным углом будет угол OCO 1 . В прямоугольном треугольнике OCO 1 имеем
OO 1 = 1; OC =
Следовательно,
13. В правильной 6-й призме A … F 1 , ребра которой равны 1, найдите у гол между плоскостями ABB 1 и CDD 1 .
Ответ: 60 о .
14. В правильной 6-й призме A … F 1 , ребра которой равны 1, найдите у гол между плоскостями ACC 1 и DEE 1 .
Ответ: 30 о .
15. В правильной 6-й призме A … F 1 , ребра которой равны 1, найдите у гол между плоскостями CDF 1 и AFD 1 .
Решение: Пусть O – центр призмы, G , G 1 – середины ребер CD и C 1 D 1 . Искомый угол равен углу GOG 1 . В треугольнике GOG 1 имеем: GG 1 = GO = G 1 O = 1. Следовательно, = 60 о .
Ответ:
Планиметрия
Здесь предлагаются примеры планиметрических задач повышенного уровня трудности, относящихся к профильной части Единого государственного экзамена и требующие развернутого решения.
1. Прямая касается окружностей радиусов R и r в точках A и B . Известно, что расстояние между центрами окружностей равно a , причем r R и r + R a . Найдите AB .
Решение. Пусть O 1 – центр окружности радиуса R , O 2 – центр окружности радиуса r . Возможны два случая: AB – внешняя касательная, AB – внутренняя касательная.
В первом случае (рис. 1) через точку O 2 проведем прямую, параллельную AB , и обозначим P ее точку пересечения с прямой O 1 A . Тогда AB =
Во втором случае (рис. 2) через точку O 2 проведем прямую, параллельную AB , и обозначим P ее точку пересечения с прямой O 1 A . Тогда AB =
Ответ. или .
2. Трапеция с основаниями 14 и 40 вписана в окружность радиуса 25. Найдите высоту трапеции.
Решение. Пусть ABCD – трапеция, вписанная в окружность с центром O и радиусом 25. Возможны два случая: основания AB и CD трапеции расположены по одну сторону от центра O , основания AB и CD расположены по разные стороны от центра O .
В первом случае (рис. 1) через точку O проведем прямую, перпендикулярную AB , и обозначим P , Q ее точки пересечения соответственно с AB и CD . Тогда высота PQ трапеции равна OQ – OP . Имеем OQ = OP = Следовательно, PQ = 9.
Во втором случае (рис. 2) через точку O проведем прямую, перпендикулярную AB , и обозначим P , Q ее точки пересечения соответственно с AB и CD . Тогда высота PQ трапеции равна OQ + OP . Имеем OQ = OP = Следовательно, PQ = 39.
Ответ. 9 или 39.
3. Окружности с центрами O 1 и O 2 пересекаются в точках A и B . Известно, что угол AO 1 B равен 90 о , угол AO 2 B равен 60 о , O 1 O 2 = a . Найдите радиусы окружностей.
Решение. Возможны два случая: точки O 1 , O 2 расположены по разные стороны от прямой AB , точки O 1 , O 2 расположены по одну сторону от прямой AB . Обозначим r радиус окружности с центром O 1 . Тогда радиус окружности с центром O 2 будет равен . Обозначим P точку пересечения прямых O 1 O 2 и AB . Тогда O 1 P = , O 2 P = .
В первом случае (рис. 1)
и, следовательно,
Во втором случае (рис. 2)
и, следовательно,
Ответ. или
4. Около треугольника ABC описана окружность с центром O , угол AOC равен 60 о . В треугольник ABC вписана окружность с центром M . Найдите угол AMC .
Решение. Возможны два случая расположения вершины B треугольника ABC .
В первом случае (рис. 1) сумма углов A и C треугольника ABC равна 150 о . Так как AM и CM – биссектрисы этих углов, то сумма углов CAM и ACM равна 75 о и, следовательно, угол AMC равен 105 о .
Во втором случае (рис. 2) сумма углов A и C треугольника ABC равна 30 о . Так как AM и CM – биссектрисы этих углов, то сумма углов CAM и ACM равна 15 о и, следовательно, угол AMC равен 165 о .
Ответ. 105 о или 165 о .
5. Треугольник ABC вписан в окружность радиуса 12. Известно, что AB = 6 и BC = 4. Найдите AC .
Решение. По теореме синусов Откуда
Возможны два случая расположения вершины C треугольника ABC .
Опустим перпендикуляр BH на прямую AC . Тогда BH = AB sin A = 1. По теореме Пифагора AH = CH = В первом случае (рис. 1)
AC = Во втором случае (рис. 2) AC =
Ответ. или
6. Прямые, содержащие высоты треугольника ABC пересекаются в точке H . Известно, что CH = AB . Найдите угол ACB .
Решение. Пусть AA 1 , BB 1 – высоты треугольника ABC . Опишем окружности на CH и AB как на диаметрах. Они пройдут через точки A 1 и B 1 . Возможны два случая расположения точки H .
В первом случае (рис. 1) угол C равен углу CAA 1 , как вписанные углы, опирающиеся на равные дуги. Следовательно, угол C равен 45 о . Во втором случае (рис. 2) угол C равен 135 о .
Ответ. 45 о или 135 о .
7. В треугольнике ABC проведены высоты BB 1 и CC 1 , O – центр вписанной окружности. Известно, что BC = 24, B 1 C 1 = 12. Найдите радиус R окружности, описанной около треугольника BOC .
Решение. Возможны два случая расположения отрезка B 1 C 1 .
На BC , как на диаметре, опишем окружность с центром P . Треугольник B 1 C 1 P равносторонний. Следовательно, сумма углов BPB 1 и CPC 1 равна 120 о . В первом случае (рис. 1) треугольники BPC 1 и CPB 1 равнобедренные. Следовательно, сумма углов B и C равна 120 о . Так как BO и CO – биссектрисы, то угол BOC равен 120 о . По теореме синусов находим R = .
Во втором случае (рис. 2) сумма углов B и C равна 60 о . Так как BO и CO – биссектрисы, то угол BOC равен 150 о . По теореме синусов находим R = 24.
Ответ. или 24.
8. В трапеции ABCD известны боковые стороны AB = 27, CD = 28. Основание BC равно 5, косинус угла BCD равен –2/7. Найдите AC .
Решение. Возможны два случая.
В первом случае (рис. 1) DF = 8, CF = BE = , AE = 3. Следовательно, AC = 28.
Во втором случае (рис. 2) DF = 8, CF = BE = , AE = 3. Следовательно, AC = .
Ответ. 28 или .
Слайд 1
Новая Школа
Подготовка к ЕГЭ по математике 2019

Слайд 2
Стереометрия. Часть 1
Задание №8 и 14

Слайд 3
План занятия
Куб
Прямоугольный параллелепипед
Составные многогранники
Призма

Слайд 4
Куб
Куб – это прямоугольный параллелепипед, все грани которого

– равные квадраты.
Слайд 5
Куб
Если сфера вписана в куб (то есть касается
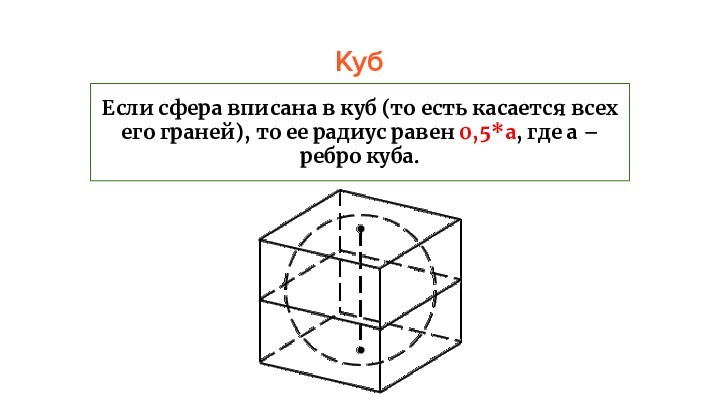
всех его граней), то ее радиус равен 0,5*a, где
a – ребро куба.
Слайд 6
Куб
Если сфера описана около куба (то есть все
вершины куба лежат на сфере), то ее радиус равен
0,5*d, где d – диагональ куба.
Слайд 7
Куб
Центр сферы, вписанной в куб или описанной около
куба, лежит в точке пересечения диагоналей куба.
Слайд 8
Задание №1
Площадь поверхности куба равна 18. Найдите его
диагональ.
Слайд 9
Задание №2
Если каждое ребро куба увеличить на 1,
то его площадь поверхности увеличится на 54. Найдите ребро
куба.
Слайд 11
Задание №4
Куб описан около шара, объем которого равен
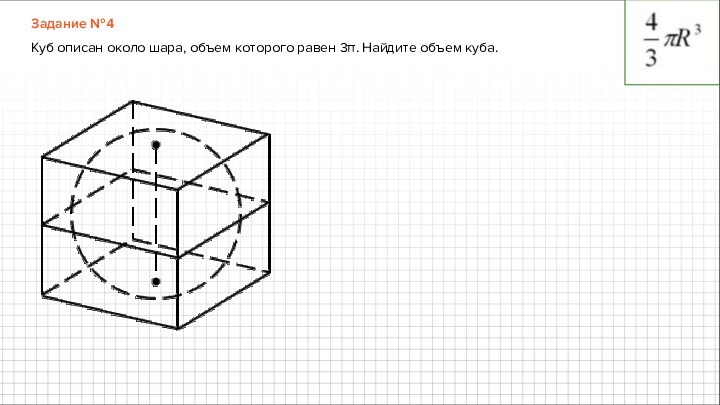
3π. Найдите объем куба.
Слайд 12
План занятия
Куб
Прямоугольный параллелепипед
Составные многогранники
Призма

Слайд 13
Прямоугольный параллелепипед
Прямоугольный параллелепипед – это параллелепипед, все грани

которого являются прямоугольниками.
Слайд 16
Задание №5
Объем прямоугольного параллелепипеда равен 24. Одно из
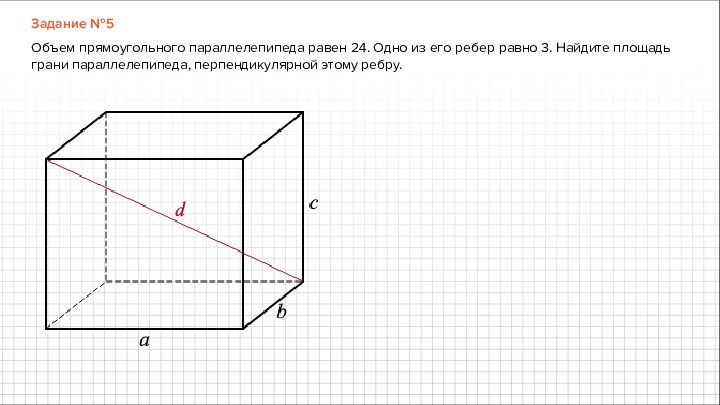
его ребер равно 3. Найдите площадь грани параллелепипеда, перпендикулярной
этому ребру.
Слайд 17
Задание №6
Два ребра прямоугольного параллелепипеда, выходящие из одной
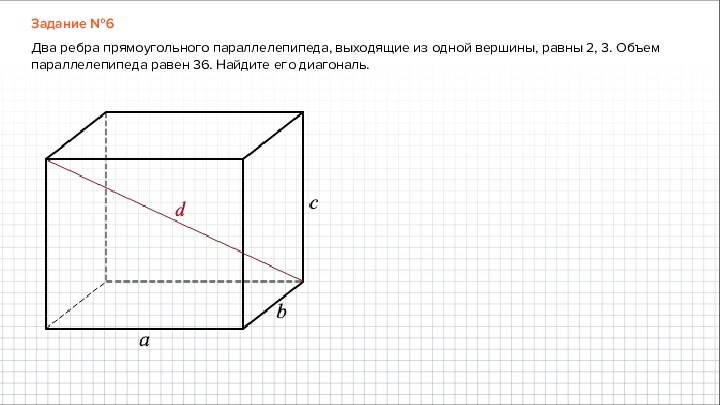
вершины, равны 2, 3. Объем параллелепипеда равен 36. Найдите
его диагональ.
Слайд 21
Задание №10
Объем первого прямоугольного параллелепипеда равен 105. Найдите
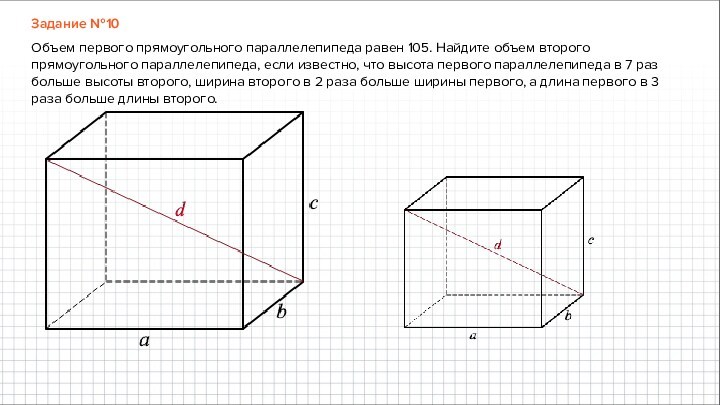
объем второго прямоугольного параллелепипеда, если известно, что высота первого
параллелепипеда в 7 раз больше высоты второго, ширина второго в
2 раза больше ширины первого, а длина первого в 3 раза больше длины второго.
Слайд 22
План занятия
Куб
Прямоугольный параллелепипед
Составные многогранники
Призма

Слайд 29
План занятия
Куб
Прямоугольный параллелепипед
Составные многогранники
Призма

Слайд 30
Призма
В основании призмы лежат многоугольники. Боковые грани представляют

собой параллелограммы. Высота призмы – перпендикуляр, опущенный из вершины
одного основания к плоскости другого основания.
Слайд 31
Призма
Площадь боковой поверхности – сумма площадей ее боковых

граней.
Площадь полной поверхности – сумма площади боковой поверхности
и площадей оснований.
Слайд 32
Прямая призма
Призма называется прямой, если ее боковые ребра
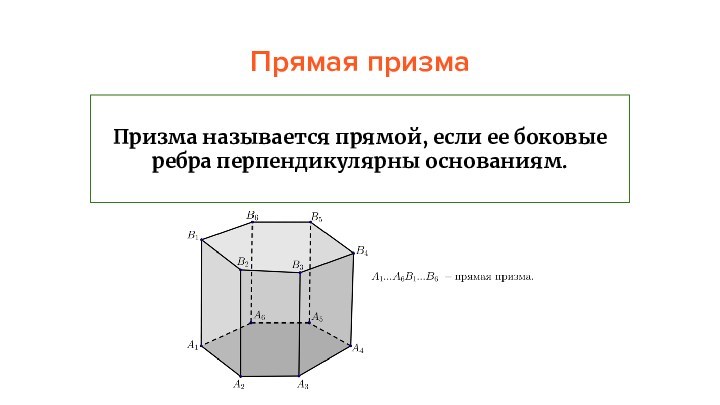
перпендикулярны основаниям.
Слайд 33
Правильная призма
Призма называется правильной, если она прямая и
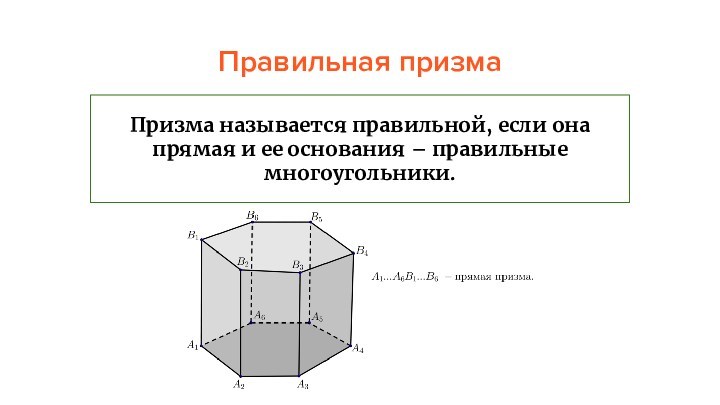
ее основания – правильные многоугольники.
Слайд 34
Задание №17
Основанием прямой треугольной призмы служит прямоугольный треугольник
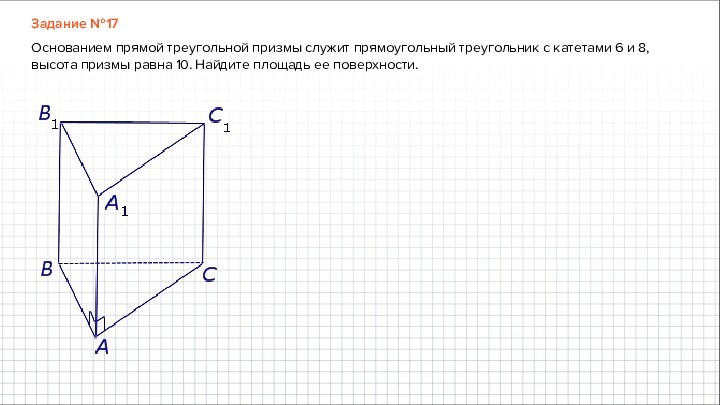
с катетами 6 и 8, высота призмы равна 10.
Найдите площадь ее поверхности.
Слайд 35
Задание №18
Через среднюю линию основания треугольной призмы, объем
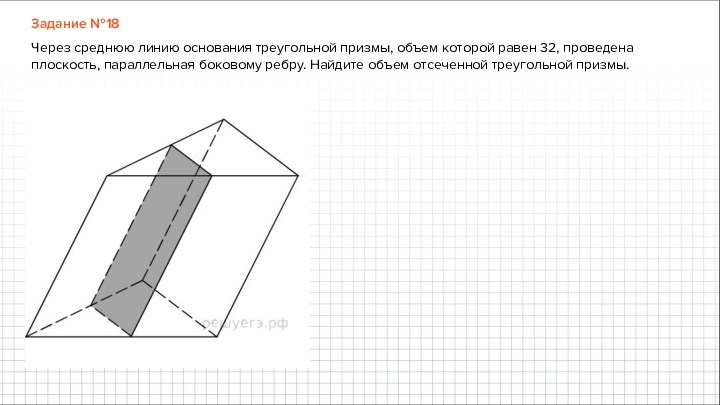
которой равен 32, проведена плоскость, параллельная боковому ребру. Найдите
объем отсеченной треугольной призмы.
Слайд 39
План занятия
Куб
Прямоугольный параллелепипед
Составные многогранники
Призма



























































































































