Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
В правильной четырёхугольной пирамиде SABCD сторона AB основания равна а высота SH пирамиды равна 3. Точки M и N — середины рёбер CD и AB, соответственно, а NT — высота пирамиды NSCD с вершиной N и основанием SCD.
а) Докажите, что точка T является серединой SM.
б) Найдите расстояние между NT и SC.
Источник: Задания 14 (С2) ЕГЭ 2016, ЕГЭ по математике 06.06.2016. Основная волна. Вариант 512 (C часть).
2
Основанием прямой треугольной призмы ABCA1B1C1 является прямоугольный треугольник ABC с прямым углом C. Грань ACC1A1 является квадратом.
а) Докажите, что прямые CA1 и AB1 перпендикулярны.
б) Найдите расстояние между прямыми CA1 и AB1, если AC = 4, BC = 7.
Источник: Задания 14 (C2) ЕГЭ 2017
3
В правильной четырёхугольной пирамиде PABCD сторона основания ABCD равна 12, боковое ребро PA ― Через вершину A проведена плоскость α, перпендикулярная прямой PC и пересекающая ребро PC в точке K.
а) Докажите, что плоскость α делит высоту PH пирамиды PABCD в отношении 2 : 1, считая от вершины P.
б) Найдите расстояние между прямыми PH и BK.
Источник: Пробный ЕГЭ по математике, Санкт-Петербург, 04.03.2018. Вариант 1.
4
В кубе ABCDA1B1C1D1 все ребра равны 6.
а) Докажите, что угол между прямыми AC и BC1 равен 60°.
б) Найдите расстояние между прямыми AC и BC1.
Источник: ЕГЭ по математике 01.06.2018. Основная волна. Вариант 991 (C часть). Он же: вариант 751 (резервная волна 25.06.2018), Задания 14 (С2) ЕГЭ 2018
5
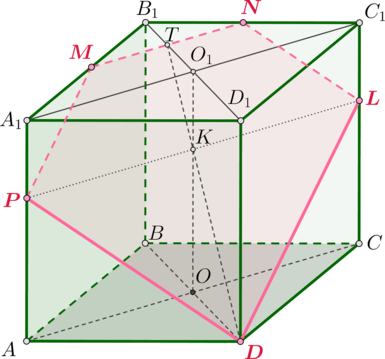
В кубе ABCDA1B1C1D1 рёбра равны 1. На продолжении отрезка A1C1 за точку C1 отмечена точка M так, что A1C1 = C1M, а на продолжении отрезка B1C за точку C отмечена точка N так, что B1C = CN.
а) Докажите, что MN = MB1.
б) Найдите расстояние между прямыми B1C1 и MN.
Источник: Резервная волна ЕГЭ по математике 24.06.2019. Вариант 992, Задания 14 (С2) ЕГЭ 2019
Пройти тестирование по этим заданиям
- ЕГЭ по математике профиль
Прототипы задания №13 ЕГЭ по математике профильного уровня — стереометрия. Практический материал для подготовки к экзамену в 11 классе.
Для успешного выполнения задания №14 необходимо уметь выполнять действия с геометрическими фигурами, координатами и векторами.
Практика
Коды проверяемых элементов содержания (по кодификатору) — 5.2–5.6
Уровень сложности задания — повышенный.
Максимальный балл за выполнение задания — 3
Примерное время выполнения задания выпускником, изучавшим математику на профильном уровне (в мин.) — 15
Связанные страницы:
Всё варианты 13 задания математика ЕГЭ Профиль 2022
Скачать задания в формате pdf.
Задания 13 ЕГЭ по математике профильного уровня 2022 год (стереометрия)
1) (28.03.2022 досрочная волна) Вне плоскости равностороннего треугольника АВС отмечена точка D, причем (cos angle DAB = cos angle DAC = 0,2.)
а) Докажите, что прямые AD и ВС перпендикулярны
б) Найдите расстояние между прямыми AD и ВС, если известно, что АВ = 2.
ОТВЕТ: (frac{{sqrt {71} }}{5}.)
2) (28.03.2022 досрочная волна) Дана треугольная пирамида SABC. Основание высоты SO этой пирамиды является серединой отрезка CH — высоты треугольника ABC.
а) Докажите, что (A{C^2} — B{C^2} = A{S^2} — B{S^2};)
б) Найдите объём пирамиды SABC, если AB = 25; AC = 10; (BC = 5sqrt {13} ;,,,,SC = 3sqrt {10} .)
3) (28.03.2022 досрочная волна) На окружности основания конуса с вершиной S отмечены точки A, B и C так, что AB — диаметр основания. Угол между образующей и плоскостью основания равен 60°.
a) Докажите, что (cos angle ASC + cos angle CSB = 1,5;)
б) Найдите объём тетраэдра SABC, если SC = 1 и (cos angle ASC = frac{2}{3}.)
ОТВЕТ: (frac{{sqrt 6 }}{{36}}.)
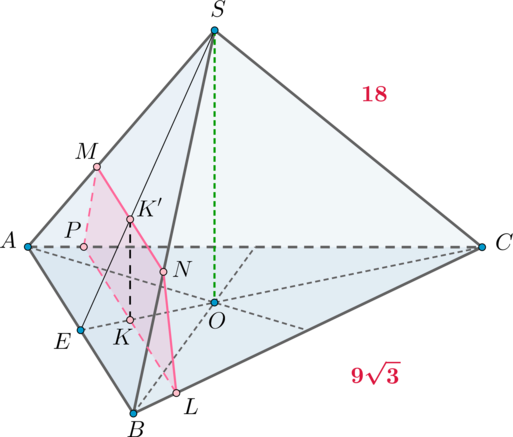
4) (02.06.2022 основная волна) Дана правильная четырёхугольная пирамида SABCD. Точка M?— середина SA, на ребре SB отмечена точка N так, что SN : NB = 1 : 2.
а) Докажите, что плоскость CMN параллельна прямой SD.
б) Найдите площадь сечения пирамиды плоскостью CMN, если все рёбра равны 12.
ОТВЕТ: (15sqrt {19} .)
5) (02.06.2022 основная волна) В основании пирамиды SABCD лежит трапеция ABCD с большим основанием AD. Диагонали пересекаются в точке O. Точки M и N — середины боковых сторон AB и CD соответственно. Плоскость α проходит через точки M и N параллельно прямой SO.
а) Докажите, что сечение пирамиды SABCD плоскостью α является трапецией.
б) Найдите площадь сечения пирамиды SABCD плоскостью α, если SO = 9, AD = 12, BC = 10, а прямая SO перпендикулярна прямой AD.
6) (02.06.2022 основная волна) В прямоугольном параллелепипеде ABCDA1B1C1D1 на диагонали BD1 отмечена точка N так, что BN : ND1 = 1 : 2. Точка O — середина отрезка CB1.
а) Докажите, что прямая NO проходит через точку A.
б) Найдите объём параллелепипеда ABCDA1B1C1D1, если длина отрезка NO равна расстоянию между прямыми BD1 и CB1 и равна (sqrt 2 .)
7) (02.06.2022 основная волна) В кубе ABCDA1B1C1D1 отмечены середины M и N отрезков AB и AD соответственно.
а) Докажите, что прямые B1N и CM перпендикулярны.
б) Найдите расстояние между этими прямыми, если ({B_1}N = 3sqrt 5 .)

а) Докажите, что SK : KC = 6 : 1.
а) Плоскость AMN делит пирамиду SABCD на два многогранника. Найдите отношение их объёмов.
9) (02.06.2022 основная волна) В прямоугольном параллелепипеде ABCDA1B1C1D1 на диагонали BD1 отмечена точка N, что BN : ND1 = 1 : 2. Точка О – середина отрезка CB1.
а) Докажите, что прямая NО проходит через точку А.
б) Найдите объём параллелепипеда ABCDA1B1C1D1, если длина отрезка NO равна расстоянию между прямыми BD1 и CB1 и равна (sqrt 6 .)
10) (02.06.2022 основная волна) В правильной четырёхугольной пирамиде SABCD точка М – середина бокового ребра SC, точка N лежит на стороне основания BC. Плоскость α проходит через точки M и N параллельно боковому ребру SA.
а) Плоскость α пересекает ребро SD в точке L. Докажите, что BN : NC = DL : LS.
б) Пусть BN : NC = 1 : 2. Найдите отношение объёмов многогранников, на которые плоскость α разбивает пирамиду.
11) (02.06.2022 основная волна) Точка O?— точка пересечения диагоналей грани CDD1C1 куба ABCDA1B1C1D1. Плоскость DA1C1 пересекает диагональ BD1 в точке F.
а) Докажите, что BF : FD1 = A1F : FO.
б) Точки M и N — середины ребер AB и AA1, соответственно. Найдите угол между прямой MN и плоскостью DA1C1.
ОТВЕТ: (arctg,sqrt 2 .)
12) (27.06.2022 резервная волна) Точка М – середина ребра АА1 треугольной призмы АВСА1В1С1, в основании которой лежит треугольник АВС. Плоскость α проходит через точки В и В1 перпендикулярно прямой С1М.
а) Докажите, что одна из диагоналей грани АСС1А1 равна одному из рёбер этой грани.
б) Найдите расстояние от точки С до плоскости α, если она делит ребро АС в отношении 1 : 5, считая от вершины А и известно, что АС = 20, АА1 = 32.
13) (27.06.2022 резервная волна) В правильной треугольной призме ABCA1B1C1 точка М – середина ребра СС1. На рёбрах АВ и А1В1 взяты точки К и N так, что АК : КВ = В1N : NA1.
а) Докажите, что плоскость MKN перпендикулярна плоскости АА1В1.
б) Найдите площадь сечения призмы плоскостью MKN, если АВ = ВВ1 = 42 и ВК : КА = 41 : 1.
Задание ЕГЭ №13 (бывшая ЕГЭ №14) по стереометрии считается очень сложным на ЕГЭ. И многие за нее не берутся.
А зря!
Если проходить стереометрию от простого к сложному освоить стереометрию можно. В 2022 году за ЕГЭ №13 дают не 2, а целых 3 балла на ЕГЭ! И вы можете их получить.
Читайте эту статью, смотрите вебинары и решайте задачи вместе с Алексеем Шевчуком и вы полюбите стереометрию.
ЕГЭ 13 Стереометрия. Расстояние между точками и от точки до прямой
Расстояние между точками и от точки до прямой – это первое видео раздела “Стереометрия”, входящее в наш курс подготовки к ЕГЭ (о нем ниже).
В этом видео мы научимся “видеть” 3-мерное пространство и изображать 3-мерные объекты на бумаге (то есть на плоской поверхности).
Затем мы научимся двум основным вещам – находить расстояние между точками на таких рисунках, а также расстояние от точки до прямой.
На этих умениях строится всё дальнейшее изучение стереометрии. В общем это очень важное, базовое видео, с которого нужно начинать изучение стереометрии. Не перескакивайте, не пропускайте его!
Даже если вы знаете стереометрию, вы найдете для себя очень много полезного и нового в этом видео.
ЕГЭ 13 (14). Стереометрия. Разбор варианта профильного ЕГЭ 2020
Нужно великолепно знать основные теоремы планиметрии, уметь рассчитывать расстояния, площади и объемы плоских и объемных фигур.
Но самое сложное, нужно научиться строить доказательства с помощью этих теорем и правильно их записывать.
Давайте этим займемся.
- 00:00 Условие задачи
- 00:25 Как нарисовать шестиугольную пирамиду
- 05:52 Как подписать вершины пирамиды
- 06:24 Как исправить рисунок, если грани пирамиды сливаются
- 10:18 Доказательство пункта А
- 14:13 Запись доказательства пункта А
- 18:50 Доказательство (решение) пункта Б (Найти объем пирамиды)
- 23:45 Запись доказательства (решения) пункта Б
- 26:08 Найдем площадь основания пирамиды (чтобы найти объем) и запишем решение
- 29:18 Нахождение объема пирамиды
- 29:59 На что рекомендуем обратить внимание
Самые бюджетные курсы по подготовке к ЕГЭ на 90+
Алексей Шевчук – ведущий мини-групп
математика, информатика, физика
+7 (905) 541-39-06 – WhatsApp/Телеграм для записи
alexei.shevchuk@youclever.org – email для записи
- тысячи учеников, поступивших в лучшие ВУЗы страны
- автор понятного всем учебника по математике ЮКлэва (с сотнями благодарных отзывов);
- закончил МФТИ, преподавал на малом физтехе;
- репетиторский стаж – c 2003 года;
- в 2021 году сдал ЕГЭ (математика 100 баллов, физика 100 баллов, информатика 98 баллов – как обычно дурацкая ошибка:);
- отзыв на Профи.ру: “Рейтинг: 4,87 из 5. Очень хвалят. Такую отметку получают опытные специалисты с лучшими отзывами”.
Как подготовиться к решению заданий ЕГЭ № 14 по стереометрии | 1С:Репетитор
Как показывают результаты профильного экзамена по математике, задачи по геометрии — в числе самых сложных для выпускников. Тем не менее, решить их, хотя бы частично, а значит заработать дополнительные баллы к общему результату возможно. Для этого необходимо, конечно, знать достаточно много о «поведении» геометрических фигур и уметь применять эти знания для решения задач. Здесь мы постараемся дать некоторые рекомендации, как подготовиться к решению задачи по стереометрии.
Эта задача обычно состоит из двух частей:
За решение данной задачи на экзамене по математике в 2018 году можно получить максимум два первичных балла. Допускается решить только «доказательную» или только «вычислительную» часть задачи и заработать в этом случае один первичный балл.
Многие школьники на экзамене даже не приступают к решению задачи №14, хотя она значительно проще, например, задачи № 16 — по планиметрии.
В задачу № 14 традиционно включается лишь несколько вопросов из всех возможных для стереометрических задач:
В соответствии с этими вопросами строится и подготовка к решению задачи.
Сначала, разумеется, нужно выучить все необходимые аксиомы и теоремы, которые понадобятся для доказательной части задачи. Помимо того, что знание аксиом и теорем поможет вам на экзамене непосредственно при решении задачи, их повторение позволит систематизировать и обобщить ваши знания по стереометрии вообще, то есть создать из этих знаний некую целостную картину.
Итак, что же нужно выучить?
После того как вы повторили теорию, можно приступать к рассмотрению методов решения задач. В курсе «1C:Репетитор» представлены все необходимые материалы для подготовки: видеолекции с теорией, тренажеры с пошаговым решением задач, тесты для самопроверки, интерактивные модели, позволяющие ученикам 10-х и 11-х классов наглядно рассмотреть методы решения задач по стереометрии, в том числе на примерах задач ЕГЭ 2017 года.
Мы рекомендуем решать задачи в такой последовательности:
- Углы в пространстве (между скрещивающимися прямыми, между прямой и плоскостью, между плоскостями);
- Расстояния в пространстве (между двумя точками, между точкой и прямой, между точкой и плоскостью, между скрещивающимися прямыми);
- Решение многогранников, то есть нахождение углов между ребрами и гранями, расстояний между ребрами, площадей поверхностей, объемов по заданным в условии задачи элементам;
- Сечения многогранников — методы построения сечений (например, метод следов) и нахождения площадей сечений и объемов получившихся после построения сечения многогранников (например, использование свойств перпендикулярной проекции и метод объемов).
Для всех указанных типов задач существуют различные методы решения:
Эти методы нужно знать и уметь применять, так как есть задачи, которые довольно сложно решаются одним методом и гораздо проще — другим.
При решении стереометрических задач более эффективным по сравнению с классическим методом нередко оказывается векторно-координатный. Классический метод решения задач требует отличного знания аксиом и теорем стереометрии, умения применять их на практике, строить чертежи пространственных тел и сводить стереометрическую задачу к цепочке планиметрических. Классический метод, как правило, быстрее приводит к искомому результату, чем векторно-координатный, но требует определенной гибкости мышления. Векторно-координатный метод представляет собой набор готовых формул и алгоритмов, но при этом требует более длительных расчетов; тем не менее, для некоторых задач, например, для нахождения углов в пространстве, он предпочтительнее классического.
Многим абитуриентам не позволяет справиться со стереометрической задачей неразвитое пространственное воображение. В этом случае мы рекомендуем использовать для самоподготовки интерактивные тренажеры с динамическими моделями пространственных тел. Такие тренажеры есть на портале «1С:Репетитор» (для перехода к их использованию необходимо зарегистрироваться): работая с ними, вы не только сможете «выстроить» решение задачи «по шагам», но и на объемной модели увидеть все этапы построения чертежа в различных ракурсах.
С помощью таких же динамических чертежей мы рекомендуем учиться строить сечения многогранников. Кроме того, что модель автоматически проверит правильность вашего построения, вы сами сможете, рассматривая сечение с разных сторон, убедиться, верно или неверно оно построено, и если неправильно, то в чем именно ошибка. Построение сечения на бумаге, с помощью карандаша и линейки, конечно, таких возможностей не дает. Посмотрите пример построения сечения пирамиды плоскостью с использованием такой модели (Нажмите на картинку, что бы перейти к тренажеру):
Последний вопрос, на который надо обратить внимание, — это нахождение площадей сечений или объемов, получившихся после построения сечения многогранников. Здесь также существуют подходы и теоремы, которые позволяют в общем случае существенно сократить трудозатраты на поиск решения и получение ответа. В курсе «1С:Репетитор» мы знакомим вас с этими приемами.
Если вы следовали нашим советам, разобрались со всеми вопросами, которые здесь затронуты, и решили достаточное количество задач, то велика вероятность, что вы практически готовы к решению задачи по стереометрии на профильном ЕГЭ по математике в 2018 году. Дальше необходимо только поддерживать себя «в форме» до самого экзамена, то есть решать, решать и решать задачи, совершенствуя свое умение применять изученные приемы и методы в разных ситуациях. Удачи!
Регулярно тренируйтесь в решении задач
Чтобы начать заниматься на портале «1С:Репетитор», достаточно зарегистрироваться.
Вы можете:
- Начать заниматься бесплатно.
- Получить доступ ко всей теории и тренажерам задачи №14. Это стоит всего 990 рублей.
- Купить доступ к этой задаче в составе экспресс-курса «Геометрия» и научиться решать задачи №14 и №16 на максимальный балл.
Все курсы состоят из методически правильной последовательности теории и практики, необходимой для успешного решения задач. Включают теорию в форме текстов, слайдов и видео, задачи с решениями, интерактивные тренажеры, модели, и тесты.
Остались вопросы? Позвоните нам по телефону 8 800 551-50-78 или напишите в онлайн-чат.
Здесь ключевые фразы, чтобы поисковые роботы лучше находили наши советы:
Как решать задание 14 на экзамене ЕГЭ, задачи по геометрии, решение задач, по стереометрии, методы решения задач, тренажеры, видео, КИМ ЕГЭ 2017, подготовка к ЕГЭ, профиль математика, математика профильного уровня, решение задачи по наклонной треугольной призме, грани, взаимно перпендикулярно, общее ребро, плоскости, точки, ребро равно, боковая поверхность, решение задач на сечение многогранника, перпендикулярное сечение, вычислить объем фигуры, в основании прямой треугольной призмы лежит, признаки равенства и подобия треугольников, примеры решения задач ЕГЭ по геометрии, вычисление сечения, задачи по математике профильного уровня, применение методов сечения, решение задач на площадь, задачи ЕГЭ 2017 по стереометрии, подготовка к ЕГЭ, выпускникам 11 класса, в 2018 году, поступающим в технический вуз.
14. Задачи по стереометрии
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Задачи по стереометрии формата ЕГЭ
Задание
1
#3868
Уровень задания: Равен ЕГЭ
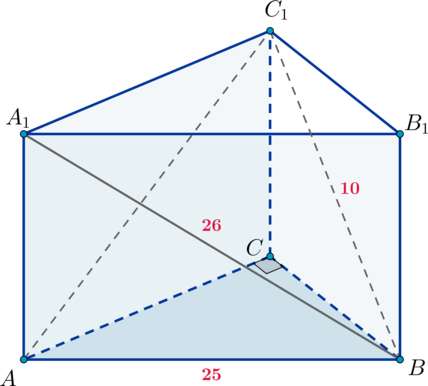
Основанием прямой треугольной призмы (ABCA_1B_1C_1) является прямоугольный треугольник (ABC), причем (angle C=90^circ). Диагонали боковых граней (AA_1B_1B) и (BB_1C_1C) равны соответственно (26) и (10), (AB=25).
а) Докажите, что (triangle BA_1C_1) – прямоугольный.
б) Найдите объем пирамиды (AA_1C_1B).
а) Так как (BB_1perp (A_1B_1C_1)), (B_1C_1perp A_1C_1), то по теореме о трех перпендикулярах (BC_1perp A_1C_1) (как наклонная). Следовательно, (triangle A_1C_1B) – прямоугольный.
б) Заметим, что (BCperp AC) и (BCperp CC_1), следовательно, по признаку (BCperp (AA_1C_1)). Следовательно, (BC) – высота пирамиды (BAA_1C_1) с основанием (AA_1C_1).
Так как (triangle AA_1C_1) прямоугольный, то [V_{BAA_1C_1}=dfrac{frac12cdot AA_1cdot A_1C_1cdot BC}3] По теореме Пифагора [begin{aligned}
&A_1C_1=sqrt{26^2-10^2}=sqrt{16cdot 36}=24\[1ex]
&AA_1=sqrt{26^2-25^2}=sqrt{1cdot 51}=sqrt{51}\[1ex]
&BC=sqrt{10^2-51}=sqrt{49}=7 end{aligned}] Тогда [V_{BAA_1C_1}=dfrac{frac12cdot 24cdot sqrt{51}cdot 7}3=28sqrt{51}]
Ответ:
б) (28sqrt{51})
Задание
2
#6924
Уровень задания: Равен ЕГЭ
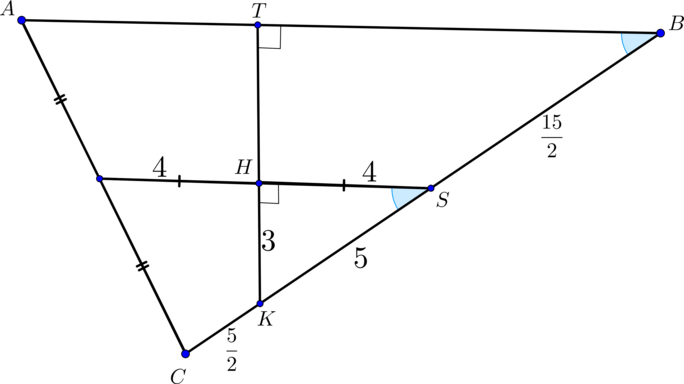
(ABCA_1B_1C_1) — прямая треугольная призма, (AB=16, BC=15,
AA_1=8), (cosangle ABC=0,8). (M, N) – середины ребер (AC) и (B_1C_1) соответственно. (K,P) – такие точки на ребрах (BC) и (B_1C_1) соответственно, что (CK=B_1P=dfrac{1}{6}BC).
а) Построить сечение призмы плоскостью (alpha), параллельной прямой (MN) и проходящей через точки (K) и (P).
б) Найти площадь сечения призмы плоскостью (alpha).
а) 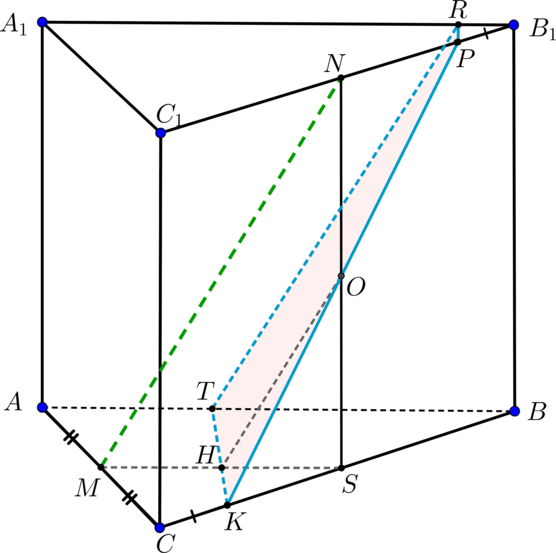
Если прямая (MNparallel alpha Rightarrow MN) параллельна некоторой прямой, лежащей в (alpha). Проведем (NSperp BC, NScap
KP=O). В плоскости (MNS) проведем (OHparallel MN Rightarrow
MH=HS). Тогда прямая (KHcap AB=T). Так как плоскости (ABC) и (A_1B_1C_1) параллельны, то (alpha) пересечет плоскость (A_1B_1C_1) по прямой, параллельной (KT). Следовательно, проведем (PRparallel
KT). Таким образом, (TRPK) – искомое сечение (трапеция).
б) Заметим, что (CK=dfrac{1}{6} cdot 15=dfrac{5}{2} Rightarrow
KS=5). Т.к. (MS) – средняя линия треугольника (ABC Rightarrow MS=8
Rightarrow HS=4). Так как (angle HSK=angle ABC), то по теореме косинусов (HK=sqrt{16+25-2cdot 4cdot 5cdot frac45}=3). Таким образом, по обратной теореме Пифагора треугольник (HKS) – прямоугольный, следовательно, (angle H =90^circ). Таким образом, по теореме о трех перпендикулярах, из того, что (NSperp (ABC),
HSperp KT Rightarrow
OHperp KT).
Проведем (PH_1 perp KT). Из подобия треугольников (HOK) и (H_1PK) следует, что (PH_1=2OH). Т.к. (OS=dfrac{1}{2}NS=4, HS=4 Rightarrow
OH=4sqrt2). Таким образом найдена высота трапеции (PH_1=8sqrt2).
Найдем основания трапеции (KT) и (PR).
(sin angle KSH = dfrac{3}{5}=sin angle B=dfrac{KT}{KB}
Rightarrow KT=dfrac{15}{2}).
(bigtriangleup PRB_1 sim bigtriangleup KTB Rightarrow
PR=dfrac{3}{2}).
Таким образом, (S_{TRPK} = dfrac{1}{2}cdot
left(dfrac{15}{2}+dfrac{3}{2}right)cdot 8sqrt2 = 36sqrt2)
Ответ:
б) (36sqrt2)
Задание
3
#2300
Уровень задания: Равен ЕГЭ
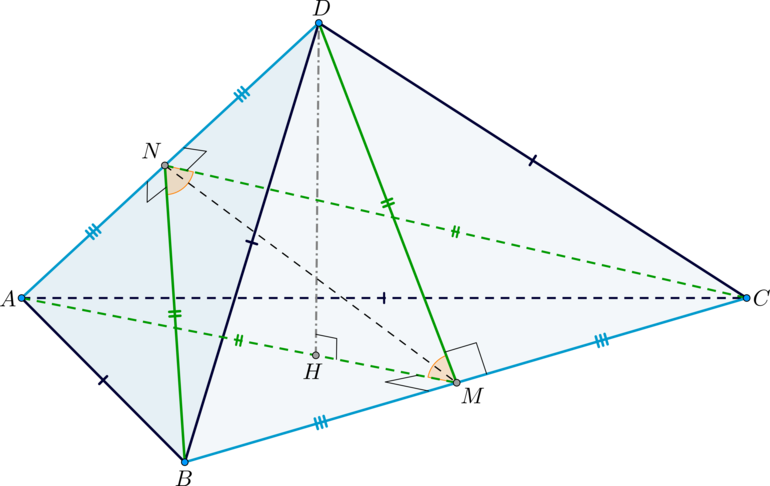
В треугольной пирамиде (DABC) двугранные углы при ребрах (AD) и (BC) равны. Известно также, что (AB=BD=DC=AC=sqrt{15}).
а) Докажите, что (AD=BC).
б) Найдите объем пирамиды, если двугранные углы при (AD) и (BC) равны по (60^circ).
а) Рассмотрим пирамиду (DABC), (AB=BD=DC=CA), (angle
(BAD,CAD)=angle (BAC,BDC)).
Т.к. (triangle ABD) и (triangle ACD) – равнобедренные, причем (AD) – общее основание, то высоты к основаниями попадут в одну точку – в середину стороны (AD), точку (N). То есть (BNperp AD), (CNperp AD). Таким образом, (angle BNC) – линейный угол двугранного угла (angle(BAD,CAD)).
Аналогичным образом строится угол (angle AMD) – линейный угол двугранного угла (angle (BAC,BDC)), где (M) – середина (BC). Таким образом, (angle BNC=angle AMD).
Т.к. (triangle ABD=triangle ACD) по трем сторонам, то (BN=CN). Аналогично (AM=DM). Значит, (triangle AMD) и (triangle BNC) – равнобедренные и подобные (по двум пропорциональным сторонам и углу между ними).
Заметим, что плоскости ((AMD)) и ((BNC)) имеют две общие точки – это точки (N) и (M). Следовательно, они пересекаются по прямой (MN). Отрезок (NM) – это высота в (triangle AMD) и (triangle BNC) к основаниям (AD) и (BC) соответственно. Следовательно, эти треугольники равны. Следовательно, (AD=BC), чтд.
б) Из пункта а) также следует, что (AM=DM=BN=CN). Т.к. двугранные углы равны (60^circ), то (triangle AMD) и (triangle BNC) – равносторонние.
Пусть (AM=DM=BN=CN=AD=BC=x).
Проведем высоту пирамиды (DH). Т.к. (DMperp BC), то по теореме о трех перпендикулярах (HMperp BC). Таким образом, точка (H) должна лежать на (AM), причем на середине, т.к. (triangle AMD) – равносторонний.
(DH=frac{sqrt3}2cdot AD=frac{sqrt3}2x). Найдем по теореме Пифагора (x) из (triangle ABM):
(AM=x), (BM=frac x2), (AB=sqrt{15}), следовательно, (x=2sqrt3).
Таким образом, [V_{DABC}=frac13cdot DHcdot S_{ABC}=dfrac13cdot
frac{sqrt3}2xcdot frac12x^2=6]
Ответ:
б) (6)
Задание
4
#1265
Уровень задания: Равен ЕГЭ
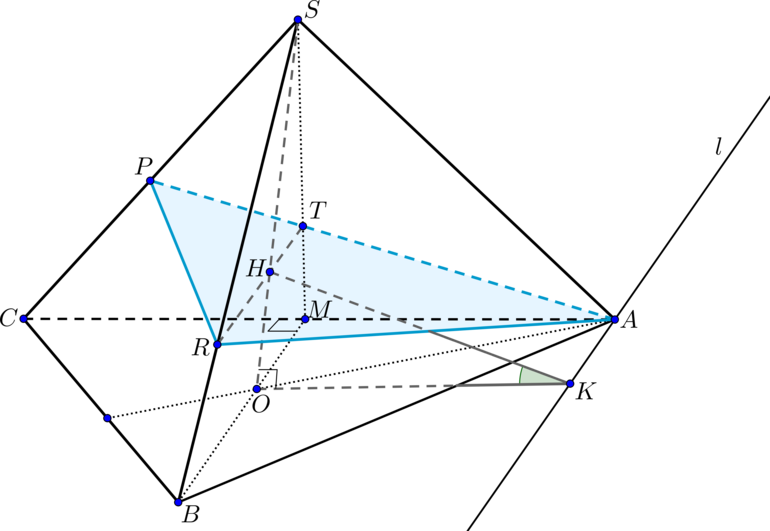
Дан правильный тетраэдр (SABC), (H) – такая точка на высоте (SO), что (OH:HS=1:3). Плоскость (alpha) проходит через точки (A) и (H) параллельно медиане (BM) треугольника (ABC) и пересекает ребро (CS) в точке (P).
а) Докажите, что (CP:PS=2:3).
б) Найдите угол между плоскостями (alpha) и (ABC).
а)
Правильный тетраэдр — это правильная треугольная пирамида, у которой все ребра равны. Пусть ребро пирамиды равно (a).
Т.к. пирамида правильная, то высота (SO) падает в точку пересечения медиан (bigtriangleup ABC). Рассмотрим плоскость (BSM), точка (H) лежит в этой плоскости. Т.к. плоскость (alpha) параллельна (BM), то она пересекает плоскость (BSM) по прямой, параллельной (BM).
Проведем (RTparallel BM, Hin RT). Тогда по теореме Фалеса (dfrac{SH}{HO}=dfrac{ST}{TM}=dfrac{3}{1}).
Прямая (AT) пересечет (CS) в точке (P). (bigtriangleup APR) – сечение пирамиды плоскостью (alpha).
Напишем теорему Менелая для (bigtriangleup CSM) и прямой (AP):
[dfrac{CP}{PS}cdot dfrac{ST}{TM}cdot dfrac{MA}{AC}=1] Из этого равенства находим, что (dfrac{CP}{PS}=dfrac{2}{3})
б) Докажем, что линия пересечения плоскостей (alpha) и (ABC) параллельна прямой (BM). Пусть это не так: пусть (l) – линия пересечения (alpha) и (ABC) и (lcap BM=Z). Тога прямая (BMcap
alpha=Z), следовательно, не может быть параллельна (alpha). Получили противоречие, следовательно, (lparallel BM). Заметим, что прямая (l) проходит через точку (A).
Построим линейный угол двугранного угла между (alpha) и (ABC). Т.к. (HOperp ABC), проведем (OKperp l), следовательно, по теореме о трех перпендикулярах (HKperp l). Таким образом, (angle HKO) – искомый угол.
1) Найдем (HO).
(BO=dfrac{2}{3}cdot BM=dfrac{2}{3}cdot
dfrac{sqrt3}{2}a=dfrac{a}{sqrt3})
Тогда (SO=sqrt{a^2 -dfrac{a^2}{3}}=sqrt{dfrac{2}{3}}a
Rightarrow HO=dfrac{1}{4}SO=dfrac{sqrt2a}{4sqrt3})
2) Найдем (OK).
(BMperp AC, BMparallel l Rightarrow ACperp l). Т.к. (OKperp l
Rightarrow OKparallel AC). Таким образом, (OMAK) – параллелограмм, следовательно, (OK=MA=dfrac{1}{2}a).
Треугольник (HOK) – прямоугольный, следовательно, (mathrm{ctg},angle
HKO=dfrac{OK}{HO}=sqrt6)
Тогда (angle HKO= mathrm{arcctg},sqrt6).
Ответ:
б) (mathrm{arcctg},sqrt6)
Задание
5
#3059
Уровень задания: Равен ЕГЭ
Дана правильная четырехугольная призма (ABCDA_1B_1C_1D_1), стороны основания которой равна (4), а боковые ребра равны (5).
а) Постройте сечение призмы плоскостью (DMN), где (M) и (N) – середины отрезков (A_1B_1) и (B_1C_1).
б) Найдите угол между данным сечением и плоскостью (ABC).
(Задача от подписчиков)
а) Из условия следует, что призма прямая и основаниями являются квадраты.
(MN) – средняя линия в (triangle A_1B_1C_1), следовательно, (MNparallel A_1C_1). Тогда плоскость (DMN) пересечет плоскость (A_1C_1CA) по прямой (l), параллельной (A_1C_1) (в противном случае (l) пересечет (A_1C_1) в некоторой точке (K), которая будет лежать и на (A_1C_1), и в плоскости (DMN), следовательно, должна будет лежать и на (MN), что невозможно, так как (MN) не пересекает (A_1C_1)).
Таким образом, найдем точку, в которой плоскость (DMN) пересекает плоскость (A_1C_1CA).
Пусть плоскость (B_1D_1DB) пересекает (MN) в точке (T). Тогда (DTin
(DMN)). Если (O) и (O_1) – точки пересечения диагоналей оснований, то прямые (DT) и (OO_1) лежат в плоскости (B_1D_1DB). Пусть точка их пересечения – точка (K). Тогда (K) – искомая точка пересечения плоскости (DMN) и плоскости (A_1C_1CA).
Проведем через точку (K) прямую (l) параллельно (A_1C_1). Пусть она пересекла (AA_1) в точке (P), (CC_1) в точке (L). Таким образом, получили сечение (DPMNL) призмы плоскостью (DMN).
б) Заметим, что (KOperp (ABC)), следовательно, так как (ODperp
AC), то и (KDperp AC) по теореме о трех перпендикулярах. Значит, (angle KDO) равен углу между плоскостями (DMN) и (ABC).
По теореме Фалеса [dfrac{A_1M}{MB_1}=dfrac11=dfrac{O_1T}{TB_1}
quadRightarrowquad O_1T=TB_1.] (triangle TO_1Ksim triangle DOK), следовательно, [dfrac{O_1T}{OD}=dfrac12=dfrac{O_1K}{OK}] Следовательно, (OK=frac23OO_1=frac23AA_1=frac23cdot
5=frac{10}3).
(OD=frac12 BD=frac12cdot sqrt2AB=2sqrt2.)
Тогда [mathrm{tg},angle KDO=dfrac{OK}{OD}=dfrac56sqrt2
quadRightarrowquad
angle KDO=mathrm{arctg},dfrac56sqrt2.]
Ответ:
б) (mathrm{arctg},dfrac56sqrt2)
Задание
6
#3064
Уровень задания: Равен ЕГЭ
В правильной треугольной пирамиде (SABC) с основанием (ABC) на медиане основания (CE) взята точка (K) так, что (CK:KE=8:1). Через точку (K) проведена плоскость (alpha), которая перпендикулярна прямой (CE) и пересекает боковые ребра (SA) и (SB) в точках (M) и (N) соответственно.
а) Докажите, что (MN:AB=2:3).
б) Найдите объем пирамиды, вершиной которой является точка (C), а основанием – сечение пирамиды (SABC) плоскостью (alpha), если известно, что (AB=9sqrt3), (SA=18).
(Задача от подписчиков)
а) Пусть (SO) – высота пирамиды, (O) – точка пересечения медиан. Следовательно, [dfrac{CO}{OE}=dfrac21] Так как по условию (CK:KE=8:1), то можно обозначить (CK=8x), (KE=x). Тогда (CE=9x). Следовательно, (CO=frac23CE=6x), (OE=3x), (OK=2x).
Так как (CE) перпендикулярна плоскости (alpha), то нужно построить две пересекающиеся прямые в плоскости (alpha), которым (CE) будет перпендикулярна.
Первая прямая: так как (CEperp AB), то проведем через точку (K) прямую (PLparallel AB). Тогда (CEperp PL) ((Pin AC, Lin BC)).
Вторая прямая: так как (SOperp (ABC)), то (SOperp CE). Следовательно, проведем (KK’parallel SO), тогда (KK’perp CE) ((K’in SE)).
Следовательно, (alpha) проходит через точки (P, L, K’).
Заметим, что (alpha) пересечет плоскость (ASB) по прямой, параллельной (AB) (в противном случае (alpha) будет иметь общую точку с (AB), что невозможно, так как (ABparallel PL
quadRightarrowquad ABparallel alpha)).
Следовательно, (MNparallel AB) и проходит через (K’).
Из подобия (triangle K’EKsim triangle SEO): [dfrac{SE}{K’E}=dfrac{OE}{KE}=dfrac31 quadRightarrowquad K’E=
dfrac13SE
quadRightarrowquad SK’=dfrac23SE.] Из подобия (triangle
MSNsim triangle ASB): [dfrac{MN}{AB}=dfrac{SK’}{SE}=dfrac23.]
б) Рассмотрим пирамиду (CPMNL). (CK) – высота этой пирамиды, (PMNL) – трапеция ((MNparallel ABparallel PL)).
Следовательно, [V=dfrac13cdot CKcdot dfrac{MN+PL}2cdot KK’] Так как (BC=9sqrt3), то (CE=sqrt{BC^2-EB^2}=frac{27}2). Следовательно, [CK=dfrac89CE=12.] Из подобия (triangle PCLsim triangle ACB): [dfrac{PL}{AB}=dfrac{CK}{CE}=dfrac89quadRightarrowquad PL=
8sqrt3.] Из пункта а) [MN=dfrac23AB=6sqrt3.] Из подобия (triangle
EK’Ksim triangle ESO): [KK’=dfrac13SO=dfrac13sqrt{SC^2-CO^2}=dfrac13sqrt{18^2-9^2}=
3sqrt3.] Следовательно, [V=dfrac13cdot 12cdot dfrac{6sqrt3+8sqrt3}2cdot 3sqrt3=252.]
Ответ:
б) 252
Задание
7
#3063
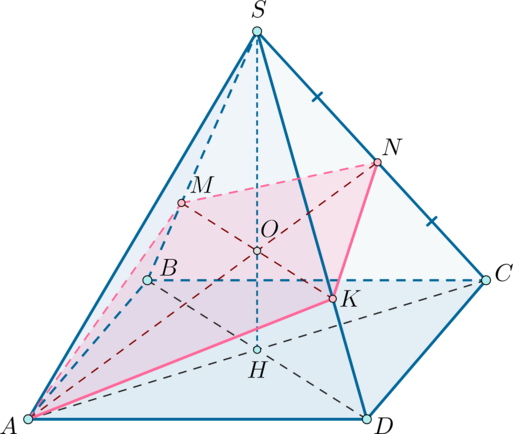
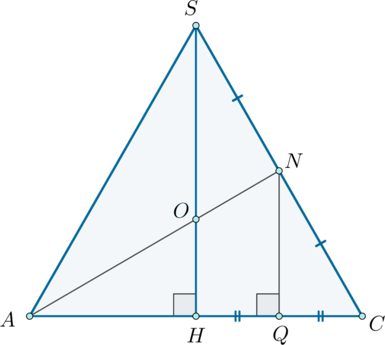
Уровень задания: Равен ЕГЭ
Дана правильная четырехугольная пирамида (SABCD) с вершиной (S), стороны основания которой равны (6sqrt2), а боковые ребра равны (21).
а) Постройте сечение пирамиды плоскостью, проходящей через точку (A) и середину ребра (SC) параллельно прямой (BD).
б) Найдите площадь построенного сечения.
(Задача от подписчиков)
а) Пусть (N) – середина ребра (SC), (SH) – высота пирамиды (падает в точку пересечения диагоналей основания).
Необходимо построить прямую, лежащую в плоскости сечения и параллельную (BD). Рассмотрим плоскость (ASC). Прямая (AN) пересекает (SH) в точке (O). Теперь рассмотрим (BSD). Проведем в этой плоскости через точку (O) прямую, параллельную (BD). Пусть она пересечет ребра (SB) и (SD) в точках (M) и (K) соответственно. Таким образом, (AMNK) – искомое сечение.
б) Заметим, что по теореме о трех перпендикулярах (так как (OHperp
(ABC), AHperp BD)) (AOperp BD). Так как (BDparallel MK), то (AOperp MK), следовательно, (ANperp MK). Следовательно, у четырехугольника (AMNK) диагонали взаимно перпендикулярны. Значит, его площадь можно найти как [S=dfrac12 ANcdot MK.]
Заметим сразу, что (BD=AC=ABsqrt2=12).
Рассмотрим плоскость (ASC).
По теореме Менелая: [dfrac{SN}
{NC}cdot dfrac{CA}{AH}cdot dfrac{HO}{OS}=1 quadRightarrow
quad dfrac{HO}{OS}=dfrac12 quadRightarrowquad OS=2OH
quadRightarrowquad dfrac{SO}{SH}=dfrac23.] (это нам понадобится позже для поиска (MK))
Проведем (NQperp AC). Тогда из подобия (triangle SHC) и (triangle
NQC): [dfrac{SH}{NQ}=dfrac{SC}{NC}=2 quadRightarrowquad
NQ=dfrac12SH=dfrac12sqrt{SC^2-HC^2}=dfrac12sqrt{21^2-6^2}=
dfrac12sqrt{81cdot 5}] (Q) – середина (HC), следовательно, (AQ=frac34AC=frac34cdot 12=9). Тогда по теореме Пифагора [AN=sqrt{AQ^2+NQ^2}=sqrt{dfrac{81cdot 5}4+81}=dfrac{27}2.]
Рассмотрим (BSD). Так как (triangle MSKsim triangle BSD), то [dfrac{MK}{BD}=dfrac{SO}{SH}=dfrac23 quadRightarrowquad
MK=dfrac23BD=dfrac23cdot 12=8.] Следовательно, площадь сечения равна [S=dfrac12cdot 8cdot dfrac{27}2=54.]
Ответ:
б) 54

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
7 февраля 2022
В закладки
Обсудить
Жалоба
Стереометрическая задача на нахождение геометрических величин (длин, углов, площадей, объёмов).
Традиционная задача по стереометрии, связанная с нахождением длин, площадей (в том числе площадей сечений многогранников и тел вращения), углов (между двумя прямыми, между прямой и плоскостью, между двумя плоскостями), связанных с призмой, пирамидой, цилиндром, конусом или шаром.
Не зная основных определений и признаков (параллельности прямой и плоскости, параллельности плоскостей, перпендикулярности прямой и плоскости, перпендикулярности плоскостей, скрещивающихся прямых), нет смысла браться за задание 13.
→ zadanie_13m.pdf
→ Пособие автора (типовые задания С2).
Типичные ошибки при решении задания 13
Типичные ошибки участников экзамена связаны в первую очередь с неверным пониманием логики построения доказательства. Например, доказательство пункта а задания 13 часто начинается так:
«Предположим, что треугольник прямоугольный, тогда …» — в случае, когда нужно доказать, что треугольник прямоугольный;
«Пусть прямые параллельны…» — в случае, когда нужно доказать параллельность прямых. И т. д.
Многие участники экзамена неверно применяют признаки:
→ параллельности прямой и плоскости, параллельности плоскостей, перпендикулярности прямой и плоскости, перпендикулярности плоскостей, скрещивающихся прямых;
→ демонстрируют непонимание взаимосвязи элементов геометрической конструкции.
При выполнении второго пункта участники:
→ допускают ошибки в геометрических формулах (например, в формулах для вычисления объемов);
→ не считают нужным доказывать неочевидные геометрические утверждения, используемые в решение.
Кроме этого участники экзамена допускают большое количество ошибок при построении чертежа.
Автор: Прокофьев Александр Александрович.