Строительство нового завода стоит 75 млн рублей. Затраты на производство x тыс. ед. продукции на таком заводе равны млн рублей в год. Если продукцию завода продать по цене p тыс. рублей за единицу, то прибыль фирмы (в млн рублей) за один год составит
Когда завод будет построен, фирма будет выпускать продукцию в таком количестве, чтобы прибыль была наибольшей. При каком наименьшем значении p строительство завода окупится не более чем за 3 года?
Спрятать решение
Решение.
Прибыль фирмы (в млн рублей) за один год выражается как
Это выражение является квадратным трёхчленом и достигает своего наибольшего значения при Наибольшее значение равно
Строительство завода окупится не более чем за 3 года, если
то есть при поскольку цена продукции не может быть отрицательной.
Таким образом, наименьшее значение
Ответ: 9.
Спрятать критерии
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получен верный ответ | 2 |
| Верно построена математическая модель | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 2 |
Источник/автор: Демонстрационная версия ЕГЭ по математике —2021. Профильный уровень.
Строительство нового завода стоит 75 млн рублей. Затраты на производство x тыс. ед. продукции на таком заводе равны 0,5x^2+ x + 7 млн рублей в год. Если продукцию завода продать по цене p тыс.рублей за единицу, то прибыль фирмы (в млн рублей) за один год составит px−(0,5x^2+x+7).
Когда завод будет построен, фирма будет выпускать продукцию в таком количестве, чтобы прибыль была наибольшей. При каком наименьшем значении p строительство завода окупится не более чем за 3 года?
математика 10-11 класс
11138
Чтобы получить за такую задачу наибольшее количество баллов следует учесть, что условие задачи » не менее» подразумевает [red]составление неравенства[/red].
За три года прибыль составит:
3•( рх–(0,5х²+х+7)).
Так как за это время должно окупиться строительство нового цеха, то эта прибыль должна быть [red]не менее [/red]75 млн. руб.
Составим [red]неравенство[/red]:
3•( рх–(0,5х²+х+7)) ≥ 75.
Запишем неравенство для р:
рх–(0,5х²+х+7) ≥ 25;
рх–0,5х²-х-7 ≥ 25;
рх≥0,5х²+х+7+25.
Так как [b]x > 0[/b], то
р≥(0,5х)+1+(32/х) .
Найдем наименьшее значение р(x)=0,5х+2+(32/х).
Применяем производную.
р`(x)=(0,5х+4+(32/x) )’=0,5–(32/x²).
р`=0.
Найдем критические точки: 0,5– (32/x²) =0.
х=8 или х=–8(отрицательное значение не удовл. условию, х – натуральное число).
x=8 — точка[red] минимума,[/red] так как при переходе через точку производная меняет знак с — на +:
p(7)=0,5-(32/49)=(49-64)/98 < 0
p(9)=0,5-(32/81)=(81-64)/81> 0
Вычислим [red]наименьшее[/red] значение р при х=8
р(8) = 0,5∙8+1+(32/8) = 9
О т в е т.[b] р=9.[/b]
Ученик, который сдает профильную математику наверняка рассчитывает поступить с ней в вуз, иначе зачем так напрягаться? Только весь масштаб катастрофы школьник средней руки осознает, когда доберется до части с развернутым ответом, ведь без нее баллов, скорее всего, не хватит. На наш взгляд, самые «дешевые» 3 балла можно получить за задачу на финансовую математику в ЕГЭ.
Напомним, что прототипы для 17-го номера делятся на три большие группы:
- банковские задачи,
- задачи на ценные бумаги,
- задачи на оптимальный выбор.
Мы уже рассказали, как научить школьника решать любую задачу на кредиты. Прелесть этих прототипов в том, что любой подобный номер решается по единому алгоритму. Однако никто не отменял менее удачливых школьников, которым попадется другой вид задач. Потому в этой статье мы покажем, как научить выпускника решать задачи на ценные бумаги и, самое страшное, оптимальный выбор. Поехали!
Финансовая математика в ЕГЭ: задачи на вклады и ценные бумаги
На самом деле это еще один «подарочный» прототип. Обычно это довольно простая задача на проценты, но нюансы, конечно, есть. Преподавателю придется сконцентрировать снимание школьника на трех вещах:
- Механизм работы вкладов и ценных бумаг. Даже если школьник может представить себе, как работает вклад, то ценные бумаги, вероятно, вообще темный лес. Как показывает, практика, каждое незнакомое слово в условии дает +50 к панике и увеличивает шансы того, что к задаче не приступят вовсе.
Предложите школьнику воспользоваться демо-режимом в каком-нибудь брокерском приложении. Например, «Сбербанк Инвестор» позволяет целый месяц торговать на виртуальном брокерском счете и дает на это 400 тысяч виртуальных рублей. Может, именно ваш ученик станет следующим Уорреном Баффетом!
- Оформление. Каждый символ в бланке ответа должен быть выверен. Например, частая ошибка оформлять математическую модель уравнением, когда в условии стоит формулировка «не больше» или «не меньше». За такие погрешности школьник лишится баллов за 17 номер.
- Вычисления. Преподаватель должен демонстрировать культуру вычислений с самой первой встречи с учеником. Какой смысл в выверенных алгоритмах решения, если подопечный закопается в цифрах? Научите школьника не спешить, продумывать расчеты на пару ходов вперед. Зачем умножать, если в следующем действии придется делить, и все лишнее сократится? Зачем считать дискриминант до конца, если из получившегося огромного числа придется извлекать нетабличный корень?
Задача 1
Алексей приобрёл ценную бумагу за 7 тыс. рублей. Цена бумаги каждый год возрастает на 2 тыс. рублей. В любой момент Алексей может продать бумагу и положить вырученные деньги на банковский счёт. Каждый год сумма на счёте будет увеличиваться на 10%. В течение какого года после покупки Алексей должен продать ценную бумагу, чтобы через тридцать лет после покупки этой бумаги сумма на банковском счёте была наибольшей?
Самый, на наш взгляд, изящный способ решить эту задачу — понять, в какой момент станет выгодно хранить деньги в банке? Покажите школьнику, как меняется стоимость каждый год:
- 1 год: если оставим бумагу, то заработаем 2000. А если продадим и положим в банк, то только 10% от 7000, то есть 700 рублей;
- 2 год: бумага все еще принесет 2000, а вот депозит уже принес бы 900;
- 3 год: 2000 против 1100…
То есть прибыль от ценной бумаги сохраняется, а депозит с ростом ее стоимости может приносить все больше. Когда же он станет выгодным? Когда 10% от стоимости бумаги перевалят за 2000:
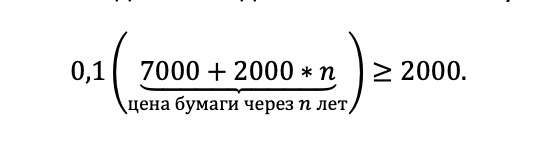
Осталось решить неравенство и не забыть, что n – целое число лет.
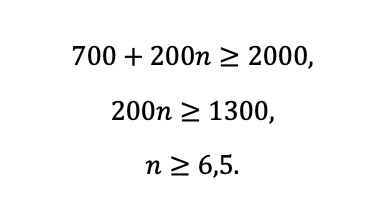
То есть, когда срок будет равен 6-ти годам, неравенство еще не выполнится. Когда пройдет 7 лет, и бумага подорожает еще на 2000, сумма станет достаточной, чтобы проценты на депозите давали больше. Значит, на восьмой год можно ее продавать.
Ответ: в течение 8-го года.
Финансовая математика в ЕГЭ: задачи на оптимальный выбор
Ну вот мы и добрались до самого неприятного варианта. Во-первых, тут надо уметь работать с условием текстовых задач. Во-вторых, бегло владеть методом исследования функций с помощью производной. И если второе укладывается в алгоритм, то первое далеко не всегда.
Если в задачах с кредитами набор прототипов очень ограничен, и там трудно придумать что-то новое, то на задачах на оптимальный выбор народ разгулялся. Тут может происходить всё что угодно:
- Покупка и продажа ценных бумаг;
- Движение двух объектов по перпендикулярным траекториям;
- Строительство заводов и оплата труда рабочим;
- Деление огорода под посадки…
Хорошая новость в том, что далеко не все задачки, которые вам попадутся, могут встретиться на экзамене. Большинство самых страшных номеров — это усложненные варианты от Александра Ларина. Ими вполне можно развлечь сильного ученика, но не стоит пугать ими того, кто «плавает». Каждый прототип, который к вам принес школьник с квадратными от испуга глазами, стоит проверить на принадлежность к авторам ФИПИ.
Мы рассмотрим 2 самых распространенных прототипа:
- Первый — из демонстрационного варианта ЕГЭ по математике 2021 года,
- Второй — более древний, но зато математическая модель из него встречается в задачах ФИПИ чаще всего.
Задача 2.1
Строительство нового завода стоит 75 млн рублей. Затраты на производство x тыс. ед. продукции на таком заводе равны 0,5x2 + x + 7 млн рублей в год. Если продукцию завода продать по цене p тыс. рублей за единицу,то прибыль фирмы (в млн рублей) за один год составит px – (0,5x2 + x + 7). Когда завод будет построен, фирма будет выпускать продукцию в таком количестве, чтобы прибыль была наибольшей. При каком наименьшем значении p строительство завода окупится не более чем за 3 года?
Первым делом убедитесь, что школьник понимает условие задачи: предложите ему пересказать ситуацию своими словами.
Если выкинуть из задачи все «лишнее», то получится, что завод хочет заработать как можно больше, и может добиться этого, выпустив больше единиц товара. То есть нам надо узнать, при каком значении x функция прибыли примет максимальное значение, цена тут будет считаться уже зафиксированной:
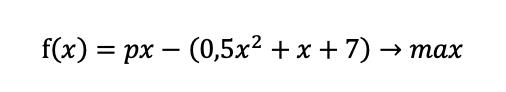
Перед нами функция, которую необходимо исследовать на максимум. Дайте школьнику подумать, вдруг он осознает, что уже владеет инструментом для такого исследования? Если не осознает, проведите аналогию с 12-ым номером.
Ищем производную, учитываем, что p – константа:
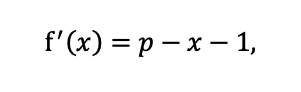
Приравниваем к нулю:
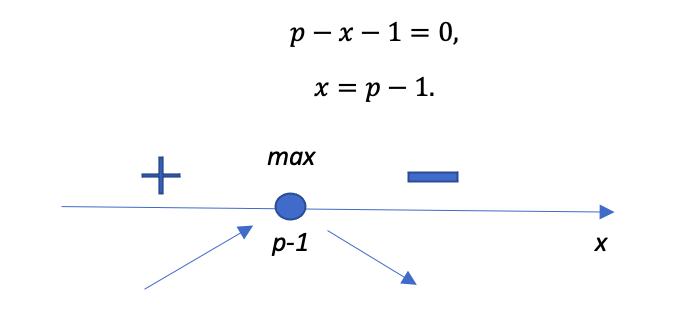
Словом, пока ничего нового, за исключением наверняка очень пугающей школьника второй переменной. Главное — чтобы подопечный не расставлял знаки интервалом по инерции, как это часто происходит в неравенствах. Напомните, что тут всегда проверяем знак подстановкой в исследуемую функцию. Например, правее точки экстремума будет точка p, а левее – p-2.
Мы выяснили, что прибыль будет максимальная, если выпускать p-1 единицу товара. Школьнику следует хорошо подумать, и понять, что дальше.От нас хотят узнать, за какую цену следует продавать товар, чтобы прибыль окупила вложенные в завод 75 млн за 3 года. Будем очень аккуратными с моделью:
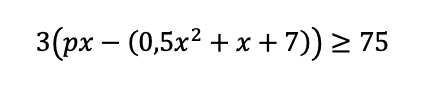
Подставим подсчитанное количество единиц товара x=p-1:
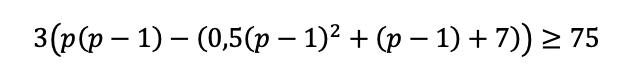
Ясно, что отрицательная цена нас не устраивает, а вот первое положительное значение, при котором неравенство выполняется — это 9. Заставляйте школьника рассуждать, иначе самостоятельно справиться с подобной задачей у него не выйдет.
Ответ: 9 тысяч.
Пробегитесь по алгоритму решения:
- Внимательно читаем и понимаем условие задачи;
- Составляем математическую модель;
- Анализируем ее на максимум с помощью производной;
- Отвечаем на вопрос задачи.
Прошлая задача, можно сказать, уже содержала математическую модель в готовом виде. Давайте теперь посмотрим, как выглядит номер без единого выражения в условии.
Задача 2.2
Григорий является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары, но на заводе, расположенном во втором городе, используется более совершенное оборудование.
В результате, если рабочие на заводе, расположенном в первом городе, трудятся суммарно t2 часов в неделю, то за эту неделю они производят 3 t единиц товара; если рабочие на заводе, расположенном во втором городе, трудятся суммарно t2 часов в неделю, то за эту неделю они производят 5 t единиц товара.
За каждый час работы (на каждом из заводов) Григорий платит рабочему 500 рублей.
Григорий готов выделять 6 800 000 рублей в неделю на оплату труда рабочих. Какое наибольшее количество единиц товара можно произвести за неделю на этих двух заводах?
Пожалуй, школьнику может быть трудно осознать, что время работы в этой задаче — это не просто t, а t2. Еще, вероятно, ему захочется вспомнить формулу работы, но тут она совершенно ни к чему:
Предприниматель хочет заработать побольше, а для этого надо произвести и продать больше товара. Но при этом и заплатить рабочим хочется меньше. Из-за того, что производительность на одном заводе выше, и товары производятся быстрее, а оплата труда та же, имеет смысл нагрузить его чуть больше. Надо посчитать, как именно следует распределить производство между заводами.
С одной стороны, нам интересно максимально много товара:
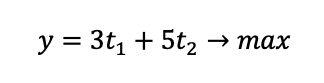
Если для ученика индексы при t станут неожиданностью, объясните, что работать на заводах будут разное количество времени.
С другой — у Григория есть ограничения по бюджету:
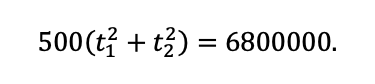
До сих пор мы не могли исследовать функцию производства товара на максимум, ведь переменных там было две, и ни одну из них зафиксировать мы не могли. Но теперь мы можем выразить, к примеру, t1 из второго уравнения, и тогда анализ станет возможным.
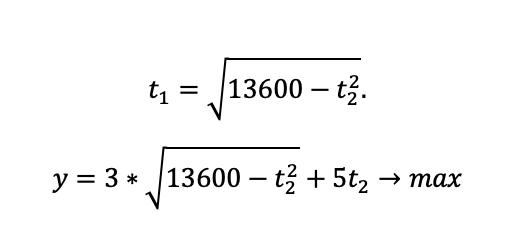
Ура! С этого момента школьник точно в курсе, что делать, дайте ему поработать самостоятельно.Ищем производную и приравниваем к нулю:
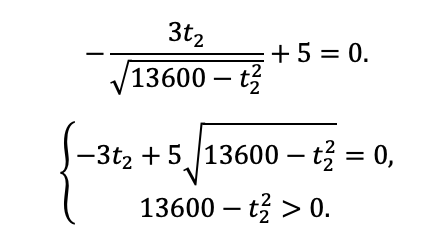
Ваш подопечный помнит, как правильно оформляется дробно-рациональное уравнение? Несмотря на то, что ОДЗ в данном случае никак на ответ не повлияет, не стоит рисковать и забывать про него.
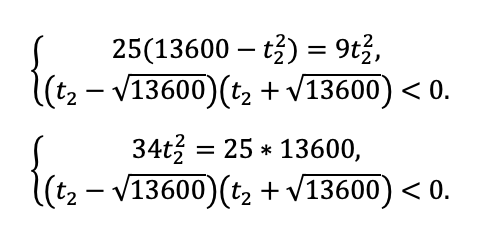
Обратите внимание школьника: мы не стали перемножать большие числа. Потому что знаем: скоро придется делить.
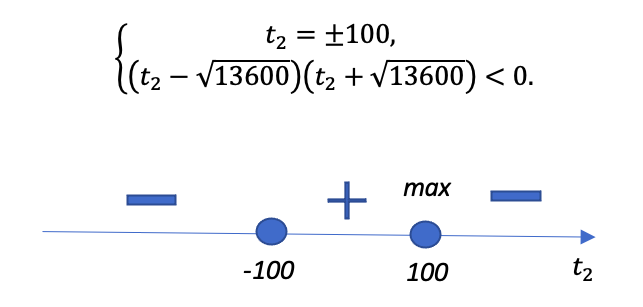
И снова повод убедиться, не забывает ли подопечный проверять тут знаки интервалов подстановкой.
Мы нашли количество рабочих часов на втором заводе. Дайте выпускнику сориентироваться в решении. Что делать дальше?
Осталось ответить на вопрос задачи:
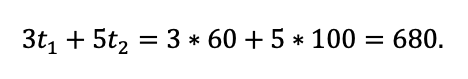
Ответ: 680 единиц товара.
Подведём итог
Мы рассмотрели 2 оставшихся прототипа 17 номера ЕГЭ по математике.
В первом случае выпускник будет работать с задачкой на проценты, где для него мало нового. Во втором ему придется вытащить из условия функцию для анализа с помощью производной.
Учитывайте, что текстовые задачи — довольно трудный для подростков формат работы, потому сопротивление ожидаемо. Однако, только экономическую задачу можно уместить всего в пару уроков разбора, все остальные номера займут гораздо больше времени! Нельзя упускать такую возможность подготовиться и урвать пару дополнительных драгоценных баллов. Донесите это до ученика, и…
Пусть удача всегда будет с вами!
(с) Голодные игры
Еще один тип заданий №15 Профильного ЕГЭ по математике — это задачи на нахождение точек максимума и минимума функций, а также их наибольших или наименьших значений. Многие из них решаются с помощью производной.
Такие задачи есть и в экономике. Например, максимизация прибыли или оптимизация издержек бизнеса — и многие другие.
1. Строительство нового завода стоит 78 млн рублей. Затраты на производство x тысяч единиц продукции на таком заводе равны млн рублей в год. Если продукцию завода продавать по цене p тыс. рублей за единицу, то прибыль фирмы (в млн рублей) за один год составит
Когда завод будет построен, фирма будет выпускать продукцию в таком количестве, чтобы прибыль была наибольшей. При каком наименьшем значении p строительство завода окупится не более, чем за 3 года?
Чтобы прибыль за три года была не меньше 78 млн рублей, необходимо, чтобы каждый год прибыль была не меньше 26 млн рублей. Это значит, что должно выполняться неравенство:
Здесь — прибыль за год. Рассмотрим функцию
Наибольшее значение этой функции должно быть не меньше, чем 26.
Графиком функции является парабола с ветвями вниз. Наибольшее значение функции достигается при
, то есть в вершине параболы.
Значит, Получим:
или
. Поскольку
, получим:
Тогда
Ответ:
2. Зависимость объема Q (в штуках) купленного у фирмы товара от цены Р (в рублях за штуку) выражается формулой , где
. Доход от продажи товара составляет PQ рублей. Затраты на производство Q единиц товара составляют 3000Q + 5000000 рублей. Прибыль равна разности дохода от продажи товара и затрат на его производство.
Стремясь привлечь внимание покупателей, фирма уменьшила цену продукции на 20%, однако ее прибыль не изменилась. На сколько процентов следует увеличить сниженную цену, чтобы добиться наибольшей прибыли?
Будем рассматривать прибыль как функцию от цены продукции. Так как прибыль, по условию, равна разности дохода от продажи товара и затрат на его производство, получим:
Обратите внимание, что можно записывать 1000 как , 1000000 как
. Работать со степенями проще, чем с длинными рядами нулей.
После того как фирма уменьшила первоначальную цену на 20%, ее прибыль не изменилась. Значит,
Приравняем эти величины.
Разделим обе части уравнения на
Получим:
руб.
Значит, первоначальная цена продукции равна 10 тысяч рублей за штуку. После снижения на 20% цена за штуку стала равна 8 тысяч рублей.
На сколько же процентов следует увеличить сниженную цену, чтобы прибыль была наибольшей? И при каком значении цены получается наибольшая прибыль?
Другими словами, мы находим наибольшее значение функции
Эта функция задает квадратичную параболу с ветвями вниз. Можно найти ее точку максимума с помощью производной. Или просто найти координату вершины параболы:
рублей.
Остается решить стандартную задачу на проценты. На сколько процентов надо увеличить 8000, чтобы получить 9000?
Ответ: на 12,5 %.
Теперь применение производной.
3. В распоряжении начальника имеется бригада рабочих в составе 24 человек. Их нужно распределить на день на два объекта. Если на первом объекте работает t человек, то их суточная зарплата составляет условных единиц. Если на втором объекте работает t человек, то их суточная зарплата составляет
у. е. (условных единиц). Как нужно распределить на эти объекты бригаду рабочих, чтобы выплаты на их суточную зарплату оказались наименьшими? Сколько у. е. в этом случае придется заплатить рабочим?
Обратите внимание, что в этой задаче переменная t — это не время! Переменная t здесь — некий параметр, через который выражены количество работающих на объекте человек и их суточная зарплата.
Сколько человек работает на каждом объекте? Мы не знаем. Нам надо найти, сколько должно быть рабочих на каждом объекте, чтобы затраты на оплату их труда оказались наименьшими.
Пусть на первом объекте работает х человек. Тогда на втором 24 —х человек, поскольку всего в бригаде 24 рабочих. Запишем данные задачи в таблицу:
Пусть функция — зависимость затрат на оплату труда рабочих от количества рабочих на первом объекте.
Найдем наименьшее значение функции Раскроем скобки в формуле функции:
Мы можем взять производную и найти . А можем просто заметить, что
— квадратичная парабола с ветвями вверх. Наименьшее ее значение достигается при
— то есть в вершине параболы.
Да, но ведь число рабочих на первом объекте — целое, и оно никак не может быть равно 4,8. Что же делать?
Найдем значения функции при
и
— то есть в ближайших к точке минимума целых точках.
Значит, оптимальное распределение рабочих по объектам — это 5 рабочих на первом объекте и 19 на втором. Затраты на оплату их труда в этом случае составляют 461 у.е.
И еще одна задача на производную.
4. Алексей приобрёл ценную бумагу за 7 тыс. рублей. Цена бумаги каждый год возрастает на 2 тыс. рублей. В любой момент Алексей может продать бумагу и положить вырученные деньги на банковский счёт. Каждый год сумма на счёте будет увеличиваться на 10%. В течение какого года после покупки Алексей должен продать ценную бумагу, чтобы через тридцать лет после покупки этой бумаги сумма на банковском счёте была наибольшей?
Пока Алексей не продал ценную бумагу, ее стоимость ежегодно увеличивается на 2 тысячи рублей. Через n лет ее стоимость равна тысяч рублей.
Когда Алексей (через n лет после покупки) продал ценную бумагу и положил деньги на банковский счет, сумма на счете ежегодно увеличивается на 10% (то есть в 1,1 раза) в течение 30 — n лет.
Значит, через 30 лет после приобретения ценной бумаги эта сумма равна
Рассмотрим функцию совпадающую с
при целых значениях х, и найдем ее наибольшее значение на отрезке
Мы знаем, как найти наибольшее значение функции на отрезке. Взять производную, приравнять ее к нулю, найти точки экстремума, сравнить значения в точке максимума и на концах отрезка.
Приравняем производную к нулю. Поскольку , исследуем знак выражения
при
если
если
Значит, точка — точка максимума функции S(x).
Хорошо, но чем это нам поможет? Ведь значение невозможно посчитать без калькулятора. Тупик? Зря вычисляли производную?
Нет, не зря. Мы выяснили, что функция стоимости ценной бумаги имеет точку максимума, причем единственную. И если в определенный момент не продать эту ценную бумагу, в итоге ее стоимость будет меньше максимально возможной.
Как же вычислить этот момент? Найдем, после скольких лет хранения будет более выгодно продать ценную бумагу и положить деньги на счет, чем продолжать хранить.
При хранении бумаги ее стоимость ежегодно увеличивается на 2 тысячи рублей. При продаже бумаги — увеличивается в 1,1 раза.
Пусть в момент продажи стоимость ценной бумаги равна
Если продать бумагу и положить деньги в банк сумма будет равна
Если продолжать хранить — получим
Необходимо выполнение условия:
Тогда k=8.
Этого условия достаточно, поскольку мы доказали, что функция S(x) имеет единственную точку максимума. Значит, ценную бумагу надо продать на восьмой год после ее приобретения.
Ответ: 8.
Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Задача 15 Профильного ЕГЭ по математике. Исследование функций и производная.» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
08.03.2023
БАЗА ЗАДАНИЙ
Задание № 15. Финансовая математика.
39. Григорий является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары, но на заводе, расположенном во втором городе, используется более совершенное оборудование. В результате, если рабочие на заводе, расположенном в первом городе, трудятся суммарно t2 часов в неделю, то за эту неделю они производят 3t единиц товара; если рабочие на заводе, расположенном во втором городе, трудятся суммарно t2 часов в неделю, то за эту неделю они производят 5t единиц товара. За каждый час работы (на каждом из заводов) Григорий платит рабочему 500 рублей. Григорий готов выделять 6 800 000 рублей в неделю на оплату труда рабочих. Какое наибольшее количество единиц товара можно произвести за неделю на этих двух заводах?
Ответ: 680
40. Владимир является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары, но на заводе, расположенном во втором городе, используется более совершенное оборудование. В результате, если рабочие на заводе, расположенном в первом городе, трудятся суммарно t2 часов в неделю, то за эту неделю они производят 4 t единиц товара; если рабочие на заводе, расположенном во втором городе, трудятся суммарно t2 часов в неделю, то за эту неделю они производят 5t единиц товара. За каждый час работы (на каждом из заводов) Владимир платит рабочему 500 рублей. Владимиру нужно каждую неделю производить 410 единиц товара. Какую наименьшую сумму придётся тратить еженедельно на оплату труда рабочих?
Ответ: 2050000 р
41. Вадим является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары при использовании одинаковых технологий. Если рабочие на одном из заводов трудятся суммарно t2 часов в неделю, то за эту неделю они производят t единиц товара. За каждый час работы на заводе, расположенном в первом городе, Вадим платит рабочему 200 рублей, а на заводе, расположенном во втором городе, — 300 рублей. Вадим готов выделять 1 200 000 рублей в неделю на оплату труда рабочих. Какое наибольшее количество единиц товара можно произвести за неделю на этих двух заводах?
Ответ: 100
42. Строительство нового завода стоит 75 млн рублей. Затраты на производство х тыс. ед. продукции на таком заводе равны 0,5x2 + x + 7 млн рублей в год. Если продукцию завода продать по цене р тыс. рублей за единицу, то прибыль фирмы (в млн рублей) за один год составит px — (0,5x2 + x + 7). Когда завод будет построен, фирма будет выпускать продукцию в таком количестве, чтобы прибыль была наибольшей. При каком наименьшем значении р строительство завода окупится не более, чем за 3 года?
Ответ: 9000 р
43. Пенсионный фонд владеет ценными бумагами, которые стоят t2 тыс. рублей в конце года t ( t=1; 2; …). В конце любого года пенсионный фонд может продать ценные бумаги и положить деньги на счёт в банке, при этом в конце каждого следующего года сумма на счёте будет увеличиваться на 10%. В конце какого года пенсионному фонду следует продать ценные бумаги, чтобы в конце двадцать пятого года сумма на его счёте была наибольшей?
Ответ: 21 год
44. Пенсионный фонд владеет ценными бумагами, которые стоят t2 тыс. рублей в конце года t (t=1; 2; … ). В конце любого года пенсионный фонд может продать ценные бумаги и положить деньги на счёт в банке, при этом в конце каждого следующего года сумма на счёте будет увеличиваться в 1+r раз. Пенсионный фонд хочет продать ценные бумаги в конце такого года, чтобы в конце двадцать пятого года сумма на его счёте была наибольшей. Расчёты показали, что для этого ценные бумаги нужно продавать строго в конце двадцать первого года. При каких положительных значениях r это возможно?
45. Первичная информация разделяется по серверам №1 и №2 и обрабатывается на них. С сервера №1 при объёме t2 Гбайт входящей в него информации выходит 20t Гбайт, а с сервера №2 при объёме t2 Гбайт входящей в него информации выходит 21t Гбайт обработанной информации; 25 < t < 55. Каков наибольший общий объём выходящей информации при общем объёме входящей информации в 3364 Гбайт?
Ответ: 1682
46. Зависимость объема Q (в шт.) купленного у фирмы товара от цены Р (в руб. за шт.) выражается формулой Q = 15000 — P, (1000 ≤ P ≤ 15000). Доход от продажи товара составляет PQ рублей. Затраты на производство Q единиц товара составляют 3000Q + 5000000 рублей.Прибыль равна разности дохода от продажи товара и затрат на его производство.Стремясь привлечь внимание покупателей, фирма уменьшила цену продукции на 20%, однако ее прибыль не изменилась. На сколько процентов следует увеличить сниженную цену, чтобы добиться наибольшей прибыли?
Ответ: 12,5%
47. Зависимость количества Q (в шт. 0 ≤ Q ≤ 15000) купленного у фирмы товара от цены P (в руб. за шт.) выражается формулой Q = 15000 — P. Затраты на производство Q единиц товара составляют 3000Q + 10000000 рублей. Кроме затрат на производство, фирма должна платить налог t рублей (0 < t < 10000) с каждой произведённой единицы товара. Таким образом, прибыль фирмы составляет PQ — 3000Q — 10000000 — tQ рублей, а общая сумма налогов, собранных государством, равна tQ рублей. Фирма производит такое количество товара, при котором её прибыль максимальна. При каком значении t общая сумма налогов, собранных государством, будет максимальной?
Ответ: 6000
48. В двух областях есть по 160 рабочих, каждый из которых готов трудиться по 5 часов в сутки на добыче алюминия или никеля. В первой области один рабочий за час добывает 0,1 кг алюминия или 0,1 кг никеля. Во второй области для добычи x кг алюминия в день требуется x2 человеко-часов труда, а для добычи у кг никеля в день требуется y2 человеко-часов труда.
Для нужд промышленности можно использовать или алюминий, или никель, причём 1 кг алюминия можно заменить 1 кг никеля. Какую наибольшую массу металлов можно за сутки суммарно добыть в двух областях?
Ответ: 120 кг
49. Строительство нового завода стоит 220 млн рублей. Затраты на производство х тыс. ед. продукции на таком заводе равны 0,5х2 + x + 7 млн рублей в год. Если продукцию завода продать по цене р тыс. рублей за единицу, то прибыль фирмы (в млн рублей) за один год составит px — (0,5х2 + x + 7). Когда завод будет построен, фирма будет выпускать продукцию в таком количестве, чтобы прибыль была наибольшей. В первый год после постройки завода цена продукции p = 9 тыс. руб. за единицу, каждый следующий год цена продукции увеличивается на 1 тыс. руб. за единицу. За сколько лет окупится строительство завода?
Ответ: 5 лет
50. Производство x тыс. единиц продукции обходится в q = 0,5x2 + x + 7 млн рублей в год. При цене p тыс. рублей за единицу годовая прибыль от продажи этой продукции (в млн рублей) составляет px − q. При каком наименьшем значении p через три года суммарная прибыль составит не менее 75 млн рублей?
Ответ: 9
51. В регионе А среднемесячный доход на душу населения в 2014 году составлял 43740 рублей и ежегодно увеличивался на 25%. В регионе Б среднемесячный доход на душу населения в 2014 году составлял 60000 рублей. В течение трех лет суммарный доход жителей региона Б увеличивался на 17% ежегодно, а население увеличивалось на m% ежегодно. В 2017 году среднемесячный доход на душу населения в регионах А и Б стал одинаковым. Найдите m.
Ответ: 4
52. По бизнес-плану четырёхлетний проект предполагает начальное вложение 12 млн рублей. По итогам каждого года планируется прирост вложенных средств на 15 % по сравнению с началом года. Начисленные проценты остаются вложенными в проект. Кроме этого, сразу после начислений процентов нужны дополнительные вложения: целое число n млн рублей в конце первого и второго года, а также целое число m млн рублей в конце третьего и четвёртого года. Найдите наименьшее значение n, при котором первоначальные вложения за два года как минимум удвоятся, и наименьшее такое значение m, что при найденном ранее значении n первоначальные вложения за четыре года как минимум утроятся.
Ответ: 4 и 2 млн руб.
53. По вкладу «А» банк в конце каждого года планирует увеличивать на 10 % сумму, имеющуюся на вкладе в начале года, а по вкладу «Б» — увеличивать эту сумму на 8 % в первый год и на одинаковое целое число n процентов и за второй, и за третий годы. Найдите наименьшее значение n, при котором за три года хранения вклад «Б» окажется выгоднее вклада «А» при одинаковых суммах первоначальных взносов.
Ответ: 12
1 2 3
54. В начале года Алексей приобрел ценные бумаги на сумму 9 тыс. рублей. В середине каждого года стоимость ценных бумаг возрастает на 2 тыс. рублей. В любой момент Алексей может продать ценные бумаги и положить вырученные деньги на банковский счет. В середине каждого года сумма на счете будет увеличиваться на 9%. В начале какого года после покупки Алексей должен продать ценные бумаги, чтобы через двадцать лет после покупки ценных бумаг сумма на банковском счете была наибольшей?
Ответ: 8
55. 15-го января планируется взять кредит в банке на 11 месяцев. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастает на 4% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
—15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.
Известно, что на шестой месяц кредитования выплата составит 25 тыс. рублей. Какую суму нужно вернуть банку в течение всего срока кредитования?
Ответ: 275 000 рублей.
56. Евгений хочет купить пакет акций быстрорастущей компании. В начале года у Евгения было недостаточно денег, а пакет стоил 195 000 рублей. В середине каждого месяца Евгений откладывает на покупку пакета акций одну и ту же сумму, а в конце месяца пакет дорожает, но не более чем на 40%. Какую наименьшую сумму нужно откладывать Евгению каждый месяц, чтобы через некоторое время выкупить желаемый пакет акций?
Ответ: 127 400 рублей.
57. Василий взял кредит в банке на срок 14 месяцев. В конце каждого месяца общая сумма оставшегося долга увеличивается на 8 %, а затем уменьшается на сумму, уплаченную Василием. Суммы, выплачиваемые в конце каждого месяца, подбираются так, чтобы в результате сумма долга каждый месяц уменьшалась равномерно, то есть на одну и ту же величину. Сколько процентов от суммы кредита составила общая сумма, уплаченная Василием банку?
Ответ: 160%.
Строительство нового завода стоит 75 млн рублей. Затраты на производство (x) тыс. ед. продукции на таком заводе равны (0{,}5x^2+x+7) млн рублей в год. Если продукцию завода продать по цене (p) тыс. рублей за единицу, то прибыль фирмы (в млн рублей) за один год составит (px-(0{,}5x^2+x+7)). Когда завод будет построен, фирма будет выпускать продукцию в таком количестве, чтобы прибыль была наибольшей. При каком наименьшем значении (p) строительство завода окупится не более чем за 3 года?
Подпишись на ютуб канал
Подписаться
Задание:
Строительство нового завода стоит 75 млн рублей. Затраты на производство x тыс. ед. продукции на таком заводе равны 0,5x2 + x + 7 млн рублей в год. Если продукцию завода продать по цене p тыс. рублей за единицу, то прибыль фирмы (в млн рублей) за один год составит px — (0.5x2 + x + 7). Когда завод будет построен, фирма будет выпускать продукцию в таком количестве, чтобы прибыль была наибольшей. При каком наименьшем значении p строительство завода окупится не более чем за 3 года?
Ответ: 9
Решение:
Экономическая задача ЕГЭ 2016 по математике. Задание №17. Строительство нового завода стоит 75 млн рублей. Затраты на производство х тыс. ед. продукции на таком заводе равны 0,5*x^2+x+7 млн рублей в год. Если продукцию завода продать по цене р тыс. рублей за единицу, то прибыль фирмы (в млн рублей) за один год составит px−(0,5*x^2+x+7). Когда завод будет построен, фирма будет выпускать продукцию в таком количестве, чтобы прибыль была наибольшей. При каком наименьшем значении р строительство завода окупится не более чем за 3 года? Дистанционные занятия онлайн для школьников и студентов здесь: http://sin2x.ru/ или здесь: http://асимптота.рф
- Категория
- Математика ЕГЭ Учеба и репетиторство
Написать комментарий
Добавил:
Upload
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Предмет:
Файл:
Скачиваний:
116
Добавлен:
20.03.2016
Размер:
21.37 Кб
Скачать
4
Лекция
14.02.2015. Задания
-
Применение
свойств квадратичной функции для
решения практических задач
-
Зависимость
объема спроса q (тыс.руб) на продукцию
предприятия-монополиста от цены p
(тыс.руб) задается формулой q=85-5p. Выручка
предприятия за месяц r (в тыс. руб)
вычисляется по формуле r(p)= q*p.
Определите наибольшую цену p, при
которой месячная выручка r(p) составит
не менее 300 тыс. руб. Ответ приведите в
тыс. руб.
Ответ:
12.
-
Задание
10 № 41337. Высота над землeй
подброшенного вверх мяча меняется по
закону,
где h — высота в метрах, t —
время в секундах, прошедшее с момента
броска. Сколько секунд мяч будет
находиться на высоте не менее 4 метров?
Ответ:
1.
-
Зависимость
температуры (в градусах Кельвина) от
времени (в минутах) для нагревательного
элемента некоторого прибора была
получена экспериментально и на
исследуемом интервале температур
даётся выражением T(t) =
T0+at+bt2 ,
где T0 = 580 К, a
= 20 К/мин, b
= -0,2 К/(мин).
Известно, что при температурах
нагревателя свыше 1000 К
прибор может испортиться, поэтому его
нужно отключать. Определите (в минутах)
через какое наибольшее время после
начала работы нужно отключать прибор.
Ответ:
30.
-
Зависимость
температуры (в градусах Кельвина) от
времени (в минутах) для нагревательного
элемента некоторого прибора была
получена экспериментально и на
исследуемом интервале температур
задаётся выражением T(t) = Т0 +
at + bt2, где Т0 =
900 К, а = 31 К/мин, Ь = —0,2 К/мин2. Известно,
что при температурах нагревателя свыше
1550 К прибор может испортиться, поэтому
его нужно отключать. Определите (в
минутах), через какое наибольшее
время после начала работы нужно
отключать прибор.
Ответ:
25.
II.
Задачи практического содержания на
нахождение наибольшего- наименьшего
значения.
Вспомогательная
задача
Найдите
наибольшее значение функции

Найдите
наименьшее значение функции
-
Владимир
является владельцем двух заводов в
разных городах. На заводах производятся
абсолютно одинаковые товары, но на
заводе, расположенном во втором городе,
используется более совершенное
оборудование. В результате, если рабочие
на заводе, расположенном в первом
городе трудятся суммарно
часов
в неделю, то за эту неделю они
производят 2t единиц товара. Если
рабочие на заводе, расположенном во
втором городе трудятся суммарно
часов
в неделю, то за эту неделю они производят 5t
единиц товара.
За
каждый час работы (на каждом из заводов)
Владимир платит рабочему 500 рублей.
Владимиру нужно каждую неделю производить
580 [410] единиц товара. Какую наименьшую
сумму придется тратить еженедельно на
оплату труда рабочих?
Ответ:5
800 000 [2050000] руб.
-
Антон
является владельцем двух заводов в
разных городах. На заводах производится
абсолютно одинаковые товары при
использовании одинаковых технологий.
Если рабочие на одном из заводов
трудятся суммарно t2 часов
в неделю, то за эту неделю они
производит t единиц товара. За
каждый час работы на заводе, расположенном
в первом городе, Антон платит рабочему
250 рублей, а на заводе, расположенном
во втором городе, — 200 рублей.
Антон
готов выделять 900 000 рублей в неделю на
оплату труда рабочих. Какое наибольшее
количество единиц товара можно произвести
за неделю на этих двух заводах?
Ответ:
90.
-
Производство
Х тыс., единиц продукции обходится в q
= 0,5
+ х+ 7 млн. рублей в год. При цене Р тыс.
рублей за единицу годовая прибыль от
продажи этой продукции (в милн. Рублей)
составляет рх-q. При каком наименьшем
значении р через три года суммарная
прибыль составит не менее 75 млн. рублей?
Ответ
: р=9.
-
Стоимость
разработки электронной версии учебника
некоторого издательства равна 800 тысяч
рублей. Если электронный учебник
продавать по цене «а» рублей за
единицу, то прибыль издательства ( в
тысячах рублей) за один год составит
«ах- (+6х+22100)».
Издательство будет выпускать электронные
учебники в таком количестве, чтобы
прибыль была наибольшей. При каком
наименьшем значении «а» разработка
учебника окупится более, чем за два
года?
Ответ:
306.
-
Строительство
нового завода обходится в 75 000 рублей.
Затраты на производство Х тыс.ед.
продукции на таком заводе равны 0,5+х+7
млн. рублей в год. При реализации
продукции завода по цене Р тыс. рублей
за единицу прибыль фирмы (в млн. рублей)
за один год составит рх-(0,5+х+7).
Когда завод будет построен, фирма будет
выпускать продукцию в таком количестве,
чтобы прибыль была наибольшей. При
каком наименьшем значении р строительство
завода окупится не более чем за 3 года? -
Строительство
нового цеха обходится в 39 млн. рублей.
Затраты на производство Х тыс.ед.
продукции в этом цеху равны 0,5+4х+19
млн. рублей в год. При реализации
продукции цеха по цене А тыс. рублей
за единицу прибыль фирмы (в млн. рублей)
за один год составит ах-(0,5+4х+19).
Когда цех будет построен, фирма будет
выпускать продукцию в таком количестве,
чтобы прибыль была наибольшей. При
каком наименьшем значении а строительство
завода окупится не более чем за 3 года?
III
Задачи
на вклады
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- Григорий является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары, но на заводе, расположенном во втором городе, используется более совершенное оборудование. В результате, если рабочие на заводе, расположенном в первом городе, трудятся суммарно t2 часов в неделю, то за эту неделю они производят t единиц товара; если рабочие на заводе, расположенном во втором городе, трудятся суммарно t2 часов в неделю, то за эту неделю они производят 2t единиц товара. За каждый час работы (на каждом из заводов) Григорий платит рабочему 500 рублей. Григорий готов выделять 30 250 000 рублей в неделю на оплату труда рабочих. Какое наибольшее количество единиц товара можно произвести за неделю на этих двух заводах?
2. Григорий является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары, но на заводе, расположенном во втором городе, используется более совершенное оборудование. В результате, если рабочие на заводе, расположенном в первом городе, трудятся суммарно t2
часов в неделю, то за эту неделю они производят 3t единиц товара; если рабочие на заводе, расположенном во втором городе, трудятся суммарно t2 часов в неделю, то за эту неделю они производят 4t единиц товара. За каждый час работы (на каждом из заводов) Григорий платит рабочему 500 рублей. Григорий готов выделять 5 000 000 рублей в неделю на оплату труда рабочих. Какое наибольшее количество единиц товара можно произвести за неделю на этих двух заводах?
3. Григорий является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары, но на заводе, расположенном во втором городе, используется более совершенное оборудование. В результате, если рабочие на заводе, расположенном в первом городе, трудятся суммарно
t2 часов в неделю, то за эту неделю они производят 3t единиц товара; если рабочие на заводе, расположенном во втором городе, трудятся суммарно t2 часов в неделю, то за эту неделю они производят 5t единиц товара. За каждый час работы (на каждом из заводов) Григорий платит рабочему 500 рублей. Григорий готов выделять 6 800 000 рублей в неделю на оплату труда рабочих. Какое наибольшее количество единиц товара можно произвести за неделю на этих двух заводах?
4. Владимир является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары, но на заводе, расположенном во втором городе, используется более совершенное оборудование. В результате, если рабочие на заводе, расположенном в первом городе, трудятся суммарно
t2 часов в неделю, то за эту неделю они производят 2t единиц товара; если рабочие на заводе, расположенном во втором городе, трудятся суммарно t2 часов в неделю, то за эту неделю они производят 5t единиц товара.
За каждый час работы (на каждом из заводов) Владимир платит рабочему 500 рублей. Владимиру нужно каждую неделю производить 580 единиц товара. Какую наименьшую сумму придётся тратить еженедельно на оплату труда рабочих?
5. Владимир является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары, но на заводе, расположенном во втором городе, используется более совершенное оборудование. В результате, если рабочие на заводе, расположенном в первом городе, трудятся суммарно
t2 часов в неделю, то за эту неделю они производят 4t единиц товара; если рабочие на заводе, расположенном во втором городе, трудятся суммарно t2 часов в неделю, то за эту неделю они производят 5t единиц товара.
За каждый час работы (на каждом из заводов) Владимир платит рабочему 500 рублей. Владимиру нужно каждую неделю производить 410 единиц товара. Какую наименьшую сумму придётся тратить еженедельно на оплату труда рабочих?
6. Владимир является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары, но на заводе, расположенном во втором городе, используется более совершенное оборудование. В результате, если рабочие на заводе, расположенном в первом городе, трудятся суммарно
t2 часов в неделю, то за эту неделю они производят 2t единиц товара; если рабочие на заводе, расположенном во втором городе, трудятся суммарно t2 часов в неделю, то за эту неделю они производят 3t единиц товара.
За каждый час работы (на каждом из заводов) Владимир платит рабочему 500 рублей. Владимиру нужно каждую неделю производить 520 единиц товара. Какую наименьшую сумму придётся тратить еженедельно на оплату труда рабочих?
7. Строительство нового завода стоит 75 млн рублей. Затраты на производство x тыс. ед. продукции на таком заводе равны 0,5х2 + х + 7 млн рублей в год. Если продукцию завода продать по цене p тыс. рублей за единицу, то прибыль фирмы (в млн рублей) за один год составит px – (0,5х2 + х + 7). Когда завод будет построен, фирма будет выпускать продукцию в таком количестве, чтобы прибыль была наибольшей. При каком наименьшем значении p строительство завода окупится не более чем за 3 года?
8. Строительство нового завода стоит 78 млн рублей. Затраты на производство x тыс. ед. продукции на таком заводе равны 0,5х2 +2х +6 млн рублей в год. Если продукцию завода продать по цене p тыс. рублей за единицу, то прибыль фирмы (в млн рублей) за один год составит px – (0,5х2 +2х +6). Когда завод будет построен, фирма будет выпускать продукцию в таком количестве, чтобы прибыль была наибольшей. При каком наименьшем значении p строительство завода окупится не более чем за 3 года?
9. Строительство нового завода стоит 122 млн рублей. Затраты на производство x тыс. единиц продукции на таком заводе равны 0,5х2 – 2х +10 − млн рублей в год. Если продукцию завода продать по цене p тыс. рублей за единицу, то прибыль фирмы (в млн рублей) за один год составит px- (0,5х2 – 2х +10). Когда завод будет построен, фирма будет выпускать продукцию в таком количестве, чтобы прибыль была наибольшей. При каком наименьшем значении p строительство завода окупится не более чем за 4 года?
10. Пенсионный фонд владеет ценными бумагами, которые стоят t2 тыс. рублей в конце года t (t = 1; 2; … ). В конце любого года пенсионный фонд может продать ценные бумаги и положить деньги на счёт в банке, при этом в конце каждого следующего года сумма на счёте будет увеличиваться на 10%. В конце какого года пенсионному фонду следует продать ценные бумаги, чтобы в конце двадцать пятого года сумма на его счёте была
наибольшей?
11. Пенсионный фонд владеет ценными бумагами, которые стоят t2 тыс. рублей в конце года t (t + 1; 2; … ). В конце любого года пенсионный фонд может продать ценные бумаги и положить деньги на счёт в банке, при этом в конце каждого следующего года сумма на счёте будет увеличиваться на 25%. В конце какого года пенсионному фонду следует продать ценные бумаги, чтобы в конце двадцатого года сумма на его счёте была наибольшей?
12. Пенсионный фонд владеет ценными бумагами, которые стоят t2 тыс. рублей в конце года t (t =1; 2; … ). В конце любого года пенсионный фонд может продать ценные бумаги и положить деньги на счёт в банке, при этом в конце каждого следующего года сумма на счёте будет увеличиваться в 1+r раз. Пенсионный фонд хочет продать ценные бумаги в конце такого года, чтобы в конце двадцатого года сумма на его счёте была наибольшей. Расчёты показали, что для этого ценные бумаги нужно продавать строго в конце девятого года. При каких положительных значениях r это возможно?
13. Пенсионный фонд владеет ценными бумагами, которые стоят t2 тыс. рублей в конце года t (t = 1; 2; … ). В конце любого года пенсионный фонд может продать ценные бумаги и положить деньги на счёт в банке, при этом в конце каждого следующего года сумма на счёте будет увеличиваться в 1+r раз. Пенсионный фонд хочет продать ценные бумаги в конце такого года, чтобы в конце двадцать пятого года сумма на его счёте была наибольшей. Расчёты показали, что для этого ценные бумаги нужно продавать строго в конце двадцать первого года. При каких положительных значениях r это возможно?




 ,
,

 часов
часов часов
часов
 +6х+22100)».
+6х+22100)». +х+7
+х+7 +х+7).
+х+7).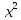 +4х+19
+4х+19 +4х+19).
+4х+19).