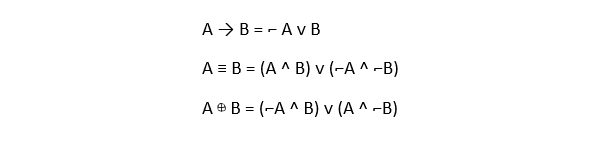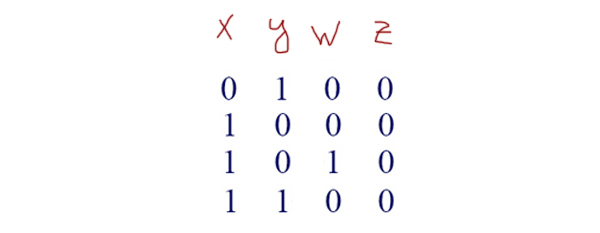На уроке рассматривается разбор 2 задания ЕГЭ по информатике, дается подробное объяснение того, как решать подобные задачи
Содержание:
- Объяснение задания 2 ЕГЭ по информатике
- Таблицы истинности и порядок выполнения логических операций
- Решение заданий 2 ЕГЭ по информатике
- Задания для тренировки
2-е задание: «Таблицы истинности»
Уровень сложности
— базовый,
Требуется использование специализированного программного обеспечения
— нет,
Максимальный балл
— 1,
Примерное время выполнения
— 3 минуты.
Проверяемые элементы содержания: Умение строить таблицы истинности и логические схемы
Типичные ошибки и рекомендации по их предотвращению:
«Игнорирование прямо указанного в условии задания требования, что заполненная таблица истинности не должна содержать одинаковых строк. Это приводит к внешне правдоподобному, но на самом деле неверному решению»
ФГБНУ «Федеральный институт педагогических измерений»
Таблицы истинности и порядок выполнения логических операций
Для логических операций приняты следующие обозначения:
| операция | пояснение | в программировании |
|---|---|---|
| ¬ A, A | не A (отрицание, инверсия) | not(A) |
| A ∧ B, A ⋅ B | A и B (логическое умножение, конъюнкция) | A and B |
| A ∨ B, A + B | A или B (логическое сложение, дизъюнкция) | A or B |
| A → B | импликация (следование) | A <= B |
| A ↔ B, A ≡ B, A ∼ B | эквиваленция (эквивалентность, равносильность) | A==B (python) A=B(pascal) |
| A ⊕ B | строгая дизъюнкция | A != B (python) A <> B (pascal) |
Егифка ©:
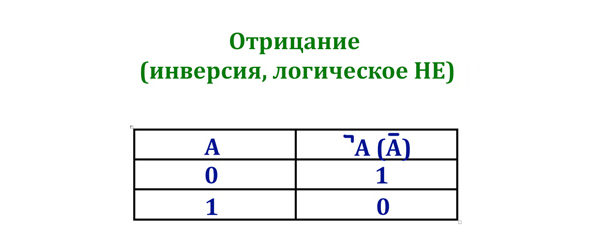
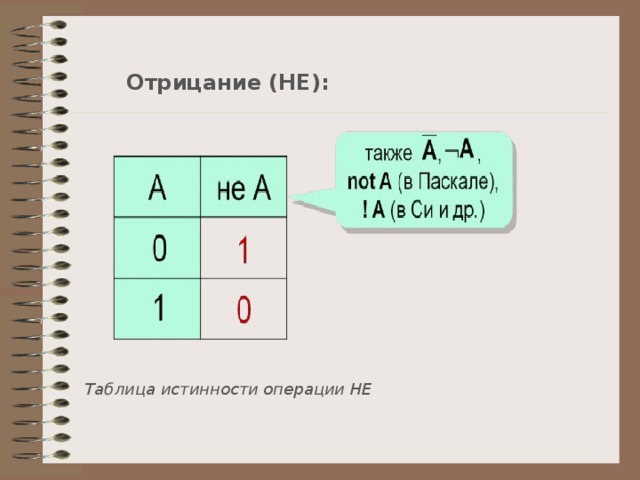
Отрицание (НЕ):
Таблица истинности операции НЕ
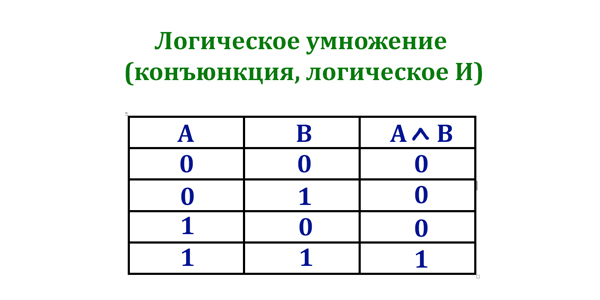
Конъюнкция (И):
Таблица истинности операции И (конъюнкция)
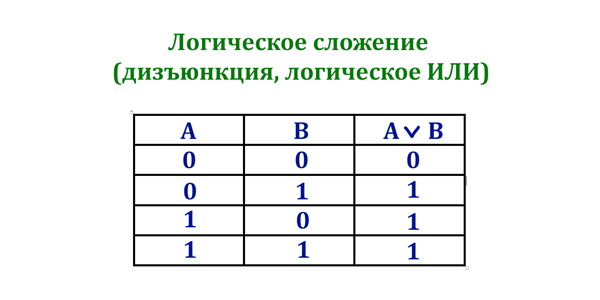
Дизъюнкция (ИЛИ):
Таблица истинности операции ИЛИ (дизъюнкция)
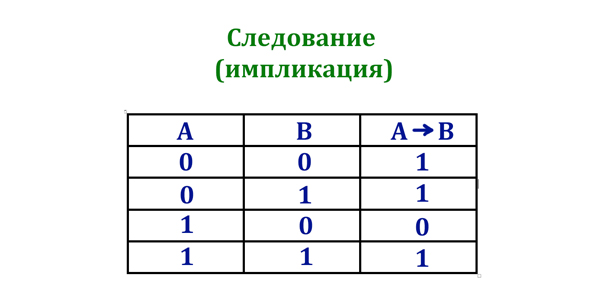
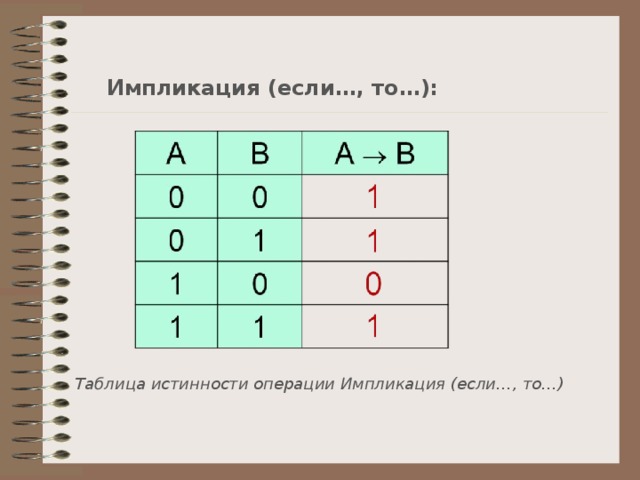
Импликация (если…, то…):
Таблица истинности операции Импликация (если…, то…)
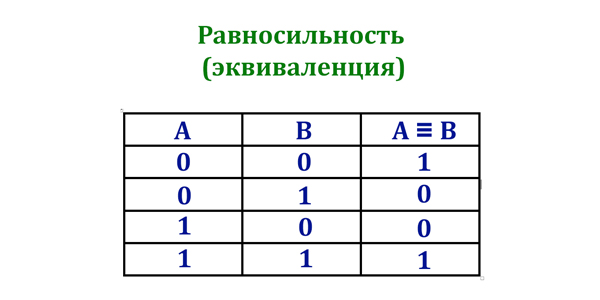
Эквивалентность (тогда и только тогда, …):
Таблица истинности операции Эквивалентность (тогда и только тогда, …)
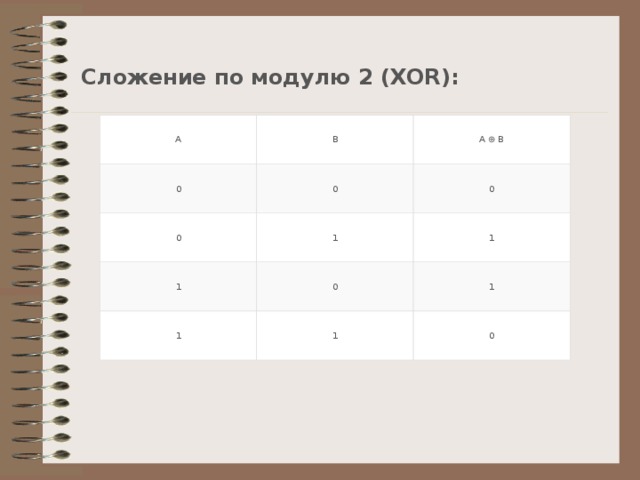
Сложение по модулю 2 (XOR):
| A | B | A ⊕ B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Порядок выполнения операций:
- если нет скобок, сначала выполняются все операции «НЕ», затем – «И», затем – «ИЛИ», импликация, равносильность
Еще о логических операциях:
- логическое произведение X∙Y∙Z∙… равно 1, т.е. выражение является истинным, только тогда, когда все сомножители равны 1 (а в остальных случаях равно 0)
- логическая сумма X+Y+Z+… равна 0, т.е. выражение является ложным только тогда, когда все слагаемые равны 0 (а в остальных случаях равна 1)
О преобразованиях логических операций читайте здесь.
Егифка ©:
Решение заданий 2 ЕГЭ по информатике
Задание 2_11: Решение 2 задания ЕГЭ по информатике:
Логическая функция F задается выражением
(¬x ∨ y ∨ z) ∧ (x ∨ ¬z ∨ ¬w)
Ниже приведен фрагмент таблицы истинности функции F, содержащей все наборы аргументов, при которых функция F ложна.
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.
| Перем.1 | Перем.2 | Перем.3 | Перем.4 | F |
| ??? | ??? | ??? | ??? | F |
| 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
В ответе запишите буквы в том порядке, в котором идут соответствующие им столбцы.
✍ Решение:
✎ Способ 1. Электронные таблицы Excel + Логические размышления:
- Отобразим перебор всех значений использующихся в выражении переменных (всю таблицу истинности). Поскольку в выражении используются 4 переменных, то строк таблицы будет 24=16:
- Далее обе скобки исходного выражения необходимо записать в виде логического выражения, каждую — в отдельном столбце. Также в отдельном столбце добавьте формулу итоговой функции F:

xwzy
-
✎ Способ 2. Программирование:
- В результате будут выведены значения для
F=0:
Язык python:
print('x y z w') for x in 0, 1: for y in 0, 1: for z in 0, 1: for w in 0, 1: F = (not(x) or y or z) and (x or not(z) or not(w)) if not(F): print(x, y, z, w)
x y z w 0 0 1 1 0 1 1 1 1 0 0 0 1 0 0 1
xwzy
Язык pascalAbc.net:
begin writeln('x':7, 'y':7, 'z':7,'w':7); for var x:=false to true do for var y:=false to true do for var z:=false to true do for var w:=false to true do if not((not x or y or z) and (x or not z or not w)) then writeln(x:7, y:7, z:7,w:7); end.
F=0:x y z w False False True True False True True True True False False False True False False True
false = 0, True = 1Ответ:
xwzy
-
✎ Способ 3. Логические размышления:
- Внешняя операция выражения — конъюнкция (∧). Во всех указанных строках таблицы истинности функция принимает значение 0 (ложь). Конъюнкция ложна аж в трех случаях, поэтому проверить на ложь очень затруднительно. Тогда как конъюнкция истинна (= 1) только в одном случае: когда все операнды истинны. Т.е. в нашем случае:
(¬x ∨ y ∨ z) ∧ (x ∨ ¬z ∨ ¬w) = 1 когда: 1. (¬x ∨ y ∨ z) = 1 И 2. (x ∨ ¬z ∨ ¬w) = 1
| x | y | z | результат |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
| x | z | w | результат |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
| x | y | z | w | F |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| x | y | z | w | F |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| x | ??? | ??? | ??? | F |
| 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| x | y | z | w | F |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| x | ??? | ??? | y | F |
| 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| x | y | z | w | F |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| x | w | z | y | F |
| 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
Результат: xwzy
🎦 Видеорешение (бескомпьютерный вариант):
📹 здесь
📹 Видеорешение на RuTube здесь
Задание 2_12: Разбор 2 задания ЕГЭ:
Миша заполнял таблицу истинности функции:
(¬z ∧ ¬(x ≡ y)) → ¬(y ∨ w)
но успел заполнить лишь фрагмент из трех различных ее строк, даже не указав, какому столбцу таблицы соответствует каждая из переменных w, x, y, z:
| Перем.1 | Перем.2 | Перем.3 | Перем.4 | F |
| ??? | ??? | ??? | ??? | F |
| 1 | 1 | 0 | ||
| 1 | 0 | 0 | ||
| 1 | 1 | 0 | 0 |
Определите, какому столбцу таблицы соответствует каждая из переменных x, y, z, w.
В ответе напишите буквы w, x, y, z в том порядке, в котором идут соответствующие им столбцы.
Подобные задания для тренировки
✍ Решение:
✎ Способ 1. Логические размышления (бескомпьютерный вариант):
- Решим задание методом построения полной таблицы истинности.
- Посчитаем общее количество строк в таблице истинности и построим ее:
4 переменных -> 24 = 16 строк
(¬z ∧ ¬(x ≡ y)) → ¬(y ∨ w) 1. Избавимся от импликации: ¬(¬z ∧ ¬(x ≡ y)) ∨ ¬(y ∨ w) 2. Внесем знак отрицания в скобки (закон Де Моргана): (z ∨ (x ≡ y)) ∨ (¬y ∧ ¬w) = 0 1 часть = 0 2 часть = 0 * Исходное выражение должно быть = 0. Дизъюнкция = 0, когда оба операнда равны 0.
(z ∨ (x ≡ y)) = 0 когда z = 0 и x ≡ y = 0 ¬y ∧ ¬w = 0 когда: 1. ¬y = 0 ¬w = 0 2. ¬y = 1 ¬w = 0 3. ¬y = 0 ¬w = 1
| x | y | w | z | F |
| 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 |
| y | w | x | z | F |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 0 |
Результат: ywxz
✎ Способ 2. Программирование:
- В результате будут выведены значения для F=0:
Язык PascalAbc.net:
begin writeln('x':7, 'y':7, 'z':7,'w':7); for var x:=false to true do for var y:=false to true do for var z:=false to true do for var w:=false to true do if not((not z and (x xor y)) <= not(y or w)) then writeln(x:7, y:7, z:7,w:7); end.
x y z w False True False False False True False True True False False True
false = 0, True = 1Сопоставив их с исходной таблицей, получим результат: ywxz
Язык Python:
print ('x y z w') for x in 0,1: for y in 0,1: for z in 0,1: for w in 0,1: F=(not z and not(x==y))<=(not(y or w)) if not F: print (x,y,z,w)
F=0:x y z w 0 1 0 0 0 1 0 1 1 0 0 1
Сопоставив их с исходной таблицей, получим результат:
Результат: ywxz
🎦 Доступно видео решения этого задания (бескомпьютерный вариант):
📹 здесь
📹 Видеорешение на RuTube здесь
🎦 Видео (решение 2 ЕГЭ в Excel):
📹 здесь
📹 Видеорешение на RuTube здесь
📹 Видеорешение на RuTube здесь (Программирование)
Задание 2_10: Решение 2 задания ЕГЭ по информатике:
Логическая функция F задается выражением
¬a ∧ b ∧ (c ∨ ¬d)
Ниже приведен фрагмент таблицы истинности функции F, содержащей все наборы аргументов, при которых функция F истинна.
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных a, b, c, d.
| Перем.1 | Перем.2 | Перем.3 | Перем.4 | F |
| ??? | ??? | ??? | ??? | F |
| 0 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 1 |
В ответе запишите буквы в том порядке, в котором идут соответствующие им столбцы.
✍ Решение:
🎦 (Бескомьютерный вариант) Предлагаем подробный разбор посмотреть на видео:
📹 здесь
📹 Видеорешение на RuTube здесь
Задание 2_3: Решение задания 2. Демоверсия ЕГЭ 2018 информатика:
Логическая функция F задаётся выражением ¬x ∨ y ∨ (¬z ∧ w).
На рисунке приведён фрагмент таб. ист-ти функции F, содержащий все наборы аргументов, при которых функция F ложна.
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных w, x, y, z.
| Перем. 1 | Перем. 2 | Перем. 3 | Перем. 4 | F |
| ??? | ??? | ??? | ??? | F |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 |
В ответе напишите буквы w, x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала – буква, соответствующая первому столбцу; затем – буква, соответствующая второму столбцу, и т.д.) Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Подобные задания для тренировки
✍ Решение:
-
✎ Логические размышления (бескомпьютерный вариант):
- Внешним действием (последним выполняемым) в исходном выражении является дизъюнкция:
¬x ∨ y ∨ (¬z ∧ w)
| x1 | x2 | F |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
¬x = 1 или 0, y = 1 или 0, ¬z ∧ w = 1 или 0).¬x = 0, иными словами x = 1. Значит первый столбец соответствует переменной x. | Перем. 1 | Перем. 2 | Перем. 3 | Перем. 4 | F |
| x | ??? | ??? | ??? | F |
| 1 | 0 | 0 | 0 | 0 |
y = 0. Значит четвертый столбец соответствует переменной y. | Перем. 1 | Перем. 2 | Перем. 3 | Перем. 4 | F |
| x | ??? | ??? | y | F |
| 1 | 1 | 1 | 0 | 0 |
¬z ∧ w должно равняться 0, чтобы функция была ложной. Конъюнкция истинна только тогда, когда оба операнда истинны (=1); в нашем случае функция должна быть ложной, но пойдем от обратного. Если ¬z = 1, т.е. z = 0, а w = 1, то это неверно для нашего случая. Значит всё должно быть наоборот: z = 1, а w = 0. Таким образом столбец второй соответствует z, а столбец третий — w. | x | z | w | y | F |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 |
Результат: xzwy
✎ Способ 2. Программирование:
Язык pascalABC.NET:
begin writeln('x ','y ','z ','w '); for var x:=false to true do for var y:=false to true do for var z:=false to true do for var w:=false to true do if not(not x or y or(not z and w)) then writeln(x:7,y:7,z:7,w:7); end.
🎦 (бескомпьютерный вариант) Подробное решение данного 2 задания из демоверсии ЕГЭ 2018 года смотрите на видео:
📹 здесь
📹 Видеорешение на RuTube здесь
Задание 2_13: Разбор досрочного егэ по информатике 2019
Логическая функция F задаётся выражением
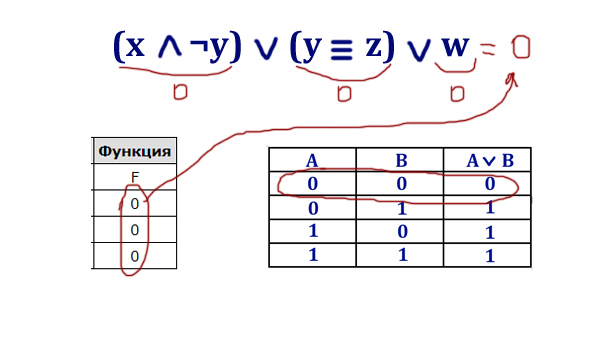
(x ∧ ¬y) ∨ (y ≡ z) ∨ ¬w
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.
В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы.
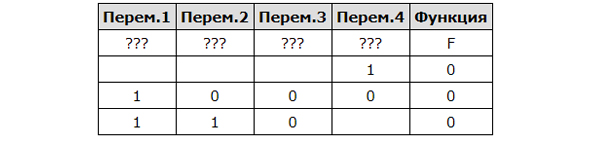
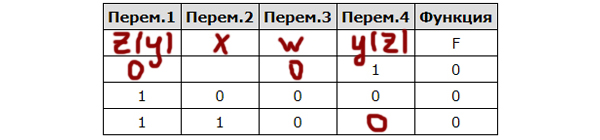
| Перем.1 | Перем.2 | Перем.3 | Перем.4 | F |
| ??? | ??? | ??? | ??? | F |
| 0 | 0 | 0 | ||
| 0 | 1 | 0 | 1 | 0 |
| 1 | 0 | 0 |
✍ Решение:
🎦 Видеорешение (бескомпьютерный вариант):
📹 здесь
📹 Видеорешение на RuTube здесь
Задания для тренировки
Задание 2_2: Задание 2 ЕГЭ по информатике:
Каждое из логических выражений F и G содержит 5 переменных. В табл. истинности для F и G есть ровно 5 одинаковых строк, причем ровно в 4 из них в столбце значений стоит 1.
Сколько строк таблицы истинности для F ∨ G содержит 1 в столбце значений?
Подобные задания для тренировки
✍ Решение:
- Поскольку в каждом из выражений присутствует 5 переменных, то эти 5 переменных порождают таблицу истинности из 32 строк: т.к. каждая из переменных может принимать оно из двух значений (0 или 1), то различных вариантов с пятью переменными будет 25=32, т.е. 32 строки.
- Из этих 32 строк и для F и для G мы знаем наверняка только о 5 строках: 4 из них истинны (=1), а одна ложна (=0).
- Вопрос стоит о количестве строк = 1 для таб. истинности F ∨ G. Данная операция — дизъюнкция, которая ложна только в одном случае — если F = 0 и одновременно G = 0
- В исходных таблицах для F и G мы знаем о существовании только одного 0, т.е. в остальных строках может быть 1. Т.о., и для F и для G в 31 строке могут быть единицы (32-1=31), а лишь в одной — ноль.
- Тогда для F ∨ G только в одном случае будет 0, когда и F = 0 и G = 0:
- Соответственно, истинными будут все остальные строки:
| № | F | G | F ∨ G |
|---|---|---|---|
| 1 | 0 | 0 | 0 |
| 2 | 0 | 1 | 1 |
| … | … | … | 1 |
| 32 | … | … | 1 |
32 - 1 = 31
Результат: 31
Подробное объяснение данного задания смотрите на видео:
📹 здесь
Задание 2_6: Решение 2 задания ЕГЭ по информатике:
Каждое логическое выражение A и B зависит от одного и того же набора из 7 переменных. В таблицах истинности каждого из этих выражений в столбце значений стоит ровно по 4 единицы.
Каково максимально возможное число единиц в столбце значений таблицы истинности выражения A ∨ B?
✍ Решение:
- Полная таблица истинности для каждого из выражений A и B состоит из 27 = 128 строк.
- В четырех из них результат равен единице, значит в остальных — 0.
- A ∨ B истинно в том случае, когда либо A = 1 либо B = 1, или и A и B = 1.
- Поскольку А = 1 только в 4 случаях, то чтобы получить максимальное количество единиц в результирующей таблице истинности (для A ∨ B), расположим все единицы т.и. для выражения A так, чтобы они были в строках, где B = 0, и наоборот, все строки, где B = 1, поставим в строки, где A = 0:
- Итого получаем 8 строк.
- Если бы в задании требовалось найти минимальное количество единиц, то мы бы совместили строки со значением = 1, и получили бы значение 4.
| A | B |
| 1 | 0 |
| 1 | 0 |
| 1 | 0 |
| 1 | 0 |
| 0 | 1 |
| 0 | 1 |
| 0 | 1 |
| 0 | 1 |
| 0 | 0 |
| … | … |
Результат: 8
Задание 2_7: Решение 2 задания ЕГЭ по информатике:
Каждое логическое выражение A и B зависит от одного и того же набора из 8 переменных. В таблицах истинности каждого из этих выражений в столбце значений стоит ровно по 6 единиц.
Каково максимально возможное число нулей в столбце значений таблицы истинности выражения A ∧ B?
✍ Решение:
- Полная таблица истинности для каждого из выражений A и B состоит из 28 = 256 строк.
- В шести из них результат равен единице, значит в остальных — 0.
- A ∧ B ложно в том случае, когда:
A ∧ B = 0 если: 1. A = 0, B = 1 2. B = 0, A = 1 3. A = 0 и B = 0
- Во всех случаях там где А=1 может стоять B=0, и тогда результат F = 0. Поскольку нам необходимо найти максимально возможное число нулей, то как раз для всех шести А=1 сопоставим B=0, и наоборот, для всех шести возможных B=1 сопоставим A=0
- Поскольку строк всего 256, то вполне возможно, что все 256 из них возвратят в результате 0
| A | B | F |
| 1 | 0 | 0 |
| 1 | 0 | 0 |
| 1 | 0 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 1 | 0 |
| 0 | 1 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 0 |
| … | … | … |
Результат: 256
Задание 2_4: 2 задание:
Дан фрагмент таблицы истинности выражения F.
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | F |
| 1 | 0 | 0 | 1 | 1 | 1 | 1 | 0 |
| 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 |
Каким из приведённых ниже выражений может быть F?
1) ¬x1 ∧ x2 ∧ ¬x3 ∧ ¬x4 ∧ x5 ∧ ¬x6 ∧ x7
2) x1 ∨ x2 ∨ x3 ∨ ¬x4 ∨ ¬x5 ∨ ¬x6 ∨ ¬x7
3) x1 ∧ ¬x2 ∧ x3 ∧ ¬x4 ∧ x5 ∧ x6 ∧ ¬x7
4) x1 ∨ ¬x2 ∨ x3 ∨ x4 ∨ ¬x5 ∨ ¬x6 ∨ x7
✍ Решение:
- В первом внешняя операция (выполняется последней) — конъюнкция. Начнем рассмотрение с нее. Соответственно, проверяем по второй строке таб. ист-ти, там где F = 1, так как в таком случае все аргументы должны быть истинными (см. таб. истинности для конъюнкции).
- Если мы подставим в нее все аргументы выражения, то функция действительно возвращает истину. Т.е. пункт первый подходит:
- Но проверим на всякий случай остальные.
- Второй пункт проверяем по первой и третьей строке, так как основная операция — дизъюнкция — ложна только в том случае, если все аргументы ложны (см. таб. истинности для дизъюнкции). Проверяя по первой строке, сразу видим, что x1 в ней равен 1. В таком случаем функция будет = 1. Т.е. этот пункт не подходит:
- Третий пункт проверяем по второй строке, так как основная операция — конъюнкция — возвратит истину только тогда, когда все операнды равны 1. Видим, что x1 = 0, соответственно функция будет тоже равна 0. Т.е. выражение нам не подходит:
- Четвертый пункт проверяем по первой и третьей строкам. В первой — x1 = 1, т.е. функция должна быть равна 1. Т.е. пункт тоже не подходит:
- Таким образом, ответ равен 1.
Результат: 1
Решение 2 задания ГВЭ по информатике смотрите на видео:
📹 здесь
Задание 2_8: Решение 2 задания ЕГЭ по информатике:
Дано логическое выражение, зависящее от 5 логических переменных:
(¬x1 ∨ ¬x2 ∨ ¬x3 ∨ x4 ∨ x5) ∧ (x1 ∨ x2 ∨ x3 ∨ ¬x4 ∨ ¬x5)
Сколько существует различных наборов значений переменных, при которых выражение истинно?
1) 0
2) 30
3) 31
4) 32
Подобные задания для тренировки
✍ Решение:
- Поскольку выражение включает 5 переменных, то таб. ист-ти состоит из 25 = 32 строк.
- Внешней операцией (последней) является конъюнкция (логическое умножение), а внутри скобок — дизъюнкция (логическое сложение).
- Обозначим первую скобку за А, а вторую скобку за B. Получим A ∧ B.
- Найдем сколько нулей существует для таб. истинности:
A B F 1. 0 0 0 2. 0 1 0 3. 1 0 0
Теперь рассмотрим каждый случай отдельно:
¬x1 ∨ ¬x2 ∨ ¬x3 ∨ x4 ∨ x5 = 0
и
x1 ∨ x2 ∨ x3 ∨ ¬x4 ∨ ¬x5 = 0.
32 - 2 = 30, что соответствует номеру 2
Результат: 2
Подробное решение задания смотрите в видеоуроке:
📹 здесь
Задание 2_5: Решение 2 задания ЕГЭ по информатике:
Дан фрагмент таблицы истинности для выражения F:
| x1 | x2 | x3 | x4 | x5 | x6 | F |
| 0 | 0 | 1 | 1 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 0 | 1 | 0 |
Укажите максимально возможное число различных строк полной таблицы истинности этого выражения, в которых значение x3 не совпадает с F.
Подобные задания для тренировки
✍ Решение:
- Полная таблица истинности будет иметь 26 = 64 строк (т.к. 6 переменных).
- 4 из них нам известны: в них x3 два раза не совпадает с F.
- Неизвестных строк:
64 - 4 = 60
60 + 2 = 62
Результат: 62
Задание 2_9: Решение 2 задания ЕГЭ по информатике:
Дан фрагмент таблицы истинности для выражения F:
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | F |
| 0 | 0 | 0 | |||||
| 0 | 0 | 1 | |||||
| 1 | 1 | 1 |
Каким выражением может быть F?
1) x1 ∧ (x2 → x3) ∧ ¬x4 ∧ x5 ∧ x6 ∧ ¬x7
2) x1 ∨ (¬x2 → x3) ∨ ¬x4 ∨ ¬x5 ∨ x6 ∨ ¬x7
3) ¬x1 ∧ (x2 → ¬x3) ∧ x4 ∧ ¬x5 ∧ x6 ∧ x7
4) ¬x1 ∨ (x2 → ¬x3) ∨ x4 ∨ x5 ∨ x6 ∧ x7
✍ Решение:
- Рассмотрим отдельно каждый пункт и найдем последнюю операцию, которая должна быть выполнена (внешнюю).
1 пункт:
(((x1 ∧ (x2 → x3) ∧ ¬x4) ∧ x5) ∧ x6) ∧ ¬x7
2 пункт:
(((x1 ∨ (¬x2 → x3) ∨ ¬x4) ∨ ¬x5) ∨ x6) ∨ ¬x7
3 пункт:
(((¬x1 ∧ (x2 → ¬x3) ∧ x4) ∧ ¬x5) ∧ x6) ∧ x7
Результат: 4
В видеоуроке рассмотрено подробное решение 2 задания:
📹 здесь
Задание 2_1: Задание 2 ЕГЭ по информатике:
Логическая функция F задается выражением
(y → x) ∧ (y → z) ∧ z.
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z.
| № | Перем. 1 | Перем. 2 | Перем. 3 | F |
|---|---|---|---|---|
| ??? | ??? | ??? | F | |
| 1 | 0 | 0 | 0 | 0 |
| 2 | 0 | 0 | 1 | 0 |
| 3 | 0 | 1 | 0 | 1 |
| 4 | 0 | 1 | 1 | 1 |
| 5 | 1 | 0 | 0 | 0 |
| 6 | 1 | 0 | 1 | 0 |
| 7 | 1 | 1 | 0 | 0 |
| 8 | 1 | 1 | 1 | 1 |
В ответе напишите буквы x, y, z в том порядке, в котором идут соответствующие им столбцы.
✍ Решение:
- Сначала необходимо рассмотреть логическую операцию, которую мы будем выполнять в последнюю очередь — это логическое И (конъюнкция) или ∧. То есть внешнюю операцию:
(y → x) ∧ (y → z) ∧ z
(y → x) ∧ (y → z) ∧ z = 1 если: 1. (y → x) = 1 2. (y → z) = 1 3. z = 1
| № | Перем. 1 | Перем. 2 | Перем. 3 | F |
|---|---|---|---|---|
| 3 | 0 | 1 | 0 | 1 |
| № | Перем. 1 | Перем. 2 | Перем. 3 | F |
|---|---|---|---|---|
| _ | ??? | z | ??? | F |
| № | Перем. 1 | z | Перем. 3 | F |
|---|---|---|---|---|
| 4 | 0 | 1 | 1 | 1 |
Результат: yzx
Детальный разбор данного задания 2 ЕГЭ по информатике предлагаем посмотреть в видео:
📹 здесь
Здравствуйте, дорогие друзья! Сегодня разберём, как решать второе задание из ЕГЭ по информатике 2020.
Во втором задании ЕГЭ по информатике у нас обычно есть логическая функция, которая зависит от логических переменных. Логические переменные могут принимать только два значения: 0 (Ложь) или 1 (Истина).
С логическими переменными можно производить логические операции. При решении второго задания из ЕГЭ по информатике необходимо твёрдо знать каждую логическую операцию, и давайте рассмотрим их.
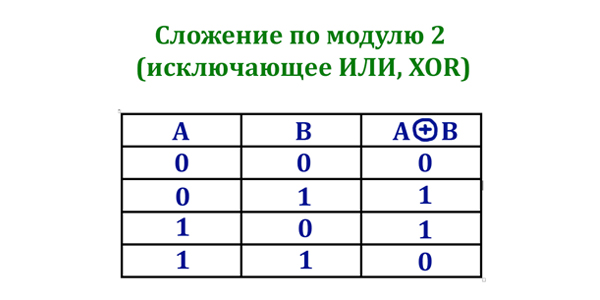
- () — операции в скобках
- ¬ — логическое отрицание
- ∧ — логическое умножение
- ∨ — логическое сложение
- ⟶ — следование
- ≡ — равнозначность
Так же на ЕГЭ по информатике будет полезно знать логические формулы :
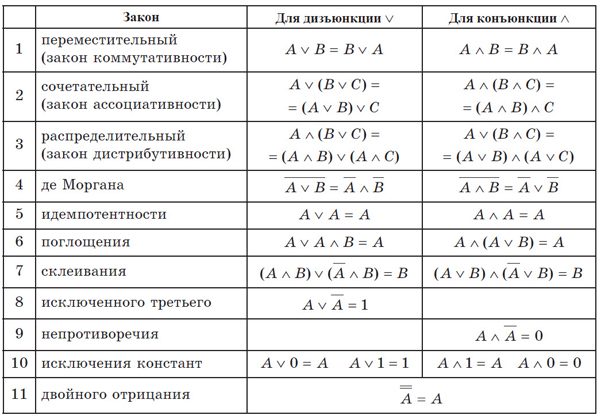
Передём к решению задач из ЕГЭ по информатике
Задача 1 (лёгкая)
Логическая функция F задаётся выражением z ∧ ¬y ∧ (w → x).
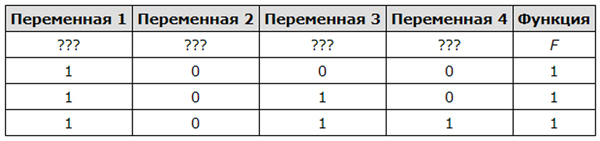
Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности функции F.
Определите, какому столбцу таблицы истинности соответствует каждая из переменных x, y, z, w.
В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы (сначала буква, соответствующая первому столбцу; затем буква, соответствующая второму столбцу, и т. д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Пример. Пусть задано выражение x → y, зависящее от двух переменных x и y, и фрагмент таблицы истинности:
Тогда первому столбцу соответствует переменная y, а второму столбцу соответствует переменная x. В ответе нужно написать: yx.
Решение:
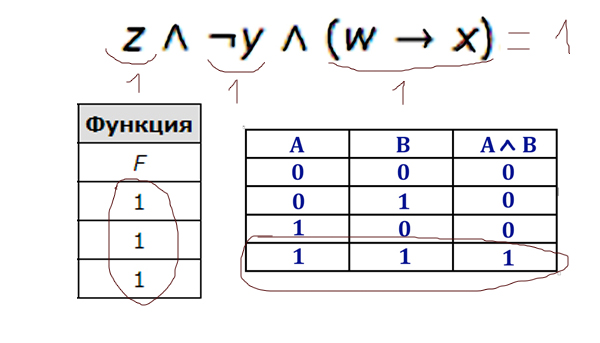
Видим, что у функции основным действием является логическое умножение. По таблице видно, что функция имеет значение только 1 . Логическое умножение даёт 1 (единицу) тогда, когда каждое выражение равно 1 (единице). Значит каждое выражение в нашей функции должно равняться единице.
Отсюда видно, что переменная z должна всегда быть равна 1 (единице). Это первый столбец. Отрицание y тоже должно быть 1 (единицей), тогда просто y всегда будет 0 (нулём). Это второй столбец.
Осталось определить положение w и x. Здесь делаем предположение, что в третьем столбце стоит w, а в 4-ом x. Проверяем построчно и видим, что во второй строчке при таком расположении из 1 следует 0, что в итоге приводит выражение (w → x) в 0, а у нас это выражение всегда должно быть 1 (единицей). Значит, мы предположение сделали неверное, и получается x — это третий столбец, а w — четвёртый.
Ответ: zyxw
Задача 2 (средний уровень)
Логическая функция F задаётся выражением (x ∧ ¬y) ∨ (y ≡ z) ∨ w.
Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности функции F.
Определите, какому столбцу таблицы истинности соответствует каждая из переменных x, y, z, w.
В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы (сначала — буква, соответствующая первому столбцу; затем — буква, соответствующая второму столбцу, и т. д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Пример. Пусть задано выражение x → y, зависящее от двух переменных x и y, и фрагмент таблицы истинности:
Тогда первому столбцу соответствует переменная y, а второму столбцу соответствует переменная x. В ответе нужно написать: yx.
Решение:
Определяем главную логическую операцию («главную скрипку»), которая соединяет разные выражения. Видим, что это логическое сложение.
Во всех строчках таблицы функция принимает значение 0 (ноль). Значит, и каждое выражение должно принимать значение 0 (ноль).
Самым слабым звеном является переменная w, потому что она стоит одна. Переменная w должна равняться всегда 0(нулю) — этому условию может удовлетворить только третий столбец. Значит w стоит на третьем месте.
Следующим слабым звеном является равносильность. Она должна «выдавать» 0 (ноль). Равносильность «выдаёт» 0 (ноль), когда переменные разные!
Проанализируем первый и второй столбец. В третьей строчке, и там, и там, стоит 1 (единица). Значит, первый и второй столбец не могут быть одновременно y и z (или z и y).
Рассмотрим второй и четвёртый столбец. Вторая строчка содержит одинаковое значение 0 (ноль), и там, и там. Значит, второй и четвёртый столбец не могут быть одновременно y и z (или z и y).
Таким образом, y и z (или z и y) будут столбцы первый и четвёртый! И теперь можно расставить недостающие значения в этих столбцах. Расставляем, чтобы были разные значения, а второй столбец получается x.
Осталось разобраться с z и y. Обратимся к первому выражению (x ∧ ¬y) и посмотрим на третью строчку. Если в четвёртом столбце будет стоять y, то отрицание на y превратит ноль(ноль) в 1(единицу) в четвёртой строчке. Тогда окажется, что у x — 1 и ¬y — 1, и выражение (x ∧ ¬y) тоже получится 1(единицей). А у нас каждое выражение должно равняться 0(нулю). Получается y будет стоять в первом столбце, а z в четвёртом.
Тогда ответ будет равен yxwz.
Ответ: yxwz
Мощнейший метод для решения второго задания из ЕГЭ по информатике
Задача 3 (хороший уровень)
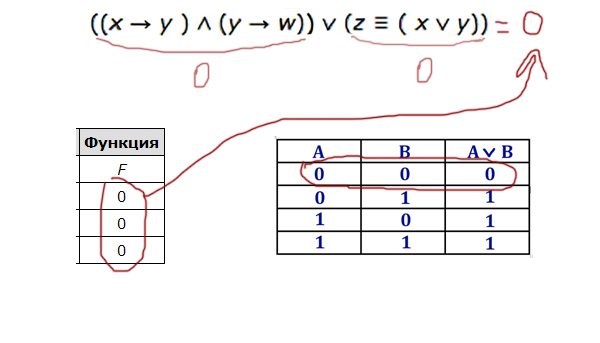
Логическая функция F задаётся выражением ((x → y ) ∧ (y → w)) ∨ (z ≡ ( x ∨ y)).
Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности функции F.
Определите, какому столбцу таблицы истинности соответствует каждая из переменных x, y, z, w.
В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы (сначала — буква, соответствующая первому столбцу; затем — буква, соответствующая второму столбцу, и т. д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Пример. Пусть задано выражение x → y, зависящее от двух переменных x и y, и фрагмент таблицы истинности:
Тогда первому столбцу соответствует переменная y, а второму столбцу соответствует переменная x. В ответе нужно написать: yx.
Решение:
«Главной скрипкой» в нашей функции является логическое сложение, потому что соединяет два выражения ((x → y ) ∧ (y → w)) и (z ≡ ( x ∨ y)).
Тогда каждое выражение должно равняться 0(нулю).
Теперь кульминация мощнейшего метода. У нас всего 4 переменных. Выпишем все комбинации для 4-х переменных. Таблица будет точно такая же, как мы писали в первом задании (её очень легко составить). Всего получается 16 комбинаций (16 = 24).
Теперь отметим зелёным плюсом те строчки, которые обращают выражение ((x → y ) ∧ (y → w)) в 0(ноль). Следующий шаг: Отметим галочкой те строчки, которые обращают в ноль второе выражение (z ≡ ( x ∨ y)) (Мы должны искать среди тех, которые уже отмечены плюсом).
При небольшой тренировке анализ подобных выражений занимает сущие секунды!
У нас получается 4 строчки, которые удовлетворяют нашей функции:
Отсюда видно, что переменная z может быть равна только 0(нулю)! Значит, она занимает третий столбец, потому что в остальных столбцах есть хотя бы одна 1(единица).
Переменная w имеет только одну 1(единицу). Значит, её ставим во второй столбец, потому что в первом и четвёртом уже по 2 единицы минимум, а третий уже занят z.
Теперь находим строчку c 1(единицей) в переменной w (Таблица данная в условии задачи) Кто в этой строчке будет иметь единицу (кроме w) — будет x! Это четвёртый столбец! Значит, x — это четвёртый столбец. Переменной y — достаётся первый столбец
Ответ: ywzx.
На этом всё! Сегодня рассмотрели теорию и основные методы для эффективного решения второго задания из ЕГЭ по информатике!
Пока!
В спецификации написано, что эту задачу нужно решать без компьютера. Тем более её решить совсем не сложно с помощью «Мощнейшего метода».
Да ужметод. На простых заданиях разбирать можно
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Логическая функция F задаётся выражением (x ∨ y) → (z ≡ x).
Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности функции F.
Определите, какому столбцу таблицы истинности соответствует каждая из переменных x, y, z.
| Переменная 1 | Переменная 2 | Переменная 3 | Функция |
|---|---|---|---|
| ??? | ??? | ??? | F |
| 0 | 0 | 0 | |
| 0 | 0 |
В ответе напишите буквы x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала – буква, соответствующая первому столбцу; затем – буква, соответствующая второму столбцу, и т. д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Пример. Пусть задано выражение x → y, зависящее от двух переменных x и y, и фрагмент таблицы истинности:
| Переменная 1 | Переменная 2 | Функция |
|---|---|---|
| ??? | ??? | F |
| 0 | 1 | 0 |
Тогда первому столбцу соответствует переменная y, а второму столбцу соответствует переменная x. В ответе нужно написать: yx.
Источник: СтатГрад: Тренировочная работа 28.11.2017 ИН10203
2
Логическая функция F задаётся выражением (x ≡ z ) ∨ (x → (y ∧ z)).
Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности функции F.
Определите, какому столбцу таблицы истинности соответствует каждая из переменных x, y, z.
| Переменная 1 | Переменная 2 | Переменная 3 | Функция |
|---|---|---|---|
| ??? | ??? | ??? | F |
| 0 | 0 | 0 | |
| 1 | 0 |
В ответе напишите буквы x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала — буква, соответствующая первому столбцу; затем — буква, соответствующая второму столбцу, и т. д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Пример. Пусть задано выражение x → y, зависящее от двух переменных x и y, и фрагмент таблицы истинности:
| Переменная 1 | Переменная 2 | Функция |
|---|---|---|
| ??? | ??? | F |
| 0 | 1 | 0 |
Тогда первому столбцу соответствует переменная y, а второму столбцу соответствует переменная x. В ответе нужно написать: yx.
3
Логическая функция F задаётся выражением (x ≡ y ) ∨ ((y ∨ z) → x).
Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности функции F.
Определите, какому столбцу таблицы истинности соответствует каждая из переменных x, y, z.
| Переменная 1 | Переменная 2 | Переменная 3 | Функция |
|---|---|---|---|
| ??? | ??? | ??? | F |
| 1 | 1 | 0 | |
| 1 | 0 |
В ответе напишите буквы x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала — буква, соответствующая первому столбцу; затем — буква, соответствующая второму столбцу, и т. д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Пример. Пусть задано выражение x → y, зависящее от двух переменных x и y, и фрагмент таблицы истинности:
| Переменная 1 | Переменная 1 | Функция |
|---|---|---|
| ??? | ??? | F |
| 0 | 1 | 0 |
Тогда первому столбцу соответствует переменная y, а второму столбцу соответствует переменная x. В ответе нужно написать: yx.
4
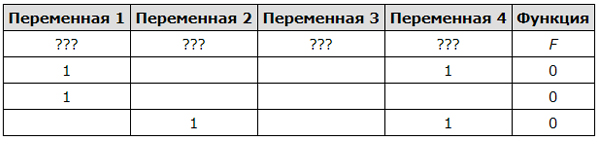
Логическая функция F задаётся выражением (x ∧ ¬y) ∨ (y ≡ z) ∨ ¬w. На рисунке приведён фрагмент таблицы истинности функции F, содержащий все наборы аргументов, при которых функция F ложна. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных w, x, y, z. Все строки в представленном фрагменте разные.
| Перем.1 | Перем.2 | Перем.3 | Перем.4 |
|---|---|---|---|
| ??? | ??? | ??? | ??? |
| 0 | |||
| 1 | 0 | 0 | |
| 1 | 0 | 0 |
В ответе напишите буквы w, x, y, z в том порядке, в котором идут соответствующие им столбцы (без разделителей).
Источник: ЕГЭ — 2018. Досрочная волна. Вариант 1., ЕГЭ — 2018. Досрочная волна. Вариант 2.
5
Логическая функция F задаётся выражением ((x → y ) ∧ (y → w)) ∨ (z ≡ ( x ∨ y)).
Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности функции F.
Определите, какому столбцу таблицы истинности соответствует каждая из переменных x, y, z, w.
| Переменная 1 | Переменная 2 | Переменная 3 | Переменная 4 | Функция |
|---|---|---|---|---|
| ??? | ??? | ??? | ??? | F |
| 1 | 1 | 0 | ||
| 1 | 0 | |||
| 1 | 1 | 0 |
В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы (сначала — буква, соответствующая первому столбцу; затем — буква, соответствующая второму столбцу, и т. д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Пример. Пусть задано выражение x → y, зависящее от двух переменных x и y, и фрагмент таблицы истинности:
| Переменная 1 | Переменная 2 | Функция |
|---|---|---|
| ??? | ??? | F |
| 0 | 1 | 0 |
Тогда первому столбцу соответствует переменная y, а второму столбцу соответствует переменная x. В ответе нужно написать: yx.
Пройти тестирование по этим заданиям
Муниципальное общеобразовательное учреждение
«Средняя общеобразовательная школа №101»
Теория и практика решения задания 2
ЕГЭ по информатике
Автор:
учитель информатики
Угулава Наталия Владимировна
Саратов, 2018
Типы задания 2
- Задания на отрезки
- Задания на множества
- Задания на поразрядную конъюнкцию
- Задания на условие делимости
Разбор 2 задания ЕГЭ 2018 по информатике и ИКТ из демоверсии.
Это задание базового уровня сложности.
Примерное время выполнения задания 3 минуты.
— умение строить таблицы истинности и логические схемы
— умение строить таблицы истинности и логические схемы
— умение строить таблицы истинности и логические схемы
Проверяемые элементы содержания:
— умение строить таблицы истинности и логические схемы.
Элементы содержания, проверяемые на ЕГЭ:
— высказывания, — логические операции, — кванторы, — истинность высказывания.
ТАБЛИЦЫ ИСТИННОСТИ И ПОРЯДОК
ВЫПОЛНЕНИЯ ЛОГИЧЕСКИХ ОПЕРАЦИЙ
Для логических операций приняты следующие обозначения :
¬ A, A
не A (отрицание, инверсия)
A ∧ B, A ⋅ B
A и B (логическое умножение, конъюнкция)
A ∨ B, A + B
A или B (логическое сложение, дизъюнкция)
A → B
импликация (следование)
A ↔ B, A ≡ B, A ∼ B
эквиваленция (эквивалентность, равносильность)
A ⊕ B
сложение по модулю 2 (XOR)
Отрицание (НЕ):
Таблица истинности операции НЕ
Конъюнкция (И):
Таблица истинности операции И (конъюнкция)
Дизъюнкция (ИЛИ):
Таблица истинности операции ИЛИ (дизъюнкция)
Импликация (если … , то … ):
Таблица истинности операции Импликация (если … , то … )
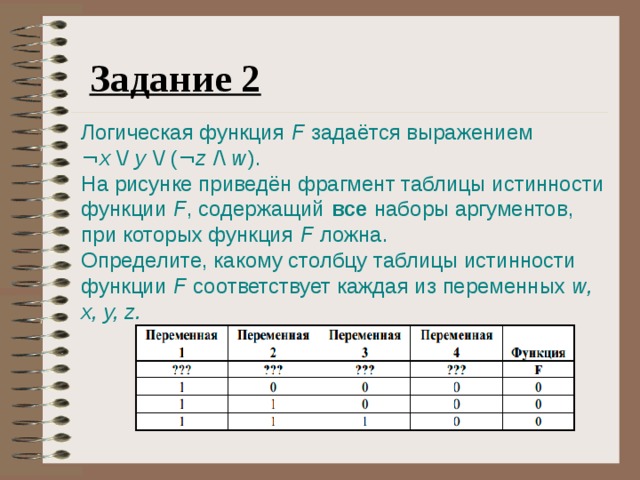
Задание 2
Логическая функция F задаётся выражением ¬ x / y / ( ¬ z / w ). На рисунке приведён фрагмент таблицы истинности функции F , содержащий все наборы аргументов, при которых функция F ложна. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных w, x, y, z.
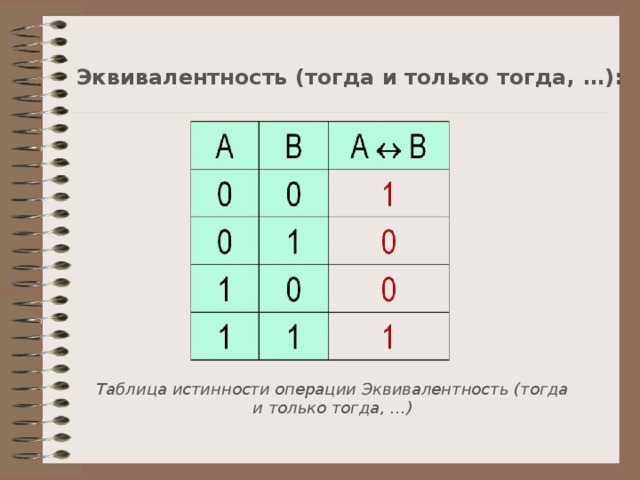
Эквивалентность (тогда и только тогда, … ):
Таблица истинности операции Эквивалентность (тогда и только тогда, … )
Сложение по модулю 2 (XOR):
A
B
0
A ⊕ B
0
0
1
0
1
1
0
1
1
1
0
Порядок выполнения операций:
- если в выражении нет скобок, сначала выполняются все операции « НЕ » , затем – « И » , затем – « ИЛИ » , импликация, равносильность
Решение заданий 2 ЕГЭ по информатике
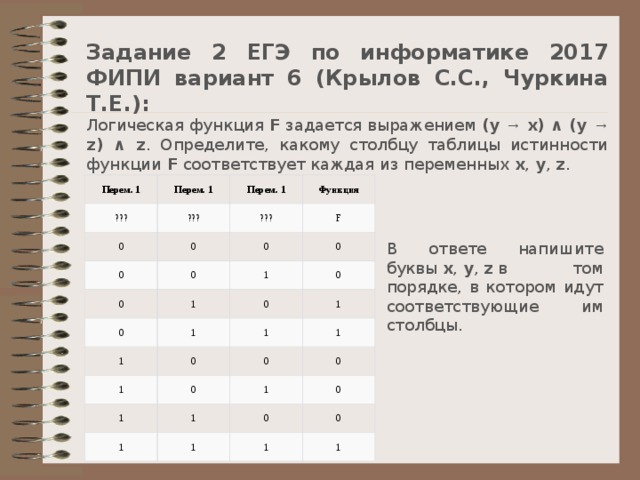
Задание 2 ЕГЭ по информатике 2017 ФИПИ вариант 6 (Крылов С.С., Чуркина Т.Е.):
Логическая функция F задается выражением (y → x) ∧ (y → z) ∧ z . Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x , y , z .
Перем. 1
Перем. 1
???
???
Перем. 1
0
Функция
???
0
0
F
0
0
0
1
0
1
0
0
1
1
0
0
1
1
1
1
0
1
0
0
1
1
1
0
1
0
0
1
1
В ответе напишите буквы x , y , z в том порядке, в котором идут соответствующие им столбцы.
Решение:
- За основу необходимо взять логическую операцию, которую мы будем выполнять в последнюю очередь — это логическое И (конъюнкция) или ∧
- Конъюнкцию легче рассматривать по тем строкам таблицы, там где функция F = 1
- Поскольку для конъюнкции функция истинна только тогда, когда все переменные истинны, то необходимо чтобы отдельно каждая скобка была истинна ((y → x) = 1 и (y → z)=1) и переменная z тоже была истинной (1)
- Поскольку со скобками сложней работать, определим сначала какому столбцу соответствует z . Для этого выберем строку, где F=1 и в остальных ячейках только одна единица, а остальные нули:
0
1
0
1
- Таким образом, из этой строки делаем вывод, что z находится во втором столбце (отсчет ведем слева):
???
z
???
F
- Рассмотрим скобку (y → x) и строку таблицы:
0
1
1
1
- Для этой строки только y может быть 0 , т.к. если x = 0 , тогда y=1 , и скобка в результате возвратит ложь ( 1 → 0 = 0 ). Соответственно, y находится в первом столбце. А x значит в третьем:
- Для этой строки только y может быть 0 , т.к. если x = 0 , тогда y=1 , и скобка в результате возвратит ложь ( 1 → 0 = 0 ). Соответственно, y находится в первом столбце. А x значит в третьем:
y
z
x
F
Результат: yzx
Задание 2 ЕГЭ по информатике 2017 ФИПИ вариант 11 (Крылов С.С., Чуркина Т.Е.): Каждое из логических выражений F и G содержит 5 переменных. В таблицах истинности выражений F и G есть ровно 5 одинаковых строк, причем ровно в 4 из них в столбце значений стоит 1 . Сколько строк таблицы истинности для выражения F ∨ G содержит 1 в столбце значений?
Решение:
- Поскольку в каждом из выражений присутствует 5 переменных, то эти 5 переменных порождают таблицу истинности из 32 строк: т.к. каждая из переменных может принимать оно из двух значений (0 или 1), то различных вариантов с пятью переменными будет 2 5 =32 , т.е. 32 строки.
- Из этих 32 строк для каждого выражения (и F и G) мы знаем наверняка только о 5 строках: в 4 из них 1, а в одной — 0.
- В исходных таблицах для каждого выражения F и G мы знаем о существовании только одного 0, т.е. в остальных строках может быть 1. Т.о. для каждого выражения и F и G в 31 строке могут быть единицы ( 32-1=31 ), а лишь в одной — ноль.
- Тогда для выражения F ∨ G только в одном случае будет 0, когда и F=0 и G = 0:
- Вопрос стоит о количестве строк = 1 для таблицы истинности выражения F ∨ G . Данной выражение — дизъюнкция, которая ложна только в одном случае — если F = 0 и одновременно G = 0
№
1
F
0
G
2
0
0
…
0
…
32
1
…
1
…
1
…
1
Результат: 31
Решение задачи на отрезки
В ответе напишите буквы w, x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала – буква, соответствующая первому столбцу; затем – буква, соответствующая второму столбцу, и т.д.) Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
¬ x / y / (¬ z / w )
Дизъюнкция (логическое сложение) истинна тогда и только тогда, когда истинно хотя бы одно высказывание.
Следовательно, для того чтобы вся функция была ложна, переменной х должен соответствовать тот столбец, в котором стоит значение 1 (так как, ¬ x превращает 1 в 0) , а переменной y столбец со значениями 0 .
Таким образом: — переменной x соответствует столбец с переменной 1 , — переменной y соответствует столбец с переменной 4 .
Решение задачи на отрезки
Конъюнкция (логическое умножение) истинна тогда и только тогда, когда истинны все высказывания (ложна — если ложно хотя бы одно высказывание). Конъюнкция ¬ z / w в нашем выражении будет истинна только если z=0, w=1.
Посмотрим на вторую строчку таблицы, где переменная 2 равна 1, а переменная 3 равна 0.
Решение задачи
Так как ¬ z / w должна равняться 0, то z = 1 и w = 0 (в противном случае произведение будет равно 1)
Таким образом: — переменной z соответствует столбец с переменной 2 (2 столбец), — переменной w соответствует столбец с переменной 3 (3 столбец).
Ответ: xzwy
Спасибо за внимание!
Автор материалов — Лада Борисовна Есакова.
В компьютере вся информация представлена в двоичной системе счисления, в которой используется две цифры – 0 и 1. Собственно, и цифр как таковых у компьютера нет, а есть электрический сигнал, проходящий по электронным схемам и соединительным проводникам (шинам) компьютера, который может принимать значения “высокий уровень электрического напряжения” (принимаемый нами за 1) и “низкий уровень электрического напряжения” (принимаемый за 0). Для различных действий над этими нулями и единичками нам необходимы специальные операции, которые работают с двоичными переменными. Такие операции называются логическими операциями.
Логические операции и их аргументы принимают только два значения: 1 (“истина”) и 0 (“ложь”).
Таблица истинности выражения определяет его значения при всех возможных комбинациях исходных данных.
Количество строк в таблице истинности выражения от N переменных равно 2N.
Основные логические операции:
1). Логическое умножение (конъюнкция, логическое И). Обозначается: AND, &, /.
Таблица истинности:
|
A |
B |
А&В |
|
1 |
1 |
1 |
|
1 |
0 |
0 |
|
0 |
1 |
0 |
|
0 |
0 |
0 |
2). Логическое сложение (дизъюнкция, логическое ИЛИ). Обозначается: OR, |, /.
Таблица истинности:
|
A |
B |
A / B |
|
1 |
1 |
1 |
|
1 |
0 |
1 |
|
0 |
1 |
1 |
|
0 |
0 |
0 |
3). Логическое отрицание (инверсия, логическое НЕ). Обозначается: NOT, ¬, .
Таблица истинности:
4). Логическое следование (импликация). Обозначается: →.
Таблица истинности:
|
A |
B |
A → B |
|
1 |
1 |
1 |
|
1 |
0 |
0 |
|
0 |
1 |
1 |
|
0 |
0 |
1 |
5). Логическое равенство (эквивалентность). Обозначается: ↔, ~.
Таблица истинности:
|
A |
B |
A ~ B |
|
1 |
1 |
1 |
|
1 |
0 |
0 |
|
0 |
1 |
0 |
|
0 |
0 |
1 |
Порядок (приоритет) выполнения логических операций:
Если в выражении нет скобок, то операции выполняются в следующем порядке:
— Логическое отрицание (инверсия, логическое НЕ);
— Логическое умножение (конъюнкция, логическое И);
— Логическое сложение (дизъюнкция, логическое ИЛИ);
— Логическое следование (импликация);
— Логическое равенство (эквивалентность).
Выбор выражения по таблице истинности
Пример 1.
Дан фрагмент таблицы истинности выражения F:
|
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
F |
|
1 |
1 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
1 |
0 |
0 |
1 |
0 |
|
1 |
0 |
0 |
1 |
0 |
0 |
0 |
Каким выражением может быть F?
1) (x1 ∧ x2) ∨ (x3 ∧ x4) ∨ (x5 ∧ x6)
2) (x1 ∧ x3) ∨ (x3 ∧ x5) ∨ (x5 ∧ x1)
3) (x2 ∧ x4) ∨ (x4 ∧ x6) ∨ (x6 ∧ x2)
4) (x1 ∧ x4) ∨ (x2 ∧ x5) ∨ (x3 ∧ x6)
Решение:
Все представленные варианты ответа — дизъюнкции трёх конъюнкций. Все значения F в таблице равны нулю. Дизъюнкция равна нулю, когда все слагаемые равны нулю.
Рассмотри поочерёдно все четыре выражения.
1) В первой строке таблицы x1=1 и x2=1, значит x1∧x2=1. Выражение не подходит.
2) Во второй строке таблицы x1=1 и x3=1, значит x1∧x3=1. Выражение не подходит.
3) Подставим в третье выражение поочередно значения всех строк таблицы:
Первая строка
(x2 ∧ x4) ∨ (x4 ∧ x6) ∨ (x6 ∧ x2) = (1 ∧ 0) ∨ (0 ∧ 0) ∨ (0 ∧ 1) = 0 ∨ 0 ∨ 0 = 0
Вторая строка
(x2 ∧ x4) ∨ (x4 ∧ x6) ∨ (x6 ∧ x2) = (0 ∧ 0) ∨ (0 ∧ 1) ∨ (1 ∧ 0) = 0 ∨ 0 ∨ 0 = 0
Третья строка
(x2 ∧ x4) ∨ (x4 ∧ x6) ∨ (x6 ∧ x2) = (0 ∧ 1) ∨ (1 ∧ 0) ∨ (0 ∧ 0) = 0 ∨ 0 ∨ 0 = 0
Выражение подходит.
4) В третьей строке таблицы x1=1 и x4=1, значит x1∧x4=1. Выражение не подходит.
Ответ:3
Пример 2.
Для таблицы истинности функции F известны значения только некоторых ячеек:
|
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
x7 |
F |
|
1 |
0 |
1 |
|||||
|
0 |
0 |
1 |
|||||
|
0 |
1 |
0 |
Каким выражением может быть F?
1) x1 ∧ x2 ∧ x3 ∧ ¬x4 ∧ x5 ∧ x6 ∧ ¬x7
2) x1 ∨ ¬x2 ∨ x3 ∨ ¬x4 ∨ ¬x5 ∨ x6 ∨ ¬x7
3) ¬x1 ∧ x2 ∧ ¬x3 ∧ x4 ∧ x5 ∧ x6 ∧ x7
4) x1 ∨ x2 ∨ ¬ x3 ∨ x4 ∨ x5 ∨ ¬x6 ∨ x7
Решение:
Рассмотри поочерёдно все четыре выражения.
1) Выражение является конъюнкцией переменных и их отрицаний. Конъюнкция равна единице, когда все операнды равны единице. В первой строке x6 = 0, а значит и все выражение F равно нулю, что не соответствует таблице истинности.
2) Выражение является дизъюнкцией переменных и их отрицаний. Дизъюнкция равна единице, когда хотя бы один операнд равен единице. Подставим во второе выражение поочередно значения всех строк таблицы:
Первая строка
x1 ∨ ¬x2 ∨ x3 ∨ ¬x4 ∨ ¬x5 ∨ x6 ∨ ¬x7 = x1 ∨ ¬x2 ∨ x3 ∨ 0 ∨ ¬x5 ∨ 0 ∨ ¬x7 может принимать значение 1, если хотя бы один из операндов равен 1.
Вторая строка
x1 ∨ ¬x2 ∨ x3 ∨ ¬x4 ∨ ¬x5 ∨ x6 ∨ ¬x7 = x1 ∨ ¬x2 ∨ x3 ∨ 1 ∨ ¬x5 ∨ x6 ∨ 1 = 1
Третья строка
x1 ∨ ¬x2 ∨ x3 ∨ ¬x4 ∨ ¬x5 ∨ x6 ∨ ¬x7 = 0 ∨ ¬x2 ∨ x3 ∨ 0 ∨ ¬x5 ∨ x6 ∨ ¬x7 может принимать значение 0, если все остальные операнды равны 0.
3) Выражение является конъюнкцией переменных и их отрицаний. Конъюнкция равна единице, когда все операнды равны единице. Во второй строке x4 = 0, а значит и все выражение F равно нулю, что не соответствует таблице истинности.
4) Выражение является дизъюнкцией переменных и их отрицаний. Дизъюнкция равна единице, когда хотя бы один операнд равен единице. В третьей строке x4 = 1, значит и все выражение F равно 1, что не соответствует таблице истинности.
Ответ:2
Пример 3.
Логическая функция F задаётся выражением (¬z) ∧ x ∨ x ∧ y. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z.
|
Перем. 1 |
Перем. 2 |
Перем. 3 |
Функция |
|
??? |
??? |
??? |
F |
|
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
1 |
|
0 |
1 |
0 |
0 |
|
0 |
1 |
1 |
1 |
|
1 |
0 |
0 |
0 |
|
1 |
0 |
1 |
0 |
|
1 |
1 |
0 |
0 |
|
1 |
1 |
1 |
1 |
В ответе напишите буквы x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала – буква, соответствующая 1-му столбцу; затем – буква, соответствующая 2-му столбцу; затем – буква, соответствующая 3-му столбцу). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Решение:
Выражение (¬z) ∧ x ∨ x ∧ y является дизъюнкцией двух конъюнкций:
((¬z) ∧ x) ∨ (x ∧ y) . В обеих конъюнкциях присутствует x. Т. е. при x = 0 все выражение равно 0. Это выполняется только при Перем.3 = x.
Выражение равно 1, если x =1 и выполняется хотя бы одно из условий: y = 1 или z = 0. Из четвертой строки следует, что Перем.1 = z, а Перем.2 = y.
Ответ: zyx
Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Задача №2. Построение таблиц истинности логических выражений. Выбор выражения, соответствующего условию.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
08.03.2023
За это задание ты можешь получить 1 балл. На решение дается около 3 минут. Уровень сложности: базовый.
Средний процент выполнения: 65.9%
Ответом к заданию 2 по информатике может быть цифра (число) или слово.
Задача 1
Дано логическое выражение, зависящее от 6 логических переменных:
¬(A → F) ∧ B ∧ ¬C ∧ (D → E).
Сколько существует различных наборов значений переменных, при которых выражение ложно?
Решение
Заметим, что все скобки и выражения связаны конъюнкцией, для которой сложно получить единицу. Поэтому будет решать от обратного. Посчитаем количество наборов, когда выражение истинно, тогда:
¬(A → F) = 1, тогда $A → F = 0$, следовательно, A = 1, F = 0.
B = 1.
¬C = 1, значит C = 0.
(D → E) = 1, тогда возможно 3 варианта: D = 0, E = 0; D = 0, E = 1; D = 1, E = 1.
Перемножим количество подходящих значений для каждой переменной: A, B, C, F — по одному набору, D и E — 3 набора. Итого:
1 х 3 = 3 набора, для которых вся функция истинна. Но нам нужно, чтобы функция была ложна. Найдём общее количество наборов по формуле $k = 2^N$, где N — количество переменных. У нас 6 переменных, значит всего наборов 64. Из них 3 нам не подходят. Тогда количество подходящих (ложных) наборов:
64 — 3 = 61.
Или при помощи программы на С++:
#include <iostream>
#include <algorithm>
#include <fstream>using namespace std;
bool f(int A, int B, int C, int D, int E, int F){
return (!(!A || F) && B && !C && (!D || E));
}int main() {
int count = 0;
for (int A = 0; A <= 1; ++A)
for (int B = 0; B <= 1; ++B)
for (int C = 0; C <= 1; ++C)
for (int D = 0; D <= 1; ++D)
for (int E = 0; E <= 1; ++E)
for (int F = 0; F <= 1; ++F)
if (f(A, B, C, D, E, F) == false)
count++;
cout << count;
return 0;
}
Ответ: 61.
Ответ: 61
Задача 2
Дано логическое выражение, зависящее от 5 логических переменных:
$(A ∨ ¬B) ∧ (¬C ∨ D ∨ ¬E)$.
Сколько существует различных наборов значений переменных, при которых выражение ложно?
Решение
В первой скобке 2 переменных, значит для неё будет 4 набора. Поскольку переменные соединяются дизъюнкцией, выражение ложно ровно в одном случае, а в трёх оставшихся — истинно.
Во второй скобке 3 переменных, значит для неё будет 8 наборов. Поскольку переменные соединяются дизъюнкцией, выражение ложно ровно в одном случае, а в семи оставшихся — истинно.
Конъюнкция ложна, когда хотя бы одна скобка ложна. Рассмотрим 3 случая:
Первая скобка ложна, вторая истинна. Первая скобка ложна в 1 случае из 4, вторая истинна в 7 случаях из 8. Итого 7 · 1 = 7.
Первая скобка истинна, вторая ложна. Первая скобка истинна в 3 случаях из 4, вторая ложна в 1 случае из 4. Итого 1 · 3 = 3.
Первая скобка ложна, вторая ложна. Первая скобка ложна в 1 случае из 4, вторая ложна в 1 случае из 8. Итого 1 · 1 = 1.
Суммарно: 7 + 3 + 1 = 11.
Ответ: 11.
Ответ: 11
Задача 3
Дано логическое выражение, зависящее от 5 логических переменных:
(¬A ∧ B ∧ C) ∨ (¬D ∧ ¬E).
Сколько существует различных наборов значений переменных, при которых выражение истинно?
Решение
В первой скобке 3 переменных, значит для неё будет 8 наборов. Поскольку переменные соединяются конъюнкцией, выражение истинно ровно в одном случае, а в семи оставшихся — ложно.
Во второй скобке 2 переменных, значит для неё будет 4 набора. Поскольку переменные соединяются конъюнкцией, выражение истинно ровно в одном случае, а в трёх оставшихся — ложно.
Дизъюнкция истинна, когда хотя бы одна скобка истинна. Рассмотрим 3 случая:
Первая скобка ложна, вторая истинна. Первая скобка ложна в 7 случаях из 8, вторая истинна в 1 случае из 4. Итого 7 · 1 = 7.
Первая скобка истинна, вторая ложна. Первая скобка истинна в 1 случае из 8, вторая ложна в 3 случаях из 4. Итого 1 · 3 = 3.
Первая скобка истинна, вторая истинна. Первая скобка истинна в 1 случае из 8, вторая истинна в 1 случае из 4. Итого 1 · 1 = 1.
Суммарно: 7 + 3 + 1 = 11.
Ответ: 11.
Ответ: 11
Задача 4
Логическая функция F задаётся выражением ((x∧z)∨¬x)∧¬w∧y. Во фрагменте таблицы истинности приведены все строки, при которых значение функции F является истиной. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.
| F | ||||
| 1 | 0 | 0 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 | 1 |
В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы (сначала букву, соответствующую 1-му столбцу; затем букву, соответствующую 2-му столбцу; затем букву, соответствующую 3-му столбцу; затем букву, соответствующую последнему столбцу). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Решение
Строим таблицу истинности для логической функции любым способом и находим наборы, при которых функция ложна. Например, при помощи программы:
bool f(int x, int y, int z, int w){
return (((x && z) || !x) && !w && y);
}int main() {
cout << "x y z w F" << endl;
for (int x = 0; x <= 1; ++x)
for (int y = 0; y <= 1; ++y)
for (int z = 0; z <= 1; ++z)
for (int w = 0; w <= 1; ++w)
if (f(x, y, z, w) == true)
cout << x << " " << y << " "
<< z << " " << w << " " << f(x, y, z, w) << endl;
return 0;
}
Получили наборы:
x y z w F
0 1 0 0 1
0 1 1 0 1
1 1 1 0 1
Начинаем сопоставление с исходной тбалицей:
1) столбец без единиц четвёртый в таблице из условия — это W
2) столбец с одной единицей третий в исходной таблице — это X
3) столбей с тремя единицами — это Y
4) столбец с двумя единицами — это Z
Результат: YZXW
Ответ: yzxw
Задача 5
Логическая функция F задаётся выражением (y → w) ∨ (¬x ∧ z). Во фрагменте таблицы истинности приведены все строки, при которых значение функции F ложно. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.
| F | ||||
| 0 | 0 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 1 | 0 |
В ответе напишите буквы w, x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала букву, соответствующую 1-му столбцу; затем букву, соответствующую 2-му столбцу; затем букву, соответствующую 3-му столбцу; затем букву, соответствующую последнему столбцу). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Решение
Строим таблицу истинности для логической функции любым способом и находим наборы, при которых функция ложна. Например, при помощи программы:
bool f(int x, int y, int z, int w){
return ((!y || w) || (!x && z));
}int main() {
cout << "x y z w F" << endl;
for (int x = 0; x <= 1; ++x)
for (int y = 0; y <= 1; ++y)
for (int z = 0; z <= 1; ++z)
for (int w = 0; w <= 1; ++w)
if (f(x, y, z, w) == false)
cout << x << " " << y << " "
<< z << " " << w << " " << f(x, y, z, w) << endl;
return 0;
}
Получили наборы:
x y z w F
0 1 0 0 0
1 1 0 0 0
1 1 1 0 0
Начинаем сопоставление с исходной тбалицей:
1) столбец без единиц второй в таблице из условия — это W
2) столбец с одной единицей третий в исходной таблице — это Z
3) столбей с тремя единицами — это Y
4) столбец с двумя единицами — это X
Результат: xwzy
Ответ: xwzy
Задача 6
Дан фрагмент таблицы истинности выражения F:
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | F |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 |
Сколько строк таблицы удовлетворяют выражению: F = (x1 ∨ x2 ∨ x3) ∧ x4 ∧ (x5 ∨ x6 ∨ x7) ∧ x8?
Решение
Данное выражение является конъюнкцией четырёх выражений. Конъюнкция нескольких высказываний истинна тогда и только тогда, когда истинными являются все входящие в неё высказывания. Следовательно, x4 = 1, x8 = 1 и в наборах значений переменных (x1, x2, x3), (x5, x6, x7) должна быть хотя бы одна 1.
Этим условиям удовлетворяют три последние строки таблицы. В каждой из этих строк значение функции F = 1. Следовательно, эти строки удовлетворяют заданному логическому выражению.
Чтобы остальные строки удовлетворяли заданному выражению, значение F должно быть равно 0. В таблице количество таких строк равно 5.
Всего значения 8 строк таблицы удовлетворяют заданному выражению.
Ответ: 8
Задача 7
Логическая функция F задаётся выражением (¬x → y) ∧ (z → y). Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z.
| Переменная 1 ??? |
Переменная 2 ??? |
Переменная 3 ??? |
Функция F |
| 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 |
В ответе напишите буквы x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала — буква, соответствующая 1-му столбцу; затем — буква, соответствующая 2-му столбцу; затем — буква, соответствующая 3-му столбцу). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Пример. Пусть задано выражение x ∨ ¬y, зависящее от двух переменных x и y, и таблица истинности:
| Переменная 1 ??? |
Переменная 2 ??? |
Функция F |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
Тогда 1-му столбцу соответствует переменная y, а 2-му столбцу соответствует переменная x. В ответе нужно написать: yx.
Решение
Преобразуем исходное выражение.
(¬x → y) ∧ (z → y) = (x ∨ y) ∧ (¬z ∨ y) = y ∨ (x ∧ ¬z).
Так как дизъюнкция ложна только в том случае, когда ложны оба высказывания, входящие в неё, то переменной y должен соответствовать тот столбец, в котором значение 0 стоит в тех же строках, что и в столбце F. Следовательно, переменной y соответствует третий столбец.
Рассмотрим строку, в которой значение функции отличается от значения переменной y. Такой строкой является четвёртая снизу. Здесь переменная y = 0, а значение функции F = 1. Это означает, что x ∧ ¬z = 1. В рассматриваемой строке значение первого столбца 0, а второго 1. Пусть x = 0, z = 1. При этих значениях логическое выражение x ∧ ¬z ложно, что не соответствует табличному значению функции F = 1. Следовательно, x = 1, z = 0. Значит, первый столбец соответствует переменной z, а второй—x.
Или при помощи программы на С++:
Выводим только ложные наборы, потому что их меньше
#include <iostream>
#include <algorithm>
#include <fstream>using namespace std;
bool f(int x, int y, int z){
return ((x || y) && (!z || y));
}int main() {
cout << "x y z F" << endl;
for (int x = 0; x <= 1; ++x)
for (int y = 0; y <= 1; ++y)
for (int z = 0; z <= 1; ++z)
if (f(x, y, z) == false)
cout << x << " " << y << " "
<< z << " " << f(x, y, z) << endl;
return 0;
}
Ответ: zxy
Задача 8
Логическая функция F задаётся выражением ((¬z∨¬x)∧z)∨w∨¬y. Во фрагменте таблицы истинности приведены все строки, при которых значение функции F ложно. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.
| F | ||||
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 |
В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы (сначала букву, соответствующую 1-му столбцу; затем букву, соответствующую 2-му столбцу; затем букву, соответствующую 3-му столбцу; затем букву, соответствующую последнему столбцу). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Пример. Пусть задано выражение x∨¬y, зависящее от двух переменных x и y, и таблица истинности
| F | ||
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
| 1 | 1 | 1 |
тогда 1-му столбцу соответствует переменная y, а 2-му столбцу соответствует переменная x. В ответе нужно написать: yx.
Задача 9
Логическая функция F задаётся выражением (y ∧ (w → x)) → g. Во фрагменте таблицы истинности приведены все строки, при которых значение функции F ложно. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, w, g.
| F | ||||
| 0 | 0 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 1 | 0 |
В ответе напишите буквы x, y, w, g в том порядке, в котором идут соответствующие им столбцы (сначала букву, соответствующую 1-му столбцу; затем букву, соответствующую 2-му столбцу; затем букву, соответствующую 3-му столбцу; затем букву, соответствующую последнему столбцу). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Пример. Пусть задано выражение x∨¬y, зависящее от двух переменных x и y, и таблица истинности
| F | ||
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
| 1 | 1 | 1 |
тогда 1-му столбцу соответствует переменная y, а 2-му столбцу соответствует переменная x. В ответе нужно написать: yx.
Задача 10
Логическая функция F задаётся выражением (x → y) → (w → g). Во фрагменте таблицы истинности приведены все строки, при которых значение функции F ложно. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, w, g.
| F | ||||
| 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 1 | 0 |
В ответе напишите буквы x, y, w, g в том порядке, в котором идут соответствующие им столбцы (сначала букву, соответствующую 1-му столбцу; затем букву, соответствующую 2-му столбцу; затем букву, соответствующую 3-му столбцу; затем букву, соответствующую последнему столбцу). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Пример. Пусть задано выражение x∨¬y, зависящее от двух переменных x и y, и таблица истинности
| F | ||
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
| 1 | 1 | 1 |
тогда 1-му столбцу соответствует переменная y, а 2-му столбцу соответствует переменная x. В ответе нужно написать: yx.
Задача 11
Логическая функция F задаётся выражением (x = y) ∨ ¬(y → w) ∨ z. Ниже приведён частично заполненный фрагмент таблицы истинности функции F, содержащий неповторяющиеся строки.
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных w, x, y, z.
| F | ||||
| 1 | 1 | 0 | 0 | |
| 1 | 1 | 0 | ||
| 0 | 1 | 0 |
В ответе напишите буквы w, x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала букву, соответствующую 1-му столбцу; затем букву, соответствующую 2-му столбцу; затем букву, соответствующую 3-му столбцу; затем букву, соответствующую последнему столбцу). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Пример. Если бы функция F была задана выражением x ∨ ¬y, зависящим от двух переменных x и y, а фрагмент таблицы истинности имел бы вид:
тогда 1-му столбцу соответствовала бы переменная y, а 2-му столбцу — переменная x. В ответе следовало бы написать: yx.
Задача 12
Логическая функция F задаётся выражением (x = y)∨(x∧w)∨¬z. Ниже приведён частично заполненный фрагмент таблицы истинности функции F, содержащий неповторяющиеся строки.
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных w, x, y, z.
| F | ||||
| 1 | 0 | 0 | ||
| 0 | 0 | 0 | ||
| 0 | 1 | 0 |
В ответе напишите буквы w, x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала букву, соответствующую 1-му столбцу; затем букву, соответствующую 2-му столбцу; затем букву, соответствующую 3-му столбцу; затем букву, соответствующую последнему столбцу). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Пример. Если бы функция F была задана выражением x ∨ ¬y, зависящим от двух переменных x и y, а фрагмент таблицы истинности имел бы вид:
тогда 1-му столбцу соответствовала бы переменная y, а 2-му столбцу — переменная x. В ответе следовало бы написать: yx.
Здравствуйте, дорогие друзья! Сегодня разберём, как решать второе задание из ЕГЭ по информатике 2020.
Во втором задании ЕГЭ по информатике у нас обычно есть логическая функция, которая зависит от логических переменных. Логические переменные могут принимать только два значения: 0 (Ложь) или 1 (Истина).
С логическими переменными можно производить логические операции. При решении второго задания из ЕГЭ по информатике необходимо твёрдо знать каждую логическую операцию, и давайте рассмотрим их.

- () — операции в скобках
- ¬ — логическое отрицание
- ∧ — логическое умножение
- ∨ — логическое сложение
- ⟶ — следование
- ≡ — равнозначность
Так же на ЕГЭ по информатике будет полезно знать логические формулы :

Передём к решению задач из ЕГЭ по информатике
Задача 1 (лёгкая)
Логическая функция F задаётся выражением z ∧ ¬y ∧ (w → x).
Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности функции F.
Определите, какому столбцу таблицы истинности соответствует каждая из переменных x, y, z, w.
В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы (сначала буква, соответствующая первому столбцу; затем буква, соответствующая второму столбцу, и т. д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Пример. Пусть задано выражение x → y, зависящее от двух переменных x и y, и фрагмент таблицы истинности:
Тогда первому столбцу соответствует переменная y, а второму столбцу соответствует переменная x. В ответе нужно написать: yx.
Решение:
Видим, что у функции основным действием является логическое умножение. По таблице видно, что функция имеет значение только 1 . Логическое умножение даёт 1 (единицу) тогда, когда каждое выражение равно 1 (единице). Значит каждое выражение в нашей функции должно равняться единице.
Отсюда видно, что переменная z должна всегда быть равна 1 (единице). Это первый столбец. Отрицание y тоже должно быть 1 (единицей), тогда просто y всегда будет 0 (нулём). Это второй столбец.
Осталось определить положение w и x. Здесь делаем предположение, что в третьем столбце стоит w, а в 4-ом x. Проверяем построчно и видим, что во второй строчке при таком расположении из 1 следует 0, что в итоге приводит выражение (w → x) в 0, а у нас это выражение всегда должно быть 1 (единицей). Значит, мы предположение сделали неверное, и получается x — это третий столбец, а w — четвёртый.
Ответ: zyxw
Задача 2 (средний уровень)
Логическая функция F задаётся выражением (x ∧ ¬y) ∨ (y ≡ z) ∨ w.
Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности функции F.
Определите, какому столбцу таблицы истинности соответствует каждая из переменных x, y, z, w.
В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы (сначала — буква, соответствующая первому столбцу; затем — буква, соответствующая второму столбцу, и т. д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Пример. Пусть задано выражение x → y, зависящее от двух переменных x и y, и фрагмент таблицы истинности:
Тогда первому столбцу соответствует переменная y, а второму столбцу соответствует переменная x. В ответе нужно написать: yx.
Решение:
Определяем главную логическую операцию («главную скрипку»), которая соединяет разные выражения. Видим, что это логическое сложение.
Во всех строчках таблицы функция принимает значение 0 (ноль). Значит, и каждое выражение должно принимать значение 0 (ноль).
Самым слабым звеном является переменная w, потому что она стоит одна. Переменная w должна равняться всегда 0(нулю) — этому условию может удовлетворить только третий столбец. Значит w стоит на третьем месте.
Следующим слабым звеном является равносильность. Она должна «выдавать» 0 (ноль). Равносильность «выдаёт» 0 (ноль), когда переменные разные!
Проанализируем первый и второй столбец. В третьей строчке, и там, и там, стоит 1 (единица). Значит, первый и второй столбец не могут быть одновременно y и z (или z и y).
Рассмотрим второй и четвёртый столбец. Вторая строчка содержит одинаковое значение 0 (ноль), и там, и там. Значит, второй и четвёртый столбец не могут быть одновременно y и z (или z и y).
Таким образом, y и z (или z и y) будут столбцы первый и четвёртый! И теперь можно расставить недостающие значения в этих столбцах. Расставляем, чтобы были разные значения, а второй столбец получается x.
Осталось разобраться с z и y. Обратимся к первому выражению (x ∧ ¬y) и посмотрим на третью строчку. Если в четвёртом столбце будет стоять y, то отрицание на y превратит ноль(ноль) в 1(единицу) в четвёртой строчке. Тогда окажется, что у x — 1 и ¬y — 1, и выражение (x ∧ ¬y) тоже получится 1(единицей). А у нас каждое выражение должно равняться 0(нулю). Получается y будет стоять в первом столбце, а z в четвёртом.
Тогда ответ будет равен yxwz.
Ответ: yxwz
Мощнейший метод для решения второго задания из ЕГЭ по информатике
Задача 3 (хороший уровень)
Логическая функция F задаётся выражением ((x → y ) ∧ (y → w)) ∨ (z ≡ ( x ∨ y)).
Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности функции F.
Определите, какому столбцу таблицы истинности соответствует каждая из переменных x, y, z, w.
В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы (сначала — буква, соответствующая первому столбцу; затем — буква, соответствующая второму столбцу, и т. д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Пример. Пусть задано выражение x → y, зависящее от двух переменных x и y, и фрагмент таблицы истинности:
Тогда первому столбцу соответствует переменная y, а второму столбцу соответствует переменная x. В ответе нужно написать: yx.
Решение:
«Главной скрипкой» в нашей функции является логическое сложение, потому что соединяет два выражения ((x → y ) ∧ (y → w)) и (z ≡ ( x ∨ y)).
Тогда каждое выражение должно равняться 0(нулю).
Теперь кульминация мощнейшего метода. У нас всего 4 переменных. Выпишем все комбинации для 4-х переменных. Таблица будет точно такая же, как мы писали в первом задании (её очень легко составить). Всего получается 16 комбинаций (16 = 24).
Теперь отметим зелёным плюсом те строчки, которые обращают выражение ((x → y ) ∧ (y → w)) в 0(ноль). Следующий шаг: Отметим галочкой те строчки, которые обращают в ноль второе выражение (z ≡ ( x ∨ y)) (Мы должны искать среди тех, которые уже отмечены плюсом).
При небольшой тренировке анализ подобных выражений занимает сущие секунды!
У нас получается 4 строчки, которые удовлетворяют нашей функции:
Отсюда видно, что переменная z может быть равна только 0(нулю)! Значит, она занимает третий столбец, потому что в остальных столбцах есть хотя бы одна 1(единица).
Переменная w имеет только одну 1(единицу). Значит, её ставим во второй столбец, потому что в первом и четвёртом уже по 2 единицы минимум, а третий уже занят z.
Теперь находим строчку c 1(единицей) в переменной w (Таблица данная в условии задачи) Кто в этой строчке будет иметь единицу (кроме w) — будет x! Это четвёртый столбец! Значит, x — это четвёртый столбец. Переменной y — достаётся первый столбец
Ответ: ywzx.
На этом всё! Сегодня рассмотрели теорию и основные методы для эффективного решения второго задания из ЕГЭ по информатике!
Пока!
Задача 1
Каждое из логических выражений A и B зависит от одного и того же набора из 5 переменных. В таблицах истинности обоих выражений совпадают ровно 10 строк. Каково максимально возможно…
Задача 2
Логическая функция F задаётся выражением (x → y) → (w → g). Во фрагменте таблицы истинности функции F приведены все строки, при которых значение функции F ложно. Определите, какому…
Задача 3
Логическая функция F задаётся выражением ¬x ⋁ y ⋁ (z ⋀ ¬w). Во фрагменте таблицы истинности функции F приведены все строки, при которых значение функции F ложно.
Определите, какому…
Задача 4
Логическая функция F задаётся выражением (¬x⋀y)⋁(z⋀¬y)⋁ w. Ниже приведён частично заполненный фрагмент таблицы истинности функции F, содержащий неповторяющиеся строки.
Определите, …
Задача 5
Логическая функция F задаётся выражением (x⋁y)⋀(¬y ≡ z)⋀ w. Ниже приведён частично заполненный фрагмент таблицы истинности функции F, содержащий неповторяющиеся строки.
Определите,…
Задача 6
Логическая функция F задаётся выражением ((¬z⋁¬x)⋀z)⋁w⋁¬y. Ниже приведён фрагмент таблицы истинности функции F, содержащий все наборы аргументов, при которых функция F ложна. Опред…
Задача 7
Логическая функция F задаётся выражением ((x ⋀ z) ⋁ ¬x) ⋀ ¬w ⋀ y. Ниже приведён фрагмент таблицы истинности функции F, содержащий все наборы аргументов, при которых функция F истин…
Задача 8
Логическая функция F задаётся выражением (y ⋀ (w → x)) → g. Во фрагменте таблицы истинности функции F приведены все строки, при которых значение функции F ложно. Определите, какому…
Задача 9
Логическая функция F задаётся выражением ¬(x → z) ⋀ (¬y ⋁ w). Во фрагменте таблицы истинности функции F приведены все строки, при которых значение функции F истинно. Определите, ка…
Задача 10
Логическая функция F задаётся выражением y ⋀ (x → z) ⋀ ¬w. Во фрагменте таблицы истинности функции F приведены все строки, при которых значение функции F истинно. Определите, каком…
Задача 11
Логическая функция F задаётся выражением (x = y) ⋁ ¬(x → w)⋁ z. Ниже приведён частично заполненный фрагмент таблицы истинности функции F, содержащий неповторяющиеся строки.
Определ…
Задача 12
Логическая функция F задаётся выражением ((y → x)⋀(¬x → z))⋁ ¬w. Ниже приведён частично заполненный фрагмент таблицы истинности функции F, содержащий неповторяющиеся строки.
Опреде…
Задача 13
Логическая функция F задаётся выражением (x = y) ⋁ ¬(y → w) ⋁ z. Ниже приведён частично заполненный фрагмент таблицы истинности функции F, содержащий неповторяющиеся строки.
Опреде…
Задача 14
Логическая функция F задаётся выражением (x → y)⋀(¬y⋁w)⋀z. Ниже приведён частично заполненный фрагмент таблицы истинности функции F, содержащий неповторяющиеся строки.
Определите, …
Задача 15
Укажите значения логических переменных X, Y, Z, T , при которых логическое выражение (X → Y ) ∨ ((X ∧ ¬Z) → T ) ложно.
Ответ запишите в виде строки из четырёх значений переменных X…
Задача 16
Дан фрагмент таблицы истинности выражения F:
…
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | F |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 |
| 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| 1 | 0 |
Задача 17
Логическая функция F задаётся выражением (x → ¬y) ≡ (z ∨ y). Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z.
Задача 18
Логическая функция F задаётся выражением ¬x∧(y → z).Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z.
| Переменная 1 ??? |
Переменн… |
Задача 19
Логическая функция F задаётся выражением (x ∧ ¬y) ∨ (¬y ∧ ¬z). Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z.
Задача 20
Логическая функция F задаётся выражением ((¬z∨¬x)∧z)∨w∨¬y. Ниже приведён фрагмент таблицы истинности функции F , содержащий все наборы аргументов, при которых функция F ложна. Опре…
На уроке рассматривается разбор 2 задания ЕГЭ по информатике, дается подробное объяснение того, как решать подобные задачи
2-е задание: «Таблицы истинности»
Уровень сложности
— базовый,
Требуется использование специализированного программного обеспечения
— нет,
Максимальный балл
— 1,
Примерное время выполнения
— 3 минуты.
Проверяемые элементы содержания: Умение строить таблицы истинности и логические схемы
Типичные ошибки и рекомендации по их предотвращению:
«Игнорирование прямо указанного в условии задания требования, что заполненная таблица истинности не должна содержать одинаковых строк. Это приводит к внешне правдоподобному, но на самом деле неверному решению»
ФГБНУ «Федеральный институт педагогических измерений»
Таблицы истинности и порядок выполнения логических операций
Для логических операций приняты следующие обозначения:
| операция | пояснение | в программировании |
|---|---|---|
| ¬ A, A | не A (отрицание, инверсия) | not(A) |
| A ∧ B, A ⋅ B | A и B (логическое умножение, конъюнкция) | A and B |
| A ∨ B, A + B | A или B (логическое сложение, дизъюнкция) | A or B |
| A → B | импликация (следование) | A |
| A ↔ B, A ≡ B, A ∼ B | эквиваленция (эквивалентность, равносильность) | A==B (python) A=B(pascal) |
| A ⊕ B | строгая дизъюнкция | A != B (python) |
Егифка ©:
Отрицание (НЕ):
Таблица истинности операции НЕ
Конъюнкция (И):
Таблица истинности операции И (конъюнкция)
Дизъюнкция (ИЛИ):
Таблица истинности операции ИЛИ (дизъюнкция)
Импликация (если…, то…):
Таблица истинности операции Импликация (если…, то…)
Эквивалентность (тогда и только тогда, …):
Таблица истинности операции Эквивалентность (тогда и только тогда, …)
Сложение по модулю 2 (XOR):
| A | B | A ⊕ B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Порядок выполнения операций:
- если нет скобок, сначала выполняются все операции «НЕ», затем – «И», затем – «ИЛИ», импликация, равносильность
Еще о логических операциях:
- логическое произведение X∙Y∙Z∙… равно 1, т.е. выражение является истинным, только тогда, когда все сомножители равны 1 (а в остальных случаях равно 0)
- логическая сумма X+Y+Z+… равна 0, т.е. выражение является ложным только тогда, когда все слагаемые равны 0 (а в остальных случаях равна 1)
О преобразованиях логических операций читайте здесь.
Егифка ©:
Решение заданий 2 ЕГЭ по информатике
Плейлист видеоразборов задания на YouTube:
Задание демонстрационного варианта 2022 года ФИПИ
Задание 2_11: Решение 2 задания ЕГЭ по информатике (Задание № 169 К. Поляков):
Логическая функция F задается выражением
(¬x ∨ y ∨ z) ∧ (x ∨ ¬z ∨ ¬w)
Ниже приведен фрагмент таблицы истинности функции F, содержащей все наборы аргументов, при которых функция F ложна.
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.
| Перем.1 | Перем.2 | Перем.3 | Перем.4 | F |
| ??? | ??? | ??? | ??? | F |
| 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
В ответе запишите буквы в том порядке, в котором идут соответствующие им столбцы.
✍ Решение:
✎ Способ 1. Электронные таблицы Excel + Логические размышления:
- Отобразим перебор всех значений использующихся в выражении переменных (всю таблицу истинности). Поскольку в выражении используются 4 переменных, то строк таблицы будет 24=16:
- Далее обе скобки исходного выражения необходимо записать в виде логического выражения, каждую — в отдельном столбце. Также в отдельном столбце добавьте формулу итоговой функции F:

xwzy
- ✎ Способ 2. Программирование:
- В результате будут выведены значения для
F=0:
Язык python:
print('x y z w') for x in 0, 1: for y in 0, 1: for z in 0, 1: for w in 0, 1: F = (not(x) or y or z) and (x or not(z) or not(w)) if not(F): print(x, y, z, w)
x y z w 0 0 1 1 0 1 1 1 1 0 0 0 1 0 0 1
xwzy
Язык pascalAbc.net:
begin writeln('x':7, 'y':7, 'z':7,'w':7); for var x:=false to true do for var y:=false to true do for var z:=false to true do for var w:=false to true do if not((not x or y or z) and (x or not z or not w)) then writeln(x:7, y:7, z:7,w:7); end.
F=0:x y z w False False True True False True True True True False False False True False False True
false = 0, True = 1Ответ:
xwzy
- ✎ Способ 3. Логические размышления:
- Внешняя операция выражения — конъюнкция (∧). Во всех указанных строках таблицы истинности функция принимает значение 0 (ложь). Конъюнкция ложна аж в трех случаях, поэтому проверить на ложь очень затруднительно. Тогда как конъюнкция истинна (= 1) только в одном случае: когда все операнды истинны. Т.е. в нашем случае:
(¬x ∨ y ∨ z) ∧ (x ∨ ¬z ∨ ¬w) = 1 когда: 1. (¬x ∨ y ∨ z) = 1 И 2. (x ∨ ¬z ∨ ¬w) = 1
| x | y | z | результат |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
| x | z | w | результат |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
| x | y | z | w | F |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| x | y | z | w | F |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| x | ??? | ??? | ??? | F |
| 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| x | y | z | w | F |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| x | ??? | ??? | y | F |
| 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| x | y | z | w | F |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| x | w | z | y | F |
| 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
Результат: xwzy
🎦 Видео решения 169 задания К.Полякова (бескомпьютерный вариант):
📹 Видеорешение на RuTube здесь
Задание 2_12: Разбор 2 задания ЕГЭ вариант № 4, 2019 Информатика и ИКТ Типовые экзаменационные варианты (10 вариантов), С.С. Крылов, Т.Е. Чуркина:
Миша заполнял таблицу истинности функции:
(¬z ∧ ¬(x ≡ y)) → ¬(y ∨ w)
но успел заполнить лишь фрагмент из трех различных ее строк, даже не указав, какому столбцу таблицы соответствует каждая из переменных w, x, y, z:
| Перем.1 | Перем.2 | Перем.3 | Перем.4 | F |
| ??? | ??? | ??? | ??? | F |
| 1 | 1 | 0 | ||
| 1 | 0 | 0 | ||
| 1 | 1 | 0 | 0 |
Определите, какому столбцу таблицы соответствует каждая из переменных x, y, z, w.
В ответе напишите буквы w, x, y, z в том порядке, в котором идут соответствующие им столбцы.
Подобные задания для тренировки
✍ Решение:
✎ Способ 1. Логические размышления (бескомпьютерный вариант):
- Решим задание методом построения полной таблицы истинности.
- Посчитаем общее количество строк в таблице истинности и построим ее:
4 переменных -> 24 = 16 строк
(¬z ∧ ¬(x ≡ y)) → ¬(y ∨ w) 1. Избавимся от импликации: ¬(¬z ∧ ¬(x ≡ y)) ∨ ¬(y ∨ w) 2. Внесем знак отрицания в скобки (закон Де Моргана): (z ∨ (x ≡ y)) ∨ (¬y ∧ ¬w) = 0 1 часть = 0 2 часть = 0 * Исходное выражение должно быть = 0. Дизъюнкция = 0, когда оба операнда равны 0.
(z ∨ (x ≡ y)) = 0 когда z = 0 и x ≡ y = 0 ¬y ∧ ¬w = 0 когда: 1. ¬y = 0 ¬w = 0 2. ¬y = 1 ¬w = 0 3. ¬y = 0 ¬w = 1
| x | y | w | z | F |
| 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 |
| y | w | x | z | F |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 0 |
Результат: ywxz
✎ Способ 2. Программирование:
- В результате будут выведены значения для F=0:
Язык PascalAbc.net:
begin writeln('x':7, 'y':7, 'z':7,'w':7); for var x:=false to true do for var y:=false to true do for var z:=false to true do for var w:=false to true do if not((not z and (x xor y)) <= not(y or w)) then writeln(x:7, y:7, z:7,w:7); end.
x y z w False True False False False True False True True False False True
false = 0, True = 1Сопоставив их с исходной таблицей, получим результат: ywxz
Язык Python:
print ('x y z w') for x in 0,1: for y in 0,1: for z in 0,1: for w in 0,1: F=(not z and not(x==y))<=(not(y or w)) if not F: print (x,y,z,w)
F=0:x y z w 0 1 0 0 0 1 0 1 1 0 0 1
Сопоставив их с исходной таблицей, получим результат:
Результат: ywxz
🎦 Доступно видео решения этого задания (бескомпьютерный вариант):
📹 Видеорешение на RuTube здесь
🎦 Видео (решение 2 ЕГЭ в Excel):
📹 Видеорешение на RuTube здесь
📹 Видеорешение на RuTube здесь (Программирование)
Задание 2_10: Решение 2 задания ЕГЭ по информатике (диагностический вариант экзаменационной работы 2018 года, С.С. Крылов, Д.М. Ушаков):
Логическая функция F задается выражением
¬a ∧ b ∧ (c ∨ ¬d)
Ниже приведен фрагмент таблицы истинности функции F, содержащей все наборы аргументов, при которых функция F истинна.
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных a, b, c, d.
| Перем.1 | Перем.2 | Перем.3 | Перем.4 | F |
| ??? | ??? | ??? | ??? | F |
| 0 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 1 |
В ответе запишите буквы в том порядке, в котором идут соответствующие им столбцы.
✍ Решение:
🎦 (Бескомьютерный вариант) Предлагаем подробный разбор посмотреть на видео:
📹 Видеорешение на RuTube здесь
Задание 2_3: Решение задания 2. Демоверсия ЕГЭ 2018 информатика:
Логическая функция F задаётся выражением ¬x ∨ y ∨ (¬z ∧ w).
На рисунке приведён фрагмент таб. ист-ти функции F, содержащий все наборы аргументов, при которых функция F ложна.
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных w, x, y, z.
| Перем. 1 | Перем. 2 | Перем. 3 | Перем. 4 | F |
| ??? | ??? | ??? | ??? | F |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 |
В ответе напишите буквы w, x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала – буква, соответствующая первому столбцу; затем – буква, соответствующая второму столбцу, и т.д.) Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Подобные задания для тренировки
✍ Решение:
- ✎ Логические размышления (бескомпьютерный вариант):
- Внешним действием (последним выполняемым) в исходном выражении является дизъюнкция:
¬x ∨ y ∨ (¬z ∧ w)
| x1 | x2 | F |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
¬x = 1 или 0, y = 1 или 0, ¬z ∧ w = 1 или 0).¬x = 0, иными словами x = 1. Значит первый столбец соответствует переменной x. | Перем. 1 | Перем. 2 | Перем. 3 | Перем. 4 | F |
| x | ??? | ??? | ??? | F |
| 1 | 0 | 0 | 0 | 0 |
y = 0. Значит четвертый столбец соответствует переменной y. | Перем. 1 | Перем. 2 | Перем. 3 | Перем. 4 | F |
| x | ??? | ??? | y | F |
| 1 | 1 | 1 | 0 | 0 |
¬z ∧ w должно равняться 0, чтобы функция была ложной. Конъюнкция истинна только тогда, когда оба операнда истинны (=1); в нашем случае функция должна быть ложной, но пойдем от обратного. Если ¬z = 1, т.е. z = 0, а w = 1, то это неверно для нашего случая. Значит всё должно быть наоборот: z = 1, а w = 0. Таким образом столбец второй соответствует z, а столбец третий — w. | x | z | w | y | F |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 |
Результат: xzwy
✎ Способ 2. Программирование:
Язык pascalABC.NET:
begin writeln('x ','y ','z ','w '); for var x:=false to true do for var y:=false to true do for var z:=false to true do for var w:=false to true do if not(not x or y or(not z and w)) then writeln(x:7,y:7,z:7,w:7); end.
🎦 (бескомпьютерный вариант) Подробное решение данного 2 задания из демоверсии ЕГЭ 2018 года смотрите на видео:
📹 Видеорешение на RuTube здесь
Задание 2_13: Разбор досрочного егэ по информатике 2019
Логическая функция F задаётся выражением
(x ∧ ¬y) ∨ (y ≡ z) ∨ ¬w
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.
В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы.
| Перем.1 | Перем.2 | Перем.3 | Перем.4 | F |
| ??? | ??? | ??? | ??? | F |
| 0 | 0 | 0 | ||
| 0 | 1 | 0 | 1 | 0 |
| 1 | 0 | 0 |
✍ Решение:
🎦 Видеорешение (бескомпьютерный вариант):
📹 Видеорешение на RuTube здесь
Задания для тренировки
Задание 2_2: Задание 2 ЕГЭ по информатике 2017 ФИПИ вариант 11 (Крылов С.С., Чуркина Т.Е.):
Каждое из логических выражений F и G содержит 5 переменных. В табл. истинности для F и G есть ровно 5 одинаковых строк, причем ровно в 4 из них в столбце значений стоит 1.
Сколько строк таблицы истинности для F ∨ G содержит 1 в столбце значений?
Подобные задания для тренировки
✍ Решение:
- Поскольку в каждом из выражений присутствует 5 переменных, то эти 5 переменных порождают таблицу истинности из 32 строк: т.к. каждая из переменных может принимать оно из двух значений (0 или 1), то различных вариантов с пятью переменными будет 25=32, т.е. 32 строки.
- Из этих 32 строк и для F и для G мы знаем наверняка только о 5 строках: 4 из них истинны (=1), а одна ложна (=0).
- Вопрос стоит о количестве строк = 1 для таб. истинности F ∨ G. Данная операция — дизъюнкция, которая ложна только в одном случае — если F = 0 и одновременно G = 0
- В исходных таблицах для F и G мы знаем о существовании только одного 0, т.е. в остальных строках может быть 1. Т.о., и для F и для G в 31 строке могут быть единицы (32-1=31), а лишь в одной — ноль.
- Тогда для F ∨ G только в одном случае будет 0, когда и F = 0 и G = 0:
- Соответственно, истинными будут все остальные строки:
| № | F | G | F ∨ G |
|---|---|---|---|
| 1 | 0 | 0 | 0 |
| 2 | 0 | 1 | 1 |
| … | … | … | 1 |
| 32 | … | … | 1 |
32 - 1 = 31
Результат: 31
Подробное объяснение данного задания смотрите на видео:
Задание 2_6: Решение 2 задания ЕГЭ по информатике (К. Поляков, вариант 89):
Каждое логическое выражение A и B зависит от одного и того же набора из 7 переменных. В таблицах истинности каждого из этих выражений в столбце значений стоит ровно по 4 единицы.
Каково максимально возможное число единиц в столбце значений таблицы истинности выражения A ∨ B?
✍ Решение:
- Полная таблица истинности для каждого из выражений A и B состоит из 27 = 128 строк.
- В четырех из них результат равен единице, значит в остальных — 0.
- A ∨ B истинно в том случае, когда либо A = 1 либо B = 1, или и A и B = 1.
- Поскольку А = 1 только в 4 случаях, то чтобы получить максимальное количество единиц в результирующей таблице истинности (для A ∨ B), расположим все единицы т.и. для выражения A так, чтобы они были в строках, где B = 0, и наоборот, все строки, где B = 1, поставим в строки, где A = 0:
- Итого получаем 8 строк.
- Если бы в задании требовалось найти минимальное количество единиц, то мы бы совместили строки со значением = 1, и получили бы значение 4.
| A | B |
| 1 | 0 |
| 1 | 0 |
| 1 | 0 |
| 1 | 0 |
| 0 | 1 |
| 0 | 1 |
| 0 | 1 |
| 0 | 1 |
| 0 | 0 |
| … | … |
Результат: 8
Задание 2_7: Решение 2 задания ЕГЭ по информатике (К. Поляков, вариант 91):
Каждое логическое выражение A и B зависит от одного и того же набора из 8 переменных. В таблицах истинности каждого из этих выражений в столбце значений стоит ровно по 6 единиц.
Каково максимально возможное число нулей в столбце значений таблицы истинности выражения A ∧ B?
✍ Решение:
- Полная таблица истинности для каждого из выражений A и B состоит из 28 = 256 строк.
- В шести из них результат равен единице, значит в остальных — 0.
- A ∧ B ложно в том случае, когда:
A ∧ B = 0 если: 1. A = 0, B = 1 2. B = 0, A = 1 3. A = 0 и B = 0
- Во всех случаях там где А=1 может стоять B=0, и тогда результат F = 0. Поскольку нам необходимо найти максимально возможное число нулей, то как раз для всех шести А=1 сопоставим B=0, и наоборот, для всех шести возможных B=1 сопоставим A=0
- Поскольку строк всего 256, то вполне возможно, что все 256 из них возвратят в результате 0
| A | B | F |
| 1 | 0 | 0 |
| 1 | 0 | 0 |
| 1 | 0 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 1 | 0 |
| 0 | 1 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 0 |
| … | … | … |
Результат: 256
Задание 2_4: 2 задание. ГВЭ 11 класс по информатике 2018 (ФИПИ):
Дан фрагмент таблицы истинности выражения F.
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | F |
| 1 | 0 | 0 | 1 | 1 | 1 | 1 | 0 |
| 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 |
Каким из приведённых ниже выражений может быть F?
1) ¬x1 ∧ x2 ∧ ¬x3 ∧ ¬x4 ∧ x5 ∧ ¬x6 ∧ x7
2) x1 ∨ x2 ∨ x3 ∨ ¬x4 ∨ ¬x5 ∨ ¬x6 ∨ ¬x7
3) x1 ∧ ¬x2 ∧ x3 ∧ ¬x4 ∧ x5 ∧ x6 ∧ ¬x7
4) x1 ∨ ¬x2 ∨ x3 ∨ x4 ∨ ¬x5 ∨ ¬x6 ∨ x7
✍ Решение:
- В первом внешняя операция (выполняется последней) — конъюнкция. Начнем рассмотрение с нее. Соответственно, проверяем по второй строке таб. ист-ти, там где F = 1, так как в таком случае все аргументы должны быть истинными (см. таб. истинности для конъюнкции).
- Если мы подставим в нее все аргументы выражения, то функция действительно возвращает истину. Т.е. пункт первый подходит:
- Но проверим на всякий случай остальные.
- Второй пункт проверяем по первой и третьей строке, так как основная операция — дизъюнкция — ложна только в том случае, если все аргументы ложны (см. таб. истинности для дизъюнкции). Проверяя по первой строке, сразу видим, что x1 в ней равен 1. В таком случаем функция будет = 1. Т.е. этот пункт не подходит:
- Третий пункт проверяем по второй строке, так как основная операция — конъюнкция — возвратит истину только тогда, когда все операнды равны 1. Видим, что x1 = 0, соответственно функция будет тоже равна 0. Т.е. выражение нам не подходит:
- Четвертый пункт проверяем по первой и третьей строкам. В первой — x1 = 1, т.е. функция должна быть равна 1. Т.е. пункт тоже не подходит:
- Таким образом, ответ равен 1.
Результат: 1
Решение 2 задания ГВЭ по информатике смотрите на видео:
Задание 2_8: Решение 2 задания ЕГЭ по информатике (К. Поляков, вариант 58):
Дано логическое выражение, зависящее от 5 логических переменных:
(¬x1 ∨ ¬x2 ∨ ¬x3 ∨ x4 ∨ x5) ∧ (x1 ∨ x2 ∨ x3 ∨ ¬x4 ∨ ¬x5)
Сколько существует различных наборов значений переменных, при которых выражение истинно?
1) 0
2) 30
3) 31
4) 32
Подобные задания для тренировки
✍ Решение:
- Поскольку выражение включает 5 переменных, то таб. ист-ти состоит из 25 = 32 строк.
- Внешней операцией (последней) является конъюнкция (логическое умножение), а внутри скобок — дизъюнкция (логическое сложение).
- Обозначим первую скобку за А, а вторую скобку за B. Получим A ∧ B.
- Найдем сколько нулей существует для таб. истинности:
A B F 1. 0 0 0 2. 0 1 0 3. 1 0 0
Теперь рассмотрим каждый случай отдельно:
¬x1 ∨ ¬x2 ∨ ¬x3 ∨ x4 ∨ x5 = 0
и
x1 ∨ x2 ∨ x3 ∨ ¬x4 ∨ ¬x5 = 0.
32 - 2 = 30, что соответствует номеру 2
Результат: 2
Подробное решение задания смотрите в видеоуроке:
Задание 2_5: Решение 2 задания ЕГЭ по информатике (К. Поляков, вариант 76):
Дан фрагмент таблицы истинности для выражения F:
| x1 | x2 | x3 | x4 | x5 | x6 | F |
| 0 | 0 | 1 | 1 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 0 | 1 | 0 |
Укажите максимально возможное число различных строк полной таблицы истинности этого выражения, в которых значение x3 не совпадает с F.
Подобные задания для тренировки
✍ Решение:
- Полная таблица истинности будет иметь 26 = 64 строк (т.к. 6 переменных).
- 4 из них нам известны: в них x3 два раза не совпадает с F.
- Неизвестных строк:
64 - 4 = 60
60 + 2 = 62
Результат: 62
Задание 2_9: Решение 2 задания ЕГЭ по информатике (К. Поляков вариант 112):
Дан фрагмент таблицы истинности для выражения F:
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | F |
| 0 | 0 | 0 | |||||
| 0 | 0 | 1 | |||||
| 1 | 1 | 1 |
Каким выражением может быть F?
1) x1 ∧ (x2 → x3) ∧ ¬x4 ∧ x5 ∧ x6 ∧ ¬x7
2) x1 ∨ (¬x2 → x3) ∨ ¬x4 ∨ ¬x5 ∨ x6 ∨ ¬x7
3) ¬x1 ∧ (x2 → ¬x3) ∧ x4 ∧ ¬x5 ∧ x6 ∧ x7
4) ¬x1 ∨ (x2 → ¬x3) ∨ x4 ∨ x5 ∨ x6 ∧ x7
✍ Решение:
- Рассмотрим отдельно каждый пункт и найдем последнюю операцию, которая должна быть выполнена (внешнюю).
1 пункт:
(((x1 ∧ (x2 → x3) ∧ ¬x4) ∧ x5) ∧ x6) ∧ ¬x7
2 пункт:
(((x1 ∨ (¬x2 → x3) ∨ ¬x4) ∨ ¬x5) ∨ x6) ∨ ¬x7
3 пункт:
(((¬x1 ∧ (x2 → ¬x3) ∧ x4) ∧ ¬x5) ∧ x6) ∧ x7
Результат: 4
В видеоуроке рассмотрено подробное решение 2 задания:
Задание 2_1: Задание 2 ЕГЭ по информатике 2017 ФИПИ вариант 6 (Крылов С.С., Чуркина Т.Е.):
Логическая функция F задается выражением
(y → x) ∧ (y → z) ∧ z.
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z.
| № | Перем. 1 | Перем. 2 | Перем. 3 | F |
|---|---|---|---|---|
| ??? | ??? | ??? | F | |
| 1 | 0 | 0 | 0 | 0 |
| 2 | 0 | 0 | 1 | 0 |
| 3 | 0 | 1 | 0 | 1 |
| 4 | 0 | 1 | 1 | 1 |
| 5 | 1 | 0 | 0 | 0 |
| 6 | 1 | 0 | 1 | 0 |
| 7 | 1 | 1 | 0 | 0 |
| 8 | 1 | 1 | 1 | 1 |
В ответе напишите буквы x, y, z в том порядке, в котором идут соответствующие им столбцы.
✍ Решение:
- Сначала необходимо рассмотреть логическую операцию, которую мы будем выполнять в последнюю очередь — это логическое И (конъюнкция) или ∧. То есть внешнюю операцию:
(y → x) ∧ (y → z) ∧ z
(y → x) ∧ (y → z) ∧ z = 1 если: 1. (y → x) = 1 2. (y → z) = 1 3. z = 1
| № | Перем. 1 | Перем. 2 | Перем. 3 | F |
|---|---|---|---|---|
| 3 | 0 | 1 | 0 | 1 |
| № | Перем. 1 | Перем. 2 | Перем. 3 | F |
|---|---|---|---|---|
| _ | ??? | z | ??? | F |
| № | Перем. 1 | z | Перем. 3 | F |
|---|---|---|---|---|
| 4 | 0 | 1 | 1 | 1 |
Результат: yzx
Детальный разбор данного задания 2 ЕГЭ по информатике предлагаем посмотреть в видео:
Построение таблиц истинности логических выражений
Содержащие более трёх переменных
№1. Дано логическое
выражение, зависящее от 5 логических переменных:
z1 ∧ ¬z2 ∧ ¬z3 ∧ ¬z4 ∧ z5
Сколько существует различных наборов значений переменных,
при которых выражение ложно?
1) 1
2) 2
3) 31
4) 32
Пояснение.
Операция конъюнкции возвращает ложное значение, если хотя бы
один из её аргументов ложен, т.е. существует только один вариант, возвращающий
истину. Следовательно, искомое число вариантов равно 25-1 = 31
(число 2 возводится в пятую степень, так как всего переменных 5 и каждая
из них может принимать два значения).
№2. Дан фрагмент
таблицы истинности выражения F:
|
x1 |
x2 |
x3 |
x4 |
x5 |
F |
|
1 |
1 |
1 |
|||
|
1 |
1 |
1 |
1 |
||
|
1 |
1 |
Какое выражение соответствует F?
1) x1 ∨ x2 ∨ x3 ∨ ¬x4 ∨ ¬x5
2) ¬x1 ∨ x2 ∨ ¬x3 ∨ x4 ∨ ¬x5
3) x1 ∧ ¬x2 ∧ x3 ∧ ¬x4 ∧ x5
4) ¬x1 ∧ x2 ∧ x3 ∧ x4 ∧ ¬x5
Пояснение.
Посмотрим внимательно на ответы. Они представляют собой либо
конъюнкцию, либо дизъюнкцию данных пяти переменных или отрицательных
к ним.
Сначала выясним, конъюнкция это или дизъюнкция.
Дизъюнкция не может принимать значение ноля дважды из трех разных
комбинаций, следовательно, в ответе должна быть конъюнкция. Вычеркиваем
1 и 2 варианты ответа.
Из 3 и 4 вариантов подходит 4. Правильный ответ — 4.
№3. Дан фрагмент
таблицы истинности выражения F:
|
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
F |
|
1 |
1 |
1 |
1 |
1 |
||
|
1 |
1 |
1 |
1 |
|||
|
1 |
1 |
1 |
1 |
Каким выражением может быть F?
1) x1 ∨ x2 ∨ x3 ∨ ¬x4 ∨ ¬x5 ∨ ¬x6
2) ¬x1 ∨ x2 ∨ ¬x3 ∨ x4 ∨ ¬x5 ∨ ¬x6
3) x1 ∧ x2 ∧ ¬x3 ∧ ¬x4 ∧ x5 ∧ x6
4) ¬x1 ∧ ¬x2 ∧ x3 ∧ x4 ∧ x5 ∧ x6
Пояснение.
Посмотрим внимательно на ответы. Они представляют собой либо
конъюнкцию, либо дизъюнкцию данных пяти переменных или отрицательных
к ним. Сначала выясним, конъюнкция это или дизъюнкция.
Конъюнкция не может принимать значение единицы дважды из трех
разных комбинаций, следовательно, в ответе должна быть дизъюнкция.
Вычеркиваем 3 и 4 варианты ответа.
Из 1 и 2 вариантов подходит 2.
Правильный ответ указан под номером 2.
№4. Дан фрагмент
таблицы истинности выражения F:
|
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
F |
|
1 |
1 |
|||||
|
1 |
1 |
1 |
||||
|
1 |
1 |
Каким выражением может быть F?
1) (x1 ∧ x2) ∨ (x3 ∧ x4) ∨ (x5 ∧ x6)
2) (x1 ∧ x3) ∨ (x3 ∧ x5) ∨ (x5 ∧ x1)
3) (x2 ∧ x4) ∨ (x4 ∧ x6) ∨ (x6 ∧ x2)
4) (x1 ∧ x4) ∨ (x2 ∧ x5) ∨ (x3 ∧ x6)
Пояснение.
Все представленные здесь варианты ответа — дизъюнкции трёх конъюнкций.
Все представленные значения F равны нулю. Дизъюнкция равна нулю тогда и
только тогда, когда все её операнды равны нулю.
Рассмотри поочерёдно все четыре выражения.
Первое выражение. В первой строке таблицы x1 и x2 равны единице,
значит x1∧x2=1. Этот вариант ответа нам не подходит.
Второе выражение. Во второй строке таблицы x1 и x3 равны единице,
значит x1∧x3=1. Этот вариант ответа нам не подходит.
Третье выражение. Проверим все строки таблицы.
Проверим первую строку таблицы. (x1 ∧ x2) ∨ (x3 ∧ x4) ∨ (x5 ∧ x6)=0∨0∨0=0 — верно.
Проверим вторую строку таблицы. (x1 ∧ x2) ∨ (x3 ∧ x4) ∨ (x5 ∧ x6)=0∨0∨0=0 — верно.
Проверим третью строку таблицы. (x1 ∧ x2) ∨ (x3 ∧ x4) ∨ (x5 ∧ x6)=0∨0∨0=0 — верно.
Четвёртое выражение. В третьей строке таблицы x1 и x4 равны единице,
значит x1∧x4=1. Этот вариант ответа нам не подходит.
Правильный ответ указан под номером 3.
№5. Дан фрагмент
таблицы истинности выражения F:
|
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
F |
|
1 |
1 |
1 |
||||
|
1 |
1 |
|||||
|
1 |
1 |
1 |
Каким выражением может быть F?
1) (x1 ∧ x2) ∨ (x3 ∧ x4) ∨ (x5 ∧ x6)
2) (x1 ∧ x3) ∨ (x3 ∧ x5) ∨ (x5 ∧ x1)
3) (x2 ∧ x4) ∨ (x4 ∧ x6) ∨ (x6 ∧ x2)
4) (x1 ∧ x4) ∨ (x2 ∧ x5) ∨ (x3 ∧ x6)
Пояснение.
Все представленные здесь варианты ответа — дизъюнкции трёх конъюнкций.
Все представленные значения F равны нулю. Дизъюнкция равна нулю тогда и
только тогда, когда все её операнды равны нулю.
Рассмотри поочерёдно все четыре выражения.
Первое выражение. В первой строке таблицы x5 и x6 равны единице,
значит x5∧x6=1. Этот вариант ответа нам не подходит.
Второе выражение. Проверим все строки таблицы.
Проверим первую строку таблицы. (x1 ∧ x2) ∨ (x3 ∧ x4) ∨ (x5 ∧ x6)=0∨0∨0=0 — верно.
Проверим вторую строку таблицы. (x1 ∧ x2) ∨ (x3 ∧ x4) ∨ (x5 ∧ x6)=0∨0∨0=0 — верно.
Проверим третью строку таблицы. (x1 ∧ x2) ∨ (x3 ∧ x4) ∨ (x5 ∧ x6)=0∨0∨0=0 — верно.
Третье выражение. В первой строке таблицы x2 и x6 равны единице,
значит x2∧x6=1. Этот вариант ответа нам не подходит.
Четвёртое выражение. В третьей строке таблицы x1 и x4 равны единице,
значит x1∧x4=1. Этот вариант ответа нам не
подходит.
Правильный ответ указан под номером 2.
№6. Дан фрагмент
таблицы истинности выражения F.
|
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
x7 |
F |
|
1 |
1 |
1 |
1 |
1 |
1 |
||
|
1 |
1 |
1 |
1 |
||||
|
1 |
1 |
1 |
1 |
Каким из приведённых ниже выражений может быть F?
1) ¬x1 ∧ x2 ∧ ¬x3 ∧ x4 ∧ x5 ∧ ¬x6 ∧ ¬x7
2) ¬x1 ∨ x2 ∨ ¬x3 ∨ x4 ∨ ¬x5 ∨ ¬x6 ∨ x7
3) x1 ∧ ¬x2 ∧ x3 ∧ ¬x4 ∧ x5 ∧ x6 ∧ ¬x7
4) x1 ∨ ¬x2 ∨ x3 ∨ ¬x4 ∨ ¬x5 ∨ x6 ∨ ¬x7
Пояснение.
Посмотрим внимательно на ответы. Они представляют собой либо
конъюнкцию, либо дизъюнкцию данных семи переменных или отрицательных
к ним. Сначала выясним, конъюнкция нам нужна или дизъюнкция.
Дизъюнкция не может принимать значение ноля дважды из трех разных
комбинаций, следовательно, в ответе должна быть конъюнкция. Вычеркиваем
2 и 4 варианты ответа.
Из 1 и 3 вариантов подходит 1. Правильный ответ — 1.
№7. Дан фрагмент
таблицы истинности выражения F:
Каким выражением может быть F?
1) х1 ∧ х2 ∧ ¬хЗ ∧ х4 ∧ ¬х5 ∧ хб ∧ ¬х7
2) x1 ∨ х2 ∨ ¬хЗ ∨ х4 ∨ ¬х5 ∨ хб ∨ ¬x7
3) x1 ∨ ¬х2 ∨ хЗ ∨ ¬х4 ∨ ¬х5 ∨ хб ∨ ¬х7
4) ¬х1 ∧ ¬х2 ∧ хЗ ∧ ¬х4 ∧ х5 ∧ ¬хб ∧ х7
Пояснение.
Посмотрим внимательно на ответы. Они представляют собой либо
конъюнкцию, либо дизъюнкцию данных семи переменных или отрицательных
к ним.
Сначала выясним, конъюнкция это или дизъюнкция.
Дизъюнкция не может принимать значение ноля дважды из трех разных
комбинаций, следовательно, в ответе должна быть конъюнкция. Вычеркиваем
2 и 3 варианты ответа.
Из 1 и 4 вариантов подходит 1. Правильный ответ — 1.
№8. Дан фрагмент
таблицы истинности выражения F:
Каким выражением может быть F?
1) х1 ∧ х2 ∧ ¬хЗ ∧ ¬х4 ∧ х5 ∧ хб ∧ ¬х7
2) x1 ∨ х2 ∨ ¬хЗ ∨ ¬х4 ∨ х5 ∨ хб ∨ ¬х7
3) ¬x1 ∨ ¬х2 ∨ хЗ ∨ х4 ∨ ¬х5 ∨ ¬хб ∨ х7
4) ¬х1 ∧ ¬х2 ∧ хЗ ∧ х4 ∧ ¬х5 ∧ ¬хб ∧ х7
Пояснение.
Сначала выясним, является F конъюнкцией или дизъюнкцией.
Каковы бы ни были логические переменные х1, х2, … х7 и отрицания
к ним, их конъюнкция может быть равна 1 только в одном случае — когда все
они равны 1. Из таблицы истинности следует, что функция F принимает
значение 1 для одного набора переменных и их отрицаний. Таким образом,
F — конъюнкция. Следовательно, второй и третий варианты ответа не
подходят.
Подставим первый вариант ответа. Во второй строке данной таблицы
значение F равно 1. Это значит, что все переменные из x1, x2, ¬x3, ¬x4,
x5, x6,¬ x7 должны быть равны 1. Значит первый вариант не подходит.
Подставим четвертый вариант ответа. Во второй строке данной
таблицы значение F равно 1. Это значит, что все переменные из ¬x1, ¬x2,
x3, x4, ¬x5, ¬x6, x7 должны быть равны 1. Следовательно, 4 вариант ответа
подходит. Проверим последовательно все строки таблицы.
Проверим третью строку таблицы. Конъюнкция равна нулю в том случае,
когда хотя бы одна из переменных ¬x1, ¬x2, x3, x4, ¬x5, ¬x6, x7 равна нулю.
И такая переменная есть: x3 = 0.
Проверим первую строку таблицы. Конъюнкция равна нулю в том случае,
когда хотя бы одна из переменных ¬x1, ¬x2, x3, x4, ¬x5, ¬x6, x7 равна нулю и
такая переменная есть: x7 = 0.
То есть ответом является четвертый вариант.
№9. Дан фрагмент
таблицы истинности выражения F:
Каким выражением может быть F?
1) x1 ∧ ¬x2 ∧ x3 ∧ ¬x4 ∧ x5 ∧ ¬x6 ∧ x7
2) x1 ∨ ¬x2 ∨ x3 ∨¬x4 ∨ x5 ∨ ¬x6 ∨ x7
3) ¬x1 ∨ x2 ∨ ¬x3 ∨ x4 ∨ ¬x5 ∨ x6 ∨ ¬x7
4) ¬x1 ∧ x2 ∧ ¬x3 ∧ x4 ∧ ¬x5 ∧ x6 ∧ ¬x7
Пояснение.
Проанализируем варианты ответов. Они представляют собой либо
конъюнкцию, либо дизъюнкцию данных семи переменных или противоположных
к ним (если x1 — переменная, то противоположная к ней — это
¬x1).
Сначала выясним, является F конъюнкцией или дизъюнкцией.
Каковы бы ни были логические переменные х1, х2, … х7 и отрицания
к ним, их конъюнкция может быть равна 1 только в одном случае — когда все
они равны 1. Из таблицы истинности следует, что функция F принимает
значение 1 для двух различных наборов переменных и их отрицаний, поэтому
F не может быть конъюнкцией. тем самым, ответы 1 и 4 не подходят.
Последовательно подставим 2 и 3 варианты ответа.
Вариант 2 (дизъюнкция x1, x3, x5, x7, ¬x2, ¬x4, ¬x6):
В первой строке данной таблицы значение F равно 1. Это значит,
что хотя бы одна переменная из x1, x3, x5, x7, ¬x2, ¬x4, ¬x6 должна быть
равна 1, и такая есть — это х5. Значит, по первой строке вариант 2
удовлетворяет функции F.
Во второй строке данной таблицы значение F равно 1. Это значит,
что хотя бы одна переменная из x1, x3, x5, x7, ¬x2, ¬x4, ¬x6 должна быть
равна 1, и такая есть — это, например, х6. Значит, по второй строке
вариант 2 удовлетворяет функции F.
В третьей строке данной таблицы значение F равно 0. Это значит,
что все переменные x1, x3, x5, x7, ¬x2, ¬x4, ¬x6 должна быть равны 0. Так
как в третьей строке переменные, около которых в варианте 2 стоит отрицание,
равны 1, а переменные без отрицания равны 0, то по третьей строке вариант
2 удовлетворяет функции F.
Вариант 2 удовлетворяет функции F по всем строкам таблицы.
Правильный ответ — 2.
№10. Дан фрагмент
таблицы истинности выражения F.
|
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
x7 |
F |
|
1 |
1 |
1 |
1 |
||||
|
1 |
1 |
1 |
1 |
1 |
|||
|
1 |
1 |
1 |
1 |
Каким из приведённых ниже выражений может быть F?
1) (х1 ∨ х2) ∧ ¬хЗ ∧ х4 ∧ ¬х5 ∧ хб ∧ ¬х7
2) (х1 ∧ х2) ∨ ¬хЗ ∨ х4 ∨ ¬х5 ∨ хб ∨ ¬х7
3) (х1 ∧ ¬х2) ∨ хЗ ∨ ¬х4 ∨ ¬х5 ∨ хб ∨ ¬х7
4) (¬х1 ∨ ¬х2) ∧ хЗ ∧ ¬х4 ∧ х5 ∧ ¬хб ∧ х7
Пояснение.
Проанализируем варианты ответов. Они представляют собой либо
конъюнкцию, либо дизъюнкцию данных семи переменных или противоположных
к ним (если x1 — переменная, то противоположная к ней — это
¬x1).
Сначала выясним, является F конъюнкцией или дизъюнкцией.
Каковы бы ни были логические переменные х1, х2, … х7 и отрицания
к ним, их дизъюнкция может быть равна 0 только в одном случае — когда все
они равны 0. Из таблицы истинности следует, что функция F принимает
значение 0 для двух различных наборов переменных и их отрицаний, поэтому
F не может быть дизъюнкцией. Тем самым, ответы 2 и 3 не подходят.
Вариант 1 (конъюнкция (х1 ∨ х2), ¬x3, x4, ¬x5, x6, ¬x7):
В первой строке данной таблицы значение F равно 0. Это значит,
что хотя бы одна переменная из (х1 ∨ х2), ¬x3, x4, ¬x5, x6, ¬x7 должна быть равна 0, и такая и есть — это ¬х5. Значит, по первой строке вариант
1 удовлетворяет функции F.
В второй строке данной таблицы значение F равно 1. Это значит,
что все переменные из (х1 ∨ х2), ¬x3, x4, ¬x5, x6, ¬x7 должны быть равны 1, Так как в третьей строке переменные, около которых стоит
отрицание, равны 0, а переменные без отрицания равны 1, то по второй
строке вариант 1 удовлетворяет функции F.
В третьей строке данной таблицы значение F равно 0. Это значит,
что хотя бы одна переменная из (х1 ∨ х2), ¬x3, x4, ¬x5, x6, ¬x7 должна быть равна 0, и такая и есть — это х6. Значит, по третьей строке вариант 1 удовлетворяет функции F.
Правильный ответ — 1.
содержащие три переменных
№1. Символом F обозначено одно из указанных
ниже логических выражений от трех аргументов: X, Y, Z. Дан фрагмент
таблицы истинности выражения F:
Какое выражение соответствует F?
1) (0 ∧ Y) ∧ (X ≡ Z)
2) (1 ∧ Y) ∧ (X ≡ Z)
3) (0 ∨ ¬Z) ∧ (X ≡ Y)
4) (¬1 ∧ Y) ∧ (X ≡ Z)
Пояснение.
1. Заметим, что первый вариант дает в результате 0
во всех случаях, так как конъюнкция ложна, если ложен хотя бы один из её аргументов,
а это не соответствует значениям F.
2. Выражение в варианте 2, как и в варианте 4, принимает
ложные значения, если X не эквивалентно Z, а значит, по первой и третьей
строчке и 2, и 4 вариант удовлетворяют F.
3. Остается сравнить их по второй строке, в которой F
– истинно. В этой строке X=0, Y=1, Z=0, значит, выражение в варианте
2 здесь истинно.
4. Так как значения F и значения функции в варианте
2 сошлись по всем трем строкам, вариант 2 является ответом к данной
задаче.
|
№2. Символом F обозначено одно из указанных Какое выражение соответствует F? 1) (0 ∧ Z) ∧ (X ≡ 2) (0 ∨ ¬Z) ∧ (X ≡ 3) (1 ∧ Z) ∧ (X ≡ 4) ( ¬1 ∧ Z) ∧ (X ≡ Пояснение. 1. Выражения из вариантов 1, 4 всегда дают результатом 2. Рассмотрим варианты 2, 3. В них обоих присутствует 3. Так как значения F и значения функции в варианте |
№3. Символом F обозначено одно из указанных
ниже логических выражений от трех аргументов: X, Y, Z. Дан фрагмент
таблицы истинности выражения F:
|
X |
Y |
Z |
F |
|
1 |
1 |
1 |
|
|
1 |
1 |
1 |
|
|
1 |
1 |
1 |
Какое выражение соответствует F?
1) ¬X ∧ ¬ Y
2) (X ≡ Y) ∧ Z
3) (X ≡ Y) ∨ Z
4) (¬X ≡ Y) ∨ Z
Пояснение.
Вариант 1) не подходит, т. к. выражение ¬X ∧
¬ Y при Х = 1, Y = 1 (строка 1) равно 0, а не 1.
Вариант 2) не подходит, т. к. выражение (X ≡ Y) ∧
Z при Х = 1, Y = 1, Z = 0 (строка 1) равно 0, а не
1.
Вариант 3) удовлетворяет таблице истинности: в
строке 1 верна эквиваленция, а в строках 2 и 3 значение
Z = 1, поэтому во всех случаях логическая сумма равна 1.
Вариант 4) не подходит, т. к. выражение (¬X ≡ Y) ∨
Z при Х = 1, Y = 1, Z = 0 (строка 1) равно 0.
Правильный ответ указан под номером 3.
№4. Символом F обозначено одно из указанных
ниже логических выражений от трех аргументов: X, Y, Z.
Дан фрагмент таблицы истинности выражения F:
Какое выражение соответствует F?
1) ¬X ∨ ¬Y ∨ ¬Z
2) ¬X ∧ ¬Y ∧ ¬Z
3) X ∧ Y ∧ ¬Z
4) X ∨ Y ∨ Z
Пояснение.
1. Выражение 1 не подходит, т.к. принимает значение
0 только при X=1, Y=1, Z=1, а F должно быть равно 0 во всех строках.
2. Выражение 2 же принимает значение 0 всегда,
кроме случая, в котором X=0, Y=0, Z=0. Такой строки в таблице нет, а значит,
значения F и значения функции в варианте 2 сходятся по всем трем строкам,
и вариант 2 является ответом к данной задаче .
3. Выражение 3 не подходит по первой строке, поскольку
при X=1, Y=1, Z=0, оно равно 1.
4. Выражение 4 не подходит по первой строке, поскольку
при X=1, Y=1, Z=0, оно равно 1.
№5. Символом F обозначено одно из указанных
ниже логических выражений от трех аргументов: X, Y, Z.
Дан фрагмент таблицы истинности выражения F:
Какое выражение соответствует F?
1) (X ≡ Z) ∧ (¬X → Y)
2) (¬X ≡ Z) ∧ (¬X → Y)
3) (X ≡ ¬Z) ∧ (¬X → Y)
4) (X ≡ Z) ∧ (¬(Y → Z))
Пояснение.
1. Заметим, что во всех трех строках X эквивалентно
Z. Это значит, что X≡Z=1, ¬X≡Z=0, X≡¬Z=0.Поэтому варианты 2 и 3 сразу
стоит исключить, ведь конъюнкция любого аргумента с 0 даст 0.
2. Рассмотрим выражение из варианта 1. Нас интересуют
значения для выражения (¬X→Y). В строке 1 это выражение – истинно, а
значит, истинно и все выражение из варианта 1, следовательно (т.к.
в первой строке F=0), вариант 1 не является решением данной задачи.
3. Методом исключения, верным остается только вариант
4. И действительно, значения F и значения функции в варианте 4 сходятся
по всем трем строкам, вариант 4 является ответом к данной задаче .
№6. Символом F обозначено одно из указанных
ниже логических выражений от трех аргументов: X, Y, Z. Дан фрагмент
таблицы истинности выражения F:
Какое выражение соответствует F?
1) (X ≡ Z) ≡ Y
2) (X ≡ Z) ≡ (¬Y)
3) (X ≡ Z) ∧ Y
4) (X ≡ Z) ∨ (¬Y)
Пояснение.
1. Заметим, что во всех трех строках X эквивалентно
Z. Это значит, что X≡Z=1.
2. Рассмотрим выражение из варианта 1. 1≡Y=1 для первой
строки, что означает исключение варианта 1 из списка возможных решений
задачи.
3. Рассмотрим вариант 2. 1≡(¬Y)=0 для первой строки, 1
для второй и 0 для третьей, следовательно, значения F и значения функции
в варианте 2 сходятся по всем трем строкам, вариант 2 является ответом
к данной задаче.
№7. Символом F обозначено одно из указанных
ниже логических выражений от трех аргументов: X, Y, Z. Дан фрагмент
таблицы истинности выражения F:
Какое выражение соответствует F?
1) ¬X ∨ ¬Y ∨ Z
2) X ∧ Y ∧ Z
3) X ∨ Y ∨ Z
4) ¬X ∧ ¬Y ∧ ¬Z
Пояснение.
Перепишем варианты ответа в других, более привычных
обозначениях:
1.
2.
3.
4.
В вариантах ответа есть либо дизъюнкция, либо конъюнкция
основных аргументов (отрицаний к ним). Прежде
всего, определим, является конъюнкцией или дизъюнкцией.
не является дизъюнкцией, поскольку
нет такой комбинации аргументов или отрицательных к ним,
чтобы из трех случаев принимало значение
1 только в одном. Значит, можно вычеркнуть 1 и 3 варианты.
Рассмотрим вариант 2. Выражение из варианта 1 —
конъюнкция всех трех аргументов. Но значения не соответствуют значениям
такой конъюнкции по второй и третьей строке, а значит, ответ — 4.
№8. Символом F обозначено одно из указанных
ниже логических выражений от трех аргументов: X, Y, Z.
Дан фрагмент таблицы истинности выражения F:
Какое выражение соответствует F?
1) (X ∧ Y) ∧ (X ≡ Z)
2) (X ∧ Y) ∨ (X ≡ Z)
3) (¬Х ∧ Y) ∧ (X ≡ Z)
4) ¬(X ∧ Y) ∧ (X ≡ Z)
Пояснение.
1. Заметим, что во всех трех строках (X ∧
Y)=0. Это значит, что выражение из варианта 1 обращается в 0 при всех
выписанных в таблицу значениях X, Y и Z.
2. Так как значения F и значения функции в варианте
1 сходятся по всем трем строкам, вариант 1 является ответом к данной
задаче .
№9. Символом F обозначено одно из указанных
ниже логических выражений от трех аргументов: X, Y, Z.
Дан фрагмент таблицы истинности выражения F:
Какое выражение соответствует F?
1) ¬(X ∧ Y) ∨ (X ≡ Z)
2) (X ∧ Y) ∨ (X ≡ Z)
3) (¬X ∧ Y) ∧ (X ≡ Z)
4) ¬(X ∧ Y) ∧ (X ≡ Z)
Пояснение.
1. Заметим, что во всех трех строках (X ∧
Y)=0. Перепишем варианты ответа с использованием этого условия:
Вариант 1: 1 ∨ (X ≡ Z)
Вариант 2: 0 ∨ (X ≡ Z)
Вариант 3: (¬X ∧ Y) ∧ (X ≡ Z)
Вариант 4: 1 ∧ (X ≡ Z)
2. Рассмотрим вариант 1. Дизъюнкция (логическое
«или») 1 и любого другого выражения возвращает 1, а по условию F = 1
для всех строк, следовательно, значения F и значения функции в варианте
1 сходятся по всем трем строкам, вариант 1 является ответом к данной
задаче .
№10. Символом F обозначено одно из указанных
ниже логических выражений от трёх аргументов: X, Y, Z.
Дан фрагмент таблицы истинности выражения F:
Какое выражение соответствует F?
1) X ∨ Y ∨ Z
2) X ∧ Y ∧ ¬Z
3) ¬X ∧ Y ∧ ¬Z
4) X ∨ ¬Y ∨ Z
Пояснение.
1. Рассмотрим первый вариант. При X = 0, Y = 0, Z = 0,
значит, X ∨ Y ∨ Z = 0 = F, следовательно, по первой
строке он подходит к нашей задаче. Во второй строке X = 0, Y = 1, Z = 0,
значит, X ∨ Y ∨ Z = 1 = F, а в третьей X = 1, Y
= 1, Z = 1, значит, X ∨ Y ∨ Z = 1 = F.
2. Так как значения F и значения функции в варианте
1 сходятся по всем трем строкам, вариант 1 является ответом к данной
задаче .
Частично заполненные таблицы истинности логических выражений
№1. Для таблицы истинности функции F известны
значения только некоторых ячеек:
|
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
x7 |
F |
|
1 |
1 |
||||||
|
1 |
|||||||
|
1 |
Каким выражением может быть F?
1) x1 ∧ x2 ∧ x3 ∧ ¬x4 ∧
x5 ∧
x6 ∧
¬x7
2) x1 ∨ ¬x2 ∨
x3 ∨
¬x4 ∨ ¬x5 ∨
x6 ∨
¬x7
3) ¬x1 ∧ x2 ∧ ¬x3 ∧
x4 ∧
x5 ∧
x6 ∧
x7
4) x1 ∨ x2 ∨ ¬ x3
∨
x4 ∨
x5 ∨
¬x6 ∨ x7
Пояснение.
Проанализируем каждый вариант.
Первый вариант не подходит, поскольку в первой строке
переменная ¬x4 = 0, следовательно, F должно обращаться в нуль, что
не соответствует таблице истинности.
Второй вариант подходит.
Третий вариант не подходит, поскольку во второй строке
переменная x4 = 0, следовательно, F должно обращаться в нуль, что не
соответствует таблице истинности.
Четвёртый вариант не подходит, поскольку в третьей
строке переменная x4 = 1, следовательно, F должно быть равно 1, что не
соответствует таблице истинности.
Ответ: 2.
№2. Для таблицы истинности функции F известны
значения только некоторых ячеек:
|
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
x7 |
F |
|
1 |
1 |
||||||
|
1 |
|||||||
|
1 |
Каким выражением может быть F?
1) x1 ∧ x2 ∧ x3 ∧ x4 ∧ x5 ∧ x6 ∧ ¬x7
2) ¬x1 ∨ ¬x2 ∨
x3 ∨
¬x4 ∨ ¬x5 ∨
x6 ∨
¬x7
3) ¬x1 ∧ x2 ∧ ¬x3 ∧
x4 ∧
x5 ∧
x6 ∧
x7
4) x1 ∨ x2 ∨ ¬ x3
∨
¬x4 ∨ x5 ∨ ¬x6 ∨
x7
Пояснение.
Проанализируем каждый вариант.
Первый вариант не подходит, поскольку в первой строке
переменная x6 = 0, следовательно, F должно обращаться в нуль, что не
соответствует таблице истинности.
Второй вариант не подходит, поскольку в третьей строке
переменная ¬ x1 = 1, следовательно, F должно быть равно 1, что не соответствует
таблице истинности.
Третий вариант не подходит, поскольку во первой строке
переменная x6 = 0, следовательно, F должно обращаться в нуль, что не
соответствует таблице истинности.
Четвёртый вариант подходит.
Ответ: 4.
№3. Маша заполняла таблицу истинности
для выражения F. Она успела заполнить лишь небольшой фрагмент таблицы:
|
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
F |
|
1 |
1 |
|||||
|
1 |
1 |
|||||
Каким выражением может быть F?
1) ¬x1 ∧ ¬x2 ∧
x3 ∧
¬x4 ∧ ¬x5 ∧
x6
2) x1 ∨ x2 ∨ x3 ∨ x4 ∨ ¬x5 ∨
¬x6
3) x1 ∧ ¬x2 ∧
¬x3 ∧ x4 ∧ ¬x5 ∧
¬x6
4) x1 ∨ x2 ∨ x3 ∨ ¬x4 ∨
x5 ∨
¬x6
Пояснение.
Поскольку F истина в одном случае из двух, второй и
четвёртый варианты не подходят.
Первый вариант не подходит, поскольку во первой строке
переменная ¬x1 = 0, следовательно, F должно обращаться в нуль, что
не соответствует таблице истинности.
Третий вариант подходит.
Ответ: 3.
№4. Маша заполняла таблицу истинности
для выражения F. Она успела заполнить лишь небольшой фрагмент таблицы:
|
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
F |
|
1 |
1 |
|||||
|
1 |
1 |
1 |
||||
Каким выражением может быть F?
1) ¬x1 ∧ x2 ∧ x3 ∧ ¬x4 ∧
¬x5 ∧ x6
2) x1 ∨ x2 ∨ x3 ∨ ¬x4 ∨
¬x5 ∨ x6
3) ¬x1 ∧ x2 ∧ ¬x3 ∧
x4 ∧
x5 ∧
¬x6
4) x1 ∨ ¬x2 ∨
¬x3 ∨ ¬x4 ∨
x5 ∨
x6
Пояснение.
Поскольку F ложно в одном случае из двух, первый и третий
варианты не подходят. Второй вариант не подходит, поскольку переменная
¬x5 = 1.
Ответ: 4.
№5. Александра заполняла таблицу истинности
для выражения F. Она успела заполнить лишь небольшой фрагмент таблицы:
|
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
x7 |
x8 |
F |
|
1 |
||||||||
|
1 |
1 |
|||||||
|
1 |
1 |
1 |
Каким из приведённых ниже выражений может быть F?
1) x1 ∧ ¬x2 ∧
x3 ∧
¬x4 ∧ x5 ∧ x6 ∧ ¬x7 ∧
¬x8
2) x1 ∨ x2 ∨ x3 ∨ ¬x4 ∨
¬x5 ∨ ¬x6 ∨
¬x7 ∨ ¬x8
3) ¬x1 ∧ x2 ∧ ¬x3 ∧
x4 ∧
x5 ∧
¬x6 ∧ x7 ∧ x8
4) x1 ∨ ¬x2 ∨
x3 ∨
¬x4 ∨ ¬x5 ∨
¬x6 ∨ ¬x7 ∨
¬x8
Пояснение.
Проанализируем каждый вариант.
Первый вариант не подходит, поскольку в третьей строке
переменная ¬x8 = 0, следовательно, F должно обращаться в нуль, что
не соответствует таблице истинности.
Второй вариант подходит по имеющимся фрагментам.
Третий вариант ответа не подходит по второй строке,
поскольку в ней x4 = 0, а F = 1.
Четвёртый вариант не подходит по первой строчке.
Правильный ответ указан под номером: 2.
Единый государственный экзамен по информатике состоит из 27 заданий. Каждое задание посвящено одной из тем, изучаемых в рамках школьной программы. Информатика является профильным предметом, поэтому ее сдают только те школьники, которым он пригодится в дальнейшем. Здесь вы можете узнать, как решать задания ЕГЭ по информатике, а также изучить примеры и способы решения на основе подробно разобранных заданий.
Все задания
ЕГЭ все задания (107)
ЕГЭ задание 1 (19)
ЕГЭ задание 3 (2)
ЕГЭ задание 4 (11)
ЕГЭ задание 5 (10)
ЕГЭ задание 6 (7)
ЕГЭ задание 7 (3)
ЕГЭ задание 9 (5)
ЕГЭ задание 10 (7)
ЕГЭ задание 11 (1)
ЕГЭ задание 12 (3)
ЕГЭ задание 13 (7)
ЕГЭ задание 16 (19)
ЕГЭ задание 17 (4)
ЕГЭ без номера (9)
У исполнителя Квадратор две команды: прибавь 3 и возведи в квадрат
У исполнителя Квадратор две команды, которым присвоены номера:
1 — прибавь 3; 2 — возведи в квадрат.
Первая из них увеличивает число на экране на 3, вторая возводит его во вторую степень. Исполнитель работает только с натуральными числами. Составьте алгоритм получения из числа A числа B, содержащий не более K команд. В ответе запишите только номера команд. Если таких алгоритмов более одного, то запишите любой из них.
Вася составляет слова, в которых встречаются только буквы
Вася составляет N-буквенные слова, в которых встречаются только буквы A, B, C, причём буква A появляется ровно 1 раз. Каждая из других допустимых букв может встречаться в слове любое количество раз или не встречаться совсем. Словом считается любая допустимая последовательность букв, не обязательно осмысленная. Сколько существует таких слов, которые может написать Вася?
Игорь составляет таблицу кодовых слов для передачи сообщений
Игорь составляет таблицу кодовых слов для передачи сообщений, каждому сообщению соответствует своё кодовое слово. В качестве кодовых слов Игорь использует N-буквенные слова, в которых есть только буквы A, B, C, причём буква A появляется ровно 1 раз. Каждая из других допустимых букв может встречаться в кодовом слове любое количество раз или не встречаться совсем. Сколько различных кодовых слов может использовать Игорь?
Задание входит в ЕГЭ по информатике для 11 класса под номером 10.
Алгоритм вычисления значения функции F(n)
Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями. Чему равно значение функции F(K)? В ответе запишите только натуральное число.
Задание входит в ЕГЭ по информатике для 11 класса под номером 11.
Сколько секунд потребуется модему, передающему сообщения
Сколько секунд потребуется модему, передающему сообщения со скоростью N бит/с, чтобы передать цветное растровое изображение размером AхB пикселей, при условии, что цвет каждого пикселя кодируется K битами? (Впишите в бланк только число.)
Задание входит в ЕГЭ по информатике для 11 класса под номером 9.
Дешифровщику необходимо восстановить поврежденный фрагмент сообщения
Дешифровщику необходимо восстановить поврежденный фрагмент сообщения, состоящий из 4-х символов. Имеется достоверная информация, что использовано не более пяти букв (A, B, C, D, E), причем на третьем месте стоит один из символов… На четвертом месте – одна из букв… На первом месте – одна из букв… На втором – … Появилась дополнительная информация, что возможен один из четырех вариантов. Какой?
Задание входит в ЕГЭ по информатике для 11 класса под номером 6.
Метеорологическая станция ведет наблюдение за влажностью воздуха
Метеорологическая станция ведет наблюдение за влажностью воздуха. Результатом одного измерения является целое число от 0 до 100 процентов, которое записывается при помощи минимально возможного количества бит. Станция сделала N измерений. Определите информационный объем результатов наблюдений.
Какой вид приобретет формула, после того как ячейку скопируют
В ячейке записана формула. Какой вид приобретет формула, после того как ячейку X скопируют в ячейку Y? Примечание: знак $ используется для обозначения абсолютной адресации.
Задание входит в ЕГЭ по информатике для 11 класса под номером 7.
Находясь в корневом каталоге только что отформатированного диска
Находясь в корневом каталоге только что отформатированного диска, ученик создал K каталогов. Затем в каждом из созданных каталогов он создал еще по N каталогов. Сколько всего оказалось на диске каталогов, включая корневой?
Задание входит в ЕГЭ по информатике для 11 класса.
На месте преступления были обнаружены четыре обрывка бумаги
На месте преступления были обнаружены четыре обрывка бумаги. Следствие установило, что на них записаны фрагменты одного IP-адреса. Криминалисты обозначили эти фрагменты буквами А, Б, В и Г. Восстановите IP-адрес. В ответе укажите последовательность букв, обозначающих фрагменты, в порядке, соответствующем IP-адресу.
Петя записал IP-адрес школьного сервера на листке бумаги
Петя записал IP-адрес школьного сервера на листке бумаги и положил его в карман куртки. Петина мама случайно постирала куртку вместе с запиской. После стирки Петя обнаружил в кармане четыре обрывка с фрагментами IP-адреса. Эти фрагменты обозначены буквами А, Б, В и Г. Восстановите IP-адрес. В ответе укажите последовательность букв, обозначающих фрагменты, в порядке, соответствующем IP-адресу.
Задание входит в ЕГЭ по информатике для 11 класса под номером 12.
При регистрации в компьютерной системе каждому пользователю выдаётся пароль
При регистрации в компьютерной системе каждому пользователю выдаётся пароль, состоящий из 15 символов и содержащий цифры и заглавные буквы. Таким образом, используется K различных символов. Каждый такой пароль в компьютерной системе записывается минимально возможным и одинаковым целым количеством байт (при этом используют посимвольное кодирование и все символы кодируются одинаковым и минимально возможным количеством бит). Определите объём памяти, отводимый этой системой для записи N паролей.
Задание входит в ЕГЭ по информатике для 11 класса под номером 13.
В некоторой стране автомобильный номер составляют из заглавных букв
В некоторой стране автомобильный номер длиной K символов составляют из заглавных букв (используется M различных букв) и любых десятичных цифр. Буквы с цифрами могут следовать в любом порядке. Каждый такой номер в компьютерной программе записывается минимально возможным и одинаковым целым количеством байт (при этом используют посимвольное кодирование и все символы кодируются одинаковым и минимально возможным количеством бит). Определите объём памяти, отводимый этой программой для записи N номеров.
Задание входит в ЕГЭ по информатике для 11 класса под номером 13.
Исполнитель А16 преобразует число, записанное на экране.
1. Прибавить 1
2. Прибавить 2
3. Умножить на 2
Первая из них увеличивает число на экране на 1, вторая увеличивает его на 2, третья умножает его на 2.
Программа для исполнителя А16 – это последовательность команд.
Сколько существует таких программ, которые исходное число 3 преобразуют в число 12 и при этом траектория вычислений программы содержит число 10?
Траектория вычислений программы — это последовательность результатов выполнения всех команд программы. Например, для программы 132 при исходном числе 7 траектория будет состоять из чисел 8, 16, 18.
Решение.
Искомое количество программ равно произведению количества программ, получающих из числа 3 число 10, на количество программ, получающих из числа 10 число 12.
Пусть R(n) — количество программ, которые число 3 преобразуют в число n, а P(n) — количество программ, которые число 10 преобразуют в число n.
Для всех n > 5 верны следующие соотношения:
1. Если n не делится на 2, то тогда R(n) = R(n — 1) + R(n — 2), так как существует два способа получения n — прибавлением единицы или прибавлением двойки. Аналогично P(n) = P(n — 1) + P(n — 2)
2. Если n делится на 2, тогда R(n) = R(n — 1) + R(n — 2) + R(n / 2). Аналогично P(n) = P(n — 1) + P(n — 2) + P(n / 2)
R(5) = R(4) + R(3) = 1 + 1 = 2
R(6) = R(5) + R(4) + R(3) = 2 + 1 + 1 = 4
R(7) = R(6) + R(5) = 4 + 2 = 6
R(8) = R(7) + R(6) + R(4) = 6 + 4 + 1 = 11
R(9) = R(8) + R(7) = 11 + 6 = 17
R(10) = R(9) + R(8) + R(5) = 17 + 11 + 2 = 30
P(11) = P(10) = 1
P(12) = P(11) + P(10) = 2
Таким образом, количество программ, удовлетворяющих условию задачи, равно 30 · 2 = 60.
Ответ:
60.
Ответ: 60
Источник: Демонстрационная версия ЕГЭ-2017 по информатике.
1. Прибавить 1
2. Прибавить 3
Сколько существует программ, для которых при исходном числе 1 результатом является число 17 и при этом траектория вычислений содержит число 9? Траектория вычислений программы — это последовательность результатов выполнения всех команд программы. Например, для программы 121 при исходном числе 7 траектория будет состоять из чисел 8, 11, 12.
Решение.
Используем метод динамического программирования. заведем массив dp, где dp[i] — количество способов получить число i с помощью таких команд.
База динамики:
Формула перехода:
dp[i]=dp + dp
При этом не учитываются значения для чисел больше 9, которые можно получить из чисел меньше 9 (перескочив тем самым траекторию 9):
Ответ:
169.
Ответ: 169
Источник: Тренировочная работа по ИНФОРМАТИКЕ 11 класс 29 ноября 2016 года Вариант ИН10203
Исполнитель Май17 преобразует число на экране.
У исполнителя есть две команды, которым присвоены номера:
1. Прибавить 1
2. Прибавить 3
Первая команда увеличивает число на экране на 1, вторая увеличивает его на 3. Программа для исполнителя Май17 — это последовательность команд.
Траектория вычислений программы – это последовательность результатов выполнения всех команд программы. Например, для программы 121 при исходном числе 7 траектория будет состоять из чисел 8, 11, 12.
Решение.
Используем метод динамического программирования. Заведем массив dp, где dp[i] — количество способов получить число i с помощью таких команд.
База динамики:
Формула перехода:
dp[i]=dp + dp
Но при этом не учитываются такие числа, которые больше 8, но в них мы можем добраться из значения меньше 8. Далее будет приведены значения в ячейках dp от 1 до 15: 1 1 1 2 3 4 6 9 9 9 18 27 36 54 81.
Ответ:
81.
Ответ: 81
Источник: Тренировочная работа по ИНФОРМАТИКЕ 11 класс 29 ноября 2016 года Вариант ИН10204
У исполнителя есть три команды, которым присвоены номера:
1) Прибавить 1;
2) Прибавить 2;
3) Прибавить 4.
Первая команда увеличивает число на экране на 1, вторая увеличивает его на 2, третья — увеличивает на 4.
Сколько существует программ, для которых при исходном числе 1 результатом является число 15 и при этом траектория вычислений содержит число 8?
Решение.
Используем метод динамического программирования: Заведем массив dp, где dp[i] — количество способов получить число i через данные команды.
База динамики dp = 1.
Переходы будут иметь вид:
dp[i] = dp + dp + dp.
При этом, если i-1 или i-2 или i-4 меньше 8, а i больше 8, то тогда его не нужно учитывать (поскольку тогда мы обойдем число 8, а этого нельзя делать по условию).
Ответ:
961.
Ответ: 961
Источник: Тренировочная работа по ИНФОРМАТИКЕ 11 класс 30 сентября 2016 года Вариант ИН10103
Исполнитель Осень16 преобразует число на экране.
У исполнителя есть три команды, которым присвоены номера:
1) Прибавить 1;
2) Прибавить 2;
3) Прибавить 3.
Первая команда увеличивает число на экране на 1, вторая увеличивает его на 2, третья — увеличивает на 3.
Программа для исполнителя Осень16 — это последовательность команд.
Сколько существует программ, для которых при исходном числе 1 результатом является число 15 и при этом траектория вычислений содержит число 8?
Траектория вычислений программы — это последовательность результатов выполнения всех команд программы. Например, для программы 121 при исходном числе 7 траектория будет состоять из чисел 8, 10, 11.
Решение.
Искомое количество программ равно произведению количества программ, получающих из числа 1 число 8, на количество программ, получающих из числа 8 число 15.
Пусть R(n) — количество программ, которые число 3 преобразуют в число n, а P(n) — количество программ, которые число 8 преобразуют в число n.
Для всех n > 3 верны следующие соотношения:
1. R(n) = R(n — 1) + R(n — 2) + R(n — 3), так как существует три способа получения n — прибавлением единицы, прибавлением двойки или прибавлением тройки. Аналогично P(n) = P(n — 1) + P(n — 2) + P(n — 3)
Последовательно вычислим значения R(n):
R(4) = R(1) + R(2) + R(3) = 4
R(5) = R(4) + R(3) + R(2) = 4 + 2 + 1 = 7
R(6) = R(5) + R(4) + R(3) = 7 + 4 + 2 = 13
R(7) = R(6) + R(5) + R(4) = 13 + 7 + 4 = 24
R(8) = R(7) + R(6) + R(5) = 24 + 13 + 7 = 44
Теперь вычислим значения P(n):
P(12) = P(11)+ P(10) + P(9) = 4 + 2 + 1 = 7
P(13) = P(12) + (11) + P(10) = 7 + 4 + 2 = 13
P(14) = P(13) + P(12) + P(11) = 13 + 7 + 4 = 24
P(15) = P(14) + P(13) + P(12) = 24 + 13 + 7 = 44
Таким образом, количество программ, удовлетворяющих условию задачи, равно 44 · 44 = 1936.
Ответ:
1936.
Ответ: 1936
Источник: Тренировочная работа по ИНФОРМАТИКЕ 11 класс 30 сентября 2016 года Вариант ИН10104
У исполнителя есть три команды, которым присвоены номера:
1. Прибавить 1
2. Умножить на 2
3. Умножить на 3
Первая команда увеличивает число на экране на 1, вторая – умножает его на 2, третья – умножает на 3.
Сколько существует программ, для которых при исходном числе 2 результатом является число 28 и при этом траектория вычислений содержит число 14?
Решение.
База динамики dp = 1.
Переходы:
dp[i] = dp + dp(если i — четно) + dp (если i — кратно 3).
При этом, если i > 14, а i-1 или i/2 или i/3 меньше 14, то этими значениями пренебрегаем, т.к. тогда не будет выполнено условие траектории. Далее будут показаны значения массива dp от 2 до 28:
1 1 2 2 4 4 6 7 9 9 15 15 19 19 19 19 19 19 19 19 19 19 19 19 19 19 38.
Ответ:
38.
Ответ: 38
Источник: Тренировочная работа по ИНФОРМАТИКЕ 11 класс 12 мая 2017 года Вариант ИН10503
Исполнитель А17 преобразует число на экране.
У исполнителя есть три команды, которым присвоены номера:
1. Прибавить 1
2. Умножить на 2
3. Умножить на 3
Первая команда увеличивает число на экране на 1, вторая умножает его на 2, третья – умножает на 3.
Программа для исполнителя А17 – это последовательность команд.
Сколько существует программ, для которых при исходном числе 2 результатом является число 30 и при этом траектория вычислений содержит число 15?
Траектория вычислений программы – это последовательность результатов выполнения всех команд программы. Например, для программы 121 при исходном числе 7 траектория будет состоять из чисел 8, 16, 17.
Решение.
Используем динамическое программирование. Заведем массив dp, где dp[i] — количество способов получить число i.
База динамики dp = 1.
Переходы:
dp[i] = dp + dp(если i — четно) + dp (если i кратно 3).
При этом если i > 15, а i-1 или i/2 или i/3 меньше 15, то этими значениями будем пренебрегать, т.к. тогда не будет выполнено условие траектории. Далее будут показаны значения массива dp от 2 до 30:
1 1 2 2 4 4 6 7 9 9 15 15 19 21 21 21 21 21 21 21 21 21 21 21 21 21 21 21 42
Ответ:
42.
Ответ: 42
Источник: Тренировочная работа по ИНФОРМАТИКЕ 11 класс 18 января 2017 года Вариант ИН10303, Тренировочная работа по ИНФОРМАТИКЕ 11 класс 12 мая 2017 года Вариант ИН10504
Исполнитель М17 преобразует число, записанное на экране. У исполнителя есть три команды, которым присвоены номера:
1. Прибавить 1
2. Прибавить 2
3. Умножить на 3
Первая из них увеличивает число на экране на 1, вторая увеличивает его на 2, третья умножает на 3. Программа для исполнителя М17 – это последовательность команд. Сколько существует таких программ, которые преобразуют исходное число 2 в число 12 и при этом траектория вычислений программы содержит числа 8 и 10? Траектория должна содержать оба указанных числа.
Траектория вычислений программы – это последовательность результатов выполнения всех команд программы. Например, для программы 132 при исходном числе 7 траектория будет состоять из чисел 8, 24, 26.
Решение.
Искомое количество программ равно произведению количества программ, получающих из числа 2 число 8, на количество программ, получающих из числа 8 число 10, и на количество программ, получающих из числа 10 число 12.
Будем решать задачу с конца. Число 12 из числа 10 можно получить двумя способами (10+1+1; 10+2). Число 10 из числа 8 можно получить двумя способами (8+1+1; 8+2). Остается узнать количество способов получения числа 8 из числа 2. Начнем свои рассуждения с числа 3, т.к. двойка это начальное число. Тройку можно получить только одним способом – прибавив 1. Четверку получим двумя способами – прибавив единицу к тройке или добавив двойку к двойке и т. д. Запишем эти рассуждения в следующем виде:
R(4) = R(3) + R(2) = 2
R(5) = R(4) + R(3) = 2 + 1 = 3
R(6) = R(5) + R(4) + R(2) = 3 + 2 + 1 = 6
R(7) = R(6) + R(5) = 6 + 3 = 9
R(8) = R(7) + R(6) = 9 + 6 = 15
Таким образом, количество программ, удовлетворяющих условию задачи, равно R(2) * R(8) * R(10) * R(12) = 1 * 15 * 2 * 2 = 60.
Ответ:
60.
Ответ: 60
Источник: Демонстрационная версия ЕГЭ-2018 по информатике.
Исполнитель Тренер преобразует число на экране.
У исполнителя есть две команды, которым присвоены номера:
1. Прибавить 1
2. Умножить на 2
Сколько существует программ, которые преобразуют исходное число 1 в число 30 и при этом траектория вычислений содержит числа 10 и 21?
Решение.
Нужно найти количество программ, которые из 1 получают 10, количество программ, которые из 10 получают 21, количество программ, которые из 21 получают 30 и перемножить найденные значения. Сначала найдём количество программ, получающих 10 из 1.
Верны следующие соотношения:
1. Если n не делится на 2, то тогда R(n) = R(n — 1), так как существует единственный способ получения n из n — 1 — прибавление единицы.
2. Пусть n делится на 2.
Если n >
У исполнителя есть две команды, которым присвоены номера:
1. Прибавить 1
2. Умножить на 2
Первая команда увеличивает число на экране на 1, вторая умножает его на 2. Программа для исполнителя Тренер — это последовательность команд.
Сколько существует программ, которые преобразуют исходное число 1 в число 40 и при этом траектория вычислений содержит числа 12 и 25?
Траектория должна содержать оба указанных числа. Траектория вычислений – это последовательность результатов выполнения всех команд программы. Например, для программы 212 при исходном числе 7 траектория будет состоять из чисел 14, 15, 30.
Решение.
Нужно найти количество программ, которые из 1 получают 12, количество программ, которые из 12 получают 25, количество программ, которые из 25 получают 40 и перемножить найденные значения. Сначала найдём количество программ, получающих 12 из 1.
Обозначим R(n) — количество программ, которые преобразуют число 2 в число n.
Верны следующие соотношения:
1. Если n не делится на 2, то тогда R(n) = R(n — 1), так как существует единственный способ получения n из n − 1 — прибавление единицы.
2. Пусть n делится на 2.
Если n > 1, то R(n) = R(n / 2) + R(n — 1).
Если n = 1, то R(n) = 1 (два способа: прибавление единицы и удвоение).
Теперь можно постепенно вычислить все значения:
R(2) = R(1) + R(1) = 1 + 1 = 2 = R(3)
R(4) = R(2) + R(3) = 2 + 2 = 4 = R(5),
R(6) = R(3) + R(5) = 2 + 4 = 6 = R(7),
R(8) = R(4) + R(7) = 4 + 6 = 10 = R(9),
R(10) = R(5) + R(9) = 4 + 10 = 14 = R(11)
R(12) = R(6) + R(11) = 6 + 14 = 20
Программ, получающих из числа 12 число 25 достаточно мало, можно их просто перечислить: 21, 1111111111111.
А программ, получающих из числа 25 число 40, всего один способ: добавление единиц.
Тем самым, находим ответ:
Ответ:
40.
Ответ: 40
Решение.
Искомое количество программ равно произведению количества программ, получающих из числа 2 число 11, на количество программ, получающих из числа 11 число 22.
Пусть R(n) — количество программ, которые число 2 преобразуют в число n, F(n) — количество программ, которые число 11 преобразуют в число n.
Верны следующие соотношения:
R(n) = R(n−2) + R(n/2)(если n — чётно) + R(n-3).
R(3) = R(3) = 0.
R(4) = R(2) + R(2) = 2.
R(5) = R(2) + R(3) = 1.
R(6) = R(3) + R(4) = 2.
R(7) = R(4) + R(5) = 3.
R(8) = R(6) + R(5) + R(4) = 5.
R(9) = R(6) + R(7) = 5.
R(10) = R(8) + R(5) + R(7) = 9.
R(11) = R(8) + R(9) = 10.
F(13) = F(11) = 1.
F(14) = F(11) + F(12) = 1.
F(15) = F(12) + F(13) = 1.
F(16) = F(14) + F(13) = 2.
F(17) = F(15) + F(14) = 2.
F(18) = F(16) + F(15) = 3.
F(19) = F(17) + F(16) = 4.
F(20) = F(18) + F(17) = 5.
F(21) = F(19) + F(18) = 7.
F(22) = F(20) + F(19) + F(11) = 10.
Таким образом, количество программ, удовлетворяющих условию задачи, равно 10 · 10 = 100.
Ответ:
100.
Муниципальное общеобразовательное учреждение
«Средняя общеобразовательная школа №101»
Теория и практика решения задания 2
ЕГЭ по информатике
учитель информатики
Угулава Наталия Владимировна
Саратов, 2018
Типы задания 2
- Задания на отрезки
- Задания на множества
- Задания на поразрядную конъюнкцию
- Задания на условие делимости
Разбор 2 задания ЕГЭ 2018 по информатике и ИКТ из демоверсии.
Это задание базового уровня сложности.
Примерное время выполнения задания 3 минуты.
—
—
умение строить таблицы истинности и логические схемы
—
умение строить таблицы истинности и логические схемы
Проверяемые элементы содержания:
Умение строить таблицы истинности и логические схемы.
Элементы содержания, проверяемые на ЕГЭ:
Высказывания, — логические операции, — кванторы, — истинность высказывания.
ТАБЛИЦЫ ИСТИННОСТИ И ПОРЯДОК
ВЫПОЛНЕНИЯ ЛОГИЧЕСКИХ ОПЕРАЦИЙ
Для логических операций приняты следующие обозначения
:
не A (отрицание, инверсия)
A ∧ B, A ⋅ B
A и B (логическое умножение, конъюнкция)
A или B (логическое сложение, дизъюнкция)
импликация (следование)
A ↔ B, A ≡ B, A ∼ B
эквиваленция (эквивалентность, равносильность)
сложение по модулю 2 (XOR)
Отрицание (НЕ):
Таблица истинности операции НЕ
Конъюнкция (И):
Таблица истинности операции И (конъюнкция)
Дизъюнкция (ИЛИ):
Таблица истинности операции ИЛИ (дизъюнкция)
Импликация (если
…
, то
…
):
Таблица истинности операции Импликация (если
…
, то
…
)
Задание 2
Логическая функция F
задаётся выражением ¬ x
/ y
/ (¬ z
/ w
). На рисунке приведён фрагмент таблицы истинности функции F
, содержащий все
наборы аргументов, при которых функция F
ложна. Определите, какому столбцу таблицы истинности функции F
w, x, y, z.
Эквивалентность (тогда и только тогда,
…
):
Таблица истинности операции Эквивалентность (тогда и только тогда,
…
)
Сложение по модулю 2 (XOR):
Порядок выполнения операций:
- если в выражении нет скобок, сначала выполняются все операции « НЕ
» , затем – « И
» , затем – « ИЛИ
» , импликация, равносильность
Задание 2 ЕГЭ по информатике 2017 ФИПИ вариант 6 (Крылов С.С., Чуркина Т.Е.):
Логическая функция F
задается выражением (y
→
x) ∧ (y
→
z) ∧
z
. Определите, какому столбцу таблицы истинности функции F
соответствует каждая из переменных x
, y
, z
.
Перем. 1
Перем. 1
Перем. 1
Функция
В ответе напишите буквы x
, y
, z
в том порядке, в котором идут соответствующие им столбцы.
Решение:
- За основу необходимо взять логическую операцию, которую мы будем выполнять в последнюю очередь — это логическое И
(конъюнкция) или ∧
- Конъюнкцию легче рассматривать по тем строкам таблицы, там где функция F = 1
- Поскольку для конъюнкции функция истинна только тогда, когда все переменные истинны, то необходимо чтобы отдельно каждая скобка была истинна ((y → x) = 1 и (y → z)=1) и переменная z
тоже была истинной (1) - Поскольку со скобками сложней работать, определим сначала какому столбцу соответствует z
. Для этого выберем строку, где F=1
и в остальных ячейках только одна единица, а остальные нули:
- Таким образом, из этой строки делаем вывод, что z
находится во втором столбце (отсчет ведем слева):
- Рассмотрим скобку (y
→
x)
и строку таблицы:
- Для этой строки только y
может быть 0
, т.к. если x = 0
, тогда y=1
1
→
0 = 0
). Соответственно, y
x
значит в третьем: - Для этой строки только y
может быть 0
, т.к. если x = 0
, тогда y=1
, и скобка в результате возвратит ложь (1
→
0 = 0
). Соответственно, y
находится в первом столбце. А x
значит в третьем:
Результат:
yzx
Задание 2 ЕГЭ по информатике 2017 ФИПИ вариант 11 (Крылов С.С., Чуркина Т.Е.):
Каждое из логических выражений F
и G
содержит 5
переменных. В таблицах истинности выражений F и G есть ровно 5
одинаковых строк, причем ровно в 4
из них в столбце значений стоит 1
. Сколько строк таблицы истинности для выражения F
∨ G
содержит 1
в столбце значений?
Решение:
- Поскольку в каждом из выражений присутствует 5 переменных, то эти 5 переменных порождают таблицу истинности из 32
строк: т.к. каждая из переменных может принимать оно из двух значений (0 или 1), то различных вариантов с пятью переменными будет 2
5
=32
, т.е. 32 строки. - Из этих 32 строк для каждого выражения (и F и G) мы знаем наверняка только о 5 строках: в 4 из них 1, а в одной — 0.
- В исходных таблицах для каждого выражения F и G мы знаем о существовании только одного 0, т.е. в остальных строках может быть 1. Т.о. для каждого выражения и F и G в 31 строке могут быть единицы
(32-1=31
), а лишь в одной — ноль. - Тогда для выражения F
∨ G
только в одном случае будет 0, когда и F=0 и G = 0: - Вопрос стоит о количестве строк = 1 для таблицы истинности выражения F
∨ G
. Данной выражение — дизъюнкция, которая ложна только в одном случае
— если F = 0
и одновременно G = 0
Результат:
31
Решение задачи на отрезки
В ответе напишите буквы w, x, y, z
в том порядке, в котором идут соответствующие им столбцы (сначала – буква, соответствующая первому столбцу; затем – буква, соответствующая второму столбцу, и т.д.) Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
¬
x
/
y
/ (¬
z
/
w
)
Дизъюнкция (логическое сложение) истинна тогда и только тогда, когда истинно хотя бы одно высказывание.
Следовательно, для того чтобы вся функция была ложна, переменной х
должен соответствовать тот столбец, в котором стоит значение 1
(так как,
¬
x
превращает 1 в 0)
, а переменной y
столбец со значениями 0
.
Таким образом: —
переменной x
соответствует столбец с переменной 1
, — переменной y
соответствует столбец с переменной 4
.
Решение задачи на отрезки
Конъюнкция (логическое умножение) истинна тогда и только тогда, когда истинны все высказывания (ложна — если ложно хотя бы одно высказывание).
Конъюнкция ¬
z
/
w
в нашем выражении будет истинна только если z=0, w=1.
Посмотрим на вторую строчку таблицы, где переменная 2 равна 1, а переменная 3 равна 0.
Решение задачи
Так как ¬
z
/
w
должна равняться 0, то z
= 1 и w
= 0 (в противном случае произведение будет равно 1)
Таким образом: — переменной z
соответствует столбец с переменной 2 (2 столбец), — переменной w
соответствует столбец с переменной 3 (3 столбец).
Ответ: xzwy
Для эффективной подготовки по информатике для каждого задания дан краткий теоретический материал для выполнения задачи. Подобрано свыше 10 тренировочных заданий с разбором и ответами, разработанные на основе демоверсии прошлых лет.
Изменений в КИМ ЕГЭ 2019 г. по информатике и ИКТ нет.
Направления, по которым будет проведена проверка знаний:
- Программирование;
- Алгоритмизация;
- Средства ИКТ;
- Информационная деятельность;
- Информационные процессы.
Необходимые действия при подготовке
:
- Повторение теоретического курса;
- Решение тестов
по информатике онлайн
; - Знание языков программирования;
- Подтянуть математику и математическую логику;
- Использовать более широкий спектр литературы – школьной программы для успеха на ЕГЭ недостаточно.
Структура экзамена
Длительность экзамена – 3 часа 55 минут (255 минут), полтора часа из которых рекомендовано уделить выполнению заданий первой части КИМов.
Задания в билетах разделены на блоки:
- Часть 1
— 23 задания с кратким ответом. - Часть 2
— 4 задачи с развернутым ответом.
Из предложенных 23 заданий первой части экзаменационной работы 12 относятся к базовому уровню проверки знаний, 10 – повышенной сложности, 1 – высокому уровню сложности. Три задачи второй части высокого уровня сложности, одна – повышенного.
При решении обязательна запись развернутого ответа (произвольная форма).
В некоторых заданиях текст условия подан сразу на пяти языках программирования – для удобства учеников.
Баллы за задания по информатике
1 балл — за 1-23 задания
2 балла — 25.
З балла — 24, 26.
4 балла — 27.
Всего: 35 баллов.
Для поступления в технический вуз среднего уровня, необходимо набрать не менее 62 баллов. Чтобы поступить в столичный университет, количество баллов должно соответствовать 85-95.
Для успешного написания экзаменационной работы необходимо четкое владение теорией
и постоянная практика в решении
задач.
Твоя формула успеха
Труд + работа над ошибками + внимательно читать вопрос от начала и до конца, чтобы избежать ошибок = максимальный балл на ЕГЭ по информатике.