Структура егэ по математике презентация - Помощь в подготовке к экзаменам и поступлению

1

О структуре и системе оценивания ЕГЭ по математике будущим участникам экзамена, учителям и родителям О структуре и системе оценивания ЕГЭ по математике будущим участникам экзамена, учителям и родителям

2

Единый государственный экзамен ЕГЭ – это основная форма государственной (итоговой) аттестации выпускников школ Российской Федерации. ЕГЭ – это основная форма государственной (итоговой) аттестации выпускников школ Российской Федерации.

3

ВУЗЫ И ССУЗЫ ИСПОЛЬЗУЮТ РЕЗУЛЬТАТЫ ЕГЭ В КАЧЕСТВЕ РЕЗУЛЬТАТОВ ВСТУПИТЕЛЬНЫХ ИСПЫТАНИЙ. ВУЗЫ И ССУЗЫ ИСПОЛЬЗУЮТ РЕЗУЛЬТАТЫ ЕГЭ В КАЧЕСТВЕ РЕЗУЛЬТАТОВ ВСТУПИТЕЛЬНЫХ ИСПЫТАНИЙ.

4

ОСОБЕННОСТИ ЕГЭ: единые правила проведения, единые правила проведения, единое расписание, единое расписание, использование заданий стандартизированной формы(КИМ), использование заданий стандартизированной формы(КИМ), использование специальных бланков для оформления ответов на задания, использование специальных бланков для оформления ответов на задания, проведение экзамена письменно на русском языке. проведение экзамена письменно на русском языке.

5

ПЛАН ЭКЗАМЕНАЦИОННОЙ РАБОТЫ ЕГЭ ПО МАТЕМАТИКЕ Всего 20 заданий: по алгебре и началам анализа 14, по алгебре и началам анализа 14, по геометрии 6. по геометрии 6.

6

Распределение заданий работы по уровню сложности: базовый — 14, повышенный — 4, высокий 2.

7

Часть 1 содержит 14 заданий (В1-В14) с кратким ответом базового уровня по материалу курса математики. Часть 1 содержит 14 заданий (В1-В14) с кратким ответом базового уровня по материалу курса математики. Часть 2 содержит 6 более сложных заданий (С1-С6). При их выполнении надо записывать полное решение и ответ. Часть 2 содержит 6 более сложных заданий (С1-С6). При их выполнении надо записывать полное решение и ответ. Работа состоит из двух частей

8

Все бланки заполняются яркими черными чернилами. Все бланки заполняются яркими черными чернилами. При выполнении заданий можно пользоваться черновиком, но записи на нем не будут учитываться при оценке работы. При выполнении заданий можно пользоваться черновиком, но записи на нем не будут учитываться при оценке работы. Можно пользоваться линейкой. Можно пользоваться линейкой.

9

Минимальный балл Минимальный балл В 2012 году минимальный балл, необходимый для получения аттестата, будет соответствовать выполнению пяти заданий части В. В 2012 году минимальный балл, необходимый для получения аттестата, будет соответствовать выполнению пяти заданий части В.

10

Правильное решение каждого Правильное решение каждого из заданий В1- В14 части 1 экзаменационной работы оценивается из заданий В1- В14 части 1 экзаменационной работы оценивается 1 баллом. 1 баллом.

11

Задание считается выполненным верно, если экзаменуемый дал правильный ответ в виде целого числа или конечной десятичной дроби. Задание считается выполненным верно, если экзаменуемый дал правильный ответ в виде целого числа или конечной десятичной дроби.

12

Правильное решение каждого из заданий С1 и С2 оценивается 2 баллами, С3 и С4 – 3 баллами, С5 и С6 – 4 баллами.

13

Главное требование в записи развернутого ответа – решение должно быть математически грамотным, из него должен быть понятен ход рассуждений автора работы. Главное требование в записи развернутого ответа – решение должно быть математически грамотным, из него должен быть понятен ход рассуждений автора работы.

14

Проверка выполнения заданий части 2 проводится экспертами на основе специально разработанной системы критериев. Проверка выполнения заданий части 2 проводится экспертами на основе специально разработанной системы критериев.

15

Максимальный первичный балл за выполнение всей работы – 32. Максимальный первичный балл за выполнение всей работы – 32.

16

Работа рассчитана на 240 минут (4 часа) (4 часа)

17

Структура и содержание работы дают возможность проверить умения: дают возможность проверить умения: использовать знания в практической деятельности; использовать знания в практической деятельности; выполнять вычисления и преобразования; выполнять вычисления и преобразования; решать уравнения и неравенства; решать уравнения и неравенства;

18

выполнять действия с функциями; выполнять действия с функциями; выполнять действия с геометрическими фигурами, координатами и векторами; выполнять действия с геометрическими фигурами, координатами и векторами; строить и исследовать математические модели. строить и исследовать математические модели.

19

Ресурсы Интернета для подготовки к ЕГЭ Ресурсы Интернета для подготовки к ЕГЭ Открытый банк задач ЕГЭ по математике Открытый банк задач ЕГЭ по математике Открытый банк задач ЕГЭ по математике Открытый банк задач ЕГЭ по математике Официальный информационный портал ЕГЭ Официальный информационный портал ЕГЭ Образовательный портал«РЕШУ ЕГЭ» Образовательный портал«РЕШУ ЕГЭ» Тесты ЕГЭ Онлайн Тесты ЕГЭ Онлайн

20

ПОСОБИЯ ДЛЯ ПОДГОТОВКИ Самое полное издание типовых вариантов заданий ЕГЭ: Математика. Высоцкий И.Р, Гущин Д.Д, Захаров П.И. и др. Самое полное издание типовых вариантов заданий ЕГЭ: Математика. Высоцкий И.Р, Гущин Д.Д, Захаров П.И. и др. ЕГЭ Математика. Типовые тестовые задания. Под ред. Семенова А.Л., Ященко И.В. ЕГЭ Математика. Типовые тестовые задания. Под ред. Семенова А.Л., Ященко И.В.

21

ЕГЭ Математика. Типовые экзаменационные варианты: 30 вариантов. Под ред. Семенова А.Л., Ященко ЕГЭ Математика. Типовые экзаменационные варианты: 30 вариантов. Под ред. Семенова А.Л., Ященко Подготовка к ЕГЭ по математике в 2012 году. Методические указания. Ященко И.В, Шестаков С.А, Трепалин А.С, Захаров П.И. Подготовка к ЕГЭ по математике в 2012 году. Методические указания. Ященко И.В, Шестаков С.А, Трепалин А.С, Захаров П.И.

22

ЕГЭ Математика. Оптимальный банк заданий для подготовки учащихся. Захаров П.И., Семенов А.В., Ященко И.В ЕГЭ Математика. Оптимальный банк заданий для подготовки учащихся. Захаров П.И., Семенов А.В., Ященко И.В Математика. ЕГЭ Контрольные тренировочные материалы с ответами и комментариями. Нейман Ю.М. и др. Математика. ЕГЭ Контрольные тренировочные материалы с ответами и комментариями. Нейман Ю.М. и др.

23

Желаю хорошо подготовиться и успешно сдать ЕГЭ по математике.

24

Для презентации использованы Демонстрационный вариант ЕГЭ по математике 2012 года Демонстрационный вариант ЕГЭ по математике 2012 года Спецификация КИМ для проведения в 2012 году единого государственного экзамена по математике Спецификация КИМ для проведения в 2012 году единого государственного экзамена по математике Ресурсы Интернета Ресурсы Интернета

Источник

Слайд 1ЕГЭ по математике
(базовый и профильный уровни)
Мегельбей Жанна Николаевна, учитель математики

МБОУ «СОШ №26»

2017-2018 уч.г.

ЕГЭ по математике
(базовый и профильный уровни) Мегельбей Жанна Николаевна, учитель математики
МБОУ «СОШ №26»

Слайд 2ЕГЭ по математике (базовый и профильный уровни) – нет изменений структуры

и содержания

Базовый уровень
(относительно простой экзамен, проверяющий в основном знания в области так называемой «реальной математики»;
результаты не принимаются при поступлении в вуз и нужны только для получения аттестата)

Профильный уровень
(гораздо более сложный, ориентированный на тех выпускников, которые планируют поступать в технические вузы, где математика является обязательным предметом для поступления)

Слайд 3Базовый уровень
Экзаменационная работа включает
20 заданий с кратким ответом базового уровня

сложности. Работы проверяются специальными считывающими машинами.
Правильное решение каждого из заданий
1–20 оценивается 1 баллом.
Все задания закрытого типа, поэтому задание считается выполненным верно, если экзаменуемый дал правильный ответ в виде целого числа, или конечной десятичной дроби, или последовательности цифр.

Слайд 4Базовый уровень
В работу включены задания по всем основным разделам предметных требований

ФК ГОС:
геометрия (планиметрия и
стереометрия) – 4 задания,
алгебра, начала математического анализа,
теория вероятностей, статистика -16 заданий.
Часть заданий имеет выраженную практическую направленность; часть заданий предназначена для проверки логических навыков.
Работа рассчитана на 180 минут.

Слайд 5Работа оценивается
по традиционной 5-балльной шкале:

Базовый уровень
Минимальный порог для получения аттестата

– 7 баллов.
Вузы не принимают результаты базовой математики!

Работа оценивается
по традиционной 5-балльной шкале: Базовый уровень Минимальный порог для получения аттестата –

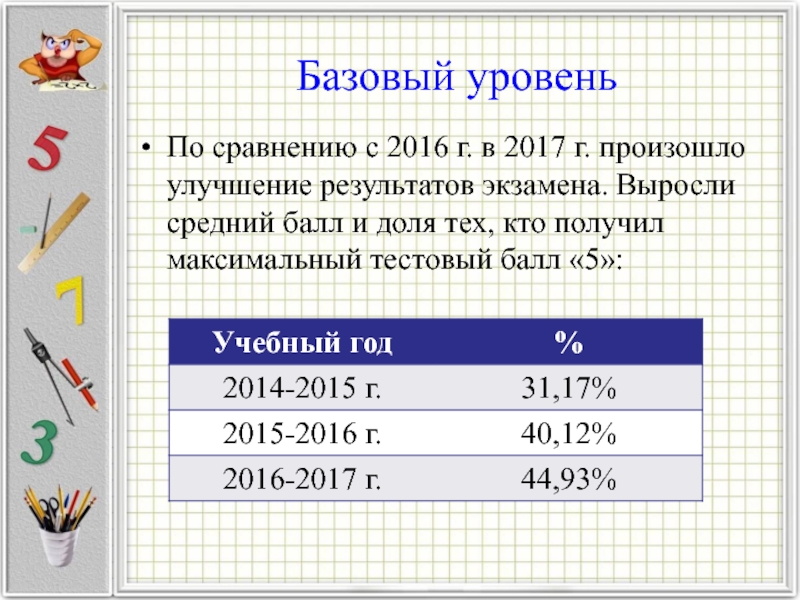
Слайд 6По сравнению с 2016 г. в 2017 г. произошло улучшение результатов

экзамена. Выросли средний балл и доля тех, кто получил максимальный тестовый балл «5»:

Базовый уровень

Слайд 7Профильный уровень
Работа состоит из двух частей и содержит 19 заданий. При

этом заданий базового уровня сложности — 8, повышенного — 9, высокого — 2.
Часть 1 содержит 8 заданий (задания 1 — с кратким числовым ответом, проверяющих наличие практических математических знаний и умений базового уровня.
Часть 2 содержит 11 заданий, проверяющих уровень профильной математической подготовки. Из них четыре задания (задания 9 – 12) с кратким ответом и семь заданий (задания 17–19) с развёрнутым ответом.

Слайд 8Профильный уровень
Задания делятся на три тематических модуля: «Алгебра и начала анализа»,

«Геометрия» и «Практико-ориентированные задания».
Задания 1, 2, 4 первой части и задания 10 и 17 второй части представляют практико- ориентированный модуль, включая задание на элементы курса теории вероятностей.
Задания 3, 6, 8 первой части, задания 14, 16 второй части – геометрические.
Задания 5, 7 первой части и задания 9, 11, 12, 13, 15, 18,19 второй части – это задания разного уровня сложности по алгебре.

Слайд 9Работа рассчитана на 3 часа 55 минут.
Работа оценивается по 100-балльной шкале

(производится перевод из первичной шкалы во вторичную):

Профильный уровень

Минимальный порог для поступления в вузы- 6 первичных баллов (27 вторичных баллов).

Слайд 10Готовимся к ЕГЭ
Официальный информационный портал ЕГЭ www.ege.edu.ru
Сайт разработчиков экзаменационных материалов

ЕГЭ ФИПИ www.Сайт разработчиков экзаменационных материалов ЕГЭ ФИПИ www.fipiСайт разработчиков экзаменационных материалов ЕГЭ ФИПИ www.fipi.ru (открытый банк заданий ЕГЭ)

Источник

Первый слайд презентации

Особенности сдачи ЕГЭ
по математике в 2022 году

Изображение слайда

ЕГЭ-2022
Удовлетворительные результаты государственной (итоговой) аттестации
по русскому языку и математике
являются основанием выдачи аттестата о среднем (полном) общем образовании.

Изображение слайда

ЕГЭ-2022
При проведении государственной (итоговой) аттестации в форме ЕГЭ используется стобалльная система оценки, кроме математики базовой.
Результаты ЕГЭ признаются удовлетворительными
в случае, если выпускник по обязательным
общеобразовательным предметам (русский язык и математика) набрал
количество баллов не ниже минимального

Изображение слайда

При проведении ЕГЭ используются контрольные измерительные материалы (КИМ), представляющие собой комплексы заданий стандартизированной формы. Для оформления ответов на задания КИМ используются специальные бланки.

Изображение слайда

Математика – обязательный экзамен

Изображение слайда

ЕГЭ-2022
Расписание ЕГЭ устанавливается
на федеральном уровне
Рособрнадзором

Изображение слайда

Слайд 7: СРОКИ СДАЧИ ЕГЭ ПО МАТЕМАТИКЕ В 2022 ГОДУ БАЗОВЫЙ УРОВЕНЬ – 03 ИЮНЯ ПРОФИЛЬНЫЙ УРОВЕНЬ -02 ИЮНЯ

Изображение слайда

ЕГЭ-2022
Предмет
Продолжительность
Математика ( профиль)
3 часа 55 минут
Математика (база)
3 часа
ПРОДОЛЖИТЕЛЬНОСТЬ
ЭКЗАМЕНА ПО МАТЕМАТИКЕ В 2022 ГОДУ

Изображение слайда

Два уровня сложности
Базовый
уровень
Профильный уровень
Для поступающих на гуманитарные и некоторые естественнонаучные специальности.
Сдают все, кто планирует поступать на специальности физико-математического направления, а также на инженерные факультеты и IT-направление.
Оценивается по 5-балльной шкале
Не учитывается при приеме в ВУЗ, но является обязательным для получения аттестата.
Оценивается по 100-балльной шкале.
Учитываются при получении аттестата, могут быть использованы в качестве вступительных испытаний при поступлении в ВУЗ

Изображение слайда

ЕГЭ-2022
Минимальное количество баллов, подтверждающее освоение образовательной программы среднего общего образования
Предмет
Количество баллов
Математика (профиль)
27 (6 первичных)
Математика (база)
3 балла по пятибалльной шкале

Изображение слайда

ЕГЭ-2022
Минимальное количество баллов, необходимое для поступления на обучение в вуз (проект)
Предмет
Количество баллов
Математика (профиль)
39 вторичных

Изображение слайда

Математика – базовый уровень

Изображение слайда

Убрали задание 2, проверяющее умение выполнять вычисления и преобразования.
Добавили новое задание 5, проверяющее умение выполнять действия с геометрическими фигурами, и задание 20, проверяющее умение строить и исследовать простейшие математические модели.
Увеличили количество заданий с 20 до 21.
Максимальный балл за выполнение всей работы в 2022 году — 21.
Изменения КИМ ЕГЭ 2022 года
по сравнению с КИМ ЕГЭ 2018-2021 годов

Изображение слайда

Структура КИМ (базовый уровень)
За каждое из заданий экзаменуемый может получить
1 первичный балл.
Тематически программа государственного экзамена охватывает все разделы математики (алгебры и геометрии) с 5 по 11 классы:
Алгебра – 10;
Геометрия – 5;
Уравнения и неравенства – 3;
Функции – 1;
Комбинаторика, статистика, теория вероятностей – 1;
Математический анализ – 1.

Изображение слайда

Оценивание (базовый уровень)
Всего за 21 задание можно получить 21 первичных баллов, которые переводятся в оценку по утвержденной Рособрнадзором шкале:

Изображение слайда

Математика – профильный уровень

Изображение слайда

Слайд 18: Характеристика контрольных измерительных материалов ЕГЭ 2022 года
по математике профильного уровня

Контрольные измерительные материалы профильного ЕГЭ 2022 года по математике претерпели ряд содержательных и структурных изменений по сравнению с 2018-2020 годами.
2. Как и ранее, работа состоит из двух частей, но содержит не 19, а 18 заданий, позволяющих участникам экзамена продемонстрировать уровень освоения требований стандарта и готовность к продолжению образования в высших учебных заведениях на специальностях с различными уровнями требований по математике.

Изображение слайда

Экзаменационная работа состоит из двух частей, которые различаются по содержанию, сложности, числу заданий и форме ответа.
Часть 1 содержит 11 заданий (задания 1–11) с кратким числовым ответом.
Часть 2 содержит 7 заданий (задания 12-18) с развернутым ответом.
Правильное решение каждого из заданий 1–11 оценивается 1 баллом. Задание считается выполненным верно, если экзаменуемый дал правильный ответ в виде целого числа или конечной десятичной дроби.
Решения заданий с развёрнутым ответом оцениваются от 0 до 4 баллов. Развёрнутый ответ предполагает полную запись решения с обоснованием выполненных действий.
Полное правильное решение каждого из заданий 12, 14 и 15 оценивается 2 баллами; каждого из заданий 13 и 16 – 3 баллами ; каждого из заданий 17 и 18 – 4 баллами. Проверка выполнения заданий 12–18 проводится экспертами на основе разработанной системы критериев оценивания.
Максимальный первичный балл за всю работу – 31.
Характеристика контрольных измерительных материалов ЕГЭ 2022 года
по математике профильного уровня

Изображение слайда

1. Удалены задания 1 и 2, проверяющие умение использовать приобретённые знания и умения в практической и повседневной жизни, задание 3, проверяющее умение выполнять действия с геометрическими фигурами, координатами и векторами.
2. Добавлены задание 9, проверяющее умение выполнять действия с функциями, и задание 10, проверяющее умение моделировать реальные ситуации на языке теории вероятностей и статистики, вычислять в простейших случаях вероятности событий.
3. Внесено изменение в систему оценивания : максимальный балл за выполнение задания повышенного уровня 13, проверяющего умение выполнять действия с геометрическими фигурами, координатами и векторами, стал равен 3; максимальный балл за выполнение задания повышенного уровня 15, проверяющего умение использовать приобретённые знания и умения в практической деятельности и повседневной жизни, стал равен 2.
4. Количество заданий уменьшилось с 19 до 18, максимальный балл за выполнение всей работы стал равным 31.
Изменения КИМ ЕГЭ 2022 года
по сравнению с КИМ ЕГЭ 2018-2021 годов

Изображение слайда

Структура КИМ
(профильный уровень)
Экзамен состоит из двух частей :
Часть 1 – задания с кратким ответом (11 заданий)
Часть 2 – задания с развернутым ответом (7 заданий)
Разделы ЕГЭ по профильной математике в 2022 году:
Алгебра и начала анализа — 8 заданий,
Геометрия — 4 задания,
Реальная математика — 6 заданий.

Изображение слайда

Оценивание (профильный уровень)
Как и ранее, ЕГЭ 2022 года по профильной математике будет оцениваться в первичных баллах
( максимальное количество первичных баллов — 31 )
которые будут переведены во вторичные по специальной таблице соответствия, разработанной ФИПИ:

Изображение слайда

ЧТО МОЖНО ВЗЯТЬ С СОБОЙ НА ЭКЗАМЕН
На экзамене по математике разрешается пользоваться линейкой, которая не содержит справочную информацию, для построения чертежей и рисунков

Изображение слайда

БАЗОВЫЙ УРОВЕНЬ

Изображение слайда

ПРОФИЛЬНЫЙ УРОВЕНЬ

Изображение слайда

Слайд 28: ЕГЭ-2022: советы тем, кто готовится сдавать математику

1. Чем раньше, тем лучше
Начинать готовиться как можно раньше, поскольку с 2022 года ЕГЭ
по математике будут сдавать по принципиально новым вариантам КИМов. ФИПИ опубликовал перспективные модели совершенно новых заданий. Конечно, какие-то старые вопросы остались, но появились и незнакомые практико-ориентированные задания, которых в ЕГЭ раньше не было.
2. Решать тесты — не всегда эффективно
Ученикам, которые хотят получить за ЕГЭ по математике высокие баллы, необходимо определить, какие задания для них являются сложными, а какие простыми. Важно сосредоточиться именно на сложных заданиях, но также постоянно возвращаться к простым заданиям. Необходимо следить за динамикой своих успехов.

Изображение слайда

Слайд 29: ЕГЭ-2022: советы тем, кто готовится сдавать математику

3. Учите формулы и теоремы
Выучить сразу все формулы и теоремы нереально. Поэтому их необходимо разместите рядом с рабочим местом дома и учить постепенно.
4. Определите «потолок» баллов и просчитайте «свои» задания
Низкий средний балл, который мы наблюдаем каждый год, связан с высочайшей сложностью заданий с развёрнутыми ответами. Не стремитесь решить весь вариант. Создайте уникальный алгоритм достижения желаемого результата, выписав те номера заданий, которые в сумме приведут вас к ожидаемым баллам.

Изображение слайда

Слайд 30: ЕГЭ-2022: советы тем, кто готовится сдавать математику

5. Тайминг — ваше тайное оружие
Каждый второй высокобалльник после реального ЕГЭ по профильной математике жалуется, что ему не хватило времени. Необходимо следить за тем, сколько времени надо на выполнение всех заданий, которые вы будете точно решать на ЕГЭ для получения определённого количества баллов.
Необходимо учиться укладываться в отведённые временные рамки
6.Пишите пробники
Необходимо писать пробники как можно чаще. Обязательно фиксировать не только количество набранных баллов, но и типичные ошибки. При этом: время пробника не должно превышать прописанного в демоверсии, необходимо решать всё без калькулятора, ни в коем случае не пользоваться подсказками и шпаргалками.

Изображение слайда

Слайд 31: ЕГЭ-2022: советы тем, кто готовится сдавать математику

7. Избегайте ошибок по невнимательности
Ещё одна специфика ЕГЭ по профильной математике: мало правильно ответить, надо ещё все правильно оформить. Недостаточно всё решить, надо ещё и убедиться, что вы не допустили никаких ошибок в вычислениях и не вписали в бланк неправильный ответ. Необходимо читать условия и проверять свои записи как минимум два раза.
8. К тяжелым заданиям необходимо делать несколько подходов
В первую очередь это касается заданий на геометрию. Не получилось решить сегодня — попробуйте вернуться к задаче

Изображение слайда

Топ-10 основных ошибок на ЕГЭ по математике.
1.90% ошибок на экзамене происходит из-за обычной невнимательности.
2. Вычислительные ошибки — 80%

Изображение слайда

ЕГЭ-2022
В случае, если математика профильная или базовая не сдана, ребенку будет рекомендовано пересдавать математику базовую, но выбор остается за учеником.

Изображение слайда

Рекомендуемые ресурсы сети Интернет
Для качественной подготовки к ЕГЭ по математике созданы сайты, обеспечивающий поддержку работы учителя и самостоятельную работу учащихся:
1. Официальный информационный портал единого государственного экзамена http://www.ege.edu.ru
2. Образовательный портал для подготовки к экзаменам «Решу ЕГЭ» https://ege.sdamgia.ru/
3. Открытый банк заданий ЕГЭ базового уровня http://fipi.ru
4. Демонстрационные варианты КИМ 2022 гг. http://fipi.ru
5. Справочные материалы http://www.mathnet.spb.ru/texts/ege_part_b/
6. Материалы для самостоятельной подготовки к ЕГЭ

Изображение слайда

Источник

Презентация содержит информацию о назначении ЕГЭ по математике базового и профильного уровня,структуре КИМ ЕГЭ, системе оценивания и другую полезную информацию для выпускников и их родителей.

Раздел: Презентации по математике для 11 класса

Скачивая материал, я соглашаюсь с условиями публичной оферты.

Скачать презентацию

Другие полезные презентации:

Задачи с параметрами
Конус
Использование определенного интеграла в экономике
Задачи по теории вероятности
Использование определителя для решения систем линейных уравнений
Логарифмическая функция в уравнениях
Конус
Использование ИКТ в преподавании математики
Особенности PISA для 10-11 классов
Сфера и шар

Для вывода других вариантов — обновите страницу.

Скачать QR-код

Автор: Петренко Елена Анатольевна
учитель математики МКОУ Баганской СОШ №1

Размер файлов: 61.50 kB

Дата публикации:

13.03.2017

Внести правки в свой материал

Выходные данные (библиографическая ссылка):

Петренко Е. А. Особенности ЕГЭ по математике // Международный каталог для учителей, учеников и преподавателей «Презентации» // URL: https://edupres.ru/prezentatsii-po-matematike/11-klass/file/19872-osobennosti-ege-po-matematike (дата обращения: 12.03.2023)

Скачать сертификат о публикации— как получить такой сертификат

Источник

1.

Тема 1. Структура и содержание контрольных
измерительных материалов по математике в 2022 г.
Роль заданий с развёрнутым ответом в КИМ ЕГЭ по
математике

2.

Содержание курса
Тема лекции
Контроль
Тема 1. Структура и содержание контрольных измерительных Теоретический
материалов по математике в 2022 г. Роль заданий с развёрнутым ответом
зачет
в КИМ ЕГЭ по математике.
Тема 2. Методика проверки и оценки заданий с развёрнутым ответом:
Тренинг
уравнения и неравенства, экономическая задача (задания 12, 14 и 15)
Тема 3. Методика проверки и оценки заданий с развёрнутым ответом:
Тренинг
геометрические задания (задания 13 и 16)
Тема 4. Методика проверки и оценки заданий с развёрнутым ответом:
Тренинг
задания высокого уровня сложности (задания 17 и 18)
Тема 5. Анализ согласованности проверки заданий с развёрнутым
Тренинг
ответом
Тема 6. Обеспечение согласованности проверки заданий с развёрнутым Итоговый зачет
ответом
2/84

3.

3/84

4.

Нормативно-правовые документы
Приказ Минпросвещения России, Рособрнадзора от 07.11.2018
№190/1512 «Об утверждении Порядка проведения государственной
итоговой аттестации по образовательным программам среднего общего
образования»
Методические документы, рекомендуемые при организации и
проведении государственной итоговой аттестации по образовательным
программам основного общего и среднего общего образования в 2022
году.
4/84

5.

Нормативно-правовые документы
Пакет региональных документов
Положение о предметной комиссии субъекта
Российской Федерации
Порядок формирования предметной комиссии
субъекта Российской Федерации
Методические рекомендации по формированию и организации работы предметных комиссий субъекта Российской Федерации при проведении
государственной итоговой аттестации по образовательным программам среднего общего образования в 2021 году), раздел 2, пункт 2.1.5
Порядок формирования предметной комиссии
субъекта Российской Федерации
Процедура подготовки экспертов
ПК, а также формирования ПК
требует
формирования
на
региональном уровне пакета
нормативных
документов,
регламентирующих организацию
работы ПК.
требования к опыту экспертов по проверке развернутых ответов
участников экзаменов с учетом положений п.38 Порядка
порядок проведения подготовки экспертов ПК
порядок допуска лиц, претендующих на включение в ПК,
квалификационного испытания
показатели согласованности оценивания по результатам квалификационного
испытания
порядок проведения анализа работы предметной комиссии
Методические рекомендации по формированию и организации работы предметных комиссий субъекта Российской Федерации при проведении
государственной итоговой аттестации по образовательным программам среднего общего образования в 2021 году), раздел 2, пункт 2.1.6
5/84

6.

Состав ПК по каждому учебному предмету формируется из лиц,
отвечающих следующим общим требованиям:
1) наличие высшего образования;
2) соответствие квалификационным требованиям, указанным в квалификационных
справочниках и (или) профессиональных стандартах;
3) наличие опыта работы в организациях, осуществляющих образовательную
деятельность и реализующих образовательные программы среднего общего,
среднего профессионального или высшего образования (не менее трех лет);
4) наличие документа, подтверждающего получение дополнительного
профессионального образования, включающего в себя практические занятия (не
менее чем 18 часов) по оцениванию образцов экзаменационных работ
в соответствии с критериями оценивания по соответствующему учебному предмету.
Приказ Министерства Просвещения Российской Федерации и Федеральной службы по надзору в сфере образования и науки от 7.11.2018 № 190/1512 «Об
утверждении Порядка проведения государственной итоговой аттестации по образовательным программам среднего общего образования», пункт 38
6/84

7.

Квалификационные требования для присвоения статуса экспертам ПК
Для присвоения экспертам ПК того или иного статуса устанавливаются
квалификационные требования:
требования к экспертам ПК, определенным п. 38 Порядка;
требования к опыту оценивания экзаменационных работ участников
экзамена;
требования к результатам квалификационных испытаний;
требование к согласованности работы при проверке в предыдущем году и к
значениям показателей статистики удовлетворенных апелляций (кроме
экспертов ПК, включаемых в ПК в первый раз).
Методические рекомендации по формированию и организации работы предметных комиссий субъекта Российской Федерации при проведении
государственной итоговой аттестации по образовательным программам среднего общего образования в 2021 году), раздел 2.3
7/84

8.

Статусы экспертов ПК
ведущий эксперт ПК;
старший эксперт ПК;
основной эксперт ПК
Методические рекомендации по формированию и организации работы предметных комиссий субъекта Российской Федерации при проведении
государственной итоговой аттестации по образовательным программам среднего общего образования в 2021 году), раздел 2.2
8/84

9.

Статусы экспертов ПК
Ведущий эксперт ПК – статус, присваиваемый председателю ПК и заместителю (ям) председателя ПК, позволяющий:
а) осуществлять руководство подготовкой и (или) подготовку экспертов ПК на
региональном уровне;
б) консультировать экспертов ПК по вопросам оценивания развернутых ответов
участников экзаменов (по поручению председателя ПК);
в) осуществлять первую, вторую, третью проверки, перепроверку развернутых
ответов участников экзаменов в составе ПК, в том числе и в рамках межрегиональной
перекрестной проверки;
г) устанавливать правильность оценивания развернутого ответа апеллянта и
присутствовать во время рассмотрения апелляции (в рамках рассмотрения
апелляции о несогласии с выставленными баллами) (по поручению председателя
ПК);
е) осуществлять межрегиональную перекрестную перепроверку в рамках
рассмотрения апелляции о несогласии с выставленными баллами;
ж) осуществлять отбор изображений незаполненных участниками экзаменов бланков
ответов № 2, дополнительных бланков ответов № 2.
Методические рекомендации по формированию и организации работы предметных комиссий субъекта Российской Федерации при проведении
9/84
государственной итоговой аттестации по образовательным программам среднего общего образования в 2021 году), раздел 2.2, пункт 2.2.2

10.

Статусы экспертов ПК
Старший эксперт ПК – статус, позволяющий:
а) консультировать экспертов ПК по вопросам оценивания развернутых
ответов участников экзаменов (по назначению председателя ПК);
б) осуществлять первую, вторую и третью проверки, перепроверку
развернутых ответов участников экзаменов в составе ПК, в том числе и в
рамках межрегиональной перекрестной проверки;
в) устанавливать правильность оценивания развернутого ответа апеллянта
и присутствовать во время рассмотрения апелляции (в рамках
рассмотрения апелляции о несогласии с выставленными баллами) (по
поручению председателя ПК);
е) осуществлять отбор изображений незаполненных участниками экзаменов
бланков ответов № 2, дополнительных бланков ответов № 2.
Методические рекомендации по формированию и организации работы предметных комиссий субъекта Российской Федерации при проведении
государственной итоговой аттестации по образовательным программам среднего общего образования в 2021 году), раздел 2.2, пункт 2.2.3
10/84

11.

Статусы экспертов ПК
Основной эксперт ПК – статус, позволяющий:
а) осуществлять первую, вторую проверки, перепроверку развернутых
ответов участников экзаменов в составе ПК, в том числе и в рамках
межрегиональной перекрестной проверки;
б) участвовать в межрегиональных перекрестных проверках в составе ПК,
осуществляя первую и вторую проверки развернутых ответов участников
экзаменов;
в) осуществлять отбор изображений незаполненных участниками экзаменов
бланков ответов № 2, дополнительных бланков ответов № 2.
Методические рекомендации по формированию и организации работы предметных комиссий субъекта Российской Федерации при проведении
государственной итоговой аттестации по образовательным программам среднего общего образования в 2021 году), раздел 2.2, пункт 2.2.4
11/84

12.

Правила для председателя и экспертов ПК
Методические рекомендации по формированию и организации работы предметных комиссий субъекта Российской Федерации при проведении
государственной итоговой аттестации по образовательным программам среднего общего образования в 2021 году), раздел 5
5.1. Правила для председателя
ПК при организации
подготовительных
мероприятий
5.2. Правила для председателя
ПК на этапе проверки
развернутых ответов
участников экзаменов
5.3. Правила для председателя
ПК по завершении работы ПК
5.4. Правила для председателя
ПК при рассмотрении
апелляций о несогласии с
выставленными баллами
5.5. Правила для экспертов ПК
12/84

13.

Демоверсии, спецификации, кодификаторы
13/84

14.

Демоверсии, спецификации, кодификаторы
Документы, определяющие структуру и содержание
контрольных измерительных материалов единого
государственного экзамена по математике:
• Кодификатор проверяемых требований к результатам освоения основной образовательной
программы среднего общего образования и элементов содержания для проведения единого
государственного экзамена по МАТЕМАТИКЕ;
• Спецификация контрольных измерительных материалов для проведения в 2022 году
единого государственного экзамена по МАТЕМАТИКЕ (профильный уровень);
• Демонстрационный вариант контрольных измерительных материалов
государственного экзамена 2022 года по МАТЕМАТИКЕ (профильный уровень).
14/84
единого

15.

Спецификация контрольных измерительных материалов для проведения в 2022 году
единого государственного экзамена по МАТЕМАТИКЕ (профильный уровень)
15/84

16.

Спецификация контрольных измерительных материалов для проведения в 2022 году
единого государственного экзамена по МАТЕМАТИКЕ (профильный уровень)
Назначение КИМ ЕГЭ.
Документы, определяющие содержание КИМ ЕГЭ.
Подходы к отбору содержания, разработке структуры КИМ ЕГЭ.
Структура варианта КИМ ЕГЭ.
Распределение заданий варианта КИМ по содержанию, видам умений и
способам действий.
6. Распределение заданий варианта КИМ по уровню сложности.
7. Продолжительность ЕГЭ по математике.
8. Дополнительные материалы и оборудование.
9. Система оценивания выполнения отдельных заданий и экзаменационной
работы в целом.
10. Изменения в КИМ ЕГЭ 2022 года в сравнении с КИМ 2021 года.
Приложение 1. Обобщенный план варианта КИМ ЕГЭ 2022 года по
математике (профильный уровень).
1.
2.
3.
4.
5.
16/84

17.

Спецификация контрольных измерительных материалов для проведения в 2022 году
единого государственного экзамена по МАТЕМАТИКЕ (профильный уровень)
17/84

18.

Спецификация контрольных измерительных материалов для проведения в 2022 году
единого государственного экзамена по МАТЕМАТИКЕ (профильный уровень)
18/84

19.

Спецификация контрольных измерительных материалов для проведения в 2022 году
единого государственного экзамена по МАТЕМАТИКЕ (профильный уровень)
19/84

20.

Спецификация контрольных измерительных материалов для проведения в 2022 году
единого государственного экзамена по МАТЕМАТИКЕ (профильный уровень)
20/84

21.

Спецификация контрольных измерительных материалов для проведения в 2022 году
единого государственного экзамена по МАТЕМАТИКЕ (профильный уровень)
21/84

22.

Спецификация контрольных измерительных материалов для проведения в 2022 году
единого государственного экзамена по МАТЕМАТИКЕ (профильный уровень)
22/84

23.

Спецификация контрольных измерительных материалов для проведения в 2022 году
единого государственного экзамена по МАТЕМАТИКЕ (профильный уровень)
23/84

24.

Спецификация контрольных измерительных материалов для проведения в 2022 году
единого государственного экзамена по МАТЕМАТИКЕ (профильный уровень)
24/84

25.

Спецификация контрольных измерительных материалов для проведения в 2022 году
единого государственного экзамена по МАТЕМАТИКЕ (профильный уровень)
25/84

26.

Спецификация контрольных измерительных материалов для проведения в 2022 году
единого государственного экзамена по МАТЕМАТИКЕ (профильный уровень)
26/84

27.

Спецификация контрольных измерительных материалов для проведения в 2022 году
единого государственного экзамена по МАТЕМАТИКЕ (профильный уровень)
27/84

28.

Спецификация контрольных измерительных материалов для проведения в 2022 году
единого государственного экзамена по МАТЕМАТИКЕ (профильный уровень)
28/84

29.

30.

31.

32.

33.

34.

35.

36.

Кодификатор проверяемых требований к результатам освоения основной
образовательной программы среднего общего образования и элементов содержания
для проведения единого государственного экзамена по МАТЕМАТИКЕ
Код раздела
1. Уметь выполнять вычисления и преобразования.
2. Уметь решать уравнения и неравенства.
3. Уметь выполнять действия с функциями.
4. Уметь выполнять действия с геометрическими фигурами,
координатами и векторами.
5. Уметь
строить
и
исследовать
простейшие
математические модели
6. Уметь использовать приобретенные знания и умения в
практической деятельности и повседневной жизни.
36/84

37.

Кодификатор проверяемых требований к результатам освоения основной
образовательной программы среднего общего образования и элементов содержания
для проведения единого государственного экзамена по МАТЕМАТИКЕ
Для теоретического зачета.
КТ (указывать только код ОДНОГО раздела)
1. Уметь выполнять вычисления и преобразования.
2. Уметь решать уравнения и неравенства.
3. Уметь выполнять действия с функциями.
4. Уметь выполнять действия с геометрическими фигурами, координатами и
векторами.
5. Уметь строить и исследовать простейшие математические модели
6. Уметь использовать приобретенные знания и умения в практической
деятельности и повседневной жизни.
37/84

38.

39.

40.

41.

42.

43.

44.

45.

46.

47.

48.

49.

50.

51.

52.

Кодификатор проверяемых требований к результатам освоения основной
образовательной программы среднего общего образования и элементов содержания
для проведения единого государственного экзамена по МАТЕМАТИКЕ
1. Алгебра
2. Уравнения и неравенства
3. Функции
4. Начала математического анализа
5. Геометрия
6. Элементы комбинаторики,
статистики и теории вероятностей
52/84
Для теоретического зачета.
КЭС
1.1. Числа, корни и степени
1.2. Основы тригонометрии
1.3. Логарифмы
1.4. Преобразование выражений
2.1. Уравнения
2.2. Неравенства
3.1. Определение и график функции
3.2. Элементарное исследование функции
3.3. Основные элементарные функции
4.1. Производная
4.2. Исследование функций
4.3. Первообразная и интеграл
5.1. Планиметрия
5.2. Прямые и плоскости в пространстве
5.3. Многогранники
5.4. Тела вращения
5.5. Измерение геометрических величин
5.6. Координаты и векторы
6.1. Элементы комбинаторики
6.2. Элементы статистики
6.3. Элементы теории вероятностей

53.

Демонстрационный вариант контрольных измерительных материалов единого
государственного экзамена 2022 года по МАТЕМАТИКЕ (профильный уровень)
53/84

54.

Демонстрационный вариант контрольных измерительных материалов единого
государственного экзамена 2022 года по МАТЕМАТИКЕ (профильный уровень)
КТ
2.1
Решать рациональные,
иррациональные,
показательные,
тригонометрические и
логарифмические уравнения,
их системы
КЭС
2.1
Уравнения
2.1.5
Показательные уравнения
2.1.3
Иррациональные уравнения
2.1.6
Логарифмические уравнения
2
2.1
54/84

55.

Демонстрационный вариант контрольных измерительных материалов единого
государственного экзамена 2022 года по МАТЕМАТИКЕ (профильный уровень)
КТ
5.4
Моделировать реальные
ситуации на языке
теории вероятностей и
статистики, вычислять
в простейших случаях
вероятности событий
КЭС
6.3
Элементы теории
вероятностей
6.3.1
Вероятности событий
5
6.3
55/84

56.

57.

Демонстрационный вариант контрольных измерительных материалов единого
государственного экзамена 2022 года по МАТЕМАТИКЕ (профильный уровень)
КТ
КЭС
1.1
Выполнять арифметические действия, сочетая
устные и письменные приёмы; находить
значения корня натуральной степени, степени
с рациональным показателем, логарифма
1.2
Вычислять значения числовых и буквенных
выражений, осуществляя необходимые
подстановки и преобразования
1.3
Проводить по известным формулам и
правилам преобразования буквенных
выражений, включающих степени, радикалы,
логарифмы и тригонометрические функции
1.1
Числа, корни и степени
1.2
Основы тригонометрии
1.3
Логарифмы
1.4
Преобразования выражений
1
1.2
57/84

58.

Демонстрационный вариант контрольных измерительных материалов единого
государственного экзамена 2022 года по МАТЕМАТИКЕ (профильный уровень)
КТ
4.2
Решать простейшие стереометрические
задачи на нахождение геометрических
величин (длин, углов, площадей, объёмов);
использовать при решении
стереометрических задач планиметрические
факты и методы
КЭС
5.2
Прямые и плоскости в
пространстве
5.3
Многогранники
5.4
Тела и поверхности вращения
5.5
Измерение геометрических
величин
4
5.4
58/84

59.

Демонстрационный вариант контрольных измерительных материалов единого
государственного экзамена 2022 года по МАТЕМАТИКЕ (профильный уровень)
КТ
КЭС
3.1
Определять значение функции по значению
аргумента при различных способах задания
функции; описывать по графику поведение
и свойства функции, находить по графику
функции наибольшее и наименьшее значения;
строить графики изученных функций
3.2
Вычислять производные и первообразные
элементарных функций
3.3
Исследовать в простейших случаях функции
на монотонность, находить наибольшее и
наименьшее значения функции
4.1
Производная
4.2
Исследование функций
4.3
Первообразная и интеграл
3
4.2
59/84

60.

Демонстрационный вариант контрольных измерительных материалов единого
государственного экзамена 2022 года по МАТЕМАТИКЕ (профильный уровень)
КТ
КЭС
6.1
Анализировать реальные числовые данные,
информацию статистического характера;
осуществлять практические расчёты по
формулам; пользоваться оценкой и
прикидкой при практических расчётах
6.2
Описывать с помощью функций различные
реальные зависимости между величинами и
интерпретировать их графики; извлекать
информацию, представленную в таблицах, на
диаграммах, графиках
6.3
Решать прикладные задачи, в том числе
социально-экономического и физического
характера, на наибольшие и наименьшие
значения, на нахождение скорости и
ускорения
2.1
Уравнения
2.2
Неравенства
6
2.1
60/84

61.

Демонстрационный вариант контрольных измерительных материалов единого
государственного экзамена 2022 года по МАТЕМАТИКЕ (профильный уровень)
КТ
5.1
Моделировать реальные
ситуации на языке алгебры,
составлять уравнения и
неравенства по условию
задачи; исследовать
построенные модели с
использованием аппарата
алгебры
КЭС
2.1
Уравнения
2.2
Неравенства
5
2.1
61/84

62.

Демонстрационный вариант контрольных измерительных материалов единого
государственного экзамена 2022 года по МАТЕМАТИКЕ (профильный уровень)
КТ
КЭС
3.1
Определять значение функции по значению
аргумента при различных способах задания
функции; описывать по графику поведение
и свойства функции, находить по графику
функции наибольшее и наименьшее значения;
строить графики изученных функций
5.1
Моделировать реальные ситуации на языке
алгебры, составлять уравнения и неравенства
по условию задачи; исследовать построенные
модели с использованием аппарата алгебры
2.1
Уравнения
2.2
Неравенства
3.1
Определение и график
функции
3.2
Элементарное исследование
функций
3.3
Основные элементарные
функции
3
2.1
62/84

63.

64.

65.

Демонстрационный вариант контрольных измерительных материалов единого
государственного экзамена 2022 года по МАТЕМАТИКЕ (профильный уровень)
КТ
КЭС
2.1
Решать рациональные, иррациональные,
показательные, тригонометрические и
логарифмические уравнения, их системы
2.2
Решать уравнения, простейшие системы
уравнений, используя свойства функций и их
графиков; использовать для приближенного
решения уравнений и неравенств графический
метод
2.3
Решать рациональные, показательные и
логарифмические неравенства, их системы
2.1
Уравнения
2.2
Неравенства
2
2.1
65/84

66.

66/84

67.

1 Оценивание
Экспертная оценка
2 балла?
67/84

68.

Демонстрационный вариант контрольных измерительных материалов единого
государственного экзамена 2022 года по МАТЕМАТИКЕ (профильный уровень)
КТ
КЭС
68/84
4
5.3
4.2
Решать простейшие стереометрические
задачи на нахождение геометрических
величин (длин, углов, площадей, объёмов);
использовать при решении
стереометрических задач планиметрические
факты и методы
4.3
Определять координаты точки; проводить
операции над векторами, вычислять длину и
координаты вектора, угол между векторами
5.2
Моделировать реальные ситуации на языке
геометрии, исследовать построенные модели
с использованием геометрических понятий
и теорем, аппарата алгебры; решать
практические задачи, связанные с
нахождением геометрических величин
5.3
Проводить доказательные рассуждения при
решении задач, оценивать логическую
правильность рассуждений, распознавать
логически некорректные рассуждения
5.2
Прямые и плоскости в
пространстве
5.3
Многогранники
5.4
Тела и поверхности вращения
5.5
Измерение геометрических
величин
5.6
Координаты и векторы

69.

2 Оценивание
Экспертная оценка
2 балла?
69/84

70.

Демонстрационный вариант контрольных измерительных материалов единого
государственного экзамена 2022 года по МАТЕМАТИКЕ (профильный уровень)
КТ
2.3
Решать рациональные,
показательные и
логарифмические
неравенства, их системы
КЭС
2.1
Уравнения
2.2
Неравенства
2
2.2
70/84

71.

3 Оценивание
Экспертная оценка
2 балла?
6; 2;
71/84
6

72.

Демонстрационный вариант контрольных измерительных материалов единого
государственного экзамена 2022 года по МАТЕМАТИКЕ (профильный уровень)
КТ
КЭС
6.1
Анализировать реальные числовые данные,
информацию статистического характера;
осуществлять практические расчёты по
формулам; пользоваться оценкой и
прикидкой при практических расчётах
6.3
Решать прикладные задачи, в том числе
социально-экономического и физического
характера, на наибольшие и наименьшие
значения, на нахождение скорости и
ускорения
1.1
Числа, корни и степени
2.1.12
Применение математических
методов для решения
содержательных задач
из различных областей науки
и практики. Интерпретация
результата, учёт реальных
ограничений
6
2.1
72/84

73.

4 Оценивание
Экспертная оценка
2 балла?
73/84

74.

Демонстрационный вариант контрольных измерительных материалов единого
государственного экзамена 2022 года по МАТЕМАТИКЕ (профильный уровень)
КТ
КЭС
4.1
Решать планиметрические задачи на
нахождение геометрических величин (длин,
углов, площадей)
4.3
Определять координаты точки; проводить
операции над векторами, вычислять длину и
координаты вектора, угол между векторами
5.2
Моделировать реальные ситуации на языке
геометрии, исследовать построенные модели
с использованием геометрических понятий
и теорем, аппарата алгебры; решать
практические задачи, связанные с
нахождением геометрических величин
5.3
Проводить доказательные рассуждения при
решении задач, оценивать логическую
правильность рассуждений, распознавать
логически некорректные рассуждения
5.1
Планиметрия
5.5
Измерение геометрических
величин
5
5.1
74/84

75.

5 Оценивание
Экспертная оценка
2 балла?
75/84

76.

Демонстрационный вариант контрольных измерительных материалов единого
государственного экзамена 2022 года по МАТЕМАТИКЕ (профильный уровень)
КТ
КЭС
76/84
5
2.1
2.1
Решать рациональные, иррациональные,
показательные, тригонометрические и
логарифмические уравнения, их системы
2.2
Решать уравнения, простейшие системы
уравнений, используя свойства функций и их
графиков; использовать для приближенного
решения уравнений и неравенств графический
метод
2.3
Решать рациональные, показательные и
логарифмические неравенства, их системы
5.1
Моделировать реальные ситуации на языке
алгебры, составлять уравнения и неравенства
по условию задачи; исследовать построенные
модели с использованием аппарата алгебры
2.1
Уравнения
2.2
Неравенства
3.1
Определение и график
функции
3.2
Элементарное исследование
функций
3.3
Основные элементарные
функции

77.

6 Оценивание
Экспертная оценка
2 балла?
77/84

78.

Демонстрационный вариант контрольных измерительных материалов единого
государственного экзамена 2022 года по МАТЕМАТИКЕ (профильный уровень)
КТ
КЭС
78/84
5.1
Моделировать реальные ситуации на языке
алгебры, составлять уравнения и неравенства
по условию задачи; исследовать построенные
модели с использованием аппарата алгебры
5.3
Проводить доказательные рассуждения при
решении задач, оценивать логическую
правильность рассуждений, распознавать
логически некорректные рассуждения
1.1
Числа, корни и степени
1.2
Основы тригонометрии
1.3
Логарифмы
1.4
Преобразования выражений
2.1
Уравнения
2.2
Неравенства
3.1
Определение и график функции
3.2
Элементарное исследование функций
3.3
Основные элементарные функции
5
1.4

79.

7 Оценивание
Экспертная оценка
2 балла?

80.

Аналитические и методические материалы
80/84

81.

Для предметных комиссий субъектов РФ
81/84

82.

Проверяйте работы
обучающихся в соответствии с
критериями.
Успехов!
82/84

Источник

Слайд 1

Система подготовки учащихся к ЕГЭ по математике. Учитель высшей категории КОУ КШИ ВО «Борисоглебский кадетский корпус» Воронина Ирина Станиславовна 24.12.2012 .

Слайд 2

В российских школах начинается поэтапный переход на федеральные государственные образовательные стандарты второго поколения общего образования (далее – ФГОС), основной миссией которых является повышение качества образования. Особенностью 2011/2012 учебного года являлось введение ФГОС начального общего образования в начальной школе и последовательная подготовка к введению ФГОС основного общего образования. Поэтому уже сейчас необходимо понять его теоретико-методологическую основу, структуру и содержание.

Слайд 3

Контрольные измерительные материалы ЕГЭ 2013 года ориентируют и учителя, и учащихся на полноценное изучение курсов алгебры и начал анализа и геометрии по учебникам из Федерального перечня. Первоочередная задача изучения курса математики – это качественное изучение предмета на базовом уровне.

Слайд 4

Анализ итогов ЕГЭ по математике показывает, что у учащихся при выполнении заданий базового и повышенного уровня наибольшие затруднения вызывают следующие темы:

Слайд 5

тригонометрические уравнения; область определения сложной функции; использование графика функции при решении неравенства; преобразование корня и степени и нахождение их значения; свойства функции; нахождение углов между плоскостями и прямыми; использование графика в решение задач с параметрами.

Слайд 6

Цели и задачи Подготовить всех учащихся к успешной сдаче ЕГЭ с хорошим качеством Для этого необходимо: Учителю обладать необходимыми компетенциями (самому уметь решать все задачи ЕГЭ) Совершенствовать структуру и содержание учебного материала в ходе подготовки к ЕГЭ Систематизировать повторение программного материала Отработать тестовые технологии в ходе работы с контрольно-измерительными материалами через личностно-ориентированный подход

Слайд 7

Схема подготовки Направления деятельности учителя математики по подготовке учащихся к ЕГЭ Методическая подготовка учителя к ЕГЭ Организация вводного, текущего и итогового повторения Психологическая подготовка учащихся Диагностика и анализ качества ЗУН учащихся по материалам ЕГЭ Создание банка тестовых заданий Организация самостоятельной работы учащихся

Слайд 8

Методическая подготовка учителя к ЕГЭ Знакомиться с нормативными документами по проведению ЕГЭ через районное МО и администрацию школы Повышать свой уровень профессиональной грамотности (развивать свои способности при решении заданий части С)

Слайд 9

Психологическая подготовка Обучение приему «Движение вверх-вниз» Обучение жесткому самоконтролю времени Обучение оценке трудности заданий и разумному выбору этих заданий Обучение прикидке границ результатов и минимальной подстановке как способам проверки результатов

Слайд 10

Организация повторения Вводное повторение Текущее повторение (по горизонтали) Итоговое повторение (по вертикали) «Числа и вычисления» «Функции» « Выражения и преобразования» «Уравнения и неравенства» «Геометрические фигуры и их свойства» Повторение, ориентированное на индивидуальный уровень подготовки учащегося

Слайд 11

Создание банка тестовых заданий Создание тестов по основным темам курса Тренировочные тесты Итоговые тесты Тесты прошлых лет Тесты пробных экзаменов

Слайд 12

Организация самостоятельной работы Работа учащихся по сборникам подготовки к ЕГЭ Организация самостоятельной работы по материалам в интернете

Слайд 13

Анализ качества ЗУН учащихся Входное диагностирование учащихся 11 кл . за курс 10 кл . Тематическое тестирование по основным разделам курса Контрольные зачеты по алгебре и началам анализа в конце 11 кл . Пробные ЕГЭ по линии администрации

Слайд 14

Для качественной подготовки к ЕГЭ созданы сайты, обеспечивающий поддержку работы учителя и самостоятельную работу учащихся по подготовке к сдаче экзамена .

Слайд 15

http://mathege.ru /

Слайд 16

http://reshuege.ru/

Слайд 17

http://www.fipi.ru/

Слайд 18

http://www.ege.edu.ru

Слайд 20

Опасность кроется в том, что демонстрационный вариант ЕГЭ по математике может сильно отличаться от того варианта, который даётся на экзамене. Экзаменационный вариант может быть сложнее демонстрационного, а многие задачи могут не соответствовать тем, к которым готовился ученик. Поэтому выпускнику необходимо заниматься самостоятельно, помимо школьной программы, и не просто “натаскаться” на задачах демонстрационного материала, но и изучить принципы и методы решения различных задач, а также научиться думать нешаблонно, сформировав цельную картину изучаемого предмета.

Слайд 22

Программа Тестариус Программа предназначена для эффективной подготовки к егэ 2013 по математике. Преимущество программы: Большое количество вариантов в темах Путь решения каждой задачи Соответствие КИМам ЕГЭ 2013 Полную версию программы можно приобрести на сайте http://www. School — testa.ru/

Источник

Слайд 12016 год

КРИТЕРИИ ОЦЕНИВАНИЯ ЗАДАНИЙ ЕГЭ С РАЗВЁРНУТЫМ ОТВЕТОМ

Слайд 4В методических материалах дается краткое описание структуры контрольных измерительных материалов 2016

г. по математике, характеризуются типы заданий с развернутым ответом, используемые в КИМ ЕГЭ по математике, и критерии оценки выполнения заданий с развернутым ответом, приводятся примеры оценивания выполнения заданий и даются комментарии, объясняющие выставленную оценку.
В пособии использованы ответы участников ЕГЭ 2013–2015 гг., а также диагностических и тренировочных работ.

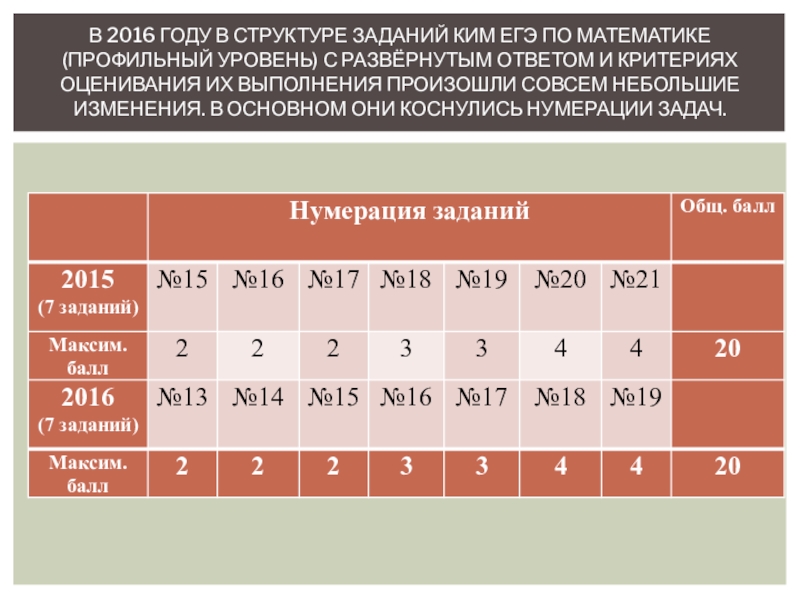
Слайд 6В 2016 году в структуре заданий КИМ ЕГЭ по математике (профильный

уровень) с развёрнутым ответом и критериях оценивания их выполнения произошли совсем небольшие изменения. В основном они коснулись нумерации задач.

Слайд 7ЗАДАНИЕ №13 – уравнение,
ЗАДАНИЕ №14 – стереометрия,
ЗАДАНИЕ №15 –

неравенство,
ЗАДАНИЕ №16 – планиметрия,
ЗАДАНИЕ №17 – текстовая задача экономического содержания,
ЗАДАНИЕ №18 – задание с параметром,
ЗАДАНИЕ №19 – дискретная математика.

Тематическая принадлежность заданий осталась неизменной.

Слайд 8Задания №13 занимают одну из важнейших позиций в структуре КИМ. К их

выполнению в 2015 г. приступало более 60% участников профильного ЕГЭ, а положительные баллы получили более 30% всех участников. Успешность выполнения заданий этого типа является характеристическим свойством, различающим базовый и профильный уровни подготовки учащихся. Поэтому при подготовке выпускников к экзамену решению заданий подобного уровня следует уделять много внимания.

Критерии проверки и оценка решений заданий 13 (15 в 2015 г., С1 ранее) вариантов КИМ ЕГЭ-2016.

Слайд 9Небольшое уточнение с «неверный ответ» до «неверные ответы» подчеркивает тот факт,

что 1 балл допускается ставить в тех случаях, когда единственная вычислительная ошибка (описка) стала причиной того, что неверны оба ответа, полученные при выполнении п. а и п. б.

Сохранена такая структура критериев и в 2016 г.

Слайд 10Возвращаясь к критериям, если:
(1) уравнение верно сведено к простейшим тригонометрическим

уравнениям и ;
(2) эти простейшие уравнения не решены или решены с ошибкой;
(3) но при этом отбор корней исходного уравнения верно произведён с помощью тригонометрической окружности, а не по неверно найденным корням простейших тригонометрических уравнений, то по критериям можно выставить 1 балл (получен верный ответ в п. б, а его получение обосновано верным сведением к простейшим уравнениям).
В то же время, при наличии (1) и (2) и «верного» отбора по неверно решенным простейшим уравнениям следует выставлять 0 баллов: любые ошибки, допущенные в тригонометрических формулах, в нахождении значений тригонометрических функций не относятся к вычислительным.

Комментарий. Отбор корней может быть обоснован любым способом: с помощью графика, решения двойных неравенств, ЕДИНИЧНОЙ ОКРУЖНОСТИ и т.п.

Слайд 11
Работа не пустая. Она цитирует УММ 2014 года, где за эту

работу был выставлен 1 балл. Объяснение состояло в том, что при переходе от

допущена очевидная вычислительная ошибка, а уравнение

решено верно, и затем произведён отбор. К сожалению, в этом отборе есть и описка в 3), есть и ошибка в 1): отобранный корень не принадлежит нужному отрезку.
Оценка эксперта: 0 баллов.

Комментарий

Слайд 12Типичный пример выставления 1 балла по критериям 2014, 2015 гг. При

решении второго простейшего тригонометрического уравнения «пропал» множитель 2 в периоде. Но верный отбор корней произведён не по формуле, а по тригонометрической окружности.

Оценка эксперта: 1 балл.

Комментарий

Слайд 13Правильные ответы обоснованно получены в пунктах а и б.

Оценка эксперта:

Слайд 14Нигде в решении нет описания значений параметра k, но при отборе

корней явно указано целое значение. Считаем, что выставление наивысшего балла возможно.

Оценка эксперта: 2 балла.

Комментарий

Слайд 15Комментарий
Странный случай. В тексте много верных вещей. В п. а сначала

написан верный ответ

Но потом появляется угол в

В результате оба ответа неверны не из-за вычислительной ошибки.

Оценка эксперта: 0 баллов.

(!!!?).

Слайд 16Комментарий
Практически всё верно, только отобранные корни не принадлежат нужному отрезку. Верно

выполнен только первый пункт.

Оценка эксперта: 1 балл.

Слайд 17Стереометрическая задача позиционируется как задача для большинства успевающих учеников, а не

только для избранных. В связи с этим в КИМах предлагается достаточно простая задача по стереометрии, решить которую возможно с минимальным количеством геометрических построений и технических вычислений. Итак, в заданиях 14 прежними остались уровень сложности, тематическая принадлежность (геометрия многогранников) и максимальный балл (2 балла) за их выполнение.
Несколько изменилась структура постановки вопроса. Как и в прошлом году, она разделена на пункты а и б примерно так же, как и задание 13. Соответственно уточнился и общий характер оценивания выполнения решений. Для получения 2 баллов нужно, чтобы выполнялись два условия одновременно (конъюнкция), а для получения 1 балла хватает выполнения хотя бы одного из этих условий (дизъюнкция).

Критерии проверки и оценка решений заданий 14 (16 в 2015 г., С2 ранее) вариантов КИМ ЕГЭ-2016.

Слайд 18Пункт а в заданиях 14 может по разному соотноситься с пунктом

б. А именно, он может быть утверждением независимым от б, дополняющим или проверяющим понимание общей конструкции.

В этой ситуации независимость условий а и б приводит и к независимости проверки их выполнения.

Слайд 19Возможен и второй вариант, когда в пункте а следует доказать утверждение,

необходимое для полной корректности вычислений в пункте б.
Во этой ситуации вполне может встретиться примерно следующий текст.
«Задание 16……
а) Докажите, что…; б) Найдите площадь….
Решение.
У меня а) не получилось. Используем а) при решении б)… далее верное и обоснованное (без выполнения пункта а) вычисление……».

ЗАДАНИЕ 14 (16 в 2015 г. и С2 раннее)

Слайд 20 Хуже того, вместо честного признания о «нерешаемости» а

может быть предъявлено неполное и, даже, неверное доказательство. И в том, и в другом случае за верное решение пункта б следует выставлять 1 балл. Позиция разработчиков КИМ состоит в том, что в первую очередь следует поощрять за достижения, а не наказывать за промахи. Тем самым, часть «обоснованно получен верный ответ в пункте б» критерия на 1 балл более точно было бы сформулировать как «обоснованно (по модулю п. а) получен верный ответ в пункте б».

ЗАДАНИЕ 14 (16 в 2015 г. и С2 раннее)

Слайд 21Это отличие не может служить основанием для снижения оценки. (Кстати, последнее

верно для проверки любого задания, не обязательно задания по стереометрии). Главное, чтобы ответ был правильным. Например, если в образце решения стоит , а у выпускника в ответе , то справедливость равенства = эксперту следует проверить самостоятельно.
Отдельно скажем о применении различных формул аналитической геометрии, которыми несколько излишне увлекаются некоторые специалисты. Разумеется, никакого запрета на их использование нет. Однако, если по критериям 2014 года адекватное использование некоторой формулы с допущенной вычислительной ошибкой можно оценить в 1 балл, то условие «обоснованно получен верный ответ в пункте б» критериев 2016 года в таком случае уже не выполнено и (если нет доказательства а) следует выставлять 0 баллов.

Вид ответа может отличаться от приведённого в критериях по проверке заданий с развёрнутым ответом.

Слайд 22Решения пункта б) нет, а в пункте а) нет обоснования того,

что при делении на 6 равных частей мы обязательно попадем в нужные точки.

Оценка эксперта: 0 баллов.

Комментарий

Слайд 23Чертёж верный, но доказательство утверждения пункта а) отсутствует и пункт б)

не выполнен. Хотя в тексте решения есть разумные выводы, которыми автор решения воспользоваться не смог. (Может создаться впечатление, что решение не до конца скопировано из оригинального текста работы. Нет, в работе действительно нет никакого продолжения.)

Оценка эксперта: 0 баллов.

Комментарий

Слайд 24Сечение построено верно и обоснованно получена величина отношения 5:1. В «Доказать»

заявлено доказательство другого отношения, но эта описка никак не повлияла на дальнейшее. В п. б есть неверный ответ и зачеркнутое решение, т.е. нет решения.
Оценка эксперта: 1 балл.

Комментарий

Слайд 25Утверждение пункта а не доказано. В пункте б найдена высота, проведенная

к гипотенузе прямоугольного треугольника, но никак не обоснованно, что это расстояние от точки до плоскости .

Оценка эксперта: 0 баллов.

Комментарий

Слайд 26Всё сделано аккуратно.

Оценка эксперта: 2 балла.

Комментарий

Слайд 27Обоснованно получено доказательство утверждения пункта а, хотя нет ссылки на признак

перпендикулярности прямой и плоскости. Верно намечен путь вычисления расстояния от вершины до плоскости, но реализовать его не удалось.
Оценка эксперта: 1 балл.

Комментарий

Слайд 28На этом месте в КИМ 2011–2014 гг была система двух неравенств,

а в 2015 и 2016 году заявлено решение одного неравенства. Грубо говоря, задание №15 «в два раза» проще прежнего задания С3.
Критерии проверки задания С3 были весьма лаконичны, жестко структурированы, но в то же время и достаточно беспощадны. Вполне грамотный и хорошо подготовленный выпускник, который допускал в решении каждого из неравенств системы хотя бы по одной неточности, получал 0 из возможных 3 баллов, несмотря на все достижения, которые он продемонстрировал в процессе решения. Например, это приводило к тому, что оценка «2 балла» из трёх была более редкой, чем оценка «3 балла» из трёх.

Критерии проверки и оценка решений заданий 15 (18 в 2015 г., С3 ранее) вариантов КИМ ЕГЭ–2016

Слайд 29При переходе к решению одного неравенства поле возможностей при выставлении 0,

1 или 2 баллов несколько расширяется. В данном случае оценка «1 балл» не есть половина оценки «2 балла». Другими словами, утверждение «1 балл ставится, если задача решена наполовину» неверно. Более точным является тезис, выражаемый равенством «1 = 2-» или словами «1 балл ставится, если задача почти решена». Для получения 1 балла за выполнение задания №15 необходимо получение итогового ответа и наличие верной последовательности всех шагов решения.

Критерии проверки и оценка решений заданий 15 (18 в 2015 г., С3 ранее) вариантов КИМ ЕГЭ–2016

Слайд 30Вот как в точности выглядят критерии оценивания выполнения задания №15.

Слайд 31При этом в первом случае выставления 1 балла допускаются только ошибки

в строгости неравенства: «≥» вместо «>», или наоборот. Если в ответ включено значение переменной, при котором одна из частей неравенства не имеет смысла, то следует выставлять оценку «0 баллов».

Слайд 32Хотя рациональное неравенство «почти» решено, в работе много ошибок. Похоже, автор

не разобрался в логарифмах даже на простейшем уровне.

Оценка эксперта: 0 баллов.

Комментарий

Слайд 33Можно отметить верную последовательность всех шагов решения, за исключением неравенства с

множителем . Далее, конечно, ошибка в применении метода интервалов. Все решения найдены, но к ним «добавлены» посторонние решения. В результате – ответ неверный.

Оценка эксперта: 0 баллов.

Комментарий

Слайд 34В результате компенсирующих ошибок и частично верных утверждений получена «часть» множества

решений неравенства. Но имеются грубейшие ошибки.

Оценка эксперта. 0 баллов.

Комментарий

Слайд 35Можно отметить не самый удачный путь к «цели», но способ решения

не оценивается. Ответ правильный и получен с приемлемым обоснованием.

Оценка эксперта: 2 балла.

Комментарий

Слайд 36 Вычислительных ошибок в ходе преобразований нет. Есть грубая ошибка

в преобразовании первого же неравенства, которое решается по правилу пропорции (см. пунктиры).
Судя по тексту решения, его автор неверно усвоил совет типа «если всё положительно, то от знаменателей можно избавляться крест-накрест»: ведь не просто так написано, что 3/2 > 0.

Оценка эксперта: 0 баллов.

Комментарий

Слайд 37Типичный 1 балл. Путаница в корнях квадратного уравнения, а потом всё

верно.

Оценка эксперта: 1 балл.

Комментарий

Слайд 38Ответ неверный, все шаги решения присутствуют, но «случайно» использовалось верное неравенство

при записи значений x. Это не может трактоваться как «получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения».

Оценка эксперта: 0 баллов.

Комментарий

Слайд 39ПРЕЗЕНТАЦИЯ СОСТАВЛЕНА ПО МАТЕРИАЛАМ «МЕТОДИЧЕСКИХ РЕКОМЕНДАЦИЙ ПО ОЦЕНИВАНИЮ ВЫПОЛНЕНИЯ ЗАДАНИЙ ЕГЭ

С РАЗВЁРНУТЫМ ОТВЕТОМ ПО МАТЕМАТИКЕ», 2016 ГОД

Источник

Слайд 1ЕГЭ по математике (базовый и профильный уровни)Мегельбей Жанна Николаевна, учитель математики

Слайд 2ЕГЭ по математике (базовый и профильный уровни) – нет изменений структуры

Слайд 3Базовый уровеньЭкзаменационная работа включает 20 заданий с кратким ответом базового уровня

Слайд 4Базовый уровеньВ работу включены задания по всем основным разделам предметных требований

Слайд 5Работа оценивается по традиционной 5-балльной шкале: Базовый уровеньМинимальный порог для получения аттестата

Слайд 6По сравнению с 2016 г. в 2017 г. произошло улучшение результатов

Слайд 7Профильный уровеньРабота состоит из двух частей и содержит 19 заданий. При

Слайд 8Профильный уровеньЗадания делятся на три тематических модуля: «Алгебра и начала анализа»,

Слайд 9Работа рассчитана на 3 часа 55 минут.Работа оценивается по 100-балльной шкале

Слайд 10Готовимся к ЕГЭ Официальный информационный портал ЕГЭ www.ege.edu.ruСайт разработчиков экзаменационных материалов

Первый слайд презентации

Слайд 7: СРОКИ СДАЧИ ЕГЭ ПО МАТЕМАТИКЕ В 2022 ГОДУ БАЗОВЫЙ УРОВЕНЬ – 03 ИЮНЯ ПРОФИЛЬНЫЙ УРОВЕНЬ -02 ИЮНЯ

Слайд 18: Характеристика контрольных измерительных материалов ЕГЭ 2022 года по математике профильного уровня

Слайд 28: ЕГЭ-2022: советы тем, кто готовится сдавать математику

Слайд 29: ЕГЭ-2022: советы тем, кто готовится сдавать математику

Слайд 30: ЕГЭ-2022: советы тем, кто готовится сдавать математику

Слайд 31: ЕГЭ-2022: советы тем, кто готовится сдавать математику

1.

2.

3.

4.

5.

6.

7.

8.

9.

10.

11.

12.

13.

14.

15.

16.

17.

18.

19.

20.

21.

22.

23.

24.

25.

26.

27.

28.

29.

30.

31.

32.

33.

34.

35.

36.

37.

38.

39.

40.

41.

42.

43.

44.

45.

46.

47.

48.

49.

50.

51.

52.

53.

54.

55.

56.

57.

58.

59.

60.

61.

62.

63.

Слайд 1ЕГЭ по математике
(базовый и профильный уровни)
Мегельбей Жанна Николаевна, учитель математики

Слайд 3Базовый уровень
Экзаменационная работа включает
20 заданий с кратким ответом базового уровня

Слайд 4Базовый уровень
В работу включены задания по всем основным разделам предметных требований

Слайд 5Работа оценивается
по традиционной 5-балльной шкале:

Базовый уровень
Минимальный порог для получения аттестата

Слайд 7Профильный уровень
Работа состоит из двух частей и содержит 19 заданий. При

Слайд 8Профильный уровень
Задания делятся на три тематических модуля: «Алгебра и начала анализа»,

Слайд 9Работа рассчитана на 3 часа 55 минут.
Работа оценивается по 100-балльной шкале

Слайд 10Готовимся к ЕГЭ
Официальный информационный портал ЕГЭ www.ege.edu.ru
Сайт разработчиков экзаменационных материалов

Слайд 18: Характеристика контрольных измерительных материалов ЕГЭ 2022 года
по математике профильного уровня

Слайд 12016 год

КРИТЕРИИ ОЦЕНИВАНИЯ ЗАДАНИЙ ЕГЭ С РАЗВЁРНУТЫМ ОТВЕТОМ

Слайд 7ЗАДАНИЕ №13 – уравнение,
ЗАДАНИЕ №14 – стереометрия,
ЗАДАНИЕ №15 –

Слайд 10Возвращаясь к критериям, если:
(1) уравнение верно сведено к простейшим тригонометрическим

Слайд 11
Работа не пустая. Она цитирует УММ 2014 года, где за эту

Слайд 13Правильные ответы обоснованно получены в пунктах а и б.

Оценка эксперта:

Слайд 15Комментарий
Странный случай. В тексте много верных вещей. В п. а сначала

Слайд 16Комментарий
Практически всё верно, только отобранные корни не принадлежат нужному отрезку. Верно

Слайд 26Всё сделано аккуратно.

Оценка эксперта: 2 балла.

Комментарий