поделиться знаниями или
запомнить страничку
- Все категории
-
экономические
43,623 -
гуманитарные
33,648 -
юридические
17,917 -
школьный раздел
611,572 -
разное
16,897
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
1. Вероятность сдачи первого экзамена 0,6, тогда вероятность его не сдать 1 — 0,6 = 0,4.
Вероятность сдачи второго экзамена равна 0,8, а неуспеха 1 — 0,8 = 0,2.
Известно, что вероятность сдать третий экзамен составляет 0,7.
Тогда вероятность его не сдать 1 — 0,7 = 0,3.
2. Вычислим вероятность сдачи одного экзамена.
Это событие происходит в случае, когда один предмет сдан, а два других нет.
Р1 = 0,6 * 0,2 * 0,3 + 0,4 * 0,8 * 0,3 + 0,4 * 0,2 * 0,7 = 0,036 + 0,096 + 0,056 = 0,188.
2. Найдем вероятность сдачи двух предметов.
Р2 = 0,6 * 0,8 * 0,3 + 0,4 * 0,8 * 0,7 + 0,6 * 0,2 * 0,7 = 0,144 + 0,224 + 0,084 = 0,452.
3. Определим вероятность сдачи трех экзаменов.
Р3 = 0,6 * 0,8 * 0,7 = 0,336.
4. Вычислим вероятность сдать хотя бы один экзамен.
Обратное этому событию — ничего не сдать.
Р = 0,4 * 0,2 * 0,3 = 0,024.
Р4 = 1 — 0,024 = 0,976.
Ответ: 0,188; 0,452; 0,336; 0,976.
1. Пусть Х – число сданных экзаменов. Составим ряд распределения Х. Возможные значения Х: 0, 1, 2, 3. Вычислим вероятности этих значений: Р(Х=0) = 0.1, Р(Х=1) = 0.9*0.2 = 0.18, Р(Х=2) = 0.9*0.8*0.3=0.216, Р(Х=3) = 0.9*0.8*0.7=0.504.
Математическое ожидание. М[X] = 0*0.1 + 1*0.18 2*0.216 + 3*0.504 = 2.124
2. Пусть Х – прибыль от инвестиций. Далее, решение можно оформить различными способами. Сначала находим все значения Х и их вероятности, а потом математическое ожидание Х. Можно немного ” повеселее”. Введём две случайные величины: Y – доход от инвестиций в фирму А, Z – доход от инвестиций в фирму В.
Значения Y: 0 , 0.5 с вероятностями 0.2 и 0.8 соответственно. M[Y] = 0.5*0.8 = 0.4.
Значения Z: 0 , 0.4 с вероятностями 0.15 и 0.85 соответственно. M[Y] = 0.4*0.85 = 0.34.
Тогда X = 10*Y + 15*Z. Поэтому М[X] = 10*M[Y] + 15*M[Z] = 9.1
Однако закон распределения Х надо найти.
Значения Х: 0, 5, 6, 11, с вероятностями 0.03, 0.12, 0.17, 0.68.
СВ является непрерывной, если
ее функция распределения непрерывна.
Для НСВ наряду с функцией распределения
вводится еще 1 закон распределения –
плотность вероятности.
Определение 4.6:
Плотностью вероятностей хназывается производная ее функции
распределения, т.е.
(плотность вероятностей может быть
обозначена
)
Свойства плотностей вероятности:
1.
2.
3.
4.
— условие нормировки
4.5. Числовые характеристики cb
Определение 4.7:
Математическим ожиданием ДСВназывается число.
Определение 4.8:
Математическим ожиданием НСВназывается число.
математическое
ожидание
Свойства математического ожидания:
1. X = с
= const,
M(C) = C
2. Постоянный множитель выносится за
знак математического ожидания, т.е.:
3. Математическое ожидание суммы СВ
равно сумме математических ожиданий
4.6. Дисперсия случайной величины
Определение 4.9:
Дисперсией СВназывается число:
Свойства дисперсии:
1. Дисперсию можно найти по формуле:
2.
3. Если X = с=const,
тоD(C)
= 0
4. Если
,
то
Формулы:
для ДСВ:
1.
2.
для НСВ:
1.
2.
Средним квадратичным отклонением
СВ Хназывается число:.
Законы распределения СВ (стр.19):
-
Биноминальное распределение.
-
Распределение Пуассона
-
Равномерное распределение
-
Показательное распределение
-
Нормальное распределение
Практическая работа № 2
№ 1.
Для данного студента вероятность
успешной сдачи первого экзамена равна
0,9, второго – 0,8, третьего – 0,7. Случайная
величина х – число успешно
сданных экзаменов. Найти: ряд распределения
ДСВ, математическое ожидание М(Х);
дисперсию D(X);
среднеквадратичное отклонение
.
Решение:
Случайная величина принимает значения:
0, 1, 2, 3
Пусть р1– вероятность
сдачи первого экзамена.
р2– вероятность сдачи
второго экзамена.
р3– вероятность сдачи
третьего экзамена.
q1– вероятность
несдачи первого экзамена.
q2– вероятность
несдачи второго экзамена.
q3– вероятность
несдачи третьего экзамена.
-
Х
0
1
2
3
Р
0,006
0,092
0,398
0,504
(методичка, стр.25, формула для доверительного
интервала)
Нормальное распределение – стр.21
П.6 зад.7 для решения к.р.
№ 2.
На сборку поступили детали с 3 конвейеров.
Первый дает 25%, второй – 30%, третий – 45%
деталей, поступающих на сборку. С первого
конвейера в среднем поступает 2% брака,
со второго – 3%, с третьего – 1%. Найти
вероятность того, что:
-
На сборку поступила бракованная
деталь. -
Поступившая бракованная деталь со
второго конвейера.
Решение:
Пункт 1.
Пусть событие А– поступившая деталь
на сборку – бракованная.
Н1– деталь с первого конвейера.
Н2– деталь со второго конвейера.
Н1– деталь с третьего конвейера.
Пункт 2.
№ 3.
Монету бросают 10 раз. Найти вероятность
того, что герб выпадет:
-
2 Раза.
-
Менее 2 раз.
-
Не менее 2 раз.
Решение:
1:
Вероятность того, что выпадет герб,
;n = 10, k
= 2
Формула Бернулли:
2:
По формуле Бернулли:
3:
Тел. кафедры – 60-27-71
Надежда Николаевна
3 студента сдают экзамен. Вероятность успешной сдачи для 1-го 0,9, для второго — 0,7, для третьего — 0,9. Найти вероятность того что:
а) все трое сдали экзамен;
б) двое сдали экзамен;
в) хотя бы один студент сдал экзамен.
вероятности
теория
задан
13 Апр ’15 21:26
мандаринка
1●2●8
20% принятых
изменен
14 Апр ’15 8:56
Виталина
99●1●7
а) Перемножьте три вероятности.
б) $%0,9cdot0,7(1-0,9)+0,9(1-0,7)0,9+(1-0,9)0,7cdot0,9$%.
в) $%1-(1-0,9)(1-0,7)(1-0,9)$%.
(14 Апр ’15 0:07)
falcao
10|600
символов нужно
символов осталось
Сессия состоит из трех экзаменов. Вероятность того, что студент сдаст первый экзамен, равна 0,9, вероятность сдачи второго — 0,9, а третьего – 0,7. Найти вероятности событий:
А – студент сдаст все три экзамена;
В – студент сдаст не менее двух экзаменов.
Решение:
Пусть событие D – студент сдает первый экзамен, событие Е — сдаст второй экзамен, событие С – сдаст третий, событие F – сдаст два экзамена.
1) Событие А – студент сдаст все три экзамена;
Р(А)= Р(D)•Р(Е)•Р(С) = 0,9•0,9•0,7= 0,567
2) В – студент сдаст не менее двух экзаменов.
Событие F = D•Е• 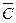
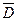

Найдем вероятность сдачи только двух экзаменов
Р(F)=Р(DЕ 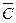
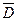

Тогда вероятность сдать не менее двух экзаменов найдем по формуле Р(В)=Р(А) + Р(F)= 0,567+0,369=0,936
Ответ: 1) 0,567; 2) 0,936.
|
Кардиналистский и ординалистский подходы Кардиналистский (количественный подход) к анализу полезности основан на представлении о возможности измерения различных благ в условных единицах полезности… |
Обзор компонентов Multisim Компоненты – это основа любой схемы, это все элементы, из которых она состоит. Multisim оперирует с двумя категориями… |
Композиция из абстрактных геометрических фигур Данная композиция состоит из линий, штриховки, абстрактных геометрических форм… |
Важнейшие способы обработки и анализа рядов динамики Не во всех случаях эмпирические данные рядов динамики позволяют определить тенденцию изменения явления во времени… |