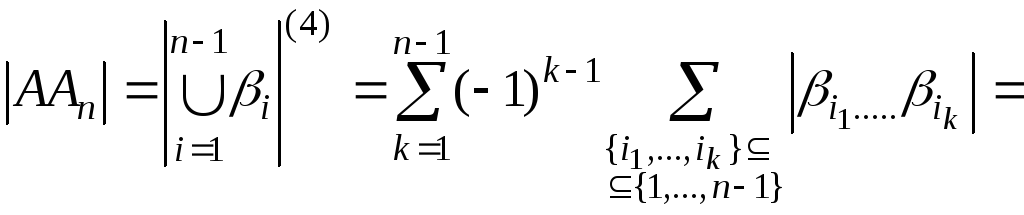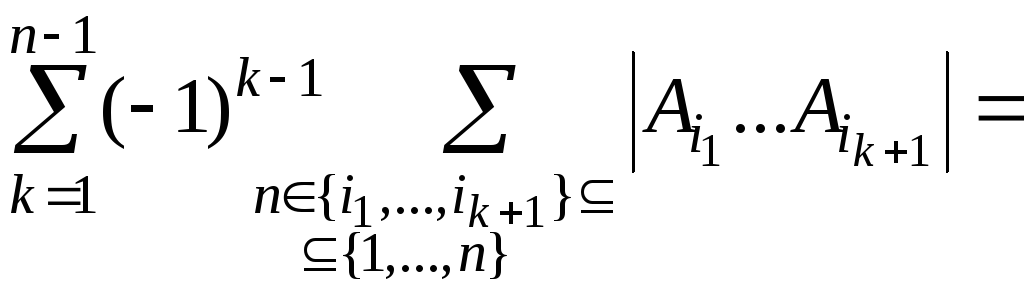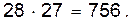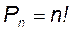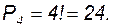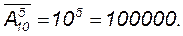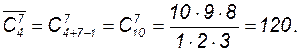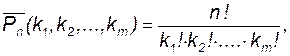Пусть
− число
всех
–сочетаний
с повторениями.
Теорема
9.
.
Доказательство. Пусть
,
–сочетание
с повторениями, в котором элемент
встречается
раз для
всех
,
причем
.
Сочетанию
поставим в соответствие двоичный набор,
в котором
единиц и
нулей, следующим образом:
.
Между множеством двоичных наборов с
единицами и k
нулями и множеством
–сочетаний
с повторениями существует взаимно-однозначное
соответствие. Отсюда получаем, что
Теорема доказана.
Задача
11. Сколькими
способами можно купить букет из 9 роз,
если в продаже имеются розы 3 цветов:
белые, розовые и красные.
Решение. Число
всех букетов совпадает с числом всех
сочетаний из трех элементов по 9 с
повторениями, тогда
§9. Формула включений и исключений
Пусть
заданы множества А
и В,
найдем число элементов в
.
Если
,
то
в силу следствия теоремы 7.
Если
,
построим диаграмму Венна 2-го порядка.
|
|
|
|
|
|
||
|
|
Рис.2
Множество
А
пометим горизонтальной штриховкой, а
В
– вертикальной, тогда в
входят все элементы универса, которые
находятся в заштрихованной области,
причем элементы множества
находятся в дважды заштрихованной
области, так как они входят и в множество
А,
и в множество
В.
Отсюда получаем, что
. (1)
Очевидно,
что формула (1) верна и в случае, если
.
Из
формулы (1) можно получить формулу для
мощности объединения трех множеств:
=.
Отсюда
получаем, что
. (2)
Аналогично
из формул (1) и (2) можно получить формулы
для мощности объединения четырех
множеств и т.д.
Теорема
10. 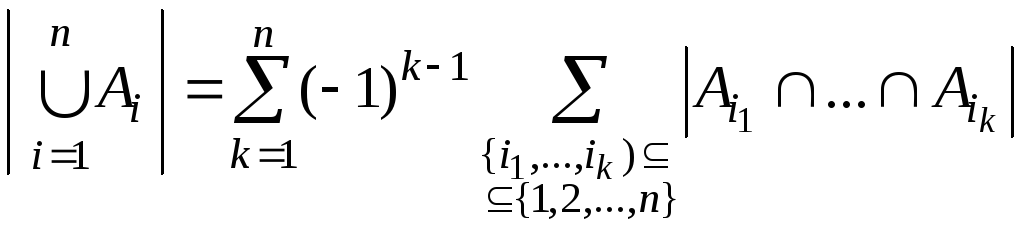
Доказательство. Утверждение
докажем индукцией по n.
Для
утверждение очевидно. Справедливость
теоремы для
вытекает согласно формуле (1).
Допустим,
что теорема выполнена для
множеств.
Пусть
.
Тогда
,
следовательно,
в силу формулы (1).
Согласно
предположению индукции,

(4)
Рассмотрим
.
Обозначим
через
,
тогда

Таким
образом, получаем, что
=
Теорема
доказана.
Задачи
-
Студенты
изучают 7 предметов. Сколькими способами
можно составить расписание на один
день, если в день следует устанавливать
не менее двух и не более четырех
предметов? -
Сколько
существует семизначных чисел, делящихся
на 5? Сколько среди них четных? -
Сколько
существует девятизначных чисел, которые
одинаково читаются как слева направо,
так и справа налево? Сколько среди них
четных? -
В
скольких точках пересекаются диагонали
выпуклого n-угольника,
если никакие три из них не пересекаются
в одной точке? -
В
комнате n
лампочек. Сколькими способами можно
зажечь k
лампочек?
Сколько существует способов освещения
комнаты? -
Сколько
существует пятизначных чисел, у которых
каждая следующая цифра больше предыдущей? -
Сколько
существует шестизначных чисел, у которых
цифры расположены в неубывающем порядке? -
Имеется
n
черных и m
белых шаров.
Сколькими способами можно их выложить
в ряд так, чтобы никакие два черных шара
не лежали рядом? -
Студенту
необходимо сдать 4 экзамена в течение
10 дней, причем известно, что в последний
день он сдает экзамен. Сколькими
способами он может это сделать? -
Сколькими
способами можно рассадить n
гостей за круглым столом? -
Имеется
4 типа открыток. Сколькими способами
можно выбрать 10 открыток? -
Сколькими
способами n
различных (одинаковых) предметов можно
разложить в k
одинаковых ящиков (разных ящиков)? -
Сколько
существует чисел не больше 100, которые
не делятся ни на 2, ни на 3, ни на 5? -
На
полке стоят n
книг. Сколькими способами можно взять
из них m
так, чтобы никакие две не стояли рядом? -
Сколькими
способами можно выбрать три различных
карандаша из имеющихся пяти карандашей
разных цветов? -
В
группе 5 девочек и 7 мальчиков. Сколькими
способами их можно разделить на 2 группы
по 6 человек? Сколькими способами это
можно сделать при условии, что в каждой
группе должно быть хотя бы по одной
девочке? -
Сколькими
способами можно рассадить за круглым
столом m
юношей и n
девушек так, чтобы никакие две девушки
не сидели рядом? -
Имеется
n
абонентов телефонной сети. Сколькими
способами можно одновременно соединить
три пары? -
Три
студента сдают экзамен. Сколькими
способами они могут сдать экзамен по
пятибалльной системе? По семибалльной? -
Сколько
различных слов можно составить из букв
слова «комбинаторика»? -
Сколькими
способами 12 одинаковых монет можно
разложить по пяти пакетам так, чтобы
ни один из пакетов не был пуст? -
В
конструкторском бюро все сотрудники
знают хотя бы один из трех языков.
Шестеро знают английский, шестеро –
немецкий, семеро – французский. Четверо
знают английский и немецкий, трое –
немецкий и французский, двое – французский
и английский. Один сотрудник знает все
три языка.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Размещения
Пример. Студенту необходимо сдать 4 экзамена за 8 дней.
Сколькими способами это можно сделать?
Решение. Искомое число способов равно числу 4–элементных
упорядоченных подмножеств из 8 элементов, т.е.
=8•7•6•5=1680
способов.
Если известно, что последний экзамен будет сдаваться на
восьмой день, то число способов равно
4•=7•6•5•4=840.
Элементы комбинаторики
Комбинаторика – это раздел математики, посвященный решению задач выбора и расположения элементов некоторого конечного множества в соответствии с заданными свойствами.
В решении комбинаторных задач применяются основные перечислительные правила: правило умножения и правило сложения.
Правило умножения. Пусть требуется выполнить одно за другим (последовательно) k действий. Если первое действие можно выполнить n1 способами, второе n2 способами, и так далее до k -го действия, которое можно выполнить nk способами, то все k действий можно выполнить n1 ∙ n2 ∙… ∙ nk способами.
Правило сложения. Если элемент А может быть выбран m способами, а элемент В – n способами, то выбрать либо А, либо В можно m + n способами.
Пример 1. В группе 28 человек. Необходимо выбрать старосту и профорга. Сколькими способами это можно сделать?
Решение. Старостой может быть выбран любой из 28 студентов, т. е. существует 28 способов выбора старосты. Профоргом можно выбрать любого из оставшихся 27 студентов, так как один уже выбран старостой. Тогда общее число способов выбора старосты и профорга равно
Пример 2. Имеется 16 изделий 1-го сорта и 25 изделий 2-го сорта. Необходимо выбрать два изделия одного сорта. Сколько способов выбора двух изделий возможно в данной ситуации?
Решение. По правилу умножения два изделия 1-го сорта можно выбрать 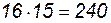
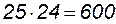
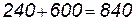
Существуют две схемы выбора m элементов из заданного множества: без возвращения и с возвращением.
Схемы выбора без возвращения предполагают, что выбранные элементы не возвращаются в исходное множество.
Размещениями из n элементов по m (0 ≤ m ≤ n) называются соединения по m элементов, которые отличаются друг от друга либо хотя бы одним элементом, либо порядком их расположения.
Число размещений обозначается символом 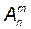
Замечание: символ 

Пример 3. Студенту необходимо сдать четыре экзамена на протяжении восьми дней. Сколькими способами это можно сделать, если деканатом запрещено сдавать более одного экзамена в день?
Решение. Искомое число способов равно
В частном случае, когда выбираются все элементы, т. е. m = n, размещения называются перестановками.
Перестановками из n элементов называются соединения, содержащие все n элементов и отличающиеся друг от друга порядком следования элементов.
Число перестановок обозначается символом 
Пример 4. Сколькими способами можно составить четырехцветный флаг из горизонтальных полос, имея четыре различных цвета?
Решение. В данном случае различные флаги отличаются друг от друга лишь порядком цветов. Число возможных флагов равно
Сочетаниями из n элементов по m называются соединения по m элементов, отличающиеся друг от друга хотя бы одним элементом.
Число сочетаний из n элементов по m обозначается 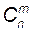
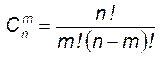
Для чисел 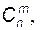
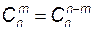

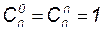
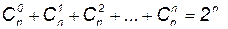
Пример 5. Акционерное собрание компании выбирает из 50 человек президента компании, председателя совета директоров и 10 членов совета директоров. Сколькими способами это можно сделать?
Решение. Президента компании можно выбрать 50 способами из 50 человек, тогда председателя компании 49 способами, а остальных членов совета директоров 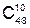

Схемы выбора с возвращением означают, что выбранные элементы возвращаются в исходное множество.
Размещения с повторениями. Если в размещении каждый отобранный элемент перед отбором следующего возвращается обратно, то в этом случае рассматриваются размещения с повторениями.
Число размещений с повторениями обозначается 
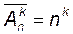
где черта указывает на возможность повторения элементов.
Пример 6. В конкурсе по 5 номинациям участвуют 10 кинофильмов. Сколько существует способов распределения призов, если по каждой номинации установлены различные премии?
Решение. Каждый из вариантов распределения призов представляет собой комбинацию 5 фильмов из 10, отличающуюся от других комбинаций как составом, так и порядком. Поскольку каждый фильм может получить призы как по одной, так и по нескольким номинациям, одни и те же фильмы могут повторяться. Число таких комбинаций равно
Сочетания с повторениями. Если в сочетаниях из n по k некоторые из элементов или все могут оказаться одинаковыми, то такие сочетания называются сочетаниями с повторениями из n по k.Число сочетаний с повторениями обозначается 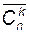
Пример 7. Сколько наборов из 7 пирожных можно составить, если в продаже имеются 4 сорта?
Решение. Искомое число равно
Перестановки с повторениями. Если множество из n различных элементов разбивается на k групп так, что в первую группу попадают k1 элементов,во вторую – k2 элементов, в k-ю группу – km элементов, то число таких разбиений равно
где 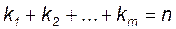
Пример 8. Наташа получила в подарок 10 просверленных шариков из оргстекла: пять белых, два красных и три голубых. Она продела в них нитку и надела ее как ожерелье на шею. Потом стала менять порядок расположения шариков, и каждый день ожерелье принимало другой вид. Сколько разных видов ожерелья может получить Наташа?
Решение. Имеем перестановки с повторениями:
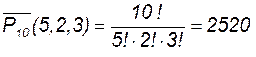
Замечание. Изменение расположения элементов, не меняющее порядка их следования (первый элемент «следует» за последним), называют циклической перестановкой. Если в примере 8 учесть, что ожерелье замкнуто, т. е. последний шарик примыкает к первому, тогда расположение первого элемента не имеет значения. В этом случае окажется, что возможны только 252 различных вида.
Пример 9. Сколько существует семизначных чисел, состоящих из цифр 4, 5 и 6, в которых цифра 4 повторяется три раза, а цифры 5 и 6 – по два раза?
Решение. Каждое семизначное число отличается от другого порядком следования цифр, при этом фактически все семь мест в этом числе делятся на три группы: на одни места ставится цифра 4, на другие – цифра 5, на третьи места – цифра 6. Таким образом, в нашем случае множество состоит из семи элементов и число таких чисел равно
Запишем основные формулы комбинаторики в табл. 1.1.
Таблица 1.1
Формулы комбинаторики
| Без повторений | С повторениями | |
| Сочетания | 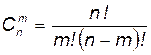
|
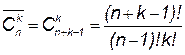
|
| Размещения | 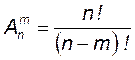
|

|
| Перестановки | 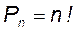
|
 
|
|
Расчетные и графические задания Равновесный объем — это объем, определяемый равенством спроса и предложения… |
Кардиналистский и ординалистский подходы Кардиналистский (количественный подход) к анализу полезности основан на представлении о возможности измерения различных благ в условных единицах полезности… |
Обзор компонентов Multisim Компоненты – это основа любой схемы, это все элементы, из которых она состоит. Multisim оперирует с двумя категориями… |
Композиция из абстрактных геометрических фигур Данная композиция состоит из линий, штриховки, абстрактных геометрических форм… |