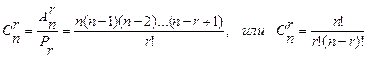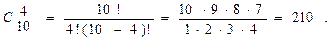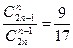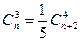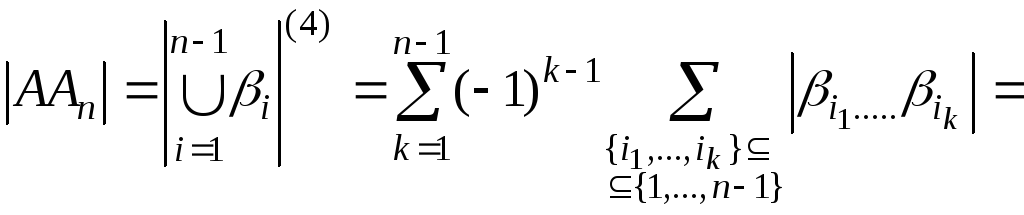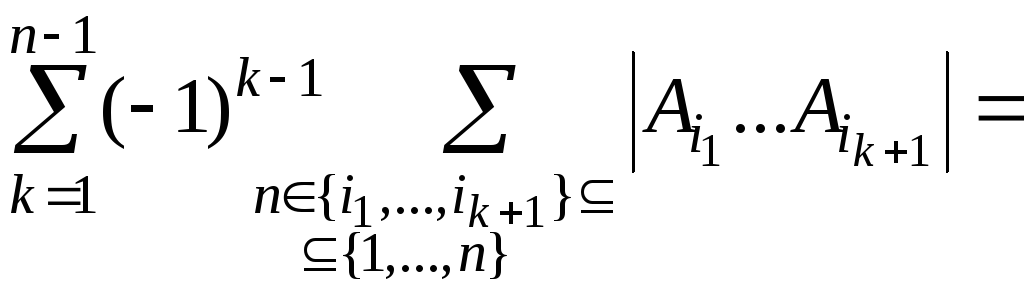Студенту необходимо сдать 4 экзамена за 10 дней сколькими способами ему можно составить расписание

Содержание

06. Размещения
Студенту необходимо сдать 4 экзамена за 10 дней сколькими способами ему можно составить расписание
Сочетания (неупорядоченные выборки)
Методические указания и контрольные задания для студентов-заочников специальности «Государственное и муниципальное управление» Братск, 2015
Главная > Методические указания
Решение типового варианта
Задание 1
Задание 2
Задание 3
Задание 4

06. Размещения

Пусть имеется некоторое множество, содержащее n элементов. Выберем из этого множества k элементов без возвращения, но упорядочивая их по мере их выбора в последовательную цепочку. Такие цепочки называются размещениями.

Размещениями из n элементов по k элементов называются такие комбинации, из которых каждое содержит k элементов, взятых из числа данных n элементов, и которые отличаются друг от друга либо самими элементами (хотя бы одного), либо порядком их расположения.

Поясним это на следующем примере. Пусть имеется три элемента: a, b и c. Тогда из этих трёх элементов можно составить шесть размещений по два элемента: ab, ac, ba, bc, ca, cb. Все приведённые размещения отличаются друг от друга хотя бы одним элементом или порядком их расположения.

Число размещений (читается: число размещений из n элементов по k элементов) можно найти из принципа умножения. Первый элемент размещения можно выбрать n способами. Как только такой выбор будет сделан, останется (n–1) возможностей, чтобы выбрать второй элемент; после этого останется (n–2) возможностей для выбора третьего элемента и т. д.; для выбора k-го элемента будет (n–k+1) возможностей. По принципу умножения находим

. (4.1)

Легко понять, что .

Пример 4.1. В некоторой газете 12 страниц. Необходимо на страницах этой газеты поместить 4 различных фотографии. Сколькими способами это можно сделать, если ни одна страница газеты не должна содержать более одной фотографии?

Решение. Для размещения фотографий следует отобрать 4 различных страницы из 12 имеющихся. Затем нужно отобранные страницы упорядочить, т. е. определить, на какую страницу поместить первую фотографию, на какую – вторую и т. д. Полученная упорядоченная совокупность страниц является, согласно определению, размещением из 12 элементов по 4, а число таких размещений является искомым результатом:

Пример 4.2. Сколькими способами можно составить трехцветный полосатый флаг, если имеются ткани пяти различных цветов? Решите эту же задачу при условии, что одна полоса должна быть красной.

Решение. Поскольку в данной задаче важен порядок следования полос и все цвета во флаге должны быть разными, то исходная задача сводится к подсчету числа размещений из 5 по 3:

способов.

При условии, что одна полоса должна быть красной, получаем, что для выбора места для красной полосы существует 3 способа, а для оставшихся двух полос останется способов. Таким образом, трехцветный полосатый флаг из имеющихся 5 цветов при условии, что один цвет должен быть красным можно составить

способами.

Пример 4.3. Сколькими способами 10 человек можно поставить парами в ряд?

Решение. Первую пару можно выбрать способами, вторую – способами, и т. д. В результате получаем

способами.

4.1. Научное общество состоит из 25 человек. Надо выбрать президента общества, вице-президента, ученого секретаря и казначея. Сколькими способами может быть сделан этот выбор, если каждый член общества может занимать лишь один пост?

Ответ: В этом случае надо число размещений из 25 элементов по 4. Здесь играет роль и то, кто будет выбран в руководство общества, и то, какие посты займут выбранные. Поэтому ответ дается формулой .

4.2. В цехе работают 8 токарей. Сколькими способами можно поручить трем из них изготовление различных видов деталей (по одному виду на каждого).

Ответ: .

4.3. Из 10 книг выбирают 4 для рассылки по разным адресам. Сколькими способами это можно сделать?

Ответ: .

4.4. Сколькими способами можно опустить 5 писем в 11 почтовых ящиков, если в каждый ящик опускают не более одного письма?

Ответ: .

4.5. Студенту необходимо сдать 5 экзаменов в течение 12 дней. Сколькими способами можно составить расписание экзаменов, если в течение дня он может сдать не более одного экзамена?

Ответ: .

4.6. Сколькими способами можно преподнести 4 различных подарка 6 ученикам таким образом, чтобы каждый ученик получил не более одного подарка?

Ответ: .

4.7. Сколько различных четырехзначных чисел можно составить из цифр 0, 1, 2, …, 9, если каждая цифра в обозначении числа встречается не более одного раза? (Учесть, что число не может начинаться с нуля.)

Ответ: .

Источник

пЮЕОШ ЮБУФП Ч ТЕБМШОПК ЦЙЪОЙ чБН РТЙИПДЙФУС ТЕЫБФШ РТПВМЕНЩ УМЕДХАЭЕЗП ФЙРБ: ЛБЛ ЙЪ НОПЦЕУФЧБ, УПУФПСЭЕЗП ЙЪ n ЬМЕНЕОФПЧ, ЧЩВТБФШ ХРПТСДПЮЕООПЕ РПДНОПЦЕУФЧП ЙЪ m ЬМЕНЕОФПЧ. оБРТЙНЕТ, ЛБЛ ТБУУБДЙФШ ЪБ РТБЪДОЙЮОЩН УФПМПН 12 ЗПУФЕК, ЕУМЙ ЧУЕЗП 15 НЕУФ ?

пртедемеойе 1.3.1
хРПТСДПЮЕООПЕ m — ЬМЕНЕОФОПЕ РПДНОПЦЕУФЧП НОПЦЕУФЧБ ЙЪ n ЬМЕНЕОФПЧ ОБЪЩЧБЕФУС тбънеэеойен ЙЪ n ЬМЕНЕОФПЧ РП m.

фептенб 1.3.1
юЙУМП ТБЪНЕЭЕОЙК НОПЦЕУФЧБ ЙЪ n ЬМЕНЕОФПЧ РП m ТБЧОП

1-К ЬМЕНЕОФ НПЦОП ЧЩВТБФШ n УРПУПВБНЙ,

2-К — (n — 1) УРПУПВПН,

m-К — (n — (m — 1)) УРПУПВБНЙ.

уМЕДПЧБФЕМШОП, ПВЭЕЕ ЮЙУМП УРПУПВПЧ ЧЩВТБФШ ХРПТСДПЮЕООПЕ РПДНОПЦЕУФЧП ВХДЕФ ТБЧОП n (n — 1) . (n — (m — 1)).

хНОПЦЙН Й ТБЪДЕМЙН ДБООПЕ ЧЩТБЦЕОЙЕ ОБ (n — m)!:

пвпъобюеойе:

уЙНЧПМ ФБЛ Й ЮЙФБЕФУС: «юЙУМП ТБЪНЕЭЕОЙК ЙЪ n РП m».

умедуфчйе 1.3.1
m ТБЪМЙЮОЩИ РТЕДНЕФПЧ РП n НЕУФБН НПЦОП ТБУУФБЧЙФШ УРПУПВБНЙ.

ч ЮБУФОПУФЙ, РТЙЗМБЫЕООЩИ чБНЙ ЗПУФЕК НПЦОП ТБУУБДЙФШ УРПУПВБНЙ.

ъбдбюб 1.3.1 уФХДЕОФХ ОЕПВИПДЙНП УДБФШ 4 ЬЛЪБНЕОБ Ч ФЕЮЕОЙЕ 10 ДОЕК. уЛПМШЛЙНЙ УРПУПВБНЙ НПЦОП УПУФБЧЙФШ ЕНХ ТБУРЙУБОЙЕ ЬЛЪБНЕОПЧ? (рТЕДРПМБЗБЕФУС, ЮФП Ч ДЕОШ УДБЕФУС ФПМШЛП ПДЙО ЬЛЪБНЕО.)

тЕЫЕОЙЕ ДБООПК ЪБДБЮЙ УЧПДЙФУС Л ПРТЕДЕМЕОЙА ЮЙУМБ УРПУПВПЧ ТБУУФБОПЧЛЙ 4-И ТБЪМЙЮОЩИ РТЕДНЕФПЧ РП 10 НЕУФБН. уМЕДПЧБФЕМШОП, ЮЙУМП УРПУПВПЧ УПУФБЧЙФШ ДБООПЕ ТБУРЙУБОЙЕ ТБЧОП:

ъбдбюб 1.3.2 уЛПМШЛП УМПЧ НПЦОП ПВТБЪПЧБФШ ЙЪ ВХЛЧ УМПЧБ жтбзнеоф, ЕУМЙ УМПЧБ ДПМЦОЩ УПУФПСФШ: Б) ЙЪ 8 ВХЛЧ; В) ЙЪ 7 ВХЛЧ; Ч) ЙЪ 3 ВХЛЧ? (нБФЕНБФЙЛБ РПД УМПЧПН РПОЙНБЕФ РТПЙЪЧПМШОЩК ОБВПТ ВХЛЧ).

Б) n = 8, m = 8. юЙУМП УРПУПВПЧ ТБЧОП = 8!.

В) n = 8, m = 7. юЙУМП УРПУПВПЧ ТБЧОП = 8!.

Ч) n = 8, m = 3. юЙУМП УРПУПВПЧ ТБЧОП = 336.

ъбдбюб 1.3.3 дЕУСФШ ЛТЕУЕМ РПУФБЧМЕОЩ Ч ТСД. уЛПМШЛЙНЙ УРПУПВБНЙ 2 ЮЕМПЧЕЛБ НПЗХФ: Б) УЕУФШ ОБ ОЙИ; В) УЕУФШ ТСДПН; Ч) УЕУФШ ФБЛ, ЮФПВЩ НЕЦДХ ОЙНЙ ВЩМП, РП ЛТБКОЕК НЕТЕ, ПДОП РХУФПЕ ЛТЕУМП?

Б) n = 10, m = 2. юЙУМП УРПУПВПЧ = 90.

В) пВПЪОБЮЙН ЬФЙИ ДЧХИ ЮЕМПЧЕЛ ХУМПЧОП и Й х.

ъБНЕФЙН, ЮФП ЮЙУМП УРПУПВПЧ ТБУУБДЙФШ ЙИ ФБЛ, ЮФПВЩ ПОЙ УЙДЕМЙ ТСДПН Й и ВЩМ УРТБЧБ ПФ х, ТБЧОП 9. бОБМПЗЙЮОП, ЮЙУМП УРПУПВПЧ ТБУУБДЙФШ ЙИ ФБЛ, ЮФПВЩ, и ВЩМ УМЕЧБ ПФ х, Й ПОЙ УЙДЕМЙ ТСДПН, ФПЦЕ — 9. (ч ЛБЦДПН ЙЪ ЬФЙИ УМХЮБЕЧ НЩ ЧЩВЙТБЕН НЕУФП ФПМШЛП ДМС и.) уМЕДПЧБФЕМШОП, ПВЭЕЕ ЮЙУМП УРПУПВПЧ: 9 + 9 = 18.

Ч) дМС РПМХЮЕОЙС ПФЧЕФБ ОБ РПУФБЧМЕООЩК ЧПРТПУ, ДПУФБФПЮОП ЧПУРПМШЪПЧБФШУС ТЕЪХМШФБФБНЙ, РПМХЮЕООЩНЙ Ч РХОЛФБИ Б) Й В). фП ЕУФШ, ЙЪ ПВЭЕЗП ЮЙУМБ УРПУПВПЧ ТБУУБДЙФШ 2-И ЮЕМПЧЕЛ РП 10 ЛТЕУМБН ЧЩЮЕУФШ ЮЙУМП УРПУПВПЧ ТБУУБДЙФШ ЙИ ФБЛ, ЮФПВЩ ПОЙ УЙДЕМЙ ТСДПН: 90 — 18 = 72.

ъБДБЮЙ ДМС УБНПУФПСФЕМШОПЗП ТЕЫЕОЙС.

ъбдбюб 1.3.1(у) чПУЕНШ НБМШЮЙЛПЧ ЧПДСФ ИПТПЧПД. ъБФЕН Л ОЙН РТЙУПЕДЙОСАФУС ЕЭЕ РСФШ ДЕЧПЮЕЛ. уЛПМШЛЙНЙ УРПУПВБНЙ ДЕЧПЮЛЙ НПЗХФ ЧУФБФШ Ч ЛПМШГП, ЕУМЙ ОЙЛБЛЙЕ ДЧЕ ДЕЧПЮЛЙ ОЕ ДПМЦОЩ УФПСФШ ТСДПН?

ъбдбюб 1.3.2(у) уЛПМШЛП ЮЕФЩТЕИЪОБЮОЩИ ЮЙУЕМ НПЦОП УПУФБЧЙФШ, ЙУРПМШЪХС ГЙЖТЩ 1, 2, 3, 4, 5; ЕУМЙ ЮЙУМБ ДПМЦОЩ ВЩФШ ОЕЮЕФОЩЕ Й РПЧФПТЕОЙК ГЙЖТ ВЩФШ ОЕ ДПМЦОП?

ъбдбюб 1.3.3(у) дПЛБЪБФШ, ЮФП ЮЙУМП ФТЕИВХЛЧЕООЩИ УМПЧ, ЛПФПТЩЕ НПЦОП ПВТБЪПЧБФШ ЙЪ ВХЛЧ, УПУФБЧМСАЭЙИ УМПЧП зйрпфеохъб, ТБЧОП ЮЙУМХ ЧУЕИ ЧПЪНПЦОЩИ РЕТЕУФБОПЧПЛ ВХЛЧ, УПУФБЧМСАЭЙИ УМПЧП ртйънб.

Источник

Сочетания (неупорядоченные выборки)

Определение: Неупорядоченные наборы, состоящие из r элементов множества А, называются сочетаниями из n элементов по r элементов. (r 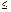n).

Пример: Студенту необходимо сдать 4 экзамена за 10 дней. Сколькими способами можно составить ему расписание, если в один день нельзя сдать более одного экзамена?

Решение: А = <1, 2, 3, 4, 5, 6, 7, 8, 9, 10>(10 дней). Поскольку в расписании учитывается порядок экзаменов, то мы имеем дело с упорядоченными выборками, т.е. с размещениями.

Пример: Подрядчику нужны 4 плотника, к нему с предложениями своих услуг обратилось 10 человек. Сколькими способами можно набрать рабочую силу?

Пример. В розыгрыше первенства по футболу участвуют 10 команд. Известно, что те, кто займет первые 3 места, получают золотую, серебряную и бронзовую медали, а последние двое выбывают. Сколько различных результатов первенства может быть?

Решение: Нужно выполнить одно за другими два действия:

I. Из десяти команд выбрать три на три первых места.

II. После выполнения первого действия из оставшихся семи команд выбрать две на два последних места.

Итак, по принципу умножения r = 2 ;

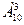
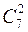
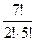
n₁= =1098=720; n₂= = =21.

Различных результатов первенства может быть:

Варианты заданий

Решить комбинаторные уравнения

Самостоятельная работа №2 Расчет количества выборок заданного типа в заданных условиях

Источник

Методические указания и контрольные задания для студентов-заочников специальности «Государственное и муниципальное управление» Братск, 2015

Главная > Методические указания

Информация о документе
Дата добавления:
Размер:
Доступные форматы для скачивания:

Решение типового варианта

Задание 1

Студенту необходимо сдать 5 экзаменов в течение 13 дней. Сколькими способами можно составить расписание?

Например, студенту нужно сдать математику (М), историю (И), философию (Ф), английский язык (А) и экономику (Э). Для этого нужно выбрать 6 дней. Допустим, это 1-й, 3-й, 8-й, 10-й и 12-й дни.

Можно получить следующие расписания:

3 10 12 1 8 и т.д.

Дни выбраны одни и те же, но расписание разное. Значит, надо воспользоваться формулой из комбинаторики:

— это число способов, с помощью которых можно выбрать k различных элементов из имеющихся n элементов с учетом порядка выборки.

В нашем случае, n = 13, k =5. Получим:

Можно составить 154440 различных вариантов сдачи экзаменов.

В конкурсе участвует 6 команд. В финал пройдут только три команды. Сколько различных составов финалистов может быть?

Например, в финал сначала прошла 2-команда, потом 6-я и затем 1-я. Или сначала могла пройти 6-я, потом 1-я и затем 2-я. Состав финалистов при этом остался прежним, поэтому воспользуемся формулой:

— это число способов, с помощью которых можно выбрать k различных элементов из имеющихся n элементов без учета порядка выборки.

В нашем случае, n = 3, k =3. Получим:

Можно получить 20 различных составов финалистов.

Чтобы открыть кодовый замок, необходимо набрать комбинацию из цифр 1, 2, 5, 7, 8, 0. Известно, что все цифры в ней различны. Сколько различных вариантов комбинаций существует?

Решение

Например, кодовый замок можно открыть при помощи комбинации 521780. Или это может быть комбинация 018257 и т.д. То есть нужно местами между собой имеющиеся 6 цифр.

Найти число комбинаций можно при помощи формулы:

— это число способов, с помощью которых можно выбрать n различных элементов из имеющихся n элементов с учетом порядка выборки.

В нашем случае имеется 6 цифр, то есть n =6. Получим: .

Чтобы открыть замок, необходимо перебрать максимум 720 комбинаций.

Задание 2

Три стрелка, попадающие в цель независимо друг от друга с вероятностями 0.6, 0.9, и 0.3 соответственно, выстрелили по мишени одновременно. Какова вероятность того, что:

а) в мишени нет пробоин;

б) в мишени будет одна пробоина;

в) в мишени будет две пробоины;

г) в мишени будет три пробоины;

д) в мишени будет хотя бы одна пробоина;

е) в мишени будет не менее двух пробоин?

а) Нас интересует вероятность события А=<в мишени нет пробоин>. Это событие возможно, когда все три стрелка промахнулись.

Сформулируем события А 1 =<первый стрелок попал в мишень>, А 2 = <второй стрелок попал в мишень>и А 3 =<третий стрелок попал в мишень>. Так как стрелки должны промахнуться, то получим события:

= <первый стрелок промахнулся>, = <второй стрелок промахнулся>и =

Они должны выполняться одновременно, т.е. .

Тогда вероятность события А найдем по формуле:

Если первый стрелок попадает в мишень с вероятностью 0,6, то промахивается он с вероятностью= 1-0,6= 0,4. Аналогично, = 0,1 и = 0,7. Отсюда

б) Нас интересует вероятность события А=<в мишени будет одна пробоина>. Это возможно, когда в мишень попал только один из стрелков, а два других промахнулись. Попасть в мишень может или первый (тогда второй и третий должны промахнуться), или второй (тогда первый и третий промахиваются), или третий стрелок (тогда первый и второй промахиваются), т.е.

Тогда вероятность события А найдем по формуле:

в) Нас интересует вероятность события А=<в мишени будет две пробоины>. Это возможно, когда в мишень попали только два стрелка, а один промахнулся. Попасть в мишень могут или первый и второй (тогда третий должен промахнуться), или второй и третий (тогда первый промахивается), или первый и третий стрелок (тогда второй промахивается), т.е.

Тогда вероятность события А найдем по формуле:

г) Нас интересует вероятность события А=<в мишени три пробоины>. Это событие возможно, когда все три стрелка попадают в мишень, т.е.

Тогда вероятность события А найдем по формуле:

д) Нас интересует вероятность события А=<в мишени хотя бы одна пробоина>. Это событие заключается в том, что в мишени или одна, или две, или три пробоины. Вероятности этих событий мы нашли выше. Так как они несовместны (в мишени не может быть одновременно и одна, и две, и три пробоины), то вероятность события А равна:

Эту же задачу можно решить другим способом. Сформулируем противоположное событие = <в мишени ни одной пробоины>. Вероятность этого события равна (из пункта а). Тогда вероятность события А равна:

е) Нас интересует вероятность события А=<в мишени не менее двух пробоин>. Значит, в мишени или две, или три пробоины. Тогда вероятность события А равна:

Задание 3

Имеются четыре одинаковые по виду коробки. В первой коробке 12 белых и 4 черных шаров, во второй – 10 белых и 6 черных шаров, в третьей – 15 белых и 1 черный, в четвертой – 8 белых и 8 черных. Наугад выбирают одну коробку и достают из нее один шар. Какова вероятность, что он белый?

Тогда вероятность события А можем найти по формуле полной вероятности:

Здесь — вероятность выполнения i -ой гипотезы, а — вероятность появления события А при выполнении i -ой гипотезы.

Из условия задачи:

, , и (вероятности выбора какой-либо коробки равны, так как коробки одинаковы);

(в первой коробке всего 16 шаров, из них удачных для нас, т.е. белых, 12). Аналогично, , и .

Задание 4

По мишени производится 6 независимых выстрелов. Вероятность попадания при каждом выстреле равна 0,6. Определите вероятность того, что будет:

а) одно попадание;

б) три попадания;

в) хотя бы одно попадание;

г) не более трех попаданий.

а) Необходимо определить вероятность события А=<одно попадание в мишень>. Это может быть попадание или первым выстрелом (тогда остальные дают промахи), или вторым (тогда при 1-ом, 3-ем, 4-ом, 5-ом и 6-ом выстреле будут промахи) и т.д. Событие достаточно сложное, и так как вероятность успеха (попадания), всегда одинаковая, то воспользуемся формулой Бернулли:

С ее помощью можно вычислить вероятность появления k успехов в n испытаниях при вероятности успеха p и вероятности неудачи q =1- p .

б) Необходимо определить вероятность события А=<три попадания в мишень>. Это могут быть первые три попадания и остальные промахи, или сначала три промаха, потом три попадания и т.д. Событие достаточно сложное, и так как вероятность успеха (попадания), всегда одинаковая, то по формуле Бернулли получим

в) Необходимо определить вероятность события А=<хотя бы одно попадание в мишень>. Это или одно попадание, или два, или три и т.д. Событие сложное, поэтому сформулируем противоположное событие =<в мишень ни разу не попали>. По схеме Бернулли вычислим вероятность появления 0 успехов:

Тогда вероятность события А равна:

г) Необходимо определить вероятность события А=<не более трех попаданий в мишень>. Это могут быть три, два, одно или ни одного попадания в мишень.

Тогда вероятность события А равна:

Вероятность рождения мальчика равна 0,505. Найдите наивероятнейшее число девочек из 100 новорожденных.

Наивероятнейшее число – это число появлений некоторого события (число успехов), которому соответствует наибольшая вероятность. Чтобы не вычислять вероятность вероятности появления одной, двух и т.д. девочек, воспользуемся формулой:

n – общее число опытов;

p – вероятность появления события (успеха);

q – вероятность неудачи;

k 0 – наивероятнейшее число успехов.

Подставим числовые данные и получим:

Отсюда, . Так как k 0 – число целое, то оно равно 49. Вероятнее всего появится 49 девочек из 100 новорожденных.

При стрельбе по мишени вероятность попадания при одном выстреле равна 0,6. При каком числе выстрелов наивероятнейшее число попаданий равно 20?

Наивероятнейшее число – это число появлений некоторого события (число успехов), которому соответствует наибольшая вероятность. Найти его можно по формуле . В данной задаче значение k 0 нам уже известно, оно равно 20. Необходимо найти общее число испытаний. Подставим известные нам данные и получим систему из двух неравенств:

или , или .

Этой системе неравенств удовлетворяют два значения n : 33 и 34.

Источник

Пусть

− число
всех
–сочетаний
с повторениями.

Теорема
9.
.

Доказательство. Пусть
,

–сочетание
с повторениями, в котором элемент

встречается
раз для
всех
,
причем
.
Сочетанию

поставим в соответствие двоичный набор,
в котором

единиц и

нулей, следующим образом:
.
Между множеством двоичных наборов с

единицами и k
нулями и множеством
–сочетаний
с повторениями существует взаимно-однозначное
соответствие. Отсюда получаем, что

Теорема доказана.

Задача
11. Сколькими
способами можно купить букет из 9 роз,
если в продаже имеются розы 3 цветов:
белые, розовые и красные.

Решение. Число
всех букетов совпадает с числом всех
сочетаний из трех элементов по 9 с
повторениями, тогда

§9. Формула включений и исключений

Пусть
заданы множества А
и В,
найдем число элементов в
.
Если
,
то

в силу следствия теоремы 7.

Если
,
построим диаграмму Венна 2-го порядка.

Рис.2

Множество
А
пометим горизонтальной штриховкой, а
В
– вертикальной, тогда в

входят все элементы универса, которые
находятся в заштрихованной области,
причем элементы множества

находятся в дважды заштрихованной
области, так как они входят и в множество
А,
и в множество
В.
Отсюда получаем, что
. (1)

Очевидно,
что формула (1) верна и в случае, если
.

Из
формулы (1) можно получить формулу для
мощности объединения трех множеств:

Отсюда
получаем, что

. (2)

Аналогично
из формул (1) и (2) можно получить формулы
для мощности объединения четырех
множеств и т.д.

Теорема
10. (3)

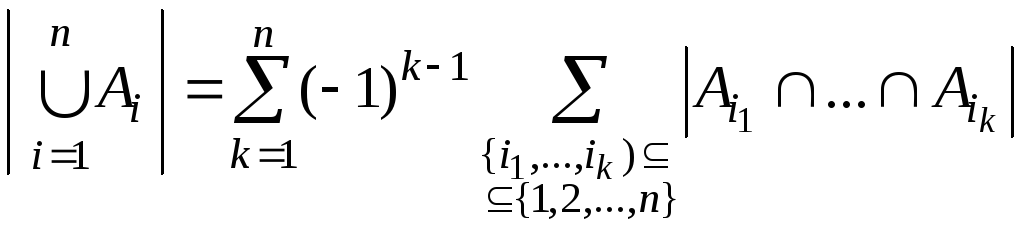
Доказательство. Утверждение
докажем индукцией по n.

Для

утверждение очевидно. Справедливость
теоремы для

вытекает согласно формуле (1).

Допустим,
что теорема выполнена для

множеств.

Пусть
.
Тогда
,
следовательно,

в силу формулы (1).

Согласно
предположению индукции,

.
(4)

Рассмотрим
.
Обозначим

через
,
тогда

Таким
образом, получаем, что
=

Теорема
доказана.

Задачи

Студенты
изучают 7 предметов. Сколькими способами
можно составить расписание на один
день, если в день следует устанавливать
не менее двух и не более четырех
предметов?
Сколько
существует семизначных чисел, делящихся
на 5? Сколько среди них четных?
Сколько
существует девятизначных чисел, которые
одинаково читаются как слева направо,
так и справа налево? Сколько среди них
четных?
В
скольких точках пересекаются диагонали
выпуклого n-угольника,
если никакие три из них не пересекаются
в одной точке?
В
комнате n
лампочек. Сколькими способами можно
зажечь k
лампочек?
Сколько существует способов освещения
комнаты?
Сколько
существует пятизначных чисел, у которых
каждая следующая цифра больше предыдущей?
Сколько
существует шестизначных чисел, у которых
цифры расположены в неубывающем порядке?
Имеется
n
черных и m
белых шаров.
Сколькими способами можно их выложить
в ряд так, чтобы никакие два черных шара
не лежали рядом?
Студенту
необходимо сдать 4 экзамена в течение
10 дней, причем известно, что в последний
день он сдает экзамен. Сколькими
способами он может это сделать?
Сколькими
способами можно рассадить n
гостей за круглым столом?
Имеется
4 типа открыток. Сколькими способами
можно выбрать 10 открыток?
Сколькими
способами n
различных (одинаковых) предметов можно
разложить в k
одинаковых ящиков (разных ящиков)?
Сколько
существует чисел не больше 100, которые
не делятся ни на 2, ни на 3, ни на 5?
На
полке стоят n
книг. Сколькими способами можно взять
из них m
так, чтобы никакие две не стояли рядом?
Сколькими
способами можно выбрать три различных
карандаша из имеющихся пяти карандашей
разных цветов?
В
группе 5 девочек и 7 мальчиков. Сколькими
способами их можно разделить на 2 группы
по 6 человек? Сколькими способами это
можно сделать при условии, что в каждой
группе должно быть хотя бы по одной
девочке?
Сколькими
способами можно рассадить за круглым
столом m
юношей и n
девушек так, чтобы никакие две девушки
не сидели рядом?
Имеется
n
абонентов телефонной сети. Сколькими
способами можно одновременно соединить
три пары?
Три
студента сдают экзамен. Сколькими
способами они могут сдать экзамен по
пятибалльной системе? По семибалльной?
Сколько
различных слов можно составить из букв
слова «комбинаторика»?
Сколькими
способами 12 одинаковых монет можно
разложить по пяти пакетам так, чтобы
ни один из пакетов не был пуст?
В
конструкторском бюро все сотрудники
знают хотя бы один из трех языков.
Шестеро знают английский, шестеро –
немецкий, семеро – французский. Четверо
знают английский и немецкий, трое –
немецкий и французский, двое – французский
и английский. Один сотрудник знает все
три языка.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

OBRAZOVALKA.COM

OBRAZOVALKA.COM — образовательный портал
Наш сайт это площадка для образовательных консультаций, вопросов и ответов для школьников и студентов .

Наша доска вопросов и ответов в первую очередь ориентирована на школьников и студентов из России и стран СНГ, а также носителей русского языка в других странах.

Для посетителей из стран СНГ есть возможно задать вопросы по таким предметам как Украинский язык, Белорусский язык, Казакхский язык, Узбекский язык, Кыргызский язык.

На вопросы могут отвечать также любые пользователи, в том числе и педагоги.

Консультацию по вопросам и домашним заданиям может получить любой школьник или студент.

Источник