Найди верный ответ на вопрос ✅ «Студент сдаёт в сессию три экзамена. Вероятность того, что студент сдаст на положительную оценку один (любой) экзамен равна 0,8. Тогда …» по предмету 📙 Математика, а если ответа нет или никто не дал верного ответа, то воспользуйся поиском и попробуй найти ответ среди похожих вопросов.
Искать другие ответы
Главная » ⭐️ Математика » Студент сдаёт в сессию три экзамена. Вероятность того, что студент сдаст на положительную оценку один (любой) экзамен равна 0,8. Тогда вероятность того, что студент сдаст на положительную оценку хотя бы один экзамен равна?
Закажите у меня новую работу, просто написав мне в чат!
Студент должен сдать в сессию три экзамена: по философии, по алгебре и по математическому анализу. Вероятности сдать каждую из этих дисциплин равны соответственно: 0.9; 0.7; 0.6. Какова вероятность того, что студент сдаст не менее двух экзаменов? а) 0.544 б) 0.834 в) 0.166 г) 0.456.
Обозначим события: 𝐴1 − студент сдал первый экзамен; 𝐴2 − студент сдал второй экзамен; 𝐴3 − студент сдал третий экзамен; 𝐴1 ̅̅̅ − студент не сдал первый экзамен; 𝐴2 ̅̅̅ − студент не сдал второй экзамен; 𝐴3 ̅̅̅ − студент не сдал третий экзамен. По условию вероятности этих событий равны: Тогда По формулам сложения и умножения вероятностей, вероятность события 𝐴 − студент сдаст не менее двух экзаменов (т.е. сдаст два или три), равна: Ответ: б) 0.834
1. Вероятность сдачи первого экзамена 0,6, тогда вероятность его не сдать 1 — 0,6 = 0,4.
Вероятность сдачи второго экзамена равна 0,8, а неуспеха 1 — 0,8 = 0,2.
Известно, что вероятность сдать третий экзамен составляет 0,7.
Тогда вероятность его не сдать 1 — 0,7 = 0,3.
2. Вычислим вероятность сдачи одного экзамена.
Это событие происходит в случае, когда один предмет сдан, а два других нет.
Р1 = 0,6 * 0,2 * 0,3 + 0,4 * 0,8 * 0,3 + 0,4 * 0,2 * 0,7 = 0,036 + 0,096 + 0,056 = 0,188.
2. Найдем вероятность сдачи двух предметов.
Р2 = 0,6 * 0,8 * 0,3 + 0,4 * 0,8 * 0,7 + 0,6 * 0,2 * 0,7 = 0,144 + 0,224 + 0,084 = 0,452.
3. Определим вероятность сдачи трех экзаменов.
Р3 = 0,6 * 0,8 * 0,7 = 0,336.
4. Вычислим вероятность сдать хотя бы один экзамен.
Обратное этому событию — ничего не сдать.
Р = 0,4 * 0,2 * 0,3 = 0,024.
Р4 = 1 — 0,024 = 0,976.
Ответ: 0,188; 0,452; 0,336; 0,976.
Сессия состоит из трех экзаменов. Вероятность того, что студент сдаст первый экзамен, равна 0,9, вероятность сдачи второго — 0,9, а третьего – 0,7. Найти вероятности событий:
А – студент сдаст все три экзамена;
В – студент сдаст не менее двух экзаменов.
Решение:
Пусть событие D – студент сдает первый экзамен, событие Е — сдаст второй экзамен, событие С – сдаст третий, событие F – сдаст два экзамена.
1) Событие А – студент сдаст все три экзамена;
Р(А)= Р(D)•Р(Е)•Р(С) = 0,9•0,9•0,7= 0,567
2) В – студент сдаст не менее двух экзаменов.
Событие F = D•Е•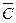 
+ 
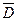
•Е•С + D • 
•С.
Найдем вероятность сдачи только двух экзаменов
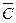
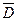
Р(F)=Р(DЕ )+Р( ЕС)+Р(D С) = 0,9•0,9•0,3+0,1•0,9•0,7+0,9•0,1•0,7 = = 0,369
Тогда вероятность сдать не менее двух экзаменов найдем по формуле Р(В)=Р(А) + Р(F)= 0,567+0,369=0,936
Ответ: 1) 0,567; 2) 0,936.
|
Шрифт зодчего Шрифт зодчего состоит из прописных (заглавных), строчных букв и цифр… |
Картограммы и картодиаграммы Картограммы и картодиаграммы применяются для изображения географической характеристики изучаемых явлений… |
Практические расчеты на срез и смятие При изучении темы обратите внимание на основные расчетные предпосылки и условности расчета… |
Функция спроса населения на данный товар Функция спроса населения на данный товар: Qd=7-Р. Функция предложения: Qs= -5+2Р,где… |
поделиться знаниями или
запомнить страничку
- Все категории
-
экономические
43,623 -
гуманитарные
33,648 -
юридические
17,917 -
школьный раздел
611,572 -
разное
16,897
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Правила форума
В этом разделе нельзя создавать новые темы.
Если Вы хотите задать новый вопрос, то не дописывайте
его в существующую тему, а создайте новую в корневом разделе «Помогите решить/разобраться (М)».
Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.
Не ищите на этом форуме халяву
, правила запрещают участникам публиковать готовые решения стандартных учебных задач. Автор вопроса обязан привести свои попытки решения
и указать конкретные затруднения.
Обязательно просмотрите тему
Правила данного раздела, иначе Ваша тема может быть удалена
или перемещена в Карантин, а Вы так и не узнаете, почему.
|
|
Теория вероятностей
|
|
05/06/13 |
Помогите пожалуйста решить задачку.
|
|
|
|
 |
26.02.2014, 13:56 
|
gris |
Re: Теория вероятностей
|
||
13/08/08 |
Как-то Вы странно считаете вторые и третьи дни. Насчёт окончательного умножения на 6 правильно. То есть остаётся посчитать количество вариантов трёх экзаменационных дней.
|
||
|
|
|||
|
|
Someone |
Re: Теория вероятностей
|
||
23/07/05 |
для первого экзамена есть 6 вариантов дней Почему? для второго экзамена в зависимости от первого — 6!
Уточните, что означает «промежуток не менее одного дня». Означает ли это, что между экзаменами должен быть пустой день? Или же это просто запрет сдавать два экзамена в один день?
|
||
|
|
|||
|
Откуда такое число?|
Jesus_in_Vegas |
Re: Теория вероятностей
|
|
05/06/13 |
в общем надо было лучше подумать прежде чем писать, я решила уже, 56 вариантов расписания для одного варианта перестановки. А для всех 6 получается 336. всего расписаний значит 336.
|
|
|
|
|
|
provincialka |
Re: Теория вероятностей
|
||
18/01/13 |
Имеем два типа дней: с экзаменом и без. Значит, надо расставить 3 «плюсика» на 10 мест. Как учесть «пустые» дни? Отвести на экзамены по 2 дня (сам экзамен и день после него). Останется еще
|
||
|
|
|||
|
дней, не связанных с экзаменами. Итак, надо расположить в некотором порядке 3 экзамена (с днем отдыха) и 5 пустых дней.Модераторы: Модераторы Математики, Супермодераторы
Найдите правильный ответ на вопрос ✅ «Студент сдаёт в сессию три экзамена. Вероятность того, что студент сдаст на положительную оценку один (любой) экзамен равна 0,8. Тогда …» по предмету 📘 Математика, а если вы сомневаетесь в правильности ответов или ответ отсутствует, то попробуйте воспользоваться умным поиском на сайте и найти ответы на похожие вопросы.
Смотреть другие ответы
Главная » ⭐️ Математика » Студент сдаёт в сессию три экзамена. Вероятность того, что студент сдаст на положительную оценку один (любой) экзамен равна 0,8. Тогда вероятность того, что студент сдаст на положительную оценку хотя бы один экзамен равна?