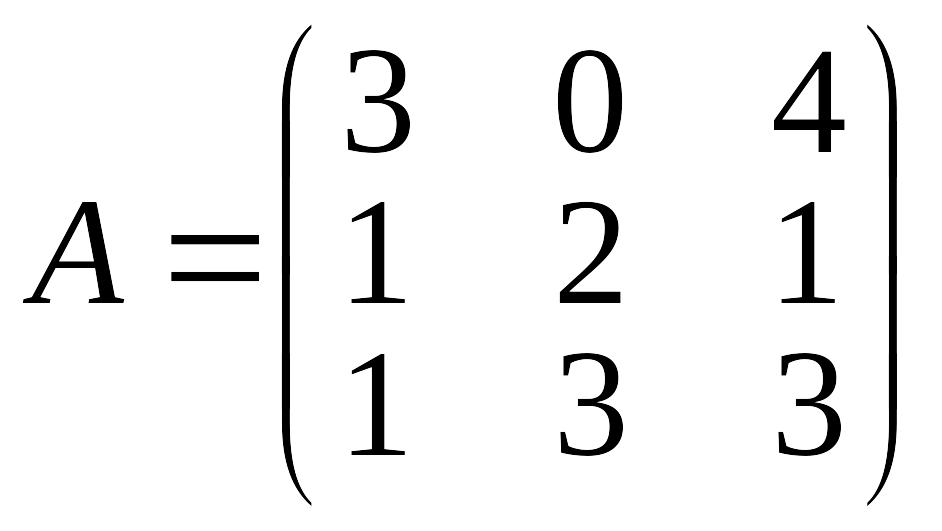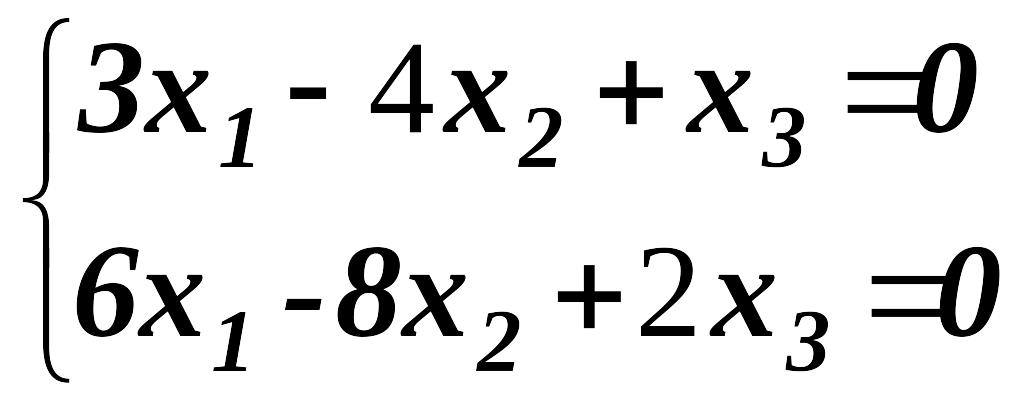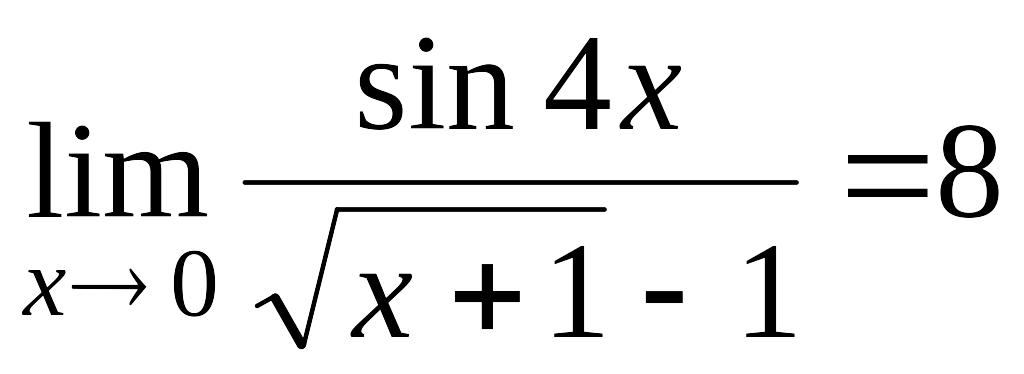Студенты первого курса сдавали экзамен по биологии среди 40 наугад выбранных студентов оказалось 10 - Помощь в подготовке к экзаменам и поступлению

Добавил:

Upload

Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Предмет:

Файл:

Занятие 3.doc

Скачиваний:

114

Добавлен:

15.03.2016

Размер:

465.41 Кб

Скачать

Вероятностный подход

Взаимоотношения
меры порядка и меры хаоса в организации
ритма сердца могут быть оценены по
информационным показателям, вычисляемым
по формуле общей энтропии:
,
гдеp_i
– вероятность попадания в тот или
иной класс кардиоинтервалов, i– номер класса кардиоинтервалов,m– количество классов кардиоинтервалов.

Максимальную
энтропию вычисляют по формуле H₀=log₂m,
гдеm– число классов межпульсовых
интервалов.

Относительную
энтропию или коэффициент сжатия h
определяют как отношение общей и
максимальной энтропии
,
а коэффициент избыточности D – как
отношение разности максимальной и общей
энтропии к максимальной энтропииили D=1-h.

Нормированную
энтропию определяют по формуле
,
гдеN– количество
кардиоинтервалов.

Перечень основных показателей вариабельности сердечного ритма

№ пп	Краткие обозначения показателей	Наименования показателей	Физиологическая интерпретация
1	ЧП	Частота пульса	Средний уровень функционирования системы кровообращения
2	SDNN	Стандартное отклонение полного массива кардиоинтервалов	Суммарный эффект вегетативной регуляции кровообращения
3	RMSSD	Квадратный корень суммы разностей последовательного ряда кардиоинтервалов	Активность парасимпатического звена вегетативной регуляции¦
4	pNN50	Число пар кардиоинтервалов с разностью более 50 мс. в % к общему числу кардиоинтервалов в массиве	Показатель степени преобладания парасимпатического звена регуляции над симпатическим (относительное значение)
5	CV	Коэффициент вариации полного массива кардиоинтервалов	Нормированный показатель суммарного эффекта регуляции
6	MxDMn	Разность между максимальным и минимальным значениями кардиоинтервалов	Максимальная амплитуда регуляторных влияний
7	Mo	Мода	Наиболее вероятный уровень функционирования сердечно-сосудистой системы
8	AMo	Амплитуда моды	Условный показатель активности симпатического звена регуляции
9	SI	Стресс индекс (Индекс напряжения регуляторных систем)	Степень напряжения регуляторных систем (степень преобладания активности центральных механизмов регуляции над автономными)
10	CC1	Значение первого коэффициента автокорреляционной функции	Степень активности автономного контура регуляции
11	CC0	Число сдвигов автокорреляционной функции до получения значения коэффициента корреляции меньше нуля	Степень активности центрального контура регуляции

Упражнения

Найти
вероятность выпадения грани с четным
номером при однократном бросании
игрального кубика.
Найти
вероятность извлечения зеленого шара
при извлечении одного шара наугад из
корзины, содержащей 4 зеленых шара и 6
белых.
На столе
находятся 5 ампул с препаратом А, 10 — с
препаратом В и 15 — с препаратом С. Наугад
берут одну ампулу. Какова вероятность
того, что выбранная ампула окажется
ампулой с препаратом В?
В
студенческой группе 6 юношей и 9 девушек.
Какова вероятность того, что наугад
вызванный студент окажется юношей?
Из 10 000
упаковок некоторого препарата, выпущенных
фармацевтической фабрикой за день,
случайным образом отобраны 100 упаковок,
и среди них обнаружены 3 бракованные.
Найти относительную частоту появления
бракованных упаковок среди отобранных
и оценить вероятность того, что упаковка,
наугад выбранная из всех выпущенных в
этот день, окажется бракованной.
Студенты
первого курса сдавали экзамен по
биологии. Среди 40 наугад выбранных
студентов оказалось 10 студентов, сдавших
экзамен на «отлично». Найти относительную
частоту появления студентов, отлично
сдавших экзамен, среди выбранных
студентов и оценить вероятность того,
что студент, наугад выбранный из всех
студентов, сдававших экзамен, сдал его
на отлично.
В ящике
находятся 4 ампулы с препаратом А, 6 —
с препаратом В и 10 — с препаратом С.
Какова вероятность того, что выбранная
наугад ампула окажется ампулой с
препаратом А или В?
В группе
из 15 студентов 5 сдали коллоквиум по
органической химии на «отлично» и 6 —
на «хорошо». Какова вероятность того,
что наугад выбранный из этой группы
студент сдал коллоквиум на «хорошо»
или «отлично»?
Аптека
получила 100 упаковок некоторого
лекарственного препарата со склада №
1, 200 — со склада № 2 и 500 — со склада № 3
. Какова вероятность того, что очередная
проданная упаковка поступила со склада
№ 1 или № 2?
Найти
вероятность того, что при двух
последовательных подбрасываниях монеты
оба раза выпадет герб.
Вероятность
осуществления некоторой химической
реакции при проведении химического
эксперимента определенного вида равна
0,9. Найти вероятность того, что данная
реакция произойдет в двух последовательно
проведенных экспериментах.
Вероятность
поражения цели первым стрелком равна
0,90, вторым — 0,95. Найти вероятность того,
что оба стрелка не промахнутся, если
произведут по одному выстрелу.
В коробке
находятся 4 ампулы с препаратом А и 10 —
с препаратом В. Какова вероятность
того, что две последовательно
выбранные ампулы окажутся ампулами с
препаратом А?
Из 12
студентов 3 не прошли профилактический
осмотр. Найти вероятность того, что оба
из 2 случайным образом выбранных из
этой группы студентов не прошли осмотр.
Принимая
вероятность появления мальчика при
рождении ребенка равной 0,5, найти
вероятность того, что в семье с 6 детьми:

а) мальчиков нет;

б) 4 мальчика;

в) все дети — мальчики.

Вероятность
осуществления некоторой химической
реакции при проведении эксперимента
определенного вида равна 0,8. Найти
вероятность того, что данная реакция
произойдет в двух из семи проведенных
экспериментов.
Вероятность
заболевания гепатитом для жителя
некоторой области в определенный период
года составляет 0,0005. Оценить вероятность
того, что из обследованных 10 000 жителей
4 окажутся заболевшими.
Если при
транспортировке ампул с некоторым
препаратом со склада в аптеку в среднем
повреждается 0,1% ампул, то какова
вероятность повреждения двух ампул
при транспортировке 3000 ампул?
Имеется
двадцать коробок с яблоками, причем
количество яблок в них составляет 10,
9, 11, 10, 12, 8, 11, 9, 10, 10, 11, 8, 9, 10, 9, 11, 12, 10, 9 и
11 штук. Составить закон распределения
случайной величины X, определяемой как
количество яблок в произвольно выбранной
коробке, и найти математическое ожидание,
дисперсию и среднее квадратическое
отклонение этой величины.
Число
фармацевтов в каждой из 15 аптек некоторого
района составляет соответственно 4, 7,
5, 6, 4, 5, 3, 6, 4, 5, 5, 4, 6, 5 и 6 человек. Составить
закон распределения случайной величины
X, определяемой как число фармацевтов
в произвольно выбранной аптеке (из этих
15 аптек), найти математическое ожидание,
дисперсию и среднее квадратическое
отклонение этой величины.
Найти
вероятность того, что значение непрерывной
нормально распределенной величины
окажется в интервале
,
где— математическое ожидание, а— среднее квадратическое отклонение
этой величины.
Предполагая,
что рН крови человека подчиняется
нормальному закону распределения
с математическим ожиданием
и средним квадратическим отклонением,
найти вероятность того, что у произвольно
выбранного человека уровень рН
находится между 7,3 и 7,5.
Предполагая
закон распределения роста студентов
нормальным с математическим ожиданием
см и дисперсиейсм2
, найти вероятность того, что рост
произвольно выбранного студента
окажется в пределах от 180 до 190 см.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Правовые документы

Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

ДЛЯ
СТУДЕНТОВ ПО ВЫПОЛНЕНИЮ

КОНТРОЛЬНОЙ
РАБОТЫ

по
разделу курса высшей математики

«Теория
вероятностей»

Методические
указания по выполнению контрольной работы разработаны для студентов СПО и ВУЗов
по разделу курса высшей математики «Теория вероятностей».

Данный
практический материал содержит краткие теоретические сведения (справочный
материал), используемые при решении задач. Изложение этих сведений
иллюстрируется решенными примерами. Приведены 15 вариантов контрольных работ (по
6 задач в каждом).

Предлагаемая
разработка адресована преподавателям и студентам, предназначена для проведения
практических занятий и самостоятельных (контрольных) работ в аудитории.

Составитель:
Сардарова В.Я., преподаватель математики

ГБПОУ
АО СПО «Астраханский технологический техникум»

Классическое
определение вероятности

При
классическом определении вероятность события определяется равенством , где число
элементарных исходов испытания, благоприятствующих появлению события ; общее
число возможных элементарных исходов испытания, образующих полную группу
событий.

Пример.
Какова вероятность того, что в наудачу выбранном двузначном числе цифры одинаковы?

Решение.
Двузначными числами являются числа от 10 до 99; всего таких чисел 90.
Одинаковые цифры имеют 9 чисел (это числа 11, 22, 33, 44, 55, 66, 77, 88, 99).
Так как в данном случае m=9,
n=90,
то

где
А – событие «число с одинаковыми цифрами».

Пример.
Из букв слова дифференциал наугад выбирается одна буква. Какова
вероятность того, что эта буква будет: а) гласной, б) согласной, в) буквой ч?

Решение.
В слове дифференциал 12 букв, из них 5 гласных и 7 согласных. Буквы ч
в этом слове нет. Обозначим события: А – «гласная буква», В –
«согласная буква», С – «буква ч». Число благоприятствующих элементарных
исходов: m₁
=5 – для события А, m₂=7 – для события В,

m₃
=0 – для события С. Поскольку n
= 12, то

Пример.
Подбрасывается два игральных кубика, отмечается число очков на верхней грани
каждого кубика. Найти вероятность того, на обоих кубиках выпало одинаковое
число очков.

Решение.
Обозначим это событие буквой А. Событию А – благоприятствуют 6
элементарных исходов: (1; 1), (2; 2), (3; 3),;4; 4), (5; 5), (6; 6). Всего
равновозможных элементарных исходов, образующих полную группу событий, в данном
случае n =
6²= 36. Значит, искомая вероятность

Пример.
В книге 300 страниц. Чему равна вероятность того, что наугад открытая страница
будет иметь порядковый номер, кратный 5?

Решение.
Из условия задачи следует, что всех равновозможных элементарных исходов, образующих
полную группу событий, будет n
= 300. Из них m
= 60 благоприятствуют наступлению указанного события. Действительно, номер,
кратный 5, имеет вид 5k,
где k
– натуральное число, причем 0<5k£300,
откуда k≤300/5≈60. Следовательно,

Где
А – событие «страница имеет порядковый номер, кратный 5».

Пример.
В партии из деталей имеется стандартных.
Наудачу отобраны деталей. Найти вероятность
того, что среди отобранных ровно стандартных.

Решение.
Общее число возможных элементарных исходов испытания равно числу способов,
которыми можно извлечь деталей из деталей, т. е. –
числу сочетаний из элементов по . Подсчитаем число исходов,
благоприятствующих интересующему нас событию: стандартных
деталей можно взять из стандартных деталей способами; при этом остальные деталей должны быть нестандартными и
берём их из нестандартных деталей способами. Следовательно, число
благоприятствующих исходов равно . Искомая вероятность
равна отношению числа исходов, благоприятствующих событию, к числу всех
элементарных исходов:

Пример.
В одном аквариуме находятся три чёрных, семь красных рыбок. Шесть случайно
выбранные рыбки переносят в другой аквариум. Какова вероятность того, что среди
них четыре красные рыбки?

Решение.
Общее число возможных элементарных исходов испытания равно числу способов,
которыми можно извлечь 6 рыбок из 10, т.е. числу сочетаний из 10 элементов по 6
элементов

Определяем
число исходов, благоприятствующих событию А – «среди 6 взятых рыбок 4
красные». Четыре красные рыбки из семи красных можно взять способами, при этом остальные 6 – 4 = 2
рыбки должны быть черные; взять же 2 черные рыбки из 3 чёрных можно способами. Следовательно, число
благоприятных исходов равно

Искомая
вероятность равна отношению числа исходов, благоприятствующих событию, к числу
всех элементарных исходов:

Пример.
Среди 25 студентов группы, в которой 10 девушек, разыгрывается 5 билетов. Найти
вероятность того, что среди обладателей билетов окажутся 2 девушки.

Решение.
Число всех равновозможных случаев распределения 5 билетов среди 25 студентов
равно числу сочетаний из 25 элементов по 5, т.е. . Число
групп по трое юношей из 15, которые могут получить билеты, равно . Каждая такая тройка может сочетаться с
любой парой из десяти девушек, а число таких пар равно .
Следовательно, число групп по 5 студентов, образованных из группы в 25
студентов, в каждую группу из которых будут входить трое юношей и две девушки,
равно произведению Это произведение равно числу
благоприятствующих случаев распределения пяти билетов среди студентов группы
так, чтобы три билета получили юноши и два билета – девушки.

В
соответствии с формулой находим искомую
вероятность

Пример.
На пяти одинаковых карточках написаны буквы И, К,
М, Н. С. Карточки перемешиваются и наугад раскладываются в ряд. Какова вероятность
того, что получится слово МИНСК?

Решение.
Из пяти различных элементов можно составить Р₅
перестановок: Р₅ = 1×2×3×4×5=120.
Значит, всего равновозможных исходов будет 120, а благоприятствующих данному
событию – только один. Следовательно,

Относительная
частота, Статистическое определение вероятности.

Классическое
определение вероятности оказывается непригодным для изучения произвольных
случайных событий. Так, оно неприемлемо, если результаты испытания не
равновозможные. Например, при бросании неправильной игральной кости выпадение
её различных граней не равновозможное. В таких случаях используется так
называемое статистическое определение вероятности. Пусть произведено n
испытаний, при этом некоторое событие А наступило m раз.

Определение.
Число m – называется абсолютной частотой события А, а отношение называется относительной частотой события А.

Пример:
При транспортировке из 10 0000 арбузов испортилось 26. Здесь m=26 –
абсолютная частота испорченных арбузов, а относительная.

Сложение
и умножение вероятностей.

Теорема
сложения вероятностей несовместных событий. Вероятность появления какого –
либо одного из нескольких несовместных событий равна сумме вероятностей этих
событий:

Замечание:
Формула имеет место только для несовместных событий. Если же события А и
В совместны, то вероятность появления хотя бы одного из них определяется
формулой .

Следствие
1: Сумма вероятностей событий, образующих полную группу событий, равна
единице.

Следствие
2: Вероятность события, противоположного данному, равна разности между
единицей и вероятностью данного события, т., е.

Теорема
умножения вероятностей. Вероятность произведения событий равна произведению их вероятностей,
вычисленных в предположении, что все события, предшествующие каждому из них,
имели место, т., е.,

Следствие.
Если события независимы
в совокупности, то вероятность совместного появления всех этих событий равна
произведению их вероятностей

Пример.
Подбрасываются два игральных кубика. Найти вероятность события А –
«сумма выпавших очков не превосходит четырех».

Решение.
Событие А есть сумма трех несовместных событий В₂ , В₃
, В_{4 ,}заключается в том, что сумма очков равна соответственно
2, 3, 4. Поскольку

то по теореме сложения вероятностей
несовместных событий получим

Пример.
Спортсмен стреляет по мишени, разделенной на три сектора. Вероятность попадания
в первый сектор равна 0,4, во второй – 0,3. Какова вероятность попадания либо в
первый, либо во второй сектор?

Решение.
События А – «попадание в первый сектор» и В – «попадание во
второй сектор» несовместны (попадание в один сектор исключает попадание во
второй), поэтому применима теорема сложения вероятностей несовместных событий.
В соответствии с этой теоремой находим искомую вероятность: Р (А + В) = Р(А)
+ Р(В) = 0,4 + 0,3 = 0,7.

Пример.
Вероятность попадания в мишень для первого спортсмена 0,85, а для второго –
0,8. Спортсмены независимо друг от друга сделали по одному выстрелу. Найти
вероятность того, что в мишень попадет хотя бы один спортсмен?

Решение.
Введем обозначения: А – «попадание первого
спортсмена», В – «попадание второго спортсмена», С – «попадание
хотя бы одного из спортсменов». Очевидно, А + В = С, причем события А
и В совместны.

В
соответствии с формулой Р(А + В) = Р(А) + Р(В) – Р(АВ) получаем

Р(С)
= Р(А) + Р(В) – Р(АВ) или Р(С) = Р(А) + Р(В) – Р(А)Р(В), поскольку А
и В – независимые события, а для них верна формула Р(АВ) =
Р(А)Р(В). Подставив данные значения Р(А) = 0,85, Р(В) = 0,8 в
формулу для Р(С), найдем искомую вероятность Р(С) = (0,85 + 0,8) –
0,85×0,8 = 0,97.

Пример.
Вероятность выживания одной клетки в течении 20 минут Р=0,7.
В пробирке с благоприятными для существования этих клеток условиями находятся
только что разделившиеся две клетки. Какова вероятность того, что через 20
минут они будут жизнеспособны?

Решение:
Пусть событие А – первая клетка жизнеспособна через 20 мин., событие В –
вторая клетка жизнеспособна. Будем считать, что между клетками нет
внутривидовой конкуренции, т. е. события независимы. Тогда по теореме умножения
независимых событий Р(АВ)=Р(А)Р(В)=0.7 0,7=0,49.

Пример.
В терапевтическом отделении больницы 70% пациентов –
женщины, а 21% – курящие мужчины. Наугад выбирают пациента. Он оказывается
мужчиной. Какова вероятность того, что он курит?

Решение:
Пусть событие М означает, что пациент мужчина, а К
– что пациент курит. Тогда в силу условия задачи Р(М)=0,3, а Р(МК)=0,21.
Тогда по теореме умножения вероятностей зависимых событий Р(МК)=Р(М)Р(К/М)
получим Р(К/М)=Р(МК)/Р(М)=0,21/0,3=0,7.

Пример.
Пусть у нас перемешаны записи нейронной активности мозга (у пяти клеток
зарегистрирована активность, характерная для клеток «внимания», у пяти другой вид
активности) и 20 – из другой области (у 15 – активность типа клеток «внимание»,
у 5 – другого вида.). Зависимы ли события А – «выбранная наугад запись
сделана в первой области» и В – на «выбранной наугад записи зарегистрирована
активность, характерная для клеток» внимания»?

Решение:
Имеем . Следовательно, события независимы

Пример.
Симметричная монета подброшена три раза. Какова вероятность того, что цифра
выпадет ровно два раза?

Решение.
Введем обозначения: А_k
– «выпадение цифры при k
– ом подбрасывании монеты (k
= 1, 2, 3)», А – «выпадение двух цифр при трех подбрасывания», тогда, Поскольку слагаемые в правой части этого
равенства попарно несовместны, то по формуле

при n
= 3 получаем

Принимая за внимание независимость
событий А₁, А₂, А₃, находим

Пример.
С помощью наблюдений установлено, что в некоторой местности в сентябре в
среднем бывает 25 дней без дождя. Какова вероятность того, что 1-го и 2-го
сентября дождя не будет?

Решение:

Вероятность
того, что 1-го сентября дождя не будет (событие А) равна Р(А) = . Найдем вероятность того, что и 2-го
сентября дождя не будет (событие В) при условии, что 1-го сентября дождя не
было. Это условная вероятность, так как событие А уже произошло. Отсюда Р
(В/A)
= . Искомую вероятность определим по теореме
умножения вероятностей зависимых событий. Р(А и В) = Р(А) Р (В/A)
= = 0,7.

Пример.
В урне находится 8 красных и 6 голубых шаров. Из урны последовательно без
возвращения извлекается 3 шара. Найти вероятность того. Что все 3 шара голубые.

Решение.
Введем обозначения: А₁ – «первый шар голубой», А₂
– «второй голубой шар», А₃ – «третий голубой шар», А –
«все три шара голубые», тогда А = А₁А₂А₃. Воспользуемся
формулой которая при n
= 3 принимает вид. Поскольку

то

Пример.
В урне 6 голубых, 5 красных и 4 белых шара. Из урны поочередно извлекают шар,
не возвращая его обратно. Найти вероятность того, что при первом извлечении
появится голубой шар (событие А), при втором – красный (событие В),
при третьем – белый (событие С).

Решение.
Вероятность появления голубого шара при первом извлечении Р(А) = 6/15 = 2/5.
Вероятность появления красного шара во втором извлечении, вычисленная в
предположении, что в первый раз появится голубой шар, т.е. условная вероятность
Р(В/А) = 5/14. Вероятность появления белого шара в третьем извлечении,
вычисленная в предположении, что в первый раз появится голубой шар, во второй –
красный, т.е. условная вероятность Р(С/АВ) = 4/13. По формуле Р(АВС)
= Р(А)Р(В/А)Р(С/АВ) находим искомую вероятность

Пример.
В каждом из трех ящиков находится по 30 деталей. В первом ящике 27, во втором
28, в третьем 25 стандартных деталей. Из каждого ящика наудачу вынимают по
одной детали. Какова вероятность того, что все три вынутые детали окажутся
стандартными.

Решение.
Вероятность того, что из первого ящика вынута стандартная деталь (событие А),
Р(А) = 27/30 = 9/10. Вероятность того, что из второго ящика вынута
стандартная деталь (событие В) Р(В) = 28/30 = 14/15. Вероятность
того, что из третьего ящика вынута стандартная деталь (событие С) Р(С)
= 25/30 = 5/6. Поскольку события А, В, С независимы, то по формуле Р(ABC)
= Р(А)Р(В)Р(С) получаем Р(АВС) =

Формула
полной вероятности. Формулы Бейеса.

Если
событие А может произойти только совместно с одним из событий Н₁,Н₂,
…, Н_n,
образующих полную группу несовместных событий (гипотез), то вероятность появления события определяется по формуле
полной вероятности:

, где –
вероятность гипотезы ; –
условная вероятность события А при этой гипотезе.

Так
как гипотезы образуют полную группу несовместных событий, то

Если
вероятности гипотез до опыта были , а после опыта
появилось событие А, то условная вероятность вычисляется по формуле
Бейеса:

Пример.
На фабрике изготовляющей болты, первая машина производит 30%, вторая – 25%,
третья – 45% всех изделий. Брак в их продукции составляет соответственно 2%,
1%, 3%. Найти вероятность того, что случайно выбранный болт оказался дефектным.

Решение.
Обозначим через А событие, состоящее в том, что случайно выбранный болт
– дефектный, а через Н₁, Н₂, Н₃ –
событие, состоящее в том, что этот болт произведен соответственно первой,
второй и третьей машинами. Из условия задачи следует, что

Р(Н₁)
= 0,30, Р(Н₂) = 0,25, Р(Н₃) = 0,45;

Р(А/Н₁)
= 0,02, Р(Н₂) = 0,01, Р(Р/Н₃)= 0,03.

По
формуле при п = 3 получаем Р(А) = Р(Н₁)Р(А/Н₁)+

+Р(Н₂)Р(Н₃)Р(А/Н₃)
= 0,3× 0,02 + 0,25×
0,1 + 0,45× 0,03 = 0,022.

Пример.
В пяти ящиках находятся одинаковые по размерам и весу шары. В двух ящиках – по
6 голубых и 4 красных шара (это ящик состава Н₁). В двух
других ящиках (состава Н₂) – по 8 голубых и 2 красных шара. В
одном ящике (состава Н₃) – 2 голубых и 8 красных шаров.
Наудачу выбирается ящик и из него извлекается шар. Какова вероятность того,
что извлеченный шар оказался красным?

Решение.
Событие «извлечен красный шар» обозначим через А. Из условия
задачи следует, что

Вероятность
вынуть красный шар, если известно, что взят ящик первого состава Н₁,
Вероятность извлечь красный шар, если
известно, что взят ящик второго состава,

Вероятность
извлечь красный шар, если известно, что взят ящик третьего состава Н₃,

В
соответствии с формулой при п = 3
находим искомую вероятность Р(А) = Р(Н₁)Р(А/Н₁) + Р(Н₂)Р(А/Н₂)+
Р(Н₃)Р(А/Н₃) = 0,4×
0,4 +

+
0,4× 0,2 + 0,2×
0,8 = 0,4.

Пример.
В группе 21 студент, в том числе 5 отличников, 10 хорошо успевающих и 6 слабо
занимающихся. На предстоящем экзамене отличники могут получить только отличные
оценки. Хорошо успевающие студенты могут получить с равной вероятностью хорошие
и отличные оценки. Слабо занимающиеся студенты могут получить с равной
вероятностью хорошие, удовлетворительные и неудовлетворительные оценки. Для
сдачи экзамена приглашается наугад один студент. Найти вероятность того, что он
получит хорошую или отличную оценку (событие А).

Решение.
Обозначим гипотезы: Н₁ – «приглашен студент-отличник», Н₂
–«приглашен хороший студент», Н₃ – «приглашен слабый
студент».

Из
условия задачи следует, что

По
формуле находим искомую вероятность

Пример.
Имеются три урны с шарами. В первой находится 5 голубых и 3 красных шара, во
второй – 4 голубых и 4 красных, в третьей – 8 голубых. Наугад выбирается одна
из урн и их нее наугад извлекается шар. Какова вероятность того, что он
окажется красным (событие А).

Решение.
Шар может быть извлечен из первой урны, либо из второй, либо из третьей.
Обозначим через Н₁,Н₂, Н₃
соответственно выбор первой, второй и третьей урны.

Поскольку
имеются одинаковые шансы выбрать любую из урн, то

Из условия задачи следует, что

В
соответствии с формулой находим искомую
вероятность

Пример.
На складе находятся детали, изготовленные на двух заводах. Известно, что объем
продукции первого завода в 4 раза превышает объем продукции второго завода.
Вероятность брака на первом заводе р₁ = 0,05, на втором
заводе – р₂ = 0,01. Наудачу взятая деталь оказалась
бракованной. Какова вероятность того, что эта деталь изготовлена первым заводом?

Решение.
Обозначим через Н₁ событие, состоящее в том, что взятая
деталь изготовлена на первом заводе, Н₂ – на втором заводе,
тогда

Пусть
А – событие, состоящее в том, что наудачу взятая деталь оказалась
бракованной.

По
условию Р(А/Н₁) = 0,05, Р(А/Н₂) = 0,01.

В
соответствии с формулой в случае п =
2 получаем

Пример.
В лаборатории есть три клетки. В первой клетке содержатся 1 серая и 2 белые
мыши, во второй – 1 серых и 3 белых, в третьей – 2 серых и 2 белых. Случайным
образом выбирают клетку и из клетки берут наудачу одну мышь. Найти вероятность
того, что мышь белая.

Решение.
Введем обозначения: событие А – «Взяли белую мышь»; гипотезы Н₁
– «выбрали первую клетку», Н₂ – «выбрали вторую клетку», Н₃
– «выбрали третью клетку».

Так
как гипотезы равновероятны, то P(H_i)=1/3
(i
= 1, 2, 3). Найдём условные вероятности.

По
формуле полной вероятности получим ответ

Формулы
Бернулли и Пуассона.

Вероятность
того, в n независимых
испытаниях, в каждом из которых вероятность появления событие А равна р,
событие наступит ровно m раз
(безразлично в какой последовательности), равна по формуле Бернулли :

, или ,

где
.

Если
число испытаний велико, а вероятность р появления события в каждом
испытании очень мала, то используют приближённую формулу Пуассона:

Где
– число появления события в независимых испытаниях, (среднее число появлений события в испытаниях).

Вероятность
того, что в испытаниях событие наступит:a)менее
раз; б) более раз; в)
не менее раз; г) не более ;
д) хотя бы один раз, – находятся соответственно по формулам:

;

Пример.
Вероятность изготовления стандартного изделия равна
0,95. Какова вероятность того, что среди десяти изделий не более одного
нестандартного?

Решение.
Пусть событие А состоит в том, что среди десяти
изделий не более одного нестандартного, а событии В – среди десяти
изделий только одно нестандартное. Тогда искомая вероятность . События А и В несовместны.
Поэтому . По формуле Бернулли находим ;

Следовательно

Пример.
С помощью наблюдений установлено, что в некоторой
местности в сентябре в среднем бывает 12 дождливых дней. Какова вероятность
того, что из наугад взятых в этом месяце 8-ми дней 3 будут дождливыми?

Решение:

Поскольку
количество испытаний невелико (n = 8), то для нахождения вероятности
того, что событие А появится точно k = 3 раза воспользуемся
формулой Бернулли:

, где .

По
условию задачи вероятность дождя равна p = 12/30 = 6/15, (в сентябре 30
дней).

Значит,
вероятность ясного дня равна q = 1 – p = 1 – 6/15 = 9/15.

Пример.
Обычный человек примерно в половине случаев правильно
угадывает, в какой руке спрятан мелкий предмет. Предположим, что верный ответ
получен в трёх случаях из четырёх. Случайно ли это? Или при таком раскладе
можно говорить о необычайных способностях угадывающего?

Решение:
Если принять вероятность угадывания в норме р=1/2,
то по формуле Бернулли ,
где

Как
видим, каждый четвёртый нормальный человек правильно угадывает в трёх случаях
из четырех.

Допустим,
что верный ответ получен в девяти случаев из десяти. Какова вероятность такого
угадывания у нормального человека?

По
формуле Бернулли

Таким
образом, нормальный человек лишь в одном случае из 100 может случайно
продемонстрировать такой результат. И если подобное угадывание происходит чаще,
то можно, по – видимому, говорить, что угадыватель – экстрасенс
(или мистификатор).

Пример.
Завод отправил на базу 500 изделий. Вероятность
повреждения изделия в пути равна 0,002. Найти вероятность того, что в пути
будет повреждено: а) ровно три изделия; б) менее трёх; в) более трёх; г) хотя
бы одно.

Решение.
Число велико, вероятность мала и рассматриваемые события
(повреждение изделий) независимы, поэтому имеет место формула Пуассона .

а)
Найдём :

Найдём
вероятность того, что будет повреждено ровно 3 изделия;

в)
Найдём вероятность того, что будет повреждено менее трёх изделий:

Найдём вероятность того, что будет
повреждено более трёх изделий. События «повреждено более трёх изделий» и «
повреждено не более трёх изделий» (обозначим вероятность этого события через ) – противоположны, поэтому . Отсюда

Используя
результаты, полученные выше, имеем

г)
Найдём вероятность того, что будет повреждено хотя бы одно изделие. Событие
«повреждено хотя бы одно изделие» и «ни одно изделие не повреждено» (обозначим
вероятность этого события через ) – противоположны,
следовательно, . Отсюда искомая вероятность
того, что будет повреждено хотя бы одно изделие, равна

Контрольная
работа «Случайные события»

Вариант
№1.1.

1. В
одном аквариуме находятся три чёрных, пять красных и две голубых рыбки. Три
случайно выбранные рыбки переносят в другой аквариум. Какова вероятность того,
что все три рыбки красные?

2. Задания
программированной контрольной работы занумерованы всеми двухзначными числами.
Какова вероятность того, что номер наугад выбранного задания состоит из
одинаковых цифр?

3. Вероятности
отказа за время Т каждого из трех станков равны 0.3, 0.4 и 0.5. Найти
вероятность того, что за это время откажет: а) только один станок, в) хотя бы
один станок.

4. Работают
три конвейера по изготовлению консервов. Вероятность поступления брака с
первого конвейера равна 0,1, со второго – 0,2, а с третьего – 0,15. Найти
вероятность того, что в данный момент брак поступает только с первого
конвейера.

5. Производится
залп 8 – разрядной реактивной установки. Вероятность попадания в цель каждым из
снарядов равна 0.2. Найти вероятность того, что цель будет поражена тремя
снарядами.

6. При
введении вакцины против гриппа иммунитет создаётся в 99,99 случаев. Какова
вероятность того, что из 1000 вакцинированных детей заболеет менее трёх детей.

Вариант
№1.2.

1. На
шести карточках записаны буквы а, е, м, о, р, ш. Какова
вероятность того, что 4 последовательно извлеченные карточки образуют слово
«море».

2. В
бассейне содержится 10 окуней и 5 карасей. Какова вероятность того, что 3
наугад выловленные рыбы окажутся карасями.

3. Три
стрелка стреляют по мишени. Вероятности попадания для них соответственно равны
0.6, 0.7 и 0.8. Найти вероятность того, что в мишень попадет 2 стрелка.

4. Лабораторное
животное либо здорово (с вероятностью 0,9), либо нет. Здоровое животное
выполняет некоторое задание в 75% все попыток. Если животное нездорово, то оно
способно выполнить эти задания, лишь в 40% всех попыток. Допустим, что
предпринималась попытка, и животное не справилось с заданием. Какова
вероятность того, что животное здорово?

5. В
операционном зале сбербанка 8 операторов. Вероятность того, что в данный момент
времени оператор зала обслуживает клиента, равна 0.7. Найти вероятность того,
что в данный момент занято 5 операторов.

6. В
некоторой лотерее вероятность крупного выигрыша равна 0.025. Найти вероятность
того, что среди 200 случайно выбранных билетов будет 4 билета с крупным
выигрышем.

Вариант
№1.3.

1. Набирая
номер телефона, абонент забыл последние две цифры и, помня лишь, что эти цифры
различны, набрал их наудачу. Найти вероятность того, что набраны нужные цифры.

2. В
бассейне находятся 20 мальков судака, 30 мальков сазана, 15 мальков карпа.
Какова вероятность того, что из двух наугад пойманных мальков окажутся либо оба
мальками судака, либо оба мальками карпа?

3. Вероятность
попадания в цель при сбрасывании одной бомбы равна 0.1. Найти вероятность
попадания в цель хотя бы одной бомбы, если бомбометание по цели производят 5
самолётов, каждый из которых сбрасывают по одной бомбе.

4. В
санатории 35 % пациентов – мужчины, остальные – женщины. Болезни сердца среди
мужчин встречаются в два раза чаще, чем среди женщин. Каково вероятность того,
что наудачу выбранный пациент – сердечник? Какова вероятность, что это мужчина?

5. Предположим,
что нормальная частота заболеваний определенной болезнью среди крупного
рогатого скота составляет 20% . Для проверки новой вакцины 15 животным делают
прививки. Какова вероятность иметь 12 здоровых среди 15 подвергающихся
прививкам?

6. Среди
семян пшеницы 0,4% семян сорняков. Найти вероятность того, что среди 5000 семян
обнаружат восемь семян сорняков. Какова вероятность того, что будет не менее
пяти семян сорняков?

Вариант
№1.4.

1. Подбрасывают
две игральные кости. Найти вероятность того, что сумма выпавших очков будет
нечётной.

2. Среди
25 студентов группы, в которой 10 девушек, разыгрывается 5 билетов. Найти
вероятность того, что среди обладателей билетов окажутся две девушки.

3. Три
подводных охотника одновременно выстрелили в редкий экземпляр акулы. Найти
вероятность того, что акула будет убита при условии, что каждое попадание
смертельно и вероятность попадания каждым охотником равна 0.6.

4. В
группе из 20 стрелков имеются 5 отличных, 9 – хороших, 6 – посредственных
стрелков. При одном выстреле отличный стрелок попадает в мишень с вероятностью
0.9, хороший — с вероятностью 0.8, посредственный – с вероятностью 0.7. Найти
вероятность того, что в цель попал хороший стрелок.

5. Знаменитый
бразильский футболист Пеле забивает пенальти с вероятностью 0.9. Какова
вероятность того, что из 10 пенальти он забьёт не менее 8

6. Вероятность
того, что семя данного растения не прорастёт, равна 0.04. Какова вероятность
того, что из 500 посеянных семян не взойдут менее пяти семян.

Вариант
№1.5.

1. В
бассейне находятся 15 судаков, из них 7 балтийских и 8 черноморских. Какова
вероятность того, что из трех взятых на исследование судаков хотя бы один будет
черноморским.

2. В
группе туристов 20 % детей, причём 12 % — девочки. Наугад выбирают ребёнка.
Какова вероятность, что это девочка?

3. В
электрическую цепь включены последовательно три элемента, работающих независимо
друг от друга. Вероятности отказа первого, второго и третьего элементов
соответственно равны 0.1, 0.15, 0.2. Найти вероятность того, что тока в цепи
не будет.

4. В
лаборатории есть три клетки. В первой клетке содержатся 2 серые и 2 белые мыши,
во второй – 4 серых и 2 белых, в третьей – 2 серых и 3 белых. Случайным образом
выбирают клетку и из клетки берут наудачу одну мышь. Найти вероятность того,
что мышь серая.

5. В
семье 5 детей. Найти вероятность того, что среди этих детей хотя бы один
мальчик. Вероятность рождения мальчика принять равной 0.51.

6. Радиоаппаратура
содержит 1000 одинаково надёжных элементов, вероятность отказа для каждого из
которых равна 0,001. Какова вероятность отказа двух элементов.

Вариант
№1.6.

1. Библиотечка
состоит из десяти различных книг, причём 5 книг стоят по 400 рублей каждая, три
книги – по 100 руб., две книги – по 300 руб. Найти вероятность того, что взятые
наудачу две книги стоят 500 рублей.

2. В
большой популяции плодовой мушки 25% мух имеют мутацию глаз, 50% — мутацию
крыльев, а 40% мух с мутацией глаз имеют мутацию крыльев. Какова вероятность
того, что у мух, наудачу выбранных из этой популяции, окажется хотя бы одна их
мутаций?

3. Вероятности
того, что нужная формула имеется в первом, втором, третьем справочнике
соответственно равны 0,9; 0,6; 0,7. Найти вероятности того, что формула
содержится: а) во всех трех справочниках; б) хотя бы в одном справочнике.

4. На
город примерно 100 дней в году дует ветер с севера, а 200 дней в году – с
запада. Промышленные предприятия, расположенные на севере, производят выброс
вредных веществ каждый третий день, а расположенные на западе – в последний
день каждой недели. Какова вероятность того, что в наугад выбранный день, город
будет накрыт промышленным смогом?

5. Вероятность
того, что стрелок попадет в десятку, равна 0.6. Чему равна вероятность того,
что при восьми выстрелах будет шесть попаданий в десятку.

6. Вероятность
того, что изделие не выдержит испытания, равна 0,0004. Найти вероятность того,
что из 1000 изделий не выдержит испытаний не менее двух изделий.

Вариант
№1.7.

1. Из
пяти карточек с буквами A, Б, В, Г, Д
наугад одна за другой выбираются три 3 и располагаются в ряд в порядке
появления. Найти вероятность, что будет слово «ДВА».

2. У
6 мальчиков и 11 девочек в классе имеются признаки инфекционного заболевания.
Чтобы определить наличие заболевания требуется взять выборочный анализ у 4
детей. Какова вероятность того, что для этого выберут 2 мальчика и 2 девочки?

3. Вероятность
выживания одной клетки в течение 20 минут р=0.7. В пробирке с
благоприятными для существования условиями находятся только разделившиеся две
клетки. Какова вероятность того, что через 20 минут они будут жизнеспособны?

4. Судоходная
компания организует средиземноморские круизы в течение летнего времени и
проводит несколько круизов в сезон. Поскольку в этом виде бизнеса очень высокая
конкуренция, то важно, чтобы все каюты зафрахтованного под круизы корабля были
полностью заняты туристами, тогда компания получит прибыль. Эксперт по туризму,
нанятый компанией, предсказывает, что вероятность того, что корабль будет полон
в течение сезона, равна 0,92, если доллар не подорожает по отношению к рублю, и
с вероятностью 0,75, если доллар подорожает. По оценкам экономистов,
вероятность того, что в течение сезона доллар подорожает по отношению к рублю,
равна 0,23. Чему равна вероятность того, что билеты на все круизы будут
проданы?

5. Для
прядения смешали поровну белый и окрашенный хлопок. Какова вероятность того,
что среди пяти случайно выбранных волокон смеси обнаружено менее двух
окрашенных.

6. Улов
из 1000 ловушек для омаров составил 1200 штук. Допустим, что имеет место
распределения Пуассона. Каково число ловушек, в которых: а) не было ни одного
омара; б) было менее двух омаров?

Вариант
№1.8.

1. В
мастерскую для ремонта поступило 12 телевизоров. Известно, что 5 штук из них
нуждаются в общей регулировке. Мастер берет первые, попавшиеся 4 телевизора.
Какова вероятность того, что 2 из них нуждаются общей регулировке.

2. Набирая
номер телефона, абонент забыл последние три цифры, помня лишь, что они
различны, набрал их наудачу. Найти вероятность того, что набраны нужные цифры.

3. Предположим,
что для одной торпеды вероятность потопить корабль равна 0.6. Какова
вероятность того, что 3торпеды потопят корабль, если для потопления корабля
достаточно одного попадания в цель.

4. Крыса
может выбирать один из 4-х лабиринтов. Известно, что вероятности выхода её из
различных лабиринтов за три минуты соответственно равны 0.7, 0.3, 0.2, 0.1.
Какова вероятность того, что крыса выберется из лабиринта за три минуты.

5. В
хлопке 75% длинных волокон. Какова вероятность того, что среди взятых наудачу
трёх волокон окажутся два длинных волокна?

6. Среди
10000 сеянцев ячменя в среднем два не имеют обычной окраски в результате
спонтанных мутаций, влияющих на хлорофилл. Какова вероятность того, что из
10000 случайно выбранных сеянцев ячменя ровно у двух из них не окажется обычной
зелёной окраски?

Вариант
№1.9.

1. В
коробке 8 резисторов, из которых 5 окрашены в черный цвет. Найти вероятность
того что, из 3-х выбранных наудачу резисторов 2 окажутся черного цвета.

2. На
шести карточках написаны буквы О, У, Х В, Д, З. После перетасовки
вынимают одну карточку за другой и раскладывают их в том порядке, в каком они
были вынуты. Какова вероятность того, что на карточках будет написано слово
«воздух».

3. Вероятность
попадания в цель при сбрасывании одной бомбы равна 0.2. Найти вероятность
попадания в цель хотя бы одной бомбы, если бомбометание по цели производят 5
самолетов.

4. На
трёх дочерей Машу, Таню и Катю возложена обязанность мыть тарелки. Маше
приходится выполнять 40% всей работы. Таня и Катя делят остальную работу
поровну. Вероятность для Маши разбить тарелку равна 0.02, для Тани – 0.05, для
– Кати – 0.07. Одна из сестер моет посуду. Родители не знают кто мыл посуду, но
слышали звук разбитой тарелки. Какова вероятность того, что посуду мыла Катя.

5. Вероятность
получения удачного результата при производстве сложного химического опыта равна
0.6. Найти вероятность того, что при проведении 7 опытов 5 закончатся успешно.

6. Средняя
плотность болезнетворных микробов в одном кубическом литре равна 100. Берётся на
пробу 2 дм³ воздуха. Найти вероятность того, что в нём обнаружат
более двух микробов.

Вариант
№1.10.

1. В
бассейне содержится 14 окуней и 6 карасей. Какова вероятность того, что 3
наугад выловленные рыбы окажутся карасями.

2. Из
пяти карточек с буквами Т, А, В, Р, И наугад одна за другой выбираются три 3 и
располагаются в ряд в порядке появления. Найти вероятность, что будет слово
«ТРИ».

3. Три
орудия ведут огонь по цели, вероятность попадания в которую при одном выстреле
из первого орудия 0.5, из второго – 0.6, а из третьего – 0.7. Зная, что каждое
орудие стреляет один раз, найти вероятность поражения цели, если для этого
достаточно двух попаданий.

4. В
эксперименте живой амёбе пересаживают ядро от одной, цитоплазму от другой и
внешнюю оболочку от третьей амёбы. Если все компоненты берут от одного и того
же штампа, то нормально воспроизводится 85% амёб. Если же компоненты берутся из
разных штампов, то только 1% амёб будет воспроизводиться. Допустим, что собрали
одинаковое количество амёб из одного и того же штампа и из разных штампов.
Наудачу выбранная амёба воспроизвелась. Какова вероятность того, что она
собрана из разных штампов?

5. Два
равносильных противника играют в шахматы. Что вероятнее: выиграть две партии из
четырёх или три партии из шести? Ничью во внимание не принимать

6. Завод
отправил на базу 500 изделий. Вероятность повреждения изделия в пути равна
0,002. Найти вероятность того, что в пути будет повреждено хотя бы одно
изделие.

Вариант
№1.11.

1. Найти
вероятность того, что наудачу взятое двузначное число окажется кранным либо 2,
либо 5, либо тому и другому одновременно

2. На
двух фермах А и В насчитывающих 1000 голов крупного рогатого
скота каждая, произошла вспышка заболевания ящуром. Доли заражённого скота
составляют соответственно 1/5 и 1/4. Выбирают случайным образом одну корову. а)
Какова вероятность того, что выбранная корова принадлежит ферме А и имеет
заболевание? б) Если на каждой ферме 70% заражённого скота младше одного года,
то какова вероятность того, что выбранная корова принадлежит ферме В,
имеет заболевание и старше одного года?

3. В
экзаменационном билете 3 вопроса. Студент может ответить на них с вероятностью
0.6, 0.6 и 0.5. Найти вероятность того, что он ответит только на один вопрос.

4. Для
проверки контагиозности нескольких штаммов бактерий большое число морских
свинок содержалось парами в отдельных клетках. По одной из каждой пары свинок
заражалось штаммом А, В или С (по каждом штамму бралось
равное количество морских свинок). Установлено, что доли здоровых свинок
заразившихся от своих соседей равны 1/3,1/4 и 3/4. В выбранной наугад
клетке обе свинки оказались заражёнными. Какова вероятность того, что заражение
вызвано штаммами А, В и С?

5. Пусть
всхожесть семян оценивается вероятностью 0.7. Какова вероятность того, что из
двух посеянных семян взойдёт какое – либо одно?

6. Многие
болезни достаточно редки или становятся такими после профилактических мер.
Однако в больших популяциях встречается некоторое число больных редкими
болезнями. Например, при введении вакцины полиомиелита иммунитет создаётся в
99,99 % случаев. Какова вероятность того, что из 10000 вакцинированных больных
заболеет один?

Вариант
№1.12.

1. В
группе туристов 20% детей. Наугад выбирают ребёнка. Какова вероятность того,
что это мальчик? Какова вероятность того, что это девочка?

2. Из
20 человек, одновременно заболевших гриппом, 15 выздоровели полностью за 5
дней. Предположим, что из этих 20 человек случайным образом выбиралось 5.
Какова вероятность того, что из 5 выздоравливают за пять дней полностью только
3 человека?

3. Охотник
выстрелил 3 раза по удаляющейся цели. Вероятность попадания при первом выстреле
равна 0.6, а при последующих выстрелах уменьшается на 0.1. . Найти вероятность
того, что он попадёт только один раз.

5. Лечение
одного заболевания приводит к выздоровлению в 75% случаев. Лечилось шесть
больных. Какова вероятность того, что будут здоровыми, по крайней мере,
четверо?

6. На
станцию скорой помощи в течение часа в среднем поступает 20 вызовов. Найти
вероятность того, что в течение 15 минут будет принято не менее четырёх
вызовов.

Вариант
№1.13.

1. На
шести карточках написаны буквы О, Т, И, Е, Р, Я. После перетасовки вынимают
наугад одну карточку за другой и раскладывают их в том порядке, в каком они
были вынуты. Найти вероятность того, что на карточках будет написано слово
«ТЕОРИЯ».

2. 25
экзаменационных билетов содержат по два вопроса, которые не повторяются.
Экзаменующийся может ответить только на 45 вопросов. Какова вероятность того,
что вытянутый экзаменационный билет состоит из подготовленных им вопросов?

3. Три
стрелка в одинаковых и независимых условиях произвели по одному выстрелу по
одной и той же цели. Вероятность поражения цели первым стрелком равна 0,9,
вторым – 0,8, третьим – 0,7. Найти вероятность того, что: а) только один из
стрелков попал в цель; б) хотя бы два стрелка попали в цель.

4. Студент
может заболеть гриппом только в результате либо переохлаждения, либо в контакте
с другим больным. Студент заболеет при переохлаждении с вероятностью 0.3. При
контакте с больным студент может заболеть с вероятностью 0.1. Считая, сто эти
события равновероятные и несовместные, найти вероятность того, что студент
заболеет.

5. Вероятность
того, что расход воды в течение дня окажется не превышающим норму, равна 0,8.
Найти вероятность того, что расход воды будет нормальным в течение пяти из семи
дней.

6. Тираж
книги 5000 экз. Вероятность брака в брошюровке составляет 0.001. Найти
вероятность того, что тираж содержит ровно 4 бракованные книги.

Вариант
№1.14.

1. В
магазин поступило 40 телевизоров. Известно, что 10 телевизоров импортные, но
неизвестно – какие. Найти вероятность того, что два наугад взятых телевизора
будут импортными.

2. В
группе обследуемых 1000 человек, из них 600 курящих. Среди курящих 240 человек
имеют те или иные лёгочные заболевания. Среди некурящих лёгочных больных 120
человек. Являются ли курение и заболевание лёгких независимыми событиями?

3. Три
крысы обучаются выполнять три различные задания (по одной крысе на каждое
задание). Вероятность того, что крысы выполнят свои задания за 1 мин.
соответствуют. Какова вероятность того, что хотя бы одна
крыса выполнит задание?

4. Имеются
по виду три одинаковых ящика. В первом ящике 20 белых шаров, во втором 10 белых
и 10 чёрных шаров, в третьем – 20 чёрных шаров. Из выбранного наугад ящика
вынули белый шар. Вычислить вероятность того, что шар вынут из первого ящика.

5. Шансы
волка добыть пищу за каждый период охоты составляет 50%. Какова вероятность
того, что успешными оказалось более половины всех периодов охоты, если было 10
периодов?

6. При
изучении пищевых ниш простейших предполагалось, что количество единиц пищи,
съеденной в течении 2 часов, является случайной величиной, имеющей
распределение Пуассона со средним 10.а) Какова вероятность того, что в течение
данного часа простейшее ничего не съест? б) Какова вероятность того, что в
течение данного часа хотя бы одна единица пищи будет потреблена конкретным
простейшим?

Вариант
№1.15.

1. На
семи карточках записаны буквы а, и, м, о, р ,в, ж. Какова
вероятность того, что 4 последовательно извлеченные карточки образуют слово
«морж».

2. В
бассейне содержится 10 окуней и 15 карасей. Какова вероятность того, что 3
наугад выловленные рыбы окажутся только карасями, либо только окунями?

3. Вероятность
того, что нужная деталь лежит в первом ящике, составляет 0.7, во втором – 0.8,
в третьем – 0.9. Найти вероятность того, что деталь лежит: а) только в одном
ящике; б) не больше, чем в двух ящиках.

4. Три
компьютерные фирмы представили в контрольное управление компьютеры для
выборочной проверки: первая – 20 компьютеров; вторая – 30 компьютеров; третья –
50 компьютеров. Вероятности того, что компьютеры без брака у этих фирм
соответственно равны: 0,8; 0,9; 0,7. Был выбран один компьютер, и он оказался
без брака. Определить вероятность того, что этот компьютер принадлежит третьей
фирме?

5. В
популяции дрозофилы у 20% особей имеются мутации крыльев. Если из популяции
выбирают 6 мух, то какова вероятность того, что есть мутации у двух из них?

6. Завод
отправил в торговую сеть 2000 изделий. Вероятность повреждения изделия в пути
0,004. Найдите вероятность того, что при транспортировке будут повреждены не
более трёх изделий.

Литература.

1. Барвин
И. И. «Теория вероятности и математическая статистика» , М.: Высшая школа,
2005.

2. Воронов
В. Н. «Математика для студентов гуманитарных факультетов», Ростов-на-Дону,
Феникс, 2002.

3. Гмурман.
В.Е. «Теория вероятностей и математическая статистика». М., Высшая школа,
1977.

4. Гресс
П. В. «Математика для гуманитариев», М.: Логос, 2004.

5. Гроссман
С., Тернер Дж. «Математика для биологов». Перевод с английского Логофета Д.О.,
М. Высшая школа, 1983

6. Данко
П. Е., Попов А. Г., Кожевникова Т. Я. «Высшая математика в упражнениях и
задачах», ч.1.2. – М.: Высшая школа, М., 1986-2001.

7. Лакин
Г.Ф.. «Биометрия». М., Высшая школа, 1980

8. Шипачёв
В. С. «Высшая математика: учебник для нематематических специальностей вузов»,
М.: Высшая школа, 1990.

Источник

Модератор

6351 / 4060 / 1509

Регистрация: 09.10.2009

Сообщений: 7,550

Записей в блоге: 4

27.02.2016, 20:10

Anna_malia, у вас лёгкий бардак в обозначениях. Задача на формулу полной вероятности и, возможно, Байеса, в зависимости от того, что брать за гипотезы.
Вы имеете события двух видов — получение/не получение «отлично» и пропуск/не пропуск занятий. Что-то нужно брать как гипотезы, а другое — как события. Как гипотезы лучше брать первое, судя по этой фразе:

Сообщение от Anna_malia

10% среди студентов, получивших «отлично», не пропустили ни одного занятия.

Дальше, вот в этой строчке

Сообщение от Anna_malia

Р(А/В) — вероятность того, что получил отл и посещал все занятия (0.1)

слева написана условная вероятность, а текст ваш означает вероятность пересечения P(AB). Это не одно и то же. $https://www.cyberforum.ru/cgi-bin/latex.cgi?Pleft(A/B right)=frac{Pleft(AB right)}{Pleft(B right)}$
Не «…И посещал», а «посещал все занятия, ЕСЛИ получил отлично». Судя по вашим обозначениям, Р(В/А)=0,1

Короче…. Давайте нормально обозначать. Гипотезы Н1={студент получил отлично}, Р(Н1)=0,1
Н2={студент получил не отлично}, Р(Н2)=1-0,1=0,9
Событие В={студент посещал все занятия} (это совпадает с вашим обозначением), Р(В)=0,4 по условию.
Тогда для решения избыточная информация. Так как по условию Р(В/Н1)=0,1, то $https://www.cyberforum.ru/cgi-bin/latex.cgi?Pleft(bar{B} /H_1right)=1-Pleft(B/H_1 right)=1-0,1=0,9$ и 0,4 вообще не нужно. Составители, наверное, перепутали вопрос. Хотя с такими данными чтобы получить где-то 0,15… Например, по формуле полной вероятности $https://www.cyberforum.ru/cgi-bin/latex.cgi?Pleft(B/H_2right)=frac{13}{30}=0,4(3)$ , а по формуле Байеса
$https://www.cyberforum.ru/cgi-bin/latex.cgi?Pleft(H_1/Bright)=frac{1}{40}\Pleft(H_2/B right)=frac{39}{40}$
Ничего не равно ни 0,15, ни 0,85

Источник

Найди верный ответ на вопрос ✅ «Десять учеников на экзамене получили следующие оценки: 2 2 5 4 5 3 3 4 5 5 найдите размах, моду и средние измерения …» по предмету 📙 Алгебра, а если ответа нет или никто не дал верного ответа, то воспользуйся поиском и попробуй найти ответ среди похожих вопросов.

Искать другие ответы

Главная » ⭐️ Алгебра » Десять учеников на экзамене получили следующие оценки: 2 2 5 4 5 3 3 4 5 5 найдите размах, моду и средние измерения

Опубликовано 2 года назад по предмету
Алгебра
от poleydima

Ответ

Ответ дан
mashadubovtseva2006

Ответ: мода 3

Объяснение:

Число которое встречается чаще всего.

Не тот ответ, который вам нужен?

Найди нужный

Самые новые вопросы

Математика — 2 года назад

Сколько здесь прямоугольников

История — 3 года назад

Какое управление было в древнейшем риме? как звали первого и последнего из царей рима?

Литература — 3 года назад

Уроки французского ответе на вопрос : расскажите о герое по следующему примерному плану: 1.почему мальчик оказался в райцентре ? 2.как он чувствовал себя на новом месте? 3.почему он не убежал в деревню? 4.какие отношения сложились у него с товарищами? 5.почему он ввязался в игру за деньги? 6.как характеризуют его отношения с учительницей ? ответе на эти вопросы пожалуйста ! сочините сочинение пожалуйста

Русский язык — 3 года назад

Помогите решить тест по русскому языку тест по русскому языку «местоимение. разряды местоимений» для 6 класса
1. укажите личное местоимение:
1) некто
2) вас
3) ни с кем
4) собой
2. укажите относительное местоимение:
1) кто-либо
2) некоторый
3) кто
4) нам
3. укажите вопросительное местоимение:
1) кем-нибудь
2) кем
3) себе
4) никакой
4. укажите определительное местоимение:
1) наш
2) который
3) некий
4) каждый
5. укажите возвратное местоимение:
1) свой
2) чей
3) сам
4) себя
6. найдите указательное местоимение:
1) твой
2) какой
3) тот
4) их
7. найдите притяжательное местоимение:
1) самый
2) моего
3) иной
4) ничей
8. укажите неопределённое местоимение:
1) весь
2) какой-нибудь
3) любой
4) этот
9. укажите вопросительное местоимение:
1) сколько
2) кое-что
3) она
4) нами
10. в каком варианте ответа выделенное слово является притяжательным местоимением?
1) увидел их
2) её нет дома
3) её тетрадь
4) их не спросили

Русский язык — 3 года назад

Переделай союзное предложение в предложение с бессоюзной связью.
1. океан с гулом ходил за стеной чёрными горами, и вьюга крепко свистала в отяжелевших снастях, а пароход весь дрожал.
2. множество темноватых тучек, с неясно обрисованными краями, расползались по бледно-голубому небу, а довольно крепкий ветер мчался сухой непрерывной струёй, не разгоняя зноя
3. поезд ушёл быстро, и его огни скоро исчезли, а через минуту уже не было слышно шума

ggg3288

Русский язык — 3 года назад

помогите прошу!перепиши предложения, расставляя недостающие знаки препинания. объясни, что соединяет союз и. если в предложении один союз и, то во втором выпадающем списке отметь «прочерк».пример:«я шёл пешком и,/поражённый прелестью природы/, часто останавливался».союз и соединяет однородные члены.ночь уже ложилась на горы (1) и туман сырой (2) и холодный начал бродить по ущельям.союз и соединяет:1) части сложного предложенияоднородные члены,2) однородные членычасти сложного предложения—.поэт — трубач зовущий войско в битву (1) и прежде всех идущий в битву сам (ю. янонис).союз и соединяет:1) части сложного предложенияоднородные члены,2)

Физика — 3 года назад

Вокруг прямого проводника с током (смотри рисунок) существует магнитное поле. определи направление линий этого магнитного поля в точках a и b.обрати внимание, что точки a и b находятся с разных сторон от проводника (точка a — снизу, а точка b — сверху). рисунок ниже выбери и отметь правильный ответ среди предложенных.1. в точке a — «от нас», в точке b — «к нам» 2. в точке a — «к нам», в точке b — «от нас» 3. в обеих точках «от нас»4. в обеих точках «к нам»контрольная работа по физике.прошу,не наугад важно

Информация

Посетители, находящиеся в группе Гости, не могут оставлять комментарии к данной публикации.

Что ты хочешь узнать на сайте Знания ком?

Задай вопрос

Модератор

6351 / 4060 / 1509

Регистрация: 09.10.2009

Сообщений: 7,550

Записей в блоге: 4

27.02.2016, 20:10

Сообщение от Anna_malia

10% среди студентов, получивших «отлично», не пропустили ни одного занятия.

Дальше, вот в этой строчке

Сообщение от Anna_malia

Р(А/В) — вероятность того, что получил отл и посещал все занятия (0.1)

Короче…. Давайте нормально обозначать. Гипотезы Н1={студент получил отлично}, Р(Н1)=0,1
Н2={студент получил не отлично}, Р(Н2)=1-0,1=0,9
Событие В={студент посещал все занятия} (это совпадает с вашим обозначением), Р(В)=0,4 по условию.
Тогда для решения избыточная информация. Так как по условию Р(В/Н1)=0,1, то $https://www.cyberforum.ru/cgi-bin/latex.cgi?Pleft(bar{B} /H_1right)=1-Pleft(B/H_1 right)=1-0,1=0,9$ и 0,4 вообще не нужно. Составители, наверное, перепутали вопрос. Хотя с такими данными чтобы получить где-то 0,15… Например, по формуле полной вероятности $https://www.cyberforum.ru/cgi-bin/latex.cgi?Pleft(B/H_2right)=frac{13}{30}=0,4(3)$ , а по формуле Байеса
$https://www.cyberforum.ru/cgi-bin/latex.cgi?Pleft(H_1/Bright)=frac{1}{40}Pleft(H_2/B right)=frac{39}{40}$
Ничего не равно ни 0,15, ни 0,85

Скачать материал

Сейчас обучается 74 человека из 35 регионов

Сейчас обучается 33 человека из 18 регионов

Сейчас обучается 355 человек из 67 регионов

Краткое описание документа:

10 спортсменов принимают участие в соревнованиях по 5 видам спорта. По каждому виду спорта спортсмен набирает не более 100 очков. Определить среди 10 спортсменов участника с наибольшим суммарным количеством очков. Построить диаграмму, показывающую соотношение количества набранных очков, каждым спортсменом по каждому виду спорта.

Скачать https://author24shop.ru/readyworks/laboratornaya_rabota/informatika/453975/

10 студентов сдают экзамены по 5 дисциплинам. По каждой дисциплине можно получить оценку – 2, 3, 4, 5. Определить среди 10 студентов человека с наибольшим средним баллом. Построить диаграмму, показывающую соотношение оценок, полученных каждым студентом по каждой дисциплине.

Скачать https://author24shop.ru/readyworks/laboratornaya_rabota/informatika/453976/

Для 10 человек по данным о ежемесячном доходе рассчитать подоходный налог 13%, единый социальный налог 5%. Округление произвести до копеек. Посчитать сумму к выдаче в рублях и $. Построить диаграмму, показывающую соотношение сумм уплаты налога по каждому виду налога.

Скачать https://author24shop.ru/readyworks/laboratornaya_rabota/informatika/453977/

Билет на пригородный поезд стоит 20 руб., если расстояние до станции не более 20 км; 50 руб., если расстояние до станции больше 20 км, но меньше 75 км; 100 руб., если расстояние больше 75 км. Составить таблицу со следующими столбцами: пункт назначения, расстояние, стоимость билета, количество проданных билетов до данного пункта назначения. Установить число станций в радиусе 50 км от города. Построить диаграмму, показывающую какая станция пользуется наибольшей популярностью по отношению к остальным.

Скачать https://author24shop.ru/readyworks/laboratornaya_rabota/informatika/453979/

Телефонная компания взимает плату за услуги телефонной связи по тарифу: 370 мин в месяц – абонентская плата 200 руб., за каждую минуту сверх нормы – 2 руб. Составить ведомость оплаты услуг телефонной связи для 10 абонентов за 1 месяц, самостоятельно указав количество потребляемого времени каждым. Построить диаграмму, показывающую сравнительную характеристику сумм оплаты услуг телефонной компании каждым абонентом.

Скачать https://author24shop.ru/readyworks/laboratornaya_rabota/informatika/453980/

Компания снабжает электроэнергией клиентов по тарифу:

5 руб. за 1 кВт/ч за первые 500 кВт/ч;

10 руб. за 1 кВт/ч свыше 500 кВт/ч, но не более 1000 кВт/ч;

15 руб. за 1 кВт/ч свыше 1000 кВт/ч. Для 10 клиентов посчитать плату. Определить число клиентов, потребляющих более 1000 кВт/ч. Построить диаграмму, демонстрирующую сравнение потребляемой электроэнергии каждым клиентом.

Скачать https://author24shop.ru/readyworks/laboratornaya_rabota/informatika/453982/

Билет на пригородный поезд стоит 10 монет, если расстояние до станции не более 20 км; 15 монет, если расстояние до станции больше 20 км, но меньше 75 км; 25 монет, если расстояние больше 75 км. Составить таблицу со следующими столбцами: пункт назначения, расстояние, стоимость билета, количество проданных билетов до данного пункта назначения. Отсортировать таблицу по полю количество проданных билетов. Установить число станций в радиусе 60 км от города. Построить диаграмму, показывающую какая станция пользуется наименьшей популярностью по отношению к остальным.

Скачать https://author24shop.ru/readyworks/laboratornaya_rabota/informatika/453984/

Билет на пригородный поезд стоит 6 монет, если расстояние до станции не более 20 км; 10 монет, если расстояние до станции больше 20 км, но меньше 75 км; 15 монет, если расстояние больше 75 км. Составить таблицу со следующими столбцами: пункт назначения, расстояние, стоимость билета, количество проданных билетов до данного пункта назначения. Отсортировать таблицу по полю количество проданных билетов. Установить число станций в радиусе более 70 км от города. Построить диаграмму, показывающую, какая станция пользуется наименьшей популярностью по отношению к остальным.

Скачать https://author24shop.ru/readyworks/laboratornaya_rabota/informatika/453986/

10 студентов сдают экзамены по 5 дисциплинам. По каждой дисциплине студент может получить оценку – 2, 3, 4, 5. Определить средний балл учащихся. Посчитать количество 5, 4, 3 и 2. Найти студента с наибольшим средним баллом и студента с наименьшим средним баллом. Построить диаграмму, показывающую соотношение оценок, полученных каждым слушателем по каждой дисциплине.

Скачать https://author24shop.ru/readyworks/laboratornaya_rabota/informatika/453987/

Для отдела из 10 человек составить ведомость расчета заработной платы. Таблица содержит следующие сведения: Ф.И.О., должность, оклад, стаж работы. Для каждого человека посчитать подоходный налог 13%, надбавку 5000 руб., если стаж работы более 3 лет и сумму к выдаче. Построить диаграмму, показывающую з/плату каждого сотрудника.

Скачать https://author24shop.ru/readyworks/laboratornaya_rabota/informatika/453990/

Для отдела из 10 человек составить ведомость расчета заработной платы. Таблица содержит следующие сведения: Ф.И.О., должность, оклад, стаж работы. Для каждого человека посчитать подоходный налог 13%, надбавку и сумму к выдаче. Надбавка составляет 10% от оклада, если стаж работы более 5 лет. Построить диаграмму, показывающую з/плату каждого сотрудника.

Скачать https://author24shop.ru/readyworks/laboratornaya_rabota/informatika/453991/

Компания снабжает электроэнергией клиентов по тарифу:

15 руб. за 1 кВт/ч за первые 500 кВт/ч;

20 руб. за 1 кВт/ч свыше 500 кВт/ч.

Для 10 клиентов посчитать плату. Определить число клиентов, потребляющих не более 500 кВт/ч и найти суммарное количество потребляемой энергии. Построить диаграмму, демонстрирующую сравнение потребляемой электроэнергии каждым клиентом.

Скачать https://author24shop.ru/readyworks/laboratornaya_rabota/informatika/453993/

Составьте экзаменационную ведомость, в которую входят следующие данные: №, Ф. И. О. студентов, оценки за экзамены. Посчитать средний балл для каждого студента. Если сданы все экзамены и средний балл равен 5,то выплачивается 50% надбавка к минимальной стипендии, если средний балл меньше 5, но больше или равен 4, то выплачивается минимальная стипендия. Построить диаграмму, показывающую количество оценок определенного вида, полученных в данной группе.

Скачать https://author24shop.ru/readyworks/laboratornaya_rabota/informatika/453995/

Телефонная компания взимает плату за услуги телефонной связи по тарифу: 300 мин в месяц – абонентская плата 250 руб., за каждую минуту сверх нормы – 2 руб. Составить ведомость оплаты услуг телефонной связи для 10 абонентов за 1 месяц, самостоятельно указав количество потребляемого времени каждым. Найти людей с максимальной и минимальной оплатой услуг. Построить диаграмму, показывающую сравнительную характеристику сумм оплаты услуг телефонной компании каждым абонентом.

Скачать https://author24shop.ru/readyworks/laboratornaya_rabota/informatika/453999/

10 спортсменов принимают участие в некотором соревновании. Каждый спортсмен может набрать не более 30 очков. Указать номер места, которое занял спортсмен в данном соревновании. За 1 место выплачивается премия 100000 руб., за 2 место 50000 руб. и за 3 место 30000 руб. Построить диаграмму, показывающую количество набранных очков, каждым спортсменом.

Скачать https://author24shop.ru/readyworks/laboratornaya_rabota/informatika/454004/

Составьте ведомость контроля остаточных знаний студентов по какой-либо дисциплине. Контроль остаточных знаний проходит в форме теста, по результатам которого выставляется оценка. Если студент набрал от 95 до 100 баллов, выставляется оценка «5», от 80 до 94 – «4», от 60 до 79 – «3», менее 60 – «2». Посчитайте: количество студентов, получивших оценку «5», «4», «3», «2», средний балл в группе, максимальный и минимальный баллы. С помощью диалогового окна Условное форматирование выделите все «2» красным цветом. Постройте круговую диаграмму, показывающую процентное соотношение оценок в группе.

Скачать https://author24shop.ru/readyworks/laboratornaya_rabota/informatika/454006/

Индивидуальные задания

Постройте графики функций.

1.	y = x⁵+x²–10, [-10;10], Скачать https://author24shop.ru/readyworks/laboratornaya_rabota/informatika/454215/
2.	y= \|tg(x)\|×x, [-1;1], Скачать https://author24shop.ru/readyworks/laboratornaya_rabota/informatika/454216/
3.	y = cos(x+x⁵)–2, [-2;2], Скачать https://author24shop.ru/readyworks/laboratornaya_rabota/informatika/454217/
4.	y = \|x³+x –10\|, [-2;2], Скачать https://author24shop.ru/readyworks/laboratornaya_rabota/informatika/454218/
5.	y = e^x-3, [-1;1], Скачать https://author24shop.ru/readyworks/laboratornaya_rabota/informatika/454219/
6.	y = e^x\|x\|, [-1;1], Скачать https://author24shop.ru/readyworks/laboratornaya_rabota/informatika/454220/
7.	y = cos(x³)–5, [-2;2], Скачать https://author24shop.ru/readyworks/laboratornaya_rabota/informatika/454221/
8.	y = x⁴-x²–х, [-5;5], Скачать https://author24shop.ru/readyworks/laboratornaya_rabota/informatika/454222/
9.	y= \|x\|, [-10;10], Скачать https://author24shop.ru/readyworks/laboratornaya_rabota/informatika/454223/
10.	y= \|x\|+5, [-10;10], Скачать https://author24shop.ru/readyworks/laboratornaya_rabota/informatika/454225/
11.	y= tg(x), [-1;1], Скачать https://author24shop.ru/readyworks/laboratornaya_rabota/informatika/454226/
12.	y = x³–2x²+5 , [-10;10], Скачать https://author24shop.ru/readyworks/laboratornaya_rabota/informatika/454228/
13.	y = 3cos(x)sin(2x+3), [-10;0], Скачать https://author24shop.ru/readyworks/laboratornaya_rabota/informatika/454229/
14.	y = \|x²+2x-5\|, [-3;3], Скачать https://author24shop.ru/readyworks/laboratornaya_rabota/informatika/454230/
15.	y = e^x2-10, [-2;2], Скачать https://author24shop.ru/readyworks/laboratornaya_rabota/informatika/454231/
16.	y = x³ – 5x–15, [-2;2], Скачать https://author24shop.ru/readyworks/laboratornaya_rabota/informatika/454232/
17.	y= \|tg(x)\|, [-1;1], Скачать https://author24shop.ru/readyworks/laboratornaya_rabota/informatika/454233/
18.	y = x³+5×\|х\|, [-5;5], Скачать https://author24shop.ru/readyworks/laboratornaya_rabota/informatika/454234/
19.	y= \|3tg(x)×cos(x)\|, [-1;1], Скачать https://author24shop.ru/readyworks/laboratornaya_rabota/informatika/454235/
20.	y = \|x²+5x-10\|, [-10;5], Скачать https://author24shop.ru/readyworks/laboratornaya_rabota/informatika/454236/

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

6 153 558 материалов в базе

Выберите категорию:
Выберите учебник и тему

Выберите класс:
Тип материала:
- Все материалы
- Статьи
- Научные работы
- Видеоуроки
- Презентации
- Конспекты
- Тесты
- Рабочие программы
- Другие методич. материалы

Найти материалы

Другие материалы

26.10.2020
330
6

26.10.2020
647
53

Вам будут интересны эти курсы:

Курс повышения квалификации «Информационные технологии в деятельности учителя физики»
Курс повышения квалификации «Внедрение системы компьютерной математики в процесс обучения математике в старших классах в рамках реализации ФГОС»
Курс повышения квалификации «Организация работы по формированию медиаграмотности и повышению уровня информационных компетенций всех участников образовательного процесса»
Курс повышения квалификации «Развитие информационно-коммуникационных компетенций учителя в процессе внедрения ФГОС: работа в Московской электронной школе»
Курс повышения квалификации «Применение MS Word, Excel в финансовых расчетах»
Курс повышения квалификации «Введение в программирование на языке С (СИ)»
Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
Курс повышения квалификации «Современные тенденции цифровизации образования»
Курс повышения квалификации «Современные языки программирования интегрированной оболочки Microsoft Visual Studio C# NET., C++. NET, VB.NET. с использованием структурного и объектно-ориентированного методов разработки корпоративных систем»
Курс повышения квалификации «Применение интерактивных образовательных платформ на примере платформы Moodle»

Задача
№ 1

Заданы
точки А (2; –2), В (–1; 3), С(4; –1). Найти:

1)
уравнение прямой АВ;

2)
уравнение перпендикуляра, опущенного
из точки С на АВ;

3)
определить угол между векторами

и ;

4)
найти расстояние от точки С до прямой
АВ.

Задача
№ 2

Стороны
параллелограмма заданы векторами

()
и

().
Найти:

длины
диагоналей параллелограмма; 2) угол
между ними.

Задача
№ 3

Даны
матрицы А и В. Найти матрицу D
= А²
– 3В

Задача
№ 4

Решить
однородную систему уравнений.

Задача
№ 5

Вычислив
пределы, убедиться в справедливости
приведенных соотношений.

Задача
№ 6

Найдя
производные от функций, убедится в
правильности приведенных соотношений.

Задача
№ 7

Из
квадратного листа картона со стороной
a
вырезаются по углам одинаковые квадраты,
и из оставшейся части склеивается
прямоугольная коробка. Какова должна
быть сторона вырезаемого квадрата,
чтобы объем коробки был наибольший?

Задача
№ 8

В
шахматном турнире участвуют 10 игроков.
Каждый из них должен сыграть по одной
партии с каждым другим. Сколько партий
будет сыграно за турнир?
В
ящике 11 деталей, из которых 6 окрашено.
Сборщик наудачу взял 5 детали. Найти
вероятность того, что среди них: а) хотя
бы одна окрашена; б) две детали окрашены;
в) не менее 3-х окрашенных?
В
урне лежит 8 белых и 6 черных шаров. Взято
4 шара. Среди них есть белые и черные.
Какова вероятность того, белых больше,
чем черных?
Три
электрические лампочки последовательно
включены в цепь. Вероятность того, что
одна (любая) лампочка перегорит, если
напряжение в цепи превысит номинальное,
равна 0,6. Найти вероятность того, что
при повышенном напряжении тока в цепи
не будет.
Из
карточек составлено слово «УНИВЕРСИТЕТ».
Поочередно (без возвращения) выбирают
3 карточки и приставляют одна к другой.
Какова вероятность, что получится слово
«ТИР»?
В
ящик, содержащий 3 одинаковые детали,
брошена стандартная деталь, а затем
наудачу извлечена одна деталь. Найти
вероятность того, что извлечена
стандартная деталь, если равновероятны
все возможные предположения о числе
стандартных деталей первоначально
находившихся в ящике.
На
экзамене оценки распределились следующим
образом: 4 студента получили «5» (I
категория), 10 студентов — «4» (II категория),
12 студентов — «3» (III категория).
Вероятность того, что предложенную
задачу решит студент I категории, равна
0,9; II категории — 0,7; III категории — 0,3.
Какова вероятность того, что наугад
выбранный студент решит задачу?
Найти
математическое ожидание числа выигрышных
лотерейных билетов, если приобретено
20 билетов, причем вероятность выигрыша
по каждому равна 0,05.

Задача № 9

Перечислить
законы распределения для дискретных
и непрерывных случайных величин.

Построить
графики плотности распределения для
непрерывных случайных величин.

Случайная
величина задана рядом распределения:

x_i	0	1	2	3	4
р_i	0,01	0,15	0,35	0,26	0,23

Найти
функцию распределения F(x) и построить
ее график.
Найти
вероятность попадания случайной
величины в интервал [0;3).
Определить
числовые характеристики случайной
величины: математическое ожидание
(M_x),
дисперсию (D_x),
среднее квадратическое
отклонение (s_x).

3.
Студенты за контрольную работу,
оцениваемую по 10-бальной шкале, получили
следующие оценки: 5; 6; 8; 7; 10; 6; 7; 4; 6; 7; 8;
10; 7; 6; 8; 9; 10; 6; 9; 8. Найти среднее значение,
дисперсию и среднее квадратическое
отклонение оценок студентов за эту
работу.

4.
Статистическое распределение выборки
имеет вид:

Х	2	3	5	6
	4	5	7	3

1.
Построить полигон распределения.

2.
Вычислить объем выборки.

3.
Найти моду, медиану и среднюю выборочную
вариационного ряда.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

1. Напишите запрос для определения количества изучаемых предметов на каждом курсе.
SELECT K AS Курс, Count(SUB) AS [Количество предметов]
FROM (SELECT STUDENT.KURS AS K, EXAM_MARKS.SUBJ_ID AS SUB
FROM STUDENT LEFT JOIN EXAM_MARKS ON STUDENT.STUDENT_ID = EXAM_MARKS.STUDENT_ID
GROUP BY STUDENT.KURS, EXAM_MARKS.SUBJ_ID)
GROUP BY K;
2. Напишите запрос для определения количества студентов, сдававших каждый экзамен.
SELECT SUBJECT.SUBJ_ID, SUBJECT.SUBJ_NAME, Count(EXAM_MARKS.STUDENT_ID) AS [Количество студентов]
FROM SUBJECT LEFT JOIN EXAM_MARKS ON SUBJECT.SUBJ_ID = EXAM_MARKS.SUBJ_ID
GROUP BY SUBJECT.SUBJ_ID, SUBJECT.SUBJ_NAME
3. Напишите запрос для получения среднего балла для каждого экзамена.
SELECT EXAM_MARKS.SUBJ_ID, SUBJECT.SUBJ_NAME, Avg(EXAM_MARKS.MARK) AS [Средний балл]
FROM SUBJECT INNER JOIN EXAM_MARKS ON SUBJECT.SUBJ_ID = EXAM_MARKS.SUBJ_ID
GROUP BY EXAM_MARKS.SUBJ_ID, SUBJECT.SUBJ_NAME
4. Напишите запрос для получения среднего балла для каждого студента.
SELECT STUDENT.STUDENT_ID, STUDENT.SURNAME, Avg(EXAM_MARKS.MARK) AS [Средний балл]
FROM STUDENT INNER JOIN EXAM_MARKS ON STUDENT.STUDENT_ID = EXAM_MARKS.STUDENT_ID
GROUP BY STUDENT.STUDENT_ID, STUDENT.SURNAME
5. Напишите запрос, который выполняет вывод данных для каждого конкретного дня сдачи экзамена о количестве студентов, сдававших экзамен в этот день.
SELECT D AS Дата, Count(S) AS [Количество студентов]
FROM (
SELECT EXAM_DATE AS D, STUDENT_ID AS S
FROM EXAM_MARKS
GROUP BY EXAM_DATE, STUDENT_ID
HAVING (EXAM_DATE) Is Not Null )
GROUP BY D
6. Напишите запрос, осуществляющий выборку для каждого студента значения его идентификатора и максимальной из полученных им оценок.
SELECT STUDENT.STUDENT_ID, STUDENT.SURNAME, Max(EXAM_MARKS.MARK) AS [Наибольший балл]
FROM STUDENT INNER JOIN EXAM_MARKS ON STUDENT.STUDENT_ID = EXAM_MARKS.STUDENT_ID
GROUP BY STUDENT.STUDENT_ID, STUDENT.SURNAME
ORDER BY STUDENT.SURNAME;
* STUDENT.SURNAME упоминать необязательно – фамилия студента в задании не оговорена, но так солиднее
* Последнюю строку вообще можно не писать – это сортировка по фамилии, в задании нет
* Если точно по заданию, то будет так
SELECT STUDENT_ID, Max(MARK) AS [Наибольший балл]
FROM EXAM_MARKS
GROUP BY STUDENT_ID;
7. Напишите запрос, который выполняет выборку для каждого студента значения его идентификатора и минимальной из полученных им оценок
SELECT STUDENT.STUDENT_ID, STUDENT.SURNAME, Min(EXAM_MARKS.MARK) AS [Наименьший балл]
FROM STUDENT INNER JOIN EXAM_MARKS ON STUDENT.STUDENT_ID = EXAM_MARKS.STUDENT_ID
GROUP BY STUDENT.STUDENT_ID, STUDENT.SURNAME
ORDER BY STUDENT.SURNAME;
* Если точно по заданию, то будет так
SELECT STUDENT_ID, Min(MARK) AS [Наименьший балл]
FROM EXAM_MARKS
GROUP BY STUDENT_ID
8. Напишите запрос, который выполняет вывод суммы баллов всех студентов для каждой даты сдачи экзаменов и представляет результаты в порядке убывания этих сумм.
SELECT EXAM_DATE, Sum(MARK) AS [Сумма баллов]
FROM EXAM_MARKS
GROUP BY EXAM_DATE
ORDER BY Sum(MARK) DESC;
9. Напишите запрос, который по таблице EXAM_MARKS позволяет найти а) максимальные и б) минимальные оценки каждого студента и который выводит их вместе с идентификатором студента.
SELECT STUDENT_ID, Max(MARK) AS [Наибольший балл], Min(MARK) AS [Наименьший балл]
FROM EXAM_MARKS
GROUP BY STUDENT_ID
10. Напишите запрос, выполняющий вывод списка предметов обучения в порядке а) убывания семестров и б) возрастания отводимых на предмет часов. Поле семестра в выходных данных должно быть первым, за ним должны следовать имя предмета обучения и идентификатор предмета.
SELECT SEMESTER, SUBJ_NAME, SUBJ_ID, HOUR
FROM SUBJECT
ORDER BY SEMESTER DESC, HOUR;
11. Напишите запрос, выполняющий вывод фамилии первого в алфавитном порядке (по фамилии) студента, фамилия которого начинается на букву «И».
SELECT TOP 1 SURNAME
FROM STUDENT
WHERE SURNAME LIKE ‘И*’
ORDER BY SURNAME
* В операторе LIKE – звёздочка – это формат MS Access; для Oracle и MS SQL было бы так LIKE ‘И%’
12. Напишите запрос, выбирающий данные о названиях университетов, рейтинг которых равен или превосходит рейтинг Воронежского государственного университета.
SELECT UNIV_NAME, RATING
FROM UNIVERSITY
WHERE NOT(
RATING<(SELECT RATING FROM UNIVERSITY
WHERE UNIV_NAME=’ВГУ’))
ORDER BY RATING;
* Последнюю строку можно не писать – это сортировка по рейтингу, в задании нет
* Здесь вложенный запрос – скобки ИМЕЮТ значение
13. Напишите запрос, выбирающий из таблицы EXAM_MARKS данные о названиях предметов обучения, для которых значение полученных на экзамене оценок (поле MARK) превышает любое значение оценки для предмета, имеющего идентификатор, равный 105.
SELECT SUBJECT.SUBJ_ID, SUBJECT.SUBJ_NAME, EXAM_MARKS.MARK
FROM SUBJECT INNER JOIN EXAM_MARKS ON SUBJECT.SUBJ_ID = EXAM_MARKS.SUBJ_ID
WHERE (EXAM_MARKS.MARK>(SELECT Max(EXAM_MARKS.MARK)
FROM EXAM_MARKS
HAVING SUBJ_ID=105))
GROUP BY SUBJECT.SUBJ_ID, SUBJECT.SUBJ_NAME, EXAM_MARKS.MARK;
*В таблице EXAM_MARKS данных о названиях предметов обучения НЕТ, их берём из таблицы SUBJECT
* В базе данных НЕТ предмета, имеющего идентификатор, равный 105. Для проверки можно подставить 22 – иначе результат запроса будет пустым
* Здесь вложенный запрос и агрегирующая функция – скобки ИМЕЮТ значение
14. Напишите запрос выполняющий выборку данных о студентах, у которых в городе их постоянного местожительства нет университета.
SELECT *
FROM STUDENT
WHERE CITY NOT IN (
SELECT CITY
FROM UNIVERSITY);
15. Напишите запрос, который выполняет выборку значений фамилии всех студентов с указанием для студентов, сдававших экзамены, идентификаторов сданных ими предметов обучения.
SELECT STUDENT.STUDENT_ID, STUDENT.SURNAME, EXAM_MARKS.SUBJ_ID
FROM STUDENT LEFT JOIN EXAM_MARKS ON STUDENT.STUDENT_ID = EXAM_MARKS.STUDENT_ID;
16. Напишите запрос, который выполняет вывод данных о фамилиях студентов, сдававших экзамены, вместе с наименованиями каждого сданного ими предмета обучения.
SELECT STUDENT.STUDENT_ID, STUDENT.SURNAME, SUBJECT.SUBJ_NAME
FROM SUBJECT INNER JOIN
(
STUDENT INNER JOIN EXAM_MARKS
ON STUDENT.STUDENT_ID = EXAM_MARKS.STUDENT_ID
)
ON SUBJECT.SUBJ_ID = EXAM_MARKS.SUBJ_ID
ORDER BY STUDENT.SURNAME;
* Последнюю строку можно не писать – это сортировка, в задании нет
17. Напишите запрос на выдачу для каждого студента названий всех предметов обучения, по которым этот студент получил оценку 4 или 5.
SELECT STUDENT.SURNAME, SUBJECT.SUBJ_NAME
FROM SUBJECT INNER JOIN
(STUDENT INNER JOIN EXAM_MARKS ON STUDENT.STUDENT_ID = EXAM_MARKS.STUDENT_ID)
ON SUBJECT.SUBJ_ID = EXAM_MARKS.SUBJ_ID
WHERE EXAM_MARKS.MARK>3
18. Напишите запрос на выдачу данных о названиях всех предметов, по которым студенты получили только хорошие (4 и 5) оценки. В выходных данных должны быть приведены фамилии студентов, названия предметов и оценка.
SELECT STUDENT.SURNAME, SUBJECT.SUBJ_NAME, EXAM_MARKS.MARK
FROM SUBJECT INNER JOIN (STUDENT INNER JOIN EXAM_MARKS ON STUDENT.STUDENT_ID = EXAM_MARKS.STUDENT_ID) ON SUBJECT.SUBJ_ID = EXAM_MARKS.SUBJ_ID
WHERE EXAM_MARKS.MARK IN (4,5)
19. Напишите запрос, который выполняет вывод списка университетов с рейтингом, превышающим 300, вместе со значением максимального размера стипендии, получаемой студентами в этих университетах.
SELECT UNIVERSITY.UNIV_ID, UNIVERSITY.UNIV_NAME, UNIVERSITY.RATING, Max(STUDENT.STIPEND) AS [Максимальная стипендия]
FROM UNIVERSITY LEFT JOIN STUDENT ON UNIVERSITY.UNIV_ID = STUDENT.UNIV_ID
GROUP BY UNIVERSITY.UNIV_ID, UNIVERSITY.UNIV_NAME, UNIVERSITY.RATING
HAVING UNIVERSITY.RATING>300
20. Напишите команду, которая вводит в таблицу SUBJECT строку для нового предмета обучения со следующими значениями полей:
SEMESTER = 4; SUBJ_NAME = ‘Алгебра’; HOUR = 72; SUBJ_ID =201.
INSERT INTO SUBJECT (SUBJ_ID, SUBJ_NAME, HOUR, SEMESTER)
VALUES (201,’Алгебра’,72,4);
21. Напишите команду, удаляющую из таблицы EXAM_MARKS записи обо всех оценках студента, идентификатор которого равен 100.
DELETE
FROM EXAM_MARKS
WHERE STUDENT_ID=100
22. Измените в таблице значение города, в котором проживает студент Иванов, на «Воронеж».
UPDATE STUDENT
SET CITY = ‘Воронеж’
WHERE SURNAME=’Иванов’;
23. Напишите команду, удаляющую из таблицы SUBJECT сведения о предметах обучения, по которым студентами не получено ни одной оценки.
DELETE
FROM SUBJECT
WHERE SUBJ_ID NOT IN
(SELECT SUBJ_ID
FROM EXAM_MARKS
WHERE SUBJECT.SUBJ_ID = EXAM_MARKS.SUBJ_ID);
24. Напишите запрос, увеличивающий данные о величине стипендии на 20% всем студентам, у которых общая сумма баллов превышает значение 50.
UPDATE STUDENT
SET STIPEND = (STIPEND + (0.2 * STIPEND))
WHERE 50 <
(SELECT SUM(MARK)
FROM EXAM_MARKS
WHERE EXAM_MARKS.STUDENT_ID = STUDENT.STUDENT_ID)

Источник