Сунц мгу вступительные экзамены варианты прошлых лет - Помощь в подготовке к экзаменам и поступлению

Поступление в СУНЦ МГУ давно признано своего рода «счастливым билетом» для ребят, которые мечтают связать свою жизнь с наукой или работой в высокотехнологичных компаниях. Школа, названная в честь крупнейшего математика ХХ века, из года в год выпускает талантливых молодых людей, которые в дальнейшем становятся успешными специалистами, работающими в самых различных сферах. Созданная академиками МГУ в 60-ых годах, СУНЦ МГУ обладает мощнейшей материально-технической базой и сильным профессорско-преподавательским составом, что гарантирует получение в этой школе реальных и востребованных знаний.

История

СУНЦ МГУ – учебное заведение, созданное на базе Московского государственного университета имени М.В. Ломоносова в 1963 году. Оно было открыто по инициативе академика Андрея Николаевича Колмогорова, который стремился обеспечить всем талантливым школьникам возможность получения лучшего физико-математического образования.

Плоды трудов Колмогорова и его коллег стали видны сразу. Уже первый выпуск СУНЦ (1964 г.) подарил стране хорошо подготовленных выпускников, многие из которых, став видными учеными, работают в своей отрасли до сих пор. Этот результат был особенно важен с учетом постоянно растущей в СССР потребности в квалифицированных технических кадрах для поднятия науки и производства по всей стране.

Изначально называвшаяся физико-математической школой-интернатом, СУНЦ МГУ обрела свое нынешнее название в 1989 году, когда сразу после присвоения ей статуса подразделения МГУ она также получила имя своего создателя.

Обучение и преподавательский состав

Профессорско-преподавательский состав образован преимущественно работающими преподавателям и научными сотрудникам МГУ имени М.В. Ломоносова. Многие из них имеют ученые степени и неоднократно отмечались государственными наградами (как в области педагогики, так и в сфере науки). Помимо этого, в учебной работе активно задействованы выпускники самой школы, а также студенты и аспиранты МГУ.

Однако поступление в СУНЦ МГУ – это не просто учеба под началом именитых преподавателей, но еще и глубокое и всестороннее образование по естественным наукам и математике. Главные принципы обучения состоят в формировании научного и критического мышления, развитии творческих способностей. Этому способствует обучение постановке вопросов и методам их решения. При том в обучении активно используются исследовательские проекты, занятия на прикладных математических курсах и семинарах, а также в предметных кружках, современная компьютерная техника и все предоставляемые ею возможности.

Преимущества и достижения школы

СУНЦ МГУ неоднократно признавалась лучшей школой страны (по версии рейтингового агентства RAEX). Критерием оценки неизменно являлся такой важный показатель, как конкурентоспособность выпускников. Статистика гласит, что 60% выпускников школы поступают в МГУ, остальные — в другие ведущие ВУЗы страны и всего мира.

Разумеется, такие успехи были бы невозможны без создания соответствующих бытовых условий для выпускников. Учащиеся школы имеют возможность жить в общежитии, а также получают полноценное ежедневное питание. При этом обучение в школе абсолютно бесплатное.

Поступление в СУНЦ МГУ

Поступление в школу имени Колмогорова подразумевает строгий отбор кандидатов. Необходимость сдачи серьезных экзаменов предполагает наличие большого объема знаний, выходящего за рамки стандартного школьного курса. В связи с этим, желающим быть зачисленными в ряды школы может понадобиться репетитор для поступления в СУНЦ МГУ, специализирующийся на конкретном предмете (прежде всего, математике и физике). Он поможет подготовиться к сложным экзаменам, которые проходят в рамках 2-ух туров.

1 тур

В рамках первого тура поступающим предстоит сдать письменные экзамены по определенным предметами (в зависимости от выбранного направления). Они могут быть сданы в Москве, а также в других городах в рамках выездного экзаменования.

2 тур

2-ой тур вступительных экзаменов проводится в рамках Колмогоровской летней школы. До него допускаются только те участники, которые успешно прошли 1 тур отбора, либо имеющие льготы. Это своего рода летний лагерь с проживанием для иногородних и двухнедельным интенсивным обучением. Форма занятий во время интенсива – семинарская. По его итогам проводится зачеты и экзамены. Также по каждому предмету проходят контрольные работы.

Ниже для примера приведён разбор письменной части вступительного экзамена по математике в 10 класс СУНЦ МГУ за 2017 год.

Письменный вступительный экзамен по математике в СУНЦ МГУ

Задание 1. Петя вышел из дома в школу, рассчитывая прийти вовремя. После 5 минут пути он вспомнил, что забыл взять с собой линейку. Он вернулся домой за линейкой со своей обычной скоростью, посмотрел на часы и понял, что опаздывает в школу. Поэтому он побежал в школу со скоростью, которая вдвое больше скорости его хотьбы. В результате он опоздал в школу на 2 минуты. Сколько времени Петя шёл бы до школы пешком, если бы не возвращался домой за линейкой?

Пусть в обычном режиме путь от дома до школы занимает у Пети минут. Тогда бегом он добирается до школы за $dfrac{t}{2}$ минут. Из-за возвращения домой Петя потерял 10 минут (по 5 минут в обе стороны). Поскольку Петя опоздал на 2 минуты, то имеет место уравнение: $10+dfrac{t}{2}=t+2$ , откуда находим, что минут.

Ответ: 16 минут.

Имеет место равенство: . Требуется найти все натуральные пары , которые бы удовлетворяли этому равенству.

Преобразуем его:

При натуральных и выражения в скобках также натуральные, причём первая скобка меньше второй, и обе скобки положительны. Значит, возможны только следующие случаи:

Первый:

$[ begin{cases} 3p-q = 1 \ 3p+q = 35 end{cases}Leftrightarrow begin{cases} p = 6 \ q=17 end{cases} ]$

Второй:

$[ begin{cases} 3p-q = 5 \ 3p+q = 7 end{cases}Leftrightarrow begin{cases} p = 2 \ q=1 end{cases} ]$

Ответ: , .

Подробный видеоразбор задания:

Пусть первый член прогрессии равен , а знаменатель прогрессии равен . Обратим сразу внимание, что , иначе все члены прогрессии должны быть равны . Но тогда сумма 200 первых членов должна быть вдвое больше суммы 100 первых членов, а это не так. Воспользуемся дважды формулой суммы первых членов геометрической прогрессии, знаменатель которой не равен 1. Тогда получим следующую систему:

$[ begin{cases} dfrac{b_1left(q^{100}-1right)}{q-1}=10 \ dfrac{b_1left(q^{200}-1right)}{q-1}=120 end{cases} ]$

Делим почленно второе уравнение на первое и приходим к уравнению:

$[ dfrac{q^{200}-1}{q^{100}-1}=12 ]$

$[ dfrac{left(q^{100}-1right)left(q^{100}+1right)}{q^{100}-1} = 12 ]$

$[ q^{100} = 11 ]$

Подставим этот результат в первое уравнение системы и получим:

$[ dfrac{b_1}{q-1} = 1 ]$

Тогда для суммы 300 первых членов имеем:

$[ S_{300} = dfrac{b_1left(q^{300}-1right)}{q-1} = 1cdot left(left(q^{100}right)^3-1right) = 1330 ]$

Ответ: 1330.

Задание 4. На катетах прямоугольного треугольника ABC с прямым углом C во внешнюю сторону построены квадраты AKMC и BCTP. Отрезок BK пересекает катет AC в точке B₁, отрезок AP пересекает катет BC в точке A₁. Найдите угол A₁B₁C.

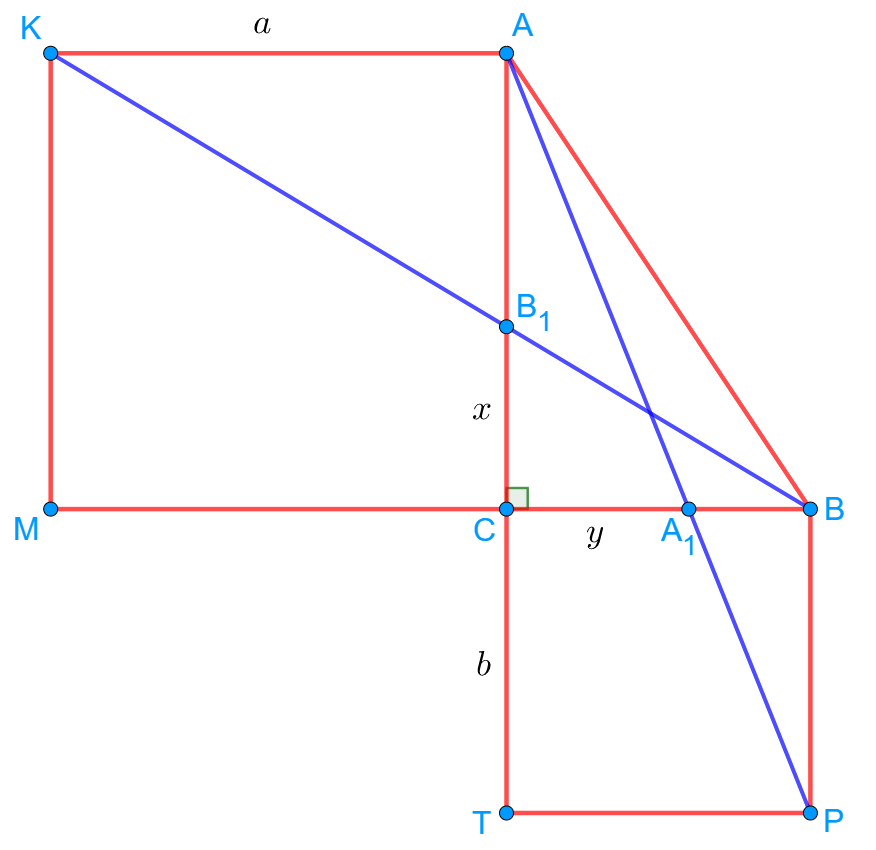
Геометрическая задача из письменного вступительного экзамена по математике в 10 класс СУНЦ МГУ

Пусть AC = CM = MK = AK = и CB = BP = PT = TC = .

Треугольник CB₁B подобен треугольнику KAB₁. Пусть B₁C = . Тогда имеет место соотношение: $dfrac{x}{a-x}=dfrac{b}{a}$ , из которого получаем, что $x = dfrac{ab}{a+b}$ .

Треугольник CA₁A подобен треугольнику PBA₁. Пусть A₁C = . Тогда имеет место соотношение: $dfrac{y}{b-y}=dfrac{a}{b}$ , из которого получаем, что $y = dfrac{ab}{a+b}$ .

То есть B₁C = CA₁, то есть прямоугольный треугольник CB₁A₁ является равнобедренным, поэтому градусная мера угла A₁B₁C равна 45 градусам.

Ответ: 45°.

Задание 5. Найдите сумму действительных корней уравнения

$[ left(x^2+dfrac{1}{x^2}right)+100left(x-dfrac{1}{x}right)+111=0 ]$

Пусть $t = x-dfrac{1}{x}$ . Тогда получаем:

$[ t^2 = left( x-dfrac{1}{x} right)^2 = x^2+dfrac{1}{x^2} - 2 ]$

$[ x^2+dfrac{1}{x^2} = t^2+2 ]$

Тогда получаем уравнение: . Обозначим его дискриминант буквой . Тогда корни этого уравнения равны:

$[ t_{1,2} = dfrac{-100+sqrt{D}}{2} = -50pmsqrt{dfrac{D}{4}} ]$

Возвращаясь к исходной переменной, получаем два уравнения:

$[ x-dfrac{1}{x}=-50-sqrt{dfrac{D}{4}} ]$

$[ x-dfrac{1}{x}=-50+sqrt{dfrac{D}{4}} ]$

Для получаем уравнения:

$[ x^2+left(50+sqrt{dfrac{D}{4}}right)x-1=0 ]$

$[ x^2+left(50-sqrt{dfrac{D}{4}}right)x-1=0 ]$

По теореме Виета сумма действительных корней первого уравнения равна $-50-sqrt{dfrac{D}{4}}$ , а сумма действительных корней второго уравнения равна $-50+sqrt{dfrac{D}{4}}$ . Тогда сумма всех действительных корней исходного уравнения равна .

Ответ: -100.

Репетитор для поступления в СУНЦ МГУ

Чтобы успешно пройти все вступительные испытания, стоит воспользоваться услугами репетитора. Это необязательно, но крайне желательно для тех, кто хочет максимально повысить вероятность успешного принятия в школу. Самостоятельная подготовка даже в течение длительного периода времени не гарантирует больших шансов на успех, поскольку объемность и сложность материала, особенно по математике, могут вызвать затруднения даже у одаренного школьника, успешно закончившего 9 или 10 классов.

В то же время, репетитор для поступления в СУНЦ МГУ поможет целенаправленно подготовиться к сдаче экзаменов обоих туров. Специализация такого преподавателя позволит быть уверенным, что ученик получит именно те знания, которые ему понадобятся. Также этому способствует опыт репетитора, отработанные годами и зарекомендовавшие себя методики. В подготовительном процессе используются варианты заданий прошлых лет, что позволяет более эффективно распорядиться ограниченным запасом времени.

Начать подготовку к поступлению стоит летом. Причем чем раньше, тем лучше, ведь освоить предстоит большой объем учебного материала. Занятия с репетитором можно проводить дистанционно. Учитывая, что в Колмогоровской школе бесплатно даётся образование высочайшего уровня, вложенные в подготовку деньги станут верной инвестицией в будущее.

Если вам требуется подготовка к вступительным экзамена в СУНЦ МГУ, обращайтесь ко мне. Я являюсь репетитором и успешно занимаюсь такого рода подготовкой. Мои контакты вы найдёте на этой странице.

Источник

Алфутова Н. Б.и др. Варианты вступительных экзаменов в Школу имени Л.Н.Колмогорова

Варианты вступительных экзаменов в Школу имени Л.Н.Колмогорова. Составители: Алфутова Н. Б., Загорский В. В., Корнеева Т.П., Смуров М. В., Устинов А. В., — М.: Школа имени А.Н.Колмогорова, «Самообразование», 2000. — 80 с.
В брошюре приведены варианты вступительных экзаменов в Школу имени А. Н.Колмогорова (по математике, физике и химии), которые проводились в 1995 -1999 годах. Большая часть задач по математике и химии сопровождается подробными решениями, к остальным задачам даны ответы и указания. С полными решениями разобраны варианты заочных и устных экзаменов по физике.
Для школьников, преподавателей, руководителей кружков.

Содержание
Предисловие…………….3
Новый прием…………….5
Математика……………..6
Физика………………7
Химия………………8
Математика…………9
Условия задач ………….9
Ответы, указания и решения…………29
Физика………..48
Заочный экзамен…………..48
Задачи устного экзамена………..57
Химия…………67
Весна- 1996…………..67
Весна 1997…………..70
Весна — 1998…………..72
Лето- 1998…………….74
Весна-1999…………..75

Источник

Демонстрационные варианты вступительных тестов

Հայերենով ուսուցմամբ դասարաններ
- 7 դասարան
  - Հայոց լեզու
    - Թեստ 1
    - Թեստ 2
    - Թեստ 3
  - Մաթեմատիկա
    - Թեստ 1
- 8 դասարան
  - Հայոց լեզու
    - Թեստ 1
    - Թեստ 2
    - Թեստ 3
  - Մաթեմատիկա
    - Թեստ 1
- 9 դասարան
  - Հայոց լեզու
    - Թեստ 1
    - Թեստ 2
    - Թեստ 3
  - Մաթեմատիկա
    - Թեստ 1
- 10, 11, 12 դասարան
  - Հայոց լեզու
    - Թեստ 1
    - Թեստ 2
    - Թեստ 3
    - Թեստ 4
    - Թեստ 5
    - Թեստ 6
    - Թեստ 7
  - Մաթեմատիկա
    - 10 դասարան
      - Թեստ 1
    - 11 դասարան
      - Թեստ 1
    - 12 դասարան
      - Թեստ 1
Классы с русским языком обучения
- 7 класс
  - Математика
    - Тест 1
    - Тест 2
  - Русский язык
    - Тест 1 (2021)
    - Тест 2 (2021)
    - Тест 3 (2021)
    - Тест 4 (2021)
    - Тест 5 (2022)
- 8 класс
  - Русский язык
    - Тест 1 (2021)
    - Тест 2 (2021)
    - Тест 3 (2021)
    - Тест 4 (2022)
  - Математика
    - Тест 1
- 9 класс
  - Русский язык
    - Тест 1 (2021)
    - Тест 2 (2021)
    - Тест 3 (2021)
    - Тест 4 (2022)
  - Математика
    - Тест 1
- 10, 11, 12 класс
  - Русский язык
    - Тест 1
    - Тест 2
    - Тест 3
    - Тест 4
    - Тест 5
    - Тест 6
  - Математика
    - 10 класс
      - Тест 1
    - 11 класс
      - Тест 1
    - 12 класс
      - Тест 1

Источник