Сессия — страшное слово для любого студента. Учащиеся не спят ночами, пытаясь выучить ответы на все билеты. Хорошо, если у преподавателя есть чувство юмора и он добавит в стопку экзаменационных билетов один счастливый. Тогда остаётся надеяться только на свою удачу. Собрали для вас билеты, которые способны осчастливить любого студента. А вы сталкивались с таким везением?
«Ридус» поздравляет всех учащихся с Днём студента и желает каждому вытянуть счастливый билет не только на экзамене, но и в жизни!
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
Каждый человек в той или иной мере применяет теорию вероятности для анализа произошедших в его жизни событий. Люди обращают внимание на вероятность вещей и прогнозируют свое дальнейшие поведение. Но к большому сожалению, не всегда возможны точно определить вероятность того или иного события. [1,3]
Примеров реального использования теории вероятности в жизни огромное множество. Так, практически вся современная экономика базируется на ней. В общем, можно сказать, что теория вероятности будет иметь большое значение в начале практически любой деятельности, а так же в её регулировании. Она дает возможность оценить шансы той или иной неполадки, позволяет нам понять, что нужно проверить и какие усилия необходимо предпринять, исходя из полученных данных. [5]
Любую деятельность любой сферы можно проанализировать, используя статистику, рассчитать благодаря теории вероятности и заметно улучшить.
Попробуем составить собственный алгоритм для решения задач по теории вероятности: [2,4]
Необходимо ознакомится с условием задачи и понять какие действия, с какими предметами выполняются.
Определить ключевой вопрос задачи и обозначить событие, вероятность которого необходимо вычислить.
Чтобы выбрать дальнейшую последовательность действий следует конкретизировать тип задачи и выяснить, какие формулы будут использоваться в дальнейшем для её решения.
Исходя из ответов на приведенные вопросы, выбрать формулы и подставить в них данные задачи.
Готово, вероятность найдена.
Одно из важных событий в жизни любого студента – это сессия. Это то время, когда нервничают все, включая отличников. Ведь всегда существует вероятность не сдать экзамен. Чтобы этого не произошло необходимо соблюдать десятки различных примет, можно даже обратиться к нумерологии. Но один из простых способов вытянуть счастливый билет – рассчитать вероятность его выпадения.
Составим и решим несколько простыхзадач, на примере которых каждый студент может вычислить вероятность выпадения счастливого билета на экзамене. [6]
Задача 1. «На экзамене по математике шесть студентов второго курса факультета агробиологии и земельных ресурсов друг за другом вытягивают билеты. Тридцать билетов включают в себя четыре простых вопроса. Необходимо вычислить вероятность, что хотя бы одному студенту попадется билет с простыми вопросами».
Решение: В первую очередь, определим ключевой вопрос задачи — вычислить вероятность, что хотя бы одному студенту попадется билет с простыми вопросами.
Далее пойдем от обратного, найдем вероятность того, что никому из студентов не попадется простой билет.
Эта вероятность будет равна
Первая дробь показывает вероятность того, что билет со сложным вопросом достался первому студенту.
Вторая дробь показывает вероятность того, что билет со сложным вопросом достался второму студенту. Третья дробь показывает вероятность того, что билет со сложным вопрос достался третьему студенту и так далее до шестого студента. Так как в задаче требуется одновременное выполнение условий, то вероятности следует перемножить.
Для того, чтобы найти искомую вероятность, надо вычесть полученную выше вероятность из единицы.
Задача 2. Леша, студент второго курса факультета механизации сельского хозяйства, сдаёт экзамен по теоретической механике, при этом из 50 билетов 35 он знает хорошо, а 15 плохо. Допустим, группа сдаёт экзамен по частям. В первый день 15 человек, включая Алексея. В каком случае Леше достанется с большей вероятностью «счастливый» билет — если он пойдет на экзамен в числе первых, в середине или же будет тянуть билет последним? Когда ему лучше зайти в кабинет?
Для начала рассмотрим случай, при котором Леша сохраняет свои шансы постоянными, то есть он не знает какие билеты вытянули однокурсники и не учит вопросы, которые знает плохо.
Пусть Алексей зайдет в аудиторию первым и вытянет «счастливый» билет, обозначим это событие . По классическому определению вероятности:
Может ли измениться вероятность извлечения нужного билета, если пропустить вперед отличника Жору? В этом случае станут возможными две несовместимые гипотезы:
— Жора вытянет «счастливый» (для Леши) билет;
— Жора вытянет «несчастливый» билет, таким образом, увеличивая шансы Леши.
Событие, при котором Леша зайдет вторым и вытянет «счастливый» билет становится зависимым.
1) Можно предположить, что Жора с вероятностью забрал у Леши «удачный» билет. Тогда останется всего 49 билетов, среди которых 34 «Счастливых». По классическому определению вероятности:
2) Допустим, что Жора с вероятностью «спас» Лешу от одного сложного билета. В этом случае останется 49 билетов, 35 из которых «счастливые». Тогда по классическому определению вероятности:
Воспользовавшись теоремами сложения вероятностей несовместных и умножение вероятностей зависимых событий, определим вероятность, что Леша вытянет «счастливый» билет, будучи вторым в очереди:
Вероятность не изменилась.
Рассмотрим следующее событие , при котором Леша пойдет третьим, пропустив перед собой Жору и Леру, и вытянет «счастливый» билет.
В данном событии гипотез будет больше: однокурсники могут забрать два удачных билета или же два неудачных, так же вытянуть один «счастливый» билет и один «несчастливый» билет. Проведем аналогичные рассуждения, воспользуемся теми же теоремами и получим значение вероятности . И так далее.
Следовательно, не важно, когда идти – первоначальные вероятности останутся неизменными. Но нужно помнить, что это лишь усредненная теоретическая оценка. Если Леша пойдет последним на экзамен, то это не значит, что ему достанутся на выбор 17 «счастливых» билетов и 19 «несчастливых» билетов в соответствии с его изначальными шансами. Это соотношение может изменяться, как в лучшую, так и в худшую сторону. Однако, маловероятно, что среди билетов останутся одни «счастливые» или же наоборот — «несчастливые».
Математика и «чистый эксперимент» — это хорошо, но чего следует придерживаться в реальных условиях? Нужно принять во внимание субъективные факторы, такие как дополнительный балл для «храбрецов» или же усталость преподавателя в конце экзамена. Часто они могут решающими факторами.
В случае, если вы хорошо подготовились к экзамену, то лучше идти в числе первых, так как есть полный комплект билетов, постулат «мало возможные события не происходят» работает в большей степени.
Если же студент готов к экзамену достаточно хорошо, но пробелы в знаниях всё-таки есть, то будет целесообразно пропустить вперед несколько человек и ожидать подходящего момента вне аудитории. Здесь нужно действовать по ситуации, когда начнет поступать информация о вытянутых билетах, и можно будет учить и повторять оставшиеся билеты, повышая первоначальную вероятность своего успеха.
В случае, если вы готовы неважно или плохо, то лучше идти в последнюю очередь. Существует небольшая вероятность, что останутся «счастливые» для вас билеты, вы можете изучить материал за время экзамена или же (в крайнем случае) сделать «шпаргалку».
Никогда невозможно точно предугадать, что произойдет с нами через день, два. Ведь событий связанных с нами в каждый момент невероятно много. Безусловно, мало кто будет высчитывать по формулам вероятность появления событий, но иногда бывает интересно проверить совпадает ли «эмпирический анализ» с математическим. Теория вероятности позволяет предугадать лишь однотипные события. Именно поэтому её применение связанно с большим количеством условий и ограничений, существуют такие задачи, вычисления в которых можно провести лишь с использованием компьютера.
Список литературы
Бондаренко В.А., Цыплакова О.Н. Задачи с экономическим содержанием на занятиях по дифференциальному исчислению / Актуальные вопросы теории и практики бухгалтерского учета, анализа и аудита: ежегодная 75-я научно-практическая конференция. Редколлегия: В.З. Мазлоев, А.В. Ткач, И.С. Санду, И.Ю. Скляров, Е.И. Костюкова, ответственный за выпуск А.Н. Бобрышев. — 2011. — С. 124-127.
Гулай Т.А., Жукова В.А., Мелешко С.В., Невидомская И.А. Математика / рабочая тетрадь / Ставрополь, 2015.
Литвин Д.Б., Гулай Т.А., Жукова В.А., Мамаев И.И. Модель экономического роста с распределенным запаздыванием в инвестиционной сфере / Вестник АПК Ставрополья. 2017. № 2 (26). С. 225-228.
Математика. Теория вероятностей и случайные величины: рабочая тетр.; учеб. пособие для студентов вузов по направлениям: 38.03.04 – «Гос. муницип. упр.», 38.03.05 – «Бизнес-информатика»/Т.А.Гулай, В.А.Жукова, С.В.Мелешко, И.А. Невидомская; СтГАУ. –Ставрополь: Сервисшкола, 2016.
Элементы теории вероятностей случайных событий. Рабочая тетрадь/ И.А. Невидомская, С.В. Мелешко,Т.А. Гулай. — Ставрополь.: Сервисшкола, — 2015.
Теория вероятностей для экономических специальностей на базе Excel (практикум)/Долгополова А.Ф., Морозова О.В., Долгих Е.В., Крон Р.В., Тынянко Н.Н., Попова С.В., Смирнова Н.Б.//Международный журнал экспериментального образования. 2009. № S4. С. 19
Как вытащить счастливый билет на экзамене?
97 ответов
Последний —
06 июня 2022, 13:12
Перейти
ТРОЛЛейбус
когда будеш тянуть билет,как размахнись рукой,и с закрытими глазами)
15 января 2012, 20:31
#10
15 января 2012, 20:35
#11
Golden
Обычно третий слева билет именно тот, который «ваш». Попробуйте, у меня всегда прокатывало
15 января 2012, 20:37
#12
Гость
берите первый.что под руку попадется.
наобум.
не выбирайте и не думайте.протянули руку и взяли.будете выбирать,самый сложный вытащите.)
15 января 2012, 20:56
#13
15 января 2012, 20:59
#14
Гость
А если все в куче лежит? ) У нас на самом сложном экзамене с самым строгим преподом было именно так ) Что п не просвечивало он так наверное складывал.
15 января 2012, 21:56
#15
Гость
Если билеты лежат в кучи,то это вообще легко!! Берёте любой билет (вы выучили, например,12) ,вам попался другой. Потм кидаете этот билет обратно в кучу с криком :»только не 12″ . Учитель спецально находит 12 билет в куче и отдаёт его вам.
Эксперты Woman.ru
-
Владимир Титаренко
Фитнес-нутрициолог
187 ответов
-
Алёшина Мария
Психолог
117 ответов
-
Иванова Светлана
Коуч
86 ответов
-
Анна Антончик
Женский психолог
163 ответа
-
Максим Сорокин
Практикующий психолог
1 053
-
Международный Институт
Психология, психотерапия,…
20 ответов
-
Токарь Дарья Анатольевна
Фитнес-тренер
53 ответа
-
Мария Бурлакова
Психолог
335 ответов
-
Мария Синяпкина
Психолог-Сексолог
92 ответа
-
Кременецкая Мария
Логопед — дефектолог
44 ответа
24 января 2014, 23:07
#42
Гость
АА ЗАВТРА МНЕ ТОЖЕ ТЯНУТЬ БИЛЕТ((((((
My name
Лучше бы билеты учили, а не в Интернете юзали)
- Авторы
- Резюме
- Файлы
- Ключевые слова
- Литература
Ревегук Ю.А.
1
Рудикова Е.С.
1
1 ФГБОУ ВО «Ставропольский государственный аграрный университет»
Вокруг нас происходит так много вещей и событий, которые, несмотря на уровень развития науки, трудно спрогнозировать. Сложно предугадать с каким номером выпадет бочонок при игре в лото или сколько будет солнечных дней в году. Но при этом, имея дополнительные сведения, возможно прогнозировать и вычислять вероятность таких событий. В данной статье идет речь о теории вероятности, составлен алгоритм решения задач по этой теме, а так же приведены примеры, с помощью которых возможно вычислить вероятность выпадения «счастливого» билета на экзамене. Теория вероятности – это отличный помощник, при предсказании наступления определенного события, в том числе выпадения «счастливого» билета на экзамене. Простые формулы позволяют провести расчеты любому человеку.
теория вероятности
«счастливый» билет
задачи
1. Бондаренко В.А., Цыплакова О.Н. Задачи с экономическим содержанием на занятиях по дифференциальному исчислению // Актуальные вопросы теории и практики бухгалтерского учета, анализа и аудита: ежегодная 75-я научно-практическая конференция / Редколлегия: В.З. Мазлоев, А.В. Ткач, И.С. Санду, И.Ю. Скляров, Е.И. Костюкова, ответственный за выпуск А.Н. Бобрышев, 2011. – С. 124–127.
2. Гулай Т.А., Жукова В.А., Мелешко С.В., Невидомская И.А. Математика: рабочая тетрадь. – Ставрополь, 2015.
3. Литвин Д.Б., Гулай Т.А., Жукова В.А., Мамаев И.И. Модель экономического роста с распределенным запаздыванием в инвестиционной сфере // Вестник АПК Ставрополья. – 2017. – № 2 (26). – С. 225–228.
4. Математика. Теория вероятностей и случайные величины: рабочая тетр.; учеб. пособие для студентов вузов по направлениям: 38.03.04 – «Гос. муницип. упр.», 38.03.05 – «Бизнес-информатика» / Т.А. Гулай, В.А. Жукова, С.В. Мелешко, И.А. Невидомская; СтГАУ. – Ставрополь: Сервисшкола, 2016.
5. Элементы теории вероятностей случайных событий: Рабочая тетрадь / И.А. Невидомская, С.В. Мелешко, Т.А. Гулай. – Ставрополь: Сервисшкола, 2015.
6. Теория вероятностей для экономических специальностей на базе Excel (практикум) / А.Ф. Долгополова, О.В. Морозова, Е.В. Долгих, Р.В. Крон, Н.Н. Тынянко, С.В. Попова, Н.Б. Смирнова // Международный журнал экспериментального образования. – 2009. – № S4. – С. 19.
Каждый человек в той или иной мере применяет теорию вероятности для анализа произошедших в его жизни событий. Люди обращают внимание на вероятность вещей и прогнозируют свое дальнейшие поведение. Но к большому сожалению, не всегда возможны точно определить вероятность того или иного события [1, 3].
Примеров реального использования теории вероятности в жизни огромное множество. Так, практически вся современная экономика базируется на ней. В общем, можно сказать, что теория вероятности будет иметь большое значение в начале практически любой деятельности, а так же в её регулировании. Она дает возможность оценить шансы той или иной неполадки, позволяет нам понять, что нужно проверить и какие усилия необходимо предпринять, исходя из полученных данных [5].
Любую деятельность любой сферы можно проанализировать, используя статистику, рассчитать благодаря теории вероятности и заметно улучшить.
Попробуем составить собственный алгоритм для решения задач по теории вероятности [2, 4]:
1. Необходимо ознакомится с условием задачи и понять какие действия, с какими предметами выполняются.
2. Определить ключевой вопрос задачи и обозначить событие, вероятность которого необходимо вычислить.
3. Чтобы выбрать дальнейшую последовательность действий следует конкретизировать тип задачи и выяснить, какие формулы будут использоваться в дальнейшем для её решения.
4. Исходя из ответов на приведенные вопросы, выбрать формулы и подставить в них данные задачи.
5. Готово, вероятность найдена.
Одно из важных событий в жизни любого студента – это сессия. Это то время, когда нервничают все, включая отличников. Ведь всегда существует вероятность не сдать экзамен. Чтобы этого не произошло необходимо соблюдать десятки различных примет, можно даже обратиться к нумерологии. Но один из простых способов вытянуть счастливый билет – рассчитать вероятность его выпадения.
Составим и решим несколько простыхзадач, на примере которых каждый студент может вычислить вероятность выпадения счастливого билета на экзамене [6].
Задача 1. «На экзамене по математике шесть студентов второго курса факультета агробиологии и земельных ресурсов друг за другом вытягивают билеты. Тридцать билетов включают в себя четыре простых вопроса. Необходимо вычислить вероятность, что хотя бы одному студенту попадется билет с простыми вопросами».
Решение. В первую очередь, определим ключевой вопрос задачи – вычислить вероятность, что хотя бы одному студенту попадется билет с простыми вопросами.
Далее пойдем от обратного, найдем вероятность того, что никому из студентов не попадется простой билет.
Эта вероятность будет равна
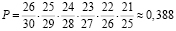
Первая дробь 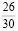
Вторая дробь 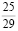
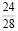
Для того, чтобы найти искомую вероятность, надо вычесть полученную выше вероятность из единицы.
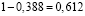
Задача 2. Леша, студент второго курса факультета механизации сельского хозяйства, сдаёт экзамен по теоретической механике, при этом из 50 билетов 35 он знает хорошо, а 15 плохо. Допустим, группа сдаёт экзамен по частям. В первый день 15 человек, включая Алексея. В каком случае Леше достанется с большей вероятностью «счастливый» билет – если он пойдет на экзамен в числе первых, в середине или же будет тянуть билет последним? Когда ему лучше зайти в кабинет?
Для начала рассмотрим случай, при котором Леша сохраняет свои шансы постоянными, то есть он не знает какие билеты вытянули однокурсники и не учит вопросы, которые знает плохо.
Пусть Алексей зайдет в аудиторию первым и вытянет «счастливый» билет, обозначим это событие 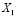
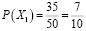
Может ли измениться вероятность извлечения нужного билета, если пропустить вперед отличника Жору? В этом случае станут возможными две несовместимые гипотезы:
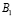
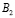
Событие 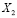
1) Можно предположить, что Жора с вероятностью
забрал у Леши «удачный» билет. Тогда останется всего 49 билетов, среди которых 34 «Счастливых». По классическому определению вероятности:
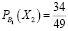
2) Допустим, что Жора с вероятностью
«спас» Лешу от одного сложного билета. В этом случае останется 49 билетов, 35 из которых «счастливые». Тогда по классическому определению вероятности:
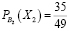
Воспользовавшись теоремами сложения вероятностей несовместных и умножение вероятностей зависимых событий, определим вероятность, что Леша вытянет «счастливый» билет, будучи вторым в очереди:
Вероятность не изменилась.
Рассмотрим следующее событие 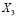
В данном событии гипотез будет больше: однокурсники могут забрать два удачных билета или же два неудачных, так же вытянуть один «счастливый» билет и один «несчастливый» билет. Проведем аналогичные рассуждения, воспользуемся теми же теоремами и получим значение вероятности
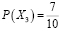
И так далее.
Следовательно, не важно, когда идти – первоначальные вероятности останутся неизменными. Но нужно помнить, что это лишь усредненная теоретическая оценка. Если Леша пойдет последним на экзамен, то это не значит, что ему достанутся на выбор 17 «счастливых» билетов и 19 «несчастливых» билетов в соответствии с его изначальными шансами. Это соотношение может изменяться, как в лучшую, так и в худшую сторону. Однако, маловероятно, что среди билетов останутся одни «счастливые» или же наоборот – «несчастливые».
Математика и «чистый эксперимент» – это хорошо, но чего следует придерживаться в реальных условиях? Нужно принять во внимание субъективные факторы, такие как дополнительный балл для «храбрецов» или же усталость преподавателя в конце экзамена. Часто они могут решающими факторами.
В случае, если вы хорошо подготовились к экзамену, то лучше идти в числе первых, так как есть полный комплект билетов, постулат «мало возможные события не происходят» работает в большей степени.
Если же студент готов к экзамену достаточно хорошо, но пробелы в знаниях всё-таки есть, то будет целесообразно пропустить вперед несколько человек и ожидать подходящего момента вне аудитории. Здесь нужно действовать по ситуации, когда начнет поступать информация о вытянутых билетах, и можно будет учить и повторять оставшиеся билеты, повышая первоначальную вероятность своего успеха.
В случае, если вы готовы неважно или плохо, то лучше идти в последнюю очередь. Существует небольшая вероятность, что останутся «счастливые» для вас билеты, вы можете изучить материал за время экзамена или же (в крайнем случае) сделать «шпаргалку».
Никогда невозможно точно предугадать, что произойдет с нами через день, два. Ведь событий связанных с нами в каждый момент невероятно много. Безусловно, мало кто будет высчитывать по формулам вероятность появления событий, но иногда бывает интересно проверить совпадает ли «эмпирический анализ» с математическим. Теория вероятности позволяет предугадать лишь однотипные события. Именно поэтому её применение связанно с большим количеством условий и ограничений, существуют такие задачи, вычисления в которых можно провести лишь с использованием компьютера.
Библиографическая ссылка
Ревегук Ю.А., Рудикова Е.С. ВЕРОЯТНОСТЬ ВЫПАДЕНИЯ «СЧАСТЛИВОГО» БИЛЕТА НА ЭКЗАМЕНЕ // Международный студенческий научный вестник. – 2018. – № 3-1.
;
URL: https://eduherald.ru/ru/article/view?id=18220 (дата обращения: 12.03.2023).
Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»
(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)
Сессия – неизбежное событие в жизни любого студента. Все понимают, что для успешной сдачи экзамена нужно знать ответы на вопросы билетов. Но далеко не всегда удается хорошо подготовиться, поэтому в критические моменты многие готовы поверить во что угодно и ищут даже не совсем рациональные способы, как вытянуть нужный билет на экзамене. Студенческий фольклор хранит богатую антологию примет и заговоров, которые помогают удачно сдать сессию. Шансы вытянуть нужные вопросы невелики, но когда другого выхода нет, говорят, и соломинка помогает.
Содержание
- Приметы, заговоры на удачу, талисманы
- Приметы и заговоры
- Талисманы
- Нумерология
- Помощь одногруппников
- Видео по теме
- Комментарии
Приметы, заговоры на удачу, талисманы
Как показывает практика, легкий билет попадается только тем, кто старательного готовится к экзаменам. Те, кто не смог выучить весь материал, могут воспользоваться приметами, которые придадут уверенности в собственных силах, настроят на удачу и помогут вытащить нужный билет на экзамене.
Некоторые преподаватели раскладывают билеты по возрастанию или в шахматном порядке, поэтому можно попробовать предугадать или понять, как расположены задания.
Приметы и заговоры
- Визуализация. Многие, кто уже не раз сдавал сессию, заверяют, что если за пару дней до экзаменов представить себе нужный билет, то он непременно
попадется.
- Если смазать руки медом или сладким сиропом перед тем, как вытягивать билет, то непременно попадутся те вопросы, которые знаешь лучше всего.
- Также можно подержаться за отличника перед тем, как заходить в аудиторию, где происходит сдача экзамена. Лучше всего выбрать того, кто уже успел получить хорошую оценку.
- Студенты верят, если надеть обувь не на ту ногу, бдительность экзаменатора снизится, а удача не заставит себя ждать.
- «Шара, приди!» Это один из наиболее известных способов призвать удачу. В ночь перед экзаменом студент должен высунуть в окно зачетку и позвать Шару, после чего удача ему обеспечена. Можно использовать другой текст – «Сегодня помашу, а завтра сдам».
- Еще один эффективный заговор необходимо использовать непосредственно перед вытягиванием билета. Следует сказать: «Чур, его, что знаю – ко мне!»
- Считается, что беременные женщины имеют развитую интуицию, поэтому попросите будущую маму предсказать номер билета. С аналогичной просьбой можно обратиться и к своей маме.
Берите билет, который приглянулся сразу, не думая и не гадая.
В топ-10 экзаменационных примет, составленный Росстуденчеством по результатам опроса учащихся вузов, кроме затоптанного поколениями студентов пятака под пяткой, кстати, разных веков эмиссии и, соответственно, фактического номинала, вошли и новшевства интернет-эры вроде сохранения на компьютере файла с ответами на вопросы экзамена под названием, к примеру, «социология на отлично».
Талисманы
Некоторые студенты для полной уверенности используют талисманы на удачу, веря, что это поможет вытащить счастливый билет на экзамене.
- Уже не одно поколение подкладывает в левый ботинок пятикопеечную монету, веря, что металл благополучно влияет на определенные зоны на пятке и позволяет активировать интуицию.
- Талисман в виде небольшой игрушки или фигурки в форме змеи и совы повышает сообразительность, добавляет мудрости.
- Также можно использовать простую нитку или шнурок в виде браслета на левое запястье, предварительно завязав девять узлов.
Талисманом может быть любая вещь или предмет, которая ассоциируется у студента с удачей и везением, – некоторые надевают «счастливые носки» или идут на экзамен с любимой ручкой.
Нумерология
Если вы еще не знаете, как выбрать нужный билет на экзамене, воспользуйтесь правилами нумерологии – науки (некоторые утверждают, что обязательно надо добавлять приставку псевдо-) о связи чисел и физических объектов.
- Постарайтесь наперед просчитать, каким по счету вы будете сдавать экзамен. Лучший вариант – нечетные цифры, особенно три и семь.
- Билет под нечетным номером будет счастливым.
- Выбирая билет, отдайте предпочтение тому, что лежит в нечетном ряду. Никогда не тяните вопросы из четного ряда, расположенные на четном месте.
Нумерологи утверждают, что четные значения имеют негативную энергетику.
Помощь одногруппников
Полагаться только на удачу и потусторонние силы не стоит. Угадать, какой билет попадется на экзамене, можно с помощью одногруппников – этот путь выглядит куда более многообещающим.
- Попросите товарища «случайно» вытянуть два билета. Один он должен оставить себе, а другой запомнить и пометить для вас, что позволит заранее подготовить необходимые шпаргалки, повторить материал билета.
- Весьма результативный вариант узнать, какой билет попадется на экзамене, – это сдавать его в числе последних. Этим методом можно воспользоваться, если все вытянутые билеты откладываются и не возвращаются обратно на стол. Спрашивайте одногруппников, которые уже сдали экзамен, что им попалось, вычеркивайте номера из списка и готовьте оставшиеся задания.
И все-таки, самый надежный способ хорошо сдать экзамен – основательно подготовиться к нему. Если каждый день учить всего по несколько вопросов, то к началу экзамена будет выучена большая часть из них, что значительно увеличивает вероятность вытянуть билет, ответы на вопросы которого известны.

Экзамен — страшное слово для любого студента. Преподаватели пытаются помочь своим ученикам и по возможности уменьшить их стресс, при этом в ход идут совершенно разные методы. Некоторые даже начали добавлять в стопку экзаменационных билетов «счастливые», которые дают возможность получить оценку неожиданно просто. Конечно, это не значит, что так надо делать всем и везде, но все-таки приятно осознавать, что такие случаи существуют. Просто представьте себе радость того, кто такой билет вытянул 🙂
Мы в Twizz собрали для вас 15 примеров таких вот счастливых билетов, глядя на которые студенты не могли поверить своим глазам. А вы сталкивались с такой удачей?
Готов ответить оба!
С таким билетом в руках с честностью проблем не будет
На третьем бы не затупить
Бывает и так
13 — это не всегда плохо
Для фанатов «Игры престолов»
Весьма приятный бонус
Вопрос из теста у медиков
Тот же счастливый тест
Не ложился
Даже такое бывает
А мне нравится эта контрольная!
Все
Этот преподаватель явно «на одной волне» со своими студентами
Даже дважды
❤️ Подписывайтесь! У нас крутые посты каждый день
Многие из нас хотят попытать свою удачу даже в обычных мелочах. Например, когда в транспорте попадается так называемый счастливый билет, появляется какой-то азарт. Пусть это и мелочь, но приятная и поднимающая настроение. Ну а определить, счастливый билет это или нет, очень просто. Каждый сможет проверить свое везение, находясь в дороге.
Определение счастливого билета
Основа счастливого билета заключается в цифрах на его нижней части. Главной считается обычная цифровая последовательность при получении проездного в маршрутке или трамвае. Удачливый билет в основном определяется шестизначным числом, но редко бывают и нечетные цифры.
Чтобы понять, какой попался талон, используем несколько интересных способов. Один из данных методов называется ленинградским. Он основан на подсчете парных и непарных чисел, сумма которых должна совпасть. Самый популярный и востребованный — московский стиль. В нем нужно сложить первых три числа, а потом вторую тройку — и их сумма должна совпасть.
Жители Новосибирска считают счастливым билетик тогда, когда с одной и с другой стороны находятся одинаковые числа. Еще один способ – это суммирование каждой предоставленной пары чисел. Если совпадают все три числа, тогда билет принесет удачу.
Еще немного о вычислении
Для каждого человека существует личное число, которое привязано к нему. Например, дата рождения, Число Души и т. д. Есть люди, которым известно, какое именно число приносит им успех в делах. Если вам попался номер билета с таким числом в сумме, он непременно знаменует удачу. Так называемый развивающий проездной билет — один из самых интересных. Для его вычисления нужно перемножить все имеющие числа, из производного отнять число их суммы. Если ответ выйдет ноль, то талон непременно принесет удачу. А приносит успех билет, который имеет ряд одинаковых чисел, при этом совпадает и их сумма.
Развлечение в дороге
В дороге можно сыграть в одну простую, но короткую игру. При этом, как определить, счастливый билет принесет удачу или нет, очень просто. В игре могут принимать участие от двух и более людей. Правила заключаются в подсчете всех чисел и определении наибольшей суммы числа. У кого самая высокая — тот победил, а у кого самая маленькая, тот получает щелбаны. Такая игра развивает умение быстро считать, а также азарт. Количество ударов устанавливается разницей между выигравшим и проигравшим человеком.
Гадание на попавшихся билетах
Как определить счастливый билет, мы выяснили. А как гадать на нем и что его результаты обозначают? Для проведения ворожбы стоит посчитать все числа. Далее полученное нужно суммировать — и мы получим число, которое что-то значит. К примеру билет с номером 333333 дает нам в сумме 18. В итоге для определения результата нужно добавить к восьми один. И мы получим девять. Каждая цифра имеет свое значение. 3 – к удаче, 9 – к свиданию и так далее.
Еще один способ заключается в сложении первых трех, а потом трех последних чисел. Далее нужно выяснить разницу предоставленных чисел. Еще таким образом можно понять, как определить счастливый билет, а вернее, какого числа не хватило до него, если это обычный проездной. По данному числу и можно определить будущее человека.
Также интересно распределение талона по определенным ролям. Например, студенческий удачный проездной или школьный билет. Студенческий счастливый талон показывает те числа, которые будут иметь выбранные вами билеты на экзамене. По такому принципу действует и школьный проездной. Удача сопутствует номерам заданий контрольной работы.
Помимо того, что билеты бывают везучими, так они могут быть еще в придачу красивыми. Все же редко, но случается и такое, что счастливый проездной билет имеет отличную комбинацию и внешний вид. Такие проездные порой отличает необычный, а самое главное, интригующий рисунок. Либо у билетика может быть нестандартный цвет. Такой проездной документ непременно нужно сохранить, и он будет приносить удачу и радовать глаз.
Таким образом, как определить счастливый билет в транспортном средстве, мы разобрали. С помощью проездного можно гадать, предсказывать судьбу. По числам билета определяют счастливые дни. А также не забываем про развлечения, которые можно воплотить с ними в жизнь. Самое главное при обнаружении счастливого талона — оставить его при себе. Тогда он точно принесет пользу и счастье владельцу.


















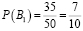
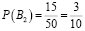
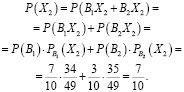
 попадется.
попадется.

















