Таблица производных егэ профильный - Помощь в подготовке к экзаменам и поступлению

Таблица производных и правила дифференцирования

О том, что такое производная, мы рассказали в статье «Геометрический смысл производной». Если функция задана графиком, её производная в каждой точке равна тангенсу угла наклона касательной к графику функции. А если функция задана формулой — вам помогут таблица производных и правила дифференцирования, то есть правила нахождения производной.

Для решения задач на исследование функции в вариантах ЕГЭ необходима таблица производных и правила дифференцирования, а также знания о том, как связана производная с поведением функции.

Смотри также, как решаются задачи ЕГЭ на применение производной: задача 7 и задача 11.

Прокомментируем несколько строк из таблицы производных.

1. Производная постоянной величины, то есть константы, равна ей самой. Так и должно быть. Ведь константа не меняется. Это постоянная величина, она всегда принимает одинаковые значения.

А производная функции, как мы знаем, – это скорость изменения функции. Подробнее об этом здесь:
Производная функции.
И поэтому производная константы равна нулю.

2. Производная функции у=х равна 1. Вспомним, что производная функции в точке – это тангенс угла наклона касательной, проведенной к графику функции в этой точке. График функции у=х образует угол 45 градусов с положительным направлением оси Х. А тангенс 45 градусов равен 1.

3. Производная функции $y=e^{x}$ равна самой этой функции. И действительно, чем больше значение х, тем больше значение функции $y=e^{x}$ … и тем круче вверх идет график по отношению к оси Х. Вот такая это функция, экспонента. Чем дальше, тем быстрее она растет.

4. Производная синуса и косинуса – тоже тригонометрические функции. Например, производная синуса – это косинус. Как это отражается в физике? Если координата тела меняется по закону синуса, то производная координаты, скорость, будет меняться по закону косинуса. Это описание гармонических колебаний: и координата, и скорость, и ускорение тела меняются по законам синуса и косинуса.

5. Производная логарифма в точке $x_{0}$ обратно пропорциональна $x_{0}$ . Чем дальше, тем медленнее растет логарифмическая функция.

Вспомним, как связаны производная и поведение функции.

Если производная {f} положительна, то функция f(x) возрастает.

Если производная отрицательная, то функция убывает.

В точке максимума производная равна нулю и меняет знак с «плюса» на «минус».

В точке минимума производная тоже равна нулю и меняет знак с «минуса» на «плюс».

Запишем эти выводы в виде таблицы:

	возрастает	точка максимума	убывает	точка минимума	возрастает
	+	0	—	0	+

Разберем задачи ЕГЭ по теме «Таблица производных, нахождение наибольших и наименьших значений функции, нахождение точек максимума и минимума». Во всех этих примерах мы пользуемся формулами из таблицы производных.

Задача 1. Найдите точки максимумам функции $displaystyle y=-frac{x^{2}+25}{x}.$

Решение:

Область определения функции:

Найдем производную функции, пользуясь формулой производной частного из таблицы.

{y} если x=pm 5.

Точки х = 5 и х = -5, а также точка ноль, разбивают числовую прямую на интервалы, на каждом из которых производная сохраняет свой знак. Это метод интервалов.

Найдем знаки производной на каждом интервале.

В точке максимума производная равна нулю и меняет знак с «плюса» на «минус». Это точка 5 на рисунке.

Ответ: 5.

Задача 2. Найдите точки минимума функции $y=e^{x+10}(8x-3).$

Решение:

Применим формулу производной произведения.

{y}

Приравняем производную к нулю:

{y} , если 8x-5=0, $displaystyle x=frac{5}{8}=0,625.$

Если то {y} функция убывает.

Если то {y} функция возрастает, значит, x=0,625 – точка минимума функции y(x).

В этой точке производная равна нулю и меняет знак с «минуса» на «плюс».

Ответ: 0,625.

Задача 3. Найдите значение функции $f(x)=x^{4}-4x^{3}-2x^{2}+12x+9$ в точке максимума.

Решение:

Найдем производную функции:

Мы применили формулы производной степени.

Решим уравнение:

$3x^{3}-12x^{2}-4x+12=0Leftrightarrow 3x^{3}(x-3)-4(x-3)=0Leftrightarrow$
$Leftrightarrow (x-3)cdot 4cdot (x-1)cdot (x+1)=0Leftrightarrow left[begin{array}{c}x=3\x=1\x=-1\end{array}right. .$

Получили критические точки, в которых производная равна нулю. Отметим их на оси Х и найдём знаки производной.

x=1 – точка максимума.

Найдём значение функции в этой точке:

Ответ: 16.

Рассмотрим задачи ЕГЭ на нахождение наибольших и наименьших значений функций.

Мы помним, что наибольшее значение функции на отрезке может достигаться либо в точке максимума, либо на конце отрезка. Эти случаи показаны на рисунке:

Это значит, что у нас есть алгоритм для нахождения наибольших и наименьших значений функции на интервале.

Пусть функция f(x) определена на некотором интервале. Чтобы найти ее наибольшее или наименьшее значение, действуем следующим образом:

Находим производную функции.
Приравниваем производную к нулю, находим точки, в которых она равна нулю.
Если производная меняет знак с «плюса» на «минус» в точке $x_{0}$ , то $x_{0}$ – точка максимума функции.
Если производная меняет знак с «минуса» на «плюс» в точке $x_{0}$ , то $x_{0}$ – точка минимума функции.
Чтобы найти наибольшее значение функции на отрезке, сравниваем значения в точке максимума и концах отрезка.
Чтобы найти наименьшее значение функции на отрезке, сравниваем значения в точке минимума и концах отрезка.

Задача 4. Найдите наибольшее значение функции на отрезке

Решение:

Найдем производную:

Приравняем производную к нулю:

$displaystyle Leftrightarrow x=frac{pi }{4}+pi n, nin Z.$

Если то $displaystyle x=frac{pi }{4}.$

Так как

Точка $displaystyle x=frac{pi }{4}$ – точка максимума функции $displaystyle y(x); y_{max}(x)=yleft (frac{pi }{4}right )=4.$

В этой точке функция принимает наибольшее значение на указанном отрезке.

Ответ: 4.

Задача 5. Найдите наименьшее значение функции $y=(x-21)e^{x-20}$ на отрезке

Решение:

Найдем производную функции:

при x=20.

Найдем знаки производной слева и справа от точки x=20.

Если то {y}

Значит, x=20 – точка минимума. Наименьшее значение функции на отрезке достигается при x=20.

Это значение равно

Ответ: -1.

Задача 6. Найдите наибольшее значение функции $y=3x^{2}-13x+7ln+5$ на отрезке $displaystyle left [ frac{13}{14};frac{15}{14} right ].$

Решение:

Область определения функции:

Найдем производную функции и приравняем ее к нулю:

$displaystyle =frac{6(x-1)left ( x-frac{7}{6} right )}{x}.$

если $6x^{2}-13x+7=0.$

или $displaystyle x=frac{7}{6}.$ Второй корень не принадлежит отрезку $displaystyle left [ frac{13}{14};frac{15}{14} right ].$

Найдем знаки производной на отрезке:

В точке x=1 производная равна нулю и меняет знак с «плюса» на «минус». Значит, это точка максимума, и наибольшее значение функции на отрезке $displaystyle left [ frac{13}{14};frac{15}{14} right ]$ достигается при x=1.

Найдем значение функции при x=1:

Ответ: -5.

В следующих задачах наименьшее значение функции достигается на конце отрезка.

Задача 7. Найдите наименьшее значение функции $y=3cosx-pi x+pi ^{2}$ на отрезке

Решение:

Найдем производную функции и приравняем ее к нулю.

У этого уравнения нет решений, так как $displaystyle-frac{pi }{3}textless -1.$

Это значит, что при любых то есть а это означает, что y(x) – убывает, наименьшее значение функции достигается в правом конце отрезка

$y_{min}=y(pi )=-3.$

Ответ: -3.

Задача 8. Найдите наибольшее значение функции на отрезке $displaystyle left [ -frac{pi }{2}; 0 right ].$

Решение:

Найдем производную функции:

Производная функции не равна нулю ни при каком .

Мы знаем, что Тогда

Прибавим 7 ко всем частям неравенства:

для всех

Значит, производная положительна при любом значении переменной, функция монотонно возрастает. Наибольшее значение функции будет достигаться в правом конце отрезка, то есть при x=0.

$y_{naim}=y(0)=7cdot 0-6sin0+8=8.$

Ответ: 8.

Задача 9. Найдите наименьшее значение функции $displaystyle y=13+frac{sqrt{3}pi }{3}-2sqrt{3}cdot x-4sqrt{3}cdot cosx$ на отрезке $displaystyleleft [ 0; frac{pi }{2} right ].$

Решение:

Найдем производную функции и приравняем ее к нулю:

тогда $displaystyle sinx=frac{1}{2}.$

На указанном отрезке это уравнение имеет единственное решение $displaystyle x=frac{pi }{6}.$

Слева от этой точки Если производная отрицательна.

Справа от этой точки производная положительна.

Значит, $displaystyle x=frac{pi }{6}$ – точка минимума функции, и наименьшее значение функции на отрезке достигается в этой точке.

Найдем значения функции в этой точке:

$displaystyle yleft ( frac{pi }{6} right )=13+frac{sqrt{3}pi }{3}-2sqrt{3}cdot frac{pi }{6}-4sqrt{3}cdot cosfrac{pi }{6}=$

$displaystyle =13+frac{sqrt{3}pi }{3}-frac{sqrt{3}pi }{3}-4sqrt{3}cdot frac{sqrt{3}}{2}=13-6=7.$

Ответ: 7.

В задачах ЕГЭ встречаются сложные функции. И найти нужно их точки максимума или минимума, наибольшие или наименьшие значения. Но производную сложной функции в школьной программе по-настоящему не проходят. Как же быть? Покажем полезные приемы, помогающие решить такие задания ЕГЭ.

Задача 10. Найдите наименьшее значение функции $y=log_{2}(x^{2}+x+0,5).$

Решение:

Рассмотрим функцию $y=log_{2}t.$

Так как функция $y=log_{2}t$ монотонно возрастает, точка минимума функции $y=log_{2}(x^{2}+x+0,5)$ будет при том же значении , что и точка минимума функции $t(x)=x^{2}+x+0,5.$ А ее найти легко:

при $displaystyle x=-frac{1}{2}.$

В точке $displaystyle x=-frac{1}{2}$ производная меняет знак с «минуса» на «плюс». Значит, $displaystyle x=-frac{1}{2}$ – единственная точка минимума функции t(x) и функции $y=log_{2}(x^{2}+x+0,5).$

$displaystyle y_{min}=yleft ( -frac{1}{2} right )=log_{2}left ( frac{1}{4}-frac{1}{2}+0,5 right )=log_{2}frac{1}{4}=-2.$

Ответ: -2.

Задача 11. Найдите наибольшее значение функции $y=sqrt{x^{2}-4x+13}$ на отрезке

Решение:

$y=sqrt{x^{2}-4x+13}, xin [-0,5; 6].$

Так как функция монотонно возрастает при tgeq 0, точка минимума функции $y=sqrt{x^{2}-4x+13}$ соответствует точке минимума подкоренного выражения $t(x)={x^{2}-4x+13}.$

Заметим, что подкоренное выражение всегда положительно.

Функция $t(x)={x^{2}-4x+13}.$ задает квадратичную параболу с ветвями вверх и точкой минимума в вершине параболы, то есть при $displaystyle x=frac{4}{2}=2.$

Если $xin [-0,5; 2], y=sqrt{x^{2}-4x+13}$ – монотонно убывает.

Если $xin [2; 6], y=sqrt{x^{2}-4x+13}$ – монотонно возрастает.

Значит, наибольшее значение функции $y=sqrt{x^{2}-4x+13}$ на отрезке достигается в одном из концов этого отрезка.

Сравним и y=(6):

$y_{max}=6.$

Ответ: 6.

Задача 12. Найдите точку максимума функции $y=log_{2}(2+2x-x^{2})-2.$

Решение:

Рассмотрим функцию $t(x)=2+2x-x^{2}.$

Ее график – парабола с ветвями вниз, и точка максимума будет в вершине параболы, при x=1. Функция $y(t)=log_{2}t$ монотонно возрастает, и значит, большему значению будет соответствовать большее значение y(t).

Точка максимума функции $y=log_{2}(2+2x-x^{2})-2$ будет такой же, как у функции $t(x)=2+2x-x^{2},$ то есть x=1.

Ответ: 1.

Читайте также: Задание 11 на ЕГЭ по математике.

Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Таблица производных и правила дифференцирования» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.

Публикация обновлена:
09.03.2023

Источник

Наверх

Шпаргалка по математике для 11 класса таблица производных, формулы и теория по производным может пригодиться при решении задания №7 ЕГЭ по математике.

Ссылка для скачивания шпаргалки №1 по производным: скачать в PDF

Ссылка для скачивания шпаргалки №2 по производным: скачать в PDF

В данной шпаргалке вы найдёте: формулы и правила дифференцирования, применение производной к исследованию функции, анализ графиков, геометрический и физический смысл производной, задачи на нахождения тангенса, задачи на нахождение коэффициента К, задачи на нахождение значения производной, условие касания функции и прямой.

Смотреть онлайн:

Кому нужно углубиться в данную тему, смотрите бесплатный видеоурок:

Смотреть видеоурок 2019-2020 производная, таблица производных

ПОДЕЛИТЬСЯ МАТЕРИАЛОМ

Источник

Что такое производная и зачем она нужна

Прежде чем переходить к таблице для вычисления производных, дадим определение производной. В учебнике оно звучит так:

Производная функции — это предел отношения приращения функции к приращению ее аргумента, при условии, что приращение аргумента стремится к нулю.

Если же говорить простыми словами, то производная функции описывает, как и с какой скоростью эта функция меняется в данной конкретной точке. Процесс нахождения производной называется дифференцированием.

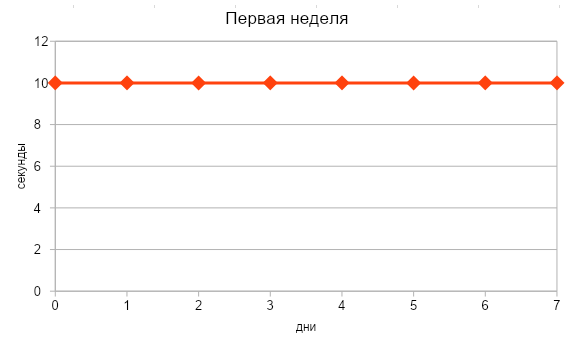
Объясним на примере: допустим, Маша решила по утрам делать зарядку и стоять в планке. В первую неделю она держалась каждый день по 10 секунд, но начиная со второй недели смогла стоять в планке с каждым днем на 3 секунды дольше. Успехи Маши можно описать следующими графиками:

Очевидно, что в первую неделю результаты Маши не менялись (т. е. были константой), скорость прироста оставалась нулевой. Если мы заглянем в таблицу производных простых функций, то увидим, что производная константы равна нулю.

у = 10

у′ = 0

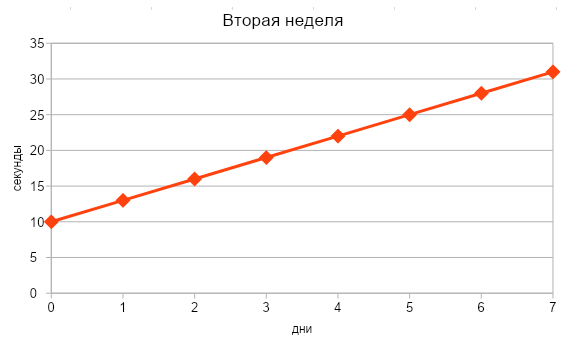
Во вторую неделю время выполнения планки с 10 сек начало увеличиваться на 3 сек ежедневно.

у = 10 + 3х

Снова смотрим в таблицу дифференцирования производных, где указано, что производная от х равна 1, а также по правилам вычисления производных (c*f(x))’=cf'(x) и (f(x)+g(x))’=f'(x)+g'(x).

у = 10 + 3х

у′ = 0 + 3

у′ = 3

Вот так с помощью таблицы производных и элементарной математики мы докажем, что успехи Маши росли со скоростью 3 сек в день.

Это был очень простой пример, который в общих чертах объясняет азы дифференциального исчисления и помогает понять, для чего нужны формулы из таблицы производных функций. Но разобраться в решении задач, где скорость меняется нелинейно, конечно, не так просто.

Быстрее освоить производные поможет
обучение на курсах по математике в онлайн-школе Skysmart.

Получай лайфхаки, статьи, видео и чек-листы по обучению на почту

Реши домашку по математике на 5.

Подробные решения помогут разобраться в самой сложной теме.

Производные основных элементарных функций

Таблица производных для 10 и 11 класса может включать только элементарные часто встречающиеся функции. Поэтому приведем стандартную таблицу производных.

Функция f (x)	Производная f’ (х)
С (т. е. константа, любое число)	0
х	1
xⁿ	nx^n-1
√x	1/(2√x)
sin x	cos x
cos x	-sin x
tg x	1/cos²(х)
ctg x	-1/sin²x
e^x	e^x
a^x	a^x * ln a
ln x	1/x
log_ax	1/(x * ln a)

Элементарные функции можно складывать, умножать друг на друга, находить их разность или частное — словом, выполнять любые математические операции. Но для этого существуют определенные правила.

Общие правила дифференцирования

Для решения задач на дифференцирование нужно запомнить (или записать в шпаргалку) пять несложных формул:

(c ⋅ f)′ = c ⋅ f′

(u + v)′ = u′ + v′

(u — v)′ = u′ — v′

(u ⋅ v)′ = u′v + v′u

(u/v)’ = (u’v — v’u)/v²

В данном случае u, v, f — это функции, а c — константа (любое число).

С константой все просто — ее можно смело выносить за знак производной. Специально запоминать придется лишь формулы, где требуется разделить одну функцию на другую или перемножить их и найти производную от результата.

Например: требуется найти производную функции y = (5 ⋅ x³).

y′ = (5 ⋅ x³)′

Вспомним, что константу, а в данном случае это 5, можно вынести за знак производной:

y′ = (5 ⋅ x³)’ = 5 ⋅ (x³)′ = 5 ⋅ 3 ⋅ х^3-1 = 15х²

Попробуйте самостоятельно решить эти примеры. Правильные ответы найдете в конце статьи:

Правила дифференцирования сложных функций

Конечно, далеко не все функции выглядят так, как в вышеуказанной таблице. Как быть с дифференцированием, например, вот таких функций: y = (3 + 2x²)⁴?

Сложной функцией называют такое выражение, в котором одна функция словно вложена в другую. Производную сложной функции f(y) можно найти по следующей формуле: (f(y))′ = f′(y) ⋅ y′. Другими словами, нужно умножить производную, условно говоря, внешней функции на производную внутренней.

Пример 1

Найдем производную функции y(x) = (3 + 2x²)⁴.

Заменим 3 + 2x² на u и тогда получим y = u⁴.

Согласно приведенному выше правилу дифференцирования сложных функций у нас получится:

y = y′_u ⋅ u′_x = 4u³ ⋅ u’_x

А теперь выполним обратную замену и подставим исходное выражение:

4u³ ⋅ u′_x = 4 (3 + 2x²)³ ⋅ (3 + 2x²)′ = 16 (3 + 2x²)³ ⋅ х

Пример 2

Найдем производную для функции y = (x³ + 4) cos x.

Для дифференцирования этой функции воспользуемся формулой (UV)′ = U′V + V′U.

y′ = (x³ + 4)′ ⋅ cos x + (x³ + 4) ⋅ cos x′ = 3x² ⋅ cos x + (x³ + 4) ⋅ (-sin x) = 3x² ⋅ cos x – (x³ + 4) ⋅ sin x

Ответы на задания

Источник

Производной функции $y = f(x)$ в данной точке $х_0$ называют предел отношения приращения функции к соответствующему приращению его аргумента при условии, что последнее стремится к нулю:

$f'(x_0)={lim}↙{△x→0}{△f(x_0)}/{△x}$

Дифференцированием называют операцию нахождения производной.

Таблица производных некоторых элементарных функций

Функция	Производная
$c$	$0$
$x$	$1$
$x^n$	$nx^{n-1}$
${1}/{x}$	$-{1}/{x^2}$
$√x$	${1}/{2√x}$
$e^x$	$e^x$
$lnx$	${1}/{x}$
$sinx$	$cosx$
$cosx$	$-sinx$
$tgx$	${1}/{cos^2x}$
$ctgx$	$-{1}/{sin^2x}$

Основные правила дифференцирования

1. Производная суммы (разности) равна сумме (разности) производных

$(f(x) ± g(x))’= f'(x)±g'(x)$

Найти производную функции $f(x)=3x^5-cosx+{1}/{x}$

Производная суммы (разности) равна сумме (разности) производных.

$f'(x) = (3x^5 )’-(cos x)’ + ({1}/{x})’ = 15x^4 + sinx — {1}/{x^2}$

2. Производная произведения

$(f(x) · g(x))’= f'(x) · g(x)+ f(x) · g(x)’$

Найти производную $f(x)=4x·cosx$

$f'(x)=(4x)’·cosx+4x·(cosx)’=4·cosx-4x·sinx$

3. Производная частного

$({f(x)}/{g(x)})’={f'(x)·g(x)-f(x)·g(x)’}/{g^2(x)}$

Найти производную $f(x)={5x^5}/{e^x}$

$f'(x)={(5x^5)’·e^x-5x^5·(e^x)’}/{(e^x)^2}={25x^4·e^x-5x^5·e^x}/{(e^x)^2}$

4. Производная сложной функции равна произведению производной внешней функции на производную внутренней функции

$f(g(x))’=f'(g(x))·g'(x)$

$f(x)= cos(5x)$

$f'(x)=cos'(5x)·(5x)’=-sin(5x)·5= -5sin(5x)$

Физический смысл производной

Если материальная точка движется прямолинейно и ее координата изменяется в зависимости от времени по закону $x(t)$, то мгновенная скорость данной точки равна производной функции.

$v(t) = x'(t)$

Точка движется по координатной прямой согласно закону $x(t)= 1,5t^2-3t + 7$, где $x(t)$ — координата в момент времени $t$. В какой момент времени скорость точки будет равна $12$?

Решение:

1. Скорость – это производная от $x(t)$, поэтому найдем производную заданной функции

$v(t) = x'(t) = 1,5·2t -3 = 3t -3$

2. Чтобы найти, в какой момент времени $t$ скорость была равна $12$, составим и решим уравнение:

$3t-3 = 12$

$3t = 15$

$t = 5$

Ответ: $5$

Геометрический смысл производной

Напомним, что уравнение прямой, не параллельной осям координат, можно записать в виде $y = kx + b$, где $k$ – угловой коэффициент прямой. Коэффициент $k$ равен тангенсу угла наклона между прямой и положительным направлением оси $Ох$.

$k = tgα$

Производная функции $f(x)$ в точке $х_0$ равна угловому коэффициенту $k$ касательной к графику в данной точке:

$f'(x_0) = k$

Следовательно, можем составить общее равенство:

$f'(x_0) = k = tgα$

На рисунке касательная к функции $f(x)$ возрастает, следовательно, коэффициент $k > 0$. Так как $k > 0$, то $f'(x_0) = tgα > 0$. Угол $α$ между касательной и положительным направлением $Ох$ острый.

На рисунке касательная к функции $f(x)$ убывает, следовательно, коэффициент $k < 0$, следовательно, $f'(x_0) = tgα < 0$. Угол $α$ между касательной и положительным направлением оси $Ох$ тупой.

На рисунке касательная к функции $f(x)$ параллельна оси $Ох$, следовательно, коэффициент $k = 0$, следовательно, $f'(x_0) = tg α = 0$. Точка $x_0$, в которой $f ‘(x_0) = 0$, называется экстремумом.

На рисунке изображён график функции $y=f(x)$ и касательная к этому графику, проведённая в точке с абсциссой $x_0$. Найдите значение производной функции $f(x)$ в точке $x_0$.

Решение:

Касательная к графику возрастает, следовательно, $f'(x_0) = tg α > 0$

Для того, чтобы найти $f'(x_0)$, найдем тангенс угла наклона между касательной и положительным направлением оси $Ох$. Для этого достроим касательную до треугольника $АВС$.

Найдем тангенс угла $ВАС$. (Тангенсом острого угла в прямоугольном треугольнике называется отношение противолежащего катета к прилежащему катету.)

$tg BAC = {BC}/{AC} = {3}/{12}= {1}/{4}=0,25$

$f'(x_0) = tg ВАС = 0,25$

Ответ: $0,25$

Производная так же применяется для нахождения промежутков возрастания и убывания функции:

Если $f'(x) > 0$ на промежутке, то функция $f(x)$ возрастает на этом промежутке.

Если $f'(x) < 0$ на промежутке, то функция $f(x)$ убывает на этом промежутке.

На рисунке изображен график функции $y = f(x)$. Найдите среди точек $х_1,х_2,х_3…х_7$ те точки, в которых производная функции отрицательна.

В ответ запишите количество данных точек.

Решение:

Отрицательным значениям производной соответствуют интервалы, на которых функция $f (x)$ убывает. Поэтому, выделим на рисунке интервалы, на которых функция убывает.

В выделенных интервалах находятся точки $х_2, х_4$. В ответ напишем их количество $2$.

Ответ: $2$

Источник

Вычисление производных – одна из самых распространенных задач школьной и вузовской программ. Как минимум один вопрос на ЕГЭ будет связан с этой темой. Эксперты Студворк составили таблицу со списком формул для вашего удобства.

Таблица производных

Функция	Производная
f(x)=constf(x)=const f(x)=xf(x)=x f(x)=xnf(x)=x^n f(x)=1xf(x)=frac{1}{x} f(x)=xf(x)=sqrt{x} f(x)=axf(x)=a^x f(x)=exf(x)=e^x f(x)=log⁡axf(x)=log_{a}x f(x)=ln⁡xf(x)=ln x f(x)=sin⁡xf(x)=sin x f(x)=cos⁡xf(x)=cos x f(x)=tg⁡xf(x)=tg x f(x)=ctg⁡xf(x)=ctg x f(x)=sec⁡xf(x)=sec x f(x)=cosec⁡xf(x)=cosec x f(x)=sh⁡xf(x)=sh x f(x)=ch⁡xf(x)=ch x f(x)=th⁡xf(x)=th x f(x)=cth⁡xf(x)=cth x f(x)=sech xf(x)=text{sech} x f(x)=csch xf(x)=text{csch} x f(x)=arcsin⁡xf(x)=arcsin x f(x)=arccos⁡xf(x)=arccos x f(x)=arctg⁡xf(x)=arctg x f(x)=arcctg⁡xf(x)=arcctg x f(x)=arsh xf(x)=text{arsh} x f(x)=arch xf(x)=text{arch} x f(x)=arth xf(x)=text{arth} x f(x)=arcth xf(x)=text{arcth} x f(x)=arsech xf(x)=text{arsech} x f(x)=arcsch xf(x)=text{arcsch} x	f′(x)=0f'(x)=0 f′(x)=1f'(x)=1 f′(x)=nxn−1f'(x)=nx^{n-1} f′(x)=−1x2f'(x)=-frac{1}{x^2} f′(x)=12xf'(x)=frac{1}{2sqrt{x}} f′(x)=axln⁡af'(x)=a^xln a f′(x)=exf'(x)=e^x f′(x)=1xln⁡af'(x)=frac{1}{xln a} f′(x)=1xf'(x)=frac{1}{x} f′(x)=cos⁡xf'(x)=cos x f′(x)=−sin⁡xf'(x)=-sin x f′(x)=1cos⁡2xf'(x)=frac{1}{cos^2 x} f′(x)=−1sin⁡2xf'(x)=-frac{1}{sin^2 x} f′(x)=tg⁡xsec⁡xf'(x)=tg xsec x f′(x)=−ctg⁡xcosec⁡xf'(x)=-ctg xcosec x f′(x)=ch⁡xf'(x)=ch x f′(x)=sh⁡xf'(x)=sh x f′(x)=sech2xf'(x)=text{sech}^2 x f′(x)=−csch2xf'(x)=-text{csch}^2 x f′(x)=−th⁡x sech xf'(x)=-th x text{sech} x f′(x)=−cth⁡x csch xf'(x)=-cth x text{csch} x f′(x)=11−x2f'(x)=frac{1}{sqrt{1-x^2}} f′(x)=−11−x2f'(x)=-frac{1}{sqrt{1-x^2}} f′(x)=11+x2f'(x)=frac{1}{1+x^2} f′(x)=−11+x2f'(x)=-frac{1}{1+x^2} f′(x)=1×2+1f'(x)=frac{1}{sqrt{x^2+1}} f′(x)=1×2−1f'(x)=frac{1}{sqrt{x^2-1}} f′(x)=11−x2 ∣x∣<1f'(x)=frac{1}{1-x^2} \|x\|<1 f′(x)=11−x2 ∣x∣>1f'(x)=frac{1}{1-x^2} \|x\|>1 f′(x)=−1×1−x2f'(x)=-frac{1}{xsqrt{1-x^2}} f′(x)=−1∣x∣1+x2f'(x)=-frac{1}{\|x\|sqrt{1+x^2}}

Функция

Производная

f(x)=constf(x)=const

f(x)=xf(x)=x

f(x)=xnf(x)=x^n

f(x)=1xf(x)=frac{1}{x}

f(x)=xf(x)=sqrt{x}

f(x)=axf(x)=a^x

f(x)=exf(x)=e^x

f(x)=log⁡axf(x)=log_{a}x

f(x)=ln⁡xf(x)=ln x

f(x)=sin⁡xf(x)=sin x

f(x)=cos⁡xf(x)=cos x

f(x)=tg⁡xf(x)=tg x

f(x)=ctg⁡xf(x)=ctg x

f(x)=sec⁡xf(x)=sec x

f(x)=cosec⁡xf(x)=cosec x

f(x)=sh⁡xf(x)=sh x

f(x)=ch⁡xf(x)=ch x

f(x)=th⁡xf(x)=th x

f(x)=cth⁡xf(x)=cth x

f(x)=sech xf(x)=text{sech} x

f(x)=csch xf(x)=text{csch} x

f(x)=arcsin⁡xf(x)=arcsin x

f(x)=arccos⁡xf(x)=arccos x

f(x)=arctg⁡xf(x)=arctg x

f(x)=arcctg⁡xf(x)=arcctg x

f(x)=arsh xf(x)=text{arsh} x

f(x)=arch xf(x)=text{arch} x

f(x)=arth xf(x)=text{arth} x

f(x)=arcth xf(x)=text{arcth} x

f(x)=arsech xf(x)=text{arsech} x

f(x)=arcsch xf(x)=text{arcsch} x

f′(x)=0f'(x)=0

f′(x)=1f'(x)=1

f′(x)=nxn−1f'(x)=nx^{n-1}

f′(x)=−1x2f'(x)=-frac{1}{x^2}

f′(x)=12xf'(x)=frac{1}{2sqrt{x}}

f′(x)=axln⁡af'(x)=a^xln a

f′(x)=exf'(x)=e^x

f′(x)=1xln⁡af'(x)=frac{1}{xln a}

f′(x)=1xf'(x)=frac{1}{x}

f′(x)=cos⁡xf'(x)=cos x

f′(x)=−sin⁡xf'(x)=-sin x

f′(x)=1cos⁡2xf'(x)=frac{1}{cos^2 x}

f′(x)=−1sin⁡2xf'(x)=-frac{1}{sin^2 x}

f′(x)=tg⁡xsec⁡xf'(x)=tg xsec x

f′(x)=−ctg⁡xcosec⁡xf'(x)=-ctg xcosec x

f′(x)=ch⁡xf'(x)=ch x

f′(x)=sh⁡xf'(x)=sh x

f′(x)=sech2xf'(x)=text{sech}^2 x

f′(x)=−csch2xf'(x)=-text{csch}^2 x

f′(x)=−th⁡x sech xf'(x)=-th x text{sech} x

f′(x)=−cth⁡x csch xf'(x)=-cth x text{csch} x

f′(x)=11−x2f'(x)=frac{1}{sqrt{1-x^2}}

f′(x)=−11−x2f'(x)=-frac{1}{sqrt{1-x^2}}

f′(x)=11+x2f'(x)=frac{1}{1+x^2}

f′(x)=−11+x2f'(x)=-frac{1}{1+x^2}

f′(x)=1×2+1f'(x)=frac{1}{sqrt{x^2+1}}

f′(x)=1×2−1f'(x)=frac{1}{sqrt{x^2-1}}

f′(x)=11−x2 ∣x∣<1f'(x)=frac{1}{1-x^2} |x|<1

f′(x)=11−x2 ∣x∣>1f'(x)=frac{1}{1-x^2} |x|>1

f′(x)=−1×1−x2f'(x)=-frac{1}{xsqrt{1-x^2}}

f′(x)=−1∣x∣1+x2f'(x)=-frac{1}{|x|sqrt{1+x^2}}

Напомним определение производной функции y=f(x)y=f(x) в точке x∈Dxin D.

DD — область определения функции f(x)f(x).

f′(x)=lim⁡Δx→0ΔyΔx=lim⁡Δx→0f(x+Δx)−f(x)Δxf'(x)=displaystylelim_{Delta xto 0}frac{Delta y}{Delta x}=lim_{Delta xto 0}frac{f(x+Delta x)-f(x)}{Delta x}

Докажем некоторые из производных и разберем примеры.

Производная от константы

f(x)=cf(x)=c

f′(x)=0f'(x)=0

Для всех c=constc=const

Доказательство

f′(x)=lim⁡Δx→0ΔyΔx=lim⁡Δx→0c−cΔx=0f'(x)=displaystylelim_{Delta xto 0}frac{Delta y}{Delta x}=lim_{Delta xto 0}frac{c-c}{Delta x}=0

Пример 1

f(x)=1f(x)=1

f′(x)=lim⁡Δx→0ΔyΔx=lim⁡Δx→01−1Δx=0f'(x)=displaystylelim_{Delta xto 0}frac{Delta y}{Delta x}=lim_{Delta xto 0}frac{1-1}{Delta x}=0

Производная степенной функции

f(x)=xaf(x)=x^a

f′(x)=axa−1f'(x)=ax^{a-1}

aa — вещественное число.

Доказательство

Начнем со случая, когда a=na=n, nn — натуральное число.

Δy=(x+Δx)n−xn=Delta y={(x+Delta x)}^n-x^n=

=Cn0xn+Cn1xn−1Δx+Cn2xn−2Δx2+…+Cnn−1xΔxn−1+CnnΔxn−xn==C^0_nx^n+C^1_nx^{n-1}Delta x+C^2_nx^{n-2}{Delta x}^2+…+C_n^{n-1}x{Delta x}^{n-1}+C_n^n{Delta x}^n-x^n=

=xn−xn+Cn1xn−1Δx+Cn2xn−2Δx2+…+Cnn−1xΔxn−1+CnnΔxn==x^n-x^n+C^1_nx^{n-1}Delta x+C^2_nx^{n-2}{Delta x}^2+…+C_n^{n-1}x{Delta x}^{n-1}+C_n^n{Delta x}^n=

=Cn1xn−1Δx+Cn2xn−2Δx2+…+Cnn−1xΔxn−1+CnnΔxn==C^1_nx^{n-1}Delta x+C^2_nx^{n-2}{Delta x}^2+…+C_n^{n-1}x{Delta x}^{n-1}+C_n^n{Delta x}^n=

=Δx(Cn1xn−1+Cn2xn−2Δx+…+Cnn−1xΔxn−2+CnnΔxn−1)=Delta x(C^1_nx^{n-1}+C_n^2x^{n-2}Delta x+…+C_n^{n-1}x{Delta x}^{n-2}+C_n^n{Delta x}^{n-1})

Здесь мы воспользовались тем, что nn натуральное и разложили первое слагаемое по формуле бинома Ньютона. Затем привели подобные слагаемые (xnx^n сократилось) и вынесли общий множитель ΔxDelta x.

f′(x)=lim⁡Δx→0ΔyΔx=lim⁡Δx→0Δx(Cn1xn−1+Cn2xn−2Δx+…+Cnn−1xΔxn−2+CnnΔxn−1)Δxf'(x)=displaystylelim_{Delta xto 0}frac{Delta y}{Delta x}=lim_{Delta xto 0}frac{Delta x(C^1_nx^{n-1}+C_n^2x^{n-2}Delta x+…+C_n^{n-1}x{Delta x}^{n-2}+C_n^n{Delta x}^{n-1})}{Delta x}

f′(x)=lim⁡Δx→0(Cn1xn−1+Cn2xn−2Δx+…+Cnn−1xΔxn−2+CnnΔxn−1)f'(x)=displaystylelim_{Delta xto 0}(C^1_nx^{n-1}+C_n^2x^{n-2}Delta x+…+C_n^{n-1}x{Delta x}^{n-2}+C_n^n{Delta x}^{n-1})

f′(x)=Cn1xn−1=n!(n−1)!xn−1=nxn−1f'(x)=C^1_nx^{n-1}=frac{n!}{(n-1)!}x^{n-1}=nx^{n-1}

Что и требовалось доказать.

Этот результат может быть обобщен на случай произвольного вещественного числа aa.

Пример 2

f(x)=x3f(x)=x^3

f′(x)=3x2f'(x)=3x^2

Пример 3

f(x)=1x35f(x)=frac{1}{sqrt[5]{x^3}}

Первым делом преобразуем это выражение так, чтобы стало очевидно, что перед нами действительно степенная функция:

1×35=1×35=x−35frac{1}{sqrt[5]{x^3}}=frac{1}{x^{frac{3}{5}}}=x^{-frac{3}{5}}

f′(x)=−35x−35−1=−35x−85f'(x)=-frac{3}{5}x^{-frac{3}{5}-1} = -frac{3}{5}x^{-frac{8}{5}}

Производная показательной функции

f(x)=axf(x)=a^x

f′(x)=axln⁡af'(x)=a^xln a

aa — вещественное число.

Следствие:

Пусть a=ea=e, тогда:

f′(x)=exln⁡e=exf'(x)=e^xln e=e^x

Поскольку по определению натурального логарифма: ln⁡e=1ln e=1.

Пример 4

f(x)=(12)xf(x)=big(frac{1}{2}big)^x

f′(x)=(12)xln⁡12f'(x)=big(frac{1}{2}big)^xln frac{1}{2}

Это выражение можно упростить, пользуясь свойствами логарифмов:

f′(x)=(12)xln⁡12=(12)x(ln⁡1−ln⁡2)=(12)x(0−ln⁡2)=−(12)xln⁡2f'(x)=Big(frac{1}{2}Big)^xln frac{1}{2}=Big(frac{1}{2}Big)^x(ln 1-ln 2)=Big(frac{1}{2}Big)^x(0-ln 2)=-Big(frac{1}{2}Big)^xln 2

Производная логарифмической функции

f(x)=log⁡axf(x)=log_a x

f′(x)=1xln⁡af'(x)=frac{1}{xln a}

Следствие:

Пусть a=ea=e, тогда:

f′(x)=1xln⁡e=1xf'(x)=frac{1}{xln e}=frac{1}{x}

Пример 5

f(x)=log⁡13exf(x)=log_{13e}x

f′(x)=1xln⁡(13e)f'(x)=frac{1}{xln(13e)}

Здесь тоже можно воспользоваться свойствами логарифмов для упрощения результата:

f′(x)=1xln⁡(13e)=1x(ln⁡13+ln⁡e)=1x(ln⁡13+1)f'(x)=frac{1}{xln(13e)}=frac{1}{x(ln 13 +ln e)}=frac{1}{x(ln 13+1)}

Тест по теме «Таблица производных»

Источник

Таблица производных

Вспомним основные функции, производные которых вам понадобятся на экзамене:

Ну и давайте разберём одну задачу из профильного ЕГЭ по математике в качестве примера:

В какой точке функция

принимает наименьшее значение?

1. Посчитаем производную функции

2. Приравняем производную к нулю и решим уравнение

3. Нанесём на числовую прямую найденную точку

4. Расставим знаки производной справа и слева от точки

5. Расставим стрелки (минус – убывание, плюс – возрастание) и определим точку (max/min).

6. Запишем ответ
Функция принимает наименьшее значение в точке минимума, то есть в точке

Ответ: -5

Источник

Таблица производных в алгебре нужна для решения целого ряда различных прикладных задач. Поскольку смысл производной иначе интерпретируется как “скорость изменения”, то, каждый раз, беря производную, мы находим величину на ступеньку более “быструю”, чем та, от которой мы берем производную. Например, беря производную от y(x) по x, мы фактически находим скорость изменения координаты y в зависимости от изменения координаты x, а беря производную от скорости изменения координаты y в зависимости от координаты x, мы находим ускорение.

Что такое производная функции

Например, при использовании производной в физике, мы знаем, что производная расстояния s по времени – это скорость. Потому что скорость – это величина, характеризующая быстроту изменения расстояния в зависимости от времени. А производная скорости – ничто иное как ускорение, так как ускорение – это величина, характеризующая быстроту изменения скорости.
Поскольку производная находится по формуле: $displaystyle f^prime(x) =lim_{Delta xto0}frac{f(x+Delta x)-f(x)}{Delta x}$ , то бесконечное количество различных функций усложняют задачу дифференцирования, так как удобно функцию, которую можно представить из различных элементарных функций, дифференцировать основываясь на уже выведенных выражениях для производных этих элементарных функций.

Характеристика производной и ее смысл

Производная характеризует быстроту изменения функции в зависимости от изменения аргумента.

Таблица производных

Таким образом, чтобы работать с производными, необходима таблица производных элементарных функций. Руководствуясь этой таблицей, можно взять производную от какой угодно функции. Но прежде чем работать с таблицей – нужно знать как брать производную функции, есть определенные правила дифференцирования, которые представим в таблице.

Правила дифференцирования

№ правила	Название правила	Правило дифференцирования
1	Производная постоянной величины	, С-постоянная
2	Производная суммы	.
3	Производная произведения постоянной на функцию	, С – постоянная
4	Производная переменной x
5	Производная произведения двух функций
6	Производная деления двух функций	$displaystyle (frac{u}{v})' = frac{u'v-v'u}{v^2}$
7	Производная сложной функции	$y{}'_x = y{}'_u cdot u{}'_x$

Таблица производных простых и сложных функций

Теперь таблица производных для элементарных и для сложных функций.

Номер формулы	Название производной	Основные элементарные функции	Сложные функции
1	Производная натурального логарифма по x	$(ln (x))' = frac{1}{x}$	$(ln(u))' = frac{1}{u}u'$
2	Производная логарифмической функции по основанию a	$displaystyle (log(x)_a)' = frac{1}{x cdot ln a}$	$displaystyle (log(u)_a)' = frac{1}{u cdot ln a}u'$
3	Производная по x в степени n	$(x^n)' = n x^{n-1}$	$(u^n)' = n u^{n-1}u'$
4	Производная квадратного корня	$(sqrt {x})' = frac{1}{2 sqrt{x}}$	$(sqrt {u})' = frac{1}{2 sqrt{u}}u'$
5	Производная a в степени x
6	Производная e в степени x
7	Производная синуса
8	Производная косинуса
9	Производная тангенса	$(tan {x})' = frac{1}{cos^2{x}}$	$(tan {u})' = frac{1}{cos^2{u}} cdot u'$
10	Производная котангенса	$(ctg {x})' = -frac{1}{sin^2{x}}$	$(ctg {u})' = -frac{1}{sin^2{u}} cdot u'$
11	Производная арксинуса	$(arcsin {x})' = frac{1}{sqr{1-x^2}}$	$(arcsin {u})' = frac{u'}{sqr{1-u^2}}$
12	Производная арккосинуса	$(arccos {x})' = -frac{1}{sqr{1-x^2}}$	$(arccos {u})' = -frac{u'}{sqr{1-u^2}}$
13	Производная арктангенса	$(arctg {x})' = frac{1}{1+x^2}$	$(arctg {u})' = frac{u'}{1+u^2}$
14	Производная арккотангенса	$(arcctg {x})' = -frac{1}{1+x^2}$	$(arcctg {u})' = -frac{u'}{1+u^2}$

Примеры нахождения производных

Пример 1

Пользуясь формулами и правилами дифференцирования, найти производную функции: .

Решение:

Мы использовали правило 2 дифференцирования суммы. Теперь найдем производную каждого слагаемого:

По формуле 3 “производная по x в степени n” (у нас в степени 2).

По правилам дифференцирования 3 и 4.

По первому правилу дифференцирования “производная постоянной равна нулю”

Итак, получим: .

Пример 2

Найти производную функции $y=frac{2x}{3x+5}$

Решение:

Находим производную, пользуясь правилам дифференцирования 6.

$[y'=frac{(2x)'(3x+5)-2x(3x+5)'}{(3x+5)^2}]$

$[y'=frac{2(3x+5)-2x cdot 3}{(3x+5)^2}]$

$[y'=frac{6x+10-6x}{(3x+5)^2}]$

$[y'=frac{10}{(3x+5)^2}]$

Ответ:

$[y'=frac{10}{(3x+5)^2}]$

Пример 3

Найти производную функции

Решение: здесь все просто, мы возьмем производную из таблицы производных.

Ответ:

Пример 4

Найдите производную функции

Решение: Здесь мы уже имеем не простую функцию, а сложную функцию и брать производную мы будем по формуле 8 таблицы производных для сложных функций.