Тела вращения презентация 11 класс егэ - Помощь в подготовке к экзаменам и поступлению

Слайд 1

Задачи по теме «Тела вращения» на вычисление объёмов и площади поверхности Выполнила: учитель математики Муниципальное казенное общеобразовательное учреждение 2020 г

Слайд 2

Содержание

Слайд 3

Базовый уровень (задания ЕГЭ базовый №16) Старт/стоп МЕНЮ

Слайд 4

Объем цилиндра ( V ц) Даны два цилиндра. Радиус основания и высота первого равны соответственно 2 и 6, а второго — 6 и 7. Во сколько раз объём второго цилиндра больше объёма первого? Решение Объём цилиндра находится по формуле: Найдём объём первого цилиндра: Найдём объём второго цилиндра: Найдём отношение объёма второго шара к первому: Ответ: 10,5. Решение Ответ Справка Каталог заданий

Слайд 5

Площадь боковой поверхности цилиндра ( S б.п.ц ) Даны два цилиндра. Радиус основания и высота первого равны соответственно 4 и 18, а второго — 2 и 3. Во сколько раз площадь боковой поверхности первого цилиндра больше площади боковой поверхности второго? Ответ: 12 Решение Ответ Справка Каталог заданий Решение Площадь боковой поверхности цилиндра находится по формуле: Найдём S б.п первого цилиндра: Найдём S б.п второго цилиндра: Найдём отношение площади боковой поверхности цилиндра первого цилиндра ко второму:

Слайд 6

Цилиндр Цилиндр – тело, ограниченное цилиндрической поверхностью и двумя кругами . Объем цилиндра (с радиусом основания R и высотой H ): S — площадь основания цилиндра, h — высота цилиндра, π — число пи (3.1415), r — радиус цилиндра, Площадь боковой и полной поверхностей цилиндра: МЕНЮ

Слайд 7

Объем конуса ( V к) Объем конуса равен 16. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса. Решение Меньший конус подобен большему с коэффициентом 0,5. Объемы подобных тел относятся как куб коэффициента подобия. Поэтому объем меньшего конуса в восемь раз меньше объема большего конуса. Ответ: 2. Решение Ответ Каталог заданий Справка

Слайд 8

Площадь боковой поверхности конуса ( S б.п.к ) Во сколько раз уменьшится площадь боковой поверхности конуса, если радиус его основания уменьшится в 1,5 раза, а образующая останется прежней? Ответ: 1,5 Решение Ответ Каталог заданий Справка Решение Площадь боковой поверхности конуса равна При уменьшении радиуса основания в 1,5 раза при неизменной величине образующей площадь боковой поверхности тоже уменьшится в 1,5 раза.

Слайд 9

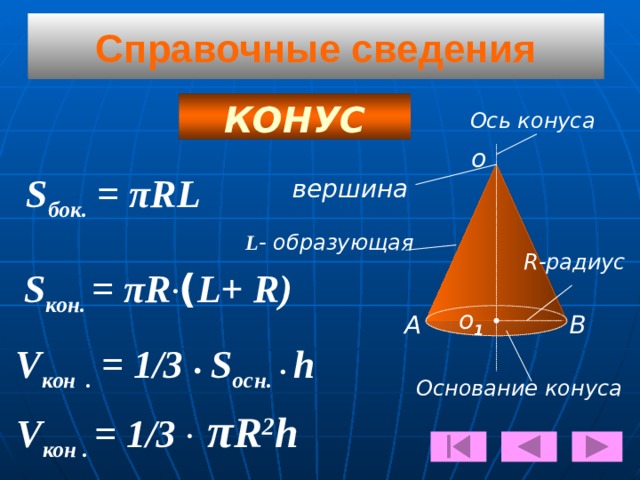
Конус Ко́нус — тело, которое состоит из круга – основания конуса , точки, не лежащей в плоскости этого круга, — вершины конуса и всех отрезков, соединяющих вершину конуса с точками основания. Площадь боковой поверхности конуса равна: где R — радиус основания, l — длина образующей. Объем конуса (с радиусом основания R и высотой H ): МЕНЮ

Слайд 10

Объем шара ( V ш) Даны два шара с радиусами 4 и 1. Во сколько раз объём большего шара больше объёма другого? Ответ: 64. Решение Ответ Каталог заданий Справка Решение Найдём отношение объёмов шаров:

Слайд 11

Площадь поверхности шара ( S ш) Даны два шара с радиусами 9 и 3. Во сколько раз площадь поверхности большего шара больше площади поверхности меньшего? Ответ: 9 Решение Ответ Каталог заданий Справка Решение Площади шаров относятся как квадраты их радиусов, следовательно, площадь поверхности второго шара в раз больше площади поверхности первого.

Слайд 12

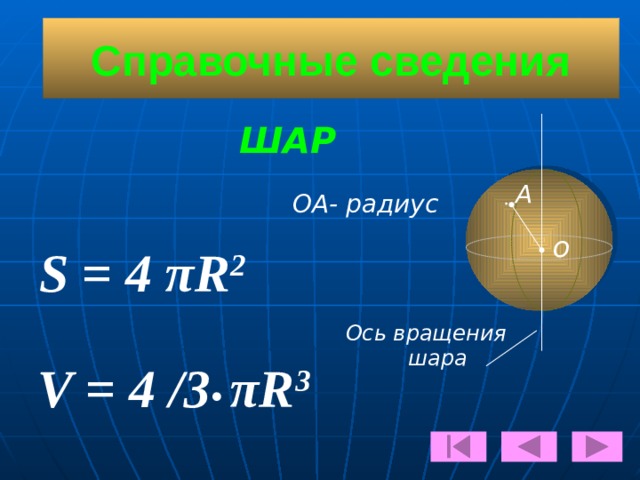
Шар Шар — геометрическое тело, ограниченное поверхностью, все точки которой отстоят на равном расстоянии от центра. Это расстояние называется радиусом шара . Площадь поверхности шара: Объем шара (с радиусом основания R ): МЕНЮ

Слайд 13

Повышенный уровень (задания ЕГЭ профильный №8) Старт/стоп МЕНЮ

Слайд 14

Объем цилиндра ( V ц) Шар, объём которого равен 42, вписан в цилиндр. Найдите объём цилиндра . Ответ: 63 Решение Ответ Справка Каталог заданий Решение Высота цилиндра равна двум радиусам вписанного в цилиндр шара, поэтому объем цилиндра, выраженный через радиус вписанного в него шара, даётся формулой Объём шара вычисляется по формуле откуда имеем: Тем самым, объём цилиндра равен 63.

Слайд 15

Площадь боковой поверхности цилиндра ( S б.п.ц ) Длина окружности основания цилиндра равна 3, высота равна 2. Найдите площадь боковой поверхности цилиндра. Ответ: 6 Решение Ответ Справка Решение Площадь боковой поверхности цилиндра равна: где C – длина окружности основания. Поэтому Каталог заданий

Слайд 16

Объем конуса ( V к) Цилиндр и конус имеют общие основание и высоту. Объём цилиндра равен 18. Найдите объём конуса. Ответ: 6. Решение Ответ Справка Решение Поскольку, конус и цилиндр имеют общую высоту и основание, имеем: Каталог заданий

Слайд 17

Площадь боковой поверхности конуса ( S б.п.к ) Длина окружности основания конуса равна 3, образующая равна 2. Найдите площадь боковой поверхности конуса. Ответ: 3 Решение Ответ Каталог заданий Справка Решение Площадь боковой поверхности конуса равна , где С — длина окружности основания, а l — образующая. Тогда

Слайд 18

Объем шара ( V ш) Цилиндр описан около шара. Объем цилиндра равен 33. Найдите объем шара. Ответ: 22 Решение Ответ Справка Решение Выразим из формулы для объёма цилиндра и подставим в формулу для объёма шара Каталог заданий

Слайд 19

Площадь поверхности шара ( S ш) Даны два шара. Радиус первого шара в 2 раза больше радиуса второго. Во сколько раз площадь поверхности первого шара больше площади поверхности второго? Ответ: 4 Решение Ответ Справка Решение Площадь поверхности шара выражается через его радиус формулой , поэтому при увеличении радиуса вдвое площадь увеличится в 2 2 = 4 раза. Каталог заданий

Слайд 20

Высокий уровень (задания ЕГЭ профильный №14) Старт/стоп МЕНЮ

Слайд 21

Объем цилиндра ( V ц) В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки A , B и C , а на окружности другого основания — точка C 1 , причём CC 1 — образующая цилиндра, а AC — диаметр основания. Известно, что , . а) Докажите, что угол между прямыми AC 1 и BC равен . б) Найдите объём цилиндра. Решение Ответ Справка Каталог заданий Ответ:

Слайд 22

Решение а) Пусть BB 1 — образующая цилиндра. Тогда BB 1 C 1 C — прямоугольник, поэтому угол между прямыми AC 1 и BС равен углу . Угол ABC опирается на диаметр основания цилиндра, поэтому он прямой. Значит, прямая B 1 C 1 , параллельная прямой BС , перпендикулярна прямым AB и BB 1 . Таким образом, прямая B 1 С 1 перпендикулярна плоскости ABB 1 , а значит, угол AB 1 C 1 прямой. В прямоугольном треугольнике АB 1 С 1 : Значит, б) Отрезок AC является диаметром основания цилиндра. Значит, площадь основания цилиндра Следовательно, объём цилиндра

Слайд 23

Площадь боковой поверхности цилиндра ( S б.п.ц ) В цилиндре на окружности одного из оснований цилиндра выбраны точки A и B , а на окружности другого основания — точки B 1 и C 1 , причём BB 1 — образующая цилиндра, а AC 1 пересекает его ось цилиндра. а) Докажите, что угол C 1 BA = 90°. б) Найдите площадь боковой поверхности, если AB = 16, BB 1 = 5, B 1 C 1 = 12. Решение Ответ Справка Каталог заданий Ответ:

Слайд 24

Решение а) Пусть точка C проекция точки C 1 на нижнее основание. Тогда AC — проекция AC 1 на плоскость нижнего основания. Так как AC 1 пересекает ось цилиндра, то и AC тоже. Следовательно, AC является диаметром окружности, а так как опирается на него. CB является проекцией C 1 B . Тогда C 1 B перпендикулярно AB по теореме о трёх перпендикулярах, то есть б) Тогда по теореме Пифагора для треугольника гипотенуза Следовательно,

Слайд 25

Объем конуса ( V к) Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем шара равен 28. Найдите объем конуса. Ответ: 7. Решение Ответ Справка Каталог заданий Решение Запишем формулу для объёма шара: Объём конуса в 4 раза меньше:

Слайд 26

Площадь боковой поверхности конуса ( S б.п.к ) Цилиндр и конус имеют общие основание и высоту. Высота цилиндра равна радиусу основания. Площадь боковой поверхности цилиндра равна Найдите площадь боковой поверхности конуса. Ответ: 3 Решение Ответ Каталог заданий Справка Решение Конус и цилиндр имеют общую высоту и равные радиусы основания. Площадь боковой поверхности цилиндра равна откуда, учитывая, что получаем: или Образующая конуса l , его высота h и радиус r основания связаны соотношением откуда, учитывая, что получаем: или Площадь боковой поверхности конуса равна следовательно:

Слайд 27

Слайд 28

Площадь поверхности шара ( S ш) Объем первого шара в 27 раз больше объема второго. Во сколько раз площадь поверхности первого шара больше площади поверхности второго? Ответ: 9 Решение Ответ Справка Каталог заданий Решение Найдем отношение объемов шаров: , откуда Площади их поверхностей соотносятся как квадраты радиусов:

Слайд 29

Список использованной литературы Ссылки на задачи из сайта https://math-ege.sdamgia.ru/ https://mathb-ege.sdamgia.ru/problem?id=509741 https://mathb-ege.sdamgia.ru/problem?id=511620 https://ege.sdamgia.ru/problem?id=27052 https://ege.sdamgia.ru/problem?id=27137 https://mathb-ege.sdamgia.ru/problem?id=509681 https://mathb-ege.sdamgia.ru/problem?id=520727 https://ege.sdamgia.ru/problem?id=525041 https://ege.sdamgia.ru/problem?id=27133 https://ege.sdamgia.ru/problem?id=27133 https://ege.sdamgia.ru/problem?id=269371 https://ege.sdamgia.ru/problem?id=27135 https://ege.sdamgia.ru/problem?id=245348 https://ege.sdamgia.ru/problem?id=27072 https://ege.sdamgia.ru/problem?id=520784 https://ege.sdamgia.ru/problem?id=520869 https://ege.sdamgia.ru/problem?id=245351 https://ege.sdamgia.ru/problem?id=324458 https://ege.sdamgia.ru/problem?id=245348 https://ege.sdamgia.ru/problem?id=27162

Источник

Скачать материал

Сейчас обучается 99 человек из 37 регионов

Сейчас обучается 898 человек из 81 региона

Сейчас обучается 54 человека из 30 регионов

Описание презентации по отдельным слайдам:

1 слайд

Задачи по стереометрии
(тела вращения)
2 слайд

Содержание:
Часть l :
Тела вращения.
Комбинации тел вращения.
Часть ll :
4 слайд

Тела вращения
Цилиндр.
Конус.
Шар.
Исторические сведения.
Проверь себя ( теоретические сведения).
Решение устных задач (ответы);
Задачи для самостоятельного решения,(подсказки, ответы).
Понятие о телах вращения
5 слайд

Стереометрия — это раздел геометрии, в котором изучаются свойства фигур в пространстве.

στερεοζ
μετρεμ
пространственный
измерять
6 слайд

Исторические сведения
Стереометрия возникла и развивалась в связи с потребностями практической деятельности человека.

Она зародилась в древнем Египте около 2000 лет до н. э., а оттуда перешла в Грецию.
7 слайд

Тела вращения
Фигура вращения получается в результате вращения плоской фигуры вокруг какой — нибудь оси, лежащей в той же плоскости.
8 слайд

Тела вращения:
Цилиндр

Конус

Шар ,(сфера)
9 слайд

ЦИЛИНДР (прямой круговой)
Тело, образованное вращением прямоугольника вокруг оси, содержащей его сторону.
10 слайд

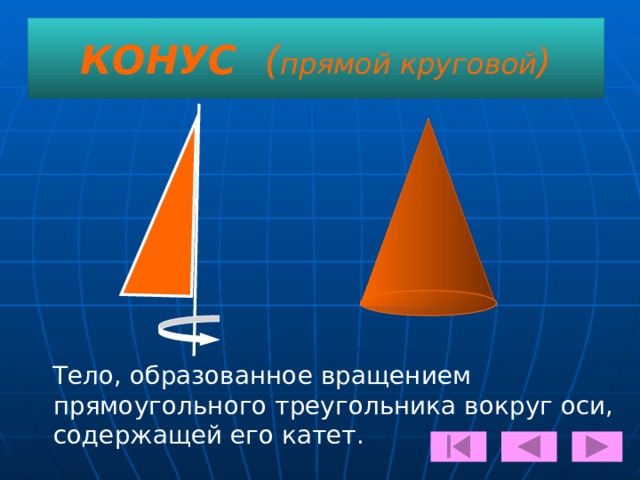
КОНУС (прямой круговой)
Тело, образованное вращением прямоугольного треугольника вокруг оси, содержащей его катет.
11 слайд

ШАР
Тело, образованное вращением полукруга вокруг оси, содержащей его диаметр.
Дополнительные сведения
12 слайд

Шар радиуса R с центром в точке О содержит все точки пространства, которые расположены от точки О на расстоянии не больше чем R (включая точку О), и не содержит других точек.
О
сфера
13 слайд

Сфера
Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии R от данной точки О.
R
О
Радиус сферы
Центр сферы
Дополнительные сведения
14 слайд

Дополнительные сведения
Отрезок,соединяющий две точки сферы и проходящий через её центр, называется её диаметром.

Диаметр сферы равен двум радиусам: D=2R.

О
•
А
В
15 слайд

ПРОВЕРЬ СЕБЯ
Что изучает стереометрия?
16 слайд

Подсказка
Стереометрия — это раздел геометрии, в котором изучаются свойства фигур в пространстве.
17 слайд

Что означает термин «стереометрия»?
18 слайд

подсказка
Στερεοζ – пространственный

Μετρεμ — измерять
19 слайд

Какие фигуры в пространстве называются фигурами вращения?
20 слайд

подсказка
Фигура вращения получается в результате вращения плоской фигуры вокруг какой — нибудь оси, лежащей в той же плоскости.
21 слайд

Приведите примеры фигур вращения.
22 слайд

Какая фигура получается при вращении прямоугольника вокруг оси, содержащей его сторону?
23 слайд

Какая фигура получается при вращении прямоугольного треугольника вокруг оси, содержащей его катет?
24 слайд

Какая фигура получается при вращении полукруга вокруг оси, содержащей его диаметр?
25 слайд

Чем отличается шар от сферы?
26 слайд

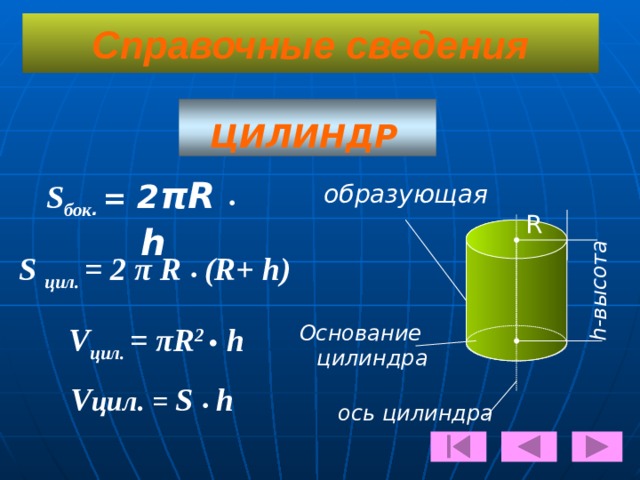
Справочные сведения
ЦИЛИНДР
образующая
ось цилиндра
Основание цилиндра
h-высота
R
Sбок. = 2πR • h
S цил. = 2 π R • (R+ h)
Vцил. = πR2 • h
Vцил. = S • h
27 слайд

( ЦИЛИНДР И ЕГО СВОЙСТВА)
УСТНЫЕ ЗАДАЧИ
1)Радиус основания цилиндра 2м.,высота 3м.Найти диагональ осевого сечения.

h=3м.
О1
R=2м.
.
ответ
28 слайд

Подсказка
4м.
3м.
?
29 слайд

ОТВЕТ:
Задача 1): 5м.
30 слайд

2)Осевое сечение цилиндра –квадрат, площадь которого S.Найдите площадь основания.
Sкв. = S
ответ
31 слайд

подсказка
Sосн.= Sкр.= πr 2
.
r
О
Sкв. = S
32 слайд

ОТВЕТ:
Задача 2): π• S/ 4.
33 слайд

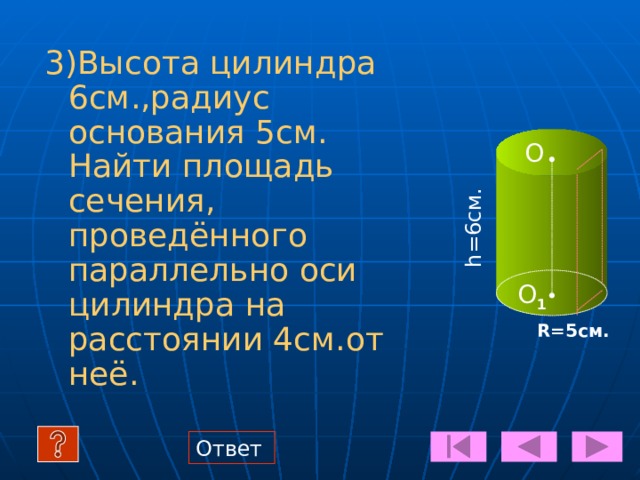
3)Высота цилиндра 6см.,радиус основания 5см. Найти площадь сечения, проведённого параллельно оси цилиндра на расстоянии 4см.от неё.
R=5см.
h=6см.
О
О1
Ответ
34 слайд

Подсказка
4см.
В
А
О
С
D
N
5см.
С
D
Sсеч.=h•СD
h=6см.
35 слайд

ОТВЕТ:
Задача 3): 36 см2.
36 слайд

Справочные сведения
КОНУС
Основание конуса
Ось конуса
вершина
L- образующая
R-радиус
о
о1
А
В
Sбок. = πRL
Sкон. = πR•(L+ R)
Vкон . = 1/3 • πR2h
Vкон . = 1/3 • Sосн. • h
37 слайд

УСТНЫЕ ЗАДАЧИ
КОНУС
1)Радиус основания конуса 3м., высота 4м.Найти образующую?
h=4м
R=3м.
ответ
38 слайд

Подсказка
R=3м.
о
о1
В
А
h=4м
?
40 слайд

2)Образующая конуса L наклонена к плоскости основания под углом в 300. Найти высоту.

ответ
41 слайд

Подсказка
о1
300
о
L
?
В
43 слайд

3)Радиус основания конуса R.Осевым сечением служит прямоугольный треугольник. Найти его площадь.
ответ
46 слайд

Справочные сведения
ШАР

•
Ось вращения шара
А
о
ОА- радиус
V = 4 /3• πR3
S = 4 πR2
47 слайд

УСТНЫЕ ЗАДАЧИ
( ШАР И ЕГО СВОЙСТВА)
1) Радиус шара 1м. Найдите объём шара.
R=1м.
ответ
48 слайд

Подсказка
V = 4 /3• πR3
R=1м.
О
49 слайд

Ответ: 4/3 • π ≈ 4,2 м3.
50 слайд

2)Во сколько раз увеличится объём шара, если радиус его увеличить в 3 раза?
ответ
51 слайд

Подсказка
V = 4 /3• πR3
R1
R
R1=3R
52 слайд

Ответ: в 27 раз.
53 слайд

Решение более сложных задач.
54 слайд

Задача 1:
Высота и образующая конуса относятся как 35:37. Полная поверхность конуса равна 588π. Найти объём конуса.

решение
ответ
55 слайд

1.Обозначим одну часть за х , тогда образующая l = 37х , а высота h = 35х. Рассм . ∆АОВ :
Дано:
конус
h:l=35:37
Sкон.=588π
Найти:Vкон.

Решение:
L АОВ=90 0, АО=h, АВ=l , ОВ=R.
А
О
В
С
l
h
R
56 слайд

Найдём радиус ОВ:
ОВ2 = АВ2 — АО2, значит
ОВ = √(37х)2-( 35х)2 = 12х ;
___________
2.Теперь найдём Sкон. т.е. полную поверхность конуса (через х):
Sкон. = S осн . + Sбок.
Sкон. = π R2+ π R l
Sкон. = π(144х2+444х2)
588π = 588πх2
х=1.
О
В
С
А
57 слайд

3. т.к. R=ОВ=12х ,
то R = 12; а т.к. h = АО = 35х , то h = 35.
4. Найдём объём конуса:
V = ⅓* π R2* h
V = ⅓* π * 144 *35= 1680 π .

Ответ: 1680 π .

О
В
С
А
59 слайд

Задачи для самостоятельного решения.
60 слайд

Задача :
Конусообразная палатка высотой в 3,5 м. с диаметром основания в 4м. покрыта парусиной. Сколько квадратных метров парусины пошло на палатку?
ответ
61 слайд

Подсказка
Sбок. = πRL
D=2R
о
о1
R
А
В
L
R
62 слайд

Ответ: ≈ 25,3м2.
63 слайд

Задача :

Боковая поверхность конуса 12 см2., расстояние от центра основания конуса до образующей 4см. Определить объём конуса.
ответ
64 слайд

Подсказка
Vкон. = 1/3• πR2h
Sбок. = πRL
∆ АОВ ~ ∆ АСО
Пропорция:
или
АО
ОВ
АС
СО
___
___
=
h
=
R .
___
___
4
l
R
О
В
С
А
h
l
D
4см.
66 слайд

Задача:
Боковая поверхность цилиндра будучи развёрнута, представляет собой прямоугольник. В котором диагональ равна в и составляет угол φ с основанием. Найти объём цилиндра?
ответ
67 слайд

Подсказка

Из прямоугольного ∆АВD:
Н=АВ = ВDsinφ= вsinφ,
АD = ВDcosφ= вcosφ.
но, сторона АD равна длине окружности основания,
т.е. 2πR = вcos φ,
отсюда найдём R.
H
в
φ
А
В
С
D
68 слайд

Ответ:
в3
____
4π
cos 2φ
sinφ
V =
69 слайд

Задача:

Шар пересечён плоскостью, перпендикулярной его радиусу и отстоящей от его центра на 9 см. Площадь сечения равна 144 π см2.
Найти объём шара и площадь сферы.

ответ
70 слайд

Подсказка
Пусть ОВ = х –радиус сферы.
В ∆ ОАВ :
АВ2= ОВ2- ОА2= х2- 81.
По условию: πR2=144 π,
значит:
π (х2 – 81) = 144 π и т. д.

О
В
А
С
х
71 слайд

Ответ:
V = 4500π см3;
S = 900 π см2.
72 слайд

Задача:

Определить площадь полной поверхности и объём цилиндра,осевое сечение которого есть квадрат и боковая поверхность равна S.

ответ
73 слайд

подсказка
По условию задачи:
S = 2πRH,
но H = 2R ,
поэтому:
S = 2πR • 2R = 4 πR 2,
Значит:
H
O
O1
R
S
__
4π ,
R2 =
R =
1
___
2
S
___
π
√
_____
74 слайд

Ответ:

Sполн.
3
___
2
S
=
V
=
S
___
4
√
___
S
π
_____
75 слайд

Задача:

Доказать ,что объём конуса равен 1/3 произведения боковой поверхности на расстояние от центра основания до образующей.
76 слайд

Задача:

Даны шар, цилиндр с квадратным осевым сечением и конус.Цилиндр и конус имеют одинаковые основания, а их высоты равны диаметру шара.Как относятся объёмы цилиндра, шара и конуса?
ответ
77 слайд

Ответ: Vц.:Vш.:Vк.= 3:2:1
78 слайд

Задача:
Равносторонний треугольник вращается вокруг своей стороны а. Найти поверхность и объём тела вращения.
а
подсказка
ответ
79 слайд

Подсказка
При вращении получается два конуса с радиусом основания ОВ.
Поверхность тела вращения – это две одинаковые боковые поверхности указанного конуса.
В
А
С
О
.
D
80 слайд

Ответ:
S
=
πа2
√3 .
__
V =
πа3
____
4
81 слайд

Задача:

Равнобедренняй треугольник вращается вокруг своей высоты. Определить стороны этого треугольника, если его периметр равен 30 см., а полная поверхность тела вращения равна 60π см2.
подсказка
ответ
82 слайд

Подсказка
При вращении этого треугольника вокруг высоты АС лучается конус.
D
А
В
С
83 слайд

Ответ: 11см., 11см., 8 см.
84 слайд

Часть ll

Комбинации тел вращения.
85 слайд

Комбинация тел вращения
Комбинация цилиндра и конуса;
Комбинация цилиндра и шара;
Комбинация конуса и шара.
Основные понятия о комбинации тел вращения:
Проверь себя (теоретические сведения).
Задачи для самостоятельного решения, (ответы).
86 слайд

Комбинация цилиндра и конуса
Цилиндр называется вписанным в конус, если окружность одного из его оснований лежит на поверхности конуса, а другое основание расположено в плоскости основания конуса.
87 слайд

Комбинация цилиндра и конуса
Конус называется вписанным в цилиндр, если основание конуса совпадает с одним из оснований цилиндра, а вершина конуса лежит в центре другого основания цилиндра.
88 слайд

Комбинация цилиндра и шара
Шар называется вписанным в цилиндр, если основания и каждая образующая цилиндра касаются шара. В этом случае цилиндр называют описанным около шара.
Дополнительные сведения
89 слайд

Дополнительные сведения
Центр шара лежит на оси цилиндра, осевое сечение цилиндра представляет собой квадрат со стороной, равной диаметру шара.

Ось цилиндра
О
•
90 слайд

Комбинация цилиндра и шара
Шар называется описанным около цилиндра, если основаниями цилиндра служат сечения шара. В этом случае цилиндр называют вписанным в шар.
дополнительные сведения
91 слайд

О
R
}
}
Ось цилиндра
Центром описанного около цилиндра, шара является середина оси цилиндра-отрезка, соединяющего центры его оснований.
Дополнительные сведения
92 слайд

Комбинация конуса и шара
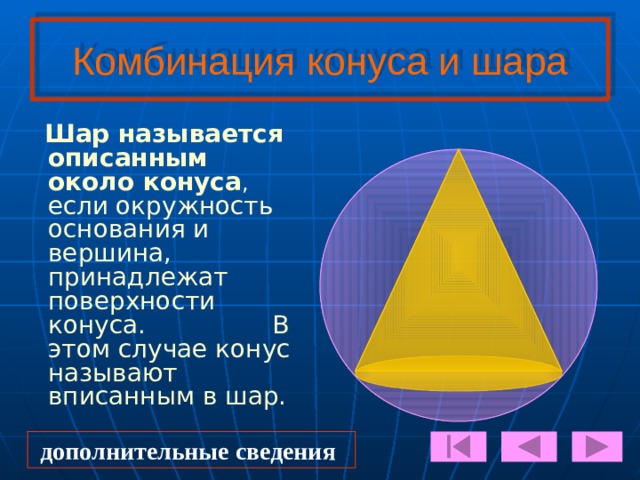
Шар называется вписанным в конус, если основание и каждая образующая конуса касаются шара.В этом случае конус называется описанным около шара.
дополнительные сведения
93 слайд

Дополнительные сведения
Шар касается боковой поверхности конуса по окружности, плоскость которой параллельна основанию.

Дополнительные сведения
94 слайд

Центр шара, вписанного в конус,лежит в точке пересечения высоты конуса и биссектрисы угла наклона образующей конуса к плоскости его основания.
О
Дополнительные сведения
95 слайд

Комбинация конуса и шара
Шар называется описанным около конуса, если окружность основания и вершина, принадлежат поверхности конуса. В этом случае конус называют вписанным в шар.

дополнительные сведения
96 слайд

Дополнительные сведения
Центром шара, описанного около конуса, является точка пересечения высоты конуса с перпендикуляром к образующей, проведённым через её середину в плоскости осевого сечения конуса.
В
О
А
С
О1
К
98 слайд

Введите понятие «цилиндр вписан в конус» и «конус вписан в цилиндр».
99 слайд

Введите понятие «конус вписан в шар» и «конус описан около шара».
100 слайд

Как расположены точки общие для шара и поверхности конуса?
101 слайд

Где расположен центр шара относительно вписанного конуса,что представляет осевое сечение данной комбинации фигур?
102 слайд

Где находится центр шара, вписанного в конус?
103 слайд

Центр шара, вписанного в конус,лежит в точке пересечения высоты конуса и биссектрисы угла наклона образующей конуса к плоскости его основания.
О
Подсказка
104 слайд

Укажите пары подобных треугольников и в них пары углов, имеющие равные величины?
В
О
А
С
О1
К
105 слайд

Во всякий ли цилиндр можно вписать сферу? Какими свойствами должен обладать цилиндр, чтобы в него можно было вписать сферу?
106 слайд

подсказка
Нет не во всякий: осевое сечение цилиндра должно быть квадратом.
107 слайд

Во всякий ли конус можно вписать сферу? Как определить положеное центра сферы, вписанной в конус?
108 слайд

подсказка
Да, во всякий.Центр вписанной сферы находится на пересечении высоты конуса и биссектрисы угла наклона образующей к плоскости основания.
109 слайд

По известному радиусу основания конуса R и его высоте h найдите радиус вписанной сферы.
подсказка
110 слайд

Подсказка:
Искомый радиус : r = R·tgφ , где φ- половина угла наклона образующей конуса к плоскости основания, причём tg2φ=h:R .
111 слайд

Задачи для самостоятельного решения.
112 слайд

Задача:

В конусе высотой 12см. вписан шар радиуса 3см. Вычислить объём конуса.

ответ
113 слайд

Ответ: 72π см3.
114 слайд

Задача:
В конус вписан цилиндр, высота которого равна радиусу основания конуса.Найти угол между осью конуса и его образующей, зная, что полная поверхность цилиндра относится к площади основания конуса как 3:2.
ответ
115 слайд

подсказка
Пусть:
R- радиус основания конуса, r-радиус основания цилиндра,
β — искомый угол.
По условию ОВ=ОD=R.
R
Е
В
}
}
r
β
β
R
С
О
D
К
А
F
подставим и решим уравнение второй степени.
r
____
R
= 1 – tgβ ,
Из ∆ЕКВ: tg β = КВ:КЕ = (R — r ) : R = 1- (r : R),
Sполн. цил.
3
Sосн. кон.
______
=
___
2
Тогда по условию задачи:
(
)
2 πR2+ 2πRr
πR2
__________
=
2
r 2
R2
r
R
+
___
____
=
3
2
__
_________
116 слайд

Ответ : β = arctg
1
2
__
117 слайд

Доказать ,что отношение объёма конуса к объёму вписанного в него шара равно отношению площади полной поверхности конуса к площади шоверхности шара.
Задача:
118 слайд

Задача
Определить боковую поверхность конуса, зная длину радиуса R, описанного вокруг него шара и угол β, под которым из центра видна образующая конуса.

ответ
119 слайд

Подсказка
∆ АОВ — равнобедренный т.к. АО=ОВ=R.
Проведём ОМ – высоту.
Тогда ВМ= ½ • ВА= ½ ·L,
L ВОМ = ½ • β ,
Из ∆ ВОМ найдём ВМ:
ВМ = ОВ·sin β /2 , т. е.
½ ·L = R·sin β /2 ,
L=2R·sin β /2 .
β
М
А
О
О1
В
С
120 слайд

Ответ: Sбок.= 2πR2sinβ·sinβ/2

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

6 156 684 материала в базе

Выберите категорию:
Выберите учебник и тему

Выберите класс:
Тип материала:
- Все материалы
- Статьи
- Научные работы
- Видеоуроки
- Презентации
- Конспекты
- Тесты
- Рабочие программы
- Другие методич. материалы

Найти материалы

Материал подходит для УМК

Другие материалы

Зачет по теме «Цилиндр. Конус. Шар»

Учебник: «Геометрия. Учебник 10-11 класс », Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б.
Тема: Глава 6. Цилиндр, конус, шар

24.02.2019
1801
57

Вам будут интересны эти курсы:

Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»
Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»
Курс профессиональной переподготовки «Маркетинг: теория и методика обучения в образовательной организации»
Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»
Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
Курс повышения квалификации «Использование активных методов обучения в вузе в условиях реализации ФГОС»
Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»
Курс профессиональной переподготовки «Черчение: теория и методика преподавания в образовательной организации»
Курс профессиональной переподготовки «Организация технической поддержки клиентов при установке и эксплуатации информационно-коммуникационных систем»
Курс повышения квалификации «Учебная деятельность по предметной области «Черчение»: основы предмета и реализация обучения в условиях ФГОС»
Курс профессиональной переподготовки «Организация системы менеджмента транспортных услуг в туризме»
Курс профессиональной переподготовки «Эксплуатация и обслуживание общего имущества многоквартирного дома»
Курс профессиональной переподготовки «Организация и управление службой рекламы и PR»
Курс профессиональной переподготовки «Технический контроль и техническая подготовка сварочного процесса»

Источник

ТЕМ ВРЕМЕНЕМ
В БЛОГАХ…

еще…

КОММЕНТАРИИ

еще…

Ольга Михайловна, спасибо за полезную разработку! Ваше творчество не имеет грани…

Спасибо, Любовь Николаевна, за то, что оценили мой комплекс как прекрасный. Спас…

Елена Владимировна, спасибо за столь приятный комментарий. Очень рада слышать Ва…

Оригинально и высококачественно подан ресурс по развитию функциональной грамотно…

Любовь Николаевна, Вы освежаете в памяти нашей форматы интереснейших шаблонов! Л…

Широта Вашей фантазии просто изумляет! Так со вкусом подаете ресурсы, что каждый…

Задачи для подготовки к ЕГЭ «Тела вращения»

ЕГЭ по математике

• 11 класс

• проверка знаний, повторение, систематизация
,
презентация

24.08.2021

Презентация «Задачи для подготовки к ГИА и ЕГЭ» содержит задания на тему «Тела вращения» (треугольник, конус, усечённый конус, шар). Подходит для любых УМК. Может быть использована при систематизации знаний и на занятиях по подготовке к ЕГЭ в 11 классе.
Цели урока:
Образовательные: повторить и закрепить знания телах вращения, научиться применять эти знания при решении конкретных задач.
Развивающие: развивать умение анализировать условие задачи.
Воспитательные: воспитание аккуратности, внимательности, быстроты мышления.

Коломина Наталья Николаевна

Понравилось? Сохраните и поделитесь:

Неограниченная бесплатная загрука материала «Задачи для подготовки к ЕГЭ «Тела вращения»» доступна всем пользователям. Разработка находится в разделе «ЕГЭ по математике» и представляет собой: «проверка знаний, повторение, систематизация».

Загрузка началась…

Понравился сайт? Получайте ссылки
на лучшие материалы еженедельно!

Подарок каждому подписчику!

Порядок вывода комментариев:

Ольга Михайловна, спасибо Вам большое!

Наталья Николаевна, Ваши работы всегда стильно, без излишеств, оформлены. Понравилось, что все ресурсы разнообразны. Спасибо Вам за творчество!

Елена Владимировна, благодарю Вас за позитивный отзыв!

Наталья Николаевна, действительно, всем Вашим работам присущ свой стиль, они легко узнаваемы и всегда вызывают восхищение!

Наталья Александровна, спасибо за добрые слова.

Наталья Николаевна, я Ваша поклонница! Такая красота в каждой работе. Хорошее оформление формирует эстетический вкус у детей. В этом Вы преуспели!

ирина Евгеньевна, приятно читать такие слова от Мастера.

Такое оформление и у взрослых формирует эстетический вкус! Я далеко не математик, но разглядываю эти работы с великим удовольствием! Учусь!

Я согласна с Вами, Наталья Александровна. Мы — учителя — должны не только учить ребят, но и воспитывать. В том числе и вкус.

«И я, и я, и я того же мнения!» tongue

/разглядываю эти работы с великим удовольствием/,
чтобы позаимствоать что-то для своей! Я ещё долго будут заходить в Ваше портфолио после марафона, Наталья Николаевна! Теперь я знаю, у кого можно поучиться «изюминкам» оформления. Спасибо за Ваше творчество.

Надежда Георгиевна, я буду только рада! Правда, не знаю, скоро ли буду что-нибудь выкладывать… Надо передохнуть.

Сняли с языка, Надежда Георгиевна! Просмотрела много Ваших презентаций, Наталья Николаевна. Различные технологические приемы используете и все для закрепления и систематизации материала. Дети в игровой форме будут с радостью изучать математику! Я скачала, теперь буду учиться у Вас. Спасибо Вам за это!

Удачи Вам, Галина Геннадьевна, в работе! Я постараюсь наблюдать за Вашими успехами!

Источник

Тела вращения. Объемы и площади их поверхностей.
Тела вращения
Тела вращения — объёмные тела, полученные при вращении плоской фигуры, ограниченной кривой, вокруг оси, лежащей в той же плоскости.
К телам вращения относят: шар, цилиндр, конус и тор.

Примеры:

Шар

— образован полукругом, вращающимся вокруг диаметра

Цилиндр

— образован прямоугольником, вращающимся вокруг одной из сторон

Конус

— образован прямоугольным треугольником, вращающимся вокруг одного из катетов

Тор

— образован окружностью, вращающейся вокруг прямой, не пересекающей его.
Цилиндр

Цилиндр — геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её. Часть поверхности цилиндра, ограниченная цилиндрической поверхностью называется боковой поверхностью цилиндра. Другая часть, ограниченная параллельными плоскостями — основания цилиндра.
Сечение цилиндра плоскостью, параллельной его оси, представляет прямоугольник.
Осевым сечением называется сечение, которое проходит через ось цилиндра.

Конус

Конус — тело, полученное объединением всех лучей, исходящих из одной точки (вершины конуса) и проходящих через плоскую поверхность. Конус — это тело, полученное при вращении прямоугольного треугольника вокруг одного из его катетов.
Сечение конуса плоскостью, проходящей через его вершину, представляет собой равнобедренный треугольник, у которого боковые стороны являются образующими конуса. В частности, равнобедренным треугольником является осевое сечение конуса

Шар

Шар — геометрическое тело; множество всех точек пространства, которые находятся на расстоянии не большем заданного от центра. Это расстояние называется радиусом шара. Шар образуется вращением полукруга около его неподвижного диаметра. Этот диаметр называется осью шара. Поверхность шара называется сферой.
Всякое сечение шара плоскостью есть круг. Центр этого круга есть основание перпендикуляра, опущенного из центра шара на секущую плоскость.

Площади боковых поверхностей

Sб.п.ц.= 2 RH

Sб.п.к.= RL

Sб.п.к =

Объемы тел вращения

Объем Шара:

Vш=

Объем Шарового Сегмента:

Объем шарового сектора

Заключение

Закончить тему можно веселым стихотворением, которое поможет запомнить две объемные формулы:

Поверхность шара знать я рад: 4 на R2 ,
Объём шаров слетает с губ: 4/3 R3

Мы узнали:

Определение понятия «Тела вращения»

Примеры таких тел

Свойства тел вращения

Формулы площадей поверхности и объемов

Источник

Задачи по стереометрии

(тела вращения)

Содержание:

Часть l :

Тела вращения.

Часть ll :

Комбинации тел вращения.

Часть l

Тела вращения

Исторические сведения.

Понятие о телах вращения

Цилиндр.

Конус.

Шар.

Проверь себя ( теоретические сведения).

Решение устных задач (ответы);

Задачи для самостоятельного решения,(подсказки, ответы).

Стереометрия — это раздел геометрии, в котором изучаются свойства фигур в пространстве.

στερεοζ

μετρεμ

пространственный

измерять

Исторические сведения

Стереометрия возникла и развивалась в связи с потребностями практической деятельности человека.

Она зародилась в древнем Египте около 2000 лет до н. э., а оттуда перешла в Грецию.

Тела вращения

Фигура вращения получается в результате вращения плоской фигуры вокруг какой — нибудь оси, лежащей в той же плоскости.

Тела вращения:

Цилиндр

Конус

Шар ,(сфера)

ЦИЛИНДР ( прямой круговой )

Тело, образованное вращением прямоугольника вокруг оси, содержащей его сторону.

КОНУС ( прямой круговой )

Тело, образованное вращением прямоугольного треугольника вокруг оси, содержащей его катет.

ШАР

Тело, образованное вращением полукруга вокруг оси, содержащей его диаметр.

Дополнительные сведения

Шар радиуса R с центром в точке О содержит все точки пространства, которые расположены от точки О на расстоянии не больше чем R (включая точку О), и не содержит других точек.

сфера

Сфера

Радиус сферы

Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии R от данной точки О.

Центр сферы

Дополнительные сведения

Дополнительные сведения

Отрезок,соединяющий две точки сферы и проходящий через её центр, называется её диаметром.

Диаметр сферы равен двум радиусам: D=2R.

•

ПРОВЕРЬ СЕБЯ

Что изучает стереометрия?

Подсказка

Стереометрия — это раздел геометрии, в котором изучаются свойства фигур в пространстве.

Что означает термин «стереометрия»?

подсказка

Στερεοζ – пространственный

Μετρεμ — измерять

Какие фигуры в пространстве называются фигурами вращения?

подсказка

Приведите примеры фигур вращения.

Какая фигура получается при вращении прямоугольника вокруг оси, содержащей его сторону?

Какая фигура получается при вращении прямоугольного треугольника вокруг оси, содержащей его катет?

Какая фигура получается при вращении полукруга вокруг оси, содержащей его диаметр?

Чем отличается шар от сферы?

h-высота

Справочные сведения

ЦИЛИНДР

S бок . = 2 πR • h

образующая

S цил. = 2 π R • (R+ h)

Основание цилиндра

V цил. = πR 2 • h

V цил. = S • h

ось цилиндра

УСТНЫЕ ЗАДАЧИ

( ЦИЛИНДР И ЕГО СВОЙСТВА)

1)Радиус основания цилиндра 2м.,высота 3м.Найти диагональ осевого сечения.

h=3м.

R=2м.

О 1

ответ

Подсказка

3м.

4м.

ОТВЕТ:

Задача 1): 5м .

2)Осевое сечение цилиндра –квадрат, площадь которого S.Найдите площадь основания.

S кв. = S

ответ

подсказка

S кв. = S

S осн. = S кр. = πr 2

ОТВЕТ:

Задача 2 ): π • S/ 4.

h=6см.

3)Высота цилиндра 6см.,радиус основания 5см. Найти площадь сечения, проведённого параллельно оси цилиндра на расстоянии 4см.от неё.

О 1

R=5см.

Ответ

h=6см.

5см .

Подсказка

S сеч.= h • СD

4см .

ОТВЕТ:

Задача 3): 36 см 2 .

Справочные сведения

КОНУС

Ось конуса

S бок. = πRL

вершина

L — образующая

R-радиус

S кон. = πR • ( L+ R)

о 1

V кон . = 1/3 • S осн. • h

Основание конуса

V кон . = 1/3 • π R 2 h

УСТНЫЕ ЗАДАЧИ

КОНУС

1)Радиус основания конуса 3м., высота 4м.Найти образующую?

h=4м

R=3м.

ответ

h=4м

Подсказка

о 1

R=3м.

Ответ: 5м .

2)Образующая конуса L наклонена к плоскости основания под углом в 30 0 . Найти высоту.

ответ

Подсказка

30 0

о 1

Ответ: ½ • L .

3)Радиус основания конуса R.Осевым сечением служит прямоугольный треугольник. Найти его площадь.

ответ

Подсказка

о 1

R 2

Ответ:

Справочные сведения

ШАР

•

ОА- радиус

S = 4 πR 2

Ось вращения шара

V = 4 /3 • πR 3

УСТНЫЕ ЗАДАЧИ

( ШАР И ЕГО СВОЙСТВА)

1) Радиус шара 1м. Найдите объём шара.

R=1 м.

ответ

Подсказка

V = 4 /3 • πR 3

R =1м.

Ответ: 4/3 • π ≈ 4,2 м 3 .

2)Во сколько раз увеличится объём шара, если радиус его увеличить в 3 раза?

ответ

Подсказка

V = 4 /3 • πR 3

R 1

R 1 =3R

Ответ: в 27 раз.

Решение более сложных задач.

Задача 1: Высота и образующая конуса относятся как 35:37. Полная поверхность конуса равна 588 π. Найти объём конуса.

решение

ответ

Дано: конус h:l=35:37 S кон. =588 π Найти: V кон .

Решение:

1.Обозначим одну часть за х , тогда образующая l = 37х , а высота h = 35х. Рассм . ∆АОВ :

L АОВ=90 0 , АО=h, АВ=l , ОВ=R.

Найдём радиус ОВ:

ОВ 2 = АВ 2 — АО 2 , значит

ОВ = √(37х) 2 -( 35х) 2 = 12х ;

___________

2.Теперь найдём Sкон. т.е. полную поверхность конуса (через х):

Sкон. = S осн . + Sбок.

Sкон. = π R 2 + π R l

Sкон. = π(144х 2 +444х 2 )

588π = 588πх 2

х=1.

3. т.к. R=ОВ=12х ,

то R = 12; а т.к. h = АО = 35х , то h = 35.

4. Найдём объём конуса:

V = ⅓ * π R 2 * h

V = ⅓ * π * 144 * 35= 1680 π .

Ответ: 1680 π .

Ответ: 1680 π .

Задачи для самостоятельного решения.

Задача :

Конусообразная палатка высотой в 3,5 м. с диаметром основания в 4м. покрыта парусиной. Сколько квадратных метров парусины пошло на палатку?

ответ

Подсказка

S бок . = π RL

D=2R

о 1

Ответ: ≈ 25,3м 2 .

Задача :

Боковая поверхность конуса 12 см 2 ., расстояние от центра основания конуса до образующей 4см. Определить объём конуса.

ответ

Подсказка

4см.

Vкон. = 1/3 • πR 2 h

Sбок. = πRL

∆ АОВ ~ ∆ АСО

Пропорция:

АО

АС

___

или

ОВ

СО

___

R .

Ответ: 16см 3

Задача:

Боковая поверхность цилиндра будучи развёрнута, представляет собой прямоугольник. В котором диагональ равна в и составляет угол φ с основанием. Найти объём цилиндра?

ответ

Подсказка

Из прямоугольного ∆ АВD :

Н = АВ = ВDsin φ= в sin φ,

АD = ВDcos φ= в cos φ.

но, сторона АD равна длине окружности основания,

т.е. 2 πR = в cos φ,

отсюда найдём R .

Ответ:

в 3

____

cos 2 φ

sin φ

V =

4 π

Задача:

Шар пересечён плоскостью, перпендикулярной его радиусу и отстоящей от его центра на 9 см. Площадь сечения равна 144 π см 2 .

Найти объём шара и площадь сферы.

ответ

Подсказка

Пусть ОВ = х – радиус сферы.

В ∆ ОАВ :

АВ 2 = ОВ 2 — ОА 2 = х 2 — 81 .

По условию: π R 2 =144 π,

значит:

π (х 2 – 81) = 144 π и т. д.

Ответ:

V = 4500 π см 3 ;

S = 900 π см 2 .

Задача:

Определить площадь полной поверхности и объём цилиндра,осевое сечение которого есть квадрат и боковая поверхность равна S.

ответ

подсказка

O 1

По условию задачи:

S = 2πRH,

но H = 2R ,

поэтому:

S = 2πR • 2R = 4 πR 2 ,

Значит:

_____

√

___

R =

R 2 =

4π ,

Ответ:

S полн.

___

_____

√

___

Задача:

Доказать ,что объём конуса равен 1/3 произведения боковой поверхности на расстояние от центра основания до образующей.

Задача:

Даны шар, цилиндр с квадратным осевым сечением и конус.Цилиндр и конус имеют одинаковые основания, а их высоты равны диаметру шара.Как относятся объёмы цилиндра, шара и конуса?

ответ

Ответ: V ц. :V ш. :V к. = 3:2:1

Задача:

Равносторонний треугольник вращается вокруг своей стороны а . Найти поверхность и объём тела вращения.

подсказка

ответ

Подсказка

При вращении получается два конуса с радиусом основания ОВ.

Поверхность тела вращения – это две одинаковые боковые поверхности указанного конуса.

√ 3 .

Ответ:

π а 2

π а 3

____

V =

Задача:

Равнобедренняй треугольник вращается вокруг своей высоты. Определить стороны этого треугольника, если его периметр равен 30 см. , а полная поверхность тела вращения равна 60 π см 2 .

подсказка

ответ

Подсказка

При вращении этого треугольника вокруг высоты АС лучается конус.

Ответ: 11см., 11см., 8 см.

Часть ll

Комбинации тел вращения.

Комбинация тел вращения

Основные понятия о комбинации тел вращения:

Комбинация цилиндра и конуса;

Комбинация цилиндра и шара;

Комбинация конуса и шара.

Проверь себя (теоретические сведения).

Задачи для самостоятельного решения, (ответы).

Комбинация цилиндра и конуса

Цилиндр называется вписанным в конус , если окружность одного из его оснований лежит на поверхности конуса, а другое основание расположено в плоскости основания конуса.

Комбинация цилиндра и конуса

Конус называется вписанным в цилиндр , если основание конуса совпадает с одним из оснований цилиндра, а вершина конуса лежит в центре другого основания цилиндра.

Комбинация цилиндра и шара

Шар называется вписанным в цилиндр , если основания и каждая образующая цилиндра касаются шара. В этом случае цилиндр называют описанным около шара.

Дополнительные сведения

Ось цилиндра

Центр шара лежит на оси цилиндра, осевое сечение цилиндра представляет собой квадрат со стороной, равной диаметру шара.

•

Комбинация цилиндра и шара

Шар называется описанным около цилиндра , если основаниями цилиндра служат сечения шара. В этом случае цилиндр называют вписанным в шар.

дополнительные сведения

}

Дополнительные сведения

Ось цилиндра

Центром описанного около цилиндра, шара является середина оси цилиндра-отрезка, соединяющего центры его оснований.

Комбинация конуса и шара

Шар называется вписанным в конус , если основание и каждая образующая конуса касаются шара.В этом случае конус называется описанным около шара.

дополнительные сведения

Дополнительные сведения

Шар касается боковой поверхности конуса по окружности, плоскость которой параллельна основанию.

Дополнительные сведения

Центр шара, вписанного в конус,лежит в точке пересечения высоты конуса и биссектрисы угла наклона образующей конуса к плоскости его основания.

Комбинация конуса и шара

Шар называется описанным около конуса , если окружность основания и вершина, принадлежат поверхности конуса. В этом случае конус называют вписанным в шар.

дополнительные сведения

Дополнительные сведения

Центром шара, описанного около конуса, является точка пересечения высоты конуса с перпендикуляром к образующей, проведённым через её середину в плоскости осевого сечения конуса.

О 1

Проверь себя

Введите понятие «цилиндр вписан в конус» и «конус вписан в цилиндр».

Введите понятие «конус вписан в шар» и «конус описан около шара».

Как расположены точки общие для шара и поверхности конуса?

Где расположен центр шара относительно вписанного конуса,что представляет осевое сечение данной комбинации фигур?

Где находится центр шара, вписанного в конус?

Подсказка

Укажите пары подобных треугольников и в них пары углов, имеющие равные величины?

О 1

Во всякий ли цилиндр можно вписать сферу? Какими свойствами должен обладать цилиндр, чтобы в него можно было вписать сферу?

подсказка

Нет не во всякий: осевое сечение цилиндра должно быть квадратом.

Во всякий ли конус можно вписать сферу? Как определить положеное центра сферы, вписанной в конус?

подсказка

Да, во всякий.Центр вписанной сферы находится на пересечении высоты конуса и биссектрисы угла наклона образующей к плоскости основания.

По известному радиусу основания конуса R и его высоте h найдите радиус вписанной сферы.

подсказка

Подсказка:

Искомый радиус : r = R·tg φ , где φ — половина угла наклона образующей конуса к плоскости основания, причём tg 2φ = h:R .

Задачи для самостоятельного решения.

Задача:

В конусе высотой 12см. вписан шар радиуса 3см. Вычислить объём конуса.

ответ

Ответ : 72 π см 3 .

Задача:

В конус вписан цилиндр, высота которого равна радиусу основания конуса.Найти угол между осью конуса и его образующей, зная, что полная поверхность цилиндра относится к площади основания конуса как 3:2.

ответ

подсказка

}

_________

Пусть:

R — радиус основания конуса, r- радиус основания цилиндра,

β — искомый угол.

По условию ОВ=ОD=R.

S полн. цил.

______

___

S осн. кон.

Тогда по условию задачи:

)

(

r 2

___

____

2 πR 2 + 2 πRr

__________

R 2

πR 2

Из ∆ ЕКВ : tg β = КВ:КЕ = (R — r ) : R = 1- (r : R),

____

подставим и решим уравнение второй степени.

= 1 – tgβ ,

Ответ : β = arctg

Задача:

Доказать ,что отношение объёма конуса к объёму вписанного в него шара равно отношению площади полной поверхности конуса к площади шоверхности шара.

Задача

Определить боковую поверхность конуса, зная длину радиуса R , описанного вокруг него шара и угол β , под которым из центра видна образующая конуса.

ответ

Подсказка

∆ АОВ — равнобедренный т.к. АО=ОВ=R.

Проведём ОМ – высоту.

Тогда ВМ= ½ • ВА= ½ ·L,

L ВОМ = ½ • β ,

Из ∆ ВОМ найдём ВМ:

ВМ = ОВ· sin β / 2 , т. е.

½ ·L = R· sin β / 2 ,

L=2 R· sin β / 2 .

О 1

Ответ: S бок. = 2π R 2 sin β · sin β / 2

Желаем удачи!

Источник

11 класс

Учитель математики

МАОУ СОШ №30, г. Челябинска

Юрченко Ольга Павловна

Цель урока:

Обобщение знаний по теме «Тела вращения»: нахождение

основных элементов фигур, площади поверхности.

Закрепление навыков решения задач уровня ЕГЭ.
Развитие самостоятельности при решении задач.
Развитие алгоритмического мышления.
Развитие пространственного воображения.
Воспитание контроля и самоконтроля.

Г. Галилей

Организационный

момент

5 мин

2. Актуализация знаний (блиц-опрос)

5 мин

3. Сообщения учащихся

(историческая справка)

5 мин

4. Решение задач уровня ЕГЭ

15 мин

5. Самостоятельная работа

10 мин

6. Итог урока.

5 мин

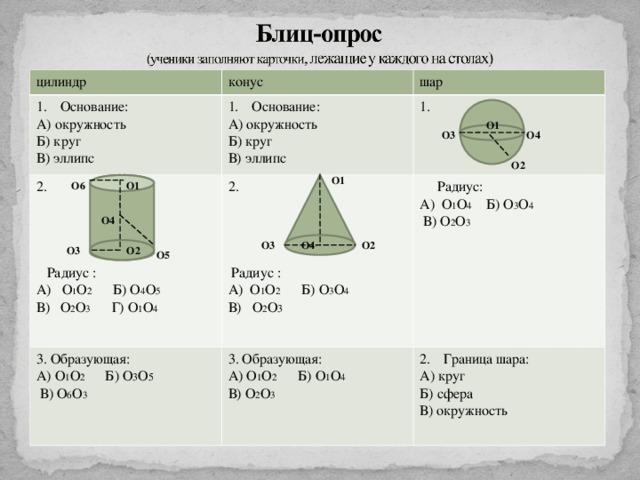
цилиндр

конус

Основание:

А) окружность

Б) круг

В) эллипс

шар

Радиус :

А) О 1 О 2 Б) О 4 О 5

В) О 2 О 3 Г) О 1 О 4

Основание:

Радиус :

А) О 1 О 2 Б) О 3 О 4

В) О 2 О 3

3. Образующая:

А) О 1 О 2 Б) О 3 О 5

В) О 6 О 3

А) окружность

Б) круг

В) эллипс

3. Образующая:

А) О 1 О 2 Б) О 1 О 4

В) О 2 О 3

Радиус:

А) О 1 О 4 Б) О 3 О 4

В) О 2 О 3

Граница шара:

А) круг

Б) сфера

В) окружность

О1

О3

О4

О2

О1

О6

О1

О4

О2

О3

О4

О3

О2

О5

цилиндр

конус

4. Высота цилиндра — это:

А) расстояние между

плоскостями его

основания Б) отрезок, который

соединяет две любые

точки оснований В) отрезок, который

соединяет центр круга

с любой точкой

цилиндра

шар

4. Высота конуса – это:

А) отрезок, соединяющий вершину с любой точкой основания

Б) расстояние от вершины конуса до основания

В) отрезок, соединяющий вершину с точкой, лежащей на окружности

Напишите формулу

3. Сечение шара:

А) окружность

Б) круг

В) эллипс

площади боковой

поверхности

цилиндра

5. Напишите формулу площади боковой поверхности конуса

4. Напишите формулу поверхности шара

ндра

Шаром принято называть тело,

ограниченное сферой, т.е. шар и сфера –

это разные геометрические тела.

Однако оба слова «шар» и «сфера» происходят от одного и того же

греческого слова «сфайра» — мяч. При этом слово «шар» образовалось

от перехода согласных сф в ш .

В Х I книге «Начала» Евклид определяет шар как фигуру, описанную

вращающимся около неподвижного диаметра полукругом.

В древности сфера была в большом почёте. Астрономические

наблюдения над небесным сводом неизменно вызывали образ сферы.

Сфера всегда широко применялась в различных областях науки и техники .

Слово цилиндр происходит от греческого слова

, что означает «валик», «каток».

Конус в переводе с греческого “konos” означает

«сосновая шишка».

С конусом и цилиндром люди знакомы с глубокой древности.

Архимед решил задачу об объеме общей части

пересекающихся цилиндров.

Демокрит получил формулу для вычисления объема

пирамиды и конуса.

Школе Платона принадлежит:

а) исследование свойств цилиндра и конуса;

б) изучение конических сечений.

Большой трактат о конических сечениях был написан

Аполлонием Пергским – учеником Евклида

В геологии существует понятие « конус выноса ». Это форма рельефа,

образованная скоплением обломочных пород (гальки, гравия, песка), вынесенными

горными реками на предгорную равнину или в более плоскую широкую долину .

В биологии есть понятие « конус нарастания ». Это верхушка побега и корня растений, состоящая из клеток образовательной ткани.

« Конусами » называется семейство морских

моллюсков. Раковина коническая (2–16 см),

ярко окрашенная.

По статистике на Земле ежегодно гибнет от разрядов

молний 6 человек на 1000 000 жителей .

Этого бы не случалось, если бы везде были громоотводы,

так как образуется конус безопасности. Чем выше

громоотвод, тем больше объем такого конуса.

Высота конуса равна 10, а диаметр основания – 48.

Найдите образующую конуса.

Ответ: 26

Высота конуса равна 6, а длина образующей – 10.

Найдите диаметр основания конуса

Ответ: 16

Площадь боковой поверхности цилиндра равна 16π, а диаметр основания – 8. Найдите высоту цилиндра.

Решение:

S = 2 π R h

→ 16 π = 8 π h

h = 2

2R =8

S = 16 π

Ответ: 2

Найдите радиус сферы, если площадь сферы равна 16π

Решение:

S = 4 π R²

16 π =

4 π R²

→

R = 2

S = 16 π

Ответ: 2

Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в 3 раза?

Решение:

S = π RL

S 1 = π R(3L) = 3 ( π RL ) = 3 S

Ответ: в 3 раза

π R² =3 4 π R²=12 Ответ: S шара = 12″ width=»640″

Задачи из банка данных ЕГЭ (устное решение задачи)

Около шара описан цилиндр, площадь

поверхности которого равна 18.

Найдите площадь поверхности шара.

Решение:

6 π² = 18

π R² =3

4 π R²=12

Ответ: S шара = 12

Прямоугольный параллелепипед

описан около единичной сферы.

Найдите его площадь поверхности .

Решение:

Т.к. сфера вписана в параллелепипед, то ABCDA 1 B 1 C 1 D 1 является кубом, в котором а = 2 R = 2 ∙ 1 = 2

Значит, S = 6a² = 6 ∙ 2²= 24

Ответ: 24

ВО = ∙ 4 = 2, Значит, S = 8 πR = 8π ∙ 2 = 16π Ответ: 16π» width=»640″

Равнобедренный треугольник, у которого боковые стороны

равны по 4см, а один из углов 120 ° , вращается вокруг прямой,

содержащей большую сторону.

Найдите площадь поверхности полученного тела.

120 ̊

Решение:

= 2 πR ∙ 4 = 8 πR

S = 2 S бок. = 2 π RL

т.е. R = 2

АВ=

Из ∆ АВО: ∟А = 30˚ = ВО =

∙ 4 = 2,

Значит, S = 8 πR = 8π ∙ 2 = 16π

Ответ: 16π

Прямоугольник с периметром 16см и площадью 15см 2 вращается

вокруг большей стороны. Найдите площадь поверхности тела вращения .

Решение:

S = S бок. + 2 S осн.

S = 2πRh + 2πR 2

Из прямоугольника ABCD : S = AB ∙ BC = 15

P = 2 ( AB + BC ) = 16

Или, Rh = 15

R + h = 8,

Ответ: 48π см 2

значит, R = 3, h = 5

Таким образом,

S = 2 π ∙15 + 2 π ∙ 3 2 =

48π (см 2 )

1 вариант

2 вариант

1. Образующая конуса

5 см, высота 4 см. Найдите площадь боковой поверхности конуса.

1. Высота конуса 4 см, а радиус основания 3см. Найдите площадь поверхности конуса.

2. Осевым сечением цилиндра является квадрат, площадь которого 100см². Найдите площадь боковой поверхности цилиндра.

2. Осевое сечение цилиндра – квадрат, длина диагонали которого равна 20см. Найдите радиус основания цилиндра.

Ответы: 1 вариант – 15 π ; 100 π

2 вариант – 24 π ; 5√2

Итог урока

1. Домашнее задание

Поставьте вопросы к данным условиям задач и решите их:

Дан шар, радиус которого 2см.
Длина окружности основания цилиндра 8 π см, а диагональ

осевого сечения 17см.

Прямоугольная трапеция с основаниями 2 и 5 см и меньшей боковой стороной 4 см вращается вокруг большего основания.

2. Рефлексия ( бланки опроса лежат на столах учащихся ).

Поставьте «плюс» или «минус» напротив каждого утверждения

Я знаю формулы для нахождения площадей поверхностей тел вращения.
Я понял, как решать типовые задачи уровня ЕГЭ.
Я расширил свои знания о телах вращения.

Источник

1. ТЕЛА ВРАЩЕНИЯ

ПОУ. Геометрия. 11 класс

2.

1.
2.
3.
4.
5.
ФИО
Место работы
Должность
Предмет
Класс
Терентьева Татьяна Авенировна
МБОУ СОШ № 62 г. Архангельск
Учитель
Математика
11
6. Цель урока: систематизация и обобщение знаний по теме
«Тела вращения».
7. Задачи:
а) повторить понятия цилиндра, конуса и сферы, их элементов;
б) повторить формулы площади поверхностей и объемов тел
вращения;
в) закрепить способы решения задач на тела вращения.
8. Формы работы учащихся:
Фронтальная, самостоятельная работа, индивидуальная работа,
работа с презентацией
9. Необходимое техническое оборудование: компьютер; проектор;
экран
10. Структура и ход урока

3. План урока

ПЛАН УРОКА
Д/з:
Прототипы В13
(открытый банк заданий)
№ 1 – 20 из 60
(письменно и обязательно).
mathege.ru

4. План урока

ПЛАН УРОКА
1.Повторение теории
2.Решение задач
3.Тест
4.Самостоятельная работа
5.Подведение итогов

5. Теория. Примеры тел вращения

ТЕОРИЯ.
ПРИМЕРЫ ТЕЛ ВРАЩЕНИЯ
Цилиндр — образован
прямоугольником, вращающимся
вокруг одной из сторон

6. Теория. Примеры тел вращения

ТЕОРИЯ.
ПРИМЕРЫ ТЕЛ ВРАЩЕНИЯ
Конус — образован
прямоугольным треугольником,
вращающимся вокруг одного из
катетов

7. Теория. Примеры тел вращения

ТЕОРИЯ.
ПРИМЕРЫ ТЕЛ ВРАЩЕНИЯ
Шар — образован полукругом,
вращающимся вокруг диаметра

8. Теория. Цилиндр

ТЕОРИЯ. ЦИЛИНДР
1
.
5
3
2
4
.
Основные понятия:
1. Ось цилиндра
2. Основание
3. Высота (h)
4. Образующая (l)
5. Радиус основания
(R)

9. Цилиндр

ЦИЛИНДР
Осевое сечение
(сечение, проходящее
через ось цилиндра) –
прямоугольник

10. Цилиндр

ЦИЛИНДР
Сечение цилиндра
плоскостью,
перпендикулярной оси
цилиндра круг

11. Цилиндр

ЦИЛИНДР
Формулы:
S осн R
2
— площадь основания
S бок 2 Rh
— площадь боковой
поверхности
V R 2 h
— объем
R радиус; h высота

12. Теория. Конус

2
ТЕОРИЯ. КОНУС
.
1
4
5
3
.
6
Основные понятия:
1. Вершина конуса
2. Ось конуса
3. Основание
4. Высота (h)
5. Образующая (l)
6. Радиус основания
(R)

13. Конус

КОНУС
Осевое сечение
(сечение, проходящее
через ось конуса) –
равнобедренный
треугольник

14. Конус

КОНУС
Сечение конуса плоскостью,
перпендикулярной оси конуса круг

15. Конус*

КОНУС*
Сечения конической поверхности плоскостью:
а) эллипс; б) парабола; в) гипербола.

16. Конус

КОНУС
Развертка боковой поверхности конуса.

17. Конус

КОНУС
Формулы:
S осн R
2
— площадь основания
Sбок Rl
— площадь боковой
поверхности
1 2
V R h
3
— объем
R радиус; h высота; l образующая

18. Теория. Усеченный конус

ТЕОРИЯ. УСЕЧЕННЫЙ КОНУС
Sбок ( R r )l
l
h
1
V h( R 2 r 2 Rr )
3

19. Теория. Сфера и шар

ТЕОРИЯ. СФЕРА И ШАР
т.О – центр
сферы
R — радиус
Площадь поверхности:
S 4 R 2
Объём:
4 3
V R
3

20. Сфера и шар

СФЕРА И ШАР
Плоскость, имеющая со
сферой только одну общую
точку, называется
касательной плоскостью к
сфере.
Т1: — касательная
плоскость, А – точка касания
ОА
Т2: ОА — касательная
плоскость, А – точка касания

21. Решение задач (№1 из 6)

РЕШЕНИЕ ЗАДАЧ (№1 ИЗ 6)
R
16
см.
В цилиндрическом сосуде уровень жидкости
достигает 16 см. На какой высоте будет
находиться уровень жидкости, если ее
перелить во второй цилиндрический сосуд,
диаметр которого в 2 раза больше диаметра
первого? Ответ выразите в сантиметрах.
V R 2 h
2R
R 2 16 (2 R) 2 x
x
R 2 16 4 R 2 x
x 4
Ответ: 4см.

22. Решение задач (№2 из 6)

РЕШЕНИЕ ЗАДАЧ (№2 ИЗ 6)
h
R
Объем конуса равен 16. Через
середину высоты параллельно
основанию конуса проведено сечение,
которое является основанием
меньшего конуса с той же вершиной.
Найдите объем меньшего конуса.
2
1 2
V R h 16
3
1 R h 1 2 1
1
Vм ен R h 16 2
3 2 2 3
8
8
Ответ: 2
Перейти к
решению теста

23. Решение задач (№3 из 6)

РЕШЕНИЕ ЗАДАЧ (№3 ИЗ 6)
2
L=3
Lокр.осн 3; l 2;
S б .пов. ?
Длина окружности основания конуса
равна 3, образующая равна 2.
Найдите площадь боковой
поверхности конуса.
3
Lокр.осн 2 R 3; R ;
2
S бок.пов Rl ;
S б .пов.
3
2 3
2
Ответ: 3
Перейти к
решению теста

24. Решение задач (№4 из 6)

РЕШЕНИЕ ЗАДАЧ (№4 ИЗ 6)
Конус вписан в шар. Радиус
основания конуса равен
радиусу шара. Объем конуса
равен 6. Найдите объем шара.
Vкон.
Vкон. 6;Vшара ?
Vшара
1 2
1 2
1 3
R h R R R 6;
3
3
3
4 3
1 3
R 4 R 4 Vкон. 4 6 24
3
3
Ответ: 24
Перейти к
решению теста

25. Решение задач (№5 из 6)

РЕШЕНИЕ ЗАДАЧ (№5 ИЗ 6)
1
1
Правильная четырехугольная призма
описана около цилиндра, радиус
основания и высота которого равны 1.
Найдите площадь боковой поверхности
призмы.
S бок.призм ы Pосн h 8 1 8
Ответ: 8
Перейти к
решению теста

26. Решение задач (№6 из 6)

РЕШЕНИЕ ЗАДАЧ (№6 ИЗ 6)
h
r
Найдите площадь боковой поверхности
правильной треугольной призмы,
описанной около цилиндра, радиус
основания которого равен 3 , а высота
равна 2.
r 3; h 2; S бок.пр. ?
а3 R 3 2r 3 2 3 3 6
R
rr
S бок.пр. Рh 3а3 h 3 6 2 36
Ответ: 36
Перейти к
решению теста

27. Тест

ТЕСТ
1. Во сколько раз увеличится объем
цилиндра, если
а) его высота увеличится в 2 раза
в2
раза
в4
раза
в 8 раз
в 16
раз

28. Тест

ТЕСТ
1. Во сколько раз увеличится объем
цилиндра, если
б) его радиус увеличится в 2 раза
в2
раза
в4
раза
в 8 раз
в 16
раз

29. Тест

ТЕСТ
1. Во сколько раз увеличится объем
цилиндра, если
в) его высота и радиус увеличатся
в 2 раза
в2
раза
в4
раза
в 8 раз
в 16
раз

30. Тест

ТЕСТ
2. Во сколько раз увеличится объем
конуса, если
а) его высота увеличится в 2 раза
в 2 раза
в 4 раза
в 8 раз
в 16 раз

31. Тест

ТЕСТ
2. Во сколько раз увеличится объем
конуса, если
б) диаметр основания увеличится
в 2 раза
в 2 раза
в 4 раза
в 8 раз
в 16 раз

32. Тест

ТЕСТ
2. Во сколько раз увеличится объем
конуса, если
в) его радиус увеличится в 2 раза,
а высота уменьшится в 2 раза
в 2 раза
в 4 раза
в 8 раз
в 16 раз

33. Тест

ТЕСТ
3. Диаметр шара увеличился в 2 раза.
а) Во сколько раз увеличился его объем
в 2 раза
в 4 раза
в 8 раз
в 16 раз

34. Тест

ТЕСТ
3. Диаметр шара увеличился в 2 раза.
б) Во сколько раз увеличилась площадь
его поверхности
в 2 раза
в 4 раза
в 8 раз
в 16 раз

35. Самостоятельная работа

САМОСТОЯТЕЛЬНАЯ РАБОТА
1. Радиус основания цилиндра равен 2, высота
равна 3. Найдите площадь боковой
поверхности цилиндра, деленную на .
2. Площадь большого круга шара равна 3.
Найдите площадь поверхности шара.
3.
Площадь боковой поверхности конуса в два
раза больше площади основания. Найдите
угол между образующей конуса и плоскостью
основания. Ответ дайте в градусах.
Дополнительны
е задачи
Перейти к
проверке

36. Самостоятельная работа (задача 1)

САМОСТОЯТЕЛЬНАЯ РАБОТА (ЗАДАЧА
1)
Радиус основания цилиндра
равен 2, высота равна 3. Найдите
площадь боковой поверхности
цилиндра, деленную на .
R 2; h 3;
S бок
?
S бок 2 Rh 2 2 3 12 ;
S бок
12
12
Ответ: 12

37. Самостоятельная работа (задача 2)

САМОСТОЯТЕЛЬНАЯ РАБОТА (ЗАДАЧА
2)
Площадь большого круга шара
равна 3. Найдите площадь
поверхности шара.
S круга 3;
S кр R 2 3;
S пов.шара ?
S пов.шара 4 R 2 4 3 12
Ответ: 12

38. Самостоятельная работа (задача 3)

САМОСТОЯТЕЛЬНАЯ РАБОТА (ЗАДАЧА
3)
A
C
B
S бок
2; ABC ?
S осн
Площадь боковой поверхности
конуса в два раза больше
площади основания. Найдите
угол между образующей конуса
и плоскостью основания. Ответ
дайте в градусах
S бок Rl
2 2;
S осн R
l
2;
R
BAC 30 ; ABC 60
Ответ: 60 .

39. Дополнительные задачи

ДОПОЛНИТЕЛЬНЫЕ ЗАДАЧИ
1. Осевое сечение конуса прямоугольный треугольник.
Найдите площадь боковой поверхности конуса, если его
радиус основания равен R.
Ответ : R
2
2
2. Цилиндр образован вращением прямоугольника
вокруг одной из его сторон. Выразите объем цилиндра
через площадь S прямоугольника и длину С окружности
основания цилиндра.
S C
Ответ :
2
Продолжение
доп. задач
Вернуться к
с/р

40. Дополнительные задачи

ДОПОЛНИТЕЛЬНЫЕ ЗАДАЧИ
3. В щар с единичным радиусом вписан конус, образующая
которого равна 3.
Найдите величину угла при вершине осевого сечения
конуса.
Ответ :120
4. В цилиндр, радиус основания которого равен 6, вписан
конус. Основание конуса совпадает с основанием
цилиндра, а вершина конуса совпадает с центром верхнего
основания цилиндра. Площадь боковой поверхности
конуса равна 60 . Найдите площадь боковой поверхности
цилиндра.
Ответ : 96
Вернуться к
с/р

41. 42. Правильно!

ПРАВИЛЬНО!

43. Не верно!

НЕ ВЕРНО!

Источник