Тела вращения в задачах егэ акчурина ответы

Предложите, как улучшить StudyLib

(Для жалоб на нарушения авторских прав, используйте

другую форму
)

Ваш е-мэйл

Заполните, если хотите получить ответ

Оцените наш проект

1

2

3

4

5

Источник

По теме: методические разработки, презентации и конспекты

Решение задач по теме: «Тела вращения

Цели урока:
• систематизировать знания учащихся;
• обобщить изученный материал;
• рассмотреть задачи на комбинацию тел;
• проверить умения и навыки при решении задач на нахождение объемов тел …

Задачи к уроку по теме «Тела вращения»

При обучении геометрии большое значение имеет умение решать задачи, требующее установление соотношений между данными и искомыми. При решении таких задач проявляется уровень математического развит…

Источник
Skip to content

ЕГЭ Профиль №5. Комбинация тел

ЕГЭ Профиль №5. Комбинация телadmin2022-08-15T15:13:25+03:00

Скачать файл в формате pdf.

ЕГЭ Профиль №5. Комбинация тел

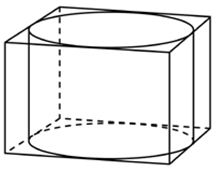
Задача 1. Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 1. Найдите объем параллелепипеда. 

Ответ

ОТВЕТ: 4.
Задача 2. Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 4. Объем параллелепипеда равен 16. Найдите высоту цилиндра.

Ответ

ОТВЕТ: 0,25.
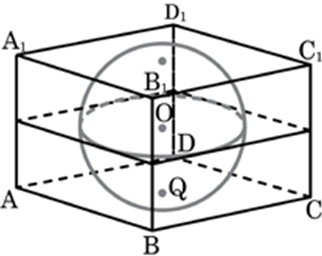
Задача 3. Прямоугольный параллелепипед описан около сферы радиуса 1. Найдите его объем.

Ответ

ОТВЕТ: 8.
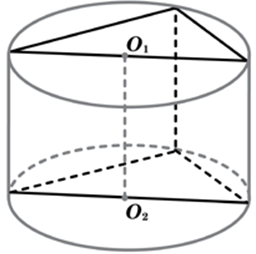
Задача 4. В основании прямой призмы лежит прямоугольный треугольник с катетами 6 и 8. Боковые ребра равны (frac{5}{pi }). Найдите объем цилиндра, описанного около этой призмы.

Ответ

ОТВЕТ: 125.
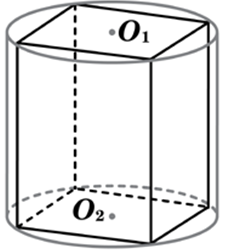
Задача 5. В основании прямой призмы лежит квадрат со стороной 2. Боковые ребра равны (frac{2}{pi }). Найдите объем цилиндра, описанного около этой призмы.

Ответ

ОТВЕТ: 4.
Задача 6. Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 25.

Ответ

ОТВЕТ: 75.
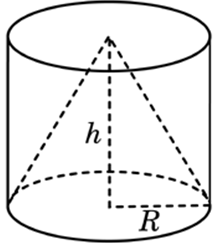Задача 7. Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 1. Найдите площадь боковой поверхности призмы.

Ответ

ОТВЕТ: 8.
Задача 8. Найдите площадь боковой поверхности правильной треугольной призмы, описанной около цилиндра, радиус основания которого равен (sqrt 3 ), а высота равна 2.

Ответ

ОТВЕТ: 36.
Задача 9. Найдите площадь боковой поверхности правильной шестиугольной призмы, описанной около цилиндра, радиус основания которого равен (sqrt 3 ), а высота равна 2.

Ответ

ОТВЕТ: 24.
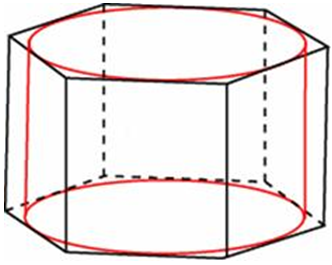Задача 10. Около шара описан цилиндр, площадь поверхности которого равна 18. Найдите площадь поверхности шара.

Ответ

ОТВЕТ: 12.
Задача 11. Из единичного куба вырезана правильная четырехугольная призма со стороной основания 0,5 и боковым ребром 1. Найдите площадь поверхности оставшейся части куба.

Ответ

ОТВЕТ: 7,5.
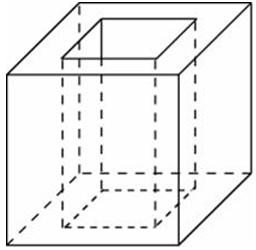Задача 12. Цилиндр и конус имеют общие основание и высоту. Найдите объем конуса, если объем цилиндра равен 150.

Ответ

ОТВЕТ: 50.
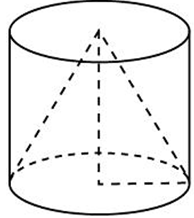Задача 13. Объем прямоугольного параллелепипеда, описанного около сферы, равен 216. Найдите радиус сферы.

Ответ

ОТВЕТ: 3.
Задача 14. Конус описан около правильной четырехугольной пирамиды со стороной основания 4 и высотой 6. Найдите его объем, деленный на (pi ).

Ответ

ОТВЕТ: 16.
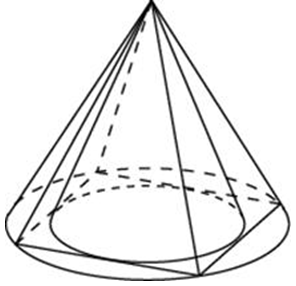
Задача 15. Во сколько раз объем конуса, описанного около правильной четырехугольной пирамиды, больше объема конуса, вписанного в эту пирамиду?

Ответ

ОТВЕТ: 2.
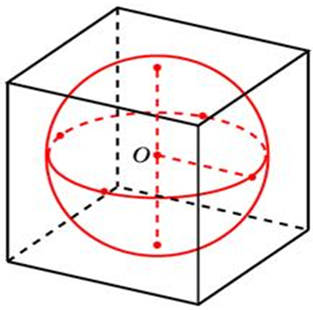
Задача 16. В куб с ребром 3 вписан шар. Найдите объем этого шара, деленный на (pi ).

Ответ

ОТВЕТ: 4,5.
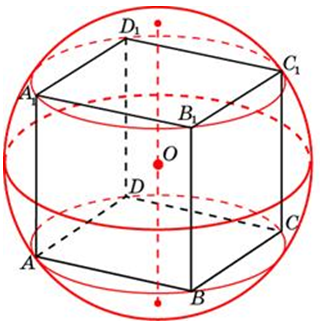
Задача17 . Около куба с ребром (sqrt 3 ) описан шар. Найдите объем этого шара, деленный на (pi ).

Ответ

ОТВЕТ: 4,5.
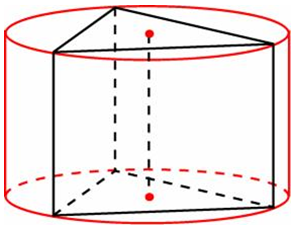
Задача 18. Найдите площадь боковой поверхности правильной треугольной призмы, вписанной в цилиндр, радиус основания которого равен (2sqrt 3 ), а высота равна 2.

Ответ

ОТВЕТ: 36.
Задача 19. Вершина A куба ABCDA1B1C1D1 со стороной 1,6 является центром сферы, проходящей через точку A1. Найдите площадь S части сферы, содержащейся внутри куба. В ответе запишите величину (frac{S}{pi }).

Ответ

ОТВЕТ: 1,28.
Задача 20. Середина ребра куба со стороной 1,9 является центром шара радиуса 0,95. Найдите площадь S части поверхности шара, лежащей внутри куба. В ответе запишите (frac{S}{pi }).

Ответ

ОТВЕТ: 0,9025.
Задача 21. Объем тетраэдра равен 1,9. Найдите объем многогранника, вершинами которого являются середины ребер данного тетраэдра.

Ответ

ОТВЕТ: 0,95.
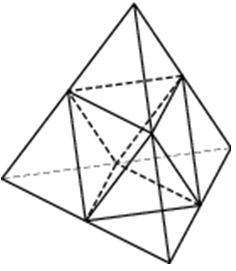Задача 22. Площадь поверхности тетраэдра равна 1,2. Найдите площадь поверхности многогранника, вершинами которого являются середины ребер данного тетраэдра.

Ответ

ОТВЕТ: 0,6.
Задача 23. Цилиндр описан около шара. Объем цилиндра равен 9. Найдите объем шара.

Ответ

ОТВЕТ: 6.
Задача 24. Цилиндр описан около шара. Объем шара равен 24. Найдите объем цилиндра.

Ответ

ОТВЕТ: 36.
Задача 25. Конус вписан в цилиндр. Объем конуса равен 16. Найдите объем цилиндра.

Ответ

ОТВЕТ: 48.
Задача 26. Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем шара равен 28. Найдите объем конуса.

Ответ

ОТВЕТ: 7.
Задача 27. Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем конуса равен 27. Найдите объем шара.

Ответ

ОТВЕТ: 108.
Задача 28. Правильная четырехугольная призма описана около цилиндра, радиус основания которого равен 2. Площадь боковой поверхности призмы равна 48. Найдите высоту цилиндра.

Ответ

ОТВЕТ: 3.
Задача 29. Куб вписан в шар радиуса (5sqrt 3 ). Найдите объем куба.

Ответ

ОТВЕТ: 1000.
Задача 30. Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы находится в центре основания конуса. Образующая конуса равна (7sqrt 2 ). Найдите радиус сферы.

Ответ

ОТВЕТ: 7.
Задача 31. Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы находится в центре основания конуса. Радиус сферы равен (28sqrt 2 ). Найдите образующую конуса.

Ответ

ОТВЕТ: 56.
Задача 32. Шар вписан в цилиндр. Площадь поверхности шара равна 111. Найдите площадь полной поверхности цилиндра.

Ответ

ОТВЕТ: 166,5.
Задача 33. Шар, объем которого равен (6pi ), вписан в куб. Найдите объем куба.

Ответ

ОТВЕТ: 36.

Источник

Зачет   «Тела вращения»

1 вариант

№13
ЕГЭ, база

1)     
Радиус ос­но­ва­ния
цилиндра равен 2, вы­со­та равна 3. Най­ди­те площадь бо­ко­вой поверхности
цилиндра, де­лен­ную на π.

2)     
Площадь бо­ко­вой поверхности ци­лин­дра
равна 2π, а диа­метр основания равен 1. Най­ди­те высоту цилиндра.

3)     
Площадь боковой поверхности цилиндра
равна 2π, а высота равна 1. Найдите диаметр основания.

4)     
Во сколь­ко раз уве­ли­чит­ся пло­щадь бо­ко­вой
по­верх­но­сти конуса, если его об­ра­зу­ю­щую уве­ли­чить в 3 раза?

5)     
Высота ко­ну­са равна 4, а диа­метр
основания — 6. Най­ди­те образующую конуса.

6)     
Площадь боль­шо­го круга шара равна 3. Най­ди­те
площадь по­верх­но­сти шара.

7)     
Даны два шара с ра­ди­у­са­ми 3 и 1. Во
сколь­ко раз пло­щадь поверхности пер­во­го шара боль­ше площади по­верх­но­сти
второго?

№16
ЕГЭ, база

8)      
Площадь осевого сечения цилиндра равна 4.
Найдите площадь боковой поверхности цилиндра, деленную на π.

9)     
Длина окружности основания конуса равна 3,
образующая равна 2. Найдите площадь боковой поверхности конуса.

10) Куб
вписан в шар радиуса . Найдите объем куба.

11)  Около
шара опи­сан цилиндр, пло­щадь поверхности ко­то­ро­го равна 18. Най­ди­те
площадь по­верх­но­сти шара.

https://mathb-ege.sdamgia.ru/get_file?id=778

12)  Около
конуса описана сфера (сфера содержит окружность основания конуса и его
вершину). Центр сферы находится в центре основания конуса. Радиус сферы
равен . Найдите образующую
конуса.

Дополнительно: (№13 ЕГЭ, профиль)

13) 
В цилиндре
образующая перпендикулярна плоскости основания. На окружности одного из
оснований цилиндра выбраны точки А и В, а на
окружности другого основания — точки В1 и С1,
причем ВВ1 — образующая цилиндра, а отрезок АС1 пересекает
ось цилиндра.

а)
Докажите, что угол АВС1 прямой.

б)
Найдите угол между прямыми ВВ1 и АС1,
если АВ = 6, ВВ1 = 15, В1С1 = 8.

Зачет   «Тела вращения»

2 вариант

№13
ЕГЭ, база

1)     
Радиус основания цилиндра
равен 7, высота равна 10. Найдите площадь боковой поверхности цилиндра,
деленную на π .

2)     
Длина
окруж­но­сти основания ци­лин­дра равна 3. Пло­щадь боковой по­верх­но­сти
равна 6. Най­ди­те высоту цилиндра.

3)      Площадь
бо­ко­вой поверхности ци­лин­дра равна 40π а диа­метр основания равен
5. Най­ди­те высоту цилиндра.

4)      Во сколько
раз уменьшится площадь боковой поверхности конуса, если радиус его основания
уменьшится в 1,5 раза, а образующая останется прежней?

5)     
Высота конуса равна 4, а
длина образующей — 5. Найдите диаметр основания конуса.

6)     
Во сколь­ко раз уве­ли­чит­ся
площадь по­верх­но­сти шара, если ра­ди­ус шара уве­ли­чить в 2 раза?

7)     
Даны два
шара. Диа­метр пер­во­го шара в 8 раз боль­ше диа­мет­ра второго. Во сколь­ко
раз пло­щадь по­верх­но­сти пер­во­го шара боль­ше пло­ща­ди по­верх­но­сти
второго?

№16
ЕГЭ, база

8)      
Радиус ос­но­ва­ния
цилиндра равен 26, а его об­ра­зу­ю­щая равна 9. Сечение, па­рал­лель­ное оси
цилиндра, уда­ле­но от неё на расстояние, рав­ное 24. Най­ди­те площадь этого
сечения.

9)     
Длина окружности основания
конуса равна 8, образующая равна 8. Найдите площадь боковой поверхности конуса.

10) Куб вписан в шар радиуса .
Найдите объем куба.

11) 
Около шара описан цилиндр,
площадь поверхности которого равна 45. Найдите площадь поверхности шара.

https://mathb-ege.sdamgia.ru/get_file?id=778

12)  Около
конуса описана сфера (сфера содержит окружность основания конуса и его
вершину). Центр сферы находится в центре основания конуса. Радиус сферы
равен . Найдите образующую
конуса.

Дополнительно: (№13 ЕГЭ, профиль)

13) В цилиндре образующая перпендикулярна плоскости основания.
На окружности одного из оснований цилиндра выбраны точки А и В,
а на окружности другого основания — точки В1 и С1,
причем ВВ1 — образующая цилиндра, а отрезок АС1 пересекает
ось цилиндра.

а) Докажите, что угол АВС1 прямой.

б) Найдите площадь боковой
поверхности цилиндра, если AB = 20, BB1 = 15, B1C1 = 21.

Источник

Практикум по теме «Цилиндр»

Тела вращения в задачах ЕГЭ

1. Осевое сечение цилиндра – квадрат, длина диагонали которого равна 36 см.

Найдите радиус основания цилиндра.

2. Площадь осевого сечения цилиндра равна 10 м

2

, а площадь основания 5 м

2

.

Найдите высоту цилиндра.

3. Длина окружности основания цилиндра равна 8π см, а диагональ осевого

сечения–17 см. Найдите образующую цилиндра.

4. Параллельно оси на расстоянии 2 см от неё проведена плоскость, отсекающая

от окружности основания дугу 90°. Найдите площадь полученного сечения,

если высота цилиндра равна 6 см.

5. Боковую поверхность равностороннего цилиндра (осевое сечение – квадрат) с

высотой 4 см разрезали по образующей. Найдите площадь полученной

развертки.

6. Отрезок, соединяющий центр верхнего основания цилиндра с точкой

окружности нижнего основания, равен 6см и образует с плоскостью нижнего

основания угол 60°. Найдите площадь осевого сечения цилиндра.

7. Параллельно оси цилиндра проведена плоскость, отсекающая от окружности

основания дугу α. Угол между диагональю полученного сечения и

образующей цилиндра равен β. Найдите площадь сечения, если радиус

цилиндра равен R.

8. Через образующую цилиндра проведены две взаимно перпендикулярных

сечения, площади которых равны 10 и 24 см

2

. Найдите площадь осевого

сечения цилиндра.

9. Отрезок, соединяющий точки окружностей верхнего и нижнего оснований

цилиндра, лежит на прямой, удаленной от оси цилиндра на 2см и образует с

плоскостью основания угол 60°. Проекция данного отрезка на плоскость

основания равна 4

см. Найдите площадь осевого сечения цилиндра.

10. Найдите площадь осевого сечения цилиндра, если диагональ осевого сечения

равна 4 и она образует с основанием угол в 45°.

Источник

Понравилась статья? Поделить с друзьями:
  • Тел миллэт сакчысы сочинение
  • Тел милл?т сакчысы сочинение
  • Тел кыйммэтле тарихи мирас сочинение
  • Тел курке суз сочинение
  • Тел к?рке с?з сочинение