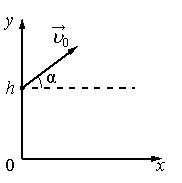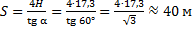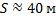Тело брошенное под углом к горизонту егэ - Помощь в подготовке к экзаменам и поступлению

в условии
в решении
в тексте к заданию
в атрибутах

Категория:

Атрибут:

Всего: 126 1–20 | 21–40 | 41–60 | 61–80 …

Добавить в вариант

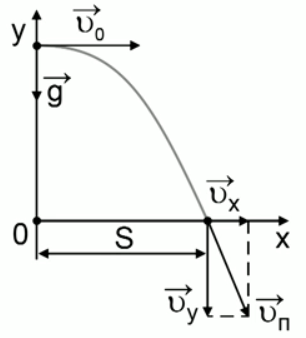
С горизонтальной плоскости вначале бросают маленький мячик под углом к горизонту со скоростью υ = 20 м/с. В момент, когда мячик достигает наивысшего положения на своей траектории, стреляют пулей из ружья со скоростью V  =  120 м/с в направлении мячика, причём пуля вылетает из той же точки, из которой был брошен мячик (см. рис.). Под каким углом varphi к горизонту надо стрелять, чтобы пуля из ружья попала в мячик? Трением мячика и пули о воздух можно пренебречь. Указание: для численного решения уравнений используйте микрокалькулятор.

Какие законы Вы использовали для описания движения тел? Обоснуйте их применение к данному случаю.

Человек ростом h  =  1,6 м, стоя на земле, кидает мяч из-за головы и хочет перебросить его через забор высотой H  =  4,8 м, находящийся на расстоянии l  =  6,4 м от него. Определите модуль скорости, с которой необходимо бросить мяч, чтобы он перелетел через забор, коснувшись его в верхней точке своей траектории? Сопротивлением воздуха пренебречь.

Какие законы Вы использовали для описания движения мяча? Обоснуйте их применение к данному случаю.

Источник: ЕГЭ по физике 11.06.2021. Основная волна. Москва

При выполнении трюка «Летающий велосипедист» гонщик движется по трамплину под действием силы тяжести, начиная движение из состояния покоя с высоты Н (см. рис.).

На краю трамплина скорость гонщика направлена под углом к горизонту. Пролетев по воздуху, гонщик приземляется на горизонтальный стол, находящийся на той же высоте, что и край трамплина. Какова высота полета h на этом трамплине? Сопротивлением воздуха и трением пренебречь.

Какие законы Вы используете для описания гонщика по трамплину? Обоснуйте их применение к данному случаю.

Прибор наблюдения обнаружил летящий снаряд и зафиксировал его горизонтальную координату x_1 и высоту м над Землёй (см. рисунок). Через 3 с снаряд упал на Землю и взорвался на расстоянии м от места его обнаружения. Известно, что снаряды данного типа вылетают из ствола пушки со скоростью 800 м/с. Какова была максимальная высота Н траектории снаряда, если считать, что сопротивление воздуха пренебрежимо мало? Пушка и место взрыва находятся на одной горизонтали.

Какие законы Вы использовали для описания движения снаряда? Обоснуйте их применение к данному случаю.

Источник: ЕГЭ по физике 06.06.2013. Основная волна. Дальний Восток. Вариант 6.

В длинном и широком спортивном зале с высотой потолка H = 10 м баскетболист бросает мяч товарищу по команде с начальной скоростью V = 20 м/с. Какова может быть максимальная дальность его передачи по горизонтали? Сопротивлением воздуха и размерами мяча можно пренебречь, бросок делается и принимается руками на уровне h = 2 м от горизонтального пола.

Какие законы Вы использовали для описания движения мяча? Обоснуйте их применение к данному случаю.

Источник: Тренировочная работа по физике 27.04.2018, вариант ФИ10503

Пружинное ружье наклонено под углом к горизонту. Энергия сжатой пружины равна 0,41 Дж. При выстреле шарик массой m=50г проходит по стволу ружья расстояние b, вылетает и падает на расстоянии L=1м от дула ружья в точку M, находящуюся с ним на одной высоте с дулом. (см. рис.). Найдите расстояние b. Трением в стволе и сопротивлением воздуха пренебречь.

Какие законы Вы использовали для описания движения шарика? Обоснуйте их применение к данному случаю.

Источник: ЕГЭ по физике 11.06.2021. Основная волна. Разные задания

Задания Д29 C2 № 3070

Наклонная плоскость пересекается с горизонтальной плоскостью по прямой AB. Угол между плоскостями Маленькая шайба начинает движение вверх по наклонной плоскости из точки A с начальной скоростью под углом к прямой AB. В ходе движения шайба съезжает на прямую AB в точке B. Пренебрегая трением между шайбой и наклонной плоскостью, найдите расстояние AB.

Небольшое тело бросили под углом α = 30º к горизонтальной плоскости с начальной скоростью V₀ = 40 м/c. В верхней точке траектории в него попало другое тело такой же массы, брошенное с той же плоскости вертикально вверх с начальной скоростью u₀ = 25 м/c, и оба тела в результате абсолютно неупругого удара слиплись и полетели дальше вместе (см. рис.). На каком расстоянии l от места броска второго тела слипшиеся тела упадут на горизонтальную плоскость? Сопротивлением воздуха можно пренебречь.

Какие законы Вы используете для описания взаимодействия тел? Обоснуйте их применение к данному случаю.

Человек ростом h, стоя на Земле, бросает из-за головы камень и хочет перебросить его через забор высотой H, находящийся на расстоянии L от человека. Найдите угол, под которым нужно бросить камень, чтобы он перелетел через забор, коснувшись его в верхней точке своей траектории.

Источник: ЕГЭ по физике 11.06.2021. Основная волна. Разные задания

На краю трамплина скорость гонщика направлена под углом к горизонту. Пролетев по воздуху, гонщик приземляется на горизонтальный стол, находящийся на той же высоте, что и край трамплина. Какова дальность полета L на этом трамплине? Cопротивлением воздуха и трением пренебречь.

Какие законы Вы используете для описания движения гонщика по трамплину? Обоснуйте их применение к данному случаю.

Первый камень бросают с горизонтальной поверхности под углом 45° к горизонту. Второй камень бросают с той же по модулю начальной скоростью, но угол, под которым она направлена к горизонту, уменьшают в 2 раза. Как для второго камня по сравнению с первым изменятся время полёта и дальность полёта, если сопротивление воздуха пренебрежимо мало?

Для каждой величины определите соответствующий характер изменения:

1)  увеличится

2)  уменьшится

3)  не изменится

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Время полёта камня	Дальность полёта камня

Источник: ЕГЭ по физике 11.06.2021. Основная волна. Москва

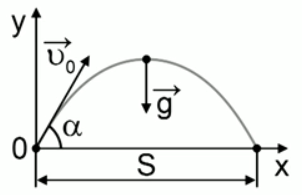
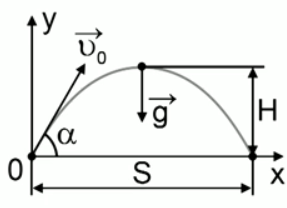
Тело, брошенное с горизонтальной поверхности со скоростью под углом к горизонту, поднимается над горизонтом на максимальную высоту h, а затем падает на расстоянии S от точки броска. Сопротивление воздуха пренебрежимо мало.

Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать. К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры.

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ

А)  Максимальная высота h над горизонтом

Б)  Расстояние S от точки броска до точки падения

Источник: ЕГЭ по физике 06.06.2013. Основная волна. Урал. Вариант 6.

Тело бросили с одинаковой начальной скоростью сначала под углом к горизонту 20°, а затем под углом 30°. Как изменились максимальная высота подъема и время полета тела? Сопротивлением воздуха пренебречь.

Для каждой величины определите соответствующий характер изменения:

1)  увеличилась;

2)  уменьшилась;

3)  не изменилась.

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Максимальная высота подъема, Н	Время полета, t

Источник: ЕГЭ по физике 11.06.2021. Основная волна. Москва

Небольшой камень бросили под углом α к горизонту с высоты h от поверхности земли с начальной скоростью v _0. Сопротивление воздуха пренебрежимо мало. Через время t после броска камень ещё не упал на землю.

Установите соответствие между физическими величинами, характеризующими движение камня, и формулами, выражающими их в рассматриваемой задаче.

К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры.

ФИЗИЧЕСКАЯ ВЕЛИЧИНА

А)  тангенс угла, который составляет вектор скорости камня с горизонтом через время t после броска

Б)  модуль скорости камня в момент его падения на землю

Ответ:

Первый камень бросают с горизонтальной поверхности под углом 45° к горизонту. Второй камень бросают с той же по модулю начальной скоростью, но угол, под которым она направлена к горизонту, увеличивают в 1,5 раза. Как для второго камня по сравнению с первым изменятся время полёта и дальность полёта, если сопротивление воздуха пренебрежимо мало?

Для каждой величины определите соответствующий характер изменения:

1)  увеличится

2)  уменьшится

3)  не изменится

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Время полёта камня	Дальность полёта камня

Тело, брошенное с горизонтальной поверхности со скоростью под углом к горизонту, в течение t секунд поднимается над горизонтом, а затем снижается и падает на расстоянии S от точки броска. Сопротивление воздуха пренебрежимо мало.

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ

А)  Время подъёма t на максимальную высоту

Б)  Расстояние S от точки броска до точки падения

Источник: ЕГЭ по физике 06.06.2013. Основная волна. Урал. Вариант 1., ЕГЭ по физике 06.06.2013. Основная волна. Урал. Вариант 5.

Источник: ЕГЭ по физике 11.06.2021. Основная волна. Разные задания

Всего: 126 1–20 | 21–40 | 41–60 | 61–80 …

Источник

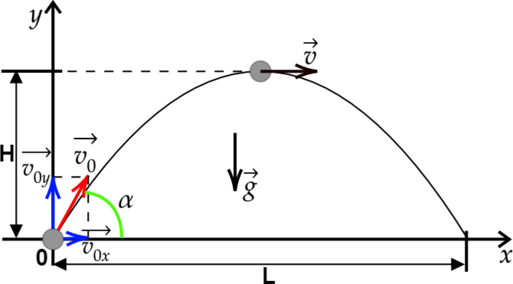
Если тело бросить под углом (displaystyle alpha) к горизонту, то в полете на него действуют сила тяжести и сила сопротивления воздуха. Если силой сопротивления пренебречь, то остается единственная сила — сила тяжести. Поэтому вследствие II закона Ньютона тело движется с ускорением, равным ускорению свободного падения, проекции ускорения на координатные оси равны (displaystyle a_x = 0), (displaystyle a_y = -g). Вдоль оси Ox тело движется равномерно, а вдоль оси Oy равноускоренно, значит можно составить следующую систему уравнений для координат тела:

[begin{cases}
x=x_0+v_text{0x}t,
\
y=y_0+v_text{0y}t+dfrac{g_yt^2}{2},
end{cases}]

Так как мы рассмотриваем случай, изображенный на рисунке, то (displaystyle x_0=0), (displaystyle y_0=0.)

Проекции скорости тела, следовательно, изменяются со временем следующим образом: [begin{cases}
v_x=v_0x=v_0cosalpha,
\
v_y=v_text{0y}t-gt,
end{cases}] Значит, координаты для тела можно записать следующие: [begin{cases}
x=v_text{0}tcosalpha,
\
y=v_text{0}tsinalpha-dfrac{gt^2}{2}, (1)
end{cases}] Определим время движения брошенного тела. Для этого положим координату (displaystyle y) равной нулю, так как в момент приземления высота тела равна нулю. Отсюда получаем для времени полета: [t_text{пол}=frac{2v_0sinalpha}{g}] Дальность полета — это значение координаты (displaystyle x) в конце полета, т.е. в момент времени, равный (displaystyle t_text{пол}). Подставляя это значение в формулу координаты (displaystyle x), получаем: [L=dfrac{2v_0cosalpha v_0sinalpha}{g}=dfrac{v_0^2sin2alpha}{g}] Так как траектория движения тела симметрична, то время подъема на высоту (displaystyle H) вдвое меньше времени всего полета [t_text{под}=dfrac{v_0sinalpha}{g}] Тогда [H=v_0sinalpha t_text{под}-dfrac{gt_text{под}^2}{2}=dfrac{v_0^2sin^2alpha}{2g}] [boxed{L=dfrac{v_0^2sin2alpha}{g}}] [boxed{H=dfrac{v_0^2sin^2alpha}{2g}}]

Источник

Движение тела, брошенного под углом к горизонту. Полный разбор движения. Вывод формул

Это движение представляет собой совокупность двух видов движения:

равномерного движения по оси X (горизонтально): скорость v=const, т.к. ускорение a=0
равнопеременного по оси Y (вертикально): скорость v=v₀+at, т.к. ускорение а=-g

Как же найти скорость?

Сначала найдем скорости по X и по Y отдельно.

Чтобы найти скорость по оси X, которая будет постоянная на всем пути, определим проекцию V₀ на ось X:

Проекция V₀ на ось Х – это прилежащий к углу α катит:

V_0x=V₀cosα

Т.к. V_x – постоянна, поэтому:

V_x= V_0x=V₀cosα

Чтобы найти скорость по оси Y, которая будет меняться, определим проекцию V₀ на ось Y, это будет начальная скорость по вертикальной оси:

Проекция V₀ на ось Y – это противолежащий к углу α катит:

V_0у=V₀sinα

Так как V_y, как мы уже говорили, равнопеременная скорость, то:

V_у= V_0у+at

Учитывая, что ускорение направлено против вертикальной оси (а=-g), и подставляя V_0y получим:

V_у= V₀sinα -gt

Итого:

Зная проекции скорости, можем ли мы восстановить саму скорость? (зная катеты треугольника можем ли мы найти гипотенузу?)

Конечно! Теорема Пифагора.

V²=V_x²+ V_y²

Скорость – дело понятное, как же быть с пройденным путем? Очень просто.

Так как мы сказали, что имеем дело с двумя видами движения в одном, а значит и пути у каждого из видов движения будут разные:

Горизонтального движение по оси Х равномерное, путь при равномерном движении:

S=V t

Обозначим путь по Х за Х и подставим нашу скорость вместо V, получим:

Х= V_xt= V₀cosα t

Вертикальное движение по оси Y равнопеременное, путь при равнопеременном движении:

Аналогично, обозначим путь по Y за Y, подставим нашу скорость вместо V₀ и ускорение а=-g получим:

В итоге:

ВАЖНО! Часто в задачах встречается ситуация, когда нужно найти высоту подъема или дальность полета.

Высота подъема находится очень просто. Все что нужно для решения большинства задач находится в получившихся уравнениях:

для скорости

для координат

Верхняя точка отличается тем, что в ней происходит изгиб. Происходит этот изгиб из-за ускорения свободного падения. Полная скорость, т.к. она направлена по касательной, становится направленной горизонтально, а значит проекция полной скорости по Y равна нулю:

V_у= V₀sinα –gt=0

Запишем концовку предыдущего уравнения и выразим время— время в этой формуле соответствует той же самой верхней точке, назовем его – время подъема (t_п).

V₀sinα –g t_п =0

Получаем:

Высота подъема – это координата Y, поэтому вставляем t_п в уравнение для Y и получаем искомую высоту собственной персоной:

Преобразуем и получим высоту подъема:

Дальность полета – это координата Х в точке падения, поэтому время уже накопится в два раза больше:

Аналогично подставим время в формулу для координаты Х:

Применим формулу из триганометрии: 2sin cos = sin, применим и получим:

Источник

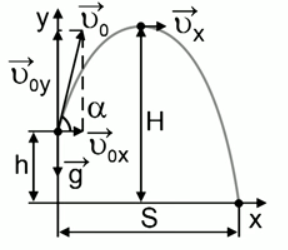
Когда тело бросают вверх под углом к горизонту, оно сначала равнозамедленно поднимается, а затем равноускорено падает. При этом оно перемещается относительно земли с постоянной скоростью.

Важные факты!График движения тела, брошенного под углом к горизонту:

α — угол, под которым было брошено тело

Вектор скорости тела, брошенного под углом к горизонту, направлен по касательной к траектории его движения.
Так как начальная скорость направлена не вдоль горизонтальной линии, обе ее проекции отличны от нуля. Проекция начальной скорости на ось ОХ равна v_0x = v₀cosα. Ее проекция на ось ОУ равна v_0y = v₀sinα.
Проекция мгновенной скорости на ось ОХ равна: v_x = v₀cosα. Ее проекция на ось ОУ равна нулю: v_y = v₀sinα – gt.
Проекция ускорения свободного падения на ось ОХ равна нулю: g_x = 0. Ее проекция на ось ОУ равна –g: g_y = –g.

Кинематические характеристики

Модуль мгновенной скорости в момент времени t можно вычислить по теореме Пифагора:

Минимальной скорости тело достигает в верхней точке траектории. Она выражается формулой:

v_min = v₀cosα = v_h

Максимальной скоростью тело обладает в момент начала движения и в момент падения на землю. Начальная и конечная скорости движения тела равны:

v_max = v_o = v

Время подъема — время, которое требуется телу, чтобы достигнуть верхней точки траектории. В этой точке проекция скорости на ось ОУ равна нулю: v_y = 0. Время подъема определяется следующей формулой:

Полное время — это время всего полета тела от момента бросания до момента приземления. Так как время падения равно времени подъема, формула для определения полного времени полета принимает вид:

Дальность полета — перемещение тела относительно ОХ. Обозначается буквой l. Так как относительно ОХ тело движется с постоянной скоростью, для вычисления дальности полета можно использовать формулу перемещения при равномерном прямолинейном движении:

l = s_x = v_0xt_полн = v₀cosα t_полн

Подставляя в выражение формулу полного времени полета, получаем:

Горизонтальное смещение тела — смещение тела вдоль оси ОХ. Вычислить горизонтальное смещение тела в любой момент времени t можно по формуле координаты x:

Учитывая, что x₀ = 0, и проекция ускорения свободного падения на ось ОХ тоже равна нулю, а проекция начальной скорости на эту ось равна v₀cosα, данная формула принимает вид:

x = v₀cosα t

Мгновенная высота — высота, на которой находится тело в выбранный момент времени t. Она вычисляется по формуле координаты y:

Учитывая, что начальная координата равна 0, проекция начальной скорости на ось ОУ равна v₀sinα, а проекция ускорения свободного падения на эту ось равна –g, эта формула принимает вид:

Наибольшая высота подъема — расстояние от земли до верхней точки траектории. Наибольшая высота подъема обозначается h и вычисляется по формуле:

Пример №1. Небольшой камень бросили с ровной горизонтальной поверхности под углом к горизонту. На какую максимальную высоту поднялся камень, если ровно через 1 с после броска его скорость была направлена горизонтально?

Скорость направляется горизонтально в верхней точке полета. Значит, время подъема равно 1 с. Из формулы времени подъема выразим произведение начальной скорости на синус угла, под которым было брошено тело:

v₀sinα = gt_под

Подставим полученное выражение в формулу для определения наибольшей высоты подъема и сделаем вычисления:

Тело, брошенное под углом к горизонту с некоторой высоты

Когда тело бросают под углом к горизонту с некоторой высоты, характер его движения остается прежним. Но приземлится оно дальше по сравнению со случаем, если бы тело бросали с ровной поверхности.

Важные факты!

График движения тела, брошенного под углом к горизонту с некоторой высоты:

Время падения тела больше времени его подъема: t_пад > t_под.

Полное время полета равно:

t_полн = t_пад + t_под

Уравнение координаты x:

x = v₀cosα t

Уравнение координаты y:

Пример №2. С балкона бросили мяч под углом 60 градусов к горизонту, придав ему начальную скорость 2 м/с. До приземления мяч летел 3 с. Определить дальность полета мяча.

Косинус 60 градусов равен 0,5. Подставляем известные данные в формулу:

x = v₀cosα t = 2 ∙ 0,5 ∙ 3 = 3 м.

Задание EF17562

С высоты Н над землёй начинает свободно падать стальной шарик, который через время t = 0,4 c сталкивается с плитой, наклонённой под углом 30° к горизонту. После абсолютно упругого удара он движется по траектории, верхняя точка которой находится на высоте h = 1,4 м над землёй. Чему равна высота H? Сделайте схематический рисунок, поясняющий решение.

Алгоритм решения

1.Записать исходные данные.

2.Построить на чертеже начальное и конечное положения тела. Выбрать систему координат.

3.Выбрать нулевой уровень для определения потенциальной энергии.

4.Записать закон сохранения энергии.

5.Решить задачу в общем виде.

6.Подставить числовые значения и произвести вычисления.

Решение

Запишем исходные данные:

• Время падения стального шарика: t = 0,4 c.

• Верхняя точка траектории после абсолютно упругого удара о плиту: h = 1,4 м.

• Угол наклона плиты: α = 30^о.

Построим чертеж и укажем на нем все необходимое:

Нулевой уровень — точка D.

Закон сохранения энергии:

E_k0 + E_p0 = E_k + E_p

Потенциальная энергия шарика в точке А равна:

E_pA = mgH

Кинетическая энергия шарика в точке А равна нулю, так как скорость в начале свободного падения нулевая.

В момент перед упругим ударом с плитой в точке В потенциальная энергия шарика минимальна. Она равна:

EpB=mgl1

Перед ударом кинетическая энергия шарика равна:

EkB=mv22

Согласно закону сохранения энергии:

EpA=EpB+EkB

mgH=mgl1+mv22

Отсюда высота H равна:

H=mgl1mg+mv22mg=l1+v22g

Относительно точки В шарик поднимется на высоту h – l₁. Но данный участок движения можно рассматривать как движение тела, брошенного под углом к горизонту. В таком случае высота полета определяется формулой:

h−l1=v2sin2β2g=v2sin2(90−2α)o2g

Отсюда:

l1=h−v2sin2(90−2α)o2g

Шарик падал в течение времени t, поэтому мы можем рассчитать высоту шарика над плитой и его скорость в точке В:

v=gt

Следовательно:

H=l1+v22g=h−(gt)2sin2(90−2α)o2g+(gt)22g

H=h−gt2sin2(90−2α)2+gt22=h−gt22(sin2(90−2α)o−1)

H=1,4−10·0,422(sin2(90−60)o−1)

H=1,4−5·0,16(sin230o−1)

H=1,4−0,8((12)2−1)=1,4−0,8(14−1)

H=1,4+0,6=2 (м)

Ответ: 20

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF17980

В момент t=0 мячик бросают с начальной скоростью v₀ под углом α к горизонту с балкона высотой h (см. рисунок).

Графики А и Б представляют собой зависимости физических величин, характеризующих движение мячика в процессе полёта, от времени t. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять. (Сопротивлением воздуха пренебречь. Потенциальная энергия мячика отсчитывается от уровня y=0).

К каждой позиции графика подберите соответствующую позицию утверждения и запишите выбранные цифры в порядке АБ.

Алгоритм решения

Установить вид механического движения, исходя из условий задачи.
Записать формулы для физических величин, указанных в таблице, в соответствии с установленным видом механического движения.
Определить, как зависят эти величины от времени.
Установить соответствие между графиками и величинами.

Решение

Исходя из условия задачи, мячик движется неравномерно. Этот случай соответствует движению тела, брошенного под углом к горизонту.

Записываем формулы для физических величин из таблицы, учитывая, что речь идет о движении тела, брошенного под углом к горизонту.

Координата x меняется согласно уравнению координаты x:

Так как начальная координата нулевая, а проекция ускорения свободного падения тоже равна нулю, это уравнение принимает вид:

Проекция скорости мячика на ось ОХ равна произведению начальной скорости на время и косинус угла, под которым мячик был брошен. Поэтому уравнение координаты x принимает вид:

В этом уравнении начальная скорость и угол α — постоянные величины. Меняется только время. И оно может только расти. Поэтому и координата x может только расти. В этом случае ей может соответствовать график, представляющий собой прямую линии, не параллельную оси времени. Но графики А и Б не могут описывать изменение этой координаты.

Формула проекции скорости мячика на ось ОХ:

Начальная скорость и угол α — постоянные величины. И больше ни от чего проекция скорости на ось ОХ не зависит. Поэтому ее может охарактеризовать график в виде прямой линии, параллельной оси времени. Такой график у нас есть — это Б.

Кинетическая энергия мячика равна половине произведения массы мячика на квадрат его мгновенной скорости. По мере приближения к верхней точке полета скорость тела уменьшается, а затем растет. Поэтому кинетическая энергия также сначала уменьшается, а затем растет. Но на графике А величина наоборот — сначала увеличивается, потом уменьшается. Поэтому он не может быть графиком зависимости кинетической энергии мячика от времени.

Остается последний вариант — координата y. Уравнение этой координаты имеет вид:

Это квадратическая зависимость, поэтому графиком зависимости координаты y от времени может быть только парабола. Так как мячик сначала движется вверх, а потом — вниз, то и график должен сначала расти, а затем — убывать. График А полностью соответствует этому описанию.

Теперь записываем установленные соответствия в порядке АБ: 42.

Ответ: 42

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF18741

Мальчик бросил стальной шарик вверх под углом к горизонту. Пренебрегая сопротивлением воздуха, определите, как меняются по мере приближения к Земле модуль ускорения шарика и горизонтальная составляющая его скорости?

Для каждой величины определите соответствующий характер изменения:

увеличивается
уменьшается
не изменяется

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Алгоритм решения

Сделать чертеж, иллюстрирующий ситуацию.
Записать формулы, определяющие указанные в условии задачи величины.
Определить характер изменения физических величин, опираясь на сделанный чертеж и формулы.

Решение

Выполняем чертеж:

Модуль ускорения шарика |g| — величина постоянная, так как ускорение свободного падения не меняет ни направления, ни модуля. Поэтому модуль ускорения не меняется (выбор «3»).

Горизонтальная составляющая скорости шарика определяется формулой:

v_x = v₀ cosα

Угол, под которым было брошено тело, поменяться не может. Начальная скорость броска тоже. Больше ни от каких величин горизонтальная составляющая скорости не зависит. Поэтому проекция скорости на ось ОХ тоже не меняется (выбор «3»).

Ответом будет следующая последовательность цифр — 33.

Ответ: 33

pазбирался: Алиса Никитина | обсудить разбор | оценить

Алиса Никитина | Просмотров: 40.3k

Источник

Эксперт ЕГЭ Н. Л. Точильникова
Задача 29 на ЕГЭ по физике – это расчетная задача на механику. До 2014 года включительно она фигурировала под номером «С2».

Это может быть кинематика, динамика, динамика движения по окружности, задача на законы сохранения в механике, статику или гидростатику.

Например, задача на движение тела, брошенного под углом к горизонту:

1. Маленький шарик падает сверху на наклонную плоскость и упруго отражается от нее. Угол наклона плоскости к горизонту равен $30^{circ}$ . На какое расстояние по горизонтали перемещается шарик между первым и вторым ударами о плоскость? Скорость шарика в момент первого удара направлена вертикально вниз и равна м/с.

Запишем «дано»:
V_0=1 м/с
$alpha = 30^{circ}$

Найти: .

Решение:

В задачах части «С» необходимо описывать все параметры, которых нет в дано, иначе оценку снижают на один балл.
Поэтому пишем:
– расстояние по горизонтали между первым и вторым ударами о плоскость.
Нарисуем наклонную плоскость и начальную скорость шарика $overrightarrow{mkern -5mu V_0}$ . Как известно из геометрии, углы с перпендикулярными сторонами равны. Начальная скорость шарика перпендикулярна основанию наклонной плоскости. Восстановим перпендикуляр к наклонной плоскости в точке падения на нее шарика. Тогда угол между этим перпендикуляром и вектором начальной скорости равен углу наклона плоскости к горизонту (углы с перпендикулярными сторонами, зеленые пунктирные линии на рисунке). Угол падения шарика (с перпендикуляром) равен углу отражения $alpha = 30^{circ}$ . Тогда угол между начальной скоростью отскочившего шарика и наклонной плоскостью равен $beta = 90^{circ} - alpha = 90^{circ} - 30^{circ} = 60^{circ} = 2 alpha$ . Модуль скорости не меняется, так как удар упругий.

Итак, убираем построения, которые нам больше не нужны:

Тело будет двигаться по параболе и упадет на расстоянии от точки бросания вдоль наклонной плоскости. Это не то расстояние, которое нам надо найти, мы ищем — расстояние по горизонтали. Но, если мы знаем , найти очень легко: .

Теперь нужно выбрать систему отсчета. С началом отсчета все ясно, очевидно, мы берем его в точке падения шарика. А вот с направлениями осей все не так просто.

Можно выбрать оси традиционным способом: «» горизонтально и «» вертикально:

Но при таком выборе осей трудно определить точку падения. Поэтому в подобных задачах оси обычно выбирают иначе: «» вдоль наклонной плоскости, а «» перпендикулярно наклонной плоскости:

При таком выборе осей точка падения определяется элементарно: там координата «» обращается в ноль. Зато движение становится равноускоренным по двум осям, поскольку ускорение проектируется на обе оси:

— противолежащий катет;
— прилежащий катет.

Начальная скорость $overrightarrow{mkern -3mu V_0mkern 3mu}$ также проектируется на обе оси:

$V_{0x} = V_0 cdot cos 2 alpha$ – прилежащий катет;
$V_{0y} = V_0 cdot sin 2 alpha$ – противолежащий катет

Зависимости координат от времени при равноускоренном движении выражаются формулами:

$x= x_0 + V_{0x}t + genfrac{}{}{}{0}{alpha_x t^2}{2}$

$y= y_0 + V_{0y}t + genfrac{}{}{}{0}{alpha_y t^2}{2}$

Подставляя значения проекций скорости и ускорения, получаем:

$left{begin{matrix}x=V_0 cdot cos 2 alpha cdot t +g cdot sin alpha cdot genfrac{}{}{}{0}{t^2}{2}=l\y = V_0 cdot sin 2 alpha cdot t - g cdot cos alpha cdot genfrac{}{}{}{0}{t^2}{2}=0end{matrix}right.$

Начальные координаты: ;

Конечная координата y также равна нулю, так как тело падает на наклонную плоскость.

Из второго уравнения получаем:

$tleft ( V_0 sin 2 alpha - g cos alpha genfrac{}{}{}{0}{t}{2}right ) = 0$

Это уравнение равносильно совокупности:

$left[ begin{matrix} t=0 phantom{sin 2 alpha - g cos alpha genfrac{}{}{}{0}{t}{2}}\V_0sin 2 alpha - g cos alpha genfrac{}{}{}{0}{t}{2}=0 end{matrix}right.$

Из второго уравнения находим :

$V_0 sin 2 alpha= g cos alpha genfrac{}{}{}{0}{t}{2}$

$t = genfrac{}{}{}{0}{2V_0 sin 2 alpha}{g cos alpha}$

Подставляем в уравнение для :

$l = V_0 cos 2 alphagenfrac{}{}{}{0}{2V_0 sin 2 alpha}{g cos alpha} + g sin alphagenfrac{}{}{}{0}{left (genfrac{}{}{}{0}{2V_0 sin 2 alpha}{g cos alpha} right ) ^2}{2},$

Откуда:

$l=2{V_0}^2 cos 2 alpha genfrac{}{}{}{0}{sin 2 alpha}{g cos alpha} + g sin alpha genfrac{}{}{}{0}{4{V_0}^2(sin 2 alpha)^2}{2 g^2 (cos alpha)^2},$

$l= genfrac{}{}{}{0}{2{V_0}^2 sin 2 alpha ( cos 2 alpha cos alpha+ sin alphasin 2 alpha)}{g (cos alpha)^2},$

Тогда:

$L=l cos alpha= genfrac{}{}{}{0}{2{V_0}^2 sin 2 alpha ( cos 2 alpha cos alpha+ sin alphasin 2 alpha)}{g (cos alpha)^2}cos alpha=$

$= genfrac{}{}{}{0}{2{V_0}^2 sin 2 alpha ( cos 2 alpha cos alpha+ sin alphasin 2 alpha)}{g cos alpha}$

Но $sin 2 alpha = sin 60^{circ} = cos 30^{circ} = cos alpha$ и $cos 2 alpha = cos 60^{circ} = sin 30^{circ} = sin alpha$

То есть:

$L= genfrac{}{}{}{0}{2{V_0}^2 sin alpha cos alpha }{g}= genfrac{}{}{}{0}{2{V_0}^2 sin 2 alpha}{g}$

$L =genfrac{}{}{}{0}{2{V_0}^2 sin 2 alpha}{g}$

$L = 2 cdot 1^2genfrac{}{}{}{0}{sin 60^{circ}}{10}= 2 cdot genfrac{}{}{}{0}{sqrt{3}}{2}cdot genfrac{}{}{}{0}{1}{10}=0,173$ м

Задача 30 на ЕГЭ по физике

Задача 30 на ЕГЭ по физике (раньше называлась С3) – это задача на газовые законы или термодинамику.

Например:

2. Вертикально расположенный замкнутый цилиндрический сосуд высотой см разделен подвижным поршнем весом 110 H на две части, в каждой из которых содержится одинаковое количество идеального газа при температуре 361 K . Сколько молей газа находится в каждой части цилиндра, если поршень расположен на высоте см от дна сосуда? Толщиной поршня пренебречь.

Дано:

H=50 см = 0,5 м
P=110 H
T=361 K
h=20 см = 0,2 м

Найти: (число молей в каждой части цилиндра.)

p_1 – давление в верхней части цилиндра;

p_2 – давление в нижней части цилиндра;

– площадь сечения поршня.

p_1S – сила давления на поршень газа в верхней части цилиндра;

p_2S — сила давления на поршень газа нижней части цилиндра.

Так как поршень неподвижен, сумма всех действующих на него сил равна нулю.

То есть:

Запишем уравнение Менделеева-Клапейрона для верхней и нижней частей цилиндра:

Где – объем верхней части цилиндра;

V_2=hS — объем нижней части цилиндра.

Выражаем p_1 и p_2 :

$p_1 = genfrac{}{}{}{0}{nu RT}{V_1};$

$p_2 = genfrac{}{}{}{0}{nu RT}{V_2}$

И подставляем в уравнение для сил:

$genfrac{}{}{}{0}{nu RT}{V_2}S=genfrac{}{}{}{0}{nu RT}{V_1}S+P$

Подставляем выражения для объемов:

$genfrac{}{}{}{0}{nu RT}{hS}S=genfrac{}{}{}{0}{nu RT}{(H-h)S}S+P$

Сокращаем :

$genfrac{}{}{}{0}{nu RT}{h}=genfrac{}{}{}{0}{nu RT}{H-h}+P$

$genfrac{}{}{}{0}{nu RT}{h}-genfrac{}{}{}{0}{nu RT}{H-h}=P$

$nu RT left ( genfrac{}{}{}{0}{1}{h}-genfrac{}{}{}{0}{1}{H-h} right ) =P$

$nu RT left ( genfrac{}{}{}{0}{H-h-h}{h(H-h)} right ) =P$

Откуда:

$nu = genfrac{}{}{}{0}{Ph(H-h)}{RT(H-2h)}$

$nu = genfrac{}{}{}{0}{110 cdot 0,5 cdot (0,5-0,2)}{8,31 cdot 361(0,5-2 cdot 0,2)} = 0,022$ моль

Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Задачи 29 и 30 на ЕГЭ по физике» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Публикация обновлена:
09.03.2023

Источник

Задачи на движение с ускорением свободного падения

Формулы для решения задач на движение тела, брошенного под углом к горизонту или горизонтально

Задачи на криволинейное движение с ускорением свободного падения чаще всего представлены в ЕГЭ как задачи на движение тела, брошенного под углом к горизонту. Рассмотрим общий вид таких задач и формулы для их решения.

Из точки, расположенной на высоте h (см. Рис. 1), со скоростью под углом к горизонту брошено тело.

Рис. 1. Движение тела, брошенного под углом к горизонту

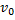
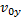
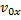
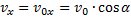
1. Для того чтобы узнать, как выглядит уравнение движения тела, нужно представить начальную скорость в виде составляющих: и .

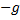
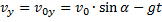
Скорость по оси x не меняется с течением времени, так как ускорение направлено по оси y () и имеет только одну составляющую. Следовательно, с течением времени изменяется скорость по оси y.

2. В решении таких задач также нужно пользоваться уравнением для координат.

– уравнение равномерного движения

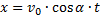
Координата y в выбранной системе координат изменяется по закону равнопеременного движения с отрицательным ускорением:

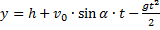
3. Модуль скорости равен:

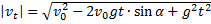
4. Уравнение траектории (зависимость координаты x от y):

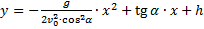
– уравнение параболы, ветви которой опущены вниз, смещённой по оси x в положительном направлении.

5. Время полёта (падения) тела:

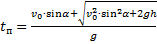
6. Дальность полёта:

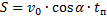
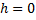
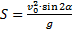
7. При дальность полёта:

8. Наивысшая высота подъёма:

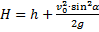
Задача 1

Снаряд вылетел из ствола со скоростью 200 м/с под углом 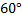к плоскости горизонта. Определить дальность полёта снаряда. Ответ выразить в километрах.

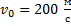
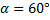
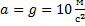
Дано: ; ; (см. Рис. 2)

Найти: S

Решение

Рис. 2. Иллюстрация к задаче

В данной задаче начальная и конечная точка полёта снаряда лежат на одной высоте, поэтому воспользуемся следующей формулой дальности полёта:

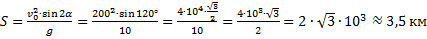
Ответ: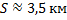

Задача 2

С вышки бросили камень в горизонтальном направлении. Через 2 с камень упал на землю на расстоянии 30 м от основания вышки. Определить конечную скорость камня.

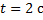
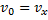
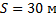
Дано: ; – начальная скорость имеет направление только по оси x; (см. Рис. 3)

Найти:

Решение

Рис. 3. Иллюстрация к задаче

Конечная скорость находится по следующей формуле (как модуль вектора):

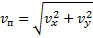
Скорость по оси x равна:

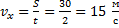
Начальной скорости по оси y не было, а далее она увеличивается с ускорением свободного падения:

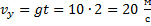
Следовательно:

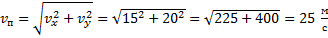
Ответ:

Задача 3

Мяч, брошенный под углом 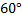к горизонту, достиг максимальной высоты 17,3 м. Какова дальность полёта мяча?

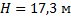
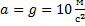
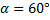
Дано: ; ; (рис. 4)

Найти: S

Решение

Рис. 4. Иллюстрация к задаче

H– максимальная высота подъёма, то есть высота, на которую тело поднимается и с которой падает.

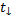
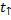
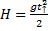
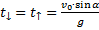
Тело падает с высоты H за время , которое равно времени подъёма , следовательно:

Поэтому:

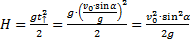
Формула для дальности полёта:

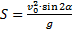
Отношение дальности полёта к максимальной высоте:

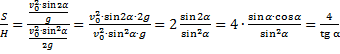
Следовательно:

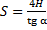
Полученную формулу дальности полёта можно использовать и в других задачах, в которых тело движется по симметричной траектории.

Ответ:

Источник

На ЕГЭ по физике эта тема может попасться в задании 29. За него дают 3 первичных балла, если вы умеете выводить формулы Hmax, L и t полёта.

Почему вообще надо что-то выводить?

В кодификаторе конечного вида этих формул нет! И если вы просто выучите конечный вид и напишите это в бланке ответов — максимальный балл вам не поставят!

Только вывод! Только хардкор! Поехали!

Проекции ускорения на координатные оси равны:

Получается, что вдоль оси Ox тело движется равномерно, а вдоль оси Oy равноускоренно, составим систему уравнений для координат тела:

2. Наше тело находится в начале координат, поэтому x0=0 и y0=0

3. А проекции скорости тела, следовательно, имеют следующий вид:

4. Объединим всё сказанное в пунктах 1,2 и 3 и получим координаты для тела в следующем виде:

Мы подготовили фундамент! Теперь давайте начнём поиски со времени полёта. Для этого положим координату y=0, так как в момент падения высота тела равна нулю. Преобразовав, получим время полёта!

Ещё две величины, и мы будем на финише!

Дальность полёта — это координата x в конце полёта, то есть в момент времени t пол. Подставляя это значение в формулу координаты, получим:

Ухххх, ну ещё одна, последняя!

Так как траектория движения тела симметрична, то время подъёма на высоту Hmax вдвое меньше времени всего полёта:

Тогда сможем подставить это время в формулу для координаты y:

Вот и всё!

👇 СКАЧАТЬ ШПАРГАЛКУ ПО ФИЗИКЕ

Методичка угол к горизонту

Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter. Мы обязательно поправим!

Источник