Темы по алгебре на егэ по

Алгебра
Числа, корни и степени
1.1.1 Целые числа
1.1.2 Степень с натуральным показателем
1.1.3 Дроби, проценты, рациональные числа
1.1.4 Степень с целым показателем
1.1.5 Корень степени и его свойства
1.1.6 Степень с рациональным показателем и ее свойства
1.1.7 Свойства степени с действительным показателем
Основы тригонометрии
1.2.1 Синус, косинус, тангенс, котангенс произвольного угла
1.2.2 Радианная мера угла
1.2.3 Синус, косинус, тангенс и котангенс числа
1.2.4 Основные тригонометрические тождества
1.2.5 Формулы приведения
1.2.6 Синус, косинус и тангенс суммы и разности двух углов
1.2.7 Синус и косинус двойного угла
Логарифмы
1.3.1 Логарифм числа
1.3.2 Логарифм произведения, частного, степени
1.3.3 Десятичный и натуральный логарифмы, число е
1.4 Преобразования выражений
1.4.1 Преобразования выражений, включающих арифметические операции
1.4.2 Преобразования выражений, включающих операцию возведения в степень
1.4.3 Преобразования выражений, включающих корни натуральной степени
1.4.4 Преобразования тригонометрических выражений
1.4.5 Преобразование выражений, включающих операцию логарифмирования
1.4.6 Модуль (абсолютная величина) числа
Уравнения и неравенства
Уравнения
2.1.1 Квадратные уравнения
2.1.2 Рациональные уравнения
2.1.3 Иррациональные уравнения
2.1.4 Тригонометрические уравнения
2.1.5 Показательные уравнения
2.1.6 Логарифмические уравнения
2.1.7 Равносильность уравнений, систем уравнений
2.1.8 Простейшие системы уравнений с двумя неизвестными
2.1.9 Основные приемы решения систем уравнений: подстановка, алгебраическое сложение, введение новых переменных
2.1.10 Использование свойств и графиков функций при решении уравнений
2.1.11 Изображение на координатной плоскости множества решений уравнений с двумя переменными и их систем
2.1.12 Применение математических методов для решения содержательных задач из различных областей науки и практики. Интерпретация результата, учет реальных ограничений
Неравенства
2.2.1 Квадратные неравенства
2.2.2 Рациональные неравенства
2.2.3 Показательные неравенства
2.2.4 Логарифмические неравенства
2.2.5 Системы линейных неравенств
2.2.6 Системы неравенств с одной переменной
2.2.7 Равносильность неравенств, систем неравенств
2.2.8 Использование свойств и графиков функций при решении неравенств
2.2.9 Метод интервалов
2.2.10 Изображение на координатной плоскости множества решений неравенств с двумя переменными и их систем
Функции
Определение и график функции
3.1.1 Функция, область определения функции
3.1.2 Множество значений функции
3.1.3 График функции. Примеры функциональных зависимостей в реальных процессах и явлениях
3.1.4 Обратная функция. График обратной функции
3.1.5 Преобразования графиков: параллельный перенос, симметрия относительно осей координат
Элементарное исследование функций
3.2.1 Монотонность функции. Промежутки возрастания и убывания
3.2.2 Четность и нечетность функции
3.2.3 Периодичность функции
3.2.4 Ограниченность функции
3.2.5 Точки экстремума (локального максимума и минимума) функции
3.2.6 Наибольшее и наименьшее значения функции
Основные элементарные функции
3.3.1 Линейная функция, ее график
3.3.2 Функция, описывающая обратную пропорциональную зависимость, ее график
3.3.3 Квадратичная функция, ее график
3.3.4 Степенная функция с натуральным показателем, ее график
3.3.5 Тригонометрические функции, их графики
3.3.6 Показательная функция, ее график
3.3.7 Логарифмическая функция, ее график
Начала математического анализа
Производная
4.1.1 Понятие о производной функции, геометрический смысл производной
4.1.2 Физический смысл производной, нахождение скорости для процесса, заданного формулой или графиком
4.1.3 Уравнение касательной к графику функции
4.1.4 Производные суммы, разности, произведения, частного
4.1.5 Производные основных элементарных функций
4.1.5 Вторая производная и ее физический смысл
Исследование функций
4.2.1 Применение производной к исследованию функций и построению графиков
4.2.2 Примеры использования производной для нахождения наилучшего решения в прикладных, в том числе социально-экономических, задачах
Первообразная и интеграл
4.3.1 Первообразные элементарных функций
4.3.2 Примеры применения интеграла в физике и геометрии
Геометрия
Планиметрия
5.1.1 Треугольник
5.1.2 Параллелограмм, прямоугольник, ромб, квадрат
5.1.3 Трапеция
5.1.4 Окружность и круг
5.1.5 Окружность, вписанная в треугольник, и окружность, описанная около треугольника
5.1.6 Многоугольник. Сумма углов выпуклого многоугольника
5.1.7 Правильные многоугольники. Вписанная окружность и описанная окружность правильного многоугольника
Прямые и плоскости в пространстве
5.2.1 Пересекающиеся, параллельные и скрещивающиеся прямые; перпендикулярность прямых
5.2.2 Параллельность прямой и плоскости, признаки и свойства
5.2.3 Параллельность плоскостей, признаки и свойства
5.2.4 Перпендикулярность прямой и плоскости, признаки и свойства; перпендикуляр и наклонная; теорема о трех перпендикулярах
5.2.5 Перпендикулярность плоскостей, признаки и свойства
5.2.6 Параллельное проектирование. Изображение пространственных фигур
Многогранники
5.3.1 Призма, ее основания, боковые ребра, высота, боковая поверхность; прямая призма; правильная призма
5.3.2 Параллелепипед; куб; симметрии в кубе, в параллелепипеде
5.3.3 Пирамида, ее основание, боковые ребра, высота, боковая поверхность; треугольная пирамида; правильная пирамида
5.3.4 Сечения куба, призмы, пирамиды
5.3.5 Представление о правильных многогранниках (тетраэдр, куб, октаэдр, додекаэдр и икосаэдр)
Тела и поверхности вращения
5.4.1 Цилиндр. Основание, высота, боковая поверхность,
образующая, развертка
5.4.2 Конус. Основание, высота, боковая поверхность,
образующая, развертка
5.4.3 Шар и сфера, их сечения
Измерение геометрических величин
5.5.1 Величина угла, градусная мера угла, соответствие между величиной угла и длиной дуги окружности
5.5.2 Угол между прямыми в пространстве; угол между прямой и плоскостью
5.5.3 Длина отрезка, ломаной, окружности, периметр многоугольника
5.5.4 Расстояние от точки до прямой, от точки до плоскости; расстояние между параллельными прямыми, параллельными плоскостями
5.5.5 Площадь треугольника, параллелограмма, трапеции, круга, сектора
5.5.6 Площадь поверхности конуса, цилиндра, сферы
5.5.7 Объем куба, прямоугольного параллелепипеда, пирамиды, призмы, цилиндра, конуса, шара
Координаты и векторы
5.6.1 Декартовы координаты на плоскости и в пространстве
5.6.2 Формула расстояния между двумя точками; уравнение сферы
5.6.3 Вектор, модуль вектора, равенство векторов; сложение векторов и умножение вектора на число
5.6.4 Коллинеарные векторы. Разложение вектора по двум неколлинеарным векторам
5.6.5 Компланарные векторы. Разложение по трем некомпланарным векторам
5.6.6 Координаты вектора; скалярное произведение векторов; угол между векторами
Элементы комбинаторики, статистики и теории
вероятностей
Элементы комбинаторики
6.1.1 Поочередный и одновременный выбор
6.1.2 Формулы числа сочетаний и перестановок. Бином Ньютона
Элементы статистики
6.2.1 Табличное и графическое представление данных
6.2.2 Числовые характеристики рядов данных
Элементы теории вероятностей
6.3.1 Вероятности событий
6.3.2 Примеры использования вероятностей и статистики при решении прикладных задач

Профильный ЕГЭ по математике сдают не все. Это вариант для тех, кто намерен поступить в технический Вуз или освоить профессию, связанную с экономикой или математикой. Чтобы сдать данный экзамен, вам нужно будет показать глубокие знания предмета.

Основные требования

Во время сдачи базового госэкзамена вам понадобятся познания, которые были получены из школьного курса алгебры и геометрии. Вы должны уметь решать разнообразные неравенства и уравнения, а также знать терминологию и алгоритмы решения разных задач. А вот чтобы выполнить тесты высокой сложности, вы должны знать:

• планиметрию;
• стереометрию;
• прогрессию.

Помимо этого от учащегося потребуется знание финансовой математики и умение работать с параметрическими системами, уравнениями, неравенствами, процентами.

Во время подготовки вам придется повторить теорию. При этом вы должны совмещать ее с практикой, чтобы уметь применять все выученные правила, теоремы, аксиомы.

Принципы подготовительного процесса

С самого начала года необходимо готовиться к ЕГЭ. Благодаря этому можно качественно усвоить весь необходимый материал.

Желательно повторять вслух все прочитанное, чтобы запомнить правила.

Некоторые аксиомы и теоремы нужно будет просто выучить. А после этого применять их при работе с тренировочными упражнениями.

Если вы готовитесь вместе с одноклассниками, контролируйте друг друга. Так материал быстрее усвоится.

Анализируйте ошибки во время решения задач. Благодаря этому вы значительно продвинетесь в подготовке.

Не забывайте про решение практических заданий. Во время сдачи тестирования этот навык вам очень пригодится.

---

0 комментария

Материалы для подготовки к ЕГЭ по математике Д. Д. Гущина

Лицензионное соглашение

Все опубликованные ниже материалы для подготовки к ЕГЭ по математике могут быть использованы в некоммерческих целях при условии сохранения авторства. Без письменного согласия автора
ЗАПРЕЩАЕТСЯ:

1. Публикация материалов в любой форме, в том числе их размещение в компьютерных сетях и на веб-сайтах.
2. Распространение неполных или измененных материалов.
3. Включение материалов в сборники на любых носителях информации.
4. Получение коммерческой выгоды от продажи или другого использования материалов.

Скачивание материалов означает, что вы приняли условия этого лицензионного соглашения.

Трёхуровневый видеокурс «Готовимся к ЕГЭ по математике»:
перейти

Избранные лекции и вебинары для учителей и учащихся:
перейти

Справочные материалы по математике

Оригинал страницы: http://mathnet.spb.ru

ЕГЭ по математике профильного уровня — один из самых сложных экзаменов. Планируете сдавать его, но не знаете, с чего начать? Этот экзамен не покажется вам таким трудным, если вы узнаете про него побольше и грамотно подготовитесь. В этой статье обсудим, что нужно знать про ЕГЭ по математике 2023, из каких разделов он состоит и как к нему подготовиться.

Какие темы важно знать для ЕГЭ по математике 2023?

В математике, как и в любом предмете, есть опорные темы. Если вы их выучите, будет легче справиться с экзаменом.

Формулы тригонометрии

Очень важно знать формулы тригонометрии и уметь применять их. Хорошая новость: в справочных материалах можно найти несколько тригонометрических формул.

Но формул гораздо больше. Я советую не зубрить их, а научиться выводить: приходить к формулам шаг за шагом, опираясь на тождества. Кстати, мы учим выводить формулы на курсах подготовки к ЕГЭ: это полезно, чтобы оказаться на экзамене во всеоружии и ничего не перепутать.

Квадратные уравнения

Эти уравнения мы учимся решать еще в 7 классе. Они встречаются в ЕГЭ по математике постоянно: и как самостоятельные задания, и внутри более сложных уравнений или неравенств. Квадратные уравнения могут встретиться в математических моделях № 9 и № 15, в задачах на геометрию и стереометрию, в задании № 17 с параметром.

Самое главное — хорошо знать универсальные методы решения. Первый — через формулу дискриминанта, второй — через теорему Виета, которая может сэкономить время на экзамене.

Треугольники

Эта замечательная тема, которую проходят в 7 классе — основа основ всей геометрии. Она нужна и для решения стереометрии, и для простейших планиметрических задач. Еще треугольники необходимы, чтобы освоить огромное количество теорем. Выучите все, что с ними связано! Особое внимание обратите на прямоугольные треугольники, которые встречаются чаще остальных — тогда геометрические задачи сразу станут проще.

Проценты

Самая нелюбимая тема моих учеников после тригонометрии, которую необходимо хорошо знать. Проценты нужны для реальной математики — это № 9 (с кратким ответом) и № 15 (с развернутым ответом). Понимание этой темы может принести вам 3 первичных балла.

План успешной подготовки к ЕГЭ по математике 2023

Если вы хотите получить больше 80 баллов на ЕГЭ, нужно идеально решать часть с кратким ответом, а также справляться с большинством заданий с развернутым ответом.

Чтобы постепенно прорабатывать материал, воспользуйтесь кодификатором. В нем обратите внимание на таблицу 2, а именно на блоки:

• Алгебра
• Уравнения и неравенства
• Элементы комбинаторики, статистики и теории вероятностей
• Функции
• Начала математического анализа
• Геометрия

Ориентируйтесь на указанную последовательность, но геометрию изучайте параллельно с остальными блоками — на нее нужно больше времени.

Самое главное — ни в коем случае не ограничивайтесь теорией. Ее у вас не спросят на экзамене, а вот задания решать придется. Поэтому тренируйте практические навыки: актуальные задания вы сможете найти в открытом банке заданий на сайте ФИПИ или в нашем тренажере «Решутест».

Как решать часть с кратким ответом

Ни в коем случае не пренебрегайте частью с кратким ответом! Иначе будет обидно: например, вы наберете за экономическую задачу № 15 полные 2 балла, но потеряете их в двух заданиях первой части. Это актуально для всех ЕГЭ: подробнее о том, как идеально справляться с первой частью экзамена, читайте здесь.

Еще одно заблуждение: «часть с кратким ответом простая, к ней можно не готовиться». Даже в первой части иногда встречаются такие задания, которые ученики даже не решают, потому что не готовились к ним.

Как я уже говорила, часть с кратким ответом содержит 11 заданий. Начинать подготовку необходимо именно с заданий базового уровня сложности, потому что это та основа, на которую потом накладывается более сложная теория.

Что касается задач повышенного уровня сложности, то среди каждого номера есть лайфхаки, например, в этой статье я уже рассказывала про № 11, в котором нужно работать с производной.

Задания с развернутым ответом: немного статистики

Многие думают, что эта часть ЕГЭ по математике очень сложная. Поэтому ребята, которые не рассчитывают на высокие баллы, даже не приступают к ней. И очень зря! С помощью этих заданий можно заработать дополнительные баллы и побороться за высокое место в рейтинге.

Сейчас будет немного статистики. В среднем около 35% учеников получают полные 2 балла за решение № 12, а вот неравенство № 14 дается хуже, только около 12% с ним справляются на полный балл. Геометрия даётся ещё хуже: стереометрию № 13 полностью решают 2% выпускников, планиметрию (№ 16) менее 5%. А вот с экономической задачей (№ 15) справляются около 20%, а это целых 2 балла! Что касается № 17 и 18, то они даются ещё хуже, но на то они и самые сложные, хотя 1 балл за № 18 по статистике получают около 25% сдающих — там нужно просто привести пример.

Особенности уровней ЕГЭ по математике

В 2015 году ЕГЭ по математике разделили на базовый и профильный уровни. Это упростило жизнь выпускникам, которые не планируют поступать на специальности, связанные с математикой. Если ЕГЭ по математике нужен только для получения аттестата, можно сдать его облегченную версию, оставив время и силы для профильных экзаменов.

Базовый уровень ЕГЭ по математике

Как устроен базовый ЕГЭ по математике? Экзамен идет 180 минут, он состоит из 21 задания, за каждое из которых можно получить 1 балл. Этот экзамен единственный, который переводится не в 100-бальную систему, а в оценки.

В ЕГЭ по математике базового уровня 6 тематических блоков:

Также обратите внимание, что базовый ЕГЭ по математике не поменялся с точки зрения наполнения, изменился лишь порядок заданий. Вот что пишут ФИПИ:

Подробнее про базовый ЕГЭ по математике, включая разбор всех заданий, читайте здесь, а мы перейдём к профильному.

Профильный уровень ЕГЭ по математике

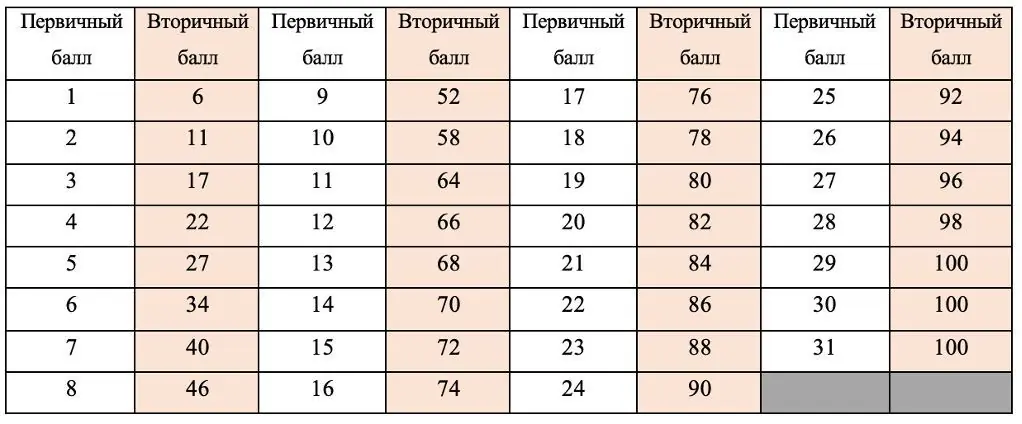
Данный экзамен, как и остальные ЕГЭ, переводится в 100-бальную систему:

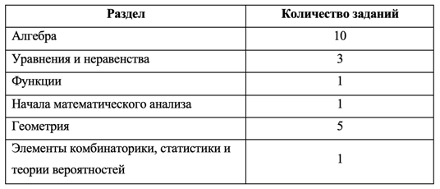
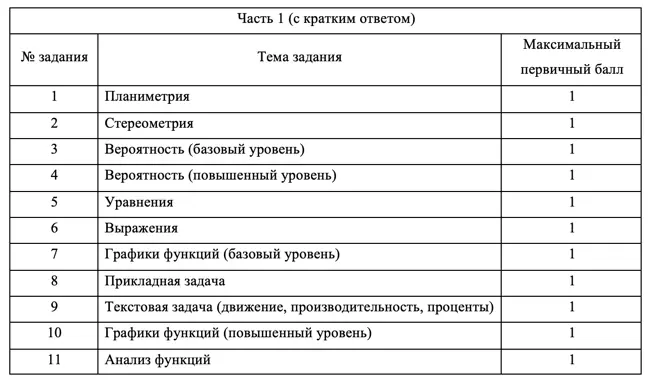
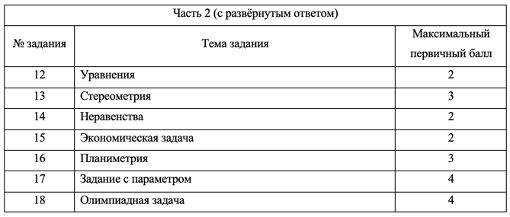
Экзамен состоит из двух частей: Часть 1 с кратким ответом, а Часть 2 — с развернутым. Длится он 235 минут. Всего есть 18 заданий, которые разделены на 3 блока: алгебра, геометрия и реальная математика. Максимальное количество первичных баллов — 31.

Структура ЕГЭ по математике 2023

Часть 1:

• Приносит 11 баллов, то есть 35% всего экзамена
• 11 заданий с кратким ответом

Часть 2:

• Приносит 20 баллов, то есть 65% всего экзамена
• 7 заданий с развернутым ответом

Внимание! Вся нумерация заданий в статье соответствует ЕГЭ 2023 года.

В заданиях с кратким ответом нужно лишь записать верное число в бланк. Заданий с развернутым ответом 7, в них нужно подробно расписать решение, которое должно соответствовать критериям оценивания.

ЕГЭ — стандартизированный экзамен, поэтому каждое задание всегда соответствует определенной теме.

Обратите внимание, что по сравнению с 2022 годом, в части 1 изменился только порядок заданий. Сами сотрудники ФИПИ говорят следующее:

Задания с кратким ответом принесут вам до 11 первичных баллов (64 вторичных). Если не понимаете, что это за баллы и откуда они берутся, почитайте эту статью. Самая популярная цель на ЕГЭ по математике — набрать 80 баллов, для этого раньше было необходимо 19 первичных баллов. Ранее многие ученики пользовались рабочей стратегией — решить всю часть с кратким ответом, а также № 12, 14 и 15. Если хорошо разбирались в геометрии, выбирали № 13 и 16 — или использовали их как запасные задания. Сейчас стратегия должна быть другая, так как № 13 (стереометрия) стал стоить дороже — 3 балла вместо 2, а № 15 (экономическая задача) — подешевел с 3 баллов до 2. Изменилась также шкала перевода баллов, поэтому подумайте, какими заданиями вы сможете набрать необходимое количество первичных баллов.

Разделы ЕГЭ по математике

• Алгебра и начала анализа — 8 заданий, 13 первичных баллов
• Геометрия — 4 задания, 8 первичных баллов
• Реальная математика — 6 заданий, 10 первичных баллов

Какие задания входят в ЕГЭ по математике?

Здесь вам на помощь приходят документы с официального сайта ФИПИ: кодификатор, демоверсия и спецификация.

• Кодификатор — это краткий перечень всех блоков и тем, которые включены в экзамен.

  Сейчас кодификатор общий для обоих уровней экзамена, как базового, так и профильного. Он снова представляет собой единый документ, так что не запутаетесь.
• Демоверсия — типовой вариант ЕГЭ. Он показывает уровень экзамена и ориентировочную сложность заданий.
• Спецификация — это документ, описывающий структуру экзамена и разбалловку.

Что в итоге