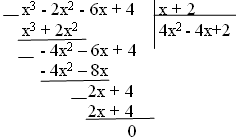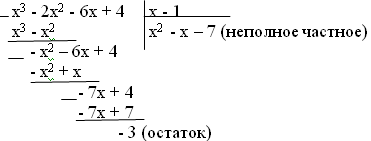Теорема безу егэ профиль

Теорема Безу и следствия из неё

19 июля 2022

Теорема Безу позволяет решать уравнения высших степеней, которые на первый взгляд не решаются, и раскладывать на множители многочлены, которые не раскладываются.:)

Формулировка теоремы довольно проста:

Терема Безу. Остаток от деления многочлена

[Pleft( x right)={{a}_{n}}{{x}^{n}}+{{a}_{n-1}}{{x}^{n-1}}+ldots +{{a}_{1}}x+{{a}_{0}}]

на двучлен $x- color{red}{a}$ равен значению этого многочлена в точке $x= color{red}{a}$:

[r=Pleft( color{red}{a} right)]

На практике нас интересует не сама теорема Безу, а некоторые следствия из неё — именно они помогают решать уравнения и раскладывать многочлены на множители. В этом уроке мы рассмотрим все такие следствия и станем настоящими мастерами в работе с многочленами.

Содержание

1. Деление с остатком
2. Разложение на множители
3. Целые корни многочленов
4. Рациональные корни многочленов
5. Доказательства

В разных учебниках теорему Безу проходят то в 9-м классе, то в 10-м. Этот урок построен так, что вы поймёте его вне зависимости от школы, класса и учебника.

1. Деление с остатком

Итак, есть многочлен $Pleft( x right)$ и двучлен $x- color{red}{a}$. Разделим $Pleft( x right)$ на $x- color{red}{a}$ с остатком:

[Pleft( x right)=Qleft( x right)cdot left( x- color{red}{a} right)+r]

Теперь найдём значение многочлена $Pleft( x right)$ в точке $x= color{red}{a}$:

[Pleft( color{red}{a} right)=Qleft( color{red}{a} right)cdot left( color{red}{a}- color{red}{a} right)+r=r]

Собственно, мы только что доказали теорему Безу. А заодно подготовили основу для первого важного следствия.

Следствие 1. Деление на произвольный двучлен

Теорема Безу прекрасно работает не только для двучлена $x-color{red}{a}$, но и для любого линейного выражения вида $color{blue}{k}x+color{red}{b}$.

Следствие 1. Остаток от деления многочлена

[Pleft( x right)={{a}_{n}}{{x}^{n}}+{{a}_{n-1}}{{x}^{n-1}}+ldots +{{a}_{1}}x+{{a}_{0}}]

на двучлен $color{blue}{k}x+color{red}{b}$ равен значению этого многочлена в точке $x=-color{red}{b}/ color{blue}{k};$:

[r=Pleft( -frac{color{red}{b}}{color{blue}{k}} right)]

На практике для большей надёжности рекомендуется приравнять двучлен $color{blue}{k}x+color{red}{b}$ к нулю:

[begin{align} color{blue}{k}x+color{red}{b} &=0 \ x &=-frac{color{red}{b}}{color{blue}{k}} \ end{align}]

Затем подставить найденное значение $x=-{color{red}{b}}/{color{blue}{k}};$ в многочлен $Pleft( x right)$ и таким образом найти $Pleft( -{color{red}{b}}/{color{blue}{k}}; right)$:

[r=Pleft( -frac{color{red}{b}}{color{blue}{k}} right)]

Пример 1. Стандартный многочлен

Не выполняя деления, найдите остаток от деления многочлена

[Pleft( x right)=4{{x}^{3}}-3{{x}^{2}}+5x-6]

на двучлен $Tleft( x right)=x-2$.

Решение. Это стандартный двучлен вида $x-color{red}{a}$, поэтому решаем по стандартной теореме Безу, согласно которой остаток от деления многочлена $Pleft( x right)$ на двучлен $x-color{red}{2}$ равен $Pleft( color{red}{2} right)$:

[begin{align}r &=Pleft( color{red}{2} right)= \ &=4cdot {color{red}{2}^{3}}-3cdot {color{red}{2}^{2}}+5cdotcolor{red}{2}-6 \ &=32-12+10-6=24 end{align}]

Ответ: 24.

Пример 2. Более сложный многочлен

Не выполняя деления, найдите остаток от деления многочлена

[Pleft( x right)={{left( {{x}^{3}}-2{{x}^{2}}+5 right)}^{3}}{{left( 2x+1 right)}^{5}}]

на двучлен $Tleft( x right)=x+1$.

Решение. Многочлен $Pleft( x right)$ представлен в виде произведения двух других многочленов, которые ещё и возведены в степени. Если раскрыть скобки и привести подобные слагаемые, получится обычный многочлен вида

[Pleft( x right)={{a}_{n}}{{x}^{n}}+{{a}_{n-1}}{{x}^{n-1}}+ldots +{{a}_{1}}x+{{a}_{0}}]

По свойствам степеней найдём степень такого многочлена:

[deg Pleft( x right)=3cdot 3+1cdot 5=14]

Раскрывать скобки и приводить подобные в многочлене 14-й степени долго и трудно, а главное — в этом нет никакой необходимости. Ведь по теореме Безу остаток от деления $Pleft( x right)$ на двучлен $x-color{red}{a}$ всегда равен $Pleft( color{red}{a} right)$ — и не важно, как записан исходный многочлен $Pleft( x right)$.

Для надёжности, чтобы найти $color{red}{a}$, приравняем к нулю двучлен $Tleft( x right)=x+1$:

[begin{align}x+1 &=0 \ x &=color{red}{-1} \ end{align}]

Теперь подставим $x=color{red}{-1}$ в многочлен $Pleft( x right)$ и найдём остаток:

[begin{align}r &=Pleft( color{red}{-1} right)= \ &={{left( {{left( color{red}{-1} right)}^{3}}-2cdot {{left( color{red}{-1} right)}^{2}}+5 right)}^{3}}cdot {{left( 2cdot left( color{red}{-1} right)+1 right)}^{5}}= \ &={{left( -1-2+5 right)}^{3}}cdot {{left( -2+1 right)}^{5}}=-8 end{align}]

Ответ: −8.

Пример 3. Рациональные коэффициенты

Не выполняя деления, найдите остаток от деления многочлена

[Pleft( x right)=3{{x}^{20}}+{{x}^{19}}-7x+1]

на двучлен $Tleft( x right)=3x+1$.

Решение. Воспользуемся Следствием 1 из теоремы Безу. Для надёжности приравняем к нулю двучлен $Tleft( x right)$ и найдём $color{red}{a}$:

[begin{align}3x+1 &=0 \ x &=color{red}{-{1}/{3};} end{align}]

Подставим найденное $x=color{red}{-{1}/{3};}$ в многочлен $Pleft( x right)$ и найдём остаток:

[begin{align} Pleft( color{red}{-frac{1}{3}} right) &=3cdot {{left( color{red}{-frac{1}{3}} right)}^{20}}+{{left( color{red}{-frac{1}{3}} right)}^{19}}-7cdot left( color{red}{-frac{1}{3}} right)+1= \ &=frac{1}{{{3}^{19}}}-frac{1}{{{3}^{19}}}+frac{7}{3}+1=frac{10}{3} end{align}]

Ответ: ${10}/{3};$.

Пример 4. Иррациональные коэффициенты

Не выполняя деления, найдите остаток от деления многочлена

[Pleft( x right)={{x}^{6}}-12{{x}^{4}}+48{{x}^{2}}+64]

на двучлен $Tleft( x right)=left( 1-sqrt{3} right)x+2$.

Решение. Вновь воспользуемся Следствием 1 из теоремы Безу. Приравняем двучлен $Tleft( x right)$ к нулю и найдём $color{red}{a}$:

[left( 1-sqrt{3} right)x+2=0]

Это линейное уравнение с иррациональными коэффициентами. Такое уравнение решается стандартно (см. урок «Линейные уравнения»):

[x=-frac{2}{1-sqrt{3}}=frac{2}{sqrt{3}-1}]

Избавимся от иррациональности в знаменателе, домножив числитель и знаменатель на сопряжённое:

[x=frac{2color{blue}{left( sqrt{3}+1 right)}}{left( sqrt{3}-1 right) color{blue}{left( sqrt{3}+1 right)}}=frac{2left( sqrt{3}+1 right)}{2}= color{red}{sqrt{3}+1}]

Степень исходного многочлена: $deg Pleft( x right)=6$. Если подставить в такой многочлен иррациональное число, то это число придётся возводить в шестую степень. Это слишком долго и трудно, поэтому перепишем многочлен $Pleft( x right)$ так:

[begin{align} Pleft( x right) &=left( {{x}^{6}}-12{{x}^{4}}+48{{x}^{2}}-64 right)+128= \ &={{left( {{x}^{2}}-4 right)}^{3}}+128 end{align}]

Мы выделили точный куб разности — классическую формулу сокращённого умножения. Как это работает — см. уроки «Формулы сокращённого умножения» и «Куб суммы и разности».

В такую формулу намного проще подставить $x=color{red}{sqrt{3}+1}$:

[begin{align}Pleft( color{red}{sqrt{3}+1} right) &={{left( {{left( color{red}{sqrt{3}+1} right)}^{2}}-4 right)}^{3}}+128= \ &={{left( {{left( sqrt{3} right)}^{2}}+2sqrt{3}+{{1}^{2}}-4 right)}^{3}}+128= \ &={{left( 2sqrt{3} right)}^{3}}+128= \ &=24sqrt{3}+128 end{align}]

Ответ получился некрасивым, но это и есть искомый остаток от деления.

Ответ: $24sqrt{3}+128$.

2. Разложение на множители

Сейчас будет немного теории, которая может показаться непонятной, но далее на примерах всё встанет на свои места.

Рассмотрим ещё раз деление многочлена $Pleft( x right)$ на двучлен $x-color{red}{a}$ с остатком:

[Pleft( x right)=Qleft( x right)cdot left( x-color{red}{a} right)+r]

По теореме Безу мы легко найдём остаток $r=Pleft( color{red}{a} right)$. В частности, при $Pleft( color{red}{a} right)=0$ многочлен примет вид

[Pleft( x right)=Qleft( x right)cdot left( x-color{red}{a} right)]

А это значит, что многочлен $Pleft( x right)$ разделился на двучлен $x-color{red}{a}$ без остатка, и мы получили разложение на множители.

Кроме того, равенство $Pleft( color{red}{a} right)=0$ означает, что число $x=color{red}{a}$ — корень многочлена $Pleft( x right)$. И это ещё одно замечательное следствие теоремы Безу.

Следствие 2. Корни многочлена и деление

Следствие 2. Число $x=color{red}{a}$ является корнем многочлена $Pleft( x right)$ тогда и только тогда, когда $Pleft( x right)$ делится без остатка на $left( x-color{red}{a} right)$.

На практике это означает, что для разложения многочлена на множители мы просто перебираем разные числа $x=color{red}{a}$ до тех пор, пока не окажется, что $Pleft( color{red}{a} right)=0$. В этот момент многочлен перепишется в виде

[Pleft( x right)=Qleft( x right)cdot left( x-color{red}{a} right)]

Такой перебор особенно эффективен в сочетании со схемой Горнера (см. урок «Схема Горнера»). Потому что параллельно с вычислением $Pleft( color{red}{a} right)$ мы получаем ещё и коэффициенты нового многочлена $Qleft( x right)$.

Пример 10. Обычный многочлен

Разложите на множители многочлен

[Pleft( x right)={{x}^{4}}+3{{x}^{3}}-3{{x}^{2}}-11x-6]

Решение. Для наглядности отметим синим цветом коэффициенты многочлена $Pleft( x right)$:

[Pleft( x right)= color{blue}{1}cdot {{x}^{4}}+color{blue}{3}cdot {{x}^{3}}+left( color{blue}{-3} right)cdot {{x}^{2}}+left( color{blue}{-11} right)cdot x+left( color{blue}{-6} right)]

Составим из них таблицу для схемы Горнера:

[begin{array}{r|r|r|r|r|r} {} & color{blue}{1} & color{blue}{3} & color{blue}{-3} & color{blue}{-11} & color{blue}{-6}\ hline{} & {} & {} & {} & {} & {}\ end{array}]

Все коэффициенты целые, поэтому логично проверять целые $x=color{red}{a}$, начиная с самых простых и маленьких чисел:

[x=pm 1; pm 2; pm 3; ldots ]

Проверим $x=color{red}{1}$ и $x=color{red}{-1}$:

[begin{array}{r|r|r|r|r|r}{} & color{blue}{1} & color{blue}{3} & color{blue}{-3} & color{blue}{-11} & color{blue}{-6}\ hline color{red}{1} & 1 & 4 & 1 & -10 & color{red}{-16}\ hline color{red}{-1} & 1 & 2 & -5 & -6 & color{green}{0}\ end{array}]

Проверка числа $x=color{red}{1}$ окончилась неудачей: остаток $r=color{red}{-16}$. Зато проверка $x=color{red}{-1}$ дала остаток $r=color{green}{0}$. Следовательно, $x=color{red}{-1}$ является корнем многочлена $Pleft( x right)$, и сам многочлен можно переписать так:

[begin{align}Pleft( x right) &=Qleft( x right)cdot left( x-left( color{red}{-1} right) right) \ &=left( {{x}^{3}}+2{{x}^{2}}-5x-6 right)left( x+1 right) end{align}]

Теперь разложим многочлен $Qleft( x right)$ по схеме Горнера. Проверим ещё раз число $x=color{red}{-1}$:

[begin{array}{r|r|r|r|r|r}{} & 1 & 3 & -3 & -11 & -6\ hline color{red}{-1} & color{blue}{1} & color{blue}{2} & color{blue}{-5} & color{blue}{-6} & color{green}{0}\ hline color{red}{-1} & 1 & 1 & -6 & color{green}{0} & {}\ end{array}]

И вновь получили $r=color{green}{0}$. Исходный многочлен примет вид

[Pleft( x right)=left( {{x}^{2}}+x-6 right){{left( x-1 right)}^{2}}]

В первой скобке стоит квадратный трёхчлен. Разложим его на множители по теореме Виета:

[{{x}^{2}}+x-6=left( x+3 right)left( x-2 right)]

Итого окончательное разложение многочлена $Pleft( x right)$:

[left( x+3 right)left( x-2 right){{left( x-1 right)}^{2}}]

Однако это было довольно простое задание: теорема Безу использовалась лишь в качестве обоснования, почему вместо $Pleft( x right)$ мы пишем $Qleft( x right)left( x-color{red}{a} right)$.

Следующее задание будет намного интереснее.:)

Пример 11. Многочлен с двумя переменными

Разложите на множители многочлен

[Pleft( x,y right)=y{{x}^{2}}+3yx+x-4y-1]

Решение. Это многочлен от двух переменных. Он квадратный относительно переменной $x$ и линейный относительно $y$. Чтобы разложить такой многочлен на множители, сгруппируем его слагаемые относительно переменной $x$:

[Pleft( x,y right)= color{blue}{y}cdot {{x}^{2}}+left( color{blue}{3y+1} right)cdot x+left( color{blue}{-4y-1} right)]

Составляем таблицу:

[begin{array}{c|c|c|c}{} & color{blue}{y} & color{blue}{3y+1} & color{blue}{-4y-1}\ hline {} & {} & {} & {}\ end{array}]

Чтобы воспользоваться теоремой Безу, нужно найти такое $x=color{red}{a}$, чтобы $r=Pleft( color{red}{a} right)= color{green}{0}$. Поскольку в роли коэффициентов выступают выражения, содержащие переменную $y$, вновь рассмотрим самые простые варианты, которые приходят в голову:

[x=pm 1; pm y]

Проверим, например, $x=color{red}{1}$:

[begin{array}{c|c|c|c}{} & color{blue}{y} & color{blue}{3y+1} & color{blue}{-4y-1}\ hline color{red}{1} & y & 4y+1 & color{green}{0}\ end{array}]

Первая же попытка привела к успеху: $r=color{green}{0}$, поэтому $x=color{red}{1}$ — крень многочлена $Pleft( x,y right)$. Разложим этот многочлен на множители согласно Следствию 2 теоремы Безу:

[Pleft( x,y right)=left( ycdot x+4y+1 right)cdot left( x-color{red}{1} right)]

В первой скобке стоит новый многочлен, линейный по $x$ и по $y$. Его уже нельзя разложить на множители, поэтому ответ окончательный:

[Pleft( x,y right)=left( xy+4y+1 right)left( x-1 right)]

Важное замечание. Строго говоря, линейность многочлена по каждой переменной ещё не означает, что его нельзя разложить на множители. Простой контрпример:

[xy-x+y-1=left( x+1 right)left( y-1 right)]

Однако в нашем случае дальнейшее применение теоремы Безу и проверки по схеме Горнера не даст никаких новых множителей.

3. Целые корни многочленов

До сих пор мы подставляли числа наугад. И если удавалось найти число $x=color{red}{a}$ такое, что $Pleft( color{red}{a} right)=0$, мы объявляли его корнем, а многочлен $Pleft( x right)$ переписывали в виде

[Pleft( x right)=Qleft( x right)cdot left( x-color{red}{a} right)]

Однако с помощью теоремы Безу можно значительно ускорить отыскание корней, отбросив заведомо неподходящие варианты. В этом нам поможет следующее утверждение.

Следствие 3. Целочисленные корни

Пусть $Pleft( x right)$ — приведённый многочлен с целыми коэффициентами:

[Pleft( x right)={{x}^{n}}+{{a}_{n-1}}{{x}^{n-1}}+ldots +{{a}_{1}}x+{{a}_{0}}]

Тогда свободный член ${{a}_{0}}$ делится на любой целый корень многочлена $Pleft( x right)$.

Обратите внимание: старший коэффициент при ${{x}^{n}}$ равен единице. Именно поэтому многочлен $Pleft( x right)$ называется приведённым. Кроме того, все коэффициенты ${{a}_{n-1}},ldots ,{{a}_{0}}$ должны быть целыми числами.

И вот тогда целые корни следует искать среди делителей свободного члена ${{a}_{0}}$.

Пример 5. Простое уравнение

Решите уравнение

[{{x}^{3}}-2{{x}^{2}}-x+2=0]

Решение. Это приведённое кубическое уравнение с целыми коэффициентами. Рассмотрим многочлен

[Pleft( x right)= color{blue}{1}cdot {{x}^{3}}+left( color{blue}{-2} right)cdot {{x}^{2}}+left( color{blue}{-1} right)cdot x+color{blue}{2}]

Если у него есть целые корни, то по Следствию 3 теоремы Безу все они находятся среди делителей свободного члена ${{a}_{0}}=2$. Таких делителей всего четыре:

[x=pm 1; pm 2]

Подставим эти числа в схему Горнера:

[begin{array}{r|r|r|r|r}{} & color{blue}{1} & color{blue}{-2} & color{blue}{-1} & color{blue}{2}\ hline color{red}{1} & 1 & -1 & -2 & color{green}{0}\ hline color{red}{-1} & 1 & -2 & color{green}{0} & {}\ end{array}]

Уже на первом шаге мы получили $r=color{green}{0}$. Следовательно, $x=color{red}{1}$ — корень многочлена $Pleft( x right)$, и сам многочлен можно переписать так:

[Pleft( x right)=left( {{x}^{2}}-x-2 right)left( x-color{red}{1} right)]

Впрочем, если учесть третью строку таблицы, то можно вообще записать

[Pleft( x right)=left( x-2 right)left( x-left( color{red}{-1} right) right)left( x-color{red}{1} right)]

В любом случае, корни многочлена, как и корни уравнения — это числа 2, 1 и −1.

Ответ: $x=1$, $x=-1$, $x=2$.

Формула понижения степени

Итак, с помощью теоремы Безу мы можем:

1. Найти целый корень многочлена;
2. Разложить исходный многочлен на множители;
3. Далее искать корни многочлена степени на единицу меньше.

В самом деле, если $Pleft( color{red}{a} right)=0$, тогда по Следствию 2 теоремы Безу мы переписываем многочлен $Pleft( x right)$ в виде

[Pleft( x right)=Qleft( x right)left( x-color{red}{a} right)]

Далее мы ищем корни многочлена $Qleft( x right)$, степень которого на единицу меньше $Pleft( x right)$.

Этот приём называется понижением степени. Он помогает свести исходный многочлен к квадратному, корни которого легко считаются, например, через дискриминант.

Пример 6. Среднее уравнение

Решите уравнение

[{{x}^{3}}-3{{x}^{2}}-4x+12=0]

Решение. Это уравнение третьей степени. Достаточно найти один корень — далее останется решить квадратное уравнение. Заметим, что многочлен

[Pleft( x right)= color{blue}{1}cdot {{x}^{3}}+left( color{blue}{-3} right)cdot {{x}^{2}}+left( color{blue}{-4} right)cdot x+color{blue}{12}]

является приведённым с целочисленными коэффициентами. По Следствию 3 теоремы Безу все целые корни этого многочлена содержатся среди делителей свободного члена ${{a}_{0}}=12$. Таких делителей довольно много:

[x=pm 1; pm 2; pm 3; pm 4; pm 6; pm 12]

Впрочем, нам достаточно найти всего один корень. Воспользуемся схемой Горнера:

[begin{array}{r|r|r|r|r}{} & color{blue}{1} & color{blue}{-3} & color{blue}{-4} & color{blue}{12}\ hlinecolor{red}{1} & 1 & -2 & -7 & color{red}{5}\ hlinecolor{red}{-1} & 1 & -4 & 0 & color{red}{12}\ hlinecolor{red}{2} & 1 & -1 & -6 & color{green}{0}\ end{array}]

Проверка закончилась неудачей для $x=color{red}{1}$ и $x=color{red}{-1}$. Но для $x=color{red}{2}$ мы нашли то, что искали: остаток $r=color{green}{0}$. Следовательно, $x=color{red}{2}$ — корень многочлена $Pleft( x right)$.

Разложим многочлен на множители согласно теореме Безу:

[Pleft( x right)=left( {{x}^{2}}-x-6 right)left( x-color{red}{2} right)]

В первой скобке стоит квадратный трёхчлен. Его корни легко найти по теореме Виета:

[Pleft( x right)=left( x-3 right)left( x+2 right)left( x-2 right)]

Приравниваем полученное произведение к нулю и решаем уравнение: $x=3$, $x=-2$, $x=2$.

Ответ: $x=2$, $x=-2$, $x=3$.

Пример 7. Сложное уравнение

Решите уравнение

[{{x}^{4}}-{{x}^{3}}-5{{x}^{2}}+3x+2=0]

Решение. Слева приведённый многочлен с целочисленными коэффициентами, поэтому все целые корни находятся среди делителей свободного члена ${{a}_{0}}=2$:

[x=pm 1; pm 2]

Достаточно подобрать два корня — далее уравнение сведётся к квадратному. Воспользуемся схемой Горнера:

[begin{array}{r|r|r|r|r|r}{} & color{blue}{1} & color{blue}{-1} & color{blue}{-5} & color{blue}{3} & color{blue}{2}\ hlinecolor{red}{-1} & 1 & -2 & -3 & 6 & color{red}{-4}\ hlinecolor{red}{1} & 1 & 0 & -5 & -2 & color{green}{0}\ hlinecolor{red}{-2} & 1 & -2 & -1 & color{green}{0} & {}\ end{array}]

Получили корни $x=color{red}{1}$ и $x=color{red}{-2}$. Разложим многочлен на множители:

[left( {{x}^{2}}-2x-1 right)left( x-color{red}{1} right)left( x-left( color{red}{-2} right) right)=0]

Решим квадратного уравнение из первой скобки:

[{{x}^{2}}-2x-1=0]

Дискриминант положителен:

[begin{align} D &={{left( -2 right)}^{2}}-4cdot 1cdot left( -1 right)= \ &=4+4=8 end{align}]

Следовательно, уравнение имеет два корня:

[x=frac{2pm 2sqrt{2}}{2}=1pm sqrt{2}]

Ответ: $x=1$, $x=-2$, $x=1pm sqrt{2}$.

4. Рациональные корни

До сих пор мы работали лишь с приведёнными многочленами, где старший коэффициент равен единице. Однако теорема Безу прекрасно работает и для неприведённых многочленов — при условии что все коэффициенты остаются целыми.

Рассмотрим уравнение

[{{a}_{n}}{{x}^{n}}+{{a}_{n-1}}{{x}^{n-1}}+ldots +{{a}_{1}}x+{{a}_{0}}=0]

где ${{a}_{n}},ldots ,{{a}_{0}}$ — целые числа, причём ${{a}_{n}}ne 0$.

Следствие 4. Если рациональное число $x=color{red}{p}/color{blue}{q};$, где $color{red}{p}in mathbb{Z}$, $color{blue}{q}in mathbb{N}$ и дробь $color{red}{p}/color{blue}{q};$ несократима, является корнем уравнения

[{{a}_{n}}{{x}^{n}}+{{a}_{n-1}}{{x}^{n-1}}+ldots +{{a}_{1}}x+{{a}_{0}}=0]

то свободный член ${{a}_{0}}$ делится на $color{red}{p}$, а старший коэффициент ${{a}_{n}}$ делится на $color{blue}{q}$.

Это утверждение будет доказано в конце урока. Сейчас важен практический смысл, который состоит в том, что все рациональные корни уравнения

[{{a}_{n}}{{x}^{n}}+{{a}_{n-1}}{{x}^{n-1}}+ldots +{{a}_{1}}x+{{a}_{0}}=0]

имеют вид $x=color{red}{p}/color{blue}{q};$, где $color{red}{p}$ следует искать среди делителей ${{a}_{0}}$, а $color{blue}{q}$ — среди положительных делителей ${{a}_{n}}$.

Пример 8. Простой многочлен

Найдите рациональные корни многочлена

[Pleft( x right)=2{{x}^{5}}-{{x}^{4}}+4x-2]

Решение. Делители свободного члена ${{a}_{0}}=-2$:

[p=pm 1; pm 2]

Положительные делители старшего коэффициента ${{a}_{4}}=2$:

[q=1; 2]

Возможные рациональные корни многочлена $Pleft( x right)$ по Следствию 4 теоремы Безу:

[x=pm 1; pm 2; pm {1}/{2};]

Проверять числа $x=color{red}{pm 1}$ нет смысла, поскольку все коэффициенты многочлена $Pleft( x right)$, за исключением одного, чётные. Следовательно, при подстановке нечётных чисел многочлен принимает нечётные значения, которые точно не равны нулю.

Остальные числа проверим по схеме Горнера:

[begin{array}{r|r|r|r|r|r|r}{} & color{blue}{2} & color{blue}{-1} & color{blue}{0} & color{blue}{0} & color{blue}{4} & color{blue}{-2}\ hlinecolor{red}{2} & 2 & 3 & 6 & 12 & 28 & color{red}{54}\ hlinecolor{red}{-2} & 2 & -5 & 10 & -20 & 44 & color{red}{-90}\ hline color{red}{{1}/{2};} & 2 & 0 & 0 & 0 & 4 & color{green}{0}\ hline color{red}{-{1}/{2};} & 2 & -2 & 1 & -{1}/{2}; & {17}/{4}; & color{red}{-{33}/{8};}\ end{array}]

Подошло лишь одно число: $x=color{red}{{1}/{2};}$. Следовательно, многочлен имеет лишь один рациональный корень.

Ответ: $x={1}/{2};$.

Обратите внимание: проверку дробных чисел можно прекращать, как только в строке таблицы появилась дробь. Потому что дальше это число будет лишь умножаться на новые дроби и складываться с другими целыми числами. При таких обстоятельствах получить $r=color{green}{0}$ уже невозможно.

Пример 9. Сложный многочлен

Найдите рациональные корни многочлена

[Pleft( x right)=3{{x}^{7}}+2{{x}^{6}}-5{{x}^{5}}+3{{x}^{3}}-{{x}^{2}}-7x+5]

Решение. Это многочлен с целыми коэффициентами. Делители свободного члена ${{a}_{0}}=5$:

[p=pm 1; pm 5]

Положительные делители старшего коэффициента ${{a}_{7}}=3$:

[q=1; 3]

Кандидаты в корни согласно Следствию 4 теоремы Безу:

[x=pm 1; pm 5; pm {1}/{3};; pm {1}/{5};]

Всего восемь кандидатов. Проверим их все по схеме Горнера:

[begin{array}{r|r|r|r|r|c|c|c|c}{} & color{blue}{3} & color{blue}{2} & color{blue}{-5} & color{blue}{0} & color{blue}{3} & color{blue}{-1} & color{blue}{-7} & color{blue}{5}\ hlinecolor{red}{1} & 3 & 5 & 0 & 0 & 3 & 2 & -5 & color{green}{0}\ hlinecolor{red}{-1} & 3 & 2 & -2 & 2 & 1 & 1 & color{red}{-6} & {}\ hlinecolor{red}{5} & 3 & 20 & 100 & color{red}{500} & color{red}{-} & color{red}{-} & color{red}{-} & {}\ hlinecolor{red}{-5} & 3 & -10 & 50 & color{red}{-250} & color{red}{-} & color{red}{-} & color{red}{-} & {}\ hlinecolor{red}{{1}/{3};} & 3 & 6 & 2 & color{red}{{2}/{3};} & color{red}{-} & color{red}{-} & color{red}{-} & {}\ hlinecolor{red}{-{1}/{3};} & 3 & 4 & color{red}{-{4}/{3};} & color{red}{-} & color{red}{-} & color{red}{-} & color{red}{-} & {}\ hlinecolor{red}{{5}/{3};} & 3 & 10 & color{red}{{50}/{3};} & color{red}{-} & color{red}{-} & color{red}{-} & color{red}{-} & {}\ hlinecolor{red}{-{5}/{3};} & 3 & 0 & 0 & 0 & 3 & -3 & color{green}{0} & {}\ end{array}]

Обратите внимание: для чисел $x=color{red}{5}$ и $x=color{red}{-5}$ мы прекратили вычисления досрочно, поскольку получили явно неадекватные числа, которые дальше будут только расти.

При проверке $x=color{red}{{1}/{3};}$, $x=color{red}{-{1}/{3};}$ и $x=color{red}{{5}/{3};}$ мы в какой-то момент возникли дроби, после чего дальнейшие вычисления теряют смысл.

Итого найдены два рациональных корня: $x=color{red}{1}$ и $x=color{red}{-{5}/{3};}$. Пожалуй, это одно из самых утомительных заданий на применение теоремы Безу, которые я когда-либо решал.:)

5. Доказательства

Рассмотрим доказательства всех ключевых утверждений сегодняшнего урока.

5.1. Теорема Безу

Мы сформулировали эту теорему в самом начале урока:

Терема Безу. Остаток от деления многочлена

[Pleft( x right)={{a}_{n}}{{x}^{n}}+{{a}_{n-1}}{{x}^{n-1}}+ldots +{{a}_{1}}x+{{a}_{0}}]

на двучлен $x-color{red}{a}$ равен значению этого многочлена в точке $x=color{red}{a}$:

[r=Pleft( color{red}{a} right)]

Доказательство. Разделим многочлен $Pleft( x right)$ на двучлен $x-color{red}{a}$ с остатком:

[Pleft( x right)=Qleft( x right)cdot left( x-color{red}{a} right)+r]

Такое представление всегда однозначно (см. урок «Деление многочленов с остатком»). Здесь многочлен $Qleft( x right)$ — неполное частное, $r$ — остаток, причём

[begin{align}deg r lt deg left( x-color{red}{a} right) &=1 \ deg r &=0 \ end{align}]

Другими словами, остаток $r$ — это просто число.

Теперь найдём значение $Pleft( x right)$ в точке $x=color{red}{a}$:

[Pleft( color{red}{a} right)=Qleft( color{red}{a} right)cdot left( color{red}{a}-color{red}{a} right)+r=r]

Теорема Безу доказана. Однако её доказательство опирается на единственность деления с остатком.

5.2. Целочисленные корни

Целочисленные корни приведённого многочлена с целыми коэффициентами следует искать среди делителей свободного члена.

Следствие 3. Пусть $Pleft( x right)$ — приведённый многочлен с целыми коэффициентами:

[Pleft( x right)={{x}^{n}}+{{a}_{n-1}}{{x}^{n-1}}+ldots +{{a}_{1}}x+{{a}_{0}}]

Тогда свободный член ${{a}_{0}}$ делится на любой целый корень многочлена $Pleft( x right)$.

Доказательство. Пусть $color{red}{b}in mathbb{Z}$ — корень многочлена $Pleft( x right)$, т.е. $Pleft( color{red}{b} right)=0$. Подставим число $x=color{red}{b}$ в формулу многочлена и получим уравнение:

[{color{red}{b}^{n}}+{{a}_{n-1}}{color{red}{b}^{n-1}}+ldots +{{a}_{1}}color{red}{b}+{{a}_{0}}=0]

Перенесём последнее слагаемое вправо, а слева из оставшихся слагаемых вынесем множитель $color{red}{b}$ за скобку:

[color{red}{b}cdot left( {color{red}{b}^{n-1}}+{{a}_{n-1}}{color{red}{b}^{n-2}}+ldots +{{a}_{1}} right)=-{{a}_{0}}]

Поскольку $-{{a}_{0}}in mathbb{Z}$, а слева стоят два целочисленных множителя, получаем, что число $-{{a}_{0}}$ делится на $color{red}{b}$. Следовательно, свободный член ${{a}_{0}}$ тоже делится на $color{red}{b}$, что и требовалось доказать.

5.3. Рациональные корни

Рассмотрим уравнение

[{{a}_{n}}{{x}^{n}}+{{a}_{n-1}}{{x}^{n-1}}+ldots +{{a}_{1}}x+{{a}_{0}}=0]

где ${{a}_{n}},ldots ,{{a}_{0}}$ — целые числа, причём ${{a}_{n}}ne 0$.

Утверждение. Если рациональное число $x=color{red}{p}/color{blue}{q};$, где $color{red}{p}in mathbb{Z}$, $color{blue}{q}in mathbb{N}$ и дробь $color{red}{p}/color{blue}{q};$ несократима, является корнем уравнения $Pleft( x right)=0$, то свободный член ${{a}_{0}}$ делится на $color{red}{p}$, а старший коэффициент ${{a}_{n}}$ делится на $color{blue}{q}$.

Доказательство. Подставим число $x=color{red}{p}/color{blue}{q};$ в исходное уравнение. Поскольку $x=color{red}{p}/color{blue}{q};$ — корень, уравнение обратится в верное числовое равенство:

[{{a}_{n}}cdot {{left( frac{color{red}{p}}{color{blue}{q}} right)}^{n}}+{{a}_{n-1}}cdot {{left( frac{color{red}{p}}{color{blue}{q}} right)}^{n-1}}+ldots +{{a}_{1}}cdot frac{color{red}{p}}{color{blue}{q}}+{{a}_{0}}=0]

Домножим обе части на ${color{blue}{q}^{n}}$. Получим

[{{a}_{n}}{color{red}{p}^{n}}+{{a}_{n-1}}{color{red}{p}^{n-1}}color{blue}{q}+ldots +{{a}_{1}}color{red}{p}{color{blue}{q}^{n-1}}+{{a}_{0}}{color{blue}{q}^{n}}=0]

Перенесём последнее слагаемое ${{a}_{0}}{color{blue}{q}^{n}}$ вправо, а в левой части из оставшихся слагаемых вынесем множитель $color{red}{p}$ за скобку:

[color{red}{p}left( {{a}_{n}}{color{red}{p}^{n-1}}+{{a}_{n-1}}{color{red}{p}^{n-2}}color{blue}{q}+ldots +{{a}_{1}}{color{blue}{q}^{n-1}} right)=-{{a}_{0}}{color{blue}{q}^{n}}]

Слева и справа от знака равенства стоят целые числа, поскольку все слагаемые и множители являются целыми. Мы видим, что левая часть делится на $color{red}{p}$. Следовательно, правая часть тоже делится на $color{red}{p}$:

[-{{a}_{0}}{color{blue}{q}^{n}} vdots color{red}{p}]

По условию теоремы дробь $color{red}{p}/color{blue}{q};$ несократима. Следовательно, числа $color{blue}{q}$ и $color{red}{p}$ не имеют общих делителей, и единственный возможный вариант — это когда ${{a}_{0}}$ делится на $color{red}{p}$.

Аналогично доказывается, что старший коэффициент ${{a}_{n}}$ делится на $color{blue}{q}$. Теорема доказана.

Вот и всё.:)

Смотрите также:

1. Схема Горнера
2. Деление многочленов уголком
3. Теорема Виета
4. Задача B3 — работа с графиками
5. Метод коэффициентов, часть 2
6. Нестандартная задача B2: студенты, гонорары и налоги

Разложение  многочлена на множители.  Теорема Безу и схема Горнера

При решении уравнений и неравенств нередко возникает необходимость разложить на множители многочлен, степень которого равна трем или выше. В этой статье мы рассмотрим,  каким образом это сделать проще всего.

Как обычно, обратимся за помощью к теории.

Теорема Безу утверждает, что остаток от деления многочлена    на  двучлен равен .

Но для нас важна не сама теорема, а следствие из нее:

Если число является корнем многочлена , то многочлен   делится без остатка на двучлен .

Перед нами стоит задача каким-то способом найти хотя бы один корень многочлена, потом разделить многочлен на , где — корень многочлена. В результате мы  получаем многочлен,    степень которого на единицу меньше, чем степень исходного. А потом при необходимости можно повторить процесс.

Эта задача распадается на две: как найти корень многочлена , и как разделить многочлен на двучлен.

Остановимся подробнее на этих моментах.

1. Как найти корень многочлена.

Сначала проверяем, являются ли числа 1 и -1 корнями многочлена.

Здесь нам помогут такие факты:

Если сумма всех коэффициентов многочлена равна нулю, то число является корнем многочлена.

Например, в многочлене сумма коэффициентов равна нулю: . Легко проверить, что является корнем многочлена.

Если сумма коэффициентов многочлена  при четных степенях равна сумме коэффициентов при нечетных степенях, то число является корнем многочлена. Свободный член считается коэффициентом при четной степени, поскольку , а — четное число.

Например, в многочлене  сумма коэффициентов при четных степенях :  , и сумма коэффициентов при нечетных степенях :   . Легко проверить, что является корнем многочлена.

Если ни 1, ни -1 не являются корнями многочлена, то двигаемся дальше.

Для приведенного многочлена степени (то есть многочлена, в котором старший коэффициент — коэффициент при — равен единице) справедлива формула Виета:

, где — корни многочлена .

Если многочлен не является приведенным, то его можно сделать таковым, разделив на старший коэффициент.

Есть ещё формул Виета, касающихся остальных коэффициентов многочлена, но нас интересует именно эта.

Из этой формулы Виета следует, что если корни приведенного многочлена целочисленные, то они являются делителями его свободного члена, который также является целым числом.

Исходя из этого, нам надо разложить свободный член многочлена на множители, и последовательно, от меньшего к большему, проверять, какой из множителей является корнем многочлена.

Рассмотрим, например, многочлен .

Для этого многочлена произведение корней равно

Делители числа : ; ;

Сумма всех коэффициентов многочлена равна , следовательно, число 1 не является корнем многочлена.

Сумма коэффициентов при четных степенях :  

Сумма коэффициентов при нечетных степенях :

, следовательно, число -1 также не является корнем многочлена.

Проверим, является ли число 2 корнем  многочлена: , следовательно, число 2  является корнем многочлена. Значит, по теореме Безу, многочлен делится без остатка на двучлен .

2. Как разделить многочлен на двучлен.

Многочлен можно разделить на двучлен столбиком.

Разделим многочлен  на двучлен столбиком:

Есть и другой способ деления многочлена на двучлен — схема Горнера.

Посмотрите это видео, чтобы понять, как делить многочлен на двучлен столбиком, и с помощью схемы Горнера.

Замечу, что если при делении столбиком какая-то степень неизвестного в исходном многочлене отсутствует, на её месте пишем 0 — так же, как при составлении таблицы для схемы Горнера.

Итак, если нам нужно разделить многочлен на двучлен и в результате деления мы получаем многочлен , то коэффициенты многочлена   мы можем найти по схеме Горнера:

Мы также можем использовать схему Горнера для того, чтобы проверить, является ли данное число корнем многочлена: если число является корнем многочлена , то остаток от деления многочлена на равен нулю, то есть в последнем столбце второй строки схемы Горнера мы получаем 0.

Используя схему Горнера, мы «убиваем двух зайцев»: одновременно проверяем, является ли число корнем многочлена и делим этот многочлен на двучлен .

Пример. Решить уравнение:

1. Выпишем делители свободного члена, и будем искать корни многочлена среди делителей свободного члена.

Делители числа 24:

2. Проверим, является ли число 1  корнем многочлена.

Сумма коэффициентов многочлена , следовательно, число 1 является корнем многочлена.

3. Разделим исходный многочлен на двучлен с помощью схемы Горнера.

А) Выпишем в первую строку таблицы коэффициенты исходного многочлена.

Так как член, содержащий отсутствует, в том столбце таблицы, в котором должен стоять коэффициент при пишем 0. Слева пишем найденный корень: число 1.

Б) Заполняем первую строку таблицы.

В последнем столбце, как и ожидалось, мы получили ноль, мы разделили исходный многочлен на двучлен без остатка. Коэффициенты многочлена, получившегося в результате деления изображены синим цветом во второй строке таблицы:

Будем делить дальше. Нам нужно найти корни многочлена . Корни также ищем среди делителей свободного члена, то есть теперь уже  числа -24.

Легко проверить, что числа 1 и -1 не являются корнями многочлена

В) Продолжим таблицу. Проверим, является ли число 2 корнем многочлена :

Так степень многочлена, который получается в результате деления на единицу меньше степени исходного многочлена, следовательно и количество коэффициентов и количество столбцов на единицу меньше.

В последнем столбце мы получили -40 — число, не равное нулю, следовательно, многочлен делится на двучлен  с остатком, и число 2 не является корнем многочлена.

Идем дальше.

В) Проверим, является ли число -2 корнем многочлена . Так как предыдущая попытка оказалась неудачной, чтобы не было путаницы с коэффициентами, я сотру строку, соответствующую этой попытке:

Отлично! В остатке мы получили ноль, следовательно, многочлен разделился на двучлен  без остатка, следовательно, число -2 является корнем многочлена. Коэффициенты многочлена, который получается в результате деления многочлена  на двучлен в таблице изображены зеленым цветом.

В результате деления мы получили квадратный трехчлен , корни которого легко находятся по теореме Виета:

Итак, корни исходного уравнения :

{}

Ответ: {}

И.В. Фельдман, репетитор по математике.

Теорема Безу: нахождение остатка от деления многочлена на двучлен

В данной публикации мы рассмотрим теорему Безу, с помощью которой можно найти остаток от деления многочлена на двучлен, а также, научимся применять ее на практике для решения примеров.

Формулировка теоремы Безу

Остаток от деления многочлена P(x) на двучлен (x-a) равняется P(a) .

Следствие из теоремы:

Число a является корнем многочлена P(x) исключительно в том случае, если многочлен P(x) без остатка делится на двучлен (x-a) .

Из этого следствия вытекает следующее утверждение: множество корней многочлена P(x) тождественно множеству корней соответствующего уравнения P(x)=0 .

Решение примеров

Пример 1
Найдите остаток от деления многочлена 5x 2 – 3x + 7 на двучлен (x – 2) .

Решение
Чтобы найти остаток от деления, согласно теореме Безу, требуется найти значение многочлена в точке a (т.е. вместо x подставляем значение a , которое в нашем случае равняется числу 2).
5 ⋅ 2 2 – 3 ⋅ 2 + 7 = 21 .

Т.е. остаток равен 21.

Пример 2
Используя теорему Безу выясните, делится ли многочлен 3x 4 + 15x – 11 на двучлен (x + 3) без остатка.

Решение
В данном случае a = -3 . Подставляем это число вместо x в многочлен и получаем:
3 ⋅ (-3) 4 + 15 ⋅ (-3) – 11 = 187 .

Это значит, что деление без остатка невозможно.

Пример 3
Выясните, при каком значении y , многочлен x 23 + yx + 16 без остатка делится на двучлен (x + 1) .

Решение
Применив теорему Безу, находим нулевой остаток от деления:
(-1) 23 + y ⋅ (-1) + 16 = 0
-1 – y + 16 = 0
y = 15

Таким образом, при y , равном 15, остаток будет равен 0.

Алгебра и начало анализа. Теорема Безу. 11-й класс

Класс: 11

Презентация к уроку

Цель урока:

• способствовать развитию навыков деления многочлена на многочлен и использованию схемы Горнера;
• закрепить навыки работы в электронных таблицах OpenOffice.org Calc;
• организовать деятельность учащихся по восприятию, осмысливанию и первичному запоминанию новых знаний;
• разобрать и доказать теорему Безу при решении проблемной ситуации: можно ли разложить многочлен третьей степени на множители;
• рассмотреть использование теорему Безу для решения уравнений высших степеней;
• содействовать развитию логического мышления, внимания, речи и умения работать самостоятельно.

Тип урока: урок ознакомления с новым материалом.

Оборудование: мультимедиа проектор, презентация к уроку, компьютерный класс.

«Для того, чтобы совершенствовать ум, надо больше рассуждать, чем заучивать».
Декарт (1596 -1650). Французский математик, физик, филолог, философ.

Ход урока

I. Организационный момент

Наша задача сегодня в совместной деятельности подтвердить слова Декарта (слайд 1). Тема нашего урока (слайд 2) «Теорема Безу» настолько значима, что даже используется в заданиях ЕГЭ и различных олимпиадах. Теорема Безу облегчает решение многих заданий, содержащих уравнения высших степеней. К сожалению, она изучается только на профильном уровне.

II. Возникновение проблемной ситуации

На этом уроке мы научимся решать уравнения высших степеней, а алгоритм решения выведем сами.

Решить уравнение: x 3 — 2x 2 — 6x + 4=0 (Слайд 3). Возникает проблема: Мы понимаем, что было бы удобно представить левую часть уравнения в виде произведения, и так как произведение равно нулю, то приравнять к нулю каждый множитель. Для этого надо разложить многочлен 3-ей степени на множители. Но как? Можно ли сгруппировать или вынести общий множитель за скобку в нашем случае? (Нет).

III. Актуализация опорных знаний

Вспомним, как разложить на множители многочлен х 2 — 5х — 6? (Слайд 4).

(По формуле разложения на множители квадратного трехчлена:

ах 2 + bх + с = a(x – x₁)(x-x₂), где х₁ и х₂ корни трехчлена).

Найдите корни трехчлена двумя способами. Какими?

(по формуле корней квадратного уравнения и по теореме Виета).

Решают на доске от каждой группы по одному ученику. Остальные учащиеся в тетрадях. Получили: х 2 — 5х — 6 = (х — 6) (х + 1).

Это значит, что трехчлен делится на каждый из двучленов: х – 6 и х + 1.

Обратите внимание на свободный член нашего трехчлена и найдите его делители (±1, ±2, ±3, ±6).

Какие из делителей являются корнями трехчлена? (-1 и 6)

Какой вывод можно сделать? (Корни трехчлена являются делителями свободного члена).

IV. Выдвижение гипотезы

Так какой же одночлен поможет подобрать корни многочлена?

Р(х) = x 3 — 2x 2 — 6x + 4=0?

Выпишите его делители: ±1; ±2; ±4.

Найдите значения многочлена для каждого делителя. С помощью электронных таблиц и непосредственно:

Об уравнениях высших степеней

Как правило в физике, информатике и экономике мы сталкиваемся с простейшими линейными, или дробно-рациональными уравнениями, реже с квадратными. А что до уравнений третьей и четвёртой степени? Если вам интересно, то прошу под кат.

Для начала рассмотрим понятие уравнения высшей степени. Уравнением высшей степени, называется уравнение вида:

В этой статье я рассмотрю:

1. Кубические уравнения.
2. Возвратные кубические.
3. Применение схемы Горнера и теоремы Безу.
4. Возвратные биквадратные уравнения.

Кубические уравнения

Кубические уравнения, это уравнения, в которых у неизвестной при старшем члене степень равна 3. Кубические уравнения имеют следующий вид:

Решать такие уравнения можно по разному, однако мы воспользуемся знаниями базовой школы, и решим кубическое уравнение методом группировки:

В данном примере используется метод группировки, группируем первые два и последние два члена, получая равные скобки, снова выносим, получая уравнение из двух скобок.

Произведение равно нулю тогда, и только тогда, если хотя бы один из множителей равен нулю, на основании этого мы каждый множитель (скобку) приравниваем к нулю, получая неполное квадратное и линейное уравнения.

Также стоит отметить, что максимальное количество корней уравнения, равно степени неизвестной при главном члене, так в кубическом уравнении может быть не более трёх корней, в биквадратном (4-ой степени) не более четырёх корней и. т. д.

Возвратные кубические уравнения

Возвратные кубические уравнения имеют вид:

Возвратными они называются потому что коэффициенты будут зеркально повторяться. Подобные уравнения тоже решаются школьными методами, но чуть хитрее:

Сначала производится группировка, потом при помощи формул сокращённого умножения мы раскладываем получаемое на множители. Снова получаем 2 равные скобки, «выносим их». Получаем два множителя (скобки) и решаем их как два различных уравнения.

Теорема Безу и схема Горнера

Теорема Безу была открыта, как ни удивительно, Этьеном Безу, французским математиком, занимавшимся в основном алгеброй. Теорему Безу, можно сформулировать следующим образом:

Давайте разберёмся. P(x) — это какой-либо многочлен от x, (x — a) — это двучлен в котором a — это один из целых корней уравнения, который мы находим среди делителей свободного члена.

Три точки, это оператор обозначающий что одно выражение делится на другое. Из этого следует что найдя хотя бы один корень данного уравнения, мы сможем применить к нему эту теорему. Но зачем нужна эта теорема, каково её действие? Теорема Безу — это универсальный инструмент, если вы хотите понизить степень многочлена. Например, при её помощи, кубическое уравнение, можно превратить в квадратное, биквадратное, в кубическое и т. д.

Но одно дело понять, а как поделить? Можно конечно, делить и в столбик, однако этот метод доступен далеко не всем, да и вероятность ошибиться очень высока. Поэтому есть и иной путь, это схема Горнера. Её работу я поясню на примере. Предположим:

И так, нам дан многочлен, и мы возможно заранее нашли один из корней. Теперь мы рисуем небольшую табличку из 6 столбцов и 2 строк, в каждый столбец первой строки (кроме первого), мы вносим коэффициенты уравнения. А в первый столбец 2 строки мы вносим значение a (найденный корень). Потом первый коэффициент, в нашем случае 5, мы просто сносим вниз. Значения последующих столбиков мы рассчитываем так:

(Картинка позаимствована здесь)
Далее поступаем точно так же и с остальными столбцами. Значение последнего столбца (2 строки) будет остатком от деления, в нашем случае 0, если получается число отличное от 0, значит надо избрать другой подход. Пример для кубического уравнения:

Возвратные биквадратные уравнения

Выше мы так же рассматривали возвратные кубические уравнения, а теперь разберём биквадратные. Их общий вид:

В отличие от кубического возвратного уравнения, в биквадратном пары, относительно коэффициентов, есть не у всех, однако в остальном они очень схожи. Вот алгоритм решения таких уравнений:

Как видно, решать такие уравнения совсем не просто. Но я всё равно разберу и этот случай. Начинается решение с деления всего уравнения на x^2. Далее мы группируем, здесь я специально ввёл дополнительную строку для ясности. После этого мы совершаем хитрость, и вводим в первую скобку 2, которую мы сначала прибавляем, а после вычитаем, сумма всё равно не изменится, зато теперь мы можем свернуть эту скобку в квадрат суммы.

Уберём -2 из скобки, предварительно домножив его на a, после чего вводим новую переменную, t и получаем квадратное уравнение.

А теперь перейдём к примеру:

Основная часть так же как и в обобщённом алгоритме, делим на x^2, группируем, сворачиваем в полный квадрат, выполняем подстановку переменной и решаем квадратное уравнение. После этого полученные корни подставляем обратно, и решаем ещё 2 квадратных уравнения (с умножением на x).

Область применения

В виду своей громоздкости и специфичности уравнения высших степеней редко находят себе применение. Однако примеры всё же есть, уравнение Пуассона для адиабатических процессов в Физике.

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

Цель урока:

• способствовать развитию навыков деления многочлена на многочлен и использованию схемы Горнера;
• закрепить навыки работы в электронных таблицах OpenOffice.org Calc;
• организовать деятельность учащихся по восприятию, осмысливанию и первичному запоминанию новых знаний;
• разобрать и доказать теорему Безу при решении проблемной ситуации: можно ли разложить многочлен третьей степени на множители;
• рассмотреть использование теорему Безу для решения уравнений высших степеней;
• содействовать развитию логического мышления, внимания, речи и умения работать самостоятельно.

Тип урока: урок ознакомления с новым материалом.

Оборудование: мультимедиа проектор, презентация к уроку, компьютерный класс.

«Для того, чтобы совершенствовать ум, надо больше рассуждать, чем заучивать».
 Декарт (1596 -1650). Французский математик, физик, филолог, философ.

Ход урока

I. Организационный момент

Наша задача сегодня в совместной деятельности подтвердить слова Декарта (слайд 1). Тема нашего урока (слайд 2) «Теорема Безу» настолько значима, что даже используется в заданиях ЕГЭ и различных олимпиадах. Теорема Безу облегчает решение многих заданий, содержащих уравнения высших степеней. К сожалению, она изучается только на профильном уровне.

II. Возникновение проблемной ситуации

На этом уроке мы научимся решать уравнения высших степеней, а алгоритм решения выведем сами.

Решить уравнение: x³ — 2x² — 6x + 4=0 (Слайд 3). Возникает проблема: Мы понимаем, что было бы удобно представить левую часть уравнения в виде произведения, и так как произведение равно нулю, то приравнять к нулю каждый множитель. Для этого надо разложить многочлен 3-ей степени на множители. Но как? Можно ли сгруппировать или вынести общий множитель за скобку в нашем случае? (Нет).

III. Актуализация опорных знаний

Вспомним, как разложить на множители многочлен х² — 5х — 6? (Слайд 4).

(По формуле разложения на множители квадратного трехчлена:

ах² + bх + с = a(x – x₁)(x-x₂), где х₁ и х₂ корни трехчлена).

Найдите корни трехчлена двумя способами. Какими?

(по формуле корней квадратного уравнения и по теореме Виета).

Решают на доске от каждой группы по одному ученику. Остальные учащиеся в тетрадях. Получили: х² — 5х — 6 = (х — 6) (х + 1).

Это значит, что трехчлен делится на каждый из двучленов: х – 6 и х + 1.

Обратите внимание на свободный член нашего трехчлена и найдите его делители (±1, ±2, ±3, ±6).

Какие из делителей являются корнями трехчлена? (-1 и 6)

Какой вывод можно сделать? (Корни трехчлена являются делителями свободного члена).

IV. Выдвижение гипотезы

Так какой же одночлен поможет подобрать корни многочлена?

Р(х) = x³ — 2x² — 6x + 4=0?

(Свободный член).

Выпишите его делители: ±1; ±2; ±4.

Найдите значения многочлена для каждого делителя. С помощью электронных таблиц и непосредственно:

1 группа вычисляет в тетради, вторая за компьютерами в OpenOffice.org Calc.

Р(1)= -3
Р(-1)=7
Р(2)=-8
Р(-2)=0
Р(4)=12
Р(-4)=-68

х	Р(х)
1	-3
-1	7
2	-8
-2	0
4	12
-4	-68

(При вычислении в электронных таблицах в ячейку В2 ученики вводят формулу: =А1^3-2*A1^2-6*A1+4. С помощью маркера автозаполнения получают значения многочлена во всем столбце).

Какой из делителей является корнем многочлена? (-2)

Таким образом, один из множителей в разложении будет х-(-2) = x + 2.

Как найти другие множители?

(Разделить «в столбик» на двучлен х + 2)

А как еще можно? (по схеме Горнера). (Слайд 5)

Что такое схема Горнера? (Схема Горнера – это алгоритм деления многочленов, записанный для частного случая, когда делитель равен двучлену x–a).

Выполняем деление: первая группа «в столбик», вторая – по схеме Горнера.

	1	-2	-6	4
-2	1	-4	2	0

Разделили без остатка.

Вернемся к уравнению: x³ — 2x² — 6x + 4= (x²-4x+2)(x+ 2)=0

x²-2x+2=0 — квадратное уравнение. Решите его:

D₁ = 4 – 2 = 2;

Ответ: -2, .

А мог получиться остаток при делении? Ответим на этот вопрос позднее. А сейчас назовите значение многочлена при х = — 2. (Значение равно нулю).

Прошу обратить ваше внимание, что x = — 2 является корнем многочлена и остаток от деления многочлена на х-(-2) равен 0.

 Рассмотрим х=1 — не является корнем уравнения.

Попробуем разделить многочлен на х-1. Вторая группа выполняет деление «в столбик». Первая – по схеме Горнера дополняет таблицу ещё одной строкой.

	1	-2	-6	4
-2	1	-4	2	0
1	1	-1	-7	-3

Итак, x³ — 2x² — 6x + 4 = (х – 1)∙( x² — х – 7) – 3.

Отметим, что x=1 не является корнем многочлена и остаток от деления многочлена на (х-1) равен значению многочлена при х=1.

Вот и ответ на вопрос об остатке. Да, остаток получился, при таком значении х, которое не является корнем многочлена.

Давайте продолжим схему Горнера для остальных делителей свободного члена. Теперь пусть первая группа вычисляет за компьютером, а вторая в тетрадях.

V. Доказательство гипотезы

(Слайд 6) Вы заметили закономерность об остатке. Какую? (остаток получился, при таком значении х, которое не является корнем многочлена).

А давайте запишем эту закономерность в общем виде.

Пусть Р(х) — многочлен, а — некоторое число.

Докажем утверждение: Остаток от деления Р(х) на (x — а) равен Р(а).

Доказательство. Разделим Р(х) c остатком на (x — а).

Получим Р(х)= (x — а)Q(х) + R; по определению остатка, многочлен r либо равен 0, либо имеет степень, меньшую степени (x — a), т.е. меньшую 1. Но степень многочлена меньше 1 только в случае, когда она равна 0, и поэтому в обоих случаях R на самом деле является числом – нулем или отличным от нуля.

Подставив теперь в равенство Р(х)= (x — а)Q(х) + R значение x = a, мы получим Р(a)= (a — а)Q(х) + R, P(a) = R, так что действительно R = P(a).

Эту закономерность отметил и математик Безу.

Сообщение ученицы

(Слайд 7) Этьенн Безу — французский математик, член Парижской Академии Наук (с 1758 года), родился в Немуре 31 марта 1730 года и умер 27 сентября 1783 года. С 1763 года Безу преподавал математику в училище гардемаринов, а с 1768 года и в королевском артиллерийском корпусе.

Основные работы Этьенна Безу относятся к высшей алгебре, они посвящены созданию теории решения алгебраических уравнений.

В теории решения систем линейных уравнений он содействовал возникновению теории определителей, развивал теорию исключения неизвестных из систем уравнений высших степеней, доказал теорему (впервые сформулированную Маклореном) о том, что две кривые порядка m и n пересекаются не более чем в mn точках.

Во Франции и за её границей вплоть до 1848 года был очень популярен его шеститомный «Курс математики», написанный им в 1764-69 годах.

Безу развил метод неопределённых множителей. В элементарной алгебре его именем назван способ решения систем уравнений, основанный на этом методе.

Часть трудов Безу посвящена внешней баллистике.

Именем ученого названа одна из основных теорем алгебры.

Следствие

Какой должен быть остаток, чтобы многочлен Р(х) делился нацело на двучлен (х – а)? (равен 0).

Получаем следствие из теоремы Безу: Для того, чтобы многочлен Р(х) делился нацело на двучлен (х – а), необходимо и достаточно, чтобы выполнялось равенство Р(а) = 0.

VI. Усвоение изученного

(Слайд Решить уравнение: х⁴ — x³ — 6x² — x + 3 = 0.

Целые корни многочлена Р(х) = х⁴ — x³ — 6x² — x + 3 должны быть делителями свободного члена, так что это могут быть числа -1, 1, 3, -3.

Подберем корень по схеме Горнера:

	1	-1	-6	-1	3
-1	1	-2	-4	3	0

х⁴ — x³ — 6x² — x + 3= (х + 1)(х³ -2х² – 4х +3) =0

	1	-2	-4	3
-1	1	-3	-1	4
1	1	-1	-5	-2
-3	1	-5	11	-30
3	1	1	-1	0

 Q(x) = х³ -2х² – 4х +3=(x- 3)(x² + x -1)=0;

x² + x -1 =0; D= 5, x =

Ответ: -1; 3; .

VII. Итог:

Итак, что дает нам Теорема Безу? (Слайд 9)

Теорема Безу дает возможность, найдя один корень многочлена, искать далее корни многочлена, степень которого на 1 меньше: если Р(а) = 0, то Р(х)= (x — а)Q(x), и остается решить уравнение Q(x) = 0. Иногда этим приемом — он называется понижением степени — можно найти все корни многочлена.

Вернуться по ссылке на слайд 1.

Удалось ли вам убедиться в справедливости слов Декарта? Как вы их поняли для себя? (Высказывания учеников: «Заучивать механически бесполезно, необходимо осмысливать изучаемое», «Без размышления ум не развивается, потому что это будет шаблонное мышление, которое никому неинтересно»).

VIII. Домашнее задание:

Решить уравнения двумя способами: а) х³ — 3х² –х + 3 = 0; б) х⁴ + 4х² – 5 = 0.

Литература:

1. Алгебра и начала математического анализа. 10 класс: учеб. Для общеобразоват. учреждений: базовый и профильный уровни / [С. М. Никольский, М. К. Потапов, Н. Н. Решетников, А. В. Шевкин]. – М.: Просвещение, 2009.
2. Алгебра: учеб. для учащихся 9 кл. с углубл. изучением математики / [Н. Я. Виленкин, Г. С. Сурвилло, А. С. Симонов, А. И. Кудрявцев]; под ред. Н. Я. Виленкина. – М.: Просвещение, 2005.
3. Числа и многочлены: Методическая разработка для учащихся заочного отделения МММФ / Автор-составитель А. В. Деревянкин. – М.: Издательство центра прикладных исследований при механико-математическом факультете МГУ, 2008.
4.  Биографический словарь деятелей в области математики. А. И. Бородин, А. С. Бугай. Пер. с укр. – К.: Радянська школа, 1979.