Теорема брахмагупты на егэ - Помощь в подготовке к экзаменам и поступлению

24
Сен 2014

Категория: Планиметрия

Формула Брахмагупты

2014-09-24
2016-09-21

Наверняка вы помните формулу площади треугольника через три известные стороны и – формулу Герона:

где – полупериметр.

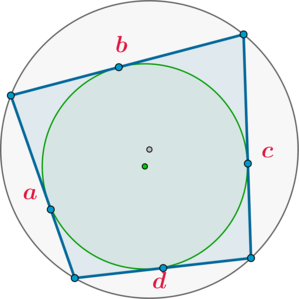
Так вот есть очень похожая формула для площади четырехугольника – формула Брахмагупты. Но вот если формула Герона работает для произвольного треугольника (около него всегда можно описать окружность), то формула Брахмагупты – только для вписанного в окружность четырехугольника.

Итак, вот формула площади вписанного в окружность четырехугольника со сторонами и :

где – полупериметр.

Доказательство:

Пусть нам дан вписанный четырехугольник со сторонами , , и .

Обозначим угол при вершине за . Тогда, так как сумма противоположных углов вписанного четырехугольника равна $180^{circ}$ , то $angle C=180^{circ}-alpha$ .

$S_{ABCD}=S_{ABD}+S_{BCD}=frac{1}{2}ad sinalpha+frac{1}{2}bcsin (180^{circ}-alpha)=$

$=frac{1}{2}sin alpha (ad+bc).$

Откуда

$S_{ABCD}^2=frac{1}{4}sin^2alpha (ad+bc)^2=frac{1}{4}(1-cos^2alpha) (ad+bc)^2$ (*)

Теперь дважды применим теорему Косинусов – сначала к треугольнику , затем к треугольнику , помня о том, что $cos (180^{circ}-alpha)=-cos alpha$ :

Откуда

$cos alpha=frac{a^2+d^2-b^2-c^2}{2(ad+bc)}.$

Вернемся к (*):

$S_{ABCD}^2=frac{1}{4}(1-cos^2alpha) (ad+bc)^2=frac{1}{4}(1-(frac{a^2+d^2-b^2-c^2}{2(ad+bc)})^2)(ad+bc)^2=$

$=frac{1}{4}(1-frac{a^2+d^2-b^2-c^2}{2(ad+bc)})(1+frac{a^2+d^2-b^2-c^2}{2(ad+bc)})(ad+bc)^2=$

$=frac{(2ad+2bc-a^2-d^2+b^2+c^2)(2ad+2bc+a^2+d^2-b^2-c^2)(ad+bc)^2}{16(ad+bc)^2}=$

$=frac{((b+c)^2-(a-d)^2)((a+d)^2-(b-c)^2)}{16}=$

$=frac{((b+c)-(a-d))((b+c)+(a-d))((a+d)-(b-c))((a+d)+(b-c))}{16}=$

$=frac{(2p-2a)(2p-2d)(2p-2b)(2p-2c)}{16}=(p-a)(p-b)(p-c)(p-d)}.$

Наконец,

$S_{ABCD}=sqrt{(p-a)(p-b)(p-c)(p-d)}.$

Что и требовалось доказать.

Применение формулы Брахмагупты можно посмотреть, например, в этой задаче или здесь.

Автор: egeMax |

комментария 2

Источник

5 февраля 2018

В закладки

Обсудить

Жалоба

Какие геометрические факты можно использовать на ЕГЭ без доказательства?

Начнём с того, что для ЕГЭ не нужны сколько-нибудь редкие теоремы, особенно где-нибудь на шпаргалке.

Нужно уметь применять всем знакомые факты, видеть рисунок и решать больше задач. Но вопрос из заголовка задают очень часто, и ответить на него нужно. Естественно, все сотни признаков и свойств, что есть в вашем школьном учебнике можно использовать. Но как насчет более редких фактов: что можно применять без доказательства, а что нет? Точный ответ: любые факты из школьных учебников, рекомендованных минобром на 2017-2018 год.

Ну а вот заветный список того, что мне все-таки удалось обнаружить в соответствующих учебниках:

→ Теорема Менелая (Атанасян. Геометрия 7-9 классы)
→ Теорема Чевы (Атанасян. Геометрия 7-9 классы)
→ Теорема Птолемея (Мерзляк. Геометрия 8 класс)
→ Прямая Эйлера (Мерзляк. Геометрия 8 класс)
→ Теорема об окружности Эйлера (Бутузов. Геометрия 8 класс)
→ Формула медианы треугольника (Шарыгин. Геометрия 7-9 классы)
→ Формула биссектрисы треугольника (Шарыгин. Геометрия 7-9 классы)
→ Теорема о четырех замечательных точках трапеции (Шарыгин. Геометрия 7-9 классы)

Формулу радиуса вневписанной окружности используйте. Каноническое уравнение эллипса — да пожалуйста! Ключевые формулы метода координат для задачи №14, опять же, есть

Но если здесь есть коллеги по цеху, которые могут уточнить еще несколько популярных вопросов насчет непопулярной теории — черкните, буду признателен! Вот интересующие факты: формула Брахмагупты, теорема Стюарта, формула Эйлера для расстояния между центрами вписанной и описанной окружностями треугольника, понятие определителя квадратной матрицы.

Ну и еще раз в заключение. Вероятность того, что задача ЕГЭ не решается без экзотики, равна нулю (такие события называются невозможными). Вероятность того, что вам вообще попадется конфигурация, для которой актуальна, например, теорема о девяти точках окружности, приблизительно равна 0,015. Вероятность того, что школьник в целом знает что-то «запрещенное», приблизительно равна, не кидайтесь камнями, 0,000037.

Источник: vk.com/wildmathing

Источник

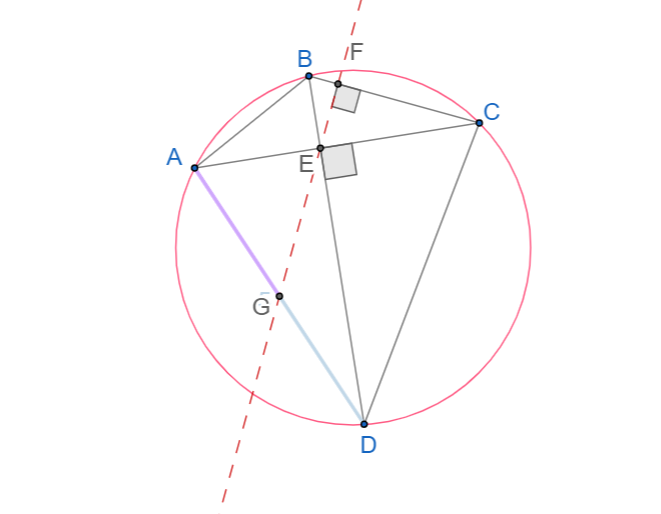
Теорема.

Если вписанный четырехугольник имеет перпендикулярные диагонали, то прямая проходящая через точку пересечения диагоналей, перпендикулярно какой-нибудь стороне четырехугольника делит противоположную ей сторону пополам.

Доказательство.

Так как ∠EAD + ∠EDA=90º, ∠FEC + ∠FCE=90º(свойство прямоугольного треугольника) и ∠ADB=∠ACB (вписанные углы, опирающиеся на дугу AB), то ∠EAD=∠FEC.

∠FEC=∠AEG (свойство вертикальных углов).

Следовательно, треугольник GAE является равнобедренным.

Аналогично доказывается, что треугольник GED — равнобедренный.

Следовательно, AG=EG=GD.

Источник

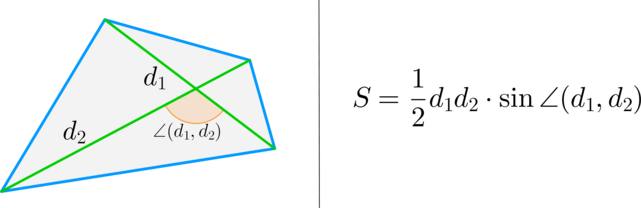
Факт 1.
(bullet) Площадь выпуклого четырехугольника равна половине произведения диагоналей на синус угла между ними.

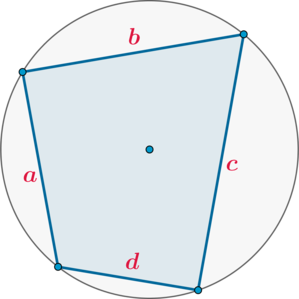
Факт 2.
(bullet) Формула Брахмагупты:
если около четырехугольника можно описать окружность, то его площадь равна [{large{S=sqrt{(p-a)(p-b)(p-c)(p-d)}}}]

где (a,b,c,d) – его стороны, (p) – полупериметр.

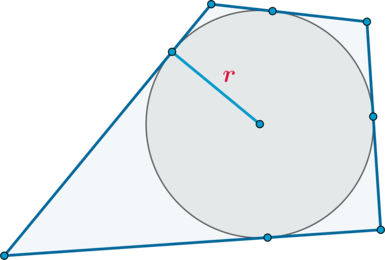
Факт 3.
(bullet) Если в четырехугольник можно вписать окружность, то его площадь равна [{large{S=pcdot r}}]

где (p) – полупериметр, (r) – радиус вписанной окружности.

Факт 4.
(bullet) Если в четырехугольник можно вписать окружность, а также около него можно описать окружность, то его площадь равна [{large{S=sqrt{abcd}}}]

где (a,b,c,d) – его стороны.

Источник

Каталог заданий.
2. Площадь четырёхугольника через четыре стороны и два противоположных угла, формула Брахмагупты

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Найдите площадь вписанного четырёхугольника со сторонами 4, 5, 7, 8.

Найдите площадь вписанного четырёхугольника со сторонами 2, 1, 4, 6.

Вокруг выпуклого четырёхугольника со сторонами а, b, c, d описана окружность.

а)  Докажите, что отношение его диагоналей равно

б)  Найдите площадь четырёхугольника, если

Пройти тестирование по этим заданиям

Источник

Егэ 2021 Математика. №3, 6, 16. Секретные Формулы Площади. Формула Брахмагупты. Синусная Теорема Чевы

Дата публикации:

26.11.2020 17:26

Продолжительность:

01:13:42

Ссылка:

https://thewikihow.com/video_pZ1Na2Luo10

Действия:

Источник:

Описание

Подписывайтесь на наш Telegram канал!@thewikihowоткрытьМониторим видео тренды 24/7

Что еще посмотреть на канале Школково Егэ, Огэ, Олимпиады

Фото обложки и кадры из видео

Егэ 2021 Математика. №3, 6, 16. Секретные Формулы Площади. Формула Брахмагупты. Синусная Теорема Чевы, Школково Егэ, Огэ, Олимпиады

https://thewikihow.com/video_pZ1Na2Luo10

Аналитика просмотров видео на канале Школково Егэ, Огэ, Олимпиады

Гистограмма просмотров видео «Егэ 2021 Математика. №3, 6, 16. Секретные Формулы Площади. Формула Брахмагупты. Синусная Теорема Чевы» в сравнении с последними загруженными видео.

Формула Брахмагупты

Какие геометрические факты можно использовать на ЕГЭ без доказательства?

Описание

Что еще посмотреть на канале Школково Егэ, Огэ, Олимпиады

Фото обложки и кадры из видео

Аналитика просмотров видео на канале Школково Егэ, Огэ, Олимпиады

Теги: