Теорема менелая егэ профиль - Помощь в подготовке к экзаменам и поступлению

Всего: 47 1–20 | 21–40 | 41–47

Добавить в вариант

На сторонах AB, BC и AC треугольника ABC отмечены точки C₁, A₁ и B₁ соответственно, причём AC₁ : C₁B  =  8 : 3, BA₁ : A₁C  =  1 : 2, CB₁ : B₁A  =  3 : 1. Отрезки BB₁ и CC₁ пересекаются в точке D.

а)  Докажите, что ADA₁B₁  — параллелограмм.

б)  Найдите CD, если отрезки AD и BC перпендикулярны, AC  =  28, BC  =  18.

Источник: ЕГЭ по математике 10.07.2020. Основная волна. Санкт-Петербург, Задания 16 ЕГЭ–2020

Дана правильная четырёхугольная пирамида SABCD. Точка M  — середина SA, на ребре SB отмечена точка N так, что

а)  Докажите, что плоскость CMN параллельна прямой SD.

б)  Найдите площадь сечения пирамиды плоскостью CMN, если все рёбра равны 12.

Источник: ЕГЭ по математике 02.06.2022. Основная волна. Краснодарский край, Задания 13 ЕГЭ–2022

На отрезке BD взята точка C. Биссектриса BL равнобедренного треугольника ABC с основанием BC является боковой стороной равнобедренного треугольника BLD с основанием BD.

а)  Докажите, что треугольник DCL равнобедренный.

б)  Известно, что В каком отношении прямая DL делит сторону AB?

Источник: Типовые тестовые задания по математике, под редакцией И. В. Ященко 2016

Точки М, N и К принадлежат соответственно ребрам АD, AB и BC тетраэдра ABCD,

причем АМ : МD  =  2 : 3, ВN : АN  =  1 : 2, ВК  =  КС.

а)  Постройте сечение тетраэдра плоскостью, проходящей через точки М, N, K.

б)  Найдите отношение, в котором секущая плоскость делит ребро CD.

Источник: А. Ларин: Тренировочный вариант № 206.

Точки B₁ и C₁ лежат на сторонах соответственно AC и AB треугольника ABC, причём AB₁ : B₁C  =  AC₁ : C₁B. Прямые BB₁ и CC₁ пересекаются в точке O.

а)  Докажите, что прямая AO делит пополам сторону BC.

б)  Найдите отношение площади четырёхугольника AB₁OC₁ к площади треугольника ABC, если известно, что AB₁ : B₁C  =  AC₁ : C₁B  =  1 : 4.

Источник: Типовые тестовые задания по математике, под редакцией И. В. Ященко 2017. Вариант 3. (Часть C)., Типовые тестовые задания по математике под редакцией И. В. Ященко, 2017. Задания С2, C4.

а)  Докажите, что треугольник DCL равнобедренный.

б)  Известно, что В каком отношении прямая DL делит сторону AB?

Источник: Типовые тестовые задания по математике, под редакцией И. В. Ященко 2016

Плоскость α проходит через середины двух противоположных ребер треугольной пирамиды и параллельна медиане одной из ее граней.

а)   Докажите, что среди медиан граней этой пирамиды в точности две являются параллельными к плоскости α.

б)   Найдите площадь сечения данной пирамиды плоскостью α, если эти медианы перпендикулярны друг другу и равны 2.

Источник: А. Ларин. Тренировочный вариант № 345.

Объем пирамиды ABCD равен 5. Через середины ребер AD и BC проведена плоскость, пересекающая ребро CD в точке M. При этом DM : MC = 2 : 3. Найти площадь сечения, если расстояние от плоскости сечения до вершины A равно 1.

Источник: А. Ларин: Тренировочный вариант № 54.

В треугольнике ABC на стороне AB расположена точка K так, что AK : KB = 3 : 5. На прямой AC взята точка E так, что AE = 2CE. Известно, что прямые BE и CK пересекаются в точке O. Найдите площадь треугольника ABC, если площадь треугольника BOC равна 20.

Источник: А. Ларин: Тренировочный вариант № 36.

Плоскость пересекает боковые ребра SA и SB треугольной пирамиды SABC в точках K и L соответственно и делит объем пирамиды пополам

а)  Постройте сечение пирамиды плоскостью, если SK : SA  =  2 : 3, SL : SB  =  4 : 5.

б)  В каком отношении эта плоскость делит медиану SN грани SBC?

Источник: А. Ларин: Тренировочный вариант № 93.

Даны треугольники ABC и A₁B₁C₁. Прямые AA₁, BB₁, CC₁ пересекаются в одной точке. Прямые AB и A₁B₁ пересекаются в точке C₂. Прямые АС и A₁C₁ пересекаются в точке B₂. Прямые BC и B₁C₁ пересекаются в точке A₂.

а)  Докажите, что точки A₂, B₂, C₂ лежат на одной прямой.

б)  Найдите отношение площади треугольника A₁B₁C₁ и площади треугольника ABC, если высоты треугольника ABC равны а высоты треугольника A₁B₁C₁ равны

Источник: А. Ларин: Тренировочный вариант № 134.

В правильной шестиугольной пирамиде SABCDEF с вершиной S боковое ребро вдвое больше стороны основания.

а)  Докажите, что плоскость, проходящая через середины рёбер SA и SE и вершину C, делит ребро SB в отношении 3 : 1, считая от вершины S.

б)  Найдите отношение, в котором плоскость, проходящая через середины рёбер SA и SE и вершину C, делит ребро SF, считая от вершины S.

Источник: Типовые тестовые задания по математике, под редакцией И. В. Ященко 2016

На сторонах AD и BC параллелограмма AВCD взяты соответственно точки M и N, причем ВN : NC  =  1 : 3. Оказалось, что прямые AN и АС разделили отрезок BM на три равные части.

а)  Докажите, что точка M — середина стороны АD параллелограмма.

б)  Найдите площадь параллелограмма ABCD, если известно, что площадь четырехугольника, ограниченного прямыми АN, AС, BM и BD равна 16.

Источник: А. Ларин: Тренировочный вариант № 152.

Источник: А. Ларин: Тренировочный вариант № 179.

Апофема правильной пирамиды SABCD равна 2, боковое ребро образует с основанием ABCD угол, равный Точки E, F, K выбраны соответственно на ребрах AB, AD и SC так, что

а)  Найдите площадь сечения пирамиды плоскостью EFK.

б)  Найдите угол между прямой SD и плоскостью EFK.

Источник: А. Ларин. Тренировочный вариант № 256.

В треугольной пирамиде SABC точка Е  — середина ребра SA, точка F  — середина ребра SB, О  — точка пересечения медиан треугольника АВС.

а)  Докажите, что плоскость CEF делит отрезок SO в отношении 3 : 2, считая от вершины S.

б)  Найдите косинус угла между плоскостями CEF и EFT, если точка Т  — середина SC, пирамида SABC правильная, площадь треугольника АВС равна а SB  =  10.

Источник: А. Ларин. Тренировочный вариант № 323. (часть C).

Дана правильная четырехугольная пирамида SABCD. Плоскость α параллельна прямой АС, проходит через точку В и середину высоты пирамиды.

а)  Докажите, что плоскость α делит ребро SD в отношении 2 : 1, считая от точки D.

б)  Найдите синус угла между плоскостью α и плоскостью ASC, если угол SAC равен 30°.

Источник: А. Ларин. Тренировочный вариант № 324. (часть C).

Окружность, построенная на стороне BC треугольника ABC как на диаметре, пересекает стороны AB и AC в точках M и N соответственно. Прямые СМ и ВN пересекаются в точке P. Точка О  — середина АР.

а)  Докажите, что треугольник ОМN равнобедренный.

б)  Найдите площадь треугольника ОМN, если известно, что AM = 3, BM = 9, AN = 4.

Источник: А. Ларин. Тренировочный вариант № 263.

В прямоугольном треугольнике АВС с прямым углом С точки М и N  — середины катетов АС и ВС соответственно, СН  — высота.

а)  Докажите, что прямые МН и NH перпендикулярны.

б)  Пусть Р  — точка пересечения прямых АС и NH, а Q  — точка пересечения прямых BC и МН. Найдите площадь треугольника PQM, если АН  =  12 и ВН  =  3.

Источник: ЕГЭ по математике 06.06.2016. Основная волна. Вариант 601 (C часть).

а)  Докажите, что прямые МН и NH перпендикулярны.

б)  Пусть Р  — точка пересечения прямых АС и NH, а Q  — точка пересечения прямых BC и МН. Найдите площадь треугольника PQM, если АН  =  4 и ВН  =  2.

Источник: Задания 16 (С4) ЕГЭ 2016, ЕГЭ по математике 06.06.2016. Основная волна. Вариант 605 (C часть).

Всего: 47 1–20 | 21–40 | 41–47

Источник

Теорема Менелая, теорема Чевы – нужны на ЕГЭ или нет?

Анна Малкова

Эти две полезные теоремы – теорема Менелая и теорема Чевы — чаще применяются при решении олимпиадных задач, чем на ЕГЭ по математике. Однако в 2020 году в ряде вариантов ЕГЭ обнаружилась задача по планиметрии (№16), которую на первый взгляд невозможно решить без теоремы Менелая или теоремы Чевы. Но на самом деле, конечно, возможно. Например, в Санкт-Петербурге попались такие задачи.

Разберемся, что это за теоремы и как применяются. И действительно ли на ЕГЭ дали задачи на применение теорем, выходящих за рамки школьной программы. И можно ли эти задачи решить по-другому?

Теорема Менелая:

Пусть прямая пересекает произвольный треугольник ABC, причем C_1 – точка ее пересечения со стороной ABC, A_1 – точка ее пересечения со стороной BC, и B_1 – точка ее пересечения с продолжением стороны AC.

Тогда выполняется равенство:

$displaystyle frac{AC_1}{C_1B} cdot frac{BA_1}{A_1C} cdot frac{CB_1}{B_1A} = 1.$

Как это запомнить? Сначала рисуем треугольник ABC. Затем прямую, пересекающую две его стороны и продолжение третьей. На этой прямой лежат точки и B_1, причем на стороне должна лежать точка C_1, на стороне – точка A_1 и на продолжении – точка B_1.

Затем записываем равенство так, как будто «обходим» весь треугольник ABC, от точки к точкам и и затем возвращаемся в точку Но по дороге нам встречаются точки и B_1 – их тоже включаем в формулу.

Один из учащихся нашей ЕГЭ-Студии предложил такое мнемоническое правило: пусть точки A, B и – это города, а точки и B_1 – заправки, где можно пополнить запас бензина. Тогда правило звучит так: «Едем из города в город, заезжаем на заправку!»Возможно, вы придумаете свое правило : -)

В некоторых задачах полезна обратная теорема Менелая.

Теорема (Менелая, обратная). Пусть дан треугольник ABC. Предположим, что точка C_1 лежит на стороне AB, точка A_1 лежит на стороне BC, а точка B_1 лежит на продолжении стороны AC, причём про эти точки известно, что

$displaystyle frac{AC_1}{C_1B} cdot frac{BA_1}{A_1C} cdot frac{CB_1}{B_1A} = 1.$

Тогда эти точки лежат на одной прямой.

Как правило, не так-то просто бывает доказать, что три точки лежат на одной прямой. Обычно мы используем для доказательства такого факта косвенные методы. Например, если для точек A, , B и выполняется равенство: – то это означает, что точка лежит на отрезке AC. Или, если нам удается доказать, что угол ABC – развернутый, это и будет означать, что точки A, , B и лежат на одной прямой. Обратная теорема Менелая дает еще один способ доказательства того, что три точки – в данном случае и C_1 – лежат на одной прямой.

Теорема Чевы

Пусть точки и C_1 лежат соответственно на сторонах и треугольника ABC, причем отрезки и CC_1 пересекаются в одной точке. В этом случае выполняется равенство:

$displaystyle frac{AC_1}{C_1B} cdot frac{BA_1}{A_1C} cdot frac{CB_1}{B_1A} = 1.$

Обратная теорема Чевы:

Теорема (Чевы, обратная). Пусть точки лежат соответственно на сторонах BC, AC и треугольника ABC, причём

$displaystyle frac{AC_1}{C_1B} cdot frac{BA_1}{A_1C} cdot frac{CB_1}{B_1A} = 1.$

Тогда отрезки и CC_1 пересекаются в одной точке.

Как применяются теоремы Менелая и Чевы?

Вот задача Профильного ЕГЭ по математике 2020 года (№16), Санкт-Петербургский вариант.

На сторонах и треугольника ABC отмечены точки и B_1 соответственно, причём Отрезки BB_1 и CC1 пересекаются в точке

а) Докажите, что — параллелограмм.
б) Найдите CD, если отрезки и перпендикулярны,

Докажем пункт (а) с помощью теоремы Менелая:

Пусть

По теореме Чевы,

$displaystyle frac{AC_1}{C_1B} cdot frac{BA_2}{A_2C} cdot frac{CB_1}{B_1A} = 1.$

$displaystyle frac{8}{3} cdot frac{BA_2}{A_2C} cdot frac{3}{1} = 1$

$displaystyle frac{BA_2}{A_2C} = frac{1}{8},$ тогда

$displaystyle BA_2 = frac{1}{9}BC$

$displaystyle A_2A_1 = left ( frac{1}{3} - frac{1}{9} right ) BC = frac{2}{9}BC,$

$displaystyle A_1C = frac{2}{3}BC,$ тогда $displaystyle A_2A_1 = frac{1}{3}A_1C$

$displaystyle A_1C : A_2C = B_1C : AC = frac{3}{4},$

Это значит, что по двум углам и то есть

Рассмотрим треугольник ABB_1.

Прямая C_1C пересекает две его стороны и продолжение третьей стороны AB_1.

По теореме Менелая,

$displaystyle frac{AC_1}{C_1B} cdot frac{BD}{DB_1} cdot frac{B_1C}{AC} = 1$

$displaystyle frac{8}{3} cdot frac{BD}{DB_1} = frac{3}{4} = 1;$

$displaystyle frac{BD}{DB_1} = frac{1}{2} = frac{BA_1}{A_1C};$

тогда $displaystyle frac{BD}{BB_1} = frac{BA_1}{BC} = frac{1}{3},$

по углу и двум сторонам, отсюда

Мы получили:

— параллелограмм по определению.

Мы доказали то, что требовалось в пункте (а).
Но что делать, если теоремы Менелая и Чевы вы не проходили в школе? Ничего страшного, докажем без теорем Менелая и Чевы. Их легко заменят подобные треугольники.

Обозначим

Докажем, что — параллелограмм.

Пусть — середина AC.

Тогда

Тогда по углу и двум пропорциональным сторонам,

Проведём

По теореме Фалеса BN = y.

Пусть

по двум углам;

$displaystyle frac{AP}{BD} = frac{AC_1}{BC_1} = frac{8}{3}.$

Пусть

по 2 углам, $displaystyle frac{AP}{B_1D} = frac{AC}{B_1C} = frac{4}{3},$
тогда $displaystyle B_1D = frac{3}{4}AP = 6k,$

$displaystyle frac{BD}{B_1D} = frac{1}{2}.$

Это значит, что по углу и двум сторонам и

При этом $displaystyle A_1D = frac{1}{3}B_1C = Z = AB_1.$

Получим, что в четырёхугольнике :

Значит, — параллелограмм.

Как видим, эти решения примерно одного уровня сложности.
А вот в пункте (б) нет необходимости применять теоремы Чевы и Менелая. Он легко решается с помощью обычной школьной геометрии.

б) Найдём , если

Поскольку получим, что — прямоугольный.

Мы доказали в пункте (а), что — трапеция, причём

По условию,

Тогда $displaystyle A_1D = frac{28}{4} = 7,$

$displaystyle B_1C = frac{28}{4} cdot 3 = 21,$

$displaystyle A_1C = frac{2}{3}BC = frac{2}{3} cdot 18 = 12.$

Пусть

Тогда A_1MCD — параллелограмм (по признаку паралелограмма)

по теореме Пифагора из

$displaystyle B_1A_1 = sqrt{21^2-12^2} = 3 sqrt{7^2 - 4^2} = 3 sqrt{33},$

$displaystyle cos angle A_1B_1C = cos angle A_1B_1M = frac{B_1A_1}{B_1C} = frac{sqrt{33}}{7}$

Найдём A_1M из по теореме косинусов.

Ответ: 17.

Вот еще одна задача, которую можно решить как с помощью теоремы Чевы, так и без нее.

На сторонах прямоугольного треугольника ABC с прямым углом построены во внешнюю сторону квадраты и Докажите, что:

а) прямые AB_2 и A_2B отсекают от катетов треугольника ABC равные отрезки
б) прямые и высота треугольника ABC, проведённая из вершины пересекаются в одной точке.

Пункт (а) доказывается легко.

а) Пусть ,
.

Докажем, что CE=CF .

Обозначим

по 2 углам,

$displaystyle frac{FC}{A_2C_1}=frac{BC}{BC_1}$ , так как

получим:

$displaystyle frac{FC}{b}=frac{a}{a+b}. ,$ (1)

по 2 углам,

$displaystyle frac{CE}{C_2B_2}=frac{AC}{AC_2}; , , frac{CE}{a}=frac{b}{a+b}. ,$ (2)

$displaystyle frac{FC cdot a}{CE cdot b} = frac{a}{b},$ отсюда FC=CE.

Решим пункт (б) с помощью теоремы Чевы:

Запишем, чему равны длины отрезков Для длин и воспользуемся тем, что в прямоугольном треугольнике каждый катет есть среднее пропорциональное между гипотенузой и проекцией этого катета на гипотенузу.

$displaystyle AH = frac{b^2}{sqrt{a^2 + b^2}}$

$displaystyle HB = frac{a^2}{sqrt{a^2 + b^2}}$

$displaystyle BE = a - frac{ab}{a+b}$

$displaystyle CE = frac{ab}{a+b}$

$displaystyle CF = frac{ab}{a+b}$

$displaystyle AF = b - frac{ab}{a+b}$

Проверим выполнение равенства

$displaystyle frac{AH}{HB} cdot frac{BE}{CE} cdot frac{CF}{AF} = 1.$

Равенство выполняется.
Согласно теореме Чевы, это значит, что и пересекаются в одной точке.
А

Источник

Анна Малкова

Теорема Менелая:

Пусть прямая пересекает произвольный треугольник ABC, причем C_1 – точка ее пересечения со стороной AB, A_1 – точка ее пересечения со стороной BC, и B_1 – точка ее пересечения с продолжением стороны AC.

Тогда выполняется равенство:

$displaystyle frac{AC_1}{C_1B} cdot frac{BA_1}{A_1C} cdot frac{CB_1}{B_1A} = 1.$

В некоторых задачах полезна обратная теорема Менелая.

Теорема (Менелая, обратная). Пусть дан треугольник Предположим, что точка лежит на стороне точка лежит на стороне а точка лежит на продолжении стороны причём про эти точки известно, что

$displaystyle frac{AC_1}{C_1B} cdot frac{BA_1}{A_1C} cdot frac{CB_1}{B_1A} = 1.$

Тогда эти точки лежат на одной прямой.

Теорема Чевы

$displaystyle frac{AC_1}{C_1B} cdot frac{BA_1}{A_1C} cdot frac{CB_1}{B_1A} = 1.$

Обратная теорема Чевы:

Теорема (Чевы, обратная). Пусть точки лежат соответственно на сторонах и треугольника причём

$displaystyle frac{AC_1}{C_1B} cdot frac{BA_1}{A_1C} cdot frac{CB_1}{B_1A} = 1.$

Тогда отрезки и пересекаются в одной точке.

Как применяются теоремы Менелая и Чевы?

Вот задача Профильного ЕГЭ по математике 2020 года (№16), Санкт-Петербургский вариант.

На сторонах и треугольника отмечены точки и соответственно, причём Отрезки и пересекаются в точке

а) Докажите, что — параллелограмм.
б) Найдите если отрезки и перпендикулярны,

Докажем пункт (а) с помощью теоремы Менелая:

Пусть

По теореме Чевы,

$displaystyle frac{AC_1}{C_1B} cdot frac{BA_2}{A_2C} cdot frac{CB_1}{B_1A} = 1.$

$displaystyle frac{8}{3} cdot frac{BA_2}{A_2C} cdot frac{3}{1} = 1$

$displaystyle frac{BA_2}{A_2C} = frac{1}{8},$ тогда

$displaystyle BA_2 = frac{1}{9}BC$

$displaystyle A_2A_1 = left ( frac{1}{3} - frac{1}{9} right ) BC = frac{2}{9}BC,$

$displaystyle A_1C = frac{2}{3}BC,$ тогда $displaystyle A_2A_1 = frac{1}{3}A_1C$

$displaystyle A_1C : A_2C = B_1C : AC = frac{3}{4},$

Это значит, что по двум углам и то есть

Рассмотрим треугольник ABB_1.

Прямая C_1C пересекает две его стороны и продолжение третьей стороны AB_1.

По теореме Менелая,

$displaystyle frac{AC_1}{C_1B} cdot frac{BD}{DB_1} cdot frac{B_1C}{AC} = 1$

$displaystyle frac{8}{3} cdot frac{BD}{DB_1} = frac{3}{4} = 1;$

$displaystyle frac{BD}{DB_1} = frac{1}{2} = frac{BA_1}{A_1C};$

тогда $displaystyle frac{BD}{BB_1} = frac{BA_1}{BC} = frac{1}{3},$

по углу и двум сторонам, отсюда

Мы получили:

— параллелограмм по определению.

Обозначим

Докажем, что — параллелограмм.

Пусть — середина AC.

Тогда

Тогда по углу и двум пропорциональным сторонам,

Проведём

По теореме Фалеса BN = y.

Пусть

по двум углам;

$displaystyle frac{AP}{BD} = frac{AC_1}{BC_1} = frac{8}{3}.$

Пусть

по 2 углам, $displaystyle frac{AP}{B_1D} = frac{AC}{B_1C} = frac{4}{3},$
тогда $displaystyle B_1D = frac{3}{4}AP = 6k,$

$displaystyle frac{BD}{B_1D} = frac{1}{2}.$

Это значит, что по углу и двум сторонам и

При этом $displaystyle A_1D = frac{1}{3}B_1C = Z = AB_1.$

Получим, что в четырёхугольнике :

Значит, — параллелограмм.

б) Найдём , если

Поскольку получим, что — прямоугольный.

Мы доказали в пункте (а), что — трапеция, причём

По условию,

Тогда $displaystyle A_1D = frac{28}{4} = 7,$

$displaystyle B_1C = frac{28}{4} cdot 3 = 21,$

$displaystyle A_1C = frac{2}{3}BC = frac{2}{3} cdot 18 = 12.$

Пусть

Тогда A_1MCD — параллелограмм (по признаку паралелограмма)

по теореме Пифагора из

$displaystyle B_1A_1 = sqrt{21^2-12^2} = 3 sqrt{7^2 - 4^2} = 3 sqrt{33},$

$displaystyle cos angle A_1B_1C = cos angle A_1B_1M = frac{B_1A_1}{B_1C} = frac{sqrt{33}}{7}$

Найдём A_1M из по теореме косинусов.

$displaystyle A_1M^2 = 9 cdot 33 + 28^2 - frac{2 cdot 28 cdot 3 sqrt{33} cdot sqrt{33}}{7} = 28^2 - 15cdot 33 = 784 - 495 = 289;$

Ответ: 17.

Вот еще одна задача, которую можно решить как с помощью теоремы Чевы, так и без нее.

На сторонах прямоугольного треугольника с прямым углом построены во внешнюю сторону квадраты и Докажите, что:

а) прямые и отсекают от катетов треугольника равные отрезки
б) прямые и высота треугольника проведённая из вершины пересекаются в одной точке.

Пункт (а) доказывается легко.

а) Пусть ,
.

Докажем, что CE=CF .

Обозначим

по 2 углам,

$displaystyle frac{FC}{A_2C_1}=frac{BC}{BC_1}$ , так как

получим:

$displaystyle frac{FC}{b}=frac{a}{a+b}. ,$ (1)

по 2 углам,

$displaystyle frac{CE}{C_2B_2}=frac{AC}{AC_2}; , , frac{CE}{a}=frac{b}{a+b}. ,$ (2)

$displaystyle frac{FC cdot a}{CE cdot b} = frac{a}{b},$ отсюда FC=CE.

Решим пункт (б) с помощью теоремы Чевы:

$displaystyle AH = frac{b^2}{sqrt{a^2 + b^2}}$

$displaystyle HB = frac{a^2}{sqrt{a^2 + b^2}}$

$displaystyle BE = a - frac{ab}{a+b}$

$displaystyle CE = frac{ab}{a+b}$

$displaystyle CF = frac{ab}{a+b}$

$displaystyle AF = b - frac{ab}{a+b}$

Проверим выполнение равенства

$displaystyle frac{AH}{HB} cdot frac{BE}{CE} cdot frac{CF}{AF} = 1.$

$displaystyle frac{frac{b^2}{sqrt{a^2+b^2}}}{frac{a^2}{sqrt{a^2+b^2}}} cdot frac{a - frac{ab}{a+b}}{frac{ab}{a+b}} cdot frac{frac{ab}{a+b}}{b - frac{ab}{a+b}} = 1.$

Равенство выполняется.
Согласно теореме Чевы, это значит, что и пересекаются в одной точке.
А вот как решается эта задача без теоремы Чевы, с помощью векторов:

Смотрите решение: https://ege-study.ru/zadacha-na-dokazatelstvo-planimetriya/

Математик Менелай Александрийский жил в I веке до нашей эры (Древний Рим).
Математик и инженер Джованни Чева – XVII век, Италия.

Как видим, теоремы Менелая и Чевы оказываются полезны в некоторых задачах. Очень хорошо, если вы знаете эти теоремы. Однако если они для вас непривычны, можно применить простой школьный прием – пары подобных треугольников.

Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Теорема Менелая, теорема Чевы – нужны на ЕГЭ или нет?» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.

Публикация обновлена:
08.03.2023

Источник

Теорема Менелая – прекрасное дополнение к вашему техническому арсеналу для решения задач ЕГЭ по стереометрии. Она позволяет найти отношение, в котором точка делит отрезок, легко и непринужденно, в одно действие. Попробуем применить ее для решения стереометрических задач.

Задача 1.

Точка лежит на ребре треугольной пирамиды , причем .

А) Постройте сечение пирамиды плоскостью, проходящей через точку и середины ребер и .

Б) В каком отношении плоскость сечения делит ребро ?

К задаче 1

Построим сечение. Для этого (по методу следов) проведем луч и луч и найдем точку их пересечения — . Через данную точку и точку проведем луч — он принадлежит плоскости . Этот луч пересечет отрезок — назовем эту точку .

Образовался четырехугольник сечения — .

Определим отношение, в котором точка делит отрезок . Для этого воспользуемся теоремой Менелая.

Откуда

То есть — середина .

Теперь найдем отношение, в котором точка делит отрезок . Для этого воспользуемся теоремой Менелая в плоскости :

Сечение пирамиды плоскостью

Ответ: .

Задача 2.

Точка — середина ребра треугольной пирамиды . Точки и лежат на прямых и соответственно, причем — середина отрезка , а — середина отрезка .

А) Постройте сечение пирамиды плоскостью, проходящей через точки , и .

Б) В каком отношении плоскость сечения делит ребро ?

К задаче 2

Соединим точки и , и — и обозначим точки пересечения этих лучей с ребрами и — и . Получено сечение .

Для треугольника и секущей составим теорему Менелая:

Сечение в задаче 2

Ответ:

Источник

Задание № 16 ЕГЭ по математике (профиль). Применение теоремы Менелая

Теорема Менелая. Рассмотрим произвольный треугольник ABC и некую прямую l, которая пересекает две стороны треугольника внутренним образом и одну — на продолжении. Обозначим точки пересечения M, N и K:

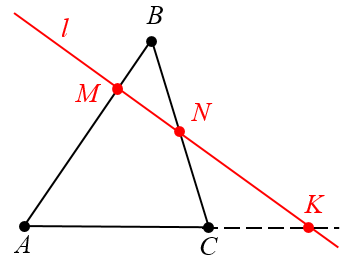
Тогда верно следующее соотношение:

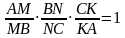
Примечание. В отношениях двигаемся от вершины к точке (в числителе), от точки к вершине (в знаменателе).

На чертеже это будет выглядеть вот так:

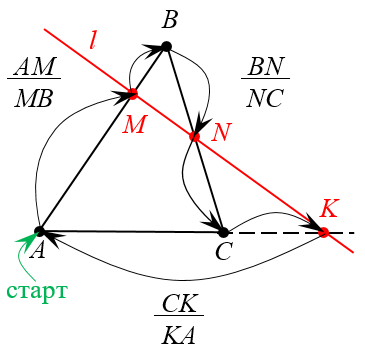
Задача 1. На сторонах АВ и ВС треугольника АВС отметили точки М и N так, что АМ : МВ = 2 : 3, ВN : NC = 2 : 1. Отрезки АN и СМ пересекаются в точке О. Найдите отношение отрезков СО и ОМ.

Р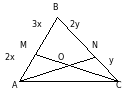 ешение.

По условию АМ : МВ = 2 : 3. Следовательно, АМ = 2х, МВ = 3х, тогда АВ = 5х. ВN : NC = 2 : 1, значит, ВN = 2у, NC = у.

Рассмотрим треугольник МВС и прямую АN. Применяя теорему Менелая, имеем:

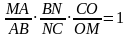
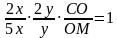
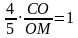
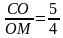
Ответ: 5 : 4.

Задача 2 (№ 514717). На отрезке BD взята точка C. Биссектриса BL равнобедренного треугольника ABC с основанием BC является боковой стороной равнобедренного треугольника BLD с основанием BD.

а) Докажите, что треугольник DCL равнобедренный.

б) Известно, что 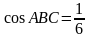. В каком отношении прямая DL делит сторону AB?

Решение.

4,5x

1,5x

2α

1,5x

а) Пусть АВL = LBC = α, тогда АВС = АСВ = 2α, как углы при основании ВС равнобедренного треугольника ABC.

Так как  LBD – равнобедренный, то D = α.

АCB – внешний угол треугольника LCD, следовательно, АCB =CDL + CLD. Поэтому CLD = α, и, следовательно,  LCD – равнобедренный.

б) Проведём высоту АН. Пусть ВН = НС = х.

Рассмотрим прямоугольный  АВН:

По свойству биссектрисы угла биссектриса BL делит сторону АС на отрезки, пропорциональные прилежащим сторонам:

Следовательно,

Так как  DCL– равнобедренный, то .

Рассмотрим  ABC и прямую DL и применим теорему Менелая:

Ответ: 9 : 7 (или 7 : 9).

Задание для самостоятельного решения

1. (№ 513277)

а) Докажите, что треугольник DCL равнобедренный.

б) Известно, что . В каком отношении прямая DL делит сторону AB?

Ответ: 21 : 4 (или 4 : 21).

Источник

Применение Теоремы Менелая в задаче 16

28 декабря 2015

Обратите внимание: у меня на сайте есть отдельный урок по теореме Менелая. Сегодня мы будем лишь применять её для решения конкретных задач из ЕГЭ.

Данная теорема в школьном курсе математики относится к категории тех знаний, которые дают далеко не во всех школах, но для успешной сдачи ЕГЭ знать её совершенно необходимо. Потому что эта теорема применяется для решения задачи 16 — сложной планиметрической задачи, состоящей из двух частей.

Сегодня мы рассмотрим, как работает теорема Менелая на примере одной довольно сложной задачи. Видео получилось довольно объёмным и отнюдь не самым простым, но очень полезным для тех, кто действительно хочет набрать много баллов на экзамене.:)

Смотрите также:

Пробный ЕГЭ 2016: задача 16 с доказательством и окружностями, для решения которой нужно знать пару теорем.:)
Угол между двумя прямыми
Тест к уроку «Округление с избытком и недостатком» (1 вариант)
Так сокращать дроби нельзя!
Задача B5: площадь сектора
Задача B4: тарифы на сотовую связь

Источник

16. Задачи по планиметрии

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

Задачи на теоремы Менелая, Чевы и Стюарта

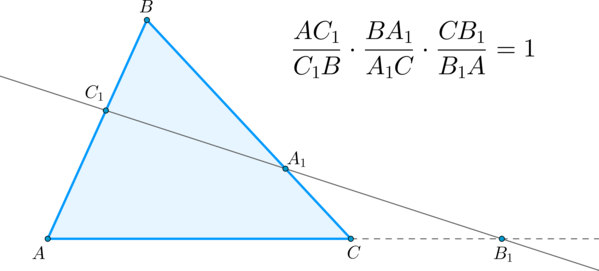
(blacktriangleright) Теорема Менелая: пусть прямая пересекает треугольник в точке (C_1) на стороне (AB), в точке (A_1) на стороне (BC) и в точке (B_1) на продолжении стороны (AC). Тогда имеет место следующее соотношение:

(blacktriangleright) Теорема, обратная теореме Менелая: пусть в треугольнике точка (B_1) лежит на продолжении стороны (AC), а точки (A_1, C_1) — на сторонах (BC) и (AB) соответственно. Тогда, если выполнено равенство [dfrac{AB_1}{B_1C}cdot dfrac{CA_1}{A_1B}cdot dfrac{BC_1}{C_1A}=1,] то точки (A_1, B_1, C_1) лежат на одной прямой.

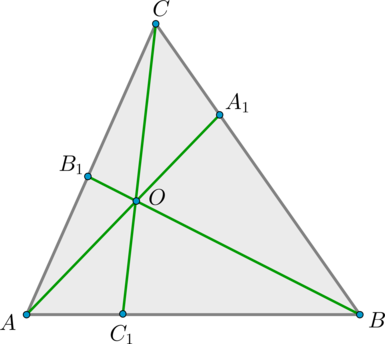
Теорема Чевы: пусть на сторонах треугольника (ABC) выбраны точки (A_1in BC, B_1in AC, C_1in AB). Отрезки (AA_1, BB_1, CC_1) пересекаются в одной точке тогда и только тогда, когда выполнено равенство [{large{dfrac{AB_1}{B_1C}cdot dfrac{CA_1}{A_1B}cdot
dfrac{BC_1}{C_1A}=1}}]

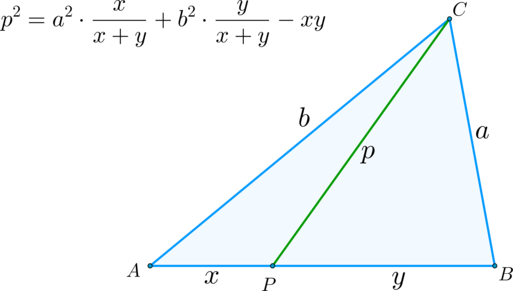
(blacktriangleright) Теорема Стюарта: пусть в треугольнике на стороне (AB) отмечена точка (P). Тогда, если (CP=p, AP=x,
BP=y,AC=b, BC=a), верно следующее соотношение:

(blacktriangleright) С помощью теоремы Стюарта выводятся формулы нахождения биссектрис и медиан треугольника:

I. Если (l_c) — биссектриса, проведенная к стороне (c) и разбивающая эту сторону на отрезки (x) и (y), а (a,b) — две другие его стороны, то [{large{l^2_c=ab-xy}}]

II. Если (m_c) — медиана, проведенная к стороне (c) треугольника, а (a,b) — две другие его стороны, то [{large{m^2_c=dfrac{2a^2+2b^2-c^2}4}}]

Задание
1

#2826

Уровень задания: Легче ЕГЭ

Докажите, что биссектрисы треугольника пересекаются в одной точке.

Пусть нам дан (triangle ABC), проведем в нем биссектрисы (AA_1,
BB_1, CC_1) и докажем что они пересекаются в одной точке.

Воспользуемся свойством биссектрисы для всех трех биссектрис:

Для биссектрисы (AA_1: dfrac{BA_1}{A_1C} =dfrac{AB}{AC})

Для биссектрисы (BB_1: dfrac{CB_1}{B_1A} =dfrac{BC}{BA})

Для биссектрисы (CC_1: dfrac{AC_1}{C_1B} =dfrac{CA}{CB})

Воспользуемся теоремой Чевы: [dfrac{BA_1}{A_1C} cdot dfrac{CB_1}{B_1A} cdot
dfrac{AC_1}{C_1B} = dfrac{AB}{AC} cdot dfrac{BC}{BA} cdot
dfrac{CA}{CB} = dfrac{ABcdot BC cdot CA}{ABcdot BC cdot CA} =1.]

Следовательно, биссектрисы треугольника пересекаются в одной точке.

Ответ:

Доказательство

Задание
2

#2827

Уровень задания: Легче ЕГЭ

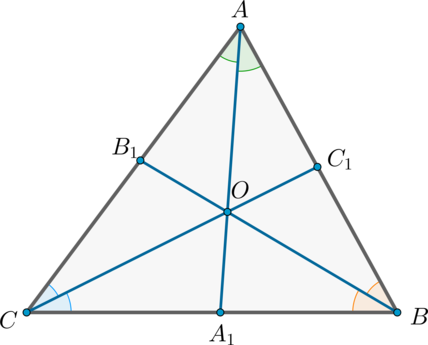
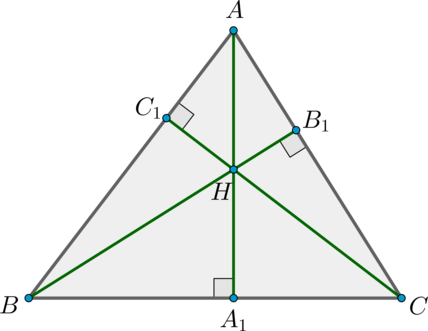
Докажите, что высоты треугольника пересекаются в одной точке.

Пусть нам дан (triangle ABC), проведем в нем высоты (AA_1,
BB_1, CC_1) и докажем что они пересекаются в одной точке.

Заметим, что: [begin{aligned}
&BA_1= cos{angle B} cdot AB,qquad
A_1C= cos{angle C} cdot AC,\
&CB_1= cos{angle C} cdot BC,qquad
B_1A= cos{angle A} cdot AB,\
&AC_1= cos{angle A} cdot AC,qquad
C_1B= cos{angle B} cdot BC.
end{aligned}] Воспользуемся теоремой Чевы: [begin{aligned}
&dfrac{BA_1}{A_1C} cdot dfrac{CB_1}{B_1A} cdot
dfrac{AC_1}{C_1B} = dfrac{cos{angle B} cdot AB}{cos{angle C}
cdot AC} cdot dfrac{cos{angle C} cdot BC}{cos{angle A}
cdot AB} cdot dfrac{cos{angle A} cdot AC}{cos{angle B}
cdot BC} =\[1.5ex]
= & dfrac{ABcdot BC cdot CA cdot cos{angle A} cdot cos{angle B} cdot cos{angle C}}{ABcdot BC cdot CA cdot cos{angle A} cdot cos{angle B} cdot cos{angle C}} =1,.
end{aligned}]

Следовательно, высоты треугольника пересекаются в одной точке.

Ответ:

Доказательство

Задание
3

#2828

Уровень задания: Легче ЕГЭ

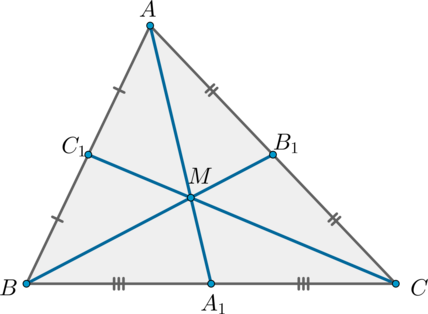
Докажите, что медианы треугольника пересекаются в одной точке.

Пусть нам дан (triangle ABC), проведем в нем медианы (AA_1, BB_1,
CC_1) и докажем что они пересекаются в одной точке.

Воспользуемся теоремой Чевы: [dfrac{AB_1}{B_1C} cdot
dfrac{CA_1}{A_1B} cdot dfrac{BC_1}{C_1A} =dfrac{1}{1} cdot
dfrac{1}{1} cdot dfrac{1}{1} =1,] так как (A_1, B_1, C_1) – середины сторон (BC, AC, AB) соответственно.
Следовательно, медианы треугольника пересекаются в одной точке.

Ответ:

Доказательство

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ

Источник