Теорема пика егэ - Помощь в подготовке к экзаменам и поступлению

ПЕРВУШКИН БОРИС НИКОЛАЕВИЧ

ЧОУ «Санкт-Петербургская Школа «Тет-а-Тет»

Учитель Математики Высшей категории

Площадь фигуры на листе в клетку. Формула Пика!

Здравствуйте, Дорогие друзья! Хочу рассказать вам о формуле, при помощи которой можно находить площадь фигуры построенной на листе в клетку (треугольник, квадрат, трапеция, прямоугольник, многоугольник). Это формула Пика.

Она секретной не является. Информация о ней в интернете имеется, но многим материал статьи будет крайне полезен. Об этой формуле обычно рассказывается применительно к нахождению площади треугольника. На примере треугольника мы её и рассмотрим.

В задачах, которые будут на ЕГЭ есть целая группа заданий, в которых дан многоугольник построенный на листе в клетку и стоит вопрос о нахождении площади. Масштаб клетки это один квадратный сантиметр.

ФОРМУЛА ПИКА

Площадь искомой фигуры можно найти по формуле:

М – количество узлов на границе треугольника (на сторонах и вершинах)

N – количество узлов внутри треугольника

*Под «узлами» имеется ввиду пересечение линий.

Найдём площадь треугольника:

Отметим узлы:

1 клетка = 1 см

M = 15 (обозначены красным)

N = 34 (обозначены синим)

Ещё пример. Найдём площадь параллелограмма:

Отметим узлы:

M = 18 (обозначены красным)

N = 20 (обозначены синим)

Найдём площадь трапеции:

Отметим узлы:

M = 24 (обозначены красным)

N = 25 (обозначены синим)

Найдём площадь многоугольника:

Отметим узлы:

M = 14 (обозначены красным)

N = 43 (обозначены синим)

Понятно, что находить площадь трапеции, параллелограмма, треугольника проще и быстрее по соответствующим формулам площадей этих фигур. Но знайте, что можно это делать и таким образом.

А вот когда дан многоугольник, у которого пять и более углов эта формула работает хорошо.

Теперь взгляните на следующие фигуры:

Это типовые фигуры, в заданиях стоит вопрос о нахождении их площади. Такие или подобные им будут на ЕГЭ. При помощи формулы Пика такие задачи решаются за минуту. Например, найдём площадь фигуры:

Отметим узлы:

M = 11 (обозначены красным)

N = 5 (обозначены синим)

Ответ: 9,5

Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см. Ответ дайте в квадратных сантиметрах.

Посмотреть решение

Конечно, можно и эти «микрофигурки» дробить на более простые фигуры (треугольники, трапеции). Способ решения выбирать вам.

Рассмотрим подход оговоренный в статье «Площадь четырёхугольника. Универсальный способ».

Найдём площадь фигуры:

Опишем около неё прямоугольник:

Из площади прямоугольника (в данном случае это квадрат) вычтем площади полученных простых фигур:

Ответ: 4,5

Источник

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

На клетчатой бумаге с размером клетки 1 см times 1 см изображены четырёхугольники. Найдите их площади.

Пройти тестирование по этим заданиям

Источник

Одна за всех

Универсальная формула

для решения заданий ОГЭ и ЕГЭ

Подгорная Вероника, 7 кл. МКОУ СОШ №3

Учитель: Ю.М. Синотова

Предмет исследования: задачи на вычисление площади многоугольника на клетчатой бумаге, методы и приёмы их решения.

Гипотеза : Площадь фигуры, вычисленная по формуле Пика равна площади фигуры, вычисленной по формулам площадей из учебника геометрии 8 кл.

Цель исследования:

Выяснение существования иной, отличной от школьной программы и доступный для моих одноклассников формулы нахождения площади решетчатого многоугольника.
Создание презентации-тренажера в помощь моим одноклассникам, ученикам 11 класса, учителям математики.

Задачи

Подобрать необходимую литературу
Отобрать материал для исследования, выбрать главную, интересную, понятную информацию
Проанализировать и систематизировать полученную информацию
Найти различные методы и приёмы решения задач на клетчатой бумаге
Создать электронную презентацию работы для представления собранного материала одноклассникам.

Этапы работы:

Георг Александр Пик

(10 августа 1859 — 26 июля 1942) — австрийский математик

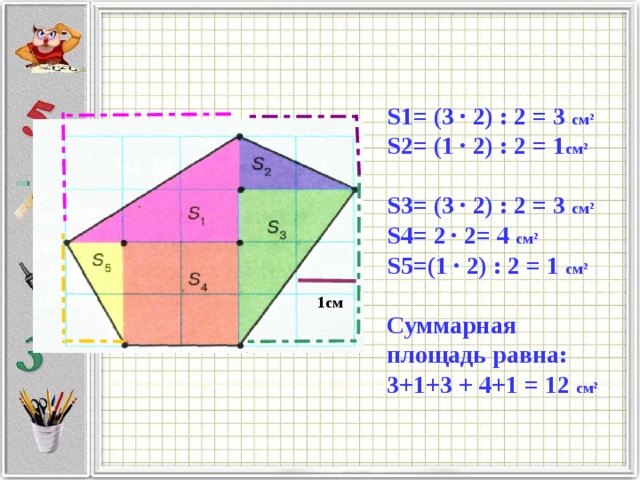
S1= (3 · 2) : 2 = 3 см²

S2= (1 · 2) : 2 = 1 см²

S3= (3 · 2) : 2 = 3 см²

S4= 2 · 2= 4 см²

S 5=(1 · 2) : 2 = 1 см²

Суммарная площадь равна: 3+1+3 + 4+1 = 12 см²

1см

Формула Пика позволит вам с необычайной легкостью находить площадь любого многоугольника на клетчатой бумаге с целочисленными вершинами.

В — количество целочисленных точек внутри многоугольника Г — количество целочисленных точек на границе многоугольника

ФОРМУЛА ПИКА

– 1

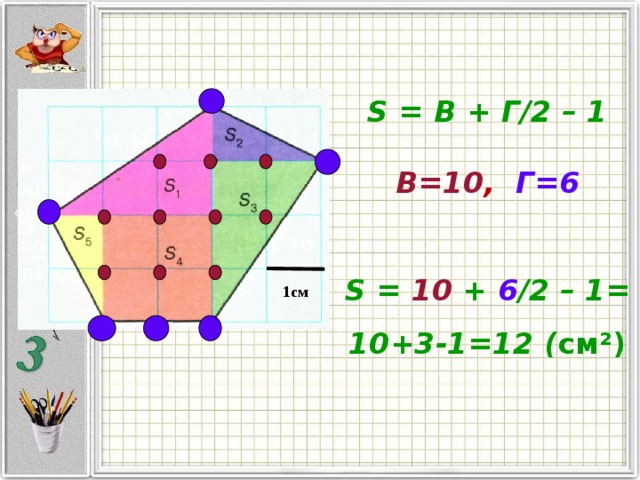
S = В + Г /2 – 1

В=10 , Г=6

S = 10 + 6 /2 – 1 =

10+3-1=12 ( см²)

1см

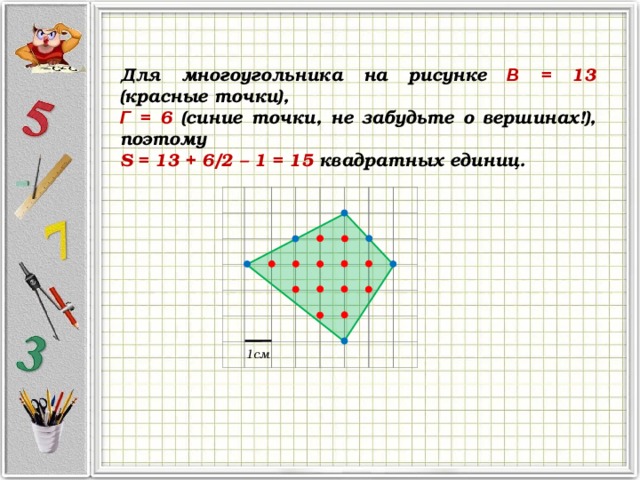
Для многоугольника на рисунке В = 1 3 (красные точки),

Г = 6 (синие точки, не забудьте о вершинах!), поэтому

S = 1 3 + 6 /2 – 1 = 1 5 квадратных единиц.

1см

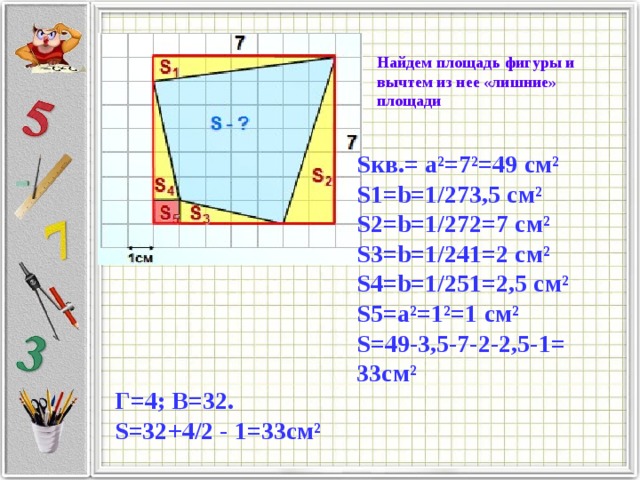
Найдем площадь фигуры и вычтем из нее «лишние» площади

S кв .= a²=7²=49 см ²

S1=b=1/273,5 см ²

S2=b=1/272=7 см ²

S3=b=1/241=2 см ²

S4=b=1/251=2,5 см ²

S5=a²=1²=1 см ²

S=49-3 , 5-7-2-2,5-1=

3 3см ²

Г=4; В=32.

S =32+ 4/2 — 1= 3 3см ²

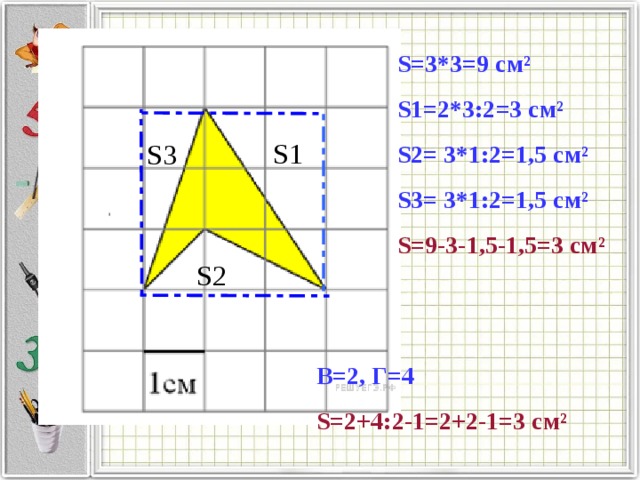
S=3*3=9 см ²

S1=2 * 3 :2=3 см ²

S 2= 3*1:2=1,5 см ²

S 3= 3*1:2=1,5 см ²

S =9-3-1,5-1,5=3 см ²

В=2, Г=4

S =2+4:2-1=2+2-1=3 см ²

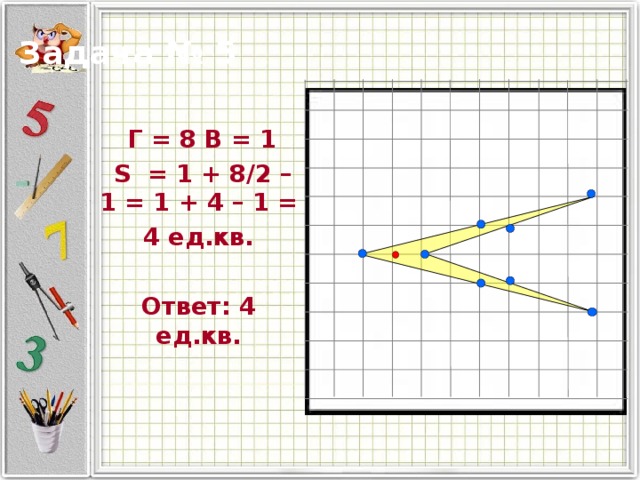
Задача № 5

Г = 8 В = 1

S = 1 + 8 / 2 – 1 = 1 + 4 – 1 =

4 ед.кв.

Ответ: 4 ед.кв.

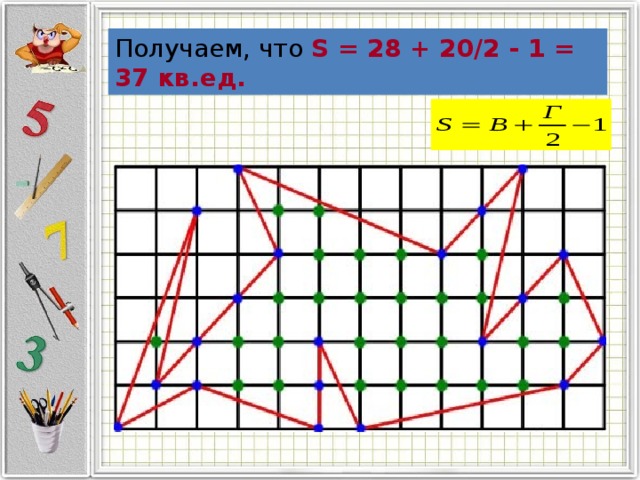
ФОРМУЛА ПИКА

Получаем, что S = 28 + 20/2 — 1 = 37 кв.ед.

Площадь кольца равна разности площадей внешнего и внутреннего кругов. R внешнего круга равен 2,9 ед., r внутреннего круга равен 2ед.

Следовательно,

S кольца= 3,14*2,9*2,9-3,14*2*2=

3,14(2,9*2,9-2*2)=3,14*(8,41-4) =

3,14*4,41= 13,87 ед.кв.

По формуле Пика площадь большого круга 21+16/2-1=28 ед.кв., а площадь маленького круга 9+12/2-1=14 ед.кв. Следовательно, площадь S кольца равна 28-14= 14ед.кв .

Для вычисления площади многоугольника нужно знать всего одну формулу:

S = В + Г/2 — 1 — формулу Пика.

Формула Пика проста для запоминания.
Формула Пика удобна и проста в применении.
Многоугольник, площадь которого необходимо вычислить, может быть любой формы.

В процессе исследования в 9 и 11 классах МКОУ СОШ № 3 был проведен практический эксперимент: решить задачи по нахождению площади многоугольника, изображенного на клетчатой бумаге.

Класс разделил на две группы. Учащиеся первой группы решали задачи по формулам геометрии, а учащиеся второй группы при решении использовали формулу Пика.

Решали по формулам

Решали по формуле Пика

Повышенный интерес к решению.
Плотность занятия.
Работоспособность учащихся.
Практически нет вычислительных ошибок.

Допущены вычислительные ошибки.
Затруднения в использовании нужных формул.

Источник

Грибановский муниципальный район

Воронежской области

Муниципальные педагогические чтения «Киселёвские чтения – 11»

«Формула Пика для нахождения площади многоугольника»

Подготовила: Табакова Ольга Николаевна

учитель МКОУ Верхнекарачанской СОШ

2021 г.

«Геометрия есть знание величин,

фигур и их границ,

а также отношений между ними

и производимых над ними операций,

разнообразных положений и движений»

Диа́дох Прокл

В 21 веке, некоторым детям, порой сложно запомнить огромное количество информации, поступающей каждый день в школе, и даже вызубренные формулы по математике, которые используются для нахождения площади различных фигур, будь то треугольник, параллелограмм или трапеция, часто забываются.

Задание, нахождение площади многоугольника, нарисованного на клетчатой бумаге очень интересное, увлекательное. Казалось бы, что увлекательного можно найти на клетчатой плоскости, то есть, на бесконечном листке бумаги, расчерченном на одинаковые квадратики? Оказывается, задачи, связанные с бумагой в клеточку, достаточно разнообразны. Мы знаем разные способы выполнения таких заданий: способ достраивания, способ разбиения и др. Одним из таких способов является формула Пика для нахождения площади многоугольника.

Актуальность данной темы заключается в том, чтобы помочь выпускникам 9-ых и 11-х классов подготовиться к сдаче ОГЭ и ЕГЭ по математике.

Немного истории:

Георг Александр Пик

(10. 09. 1859 – 13. 07. 1942)

Георг Александр Пик – австрийский математик. Родился Георг Пик в еврейской семье Он был одарённым ребёнком, его обучал отец, возглавлявший частный институт. До одиннадцати лет Георг получал образование дома (с ним занимался отец), а затем поступил сразу в четвёртый класс гимназии. В шестнадцать лет Пик сдал выпускные экзамены и поступил в университет в Вене. Уже в следующем году Пик опубликовал свою первую работу по математике. После окончания университета в 1879 году он получил право преподавать математику и физику. В 1880 году Пик защитил докторскую диссертацию, а в 1881 году получил место ассистента на кафедре физики Пражского университета. В 1888 году он был назначен экстраординарным профессором математики, затем в 1892 году в Немецком университете в Праге был назначен ординарным профессором (полным профессором).

Круг математических интересов Пика был чрезвычайно широк. В частности, им написаны работы в области функционального анализа и дифференциальной геометрии, эллиптических и абелевых функций, теории дифференциальных уравнений и комплексного анализа, всего более 50 тем. С его именем связаны матрица Пика, интерполяция Пика — Неванлинны, лемма Шварца — Пика.

Широкую известность получила открытая им в 1899 году теорема Пика для расчёта площади многоугольника. Эта теорема оставалась незамеченной в течение некоторого времени, однако в 1949 году польский математик Гуго Штейнгауз включил теорему в свой знаменитый «Математический калейдоскоп». С этого времени теорема Пика стала широко известна.

Теорема привлекла довольно большое внимание и начала вызывать восхищение своей простотой и элегантностью.

В Германии эта теорема включена в школьные учебники.

Когда нацисты вошли в Австрию 12 марта 1938 года, он вернулся Прагу. В марте 1939 года нацисты вторглись в Чехословакию. 13 июля 1942 года Пик был депортирован в созданный нацистами в северной Чехии лагерь Терезиенштадт, где умер две недели спустя в возрасте 82 лет.

Формула Пика.

, где

S- площадь многоугольника

В-количество узлов сетки, лежащих внутри многоугольника;

Г-количество узлов сетки, лежащих на границе многоугольника.

Основное условие для применения формулы Пика: у многоугольника, изображённого на клетчатой бумаге (решётке), должны быть только целочисленные вершины, то есть они обязательно должны находиться в узлах решётки. ( узел –это пересечение клеток ).

В -7 узлов

Г- 8 узлов

Формула Пика универсальна, по ней можно вычислить площадь любого многоулольника на клетчатой бумаге.

В-15 узлов

Г-4 узла

Свавним различные способы вычисления площади многоугольника на клетчатой бумаге:

Задача 1. Найти площадь четырехугольника

Метод достраивания

Формула Пика

В- 32

Г- 4

Задача 2.

Метод разбиения на треугольники

Формула Пика

В- 28

Г-18

Сравнивая, полученные результаты, видно, что ответ получается одинаковый. Найти площадь фигуры по формуле Пика, оказалось быстрее и легче, ведь вычислений было меньше.

Таким образом, видно, что формула Пика имеет ряд преимуществ перед другими способами вычисления площадей многоугольников на клетчатой бумаге:

для вычисления площади многоугольника, нужно знать всего одну формулу:

формула Пика проста для запоминания;
формула Пика очень удобна и проста в применении;
многоугольник, площадь которого необходимо вычислить может быть любой, даже самой причудливой.

Вывод: вычисление площадей сложных фигур с помощью формулы Пика легче, чем вычисление методом достраивания и разбивания фигур на части, так как требуется меньше вычислений, а, следовательно, меньше времени.

Формула Пика — это настоящее спасение для тех учеников, которые так и не смогли выучить все формулы для вычисления площадей фигур, для тех, кто так и не уяснил до конца, как выполнить разбиение фигуры или дополнительное построение, чтобы подобраться к вычислению её площади «через знакомых».

С другой стороны, для тех, кто площадь многоугольника, изображённого на клетчатой бумаге, умеет находить с помощью вышеперечисленных приёмов, формула Пика послужит дополнительным инструментом, с помощью которого можно будет решить задачу ещё и этим способом (и тем самым проверить правильность своего предыдущего решения, сверив полученные ответы).

Источник

1

Решение заданий В3 Готовимся к ЕГЭ

2

Теорема Пика Пусть L число целочисленных точек внутри многоугольника, B количество целочисленных точек на его границе, S его площадь. Тогда справедлива формула Пика: S = L + B/2 – 1 Пример 1. Для многоугольника на рисунке L = 13 (красные точки), B = 6 (синие точки, не забудьте о вершинах!), поэтому S = /2 – 1 = 15 квадратных единиц. 1см

3

Теорема Пика Пример 2. L = 18 (красные точки), B = 10 (синие точки), поэтому S = /2 – 1 = 22 квадратных единиц. 1см

4

Площадь прямоугольного треугольника Пусть а и b катеты прямоугольного треугольника, c – гипотенуза, h – высота, проведенная из вершины прямого угла на гипотенузу, S его площадь. Тогда справедливы формулы: 2 1 S = ab a b 2 1 S = ch c h

5

Площадь произвольного треугольника Пусть а сторона треугольника, h а – высота, проведенная к этой стороне, S его площадь. Тогда справедлива формула: 2 1 S = ah a a haha a haha

6

Площадь параллелограмма Пусть а сторона параллелограмма, h а – высота, проведенная к этой стороне, S его площадь. Тогда справедлива формула: S = ah a a haha haha a

7

Площадь трапеции Пусть а и b основания трапеции, h – высота, S площадь трапеции. Тогда справедлива формула: b h 2 a + b S = h a b h a

8

Площадь четырехугольника Пусть d 1 и d 2 диагонали произвольного четырехугольника, α – угол между ними, S его площадь. Тогда справедлива формула: 2 1 S = d 1 d 2 sin α d2d2 d1d1 d2d2 d1d1

9

Площадь круга Пусть R радиус круга, d = 2R – диаметр, С = 2πR – длина окружности, S его площадь. Тогда справедливы формулы: S = πR 2 R d СdСd 4 1 S = πd2πd2 4 1 О

10

Площадь кругового сектора Пусть R радиус круга, α – градусная мера соответствующего центрального угла, S его площадь. Тогда справедлива формула: R πR2πR2 360 S = · α α О

11

Площадь кольца Пусть R радиус внешней окружности, r – радиус внутренней окружности, S его площадь. Тогда справедлива формула: О R r S = π(R 2 – r 2 )

12

Задания открытого банка задач 1. Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1см×1см. Ответ дайте в квадратных сантиметрах. Ответ: 10,5. Решение: 7 3 1см

13

Задания открытого банка задач 2. Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1см×1см. Ответ дайте в квадратных сантиметрах. Ответ: 16. Решение: 8 4 1см haha

14

Задания открытого банка задач 3. Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1см×1см. Ответ дайте в квадратных сантиметрах. Ответ: 12. Решение: 8 1см haha 3

15

Задания открытого банка задач 4. Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1см×1см. Ответ дайте в квадратных сантиметрах. Ответ: 12. Решение: 4 6 1см haha

16

Задания открытого банка задач 5. Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1см×1см. Ответ дайте в квадратных сантиметрах. Ответ: 12. Решение: 3 8 1см haha

17

Задания открытого банка задач 6. Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1см×1см. Ответ дайте в квадратных сантиметрах. Ответ: 33. Решение: 1см

18

Задания открытого банка задач 7. Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1см×1см. Ответ дайте в квадратных сантиметрах. Ответ: 15,5. Решение: 1см

19

Задания открытого банка задач 8. Найдите площадь квадрата, изображенного на клетчатой бумаге с размером клетки 1см×1см. Ответ дайте в квадратных сантиметрах. Ответ: 50. Решение: 1см 1 7 по теореме Пифагора: а а

20

Задания открытого банка задач 9. Найдите площадь прямоугольника, изображенного на клетчатой бумаге с размером клетки 1см×1см. Ответ дайте в квадратных сантиметрах. Ответ: 20. Решение: 1см 2 6 по теореме Пифагора: а b 1 3

21

Задания открытого банка задач 10. Найдите площадь ромба, изображенного на клетчатой бумаге с размером клетки 1см×1см. Ответ дайте в квадратных сантиметрах. Ответ: 16. Решение: 1см 4 8

22

Задания открытого банка задач 11. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1см×1см. Ответ дайте в квадратных сантиметрах. Ответ: 17,5. Решение: 1см 5 4 3

23

Задания открытого банка задач 12. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1см×1см. Ответ дайте в квадратных сантиметрах. Ответ: 8. Решение: 1см 6 4 8

24

Задания открытого банка задач 13. Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки 1см×1см. Ответ дайте в квадратных сантиметрах. Ответ: 30. Решение: 1см 5 4 8

25

Задания открытого банка задач Ответ: 36. Решение: 1см Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки 1см×1см. Ответ дайте в квадратных сантиметрах.

26

Задания открытого банка задач 15. Найдите площадь параллелограмма, изображенного на клетчатой бумаге с размером клетки 1см×1см. Ответ дайте в квадратных сантиметрах. Ответ: 28. Решение: 1см 7 4

27

Задания открытого банка задач 17. Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1см×1см. Ответ дайте в квадратных сантиметрах. Ответ: 25,5. Решение: 1см

28

Задания открытого банка задач Ответ: 13,5. Решение: (1 способ) 1см Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки 1см×1см. Ответ дайте в квадратных сантиметрах. 2 3

29

Задания открытого банка задач Ответ: 13,5. Решение: (2 способ) 1см Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки 1см×1см. Ответ дайте в квадратных сантиметрах S2S2 S3S3 S4S4

30

Задания открытого банка задач 19. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1см×1см. Ответ дайте в квадратных сантиметрах. Ответ: 51. Решение: 1см

31

Задания открытого банка задач 20. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1см×1см. Ответ дайте в квадратных сантиметрах. Ответ: 31. Решение: 1см

32

Задания открытого банка задач 21. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1см×1см. Ответ дайте в квадратных сантиметрах. Ответ: 33,5. Решение: 1см

33

Задания открытого банка задач 22. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1см×1см. Ответ дайте в квадратных сантиметрах. Ответ: 24. Решение: 1см

34

Задания открытого банка задач 23. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1см×1см. Ответ дайте в квадратных сантиметрах. Ответ: 14,5. 1см Решение:

35

Задания открытого банка задач 24. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1см×1см. Ответ дайте в квадратных сантиметрах. Ответ: 18. 1см 7 8 Решение: 3 2

36

Задания открытого банка задач 25. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1см×1см. Ответ дайте в квадратных сантиметрах. Ответ: 16. 1см Решение: (1 способ) Площадь четырехугольника (в том числе невыпуклого) равна половине произведения диагоналей на синус угла между ними. Диагонали данного четырехугольника являются взаимно перпендикулярными диагоналями квадратов со стороной 4. Поэтому длины диагоналей равны 4 2, а синус угла между ними равен 1. Тем самым, площадь данного четырехугольника равна

37

Задания открытого банка задач 26. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1см×1см. Ответ дайте в квадратных сантиметрах. Ответ: 16. 1см Решение: (2 способ) L = 15 (красные точки), B = 4 (синие точки), тогда по теореме Пика S = L + B/2 – 1 S = /2 – 1 = 16

38

Задания открытого банка задач 27. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1см×1см. Ответ дайте в квадратных сантиметрах. Ответ: 19,5. 1см Решение: (1 способ)

39

Задания открытого банка задач 28. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1см×1см. Ответ дайте в квадратных сантиметрах. Ответ: 19,5. 1см Решение: (2 способ) L = 16 (красные точки), B = 9 (синие точки), тогда по теореме Пика S = L + B/2 – 1 S = /2 – 1 = 19,5

40

Задания открытого банка задач 29. Найдите площадь S фигуры, изображенной на клетчатой бумаге с размером клетки 1см×1см. В ответе запишите S/π. Ответ: 11,25. Решение: 3 3 R по теореме Пифагора: 1см

41

Задания открытого банка задач 30. Найдите площадь S круга, считая стороны квадратных клеток равными 1. В ответе укажите S/π. Ответ: 5. Решение: по теореме Пифагора: 1см 2 R 1 О

42

Задания открытого банка задач 31. Найдите (в см 2 ) площадь S фигуры, изображенной на клетчатой бумаге с размером клетки 1см×1см. В ответе запишите S/π. Ответ: 13. Решение: по теореме Пифагора: 3 3 R 1см 1 2 r

43

Задания открытого банка задач 32. На клетчатой бумаге нарисованы два круга. Площадь внутреннего круга равна 12. Найдите площадь заштрихованной фигуры. Ответ: 180. Решение: R r

44

Задания открытого банка задач 33. На клетчатой бумаге нарисованы два круга. Площадь внутреннего круга равна 4. Найдите площадь заштрихованной фигуры. Ответ: 21. Решение: R r

45

Задания открытого банка задач 34. На клетчатой бумаге нарисованы два круга. Площадь внутреннего круга равна 9. Найдите площадь заштрихованной фигуры. Ответ: 16. Решение: R r

46

Задания открытого банка задач 35. На клетчатой бумаге нарисован круг площадью 93. Найдите площадь заштрихованного сектора. Ответ: 31. Решение: R Найдем величину смежного с центральным угла α : О С М α Значит, круговой сектор имеет величину: 180º 60º = 120º, что составляет 1/3 часть круга R

47

Задания открытого банка задач 36. На клетчатой бумаге изображён круг. Какова площадь круга, если площадь заштрихованного сектора равна 27? Ответ: 36. Решение: О

Источник

Научно-исследовательская работа «Формула Пика»

Авторы
Руководители
Файлы работы
Наградные документы

Рассохина Е.О. 1

1МАОУ СОШ №15 г. Челябинска

Васильева И.В. 1

1МАОУ СОШ №15, г. Челябинска

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF

“Если вы хотите научиться плавать,

то смело входите в воду,
а если хотите научиться решать задачи,

то решайте их”.
Д. Пойя

Введение

Размышляя над какой-то задачей, мы начинаем увлекаться математикой. Многие ученики сталкиваются с задачами на нахождение площади треугольника, параллелограмма, многоугольника и других геометрических фигур по рисунку на клетчатой бумаге. Такие задачи чаще всего встречаются в ВПР по математике, а также они есть в контрольно-измерительных материалах ОГЭ и ЕГЭ. Применяя правила и теоремы из геометрии, ученик может запутаться или забыть, да и к тому же уходит много времени на дополнительное построение, а в условиях экзамена дорога каждая минута. Чтобы не тратить много усилий, времени и не вспоминать впопыхах теоремы, аксиомы, правила, существует теорема Пика, с помощью которой можно без проблем и траты времени вычислить площадь фигуры, расположенной на клетчатой бумаге. Но в чём же заключается особенность таких задач, какие методы и приёмы используются для решения задач на клетчатой бумаге?

Актуальность: Выбор темы проекта не случаен. Способы нахождения площади многоугольника, нарисованного на клетчатой бумаге, очень интересная и актуальная тема, особенно, при подготовке к экзаменам. При решении задач по математике и геометрии часто встречаются задачи, где нужно вычислить площадь фигур. Если фигура сложная, то её площадь находить довольно долго одним из способов: либо достроим до известной фигуры, либо разделим на фигуры.

Гипотеза: мы считаем, что вычисление площадей сложных фигур с помощью формулы Пика легче, чем вычисление методом достраивания и разбивания фигур на части и его может освоить каждый школьник.

Объект исследования: формула Пика для вычисления площадей многоугольников.

Предмет исследования: применение формулы Пика при решении задач, на нахождение площади фигур, изображённых на клетчатой бумаге.

Таким образом, целью моего исследования является: донести и объяснить материал о Формуле Пика учащимся 8-9 классам; доказать рациональность использования формулы Пика при решении задач на нахождение площади фигур, изображённых на клетчатой бумаге. Изучение данной темы поможет лучше подготовиться к олимпиадам и экзаменам.

Задачи:

1. Изучить методы вычисления площадей сложных фигур на клетчатой бумаге.

2. Научиться применять формулу Пика для вычисления площадей различных фигур.

3. Сделать видео разбор для учащихся старших классов.

4. Сравнить и проанализировать результаты исследования проведенных среди старшеклассников.

5. Донести учащимся рекомендации по применению формулы Пика при решении задач ОГЭ и ЕГЭ.

Методы: системный анализ; обобщение; сравнение; поиск.

Глава 1. Теоретическая часть

1.1. Методы вычисления площадей

В процессе изучения математики, мы заметили, что площади одних и тех же фигур можно находить различными способами. В быту мы часто сталкиваемся с задачами нахождения площади. Например, высчитать площадь стен, на которые необходимо наклеить обои, или вычислить площадь напольного покрытия. Вычисление площади квадрата, прямоугольника и прямоугольного треугольника не вызвало у нас затруднений.

В жизни очень часто мы сталкиваемся с тем, что нам приходится находить площадь геометрической фигуры неправильной формы. Как это сделать?

Наверное, проще всего разбить его на прямоугольные треугольники и прямоугольники, площади которых нетрудно вычислить по формулам.

Способы нахождения площадей фигур на клетчатой бумаге.

Площадь фигуры как сумма площадей ее частей
Найти площадь фигуры №1 на рисунке 1 (клетки размером 1х1 см). Разбиваем данную фигуру на четыре части, и находим площадь каждой части. Затем складываем все части, и получаем площадь данной фигуры.

Рис 1. Фигура №1

Разобьем многоугольник на четыре геометрические фигуры:

S=S₁+ S₂+ S₃+S₄

Площадь прямоугольного треугольника находится S₁= ½ · 5 · 1 = 2,5 см²;

Площадь прямоугольника находится S₂=4·2=8 см²

Площадь прямоугольного треугольника находится S₃= ½ · 1· 2= 1 см²

Площадь прямоугольного треугольника находится S₄= ½ · 2 · 4= 4 см²

S= 2,5+8+1+4= 15,5 см².

Ответ: 15,5 см^2.

Площадь фигуры как часть площади прямоугольника

Найти площадь фигуры на рисунке 2 фигура №2 (клетки размером 1х1см). Опишем около данной фигуры прямоугольник. Из площади прямоугольника (в данном случае квадрата) вычтем площади полученных фигур:

Рис. 2. Фигура №2

S= Sпрям. – S₁ – S₂; Sпрям. =5^.5=25 см²; S₁= ½ ^.3^.1=1,5 см²; S₂= ½ ^.4^.5=10 см²;

S= 25 − 1,5 − 10=13,5 см².

Ответ: 13,5 см².

Вывод: анализ показал, что вычислять площади фигур «достраиванием» или «разбиением» долгий процесс и требует большого количество промежуточных действий. Оказывается, есть другой способ для вычисления площади фигур на клетчатой бумаге, используя Формулу Пика.

1.2. Формула Пика

Формула Пика (или теорема Пика) — классический результат комбинаторной геометрии и геометрии чисел, согласно которому площадь многоугольника с целочисленными вершинами равна:

S = В + Г : 2 — 1

Где В — количество целочисленных точек внутри многоугольника, а Г — количество целочисленных точек на границе многоугольника. Историю открытия формулы Пика можно посмотреть в приложении А.

Многоугольник без самопересечений называется решётчатым, если все его вершины находятся в точках с целочисленными координатами в декартовой системе координат.

Теорема Пика. Нахождение площади решётчатого многоугольника (Рис.3)

S = В + Г : 2 — 1, где В — к-во целых точек внутри многоугольника, Г — к-во целых точек на границе многоугольника. В = 7, Г = 8, S = В + Г : 2 — 1 = 10

Рис. 3. Четырехугольник

Проведем сравнительный анализ нахождения площади многоугольника тремя разными способами (Таблица 1). Из таблицы видно, что самым рациональным и быстрым способом решения является формула Пика, в других способах используется 8 и 9 действий, а значит, вероятность допустить ошибку увеличивается во много раз.

Таблица 1

Нахождения площади геометрической фигура разными методами

Методы решения
Метод достраивания до прямоугольника	Метод разделения на геометрические фигуры	Формула Пика

S₁ = 4 ^. 7 – ((4 ^.7 : 2) + (2 ^.4 : 2)) = =28 – 18 = 10 см.² S₂ = 2 ^.1 : 2 = 1 см.² S₃ = 5 ^.1 : 2 = 2,5 см.² S₄ = 5 ^. 3 = 15 см.² S₅ = 2 ^.3 : 2 = 3 см.² S₆ = 3 ^.3 : 2 = 4,5 см.² S₇ = 2 ^.3 : 2 = 3 см.² S_Ф = S₁ + S₂ + S₃ + S₄ + S₅ + S₆ + S₇ 10 + 1 + 2,5 + 15 + 3 + 4,5 + 3 = =39см.² Ответ: 39 см.²	S₁= (4 ^.5) : 2 = 10 см.² S₂= (1 ^.2) : 2 = 1 см.² S₃= ( 1^.5) : 2 = 2,5 см.² S₄= 3 ^.5 = 15 см.² S₅= ( 2^.3 ) : 2 = 3 см.² S₆= ( 3^.3) : 2 = 4,5 см.² S₇= ( 2^.3 ) : 2 = 3 см.² S_ф= 10 + 1+ 2,5 + 15 + 3 + +4,5 + 3 = 39 см.² Ответ :S_ф= 39 см.²	Г=10 (синие) В=35 (красные) S = 35 + 10:2-1 = 39

Глава 2. Практическая часть

2.1. Создание видеоуроков

Так как тема формула Пика не изучается в курсе геометрии 7-9 класса, поэтому мной было принято решение записать видеоуроки, в которых я объясняю материал по данной теме. В итоге, мной были созданы три видеоурока на следующие темы:

Методы нахождения площадей на клетчатой бумаге;

Формула Пика (теоретическая часть);

Формула Пика (практическая часть).

Видеоуроки размещены на моей странице сообщество в социальной сети Вконтакте https://vk.com/club199771244.

Рис. 1. Фрагменты видеоурока про методы нахождения площадей на клетчатой бумаге

Рис.2. Фрагменты видеоурока по теме «Формула Пика»

2.2. Педагогическое исследование

Мной был проведен эксперимент, в котором учащиеся 9 класс школы № 15 в течение 10 минут должны были решить как можно больше задач по нахождению площадей разных геометрических фигур на клетчатой бумаге (Приложение В). Критерии оценивая данной работы следующие:

«5» — от 9 до 10 правильно решенных задач;

«4» — от 7 до 8 правильно решенных задач;

«3» — от 5 до 6 правильно решенных задач;

Результаты выполнения данной работы показали, что у школьников 9 класса есть проблемы при вычислении площадей различных геометрических фигур. Они продемонстрировали незнание формул и плохо различают фигуры.

Затем мной на уроке геометрии для учащихся этого же класса были показаны снятые видеоуроки по теме «Формула Пика» и предложено выполнить второй вариант работы по нахождению площадей фигур на клетчатой бумаге. Результаты можно посмотреть в таблице 2.

Таблица 2

Сравнение и анализ результатов исследования

До изучения материала видеоурока	После изучения материала видеоурока
«2»	«3»	«4»	«5»	«2»	«3»	«4»	«5»
3	10	7	0	0	7	11	2

Сравнительный анализ показывает, что учащиеся 9 класса без особых проблем восприняли материал видеоурока и применили его при решении самостоятельной работы. Таким образом, можно сделать вывод, что формула Пика легко может применяться при решении задач, а также при подготовке к экзаменам. Соответственно, мой труд по созданию данного материала был оценен должным образом. В дальнейшем, мной планируется создание такого материала, который бы облегчил жизнь школьников при подготовке к экзаменам и размещение данного материала на страницах моего сообщества в социальной сети Вконтакте «Интересная математика» https://vk.com/club199771244, доступ к которому позволяет учащимся в любое время изучить и применить данный материал на практике.

Заключение

Любители головоломок увлекаются решением задач на клетчатой бумаге, прежде всего потому, что универсального метода решения таких задач не существует, и каждый, кто берётся за их решение, может в полной мере проявить свою смекалку, интуицию и способность к творческому мышлению, поскольку здесь не требуется глубокого знания геометрии. Вместе с тем, задачи на клетчатой плоскости не являются несерьёзными или бесполезными, они не так уж и далеки от серьёзных математических задач.

Формула Пика проста в понимании и удобна в применении. Во-первых, достаточно уметь считать, делить на 2, складывать и вычитать. Во-вторых, можно найти площадь и сложной фигуры, не затратив много времени. В-третьих, эта формула работает для любого многоугольника.

Недостаток в том, что Формула Пика применима только для фигур, которые нарисованы на клетчатой бумаге и вершины лежат на узлах клеток.

При выполнении нашей работы мы рассмотрели решение задач на вычисление площади многоугольников неправильной формы разными способами. Ознакомление учащихся с формулой Пика особенно актуально накануне сдачи ЕГЭ и ГИА. С помощью этой формулы можно без проблем решать большой класс задач, предлагаемых на экзаменах, — это задачи на нахождение площади многоугольника, изображённого на клетчатой бумаге.

Маленькая формула Пика заменит учащимся целый комплект формул, необходимых для решения таких задач. Формула Пика будет работать «одна за всех…»!

Таким образом, цель нашего исследования была выполнена в полном объеме, а именно, донести и объяснить материал о Формуле Пика учащимся 9 классам; доказать рациональность использования формулы Пика при решении задач на нахождение площади фигур на примере разбора трех методов. Реализованы следующие задачи:

1. Изучила методы вычисления площадей сложных фигур на клетчатой бумаге.

2. Научилась применять формулу Пика для вычисления площадей различных фигур.

3. Сделала видеоуроки для учащихся старших классов.

4. Сравнила и проанализировала результаты исследования проведенных среди старшеклассников.

5. Донесла учащимся рекомендации по применению формулы Пика при решении задач ОГЭ и ЕГЭ.

Список литературы

Васильев Н.Б. Вокруг формулы Пика. //Квант. — 1974.-№2, № 12.

Формула Пика http://turboreferat.ru/geometry/formula-pika/10094-52632-page1.html

Математика, которая мне нравится http://hijos.ru/2011/12/30/georg-aleksandr-pik-1859-1942/

Образовательный портал «Решу ЕГЭ» https://ege.sdamgia.ru

«Математические этюды» www.etudes.ru/ru/etudes/pick—theorem/

Дидактическая библиотека http://gorinalw.3dn.ru/OSNOVA/osnova-3-2013.pdf

И.В. Ященко.ОГЭ. Математика: типовые экзаменационные варианты: О-39 36 вариантов

М.: Издательство «Национальное образование», 2017. -240 с. — (ОГЭ. ФИПИ- школе).

Бунимович Е.А., Дорофеев Г.В., Суворова С.Б. и др. Математика. Арифметика. Геометрия.

5 класс: учебн. для общеобразоват. организаций с прил. на электрон. носителе -3-е изд.-М;Просвещение, 2014.- 223, с.: ил. — (Сферы).

Просмотров работы: 59

Источник

Чтобы уверенно решать задачи по геометрии — даже такие простые — необходимо выучить основные понятия и формулы.

Это формулы площадей фигур — треугольника (5 формул), параллелограмма, ромба, прямоугольника, произвольного четырехугольника, а также круга. Формулы для длины окружности, длины дуги и площади сектора. Для средней линии треугольника и средней линии трапеции.

Надо знать, что такое центральный и вписанный угол. Знать основные тригонометрические соотношения. В общем, учите основы планиметрии.

Больше полезных формул — в нашем ЕГЭ-Справочнике.

Смотри также материал: Как быстро выучить формулы

В этой статье — основные типы заданий №1 Базового ЕГЭ по математике. Задачи взяты из Банка заданий ФИПИ.

Вычисление длин отрезков, величин углов и площадей фигур по формулам

1. На клетчатой бумаге с размером клетки изображена трапеция. Найдите длину средней линии этой трапеции.

Средняя линия трапеции равна полусумме её оснований: $frac{AD+BC}{2}=frac{4+2}{2}=3.$

Ответ: 3.

2. Найдите величину угла ABC. Ответ дайте в градусах.

Величина вписанного угла alpha равна половине величины центрального угла, опирающегося на ту же дугу. Соединим точки А и С с центром окружности и проведем диаметры через точки А и С. Видим, что величина центрального угла АОС равна ${90}^{circ}.$ Тогда $angle alpha =frac{{90}^{circ}}{2}={45}^{circ}.$

Ответ: 45.

3. Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на $frac{sqrt{5}}{2}.$

Решение:

Проведем из точки В перпендикуляр к прямой ОА. Из прямоугольного треугольника ОВС по теореме Пифагора:

${sin alpha }={sin angle AOB}=frac{4}{2sqrt{5}}=frac{2}{sqrt{5}}.$ Осталось умножить найденное значение синуса на $frac{sqrt{5}}{2}.$

$frac{2}{sqrt{5}}cdot frac{sqrt{5}}{2}=1$

Ответ: 1.

4. Найдите площадь ромба, изображенного на клетчатой бумаге с размером клетки Ответ дайте в квадратных сантиметрах.

Самый простой способ — воспользоваться формулой площади ромба, выраженной через его диагонали:

, где d_1 и d_2 — диагонали.

Получим:

Ответ: 12.

5. Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки Ответ дайте в квадратных сантиметрах.

Площадь трапеции равна произведению полусуммы оснований на высоту:

Основания нашей трапеции равны 4 и 8, а высота равна боковой стороне (поскольку трапеция прямоугольная), то есть 3 см. Площадь трапеции

Ответ: 18.

Нахождение площадей многоугольников сложной формы

А что делать, если надо найти не площадь трапеции или треугольника, а площадь какой-либо сложной фигуры? Есть универсальные способы! Покажем их на примерах из банка заданий ФИПИ и на авторских задачах.

6. Как найти площадь нестандартной фигуры? Например, произвольного четырёхугольника? Простой приём — разобьём эту фигуру на такие, о которых мы всё знаем, и найдем её площадь — как сумму площадей этих фигур.

Разделим этот четырёхугольник горизонтальной линией на два треугольника с общим основанием, равным . Высоты этих треугольников равны и . Тогда площадь четырёхугольника равна сумме площадей двух треугольников: .

Ответ: 12,5 .

7. В некоторых случаях площадь фигуры можно представить как разность каких-либо площадей.

Не так-то просто посчитать, чему равны основание и высота в этом треугольнике! Зато мы можем сказать, что его площадь равна разности площадей квадрата со стороной и трёх прямоугольных треугольников. Видите их на рисунке? Получаем: .

Ответ: 10,5 .

Многие репетиторы рекомендуют в таких задачах пользоваться формулой Пика. В ней нет необходимости, однако эта формула довольно интересна.

Согласно формуле Пика, площадь многоугольника равна В+Г/2-1

где В — количество узлов внутри многоугольника, а Г — количество узлов на границе многоугольника.

Узлами здесь названы точки, в которых пересекаются линии нашей клетчатой бумаги.

Посмотрим, как решается задача 7 с помощью формулы Пика:

Синим на рисунке отмечены узлы внутри треугольника. Зеленым — узлы на границе.

Аккуратно посчитав те и другие, получим, что В = 9, Г = 5, и площадь фигуры равна S = 9 + 5/2 — 1 = 10,5.

Выбирайте — какой способ вам больше нравится.

8. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки

Такой четырехугольник получится, если от квадрата размером отрезать 2 прямоугольника и 4 треугольника. Найдите их на рисунке.

Площадь каждого из больших треугольников равна $frac{1}{2}cdot 3cdot 2=3.$

Площадь каждого из маленьких треугольников равна $frac{1}{2}cdot 1cdot 2=1.$

Тогда площадь четырехугольника

9. Авторская задача. Найдите площадь закрашенной фигуры, изображенной на клетчатой бумаге с размером клетки

Решение:

На рисунке изображен ромб с вырезанным из него квадратом.

Площадь ромба равна половине произведения его диагоналей.

Площадь вырезанного квадрата равна 4.

Площадь фигуры равна 36 — 4 = 32.

Ответ: 32.

Площадь круга, длина окружности, площадь части круга

Длина дуги во столько раз меньше длины окружности, во сколько раз ее градусная мера меньше, чем полный круг, то есть 360 градусов.

Площадь сектора во столько раз меньше площади всего круга, во сколько раз его градусная мера меньше, чем полный круг, то есть 360 градусов.

10. Иногда в задании надо найти площадь не всей фигуры, а её части. Обычно речь здесь идет о площади сектора — части круга.Найдите площадь сектора круга радиуса , длина дуги которого равна .

На этом рисунке мы видим часть круга. Площадь всего круга равна , так как R=1 . Остается узнать, какая часть круга изображена. Поскольку длина всей окружности равна (так как R=1 ), а длина дуги данного сектора равна , следовательно, длина дуги в раз меньше, чем длина всей окружности. Угол, на который опирается эта дуга, также в раз меньше, чем полный круг (то есть 360 градусов). Значит, и площадь сектора будет в раз меньше, чем площадь всего круга.

Ответ: .

11. На клетчатой бумаге нарисован круг площадью 2,8. Найдите площадь закрашенного сектора.

На рисунке изображен сектор, то есть часть круга. Но какая же это часть? Это четверть круга и еще $frac{1}{8}$ круга, то есть $frac{3}{8}$ круга.

Значит, нам надо умножить площадь круга на $frac{3}{8}$ . Получим:

$frac{3}{8}cdot 2,8 =1,05$

Ответ: 1,05.

12. На клетчатой бумаге изображены два круга. Площадь внутреннего круга равна 9. Найдите площадь закрашенной фигуры.

Площадь фигуры равна разности площадей двух кругов, один из которых расположен внутри другого. По условию, площадь внутреннего круга равна 9. Радиус внешнего круга относится к радиусу внутреннего как 4 к 3. Площадь круга равна pi R^2 , то есть пропорциональна квадрату радиуса. Значит, площадь внешнего круга в ${frac{4}{3}}^2 = frac{16}{9}$ раза больше площади внутреннего и равна 16. Тогда площадь фигуры равна 16 — 9 = 7.

Ответ: 7.

Задачи на координатной плоскости

13. Найдите площадь четырехугольника, вершины которого имеют координаты (4;2), (8;4), (6;8), (2;6).

Заметим, что этот четырехугольник — квадрат. Сторона квадрата a является гипотенузой прямоугольного треугольника с катетами, равными 2 и 4. Тогда

Ответ: 20

14. Найдите площадь четырехугольника, вершины которого имеют координаты

На рисунке изображен параллелограмм (четырехугольник, имеющий две пары параллельных сторон). Площадь параллелограмма равна произведению основания на высоту. Основание равно 2, высота 8, площадь равна 16.

Ответ: 16.

Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Геометрия. Применение формул. Задача 1 Базового ЕГЭ по математике» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.

Публикация обновлена:
09.03.2023

Источник