Всего: 8 1–8
Добавить в вариант
В выпуклом четырёхугольнике ABCD известны стороны и диагональ: AB = 3, BC = CD = 5, AD = 8, AC = 7.
а) Докажите, что вокруг этого четырёхугольника можно описать окружность.
б) Найдите BD.
Источник: ЕГЭ по математике 11.04.2018. Досрочная волна, резервная волна. Запад (часть С)
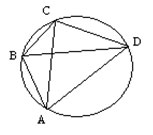
Равносторонний треугольник АВС вписан в окружность. На окружности отмечена точка М, не совпадающая ни с одной из точек А, В и С.
а) Докажите, что расстояние от точки М до одной из вершин треугольника равно сумме расстояний до двух других вершин.
б) Найдите периметр четырехугольника с вершинами в точках А, В, С и М, если известно, что площадь равна а радиус окружности равен
Источник: А. Ларин: Тренировочный вариант № 104.
На стороне АВ треугольника АВС отмечена точка М, отличная от вершин, что МС = АС. Точка Р симметрична точке А относительно прямой ВС.
а) Докажите, что около четырехугольника ВМСР можно описать окружность.
б) Найдите длину отрезка МР, если известно, что АВ = 6, ВС = 5, СА = 3.
Источник: А. Ларин: Тренировочный вариант № 180.
Из точки M, взятой на окружности с центром в точке О, на диаметры AB и СD опущены перпендикуляры MK и MP соответственно.
а) Докажите, что существует точка, одинаково удалённая от точек M, О, P, K.
б) Найдите площадь треугольника MKP, если известно, что ∠MKP = 30°, ∠AOC = 15°, а радиус окружности равен 4.
Источник: А. Ларин: Тренировочный вариант № 140.
Четырехугольник ABCD со взаимно перпендикулярными диагоналями АС и BD вписан в окружность.
а) Докажите, что квадрат диаметра окружности равен сумме квадратов противоположных сторон четырехугольника.
б) Найдите площадь четырехугольника ABCD, если известно, что
Источник: А. Ларин: Тренировочный вариант № 163.
В трапеции ABCD с основаниями ВС и AD углы ABD и ACD прямые.
а) Докажите, что АВ = CD.
б) Найдите AD, если AB = 2, BC = 7.
Источник: ЕГЭ по математике 01.06.2018. Основная волна. Вариант 991 (C часть). Он же: вариант 751 (резервная волна 25.06.2018), Задания 16 (С4) ЕГЭ 2018
Параллелограмм и окружность расположены так, что сторона AB касается окружности, CD является хордой, а стороны DA и BC пересекают окружность в точках P и Q соответственно.
а) Докажите, что около четырехугольника ABQP можно описать окружность.
б) Найдите длину отрезка DQ, если известно, что AP = a, BC = b, BQ = c.
Источник: Пробный экзамен Санкт-Петербург, 11.04.2017. Вариант 1., Пробный экзамен Санкт-Петербург, 11.04.2017. Вариант 1. (C часть).
Окружность проходит через вершины A и B параллелограмма ABCD, пересекает стороны AD и BC в точках M и N соответственно и касается стороны CD.
а) Докажите, что точки C, D, M и N лежат на одной окружности.
б) Найдите длину отрезка AD, зная, что BM = a, MD = b, NC = c.
Источник: Пробный экзамен Санкт-Петербург, 11.04.2017. Вариант 2., Пробный экзамен Санкт-Петербург, 11.04.2017. Вариант 2. (C часть).
Всего: 8 1–8
(Решение Leonid Argail) 2 способ) через теорему Птолемея — Решение Елены Ильиничны Хажинской
1. Метод проведения вспомогательной
окружности.
Проведение вспомогательной окружности около
четырехугольника позволяет установить
равенство вписанных углов, либо использовать
свойства четырехугольника, вписанного в
окружность и свойства описанной окружности.
Задача 1. В треугольнике АВС
проведены биссектрисы из вершин А и С. Пусть К и L
– основания перпендикуляров, опущенных из
вершины В на эти биссектрисы.
Докажите, что прямая КL параллельна АС. [3]
Задача 2. Внутри острого угла,
равного ,
взята точка М, удаленная от сторон угла на
расстояния k и n.
Найти расстояние от вершины угла до точки М.
[3]
Задача 3. Дан остроугольный
треугольник АВС. На сторонах АВ и ВС во внешнюю
сторону построены равные прямоугольники АВМN и
LВСК так, что АВ = КС.
Докажите, что прямые АL, NК и МС пересекаются
в одной точке. [3]
Задача 4. В треугольнике NMF
медиана МА делит угол М так, что NMА = 20° и
АMF= 30°. Из точки А опущены
перпендикуляры АК и АС на стороны NM и MF
соответственно.
Вычислить площадь треугольника АКС, если АК
= 5 и КС = 7. [2]
Задача 5. Пусть А1 , В1
, С1 – точки касания вписанной
окружности остроугольного треугольника АВС со
сторонами ВС, АС, АВ соответственно. Обозначим
через Н1 и Н ортоцентры треугольников ВС1А1
и СА1В1 соответственно.
Доказать, что четырехугольник ВН1НС —
вписанный. [3]
2. Применение теоремы Птолемея
Теорема Птолемея: В любом вписанном
четырехугольнике произведение диагоналей равно
сумме произведений противоположных сторон, т.е.
АС•ВD=AB•CD+BC•AD.
Задача 1. В окружность вписан
равнобедренный треугольник АВС (АВ = ВС). На дуге
АВ взята произвольная точка К и соединена
хордами с вершинами треугольника.
Доказать, что АК • КС = АВ2 – КВ2.
[3]
Задача 2. Длины катетов
прямоугольного треугольника равны а и в. На его
гипотенузе во внешнюю сторону треугольника
построен квадрат, одна из сторон которого
совпадает с гипотенузой.
Найдите расстояние от вершины прямого угла
треугольника до центра квадрата. [3]
Задача 3. В равнобочной
трапеции основание АD равно диагонали АС.
Известно, что САD
= СDМ, где М –
середина ВС.
Найти углы трапеции. [1]
Задача 4. Вокруг
равностороннего треугольника АВС описана
окружность радиуса R и на дуге ВС окружности
взята точка М так, что дуга ВС делится этой точкой
в отношении 1:3, считая от вершины В.
Найти расстояние АМ. [1]
Задача 5. Доказать, что в
равнобочной трапеции произведение длин
оснований равно разности квадратов диагонали и
боковой стороны. [2]
Используемая литература
1. И.Ф. Шарыгин. Факультативный курс по
математике для 10 кл. М., Просвещение, 1989 г.
2. О.Ю. Черкасов. Планиметрия на вступительном
экзамене, “Московский лицей”, 1996г.
3. Задачи математических конкурсов и олимпиад
2007-2010 гг.
4. Теорема Птолемея
Клавдий Птолемей (ок.100-ок.178)– древнегреческий астроном, математик, географ. Он ввёл понятия широты и долготы местности. Автор «Великого математического построения астрономии в 13 книгах» («Альмагест»), в котором, в частности, изложены сведения по прямолинейной и сферической тригонометрии и дана теорема о выпуклом четырёхугольнике, вписанном в окружность. Благодаря теореме он составил таблицу хорд, которой воспользовался для астрономических вычислений.
Сумма произведений двух пар противоположных сторон вписанного четырёхугольника равна произведению его диагоналей
Запишем теоремы синусов для треугольников АВD, АВС, ВСD:
, , , , , .
Теорема будет доказана, если будет показано равенство тригонометрических выражений, получившихся при подстановке в формулу после сокращения на :
и . После тригонометрических преобразований левой и правой части и получаем тождественное равенство.
Другое доказательство прямой теоремы связано с небольшим дополнительным построением. Проведём отрезок АQ так, чтобы углы QАD и ВАС были равны. Из подобия треугольников QАD и ВАС следует равенство или . Из подобия треугольников QАВ и АСD следует равенство или .
Сложив равенства , получаем .
Покажем, как Птолемей составил таблицу хорд. Допустим, дан диаметр окружности d и хорды двух дуг: а и b.
Найдём хорду разности этих дуг.
Запишем теорему с учётом того, что треугольники МАС и МВС прямоугольные:
, откуда получаем формулу для хорды . Следует заметить, что . Разделив дугу пополам, можно найти хорду половины дуги. Птолемей установил длину хорды дуги 0,50 и, пользуясь этим, вычислил хорды всех дуг с шагом в 0,50. Это были первые тригонометрические таблицы в истории математики.
Задачи на теорему Птолемея
- На окружности, описанной около равностороннего треугольника АВС, взята произвольная точка М, отличная от А, В и С. Доказать, что один из отрезков АМ, АВ, АС равен сумме двух других.
- В шестиугольнике АВСDЕF, вписанном в окружность, АС = СЕ = ЕА, . Найти периметр шестиугольника.
- Биссектриса угла А треугольника АВС пересекает описанную около треугольника окружность в точке D. Докажите, что .
5. Определение радиуса вневписанной окружности в треугольнике
Пусть в треугольнике АВС точка О – центр вневписанной окружности, точка Р – центр описанной окружности, Е – центр вписанной окружности, угол ВАС равен α, R – радиус описанной окружности, r – радиус вписанной окружности, ρ – радиус вневписанной окружности, M, F, D, H, K, Q – точки касания окружностей со сторонами треугольника или угла.
Запишем следующую систему равенств: . Из системы следует формула . Запишем теорему косинусов для стороны а:
Таким образом, и .
Можно получить формулу для r следующим образом: , , , следовательно
Воспользовавшись формулой для ρ несложно получить следующие равенства:
и .
Теорема Мансиона
Отрезок, соединяющий центры вписанной и вневписанной окружностей треугольника, делится описанной окружностью пополам. Пауль Мансион – бельгийский математик, 1844-1919 г.
Пусть N – середина отрезка ЕО. Докажем, что в этом случае отрезок РN есть радиус описанной окружности. Итак, .
Вопрос от Юлии:
Подскажите, как можно решить задачу: В треугольнике MNP угол M равен 40 градусов, угол N равен 20 градусов, а MN-NP=8. Найти длину биссектрисы, проведенной из вершины угла P. Задача взята из вступительной работы по математике в 8 класс физико — математического лицея.
Решение репетитора по математике к задаче про биссектрису (Колпаков А.Н.):
Пусть NP=x, MN=x+8. Очевидно, что 



В треугольнике KNP снова по теореме синусов запишем:
Как и следовало ожидать, вся тригонометрия сокращается. Задача интересна тем, что имеет весьма красивое и простое решение (которое я показал) в противовес долгому и мучительному стандартному решению (через отрезок KN и теорему косинусов в треугольнике PKN).
Вопрос от Людмилы: Подскажите, как решить задачу: в равнобедренном треугольнике с углом альфа при основании высота, опущенная на основание, больше радиуса вписанного в треугольник круга на m. Основание треугольника равно? Спасибо.
Задача про высоту и радиус. Решение репетитора по математике.(Колпаков А.Н. )









Тогда 
Тогда
Вопрос репетитору по математике от Жанат:
Пожалуйста. Помогите решить задачу на площадь по геометрии. Прошу вас…
В треугольнике АВС AB=AC=13; AC=24. На его стороне АС дана точка D так, что CD=6. Найдите
Решение репетитора (Колпаков А.Н.).
Найдем сначала площадь всего треугольника ABC. Есть возможность действовать или по формуле Герона 

Воспользуемся известным фактом: при равных высотах отношение площадей двух треугольников равно отношению их оснований
Вопрос от Роберта:
Здравствуйте! Помогите пожалуйста решить задачу из типовых вариантов ЕГЭ под номером C4 (задача представлена ниже).Треугольник ABC вписан в окружность. Ее радиус равен 12 см. Известно, что BC=4cм и AB = 6 см . Найдите AC.
Репетитор по математике использует теорему Птолемея (А.Н. Колпаков)
Самое быстрое и красивое решение задачи дает редкая, но в некоторых ситуациях незаменимая теорема Птолемея. Она есть у меня в справочном отделе сайта: если четырехугольник вписан в окружность, то сумма произведений его сторон равна произведению его диагоналей. У нас никакого, казалось бы, четырехугольника нет. Построим его. Дополнительное построение репетитора по математике будет следующим:


Применяем терему Птолемея:
Сокращая на 24 получим окончательно:
Комментарий репетитора о применении теоремы Птолемея: на ЕГЭ можно использовать любой известный в математике факт, не обязательно соответствующий программе 5-11 класса. Надо только на него не забыть сослаться при оформлении. Если нужно школьное решение — можно действовать через поиск углов A и C (по формуле 


Вопрос репетитору по математике от Светланы Ивановны:Уважаемый Александр Николаевич! Если Вам не трудно, помогите решить задачу: В трапеции АВСД сумма острых углов 90 градусов, меньшая диагональ ВД перпендикулярна основаниям ВС и АД. Найдите площадь трапеции, если основание АД = 2, СД = 18.
Репетитор о задаче с трапецией (А.Н. Колпаков)





У меня получился корень 
Тогда 

Вопрос репетитору от Артема Иванова.Треугольник KLM подобен треугольнику NPR.Докажите,что отношение длин медиан,проведенных из K и N,равно коэффициенту подобия треугольников. Помогите, пожалуйста, задача с контрольной. Я ученик 8 класса. Не из России.
Репетитор по математике о задаче про медианы.






Вопрос репетитору по математике от Тимерлана Селахова
Помогите с решениями этой задачи:
Решение (Колпаков А.Н.):
Треугольник ABD равнобедренный по определению (т.к. AB=DB по условию) и ВМ — медиана (т.к. АМ=DМ по условию). Следовательно ВМ — биссектриса и высота (по тереме о совпадении медианы с биссектрисой и высотой). Тогда 



Вопрос от Тамины. Помогите найти площадь большого прямоугольника, разделенного на 12 квадратов, если площадь закрашенного квадрата равна 1 кв.см.
Задача про закрашенный квадрат. Решение репетитора по математике:
Очевидно, что площадь пяти нижних квадратов равна 8 и длина прямоугольника ABCD равна 4 см. Пусть BE=x, тогда NK=4-2x и соответственно NP=NM=2-x 
4-2x=3 (2x-2)
откуда x=1,25. Следовательно
Pages: 1 2
Мы с вами разберем задания ЕГЭ, которые предлагаются на экзамене разработчиками самого ЕГЭ по математике И.В. Ященко, П.В. Семеновым и другими. Многие задания опубликованы на сайте «Решу ЕГЭ» и на сайте ФИПИ.
Хочу отметить, что для лучшего усвоения материала, я рекомендую вам выполнить домашнее задание, которое будет прикреплено к этой статье. Это будет небольшой набор задач с ответами для самостоятельного решения и самопроверки.
Итак, начнем. Задание № 1 по математике предполагает умение решать простейшие текстовые задачи, которые делятся на:
- задачи на вычисление;
- задачи на округление с избытком;
- задачи на округление с недостатком;
- задачи на проценты.
Начнем с задач на вычисление. Предлагаемые задачи на вычисления условно делятся на несколько типов, поэтому и наши с вами занятия будут разделены на части.
- Задачи на вычисление. Часть 1
- Задачи на вычисление. Часть 2
- Задачи на вычисление. Часть 3
Задачи на вычисление. Часть 1
Задача 1. Килограмм моркови стоит 40 рублей. Олег купил 2 килограмма моркови. Сколько рублей сдачи он должен получить со 100 рублей?
Решение.
Простейшая жизненная задача. Всегда представляйте себя. Вы покупаете морковь. У вас есть 100 рублей и вы купили 2 кг моркови.
Так как килограмм моркови стоит 40 рублей, то за 2 кг надо заплатить 80 рублей. То есть . Значит, сдачи Олег получит
рублей.
Ответ: 20 рублей.
Задача 2. Летом килограмм клубники стоит 80 рублей. Мама купила 1 кг 200 г клубники. Сколько рублей сдачи она получит с 500 рублей?
Решение.
Аналогичная задача. Отличается только тем, что надо граммы перевести в килограммы.
Напомню, что 1 кг = 1000 г. Тогда 1кг 200г = 1,2 кг. Как это можно сделать иначе? Можно сначала 1кг 200 г перевести в граммы, т.е. 1 кг 200 г = 1200 г, после этого 1200 : 1000 =1,2 (кг).
Теперь у нас есть 1,2 кг, а 1 кг стоит 80 рублей, значит, нам надо умножить . То есть мама заплатит 96 рублей за свою покупку. А сдача с 500 рублей составит 500 – 96 = 404 (рубля).
Ответ: 404
Задача 3. В квартире, где проживает Алексей, установлен прибор учёта расхода холодной воды (счётчик). 1 сентября счётчик показывал расход 103 куб. м воды, а 1 октября — 114 куб. м. Какую сумму должен заплатить Алексей за холодную воду за сентябрь, если цена 1 куб. м холодной воды составляет 19 руб. 20 коп.? Ответ дайте в рублях.
Решение.
Для решения этой задачи надо вспомнить, что месяцы сентябрь и октябрь идут друг за другом (кто не помнит, посмотрите календарь).
Далее, не надо бояться слов «куб.м.». Это просто единица измерения. Запись «куб.м.» и «м3» — одно и то же. В этой задаче, переводить в какую- либо другую единицу измерения кубические метры не надо. Единственное, что при выполнении действий, помним, что действия выполняем с одноименными величинами: рубли с рублями, кубические метры с кубическими метрами.
1) Итак, с 1 сентября по 1 октября прошел ровно один месяц. О чем нас и спрашивают в задаче.
1 сентября – 103 куб.м.
1 октября – 114 куб.м.
Значит, за полный месяц сентябрь было потрачено 114 – 103 = 11 (куб.м.) холодной воды. Акцент на «холодной воде» тоже делать не надо, для задачи это не принципиально.
2) Известно, что 1 куб.м. стоит 19 рублей 20 копеек. Здесь надо перевести копейки в рубли, так как в ответе нас спрашивают про рубли.
1 рубль – 100 копеек
x рублей – 20 копеек
Можно воспользоваться знанием пропорции (в верной пропорции произведение крайних членов равно произведению средних членов). А также помним, что в пропорции одноименные единицы измерения подписываем друг под другом.
Находим х из уравнения: , х=0,2.
Значит 20 копеек = 0,2 рубля. Но у нас еще есть 19 рублей. Тогда 19 рублей 20 копеек = 19 + 0,2 = 19,2 (руб.).
3) Тогда за 11 кубических метров (из пункта 2) будет заплачено
1 куб.м. – 19,2 руб
11 куб.м – х руб
Находим х из пропорции , х= 211,2 (руб)
Замечание. Хотя можно поступить и иначе (просто немного дольше). Можно рубли сначала перевести в копейки.
1 руб = 100 копеек. Значит 19 рублей = (коп). Тогда 19 рублей 20 коп = 1900 + 20 = 1920 (коп).
Дальше вычисления выполняем уже с копейками. Тогда пункт 4) будет таким:
1 куб.м. – 1920 коп
11 куб. м. – х коп
, x = 21 120 (коп)
Но на этом остановиться нельзя, так как в ответе требуется указать рубли. Надо 21 120 : 100 =211,2 (руб)
Ответ: 211,2
Подведем итог разбора задания 1 (часть1)
Итак, мы с вами выполнили разбор некоторых заданий ЕГЭ по математике (профильный уровень), которые встречаются в задании № 1 и теперь вы умеете решать простейшие задачи на вычисление. Вы наверняка заметили сами, что ничего сложного нет. А для закрепления знаний, я рекомендую вам обязательно выполнить задачи для самостоятельного решения. Калькулятором пользоваться нельзя. Тренируйтесь выполнять действия в столбик. Это важно.
Если у вас будут вопросы, пишите их в комментариях. Обязательно отвечу и помогу разобраться. Главное — не падать духом и не паниковать.
Успехов!
P.S. Задачи для самостоятельного решения и ответы к ним вы найдете на моем канале Telegram @egematem (через поиск) или по ссылке https://t.me/egematem
Добавляйтесь в группу Telegram для обсуждения и ответов на ваши вопросы.
Спасибо, что поделились статьей в социальных сетях
��������: 1 2 3 4 5 6 7 >> [����� �����: 34]
��������, ��� ���� ����ң��������� ������ � ����������, �� ����� ������������ ���� ���� ��� ��� ��������������� ������ ����� ������������ ���� ��� ����������.
� ������������ ABC ������� BC ����� ��������� ���� ������ ������. ����� ����� A � �������� B’, C’ ������ AB � AC ��������� ���������� Ω � � ��� �� ������ ������� ������������ ��������� �����������. ��������, ��� ���� �� ����� ������� �������� ������� I ��������� ���������� ������������ ABC.
������ 78539 |
���������: 4+ ������: 9,10 |
� ������������ ABC ������� BC ����� ��������� ���� ������ ������. ��������,
��� ����������� ���� A ��������������� �������, ������������ ������ ���������
� ��������� ����������� ������������.
��� ����������� ABC, ���ޣ� ������� BC ����� ��������� ���� ������ ������.
��������, ��� � ����� ������������ ������� A, �������� ������ AB � AC �
������ ��������� � ��������� ����������� ����� �� ����� ���������� (�������� � ������� 4 ��� 9 ������).
������ 55464 |
���������: 5- ������: 8,9 |
����� A1A2…An – ���������� ������������� � ��ޣ���� ������ ������, M – ������������ ����� �� ���� A1An ����������, ��������� ����� ��������������. ��������, ��� ����� ���������� �� ����� M �� ������ � ��ޣ����� �������� ����� ����� ���������� �� M �� ������ � ޣ����� ��������.
��������: 1 2 3 4 5 6 7 >> [����� �����: 34]