Теорема синусов решу егэ

в условии
в решении
в тексте к заданию
в атрибутах

Категория:

Атрибут:

Всего: 132    1–20 | 21–40 | 41–60 | 61–80 …

Добавить в вариант

Четырёхугольник ABCD вписан в окружность радиуса R = 10. Известно, что AB = BC = CD = 6.

а)  Докажите,что прямые BC и AD параллельны.

б)  Найдите AD.

Источник: ЕГЭ — 2018. Основная волна 01.06.2018. Вариант 402 (C часть)., Задания 16 (С4) ЕГЭ 2018

Стороны BC и CD квадрата ABCD являются сторонами равносторонних треугольников BCM и DCN соответственно, точки M и N лежат вне квадрата. Прямая AM пересекает BC в точке K.

а)  Докажите, что angle AMC=45 градусов .

б)   Найдите KN, если AB= корень из 8 плюс 3 корень из 3.

Источник: А. Ларин. Тренировочный вариант № 395.

На отрезке BD взята точка C. Биссектриса BL равнобедренного треугольника ABC с основанием BC является боковой стороной равнобедренного треугольника BLD с основанием BD.

а)  Докажите, что треугольник DCL равнобедренный.

б)  Известно, что косинус angle ABC= дробь: числитель: 1, знаменатель: 6 конец дроби . В каком отношении прямая DL делит сторону AB?

Источник: Типовые тестовые задания по математике, под редакцией И. В. Ященко 2016

В треугольнике ABC угол В прямой, точка М лежит на стороне АС, причем АМ : СМ= корень из 3:4. Величина угла АВМ равна 60 градусам, BM = 8.

а)  Найдите величину угла ВАС;

б)  Найдите расстояние между центрами окружностей, описанных вокруг треугольников ВСМ и ВАМ.

Источник: А. Ларин: Тренировочный вариант № 45.

В остроугольном треугольнике ABC, angle A=60 градусов. Высоты BN и CM треугольника ABC пересекаются в точке H. Точка O  — центр окружности, описанной около Delta ABC.

а)  Докажите, что AH=AO.

б)  Найдите площадь Delta AHO, если BC=6 корень из 3, angle ABC = 45 градусов.

Источник: Основная волна ЕГЭ по математике 29.05.2019. Вариант 405, Основная волна ЕГЭ по математике 29.05.2019. Вариант 409, Задания 16 (С4) ЕГЭ 2019

Дана трапеция ABCD с основаниями BC и AD. Точки M и N являются серединами сторон AB и CD соответственно. Окружность, проходящая через точки B и С, пересекает отрезки BM и CN в точках P и Q (отличных от концов отрезков).

а)  Докажите, что точки M, N, P и Q лежат на одной окружности.

б)  Найдите длину отрезка QN, если BC  =  4,5, AD  =  21,5, AB  =  26, CD  =  25, а угол CPD  — прямой.

Источник: ЕГЭ по математике 29.03.2019. Досрочная волна. Вариант 3 (только часть С)., Задания 16 (С4) ЕГЭ 2019

Угол C треугольника ABC равен 30°, D  — отличная от A точка пересечения окружностей, построенных на сторонах AB и AC как на диаметрах. Известно, что BD:DC  =  1:6. Найдите синус угла A.

Источник: ЕГЭ по математике 10.06.2013. Вторая волна. Центр. Вариант 602., Задания 16 (С4) ЕГЭ 2013

Угол C треугольника ABC равен 60°, D  — отличная от A точка пересечения окружностей, построенных на сторонах AB и AC как на диаметрах. Известно, что ВD : DC = 1 : 3. Найдите синус угла A.

Источник: ЕГЭ по математике 03.06.2013. Основная волна. Восток. Вариант 701.

Угол C треугольника ABC равен 60°, D  — отличная от A точка пересечения окружностей, построенных на сторонах AB и AC как на диаметрах. Известно, что ВD : DC = 1 : 4. Найдите синус угла A.

Источник: ЕГЭ по математике 03.06.2013. Основная волна. Восток. Вариант 702.

Четырёхугольник ABCD вписан в окружность радиуса R  =  8. Известно, что AB = BC = CD = 12.

а)  Докажите,что прямые BC и AD параллельны.

б)  Найдите AD.

Источник: ЕГЭ — 2018. Основная волна 01.06.2018. Вариант 401 (C часть)., Задания 16 (С4) ЕГЭ 2018

Дана трапеция ABCD с основаниями BC и AD. Точки M и N являются серединами сторон AB и CD соответственно. Окружность, проходящая через точки B и С, пересекает отрезки BM и CN в точках P и Q (отличных от концов отрезков).

а)  Докажите, что точки M, N, P и Q лежат на одной окружности.

б)  Найдите QN, если отрезки DP и PC перпендикулярны, AB  =  21, BC  =  4, CD  =  20, AD  =  17.

Источник: Досрочная волна ЕГЭ по математике 29.03.2019. Вариант 1, Задания 16 (С4) ЕГЭ 2019

Окружность проходит через вершины B и C треугольника ABC и пересекает AB и AC в точках C1 и B1 соответственно.

а)  Докажите, что треугольник ABC подобен треугольнику AB1C1.

б)  Найдите радиус данной окружности, если ∠A  =  45°, B1C1  =  6 и площадь треугольника AB1C1 в восемь раз меньше площади четырёхугольника BCB1C1.

Окружность проходит через вершины B и C треугольника ABC и пересекает AB и AC в точках C1 и B1 соответственно.

а)  Докажите, что треугольник ABC подобен треугольнику AB1C1.

б)  Найдите радиус данной окружности, если ∠A  =  135°, B1C1  =  10 и площадь треугольника AB1C1 в семь раз меньше площади четырёхугольника BCB1C1.

Окружность проходит через вершины В и С треугольника АВС и пересекает АВ и АС в точках С1 и В1 соответственно.

а)  Докажите, что треугольник АВC подобен треугольнику АВ1С1

б)  Вычислите радиус данной окружности, если angle A= 120 градусов, BC=10 корень из 7 и площадь треугольника АВ1С1 в три раза меньше площади четырёхугольника ВСВ1С1.

Окружность проходит через вершины В и С треугольника АВС и пересекает АВ и АС в точках С1 и В1 соответственно.

а)  Докажите, что треугольник АВC подобен треугольнику АВ1С1

б)  Вычислите радиус данной окружности, если angle A= 150 градусов, BC=5 корень из 5 и площадь треугольника АВ1С1 в четыре раза меньше площади четырёхугольника ВСВ1С1.

В треугольнике ABC угол A равен 120°. Прямые, содержащие высоты BM и CN треугольника ABC, пересекаются в точке H. Точка O  — центр окружности, описанной около треугольника ABC.

а)  Докажите, что AH  =  AO.

б)  Найдите площадь треугольника AHO, если BC = корень из 15 , angle ABC=45 градусов.

Источник: ЕГЭ по математике 27.03.2020. Досрочная волна. Вариант 1, Задания 16 ЕГЭ–2020

В треугольнике ABC угол A равен 120° . Прямые, содержащие высоты BM и CN треугольника ABC, пересекаются в точке H. Точка O  — центр окружности, описанной около треугольника ABC .

а)  Докажите, что AH  =  AO.

б)  Найдите площадь треугольника AHO, если BC = 3 , angle ABC=15 градусов.

Источник: ЕГЭ по математике 27.03.2020. Досрочная волна. Вариант 2

На гипотенузу AB прямоугольного треугольника ABC опустили высоту CH. Из точки H на катеты опустили перпендикуляры HK и HE.

а)  Докажите, что точки A, B, K и E лежат на одной окружности.

б)  Найдите радиус этой окружности, если AB = 12, CH = 5.

Высоты BB1 и CC1 остроугольного треугольника ABC пересекаются в точке H.

а)  Докажите, что ∠AHB1 = ∠ACB.

б)  Найдите BC, если AH  =  4 и ∠BAC  =  60°.

Источник: ЕГЭ по математике 05.06.2014. Основная волна. Запад. Вариант 302.

Всего: 132    1–20 | 21–40 | 41–60 | 61–80 …

Источник

6. Геометрия на плоскости (планиметрия). Часть II


1. Вспоминай формулы по каждой теме


2. Решай новые задачи каждый день


3. Вдумчиво разбирай решения

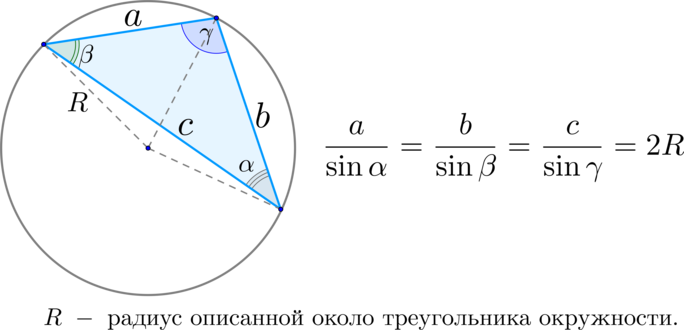
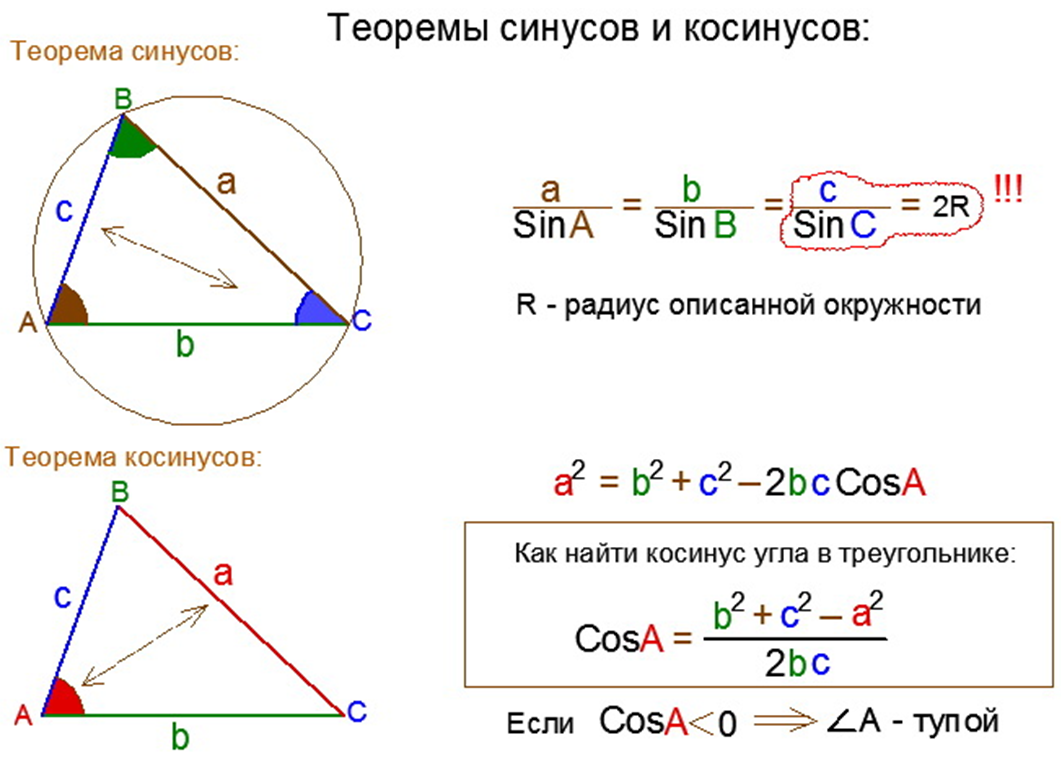
Теорема синусов и теорема косинусов

(blacktriangleright) Теорема синусов:

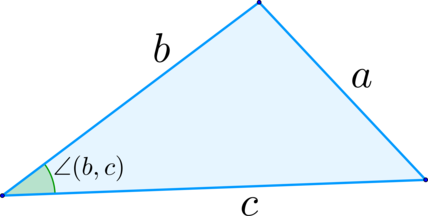
(blacktriangleright) Теорема косинусов: (Large{a^2=b^2+c^2-2bccdot cos angle(b,c)})


Задание
1

#656

Уровень задания: Равен ЕГЭ

В треугольнике (ABC): (sin{angle B} = 0,55), радиус описанной около (ABC) окружности равен 5. Найдите (AC).

По теореме синусов [dfrac{AB}{sin{angle C}} = dfrac{BC}{sin{angle A}} = dfrac{CA}{sin{angle B}} = 2R,] где (R) – радиус описанной около (ABC) окружности.
Тогда [dfrac{CA}{sin{angle B}} = 2R] и, значит, (dfrac{CA}{0,55} = 10), откуда (CA = 5,5).

Ответ: 5,5


Задание
2

#3586

Уровень задания: Равен ЕГЭ

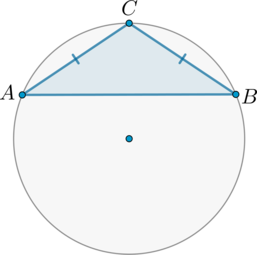
Найдите хорду, на которую опирается угол (120^circ), вписанный в окружность радиуса (sqrt3).

Рассмотрим (triangle ABC). По теореме синусов [dfrac a{sin
alpha}=2R] где (a) – сторона треугольника, (alpha) – противолежащий этой стороне угол, (R) – радиус описанной окружности. Следовательно, [AB=2Rcdot sin angle C=2cdot sqrt3cdot dfrac{sqrt3}2=3]

Ответ: 3


Задание
3

#3585

Уровень задания: Равен ЕГЭ

Боковая сторона равнобедренного треугольника равна (1), угол при вершине, противолежащей основанию, равен (120^circ). Найдите диаметр описанной окружности этого треугольника.

По теореме косинусов (AB^2=AC^2+BC^2-2cdot ACcdot BCcdot
cos120^circ=2AC^2(1-cos 120^circ)=2cdot 1^2cdot
left(1+dfrac12right)=3). Следовательно, (AB=sqrt3).
По теореме синусов [dfrac a{sin alpha}=2R] где (a) – сторона треугольника, (alpha) – противолежащий этой стороне угол, (R) – радиус описанной окружности. Следовательно, [D=2R=dfrac{sqrt3}{sin 120^circ}=dfrac{sqrt3}{frac{sqrt3}2}=2]

Ответ: 2


Задание
4

#3584

Уровень задания: Равен ЕГЭ

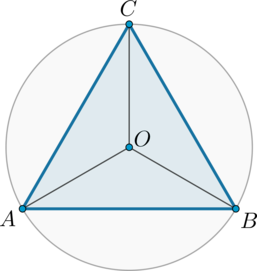
Радиус окружности, описанной около правильного треугольника, равен (sqrt3). Найдите сторону этого треугольника.

По теореме синусов [dfrac a{sin alpha}=2R] где (a) – сторона треугольника, (alpha) – противолежащий этой стороне угол, (R) – радиус описанной окружности. Так как в правильном треугольнике все углы равны по (60^circ), то [a=2Rcdot sin60^circ=2cdot sqrt3cdot dfrac{sqrt3}2=3]

Ответ: 3


Задание
5

#3583

Уровень задания: Равен ЕГЭ

Сторона правильного треугольника равна (sqrt3). Найдите радиус окружности, описанной около этого треугольника.

По теореме синусов [dfrac a{sin alpha}=2R] где (a) – сторона треугольника, (alpha) – противолежащий этой стороне угол, (R) – радиус описанной окружности. Так как в правильном треугольнике все углы равны по (60^circ), то [2R=dfrac {sqrt3}{sin60^circ}=dfrac{sqrt3}{frac{sqrt3}2}=2
quadRightarrowquad R=1]

Ответ: 1


Задание
6

#654

Уровень задания: Равен ЕГЭ

В треугольнике (ABC): (sin{angle B} = 0,6), (AC = 3), (angle C = 30^{circ}). Найдите (AB).

По теореме синусов [dfrac{AB}{sin{angle C}} = dfrac{BC}{sin{angle A}} = dfrac{CA}{sin{angle B}} = 2R,] где (R) – радиус описанной около (ABC) окружности. Тогда [dfrac{AB}{sin{angle C}} = dfrac{CA}{sin{angle B}}] и, значит, (dfrac{AB}{0,5} = 5), откуда (AB = 2,5).

Ответ: 2,5


Задание
7

#2741

Уровень задания: Равен ЕГЭ

Радиус окружности, описанной около треугольника (ABC), равен (R). Большая сторона треугольника (ABC) равна (10), а (angle ABC = 150^circ). Найдите (R).

В треугольнике против большего угла лежит большая сторона, тогда (AC = 10).

По теореме синусов [2R = dfrac{AC}{sin angle ABC} = dfrac{10}{0,5} = 20,,] откуда (R = 10).

Ответ: 10

Выпускники, которые готовятся сдавать ЕГЭ по математике и хотят получить достаточно высокие баллы, обязательно должны освоить принцип решения задач на применение теоремы синусов и косинусов. Многолетняя практика показывает, что подобные задания из раздела «Геометрия на плоскости» являются обязательной частью программы аттестационного испытания. Поэтому, если одним из ваших слабых мест являются задачи на теорему косинусов и синусов, рекомендуем обязательно повторить базовую теорию по данной теме.

Готовьтесь к экзамену вместе с образовательным порталом «Школково»

Занимаясь перед сдачей ЕГЭ, многие выпускники сталкиваются с проблемой поиска базовой теории, необходимой для решения практических задач на применение теоремы синусов и косинусов.

Учебник далеко не всегда оказывается под рукой в нужный момент. А найти необходимые формулы иногда бывает достаточно проблематично даже в Интернете.

Подготовка к аттестационному испытанию вместе с образовательным порталом «Школково» будет максимально качественной и эффективной. Чтобы задачи на теорему синусов и косинусов давались легко, рекомендуем освежить в памяти всю теорию по данной теме. Этот материал наши специалисты подготовили на основе богатого опыта и представили в понятной форме. Найти его вы можете в разделе «Теоретическая справка».

Знание базовых теорем и определений — это половина успеха при прохождении аттестационного испытания. Отточить навык решения примеров позволяют соответствующие упражнения. Чтобы их найти, достаточно перейти в раздел «Каталог» на образовательном сайте «Школково». Там представлен большой перечень заданий различного уровня сложности, который постоянно дополняется и обновляется.

Задачи на теоремы синусов и косинусов, подобные тем, что встречаются в ЕГЭ по математике, учащиеся могут выполнять в онлайн-режиме, находясь в Москве или любом другом российском городе.

В случае необходимости любое упражнение, например, на вычисление синуса угла треугольника, можно сохранить в разделе «Избранное». Это позволит в дальнейшем вернуться к нему, чтобы еще раз проанализировать алгоритм нахождения правильного ответа и обсудить его с преподавателем в школе или репетитором.

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ

Источник
Skip to content

Геометрия 7-9 класс. Теорема синусов

Геометрия 7-9 класс. Теорема синусовadmin2022-12-26T22:20:53+03:00

Скачать файл в формате pdf.

Геометрия 7-9 класс. Теорема синусов

Задача 1. В треугольнике АВС  ВС = 12,  (sin ,A = frac{4}{5},,,,sin C = frac{3}{5}.)  Найдите АВ.

Ответ

ОТВЕТ: 9.
Задача 2. В треугольнике АВС  ВС = 18,  АС = 30,  (sin B = frac{5}{6}.)  Найдите (angle ,A.) Ответ дайте в градусах.

Ответ

ОТВЕТ: 30.
Задача 3. В треугольнике АВС  (BC = 3sqrt 6 ,)  (angle ,A = {45^ circ },,,,angle C = {60^ circ }.)  Найдите АВ.

Ответ

ОТВЕТ: 9.
Задача 4. В остроугольном треугольнике АВС (BC = 6sqrt 3 ,) (AB = 6sqrt 2 ,)  (angle ,A = {60^ circ }.)  Найдите (angle ,C.)  Ответ дайте в градусах.

Ответ

ОТВЕТ: 45.
Задача 5. Найдите радиус окружности описанной вокруг треугольника  АВС, если  (BC = 4sqrt 3 ,)  (angle ,A = {60^ circ }.)

Ответ

ОТВЕТ: 4.
Задача 6. В треугольнике АВС (angle ,A = {30^ circ },) а радиус описанной окружности равен 14. Найдите ВС.

Ответ

ОТВЕТ: 14.
Задача 7. В треугольнике ABC угол B равен 72°, угол C равен 63°, (BC = 2sqrt 2 .) Найдите радиус описанной около этого треугольника окружности.

Ответ

ОТВЕТ: 2.
Задача 8. В треугольнике ABC угол B равен 56°, угол C равен 64°, (BC = 3sqrt 3 ). Найдите радиус описанной около этого треугольника окружности.

Ответ

ОТВЕТ: 3.
Задача 9. Найдите радиус окружности описанной около треугольника  АВС, если  ВС = 36,  а синус внешнего угла при вершине  А  равен  (frac{4}{5}.)

Ответ

ОТВЕТ: 22,5.
Задача 10. Радиус окружности описанной около треугольника АВС равен 13. Найдите ВС, если косинус внешнего угла при вершине А равен (frac{5}{{13}}.)

Ответ

ОТВЕТ: 24.
Задача 11. В треугольнике АВС  (AB = 8sqrt 2 ,,,,angle ,A = {30^ circ },,,,angle ,B = {105^ circ }.)  Найдите ВС.

Ответ

ОТВЕТ: 8.
Задача 12. В равнобедренной трапеции ABCD с основаниями AD = 6 и ВС боковые стороны равны (2sqrt 6 .)  Найдите (angle ,BDC,) если (angle ,ADB = {45^ circ }.)

Ответ

ОТВЕТ: 30.
Задача 13. Углы B и C треугольника ABC равны соответственно 73° и 77°. Найдите BC, если радиус окружности описанной около треугольника ABC, равен 9.

Ответ

ОТВЕТ: 9.
Задача 14. Углы B и C треугольника ABC равны соответственно 64° и 86°. Найдите BC, если радиус окружности описанной около треугольника ABC, равен 7.

Ответ

ОТВЕТ: 7.
Задача 15. Вершины треугольника делят описанную около него окружность на три дуги, длины которых относятся как 2 : 3 : 7. Найдите радиус окружности, если меньшая из сторон равна 16.

Ответ

ОТВЕТ: 16.
Задача 16. Вершины треугольника делят описанную около него окружность на три дуги, длины которых относятся как 1 : 2 : 3. Найдите радиус окружности, если меньшая из сторон равна 17.

Ответ

ОТВЕТ: 17.
Задача 17. В равнобедренном треугольнике АВС с основанием (AC = sqrt 2 ) угол при основании равен ({30^ circ }.) Найдите биссектрису АК.

Ответ

ОТВЕТ: 1.
Задача 18. В равнобедренной трапеции ABCD с основаниями AD = 12 и ВС  (sin angle BAC = frac{4}{9},,,,sin angle ACD = frac{2}{3}.) Найдите среднюю линию трапеции.

Ответ

ОТВЕТ: 10.
Задача 19. Две стороны треугольника равны 6 и 12, а высота, проведённая к третьей стороне равна 4. Найдите радиус окружности, описанной около данного треугольника.

Ответ

ОТВЕТ: 9.
Задача 20. Найдите радиус окружности, описанной около равнобедренного треугольника с основанием 16 и боковой стороной 10.

Ответ

ОТВЕТ: (frac{{25}}{3}.)
Задача 21. В прямоугольном треугольнике АВС через вершины А и С и середину М гипотенузы АВ проведена окружность радиуса (5sqrt 3 .) Найдите радиус описанной окружности треугольника СМВ, если (angle ,A = {30^ circ }.)

Ответ

ОТВЕТ: 5.
Задача 22. В четырёхугольнике ABCD известно, что (CD = 10sqrt 2 ,) (angle ,CAD = {45^ circ }) и  (angle ,BAC = angle ,BDC = {30^ circ }.)  Найдите ВС.

Ответ

ОТВЕТ: 10.
Задача 23. Радиус окружности описанной около треугольника АВС равен 6. Найдите высоту треугольника  BH,  если  АВ = 9  и  ВС = 4.

Ответ

ОТВЕТ: 3.
Задача 24. Радиус окружности описанной около треугольника АВС равен 8. Найдите АВ, если  ВС = 14  и высота треугольника  ВН = 5,25.

Ответ

ОТВЕТ: 6.
Задача 25. В равнобедренном треугольнике АВС на основании АС выбрана точка D так, что AD = 5. Около треугольника DBC описана окружность и прямая АВ является касательной к этой окружности. Найдите диаметр этой окружности, если (angle ,ABD = {30^ circ }.)

Ответ

ОТВЕТ: 10.

Источник

Поиск

в условии
в решении
в тексте к заданию
в атрибутах

Класс: 10 11 6 7 8 9
Атрибут:

Всего: 89    1–20 | 21–40 | 41–60 | 61–80 …

Добавить в вариант

Точка A лежит на стороне LM треугольника KLM с углом 120° при вершине K. В треугольники AKL и AKM вписаны окружности с центрами F и O соответственно. Найти радиус окружности, описанной около треугольника FKO, если AO  =  2, AF  =  7.

Точка A лежит на стороне LM треугольника KLM с углом 60 в степени левая круглая скобка circ правая круглая скобка при вершине K. В треугольники AKL и AKM вписаны окружности с центрами F и O соответственно. Найти радиус окружности, описанной около треугольника FKO, если AO  =  6, AF  =  3.

Различные прямые a и b пересекаются в точке О. Рассмотрим всевозможные отрезки АВ длины l, концы А и В которых лежат на a и b соответственно, и обозначим за Р точку пересечения перпендикуляров к прямым a и b, восстановленным из А и В соответственно. Найти геометрическое место точек Р.

В треугольнике ABC сторона BC равна 4, а угол ABC равен дробь: числитель: 2 Пи , знаменатель: 3 конец дроби . Окружность Г радиуса 2 корень из 3 касается сторон BC и AC треугольника ABC в точках K и L соответственно и пересекает сторону AB в точках M и N (M лежит между A и N) так, что отрезок MK параллелен AC. Найдите длины отрезков CL, MK, AB и площадь треугольника CMN.

В треугольнике ABC, angle A=2 альфа , биссектрисы BD и CE пересекаются в точке I. Найдите наименьший возможный радиус окружности, описанной около треугольника DEI, если сумма длин отрезков DI и EI равна 2d.

В остроугольном треугольнике ABC angleB=75 градусов, длина AC  =  2 cм, H  — точка пересечения его высот. Площадь треугольника AHC равна корень из 12 минус 3 см2. Найти площадь треугольника ABC.

В треугольнике ABC проведена медиана AM, точка O  — центр описанной около него окружности, точка Q  — центр вписанной в него окружности. Отрезки AM и OQ пересекаются в точке S, при этом

2 дробь: числитель: OS, знаменатель: MS конец дроби =3 корень из 3 дробь: числитель: QS, знаменатель: AS конец дроби .

Найдите сумму синусов величин углов ABC и ACB, если известно, что angle BAC= дробь: числитель: Пи , знаменатель: 3 конец дроби . Ответ при необходимости округлите до сотых.

Точка M лежит на описанной около правильного треугольника ABC окружности и не совпадает с его вершинами. Докажите, что сумма расстояний от точки M до прилегающих вершин треугольника равна расстоянию от точки M до третей его вершины: AM + CM  =  BM.

В треугольнике со сторонами AB  =  BC  =  5 и AC  =  6 на основании AC выбрана точка N так, что AN : NC  =  2 : 1. Найдите расстояние между центрами окружностей, описанных вокруг треугольников ABN и CBN. При необходимости округлите результат до двух знаков после запятой.

В треугольнике ABC проведена средняя линия MN, соединяющая стороны AB и BC. Окружность радиуса корень из 2, проведенная через точки M, N и C, касается стороны AB. Длина стороны AC равна 2. Найти синус угла angle ACB.

Всего: 89    1–20 | 21–40 | 41–60 | 61–80 …

Источник

Понравилась статья? Поделить с друзьями:
  • Темы сочинения мертвые души для 9 класса с планом
  • Теорема птолемея задача егэ
  • Темы сочинения итогового сочинения 2019 2020
  • Теорема по русскому языку егэ
  • Темы сочинения итогового сочинения 2016