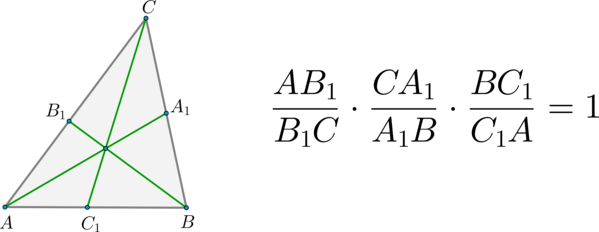Теорема ван обеля задачи егэ

Источник: Типовые тестовые задания по математике, под редакцией И. В. Ященко 2016

Источник: А. Ларин. Тренировочный вариант № 323. (часть C).

Источник: А. Ларин. Тренировочный вариант № 324. (часть C).

Источник: А. Ларин. Тренировочный вариант № 397.

К задаче 1

К задаче 2

К задаче 3

Факт 1.
(bullet) Теорема Вариньона:
Середины сторон выпуклого четырехугольника являются вершинами параллелограмма.

Факт 2.
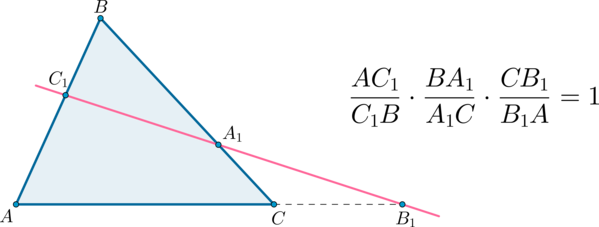
(bullet) Теорема Менелая:
Если прямая пересекает стороны (AB) и (BC) в точках (C_1) и (A_1) соответственно, а также продолжение прямой (AC) в точке (B_1), то выполнено следующее соотношение:

Факт 3.
(bullet) Теорема Чевы:
Если (AA_1, BB_1) и (CC_1) – чевианы, пересекающиеся в одной точке, то для них выполнено следующее соотношение:

(чевиана – отрезок, соединяющий вершину треугольника с точкой на противоположной стороне)

Факт 4.
(bullet) Теорема Ван-Обеля:
Если (AA_1, BB_1) и (CC_1) – чевианы, пересекающиеся в одной точке, то для них выполнено следующее соотношение:

Пусть все углы треугольника ABC меньше 120° и Рассмотрим точку  внутри треугольника, для которой

Пусть прямая BT пересекает сторону AC в точке E, а прямая CT пересекает сторону AB в точке F. Докажите, что прямые EF и BC пересекаются в некоторой точке M, причём MB : MC  =  TB : TC.

Дан равнобедренный треугольник PQR (PQ = QR) с углом при вершине, равным 108°. Точка O расположена внутри треугольника PQR так, что а Найдите величину угла QOR.

На сторонах AB и AC треугольника ABC расположены точки D и E так, что AD : AB  =  1 : 3 и CE : CA  =  1 : 4. Прямые CD, BE и медиана, проведенная из вершины A, попарно пересекаются в точках M, N и P. Найти отношение площадей треугольников MNP и ABC.

Через вершины треугольника ABC проведены три параллельные прямые a, b, c соответственно, не параллельные сторонам треугольника. Пусть A₀, B₀, C₀  — середины сторон BC, CA, AB. Пусть A₁, B₁, C₁  — точки пересечения пар прямых a и B₀C₀, b и C₀A₀, c и A₀B₀ соответственно. Докажите, что прямые A₀A₁, B₀B₁ и C₀C₁ пересекаются в одной точке.

Точки P и Q лежат соответственно на сторонах BC и CD квадрата ABCD. Прямые AP и AQ пересекают BD в точках M и N соответственно, а прямые PN и QM пересекаются в точке H. Докажите, что AH ⊥ PQ тогда и только тогда, когда точки P, Q, M, N лежат на одной окружности.

Внутри четырехугольника ABCD взяли точку P. Прямые BC и AD пересекаются в точке X. Оказалось, что прямая XP является внешней биссектрисой углов APD и Пусть PY и PZ  — биссектрисы треугольников APB и DPC. Докажите, что точки X, Y и Z лежат на одной прямой.

В треугольнике ABC точки A₁, B₁, C₁  — середины сторон BC, AC, AB соответственно. Точки A₂, B₂, C₂  — середины ломанных BAC, ABC, ACB соответственно (точка называется серединой ломанной если принадлежит ломанной и делит ее на две ломанных равной длины). Докажите, что прямые A₁A₂, B₁B₂, C₁C₂ проходят через одну точку.

Плоскость пересекает ребра тетраэдра ABCD, выходящие из вершины D, и делает их в отношении 5 : 1 (не обязательно от вершины D). Так же эта плоскость пересекает прямые AB и AC в точках E и F. Найдите отношение площадей треугольников AEF и ABC.

В треугольнике ABC на сторонах BC, AC, AB отметили точки D, E, F соответственно так, что

Отрезки AD, BE, CF попарно пересекаются в точках P, Q, R. Площадь треугольника ABC равна Найдите площадь треугольника PQR.

На высоте BH треугольника ABC отмечена некоторая точка D. Прямая AD пересекает сторону BC в точке E, прямая CD пересекает сторону AB в точке F. Точки G и J являются проекциями соответственно точек F и E на сторону AC. Площадь треугольника HEJ вдвое больше площади треугольник HFG. В каком отношении высота BH делит отрезок FE?

В треугольнике ABC проведена медиана AM, точка O  — центр описанной около него окружности, точка Q  — центр вписанной в него окружности. Отрезки AM и OQ пересекаются в точке S, при этом

Найдите сумму синусов величин углов ABC и ACB, если известно, что Ответ при необходимости округлите до сотых.

Внутри треугольника ABC отмечена точка P так, что Точки M и N  — проекции точки P на стороны AC и BC соответственно, D  — середина AB. Докажите, что DM = DN.

В треугольнике ABC на сторонах AB и AC выбраны точки D и E соответственно так, что AD : DB  =  2 : 1 и AE : EC  =  3 : 1. Пусть отрезки BE и CD пересекаются в точке F. Найти площадь треугольника ABC, если площадь четырехугольника ADFE равна SADFE  =  7.

Дан неравнобедренный треугольник ABC. Выберем произвольную окружность ω, касающуюся описанной окружности треугольника ABC внутренним образом в точке B и не пересекающую прямую AC. Отметим на ω точки P и Q так, чтобы прямые AP и CQ касались ω, а отрезки AP и СQ пересекались внутри треугольника ABC. Докажите, что все полученные таким образом прямые РQ проходят через одну фиксированную точку, не зависящую от выбора окружности.

Объем тетраэдра ABCD равен 4(m + n). Точка M делит ребро AB в отношении m : n. Через точку M и середины ребер BC и AD проведено сечение. Найдите площадь этого сечения, если расстояние от точки D до него равно h.