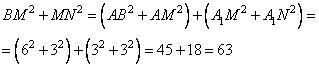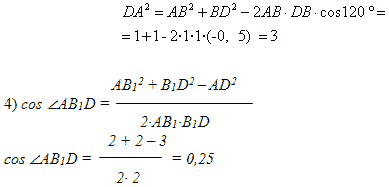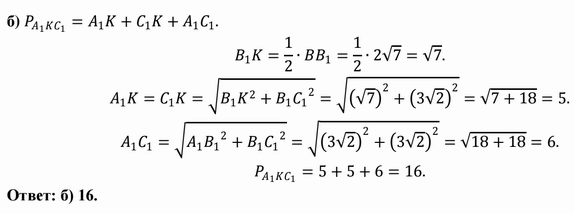Теоремы для егэ по математике профиль 14 задание

Цилиндр – тело, ограниченное цилиндрической поверхностью и двумя кругами с границами $М$ и $М_1$. Цилиндрическая поверхность называется боковой поверхностью цилиндра, а круги – основаниями цилиндра.

Образующие цилиндрической поверхности называются образующими цилиндра, на рисунке образующая $L$.

Цилиндр называется прямым, если его образующие перпендикулярны основаниям.
Осевое сечение цилиндра — это прямоугольник, у которого одна сторона равна диаметру основания, а вторая – высоте цилиндра.

Основные понятия и свойства цилиндра:

1. Основания цилиндра равны и лежат в параллельных плоскостях.
2. Все образующие цилиндра параллельны и равны.
3. Радиусом цилиндра называется радиус его основания ($R$).
4. Высотой цилиндра называется расстояние между плоскостями оснований (в прямом цилиндре высота равна образующей).
5. Осью цилиндра называется отрезок, соединяющий центры оснований ($ОО_1$).
6. Если радиус или диаметр цилиндра увеличить в n раз, то объем цилиндра увеличится в $n^2$ раз.
7. Если высоту цилиндра увеличить в m раз, то объем цилиндра увеличится в то же количество раз.
8. Если призму вписать в цилиндр, то ее основаниями будут являться равные многоугольники, вписанные в основание цилиндра, а боковые ребра — образующими цилиндра.
9. Если цилиндр вписан в призму, то ее основания — равные многоугольники, описанные около оснований цилиндра. Плоскости граней призмы касаются боковой поверхности цилиндра.
10. Если в цилиндр вписана сфера, то радиус сферы равен радиусу цилиндра и равен половине высоты цилиндра.

$R_{сферы}=R_{цилиндра}={h_{цилиндра}}/{2}$

Площадь поверхности и объем цилиндра.

Площадь боковой поверхности цилиндра равна произведению длины окружности основания на высоту.

$S_{бок.пов.}=2πR·h$

Площадь поверхности цилиндра равна сумме двух площадей оснований и площади боковой поверхности.

$S_{полной.пов.}=2πR^2+2πR·h=2πR(R+h)$

Объем цилиндра равен произведению площади основания на высоту.

$V=πR^2·h$

Объем части цилиндра, в основании которого лежит сектор: $V={πR^2·n°·h}/{360}$, где $n°$ — это градусная мера центрального угла, отсекающего заданный сектор.

Конусом (круговым конусом) называется тело, которое состоит из круга, точки, не лежащей в плоскости этого круга, и всех отрезков, соединяющих заданную точку с точками круга.

Отрезки, соединяющие вершину конуса с точками окружности основания, называются образующими и обозначаются (l).

$l=SA$

Высотой конуса называется перпендикуляр, опущенный из его вершины на плоскость основания. Ось прямого конуса и его высота равны.

$SО$ — высота и ось конуса.

Свойства конуса:

1. Все образующие конуса равны.
2. Осевым сечением конуса является равнобедренный треугольник, основание которого равно двум радиусам, а боковые стороны равны образующим конуса.
3. Если боковая поверхность конуса – полукруг, то осевым сечением является равносторонний треугольник, угол при вершине равен $60°$.
4. Если радиус или диаметр конуса увеличить в n раз, то его объем увеличится в $n^2$ раз.
5. Если высоту конуса увеличить в m раз, то объем конуса увеличится в то же количество раз.

Площадь поверхности и объем конуса.

Площадь боковой поверхности конуса равна произведению половины длины окружности основания на образующую.

$S_{бок.пов.}=πR·l$

Площадь поверхности конуса равна сумме площади основания и площади боковой поверхности.

$S_{полной.пов.}=πR^2+πR·l=πR(R+l)$

Объем конуса равен трети произведения площади основания на высоту.

$V={πR^2·h}/{3}$

Объем части конуса, в основании которого лежит сектор: $V={πR^2·n°·h}/{360·3}$, где $n°$ — это градусная мера центрального угла, отсекающего заданный сектор.

Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии ($R$) от данной точки (центра сферы $О$).

Тело, ограниченное сферой, называется шаром.

Осевое сечение шара это круг, радиус которого равен радиусу шара. Осевым сечением является самый большой круг шара.

Площадь поверхности сферы: $S_{п.п}=4π·R^2=π·d^2$, где $R$ — радиус сферы, $d$ — диаметр сферы

Объем шара: $V={4π·R^3}/{3}={π·d^3}/{6}$, где $R$ — радиус шара, $d$ — диаметр шара.

Если радиус или диаметр шара увеличить в n раз, то площадь поверхности увеличится в $n^2$ раз, а объем в $n^3$ раз.

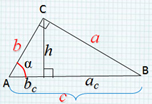
Теорема Пифагора

В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.

$АС^2+ВС^2=АВ^2$

Соотношение между сторонами и углами в прямоугольном треугольнике:

В прямоугольном треугольнике $АВС$, с прямым углом $С$:

Для острого угла $В: АС$ — противолежащий катет; $ВС$ — прилежащий катет.

Для острого угла $А: ВС$ — противолежащий катет; $АС$ — прилежащий катет.

1. Синусом ($sin$) острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
2. Косинусом ($cos$) острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
3. Тангенсом ($tg$) острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету.

Значения тригонометрических функций некоторых углов:

$α$	$30$	$45$	$60$
$sinα$	${1}/{2}$	${√2}/{2}$	${√3}/{2}$
$cosα$	${√3}/{2}$	${√2}/{2}$	${1}/{2}$
$tgα$	${√3}/{3}$	$1$	$√3$
$ctgα$	$√3$	$1$	${√3}/{3}$

Признаки подобия треугольников:

1. Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.
2. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между ними равны, то такие треугольники подобны.
3. Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны. Периметры подобных треугольников и их линейные величины (медианы, биссектрисы, высоты) относятся друг к другу как коэффициент подобия $k$. Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.

Задание 13 Профильного ЕГЭ (Стереометрия) многие старшеклассники считают самой сложной задачей в варианте. И напрасно! Ничего особенного в ней нет. Просто начинать надо вовремя, лучше всего в десятом классе. И конечно, не с самых сложных задач. Действуем по порядку!

1. Подготовительный этап — решение задач по стереометрии из первой части ЕГЭ. Повторите формулы объемов и площадей поверхности многогранников и тел вращения. Посмотрите, как решаются типовые задачи.

2. Повторите необходимую теорию. Вот краткая Программа по стереометрии. Проверьте себя. Все ли вы знаете? В освоении стереометрии вам поможет наш ЕГЭ-Справочник.

3. Посмотрите, как правильно строить чертежи.

4. Выучили теорию? Применяем на практике — строим сечения.

5. Решаем простые задачи по стереометрии. И после этого — переходим к реальным задачам ЕГЭ.

6. Задачи 13 по стереометрии из Профильного ЕГЭ по математике обычно относятся к одному из типов. Смотрите нашу Классификацию задач по стереометрии и методы их решения.

Вот примеры простых подготовительных задач по стереометрии:

1. Высота правильной треугольной пирамиды равна 4, а угол между боковой гранью и плоскостью основания равен 60 градусов. Найдите расстояние от вершины основания до плоскости противолежащей ей боковой грани.

Посмотреть решение

2. В правильной шестиугольной призме , все ребра которой равны 1, точка G — середина ребра Найдите угол между прямой АG и плоскостью

Посмотреть решение

3. В правильной шестиугольной призме все рёбра равны 1. Найдите расстояние от точки В до плоскости

Посмотреть решение

4. В основании прямой призмы лежит ромб. Найти угол между прямыми и

Посмотреть решение

5. Точка E — середина ребра куба Найдите угол между прямыми и

Посмотреть решение

6. В правильной треугольной призме , все рёбра которой равны . Найдите расстояние между прямыми и

Посмотреть решение

7. Радиус основания конуса с вершиной P равен 6, а длина его образующей равна 9. На окружности основания конуса выбраны точки A и B, делящие окружность на две дуги, длины которых относятся как 1 : 5. Найдите площадь сечения конуса плоскостью ABP.

Посмотреть решение

А теперь — реальные задачи по стереометрии, встретившиеся выпускникам на Профильном ЕГЭ по математике.

8. Точки М и N — середины ребер соответственно АВ и СD треугольной пирамиды АВСD, О — точка пересечения медиан грани АВС.

а) Докажите, что прямая DO проходит через середину отрезка MN.

б) Найдите угол между прямыми MN и ВС, если АВСD — правильный тетраэдр.

Посмотреть решение

9. В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки A, B и C, а на окружности другого основания — точка , причём — образующая цилиндра, а AC — диаметр основания. Известно, что

а) Докажите, что угол между прямыми и равен

б)Найдите объём цилиндра.

Посмотреть решение

10. В основании призмы лежит правильный треугольник, вершина проецируется в центр Q основания АВС.

а) Докажите, что плоскости и перпендикулярны.

б) Найдите угол между прямой и плоскостью если боковое ребро призмы равно стороне основания.

Посмотреть решение

11. Сечением прямоугольного параллелепипеда плоскостью , содержащей прямую и параллельной прямой АС, является ромб.

а) Докажите, что грань ABCD — квадрат.

б) Найдите угол между плоскостями и , если

Посмотреть решение

12. На ребрах АВ и ВС треугольной пирамиды АВСD отмечены точки М и N соответственно, причем

Точки P и Q — середины ребер DA и DC соответственно.

а) Докажите, что точки P, Q, M и N лежат в одной плоскости.

б) Найдите, в каком отношении эта плоскость делит объем пирамиды.

Посмотреть решение

Решаем задачи из сборника И. В. Ященко, 2020. Вариант 6, задача 14

7 лайфхаков для решения задач по стереометрии:

1. Задача по стереометрии не решается без хорошего чертежа! Чертеж строим по линейке, черной ручкой, на клетчатой бумаге, по правилам построения чертежей. На ЕГЭ можно и нужно пользоваться линейкой! А бланк будет в клеточку.

2. Все, что нужно, на чертеже должно быть хорошо видно! Если вам не понравился чертеж — не сидите над ним, бросьте и нарисуйте другой. Одного объемного чертежа будет недостаточно — понадобится один или несколько плоских.

3. Учимся записывать решение кратко. Вспомним основные обозначения

— точка M принадлежит плоскости АВС.

— прямые а и b пересекаются в точке О.

— прямые а и b параллельны.

— прямые а и b перпендикулярны.

4. Почти в каждой задаче по стереометрии встречаются «особенные треугольники»

Давайте вспомним:

— В прямоугольном равнобедренном треугольнике гипотенуза в раз больше катета.

— В треугольнике с углами 30, 60 и 90 градусов гипотенуза в 2 раза больше меньшего катета, а больший катет в раз больше меньшего.

5. Формула для площади прямоугольной проекции фигуры  помогает найти угол между плоскостями. Здесь — угол между плоскостью фигуры и плоскостью проекции.

6. Метод объемов помогает найти расстояние от точки до плоскости. Надо выбрать треугольную пирамиду, записать ее объем двумя способами и найти из полученного уравнения нужное расстояние.

7. Сначала изучаем «классику». После этого, если время есть, можно браться и за координатный метод

Почему именно в таком порядке?

Конечно, координатный метод удобен. Однако большинство задач по стереометрии из вариантов ЕГЭ «заточены» под классику.

И если в решении задачи координатным методом вы сделаете арифметическую ошибку — можете потерять все баллы. Эксперт не будет разбираться, правильно ли вы посчитали определитель или смешанное произведение векторов. Потому что эти темы не входят в школьную программу, и составители «конструировали» задачи по стереометрии так, чтобы они решались обычными, «классическими» способами.

• Главная

  
  

• Теория ЕГЭ

  
  
• Математика — теория ЕГЭ

  
  

• 
  Задание 14 ЕГЭ 2021 по математике, теория

08.10.2018

Необходимая теория для успешного освоения и решения заданий №14 по математике профильного уровня на ЕГЭ в 2021 году.

Представлена вся теория и алгоритм решения различных заданий такого типа.

• Тренировочные кимы ЕГЭ по математике
• Практика — примеры для решения каждого типа заданий

Обсудить решение конкретных заданий вы можете в комментариях ниже.

Смотреть в PDF:

Или прямо сейчас: cкачать в pdf файле.

Сохранить ссылку:

Комментарии (0)
Добавить комментарий

Добавить комментарий

Комментарии без регистрации. Несодержательные сообщения удаляются.

Имя (обязательное)

E-Mail

Подписаться на уведомления о новых комментариях

Отправить

Как подготовиться к решению заданий ЕГЭ № 14 по стереометрии | 1С:Репетитор

Задание ЕГЭ №13 (бывшая ЕГЭ №14) по стереометрии считается очень сложным на ЕГЭ. И многие за нее не берутся.

А зря!

Если проходить стереометрию от простого к сложному освоить стереометрию можно. В 2022 году за ЕГЭ №13 дают не 2, а целых 3 балла на ЕГЭ! И вы можете их получить.

Читайте эту статью, смотрите вебинары и решайте задачи вместе с Алексеем Шевчуком и вы полюбите стереометрию.

ЕГЭ 13 Стереометрия. Расстояние между точками и от точки до прямой

Расстояние между точками и от точки до прямой – это первое видео раздела “Стереометрия”, входящее в наш курс подготовки к ЕГЭ (о нем ниже).

В этом видео мы научимся “видеть” 3-мерное пространство и изображать 3-мерные объекты на бумаге (то есть на плоской поверхности).

Затем мы научимся двум основным вещам – находить расстояние между точками на таких рисунках, а также расстояние от точки до прямой.

На этих умениях строится всё дальнейшее изучение стереометрии. В общем это очень важное, базовое видео, с которого нужно начинать изучение стереометрии. Не перескакивайте, не пропускайте его!

Даже если вы знаете стереометрию, вы найдете для себя очень много полезного и нового в этом видео.

ЕГЭ 13 (14). Стереометрия. Разбор варианта профильного ЕГЭ 2020

Нужно великолепно знать основные теоремы планиметрии, уметь рассчитывать расстояния, площади и объемы плоских и объемных фигур.

Но самое сложное, нужно научиться строить доказательства с помощью этих теорем и правильно их записывать.

Давайте этим займемся.

• 00:00 Условие задачи
• 00:25 Как нарисовать шестиугольную пирамиду
• 05:52 Как подписать вершины пирамиды
• 06:24 Как исправить рисунок, если грани пирамиды сливаются
• 10:18 Доказательство пункта А
• 14:13 Запись доказательства пункта А
• 18:50 Доказательство (решение) пункта Б (Найти объем пирамиды)
• 23:45 Запись доказательства (решения) пункта Б
• 26:08 Найдем площадь основания пирамиды (чтобы найти объем) и запишем решение
• 29:18 Нахождение объема пирамиды
• 29:59 На что рекомендуем обратить внимание

Самые бюджетные курсы по подготовке к ЕГЭ на 90+

Алексей Шевчук – ведущий мини-групп

математика, информатика, физика

+7 (905) 541-39-06 – WhatsApp/Телеграм для записи

alexei.shevchuk@youclever.org – email для записи

• тысячи учеников, поступивших в лучшие ВУЗы страны
• автор понятного всем учебника по математике ЮКлэва (с сотнями благодарных отзывов);
• закончил МФТИ, преподавал на малом физтехе;
• репетиторский стаж – c 2003 года;
• в 2021 году сдал ЕГЭ (математика 100 баллов, физика 100 баллов, информатика 98 баллов – как обычно дурацкая ошибка:);
• отзыв на Профи.ру: “Рейтинг: 4,87 из 5. Очень хвалят. Такую отметку получают опытные специалисты с лучшими отзывами”.

---

Стереометрия

---

Задание №14 – стереометрия в профильном ЕГЭ по математике. В задачах данного уровня необходимо проявить знания как по планиметрии, так и по стереометрии. Однако многие задания опираются на теорему Пифагора, поэтому опыт решения аналогичных задач будет только плюсом. Перейдем к рассмотрению одного из таких заданий.

---

Разбор типовых вариантов заданий №14 ЕГЭ по математике профильного уровня

---

Первый вариант задания (демонстрационный вариант 2018)

[su_note note_color=”#defae6″]

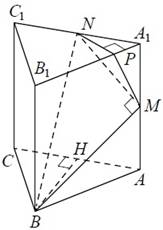
Все рёбра правильной треугольной призмы ABCA₁B₁C₁ имеют длину 6. Точки M и N— середины рёбер AA₁ и A₁C₁ соответственно.

а) Докажите, что прямые BM и MN перпендикулярны.

б) Найдите угол между плоскостями BMN и ABB₁.

[/su_note]

Алгоритм решения:

а)

1. Выполняем чертеж, соответствующий условию и проводим высоту ВН.
2. Вычисляем длину высоты ВН.
3. Вычисляем BN.
4. Показываем, что BM и MN перпендикулярны.

б)

1. Проводим перпендикуляр NP к ребру A₁B₂,
2. Показываем, что отрезок MN перпендикулярен плоскости ABB₁.
3. Определяем линейный угол между плоскостями BMN и ABB₁ и вычисляем его.

Решение:

1. Выполняем чертеж к задаче.

Призма правильная, следовательно, основанием ее является равносторонний треугольник. H делит AC пополам, поскольку в равностороннем треугольнике высота является биссектрисой и медианой.

2. Тогда высоту BH можно вычислить по теореме Пифагора из треугольника АВН:

3. Вычисляем длину BN² из треугольника BNH. Он тоже прямоугольный. По теореме Пифагора:

4. Отрезки BM и MN перпендикулярны, поскольку сумма квадратов их длин равна BN², то есть 63:

По теореме, обратной теореме Пифагора, BMN – прямоугольный, причем угол M прямой.

Первая часть задания выполнена: утверждение доказано.

б)

1. Проводим перпендикуляр NP к ребру A₁B₂.

Показываем , что NP перпендикулярна плоскости ABB₁. Из построения и условия (призма правильная) следует:

А это означает, что .и прямая NP является проекцией MN на плоскость ABB₁.

3. Выше было доказано, что . Тогда согласно теореме о трех перпендикулярах . Их этого следует, что NMP – линейный угол искомого угла.

Вычисляем его.

N – середина отрезка A₁C₁, тогда NP = 1/2∙h, где h – высота в треугольнике A₁B₁C₁. А он равносторонний и равен треугольнику АВС. Следовательно, , то есть . По соотношениям в прямоугольном треугольнике.

, откуда .

Ответ:

---

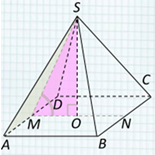
Второй вариант задания (из Ященко, № 1)

[su_note note_color=”#defae6″]

На ребре SA правильной четырёхугольной пирамиды SABCD с основанием ABCD отмечена точка М, причём SM : МА = 5:1. Точки P и Q — середины рёбер ВС и AD соответственно.

а) Докажите, что сечение пирамиды плоскостью MPQ является равнобедренной трапецией.

б) Найдите отношение объёмов многогранников, на которые плоскость MPQ разбивает пирамиду.

[/su_note]

Алгоритм решения:

а)

1. Выполняем чертеж.
2. Устанавливаем подобие треугольников SAB и SMN.
3. Определяем вид сечения.

б)

1. Полагаем объем пирамиды равным V.
2. Определяем какую часть от всего объема пирамиды составляет каждая часть.
3. Находим отношение определенных объемов частей.
4. Записываем ответ.

Решение:

а)

1. Выполняем чертеж для задачи.

2. Пусть N — точка на ребре SB, причем SN:NB = 5:1. Треугольник SAB подобен треугольнику SMN, потому что в них две стороны пропорциональны и углы между ними равны.

3. Из подобия следует: , сторона AB параллельна отрезку MN и . PQ параллельна стороне АВ. Имеем: отрезки MN и PQ параллельны и не равны.

Рассмотрим треугольники MAQ и NBP. У них:

MA = NB, QA = PB

. Значит, эти треугольники равны. А по свойству равных фигур MQ = NP. Тогда трапеция MNPQ является равнобедренной.

Отсюда следует, что сечение пирамиды плоскостью MPQ является трапецией MNPQ.

б)

1. Обозначаем объём пирамиды SABCD буквой V.

2. Многогранник AMQBNP составлен из пирамиды MABPQ (ее основание ABPQ) и пирамиды MBNP (ее с основание BNP).

Расстояния от точки М до (BNP) и от точки A до этой же плоскости равно 5:6, и S_BNP:S_SBC = 1:12.

3. Найдем отношение объёмов пирамид MBNP и ASBC: Оно равно 5:72. То есть объём V_MBNP = 5V|144.

S_ABPQ = ½ S_ABCD. Точка М отстоит от плоскости основания на расстоянии в 6 раз меньшем расстояния от вершины S до этого основании. Потому V_MABPQ = V|12.

Таким образом, V_AMQBNP = 5V|144+V|12=5V|144+12V|144=17V|144

Тогда отношение объёмов частей AMQBNP и CDSNPQM пирамиды равно

17:(144 – 17)127=17:127.

Ответ: 17 : 127.

Даниил Романович | Просмотров: 5.9k

1. Повторение.

1.1.Соотношения между сторонами и углами
прямоугольного треугольника

Формулы: a² + b²= c²

1.2.Теорема косинусов

Квадрат стороны треугольника равен сумме
квадратов двух других сторон минус удвоенное
произведение этих сторон на косинус угла между
ними.

a² = b² + c²– 2bc·cosA

1.3. Угол между пересекающимися и
скрещивающимися прямыми.

За
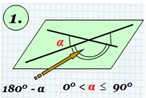
угол между пересекающимися прямыми принимают
острый угол, образованный этими прямыми.

 Угол между скрещивающимися прямыми АВ и СD
определяется как угол между пересекающимися
прямыми А₁В₁ и С₁D₁, при
этом А₁В₁|| АВ и С₁D₁|| CD.

1.4. Угол между плоскостями (АСН) и (СНD) – это
двугранный угол АСНD, где СН ребро.

Точки
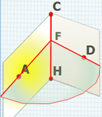
А и D лежат на гранях этого угла. AF CH, FD CH.

Угол AFD – линейный угол двугранного угла АCHD

2. Решение задач.

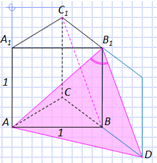
Задача №1.В правильной треугольной
призме ABCA₁B₁C₁, все рёбра которой
равны 1, найдите косинус угла между прямыми АВ₁
и ВС₁.

Решение:

1) Продлим плоскость ВСС₁, тогда (AB₁, ВС₁) = (AB₁, DВ₁) =
AВ₁D, т. к. C₁В || B₁D.

2) AB_{1 =} B₁D =из ABB_1.

3) из ABD по теореме
косинусов:

Ответ: 0,25.

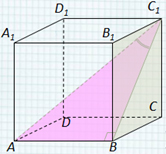
Задача №2. В кубе ABCDA₁B₁C₁D₁
найдите угол между прямой AC₁ и плоскостью
ВСC₁.

Решение:

1) ВС₁ — проекция прямой АС₁ на
плоскость (ВCС₁), так как AB (ВCС₁), то AB ВС₁;

(AC₁, (ВCС₁))
= (AС₁,С₁В) = AC₁B, т.е. АВC₁ – прямоугольный.

2) Пусть АВ = а, тогда ВС₁ = а из C₁CB.

3) .

4) AC₁B = arctg .

Ответ: arctg .

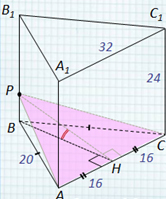
Задача №3. Основанием прямой
треугольной призмы ABCA₁B₁C₁,
является равнобедренный треугольник АВС, в
котором АВ = ВС = 20, АС = 32. Боковое ребро
призмы равно 24. Точка Р принадлежит ребру ВВ₁,
причем ВР : РВ₁= 1 : 3. Найдите тангенс
угла между плоскостями А₁В₁С₁
и АСР.

Решение:

1) Так как (АВС) || (А₁В₁С₁), то (( А₁В₁С₁) ,
(АСР)) = ((АВС),(АСР)).

2) Т.к. ВН АС (высота
р/б ),то по теореме о
трех перпендикулярах РН АС.

3) Тогда РНВ –
линейный угол двугранного РАСВ. Найдем его из прямоугольного РНВ.

4) РВ = 1/4 ВВ₁ = 1/4 · 24 = 6,

5) ВН² = АВ² – АН² (из AНВ)

ВН² = 20² – 16² = 144, ВН = 12;

6) tg РНВ = PB/HB = 6/12 = 0,5.

Ответ: 0,5.

Задача №4. В правильной
четырехугольной пирамиде SABCD, все ребра которой
равны 1, найдите косинус угла между прямой AB и
плоскостью SAD.

Решение:

1) Так как ABCD – квадрат, то АВ AD. Поэтому проекция AB на плоскость (SAD)
будет AD. Значит,
искомый угол – двугранный угол при ребре
основания AD.

2) SM – высота грани SAD, SM =/2,
МО || АВ, МО = 0,5АВ = 0,5.

3) ?SMO – искомый угол, косинус которого найдем из
прямоугольного SMO.

сos ?SMO =
= =

Ответ :.

3. Повторение.

3.1. Расстояние от точки до прямой.

Определение. Расстоянием от
точки до прямой в пространстве называется длина
перпендикуляра, проведённого из данной точки к
данной прямой.

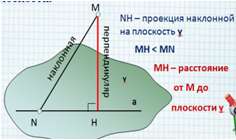
3.2. Расстояние от точки до плоскости.

Определение. Расстоянием от
точки до плоскости является длина
перпендикуляра, проведённого из данной точки к
данной плоскости.

3.3. Расстояние между скрещивающимися
прямыми.

Общим перпендикуляром двух скрещивающихся
прямых называют отрезок с концами на этих прямых,
являющийся перпендикуляром к каждой из них.

Определение. Расстоянием между
скрещивающимися прямыми называют длину их
общего перпендикуляра.

• 1 способ. Расстояние между скрещивающимися
  прямыми равно расстоянию от любой точки одной из
  этих прямых до плоскости, проходящей через
  вторую прямую параллельно первой прямой.

• 2 способ. Расстояние между скрещивающимися
  прямыми равно расстоянию между двумя
  параллельными плоскостями, содержащими эти
  прямые.

• 3 способ. Расстояние между скрещивающимися
  прямыми равно расстоянию между их проекциями на
  плоскость, перпендикулярную одной из них.

4. Решение задач.

Задача №5. В правильной шестиугольной
призме ABCDEFA₁B₁C₁D₁E₁F₁,
стороны основания которой равны 5, а боковые
рёбра равны 11, найдите расстояние от точки С
до прямой A₁F₁.

Решение:

1) Так как ABCDEF – правильный шестиугольник, то
прямые AC и AF перпендикулярны.

CA AFпо доказанному,

CA A₁А по
определению правильной призмы

CA (АA₁F₁)
по признаку перпендикулярности прямой и
плоскости, т.е.

СА – перпендикуляр к плоскости, CA₁ —
наклонная, A₁А – проекция наклонной,

A₁А A₁F₁;
A₁F₁ – прямая в плоскости.

Тогда по теореме о трёх перпендикулярах CA₁ A₁F₁, значит,
длина отрезка CA₁ равна искомому расстоянию.

2) Из АВС (АВ=ВС=5, B = 120^o)

по теореме косинусов найдём СА: , ,

3) Из CAA_1, по теореме
Пифагора найдём CA₁:

CA₁ ² = 75 + 121 = 196

CA₁ = 14

Ответ: 14.

Задача №6.

Ребро AD пирамиды DABC перпендикулярно
плоскости основания АВС. Найдите расстояние
от А до плоскости, проходящей через середины
ребер АВ, АС и АD, если АD = 2, АВ = АС = 10, ВС
= 4.

Решение:

1) Построим плоскость КМN.

Т. к. КМ – средняя линия АDВ,
КМ?DВ,

MN — средняя линия АВC, МN
||| CВ, то (KMN) || (BCD) по признаку

параллельности плоскостей. АР – медиана и
высота р/б АВC.

KF – медиана и высота р/б KMN.

DP BC по теореме о трёх
перпендикулярах, KF || DP.

Искомое расстояние AH равно половине расстояния
от вершины А до плоскости BCD, т.к. (KMN) || (BCD) и KF –
средняя линия ADP.

2) LDA и ADP подобны по двум углам, тогда LA:AP=AD:DP,
тогда AL = (AP*AD):DP.

Найдём АР из АВР по
теореме Пифагора (АВ=10, ВР = 2 ):

AP² = AB² – BP² = 100 – 20 = 80, АР= 4

Найдём DР из АDР по
теореме Пифагора: DP² = AD² + AP² = 20 +
80 = 100, DP = 10.

Тогда AL =( 4 · 2):10=4. Итак, АН = 1/2 AL =
2.

Ответ: 2.

Задача №7.

В правильной шестиугольной призме АВCDEFA₁B₁C₁D₁E₁F₁ все
рёбра равны 1.

а) Постройте сечение призмы плоскостью,
проходящей через точки B, С₁ и F.

б) Найдите расстояние от точки В до прямой C₁F.

Решение.

а) Сечение – четырёхугольник BC₁E₁F с
диагональю C₁F.

Сторона ВC₁= — диагональ квадрата ВВ1С1С со
стороной 1.

Сторону BF найдём из ABF по
теореме косинусов:

BF²=AB²+AF²-2 * AB * AF * cosBAF;

BF²=AB²+AF²-2 * AB * AF * cos120⁰ = 3.

Тогда

Так как CBF=90°, то по
теореме о трёх перпендикулярах, BF BC₁.

Значит,
сечение BC₁E₁F – прямоугольник.
Диагональ прямоугольника C₁F²=BF²+BC₁²;
C₁F²=3+2=5.

Отсюда

б) Сечение – прямоугольник BC₁E₁F.

ВК C₁F, ВК –
искомое расстояние от точки В до прямой C₁F.

Найдем ВК как высоту из FBС₁, 

Используя 2 формулы площади треугольника.

Задача №8.

Основанием прямой четырехугольной призмы
является квадрат ABCD со стороной , высота призмы равна . Точка K — середина ребра ВВ1.
Через точки K и С₁ проведена плоскость a,
параллельная прямой BD₁.

а) Докажите, что сечение призмы плоскостью a
является равнобедренным треугольником.

б) Найдите периметр треугольника, являющегося
сечением призмы плоскостью a.

Решение.

а) Для построения сечения призмы плоскостью a,
проведём КЕ || BD₁, E € B₁ D₁.

Плоскость a проходит через точки К, С₁ и
Е.

Так как К – середина ВВ₁ и КЕ || BD₁, то
Е – середина диагонали А₁ С₁ квадрата
А₁ В₁ С₁ Д₁. Значит,
плоскость a пересекает

грань А₁ В₁ С₁ Д₁ по
диагонали А₁ С₁ .

Соединив точки К, С₁ и А₁, получаем А₁ КС₁ — сечение
призмы плоскостью a.

А₁КВ₁ = С₁ КВ₁ по двум
сторонам и углу между ними (А₁ В₁ = С ₁В₁
, , В₁ К –
общая сторона).

Из равенства треугольников следует, что А₁К
= С₁К, значит А₁
КС₁ — равнобедренный.

5. Задачи для самостоятельного решения.

На ребре AA₁ прямоугольного
параллелепипеда ABCDA₁B₁C₁D₁
взята точка E так, что A₁E : EA = 2:5, на ребре BB₁
— точка F так, что B₁F : FB =1: 6, а точка Т —
середина ребра B₁ C₁. Известно, что AB = 5,
AD = 6 , AA₁ =14.

а) Докажите, что плоскость EFT проходит через
вершину D₁ .

б) Найдите угол между плоскостью EFT и плоскостью
AA₁B₁ .

Ответ. б) arctg .

2) Дана правильная треугольная призма ABCA₁B₁C₁,
все рёбра которой равны 4.

Через точки A, С₁ и середину T ребра
А₁В₁ проведена плоскость.

а) Докажите, что сечение призмы указанной
плоскостью является прямоугольным
треугольником.

б) Найдите угол между плоскостью сечения и
плоскостью ABC .

Ответ. б) arctg 2.

3) В правильной шестиугольной призме А…F₁
все рёбра равны 2.

а) Докажите, что плоскость ВВ₁F
перпендикулярна прямой В₁С_1.

б) Найдите расстояние от точки В до плоскости F В₁С_1.

Ответ. б) .

4) В пирамиде DАВС известны длины ребер
АВ=АС=DВ=DС=13, DА =6, ВС=24.

а) Постройте прямую, перпендикулярную прямым DА
и ВС.

б) Найдите расстояние между прямыми DА и ВС.

Ответ. б) 4.

5) Высота правильной треугольной пирамиды равна
20, а медиана её основания равна 6.

а) Постройте сечение пирамиды плоскостью,
проходящей через её вершину и перпендикулярной
ребру основания.

б) Найдите тангенс угла, который образует
боковое ребро с плоскостью основания.

Ответ. б) 5.

6) В правильной четырёхугольной пирамиде МАВСD с
вершиной М сторона основания равна 3, а боковое
ребро равно 6.

а) Постройте сечение пирамиды плоскостью,
проходящей через точку С и середину ребра МА
параллельно прямой ВD.

б) Найдите площадь этого сечения.

Ответ. б) 6.

Презентация.

Используемая литература.

1) И.В. Ященко, С.А. Шестаков, А.С. Трепалин
“Подготовка к ЕГЭ по математике 2016, профильный
уровень”, Москва, издательство МЦНМО, 2016.

2) Интернет-ресурсы:

• http://www.fipi.ru/
• http://mathege.ru/or/ege/Main
• https://math-ege.sdamgia.ru/
• http://alexlarin.net/
• https://ege-ok.ru/